ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Приклади розв'язування задач
Задача 17.3
Скляний клин (показник заломлення n = 1,5) має кут при вершині \(\varphi=2^{\prime}\). На клин падає нормально монохроматичне світло з довжиною хвилі \(\lambda=600\) нм
Визначити
відстань x між сусідніми темними інтерференційними смугами, що спостерігаються у відбитих променях.
|
Дано: n = 1,5
φ = 2′
λ = 600 нм = 6·10-7 м
|
|
x - ?
|
Розв’язання
Промінь світла, який падає на клин, частково відбивається, а частково проходить у скло. Оскільки кут клина дуже малий, можна вважати, що кут заломлення практично дорівнює куту падіння, тобто \(\alpha=\beta=0\) Промінь, що зайшов у скло, відбивається від нижньої грані клина і після виходу зі скла інтерферує з променем, відбитим від верхньої грані. Умови утворення темних смуг (мінімумів інтерференції) цих променів такі ж, як у попередній задачі. Слід тільки врахувати, що в даній задачі \(\alpha=0\). Отже, згідно з виразом (6) з задачі 17.2 маємо таку умову мінімумів:
|
|
\(2dn=\lambda\), |
(1) |
де m – порядок (номер) мінімуму.
Припустимо, що в точці A (рис.3) спостерігається (m + 1)-й мінімум. Тоді, позначивши товщину клина в цій точці d1, можемо записати:
|
|
\(2d_{1}n=(m+1)\lambda\). |
(2) |
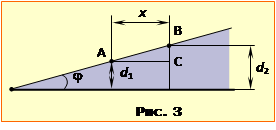
Аналогічно для точки B де спостерігається наступний інтерференційний мінімум порядку m +2 і товщина клина дорівнює d2:
|
|
\(2d_{2}n=(m+2)\lambda\). |
(3) |
Віднявши ліві та праві частини виразів (3) та (2), дістанемо:
\(2(d_{2}-d_{1})n=\lambda\) \(\Rightarrow\) \(d_{2}-d_{1}=\frac{\lambda}{2n}\).
Різниця d2 – d1 = s дуже мала. Тому з трикутника ABC, враховуючи малість кута \(\varphi\) (звичайно, вираженого в радіанах), маємо
\(\frac{S}{\varphi}=\frac{\lambda}{2n\varphi}=\frac{6\cdot{10^{-7}}}{2\cdot{1,5}\cdot{5,82}\cdot{10}^{-4}}=0,00034\) м = 0,34 мм.