ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 06:33 |
Оглавление
Вступ
|
Оптика – це наука, яка вивчає випромінювання світла, його розповсюдження у різноманітних середовищах і взаємодію з речовиною. Оптика досить об'ємна наука. Вона складається з різних розділів: геометричної, хвильової, квантової оптики та ін. В даний посібник включено наступні розділи оптики: |
Розділ 16. Геометрична оптика
|
У відповідності до основних законів електродинаміки Максвелла світло являє собою електромагнітні хвилі, тобто коливання електромагнітного поля, що поширюються в просторі. Але у більшості випадків поширення світла можна досліджувати методами геометричної оптики, тобто на основі простих геометричних співвідношень, що використовують уявлення про світлові промені.
Теоретичні відомості
Приклади розв’язування задач |
Теоретичні відомості. Характеристики світла; показник заломлення
|
До основних характеристик світла належать: швидкість поширення, частота і довжина хвилі; інтенсивність. |
Швидкість світла у вакуумі дорівнює
\(c=3\cdot{10^{8}}\) м/с.
Усі прозорі для світла речовини – це слабко магнітні діелектричні середовища. Тому швидкість світла в речовині виражається формулою (15.10а):
\(v=\frac{c}{\sqrt{\varepsilon}}\)
Відміна швидкості поширення світла в різних речовинах є причинною ефекту заломлення. Тому вводять величину
\(n=\sqrt{\varepsilon}\),
яку називають показником заломлення (точніше – абсолютним показником заломлення) або оптичною густиною речовини (середовища).
Показник заломлення дорівнює відношенню швидкості світла у вакуумі до швидкості світла в даній речовині:
|
|
\(n=\frac{c}{v}\). |
(16.1) |
Таким чином, швидкість світла в речовині визначається формулою
|
|
\(v=\frac{c}{n}\). |
(16.2) |
Частота \(\nu\) і довжина хвилі \(\lambda\) є спектральними характеристиками світла. Вони пов'язані між собою через швидкість поширення світла v:
|
|
\(\lambda=\frac{v}{\nu}\). |
(16.3) |
При переході з вакууму в речовину частота світла не змінюється, а швидкість зменшується (формула (16.2)). Тому
|
|
\(\lambda=\frac{\lambda}{n}\). |
(16.4) |
тобто довжина світлової хвилі зменшується, причому тим сильніше, чим більший показник заломлення речовини n.
Видиме світло – це випромінювання з частотою в інтервалі
\(\nu=(0,75\div{0,4})\cdot{10^{15}}\) Гц,
що відповідає інтервалу довжин хвиль у вакуумі
\(\lambda=(0,4\div{0,75})\cdot{10^{-6}}\) м.
Оскільки для світла величини \(\lambda\) дуже малі, в оптиці використовують дольові одиниці довжини: мікрометри (1 мкм = 10-6 м) і нанометри (1 нм = 10-9 м).
Частота (або довжина хвилі у вакуумі) визначає суб'єктивне відчуття кольору. При збільшенні частоти (зменшенні довжини хвилі) колір видимого світла поступово змінюється від червоного до фіолетового. Усю гаму кольорів умовно поділяють на сім "кольорів веселки": червоний, помаранчевий, жовтий, зелений, блакитний, синій і фіолетовий. (Формально кожній частоті відповідає свій "колір", тобто кількість кольорів нескінченна. Але око людини не розрізняє кольори світлових хвиль з дуже близькими частотами. І все ж таки кількість різних відтінків кожного серед зазначених кольорів вимірюється десятками і сотнями. Подивіться, наприклад, яку кількість кольорів, може відтворювати монітор вашого комп'ютера).
Випромінювання прилеглих до видимого світла діапазонів має близькі до видимого світла властивості і досліджується тими ж методами. Тому таке випромінювання теж називається світлом: ультрафіолетовим (для \(\nu\gt{0,75\cdot{10^{15}}}\) Гц; \(\lambda_{0}\lt{10^{-6}}\) м) та інфрачервоним (для \(\nu\lt{0,4}\cdot{10^{15}}\) Гц; \(\lambda_{0}\gt{0,75}\cdot{10^{15}}\) м). Ультрафіолетове, видиме та інфрачервоне світло разом утворюють оптичний діапазон електромагнітного спектра.
Світло переносить енергію. Мірою переносу енергії є інтенсивність світла, що визначається виразом (15.11).
Інтенсивність пропорційна квадрату амплітуди хвилі, під якою для світла розуміють амплітуду електричного поля. Це пояснюється двома причинами: 1) енергія електричного і магнітного поля у світловій хвилі однакові; 2) більшість оптичних явищ визначається саме електричним полем світлової хвилі.
Інтенсивність світла визначає суб'єктивні відчуття яскравості джерела і освітленості поверхні, на яку падає світло.
Теоретичні відомості. Основні поняття геометричної оптики
|
Геометрична оптика використовує такі основні поняття: світловий промінь, кут падіння, кут відбиття, кут заломлення, площина падіння. |
Світловим променем називається лінія, уздовж якої світлова енергія від певної точки джерела переноситься в дану точку простору. світловий промінь є геометричним поняттям. У фізиці променем можна вважати вузькі світлові пучки, що утворюються при проходженні світла крізь маленькі отвори (діафрагми). Однак реальний світловий пучок неможливо зробити гранично вузьким унаслідок дифракції. Тому закони геометричної оптики можна застосовувати не завжди. В оптично однорідному середовищі, тобто такому, у якому показник заломлення однаковий в усіх точках, світлові промені прямолінійні.
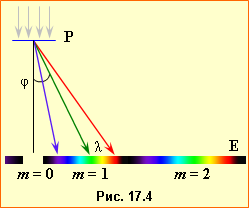
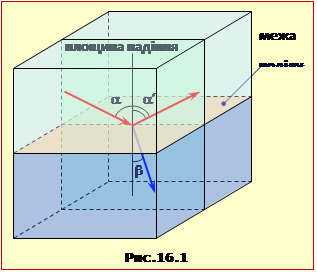
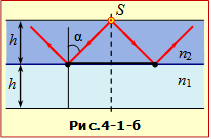
При падінні і проходженні світла крізь межу поділу двох середовищ напрямки променів визначається відповідними кутами, що відраховуються від нормалі до межі поділу в точці падіння променя (рис.16.1):
 \(\alpha\) – кут падіння;
\(\alpha\) – кут падіння;
\(\alpha^{\prime}\) – кут відбивання;
\(\beta\) – кут заломлення.
Площина, в якій лежать падаючий промінь і нормаль, називається площиною падіння.
Теоретичні відомості. Закони відбивання і заломлення світла
|
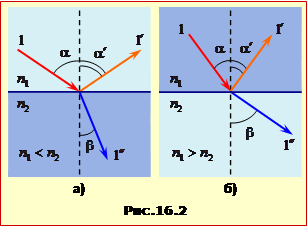
При падінні на межу поділу двох середовищ з різною оптичною густиною світлова хвиля поділяється на відбиту і заломлену. Відбита хвиля поширюється в першому середовищі, а заломлена – проходить у друге середовище. В ізотропних середовищах напрямки поширення відбитої і заломленої хвиль підпорядковані законам відбивання і заломлення світла. За відповідних умов на межі поділу двох прозорих речовин спостерігається явище повного відбивання. |
На межі поділу середовищ з різними показниками заломлення падаючий промінь 1 поділяється на відбитий промінь 1’ і заломлений промінь 1’’ (рис.16.2).
|
В ізотропних середовищах усі три промені – падаючий, відбитий і заломлений – лежать у площині падіння. |
Кути \(\alpha\), \(\alpha^{\prime}\), і \(\beta\) пов'язані законом відбивання і законом заломлення.
|
Закон відбивання світла Кут відбивання дорівнює куту падіння: |
|||
|
\(\alpha^{\prime}=\alpha\). |
(16.5) |
||
|
Закон заломлення світла Відношення синуса кута падіння до синуса кута заломлення дорівнює оберненому відношенню показників заломлення двох даних середовищ: |
|||
|
\(\frac{\sin\alpha}{\sin\beta}=\frac{n_{2}}{n_{1}}\) |
або |
\(n_{1}\sin\alpha=n_{2}\sin\beta\). |
(16.6) |
Закон заломлення відображає той факт, що
|
співвідношення між зазначеними кутами не залежить від кута падіння і визначається тільки оптичними густинами середовищ, |
тобто швидкостями поширення світла в них (див. формулу (16.2)).
 З формул (16.6) видно, що напрям заломленого променя залежить від співвідношення між оптичними густинами.
З формул (16.6) видно, що напрям заломленого променя залежить від співвідношення між оптичними густинами.
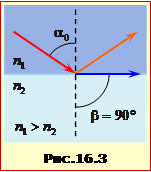
При переході світла із середовища, що має малу густину в середовище з більшою густиною (n1 < n2) заломлений промінь відхиляється до нормалі (рис.16.2а), а за умови n1 > n2 він відхиляється до границі розподілу (рис.16.2б). В останньому випадку, при певному значенні кута падіння \(\alpha_{0}\) кут заломлення набуває свого найбільш можливого значення \(\beta=90^{\circ}\) (рис.16.3). При цьому відповідно до закону (16.6)
|
|
\(\sin\alpha_{0}=\frac{n_{2}}{n_{1}}\), \(n_{2}\lt{n}_{1}\). |
(16.7) |
Кут \(\alpha_{0}\), що визначається умовою (16.7), називається граничним кутом для даних двох середовищ.
Зрозуміло, що при кутах падіння \(\alpha\gt\alpha_{0}\) рівняння (16.6) не виконується. Причина цього полягає в тому, що при кутах падіння \(\alpha\gt\alpha_{0}\) спостерігається явище повного відбивання. Енергія світла, що падає на прозору межу поділу середовищ, не проходить крізь неї, а повністю відбивається, як від ідеального дзеркала.
Таким чином повне відбивання спостерігається якщо:
1) світло падає на межу поділу з оптично більш густого середовища (n1 > n2);
2) кут падіння не менший за граничний кута для цих середовищ (\(\alpha\ge\alpha_{0}\)).
Теоретичні відомості. Дзеркала і лінзи
|
На законах геометричної оптики заснований принцип дії різноманітних оптичних приладів, призначених для одержання зображень. Основними елементами оптичних приборів є лінзи та дзеркала – прилади, які формують дійсні та уявні зображення. Загальна теорія зображень в оптичних приборах є складною. Тому в елементарній теорії світлові промені вважають параксіальними, а лінзи – тонкими. (Пояснення: "параксіальний" у перекладі означає "приосьовий". Параксіальний пучок створюється вузьким пучком променів, що падають на поверхню дзеркала або лінзи у області її оптичного центра). Найпростішим оптичними приладами є плоске дзеркало і сферичні дзеркала. Положення і характеристики зображень у дзеркалах визначаються формулою сферичного дзеркала. Для одержання зображень використовуються різні сферичні лінзи. Положення і характеристики зображень у лінзах визначаються формулою тонкої лінзи. |
Якщо промені, що попадають в оптичний пристрій – ОП (наприклад, лінзу), виходять з однієї точки (рис.16.4), тоді або самі промені, що пройшли через пристрій (рис.16.4а), або їхні продовження (рис.16.4б) також перетинаються в одній точці \(S^{\prime}\) (винятком є випадок, коли точка S знаходиться у фокусі збірної лінзи).
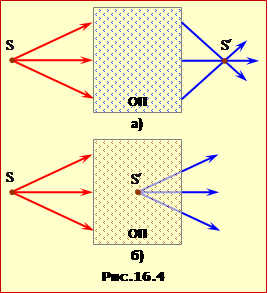
В першому випадку точка \(S^{\prime}\) називається дійсним, а в другому – уявним зображенням точки S. У точках дійсного зображення відбувається концентрація світлової енергії, і його можна спостерігати на екрані, розташованому в потрібному місці. Уявне зображення на екрані спостерігати неможливо. При візуальному спостереженні кришталик ока перетворює уявне зображення в дійсне на "екрані" – сітківці.
Зображення класифікують за:
- типом (дійсне або уявне);
- розміром (збільшене або зменшене);
- орієнтацією (пряме або перевернуте).
Одним з найпростіших приладів, що утворять зображення, є плоске дзеркало.
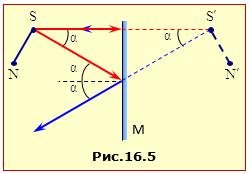
Рис.16.5 ілюструє утворення зображення точки S і предмета SN у плоскому дзеркалі M. На основі закону відбивання (16.5) легко збагнути, що продовження відбитих від дзеркала променів, які виходять з точки S, перетинаються в точці \(S^{\prime}\), розташованій симетрично точці S. Те ж саме стосується будь-якої іншої точки. Звідси випливає, що плоске дзеркало дає уявне пряме зображення \(S^{\prime}N^{\prime}\) предмета SN у натуральну величину, симетричне відносно дзеркала.
Сферичні дзеркала, на відміну від плоских, дають зображення різного типу, розміру та положення. Поверхня такого дзеркала має форму угнутого (рис.16.6а) або опуклого (рис.16.6б) сферичного сегмента.

Основні характеристики сферичного дзеркала (див. рис.16.6):
- оптичний центр С – геометричний центр сфери, частиною якої є дзеркало;
- полюс O – вершина сферичного сегмента, що утворює дзеркало;
- головна оптична вісь CO – пряма, що проходить через центр і полюс дзеркала;
- побічна вісь – будь-яка пряма, що проходить через оптичний центр дзеркала;
- головний фокус F – точка на головній оптичній осі, у якій перетинаються відбиті промені (угнуте дзеркало), або їхні продовження (опукле дзеркало), якщо падаючі промені паралельні головній оптичній осі (рис.16.6). Фокус угнутого дзеркала дійсний, а опуклого – уявний.
- головна фокусна відстань F = OF – відстань між полюсом і головним фокусом дзеркала. Вона дорівнює половині радіуса кривизни поверхні дзеркала:
|
|
\(F=\frac{R}{2}\) |
(16.8) |
- фокальна площина – площина, що проходить через головний фокус і перпендикулярна головній оптичній осі.
Фокальна площина угнутого дзеркала дійсна, а опуклого – уявна.
Збиральна властивість фокальної площини:
|
будь-які паралельні між собою промені після відбивання від дзеркала перетинаються (самі або їхні продовження) в одній точці фокальної площини. |
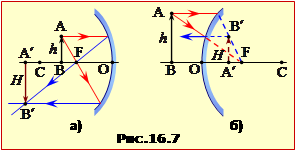
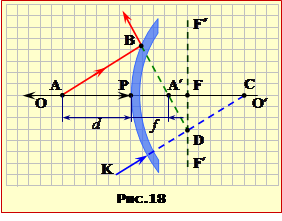
Положення предмета AB та його зображення A′B′ у дзеркалі (рис.16.7) пов'язані формулою сферичного дзеркала:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(16.9) |
де d = OA – відстань від предмета до дзеркала; f = OA′ – відстань від дзеркала до зображення; F = OF – головна фокусна відстань дзеркала.
Величини d, f, F, розглядаються як алгебраїчні. Для них чинне таке правило знаків:
|
відстані між полюсом дзеркала і дійсними точками беруть зі знаком "+", а між полюсом і уявними точками – зі знаком "–". |
(Дійсна точка – це точка, з якої промені виходять чи сходяться(перетинаються). Уявна точка – це точка перетину не самих променів, але їхніх продовжень).
Відношення висоти зображення H = A′B′ до висоти предмета h = AB називається поперечним збільшенням: Г = H/h. Для сферичного дзеркала
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(16.10) |
Знак Г визначає тип зображення: при Г > 0 зображення дійсне, а при Г < 0 – уявне. Виразивши f з рівняння (16.9) і підставивши його у формулу (16.10), можна одержати
|
|
\(\Gamma=\frac{F}{d-F}\), |
(16.10а) |
Збільшення зображення визначається положенням предмета, фокусною відстанню і типом дзеркала.
Для опуклого дзеркала F < 0 (фокус F – уявний), тому при будь-якому значенні d Г < 0 і |Г| < 1. Таким чином, незалежно від положення предмета, опукле дзеркало дає уявне зменшене зображення.
В увігнутому дзеркалі F > 0, і можливі різні ситуації:
1) якщо d > 2F, то 0 < Г < 1, зображення дійсне зменшене;
2) якщо d = 2F, то Г = 1, зображення дійсне в натуральну величину;
3) F < d, то Г > 1, зображення дійсне збільшене;
4) якщо d < F, то Г < 0 та |Г| > 1, зображення уявне збільшене;
5) якщо d = F маємо особливий випадок \(\Gamma\to\infty\) і, відповідно до формули (16.10), \(f\to\infty\), тобто відбиті промені ніде не перетинаються (йдуть паралельно), і зображення не існує.
Сферичні лінзи являють собою прозорі тіла, обмежені з двох боків сферичними поверхнями. В окремому випадку одна з поверхонь може бути плоскою. На рис.16.8 показані (у розрізі) різні типи лінз: двоопукла (а), плоскоопукла (б), двоввігнута (в), плосковігнута (г), опукловігнуті або меніски (д, е).
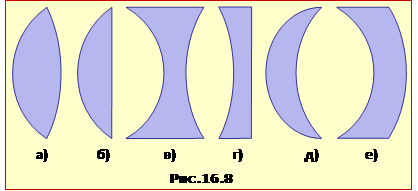
За характером дії на світлові промені лінзи поділяють на збиральні та розсіювальні. Збральна лінза перетворює паралельний пучок променів на збіжний, а розсіювальна – на розбіжний. Дія лінзи на промені визначається як формою поверхонь, так і співвідношенням між оптичними густинами лінзи і навколишнього середовища (див. нижче формулу (16.12)). Тому одна й та ж лінза в залежності від умов може бути як збиральною, так і розсіювальною. У повітрі лінзи типів а), б), д) є збиральними, а типів в), г), е) – розсіювальними. В оптично більш густому середовищі – навпаки.
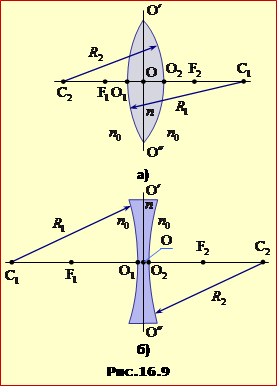 Лінзи характеризують наступними параметрами (див. рис.16.9):
Лінзи характеризують наступними параметрами (див. рис.16.9):
- радіуси кривизни R1, R2 сфер, що утворюють поверхні лінзи;
- головна оптична вісь C1C2 – пряма, що проходить через центри C1, C2 зазначених сфер;
- у тонкій лінзі можна вважати, що точки перетину O1, O2 поверхонь лінзи з головною оптичною віссю зливаються в одну точку O, яка називається оптичним центром лінзи;
- побічна вісь – будь-яка пряма, що проходить через оптичний центр лінзи;
- площина лінзи O′O″ – площина, що проходить через оптичний центр лінзи перпендикулярно до головної оптичній осі;
- фокуси F1, F2 – точки на головній оптичній осі, у яких перетинаються заломлені промені (збірна лінза) або їхні продовження (розсівна лінза), що падають на лінзу паралельно головній оптичної осі. У збірній лінзі фокуси дійсні, а в розсівній лінзі – уявні. У тонкій лінзі фокуси розташовані симетрично відносно площини лінзи, тобто на однакових відстанях від центра ;
- фокусна відстань F = OF1 = OF2 – відстань між головним фокусом і оптичним центром лінзи;
- оптична сила лінзи D – величина, обернена головній фокусній відстані:
|
|
\(D=\frac{1}{ F}\). |
(16.11) |
Одиницею оптичної сили є діоптрія (дптр). 1 дптр = 1 м-1 – оптична сила лінзи з головною фокусною відстанню 1 м. Оптична сила збиральної лінзи додатня, розсіювальної – від'ємна. Оптична сила тонкої лінзи визначається за формулою
|
|
\(D=\left(\frac{n}{n_{0}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\). |
(16.12) |
де n, n0 – показники заломлення речовини лінзи і навколишнього середовища; R1, R2 – радіуси кривизни передньої (відносно падаючого променя) і задньої поверхонь лінзи. Величини R1, R2 у формулі (16.12) розглядаються як алгебраїчні: радіус опуклої поверхні береться зі знаком "+", а увігнутої – зі знаком "–".
- фокальна площина – площина, що проходить через фокус перпендикулярно головній оптичній осі.
Фокальна площина збиральної лінзи дійсна, а розсіювальної– уявна.
Збиральна властивість фокальної площини:
|
будь–які паралельні між собою промені після проходження крізь лінзу перетинаються (самі або їхні продовження) в одній точці фокальної площини. |
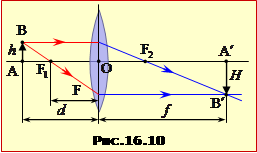
Положення предмета AB та його зображення A′B′ у лінзі (рис.16.10) пов'язані формулою тонкої лінзи:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\). |
(16.13) |
де d = AO – відстань від предмета до лінзи; f = OA′ – відстань від лінзи до зображення; F = OF – фокусна відстань лінзи.
Величини d, f, F розглядаються як алгебраїчні відповідно до такого правила знаків:
|
відстані між центром лінзи і дійсними точками беруть із знаком "+", а відстані між центром лінзи і уявними точками беруть із знаком "–". |
Відношення розміру зображення H = A′B′ до розміру предмета h = AB: Г = H/h називається поперечним збільшенням. Воно визначається формулою
|
|
\(\Gamma=\frac{f}{d}\). |
(16.14) |
Визначивши відстань f з формули лінзи (16.13), одержимо ще один вираз для збільшення:
|
|
\(\Gamma=\frac{F}{d-F}\). |
(16.14а) |
Формули (16.13), (16.14) і (16.14а) ідентичні формулам (16.9), (16.10) і (16.10a) для сферичного дзеркала. Це означає, що властивості збиральної лінзи аналогічні властивостям увігнутого, а властивості розсіювальної лінзи – властивостям опуклого дзеркала. Тому наведений вище аналіз зображень у дзеркалах цілком придатний і для лінз.
На практиці в різних оптичних приладах використовують не окремі лінзи, а системи лінз. Найпростішою є система з двох складених разом тонких лінз. Такою ж системою можна вважати око людини, що "озброєне" окулярами. Оптична сила системи лінз, розташованих впритул одна до одної, дорівнює алгебраїчній сумі оптичних сил кожної з лінз:
|
|
D = D1 + D2. |
(16.15) |
Приклади розв’язування задач
Приклади розв'язування задач цього розділу поділені на теми:
Закони відбивання та заломлення
Побудова зображень у дзеркалах і лінзах
Формули дзеркала і лінзи
Закони відбивання та заломлення
Задача 16.1. Визначити кут \(\vartheta\) відхилення променя світла, відбитого від двох плоских дзеркал, що утворять двогранний кут \(\varphi\). Площина, у якій лежить падаючий промінь, перпендикулярна ребру двогранного кута.
Задача 16.2. При падінні променя світла на межу поділу двох середовищ відбитий та заломлений промені виявились взаємно перпендикулярними. Визначити кут падіння, якщо відношення показників заломлення середовищ k = 1,5.
Задача 16.3. У точці K на дні непрозорої кубічної посудини лежить маленька важка кулька. Око спостерігача розташоване так, що дно невидиме. У посудину починають наливати воду (n = 1,33). Визначити висоту рівня води h, при якій спостерігач зможе побачити кульку, не змінюючи положення ока, якщо відстань між точками K і N S = 10 см (див. рис.3).
Задача 16.4. Дві пластини товщиною по h = 2 см кожна з показниками заломлення n1 = 1,35 i n2 = 1,95 складені впритул. На поверхні дотику на одній з пластин зафарбовано диск радіусом r = h. На зовнішній поверхні однієї з пластин прямо над центром диска O розміщене точкове джерело світла S (рис.4). Визначити радіус тіні R від диска на зовнішній поверхні іншої пластини у випадку, коли джерело знаходиться на поверхні: А) першої пластини; В) другої пластини.
Задача 16.5. Промінь світла падає під кутом \(\alpha=60^{\circ}\) на скляну (n = 1,5) плоскопаралельну пластину товщиною d = 3 см, що знаходиться в повітрі. Визначити зміщення x променя відносно його початкового напрямку після проходження крізь пластину.
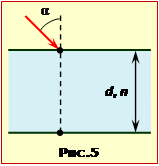
Задача 16.6. Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис.6). Визначити відстань S на яку зміститься цятка, якщо на папір покласти скляну (n = 1,5) пластину товщиною d = 5 см.
Задача 16.7. Рибалка, що сидить у човні, розглядає камінчик на дні озера безпосередньо під човном. Рибалці здається, що камінчик знаходиться на глибині h = 3 м. Визначити істину глибину озера H. Показник заломлення води n = 1,33.
Задача 16.8. Хід променя крізь скляну трикутну призму показаний на рис., на якому \(\alpha_{1}=30^{\circ}\), \(\alpha_{2}=60^{\circ}\), \(\delta=45^{\circ}\). Визначити заломний кут призми \(\varphi\).
Задача 16.9. На бічну грань скляної (n = 1,5) призми, що має заломний кут \(\varphi=0,1\) рад, під малим кутом падає промінь світла. Визначити кут відхилення \(\delta\) променя призмою.
Задача 16.10. Промінь світла падає на бічну грань тригранної скляної (n = 1,5) призми з кутом заломлення \(\varphi=60^{\circ}\). Визначити мінімальне значення кута падіння \(\alpha_{m}\), при якому світло буде проходити крізь призму.
Задача 16.1
Визначити кут \(\vartheta\) відхилення променя світла, відбитого від двох плоских дзеркал, що утворять двогранний кут \(\varphi\). Площина, у якій лежить падаючий промінь, перпендикулярна ребру двогранного кута.
|
Дано: \(\varphi\)
|
|
\(\vartheta\) - ?
|
Розв’язання
На рис.1 ребро двогранного кута є перпендикулярним площині рисунка і проходить через точку O. Промінь світла, що падає на одне з дзеркал під кутом \(\alpha_{1}\) (у точці o1), після відбивання падає на друге дзеркало під кутом \(\alpha_{2}\) (у точці O2).
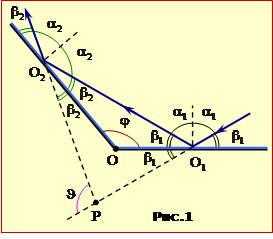
На рис.1 також показані всі кути, необхідні для подальшого розв’язування. Рівність відповідних кутів випливає із закону відбивання (16.5) і очевидних геометричних співвідношень. Кут відхилення \(\vartheta\) – це кут між напрямками променя, відбитого від другого дзеркала в точці O2 і променя, який падає на перше дзеркало в точку O1 (див. рис.1). Цей кут є зовнішнім кутом трикутника PO1O2, тому
\(\vartheta=2\beta_{1}+2\beta_{2}=2(\beta_{1}+\beta_{2})\).
З трикутника O1OO2 маємо
\(\beta_{1}+\beta_{2}=180^{\circ}-\varphi\),
Отже шуканий кут відхилення
\(\vartheta=360^{\circ}-2\varphi\).
Зверніть увагу на те, що цей кут визначається тільки двогранним кутом \(varphi\) і не залежить від напрямку падаючого променя. Зокрема, при \(\varphi=90^{\circ}\) \(\vartheta=180^{\circ}\). Це означає, що будь-який промінь відбивається у зворотному напрямку. Таку ж властивість має і тригранне прямокутне дзеркало. Воно використовується у так званих кутових відбивачах, якими, зокрема, є катофоти автомобілів і велосипедів, а також рефлектори на ранцях школярів.
Задача 16.2
При падінні променя світла на межу поділу двох середовищ відбитий та заломлений промені виявились взаємно перпендикулярними.
Визначити
кут падіння, якщо відношення показників заломлення середовищ k = 1,5.
|
Дано: k = 1,5
\(\varphi=90^{\circ}\)
|
|
\(\alpha\) - ?
|
Розв’язання
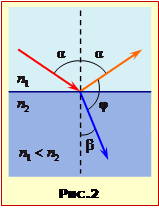 На рис.2 показано хід променів для випадку n1 < n2. З рисунка видно, що \(\alpha+\varphi+\beta=17=80^{\circ}\) отже при \(\varphi=90^{\circ}\), \(\beta=90^{\circ}-\alpha\), і згідно із законом заломлення (16.6)
На рис.2 показано хід променів для випадку n1 < n2. З рисунка видно, що \(\alpha+\varphi+\beta=17=80^{\circ}\) отже при \(\varphi=90^{\circ}\), \(\beta=90^{\circ}-\alpha\), і згідно із законом заломлення (16.6)
\(\frac{\sin\alpha}{\sin(90^{\circ}-\alpha)}\) \(\Rightarrow\) \(\mathrm{tg}\alpha=\frac{n_{2}}{n_{1}}\).
Таким чином шуканий кут падіння
\(\alpha=\mathrm{arctg}\left(\frac{n_{2}}{n_{1}}\right)\).
Числове значення \(\alpha\) залежить від того, яке з середовищ більш оптично густе. Є дві можливості:
|
1) \(\frac{n_{2}}{n_{1}}=k\) |
і |
2) \(\frac{n_{2}}{n_{1}}=\frac{1}{k}\). |
Відповідно задача має дві числові відповіді:
\(\alpha_{1}=\mathrm{arctg}_{2}{1,5}=56,3^{\circ}\);
\(\alpha_{1}=\mathrm{arctg}_{2}\frac{1}{1,5}=33,7^{\circ}\)
Корисно звернути увагу на те, що за умов задачі незалежно від послідовності розміщення середовищ одне з отриманих значень є кутом падіння, а інше - кутом заломлення.
Задача 16.3
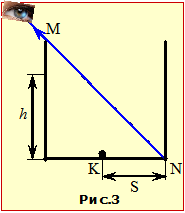 У точці K на дні непрозорої кубічної посудини лежить маленька важка кулька. Око спостерігача розташоване так, що дно невидиме (рис.3). У посудину починають наливати воду (n = 1,33).
У точці K на дні непрозорої кубічної посудини лежить маленька важка кулька. Око спостерігача розташоване так, що дно невидиме (рис.3). У посудину починають наливати воду (n = 1,33).
Визначити
висоту рівня води h, при якій спостерігач зможе побачити кульку, не змінюючи положення ока, якщо відстань між точками K і N S = 10 см (див. рис.3).
|
Дано: n = 1,33
S = 10 см
|
|
h - ?
|
Розв’язання
Аби спостерігач зміг бачити кульку, частина відбитих нею променів повинна потрапляти в око, як показано на рис.3-1.
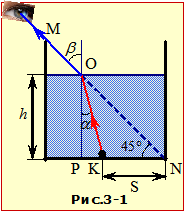 Це можливо лише при такій висоті рівня води h, при якій промені KO та OM задовольняють закону заломлення світла (16.6)
Це можливо лише при такій висоті рівня води h, при якій промені KO та OM задовольняють закону заломлення світла (16.6)
|
\(\frac{\sin\alpha}{\sin\beta}=\frac{1}{n}\). |
(1) |
(Тут враховано, що показник заломлення повітря практично дорівнює одиниці).
За умовою \(\beta=45^{\circ}\) (посудина - куб), отже
|
\(\sin\alpha=\frac{1}{2\sqrt{2}}\). |
(2) |
З рис.3-1 видно, що висота рівня води
|
\(h=\frac{\mathrm{PK}}{\mathrm{tg}\alpha}\), |
(3) |
а PK = htg\(\alpha\), PN = htg\(\beta\), S = KN = PN - PK. Отже
\(S=h(\mathrm{tg}\alpha-\mathrm{tg}\beta)\) \(\Rightarrow\) \(h=\frac{S}{\mathrm{tg}\alpha-\mathrm{tg}\beta}\).
Враховуючи співвідношення
\(\mathrm{tg}\alpha=\frac{\sin\alpha}{\sqrt{1-\sin^{2}\alpha}}=\frac{1}{\sqrt{1/\sin^{2}\alpha-1}}\)
та формулу (1), маємо
\(\mathrm{tg}\alpha=\frac{1}{\sqrt{n^{2}/\sin^{2}\beta-1}}\).
Отже
\(h=\frac{S}{\mathrm{tg}\beta-\sqrt{n^{2}/\sin^{2}\beta-1}}\).
Оскільки посудина куб, то \(\beta=45^{\circ}\) і
\(h=\frac{S}{1-1/\sqrt{2n^{2}-1}}=\frac{10}{1-1/\sqrt{2\cdot{1,33}^{2}-1}}=26,9\) см.
Задача 16.4
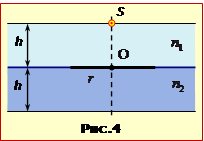 Дві пластини товщиною по h = 2 см кожна з показниками заломлення n1 = 1,35 i n2 = 1,95 складені впритул. На поверхні дотику на одній з пластин зафарбовано диск радіусом r = h. На зовнішній поверхні однієї з пластин прямо над центром диска O розміщене точкове джерело світла S (рис.4).
Дві пластини товщиною по h = 2 см кожна з показниками заломлення n1 = 1,35 i n2 = 1,95 складені впритул. На поверхні дотику на одній з пластин зафарбовано диск радіусом r = h. На зовнішній поверхні однієї з пластин прямо над центром диска O розміщене точкове джерело світла S (рис.4).
Визначити
радіус тіні R від диска на зовнішній поверхні іншої пластини у випадку, коли джерело знаходиться на поверхні:
А) першої пластини;
В) другої пластини.
|
Дано: h = 2 см
\(n_{1}\) = 1,35
\(n_{2}\) = 1,95
|
|
R - ?
|
Розв’язання
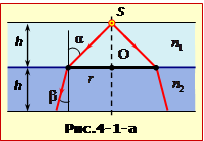 А) У цьому випадку світло переходить з оптично менш густого середовища n1 в більш густе n2. За законом заломлення (16.6) маємо:
А) У цьому випадку світло переходить з оптично менш густого середовища n1 в більш густе n2. За законом заломлення (16.6) маємо:
\(R=r+h\mathrm{tg}\beta\).
За умовою r = h, отже
\(R= h(1+\mathrm{tg}\beta)=h\left(1+\frac{1}{\sqrt{1/\sin^{2}\beta-1}}\right)\).
Величину \(1/\sin^{2}\beta\) знайдемо через співвідношення (16.7), врахувавши, що за умовою задачі (r = h) \(\alpha=45^{\circ}\), отже \(\sin\alpha=1/\sqrt{2}\):
\(\frac{1}{\sin^{2}\beta}=\frac{2n_{2}^{2}}{n_{1}^{2}}\).
Тепер
\(R=h\left(1+\frac{1}{\sqrt{2(n_{2}/n_{1})^{2}-1}}\right)\approx3,1\) см.
 Б) В цьому випадку світло падає на межу поділу з більш густого середовища, тому, перш ніж виконувати обчислення, слід з'ясувати, чи зможе світло взагалі пройти через межу поділу. Для цього визначимо граничний кут, для межі заданих речовин (формула (16.7)):
Б) В цьому випадку світло падає на межу поділу з більш густого середовища, тому, перш ніж виконувати обчислення, слід з'ясувати, чи зможе світло взагалі пройти через межу поділу. Для цього визначимо граничний кут, для межі заданих речовин (формула (16.7)):
\(\alpha_{0}=\mathrm{arcsin}\left(\frac{n_{1}}{n_{2}}\right)=43,8^{\circ}\).
Згідно з умовою r = h кут падіння \(\alpha=45^{\circ}\), тобто \(\alpha\gt\alpha_{0}\). Отже на межі пластин здійснюється повне відбивання і жоден падаючий на поверхню дотику промінь не пройде в іншу пластину. Тому формальна відповідь
\(R\to\infty\).
Задача 16.5
 Промінь світла падає під кутом \(\alpha=60^{\circ}\) на скляну (n = 1,5) плоскопаралельну пластину товщиною d = 3 см, що знаходиться в повітрі.
Промінь світла падає під кутом \(\alpha=60^{\circ}\) на скляну (n = 1,5) плоскопаралельну пластину товщиною d = 3 см, що знаходиться в повітрі.
Визначити
зміщення x променя відносно його початкового напрямку після проходження крізь пластину.
|
Дано: \(\alpha\) = \(60^{\circ}\)
n = 1,5
d = 3 см
|
|
x - ?
|
Розв’язання
Розглянемо хід променя крізь плоскопаралельну пластинку (рис.5-1) для цього запишемо закон заломлення світла (формула (16.6)), на верхній і на нижній гранях:
\(\frac{\sin\alpha}{\sin\beta}=n\), \(\frac{\sin\beta}{\sin\alpha^{\prime}}=\frac{1}{n}\).
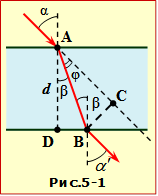
З цих виразів випливає, що \(\alpha^{\prime}=\alpha\). Це значить, що після проходження промінь не змінює напрямку, а тільки зміщується відносно падаючого на відстань x рівну довжині спільного перпендикуляра до цих променів: x = BC.
З прямокутного трикутника ABC:
|
\(x=\mathrm{AB}\cdot\sin\varphi=\mathrm{AB}\cdot\sin(\alpha-\beta)=\) \(=\mathrm{AB}(\sin\alpha\cos\beta-\sin\beta\cos\alpha)=\) \(=\mathrm{AB}\sin\alpha\cos\beta\left(1-\frac{\sin\beta}{\sin\alpha}\cdot\frac{\cos\alpha}{\cos\beta}\right)\), |
(1) |
де \(\beta\) – кут заломлення. За законом заломлення
|
\(\frac{\sin\alpha}{\sin\beta}=n\) \(\Rightarrow\) \(\sin\beta=\frac{\sin\alpha}{n}\), \(\cos\beta=\sqrt{1-\sin^{2}\beta}=\sqrt{1-(\sin\alpha/n)^{2}}\). |
(2) |
З прямокутного трикутника AB:
|
\(\mathrm{AB}=\frac{\mathrm{AD}}{\cos\alpha}=\frac{d}{\cos\alpha }\). |
(3) |
Підставивши вирази (2) і (3) у формулу (1), після нескладних перетворень одержимо:
|
\(x=d\sin\alpha\left(1-\frac{\cos\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\). |
(4) |
Виконаємо обчислення:
\(x=3\cdot\frac{\sqrt{3}}{2}\cdot\left(1-\frac{1/2}{\sqrt{1,5^{2}-3/4}}\right)=1,53\) см.
Задача 16.6
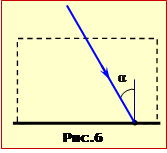 Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис.6).
Вузький паралельний пучок променів падає на аркуш паперу під кутом \(\alpha=60^{\circ}\) і створює світлову пляму (рис.6).
Визначити
відстань S на яку зміститься цятка, якщо на папір покласти скляну (n = 1,5) пластину товщиною d = 5 см.
|
Дано: α = 60°
n = 1,5
d = 5 см
|
|
S - ?
|
Розв’язання
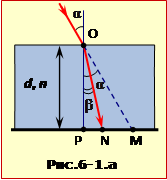 Нехай спочатку світна цятка розміщена в точці M (рис.6-1.а). Після того як на папір поклали пластину, цятка внаслідок заломлення переміститься в точку N.
Нехай спочатку світна цятка розміщена в точці M (рис.6-1.а). Після того як на папір поклали пластину, цятка внаслідок заломлення переміститься в точку N.
Шукана відстань S = MN. З рисунка видно, що
|
|
S = PM – PN = \(d(\mathrm{tg}\alpha-\mathrm{tg}\beta)\). |
(1) |
Величину \(\mathrm{tg}\beta\) легко визначити через відомі тригонометричні співвідношення та закон заломлення (16.6), згідно з яким \(\sin\beta=\sin\alpha/n\)
\(d(\mathrm{tg}\beta=\frac{\sin\beta}{\cos\beta}=\frac{\sin\beta}{\sqrt{1-\sin^{2}\beta}}=\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\).
Підставивши цей вираз у формулу (1), дістанемо відповідь:
\(S=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).
Обчислення дають:
\(S=5\cdot\left(\sqrt{3}-\frac{\sqrt{3}}{2\cdot\sqrt{1,5^{2}-3/4}}\right)\approx\) 5,1 см.
Одержати відповідь у цій задачі також можна інакше.
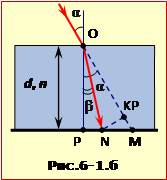 Дійсно, якщо з точки N опустити перпендикуляр на лінію OM (рис. 16-1.б), то з трикутника NKM: NM = NK/\(\cos\alpha\). Відрізок NK = x був визначений у задачі 16.5 формула (4).
Дійсно, якщо з точки N опустити перпендикуляр на лінію OM (рис. 16-1.б), то з трикутника NKM: NM = NK/\(\cos\alpha\). Відрізок NK = x був визначений у задачі 16.5 формула (4).
Отже маємо:
\(S=d\mathrm{tg}\alpha\left(1-\frac{\cos\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)=d\left(\mathrm{tg}\alpha-\frac{\sin\alpha}{\sqrt{n^{2}-\sin^{2}\alpha}}\right)\).
Задача 16.7
Рибалка, що сидить у човні, розглядає камінчик на дні озера безпосередньо під човном. Рибалці здається, що камінчик знаходиться на глибині h = 3 м.
Визначити
істину глибину озера H. Показник заломлення води n = 1,33.
|
Дано: h = 3 м
n = 1,33
|
|
H - ?
|
Розв’язання
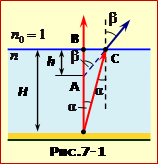 Рибалка бачить камінчик завдяки тим відбитим від нього променям світла, що попадають в око. На рис.7-1 показані два таких промені, що виходять з точки розташування камінчика на дні A. Ці промені розходяться, тому рибалці буде здаватися, що вони виходять з точки A, розташованої на глибині h. Так виникає оптичний обман: удавана глибина водойми h виявляється меншою, ніж істинна глибина H.
Рибалка бачить камінчик завдяки тим відбитим від нього променям світла, що попадають в око. На рис.7-1 показані два таких промені, що виходять з точки розташування камінчика на дні A. Ці промені розходяться, тому рибалці буде здаватися, що вони виходять з точки A, розташованої на глибині h. Так виникає оптичний обман: удавана глибина водойми h виявляється меншою, ніж істинна глибина H.
Для розрахунків позначимо \(\alpha\) кут падіння променя на межу вода-повітря і \(\beta\) кут заломлення (рис.7-1). За законом заломлення (16.6)
|
|
\(\frac{\sin\alpha}{\sin\beta}=\frac{1}{n}\), |
(1) |
де враховано, що показник заломлення повітря n0 = 1. Трикутники ABC і A¢BC мають спільний катет BC, тому
|
|
\(\frac{H}{h}=\frac{\mathrm{tg}\beta}{\mathrm{tg}\alpha}\). |
(2) |
Розв’язавши сумісно рівняння (1) і (2), одержимо:
|
|
\(H=nh\sqrt{\frac{1-\sin^{2}\alpha}{1-(n\sin\alpha)^{2}}}\). |
(3) |
З цього результату може здатися, що глибина озера H залежить від кута \)\alpha\). Звичайно це не так. Від кута \(\alpha\) залежить не H, а h, тобто положення точки A¢. Це означає, що продовження заломлених променів, що виходять з точки A під різними кутами, перетинаються в різних точках, і, отже, не створюють її зображення. Чому ж тоді ми чітко бачимо предмети на дні (звичайно, якщо вода прозора)? Відповідь така: тому що розміри зіниці дуже малі, в око попадають тільки промені, що виходять з води під дуже малими кутами (\(\alpha\ll{1}\)). У такому випадку величини \(\sin\alpha\) і \(n\sin\alpha\) у формулі (3) нехтовно малі і відповідь задачі фактично має вигляд:
\(H=nh=1,33\cdot{3}=4\) м.
Зверніть увагу на наступне. Подібна ситуація зустрічається в усіх задачах, зв'язаних з візуальними спостереженнями. Тому малість кутів необхідно враховувати із самого початку. Наприклад, у даній задачі необхідно було б одразу врахувати, що для малих кутів \(\sin\alpha=\mathrm{tg}\alpha=\alpha\) і записати закон заломлення у вигляді.
\(\frac{\alpha}{\beta}=\frac{1}{n}\).
Тоді відразу і набагато простіше була б отримана правильна відповідь:
\(\frac{H}{h}=n\) \(\Rightarrow\) \(H=nh\).
Задача 16.8
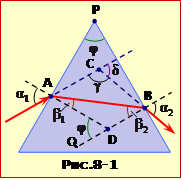
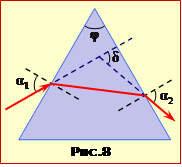 Хід променя крізь скляну трикутну призму показаний на рис.8, на якому \(\alpha_{1}=30^{\circ}\), \(\alpha_{2}=60^{\circ}\), \(\delta=45^{\circ}\).
Хід променя крізь скляну трикутну призму показаний на рис.8, на якому \(\alpha_{1}=30^{\circ}\), \(\alpha_{2}=60^{\circ}\), \(\delta=45^{\circ}\).
Визначити заломний кут призми \(\varphi\).
|
Дано: α1 = 30°
α2 = 60°
δ = 45°
|
|
φ - ?
|
Розв’язання
Позначимо кут заломлення на першій грані \(\beta_{1}\), а кут падіння на другу грань \(\beta_{2}\) (рис.8-1).
 Кут відхилення променя \(\delta\) – то є кут між напрямками променя, що вийшов з призми та променя, що падає на призму. Він є зовнішнім кутом трикутника ABC, отже
Кут відхилення променя \(\delta\) – то є кут між напрямками променя, що вийшов з призми та променя, що падає на призму. Він є зовнішнім кутом трикутника ABC, отже
|
|
\(\delta=\pi-\gamma\) \(\Rightarrow\) \(\gamma=\pi-\delta\). |
(1) |
В цьому трикутнику \(\angle\)BAC = \(\alpha_{1}-\beta_{1}\) і \(\angle\)ABC = \(\alpha_{2}-\beta_{2}\). Тому
|
|
\(\gamma=\pi-(\alpha_{1}-\beta_{1})-(\alpha_{2}-\beta_{2})=\pi-(\alpha_{1}+\alpha_{2})+(\beta_{1}+\beta_{2})\). |
(2) |
Прирівнюючи праві частини виразів (1) і (2), отримаємо:
|
|
\(\delta=(\alpha_{1}+\alpha_{2})-(\beta_{1}+\beta_{2})\). |
(3) |
Зовнішній кут \(\angle\)ADQ трикутника ABD дорівнює заломному кутові призми \(\varphi\), оскільки він утворений перпендикулярами до бічних граней призми. Отже
|
|
\(\varphi=\beta{1}+\beta_{2}\). |
(4) |
Підставивши цей вираз у формулу (3), дістанемо відповідь:
\(\delta=\alpha_{1}+\alpha_{2}-\varphi\) \(\Rightarrow\) \(\varphi=\alpha_{1}+\alpha_{2}-\delta=30^{\circ}+60^{\circ}-45^{\circ}\)
Задача 16.9
На бічну грань скляної (n = 1,5) призми, що має заломний кут \(\varphi=0,1\) рад, під малим кутом падає промінь світла.
Визначити кут відхилення \(\delta\) променя призмою.
|
Дано: φ = 0,1 рад
n = 1,5
|
|
δ - ?
|
Розв’язання
Скористаємося результатами задачі 16.8 (формули (3) і (4)):
|
|
\(\delta=(\alpha_{1}+\alpha_{2})-(\beta_{1}+\beta_{2})\); |
(1) |
|
|
\(\varphi=\beta_{1}+\beta_{2}\). |
(2) |
Відтак залишається визначити суму кутів \(\alpha_{1}\) та \(\alpha_{2}\). При малих кутах \(\sin\alpha\approx\alpha\), отже, за законом заломлення (16.6) можна наближено записати
|
|
\(\frac{\alpha_{1}}{\beta_{1}}=n\) \(\Rightarrow\) \(\alpha_{1}=n\beta_{1}\), \(\frac{\beta_{2}}{\alpha_{2}}=\frac{1}{n}\) \(\Rightarrow\) \(\alpha_{2}=n\beta_{2}\). |
(3) |
де n – показник заломлення призми. Підставивши вирази (3) у формулу (1) і врахувавши співвідношення (2), отримаємо:
\(\delta=n(\beta_{1}+\beta_{2})-(\beta_{1}+\beta_{2})=(n-1)\varphi\).
Таким чином, при малих кутах падіння кут відхилення променя в призмі з малим заломним кутом залежить тільки від показника заломлення та заломного кута.
Виконаємо обчислення:
\(\delta=(1,5-1)\cdot{0,1}=0,05\) рад = \(2,86^{\circ}\).
Задача 16.10
Промінь світла падає на бічну грань тригранної скляної (n = 1,5) призми з кутом заломлення \(\varphi=60^{\circ}\).
Визначити
мінімальне значення кута падіння \(\alpha_{m}\), при якому світло буде проходити крізь призму.
|
Дано: n = 1,5
φ = 60°
|
|
αm - ?
|
Розв’язання
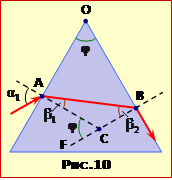 На рис.10 показаний хід граничного променя крізь призму і відповідні кути.
На рис.10 показаний хід граничного променя крізь призму і відповідні кути.
Світло буде проходити крізь призму за умови
|
\(\beta_{2}\le\beta_{г}\), |
(1) |
де \(\beta_{г}\) – граничний кут, для якого відповідно до формули (16.7), умову (1) можна записати, як
\(\sin\beta_{2}\le\frac{1}{n}\).
З іншого боку (див. задачу 16.8, формула (4))
|
|
\(\varphi=\beta_{1}+\beta_{2}\) \(\Rightarrow\) \(\beta_{2}=\varphi-\beta_{1}\). |
(2) |
відповідно до цього світло проходить крізь призму за умови
\(\sin(\varphi-\beta_{1})\le\frac{1}{n}\).
З виразів (1) і (2) слідує, що найбільшій величині \(\beta_{1}=\beta_{г}\) відповідає таке значення \(\beta_{1}=\beta_{m}\), при якому
|
|
\(\sin(\varphi-\beta_{m})=\frac{1}{n}\). |
(3) |
За законом заломлення (16.6) найменшому значенню \(\beta_{1}=\beta_{m}\) відповідає шуканий найменший кут падіння \(\alpha_{1}=\alpha_{m}\), причому
\(\sin\beta_{m}=\frac{\sin\alpha_{m}}{n}\).
Підставляючи цей вираз в рівність (3) і використовуючи відому тригонометричну формулу, одержимо
\(\frac{1}{n}=\sin\varphi\cdot\frac{1}{n}\sqrt{n^{2}-\sin^{2}\alpha_{m}}-\frac{1}{n}\sin\alpha_{m}\cos\varphi\) \(\Rightarrow\)
\(\Rightarrow\) \(1+\sin\alpha_{m}\cos\varphi=\sin\varphi\sqrt{n^{2}-\sin^{2}\alpha_{m}}\).
Зведемо останній вираз в квадрат і виконаємо перетворення:
\(\sin^{2}\alpha_{m}+2\sin\alpha_{m}\cos\varphi+1-n^{2}\sin^{2}\varphi=0\).
Рішення цього квадратного рівняння відносно \(\sin\alpha_{m}\) дає
\(\sin\alpha_{m}=-\cos\varphi+\sqrt{\cos^{2}\varphi-1+n^{2}\sin\varphi}=-\cos\varphi+\sin\varphi\sqrt{n^{2}-1}\).
(Другий корінь не має фізичного змісту).
Виконаємо обчислення:
\(\sin\alpha{m}=-\cos{60^{\circ}}+\sin{60^{\circ}}\sqrt{1,5^{2}-1}\) \(\Rightarrow\) \(\alpha_{m}=27,9^{\circ}\).
Побудова зображень у дзеркалах і лінзах
Рекомендації до теми
Задача 16.11. Предмет AB розташований між фокусом F і полюсом P угнутого сферичного дзеркала. Визначити побудовою зображення \(\mathrm{A^{\prime}B^{\prime}}\) предмета.
Задача 16.12. Предмет AB розташований між фокусом F і подвійним фокусом 2F збиральної лінзи. Визначити побудовою зображення предмета і охарактеризувати його.
Задача 16.13. На рис.13 показаний хід заданого променя крізь збиральну лінзу. Визначити побудовою положення головних фокусів лінзи.
Задача 16.14. На рис.14 показаний хід променя 1 і напрямок падіння променя 2 на розсіювальну лінзу. Визначити побудовою хід променя після проходження лінзи.
Задача 16.15. По заданому положенню точки S і головної оптичної осі лінзи O′O″. Визначити побудовою положення оптичного центра і фокусів, а також визначити тип лінзи, якщо точки S і S′ розташовані, як показано А) на рис.15а; Б) на рис.15б.
Задача 16.16. На рис.16 показане положення точок A, B та їхніх зображень A′, B′ у лінзі. Визначити побудовою положення лінзи та її фокусів, а також визначити тип лінзи.
Задача 16.11
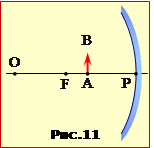 Предмет AB розташований між фокусом F і полюсом P угнутого сферичного дзеркала (рис.11).
Предмет AB розташований між фокусом F і полюсом P угнутого сферичного дзеркала (рис.11).
Визначити
побудовою зображення \(\mathrm{A^{\prime}B^{\prime}}\) предмета.
Розв’язування
Очевидно, що зображення точки A знаходиться на головній оптичній осі OP дзеркала. Точки A і B розташовані на однаковій відстані від дзеркала, тому точки зображення \(\mathrm{A^{\prime}}\), \(\mathrm{ B^{\prime}}\) також рівновіддалені від дзеркала (див. формулу (16.9)). Отже, для розв’язування задачі досить побудувати тільки зображення точки B. Побудову проводимо в порядку, відповідно до пункту 1 рекомендацій (рис. 16.12). Ці дії показані на рис.11-1.
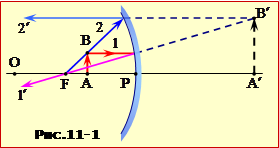 1. Проводимо з точки B паралельно головній оптичній осі OP промінь 1 і відбитий промінь 1′, що проходить через фокус дзеркала F;
1. Проводимо з точки B паралельно головній оптичній осі OP промінь 1 і відбитий промінь 1′, що проходить через фокус дзеркала F;
2. Проводимо другий промінь 2 через точки F, B і відбитий промінь 2′, що є паралельним OP;
3. Продовжуємо промені 1′ і 2′ до перетину і знаходимо уявне зображення B′ точки B;
4. Опускаємо з точки B′ перпендикуляр на головну оптичну вісь дзеркала OP і визначаємо положення A′ зображення точки A і всього предмета (стрілка A′B′).
Таким чином, якщо предмет розташований між полюсом і фокусом, то угнуте дзеркало дає уявне, пряме і збільшене зображення. (Ця властивість угнутого дзеркала зокрема використовується в дзеркалах, що збільшують зображення, для гоління).
Задача 16.12
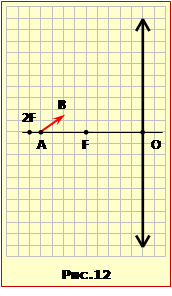 Предмет AB розташований між фокусом F і подвійним фокусом 2F збиральної лінзи так, як показано на рис.12.
Предмет AB розташований між фокусом F і подвійним фокусом 2F збиральної лінзи так, як показано на рис.12.
Визначити
побудовою зображення предмета і охарактеризувати його.
Розв’язування
Задача зводиться до побудови зображень точок A і B.
Точка A. Для побудови зображення точки A використовуємо два промені: промінь 1, що збігається з головною оптичною віссю, і промінь 2, що йде уздовж відрізка AB і падає на лінзу в точці C (рис.12-1). Для побудови ходу променя після заломленні в лінзі побудуємо побічну оптичну вісь, яка паралельна до променя 2, а також фокальну площину F′F″ згідно з пунктом 3) рекомендацій. Після заломленні у лінзі промінь 2 перетинається з побічною оптичною віссю у фокальній площині. На перетині променів 1 і 2′, що пройшли, одержуємо зображення точки A (точка A′).
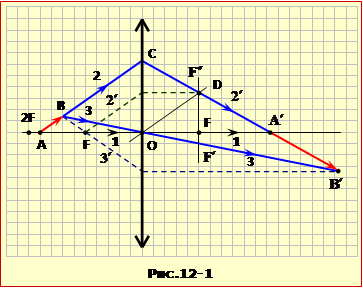 Точка B. Для побудови зображення точки B теж треба визначити хід крізь лінзу двох променів, що виходять з цієї точки. У якості одного зручно взяти використаний вище промінь 2. Інший промінь 3 проводимо через оптичний центр лінзи O. Зображення точки B (точка B′) одержуємо на перетині променів 2′ і 3. Стрілка A′B′ є шуканим зображенням. Воно дійсне, збільшене і перевернуте.
Точка B. Для побудови зображення точки B теж треба визначити хід крізь лінзу двох променів, що виходять з цієї точки. У якості одного зручно взяти використаний вище промінь 2. Інший промінь 3 проводимо через оптичний центр лінзи O. Зображення точки B (точка B′) одержуємо на перетині променів 2′ і 3. Стрілка A′B′ є шуканим зображенням. Воно дійсне, збільшене і перевернуте.
Примітка. Для побудови можна використовувати й інші промені. Наприклад, замість допоміжного променя 2 – промінь 2′, а замість променя 3 – промінь 3’ (див.рис.12-1).
Задача 16.13
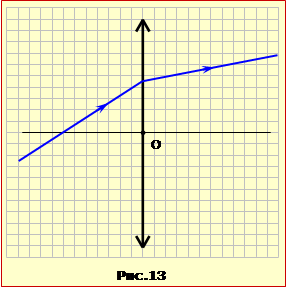 На рис.13 показаний хід заданого променя крізь збиральну лінзу.
На рис.13 показаний хід заданого променя крізь збиральну лінзу.
Визначити
побудовою положення головних фокусів лінзи.
Розв’язування
Для розв’язання використовуємо властивості фокальної площини (див. Характеристики лінзи):
1) фокальна площина проходить через фокус перпендикулярно головної оптичної осі;
2) будь-які паралельними між собою промені після лінзи перетинаються в одній точці фокальної площини.
Побудову проводимо в такій послідовності (див.рис.13-1):
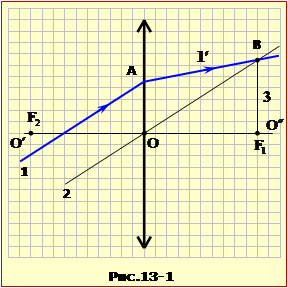
1. Проводимо через центр лінзи O допоміжний промінь 2 паралельний заданому падаючому променю 1 – A (див. Рекомендації, п.2);
2. Знаходимо точку перетину променів 2 і 1′ (точці B), яка належить фокальній площині;
3. Опускаємо перпендикуляр 3 із точки B на головну оптичну вісь лінзи O′O″ і визначаємо положення правого фокуса лінзи F1.
4. Симетрично точці F1 відзначаємо положення лівого фокуса F2. Строго кажучи для визначення положення F2 треба було б повторити побудову п.п.1-3, використовуючи в якості падаючого промінь 1′ – лінія BA (оборотність променів). Але для тонких лінз це можна не робити.
Задача 16.14
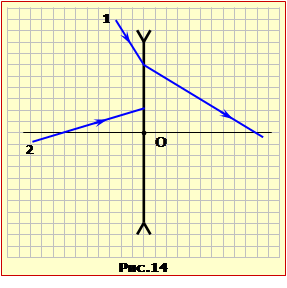 На рис.14 показаний хід променя 1 і напрямок падіння променя 2 на розсіювальну лінзу.
На рис.14 показаний хід променя 1 і напрямок падіння променя 2 на розсіювальну лінзу.
Визначити
побудовою хід променя після проходження лінзи.
Розв’язування
Побудова ходу променів показане на рис.14-1. Воно виконується в два етапи.
1. За допомогою допоміжного променя 1 так, як описано в задачі 16.13, визначаємо положення фокальної площини лінзи CF;
2. Проводимо через оптичний центр лінзи O паралельно променю 2 допоміжний промінь DO, і знаходимо точку перетину D його з фокальною площиною;
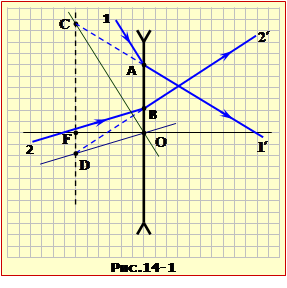 3. Оскільки напрямок шуканого заломленого променя теж проходить через точку D, проводимо через точки D і B відрізок і одержуємо шуканий промінь 2′.
3. Оскільки напрямок шуканого заломленого променя теж проходить через точку D, проводимо через точки D і B відрізок і одержуємо шуканий промінь 2′.
Задача 16.15
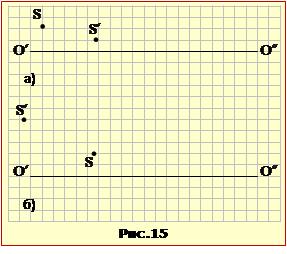 По заданому положенню точки S і головної оптичної осі лінзи O′O″.
По заданому положенню точки S і головної оптичної осі лінзи O′O″.
Визначити
побудовою положення оптичного центра і фокусів, а також визначити тип лінзи, якщо точки S і S′ розташовані, як показано
А) на рис.15а;
Б) на рис.15б.
Розв’язування
Ключем до розв’язування задачі є той факт, що точка і її зображення завжди лежать на одному промені, що проходить через оптичний центр лінз (див. Рекомендації п.3).
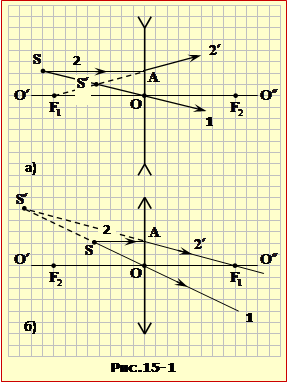
Побудова виконаємо паралельно для обох випадків у такій послідовності (рис.15-1а,б):
1. Проводимо промінь 1 через точки S і S′ і на перетині його з оптичною віссю O’O” одержуємо положення оптичного центра O лінзи.
2. Проводимо через точку O перпендикуляр до O′O″, що показує положення площини лінзи.
3. Направляємо з точки S на лінзу промінь 2, паралельний O′O″, і визначаємо точку його падіння на лінзу (точка A).
4. Заломлений промінь 2′ (сам чи його продовження) перетинає головну оптичну вісь лінзи у фокусі. З іншого боку зображення (точка S′) теж знаходиться на цьому промені. Тому, провівши промінь 2′ через точки S′ і A, на перетині з віссю O′O″ знаходимо положення фокуса F1. Положення другого фокуса відзначаємо симетрично з іншого боку лінзи.
5. З ходу променя 2 (очевидно, що у випадку A) розсіювальна лінза, а у випадку Б) збиральна. Показуємо це на рисунку відповідно «вилочками» (рис.15-1а) і «стрілочками» (рис.15-1б).
Задача 16.16
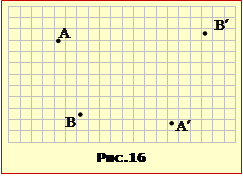 На рис.16 показане положення точок A, B та їхніх зображень A′, B′ у лінзі.
На рис.16 показане положення точок A, B та їхніх зображень A′, B′ у лінзі.
Визначити
побудовою положення лінзи та її фокусів, а також визначити тип лінзи.
Розв’язування
Розв’язування задачі проводимо в кілька етапів. Для зручності побудови виконані на окремих рисунках-фрагментах (рис.16-1).
 1. Визначення положення оптичного центра лінзи (рис.16-1а). Точка і її зображення лежать на одному промені, що проходить через центр лінзи (див. Рекомендації, п.2). Тому проводимо промені AA′, BB′ і на їх перетині одержуємо оптичний центр лінзи .
1. Визначення положення оптичного центра лінзи (рис.16-1а). Точка і її зображення лежать на одному промені, що проходить через центр лінзи (див. Рекомендації, п.2). Тому проводимо промені AA′, BB′ і на їх перетині одержуємо оптичний центр лінзи .
2. Визначення положення площини лінзи (рис.16-1б). Для визначення положення площини лінзи треба, крім точки O, знати положення ще однієї точки, що належить площині лінзи. Таку точку легко визначити, прийнявши до уваги, що, якщо дві точки лежать на одному промені, що падає на лінзу, те їхні зображення також лежать на одному промені, що пройшов крізь лінзу.
Тому проводимо промені через точки A, B і A′, B′ і на їх перетині знаходимо необхідну точку D. Площина лінзи проходить через точки O, D і зображується на кресленні прямою P′P″.
3. Визначення головної оптичної осі і типу лінзи (рис.16-1б). Головну оптичну вісь O′O² проводимо через точку перпендикулярно P′P″. Точки A, B і їхні зображення A′, B′ розташовані по різні сторони від головної оптичної осі лінзи. Отже, це лінза збиральна. Показуємо це на кресленні «стрілочками».
4. Визначення фокусів (рис.16-1г,д). Для визначення положення фокусів лінзи проводимо промені, паралельні головній оптичній осі O′O″: AE (рис.16-1г) і A′G (рис.16-1д). Після заломлення ці промені проходять через точки A¢ і A, відповідно, і перетинають O′O″ у фокусах F1 і F2.
Примітка. Побудову рис.16-1д можна не робити, тому що в тонкій лінзі фокуси розташовуються симетрично, тобто на рівних відстанях від центра лінзи.
Рис.16-1е являє собою узагальнений рисунок, на якому показане все розв’язання задачі (за винятком необов'язкової побудови д). Цифри вказують послідовність побудов.
Рекомендації до теми "Побудова зображень у дзеркалах і лінзах"
|
Задачі на побудову зображень передбачають виконання певних "правил гри":
При розв'язуванні графічних задач на дзеркала та лінзи корисно керуватись такими порадами. |
|
1) |
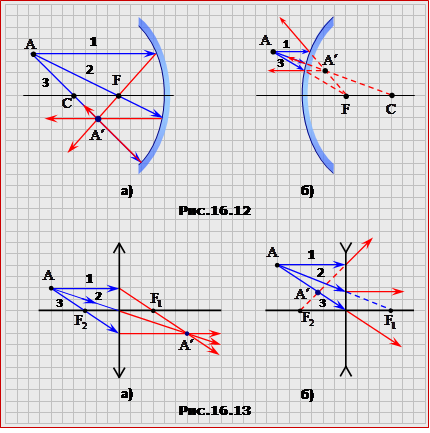
Всі промені, що виходять з однієї точки "предмета", після лінзи (дзеркала) перетинаються (самі чи їх продовження) теж в одній точці - зображенні. Тому для отримання зображення точки А необхідно і достатньо побудувати хід через лінзу (дзеркало) будь-яких двох променів, що виходять з цієї точки. Зображення А' знаходиться на перетині цих променів (або їхніх продовжень). Звичайно для побудови використовують будь-які два з трьох "зручних" променів, хід яких заздалегідь відомий. Ці зручні промені, а також побудова зображення точки, показані на рис.16.12 для дзеркал і на рис.16.13 - для лінз.
Примітка. Промені 2, що падають в оптичний центр тонкої лінзи, проходять без відхилення і зміщення через те, що поверхні лінзи в області центра взаємно паралельні, і відстань між ними гранично мала. |
|
|
|
|
2) |
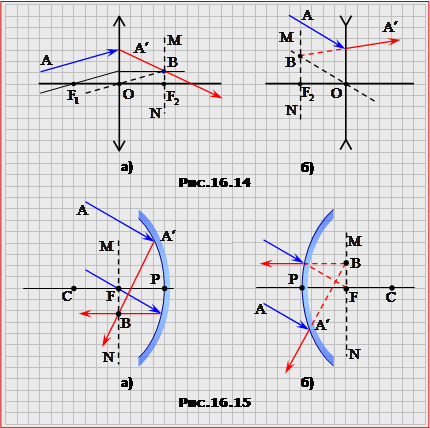
В деяких задачах за умовою можна використати тільки один з названих зручних променів (наприклад, треба побудувати зображення точки, що лежить на головній оптичній осі лінзи (дзеркала), як на рис.16.11д). Відтак другим необхідним для побудови може бути довільний промінь. Хід довільного променя після лінзи (дзеркала) будується з використанням фокальної площини. Побудову ходу довільного променя АА' для лінз показано на рис.16.14 (а) - збірна лінза, б) - розсівна лінза), а для дзеркал - на рис.16.15 (а) - увігнуте дзеркало, б) - опукле дзеркало).
Побудова виконується у такій послідовності: а) проводиться робоча фокальна площина MN (у збірній лінзі вона знаходиться за лінзою, а в розсіювальній - перед лінзою); б) паралельно до заданого променя АА' проводиться допоміжний промінь з відомим подальшим ходом і знаходиться точка В його перетину з фокальною площиною; шуканий заломлений (відбитий) промінь проходить через точки А' и В. (Примітка. Для такої побудови можна використовувати бути якийсь з трьох розглянутих вище "зручних" променів (рис.16.13). Звичайно вибирають той, що проходить найближче до заданого: при цьому легше витримати паралельність допоміжного та заданого променів). |
|
|
|
|
3) |
В деяких задачах на побудову необхідно визначати положення і характеристики лінзи (дзеркала) за заданим положенням точки та її зображення. При розв'язуванні таких задач необхідно пам'ятати, що:
Точка A та її зображення A' у випадку дійсного зображення розташовані по різні боки головної оптичної осі (рис.16.12а, 16.13а), а у випадку уявного зображення - по один бік (рис.16.12б, 16.13б). |
|
|
|
|
4) |
Для більшої виразності креслення усі дійсні промені має сенс проводити суцільними лініями, а всі уявні - штриховими; допоміжні промені, на відміну від основних, доцільно проводити тоншими лініями. |
Формули дзеркала і лінзи
Задача 16.17. Рефлектор прожектора являє собою угнуте сферичне дзеркало з радіусом кривизни R = 30 см. Визначити на якій відстані l від фокуса дзеркала треба розташувати на головній оптичній осі точкове джерело світла, щоб одержати конічний пучок відбитих променів, що сходиться в точку на відстані L = 10 м від полюса дзеркала.
Задача 16.18. Мурашка повзе зі швидкістю v = 5 мм/с уздовж головної оптичної осі опуклого дзеркала. Визначити швидкість руху зображення мурашки u у момент, коли вона знаходиться на відстані d = 1,5F від дзеркала (F – фокусна відстань).
Задача 16.19. Малий предмет розглядають, приклавши до ока збірну лінзу (лупу) з фокусною відстанню F = 5 см так, що утворюється пряме зображення предмета, розміщене на відстані найкращого зору L = 25 см від лінзи. Визначити положення d предмета та збільшення \(\Gamma\) зображення.
Задача 16.20. Відстань між предметом та його зображенням у розсіювальній лінзі l = 5 см, а збільшення \(\Gamma=0,5\). Визначити фокусну відстань F та оптичну силу лінзи D.
Задача 16.21.Збірна лінза має фокусну відстань F. Визначити: А) при якій відстані d0 між предметом та лінзою, відстань між предметом та його дійсним зображенням буде найменшою L = Lmin; Б) величину Lmin.
Задача 16.22. Світна точка S та екран E розташовані на відстані L = 1 м одне від одного. Збірна лінза, вміщена між ними, дає чітке зображення \(\mathrm{S}^{\prime}\) на екрані при двох положеннях, відстань між якими l = 60 см (див. схематичний рис. 22). Визначити фокусну відстань лінзи F.
Задача 16.23. Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються в точці В головної оптичної осі на відстані L = 60 см від центра лінзи O (рис.23). Визначити відстань l на яку, зміститься точка перетину променів, якщо лінзу прибрати.
Задача 16.24. Короткозорий хлопець читає книжку, тримаючи її на відстані d0 = 16 см від очей. Визначити оптичну силу Dл окулярів, які потрібні хлопцеві для корекції зору.
Задача 16.25. Оптична система складається із збірної лінзи Л1 з відомою фокусною відстанню F1 і розсівної лінзи Л2, що розміщена у фокальній площині лінзи Л1 так, що головні оптичні осі лінз співпадають (рис.25). Предмет AB розташований на відстані d1 = 3F1 перед збиральною лінзою. Визначити фокусну відстань розсіювальної лінзи F2, якщо система дає дійсне зображення предмета із збільшенням \(\Gamma=2\).
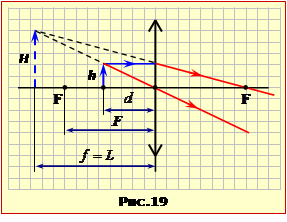
Задача 16.17
Рефлектор прожектора являє собою угнуте сферичне дзеркало з радіусом кривизни R = 30 см.
Визначити
на якій відстані l від фокуса дзеркала треба розташувати на головній оптичній осі точкове джерело світла, щоб одержати конічний пучок відбитих променів, що сходиться в точку на відстані L = 10 м від полюса дзеркала.
|
Дано: R = 30 см = 0,1 м
L = 10 м
|
|
l - ?
|
Розв’язання
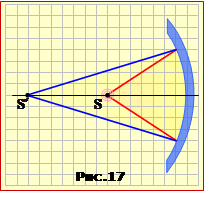 Положення вершини відбитого пучка S′ (рис.17) і джерела S зв'язані формулою дзеркала (16.9). Оскільки дзеркало угнуте і точка S′ є дійсним зображенням точки S, усі величини у формулі (16.9) мають знак «+» (див. правило знаків). Відповідно до тексту задачі f = L і d = F + l, де F – головна фокусна відстань дзеркала. Тому формула (16.9) здобуває вигляд:
Положення вершини відбитого пучка S′ (рис.17) і джерела S зв'язані формулою дзеркала (16.9). Оскільки дзеркало угнуте і точка S′ є дійсним зображенням точки S, усі величини у формулі (16.9) мають знак «+» (див. правило знаків). Відповідно до тексту задачі f = L і d = F + l, де F – головна фокусна відстань дзеркала. Тому формула (16.9) здобуває вигляд:
\(\frac{1}{F+l}+\frac{1}{L}=\frac{1}{F}\).
Звідси, після елементарних викладок одержуємо
\(l=\frac{F^{2}}{L-F}\).
Для сферичного дзеркала \(F=\frac{R}{2}\) (формула (16.8)), тому
\(l=\frac{R^{2}}{2(2L-R)}\).

З урахуванням того, що за умовою L >> R, остаточну відповідь доцільно представити у вигляді:
\(l\approx\frac{R^{2}}{4L}=4\cdot{10^{-3}}\) м = 4 мм
У такий спосіб джерело варто розташувати на 4 мм далі від полюса P, ніж фокус F. На рис.17-1 для ілюстрації показана побудова ходу одного з променів. (При побудові враховано, що показник заломлення повітря практично рівний одиниці).
Задача 16.18
Мурашка повзе зі швидкістю v = 5 мм/с уздовж головної оптичної осі опуклого дзеркала.
Визначити
швидкість руху зображення мурашки u у момент, коли вона знаходиться на відстані d = 1,5F від дзеркала (F – фокусна відстань).
|
Дано: v = 5 мм/с
d = 1,5F
|
|
u - ?
|
Розв’язання
 Побудуємо зображення мурашки в дзеркалі на момент, коли вона знаходиться в точці A на головній оптичній осі (рис.18).
Побудуємо зображення мурашки в дзеркалі на момент, коли вона знаходиться в точці A на головній оптичній осі (рис.18).
Для цього (див. Рекомендації, п.3. рис.16.15б):
1) показуємо положення фокальної площини дзеркала F′F″;
2) проводимо допоміжний промінь KC, продовження якого за дзеркалом проходить через центр кривизни дзеркала C. Він перетинає фокальну площину в точці D;
3) будуємо хід променя AB, паралельного KC: після відбивання він йде так, щоб його продовження за дзеркалом перетинається з променем KC у точці D фокальної площини;
4) другий промінь AP, необхідний для побудови зображення, направимо уздовж головної оптичної осі; (після відбивання в точці P (полюс дзеркала) він змінить напрямок на протилежний);
5) На перетині відрізків BD і AC одержуємо уявне зображення A′ точки A.
Відповідно до формули сферичного дзеркала (16.9) з урахуванням правила знаків, маємо:
|
\(-\frac{1}{F}=\frac{1}{d}-\frac{1}{f}\) \(\Rightarrow\) \(f=\frac{Fd}{d+F}\), |
(1) |
де F – фокусна відстань дзеркала, d, f – відстані від предмета (мурашки) і її зображення у дзеркалі (рис.18).
Відстань (координата) мурашки до дзеркала змінюється за законом d = d0 + vt, де d0 – відстань у початковий момент часу. Підставимо вираз d у формулу (1):
|
\(f=\frac{F(d_{0}+vt)}{d_{0}+vt+F}\). |
За умовою задачі необхідно визначити миттєву швидкість, що визначається як похідна координати за часом \(u=f^{\prime}(t)\) (див. формулу (1.5)). За правилами визначення похідної дробу маємо:
\(u=f^{\prime}(t)=\frac{Fv(d_{0}+vt+F)-F(d_{0}+vt)v}{(d_{0}+vt+F)^{2}}=\frac{vF^{2}}{(d+F)^{2}}\).
За умовою в заданий момент часу f = 1,5F , тому
|
\(u=\frac{vF^{2}}{(1,5F+F)^{2}}=\frac{v}{6,25}=\frac{5}{6,25}=0,8\) мм/с |
(2) |
Ті ж, хто не володіють вищою математикою, можуть міркувати так. Нехай у заданий момент часу відстань від мурашки до дзеркала дорівнює d. Тоді відстань f від дзеркала до зображення визначається формулою (1). За деякий проміжок часу \(\Delta{t}\) ці відстані зміняться і стануть рівними відповідно d1 і f1. Переміщення зображення
|
\(\Delta{f}=f_{1}-f=\frac{Fd_{1}}{d_{1}+F}-\frac{Fd}{(d+F)}\), |
звідки
|
\(\Delta{f}=\frac{F^{2}\Delta{d}}{(d+F)(d_{1}+F)}\), |
(3) |
де \(\Delta{d}\) – переміщення мурахи за час \(\Delta{t}\).
З формул (1) і (3) можна зрозуміти, що рух зображення нерівномірний. Отже, для визначення його швидкості треба розглядати переміщення \(\Delta{f}\) і \(\Delta{d}\), за гранично малий проміжок часу \(\Delta{t}\to{0}\). У такому випадку величини d і d1 у формулі (3) можна вважати рівними і записати:
\(\Delta{f}=\frac{F^{2}\Delta{d}}{(d+F)^{2}}\)
звідки одержуємо швидкість зображення
\(u=\frac{\Delta{f}}{\Delta{t}}=\frac{F^{2}}{(d+F)^{2}}\cdot\frac{\Delta{d}}{\Delta{t}}=\frac{F^{2}v}{(d+F)^{2}}\),
що співпадає з виразом (2).
Задача 16.19
Малий предмет розглядають, приклавши до ока збірну лінзу (лупу) з фокусною відстанню F = 5 см так, що утворюється пряме зображення предмета, розміщене на відстані найкращого зору L = 25 см від лінзи.
Визначити
положення d предмета та збільшення \(\Gamma\) зображення.
|
Дано: F = 5 см
L = 25 см
|
|
d, \(\Gamma\) - ?
|
Розв’язання
Лупа є найпростішим приладом, що "озброює" око. Для того, щоб зображення було прямим (неперевернутим), точки предмета та їх зображення повинні бути розташовані по один бік від головної оптичної осі лінзи. В збіральній лінзі це можливо, тільки коли предмет розміщений між оптичним центром та фокусом. При цьому зображення є уявним і збільшеним, як видно з побудови рис.19.
Отже, згідно з формулою лінзи (16.13) та правилом знаків і умовою задачі f = L, маємо:
|
\(\frac{1}{d}-\frac{1}{L}=\frac{1}{F}\) \(\Rightarrow\) \(d=\frac{LF}{L+F}\approx{4,2}\) см. |
(1) |
Збільшення зображення визначимо, підставивши вираз (1) у формулу (16.14):
\(\Gamma=\frac{f}{d}=\frac{L+F}{F}=6\).
З останнього виразу видно, що збільшення тим більше, чим менша фокусна відстань лінзи. Тому в якості луп використовують короткофокусні лінзи, і при розгляданні предмета його розміщують у безпосередньо біля фокуса лупи. Це очевидно з формули (1) за умови F << L.
Задача 16.20
Відстань між предметом та його зображенням у розсіювальній лінзі l = 5 см, а збільшення \(\Gamma=0,5\).
Визначити
фокусну відстань F та оптичну силу лінзи D.
|
Дано: l = 5 см
\(\Gamma=0,5\)
|
|
F, D - ?
|
Розв’язання
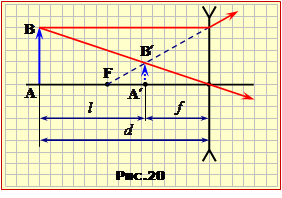 Побудова зображення предмета AB в розсіювальній лінзі та відповідні відстані показані на рис.20, з якого видно що
Побудова зображення предмета AB в розсіювальній лінзі та відповідні відстані показані на рис.20, з якого видно що
|
l = d – f. |
(1) |
Лінійне збільшення лінзи \(\Gamma\) визначається формулою (16.14):
|
\(\Gamma=\frac{H}{h}=\frac{f}{d}\). |
(2) |
З рівнянь (1) та (2) знайдемо f та d:
\(-\frac{1}{F}=\frac{1}{d}-\frac{1}{f}\) \(\Rightarrow\) \(F=\frac{fd}{d-f}=\frac{l\Gamma}{(1-\Gamma)^{2}}=\frac{5\cdot{0,5}}{1-0,5}=10\) см.
Оптична сила лінзи
\(D=-\frac{1}{F}=-10\) дптр.
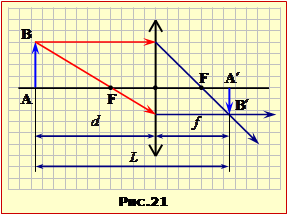
Задача 16.21
Збірна лінза має фокусну відстань F.
Визначити:
А) при якій відстані d0 між предметом та лінзою, відстань між предметом та його дійсним зображенням буде найменшою L = Lmin;
 Б) величину Lmin.
Б) величину Lmin.
|
Дано: F
|
|
d0 - ?
Lmin - ?
|
Розв’язання
Предмет та його дійсне зображення знаходяться по різні боки від лінзи (рис.21). Тому відстань l між предметом та його дійсним зображенням
|
L = d + f. |
(1) |
Отже
f = L – d.
Підставивши цей вираз у формулу лінзи (16.9), отримаємо залежність L від d:
|
\(\frac{1}{d}+\frac{1}{L-d}=\frac{1}{F}\) \(\Rightarrow\) \(L=\frac{d^{2}}{d-F}\). |
(2) |
Далі задачу можна розв'язувати двома способами:
1) з використанням методів вищої математики;
2) алгебраїчно.
I спосіб.
А) Щоб визначити, при якому значенні d = d0 величина L буде найменшою (L = Lmin), знайдемо похідну від L по d і прирівняємо її до нуля. За правилом диференціювання дробу
|
\(L^{\prime}=\frac{2d(d-F)-d^{2}}{(d-F)^{2}}=\frac{d(d-2F)}{(d-F)^{2}}\). |
(3) |
Мінімальній відстані L = Lmin відповідає така величина d = d0, при якій \(L^{\prime}(d_{0})=0\), отже
|
\(\frac{d_{0}( d_{0}-2F)}{( d_{0}-F)}=0\) \(\Rightarrow\) \(d_{0}=2F\). |
(4) |
Зауважимо, що рівність нулю похідної відповідає також умові максимуму L. Однак відстань d може бути якою завгодно то, згідно з виразом (1), те ж саме можна сказати і про L. Таким чином, відсутні чинники, які б зумовили можливість досягнення максимуму функції L(d).
При цьому враховано те, що \( d_{0}\ne{F}\) і \( d_{0}\ne{0}\), оскільки при \( d_{0}=F\) зображення не існує (див. формулу (16.13)), а \(d_{0}=0\) не має фізичного змісту: предмет не може знаходитись всередині лінзи
Б) Підставивши значення \(d_{0}=2F\) у вираз (2), отримаємо для мінімальної відстані Lmin:
\(L_{min}=\frac{4F^{2}}{2F-F}=4F\).
За такої умови з виразу (1) випливає, що f = 2F.
Отже при мінімальній відстані L = Lmin: предмет і його дійсне зображення розміщені у подвійному фокусі лінзи. Як наслідок, збільшення \(\Gamma=f/d=1\). Сказане свідчить про те, що для збірної лінзи не лише головні фокуси, а й подвійні фокуси є особливими точками.
II спосіб. Перепишемо вираз (2) у вигляді квадратного рівняння відносно величини d:
|
\(d^{2}-Ld+LF=0\). |
(5) |
Корені цього рівняння можна подати у вигляді:
|
\(d_{1,2}=\frac{L}{2}\left(1\pm\sqrt{1-\frac{4F}{L}}\right)\). |
(6) |
Обидва корені d1 і d2 мають фізичний зміст і визначають два положення предмета відносно збиральної лінзи, при яких на заданій відстані утворюються дійсні зображення (в одному випадку збільшене, а в іншому зменшене). Але з виразу (6) очевидно, що дійсні корені, а отже – розв'язок задачі, існують лише за умови
\(1-\frac{4F}{L}\ge{0}\) \(\Rightarrow\) \(L\ge{4F}\).
Звідси відразу випливає відповідь на запитання Б):
\(L_{min}=4F\).
Підстановка цього значення у виразі (6) дає величину d. (завдання А)):
\(d_{0}=\frac{L_{min}}{2}=2F\).
Задача 16.22
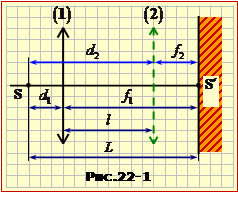
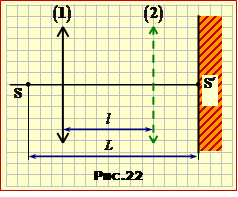 Світна точка S та екран E розташовані на відстані L = 1 м одне від одного. Збірна лінза, вміщена між ними, дає чітке зображення \(\mathrm{S}^{\prime}\) на екрані при двох положеннях, відстань між якими l = 60 см (див. схематичний рис. 22).
Світна точка S та екран E розташовані на відстані L = 1 м одне від одного. Збірна лінза, вміщена між ними, дає чітке зображення \(\mathrm{S}^{\prime}\) на екрані при двох положеннях, відстань між якими l = 60 см (див. схематичний рис. 22).
Визначити фокусну відстань лінзи F.
|
Дано: L = 1 м
l = 60 см
|
|
F - ?
|
Розв’язання
На рис.22-1 схематично показані точка S, її зображення \(\mathrm{S}^{\prime}\) на екрані E, два положення лінзи (1), (2) та відповідні відстані.
 Задачу можна розв'язати декількома способами.
Задачу можна розв'язати декількома способами.
I спосіб. Логічно найпростішими є такий шлях. Запишемо формулу лінзи (16.9) для обох положень лінзи та співвідношення, що випливають безпосередньо з умови задачі та рис.22-1:
|
\(\frac{1}{d_{1}}+\frac{1}{f_{1}}=\frac{1}{F}\), \(\frac{1}{d_{2}}+\frac{2}{f_{2}}=\frac{1}{F}\), |
(1) |
|
|
\(d_{1}+f_{1}=L\), \(d_{2}+f_{2}=L\), |
(2) |
|
|
\(d_{2}-d_{1}=L\). |
(3) |
Ця система з п'яти рівнянь містить 5 невідомих (d1, f1, d2, f2, F), отже є повною. Розв'язавши її, можна визначити шукану фокусну відстань F. Але такий спосіб не є раціональним, оскільки пов'язаний з громіздкими викладками.
II спосіб. Розв'язання значно спрощується, якщо врахувати оборотність світлових променів, яка дозволяє міняти місцями предмет і його зображення. Відтак стає зрозумілим, що d2 = f1 , f2 = d1 і рівняння (3) набуває вигляду
|
\(f_{1}-d_{1}=l\). |
(4) |
Почленно додавши, а потім віднявши, рівняння (2) і (3), легко отримаємо
\(d_{1}=\frac{L-l}{2}\), \(f_{1}=\frac{L+l}{2}\).
Підставивши ці вирази в рівняння (1), після нескладних викладок знайдемо відповідь:
\(\frac{2}{L-l}+\frac{2}{L+l}=\frac{1}{F}\) \(\Rightarrow\) \(F=\frac{L^{2}-l^{2}}{4l}=16\) см.
III спосіб. Скористаємось виразами d1 і d2 з задачі 16.19 (формула (6)):
\(d_{1}=\frac{L}{2}\left(1-\sqrt{1-\frac{4F}{L}}\right)\),
\(d_{2}=\frac{L}{2}\left(1+\sqrt{1-\frac{4F}{L}}\right)\).
В такому виразі, згідно з співвідношенням (3)
\(l=L\sqrt{1-\frac{4F}{L}}\) \(\Rightarrow\) \(F=\frac{L^{2}-l^{2}}{4L}\).
Задача 16.23
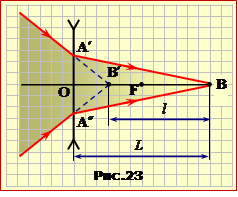 Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються в точці В головної оптичної осі на відстані L = 60 см від центра лінзи O (рис.23).
Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються в точці В головної оптичної осі на відстані L = 60 см від центра лінзи O (рис.23).
Визначити
відстань l на яку, зміститься точка перетину променів, якщо лінзу прибрати.
|
Дано: F = 30 см
L = 60 см
|
|
l - ?
|
Розв’язання
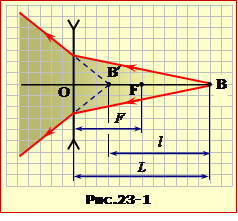
Промені, що падають на лінзу, не виходять з якоїсь світної точки (джерела). Тому може здатись, що формула лінзи (16.13) тут непридатна через невизначеність параметра d – відстані від "предмета" до лінзи. Але завдяки оборотності світлових променів можна "обернути" задачу в такий спосіб. Розмістимо в точці B точкове джерело, що напрямляє на лінзу конічний світловий пучок, обмежений променями BA′ і BA″ (рис.23-1). Тоді заломлені промені утворять такий самий, як падаючі, але розбіжний пучок, і точка B’ буде уявним зображенням точки B. При цьому OB = L = d і OB′ =L – l = f.
З формули лінзи (16.9), враховуючи правило знаків, маємо
|
|
\(\frac{1}{L}-\frac{1}{L-l}=-\frac{1}{F}\), |
(1) |
звідки
\(l=\frac{L^{2}}{L+F}=40\) см.
Цікаво і корисно звернути увагу на те, що формулі (1) можна надати іншої інтерпретації, яка дозволяє отримати відповідь у цій та подібних задачах одразу, не розглядаючи оберненої задачі. Точка B′ за умовою є точкою перетину продовжень падаючих на лінзу променів. Тому її можна формально трактувати як уявне джерело, тобто як уявний зображуваний предмет. Натомість точка B є дійсним зображенням уявної точки B′. В такому разі OB′ = L – l = d i OB = L = f, і вираз (1) набуває вигляду:
\(-\frac{1}{d}+\frac{1}{f}=-\frac{1}{F}\),
що співпадає з формулою лінзи (16.9) і відповідає правилу знаків (величина 1/d взята зі знаком "–", а 1/f – зі знаком "+").
Задача 16.24
Короткозорий хлопець читає книжку, тримаючи її на відстані d0 = 16 см від очей.
Визначити
оптичну силу Dл окулярів, які потрібні хлопцеві для корекції зору.
|
Дано: d0 = 16 см
|
|
Dл - ?
|
Розв’язання
Людина з нормальним зором найкраще розрізняє дрібні деталі, якщо предмет розташований на відстані найкращого бачення d = 25 см. Люди з дефектами зору змушені роздивлятися дрібні предмети, тримаючи їх на відстанях d0, що відрізняються від вказаної. Для корекції зору застосовують окуляри, при цьому кришталик ока та лінзу окулярів можна вважати оптичною системою, в якій лінзи розташовані впритул одна до одної. Оптична сила такої системи D, тобто «скорегованого» ока, визначається формулою (16.15):
|
|
D = D0 + Dл, |
(1) |
де D0 – оптична сила кришталика, Dл – оптична сила лінзи окулярів.
За формулою тонкої лінзи (16.13)
|
|
\(D_{0}=\frac{1}{d_{0}}+\frac{1}{f}\); \(D=\frac{1}{d}+\frac{1}{f}\), |
(2) |
де f – відстань між кришталиком та дном ока. (Нагадаємо, що на дні ока знаходиться сітківка, що відіграє роль "екрана", на який фокусується зображення розглядуваних об'єктів). Підставивши вирази (2) у формулу (1), після перетворень дістанемо
\(D_{л}=D-D_{0}=\frac{1}{d}-\frac{1}{d_{0}}=\frac{1}{0,25}-\frac{1}{0,16}=-2,25\) дптр.
Оптична сила від'ємна, отже для короткозорих людей окуляри виготовляються з розсіювальних лінз.
Задача 16.25
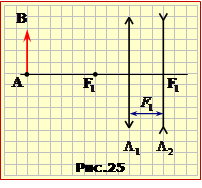 Оптична система складається із збірної лінзи Л1 з відомою фокусною відстанню F1 і розсівної лінзи Л2, що розміщена у фокальній площині лінзи Л1 так, що головні оптичні осі лінз співпадають (рис.25). Предмет AB розташований на відстані d1 = 3F1 перед збиральною лінзою.
Оптична система складається із збірної лінзи Л1 з відомою фокусною відстанню F1 і розсівної лінзи Л2, що розміщена у фокальній площині лінзи Л1 так, що головні оптичні осі лінз співпадають (рис.25). Предмет AB розташований на відстані d1 = 3F1 перед збиральною лінзою.
Визначити
фокусну відстань розсіювальної лінзи F2, якщо система дає дійсне зображення предмета із збільшенням \(\Gamma=2\).
|
Дано: d1 = 3F1
\(\Gamma=2\)
|
|
F2 - ?
|
Розв’язання
Приблизний хід променів і необхідні для аналізу відстані показані на рис.25-1.
Ключ до аналітичного розв'язання задач на зображення в оптичних системах полягає в тому, що зображення, яке створюється (або створювалося б) одним елементом системи можна розглядати як зображуваний предмет для наступного елемента.
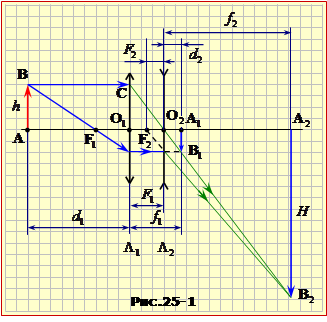
В даній задачі це стосується зображення A1B1 (див. рис.25-1), яке створювала б лінза Л1 за відсутності Л2. Тому варто визначити положення цього зображення. Згідно з формулою лінзи (16.13) та умовою задачі d1 = 3F1 маємо:
|
|
\(\frac{1}{3F_{1}}+\frac{1}{f_{1}}=\frac{1}{F_{1}}\) \(\Rightarrow\) \(f_{1}=\frac{3}{2}F_{1}\). |
(1) |
По відношенню до лінзи Л2 відрізок A1B1 є уявним предметом, а A2B2 – його дійсним зображенням (див. Задачу 16.23). Тому згідно з правилом знаків для Л2 формула (16.13) набуває вигляду:
|
|
\(-\frac{1}{d_{2}}+\frac{1}{f_{2}}=\frac{1}{F_{2}}\). |
(2) |
З рис.25-1 видно, що d2 = f1 – F1 і з урахуванням значення (1)
\(d_{2}=\frac{3}{2}F_{1}-F_{2}=\frac{1}{2}F_{1}\).
З подібних трикутників O2A2B2 і O2O1C маємо:
\(\frac{f_{2}}{F_{1}}=\frac{H}{h}\) \(\Rightarrow\) \(f_{2}=\Gamma{F}_{1}=2F_{2}\),
де \(\Gamma=2\) – задане збільшення системи.
Підставивши ці значення d2 і f2 у формулу (2), дістанемо відповідь:
\(-\frac{2}{F_{1}}+\frac{1}{\Gamma{F}_{1}}=-\frac{1}{F_{2}}\) \(\Rightarrow\) \(F_{2}=\frac{2}{3}F_{1}\).
Рекомендації до теми "Формули дзеркала і лінзи"
|
Формули дзеркала (16.9) і тонкої лінзи (16.13) ідентичні. Тому в обох випадках аналітичні задачі на зображення слід розв'язувати за наступною схемою. |
|
1) |
Зобразити на рисунку положення лінзи (дзеркала) і приблизні положення предмета та його зображення. Примітка. У найпростіших ситуаціях цього можна й не робити. Рисунок робиться схематично, без побудови ходу променів. У деяких складних задачах треба показувати хід променів. |
|
|
|
|
2) |
Скласти рівняння, тобто записати формулу лінзи (дзеркала) з урахуванням правила знаків та додаткових умов задачі (задано відстань між предметом та екраном, задано збільшення, тощо). При цьому слід пам'ятати, що фокусні відстані (або оптична сила ) увігнутого дзеркала і збірної лінзи завжди додатні, а опуклого дзеркала та розсіювальної лінзи - завжди від'ємні. Якщо знак шуканої відстані від лінзи (дзеркала) до зображення не є очевидним, то вона береться додатною. Знак кінцевого результату вкаже характер зображення: "+" буде означати, що зображення дійсне, а "-" покаже на те, що воно уявне. |
|
|
|
|
3) |
В деяких задачах складання рівнянь і розв'язування задачі полегшується, якщо скористатись оборотністю світлових променів. Ця властивість променів випливає з законів відбивання і заломлення світла і полягає в наступному. Якщо промінь світла виходить з певної точки А і, пройшовши крізь оптичну систему, попадає в точку А', то промінь, що виходить з точки А' у зворотному напрямку, потрапить у точку А, повністю повторивши шлях першого променя. Це дозволяє при необхідності міняти місцями предмет та його зображення без зміни ходу променів. |
|
|
|
|
4) |
Розв'язати отримане рівняння (або систему рівнянь) і знайти аналітичну відповідь, яка покаже положення, розміри та характер зображення. Згідно з аналітичною відповіддю виконати рисунок з побудовою ходу променів. Це потрібно як для ілюстрації розв'язку, так і для його загальної перевірки. Наприклад, може виявитись, що згідно з аналітичною відповіддю зображення уявне, а побудова ходу променів засвідчить, що воно дійсне. |
Розділ 17. Хвильова оптика
|
Хвильова оптика досліджує явища, розгляд яких неможливий без урахування хвильових властивостей світлового випромінення. До таких явищ, зокрема, відносяться інтерференція та дифракція. Ці явища спостерігаються при утворенні та накладанні певним чином узгоджених хвиль. Теоретичні відомості Приклади розв’язування задач |
Теоретичні відомості. Інтерференція світла
|
При накладанні хвиль від двох чи більше джерел за певних умов спостерігається специфічне явище інтерференції. Інтерференція спостерігається при накладанні когерентних хвиль. При інтерференції в залежності від різниці фаз (різниці ходу) на екрані створюється інтерференційна картина - зони збільшення та зменшення інтенсивності світла (інтерференційні смуги). Найбільша та найменша інтенсивності спостерігаються при виконанні загальних умов максимумів і мінімумів. |
|
Накладання хвиль від декількох джерел створює у кожній точці простору відповідні результуючі коливання. Нехай маємо два точкових джерела (рис.17.1) S1 та S2 в однорідному прозорому середовищі, що випромінюють монохроматичні світлові хвилі однієї частоти \(\omega\) (довжини хвилі \(\lambda\)). Приймемо, що в певній точці спостереження P кожна з хвиль збуджує коливання електричного поля вздовж одного напрямку і однакової амплітуди Em. (саме такі умови створюються при реальному спостереженні інтерференції світла). В такому разі рівняння цих коливань мають вигляд \(E_{1}=E_{m}\cos(\omega{t}-\varphi_{1})\); \(E_{2}=E_{m}\cos(\omega{t}-\varphi_{2})\). Початкові фази \(\varphi_{1}\) і \(\varphi_{2}\) залежать від початкових фаз кожної з хвиль \(\varphi_{01}\), \(\varphi_{02}\) і відстаней l1, l2 від джерел до даної точки P. Згідно з рівнянням монохроматичної хвилі (15.5)) і формулою (15.6))
де \(\lambda\) – довжина світлової хвилі. За принципом суперпозиції результуюча напруженість
або
Отже, при накладанні двох монохроматичних хвиль однакової частоти створюються гармонічні коливання \(E=E_{0}\cos(\omega{t}-\varphi)\) з початковою фазою \(\varphi=(\varphi_{1}+\varphi_{2})/2\) і амплітудою
яка залежить від різниці фаз
хвиль, що накладаються. |
|
Оскільки інтенсивність прямо пропорційна квадрату амплітуди \(I\sim{E}_{0}^{2}\), тому з виразу (17.2)) випливає, що
де \(I_{1}\) – інтенсивність, що створюється кожною з хвиль окремо. Очевидно, що \(I\ne2I_{1}\). У цьому і полягає ефект інтерференції. Інтерференцією називається таке накладання хвиль, при якому результуюча інтенсивність у точці накладання не дорівнює сумі інтенсивностей, створюваних кожною з хвиль окремо. Зазначимо, що інтерференція не суперечить закону збереження енергії. Енергія не виникає (у точках, де \(I\gt{2}I_{1}\)) і не щезає (якщо \(I\lt{2}I_{1}\)), вона лише відповідним чином перерозподілюється у просторі. |
|
З виразу (17.4) зрозуміло, що для спостереження інтерференції необхідно, щоб величина \(\delta\) не змінювалася з часом, тобто, щоб хвилі, що накладаються були узгодженими, або когерентними. Когерентними називаються хвилі, різниця фаз яких \(\delta\) у даній точці простору не залежить від часу. Точно ця умова виконується лише для ідеальних монохроматичних хвиль однієї частоти. Для реальних хвиль когерентність означає достатньо повільну зміну \(\delta\) з часом. Отже,
Світло від реальних джерел не є неперервною хвилею з заданою початковою фазою. Воно складається з безлічі елементарних порцій випромінення, що випускаються окремими атомами протягом дуже коротких проміжків часу. Фази таких порцій ніяк не узгоджені між собою. Тому при накладанні хвиль від двох незалежних джерел різниця фаз \(\delta\) швидко і невпорядковано змінюється. Як наслідок, світлові хвилі від незалежних джерел є некогерентними, і при їх накладанні інтерференція не спостерігається. Виняток становлять оптичні квантові генератори – лазери, – випромінення яких є високомонохроматичним і має стабільну фазу. Отримати когерентні світлові хвилі і спостерігати інтерференцію можна, якщо поділити випромінювання від одного джерела на два промені і потім звести їх у просторі. В такому випадку початкові фази в обох пучках у будь який момент однакові \(\varphi_{01}=\varphi_{02}=\varphi_{0}\), а різниця фаз \(\delta=\varphi_{2}-\varphi_{1}\), згідно з виразами (17.1), залежить тільки від відстаней l1, l2 і не залежить від часу. Для такого поділу використовують різні способи, що базуються на відбиванні та заломленні світла. Зокрема, когерентні хвилі утворюються при відбиванні світла від поверхонь тонких прозорих плівок. Завдяки інтерференції таких хвиль спостерігається яскраве райдужне забарвлення плівок бензину в калюжах або мильних бульбашок, видуванням яких полюбляють бавитися діти. |
|
З виразу (17.4) очевидно, що результат інтерференції (величина I) при накладанні двох заданих когерентних хвиль залежить від значення різниці фаз \(\delta=\varphi_{2}-\varphi_{1}\). Підставивши сюди вирази (17.1) і врахувавши, що в реальних умовах спостереження \(\varphi_{01}=\varphi_{02}\), отримаємо
Різниця відстаней від джерел до даної точки (див. рис.17.1) \(\Delta_{0}=l_{2}-l_{1}\) називається геометричною різницею ходу хвиль (або променів), що приходять у дану точку. Таким чином, в однорідному середовищі різниця фаз пов'язана з різницею ходу співвідношенням
Якщо світлові хвилі від джерел до даної точки розповсюджуються у двох різних середовищах з показниками заломлення n1 і n2, тоді довжини хвиль не є однаковими (див. формулу (16.4)): \(\lambda_{1}=\frac{\lambda_{0}}{n_{1}}\) і \(\lambda_{2}=\frac{\lambda_{0}}{n_{2}}\). Тому фази коливань \(\varphi_{1}=\frac{2\pi}{\lambda_{1}}\), \(\varphi_{2}=\frac{2\pi}{\lambda_{2}}\), і \(\delta=2\pi\left(\frac{l_{2}}{\lambda_{2}}-\frac{l_{1}}{\lambda_{1}}\right)=\frac{2\pi}{\lambda_{0}}(l_{2}n_{2}-l_{1}n_{1})\), де \(\lambda_{0}\) – довжина світлової хвилі у вакуумі. Величина \(L=l\cdot{n}\) називається оптичною довжиною шляху, а
оптичною різницею ходу. Таким чином, для неоднорідних середовищ
|
|
При переході від точки до точки у певному напрямку різниця фаз \(\delta\), згідно з формулою (17.5), монотонно змінюється (зростає або спадає), а величина \(\cos^{2}(\delta/2)\) у формулі (17.4) періодично змінюється між значеннями 0 та 1. З цієї причини у просторі створюється система інтерференційних смуг – зон з великою та з малою інтенсивністю. Максимальна інтенсивність спостерігається, якщо \(\cos^{2}(\delta/2)=1\), тобто при
Мінімумам інтенсивності відповідають точки зі значенням \(\cos^{2}(\delta/2)=0\), і
Підставивши ці значення \(\delta\) у вираз (17.6a), дістанемо зручні для розрахунків загальні умови максимумів та мінімумів при інтерференції двох хвиль. Умова максимумів:
Умова минимумів:
Таким чином,
|
Теоретичні відомості. Дифракція світла
|
Якщо на шляху поширення хвиль трапляються різкі неоднорідності, то спостерігається дифракція. На явищі дифракції світла заснована дія оптичного приладу, що зветься дифракційною граткою. Дифракційна гратка має важливі практичні застосування. |
|
Дифракцією називаються явища, зумовлені здатністю хвиль змінювати напрям поширення при зустрічі з різкими неоднорідностями – невеликими непрозорими перешкодами або з отворами у непрозорому екрані. Можливість практичного спостереження дифракції залежить від розмірів перешкод: вони повинні бути співвимірними з довжиною хвилі (оптимально – (10 – 100)\(\lambda\). Дифракційні явища можна аналізувати на основі принципу Гюйгенса-Френеля, згідно з яким
Оскільки вторинні хвилі когерентні, то при накладанні вони інтерферують з утворенням максимумів і мінімумів інтенсивності. З цієї причини при проходженні світла крізь малий отвір (рис.17.2а) на поставленому за ним екрані спостерігається не просто розмите зображення отвору, а сукупність світлих і темних смуг (кілець) – дифракційних максимумів і мінімумів (рис.17.2б).
|
|
Дифракційні смуги від одного отвору через його малі розміри дуже слабкі. Але інтенсивність дифракційних максимумів різко збільшується у дифракційній гратці. Найпростіша дифракційна гратка являє собою плоску прозору пластинку, на поверхні якої створена система однакових вузьких прозорих смуг (щілин), розділених однаковими непрозорими проміжками (рис.17.3). Відстань d між сусідніми щілинами називається періодом гратки, і є одним з її основних параметрів. Часто замість d використовують сталу дифракційної гратки n = 1/d – кількість щілин на одиницю довжини гратки. Ще одним параметром гратки є загальна кількість щілин N. Для дифракційних граток високого класу d ~ 1 мкм (10-6 м) і N ~ 105.
При опроміненні гратки паралельним пучком променів внаслідок дифракції після неї під будь-яким кутом \(\varphi\) поширюється N когерентних пучків від усіх щілин. Кут, під яким поширюється певний пучок, називають кутом дифракції. В результаті інтерференції цих пучків на розташованому за ґраткою екрані виникає складна дифракційна картина, що складається з великої кількості мінімумів та максимумів різної інтенсивності. Серед них вирізняються дуже інтенсивні головні максимуми. Вони визначаться умовою головних максимумів ґратки:
У цій формулі d – період гратки, \(\varphi\) – кут дифракції (див. рис.17.3), \(\lambda\) – довжина хвилі світла, яким опромінюється гратка, m – ціле число, що називається порядком дифракційного спектра. Умова (17.9) і велика інтенсивність головних максимумів мають просте пояснення. З рис.17.3 можна зрозуміти, що величина \(\Delta=d\sin\varphi \) – то є різниця ходу променів, які йдуть під кутом \(\varphi\) від двох сусідніх щілин. Це означає, що при виконанні умови (17.9) фази коливань електричного поля від усіх N щілин кратні \(2\pi\). Тому результуюча амплітуда \(E=NE_{1}\), а результуюча інтенсивність
де \(I_{1}\) – інтенсивність світла, що створюється однією щілиною, N – загальна кількість щілин гратки. |
|
З формули (17.10) випливає, що в головних максимумах спостерігається дуже велика концентрація світлової енергії. Це визначає практичні застосування дифракційної гратки. Згідно з умовою (17.9), кожній довжині хвилі \(\lambda\) відповідає свій власний кут дифракції \(\varphi\), а отже своє власне положення головного максимума при заданому m. Тому, якщо на гратку P з відомим періодом напрямити пучок білого світла (рис.17.4), то на екрані E для всіх \(m\ne{0}\) замість вузьких яскравих смуг утворюються спектри – широкі смуги, що забарвлені у кольори веселки. У центрі екрана m = 0, \(\sin\varphi=0\) і умова (17.9) виконується для будь-якої довжини хвилі. Тому в центрі екрана спостерігається вузька незабарвлена смуга.
Вимірявши кут дифракції \(\varphi\) (або координату відповідної точки на екрані), можна визначити довжину хвилі \(\lambda\) світла, що дає дифракційний максимум у даній точці екрана: \(\lambda=\frac{d\sin\varphi}{m}\). Властивість дифракційної гратки розгортати світло у спектр використовується в оптичних приладах для отримання монохроматичного світла та для визначення спектрального складу невідомого випромінення. |
Приклади розв'язування задач
*********************************
Задача 17.1
*********************************
Задача 17.2
*********************************
Задача 17.3
*********************************
Задача 17.4
*********************************
Задача 17.5
Задача 17.1
Два точкові когерентні джерела світла розташовані на відстані l = 0,5 м від екрана. Довжина хвилі світла \(\lambda=620\) нм. Відстань між джерелами d = 0,4 мм.
Визначити
відстань \(\Delta{x}\) між інтерференційними максимумами на екрані.
|
Дано: l = 0,5 м
\(\lambda=620\) нм = 6,2·10-7 м
d = 0,4 мм = 0,4·10-3 м
|
|
\(\Delta{x}\) - ?
|
Розв’язання
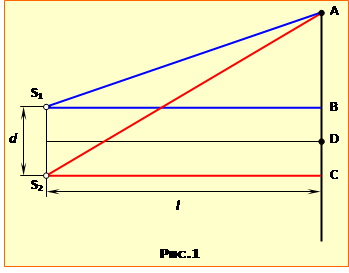
Припустимо, що в точці А на екрані (рис.1) спостерігається максимум інтерференції. Це можливо, якщо різниця ходу \(\Delta\) двох променів S1A та S2A задовольняє умові (17.8a):
|
|
\(\Delta=\pm{m}\lambda\), |
(1) |
де m – цілі числа. Знайдемо різницю ходу, скориставшись геометричною побудовою на рис.1. З трикутників S1AB та S2AC за теоремою Піфагора маємо:
S1A2 = S1B2 + AB2; S2A2 = S2C2 + AC2.
Відрізки AB та AC відповідно дорівнюють
AB = AD - \(\frac{1}{2}\)BC; AC = AD + \(\frac{1}{2}\)BC.
Позначимо AD = x. Оскільки S1B = S2C = l, BC = d, маємо:
|
|
S1A2 = l2 + (x – d/2)2; S2A2 = l2 +(x + d/2)2. |
(2) |
Різницю квадратів (S2A2 – S1A2) запишемо у вигляді:
S2A2 – S1A2 = (S2A – S1A)(S2A + S1A).
Інтерференційна картина в таких випадках завжди спостерігається поблизу центра екрана (точка D на рис.1), тобто \(x\ll{l}\). За цих умов S2A + S1A \(\approx\) 2l, S2A – S1A = \(\Delta\)отже
S2A2 – S1A2 = \(\Delta\cdot{2l}\).
Підставимо сюди вирази (2) і дістанемо:
\(l^{2}+(x+d/2)^{2}-l^{2}-(x-d/2)^{2}=\Delta{2l}\) \(\Rightarrow\) \(x=\frac{\Delta\cdot{l}}{d}\).
Врахувавши умову (1), знаходимо, що точка A, в якій спостерігається максимум інтерференції з номером m, віддалена від точки D на відстань
\(x_{m}=\frac{m\lambda{l}}{d}\).
Точка А1, в якій спостерігається максимум з номером (m + 1), віддалена від точки О на відстань
\(x_{m+1}=\frac{(m+1)\lambda{l}}{d}\),
отже відстань між максимумами
\(\Delta{x}=x_{m+1}-x_{m}=\frac{\lambda{l}}{d}\).
З останнього виразу зрозуміло, що для покращення умов спостереження інтерференції необхідно збільшувати відстань від джерел до екрана l і зменшувати відстань між джерелами d.
Виконаємо обчислення:
\(\Delta{x}=\frac{6,2\cdot{10^{-7}}\cdot{0,5}}{0,4\cdot{10^{-3}}}=7,75\cdot{10}^{-4}\) м \(\approx{0,8}\) мм.
Задача 17.2
На тонку плівку з показником заломлення n = 1,33 падає паралельний пучок білого світла під кутом \(\alpha=30^{\circ}\).
Визначити
мінімальну товщину плівки d, при якій відбите світло з довжиною хвилі \(\lambda_{1}=0,64\) мкм максимально підсилене внаслідок інтерференції, а з довжиною хвилі \(\lambda_{2}=0,40\) мкм – зовсім не відбивається. Врахувати, що при відбиванні від оптично більш густого середовища фаза відбитої хвилі стрибком змінюється на \(\delta=\pi\).
|
Дано: n = 1,33
\(\alpha=30^{\circ}\)
\(\lambda_{1}=0,64\) мкм
\(\lambda_{2}=0,40\) мкм
|
|
d - ?
|
Розв’язання
Світло, що падає на плівку, частково відбивається від її верхньої поверхні, частково входить у плівку, відбивається від її нижньої поверхні та виходить назовні. Хід одного з падаючих променів показаний на рис.2. Промені 1 та 2 є когерентними, оскільки утворені поділом одного падаючого променя. Якщо на шляху променів поставити лінзу, що збере їх в одну точку (такою лінзою може бути кришталик ока), то буде спостерігатись інтерференція. Як наслідок, інтенсивність відбитого світла в залежності від різниці фаз \(\delta\) може підсилюватися (при виконанні умови (17.7а)), або послаблятися (при виконанні умови (17.7б)).
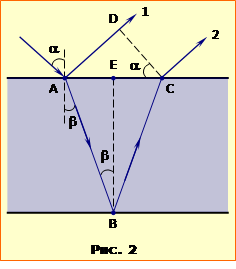
Різниця фаз залежить від різниці ходу променів (формула (17.5)). Визначимо геометричні довжини шляху променів 1 та 2 від точки падіння А до точок D та С (подальші шляхи променів до екрана однакові, тому їх не треба враховувати). Шлях променя 1 l1 = AD. З трикутника ACD:
l1 = AC\(\cdot\sin\alpha\)=2AE\(cdot\sin\alpha\).
З трикутника ABE: AE = \(d\cdot\mathrm{tg}\beta\), отже \(l_{1}=2d\cdot\frac{\sin\alpha\cdot\sin\beta}{\sqrt{1-\sin^{2}\beta}}\)
Підставивши вираз \(\sin\beta=\sin\alpha/n\) з закону заломлення світла (16.6), дістанемо:
|
|
\(l_{1}=2d\frac{\sin^{2}\alpha}{n\sqrt{1-\sin^{2}\alpha/n}}=\frac{2d\sin^{2}\alpha}{\sqrt{n^{2}-sin^{2}\alpha}}\). |
(1) |
Аналогічно визначаємо шлях променя 2 (див. рис.2):
|
|
\(l_{2}=AB+BC=2AB=\frac{2d}{\cos\beta}=\frac{2d}{\sqrt{1-\sin^{2}\beta}}=\frac{2dn}{\sqrt{n^{2}-\sin^{2}\alpha}}\). |
(2) |
В однорідному середовищі різниця фаз пов’язана з шляхами променів співвідношенням (17.5). Але в даній задачі промені поширюються в різних середовищах: промінь 1 у повітрі (n = 1), а промінь 2 у плівці (n = 1,33). Тоді довжини хвиль цих променів різні: у променя 1 задане в умові значення \(\lambda_{0}\), а у променя 2 \(\lambda=\lambda_{0}/n\) (див. формулу (16.4)), і формула (17.5) набуває вигляду:
\(\delta=\frac{2\pi{l_{2}}}{\lambda}-\frac{2\pi{l_{1}}}{\lambda_{0}}\) \(\Rightarrow\) \(\delta=\frac{2\pi}{\lambda}(l_{2}n-l_{1})\).
Підставивши в це співвідношення вирази (2) і (1), після спрощення отримаємо:
|
|
\(\delta=\frac{2\pi}{\lambda_{0}}\cdot{2d}\sqrt{1-\sin^{2}\alpha}\). |
(3) |
Для визначення результату інтерференції цих променів слід урахувати вказаний в умові ефект зміни фази на \(\delta_{0}=\pi\) променя 1, який відбивається від плівки (оптично більш густої, ніж повітря). Промінь 2 в точці В відбивається від повітря, тому його фаза не змінюється. Тому повна різниця фаз променів 1 і 2 \(\delta_{n}=\delta-\delta_{0}=\delta-\pi\). З урахуванням виразу (3), маємо:
|
|
\(\delta=\frac{2\pi}{\lambda_{0}}\cdot\left(2d\sqrt{n^{2}-\sin^{2}\alpha}-\frac{\lambda_{0}}{2}\right)\). |
(4) |
Максимум інтерференції для довжини хвилі \)\lambda_{0}=\lambda_{1}\) спостерігається при виконанні умови (17.7a), тобто
|
|
\(\frac{2\pi}{\lambda_{0}}\left(2d\sqrt{n^{2}-\sin^{2}\alpha}-\frac{\lambda_{0}}{2}\right)=2m_{1}\pi\) \(\Rightarrow\) \(\Rightarrow\) \(2d\sqrt{n^{2}-\sin^{2}\alpha}=(2m+1)\frac{\lambda_{0}}{2}\). |
(5) |
Мінімум інтерференції для довжини хвилі \(\lambda_{0}=\lambda\) спостерігається при виконанні умови (17.7б), тобто
|
|
\(\frac{2\pi}{\lambda_{0}}\left(2d\sqrt{n^{2}-\sin^{2}\alpha}-\frac{\lambda_{0}}{2}\right)=(2m_{2}+1)\pi\) \(\Rightarrow\) \(\Rightarrow\) \(2d\sqrt{n^{2}-\sin^{2}\alpha}=(m_{2}+1)\lambda_{0}\). |
(6) |
Порядки інтерференції (числа m1, m2) у формулах (5) та (6) є незалежними і, звичайно, можуть бути різними.
Оскільки умови (5) і (6) повинні виконуватись одночасно, то, прирівнюючи праві частини, дістанемо
\((2m_{1}+1)\frac{\lambda_{1}}{2}=(m_{2}+1)\lambda_{2}\) \(\Rightarrow\) \(\frac{2m_{2}+2}{2m_{1}+1}=\frac{\lambda_{1}}{\lambda_{2}}\)
Мінімальній можливій товщині плівки відповідають мінімальні значення цілих чисел m2 та m1, що з урахуванням значень \(\lambda_{1}\) та \(\lambda_{2}\) дає
\(\frac{2m_{2}+2}{2m_{1}+1}=\frac{8}{5}\) \(\Rightarrow\) \(\frac{m_{2}+1}{2m_{1}+1}=\frac{4}{5}\).
Звідси: m2 + 1 = 4; 2m1 + 1 =5.
Підставивши будь-яке з цих чисел у відповідну формулу ((6) або (5)), отримаємо відповідь. Наприклад:
\(d=\frac{(2m+1)\lambda}{4\sqrt{n^{2}-sin^{2}\alpha}}=\frac{5\cdot{0,64}\cdot{10^{-6}}}{4\sqrt{1,33^{2}-\sin^{2}30^{\circ}}}=6,49\cdot{10}^{-7}\) м \(\approx\) 0,65 мкм.
Задача 17.3
Скляний клин (показник заломлення n = 1,5) має кут при вершині \(\varphi=2^{\prime}\). На клин падає нормально монохроматичне світло з довжиною хвилі \(\lambda=600\) нм
Визначити
відстань x між сусідніми темними інтерференційними смугами, що спостерігаються у відбитих променях.
|
Дано: n = 1,5
φ = 2′
λ = 600 нм = 6·10-7 м
|
|
x - ?
|
Розв’язання
Промінь світла, який падає на клин, частково відбивається, а частково проходить у скло. Оскільки кут клина дуже малий, можна вважати, що кут заломлення практично дорівнює куту падіння, тобто \(\alpha=\beta=0\) Промінь, що зайшов у скло, відбивається від нижньої грані клина і після виходу зі скла інтерферує з променем, відбитим від верхньої грані. Умови утворення темних смуг (мінімумів інтерференції) цих променів такі ж, як у попередній задачі. Слід тільки врахувати, що в даній задачі \(\alpha=0\). Отже, згідно з виразом (6) з задачі 17.2 маємо таку умову мінімумів:
|
|
\(2dn=\lambda\), |
(1) |
де m – порядок (номер) мінімуму.
Припустимо, що в точці A (рис.3) спостерігається (m + 1)-й мінімум. Тоді, позначивши товщину клина в цій точці d1, можемо записати:
|
|
\(2d_{1}n=(m+1)\lambda\). |
(2) |
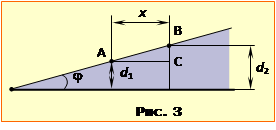
Аналогічно для точки B де спостерігається наступний інтерференційний мінімум порядку m +2 і товщина клина дорівнює d2:
|
|
\(2d_{2}n=(m+2)\lambda\). |
(3) |
Віднявши ліві та праві частини виразів (3) та (2), дістанемо:
\(2(d_{2}-d_{1})n=\lambda\) \(\Rightarrow\) \(d_{2}-d_{1}=\frac{\lambda}{2n}\).
Різниця d2 – d1 = s дуже мала. Тому з трикутника ABC, враховуючи малість кута \(\varphi\) (звичайно, вираженого в радіанах), маємо
\(\frac{S}{\varphi}=\frac{\lambda}{2n\varphi}=\frac{6\cdot{10^{-7}}}{2\cdot{1,5}\cdot{5,82}\cdot{10}^{-4}}=0,00034\) м = 0,34 мм.
Задача 17.4
При опроміненні дифракційної гратки білим світлом спектри другого та третього порядків частково перекриваються.
Визначити
довжину хвилі \(\lambda_{2}\) у спектрі другого порядку (m2 = 2), на яку накладається фіолетова (\(\lambda_{3}=400\) нм) межа спектра третього порядку (m3 = 3).
|
Дано: m2 = 2
m3 = 3
λ3 = 400 нм
|
|
λ3 - ?
|
Розв’язання
З умови задачі зрозуміло, що кути дифракції \(\varphi\) для хвиль \(\lambda_{2}\) та \(\lambda_{3}\) однакові. Тому, згідно з умовою (17.9), маємо:
\(d\sin\varphi=m_{2}\lambda_{2}\); \(d\sin\varphi=m_{3}\lambda_{3}\)
Прирівнюючи праві частини цих виразів, одержимо
\(m_{2}\lambda_{2}= m_{3}\lambda_{3}\) \(\Rightarrow\) \(\lambda_{2}=\frac{m_{3}}{m_{2}}\lambda_{3}=\frac{3}{2}\cdot{400}=600\) нм.
Задача 17.5
Монохроматичне світло нормально падає на дифракційну гратку, яка має 45 штрихів на кожний міліметр довжини. Кут між напрямками на максимуми другого (m1 = 2) та третього (m2 = 3) порядків \(\Theta=1,6^{\circ}\).
Визначити
довжину хвилі світла \(\lambda\).
|
Дано: N = 45 1/мм
m1 = 2
m2 = 3
Θ = 1,6°
|
|
λ - ?
|
Розв’язання
Відповідно до умови головних максимумів дифракційної гратки (формула (17.9)), і з урахуванням умови задачі для максимумів порядку m1 і m2 можна записати:
|
|
\(\d\sin\varphi=m_{1}\lambda\), |
(1) |
|
|
\(\d\sin(\varphi+\Theta)=m_{2}\lambda\), |
(2) |
де \(\varphi\) – кут між нормаллю до ґратки і напрямком на максимум порядку m1 (рис.1), d – період гратки, що зв'язаний з числом штрихів на одиницю довжини співвідношенням
\(d=\frac{1}{N}\).
Представимо вираз (2) у вигляді
|
|
\(\frac{m_{2}\lambda}{d}=\sin\varphi\cos\Theta+\sin\Theta\cos\varphi\). |
(3) |
Оскільки кут \(\Theta\ll{1}\) (1,6° = 0,028 рад), то можна прийняти \(\cos\Theta=1\) та \(\sin\Theta=\Theta\) (рад). Крім того
\(\cos\varphi=\sqrt{1-\sin^{2}\varphi}\).
Зробивши ці підстановки у вираз (3), одержимо
\(\frac{m_{2}\lambda}{d}=\sin\varphi+\Theta\sqrt{1-\sin^{2}\varphi}\).
Підставивши вираз \(\sin\varphi=m_{1}\lambda/d\) з формули (1) в останній вираз, після перетворень знаходимо:
\(\lambda=\frac{\Theta}{N\sqrt{(m_{2}-m_{1})^{2}+m_{1}^{2}\Theta}}=\frac{\Theta}{N\sqrt{1+\Theta^{2}}}\approx\frac{\Theta}{N}\).
Обчислення дають:
\(\lambda=\frac{0,028}{45}\approx{620}\) нм.