ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
Розділ 15. Хвилі
Приклади розв'язування задач
Розв'язування задач на хвилі проводять за схемою, викладеною у вступі (див. "Етапи розв'язування задач"), з урахуванням специфіки хвильових процесів.
1. При розгляді механічних хвиль, зокрема звукових, потрібно пам'ятати, що швидкість поширення хвилі і швидкість руху часток середовища – це зовсім різні швидкості. Перша визначається фізичними властивостями середовища, а друга – амплітудою і частотою хвилі.
2. Стандартні рівняння і формули, наведені в теоретичних відомостях, стосуються випадку, коли джерело і приймач (спостерігач) нерухомі відносно середовища, у якому поширюється хвиля. Але у випадку руху джерела або приймача (спостерігача) характеристики хвилі змінюються. Тому такі задачі вимагають особливої уваги.
Задача 15.1. Точки A, B та C лежать на лінії поширення плоскої монохроматичної хвилі. Точки B та C віддалені від точки A на відстані l1 = 15 см та l2 = 30 см відповідно. Швидкість поширення хвилі v = 0,6 м/с. Коливання в точці A відбуваються за законом \(\xi_{A}=0,05\cos(2\pi{t})\), м.
Задача 15.2. Джерело створює плоску звукову хвилю з частотою \(\nu\) = 500 Гц і амплітудою \(\xi_{m}=5\) мкм. Коливання в джерелі відбуваються за законом косинуса з нульовою початковою фазою. Для точки, що віддалена від джерела на відстань l = 170 м, і моменту часу t = 1 c. Визначити: А) зміщення частинок середовища від положення рівноваги \(\xi\); Б) швидкість їх коливального руху u; В) прискорення частинок a. Швидкість звуку прийняти v = 340 м/с.
Задача 15.3. У плоскій монохроматичній хвилі частота коливань частинок середовища \(\nu=10\) Гц. Різниця фаз коливань у двох точках, які лежать на лінії поширення хвилі на відстані \(\Delta{l}=100\) см одна від одної, дорівнює \(\Delta\varphi=\pi/4\). Визначити швидкість поширення хвилі v.
Задача 15.4. По озеру рухається катер, хвилі від якого дістаються до берега за час t = 1 хв. Відстань між гребенями хвиль l = 0,5 м, час між ударами хвиль об берег \(\tau=0,5\) с. Визначити відстань L від катера до берега.
Задача 15.5. Літак рухається горизонтально з надзвуковою швидкістю на висоті H = 4 км над землею. Спостерігач чує звук через час \(\tau= 10\) c після того, як літак пролетів над ним. Визначити швидкість літака u. Швидкість звуку взяти v = 330 м/с.
Задача 15.6. Тепловоз подає звуковий сигнал з частотою \(\nu_{0}=400\) Гц. Пасажир, який стоїть на платформі сприймає частоту сигналу \(\nu=380\) Гц. Визначити: швидкість V та напрям руху тепловоза. Швидкість звуку в повітрі прийняти v = 340 м/с.
Задача 15.7. Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n1 = 2 удари за секунду. Якщо ж катер рухається назустріч хвилям, то удари в ніс йдуть з частотою n2 = 4 удари за секунду. Визначити швидкість поширення хвиль v та швидкість руху катера V.
Задача 15.8. Вхідний коливальний контур радіоприймача з плоским повітряним конденсатором налаштований на довжину хвилі \(\lambda_{1}=200\) м. Визначити довжину хвилі \(\lambda_{2}\), на яку буде налаштований контур, якщо між обкладинками конденсатора розмістити діелектричну пластину з проникністю \(\varepsilon=6\), товщина якої в k = 3 рази менша ніж відстань між пластинами.
Задача 15.9. Частота електромагнітної хвилі \(\nu=1\) МГц. Визначити довжину електромагнітної хвилі: А) \(\lambda_{0}\) у вакуумі; Б) \(\lambda\) у немагнітному (\(\mu=1\)) діелектричному середовищі з діелектричною проникністю \(\varepsilon=2,25\).
Задача 15.10. На відстані l = 30 км від радіолокатора знаходиться літак. Визначити максимальне число імпульсів n, що може випромінювати локатор за \(\tau=1\) с для спостереження за літаком.
Задача 15.1
 Точки A, B та C лежать на лінії поширення плоскої монохроматичної хвилі. Точки B та C віддалені від точки A на відстані l1 = 15 см та l2 = 30 см відповідно. Швидкість поширення хвилі v = 0,6 м/с. Коливання в точці A відбуваються за законом \(\xi_{A}=0,05\cos(2\pi{t})\), м.
Точки A, B та C лежать на лінії поширення плоскої монохроматичної хвилі. Точки B та C віддалені від точки A на відстані l1 = 15 см та l2 = 30 см відповідно. Швидкість поширення хвилі v = 0,6 м/с. Коливання в точці A відбуваються за законом \(\xi_{A}=0,05\cos(2\pi{t})\), м.
Записати:
рівняння коливань в точках B та C.
|
Дано: \(\xi_{A}=0,05\cos(2\pi{t})\), м
l1 = 15 см = 0,15 м
l2 = 30 см = 0,3 м
|
|
\(x_{A}(t)\) - ?
\(x_{B}(t)\) - ?
|
Розв’язання
Коливання в заданій точці хвилі визначаються рівнянням (15.2) і співвідношенням (15.2a). Згідно з умовою задачі в точці A початкова фаза \(\varphi=0\), її координату приймемо xA = 0. Тоді, xB = l1, xC = l2. Оскільки хвиля поширюється зі швидкістю v, то коливання в точках B та C відстають по фазі від коливань у точці A і згідно з рівнянням (15.2) мають вигляд:
\(x_{B}=x_{m}\cos\left(2\pi{t}-\frac{2\pi{l_{1}}}{v}\right)\);
\(x_{C}=x_{m}\cos\left(2\pi{t}-\frac{2\pi{l_{2}}}{v}\right)\).
У числовому вигляді:
\(x_{B}=0.05\cdot\cos\left(2\pi{t}-\frac{2\pi\cdot{0,15}}{0,06}\right)=0,05\sin(2\pi{t})\);
\(x_{B}=0.05\cdot\cos\left(2\pi{t}-\frac{2\pi\cdot{0,3}}{0,06}\right)=-0,05\cos(2\pi{t})\).
Задача 15.2
Джерело створює плоску звукову хвилю з частотою \(\nu\) = 500 Гц і амплітудою \(\xi_{m}=5\) мкм. Коливання в джерелі відбуваються за законом косинуса з нульовою початковою фазою. Для точки, що віддалена від джерела на відстань l = 170 м, і моменту часу t = 1 c.
визначити:
А) зміщення частинок середовища від положення рівноваги \(\xi\);
Б) швидкість їх коливального руху u;
В) прискорення частинок a.
Швидкість звуку прийняти v = 340 м/с.
|
Дано: \(\nu\) = 500 Гц
\(\xi_{m}=5\) мкм = 5·10-6 м
l = 170 м
v = 340 м/с
t = 1 c
|
|
\(\xi\), u, a - ?
|
Розв’язання
A) Згідно з рівнянням (15.1) і формулою (13.2) можна записати:
|
|
\(\xi=\xi_{m}\cos\left(2\pi\nu{t}-\frac{2\pi\nu{l}}{v}\right)\) |
(1) |
Підставивши числові дані, отримаємо:
\(\xi=5\cdot{10^{-6}}\cdot\cos\left(1000\pi-\frac{1000\pi\cdot{170}}{340}\right)=5\cdot{10^{-6}}\) м = 5 мкм.
Б) Швидкість коливального руху частинок у хвилі – це похідна від зміщення по часу (формула (1.5)): \(u=\xi^{\prime}(t)\). Взявши похідну від функції (1), дістанемо
|
|
\(u=-2\pi\nu\xi_{m}\cdot\sin\left(2\pi\cdot{5}\cdot{10^{-5}}{t}-\frac{2\pi\nu{l}}{v}\right)\). |
(2) |
У числах
\(u=-1000\pi\cdot{5}\cdot{10^{-6}}\cdot\sin\left(1000\pi\cdot{1}-\frac{1000\pi\cdot{170}}{340}\right)=0\).
В) Прискорення частинок – це похідна швидкості коливального руху по часу (формула (1.7)): \(a=u^{\prime}(t)\). Взявши похідну від функції (2), знаходимо:
\(a=-(2\pi\nu)^{2}\xi\),
де, згідно з результатом пункту А), \(\xi=5\cdot{10^{-5}}\) м. Отже
\(a=-(2\pi\cdot{500})^{2}\cdot{5}\cdot{10^{-6}}=-49,3\) м/с2.
Задача 15.3
У плоскій монохроматичній хвилі частота коливань частинок середовища \(\nu=10\) Гц. Різниця фаз коливань у двох точках, які лежать на лінії поширення хвилі на відстані \(\Delta{l}=100\) см одна від одної, дорівнює \(\Delta\varphi=\pi/4\).
Визначити
швидкість поширення хвилі v.
|
Дано: \(\nu=10\) Гц
\(\Delta{l}=100\) см = 1 м
\(\Delta\varphi=\pi/4\)
|
|
v - ?
|
Розв’язання
Відповідно до формули (15.9) можна записати:
|
|
\(\Delta\varphi=\frac{2\pi}{\lambda}\Delta{l}\), |
(1) |
де \(\Delta{l}\) – задана відстань між точками, \(\lambda\) – довжина хвилі.
Швидкість поширення хвилі v виражається через довжину хвилі на основі формули (15.4a):
|
|
\(v=\lambda\nu\), |
(2) |
Виразивши величину l з співвідношення (1) і підставивши її у формулу (2), дістанемо
\(v=\frac{2\pi\nu\Delta{l}}{\Delta\varphi}=\frac{2\pi\cdot{10}\cdot{1}}{\pi/4}=80\) м/с.
Задача 15.4
По озеру рухається катер, хвилі від якого дістаються до берега за час t = 1 хв. Відстань між гребенями хвиль l = 0,5 м, час між ударами хвиль об берег \(\tau=0,5\) с.
Визначити
відстань L від катера до берега.
|
Дано: t = 1 хв = 60 c
l = 0,5 м
\(\tau=0,5\) с
|
|
L - ?
|
Розв’язання
Відстань між гребнями хвиль – то є довжина хвилі, час між ударами хвиль об берег дорівнює періоду коливань. Скориставшись зв'язком між довжиною хвилі \(\lambda\), періодом коливань T та швидкістю поширення хвилі v (формула (15.4)), знайдемо
\(v=\frac{\lambda}{T}=\frac{l}{\tau}\).
Тоді відстань, яку проходить хвиля за час t, становить
\(L=vt=\frac{l}{\tau}t=\frac{0,5}{0,5}\cdot{60}=60\) м.
тобто катер пливе на відстані 60 м від берега.
Задача 15.5
Літак рухається горизонтально з надзвуковою швидкістю на висоті H = 4 км над землею. Спостерігач чує звук через час \(\tau= 10\) c після того, як літак пролетів над ним.
Визначити
швидкість літака u. Швидкість звуку взяти v = 330 м/с.
|
Дано: H = 4 км = 4000 м
\(\tau= 10\) c
v = 330 м/с
|
|
u - ?
|
Розв’язання
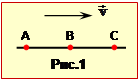
Літак у кожній точці свого перебування випромінює сферичну хвилю. Обвідна всіх цих сферичних хвильових поверхонь утворює конус, який являє собою фронт звукової хвилі, що поширюється від літака. На рис.5 показаний перетин деяких з цих сферичних поверхонь з площиною рисунка та слід обвідної O2C. З рис.5 можна збагнути, що спостерігач (точка C) чує звук, який був випромінений літаком у точці O1. В той момент, коли хвиля дійшла до спостерігача, літак вже знаходиться у точці O2.
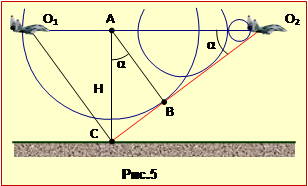 Врахуємо, що обвідна сферичних хвиль O2C перпендикулярна до радіусів сфер. Отже на рис.5 трикутники \(\Delta{O}_{1}O_{2}C\), \(\Delta{A}O_{2}B\) та \(\Delta{A}CB\) прямокутні та подібні. За умовою задачі літак долає відстань AO2 за час \(\tau\), тому
Врахуємо, що обвідна сферичних хвиль O2C перпендикулярна до радіусів сфер. Отже на рис.5 трикутники \(\Delta{O}_{1}O_{2}C\), \(\Delta{A}O_{2}B\) та \(\Delta{A}CB\) прямокутні та подібні. За умовою задачі літак долає відстань AO2 за час \(\tau\), тому
\(AO_{2}=u\tau\).
За цей же час звукова хвиля, що була випромінена літаком у точці A, доходить до точки B, отже
\(AB=v\tau\).
З трикутника AO2B маємо:
\(\sin\alpha=\frac{AB}{AO_{2}}=\frac{v}{U}\).
З трикутника ABC:
\(H=\frac{AB}{\cos\alpha}=\frac{v\tau}{\sqrt{1-\sin^{2}\alpha}}=\frac{v\tau}{\sqrt{1-(v/u)^{2}}}\).
Після нескладних перетворень з останнього виразу знаходимо
\(u=\frac{v}{\sqrt{1-(v\tau/H)^{2}}}=\frac{330}{\sqrt{1-(330\cdot{10}/4000)^{2}}}=584\) м/с \(\approx{2100}\) км/год.
Задача 15.6
Тепловоз подає звуковий сигнал з частотою \(\nu_{0}=400\) Гц. Пасажир, який стоїть на платформі сприймає частоту сигналу \(\nu=380\) Гц.
Визначити:
швидкість V та напрям руху тепловоза. Швидкість звуку в повітрі прийняти v = 340 м/с.
|
Дано: \(\nu_{0}=400\) Гц
\(\nu=380\) Гц
v = 340 м/с
|
|
V - ?
|
Розв’язання
Приступаючи до розв'язання цієї і подібних задач, слід чітко усвідомити таке. В загальній теорії рівняння хвилі ((15.1), (15.5), (15.7)), а також її параметри (період T, частоти \(\nu\) та \(\omega\), швидкість v, довжина хвилі \(\lambda\)) визначені для випадку, коли джерело і спостерігач нерухомі відносно середовища, в якому поширюється хвиля. В такому разі частота (або період) хвилі дорівнює частоті коливань в джерелі. При цьому швидкість поширення хвилі (швидкість поширення коливань відносно середовища, яку можна знайти у довідкових таблицях) залежить тільки від властивостей середовища.
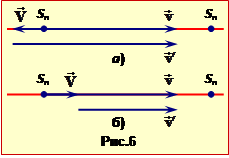 Але якщо джерело або спостерігач (чи обоє) рухаються відносно середовища, характеристики хвилі змінюються. Цим і пояснюється те, що для пасажира на платформі (точка Sп на рис.6) частота звуку \(\nu\) відрізняється від частоти джерела \(\nu_{0}\), розміщеного на рухомому тепловозі.
Але якщо джерело або спостерігач (чи обоє) рухаються відносно середовища, характеристики хвилі змінюються. Цим і пояснюється те, що для пасажира на платформі (точка Sп на рис.6) частота звуку \(\nu\) відрізняється від частоти джерела \(\nu_{0}\), розміщеного на рухомому тепловозі.
Згідно з формулою (15.4a) пасажир (спостерігач) зафіксує частоту сигналу
|
|
\(\nu=\frac{v}{\lambda}\), |
(1) |
де \(\lambda\) – довжина звукової хвилі, створюваної рухомим тепловозом. Довжина хвилі – це відстань між сусідніми "гребенями" хвилі (для звукової хвилі такими "гребенями" є точки з максимальним значеннями тиску або концентрації молекул (густини) повітря). Джерело на тепловозі посилає ці гребені з інтервалом часу T0, отже
|
|
\(\lambda=v^{\prime}T_{0}=\frac{v^{\prime}}{\nu_{0}}\), |
(2) |
де \(v^{\prime}\) – швидкість хвилі відносно тепловоза у напрямку до пасажира.
Швидкість \(\vec{v}^{\prime}\) виражається через швидкість звуку \(\vec{v}\) та швидкість тепловоза \(\vec{V}\) класичною формулою додавання швидкостей (1.10):
|
|
\(\vec{v}^{\prime}=\vec{v}-\vec{V}\) \(\Rightarrow\) \(v^{\prime}=v\pm{V}\), |
(3) |
де знак "+" відноситься до випадку, коли тепловоз віддаляється від пасажира (рис.6а), а знак "-" – коли наближається (рис.6б).
Підставивши вираз (3) у формулу (2), отримаємо
\(\lambda=\frac{v\pm{V}}{\nu_{0}}\).
Таким чином, у відповідності з формулою (1)
\(\nu=\frac{v\nu_{0}}{v\pm{V}}=\frac{\nu_{0}}{1\pm{V/v}}\).
Згідно з умовою \nu\lt\nu_{0}\), отже
|
|
\(\nu=\frac{\nu_{0}}{1+(V/v)}\), |
(4) |
тобто тепловоз віддаляється від пасажира.
З формули (4) після елементарних викладок отримаємо:
\(V=\left(\frac{\nu_{0}}{\nu}-1\right)v\).
У числах
\(V=\left(\frac{400}{380}-1\right)\cdot(340)=17,9\) м/с = 64,4 км/год.
Примітка. Аналогічно до наведених міркувань і викладок можна отримати формули частоти звуку для випадку, коли рухаються як джерело, так і спостерігач. Вперше такі співвідношення були отримані Доплером. Тому зміна частоти, що сприймається при русі джерела і приймача, називається ефектом Доплера. Його прояв ви можете подивитися і почути.
Задача 15.7
Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n1 = 2 удари за секунду. Якщо ж катер рухається назустріч хвилям, то удари в ніс йдуть з частотою n2 = 4 удари за секунду.
Визначити
швидкість поширення хвиль v та швидкість руху катера V.
|
Дано: l = 5 м
\(n_{1}=2\)
\(n_{2}=4\)
|
|
v, V - ?
|
Розв’язання
Відстань між гребенями l – це довжина хвилі, а кількість ударів об корпус дорівнює частоті коливань для рухомого спостерігача, що знаходиться на катері. Отже згідно з формулою (15.4a) можна записати:
|
|
n1l = v1, |
(1) |
|
|
N2l = v2, |
(2) |
де v1, v2 – швидкості поширення хвиль відносно катера у випадках руху вздовж та проти напрямку поширення хвиль. Згідно з законом додавання швидкостей (1.9)
v1 = V – v;
v2 = V + v,
де V, v – швидкості руху катера та поширення хвиль відносно води.
Підставивши сюди вирази (1), (2) для швидкостей і розв'язавши отриману систему, дістанемо відповіді:
\(\left.\begin{align} {}n_{1}l=V-v \\ {}n_{2}l=V+v \\ \end{align}\right\}\) \(\Rightarrow\) \( \begin{align} {}V=l\frac{n_{1}+n_{2}}{2}=5\frac{2+4}{2}=15\ {м/с}; \\ {}v=l\frac{n_{2}-n_{1}}{2}=5\frac{4-2}{2}=5\ {м/с}. \\ \end{align}\)
Задача 15.8
Вхідний коливальний контур радіоприймача з плоским повітряним конденсатором налаштований на довжину хвилі \(\lambda_{1}=200\) м.
Визначити
довжину хвилі \(\lambda_{2}\), на яку буде налаштований контур, якщо між обкладинками конденсатора розмістити діелектричну пластину з проникністю \(\varepsilon=6\), товщина якої в k = 3 рази менша ніж відстань між пластинами.
|
Дано: \(\lambda_{1}=200\) м
\(\varepsilon=6\)
k = 3
|
|
\(\lambda_{2}\) - ?
|
Розв’язання
Резонанс у контурі настає за умови, що період його власних коливань (формула (14.6)) співпадає з періодом коливань в електромагнітній хвилі. В свою чергу довжина хвилі пов'язана з періодом формулою (15.4). Тому для резонансної довжини хвилі маємо
|
|
\(\lambda=vT=v2\pi\sqrt{LC}\), |
(1) |
де v – швидкість поширення хвилі (Для позначення швидкості електромагнітної хвилі використана літера v замість загальноприйнятої літери c, щоб не сплутати її з ємністю конденстора).
Якщо позначити ємність конденсатора без діелектрика C1, з діелектриком – C2, то
\(\lambda_{1}=2\pi{v}\sqrt{LC_{1}}\),
\(\lambda_{2}=2\pi{v}\sqrt{LC_{2}}\),
звідки
\(\lambda_{2}=\lambda_{1}\sqrt{\frac{C_{2}}{C_{1}}}\).
Ємність конденсатора з двома шарами діелектрика, які мають товщину d1 та d2 і діелектричні проникненості \(\varepsilon_{1}\) та \(\varepsilon_{2}\), була визначена в задачі 10.17. З урахуванням того, що в даній задачі \(\varepsilon_{1}=1\) (повітря) та \(\varepsilon_{2}=\varepsilon\) ємність C2, визначається формулою
\(C_{2}=C_{1}\frac{\varepsilon{k}}{\varepsilon(k-1)+1}\).
Підставивши цей вираз у формулу (1), знайдемо
\(\lambda_{2}=\lambda_{1}\sqrt{\frac{\varepsilon{k}}{\varepsilon(k-1)+1}}=200\cdot\frac{6\cdot{3}}{6\cdot(3-1)+1}=235,3\) м.
Задача 15.9
Частота електромагнітної хвилі \(\nu=1\) МГц.
Визначити
довжину електромагнітної хвилі:
А) \(\lambda_{0}\) у вакуумі;
Б) \(\lambda\) у немагнітному (\(\mu=1\)) діелектричному середовищі з діелектричною проникністю \(\varepsilon=2,25\).
|
Дано: \(\nu=1\) МГц = 106 Гц
\(\varepsilon=2,25\)
\(\mu=1\)
|
|
\(\lambda_{0}\) - ?
\(\lambda\) - ?
|
Розв’язання
Відповідно до формули (15.4a) довжина електромагнітної хвилі
\(\lambda=\frac{v}{\nu}\),
де \(\nu\) – частота, а v – швидкість поширення хвилі.
Швидкість поширення електромагнітних хвиль визначається загальною формулою (15.10), а з урахуванням умови \(\mu=1\) – формулою (15.10а):
\(v=\frac{c}{\sqrt{\varepsilon}}\),
де \(c=3\cdot{10^{8}}\) м/с – швидкість поширення електромагнітних хвиль у вакуумі (швидкість світла). Підставляючи вираз швидкості v з формули довжини хвилі, одержимо:
\(\lambda=\frac{c}{\nu\sqrt{\varepsilon}}\).
Для вакууму формально \(\varepsilon=1\), тому
\(\lambda_{0}=\frac{3\cdot{10^{8}}}{10^{6}}=300\) м.
Для діелектричного середовища
\(\lambda=\frac{3\cdot{10^{8}}}{10^{6}\cdot\sqrt{2,25}}\)=200 м.
Задача 15.10
На відстані l = 30 км від радіолокатора знаходиться літак.
Визначити
максимальне число імпульсів n, що може випромінювати локатор за \(\tau=1\) с для спостереження за літаком.
|
Дано: l = 30 км = 3·104 м
\(\tau=1\) с
|
|
n - ?
|
Розв’язання
Кожен імпульс радіохвиль, випромінюваний антеною локатора, досягає літака і, відбивши від нього, повертається до локатора. Кожен наступний імпульс може бути випроменений антеною тільки після повернення попереднього, інакше антена може вийти з ладу. Таким чином, мінімальний час між послідовним випромінюванням двох імпульсів повинний бути не меншим, ніж час проходження електромагнітних хвиль від антени до літака і назад. З огляду на те, що швидкість поширення електромагнітних хвиль \(c=3\cdot{10^{8}}\) м/с, визначаємо час проходження імпульсу радіохвиль
\(\tau=\frac{2l}{c}\).
При цьому період випромінювання
\(T\ge\tau\) \(\Rightarrow\) \(T\ge\frac{2l}{c}\).
Кількість імпульсів, випромінюваних за одиницю часу, – це частота, що зв'язана з періодом співвідношенням n = 1/T, тоді
\(n\le\frac{c}{2l}\).
Максимальному числу імпульсів відповідає знак рівності, отже
\(n=\frac{c}{2l}=\frac{3\cdot{10^{8}}}{2\cdot{3}\cdot{10^{4}}}=5000\).