ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 03:59 |
Оглавление
- Розділ 13. Механічні коливання
- Теоретичні відомості. Рівняння і характеристики гармонічних коливань
- Теоретичні відомості. Швидкість, прискорення і сила при гармонічних коливаннях
- Теоретичні відомості. Найпростіші коливальні системи
- Теоретичні відомості. Енергія гармонічних коливань
- Теоретичні відомості. Диференціальне рівняння вільних гармонічних коливань
- Приклади розв’язування задач
- Розділ 14. Електромагнітні коливання. Змінний струм
- Приклади розв'язування задач
- Розділ 15. Хвилі
Розділ 13. Механічні коливання
|
Коливаннями називають фізичні процеси, характеристики котрих точно, або наближено багаторазово відтворюються з часом. Найбільш простими й важливими є гармонічні коливання, за допомогою яких можна описати й будь-які складні коливальні процеси. Гармонічними коливаннями називаються процеси, в яких фізичні величини змінюються за законом синуса або косинуса. Загальні властивості гармонічних коливань зручн0 вивчати на прикладі механічних гармонічних коливань, при яких за законом синуса або косинуса змінюються координата, швидкість і прискорення тіла. Далі розглянуто наступні розділи. Теоретичні відомості:
Приклади розв’язування задач |
Теоретичні відомості. Рівняння і характеристики гармонічних коливань
|
Гармонічний коливальний рух описується рівнянням гармонічних коливань, яке визначає значення відповідної величини (зміщення, швидкість, прискорення) через основні характеристики гармонічних коливань у кожний момент часу. Основними характеристиками гармонічних коливань є амплітуда, період або частота (лінійна і циклічна). Крім цих величин миттєве положення точки визначається фазою. |
Рівняння гармонічних коливань визначає залежність зміщення x точки з положення рівноваги від часу t і має вигляд:
|
|
\(x=x_{m}\cos\left(\frac{2\pi}{T}+\varphi_{0}\right)\), |
(13.1) |
де xm, T, \(\varphi_{0}\) – постійні величини, \(\pi=\) 3,14… рад.
Рівняння (13.1) можна записати і так:
|
|
\(x=x_{m}\sin\left(\frac{2\pi}{T}+\varphi_{0}^{\prime}\right)\), |
(13.1а) |
де \(\varphi_{0}^{\prime}=\varphi_{0}+\pi/2\).
Графік x(t) показаний на рис.13.1.
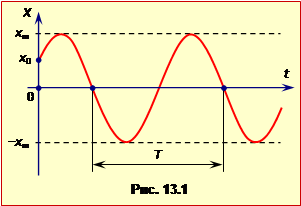
Амплітудою xm коливань (її також часто позначають А) називається максимальне зміщення точки з положення рівноваги. Амплітуда визначає "розмах" коливань: усі можливі значення координати коливної точки належать інтервалу \(\left[-x_{m},\ x_{m}\right]\), (рис.13.1).
Період T – це проміжок часу, протягом якого відбувається одне повне коливання, (рис.13.1). Через час t = T стан коливаної системи повністю повторюється. Періодичність коливань характеризують також лінійною і циклічною (коловою) частотами.
Линійна частота \(\nu\) дорівнює кількості коливань, що відбуваються протягом часу 1 с:
|
|
\(\nu=\frac{1}{T}\), |
(13.2) |
Лінійна частота вимірюється у герцах (Гц). 1 Гц = 1 с-1 – частота, при якій за 1 с відбувається одне коливання. На практиці широко застосовуються високі частоти, які виражають у кілогецах (1 кГц = 103 Гц), мегагерца (1 МГц = 106 Гц) та інші.
Циклічна (колова) частота \(\omega\) пов'язана з періодом і лінійною частотою співвідношеннями:
|
|
\(\omega=\frac{2\pi}{T}=2\pi\nu\). |
(13.3) |
Циклічна частота вимірюється у "радіанах за секунду" (рад/с, але часто пишуть 1/с).
Використовуючи співвідношення (13.3), рівняння гармонічних коливань (13.1) можна записати через частоти:
|
|
\(x=x_{m}\cos(\omega{t}+\varphi_{0})\), |
(13.4) |
або
|
|
\(x=x_{m}\cos(2\pi\nu{t}+\varphi_{0})\) |
(13.4а) |
Фазою \(\varphi\) називається значення аргументу тригонометричної функції в рівнянні коливань (13.1), (13.4), (13.4a):
\(\varphi=\frac{2\pi}{T}t+\varphi_{0}=\omega{t}+\varphi_{0}=2\pi\nu{t}+\varphi_{0}\).
У момент часу t = 0 \(\varphi=\varphi_{0}\), тому величина \(\varphi_{0}\) називається початковою фазою коливань. Початкова фаза \(\varphi_{0}\) визначається вибором моменту початку відліку часу і може мати будь-які значення в інтервалі від 0 до \(2\pi\) рад.
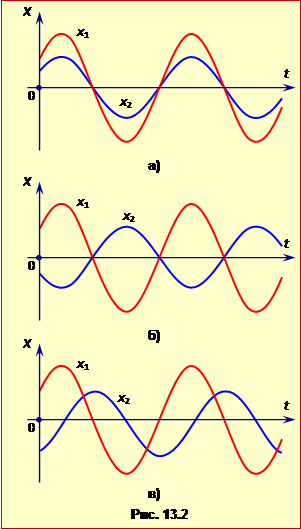
Фаза визначає стан тіла, що коливається, у даний момент часу, а також дозволяє порівнювати різні коливання однакової частоти. В останньому випадку розглядають різницю фаз \(\delta=\varphi_{01}-\varphi_{02}\). Якщо різниця фаз \(\delta=0\) (рис.13.2а), то говорять, що коливання відбуваються "у фазі", інакше – синфазно, а якщо \(\delta=\pi\) (рис.13.2б) – "у протилежних фазах" або "в протифазі". В інших випадках говорять, що коливання відбуваються з "зсувом фаз" \(\delta\) (на рис.13.2в зсув фаз \(\delta=\frac{\pi}{2}\)).
Теоретичні відомості. Швидкість, прискорення і сила при гармонічних коливаннях
|
При гармонічних коливаннях періодично змінюється не тільки координата точки, але й швидкість і прискорення. Миттєві значення цих величин визначаються рівнянням швидкості та рівнянням прискорення. Для того щоб коливання були гармонічними, прикладена до тіла рівнодійна сила повинна задовольняти жорстким умовам. |
Рівняння швидкості точки при гармонічних коливаннях одержують, знаходячи першу похідну координати по часу, наприклад (13.4), і воно має вигляд
|
|
\(v_{x}=x^{\prime}(t)=-\omega{x}_{m}\sin(\omega{t}+\varphi_{0})\), |
(13.5) |
або
|
|
\(v_{x}=v_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\), |
(13.5a) |
де vm – амплітуда швидкості, що зв'язана з амплітудою відхилення точки співвідношенням
|
|
\(v_{m}=\omega{x}_{m}\). |
(13.5б) |
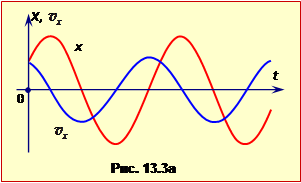
Порівняння рівнянь (13.4) і (13.5) свідчить, що коливання швидкості випереджають коливання координати точки на \(\pi/2\) або на ¼ періода (рис.13.3а).
Рівняння прискорення при гармонічних коливаннях одержуємо, знаходячи похідну за часом від рівняння (13.5):
|
|
\(a_{x}=v_{x}^{\prime}=-\omega^{2}x_{m}\cos(\omega{t}+\varphi_{0})\), |
(13.5) |
або
|
|
\(a_{x}==a_{m}\cos(\omega{t}+\varphi_{0})=a_{m}\cos(\omega{t}+\varphi_{0}+\pi)\), |
(13.6) |
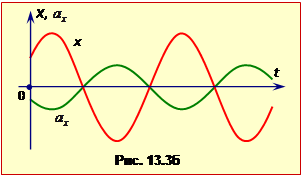
З рівняння (13.6а) випливає, що коливання прискорення відбуваються з різницею фаз \(\pi\), тобто в протифазі відносно коливань координати (рис.13.3б).
Амплітуда прискорення am пов'язана з амплітудою швидкості vm і з амплітудою відхилення xm співвідношеннями:
|
|
\(a_{m}=\omega^{2}x_{m}\), |
(13.7) |
||
|
|
\(a_{m}=\omega{v}_{m}\). |
(13.8) |
||
Примітка. Тригонометрична функція в рівняннях швидкості і прискорення визначена неоднозначно і залежить від вигляду цієї функції в рівнянні зміщення. Наприклад при використанні рівняння (13.1a) у рівнянні (13.5) буде присутня функція \(\cos\), а в рівняннях(13.6) та (13.6а) – функція \(\sin\).
З рівнянь (13.6) та (13.4), видно, що
|
|
\(a_{x}=-\omega^{2}{x}\). |
(13.9) |
Це означає, що
|
при гармонічних коливаннях прискорення точки в будь-який момент часу прямо пропорційне зміщенню і напрямлене до положення рівноваги. |
Відповідно до другого закону Ньютона (F = ma) та рівняння (13.9), прикладена до кожної точки рівнодійна сила у будь-який момент часу визначається формулою
|
|
\(F_{x}=-kx\), |
(13.10) |
де
|
|
\(k=m\omega^{2}\). |
(13.11) |
Ці формули виражають критерій гармонічності механічних коливань:
|
якщо рівнодійна сил, прикладених до матеріальної точки, прямо пропорційна зміщенню і спрямована до положення рівноваги, то рух точки є гармонічними коливаннями. |
При цьому частота і період коливань визначаються загальними формулами
|
|
\(\omega=\sqrt{\frac{k}{m}}\). |
(13.12) |
||
|
|
\(\nu=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\). |
(13.12а) |
||
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(13.13) |
||
де m – маса матеріальної точки, що коливається, k – коефіцієнт пропорційності між рівнодійною силою і відхиленням точки від положення рівноваги.
Теоретичні відомості. Найпростіші коливальні системи
|
Найпростішими коливальними системами, в яких можливі вільні гармонічні коливання, є пружинний і математичний маятники. |
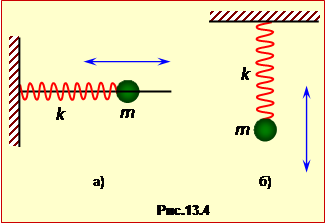 Пружинний маятник являє собою тіло маси m, з'єднане з невагомою пружиною, що має жорсткість k, інший кінець якої закріплений (рис.13.4). За відсутності сил тертя і опору повітря, тобто за умов, коли цими силами можна знехтувати, рух тіла визначається тільки силою пружності
Пружинний маятник являє собою тіло маси m, з'єднане з невагомою пружиною, що має жорсткість k, інший кінець якої закріплений (рис.13.4). За відсутності сил тертя і опору повітря, тобто за умов, коли цими силами можна знехтувати, рух тіла визначається тільки силою пружності
\(F=-kx\),
де x – величина деформації, зумовленої відхиленням тіла від положення рівноваги. Якщо тіло висить на пружині (рис. 13.4б), величина x на включає статичної деформації пружини, створеної вагою вантажу.
Сила пружності задовольняє умові (13.10), тому за відсутності сил тертя і опору пружинний маятник (вантаж на пружині), виведений з положення рівноваги і наданий сам собі, здійснює гармонічні коливання з циклічною частотою
|
|
\(\omega=\sqrt{\frac{k}{m}}\) |
(13.14) |
і періодом
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(13.15) |
де m – маса маятника, k – жорсткість пружини. Це в однаковій мірі стосується і горизонтальних (рис.13.4а), і вертикальних (рис.13.4б) коливань. Відмінність цих коливань тільки в тому, що в першому випадку в положенні рівноваги пружина недеформована, а в другому – вона розтягнута внаслідок притягання вантажу до Землі.
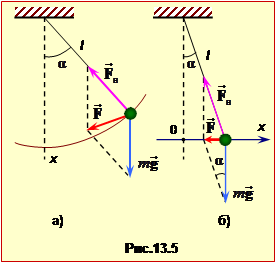
Математичним маятником називається матеріальна точка маси m, підвішена на невагомій нерозтяжній нитці довжиною l (рис.13.5).
За відсутності сил тертя в підвісі і опору середовища рух маятника відбувається тільки під дією сил тяжіння \(m\vec{g}\) і натягу нитки \(\vec{F}_{н}\) (рис.13.5).
Рівнодійна
\(\vec{F}=m\vec{g}+\vec{F}_{н}\)
у загальному випадку складно залежить від кута відхилення нитки \(\alpha\) і зміщення x маятника з положення рівноваги. Тому довільні коливання математичного маятника (рис.13.5а) не є гармонічними. Однак при невеликих амплітудах (\(\alpha\ll{1}\)) \(\mathrm{tg}\alpha=\sin\alpha=\alpha\). Тому можна вважати, що маятник рухається уздовж осі OX під дією рівнодійної сили
\(F_{x}=-mg\cdot\mathrm{tg}\alpha=-mg\alpha\).
З тієї ж причини можна прийняти \alpha=x/l\) (див. рис.13.5б). У результаті одержуємо
\(F_{x}=-kx\),
де x – зміщення маятника з положення рівноваги,
|
|
\(k=\frac{mg}{l}\), |
(13.16) |
Отже, у відповідності до умови (13.10)
|
малі вільні коливання математичного маятника є гармонічними. |
Зіставивши вираз (13.16) з формулами (13.12) та (13.13), знаходимо, що циклічна частота \(\omega\) і період T гармонічних коливань математичного маятника визначається формулами
|
|
\(\omega=\sqrt{\frac{g}{l}}\), |
(13.17) |
і
|
|
\(T=2\pi\sqrt{\frac{l}{g}}\), |
(13.18) |
Теоретичні відомості. Енергія гармонічних коливань
|
Тіло, яке здійснює коливання, має відповідний запас механічної енергії. У процесі гармонічних коливань відбуваються тільки взаємні перетворення потенціальної і кинетичної енергії тіла, що коливається. Повна енергія гармонічних коливань не змінюється з часом. |
У випадку пружинного маятника потенціальна енергія гармонічних коливань – це енергія пружини, зумовлена відхиленням вантажу від положення рівноваги:
|
|
\(W_{п}=\frac{kx^{2}}{2}\). |
(13.19) |
Потенціальна енергія статичної деформації пружини під дією ваги вантажу і потенціальна енергія вантажу в полі сил тяжіння до енергії коливань не входять.
Відповідно до рівняння (13.1)
|
|
\(W_{п}=\frac{kx_{m}^{2}}{2}\cos^{2}(\omega{t}+\varphi_{0})\), |
(13.19a) |
де k – жорсткість пружини, xm – амплітуда коливань.
Рівняння (13.19) визначає потенціальну енергію також й інших механічних гармонічних коливань. У таких випадках k – це коефіцієнт пропорційності між рівнодійною і зміщенням (формула (13.10)). Зокрема, для математичного маятника значення k визначається виразом (13.16).
Кінетична енергія гармонічних коливань
|
|
\(W_{к}=\frac{mv^{2}}{2}\) |
(13.20) |
у відповідності до рівняння (13.5) виражається як
|
|
\(W_{к}=\frac{mv_{m}^{2}}{2}\sin^{2}(\omega{t}+\varphi_{0})\), |
(13.20a) |
де m – маса, vm – амплітуда швидкості тіла.
За допомогою співвідношень (13.5б) і (13.11) максимальну потенціальну енергію у рівнянні (13.19) і максимальну кінетичну енергію у рівнянні (13.20) можна виразити через масу тіла m, частоту \(\omega\) і амплітуду зміщення xm. В такому разі виходить, що
|
|
\(\frac{mv_{m}^{2}}{2}=\frac{kx_{m}^{2}}{2}=\frac{m\omega^{2}x_{m}^{2}}{2}=W_{0}\). |
(13.21) |
З урахуванням цього повна енергія гармонічних коливань у будь-який момент часу
\(W=W_{к}+W_{п}=W_{0}\left(\cos^{2}(\omega{t}+\varphi_{0})+\sin^{2}(\omega{t}+\varphi_{0})\right)=W_{0}\),
Тобто
\(W=W_{0}\).
Отже,
|
повна енергія гармонічних коливань зберігається: |
|||
|
|
\(W_{п}+W_{к}=\) const. |
(13.21a) |
|
Цей результат має просте пояснення: гармонічні коливання можливі тільки тоді, коли відсутні сили тертя й опору, тобто не відбувається перетворення механічної енергії в інші форми.
Теоретичні відомості. Диференціальне рівняння вільних гармонічних коливань
Якщо в рівнянні (13.9) величину ax представити у вигляді другої похідної (див. ч.1. Механіка, формула (1.7, 1.7a)) координати по часу, то одержимо диференціальне рівняння гармонічних коливань:
|
|
\(x^{\prime\prime}=-\omega^{2}x\). |
(13.22) |
(Диференціальним називається рівняння, до складу якого входить не тільки невідома функція, але й її похідні).
У математиці доводиться, що єдиними функціями, які є розв'язником рівняння (13.22) є функції sin або cos. При цьому зміст, тобто фізична природа величини x не має значення. Наприклад, для математичного маятника роль x відіграє кут відхилення нитки від вертикалі, а при розгляді електромагнітних коливань у коливальному контурі – це заряд конденсатора, або сила струму в котушці.
Рівняння (13.22) виражає загальну ознаку гармонічних коливань:
|
якщо друга похідна по часу деякої фізичної величини прямо пропорційна самій величині і має протилежний знак, то ця величина здійснює гармонічні коливання, частота яких визначається з співвідношення (13.22). |
Приклади розв’язування задач
При розв'язуванні задач на коливальний рух необхідно дотримуватися порад, викладених у рекомендаціях до розділу, з огляду на поради з організації роботи і оформленню розв'язку задач (див. "Етапи розв'язування задач").
Приклади розв'язування розділені по темах:
Рівняння і характеристики гармонічних коливань
Динаміка гармонічних коливань
Енергія гармонічних коливань
Рівняння і характеристики гармонічних коливань
У задачах, де потрібно складати рівняння гармонічних коливань за заданими характеристиками і початковими умовами, іноді виникають проблеми з визначенням початкової фази. Необхідно пам'ятати, що для визначення початкової фази потрібно використовувати обидві початкові умови (x(0), v(0)), оскільки при використанні тільки однієї з них початкова фаза визначається неоднозначно.
Для визначення характеристик гармонічних коливань за заданим рівнянням необхідно виконати наступне.
|
1) |
Записати загальний вигляд рівняння коливань через ту функцію, що використана в умові задачі. |
|
|
|
|
2) |
Порівнюючи задане числове рівняння із загальним, визначити значення необхідних характеристик (амплітуда, період і ін.). При цьому треба взяти до уваги, що коли в заданому рівнянні не зазначені одиниці фізичних величин, то вони задані в основних одиницях СІ. |
|
|
|
|
3) |
Якщо потрібно визначити якісь характеристики, що не входять у задане рівняння (наприклад, швидкість за заданим рівнянням координати), то спочатку треба із заданого рівняння одержати рівняння коливань необхідної величини, а потім діяти аналогічно п.2). |
Задача 13.1. Точка здійснює гармонічні коливання з періодом T = 1,57 c і амплітудою A = 12 см. Визначити рівняння руху точки x(t), якщо в початковий момент часу її координата x0 = 6 см і вона віддаляється від положення рівноваги.
Задача 13.2. Точка здійснює гармонічні коливання. На відстані x1 = 3 см від положення рівноваги її швидкість v1 = 10 см/с, а на відстані x2 = 5 см – швидкість v2 = 6 см/с. Визначити циклічну частоту \(\omega\) й амплітуду A коливань.
Задача 13.3. Тіло здійснює гармонічні коливання між точками C і D. Його максимальна швидкість \(v_{m}\) = 10 м/с. Визначити середню швидкість \(\langle{v}\rangle\) на шляху від C до D.
Задача 13.1
Точка здійснює гармонічні коливання з періодом T = 1,57 c і амплітудою A = 12 см.
Визначити
рівняння руху точки x(t), якщо в початковий момент часу її координата x0 = 6 см і вона віддаляється від положення рівноваги.
|
Дано: T = 1,57 c
A = 12 см
\(x_{0}\) = 6 см
|
|
x(t) - ?
|
Розв’язання
Оскільки в початковий момент часу ні координата, ні швидкість точки не дорівнюють нулю, то немає значення, яку функцію вибрати для опису коливань. Будемо вважати, що рівняння x(t) має вигляд
|
|
\(x(t)=A\cos\left(\frac{2\pi}{T}t+\varphi_{0}\right)\). |
(1) |
Значення A і T задані, отже, задача зводиться до визначення початкової фази \(\varphi_{0}\). Підставивши в рівняння (1) значення t = 0, x0 і A, одержимо
\(6=12\cos\varphi_{0}\) \(\Rightarrow\) \(\cos\varphi_{0}=\frac{1}{2}\) \(\Rightarrow\) \(\varphi_{0}=\pm\frac{\pi}{3}\).
Для вибору знаку \(\varphi_{0}\) врахуємо, що за умовою у початковий момент часу напрям швидкості точки співпадає з напрямом осі OX, тобто \(v_{0x}>0\). Проекція швидкості \(v_{0x}=x^{\prime}(t)\), тому з рівняння (1):
\(v_{x}=x^{\prime}(t)=-A\frac{2\pi}{T}\cos\left(\frac{2\pi}{T}\cdot{t}+\varphi_{0}\right)\).
При t = 0
\(v_{0x}=-A\frac{2\pi}{T}\sin\varphi_{0}\).
Оскільки \(v_{0x}>0\), то
\(\sin\varphi_{0}<0\) \(\Rightarrow\) \(\varphi_{0}<0\).
Отже, початкова фаза \(\varphi_{0}=-\pi/3\).
Підставивши в рівняння (1) всі числові значення, отримаємо відповідь:
\(x(t)=12\cos\left(4t-\pi/3\right)\), см.
Зауваження. Зверніть увагу на те, що при складанні рівняння коливань у відповіді всі величини, окрім часу, повинні бути представлені в числовому вигляді.
Задача 13.2
Точка здійснює гармонічні коливання. На відстані x1 = 3 см від положення рівноваги її швидкість v1 = 10 см/с, а на відстані x2 = 5 см – швидкість v2 = 6 см/с.
Визначити
циклічну частоту \(\omega\) й амплітуду A коливань.
|
Дано: \(x_{1}\) = 3 см
\(v_{1}\) = 10 см/с
\(x_{2}\) = 5 см
\(v_{2}\) = 6 см/с
|
|
A - ?
\(\omega\) - ?
|
Розв’язання
Припустимо, що рівняння руху точки має вигляд
|
|
\(x=A\sin(\omega{t}+\varphi_{0})\), |
(1) |
де \(\varphi_{0}\) – початкова фаза, t – час. Тоді її швидкість
|
|
\(v_{x}=x^{\prime}(t)=A\omega\cos(\omega{t}+\varphi_{0})\). |
(2) |
Виключимо з рівнянь (1) і (2) час t, скориставшися основною тригонометричною тотожністю \(\sin^{2}\alpha+\cos^{2}\alpha=1\):
|
|
\(\left. \begin{align} \sin(\omega{t}+\varphi_{0})=\frac{x}{A} \\ \cos(\omega{t}+\varphi_{0})=\frac{x}{A\omega} \\ \end{align} \right\} \) \(\Rightarrow\) \(\frac{x^{2}}{A^{2}}+\frac{v^{2}}{A^{2}\omega^{2}}=1\). |
(3) |
(Такий прийом дуже часто використовують в задачах на гармонічні коливання, коли немає необхідності у визначенні моменту часу, або він не заданий в умові задачі).
Записавши вираз (3) для двох випадків (x1, v1, x2, v2), отримаємо систему рівнянь:
\( \left\{ \begin{align} {}x_{1}^{2}+\frac{v_{1}^{2}}{\omega^{2}}=A^{2}; \\ {}x_{2}^{2}+\frac{v_{2}^{2}}{\omega^{2}}=A^{2}. \\ \end{align} \right. \)
Розв’язування цієї системи дає:
\(\omega=\sqrt{\frac{v_{1}^{2}-v_{2}^{2}}{x_{2}^{2}-x_{1}^{2}}}=\sqrt{\frac{100-36}{25-9}}\) = 2 c-1;
\(A=\sqrt{\frac{v_{1}^{2}x_{2}^{2}}{v_{1}^{2}-v_{2}^{2}}}=\sqrt{\frac{100\cdot{25}-36\cdot{9}}{100-36}}=\) 5,83 см.
Задача 13.3
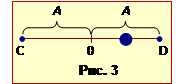 Тіло здійснює гармонічні коливання між точками C і D. Його максимальна швидкість \(v_{m}\) = 10 м/с.
Тіло здійснює гармонічні коливання між точками C і D. Його максимальна швидкість \(v_{m}\) = 10 м/с.
Визначити
середню швидкість \(\langle{v}\rangle\) на шляху від C до D.
|
Дано: \(v_{m}\) = 10 м/с
|
|
\(\langle{v}\rangle\) - ?
|
Розв’язання
Середня шляхова швидкість - це відношення пройденого шляху до часу (див. розділ 1. Кінематика, формула (1.4)):
\(\langle{v}\rangle=\frac{S}{t}\).
Точки C і D максимально віддалені від положення рівноваги (точка O на рис.3), тобто знаходяться на відстані амплітуди від неї, тому шлях точки дорівнює подвоєній амплітуді коливань S = 2A. Якщо припустити, що рух починається в точці C, то за час одного періоду тіло доходить до точки D і повертається в точку C, тому час руху від точки С до точки D дорівнює половині періоду коливань t = T/2, отже:
|
|
\(\langle{v}\rangle=\frac{4A}{T}\). |
(1) |
Максимальна швидкість тіла визначається формулою (13.5б):
\(v_{m}=A\omega=A\cdot\frac{2\pi}{T}\) \(\Rightarrow\) \(T=\frac{2\pi{A}}{v_{m}}\),
де \(\omega\) – кругова (циклічна) частота. Підставивши вираз періоду коливань у формулу (1), остаточно знаходимо:
\(\langle{v}\rangle=\frac{4Av_{m}}{2\pi{A}}=\frac{2v_{m}}{\pi}=\frac{2\cdot{10}}{\pi}\approx\) 6,4 м/с.
Динаміка гармонічних коливань
Для аналізу і визначення періоду (частоти) гармонічних коливань у складній коливальній механічній системі необхідно виконати наступне.
|
1) |
Показати на рисунку вектори всіх прикладених сил і рівнодійної для довільного положення тіла. Якщо рівнодійна напрямлена до положення рівноваги, то тіло здійснює коливання. |
|
|
|
|
2) |
Встановити вираз залежності проекції рівнодійної сили залежно від зміщення тіла з положення рівноваги. Якщо він задовольняє умові (13.10), то коливання є гармонічними. |
|
|
|
|
3) |
Використовуючи отриманий в п.2) вираз коефіцієнта пропорційності між силою і зміщенням, за формулами (13.12), (13.12a), або (13.13), визначити період або частоту коливань. |
Задача 13.4. До стіни, нахиленої під кутом \(\alpha=3^{\circ}\) до вертикалі, прикріплена нитка математичного маятника завдовжки l = 0,5 м. Нитку відвели на кут \(\Theta_{0}=6^{\circ}\) від вертикалі і відпустили. Вважаючи удар кульки маятника об стіну абсолютно пружним, визначити період коливань маятника T.
Задача 13.5. Маленька кулька масою m = 20 г, що несе заряд q = 1 мкКл, підвішена на тонкій шовковій нитці завдовжки l = 40 см і здійснює малі коливання у вертикальному електричному полі напруженістю E = 50 кВ/м. Визначити період коливань T, якщо вектор \(\vec{E}\) напрямлений: А) вгору (T1); Б) вниз (T2).
Задача 13.6. В середині закритого з обох торців горизонтального циліндра довжиною 2l = 0,8 м, розташований поршень масою m = 2 кг і площею S = 50 см2. Тиск повітря в циліндрі P = 50 кПа. В результаті легкого поштовху поршень починає здійснювати малі коливання. Нехтуючи товщиною поршня і тертям, визначити період коливань T. Температуру повітря вважати постійною.
Задача 13.7. На вертикальній пружині жорсткістю k = 245 Н/м укріплена горизонтальна чашка масою M = 1,5 кг. З висоти h = 20 см на чашку падає шматок пластиліну масою m = 0,5 кг і прилипає до неї. Визначити період T і амплітуду xm коливань чашки.
Задача 13.4
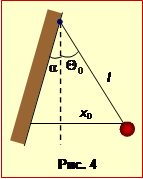 До стіни, нахиленої під кутом \(\alpha=3^{\circ}\) до вертикалі, прикріплена нитка математичного маятника завдовжки l = 0,5 м. Нитку відвели на кут \(\Theta_{0}=6^{\circ}\) від вертикалі (рис.4) і відпустили. Вважаючи удар кульки маятника об стіну абсолютно пружним,
До стіни, нахиленої під кутом \(\alpha=3^{\circ}\) до вертикалі, прикріплена нитка математичного маятника завдовжки l = 0,5 м. Нитку відвели на кут \(\Theta_{0}=6^{\circ}\) від вертикалі (рис.4) і відпустили. Вважаючи удар кульки маятника об стіну абсолютно пружним,
визначити
період коливань маятника T.
|
Дано: \(\alpha=3^{\circ}\)
l = 0,5 м
\(\Theta_{0}=6^{\circ}\)
|
|
T - ?
|
Розв’язання
Період – це час, за який тіло здійснює одне повне коливання. В даній задачі період дорівнює часу, за який маятник з початкового положення дійде до стіни і повернеться назад. Оскільки удар об стіну пружний, швидкість маятника при ударі змінює тільки напрям, не змінюючи величини. Звідси очевидно, що час t0 руху з крайнього положення до стіни і назад однаковий, отже період коливань
|
|
T = 2t0. |
(1) |
Зміщення маятника з положення рівноваги задається кутом \(\Theta\) відхилення нитки від вертикалі. Визначимо закон, за яким змінюється з часом цей кут. Оскільки \(\Theta\ll{1}\) рад, координата x маятника при вільному русі від початкового положення і до удару об стіну виражається рівнянням (13.4):
|
|
\(x=x_{0}\sin(\omega{t})\), |
(2) |
де частота \(\omega\) визначається формулою (13.17).
Розділивши обидві частини рівняння (2) на довжину маятника l і врахувавши малість кутів \(\Theta\) і \(\Theta_{0}\), отримаємо:
\(\Theta=\Theta_{0}\cos(\omega{t})\).
У момент удару об стіну t = t0 кут відхилення \(\Theta=-\alpha\), тому
\(-\alpha=\Theta_{0}\cos\omega{t}_{0}\) \(\Rightarrow\) \(t_{0}=\frac{1}{\omega}\mathrm{arccos}\left(\frac{\alpha}{\Theta_{0}}\right)=\sqrt{\frac{l}{g}}\left(\pi-\mathrm{arccos\frac{\alpha}{\Theta_{0}}}\right)\).
Підставимо цей вираз у формулу (1) і остаточно отримаємо:
\(T=2\sqrt{\frac{l}{g}}\left(\pi-\mathrm{arccos\frac{\alpha}{\Theta_{0}}}\right)=2\sqrt{\frac{0,5}{9,8}}\left(\pi-\mathrm{arccos}\frac{3}{6}\right)\approx\) 0,95 c,
де кути виражені в радіанах, \(\mathrm{arccos}\frac{3}{6}=\frac{\pi}{3}\).
Задача 13.5
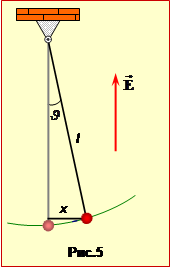 Маленька кулька масою m = 20 г, що несе заряд q = 1 мкКл, підвішена на тонкій шовковій нитці завдовжки l = 40 см і здійснює малі коливання у вертикальному електричному полі напруженістю E = 50 кВ/м (рис.5).
Маленька кулька масою m = 20 г, що несе заряд q = 1 мкКл, підвішена на тонкій шовковій нитці завдовжки l = 40 см і здійснює малі коливання у вертикальному електричному полі напруженістю E = 50 кВ/м (рис.5).
Визначити
період коливань T, якщо вектор \(\vec{E}\) напрямлений:
А) вгору (T1);
Б) вниз (T2).
|
Дано: m = 20 г = 0,02 кг
q = 1 мкКл = 10-6 Кл
l = 40 см = 0,4 м
E = 50 кВ/м = 5·104 В/м
|
|
T1, T2 - ?
|
Розв’язання
Нехай кулька рухається від положення рівноваги (рис.5-1). На кульку діє сила тяжіння \(m\vec{g}\), сила натягу нитки \(\vec{F}_{н}\) і сила \(\vec{F}_{е}=q\vec{E}\) в електричному полі. Якщо вектор \(\vec{E}\) направлений вертикально вгору, то і сила \(\vec{F}_{е}\) також направлена вгору.
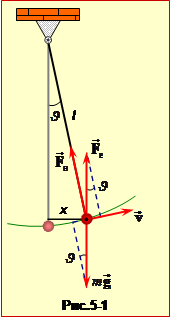 Проекції сил на напрям вектора швидкості дорівнює відповідно: \(-mg\sin\vartheta\), 0 і \(qE\sin\vartheta\). Проекція сили натягну нитки на напрям вектора \(\vec{v}\) дорівнює нулю, оскільки цей вектор перпендикулярний нитці (направлений по дотичній до траєкторії).Проекція рівнодійної цих сил
Проекції сил на напрям вектора швидкості дорівнює відповідно: \(-mg\sin\vartheta\), 0 і \(qE\sin\vartheta\). Проекція сили натягну нитки на напрям вектора \(\vec{v}\) дорівнює нулю, оскільки цей вектор перпендикулярний нитці (направлений по дотичній до траєкторії).Проекція рівнодійної цих сил
|
|
\(F=-(mg-qE)\sin\vartheta=-\frac{(mg-qE)}{l}\cdot{x}=-kx\), |
(1) |
де введено позначення \(k=(mg-qE)/l\), і враховано, що \(\sin\vartheta=x/l\), оскільки відхилення від положення рівноваги x є малим у порівнянні з довжиною нитки l від положення рівноваги.
Вигляд виразу (1) співпадає з формулою (13.10). Це значить, що коливання гармонічні і згідно формулі (13.13), їх період
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\) = \(2\pi\sqrt{\frac{ml}{mg-qE}}\). |
(2) |
Якби ми припустили спочатку, що вектор \(\vec{E}\) направлений вертикально вниз, то проекція вектора \(\vec{F}_{е}\) на напрям вектора швидкості була б негативною, і період коливань був би
|
|
\(T=2\pi\sqrt{\frac{ml}{mg+qE}}\). |
(3) |
Об'єднавши вирази (2) і (3), можна записати:
|
|
\(T=2\pi\sqrt{\frac{ml}{mg\pm{qE}}}\). |
(4) |
Підставивши сюди числові значення величин, знаходимо
\(T_{1}=2\pi\sqrt{\frac{2\cdot{10^{-2}}\cdot{0,4}}{2\cdot{10^{-2}}\cdot{9,8}-10^{-6}\cdot{5}\cdot{10^{4}}}}\) = 1,47 c;
\(T_{1}=2\pi\sqrt{\frac{2\cdot{10^{-2}}\cdot{0,4}}{2\cdot{10^{-2}}\cdot{9,8}+10^{-6}\cdot{5}\cdot{10^{4}}}}\) = 1,13 c
Корисно провести аналіз загального виразу (4).
 1) Якщо електричне поле відсутнє (E = 0), то
1) Якщо електричне поле відсутнє (E = 0), то
\(T=2\pi\sqrt{\frac{l}{g}}\),
що природно співпадає з формулою (13.18) періоду вільних коливань математичного маятника.
2) Якщо виявиться, що qE > mg, то формально під коренем виходить від’ємна величина, чого бути не може. Річ у тім, що за таких умов рівноважним є положення маятника, показане на рис.5-2, і маятник здійснюватиме коливання відносно цього положення з періодом
\(T=2\pi\sqrt{\frac{ml}{qE-mg}}\).
3) У випадку mg = qE повертаюча сила F = 0 і період коливань \(T\to\infty\), тобто кулька знаходиться в стані байдужої рівноваги.
Задача 13.6
В середині закритого з обох торців горизонтального циліндра довжиною 2l = 0,8 м, розташований поршень масою m = 2 кг і площею S = 50 см2. Тиск повітря в циліндрі P = 50 кПа. В результаті легкого поштовху поршень починає здійснювати малі коливання. Нехтуючи товщиною поршня і тертям,
визначити
період коливань T. Температуру повітря вважати постійною.
|
Дано: 2l = 0,8 м
m = 2 кг
S = 50 см2 = 5·10-3 м2
P = 50 кПа = 5·104 Па
|
|
T - ?
|
Розв’язання
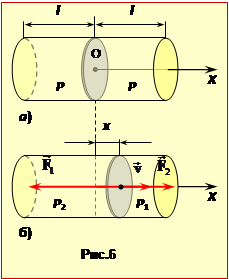 В положенні рівноваги поршня (рис.6а) тиск в обох половинах циліндра однаковий. При зсуві поршня на відстань x, наприклад управо (рис.6б), тиск у лівій частині зменшується, а у правій - зростає. У результаті виникають сили F1 = P1S і F2 = P2S (рис.6б), рівнодійна яких напрямлена до положення рівноваги (повертаюча сила). Знайдемо її вираз.
В положенні рівноваги поршня (рис.6а) тиск в обох половинах циліндра однаковий. При зсуві поршня на відстань x, наприклад управо (рис.6б), тиск у лівій частині зменшується, а у правій - зростає. У результаті виникають сили F1 = P1S і F2 = P2S (рис.6б), рівнодійна яких напрямлена до положення рівноваги (повертаюча сила). Знайдемо її вираз.
Оскільки за умовою температура повітря не змінюється, зміни тиску в частинах циліндра зв'язані законом Бойля-Маріотта (формула (7.10)). Якщо поршень змістився на x, то об'єм правої частини V1 = S(l - x), і тоді
\(PS=P_{1}S(l-x)\) \(\Rightarrow\) \(P_{1}=\frac{Pl}{l-x}\).
Аналогічно, для лівої частини
\(PS=P_{2}S(l+x)\) \(\Rightarrow\) \(P_{2}=\frac{Pl}{l+x}\).
Нехай поршень зміщений управо (рис.6б). Проектуючи сили тиску на вісь OX, для рівнодійної отримаємо:
\(F_{x}=-F_{1}+F_{2}=(-P_{1}+P_{2})S=PlS\left(\frac{1}{l+x}-\frac{1}{l-x}\right)=-PlS\frac{2x}{l^{2}-x^{2}}\).
При малих коливаннях \(x\ll{l}\), в знаменнику можна знехтувати \(x^{2}\) у порівнянні з \(l^{2}\), тоді
|
|
\(F_{x}=-\frac{2PS}{l}x=-kx\), |
(1) |
де
|
|
\(k=\frac{2PS}{l}\). |
(2) |
Вираз (1) співпадає з (13.10), отже коливання поршня є гармонічними з періодом, який визначається формулою (13.13):
\(T=2\pi\sqrt{\frac{ml}{2PS}}=2\pi\sqrt{\frac{2\cdot{0,4}}{2\cdot{5}\cdot{10^{-4}}\cdot{5}\cdot{10^{-3}}}}\) = 0,25 c.
Задача 13.7
На вертикальній пружині жорсткістю k = 245 Н/м укріплена горизонтальна чашка масою M = 1,5 кг. З висоти h = 20 см на чашку падає шматок пластиліну масою m = 0,5 кг і прилипає до неї.
Визначити
період T і амплітуду xm коливань чашки.
|
Дано: k = 245 Н/м
M = 1,5 кг
h = 20 см = 0,2 м
m = 0,5 кг
|
|
T - ?
xm - ?
|
Розв’язання
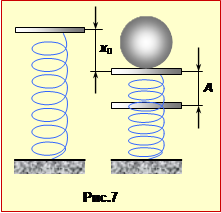 Період коливання вантажу на пружині визначається формулою (13.15). Після того, як пластилін прилипнув до чашки, маса вантажу дорівнює m + M, отже період коливань
Період коливання вантажу на пружині визначається формулою (13.15). Після того, як пластилін прилипнув до чашки, маса вантажу дорівнює m + M, отже період коливань
| \(T=2\pi\sqrt{\frac{m+M}{k}}=2\pi\sqrt{0,5+1,5}{245}\) = 0,57 c. | (1) |
Якщо пластилін обережно покласти на чашку, то пружина стиснеться на величину x0 (рис.7), яка знаходиться з умови рівності сил тяжіння і пружності:
|
|
\(mg=kx_{0}\) \(\Rightarrow\) \(x_{0}=\frac{mg}{k}\). |
(2) |
 Очевидно, що це положення є положенням рівноваги системи "пластилін – чашка – пружина". Впавши з висоти h, (рис.7-1) пластилін має швидкість (формула (1.19)).
Очевидно, що це положення є положенням рівноваги системи "пластилін – чашка – пружина". Впавши з висоти h, (рис.7-1) пластилін має швидкість (формула (1.19)).
\(v=\sqrt{2gh}\).
Оскільки тривалість удару мала (частки секунди), то можна вважати, що виконується закон збереження імпульсу. Тому початкова швидкість чашки з пластиліном v0 визначається з рівняння балансу імпульсів:
|
|
\(mv=(M+m)v_{0}\) \(\Rightarrow\) \(v_{0}=\frac{mv}{m+M}=\frac{m\sqrt{2gh}}{m+M}\). |
(3) |
Нехай коливальний рух чашки після удару відбувається згідно із законом
|
|
\(x=x_{m}\cos(\omega{t}+\varphi_{0})\). |
(4) |
Тоді швидкість чашки після удару змінюється з часом згідно із законом
|
|
\(v(t)=x^{\prime}(t)=-x_{m}\omega\sin(\omega{t}+\varphi_{0})\). |
(5) |
Для знаходження амплітуди xm виразимо з рівнянь (4) і (5) \(\cos(\omega{t}+\varphi_{0})\) і \(\sin(\omega{t}+\varphi_{0})\), піднесемо їх до квадрату і додамо:
|
|
\(\frac{x^{2}}{x_{m}^{2}}+\frac{v^{2}}{x_{m}^{2}\omega^{2}}=1\) \(\Rightarrow\) \(x_{m}=\sqrt{x^{2}+\frac{v^{2}}{\omega^{2}}}=\sqrt{x^{2}+\frac{v^{2}T^{2}}{4\pi^{2}}}\). |
(6) |
(Тут ми скористалися формулою (13.3)).
Співвідношення (6) виконується у будь-який момент часу, у тому числі і у момент початку коливань. Тому, підставивши в (6) вирази T, x0, v0 з формул (1), (2) і (3), отримаємо:
\(x_{m}=\sqrt{\left(\frac{mg}{k}\right)^{2}+\left(\frac{m}{M+m}\right)^{2}\cdot\frac{2gh(M+m)}{k}}=\frac{mg}{k}\sqrt{1+\frac{2hk}{(M+m)g}}\).
Обчислення дають:
\(x_{m}=\frac{0,5\cdot{9,8}}{245}\cdot\sqrt{1+\frac{2\cdot{0,2}\cdot{245}}{2\cdot{9,8}}}\) = 0,049 м = 4,9 см.
Енергія гармонічних коливань
При розв'язуванні задач на енергію гармонічних коливань часто буває необхідно скласти рівняння енергетичного балансу (13.21a) з використанням виразів (13.19), (13.20), (13.21).
У зв'язку з цим нагадаємо, що формули (13.20) і (13.19) можна застосоувати не лише до коливань вантажу на пружині, але й до будь-яких інших гармонічних коливань. При цьому k - коефіцієнт пропорційності між рівнодійною силою і зміщенням тіла з положення рівноваги.
Нагадаємо також, що вигляд тригонометричної функції в рівняннях (13.19) та (13.20) не відомий заздалегідь, а залежить від вибору вихідної функції, що описує коливання.
Задача 13.8. Математичний маятник з довжиною нитки l здійснює малі коливання. Показати, що потенціальна енергія малих коливань маятника визначається формулою (13.19): \(W_{п}=\frac{kx^{2}}{2}\), в якій коефіцієнт k задається виразом (13.16): \(k=\frac{mg}{l}\).
Задача 13.9. Тіло, прикріплене до пружини, здійснює гармонічні коливання, амплітуда коливань A = 2 см. Повна енергія коливань W = 0,3 мДж. Визначити зміщення x з положення рівноваги, при якому на тіло діє повертаюча сила |F| = 22,5 мН.
Задача 13.10. Тіло, прикріплене до пружини жорсткістю k = 1200 Н/м, Здійснює в горизонтальній площині коливання за законом синуса з амплітудою A = 10 см. Нехтуючи тертям і опором повітря, визначити повну W, кінетичну Wк і потенціальну Wп енергії коливань при фазі \(\varphi=50^{\circ}\).
Задача 13.11. Тіло, прикріплене до пружини, здійснює гармонічні коливання в горизонтальній площині. В момент, коли потенціальна енергія системи складає n = 80 % її повної енергії, зміщення тіла з положення рівноваги x = 2 см, а його швидкість v = 3,1 см/с. Визначити період коливань T.
Задача 13.8
Математичний маятник з довжиною нитки l здійснює малі коливання.
Показати,
що потенціальна енергія малих коливань маятника визначається формулою (13.19): \(W_{п}=\frac{kx^{2}}{2}\), в якій коефіцієнт k задається виразом (13.16): \(k=\frac{mg}{l}\).
Розв’язання
Потенціальна енергія маятника обумовлена дією на нього сили тяжіння і виражається формулою
|
|
\(W_{п}=mgh\), |
(1) |
де m – маса маятника, h – висота підйому над положенням рівноваги (див. рис.8). З рис.8 видно, що
|
|
\(h=AO-AB=l-l\cos\alpha\) \(\Rightarrow\) \(h=l(1-\cos\alpha)=2l\sin^{2}\frac{\alpha}{2}\). |
(2) |
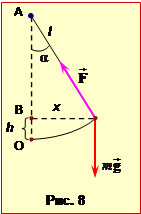 Оскільки маятник здійснює малі коливання (\(x\ll{l}\)), то \(\alpha\ll{1}\) рад. Тому \(\sin\frac{\alpha}{2}=\frac{\alpha}{2}\), і вираз (2) набуває вигляду:
Оскільки маятник здійснює малі коливання (\(x\ll{l}\)), то \(\alpha\ll{1}\) рад. Тому \(\sin\frac{\alpha}{2}=\frac{\alpha}{2}\), і вираз (2) набуває вигляду:
\(h=2l\left(\frac{\alpha}{2}\right)^{2}=\frac{l\alpha^{2}}{2}\).
Підставивши його у формулу (1) і зробивши заміну \(\alpha=x/l\), отримаємо
\(W_{п}=\frac{mgx^{2}}{2l}=\frac{kx^{2}}{2}\),
де \(k=\frac{mg}{l}\), що і треба було довести.
Ця задача ілюструє універсальність формули (13.19): вона може бути застосовна до будь-яких гармонічних коливань, а не тільки до коливань під дією сили пружності.
Задача 13.9
Тіло, прикріплене до пружини, здійснює гармонічні коливання, амплітуда коливань A = 2 см. Повна енергія коливань W = 0,3 мДж.
Визначити
зміщення x з положення рівноваги, при якому на тіло діє повертаюча сила |F| = 22,5 мН.
|
Дано: A = 2 см = 0,02 м
W = 0,3 мДж = 3·10-4 Дж
|F| = 22,5 мН = 2,25·10-2 Н
|
|
x - ?
|
Розв’язання
Повна енергія тіла, що здійснює гармонічні коливання, визначається формулою (13.21):
|
|
\(W=\frac{kA^{2}}{2}\). |
(1) |
Повертаюча сила в залежності від зміщеня виражається формулою (13.10), причому її модуль
|
|
\(|F|=kx\), |
(2) |
Виключивши з виразів (1) і (2) величину k, знаходимо:
\(x=\frac{|F|A^{2}}{2W}=\frac{2,25\cdot{10^{-2}}\cdot{4}\cdot{10^{-4}}}{2\cdot{3}\cdot{10^{-4}}}=1,5\cdot{10^{-2}}\) м = 1,5 см.
Задача 13.10
Тіло, прикріплене до пружини жорсткістю k = 1200 Н/м, Здійснює в горизонтальній площині коливання за законом синуса з амплітудою A = 10 см. Нехтуючи тертям і опором повітря,
визначити
повну W, кінетичну Wк і потенціальну Wп енергії коливань при фазі \(\varphi=50^{\circ}\).
|
Дано: k = 1200 Н/м
A = 10 см = 0,1 м
\(\varphi=50^{\circ}\)
|
|
W, Wк, Wп - ?
|
Розв’язання
Повна енергія коливань тіла на пружині визначається виразом (13.21):
\(W=\frac{kA^{2}}{2}=\frac{1200\cdot{10^{-2}}}{2}=6\) Дж.
Згідно з умовою, коливання відбуваються за законом
\(x=A\sin(\omega{t}+\varphi_{0})=A\sin\varphi\),
де \(\varphi=\omega+\varphi_{0}\) – фаза коливань. Потенціальна енергія коливань відповідно до формули (13.19)
\(W_{п}=\frac{kx^{2}}{2}=\frac{kA^{2}\sin^{2}\varphi}{2}\)=\(\frac{1200\cdot{10^{-2}}\sin^{2}50^{\circ}}{2}\) = 3,52 Дж.
Оскільки повна енергія рівна сумі кінетичної і потенціальної W = Wк + Wп, то кінетична енергія коливань
Wк = W – Wп = 6 – 3,52 = 2,48 Дж.
Звичайно, кінетичну енергію можна було б шукати як \(W_{к}=\frac{mv^{2}}{2}\), але для цього треба було б визначати швидкість як похідну від координати x по часу, і врахувати, що амплітуда швидкості \(v_{m}=A\omega\), і далі скористатися тим, що \(k=m\omega^{2}\). Все це вимагає додаткових перетворень, а використання закону збереження енергії дозволило одержати значення кінетичної енергії за одну дію.
Задача 13.11
Тіло, прикріплене до пружини, здійснює гармонічні коливання в горизонтальній площині. В момент, коли потенціальна енергія системи складає n = 80 % її повної енергії, зміщення тіла з положення рівноваги x = 2 см, а його швидкість v = 3,1 см/с.
Визначити
період коливань T.
|
Дано: n = 80 %
x = 2 см
v = 3,1 см/с
|
|
T - ?
|
Розв’язання
Період коливань тіла на пружині визначається формулою:
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\). |
(1) |
Відношення m/k знайдемо з умови збереження повної енергії коливань:
|
|
\(W=W_{к}+W_{п}=\frac{mv^{2}}{2}+\frac{kx^{2}}{2}=W_{п}\left(\frac{mv^{2}}{kx^{2}}+1\right)\), |
(2) |
де \(W_{к}=mv^{2}/2\) – кінетична енергія, \(W_{п}=kx^{2}/2\) – потенціальна енергія. З формули (2) одержуємо:
\(\frac{m}{k}=\frac{x^{2}}{v^{2}}\left(\frac{W}{W_{п}}-1\right)\).
Підставивши цей вираз у формулу (1), маємо
\(T=2\pi\frac{x}{v}\sqrt{\frac{W}{W_{п}}-1}=2\pi\cdot\frac{2}{3,1}\sqrt{\frac{1}{0,8}-1}\approx\) 2 c.
Підкреслимо, що методи розв’язування задач, які ґрунтуються на законі збереження енергії, часто дозволяють визначити період (частоту) коливань простіше, ніж інші методи.
Розділ 14. Електромагнітні коливання. Змінний струм
|
Електромагнітними коливаннями називають процеси в електричних колах, коли багаторазово змінюється величина і напрямок струму і, відповідно, величина і полярність напруги на кожній ділянці кола. Існують і знаходять широке застосування різні типи електричних коливань – вільні, вимушені та ін. Вільні коливання спостерігаються в коливальних контурах – колах, в яких окрім звичайних провідників (резисторів) є конденсатори і котушки індуктивності. Вимушені електричні коливання називаються змінним струмом. Вони створюються в будь-якому електричному колі при його підключенні до джерела змінної ЕРС (генератора). Теоретичні відомості |
Теоретичні відомості. Вільні коливання у контурі
|
Вільні електричні коливання спостерігаються у коливальному контурі, причому в ідеальному контурі вони є гармонічними. Повну інформацію про коливання містить диференціальне рівняння коливального контуру. Зокрема, з нього можна визначити частоту і період вільних коливань, одержати рівняння коливань заряду, напруги і сили струму в контурі. У коливальному контурі відбуваються перетворення електричної і магнітної енергії коливань. |
Коливальним контуром називається електричне коло, що складається з резистора (резистором у контурі часто є дроти), конденсатора і котушки індуктивності. При певних співвідношеннях між параметрами кола R, L, C, в ньому можливі вільні електричні коливання.
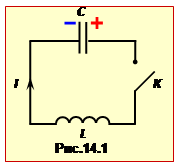 У теорії електричних коливань базовою моделлю є ідеальний коливальний контур. Такий контур (рис.14.1) складається тільки з ідеальних конденсатора і котушки індуктивності і не має опору (R = 0). (Ідеальний конденсатор заповнений ідеальним діелектриком, і його електричне поле зосереджене тільки між обкладками. Ідеальна котушка не має опору (R = 0) , і її магнітне поле зосереджене тільки усередині котушки).
У теорії електричних коливань базовою моделлю є ідеальний коливальний контур. Такий контур (рис.14.1) складається тільки з ідеальних конденсатора і котушки індуктивності і не має опору (R = 0). (Ідеальний конденсатор заповнений ідеальним діелектриком, і його електричне поле зосереджене тільки між обкладками. Ідеальна котушка не має опору (R = 0) , і її магнітне поле зосереджене тільки усередині котушки).
Вільні електричні коливання у контурі виникають так. Якщо зарядити конденсатор і замкнути ключ K, то конденсатор почне розряджатися через котушку, і в ній виникне струм, що змінюється за величиною. Цей струм створює ЕРС самоіндукції (див. формулу (12.14)), яка за правилом Ленца перешкоджає зміні струму. Як наслідок, після замикання ключа К сила струму розрядки конденсатора спочатку поступово збільшується, а потім поступово зменшується. При цьому за рахунок ЕРС самоіндукції на момент повної розрядки конденсатора (q, U = 0) струм не припиняється, а продовжує текти в тому ж напрямку, що призводить до перезаряджання конденсатора. Далі всі процеси повторюються у зворотному напрямку, тобто виникають коливання.
Диференціальне рівняння ідеального контуру виходить з тієї очевидної умови, що, оскільки котушка приєднана безпосередньо до конденсатора (рис.14.1), то в будь–який момент часу напруга на конденсаторі u дорівнює ЕРС самоіндукції \(\mathcal{E}_{с}\):
|
\(u=\mathcal{E}_{с}\). |
Величини u і \(\mathcal{E}_{с}\) визначаються формулами (10.23) і (12.14), отже
|
|
\(\frac{q}{C}=-Li^{\prime}\), |
(14.1) |
де q – заряд конденсатора, \(i^{\prime}\) – похідна сили струму по часу.
Струм у контурі створюється переміщенням заряду з однієї обкладки конденсатора на іншу. Тому заряд, що проходить протягом часу dt через переріз провідників контуру, дорівнює зміні заряду конденсатора dq протягом цього ж часу. Отже, сила струму
|
|
\(i=q^{\prime}\), |
(14.2) |
де \(a^{\prime}\) – похідна заряду конденсатора по часу, тобто
|
|
\(i^{\prime}=q^{\prime\prime}(t)\), |
(14.3) |
Після підстановки цього виразу до рівняння (14.1) маємо диференціальне рівняння ідеального контуру
|
|
\(q^{\prime\prime}=-\frac{1}{LC}q\). |
(14.4) |
Рівняння (14.4) ідентичне рівнянню (13.22). З цього випливають два висновки.
|
По–перше, вільні електричні коливання в ідеальному контурі є гармонічними. По–друге, |
|
|
\(\frac{1}{LC}=\omega^{2}\). |
(14.5) |
де \(\omega\) – циклічна частота коливань.
Частоти і період вільних коливань в ідеальному контурі виражаються наступними формулами.
Циклична частота
|
|
\(\omega=\frac{1}{\sqrt{LC}}\). |
(14.5a) |
Період коливань (див. формулу (13.3))
|
|
\(T=2\pi\sqrt{LC}\). |
(14.6) |
Останній вираз називається формулою Томсона.
Лінійна частота (див. формулу (13.2))
|
|
\(\nu=\frac{1}{2\pi\sqrt{LC}}\). |
(14.7) |
Рівняння коливань заряду конденсатора в ідеальному контурі можна одержати з рівняння механічних коливань (13.4) або (13.1), (13.1a), (13.4a), замінивши зміщення x на заряд q:
|
|
\(q=q_{m}\cos(\omega{t}+\varphi_{0})\), |
(14.8) |
де qm – амплітуда заряду, \(\omega\) – циклічна частота (формула (14.5)) і \(\varphi_{0}\) – початкова фаза коливань.
Напруга на конденсаторі \(u=q/C\) (формула (10.23)), тому рівняння коливань напруги на конденсаторі ідеального контуру має вигляд:
|
|
\(u=U_{m}\cos(\omega{t}+\varphi_{0})\), |
(14.9) |
де Um – амплітуда напруги, що визначається як
|
|
\(U_{m}=\frac{q_{m}}{C}\). |
(14.10) |
Оскільки сила струму в контурі \(i=q^{\prime}(t)\), то сила струму в ідеальному контурі:
|
|
\(i=-\omega{q}_{m}\sin(\omega{t}+\varphi_{0})\) |
(14.11) |
|
|
\(i=I_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\), |
(14.11a) |
де амплітуда сили струму
|
|
\(I_{m}=\omega{q}_{m}\). |
(14.12) |
З рівнянь (14.9) і (14.11а) видно, що в ідеальному контурі коливання сили струму випереджають по фазі коливання напруги на конденсаторі на \(\pi/2\) або на ¼ періоду (рис.14.2).
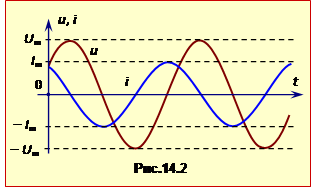
(Коливання заряду на конденсаторі завжди мають таку ж фазу, як і коливання напруги (див. рівняння (14.8) та (14.9)). Тому графік q(t) на рисунку не показаний).
Енергія коливань в ідеальному контурі складається з енергії електричного поля конденсатора WE та енергії магнітного поля котушки індуктивності WB:
|
|
W = WE + WB. |
(14.13) |
Відповідно до формул (10.32), (12.15) і рівнянь (14.9), (14.11а)
|
|
\(W_{Е}=\frac{q_{m}^{2}}{2C}\cos^{2}(\omega{t}+\varphi_{0})\) =\(\frac{q_{m}^{2}}{4C}\left(1+cos(2\omega{t}+2\varphi_{0})\right)\), |
(14.14) |
|
|
\(W_{В}=\frac{LI_{m}^{2}}{2}\sin^{2}(\omega{t}+\varphi_{0})=\frac{LI_{m}^{2}}{2}\left(1-\cos(2\omega{t}+2\varphi_{0})\right)\). |
(14.15) |
З виразів (14.12) та (14.5) виходить:
\(LI_{m}^{2}=L\omega^{2}q_{m}^{2}\) \(\Rightarrow\) \(LI_{m}^{2}=\frac{q_{m}^{2}}{C}\).
Тому з виразів (14.13), (14.14) і (14.15) очевидно, що
|
|
\(W=\frac{q_{m}^{2}}{2C}=\frac{LI_{m}^{2}}{2}\) = const. |
(14.13) |
Таким чином,
|
повна енергія вільних коливань в ідеальному контурі не залежить від часу, тобто зберігається. |
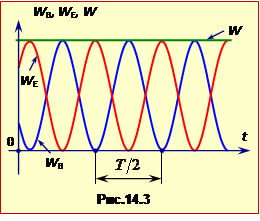 На рис.14.3 зображені графіки залежності від часу електричної WE, магнітної WB і повної енергії коливань W в ідеальному контурі.
На рис.14.3 зображені графіки залежності від часу електричної WE, магнітної WB і повної енергії коливань W в ідеальному контурі.
Ці графіки наочно показують, що при вільних коливаннях в ідеальному контурі відбуваються неперервні взаємні перетворення електричного та магнітного полів без втрати енергії. Крім того, з рівнянь (14.14) і (14.15) випливає, що коливання енергії кожного з полів відбуваються з подвоєною частотою \(\omega^{\prime}\) відносно коливань напруги і струму:
|
\(\omega^{\prime}=2\omega\) |
або |
\(T^{\prime}=\frac{T}{2}\). |
Порівняння формул (14.16) і (13.21) показує їх математичну ідентичність. При цьому для контуру величини 1/C і L виконують ту ж саму роль, що й жорсткість пружини k та маса вантажу m у випадку пружинного маятника.
Теоретичні відомості. Змінний струм
|
Змінним струмом називаються вимушені коливання в електричному колі, підключеному до генератора. В елементарній фізиці розглядаються тільки синусоїдальні змінні струми. Такі струми повсюди використовуються в силових електричних установках (двигуни, нагрівачі, освітлювачі й ін.). Але в електроніці широко застосовують різноманітні змінні струми інших видів. У загальному випадку коло змінного струму, крім генератора, включає резистори, конденсатори і котушки індуктивності. Кожний з цих елементів створює певний опір струмові. Розрізняють три види опорів змінному струмові: активний опір, реактивний ємнісний та реактивний індуктивний опори. Зв'язок між струмом і напругою (ЕРС) генератора залежить від повного опору кола і описується законом Ома для змінного струму. За певних умов у колах змінного струму спостерігається резонанс – явище, яке має важливі практичні застосування. Потужність змінного струму залежить не тільки від напруги і сили струму, але й від різниці фаз між коливаннями цих величин. Для перетворення напруги і сили змінного струму використовують трансформатори. |
Синусоїдальним називається змінний струм, при якому сила струму і напруги на ділянках кола здійснюють гармонічні коливання.
Синусоїдальний струм створюється генератором змінної напруги (ЕРС), яке залежить від часу за законом:
|
|
\(u=U_{m}\sin\omega{t}\), |
(14.17) |
де Um – амплітуда напруги генератора, \(\omega\) – циклічна частота. На практиці використовують лінійну частоту \(\nu\). Наприклад, на пристроях, що використовують промисловий змінний струм, вказують: \(\nu\) = 50 Гц. (Зауважимо, що зміна напруги з часом може описуватися і законом косинуса).
![]()
Генератор змінного струму на електричних схемах зображують так:
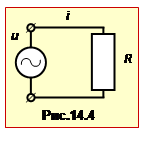 Активним опором у колі (мається на увазі, що коло нерухоме, тобто відсутнє перетворення електричної енергії у механічну) змінного струму (рис.14.4) називають опір резисторів. Він має таку ж природу, що й при постійному струмі, тобто обумовлений гальмуванням носіїв струму іншими частинками провідника. Всі формули, співвідношення і закони постійного струму залишаються чинними і для змінного струму в резисторах. Зокрема, для них виконується закон Ома
Активним опором у колі (мається на увазі, що коло нерухоме, тобто відсутнє перетворення електричної енергії у механічну) змінного струму (рис.14.4) називають опір резисторів. Він має таку ж природу, що й при постійному струмі, тобто обумовлений гальмуванням носіїв струму іншими частинками провідника. Всі формули, співвідношення і закони постійного струму залишаються чинними і для змінного струму в резисторах. Зокрема, для них виконується закон Ома
|
|
\(i=\frac{u}{R}\), |
(14.18) |
де i, u – миттєві значення сили струму і напруги на резисторі, R – активний опір.
Якщо резистор підключити до генератора змінної напруги u (формула (14.17)), то сила струму у резисторі
|
|
\(i=I_{m}\sin\omega{t}\), |
(14.19) |
тобто коливання сили струму в резисторі відбуваються в однаковій фазі з коливаннями напруги і мають амплітуду
|
|
\(I_{m}=\frac{U_{m}}{R}\). |
(14.20) |
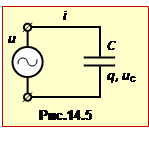 Реактивним ємнісним опором називається опір, що створюється ідеальним конденсатором при протіканні змінного струму.
Реактивним ємнісним опором називається опір, що створюється ідеальним конденсатором при протіканні змінного струму.
Напруга на конденсаторі, підключеному до генератора (рис.14.5), дорівнює напрузі генератора (формула (14.17)): uC = u. Отже, заряд конденсатора неперервно змінюється за законом
|
|
\(q=Cu=CU_{m}\sin\omega{t}\). |
(14.21) |
При цьому через з'єднувальні провідники і генератор тече струм, який визначається формулою (14.2):
\(i=q^{\prime}(t)\).
У теорії змінного струму цю величину називають струмом конденсатора. (Струм конденсатора – абстрактне поняття, оскільки ніякого руху носіїв між обкладками немає. Струм в конденсаторі визначається не швидкістю носіїв, як звичайний струм, а швидкістю зміни в ньому електричного поля). Відповідно до рівняння (14.21) струм конденсатора
|
|
\(i=\omega{C}U_{m}\cos\omega{t}\), |
(14.22) |
або
|
|
\(i=I_{m}\sin\left(\omega{t}+\frac{\pi}{2}\right)\), |
(14.22a) |
де Im – амплітуда струму, яку можна записати як
\(I_{m}=\frac{U_{m}}{(1/\omega{C})}\).
Цей вираз і за виглядом, і за змістом аналогічний формулі (14.20). Отже, величина
|
|
\(X_{C}=\frac{1}{\omega{C}}=\frac{1}{2\pi\nu{C}}\) |
(14.23) |
описує опір конденсатора змінному струмові. Вона називається реактивним ємнісним опором.
Таким чином, для змінного струму в конденсаторі з'вязок між амплітудами сили струму Im і напруги Um аналогічний зв'язку між силою струму і напругою в колі постійного струму:
|
|
\(I_{m}=\frac{U_{m}}{X_{C}}\), |
(14.24) |
Але, як видно з рівнянь (14.22) і (14.17), \(i(t)\ne{u}(t)/X_{C}\), тобто
|
для миттєвих значень сили змінного струму і напруги на конденсаторі закон Ома не виконується. |
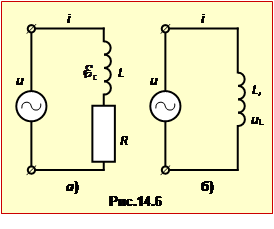 Реактивним індуктивним опором називається опір змінному струмові, створюваний ідеальною котушкою індуктивності.
Реактивним індуктивним опором називається опір змінному струмові, створюваний ідеальною котушкою індуктивності.
Якщо до генератора підключити котушку з індуктивністю L і активним опором R (рис.14.6а), то відповідно до формули (11.15)
\(iR=u+\mathcal{E}_{с}\),
де i – сила струму, u – напруга (ЕРС) генератора, \(\mathcal{E}_{с}\) – ЕРС самоіндукції в котушці. Для ідеальної котушки R = 0 (рис.14.6б), отже
|
|
\(-\mathcal{E}_{с}=u\). |
(14.25) |
Оскільки котушка підключена до генератора прямо, то напруга на ній дорівнює напрузі генератора: uL = u. Тому, підставивши вирази u (14.17), та \(\mathcal{E}_{с}\) (12.14) у співвідношення (14.25), одержуємо
|
|
\(Li^{\prime}=U_{m}\sin\omega{t}\). |
(14.26) |
З цього рівняння випливає, що
|
|
\(i=I_{m}\sin\left(\omega{t}-\frac{\pi}{2}\right)\). |
(14.27) |
де амплітуда сили струму Im визначається виразом
\(I_{m}=\frac{U_{m}}{\omega{L}}\).
(Розв'язання рівняння (14.26) можна визначити або прямим інтегруванням, або підстановкою загального рівняння коливань струму \(i=I_{m}\sin(\omega{t}+\varphi_{0})\).
Порівняння цього виразу з формулами (14.20) і (14.23) показує, що котушка індуктивності створює для змінного струму опір
|
|
\(X_{L}=\omega{L}=2\pi\nu{L}\), |
(14.28) |
який називається реактивним індуктивним опором.
Індуктивний опір XL визначає зв'язок між амплітудами сили струму Im і напруги Um на котушці індуктивності в колі змінного струму:
|
|
\(I_{m}=\frac{U_{m}}{X_{L}}\). |
(14.29) |
Але для миттєвих значень (див. рівняння (14.27) та (14.17)) такого зв'язку немає: \(i\ne{u}/X_{L}\). Отже,
|
для миттєвих значень сили змінного струму і напруги на котушці індуктивності закон Ома не виконується. |
Прямо пропорційний зв'язок між амплітудою сили струму і амплітудою напруги зберігається в будь-якому колі змінного струму. У цьому полягає закон Ома для змінного струму:
|
амплітуда сили змінного струму в колі прямо пропорційна амплітуді напруги (ЕРС) генератора і обернено пропорційна повному опору кола: |
|
|
\(I_{m}=\frac{U_{m}}{Z}\). |
(14.30) |
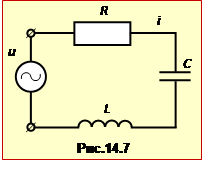 При цьому повний опір Z (його ще називають ще "імпедансом") визначається параметрами елементів кола (R, L, C) і способом їх з'єднання. Для найпростішого послідовного кола (рис.14.7)
При цьому повний опір Z (його ще називають ще "імпедансом") визначається параметрами елементів кола (R, L, C) і способом їх з'єднання. Для найпростішого послідовного кола (рис.14.7)
|
\(Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}\), |
(14.31) |
або
|
\(Z=\sqrt{R^{2}+\left(\omega{L}-\frac{1}{\omega{C}}\right)^{2}}\). |
(14.31a) |
Закон Ома для змінного струму стосується амплітуд. Для миттєвих значень сили струму він не виконується, тобто сила струму в даний момент часу не дорівнює відношенню напруги в цей же момент часу до повного опору. (Це не суперечить співвідношенню (14.30), тому що сила струму і напруга здійснюють коливання зі зсувом фаз і досягають своїх максимальних значень Im і Um не одночасно).
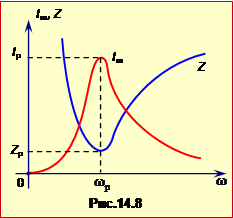 Згідно з формулами (14.23), (14.28) та (14.30), повний опір кола Z залежить від частоти. Відповідно, від частоти залежить і амплітуда сили струму Im. Вигляд цих залежностей для послідовного кола показаний на рис.14.8. На рисунку виразно простежується явище резонансу в електричному колі, яке полягає у різкому збільшенні амплітуди коливань при при наближенні частоти струму до резонансної частоти \(\omega_{р}\). Резонансна частота відповідає мінімуму повного опору і знаходиться з умови
Згідно з формулами (14.23), (14.28) та (14.30), повний опір кола Z залежить від частоти. Відповідно, від частоти залежить і амплітуда сили струму Im. Вигляд цих залежностей для послідовного кола показаний на рис.14.8. На рисунку виразно простежується явище резонансу в електричному колі, яке полягає у різкому збільшенні амплітуди коливань при при наближенні частоти струму до резонансної частоти \(\omega_{р}\). Резонансна частота відповідає мінімуму повного опору і знаходиться з умови
|
\(\omega_{р}L-\frac{1}{\omega_{р}C}\) \(\Rightarrow\) \(\omega_{р}=\frac{1}{\sqrt{LC}}\). |
(14.32) |
При \(\omega=\omega_{р}\) повний опір Zр і резонансна амплітуда сили струму Iр відповідно до формул (14.31a) та (14.30), дорівнюють
\(Z_{р}=R\),
\(I_{р}=\frac{U_{m}}{R}\).
Видно, що при резонансі відбувається компенсація ємнісного й індуктивного опорів. Це пояснюється тим, що коливання напруги на конденсаторі і на котушці протилежні по фазі і, отже, віднімаються. Тому при резонансі сумарний спад напруги на них дорівнює нулю.
Потужність змінного струму, що виділяється в колі у кожний момент часу, дорівнює добутку миттєвих значень сили струму і напруги. Ця миттєва потужність змінюється з великою частотою і її достатньо складно безпосередньо виміряти.
Тому потужністю змінного струму називають середнє значення добутку сили струму і напруги.
Повна потужність у колі змінного струму виражається формулою
|
|
\(P=\frac{1}{2}I_{m}U_{m}\cos\varphi\), |
(14.33) |
де Im, Um – амплітуди сили струму і напруги генератора, \(\varphi\) – різниця фаз між коливаннями струму і напруги генератора.
Величина \(\cos\varphi\) називається коефіцієнтом потужності і виражається через активний і повний опір кола формулою
|
|
\(\cos\varphi=\frac{R}{Z}\). |
(14.34) |
Якщо підставити цей вираз у формулу (14.33) і врахувати закон Ома (формула (14.30), то виходить
|
|
\(P=\frac{I_{m}^{2}}{2}R=\frac{U_{Rm}^{2}}{2R}\), |
(14.35) |
де URm = ImR – напруги на активному опорі кола.
Така ж потужність виділялася б у колі постійного струму з опором R при силі струму і напрузі
|
|
\(I=\frac{I_{m}}{\sqrt{2}}\), \(U=\frac{U_{m}}{\sqrt{2}}\). |
(14.34) |
Величини I та U, що визначаються формулами (14.36), називаються діючими, або ж ефективними значеннями сили струму і напруги.
Діючі значення є загальноприйнятими практичними характеристиками змінного струму. Зокрема, електровимірювальні прилади показують діючі значення, робочі величини струмів і напруг на різних побутових приладах теж вказують у діючих значеннях.
Із застосуванням діючих значень струму й напруги формули потужності (14.33) і (14.35) записуються у вигляді
|
|
\(P=IU\cos\varphi\), |
(14.37) |
та
|
|
\(P=I^{2}R=\frac{U_{m}^{2}}{R}\). |
(14.38) |
Остання формула показує, що споживана від генератора потужність змінного струму, виділяється тільки на активному опорі, а реактивні елементи – конденсатор і котушка індуктивності – енергії не споживають. Це пов'язано з тим, що при зарядці конденсатор поглинає відповідну енергію, а при розрядці – повністю повертає її в коло. Те ж саме відбувається і у котушці індуктивності при збільшенні і зменшенні сили струму.
Трансформатор – це пристрій для перетворення ("трансформації") величини напруги та сили змінного струму.
Робота трансформатора грунтується на явищі електромагнітної індукції.
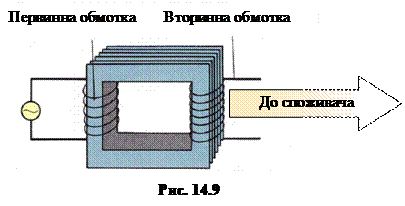
Трансформатор складається з двох (або більше) обмоток, надітих на спільне залізне осердя. Та обмотка, яка підключається до джерела живлення, называється первинною, а та, до якої підключають навантаження, – вторинною. Якщо напруга на вторинній обмотці u2 більша, ніж на первинній u1, трансформатор називають підвищувальним, інакше (u2 < u1) – знижувальним.
Роботу трансформатора якісно можна пояснити так. При протіканні в первинній обмотці змінного струму в залізному осерді виникає змінний магнітный потік, який пронизує обидві обмотки і створює в кожному витку однакову ЕРС індукції ei. Активний опір первинної обмотки малий порівняно з індуктивним. Тому спадом напруги на активному опорі можно нехтувати і вважати, що напруга на первинній обмотці
\(u_{1}=\mathcal{E}_{1}=Ne_{i}\),
де N1 – кількість витків у первинній обмотці.
При розімкненій вторинній обмотці (режим "холостого ходу") напруга на ній
\(u_{2}=\mathcal{E}_{2}=N_{2}e_{i}\),
де N2 – кількість витків у вторинній обмотці.
Отже, відношення напруг
|
|
\(k=\frac{U_{1}}{U_{2}}=\frac{\mathcal{E}_{1}}{\mathcal{E}_{2}}=\frac{N_{1}}{ N_{2}}\). |
(14.39) |
Величину k називають коефіцієнтом трансформації. Для знижувального трансформатора k > 1, для підвищувального k < 1. Однак на практиці коефіцієнт трансформації підвищувального трансформатора виражають числом \(k^{\prime}=\frac{1}{k}\), яке більше за одиницю. Наприклад, говорять: "підвищувальний трансформатор з коефіцієнтом трансформації 10".
В трансформаторі певна частка енергії електричного струму втрачається внаслідок виділення тепла на активних опорах обмоток та при перемагнічуванні осердя. Але ці втрати невеликі, і ККД трансформації близький до 1. Тому з достатньою точністю можна вважати, що потужності струму у обмотках однакові:
|
|
\(U_{1}I_{1}= U_{2}I_{2}\) \(\Rightarrow\) \(\frac{I_{2}}{I_{1}}=\frac{U_{1}}{U_{2}}=\frac{1}{k}\). |
(14.38) |
Отже, у скільки разів трансформатор змінює напругу, у стільки ж разів (тільки в зворотному напрямку) він змінює й силу струму.
Приклади розв'язування задач
Розв'язуючи задачі на коливання в ідеальному коливальному контурі і на змінний електричний струм, слід пригадати порядок організації та оформлення розв'язку задач (див. "Етапи розв'язування задач").
У прикладах цього розділу розглянуті:
1. Вільні коливання у контурі
2. Змінний струм
Вільні коливання у контурі
|
Задачі, в яких розглядаються коливання в ідеальному коливальному контурі, не вимагають спеціальних рекомендацій. Необхідно лише прийняти до відома, що розв’язування багатьох задач на коливання в контурі суттєво полегшується при застосуванні закону збереження енергії. |
Задача 14.1. Конденсатор ємністю C = 1000 пФ зарядили від джерела ЕРС \(\mathcal{E}\) = 10 В (рис.1) і у момент часу t = 0 замкнули на котушку індуктивності L = 10 мкГн. Нехтуючи опором провідників, визначити: А) частоту коливань \(\nu\) в контурі; Б) залежність від часу: – заряду конденсатора q(t); – струму в контурі i(t); – напруги uL(t) на котушці.
Задача 14.2. До конденсатора C ідеального контуру приєднали ще один такий же конденсатор. Визначити, у скільки разів (\(\eta\)) змінилася частота вільних коливань у контурі.
Задача 14.3. Коливальний контур з повітряним конденсатором має певну власну частоту (власною називається частота вільних коливань в ідеальному контурі). Контур помістили під вакуумний ковпак і відкачали повітря. В результаті власна частота контура змінилася на \(\Delta\nu=13\) Гц. Нехтуючи опором контура R, визначити діелектричну проникність \(\varepsilon\) повітря в умовах досліду.
Задача 14.4. В ідеальному коливальному контурі ємність конденсатора C = 1 мкФ, індуктивність котушки L = 100 мкГн. При вільних коливаннях в контурі максимальний заряд конденсатора qm = 1 мкКл. Визначити силу струму i в контурі в момент, коли заряд конденсатора в k = 3 рази менший за максимальний.
Задача 14.5. У коливальному контурі ємність конденсатора C = 20 мкФ, індуктивність котушки L = 2 мГн. В деякий момент часу напруга на конденсаторі u = 10 В, а сила струму в котушці i1 = 2 A. Визначити заряд конденсатора q в момент, коли сила струму в котушці i2 = 1 A.
Задача 14.6. У коливальному контурі, що має котушку індуктивності L = 0,2 Гн, амплітуда сили струму Im = 40 мА. Визначити енергію електричного WE і магнітного WB полів на момент, коли сила струму в n = 2 рази менша свого амплітудного значення.
Задача 14.7. У початковий момент часу напруга на конденсаторі контура має максимальне значення U0 = 400 В. Ємність конденсатора C = 10 мкФ. Унаслідок наявності опору провідників, амплітуда вільних коливань в контурі поступово зменшується. Визначити кількість теплоти Q, що виділяється в контурі за час, протягом якого амплітуда напруги на конденсаторі зменшиться в n = 2 рази.
Задача 14.1
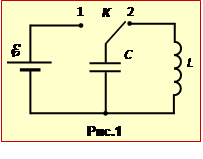 Конденсатор ємністю C = 1000 пФ зарядили від джерела ЕРС \(\mathcal{E}\) = 10 В (рис.1) і у момент часу t = 0 замкнули на котушку індуктивності L = 10 мкГн. Нехтуючи опором провідників,
Конденсатор ємністю C = 1000 пФ зарядили від джерела ЕРС \(\mathcal{E}\) = 10 В (рис.1) і у момент часу t = 0 замкнули на котушку індуктивності L = 10 мкГн. Нехтуючи опором провідників,
визначити:
А) частоту коливань \(\nu\) в контурі;
Б) залежність від часу:
– заряду конденсатора q(t);
– струму в контурі i(t);
– напруги uL(t) на котушці.
|
Дано: C = 1000 пФ = 10-9 Ф
L = 10 мкГн = 10-5 Гн
\(\mathcal{E}\) = 10 В
|
|
\(\nu\) - ?
q(t) - ?
i(t) - ?
uL(t) - ?
|
Розв’язання
При замиканні зарядженого конденсатора C на котушку L (ключ K на рис.1 в положенні 2) утворюється коливальний контур, в якому виникають вільні коливання. Оскільки по умові R = 0, то контур ідеальний, і коливання в ньому є гармонічними.
Частота коливань визначається формулою (14.7):
|
|
\(\nu=\frac{1}{2\pi\sqrt{LC}}=\frac{1}{2\cdot{3,14}\cdot\sqrt{10^{-5}\cdot{10^{-9}}}}=1,59\cdot{10^{6}}\) Гц = 1,59 МГц. |
(1) |
При цьому циклічна частота \(\omega=2\pi\nu=10^{-7}\) c-1. З умови задачі в початковий момент часу t = 0 напруга на конденсаторі, а значить і заряд, мають максимальні значення. Тому в рівнянні (14.8) початкову фазу слід узяти \(\varphi=0\). З урахуванням співвідношення (13.3), рівняння коливань заряду на конденсаторі має вигляд:
|
|
\(q(t)=q_{m}\cos(2\pi\nu{t})\). |
(2) |
При підключенні до джерела на конденсаторі встановилася максимальна напруга Um, що дорівнює ЕРС джерела \(U_{m}=\mathcal{E}\). Відповідно до формули (10.23), максимальний заряд
|
|
\(q_{m}=C\mathcal{E}=10^{-9}\cdot{10}=10^{-8}\) Кл. |
(3) |
З урахуванням величини qm і \(\nu\) (формула (1)), рівняння (2) в числовому вигляді записується як
|
|
\(q(t)=10^{-8}\cdot\cos(10^{7}\cdot{t})\), Кл. |
(4) |
Коливання сили струму в контурі визначаються загальним рівнянням (14.11). В даній задачі \(\varphi=0\), тому з урахуванням співвідношень (13.3):
|
|
\(i(t)=-2\pi\nu{q}_{m}\sin(2\pi\nu{t})\). |
(5) |
Підставивши значення \(\nu\) (формула (1)) і qm (формула (3)), отримаємо рівняння з числовими коефіцієнтами:
\(i(t)=-0,1\cdot\sin(10^{7}t)\), A.
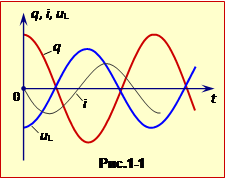
Напруга на ідеальній котушці індуктивності (R = 0) виникає тільки завдяки явищу самоіндукції. Згідно співвідношенням (12.14), (14.25) і рівнянню (5), для будь-якого моменту часу
\(u_{L}(t)=-L(2\pi\nu)^{2}q_{m}\cos(2\pi\nu{t})\).
З урахуванням формули (14.7) і виразу (3) одержуємо:
\(u_{L}(t)=-\mathcal{E}\cos(2\pi\nu{t})=\mathcal{E}\cos(2\pi\nu{t}+\pi)\).
Це означає, що коливання напруги на котушці відбуваються в протифазі з коливаннями напруги на конденсаторі. В числовому вигляді рівняння (6) записується як
\(u_{L}=10\cdot\cos(10^{-7}t+\pi)\).
Графіки залежності від часу q(t), i(t) і uL(t) показані на рис.1–1.
Задача 14.2
До конденсатора C ідеального контуру приєднали ще один такий же конденсатор.
Визначити,
у скільки разів (\(\eta\)) змінилася частота вільних коливань у контурі.
Розв’язання
Відповідно до формули (14.5a), шукане відношення частот
|
|
\(\eta=\frac{\omega_{2}}{\omega_{1}}=\sqrt{\frac{C}{C^{\prime}}}\), |
(1) |
де \(C,\ C^{\prime}\) – початкова і кінцева ємності контура.
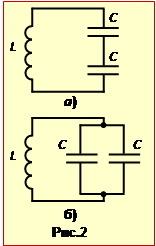 Оскільки в умові не вказаний спосіб приєднання додаткового конденсатора, треба розглянути два випадки:
Оскільки в умові не вказаний спосіб приєднання додаткового конденсатора, треба розглянути два випадки:
1) послідовне з'єднання (рис.2а),
2) паралельне з'єднання (рис.2б).
В першому випадку відповідно до формули (10.26), \(C^{\prime}=C/2\), а в другому, відповідно до формули (10.29), \(C^{\prime}=2C\).
Підставивши ці значення в співвідношення (1), отримаємо відповідь:
\(\eta_{1}=\sqrt{\frac{C}{(C/2)}}=\sqrt{2}\approx\) 1,41;
\(\eta_{2}=\sqrt{\frac{C}{(2C)}}=\frac{1}{\sqrt{2}}\approx\) 0,707.
Таким чином, при послідовному з'єднанні частота контура зростає в \(\sqrt{2}\approx\) 1,4 рази, а при паралельному – в стільки ж разів зменшується.
Задача 14.3
Коливальний контур з повітряним конденсатором має певну власну частоту (власною називається частота вільних коливань в ідеальному контурі). Контур помістили під вакуумний ковпак і відкачали повітря. В результаті власна частота контура змінилася на \(\Delta\nu=13\) Гц. Нехтуючи опором контура R,
визначити
діелектричну проникність \(\varepsilon\) повітря в умовах досліду.
|
Дано: \(\Delta\nu=13\) Гц
|
|
\(\varepsilon\) - ?
|
Розв’язання
При відкачуванні з конденсатора віддаляється діелектрик (повітря) і зменшується його ємність (формула (10.24)). В результаті (формула (14.7)) збільшується власна частота контура. Отже, після відкачування власна частота контура:
|
|
\(\nu_{0}=\nu+\Delta\nu\), |
(1) |
де \(\nu_{0}\) - частота після відкачування. З формули (14.7):
|
|
\(\nu_{0}=\frac{1}{2\pi\sqrt{LC_{0}}}\), \(\nu=\frac{1}{\sqrt{LC}}\), |
(2) |
де L – індуктивність контура, C0 і C – ємність конденсатора після і до відкачування повітря.
Розділивши почленно вирази (2) і врахувавши співвідношення (1), отримаємо:
\(1+\frac{\Delta\nu}{\nu}=\frac{C}{C_{0}}\).
Звідси, використовуючи формулу (10.24), отримаємо відповідь:
\(\varepsilon=\left(1+\frac{\Delta\nu}{\nu}\right)^{2}\) = 1,00063.
Примітка. Існують прилади, які дозволяють виміряти власні частоти контурів з великою точністю. Тому описаний в задачі експеримент є одним з лабораторних способів вимірювання діелектричних проникність газів, які дуже мало відрізняються від одиниці.
Задача 14.4
В ідеальному коливальному контурі ємність конденсатора C = 1 мкФ, індуктивність котушки L = 100 мкГн. При вільних коливаннях в контурі максимальний заряд конденсатора qm = 1 мкКл.
Визначити
силу струму i в контурі в момент, коли заряд конденсатора в k = 3 рази менший за максимальний.
|
Дано: C = 1 мкФ = 10-6 Ф
L = 100 мкГн = 10-4 Гн
\(q_{m}\) = 1 мкКл = 10-6 Кл
k = 3\(\)
|
|
i - ?
|
Розв’язання
Задачу можна розв’язати двома способами.
I спосіб. Нехай заряд конденсатора змінюється з часом за законом
|
|
\(q=q_{m}\cos(\omega{t}+\varphi_{0})\), |
(1) |
де qm – амплітуда заряду, \(\omega\) – частота коливань, \(\varphi_{0}\) – початкова фаза. Згідно з рівнянням (14.11), сила струму в контурі
|
|
\(i=q^{\prime}(t)=\frac{\mathrm{d}q}{\mathrm{d}t}=-q_{m}\omega\sin(\omega{t}+\varphi_{0})\), |
(2) |
Щоб не визначати фазу для обумовленого в умові моменту часу, виразимо з формул (1) і (2) тригонометричні функції:
\(\cos(\omega{t}+\varphi_{0})=\frac{q}{q_{m}}\); \(\sin(\omega{t}+\varphi_{0})=-\frac{i}{q_{m}\omega}\).
Якщо піднести ці вирази в квадрат і додати, отримаємо
\(\left(\frac{q}{q_{m}}\right)^{2}+\left(\frac{1}{q_{m}\omega}\right)^{2}=1\) \(\Rightarrow\) \(i=\omega\sqrt{1-\left(\frac{q}{q_{m}}\right)^{2}}\).
Враховуючи, що \(\frac{q}{q_{m}}=\frac{1}{k}\), \(\omega=\frac{1}{\sqrt{LC}}\), з виразу (3) після перетворення знаходимо:
\(i=\frac{q_{m}}{k}\sqrt{\frac{k^{2}-1}{LC}}=\frac{10^{-6}}{3}\sqrt{\frac{9-1}{10^{-4}\cdot{10^{-6}}}}=0,094\) А = 94 мА.
II спосіб. Відповідь задачі можна отримати за допомогою закону збереження енергії.
В ідеальному контурі повна енергія W, яка дорівнює сумі енергій електричного WE, і магнітного WB полів, не зміниться:
WE + WB = const.
Повна енергія, згідно виразу (14.16), дорівнює максимальному значенню енергії електричного WE або магнітного WB полів:
\(W=\frac{q_{m}^{2}}{2C}=\frac{Li_{m}^{2}}{2}\).
Енергії WE, і WB визначаються за формулами (14.14) і (14.15), тому
\(\frac{q^{2}}{2C}+\frac{Li^{2}}{2}=\frac{q_{m}^{2}}{2C}\) \(\Rightarrow\) \(i=\sqrt{\frac{q_{m}^{2}-q^{2}}{LC}}=\frac{q_{m}}{k}\sqrt{\frac{k^{2}-1}{LC}}\),
що, природно, співпадає з отриманим вище результатом. Зазначимо, що використовування закону збереження енергії істотно спростило розв’язування.
Задача 14.5
У коливальному контурі ємність конденсатора C = 20 мкФ, індуктивність котушки L = 2 мГн. В деякий момент часу напруга на конденсаторі u = 10 В, а сила струму в котушці i1 = 2 A.
Визначити
заряд конденсатора q в момент, коли сила струму в котушці i2 = 1 A.
|
Дано: C = 20 мкФ = 2·10-5 Ф
L = 2 мГн = 2·10-3 Гн
u = 10 В
\(i_{1}\) = 2 А
\(i_{2}\) = 1 А
|
|
q - ?
|
Розв’язання
Для розв’язання задачі використаємо законом збереження енергії.
В ідеальному коливальному контурі повна енергія залишається незмінною: W = const. Ця енергія складається з енергій електричного і магнітного полів, отже, для будь-яких двох моментів часу t1 і t2 можна записати
|
|
WE(t1) + WB(t1) = WE(t2) + WB(t2). |
(1) |
Енергія електричного поля конденсатора і магнітного поля котушки виражається формулами (10.32) і (12.15) відповідно:
\(W_{E}=\frac{q^{2}}{2C}=\frac{Cu^{2}}{2}\); \(W_{B}=\frac{Li^{2}}{2}\).
Підставивши ці формули у вираз (1), знайдемо
\(\frac{Cu^{2}}{2}+\frac{Li_{1}^{2}}{2}=\frac{q^{2}}{2C}+\frac{Li_{2}^{2}}{2}\) \(\Rightarrow\) \(q=\sqrt{C^{2}u^{2}+LC(Li_{1}^{2}-Li_{2}^{2})}\).
Виконаємо обчислення
\(q=\sqrt{4\cdot{10^{-10}}\cdot{10^{2}}+2\cdot{10^{-5}}\cdot{2}\cdot{10^{-3}}\cdot{(4-1)}}=4\cdot{10^{-4}}\) Кл = 400 мкКл.
Примітка. Цю задачу, як і попередню, можна розв'язати, розглядаючи рівняння коливань в конденсаторі. Але це набагато більш громіздкий спосіб.
Задача 14.6
У коливальному контурі, що має котушку індуктивності L = 0,2 Гн, амплітуда сили струму Im = 40 мА.
Визначити
енергію електричного WE і магнітного WB полів на момент, коли сила струму в n = 2 рази менша свого амплітудного значення.
|
Дано: L = 0,2 Гн
Im = 40 мА = 4·10-2 А
n = 2
|
|
WE, WB - ?
|
Розв’язання
Енергія магнітного поля котушки для будь-якого моменту часу визначається формулою (12.15)
\(W_{B}=\frac{Li^{2}}{2}\).
Звідси одержуємо значення повної енергії контура W (формула (14.16)) і енергії магнітного поля WB на момент часу, коли I = Im/2:
\(W=\frac{LI_{m}^{2}}{2}=\frac{0,2\cdot(4\cdot{10^{-2}})^{2}}{2}=1,6\cdot{10^{-4}}\) Дж = 160 мкДж.
\(W_{B}=\frac{LI_{m}^{2}}{2\cdot{4}}=\frac{W}{4}=40\) мкДж.
Енергію електричного поля WE визначимо із співвідношення (14.13):
WE = W – WB = 120 мкДж.
Задача 14.7
У початковий момент часу напруга на конденсаторі контура має максимальне значення U0 = 400 В. Ємність конденсатора C = 10 мкФ. Унаслідок наявності опору провідників, амплітуда вільних коливань в контурі поступово зменшується.
Визначити
кількість теплоти Q, що виділяється в контурі за час, протягом якого амплітуда напруги на конденсаторі зменшиться в n = 2 рази.
|
Дано: U0 = 400 В
C = 10 мкФ = 10-5 Ф
n = 2
|
|
Q - ?
|
Розв’язання
Кількість теплоти, яка виділяється при протіканні струму по провідниках контура, дорівнює зменшенню енергії коливань:
Q = W1 – W2.
Відповідно до формул (14.16) і (10.32), енергія конденсатора
\(W=\frac{CU^{2}}{2}=\frac{q^{2}}{2C}\).
отже, записавши вирази енергій для заданих моментів часу, маємо
\(Q= \frac{CU_{0}^{2}}{2}-\frac{C(U_{0}/n)^{2}}{2}=\frac{CU_{0}^{2}}{2}\cdot\frac{n^{2}-1}{n^{2}}\)
Виконаємо обчислення:
\(Q=\frac{10^{-5}\cdot{400^{2}}}{2}\cdot\frac{4-1}{4}=0,6\) Дж.
Змінний струм
|
Задачі, в яких розглядаються характеристики змінного електричного струму, не вимагають спеціальних рекомендацій. В задачах на змінний струм (якщо немає спеціальних вказівок) завжди задається діюче (ефективне) значення сили струму і напруги. |
Задача 14.8. Неонова лампочка горить, коли напруга на її електродах перевищує строго певне значення – напругу запалення Uз (незалежно від полярності). Лампочку включають в мережу з діючим значенням напруги, рівним напрузі запалення, U = Uз. Визначити, яку частину часу \(\eta\) (в частках періоду) горить лампочка.
Задача 14.9. У мережу змінного струму з частотою \(\nu\) = 50 Гц послідовно включені резистор R = 100 Ом і два однакові конденсатори по C = 30 мкФ. Один з конденсаторів пробивається. (При електричному пробої в діелектрику, який заповнює конденсатор, утворюється провідний канал, який сполучає (закорочує) пластини конденсатора). Визначити відношення сил струмів в колі до (I1) та після (I2) пробою одного з конденсаторів.
Задача 14.10. Якщо котушку з індуктивністю L = 0,03 Гн приєднати до батареї з нульовим внутрішнім опором і ЕРС \(\mathcal{E}\) = 9 В (рис.10а), то сила струму в котушці I1 = 1 A. Визначити силу струму в котушці I2, якщо її приєднати до джерела змінного струму з частотою \(\nu=50\) Гц і напругою \(U=\mathcal{E}\) (рис.10б)
Задача 14.11. Послідовно з’єднанні конденсатор C, котушка індуктивності L = 0,338 Гн і резистор R = 2 Ом підключені до джерела напруги U = 220 В з частотою \(\nu=50\) Гц. Визначити: А) ємність конденсатора C, при якій струм у колі буде максимальним; Б) напруга на кожному з елементів схеми (конденсаторі UC, котушці UL, резисторі UR) при максимальному струмі.
Задача 14.12. Електричне коло складається з послідовно з’єднаних котушки індуктивності L = 6 мкГн, конденсатора С = 0,01 мкФ і резистора R = 0,5 Ом. Визначити потужність P, яку необхідно підводити від джерела змінної напруги, щоб амплітуда напруги на конденсаторі при резонансі була U = 10 В.
Задача 14.13. Трансформатор, що підвищує напругу від U1 = 100 В до U2 = 3300 В, має замкнуте осердя у вигляді кільця. Крізь кільце пропущений дріт, кінці якого приєднані до вольтметра (рис.13). Вольтметр показує U = 0,5 В. Визначити кількість витків первинної N1 і вторинної N2 обмоток.
Задача 14.14. Трансформатор має осердя, показане на рис.14. Якщо обмотку I підключити до джерела з напругою U1 = 160 В, то напруга на обмотці II буде дорівнювати U. Джерело U1 відключають від обмотки I, і обмотку II підключають до джерела напруги U. Вважаючи, що магнітний потік ділиться порівну між розгалуженнями осердя визначити напругу U2 на виводах обмотки I. Опором обмотки нехтувати.
Задача 14.15. На первинну обмотку знижувального трансформатора з коефіцієнтом трансформації k = 20 подана напруга U1 = 220 В. При цьому у вторинній обмотці, яка замкнута на певне навантаження, тече струм I2 = 5 А. Активний опір вторинної обмотки r2 = 0,5 Ом. Нехтуючи втратами у первинній обмотці, визначити напругу \(U_{2}\) на клемах вторинної обмотки.
Задача 14.8
Неонова лампочка горить, коли напруга на її електродах перевищує строго певне значення – напругу запалення Uз (незалежно від полярності). Лампочку включають в мережу з діючим значенням напруги, рівним напрузі запалення, U = Uз.
Визначити,
яку частину часу \(\eta\) (в частках періоду) горить лампочка.
|
Дано: \(U=U_{з}\)
|
|
\(\eta\) - ?
|
Розв’язання
Відповідно до означення (формула 14.36), діюче (або ефективне) значення напруги дорівнює
\(U=\frac{U_{m}}{\sqrt{2}}\),
де Um – амплітуда напруги.
Залежність напруги від часу визначається законом (14.17):
\(u=U_{m}\sin\omega{t}\),
 Графік цієї функції, а також рівні діючого значення напруги і рівного йому напруги запалення показані на рис.8. З нього зрозуміло, що лампочка горітиме в проміжках часу \(\left[t_{1},\ t_{2}\right]\) і \(\left[t_{3},\ t_{4}\right]\). З симетрії графіка функції \(\sin\omega{t}\) очевидно, що час горіння лампочки протягом одного періоду визначається за формулою
Графік цієї функції, а також рівні діючого значення напруги і рівного йому напруги запалення показані на рис.8. З нього зрозуміло, що лампочка горітиме в проміжках часу \(\left[t_{1},\ t_{2}\right]\) і \(\left[t_{3},\ t_{4}\right]\). З симетрії графіка функції \(\sin\omega{t}\) очевидно, що час горіння лампочки протягом одного періоду визначається за формулою
\(\tau=T-4t_{1}\).
Час t1 знайдемо з умови загорання лампочки, враховуючи задану в умові рівність u = Uз:
\(U_{з}=\frac{U_{m}}{\sqrt{2}}=U_{m}\sin\omega{t}_{1}\) \(\Rightarrow\) \(\sin\omega{t}_{1}=\frac{1}{\sqrt{2}}\) \(\Rightarrow\) \(\omega{t}_{1}=\frac{\pi}{4}\).
Беручи до уваги, що циклічна частота пов'язана з періодом як \(\omega=2\pi/T\), знаходимо:
\(\frac{2\pi}{T}t_{1}=\frac{\pi}{4}\) \(\Rightarrow\) \(t_{1}=\frac{T}{8}\).
Отже
\(\tau=T-4\frac{T}{8}=\frac{T}{2}\) \(\Rightarrow\) \(\eta=\frac{\tau}{T}=0,5=50\) %.
Отже, лампочка горітиме половину часу, протягом якого вона підключена до електромережі.
Задача 14.9
 У мережу змінного струму з частотою \(\nu\) = 50 Гц послідовно включені резистор R = 100 Ом і два однакові конденсатори по C = 30 мкФ (рис.9). Один з конденсаторів пробивається. (При електричному пробої в діелектрику, який заповнює конденсатор, утворюється провідний канал, який сполучає (закорочує) пластини конденсатора).
У мережу змінного струму з частотою \(\nu\) = 50 Гц послідовно включені резистор R = 100 Ом і два однакові конденсатори по C = 30 мкФ (рис.9). Один з конденсаторів пробивається. (При електричному пробої в діелектрику, який заповнює конденсатор, утворюється провідний канал, який сполучає (закорочує) пластини конденсатора).
Визначити
відношення сил струмів в колі до (I1) та після (I2) пробою одного з конденсаторів. (Якщо говорять "сила струму" або "напруга" в колі змінного струму, то завжди мають на увазі діючі значення).
|
Дано: \(\nu\) = 50 Гц
R = 100 Ом
C = 30 мкФ = 3·10-5 Ф
|
|
\(I_{1}/I_{2}\) - ?
|
Розв’язання
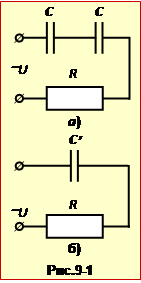 Унаслідок пробою, замість початкового кола (рис.9–1а) утворюється нове коло (рис.9–1б). Сила змінного струму в колі визначається законом Ома. Тому шукане відношення дорівнює оберненому відношенню імпедансів:
Унаслідок пробою, замість початкового кола (рис.9–1а) утворюється нове коло (рис.9–1б). Сила змінного струму в колі визначається законом Ома. Тому шукане відношення дорівнює оберненому відношенню імпедансів:
\(\frac{I_{2}}{I_{1}}=\frac{Z_{1}}{Z_{2}}\).
Оскільки в колі відсутня індуктивність, то імпеданс кола
\(Z=\sqrt{R^{2}+X_{C}^{2}}\).
Реактивний ємнісний опір XC визначається формулою (14.23)
\(X_{C}=\frac{1}{2\pi\nu{C}}\).
Враховуючи, що в даній задачі C2 = C, а C1 = C/2 (див. формулу (10.26)), знаходимо:
\(Z_{1}=\sqrt{R^{2}+\left(\frac{1}{2\pi\nu(C/2)}\right)^{2}}\) = 234,6 Ом.
\(Z_{2}=\sqrt{R^{2}+\left(\frac{1}{2\pi\nu{C}}\right)^{2}}\) =145,8 Ом.
Таким чином:
\(\frac{I_{1}}{I_{2}}=\frac{145,8}{234,6}\approx\) 0,62,
тобто сила струму після пробою збільшиться в \(\approx{1,6}\) рази.
Задача 14.10
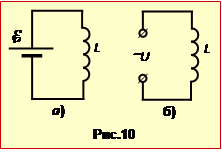 Якщо котушку з індуктивністю L = 0,03 Гн приєднати до батареї з нульовим внутрішнім опором і ЕРС \(\mathcal{E}\) = 9 В (рис.10а), то сила струму в котушці I1 = 1 A.
Якщо котушку з індуктивністю L = 0,03 Гн приєднати до батареї з нульовим внутрішнім опором і ЕРС \(\mathcal{E}\) = 9 В (рис.10а), то сила струму в котушці I1 = 1 A.
Визначити
силу струму в котушці I2, якщо її приєднати до джерела змінного струму з частотою \(\nu=50\) Гц і напругою \(U=\mathcal{E}\) (рис.10б)
|
Дано: L = 0,03 Гн
\(\mathcal{E}\) = 9 В
\(I_{1}\) = 1 A
\(\nu=50\) Гц
\(U=\mathcal{E}\)
|
|
I2 - ?
|
Розв’язання
В першому випадку в котушці тече постійний струм, сила якого залежить тільки від активного опору R (опора дроту, яким намотана котушка) і ЕРС джерела. Еквівалентна схема кола для цього випадку показана на рис.10а. Якщо ж струм змінний, то повний опір кола визначається не тільки опором дроту R, але й індуктивністним опором котушки XL (рис.10б). Відповідно до закону Ома для постійного (11.15) і змінного (14.30) струму маємо:
|
|
\(I_{1}=\frac{\mathcal{E}}{R}\), \(I_{2}=\frac{U}{Z}\). |
(1) |
Звідси, з урахуванням умови \(U=\mathcal{E}\), одержуємо:
|
|
\(\frac{I_{2}}{I_{1}}=\frac{R}{Z}\) \(\Rightarrow\) \(I_{2}=I_{1}\frac{R}{Z}\), |
(2) |
де Z – імпенданс (повний опір) котушки. Оскільки в колі немає конденсатора, то опір ємності XC = 0, і з формул (14.31) і (14.28) випливає
\(Z=\sqrt{R^{2}+(2\pi\nu{L})^{2}}\).
Підставивши цей вираз у формулу (2), отримаємо:
|
|
\(I_{2}=I_{1}\frac{R}{\sqrt{R^{2}+(2\pi\nu{L})^{2}}}\) = \(I_{1}\frac{1}{\sqrt{1+\left(2\pi\nu{L}/{R}\right)^{2}}}\). |
(3) |
З формули (1) \(R=\mathcal{E}/I_{1}\), тому остаточна відповідь має вигляд:
\(I_{2}=\frac{1}{\sqrt{1/I_{1}^{2}+\left(2\pi\nu{L}/\mathcal{E}\right)^{2}}}\).
Виконавши обчислення одержимо:
I2 = 0,7 A.
Задача 14.11
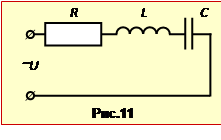 Послідовно з’єднанні конденсатор C, котушка індуктивності L = 0,338 Гн і резистор R = 2 Ом підключені до джерела напруги U = 220 В з частотою \(\nu=50\) Гц (рис.11)
Послідовно з’єднанні конденсатор C, котушка індуктивності L = 0,338 Гн і резистор R = 2 Ом підключені до джерела напруги U = 220 В з частотою \(\nu=50\) Гц (рис.11)
Визначити:
А) ємність конденсатора C, при якій струм у колі буде максимальним;
Б) напруга на кожному з елементів схеми (конденсаторі UC, котушці UL, резисторі UR) при максимальному струмі.
|
Дано: L = 0,338 Гн
R = 2 Ом
\(\nu=50\) Гц
|
|
C - ?
UC, UL, UR - ?
|
Розв’язання
А) Струм в колі (рис.11) буде найбільшим при мінімальному значенні повного опору, тобто при виконанні умови Z = R (див. формули (14.31), (14.31a)). Тому
\(\omega{L}-\frac{1}{\omega{C}}=0\) \(\Rightarrow\) \(\omega{L}=\frac{1}{\omega{C}}\).
Звідси знаходимо:
\(C=\frac{1}{\omega^{2}L}=\frac{1}{(2\pi\nu)^{2}L}=\frac{1}{(2\pi\cdot{50})^{2}\cdot{0,338}}=3\cdot{10^{-5}}\) Ф = 30 мкФ.
Б) За законом Ома (14.30) при Z = R маємо:
\(I_{m}=\frac{U}{R}\).
Підставивши цей вираз у формули (14.24), (14.29), (14.20), знаходимо:
\(U_{C}=\frac{I}{\omega{C}}=\frac{U}{2\pi\nu{CR}}=\frac{220}{22\cdot{2}\cdot{3,14}\cdot{50}\cdot{3}\cdot{10^{-5}}}=1061\) В;
\(U_{L}=I\omega{L}=\frac{U}{R}2\pi\nu{L}=\frac{220}{22}\cdot{2}\cdot{3,14}\cdot{50}\cdot{0,338}=1061\) В.
В отриманих результатах впадає в очі здавалося б парадоксальний факт – напруги на конденсаторі і котушці майже в 5 разів перевищують напругу джерела, а напруга на резисторі дорівнює напрузі джерела так, ніби конденсатора і котушки у колі немає. Ці особливості зв'язані з тим, що напруги на котушці і конденсаторі мають протилежні фази і виявляються рівними по величині.
Задача 14.12
Електричне коло складається з послідовно з’єднаних котушки індуктивності L =6 мкГн, конденсатора С = 0,01 мкФ і резистора R = 0,5 Ом.
Визначити
потужність P, яку необхідно підводити від джерела змінної напруги, щоб амплітуда напруги на конденсаторі при резонансі була U = 10 В.
Вказівка: Для змінного струму слово "потужність" без спеціальних домовленостей означає середню потужність за період.
|
Дано: L =6 мкГн = 6·10-6 Гн
С = 0,01 мкФ = 10-8 Ф
R = 0,5 Ом
U = 10 В
|
|
P - ?
|
Розв’язання
 Схема заданого кола зображена на рис.12. В колі змінного струму енергію споживає тільки резистор і вона визначається формулами (14.33), (14.34). В умовах резонансу з формул (14.31a), (14.32) і (14.34), маємо:
Схема заданого кола зображена на рис.12. В колі змінного струму енергію споживає тільки резистор і вона визначається формулами (14.33), (14.34). В умовах резонансу з формул (14.31a), (14.32) і (14.34), маємо:
\(Z=R\), \(\cos\varphi=1\)
Тому потужність, яка виділяється в колі, відповідно до формул (14.33) і (14.30), дорівнює:
|
|
\(P=\frac{1}{2}I_{р}U_{р}=\frac{1}{2}I_{р}^{2}R\), |
(1) |
де Iр – резонансна амплітуда сили струму в колі.
Значення Iр знаходимо через задану величину Uр за допомогою закону Ома (формула (14.24)), врахувавши вираз (14.32):
\(I_{р}=\frac{U_{р}}{X_{р}}=\omega{C}U_{р}=\frac{CU_{р}}{\sqrt{LC}}\) \(\Rightarrow\) \(I_{р}=U\sqrt{\frac{C}{L}}\).
Підставивши цей вираз у формулу (1), отримаємо відповідь:
\(P=\frac{RCU_{р}^{2}}{2L}\approx{4,17}\cdot{10^{-2}}\) Вт = 41,7 мВт.
Задача 14.13
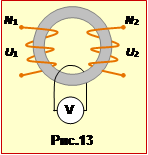 Трансформатор, що підвищує напругу від U1 = 100 В до U2 = 3300 В, має замкнуте осердя у вигляді кільця. Крізь кільце пропущений дріт, кінці якого приєднані до вольтметра (рис.13). Вольтметр показує U = 0,5 В.
Трансформатор, що підвищує напругу від U1 = 100 В до U2 = 3300 В, має замкнуте осердя у вигляді кільця. Крізь кільце пропущений дріт, кінці якого приєднані до вольтметра (рис.13). Вольтметр показує U = 0,5 В.
Визначити
кількість витків первинної N1 і вторинної N2 обмоток.
|
Дано: \(U_{1}\) = 100 В
\(U_{2}\) = 3300 В
\(U\) = 0,5 В
|
|
N1, N2 - ?
|
Розв’язання
Дріт разом з вольтметром утворюють замкнутий контур. Його поверхня пронизується магнітним потоком, створеним струмом в первинній обмотці. Це дозволяє вважати дріт (разом з вольтметром) обмоткою трансформатора, що має один виток. Для цієї "обмотки" формула трансформатора (14.39) набуває вигляд:
\(\frac{U}{U_{1}}=\frac{1}{N_{1}}\) \(\Rightarrow\) \(N_{1}=\frac{U_{1}}{U}=\frac{100}{0,5}=200\).
Таким чином, первинна обмотка трансформатора складається з N1 = 200 витків. Число витків вторинної обмотки трансформатора N2 також знаходимо з формули (14.39):
\(\frac{U_{1}}{U_{2}}=\frac{N_{1}}{N_{2}}\) \(\Rightarrow\) \(N_{2}=N_{1}\frac{U_{2}}{U_{1}}=200\cdot\frac{3300}{100}=6600\),
або
\(\frac{U}{U_{2}}=\frac{1}{N_{2}}\) \(\Rightarrow\) \(N_{2}=\frac{U_{2}}{U}=\frac{3300}{0,5}=6600\).
Задача 14.14
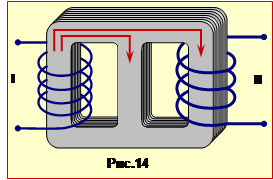 Трансформатор має осердя, показане на рис.14. Якщо обмотку I підключити до джерела з напругою U1 = 160 В, то напруга на обмотці II буде дорівнювати U. Джерело U1 відключають від обмотки I, і обмотку II підключають до джерела напруги U. Вважаючи, що магнітний потік ділиться порівну між розгалуженнями осердя
Трансформатор має осердя, показане на рис.14. Якщо обмотку I підключити до джерела з напругою U1 = 160 В, то напруга на обмотці II буде дорівнювати U. Джерело U1 відключають від обмотки I, і обмотку II підключають до джерела напруги U. Вважаючи, що магнітний потік ділиться порівну між розгалуженнями осердя
визначити
напругу U2 на виводах обмотки I. Опором обмотки нехтувати.
|
Дано: \( {U}_{1}\) = 160 В
|
|
U2 - ?
|
Розв’язання
Припустимо, що кількість витків в обмотках I і II рівні N1 і N2 відповідно. Тоді напруга на обмотці I згідно з формулою (12.12)
|
|
\(U_{1}=N_{1}\Phi_{1}^{\prime}(t)\), |
(1) |
де \(\Phi_{1}\) – магнітний потік, створений в осерді струмом в обмотці I, \(\Phi_{1}^{\prime}(t)\) – похідна магнітного потоку по часу. Оскільки потік \(\Phi_{1}\) ділиться порівну між розгалуженнями, обмотку II пронизує потік \(\Phi_{2}=\Phi_{1}/2\), індукуючи напругу U, яка дорівнює ЕРС у цій обмотці (обмотка розімкнена):
|
|
\(U=N_{2}\Phi_{2}^{\prime}(t)=\frac{N_{2}}{2}\Phi_{1}^{\prime}(t)\). |
(2) |
З формули (1) і (2) знаходимо
|
|
\(\frac{U}{U_{1}}=\frac{N_{2}}{2N_{1}}\). |
(3) |
Якщо джерело напруги U підключити до обмотки II, то міркуючи аналогічно попередньому, нескладно отримати
|
|
\(\frac{U_{2}}{U}=\frac{N_{1}}{2N_{2}}\). |
(4) |
Помноживши отриманий вираз (4) на (3), знаходимо відповідь:
\(\frac{U_{2}}{U_{1}}=\frac{1}{4}\) \(\Rightarrow\) \(U_{2}=\frac{U_{1}}{4}=\frac{160}{4}=40\) В.
Задача 14.15
На первинну обмотку знижувального трансформатора з коефіцієнтом трансформації k = 20 подана напруга U1 = 220 В. При цьому у вторинній обмотці, яка замкнута на певне навантаження, тече струм I2 = 5 А. Активний опір вторинної обмотки r2 = 0,5 Ом. Нехтуючи втратами у первинній обмотці,
Визначити
напругу \(U_{2}\) на клемах вторинної обмотки.
|
Дано: k = 20
\(U_{1}=\) 220 В
\(I_{2}=\) 5 A
\(r_{2}=\) 0,5 Ом
|
|
\(U_{2}\) - ?
|
Розв’язання
Відповідно до означення (14.39), коефіцієнт трансформації
|
|
\(k=\frac{\mathcal{E}_{1}}{\mathcal{E}_{2}}\). |
(1) |
де \(\mathcal{E}_{1}\) – ЕРС самоіндукції в первинній обмотці, \(\mathcal{E}_{2}\) – ЕРС індукції у вторинній обмотці.
За умовою в первинній обмотці втрат немає, тому можна записати:
|
|
\(U_{1}=\mathcal{E}_{1}\). |
(2) |
Для вторинної обмотки, згідно із законом Ома (формула (11.17)),
|
|
\(U_{2}=\mathcal{E}_{2}-I_{2}r_{2}\). |
(3) |
де \( I_{2}r_{2}\) – спад напруги на активному опорі обмотки.
Відповідно до співвідношень (1) і (2),
\(\mathcal{E}_{2}=\frac{\mathcal{E}_{1}}{k}=\frac{U_{1}}{k}\).
Підставивши цей вираз в співвідношення (3), отримаємо відповідь:
\(U_{2}=\frac{U_{1}}{k}-I_{2}r_{2}\) = 8,5 В.
Розділ 15. Хвилі
|
Хвилями називаються збурення різної фізичної природи, що поширюються в просторі з часом. Найчастіше, ці збурення являють собою коливання того або іншого виду і походження. У природі спостерігаються та широко використовуються людиною механічні і електромагнітні хвилі, проявами яких, зокрема, є звук і світло. Зауважимо, що у теоретичній фізиці розглядаються й інші хвилі. Незалежно від природи, усі хвилі мають низку спільних властивостей і ознак, за якими їх класифікують і описують математично. Теоретичні відомості |
Теоретичні відомості. Типи хвиль
|
Хвилі класифікують за різними ознаками. Зокрема, за напрямком коливань усі хвилі поділяють на поперечні і повздовжні. Іншою визначальною ознакою є закон, за яким відбуваються коливання у хвилі. За цією ознакою найпростішим і найважливішим типом хвиль є монохроматичні хвилі. |
Поперечною називається хвиля, у якій коливання відбуваються в напрямках, перпендикулярних до напрямку поширення хвилі. Наочним прикладом поперечних хвиль є хвилі на поверхні води.
Повздовжньою називається така хвиля, в якій коливання відбуваються уздовж напрямку поширення хвилі. Прикладом повздовжніх хвиль є звукові хвилі у газах.
Поперечні хвилі можуть існувати тільки в середовищах, здатних зберігати форму (яким властива «пружність форми»). Таку здатність мають тверді тіла і вільна поверхня рідин. Тому у твердому тілі можливі як повздовжні, так і поперечні хвилі. Хвилі в об'ємі рідини є повздовжніми, а на поверхні – поперечними. У газах можливі тільки повздовжні хвилі.
Монохроматичною хвилею називається поширення гармонічних коливань (походження терміну "монохроматична" наводиться далі в р. 5. Оптика).
Відповідно до критерію гармонічних коливань (див. розділ 13 , формулу (13.10)), механічні монохроматичні хвилі можливі тільки в пружних середовищах, в яких енергія механічних коливань не перетворюється в інші форми.
Аналогічно монохроматичні електромагнітні хвилі можливі тільки в діелектриках – середовищах, в яких енергія електромагнітних коливань не перетворюється у внутрішню (теплову) енергію.
Теоретичні відомості. Рівняння і параметри монохроматичної хвилі
Найпростішою за властивостями монохроматичною хвилею є плоска хвиля. У рівнянні плоскої монохроматичної хвилі міститься інформація про основні параметри монохроматичної хвилі: амплітуду, період (частоти), швидкість поширення і довжину хвилі (хвильове число). Крім того використовуються такі поняття: фаза, хвильові поверхні, промінь, різниця фаз та різниці ходу.
 Уявлення про плоску монохроматичну хвилю можна одержати, якщо уявити нескінченну площину-мембрану, яка здійснює гармонічні коливання в пружному середовищі (рис.15.1). Завдяки силам зчеплення між частинками середовища, ці коливання в усіх точках поширюються паралельно осі OX. Звичайно, коливання поширюються в обидва боки від мембрани. Але оскільки їхні властивості не залежать від напрямку, то надалі будемо вважати, що хвиля поширюється в додатному напрямку осі OX.
Уявлення про плоску монохроматичну хвилю можна одержати, якщо уявити нескінченну площину-мембрану, яка здійснює гармонічні коливання в пружному середовищі (рис.15.1). Завдяки силам зчеплення між частинками середовища, ці коливання в усіх точках поширюються паралельно осі OX. Звичайно, коливання поширюються в обидва боки від мембрани. Але оскільки їхні властивості не залежать від напрямку, то надалі будемо вважати, що хвиля поширюється в додатному напрямку осі OX.
З огляду симетрії зрозуміло, що коливання всіх точок середовища в будь-якій площині, паралельній мембрані, повністю однакові. Тому така хвиля називається плоскою.
У пружному середовищі відсутнє поглинання енергії коливань. Тому коливання частинок середовища в плоскій хвилі мають однакову амплітуду і частоту. Але оскільки хвиля поширюється з кінцевою швидкістю, коливання у віддалених від джерела (мембрани) точках починаються з деяким запізненням.
Нехай мембрана і частинки середовища, що безпосередньо прилягають до неї, здійснюють коливання за законом
\(\xi(0,t)=\xi_{0}\cos\frac{2\pi}{t}t\),
де \(\xi\) – відхилення від положення рівноваги в момент часу t частинок середовища (у випадку немеханічної хвилі – це, відповідно, інша величина), розташованих в площині x = 0, \(\xi_{0}\) – амплітуда, T – період коливань.
Частинки, розташовані на відстані x від джерела, почнуть коливання з деяким запізненням \(\tau\). Отже, ці коливання описуються рівнянням
\(\xi(x,t)=\xi_{0}\cos\frac{2\pi}{T}(t-\tau)\).
Якщо хвиля поширюється зі швидкістю v, то \(\tau=x/v\) (див. рис.15.1), і
|
|
\(\xi(x,t)=\xi_{0}\cos\frac{2\pi}{T}\left(t-\frac{x}{v}\right)\). |
(15.1) |
Рівняння (15.1) називається рівнянням плоскої монохроматичної хвилі, що поширюється уздовж осі OX. Так само, як у випадку гармонічних коливань, існує кілька рівнозначних способів представлення рівняння монохроматичної хвилі, див. нижче. Рівняння (15.1) дає значення величини \(\xi\) у будь-якій точці простору і у будь-який момент часу.
Усі характеристики гармонічних коливань є також параметрами монохроматичної хвилі. Зокрема, – це амплітуда, період, циклічна або лінійна частота (див. розділ 13 ("Механічні коливання"), формули (13.1), (13.2), (13.3)).
Коливання в монохроматичній хвилі вимушені, вони створюються і підтримуються джерелом. Тому
|
амплітуда і період (частота) хвилі визначаються тільки джерелом і не залежать від властивостей середовища. |
Швидкість поширення хвилі характеризується швидкістю хвилі v, тобто відстанню, на яку поширюються коливання від джерела за одиницю часу.
|
Швидкість хвилі залежить тільки від її фізичної природи і властивостей середовища. |
У будь-якій заданій точці x = x0 відповідно до рівняння (15.1) збуджуються гармонічні коливання (рис.15.2а):
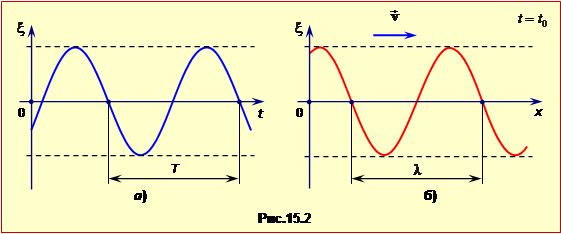
|
|
\(\xi(t)=\xi_{0}\cos\left(\frac{2\pi}{T}t-\varphi_{0}\right)\). |
(15.2) |
початкова фаза яких \(\varphi_{0}\) визначається положенням цієї точки:
|
|
\(\varphi_{0}=\frac{2\pi{x}}{Tv}\). |
(15.2а) |
Аналогічно в будь-який заданий момент часу t = t0 значення \(\xi\) залежать від координати за законом:
|
|
\(\xi(x)=\xi_{0}\cos\left(\frac{2\pi}{Tv}x-\varphi_{0}^{\prime}\right)\), |
(15.3) |
де
|
|
\(\varphi_{0}^{\prime}=\frac{2\pi{t}_{0}}{T}\). |
(15.3а) |
Таким чином, величина \(\xi\) змінюється від точки до точки теж за гармонічним законом (рис.15.2б). При цьому значення \(\xi\) повністю повторюються на відстані \(\lambda\) (рис.15.2.б), яка називається довжиною хвилі. З рівняння (15.3) випливає, що
|
|
\(\lambda=vT\). |
(15.4) |
Можна сказати, що довжина хвилі – це відстань, на яку поширюється хвиля за час одного періоду коливань.
Очевидно також, що
|
довжина хвилі визначається як джерелом (через період T), так і властивостями середовища (через швидкість v). |
Величину \(\lambda\) можливо також виражати через швидкість v і частоти \(\nu\) або \(\omega\) співвідношеннями:
|
|
\(\lambda=\frac{v}{\nu}\); |
(15.4а) |
|
|
\(\lambda=\frac{2\pi{v}}{\omega}\) |
(15.4б) |
З використанням \(\lambda\) рівняння хвилі (15.1) можна записати як
|
|
\(\xi(x,t)=\xi_{0}\cos\left(\frac{2\pi}{T}t-\frac{2\pi}{\lambda}x\right)\) |
(15.5) |
Замість періоду T використовують також частоту \(\omega=2\pi/T\), а замість довжини хвилі \(\lambda\) – так зване хвильове число:
|
|
\(k=\frac{2\pi}{\lambda}\). |
(15.6) |
При цьому рівняння монохроматичної хвилі записується найбільш компактно:
|
|
\(\xi(x,t)=\xi_{0}\cos(\omega{t}-kx)\). |
(15.7) |
Коливання у хвилі в кожній точці в кожен момент часу визначаються фазою.
Фазою хвилі називається аргумент функції в рівнянні хвилі, наприклад у (15.7)
|
|
\(\phi=\omega{t}-kx\). |
(15.8) |
У будь-якій заданій точці фаза безперервно змінюється з часом, а в будь-який заданий момент часу вона безперервно змінюється від точки до точки. Для наочного уявлення про розподіл фаз у просторі використовують поняття хвильових поверхонь, а для характеристики напрямків поширення хвилі використовують поняття променів.
Хвильова поверхня (іноді її називають фронтом хвилі) – це поверхня, у всіх точках якої фаза хвилі має одне і теж значення в даний момент часу.
Форма хвильових поверхонь дає наочне уявлення про хвилю. Вона залежить від типу джерела і властивостей середовища. Рівняння хвильових поверхонь знаходять підстановкою фіксованих значень \(\varphi=\varphi_{0}\) та t = t0 до рівняння фази. Для розглянутої тут хвилі з рівняння (15.8) виходить
\(\varphi_{0}=\omega{t}-kx\) \(\Rightarrow\) x = const.
Це означає, що хвильові поверхні являють собою площини, перпендикулярні осі OX, тобто напрямку поширення хвилі (рис.15.3а). Саме тому така хвиля називається плоскою.
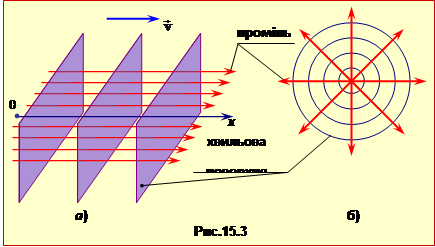
Іншим поширеним типом хвиль є сферична хвиля, що створюється точковим джерелом в однорідному ізотропному середовищі. Хвильові поверхні такої хвилі – сфери з центром у джерелі (рис.15.3б).
Промінь – це лінія, уздовж якої хвиля переносить енергію від джерела до даної точки.
У випадку однорідного та ізотропного середовища промені в кожній точці співпадають з напрямком швидкості хвилі і спрямовані уздовж нормалі до хвильової поверхні, що проходить через дану точку.
При розгляді різних хвильових явищ важливу роль відіграє різниця фаз хвилі \(\delta=\varphi_{2}-\varphi_{1}\) у двох точках в один і той же момент часу. Відповідно до рівняння (15.8) і формули (15.6)
|
|
\(\delta=\frac{2\pi}{\lambda}(x_{2}-x_{1})=\frac{2\pi}{\lambda}\Delta{x}\), |
(15.8) |
де \(\Delta{x}=x_{2}-x_{1}\) – різниця відстаней від цих точок до джерела.
Формулою (15.9) визначається також
|
різниця фаз двох монохроматичних хвиль однакової довжини хвилі (частоти), що приходять в одну точку від двох джерел. |
При цьому \(\Delta{x}\) – різниця відстаней від джерел до даної точки – називається різницею ходу хвиль (або променів).
Теоретичні відомості. Звукові хвилі
Механічні хвилі при визначених частотах коливань, діючи на органи слуху – вуха, створюють слухове відчуття і називаються чутним звуком. Крім чутного звуку, існують інфразвук та ультразвук. За суб'єктивним сприйняттям всі звуки поділяються на музичні звуки та шуми. Усі звуки характеризуються гучністю, а музичні ще й висотою тону та тембром.
Чутний для людини звук утворюють механічні хвилі в середовищі, що мають частоти в діапазоні:
\(\nu=(16\div{20000})\) Гц.
Діапазон частот чутного звуку для інших істот може відрізнятися. Так, кажани чують в ультразвуковому діапазоні частот.
Хвилі с частотами \(\nu<16\) Гц називаються інфразвуком, а з частотами \(\nu>20000\) Гц – ультразвуком.
Звукові хвилі практично ніколи не бувають монохроматичними. Вони несуть коливання різних частот або, як говорять, мають певний спектральний склад. Сприйняття звуку людиною сильно залежить від характеру спектра. Якщо звук складається з усіх можливих частот у широкому діапазоні, то спектр такого звуку називають безперервним. Звуки з безперервним спектром людина сприймає як шуми. Якщо ж звик складається з визначеного набору хвиль з окремими частотами у заданому діапазоні частот, то кажуть, що спектр такого звуку є дискретним. Звуки з дискретним спектром сприймаються як музичні.
Музичні звуки характеризуються висотою і тембром (колоратурою). Висота звуку визначається частотою основного тону, тобто найнижчою частотою в спектрі даного звуку. Більш високі частоти, кратні до основного тону, називаються обертонами або гармоніками.
Набір обертонів і їхні амплітуди визначають тембр звуку – специфічне «забарвлення», що робить звук приємним для слуху і визначає індивідуальне звучання людського голосу і кожного музичного інструмента
Незалежно від спектру всі звуки за силою впливу на вухо характеризуються гучністю. Гучність звуку визначається амплітудою звукової хвилі і чутливістю вуха, яка максимальна в середині звукового діапазону і різко зменшується на краях.
Теоретичні відомості. Електромагнітні хвилі
Іншим розповсюдженим типом хвиль є електромагнітні хвилі. Їх виникнення обумовлене здатністю електричних і магнітних полів до взаємних перетворень. Властивості цих полів визначають характерні властивості електромагнітних хвиль: поперечність, гранично велику швидкість поширення і здатність переносити енергію на дуже великі відстані.
Перенесення енергії характеризується інтенсивністю хвилі.
Змінне магнітне поле породжує вихрове електричне поле, а змінне електричне поле, у свою чергу, породжує магнітне поле. Як наслідок, змінне електромагнітне поле здатне "самовідтворюватися", тобто існувати незалежно від тих зарядів, що його створили. При цьому коливання електричних і магнітних полів у відкритому просторі відбуваються не в тому самому місці, як, наприклад, у коливальному контурі, а поширюються з кінцевою швидкістю, утворючи хвилю.
Зауваження. Вихровим поле називають тому, що його силові лінії замкнуті. Вихрове електричне поле може виконувати роботу при переміщенні заряду уздовж замкнутої траєкторії і створювати електричний струм у замкнутому провідному контурі.
Коливання напруженості електричного \(\vec{E}\) і індукції магнітного \(\vec{B}\) полів відбуваються в напрямках, перпендикулярних напрямку поширення хвилі, тобто
|
електромагнітні хвилі є поперечними. |
Крім того, коливання полів відбуваються в однаковій фазі і у взаємно перпендикулярних напрямках так, що вектори \(\vec{E}\) і \(\vec{B}\) утворюють з вектором швидкості хвилі \(\vec{v}\) праву трійку, як показано на рис.15.4.
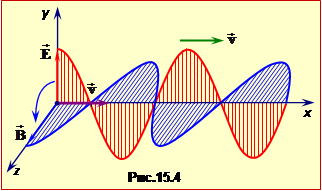
З рис. 15.4 видно, напрямки векторів у послідовності \(\vec{E}\), \(\vec{B}\), \(\vec{v}\), або \(\vec{B}\), \(\vec{v}\), \(\vec{E}\), або \(\vec{v}\), \(\vec{B}\), \(\vec{E}\), пов'язані правилом правого гвинта.
Швидкість поширення електромагнітних хвиль у вакуумі є універсальною фізичною сталою, яка майже точно дорівнює
\(c=3\cdot{10^{8}}\) м/с.
(Точне значення \(c=(299792458\pm{1,2})\) м/с)
Швидкість поширення електромагнітних хвиль у речовині залежить від діелектричної \(\varepsilon\) і магнітної \(\mu\) проникностей речовини:
|
|
\(v=\frac{c}{\sqrt{\varepsilon\mu}}\). |
(15.10) |
Практично всі речовини, в яких можуть поширюватися електромагнітні хвилі, є слабо магнітними (у них \(|\mu-1|\lt{0,0001}\)). Для них можна вважати \(\mu=1\) і
|
|
\(v=\frac{c}{\sqrt{\varepsilon}}\). |
(15.10а) |
Швидкість електромагнітних хвиль співпадає зі швидкістю поширення світла, що свідчить про електромагнітну природу світла. Тому електродинаміка є теоретичною базою хвильової оптики.
Електромагнітна хвиля переносить енергію, що випромінюється джерелом, в різні точки простору. Основною енергетичною характеристикою хвилі є інтенсивність.
Інтенсивність I чисельно дорівнює енергії, що переноситься хвилею за одиницю часу крізь одиничну площину, перпендикулярну до напрямку поширення хвилі:
|
|
\(I=\frac{\Delta{W}}{\Delta{t}\Delta{S}_{\bot}}\). |
(15.11) |
де \(\Delta{W}\) – енергія, що переноситься протягом часу \(\Delta{t}\) через площину \(\Delta{S}_{\bot}\).
Одиниця інтенсивності – 1 Вт/м2.
Приклади розв'язування задач
Розв'язування задач на хвилі проводять за схемою, викладеною у вступі (див. "Етапи розв'язування задач"), з урахуванням специфіки хвильових процесів.
1. При розгляді механічних хвиль, зокрема звукових, потрібно пам'ятати, що швидкість поширення хвилі і швидкість руху часток середовища – це зовсім різні швидкості. Перша визначається фізичними властивостями середовища, а друга – амплітудою і частотою хвилі.
2. Стандартні рівняння і формули, наведені в теоретичних відомостях, стосуються випадку, коли джерело і приймач (спостерігач) нерухомі відносно середовища, у якому поширюється хвиля. Але у випадку руху джерела або приймача (спостерігача) характеристики хвилі змінюються. Тому такі задачі вимагають особливої уваги.
Задача 15.1. Точки A, B та C лежать на лінії поширення плоскої монохроматичної хвилі. Точки B та C віддалені від точки A на відстані l1 = 15 см та l2 = 30 см відповідно. Швидкість поширення хвилі v = 0,6 м/с. Коливання в точці A відбуваються за законом \(\xi_{A}=0,05\cos(2\pi{t})\), м.
Задача 15.2. Джерело створює плоску звукову хвилю з частотою \(\nu\) = 500 Гц і амплітудою \(\xi_{m}=5\) мкм. Коливання в джерелі відбуваються за законом косинуса з нульовою початковою фазою. Для точки, що віддалена від джерела на відстань l = 170 м, і моменту часу t = 1 c. Визначити: А) зміщення частинок середовища від положення рівноваги \(\xi\); Б) швидкість їх коливального руху u; В) прискорення частинок a. Швидкість звуку прийняти v = 340 м/с.
Задача 15.3. У плоскій монохроматичній хвилі частота коливань частинок середовища \(\nu=10\) Гц. Різниця фаз коливань у двох точках, які лежать на лінії поширення хвилі на відстані \(\Delta{l}=100\) см одна від одної, дорівнює \(\Delta\varphi=\pi/4\). Визначити швидкість поширення хвилі v.
Задача 15.4. По озеру рухається катер, хвилі від якого дістаються до берега за час t = 1 хв. Відстань між гребенями хвиль l = 0,5 м, час між ударами хвиль об берег \(\tau=0,5\) с. Визначити відстань L від катера до берега.
Задача 15.5. Літак рухається горизонтально з надзвуковою швидкістю на висоті H = 4 км над землею. Спостерігач чує звук через час \(\tau= 10\) c після того, як літак пролетів над ним. Визначити швидкість літака u. Швидкість звуку взяти v = 330 м/с.
Задача 15.6. Тепловоз подає звуковий сигнал з частотою \(\nu_{0}=400\) Гц. Пасажир, який стоїть на платформі сприймає частоту сигналу \(\nu=380\) Гц. Визначити: швидкість V та напрям руху тепловоза. Швидкість звуку в повітрі прийняти v = 340 м/с.
Задача 15.7. Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n1 = 2 удари за секунду. Якщо ж катер рухається назустріч хвилям, то удари в ніс йдуть з частотою n2 = 4 удари за секунду. Визначити швидкість поширення хвиль v та швидкість руху катера V.
Задача 15.8. Вхідний коливальний контур радіоприймача з плоским повітряним конденсатором налаштований на довжину хвилі \(\lambda_{1}=200\) м. Визначити довжину хвилі \(\lambda_{2}\), на яку буде налаштований контур, якщо між обкладинками конденсатора розмістити діелектричну пластину з проникністю \(\varepsilon=6\), товщина якої в k = 3 рази менша ніж відстань між пластинами.
Задача 15.9. Частота електромагнітної хвилі \(\nu=1\) МГц. Визначити довжину електромагнітної хвилі: А) \(\lambda_{0}\) у вакуумі; Б) \(\lambda\) у немагнітному (\(\mu=1\)) діелектричному середовищі з діелектричною проникністю \(\varepsilon=2,25\).
Задача 15.10. На відстані l = 30 км від радіолокатора знаходиться літак. Визначити максимальне число імпульсів n, що може випромінювати локатор за \(\tau=1\) с для спостереження за літаком.
Задача 15.1
 Точки A, B та C лежать на лінії поширення плоскої монохроматичної хвилі. Точки B та C віддалені від точки A на відстані l1 = 15 см та l2 = 30 см відповідно. Швидкість поширення хвилі v = 0,6 м/с. Коливання в точці A відбуваються за законом \(\xi_{A}=0,05\cos(2\pi{t})\), м.
Точки A, B та C лежать на лінії поширення плоскої монохроматичної хвилі. Точки B та C віддалені від точки A на відстані l1 = 15 см та l2 = 30 см відповідно. Швидкість поширення хвилі v = 0,6 м/с. Коливання в точці A відбуваються за законом \(\xi_{A}=0,05\cos(2\pi{t})\), м.
Записати:
рівняння коливань в точках B та C.
|
Дано: \(\xi_{A}=0,05\cos(2\pi{t})\), м
l1 = 15 см = 0,15 м
l2 = 30 см = 0,3 м
|
|
\(x_{A}(t)\) - ?
\(x_{B}(t)\) - ?
|
Розв’язання
Коливання в заданій точці хвилі визначаються рівнянням (15.2) і співвідношенням (15.2a). Згідно з умовою задачі в точці A початкова фаза \(\varphi=0\), її координату приймемо xA = 0. Тоді, xB = l1, xC = l2. Оскільки хвиля поширюється зі швидкістю v, то коливання в точках B та C відстають по фазі від коливань у точці A і згідно з рівнянням (15.2) мають вигляд:
\(x_{B}=x_{m}\cos\left(2\pi{t}-\frac{2\pi{l_{1}}}{v}\right)\);
\(x_{C}=x_{m}\cos\left(2\pi{t}-\frac{2\pi{l_{2}}}{v}\right)\).
У числовому вигляді:
\(x_{B}=0.05\cdot\cos\left(2\pi{t}-\frac{2\pi\cdot{0,15}}{0,06}\right)=0,05\sin(2\pi{t})\);
\(x_{B}=0.05\cdot\cos\left(2\pi{t}-\frac{2\pi\cdot{0,3}}{0,06}\right)=-0,05\cos(2\pi{t})\).
Задача 15.2
Джерело створює плоску звукову хвилю з частотою \(\nu\) = 500 Гц і амплітудою \(\xi_{m}=5\) мкм. Коливання в джерелі відбуваються за законом косинуса з нульовою початковою фазою. Для точки, що віддалена від джерела на відстань l = 170 м, і моменту часу t = 1 c.
визначити:
А) зміщення частинок середовища від положення рівноваги \(\xi\);
Б) швидкість їх коливального руху u;
В) прискорення частинок a.
Швидкість звуку прийняти v = 340 м/с.
|
Дано: \(\nu\) = 500 Гц
\(\xi_{m}=5\) мкм = 5·10-6 м
l = 170 м
v = 340 м/с
t = 1 c
|
|
\(\xi\), u, a - ?
|
Розв’язання
A) Згідно з рівнянням (15.1) і формулою (13.2) можна записати:
|
|
\(\xi=\xi_{m}\cos\left(2\pi\nu{t}-\frac{2\pi\nu{l}}{v}\right)\) |
(1) |
Підставивши числові дані, отримаємо:
\(\xi=5\cdot{10^{-6}}\cdot\cos\left(1000\pi-\frac{1000\pi\cdot{170}}{340}\right)=5\cdot{10^{-6}}\) м = 5 мкм.
Б) Швидкість коливального руху частинок у хвилі – це похідна від зміщення по часу (формула (1.5)): \(u=\xi^{\prime}(t)\). Взявши похідну від функції (1), дістанемо
|
|
\(u=-2\pi\nu\xi_{m}\cdot\sin\left(2\pi\cdot{5}\cdot{10^{-5}}{t}-\frac{2\pi\nu{l}}{v}\right)\). |
(2) |
У числах
\(u=-1000\pi\cdot{5}\cdot{10^{-6}}\cdot\sin\left(1000\pi\cdot{1}-\frac{1000\pi\cdot{170}}{340}\right)=0\).
В) Прискорення частинок – це похідна швидкості коливального руху по часу (формула (1.7)): \(a=u^{\prime}(t)\). Взявши похідну від функції (2), знаходимо:
\(a=-(2\pi\nu)^{2}\xi\),
де, згідно з результатом пункту А), \(\xi=5\cdot{10^{-5}}\) м. Отже
\(a=-(2\pi\cdot{500})^{2}\cdot{5}\cdot{10^{-6}}=-49,3\) м/с2.
Задача 15.3
У плоскій монохроматичній хвилі частота коливань частинок середовища \(\nu=10\) Гц. Різниця фаз коливань у двох точках, які лежать на лінії поширення хвилі на відстані \(\Delta{l}=100\) см одна від одної, дорівнює \(\Delta\varphi=\pi/4\).
Визначити
швидкість поширення хвилі v.
|
Дано: \(\nu=10\) Гц
\(\Delta{l}=100\) см = 1 м
\(\Delta\varphi=\pi/4\)
|
|
v - ?
|
Розв’язання
Відповідно до формули (15.9) можна записати:
|
|
\(\Delta\varphi=\frac{2\pi}{\lambda}\Delta{l}\), |
(1) |
де \(\Delta{l}\) – задана відстань між точками, \(\lambda\) – довжина хвилі.
Швидкість поширення хвилі v виражається через довжину хвилі на основі формули (15.4a):
|
|
\(v=\lambda\nu\), |
(2) |
Виразивши величину l з співвідношення (1) і підставивши її у формулу (2), дістанемо
\(v=\frac{2\pi\nu\Delta{l}}{\Delta\varphi}=\frac{2\pi\cdot{10}\cdot{1}}{\pi/4}=80\) м/с.
Задача 15.4
По озеру рухається катер, хвилі від якого дістаються до берега за час t = 1 хв. Відстань між гребенями хвиль l = 0,5 м, час між ударами хвиль об берег \(\tau=0,5\) с.
Визначити
відстань L від катера до берега.
|
Дано: t = 1 хв = 60 c
l = 0,5 м
\(\tau=0,5\) с
|
|
L - ?
|
Розв’язання
Відстань між гребнями хвиль – то є довжина хвилі, час між ударами хвиль об берег дорівнює періоду коливань. Скориставшись зв'язком між довжиною хвилі \(\lambda\), періодом коливань T та швидкістю поширення хвилі v (формула (15.4)), знайдемо
\(v=\frac{\lambda}{T}=\frac{l}{\tau}\).
Тоді відстань, яку проходить хвиля за час t, становить
\(L=vt=\frac{l}{\tau}t=\frac{0,5}{0,5}\cdot{60}=60\) м.
тобто катер пливе на відстані 60 м від берега.
Задача 15.5
Літак рухається горизонтально з надзвуковою швидкістю на висоті H = 4 км над землею. Спостерігач чує звук через час \(\tau= 10\) c після того, як літак пролетів над ним.
Визначити
швидкість літака u. Швидкість звуку взяти v = 330 м/с.
|
Дано: H = 4 км = 4000 м
\(\tau= 10\) c
v = 330 м/с
|
|
u - ?
|
Розв’язання
Літак у кожній точці свого перебування випромінює сферичну хвилю. Обвідна всіх цих сферичних хвильових поверхонь утворює конус, який являє собою фронт звукової хвилі, що поширюється від літака. На рис.5 показаний перетин деяких з цих сферичних поверхонь з площиною рисунка та слід обвідної O2C. З рис.5 можна збагнути, що спостерігач (точка C) чує звук, який був випромінений літаком у точці O1. В той момент, коли хвиля дійшла до спостерігача, літак вже знаходиться у точці O2.
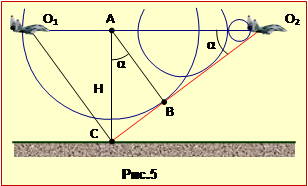 Врахуємо, що обвідна сферичних хвиль O2C перпендикулярна до радіусів сфер. Отже на рис.5 трикутники \(\Delta{O}_{1}O_{2}C\), \(\Delta{A}O_{2}B\) та \(\Delta{A}CB\) прямокутні та подібні. За умовою задачі літак долає відстань AO2 за час \(\tau\), тому
Врахуємо, що обвідна сферичних хвиль O2C перпендикулярна до радіусів сфер. Отже на рис.5 трикутники \(\Delta{O}_{1}O_{2}C\), \(\Delta{A}O_{2}B\) та \(\Delta{A}CB\) прямокутні та подібні. За умовою задачі літак долає відстань AO2 за час \(\tau\), тому
\(AO_{2}=u\tau\).
За цей же час звукова хвиля, що була випромінена літаком у точці A, доходить до точки B, отже
\(AB=v\tau\).
З трикутника AO2B маємо:
\(\sin\alpha=\frac{AB}{AO_{2}}=\frac{v}{U}\).
З трикутника ABC:
\(H=\frac{AB}{\cos\alpha}=\frac{v\tau}{\sqrt{1-\sin^{2}\alpha}}=\frac{v\tau}{\sqrt{1-(v/u)^{2}}}\).
Після нескладних перетворень з останнього виразу знаходимо
\(u=\frac{v}{\sqrt{1-(v\tau/H)^{2}}}=\frac{330}{\sqrt{1-(330\cdot{10}/4000)^{2}}}=584\) м/с \(\approx{2100}\) км/год.
Задача 15.6
Тепловоз подає звуковий сигнал з частотою \(\nu_{0}=400\) Гц. Пасажир, який стоїть на платформі сприймає частоту сигналу \(\nu=380\) Гц.
Визначити:
швидкість V та напрям руху тепловоза. Швидкість звуку в повітрі прийняти v = 340 м/с.
|
Дано: \(\nu_{0}=400\) Гц
\(\nu=380\) Гц
v = 340 м/с
|
|
V - ?
|
Розв’язання
Приступаючи до розв'язання цієї і подібних задач, слід чітко усвідомити таке. В загальній теорії рівняння хвилі ((15.1), (15.5), (15.7)), а також її параметри (період T, частоти \(\nu\) та \(\omega\), швидкість v, довжина хвилі \(\lambda\)) визначені для випадку, коли джерело і спостерігач нерухомі відносно середовища, в якому поширюється хвиля. В такому разі частота (або період) хвилі дорівнює частоті коливань в джерелі. При цьому швидкість поширення хвилі (швидкість поширення коливань відносно середовища, яку можна знайти у довідкових таблицях) залежить тільки від властивостей середовища.
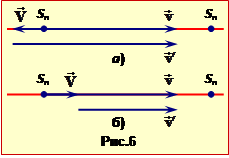 Але якщо джерело або спостерігач (чи обоє) рухаються відносно середовища, характеристики хвилі змінюються. Цим і пояснюється те, що для пасажира на платформі (точка Sп на рис.6) частота звуку \(\nu\) відрізняється від частоти джерела \(\nu_{0}\), розміщеного на рухомому тепловозі.
Але якщо джерело або спостерігач (чи обоє) рухаються відносно середовища, характеристики хвилі змінюються. Цим і пояснюється те, що для пасажира на платформі (точка Sп на рис.6) частота звуку \(\nu\) відрізняється від частоти джерела \(\nu_{0}\), розміщеного на рухомому тепловозі.
Згідно з формулою (15.4a) пасажир (спостерігач) зафіксує частоту сигналу
|
|
\(\nu=\frac{v}{\lambda}\), |
(1) |
де \(\lambda\) – довжина звукової хвилі, створюваної рухомим тепловозом. Довжина хвилі – це відстань між сусідніми "гребенями" хвилі (для звукової хвилі такими "гребенями" є точки з максимальним значеннями тиску або концентрації молекул (густини) повітря). Джерело на тепловозі посилає ці гребені з інтервалом часу T0, отже
|
|
\(\lambda=v^{\prime}T_{0}=\frac{v^{\prime}}{\nu_{0}}\), |
(2) |
де \(v^{\prime}\) – швидкість хвилі відносно тепловоза у напрямку до пасажира.
Швидкість \(\vec{v}^{\prime}\) виражається через швидкість звуку \(\vec{v}\) та швидкість тепловоза \(\vec{V}\) класичною формулою додавання швидкостей (1.10):
|
|
\(\vec{v}^{\prime}=\vec{v}-\vec{V}\) \(\Rightarrow\) \(v^{\prime}=v\pm{V}\), |
(3) |
де знак "+" відноситься до випадку, коли тепловоз віддаляється від пасажира (рис.6а), а знак "-" – коли наближається (рис.6б).
Підставивши вираз (3) у формулу (2), отримаємо
\(\lambda=\frac{v\pm{V}}{\nu_{0}}\).
Таким чином, у відповідності з формулою (1)
\(\nu=\frac{v\nu_{0}}{v\pm{V}}=\frac{\nu_{0}}{1\pm{V/v}}\).
Згідно з умовою \nu\lt\nu_{0}\), отже
|
|
\(\nu=\frac{\nu_{0}}{1+(V/v)}\), |
(4) |
тобто тепловоз віддаляється від пасажира.
З формули (4) після елементарних викладок отримаємо:
\(V=\left(\frac{\nu_{0}}{\nu}-1\right)v\).
У числах
\(V=\left(\frac{400}{380}-1\right)\cdot(340)=17,9\) м/с = 64,4 км/год.
Примітка. Аналогічно до наведених міркувань і викладок можна отримати формули частоти звуку для випадку, коли рухаються як джерело, так і спостерігач. Вперше такі співвідношення були отримані Доплером. Тому зміна частоти, що сприймається при русі джерела і приймача, називається ефектом Доплера. Його прояв ви можете подивитися і почути.
Задача 15.7
Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n1 = 2 удари за секунду. Якщо ж катер рухається назустріч хвилям, то удари в ніс йдуть з частотою n2 = 4 удари за секунду.
Визначити
швидкість поширення хвиль v та швидкість руху катера V.
|
Дано: l = 5 м
\(n_{1}=2\)
\(n_{2}=4\)
|
|
v, V - ?
|
Розв’язання
Відстань між гребенями l – це довжина хвилі, а кількість ударів об корпус дорівнює частоті коливань для рухомого спостерігача, що знаходиться на катері. Отже згідно з формулою (15.4a) можна записати:
|
|
n1l = v1, |
(1) |
|
|
N2l = v2, |
(2) |
де v1, v2 – швидкості поширення хвиль відносно катера у випадках руху вздовж та проти напрямку поширення хвиль. Згідно з законом додавання швидкостей (1.9)
v1 = V – v;
v2 = V + v,
де V, v – швидкості руху катера та поширення хвиль відносно води.
Підставивши сюди вирази (1), (2) для швидкостей і розв'язавши отриману систему, дістанемо відповіді:
\(\left.\begin{align} {}n_{1}l=V-v \\ {}n_{2}l=V+v \\ \end{align}\right\}\) \(\Rightarrow\) \( \begin{align} {}V=l\frac{n_{1}+n_{2}}{2}=5\frac{2+4}{2}=15\ {м/с}; \\ {}v=l\frac{n_{2}-n_{1}}{2}=5\frac{4-2}{2}=5\ {м/с}. \\ \end{align}\)
Задача 15.8
Вхідний коливальний контур радіоприймача з плоским повітряним конденсатором налаштований на довжину хвилі \(\lambda_{1}=200\) м.
Визначити
довжину хвилі \(\lambda_{2}\), на яку буде налаштований контур, якщо між обкладинками конденсатора розмістити діелектричну пластину з проникністю \(\varepsilon=6\), товщина якої в k = 3 рази менша ніж відстань між пластинами.
|
Дано: \(\lambda_{1}=200\) м
\(\varepsilon=6\)
k = 3
|
|
\(\lambda_{2}\) - ?
|
Розв’язання
Резонанс у контурі настає за умови, що період його власних коливань (формула (14.6)) співпадає з періодом коливань в електромагнітній хвилі. В свою чергу довжина хвилі пов'язана з періодом формулою (15.4). Тому для резонансної довжини хвилі маємо
|
|
\(\lambda=vT=v2\pi\sqrt{LC}\), |
(1) |
де v – швидкість поширення хвилі (Для позначення швидкості електромагнітної хвилі використана літера v замість загальноприйнятої літери c, щоб не сплутати її з ємністю конденстора).
Якщо позначити ємність конденсатора без діелектрика C1, з діелектриком – C2, то
\(\lambda_{1}=2\pi{v}\sqrt{LC_{1}}\),
\(\lambda_{2}=2\pi{v}\sqrt{LC_{2}}\),
звідки
\(\lambda_{2}=\lambda_{1}\sqrt{\frac{C_{2}}{C_{1}}}\).
Ємність конденсатора з двома шарами діелектрика, які мають товщину d1 та d2 і діелектричні проникненості \(\varepsilon_{1}\) та \(\varepsilon_{2}\), була визначена в задачі 10.17. З урахуванням того, що в даній задачі \(\varepsilon_{1}=1\) (повітря) та \(\varepsilon_{2}=\varepsilon\) ємність C2, визначається формулою
\(C_{2}=C_{1}\frac{\varepsilon{k}}{\varepsilon(k-1)+1}\).
Підставивши цей вираз у формулу (1), знайдемо
\(\lambda_{2}=\lambda_{1}\sqrt{\frac{\varepsilon{k}}{\varepsilon(k-1)+1}}=200\cdot\frac{6\cdot{3}}{6\cdot(3-1)+1}=235,3\) м.
Задача 15.9
Частота електромагнітної хвилі \(\nu=1\) МГц.
Визначити
довжину електромагнітної хвилі:
А) \(\lambda_{0}\) у вакуумі;
Б) \(\lambda\) у немагнітному (\(\mu=1\)) діелектричному середовищі з діелектричною проникністю \(\varepsilon=2,25\).
|
Дано: \(\nu=1\) МГц = 106 Гц
\(\varepsilon=2,25\)
\(\mu=1\)
|
|
\(\lambda_{0}\) - ?
\(\lambda\) - ?
|
Розв’язання
Відповідно до формули (15.4a) довжина електромагнітної хвилі
\(\lambda=\frac{v}{\nu}\),
де \(\nu\) – частота, а v – швидкість поширення хвилі.
Швидкість поширення електромагнітних хвиль визначається загальною формулою (15.10), а з урахуванням умови \(\mu=1\) – формулою (15.10а):
\(v=\frac{c}{\sqrt{\varepsilon}}\),
де \(c=3\cdot{10^{8}}\) м/с – швидкість поширення електромагнітних хвиль у вакуумі (швидкість світла). Підставляючи вираз швидкості v з формули довжини хвилі, одержимо:
\(\lambda=\frac{c}{\nu\sqrt{\varepsilon}}\).
Для вакууму формально \(\varepsilon=1\), тому
\(\lambda_{0}=\frac{3\cdot{10^{8}}}{10^{6}}=300\) м.
Для діелектричного середовища
\(\lambda=\frac{3\cdot{10^{8}}}{10^{6}\cdot\sqrt{2,25}}\)=200 м.
Задача 15.10
На відстані l = 30 км від радіолокатора знаходиться літак.
Визначити
максимальне число імпульсів n, що може випромінювати локатор за \(\tau=1\) с для спостереження за літаком.
|
Дано: l = 30 км = 3·104 м
\(\tau=1\) с
|
|
n - ?
|
Розв’язання
Кожен імпульс радіохвиль, випромінюваний антеною локатора, досягає літака і, відбивши від нього, повертається до локатора. Кожен наступний імпульс може бути випроменений антеною тільки після повернення попереднього, інакше антена може вийти з ладу. Таким чином, мінімальний час між послідовним випромінюванням двох імпульсів повинний бути не меншим, ніж час проходження електромагнітних хвиль від антени до літака і назад. З огляду на те, що швидкість поширення електромагнітних хвиль \(c=3\cdot{10^{8}}\) м/с, визначаємо час проходження імпульсу радіохвиль
\(\tau=\frac{2l}{c}\).
При цьому період випромінювання
\(T\ge\tau\) \(\Rightarrow\) \(T\ge\frac{2l}{c}\).
Кількість імпульсів, випромінюваних за одиницю часу, – це частота, що зв'язана з періодом співвідношенням n = 1/T, тоді
\(n\le\frac{c}{2l}\).
Максимальному числу імпульсів відповідає знак рівності, отже
\(n=\frac{c}{2l}=\frac{3\cdot{10^{8}}}{2\cdot{3}\cdot{10^{4}}}=5000\).