physics.zfftt.kpi.ua

Для аналізу і визначення періоду (частоти) гармонічних коливань у складній коливальній механічній системі необхідно виконати наступне.

Задача 13.4. До стіни, нахиленої під кутом \(\alpha=3^{\circ}\) до вертикалі, прикріплена нитка математичного маятника завдовжки l = 0,5 м. Нитку відвели на кут \(\Theta_{0}=6^{\circ}\) від вертикалі  і відпустили. Вважаючи удар кульки маятника об стіну абсолютно пружним, визначити період коливань маятника T.

Задача 13.5. Маленька кулька масою m = 20 г, що несе заряд q = 1 мкКл, підвішена на тонкій шовковій нитці завдовжки l = 40 см і здійснює малі коливання у вертикальному електричному полі напруженістю E = 50 кВ/м. Визначити період коливань T, якщо вектор \(\vec{E}\) напрямлений: А) вгору (T₁); Б) вниз (T₂).

Задача 13.6. В середині закритого з обох торців горизонтального циліндра довжиною 2l = 0,8 м, розташований поршень масою m = 2 кг і площею S = 50 см². Тиск повітря в циліндрі P = 50 кПа. В результаті легкого поштовху поршень починає здійснювати малі коливання. Нехтуючи товщиною поршня і тертям, визначити період коливань T. Температуру повітря вважати постійною.

Задача 13.7. На вертикальній пружині жорсткістю k = 245 Н/м укріплена горизонтальна чашка масою M = 1,5 кг. З висоти h = 20 см на чашку падає шматок пластиліну масою m = 0,5 кг і прилипає до неї. Визначити період  T  і амплітуду x_m коливань чашки.

Задача 13.4

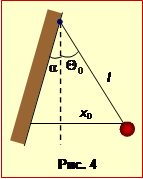До стіни, нахиленої під кутом \(\alpha=3^{\circ}\) до вертикалі, прикріплена нитка математичного маятника завдовжки l = 0,5 м. Нитку відвели на кут \(\Theta_{0}=6^{\circ}\) від вертикалі (рис.4) і відпустили. Вважаючи удар кульки маятника об стіну абсолютно пружним,

визначити
період коливань маятника T.

Розв’язання

Період – це час, за який тіло здійснює одне повне коливання. В даній задачі період дорівнює часу, за який маятник з початкового положення дійде до стіни і повернеться назад. Оскільки удар об стіну пружний, швидкість маятника при ударі змінює тільки напрям, не змінюючи величини. Звідси очевидно, що час t₀ руху з крайнього положення до стіни і назад однаковий, отже період коливань

Зміщення маятника з положення рівноваги задається кутом \(\Theta\) відхилення нитки від вертикалі. Визначимо закон, за яким змінюється з часом цей кут. Оскільки \(\Theta\ll{1}\) рад, координата x  маятника при вільному русі від початкового положення і до удару об стіну виражається рівнянням (13.4):

де частота \(\omega\) визначається формулою (13.17).

Розділивши обидві частини рівняння (2) на довжину маятника l і врахувавши малість кутів \(\Theta\) і \(\Theta_{0}\), отримаємо:

\(\Theta=\Theta_{0}\cos(\omega{t})\).

У момент удару об стіну t = t₀ кут відхилення \(\Theta=-\alpha\), тому

\(-\alpha=\Theta_{0}\cos\omega{t}_{0}\)     \(\Rightarrow\)     \(t_{0}=\frac{1}{\omega}\mathrm{arccos}\left(\frac{\alpha}{\Theta_{0}}\right)=\sqrt{\frac{l}{g}}\left(\pi-\mathrm{arccos\frac{\alpha}{\Theta_{0}}}\right)\).

Підставимо цей вираз у формулу (1) і остаточно отримаємо:

\(T=2\sqrt{\frac{l}{g}}\left(\pi-\mathrm{arccos\frac{\alpha}{\Theta_{0}}}\right)=2\sqrt{\frac{0,5}{9,8}}\left(\pi-\mathrm{arccos}\frac{3}{6}\right)\approx\) 0,95 c,

де кути виражені в радіанах, \(\mathrm{arccos}\frac{3}{6}=\frac{\pi}{3}\).

Задача 13.5

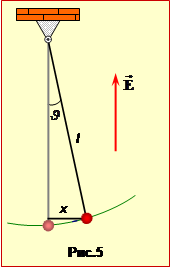Маленька кулька масою m = 20 г, що несе заряд q = 1 мкКл, підвішена на тонкій шовковій нитці завдовжки l = 40 см і здійснює малі коливання у вертикальному електричному полі напруженістю E = 50 кВ/м (рис.5).

Визначити
період коливань T, якщо вектор \(\vec{E}\) напрямлений:

А) вгору (T₁);

Б) вниз (T₂).

Розв’язання

Нехай кулька рухається від положення рівноваги (рис.5-1). На кульку діє сила тяжіння \(m\vec{g}\), сила натягу нитки \(\vec{F}_{н}\) і сила \(\vec{F}_{е}=q\vec{E}\) в електричному полі. Якщо вектор \(\vec{E}\) направлений вертикально вгору, то і сила \(\vec{F}_{е}\) також направлена вгору.

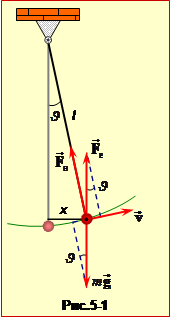Проекції сил на напрям вектора швидкості дорівнює відповідно: \(-mg\sin\vartheta\), 0 і \(qE\sin\vartheta\). Проекція сили натягну нитки на напрям вектора \(\vec{v}\) дорівнює нулю, оскільки цей вектор перпендикулярний нитці (направлений по дотичній до траєкторії).Проекція рівнодійної цих сил

де введено позначення \(k=(mg-qE)/l\), і враховано, що \(\sin\vartheta=x/l\), оскільки відхилення від положення рівноваги x є малим у порівнянні з довжиною нитки l від положення рівноваги.

Вигляд виразу (1) співпадає з формулою (13.10). Це значить, що коливання гармонічні і згідно формулі (13.13), їх період

Якби ми припустили спочатку, що вектор \(\vec{E}\) направлений вертикально вниз, то проекція вектора \(\vec{F}_{е}\) на напрям вектора швидкості була б негативною, і період коливань був би

Об'єднавши вирази (2) і (3), можна записати:

Підставивши сюди числові значення величин, знаходимо

\(T_{1}=2\pi\sqrt{\frac{2\cdot{10^{-2}}\cdot{0,4}}{2\cdot{10^{-2}}\cdot{9,8}-10^{-6}\cdot{5}\cdot{10^{4}}}}\) = 1,47 c;

\(T_{1}=2\pi\sqrt{\frac{2\cdot{10^{-2}}\cdot{0,4}}{2\cdot{10^{-2}}\cdot{9,8}+10^{-6}\cdot{5}\cdot{10^{4}}}}\) = 1,13 c

Корисно провести аналіз загального виразу (4).

1)   Якщо електричне поле відсутнє (E = 0), то

\(T=2\pi\sqrt{\frac{l}{g}}\),

що природно співпадає з формулою (13.18) періоду вільних коливань математичного маятника.

2) Якщо виявиться, що qE > mg, то формально під коренем виходить від’ємна величина, чого бути не може. Річ у тім, що за таких умов рівноважним є положення маятника, показане на рис.5-2, і маятник здійснюватиме коливання відносно цього положення з періодом

\(T=2\pi\sqrt{\frac{ml}{qE-mg}}\).

3) У випадку mg = qE повертаюча сила F = 0 і період коливань \(T\to\infty\), тобто кулька знаходиться в стані байдужої рівноваги.

Задача 13.6

В середині закритого з обох торців горизонтального циліндра довжиною 2l = 0,8 м, розташований поршень масою m = 2 кг і площею S = 50 см². Тиск повітря в циліндрі P = 50 кПа. В результаті легкого поштовху поршень починає здійснювати малі коливання. Нехтуючи товщиною поршня і тертям,

визначити

період коливань T. Температуру повітря вважати постійною.

Розв’язання

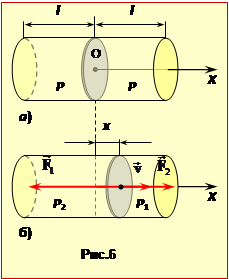В положенні рівноваги поршня (рис.6а) тиск в обох половинах циліндра однаковий. При зсуві поршня на відстань x, наприклад управо (рис.6б), тиск у лівій частині зменшується, а у правій - зростає. У результаті виникають сили F₁ = P₁S і F₂ = P₂S (рис.6б), рівнодійна яких напрямлена до положення рівноваги (повертаюча сила). Знайдемо її вираз.

Оскільки за умовою температура повітря не змінюється, зміни тиску в частинах циліндра зв'язані законом Бойля-Маріотта (формула (7.10)). Якщо поршень змістився на x, то об'єм правої частини V₁ = S(l - x), і тоді

\(PS=P_{1}S(l-x)\)      \(\Rightarrow\)      \(P_{1}=\frac{Pl}{l-x}\).

Аналогічно, для лівої частини

\(PS=P_{2}S(l+x)\)      \(\Rightarrow\)      \(P_{2}=\frac{Pl}{l+x}\).

Нехай поршень зміщений управо (рис.6б). Проектуючи сили тиску на вісь OX, для рівнодійної отримаємо:

\(F_{x}=-F_{1}+F_{2}=(-P_{1}+P_{2})S=PlS\left(\frac{1}{l+x}-\frac{1}{l-x}\right)=-PlS\frac{2x}{l^{2}-x^{2}}\).

При малих коливаннях \(x\ll{l}\), в знаменнику можна знехтувати \(x^{2}\) у порівнянні з \(l^{2}\), тоді

де

Вираз (1) співпадає з (13.10), отже коливання поршня є гармонічними з періодом, який визначається формулою (13.13):

\(T=2\pi\sqrt{\frac{ml}{2PS}}=2\pi\sqrt{\frac{2\cdot{0,4}}{2\cdot{5}\cdot{10^{-4}}\cdot{5}\cdot{10^{-3}}}}\) = 0,25 c.

Задача 13.7

На вертикальній пружині жорсткістю k = 245 Н/м укріплена горизонтальна чашка масою M = 1,5 кг. З висоти h = 20 см на чашку падає шматок пластиліну масою m = 0,5 кг і прилипає до неї.

Визначити
період  T  і амплітуду x_m коливань чашки.

Розв’язання

Період коливання вантажу на пружині визначається формулою (13.15). Після того, як пластилін прилипнув до чашки, маса вантажу дорівнює m + M, отже період коливань

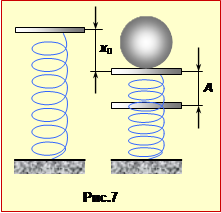
Якщо пластилін обережно покласти на чашку, то пружина стиснеться на величину  x₀ (рис.7), яка знаходиться з умови рівності сил тяжіння і пружності:

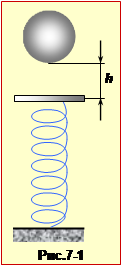Очевидно, що це положення є положенням рівноваги системи "пластилін – чашка – пружина". Впавши з висоти h, (рис.7-1) пластилін має швидкість (формула (1.19)).

\(v=\sqrt{2gh}\).

Оскільки тривалість удару мала (частки секунди), то можна вважати, що виконується закон збереження імпульсу. Тому початкова швидкість чашки з пластиліном v₀ визначається з рівняння балансу імпульсів:

Нехай коливальний рух чашки після удару відбувається згідно із законом

Тоді швидкість чашки після удару змінюється з часом згідно із законом

Для знаходження амплітуди x_m виразимо з рівнянь (4) і (5) \(\cos(\omega{t}+\varphi_{0})\) і \(\sin(\omega{t}+\varphi_{0})\), піднесемо їх до квадрату і додамо:

(Тут ми скористалися формулою (13.3)).

Співвідношення (6) виконується у будь-який момент часу, у тому числі і у момент початку коливань. Тому, підставивши в (6) вирази T, x₀, v₀ з формул (1), (2) і (3), отримаємо:

\(x_{m}=\sqrt{\left(\frac{mg}{k}\right)^{2}+\left(\frac{m}{M+m}\right)^{2}\cdot\frac{2gh(M+m)}{k}}=\frac{mg}{k}\sqrt{1+\frac{2hk}{(M+m)g}}\).

Обчислення дають:

\(x_{m}=\frac{0,5\cdot{9,8}}{245}\cdot\sqrt{1+\frac{2\cdot{0,2}\cdot{245}}{2\cdot{9,8}}}\) = 0,049 м = 4,9 см.