ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
СТАТИКА. Приклади розв'язування задач
Рівновага тіла з закріпленою віссю обертання
Задача 5.6. Конічна колода знаходиться в рівновазі на підпірці, що встановлена на третині довжини колоди від товщого кінця. Якщо підпірку розмістити посередині, а на тонший край посадити людину масою m = 70 кг, то колода знову буде зрівноважена. Визначити масу колоди M.
Задача 5.7. Стрижень масою m = 2 кг і довжиною l = 50 см, який шарнірно прикріплено одним кінцем до вертикальної стіни, за інший кінець утримується під кутом α = 30° до вертикалі горизонтальною ниткою. Визначити силу натягу цієї нитки, якщо до кінця стрижня підвішено тягар масою m1 = 4 кг.
Задача 5.8. Прут, зігнутий у формі прямого кута з нерівними сторонами, шарнірно підвішено за коротший край. Визначити відношення n довжин сторін кута, якщо менша утворює з вертикаллю кут \(\vartheta =50^{\circ} \).
Конічна колода знаходиться в рівновазі на підпірці, що встановлена на третині довжини колоди від товщого кінця. Якщо підпірку розмістити посередині, а на тонший край посадити людину масою m = 70 кг, то колода знову буде зрівноважена.
Визначити
масу колоди M.
|
Дано: m = 70 кг |
|
M - ? |
Розв’язання
З умови зрозуміло, що в першому випадку підпірка розташована під центром ваги колоди С, (рис. 6а). У другому випадку за умовою рівноваги (5.4) моменти сил
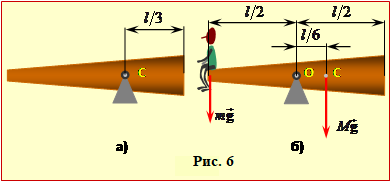
тяжіння \( {M}\vec{g}\) і \( {m}\vec{g}\), що діють на колоду та на людину (рис.6б) відносно осі О мають бути однакові. Плечі цих сил дорівнюють \({{h}_{1}}={l}/{2}\;-{l}/{3}\;={l}/{6}\; \) і \( {{h}_{2}}={l}/{2}\;\), відповідно. Отже,
\( {Mgl}/{6}={mgl}/{2}\); \( \Rightarrow \) \( {M}=3m\) = 210кг.
Стрижень масою m = 2 кг і довжиною l = 50 см, який шарнірно прикріплено одним кінцем до вертикальної стіни, за інший кінець утримується під кутом α = 30° до вертикалі горизонтальною ниткою.
Визначити
силу натягу цієї нитки, якщо до кінця стрижня підвішено тягар масою m1 = 4 кг.
|
Дано: m = 2 кг
l = 0,5 м
α =30°
m1 = 4 кг
|
|
F - ? |
Розв’язання
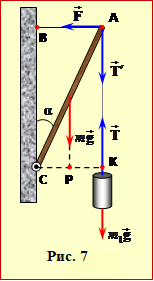Стрижень має закріплену вісь обертання в точці О (рис. 7), тож згідно з правилом моментів (5.4),
|
M1 + M2 + M3 = 0, |
(1) |
де M1, M2, M3 – моменти відносно осі О наступних сил: 1) натягу горизонтальної нитки \( \vec{F}\), 2) ваги (сили тяжіння) стрижня \({m}\vec{g}\) і 3) натягу підвісу тягаря \({\vec{T}}\) = ${{m}_{1}}\vec{g}$. Плечі цих сил ОС, ВС і АС (рис. 5) дорівнюють: 1) h1 = l·cosα, h2 = (l/2)·sinα і h3 = l·sinα, відповідно. Тож, підставивши указані величини сил і пліч в рівняння (1) і, врахувавши знаки моментів, дістанемо відповідь:
|
\( {l}T\sin\alpha+\frac{l}{2}mg\sin\alpha-lF\cos\alpha={0}\) \( \Rightarrow \) \(F=\left(\frac{m}{2}+{m}_{1}\right)g\mathrm{tg}\alpha \), |
|
і після обчислень
F = 28,3 H.
Прут, зігнутий у формі прямого кута з нерівними сторонами, шарнірно підвішено за короткий кінець.
Визначити
відношення n довжин сторін кута, якщо менша утворює з вертикаллю кут \(\vartheta =50^{\circ} \).
|
Дано: \(\vartheta =50^{\circ} \) |
|
n - ? |
Розв’язання
Згідно умовою (5.4) при рівновазі прута моменти сил тяжіння, що діють на частини прута, відносно осі О (рис. 6) мають мати однакову величину:
M1 = M2.
Позначимо для їхнього визначення довжину та масу короткої сторони прута як l і m. Тоді для довгої матимемо nl і nm і для сил тяжіння – mg і nmg, відповідно. Ці сили є прикладені в центрах ваги (посередині) сторін (рис. 6), отже, їхні плечі дорівнюють:
\({{h}_{1}}=\frac{l}{2}\sin\vartheta \),
\({{h}_{2}}=\frac{nl}{2}\cos\vartheta -l\sin\vartheta\),
а моменти
\( {{M}_{1}}=\frac{mgl}{2}\sin \vartheta \),
\({M}_{2}=nmgl\left(\frac{n}{2}\cos\vartheta -\sin\vartheta\right)\).
${{n}^{2}}-2n\operatorname{tg}\vartheta -{{\operatorname{tg}}}\vartheta $ = 0,
з якого знайдемо відповідь (від'ємний корінь не має змісту):