ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 11:25 |
Оглавление
- Вступ. Механіка
- Розділ І. КІНЕМАТИКА
- Приклади розв'язування задач
- Задачі для самостійної роботи
- Розділ ІІ. ДИНАМІКА
- Приклади розв’язування задач
- Задачі для самостійної роботи
- Розділ ІІІ. ЗАКОН ЗБЕРЕЖЕННЯ ІМПУЛЬСУ
- Приклади розв'язування задач
- Задачі для самостійної роботи
- Розділ ІV. РОБОТА ТА ЕНЕРГІЯ
- Короткі теоретичні відомості
- Приклади розв'язування задач
- Задачі для самостійної роботи.
- Розділ V. СТАТИКА
- СТАТИКА. Приклади розв'язування задач
- Задачі для самостійної роботи
- Розділ VI. ГІДРО-АЕРОСТАТИКА
- Теоретичні відомості
- Приклади розв’язування задач
- Задачі для самостійної роботи
Вступ. Механіка
В механіці вивчаються найпростіші фізичні явища – механічний рух і рівновага тіл.
Механічним рухом називається зміна положення тіл у просторі з плином часу. Про положення тіла у просторі та його рух можна судити лише по відношенню до якогось іншого тіла (тіло відліку). Тому точний математичний опис руху можливий тільки в обраній системі відліку.
Системою відліку називається сукупність тіла відліку, зв'язаної з ним системи координат та годинника.
(Примітка. Під годинником розуміють не прилад, а прийнятий принцип визначення інтервалів часу в кожній точці простору).
Систему відліку, в принципі, можна обирати як завгодно. При цьому вид та характеристики руху даного тіла відносно різних систем відліку будуть різними. Тому
рух є відносним за самою своєю природою.
Слід зауважити, що не лише механічні, а й усі інші фізичні явища відбуваються у просторі і часі, тобто "десь" і "колись". Тому система відліку є фундаментальним поняттям: будь-яку фізичну задачу ми завжди аналізуємо і розв'язуємо у певній системі відліку, інколи навіть не усвідомлюючи цього.
Залежно від умов і цілей фізика у своїх дослідженнях використовує ті чи інші моделі. Основними моделями механіки є матеріальна точка та абсолютно тверде тіло.
Матеріальною точкою називається тіло, розмірами якого можна нехтувати в умовах даної задачі, тобто по відношенню до інших лінійних розмірів (відстаней), які фігурують у задачі.
Абсолютно твердим називається тіло, відстань між будь-якими точками котрого лишається незмінною за будь-яких умов. Абсолютно тверде тіло можна розглядати як систему жорстко зв'язаних між собою матеріальних точок.
Даний посібник складається з наступних розділів:
ІІІ. Імпульс. Закон збереження імпульсу
Кожен розділ містить:
1. Короткі теоретичні відомості
2. Приклади розв’язування задач
3. Задачі для самостійної роботи
Перед початком роботи варто відновити в пам'яті рекомендації з організації розв'язування задач та відомі спрощення й наближення, що приймаються в текстах умов за умовчанням .
Для перевірки засвоєння матеріалів розділу можна пройти тестування, але для цього необхідно зареєструватися в адміністраторів сайту.
Розділ І. КІНЕМАТИКА
Кінематика – це розділ механіки, в якому вивчається рух тіл без з’ясування причин, які його визначають. В кінематиці встановлюються основні поняття, кількісні характеристики руху та рівняння для різних видів руху, що спостерігаються у природі та техніці.
2. Приклади розв'язування задач
3. Задачі для самостійної роботи
1.1. Основні поняття та величини кінематики
Основні поняття й величини кінематики кількісно характеризують просторове положення та рух тіла.
Положення точки у просторі задається її радіус-вектором або координатами, зміна положення — траєкторією, шляхом і переміщенням, а сам процес руху — швидкістю та прискоренням.
Радіус-вектор \( \vec{r} \) – це вектор проведений з початку відліку в дану точку. Радіус-вектор визначає положення рухомої точки (тіла) в даний момент часу. Координати точки є проєкціями радіус-вектора на осі координат (рис.1.1):
rx = x; ry = y.
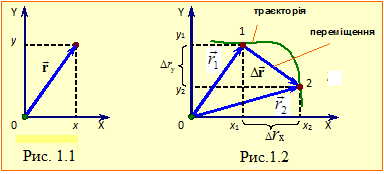 |
Траєкторією називається неперервна лінія у просторі, вздовж якої рухається матеріальна точка. Можна також сказати, що траєкторія – це лінія, яку описує кінець радіус-вектора рухомої точки (рис.1.2). Довжина відрізка траєкторії між заданими двома точками називається шляхом S, пройденим тілом за відповідний проміжок часу. Шлях є скалярною додатньою величиною, що в процесі руху невпинно зростає.
Переміщення \( \Delta\vec{r} \) – це вектор, проведений з початкового (1) у кінцеве (2) положення тіла, рис.1.2. Переміщення визначає зміну положення тіла в просторі за заданий проміжок часу. На відміну від шляху, величина (модуль) переміщення в процесі руху може як збільшуватися, так і лишатися незмінним, або зменшуватись.
Із рис. 1.2 видно, що переміщення дорівнює зміні радіус-вектора, а його проєкції є змінами координат рухомої точки:
|
\( \Delta\vec{r}=\vec{r}_{2}-\vec{r}_{1} \). |
(1.1) |
|
\( \Delta{r}_{x}=x_{2}-x_{1}=\Delta{x} \); \( \Delta{r}_{y}=y_{2}-y_{1}=\Delta{y} \). |
(1.1а) |
Середня швидкість переміщення \( \langle{\vec{v}}\rangle \), або вектор середньої швидкості, – це відношення переміщення \( \Delta\vec{r} \) до проміжку часу Δt = t2 – t1, за який воно відбулося:
| \( \langle{\vec{v}}\rangle=\frac{\Delta\vec{r}}{\Delta{t}}\). | (1.2) |
Модуль вектора середньої швидкості дорівнює:
| \( \left|\langle\vec{v}\rangle\right|=\frac{\left|\Delta\vec{r}\right|}{\Delta{t}} \). | (1.2а) |
Напрям вектора \( \langle\vec{v}\rangle \) збігається з напрямом вектора \( \Delta\vec{r} \).
Середня шляхова швидкість (або просто середня швидкість) \( \langle{v}\rangle \) це відношення шляху S до проміжку часу його проходження Δt:
| \( \langle{v}\rangle=\frac{S}{\Delta{t}} \). | (1.3) |
Середні швидкості (1.2) і (1.3) не містять інформації про стан руху тіла в кожен момент часу (або в кожній точці траєкторії). Таку інформацію містить миттєва швидкість.
Миттєва швидкість \( \vec{v}\) (у контексті вектор швидкості, або просто швидкість) – це границя відношення переміщення \( \Delta\vec{r} \) до відповідного проміжку часу Δt при його необмеженому зменшенні. Іншими словами
миттєва швидкість є похідною радіус-вектора рухомої точки по часу:
| \( \vec{v}=\underset{\Delta t\to{0}}\lim\frac{\Delta\vec{r}}{\Delta{t}}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\equiv {\vec{r}}^{\prime}{(t)}\). | (1.4) |
(Примітка. Тут наведені два прийняті позначення похідної функції f(t): f′(t) і df/dt; те ж саме стосується й другої похідної: f″(t) та ${{{d}^{2}}f}/{d{{t}^{2}}}\;$).
Можна сказати, що миттєва швидкість дорівнює відношенню гранично малого переміщення \(d\vec{r}\) точки до відповідного гранично малого проміжку часу dt. Тому вектор швидкості \( \vec{v}\) завжди є спрямований вздовж дотичної до траєкторії (рис. 1.2).
Проєкції швидкості на координатні осі є похідними відповідних координат по часу:
|
\( {v}_{x}=x^{\prime}=\frac{\mathrm{d}x}{\mathrm{d}t}\); \( {v}_{y}=y^{\prime}=\frac{\mathrm{d}y}{\mathrm{d}t}\). |
(1.4a) |
У довільному русі швидкість точки неперервно змінюється як за величиною, так і за напрямом . Мірою такої зміни є середнє та миттєве прискорення.
Середнє прискорення \( \langle\vec{a}\rangle \) – то є відношення зміни вектора швидкості \( \Delta\vec{v}=\vec{v}_{2}-\vec{v}_{1} \) до проміжку часу \( \Delta{t} \), за який сталася ця зміна:
| \( \langle\vec{a}\rangle=\frac{\Delta\vec{v}}{\Delta{t}}\) | (1.5) |
Миттєве прискорення є точною характеристикою зміни вектора швидкості в кожен момент часу і визначається аналогічно до миттєвої швидкості:
| \( \vec{a}=\underset{\Delta t\to{0}}\lim\frac{\Delta\vec{v}}{\Delta{t}}=\vec{v}^{\prime}(t)=\frac{\text{d}\vec{v}}{\text{d}t}\) | (1.6а) |
або
| \( \vec{a}=\vec{r}^{\prime\prime}(t)=\frac{\mathrm{d}^{2}\vec{r}}{\mathrm{d}t^{2}}\). | (1.6б) |
Іншими словами,
миттєве прискорення є першою похідною вектора швидкості або другою похідною радіус-вектора по часу.
Проєкції вектора прискорення на осі координат визначаються аналогічно через проєкції швидкості та координат точки:
|
\({{a}_{x}}={{{v}'}_{x}}(t)=\frac{d{{v}_{x}}}{dt}\) \({{a}_{y}}={{{v}'}_{y}}(t)=\frac{d{{v}_{y}}}{dt}\) |
(1.7) |
|
\({{a}_{x}}={x}''(t)=\frac{{{d}^{2}}x}{d{{t}^{2}}}\) \({{a}_{y}}={y}''(t)=\frac{{{d}^{2}}y}{d{{t}^{2}}}\) |
(1.8) |
При русі точки з постійним прискоренням воно будь-якої миті визначається формулою (1.5).
1.2. Відносність руху
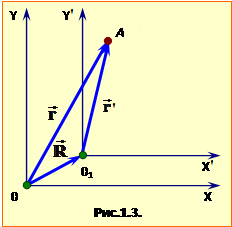
Положення тіла в просторі є визначеним не саме по собі, а тільки по відношенню до вибраної ''системи відліку'' – якогось іншого тіла й жорстко зв'язаної з ним системи координат. Те саме стосується й руху, тож він за самою природою є відносним. Через це положення точки та її рух у двох різних системах відліку – нерухомій (ХОY) та рухомій (Х′О′Y′) – визначаються різними, хоч і взаємопов'язаними, значеннями радіус-вектора, швидкості та прискорення. Радіус-вектори \( \vec{r}\) і \(\vec{r}^{\prime}\) точки в нерухомій та в рухомій системі відліку (рис.1.3) є зв'язані співвідношенням:
| \( \vec{r}={\vec{r}}'+\vec{R}\), | (1.9) |
де \( \vec{R} \) – радіус-вектор, що задає положення початку відліку рухомої системи відносно нерухомої (рис.1.3). Аналогічно для переміщень
| $\Delta \vec{r}=\Delta \vec{{r}'}+\Delta \vec{R}$ | (1.9а) |
Звідси відповідно до формули (1.4) випливає класичний закон додавання швидкостей:
| \( \vec{v}={\vec{v}}'+\vec{V}\) | (1.10) |
 |
тобто,
вектор швидкості тіла в нерухомій системі відліку \( \vec{v}\) дорівнює сумі вектора його швидкості в рухомій системі відліку ${\vec{v}}'$ та вектора швидкості \( \vec{V} \) рухомої системи відліку відносно нерухомої.
Швидкість \(\vec{v}^{\prime}\) тіла відносно рухомої системи через його швидкість \( \vec{v}\) у нерухомій системі визначається зворотнім співвідношенням:
| \( {\vec{v}^{\prime}}=\vec{v}-\vec{V}\). | (1.10а) |
Співвідношення (1.11) і (1.11а) є універсальними і виконуються в будь-яких системах відліку та при будь-яких рухах тіла. Але зв'язок між прискореннями є більш складним і залежить від систем відліку. І тільки в системах відліку, що рухаються одна відносно одної поступально, прискорення тіла \( \vec{a}\) і \({\vec{a}}'\) пов'язані таким самим співвідношенням, що й швидкості:
|
\(\vec{a}={\vec{a}}'+{{\vec{a}}_{0}}\) |
(1.11) |
i
|
\({\vec{a}}'=\vec{a}-{{\vec{a}}_{0}}\) |
(1.11а) |
де \( \vec{a}_{0}\) – прискорення рухомої системи відліку відносно нерухомої.
1.3. Рух з постійним прискоренням
Усі миттєві характеристики руху точки можна обчислити, якщо відомий закон руху, тобто, залежність її радіуса-вектора від часу \(\vec{r}\left( t \right)\). Ця залежність визначається змінами прискорення і може виявитися складною. Але при русі з постійним прискоренням \( \vec{a}=\mathrm{const} \), закон руху спрощується і має вигляд:
|
\(\vec{r}\left( t \right)={{\vec{r}}_{0}}+{{\vec{v}}_{0}}t+\frac{\vec{a}{{t}^{2}}}{2}\), |
(1.12) |
де \( \vec{r}_{0}=\vec{r}(0) \), \( \vec{v}_{0}=\vec{v}(0) \) – радіус-вектор та вектор швидкості в початковий момент часу (t = 0), відповідно.
Із рівняння (1.12) можна знайти будь-яку величину, що визначає рух (див. п.1.1), тож воно містить всю інформацію про рух точки із сталим прискоренням. Але задля зручності для загальної характеристики рівнозмінного руху записують два окремі рівняння – рівняння переміщення та рівнянням швидкості. Вони безпосередньо випливають з рівняння (1.12) і формул (1.1), (1.4) і мають вигляд:
| \( \Delta\vec{r}=\vec{v}_{0}t+\frac{\vec{a}t^{2}}{2}\), | (1.13) |
| \( \vec{v}=\vec{v}_{0}+\vec{a}t \). | (1.14) |
Слід наголосити на тому, що наведені рівняння є однаково чинні як для прямолінійного, так і для криволінійного рухів. При цьому, яким буде рух, залежить від напрямків початкової швидкості та прискорення: якщо ці вектори напрямлені вздовж однієї прямої (однаково, або протилежно), рух є прямолінійним; якщо ж вони напрямлені під кутом один до одного, то рух відбувається по криволінійній траєкторії. Це ілюструє рух тіла, що кинуте вертикально та під кутом до горизонту.
Рівняння (1.12) або (1.13) і (1.14) включають як окремий випадок і кінематику рівномірного прямолінійного руху. При такому русі \( \vec{a}=0 \) і \(\vec{v}=\mathrm{const} \), тому
| \( \vec{r}(t)=\vec{r}_{0}+\vec{v}t \) | (1.15) |
У задачах для обчислень використовують скалярні рівняння руху, тобто рівняння для проєкцій векторів на координатні осі:
| \( {x}=x_{0}+v_{0x}t+\frac{a_{x}t^2}{2}\) | \( {y}=y_{0}+v_{0y}t+\frac{a_{y}t^{2}}{2}\) | (1.16) | |
| \( {v}_{x}=v_{0x}+a_{x}t \) | \( {v}_{y}=v_{0y}+a_{y}t \) | ||
| \( {a}_{x}=\mathrm{const} \) | \( {a}_{y}=\mathrm{const} \) |
(Примітка. Вісь ОZ в рівняннях не фігурує, бо при вивченні теорії та для вправ достатньо розглядати лише рухи, що відбуваються по плоских траєкторіях).
При рівномірному прямолінійному русі координатну вісь ОХ вибирають паралельно до напряму руху, тож рух визначається одним рівнянням:
|
\(x={{x}_{0}}+{{v}_{x}}t\). |
(1.17) |
При цьому, позаяк vх = ± v, індекс проєкції зазвичай опускають, а напрям швидкості в рівнянні (1.17) враховують знаком.
У багатьох задачах зручно користуватись формулами, що випливають з рівнянь (1.16) і прямо пов'язують між собою переміщення, швидкість і прискорення:
| \( {v}_{x}^{2}-v_{0x}^{2}=2a_{x}(x-x_{0}) \), | (1.18) | |
| \( {v}_{y}^{2}-v_{0y}^{2}=2a_{y}(y-y_{0}) \). |
У найпростішому випадку прямолінійного руху, що відбувається без зміни напрямку, аналогічна формула пов'язує модулі векторів і пройдений точкою шлях:
|
\(\left| {{v}^{2}}-v_{0}^{2} \right|=2aS\). |
(1.19) |
1.4. Графіки руху
Графіками руху називають графіки залежності від часу кінематичних величин: проєкцій та модулів прискорення, швидкості, переміщення, а також координати й шляху. Графіки руху наочно відображають його властивості і в багатьох випадках полегшують розв'язування задачі.
Згідно з рівняннями (1.16), для руху зі сталим прискоренням графіки прискорення та швидкості зображуються відрізками прямої, а переміщення, координати та шляху – відрізками параболи, як, до прикладу, на рис.1.4.
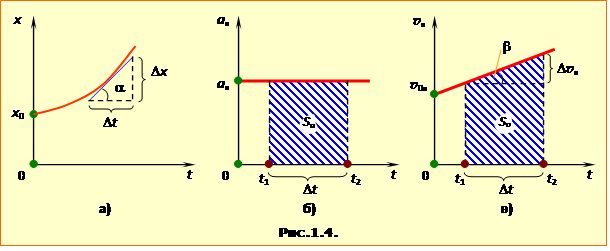 |
Графіки руху мають певні загальні властивості, що дозволяють за графіком якоїсь величини отримати інформацію не лише про неї, а й про інші кінематичні величини. Конкретно:
1. Тангенс кута нахилу графіка проєкції швидкості (рис.1.4в) чисельно дорівнює проєкції прискорення на ту саму вісь:
| \( \mathrm{tg}\beta=\frac{\Delta{v}_{x}}{\Delta{t}}=a_{x} \) | (1.20) |
2. Тангенс кута нахилу дотичної до графіка координати (рис.1.4а) чисельно дорівнює проєкції миттєвої швидкості тіла на дану координатну вісь:
| \( \mathrm{tg}\alpha=\frac{\Delta{x}}{\Delta{t}}=v_{x} \). | (1.20а) |
(Примітка. Позаяк на графіку дотичну до кривої точно провести не можна, на практиці tgα визначається через відношення малого приросту координати до відповідного проміжку часу).
3. Площа під заданою ділянкою графіка проєкції швидкості на вісь (заштрихована на рис.1.4в) чисельно дорівнює проєкції на цю вісь переміщення (зміні координати) тіла за відповідний проміжок часу.
| \( {S}_{v}=\Delta{x}\) |
4. Шлях чисельно дорівнює площі під відповідною ділянкою графіка модуля швидкості.
5. Площа під ділянкою графіка проєкції прискорення (заштрихована на рис.1.4б) чисельно дорівнює зміні проєкції швидкості на цю вісь за відповідний проміжок часу:
| \( {S}_{a}=\Delta{v}_{x} \) |
На завершення, як приклад застосування графіків руху при розв'язуванні задач, визначимо формулу середньої швидкості у випадку руху із сталим прискоренням. Графік швидкості такого руху (рис. 1.4в) зображується відрізком прямої, а його виділена ділянка має форму трапеції. Отже, на проміжку часу Δt, за який швидкість тіла змінюється від v1 до v2, пройдений тілом шлях дорівнює
$S=\frac{1}{2}\left( ~{{v}_{1}}+{{v}_{2}} \right)\Delta t$,
і середня швидкість
|
$\left\langle v \right\rangle =\frac{{{v}_{1}}+{{v}_{2}}}{2}$. |
(1.21) |
Примітка. Ця формула відповідає нашому інтуїтивному уявленню про середнє значення змінної величини і може здатися самоочевидною. Але це не так, і середні швидкості для різних змінних рухів визначаються різними формулами.
1.5. Рівномірний рух по колу
Одним із поширених простих рухів є рівномірний рух по колу, що визначається радіусом кола R та швидкістю v, яка в цьому випадку називається лінійною швидкістю.
Рівномірне обертання є циклічним рухом, тому його характеризують також періодом T і частотою n.
Періодом T (с) називається час, за який тіло здійснює один повний оберт по колу.
Частота n (об/с) – це кількість обертів, яку тіло здійснює за одиницю часу:
| \( {n}=\frac{1}{T} \). | (1.22) |
Зв’язок між швидкістю і періодом (частотою) обертання:
|
\(v=\frac{2\pi R}{T}=2\pi Rn\) |
(1.23) |
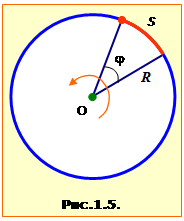
Крім указаних величин при описі колового руху точки та обертання твердого тіла використовують також кутові величини: кут повороту та кутову швидкість.
| \( \varphi=\frac{S}{R} \). | (1.24) |
| \( \omega=\frac{\Delta\varphi}{\Delta{t}} \). | (1.25) |
Лінійна та кутова швидкості пов'язані співвідношенням
| \( {v}=\omega{R} \), | (1.26) |
а кутова швидкість і період (частота) обертання – співвідношенням
| \( \omega=\frac{2\pi}{T}=2\pi{n} \). | (1.27) |
При рівномірному обертовому русі модуль лінійної швидкості не змінюється, але змінюється її напрям. Тому такий рух характеризується доцентровим прискоренням, модуль якого дорівнює:
| aдц = \( \frac{v^{2}}{R}=4\pi^{2}n^{2}R=\frac{4\pi^{2}R}{T^{2}}=\omega^{2}R=\omega{v} \). | (1.28) |
Вектор доцентрового прискорення ${{\vec{a}}_{\text{дц}}}$ є напрямлений до центра кола, по якому рухається точка.
Кінематичні величини, відносність руху
У всіх наведених задачах для прискорення вільного падіння прийнято значення g = 10 м/с2.
Задача 1.1. Автомобіль проїхав прямою дорогою відстань l1 = 1 км. Потім, рухаючись по дузі кола радіусом R = 300 м, розвернувся на 180° і, проїхавши далі прямо ще l2 = 200 м, зупинився. Загальний час руху склав t = 4 хв. Визначити за час руху: А) середню шляхову швидкість автомобіля; Б) модуль вектора середньої швидкості переміщення; В) кут між напрямом вектора переміщення та початковим напрямом руху.
Задача 1.2. На першій половині шляху автомобіль мав швидкість v1 = 36 км/год, а на другій – половину часу рухався зі швидкістю v2 = 72 км/год і стільки ж із швидкістю v3 = 90 км/год. Визначити середню швидкість автомобіля на всьому шляху.
Задача 1.3. Сліди дощових крапель на бічному склі трамвая є вертикальні під час руху і відхилені на кут α = 30° при зупинці. Визначити кут β, на який відхилені від вертикалі сліди дощових крапель на склі зустрічного трамвая, що рухається з такою самою швидкістю.
Задача 1.4. Хлопчик, який може плисти відносно води зі швидкістю u, що складає половину швидкості течії v, хоче переплисти річку. Визначити, під яким кутом α до берега хлопчик має тримати курс, аби його знесло течією якнайменше?
Задача 1.5. Визначити мінімальну швидкість umin, з якою має рухатись човен відносно води, аби потрапити з точки А на одному березі ріки у точку B на іншому. Швидкість течії V , ширина ріки h і відстань між точками А і В вздовж берега S є задані.
Задача 1.6. Від бакена, що стоїть посеред ріки, одночасно відпливають два човни: один за, а другий – поперек течії. Пройшовши однакову відстань, човни вертаються назад тими самими шляхами.
Визначити відношення часів руху човнів τ1/τ2, якщо їхня швидкість відносно води в η = 1,8 разів перевищує швидкість течії.
Задача 1.7. Два катери, рухаючись річкою назустріч один одному, порівнялись і розійшлися під мостом. Відтак, розвернувшись через τ =0,5 год, вони знов зустрілися на відстані L = 2 км від мосту. Визначити швидкість течії V, якщо швидкості катерів відносно води лишалися незмінними.
Задача 1.8. Два автомобілі рухаються зі швидкостями v1 і v2 по двох взаємно перпендикулярних дорогах до перехрестя. Визначити, на якій найменшій відстані Lmin вони пройдуть один поз одного, якщо в початковий момент часу перебували на відстанях L1 і L2 від перехрестя.
Автомобіль проїхав прямою дорогою відстань L1 = 1 км. Потім, рухаючись по дузі кола радіусом R = 300 м, розвернувся на 180° і, проїхавши далі прямо ще L2 = 200 м, зупинився. Загальний час руху t = 4 хв.
Визначити за час руху:
А) середню шляхову швидкість автомобіля;
Б) модуль вектора середньої швидкості переміщення;
В) кут між напрямом вектора переміщення та початковим напрямом руху.
Розв'язання
|
Дано: L1 = 1 км
L2 = 200 м
R = 300 м
t = 4 хв
|
|
\( \langle{v}\rangle,\,\left|\langle\vec{v}\rangle\right|,\,\alpha \) - ? |
А) Пройдений автомобілем шлях (рис. 1.1) складається з довжин відрізків AC = L1 і EF = L2 та половини кола CDE:
S = L1 + πR + L2 = 2,14 км.
Тож середня шляхова швидкість (відношенню шляху до часу його проходження) дорівнює:
\( \langle{v}\rangle=\frac{S}{t}=\frac{2140}{240}\approx \) 8,9 м/с = 32,1 км/год.
Б) Модуль середньої швидкості переміщення є відношенням модуля вектора переміщення до часу руху автомобіля:
$\left| \left\langle {\vec{v}} \right\rangle \right|=\frac{\left| \Delta \vec{r} \right|}{\Delta t}$.
Із рис. 1.1 видно, що
$\left| \Delta \vec{r} \right|=\sqrt{{{\left( {{l}_{1}}-{{l}_{2}} \right)}^{2}}+{{\left( 2R \right)}^{2}}}$ = 1 км.
За умовою час руху t = (1/15) год, отже,
$\left| \Delta \vec{r} \right|$ = 15 км/год.
В) Напрям \( \left|\langle\vec{v}\rangle\right| \) збігається з напрямом \( \Delta\vec{r} \) і визначається кутом
$\alpha =\arcsin \left( \frac{2R}{\left| \Delta \vec{r} \right|} \right) $ ≈ 37°.
| Задача 1.2. |
На першій половині шляху автомобіль мав швидкість v1 = 36 км/год, а другу половину часу він рухався зі швидкостями v2 = 72 км/год і v3 = 90 км/год протягом двох рівних інтервалів.
Визначити
середню швидкість автомобіля на всьому шляху.
Розв'язання
|
Дано: v1 = 36 км/год
v2 = 72 км/год
v3 = 90 км/год
|
|
\( \langle{v}\rangle\) - ? |
Середня швидкість дорівнює відношенню пройденого шляху до часу, за який його подолано. Тож, позначивши як S половину всього шляху, t1 – час проходження першої половини шляху і τ – час руху на кожній з двох частин решти шляху, можемо записати:
| \(\left\langle v \right\rangle =\frac{2S}{{{t}_{1}}+2\tau }\). | (1) |
На всій дистанції автомобіль рухався із заданими сталими швидкостями, тож для кожної з двох половин шляху маємо:
$S={{v}_{1}}{{t}_{1}}$ $\Rightarrow $ ${{t}_{1}}=\frac{S}{{{v}_{1}}}$, $S={{v}_{2}}{{τ}}$ + ${{v}_{3}}{{τ}}$ $\Rightarrow $ $2\tau =\frac{2S}{{{v}_{2}}+{{v}_{3}}}$.
Відтак загальний час руху
${{t}_{1}}+2\tau $ = $\left( \frac{1}{{{v}_{1}}}+\frac{2}{{{v}_{2}}+{{v}_{3}}}\right)S$ = $\frac{2{{v}_{1}}+{{v}_{2}}+{{v}_{3}}}{2{{v}_{1}}\left( {{v}_{2}}+{{v}_{3}} \right)}S$,
і середня швидкість на всьому шляху
$\left\langle v \right\rangle =\frac{2v\left( {{v}_{2}}+{{v}_{3}} \right)}{2v+{{v}_{2}}+{{v}_{3}}}$ = 49,8 км/год.
На завершення, відмітимо, що середня швидкість автомобіля зовсім не дорівнює величині (v1 + v2 +v3)/3, як може здатися на перший погляд.
| Задача 1.3 |
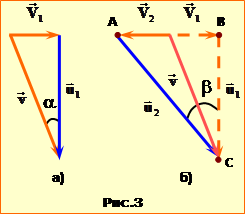 Сліди дощових крапель на бічному склі трамвая є вертикальні під час руху і відхилені на кут α = 30° при зупинці.
Сліди дощових крапель на бічному склі трамвая є вертикальні під час руху і відхилені на кут α = 30° при зупинці.
Визначити
кут \( \beta \), на який відхилені від вертикалі сліди дощових крапель на склі зустрічного трамвая, що рухається з такою самою швидкістю.
Розв'язання:
|
Дано: \( \alpha=30^{\circ} \) |
|
\( \beta \) - ? |
Вертикальні сліди вказують напрям швидкості крапель відносно трамвая, що рухається (рухома система відліку). Аналогічно, нахилені сліди вказують напрям швидкості крапель відносно нерухомого трамвая та землі (нерухома система відліку).
За законом додавання швидкостей (1.10) краплі відносно землі рухаються із швидкістю \( \vec{v} \), що в обох випадках дорівнює сумі їхніх швидкостей відносно трамвая \( \vec{u}\) та швидкості трамвая відносно землі \( \vec{V}\):
\( \vec{v}=\vec{u}_{1}+\vec{V}_{1}\),
\( \vec{v}=\vec{u}_{2}+\vec{V}_{2}\).
Із векторних діаграм цих рівнянь (рис. 3а,б) можна встановити зв'язок між напрямком руху крапель і величиною швидкості трамвая в обох випадках:
$\operatorname{tg}\beta =\frac{{{V}_{1}}+{{V}_{2}}}{{{u}_{1}}}$, $\operatorname{tg}\alpha =\frac{{{V}_{1}}}{{{u}_{1}}}$ .
Тож враховуючи умову V2 = V1 , маємо:
$\operatorname{tg}\beta =2\operatorname{tg}\alpha$.
Відтак, підставивши значення tgα, отримуємо відповідь:
$\operatorname{tg}\beta =\frac{2}{\sqrt{3}}$ $\Rightarrow $ β = 49,1°
| Задача 1.4 |
Хлопчик, який може відносно води плисти зі швидкістю u, що складає половину швидкості течії v, хоче переплисти річку.
Визначити,
під яким кутом \( \alpha \) до берега хлопчик має тримати курс, аби його знесло течією якнайменше?
Розв'язання
|
Дано: v/u = 2 |
|
α - ? |
Величина знесення хлопця L (рис. 4) залежить від ширини річки h та величини й напряму його швидкості \( \vec{v}\) відносно берега, котра визначається законом додавання швидкостей (1.10):
| \( \vec{v}=\vec{u}+\vec{V}\), | (1) |
де \( \vec{u}\) – швидкість руху хлопчика відносно води, \( \vec{V} \) – швидкість течії.
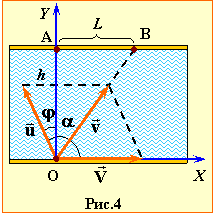 Аби встановити цю залежність, оберемо систему відліку, як на рис. 1.4. Тоді, коли хлопець тримає курс під кутом \( \varphi \) до осі OY, проєкції його швидкості \( \vec{v}\) на координатні осі складають:
Аби встановити цю залежність, оберемо систему відліку, як на рис. 1.4. Тоді, коли хлопець тримає курс під кутом \( \varphi \) до осі OY, проєкції його швидкості \( \vec{v}\) на координатні осі складають:
\( {v}_{x}=V-u\sin\varphi \),
\( v_{y}=u\cos\varphi \).
Час переправи визначається складовою швидкості \( {v}_{y}\) та шириною ріки h:
\( {t}=\frac{h}{v_{y}}=\frac{h}{u\cos\varphi}\).
За цей час хлопчик зноситься течією на відстань
| \( {L}({\varphi})=v_{x}t=h\cdot\frac{V-u\sin\varphi}{u\cos\varphi}\), | (2) |
За умовою задачі відстань L має бути якнайменшою. Але, при якому напрямку руху плавця так буде, безпосередньо з отриманого виразу не видно. Тому скористаємося методами математичного аналізу й дослідимо отриману функцію L(φ) на екстремум. Для цього спочатку знайдемо похідну L′(φ):
| \( {L}^{\prime}({\varphi})=\frac{h}{u}\cdot\frac{(-u\cos^{2}\varphi+(V-u\sin\varphi)\sin\varphi)}{\cos^{2}\varphi}\). | (3) |
Відтак згадаємо, що величина L(φ) буде мінімальною при значенні кута \(\varphi=\varphi_{m}\), для якого \( {L}^{\prime}({\varphi}_{m})\) дорівнює нулю. Отже, згідно з виразом (3),
\( {(V-u\sin\varphi_{m})\sin\varphi_{m}}-u\cos^{2}\varphi_{m}={0}\),
звідки
\( \sin\varphi_{m}=\frac{u}{V}=\frac{1}{2}\) \( \Rightarrow \) \( \varphi_{m}=30^{\circ}\).
Таким чином, необхідний кут між напрямком руху хлопця та напрямком течії дорівнює
\( \alpha=90^{\circ}+\varphi_{m}=120^{\circ}\).
| Задача 1.5 |
Визначити
мінімальну швидкість umin, з якою має рухатись човен відносно води, аби потрапити із заданої точки А на одному березі ріки в задану точку B на іншому. Швидкість течії V , ширина ріки h і відстань S між заданими точками відомі.
Розв'язання
|
Дано V, h, S |
|
umin - ? |
Цю задачу можна розв'язати аналогічно до попередньої, склавши рівняння для шуканої швидкості u і проаналізувавши його на мінімум. Але відповідь можна отримати значно простіше за допомогою геометричної побудови, показаної на рис. 5-1.
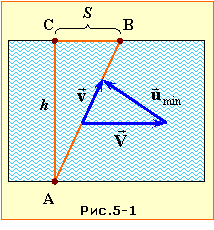 При переправі вектор швидкості човна \( \vec{v}\) відносно берега, що спрямовано по лінії AB, за законом додавання швидкостей (1.9) є пов'язаний із швидкістю човна відносно води \( \vec{u}\) та швидкістю течії \( \vec{V}\) співвідношенням
При переправі вектор швидкості човна \( \vec{v}\) відносно берега, що спрямовано по лінії AB, за законом додавання швидкостей (1.9) є пов'язаний із швидкістю човна відносно води \( \vec{u}\) та швидкістю течії \( \vec{V}\) співвідношенням
\( \vec{v}=\vec{u}+\vec{V}\).
Це відображає рис. 1.5, з якого очевидно, що швидкість човна відносно води буде мінімальною, коли вектор \( \vec{u}\) буде перпендикулярним до вектора \( \vec{v}\). В такому разі трикутник швидкостей є подібний до трикутника ABC, тож
\( \frac{u_{min}}{V}=\frac{h}{\sqrt{h^{2}+S^{2}}}\) \( \Rightarrow \) \( {u}_{min}=\frac{Vh}{\sqrt{h^{2}+S^{2}}}\).
| Задача 1.6 |
Від бакена, що стоїть посеред ріки, одночасно відпливають два човни: один за, а другий – поперек течії. Пройшовши однакову відстань, човни вертаються назад тими самими шляхами.
Визначити
відношення часів руху човнів \( \tau_{1}/\tau_{2}\), якщо їхня швидкість відносно води є в \( \eta{=1,8} \) раза більша за швидкість течії.
Розв'язання
|
Дано: η = 1,8 |
|
τ1/τ2 - ? |
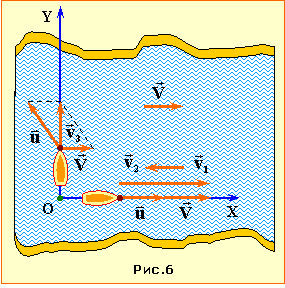
Позаяк за умовою швидкості човнів відносно води і пройдені ними відстані однакові, відміна у часах руху залежить тільки від швидкостей човнів відносно бакена.
Проаналізуємо їх, задля чого пов'яжемо систему відліку з бакеном (рис. 6) і приймемо що перший човен рухається вздовж осі ОХ. У такому разі модулі швидкості першого човна при русі вниз за течією v11 та вгору v12 дорівнюють
\( {v}_{11}={u+V}\) і \( {v}_{12}=u-{V}\),
де u – швидкість човна відносно води, V – швидкість течії. Відповідно до цього, якщо відстань в один кінець складає S, то повний час руху першого човна дорівнює
\( \tau_{1}=\frac{S}{V}\cdot\frac{2\eta}{\eta^{2}-1}\).
Аби рухатися перпендикулярно до берега, другий човен має правити під під певним кутом до осі OY, як показано на рис. 6. За такої умови швидкість човна відносно бакена в обох напрямках однакова і за теоремою Піфагора складає
\( {v}_{2}=\sqrt{u^{2}-V^{2}}=V\sqrt{\eta^{2}-1}\),
а час руху
| \( \tau_{2}=\frac{S}{V}\cdot\frac{2\eta}{\eta^{2}-1}\). | (2) |
Таким чином, відношення часів руху човнів дорівнює
\( \frac{\tau_{1}}{\tau_{2}}=\frac{\eta\cdot\sqrt{\eta^{2}-1}}{\eta^{2}-1}=\frac{\eta}{\sqrt{\eta^{2}-1}}={1,2} \).
| Задача 1.7 |
Два катери, рухаючись річкою назустріч один одному, порівнялися й розійшлись під мостом. Відтак, розвернувшись через τ =0,5 год, вони знов зустрілися на відстані L = 2 км від мосту.
Визначити
швидкість течії V, якщо швидкості катерів відносно води лишалися незмінними.
Розв'язання
|
Дано: L = 2 км
τ = 0,5 год
|
|
\( {V}\) - ? |
Цю задачу можна розв'язувати в нерухомій системі відліку, пов'язаній з берегом ріки (мостом), відносно якої сформульовані умова та завдання задачі. Для цього слід скласти рівняння руху катерів, врахувавши, що швидкість кожного з них при русі за течією становить u + V, а при русі проти дорівнює u – V (V – швидкість течії, u – швидкість катера відносно води). А далі треба розв'язати отриману систему рівнянь, врахувавши, що початкові та кінцеві положення катерів однакові.
Але задачу значно зручніше розглядати в рухомій системі відліку, пов'язаній з водою. Задля наочності приймемо, що під мостом в момент зустрічі катерів знаходиться ще й пліт, з яким і пов'яжемо рухому систему відліку. Позаяк ця система відліку рухається відносно берега зі швидкістю течії, то в ній швидкості катерів не залежать від напрямку руху і є однаковими. Тому катери віддаляються після першої зустрічі й повертаються до другої однаковий час, тож повний час їхнього руху між зустрічами t = 2τ. За цей час пліт, пливучи зi швидкістю V, проходить відстань L, тож швидкість течії дорівнює
\( {V}=\frac{L}{2\tau}\) = 2 км/год.
Як бачимо, при такому підходів задача практично є усною. Тож варто не забувати, що систему відліку, що мається на увазі в тексті задачі, не обов'язково, а інколи й недоцільно, використовувати для її розв'язування.
| Задача 1.8 |
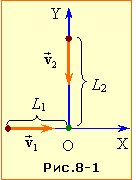 Два автомобілі рухаються зі швидкостями v1 і v2 по двох взаємно перпендикулярних дорогах у напрямку перехрестя.
Два автомобілі рухаються зі швидкостями v1 і v2 по двох взаємно перпендикулярних дорогах у напрямку перехрестя.
Визначити,
на якій найменшій відстані Lmin вони пройдуть один поз одного, якщо в початковий момент часу перебували на відстанях L1 і L2 від перехрестя.
|
Дано: v1, v2 L1, L2 |
|
Lmin - ?
|
Розв'язання
Розв'яжемо задачу теж у двох різних системах відліку.
I спосіб. Розмістимо початок координат нерухомої системи відліку ХОY у перехресті і спрямуємо осі координат уздовж доріг (рис. 8-1). В такому разі початкові координати автомобілів x01 = – L1, y01 = 0, x02 = 0, y02 = L2, і рівняння руху автомобілів мають вигляд:
|
\( {x_{1}}=-L_{1}+v_{1}{t}\) \( {y}_{1}={0}\) |
\(x_{2}={0}\) \( {y}_{2}=L_{2}-v_{2}{t}\) |
(1) |
Тож відстань між автомобілями \( {L}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\) визначається виразом:
| L(t) = \(\sqrt{(v_{1}t-L_{1})^{2}+(L_{2}-v_{2}t)^{2}}\). | (2) |
Проаналізувавши отриману функцію L(t) на мінімум, отримаємо відповідь задачі. Для цього спочатку знайдемо похідну L′(t):
\( {L}^{\prime}(t)=\frac{2(v_{1}t-L_{1})v_1+2(L_{2}-v_{2}t)(-v_{2})}{2\sqrt{(v_{1}t-L_{1})^{2}+(L_{2}-v_{2}t)^{2}}}\) =
=\( \frac{\left( v_{1}^{2}+v_{2}^{2} \right)t-\left( {{L}_{1}}{{v}_{1}}+{{L}_{2}}{{v}_{2}} \right)}{\sqrt{{{\left( {{v}_{1}}t-{{L}_{1}} \right)}^{2}}+{{\left( {{L}_{2}}-{{v}_{2}}t \right)}^{2}}}} \).
У момент t0 розташування автомобілів на найменшій відстані, похідна L′(t0) = 0, отже,
\( \left(v_{1}^{2}+v_{2}^{2}\right)t_{0}-(L_{1}v_{1}+L_{2}x_{2})={0}\),
звідки
\( {t}_{0}=\frac{L_{1}v_{1}+L_{2}v_{2}}{v_{1}^{2}+v_{2}^{2}}\).
Підставивши це значення у вираз (2), знайдемо шукану відстань:
\( {{L}_{\min }}=\sqrt{{{\left( \frac{{{v}_{1}}{{\left( {{L}_{1}}{{v}_{1}}+{{L}_{2}}{{v}_{2}} \right)}^{2}}}{v_{1}^{2}+v_{2}^{2}}-{{L}_{1}} \right)}^{2}}+{{\left( {{L}_{2}}-\frac{{{v}_{2}}{{\left( {{L}_{1}}{{v}_{1}}+{{L}_{2}}{{v}_{2}} \right)}^{2}}}{v_{1}^{2}+v_{2}^{2}} \right)}^{2}}} \) =
=\( \frac{\left|L_{2}v_{2}-L_{1}x_{1}\right|}{\sqrt{v_{1}^{2}+v_{2}^{2}}}\).
II спосіб. Розв'яжемо тепер задачу в пов'язаній з першим автомобілем рухомій системі відліку X1O1Y1, швидкість якої відносно нерухомої системи ХОY складає \(\vec{V}=\vec{v}_{1}\). Тепер перший автомобіль весь час перебуває в початку відліку O1, а другий рухається відносно нього під певним кутом \( \alpha \) до осі O1X1 (рис. 8-2). Його швидкість \( \vec{u}\) за законом (1.11) дорівнює
| \( \vec{u}=\vec{v}_{2}-\vec{v}_{1}\), | (3) |
отже,
|
\( {u}=\sqrt{v_{1}^{2}+v_{2}^{2}}\). |
(4) |
|
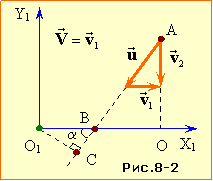
Із рис. 1.8-2 видно, що відстань L буде найменша, коли другий автомобіль знаходитиметься в т. С. Тому, якщо позначити довжину відрізка ВО як S, то
|
\({{L}_{\min }}=\left( {{L}_{1}}-S \right)\sin \alpha \). |
(5) |
Також є зрозуміло, що $S=\frac{{{L}_{2}}}{\operatorname{tg}\alpha }$, $\sin \alpha =\frac{{{v}_{2}}}{u}$ i $\operatorname{tg}\alpha =\frac{{{v}_{2}}}{{{v}_{1}}}$.
Відтак підставивши ці значення у вираз (5) і, замінивши величину u за формулою (4), отримаємо відповідь:
\( {L}_{min}=\left(L_{1}-\frac{L_{2}v_{1}}{v_{2}}\right)\frac{v_{2}}{u}=\frac{\left|L_{2}v_{1}-L_{1}v_{2}\right|}{\sqrt{v_{1}^{2}+v_{2}^{2}}}\).
Очевидно, що цей спосіб (використання рухомої системи відліку) робить розв'язок набагато коротшим.
Прямолінійний рівнозмінний рух одного тіла
Задача 1.9. Літак рухається прямолінійно спочатку зі швидкістю \(v_{0}\) = 720 км/год, а потім протягом t = 10 с рівно-прискорено так, що за останню секунду (проміжок часу \( \tau \) ) долає відстань S = 295 м. Визначити кінцеву швидкість літака \( {v}\).
Задача 1.10. Потяг, який рухається прямолінійно рівно-прискорено, на певній ділянці шляху збільшує швидкість на \( \Delta{v} \) = 60 км/год при середній швидкості \( \langle{v}\rangle \) = 40 км/год. Визначити швидкість поїзда \( {v}\) посередині згаданої ділянки.
Задача 1.11. Тіло вільно падає з висоти h = 25 м. Визначити його середню швидкість \( \langle{v}\rangle \) на другій половині шляху.
Задача 1.12. По похилій дошці знизу вгору пустили кульку. На відстані S = 30 см від початкової точки кулька побувала двічі: через t1 = 1 c та t2 = 2 c . Визначити мінімально можливу довжину дошки L. Тертя відсутнє.
Задача 1.13. Тіло кинули зі швидкістю \( {v}_{0}\) = 15 м/с вертикально вгору з балкона, розташованого на висоті h = 25 м. Визначити: а) максимальну висоту підйому H тіла над землею; б) час \( \tau \), через який воно впаде на землю; в) швидкість \( {v}\) тіла на момент падіння.
Задача 1.14. Кабіна ліфта висотою h = 2,25 м починає підійматись із прискоренням a = 0,5 м/с2. На момент, коли її швидкість досягла значення \( {v}_{0}=2,5 \) м/с, зі стелі відірвалася пластилінова кулька. Визначити: а) час \( \tau \) падіння кульки на підлогу, б) величину (модуль) переміщення \( {l}\) та в) шлях S, який пройшла кулька відносно шахти ліфта.
| Задача 1.9 |
Літак рухається прямолінійно спочатку зі швидкістю \(v_{0}\) = 720 км/год, а потім протягом t = 10 с рівно-прискорено так, що за останню секунду (проміжок часу τ = 1 c) долає відстань S = 295 м.
Визначити
кінцеву швидкість літака \( {v}\).
Розв'язання
|
Дано: v0 = 720 км/год=
=200 м/с
t = 10 c
τ = 1 c
S = 295 м
|
|
\( {v}\) - ? |
Літак починає прискорюватися при заданій швидкості v0, тож шукана кінцева швидкість визначається рівнянням
|
\( {v}=v_{0}+at \). |
(1) |
Потрібне для отримання відповіді прискорення а можна знайти через заданий шлях S. Для цього в напрямку руху літака спрямуємо вісь OX із початком відліку в точці початку розгону, рис. 9. Тоді рівняння кінцевої координати літака має вигляд:
|
\( {x}=v_{0}t+\frac{at^{2}}{2}\). |
(2) |
Із цього ж рівняння, замінивши t на t1 = t – τ, отримаємо вираз координати на передостанню секунду:
\( {x}_{1}\) = \( v_{0}(t-\tau)+\frac{a(t-\tau)^{2}}{2}\).
Отже, літака за останню секунду S = x – x1 визначається, як
\( {S}=x-x_{1}\) = ${{v}_{0}}\tau +\frac{a\tau \left(2t-\tau \right)}{2}$,
Відтак після простих перетворень знайдемо прискорення
\( {a}=\frac{2(S-v_{0}\tau)}{{\tau}(2t-\tau)} \) = 10 м/с2
і за формулою (1) – кінцеву швидкість літака:
\( {v}\) = 300 м/с.
| Задача 1.10 |
Потяг, який рухається прямолінійно рівно-прискорено, на певній ділянці шляху збільшує швидкість на \( \Delta{v} \) = 60 км/год при середній швидкості \( \langle{v}\rangle \) = 40 км/год..
Визначити
швидкість поїзда \( {v}\) посередині згаданої ділянки.
|
Дано: \( \langle{v}\rangle \) = 40 км/год
\( \Delta{v}\) = 60 км/год
|
|
\( {v} \) - ? |
Розв'язання
В умові немає інформації про час руху потяга на згадуваній ділянці шляху. Тому пошук відповіді почнемо з формули (1.19), яка опосередковано встановлює зв'язок між шляхом і швидкістю. Отже, увівши для початкової, кінцевої і шуканої швидкостей, а також прискорення і пройденого шляху відповідні позначення v1, v2, v, а, S, запишемо:
\({{v}^{2}}-v_{1}^{2}=aS\),
\({v_{2}^{2}-{v}^{2}}=aS\),
і, прирівнявши ліві частини, отримаємо:
| \({{v}^{2}}=\frac{v_{1}^{2}+v_{2}^{2}}{2}\) \(\Rightarrow \) v = \(\sqrt{{\left( v_{1}^{2}+v_{2}^{2} \right)}/{2}}\) | (1) |
Швидкості v1 і v2 можна виразити через задані величини \( \langle{v}\rangle \) і \( \Delta{v} \) за допомогою рівняння (1.16):
|
\(S={{v}_{1}}t+\frac{a{{t}^{2}}}{2}=\left( {{v}_{1}}+\frac{at}{2} \right)t\). |
Звідси, зробивши очевидні заміни S = \( \langle{v}\rangle\)t, a = (Δv/t) і v2 = v1 + Δv, дістанемо:
|
\({{v}_{1}}=\left\langle v \right\rangle -\frac{\Delta v}{2}\quad \ , \quad {{v}_{2}}=\left\langle v \right\rangle+\frac{\Delta v}{2}\) |
Відтак, підставивши отримані вирази у формулу (1), після спрощень отримуємо відповідь:
\( {v}=\sqrt{\langle{v}\rangle^{2}+\left(\frac{\Delta{v}}{2}\right)^{2}}\) = 50 км/год.
| Задача 1.11 |
Тіло вільно падає з висоти h = 25 м.
Визначити
його середню швидкість \( \langle{v}\rangle \) на другій половині шляху.
Дано:
| h = 25,0 м |
|
\( \langle{v}\rangle \)-? |
Розв'язання
Розв'яжемо задачу двома способами.
Спосіб 1. Середня швидкість тіла кульки дорівнює відношенню пройденого шляху (h/2) до часу його проходження Δt:
$\left\langle v \right\rangle =\frac{h}{2\Delta t}$,
Величина \( \Delta{t}=t_{2}-t_{1}\), де час проходження тілом верхньої половини шляху t1 і повний час руху t2 визначаються з рівняння (1.16):
\( \frac{h}{2}=\frac{gt_{1}^{2}}{2}\); \( \Rightarrow \) \( {t}_{1}=\sqrt{\frac{h}{g}}\);
\( {h}=\frac{gt_{2}^{2}}{2}\); \( \Rightarrow \) \( {t}_{2}=\sqrt{\frac{2h}{g}}\).
Отже,
\( \Delta{t}=t_{2}-t_{1}=\sqrt{\frac{h}{g}}\left(\sqrt{2}-1\right) \).
Відтак для шуканої і середньої швидкості виходить:
|
$\left\langle v \right\rangle =\frac{\sqrt{gh}}{2\left( \sqrt{2}-1 \right)}$ |
Помноживши цей вираз у чисельнику й знаменнику на $\left( \sqrt{2}+1 \right)$, відповідь можна подати також у наступному вигляді:
|
$\left\langle v \right\rangle =\frac{\sqrt{gh}}{2}\left( \sqrt{2}+1 \right)$. |
Обчислення дають
\(\left\langle v \right\rangle \) = 19 м/с
Спосіб 2. Відповідь можна отримати легше, якщо зобразити графік швидкості тіла v(t), визначити за ним вказану в умові частину шляху кульки (див. п. 1.4), отримати формулу (1.21)
$\left\langle v \right\rangle =\frac{{{v}_{1}}+{{v}_{2}}}{2}$
і відтак, врахувавши, що за формулою (1.19) \({{v}_{1}}=\sqrt{gh}\) і \({{v}_{2}}=\sqrt{2gh}\), отримати відповідь:
\(\left\langle v \right\rangle =\frac{\sqrt{gh}}{2}\left( \sqrt{2}+1 \right) \).
| Задача 1.12 |
Кулька, пущена вгору по похилій дошці, на відстані S = 30 см від початкового положення побувала двічі: через t1 = 1 c та t2 = 2 c .
Визначити
мінімально можливу довжину дошки L. Тертя відсутнє.
|
Дано: S = 30 см
t1 = 1 c
t2 = 2 c
|
|
L - ? |
Розв'язання
Кулька рухається вздовж дошки з наданою їй початковою швидкістю v0 і прискоренням a, що створюється "скочувальною" складовою сили тяжіння. Спочатку вона опиняється на відстані S в момент t1, підіймаючись угору, а потім у момент t2 знов опиняється в тому самому положенні, скочуючись. Отже, найменша необхідна довжина дошки дорівнює максимальній відстані L, на яку може віддалитися кулька від початкового положення.
Для визначення величини L спрямуємо вісь OX уздовж дошки, розмістивши початок координат в початковому положенні кульки (х0 = 0). У такому разі проєкція прискорення ах = – а, і, згідно з рівнянням (1.18),
| \(x=\frac{v_{0}^{2}-{{v}^{2}}}{2a}\). |
При максимальному віддаленні х = L швидкість кульки v = 0, отже,
| \( {L}=\frac{v_{0}^{2}}{2a}\). | (1) |
Величини v0 і a можна знайти з рівняння координати кульки (1.16). Поклавши x = S , отримаємо:
|
\( {S}=v_{0}t-\frac{at^{2}}{2}\) \(\Rightarrow \) \(a{{t}^{2}}-2{{v}_{0}}t+2S=0\), |
Коренями цього рівняння є задані моменти часу t1 і t2, тож за теоремою Вієта
${{t}_{1}}+{{t}_{2}}=\frac{2{{v}_{0}}}{a}$ i ${{t}_{1}}{{t}_{2}}=\frac{S}{2a}$,
і
\( {a}=\frac{2S}{t_{1}t_{2}}\), \( {v}_{0}=\frac{a(t_{1}+t_{2})}{2}=\frac{S(t_{1}+t_{2})}{t_{1}t_{2}}\).
Підставивши отримані величини у вираз (1), дістанемо відповідь:
\( {L}=\frac{S(t_{1}+t_{2})^{2}}{4t_{1}t_{2}}\) ≈ 34 см.
| Задача 1.13 |
Тіло кинули зі швидкістю \( {v}_{0}\) = 15 м/с вертикально вгору з балкона, розташованого на висоті h = 25 м.
Визначити:
а) максимальну висоту підйому H тіла над землею;
б) час \( \tau \), через який воно впаде на землю;
в) швидкість \( {v}\) тіла на момент падіння.
|
Дано: h = 25 м
v0 = 15 м/с
|
|
H - ?
τ - ?
v - ?
|
Розв'язання
Напрямимо вгору вісь OY з початком відліку на землі (рис. 13). У такому разі початкова координата тіла y0 = h, проєкції швидкості та прискорення \(v_{0y}=v_{0}\) і \(g_{y}=-g\), і, згідно з (1.16), 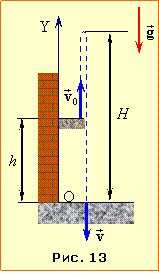 поточні координата та проєкція швидкості задовольняють рівняння:
поточні координата та проєкція швидкості задовольняють рівняння:
| \(y=h+v_{0}t-\frac{gt^{2}}{2}\), | (1) |
| vy = v0 – gt. | (2) |
а) У найвищій точці підйому швидкість тіла дорівнює нулю, тож час підйому:
| \(t=\frac{v_{0}}{g}\). |
Максимальна висота підйому дорівнює координаті тіла в цей момент:
\(H=h+v_{0}t-\frac{gt^{2}}{2}=h+\frac{v_{0}^{2}}{2g}\approx\) 36,5 м.
б) На момент падіння на землю t =\(\tau\) координата тіла y = 0:
\(y(\tau)=h+v_{0}\tau-\frac{g\tau^{2}}{2}=\) 0.
Розв'язавши це квадратне рівняння, знайдемо:
\(\tau=\frac{v_{0}+\sqrt{v_{0}^{2}+2gh}}{g}=\) 4,26 c.
(від'ємний корінь не має фізичного змісту).
в) Підставивши знайдене значення \(\tau\) в рівняння (2), дістанемо
vy = v0 – gτ= –26,75 м/с.
Знак "–" означає, що вектор швидкості в момент падіння тіла на землю напрямлений проти осі OY, тобто вертикально вниз.
| Задача 1.14 |
Кабіна ліфта висотою h = 2,25 м починає підійматися з прискоренням a = 0,5 м/с2. У момент, коли її швидкість досягла значення v0 = 2,5 м/с, зі стелі відірвалася пластилінова кулька.
Визначити:
а) час \( \tau \) руху кульки до підлоги;
б) переміщення \( {l}\) та
в) шлях S, який пройшла кулька відносно шахти.
|
Дано: h = 2,25 м
a = 0,5 м/с2
v0 = 2,5 м/с
|
|
τ - ? l - ? S - ? |
Розв'язання
Рух кульки, залежно від ситуації, зручно розглядати або відносно кабіни ліфта (система відліку O′Y′, рис. 1.14а), або відносно шахти (система відліку OY, рис. 1.14б).
а) Для визначення часу падіння кульки є доцільно розглянути її рух відносно кабіни ліфта (рухомої системи відліку О′Y′, рис. 14а.
Відносно землі ліфт рухається з прискоренням \( \vec{a}\) а кулька – з прискоренням \( \vec{g}\). Тож
відносно ліфта її прискорення \( \vec{a}^{\prime}=\vec{g}-\vec{a}\) має модуль
a′ = (a + g).
При цьому початкова швидкість кульки відносно ліфта ${{{v}'}_{0}}=0$ і початкова координата ${{{y}'}_{0}}=h$. Отже за рівнянням (1.16) її координата в довільний момент часу
\( {y}^{\prime}=h-\frac{(g+a)t^{2}}{2}\).
Тож на момент падіння t = \( \tau \), коли \( {y}^{\prime}\) = 0, маємо:
\( h-\frac{(g+a)t^{2}}{2}={0}\) \( \Rightarrow \) \( \tau=\sqrt{\frac{2h}{g+a}}\) = 0,65 c.
б) Величина переміщення l кульки в нерухомій системі відліку OY , що є пов'язана із шахтою ліфта (тобто землею), дорівнює відстані (модулю різниці координат) між точками падіння на підлогу та відриву кульки від стелі ліфта:
$l=\left| y(\tau )-h \right|$.
Прискорення кульки відносно шахти дорівнює g, отже,
\( {y}(\tau)=h+v_{0}\tau-\frac{g{\tau}^{2}}{2}\).
Відповідно, переміщення
| \( {l}=\left|v_{0}\tau-\frac{g\tau^{2}}{2}\right|={0,5}\) м. | (1) |
в) На рис. 1.14б умовно показано положення кабіни ліфта відносно шахти (в системі відліку OY) на момент падіння кульки на підлогу та її початкове (y0 = h) і найвище (ym) положення. З рисунка видно, що шлях S кульки складається з двох частин – шляху підйому до найвищої точки траєкторії S1 і шляху S2 падіння на підлогу ліфта, причому \( {S}_{2}=S_{1}+{l}\). Отже,
| \( {S}=S_{1}+S_{2}=2S_{1}+{l}\) |
Позаяк у найвищій точці підйому швидкість кульки v = 0, то згідно з формулою (1.19),
\( {S}_{1}=\frac{v_{0}^{2}}{2g}\) = 0,3 м,
і згідно з результатом (1) шуканий шлях кульки від точки відриву до підлоги ліфта складає
S = 1,1 м.
Графіки руху та їхнє використання
Задача 1.15. Тіло рухається з початку координат у напрямку осі ОХ перші 5 с рівномірно зі швидкістю v0 = 10 м/с, а наступні 15 c – із протилежно напрямленим прискоренням a = 2 м/с2. Побудувати графіки: а) проєкції швидкості \( {v}_{x}(t) \) та б) координати x(t) тіла.
Задача 1.16. За заданим графіком швидкості тіла, що рухається з початку координат уздовж осі OX побудувати графіки: прискорення тіла ax(t), його координати x(t) і пройденого шляху s(t).
Задача 1.17. На перегоні між двома станціями метро довжиною s = 4 км потяг рухається з середньою швидкістю \( \langle{v}\rangle \) = 68,4 км/год. На розгін та гальмування з однаковим прискоренням він витрачає по \( \tau=20 \) c, а решту часу рухається рівномірно. Визначити максимальну швидкість потяга v0.
Задача 1.18. Від потяга, що рухається рівномірно, відчіплюють останній вагон, який, рівномірно сповільнюючись, проходить до до зупинки шлях S. Визначити шлях S1, який пройде за цей час потяг.
Задача 1.19. Дві кульки, що рухаються без тертя з однаковою швидкістю, одночасно підходять до викривлених симетричних профілів, перша – до опуклого, друга – до угнутого. Обґрунтувати, яка з кульок раніше пройде свій профіль.
| Задача 1.15 | |
|
Задача 1.15 |
Тіло рухається з початку координат у напрямку осі ОХ перші 5 с рівномірно зі швидкістю v0 = 10 м/с, а наступні 15 c – із протилежно напрямленим прискоренням a = 2 м/с2.
Побудувати графіки
а) проєкції швидкості \( {v}_{x}(t) \);
б) координати x(t) тіла.
|
Дано: v0 = 10 м/с
a = 2 м/c2
τ1 = 5 c
τ2 = 15 c
x0 = 0
|
|
\( {v}_{x}(t) \)?, x(t)? |
Розв'язання
а) На першому відтинку часу (від 0 до t=τ1) швидкість тіла vх = v0 = const, тож графік \( {v}_{x}{(t)}\) є відрізком прямої, паралельної до осі t, рис. 1.15, а.
На другому проміжку часу тривалістю τ2 тіло рухається з прискоренням, проєкція котрого ax = –a. Отже, згідно з рівняннями швидкості (1.16), графік \( {v}_{x}{(t)}\) зображується відрізком спадної прямої, рис. 15, а. При цьому в точці перетину графіка з віссю t величина vх змінює знак, тобто тіло змінює напрям руху на протилежний. 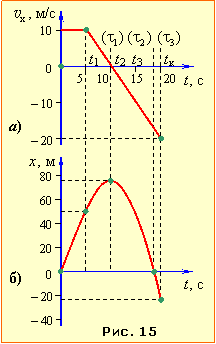
б) Розглянемо тепер графік координати х(t). На першому проміжку часу (від t = 0 до t = t1) координата змінюється за законом x = v0t, а на другому – згідно з рівнянням координати х (1.16), яке зручно записати у вигляді:
|
\(x={{x}_{1}}+{{v}_{0}}\tau -\frac{a{{\tau }^{2}}}{2}\), |
(1) |
де х1 – початкова координата тіла і τ = (t – τ1) – поточний час на другому інтервалі руху. Відповідно, графік х(t) зображується відрізками прямої та параболи, що мають бути спряжені (плавно переходити один в один, як на рис. 15, б), бо їхній нахил до осі часу визначає одну й ту саму величину v0. При цьому вершина параболи орієнтована догори (ax < 0) і визначає точку повороту, тобто точку максимального віддалення тіла від початкового положення й зміни напрямку руху.
Відтак для коректного відображення на рисунку умов задачі знайдемо числові значення необхідних параметрів графіків. А саме:
– координату тіла в момент t1
х1 = v0τ1 = 50 м;
– проєкцію кінцевої швидкості
vк = v0 – aτ2 = –20 м/с;
– координати вершини параболи, які визначають момент повороту tп і координату xп точки, в якій він відбувається. Обидві величини легко визначаються з рівнянь (1.16) і (1.18). Позаяк у момент tп швидкість тіла v = 0, то
tп = τ1 + \(\frac{v_{0}}{a}\) = 10 c,
і
|
\(v_{0}^{2}=2a\left( {x}_{п}-{{x}_{1}} \right)\) \(\Rightarrow \) \({{x}_{\text{п}}}={{x}_{1}}+\frac{v_{0}^{2}}{2a}\); |
– кінцеву координату тіла хк :
xк = \({{x}_{1}}+{{v}_{0}}{{\tau }_{2}}-\frac{a\tau _{2}^{2}}{2}\) = –25 м;
– час повернення тіла в початкове положення x0 = 0, який дорівнює t0 = τ1 + τ0, де величина τ0 є коренем рівняння:
\( {x}_{1}+v_{0}\tau_{0}-\frac{a\tau^{0}}{2}={0}\) \( \Rightarrow \) τ0 ≈ 13,7 с \( \Rightarrow \) τ0 ≈ 18,7 с.
(Другий корінь не задовольняє умову задачі).
Згідно з обчисленнями, відмічаємо на графіку всі розраховані точки і проводимо через них відрізок прямої та відрізок параболи, як показано на рис. 15, б).
| Задача 1.16 |
| Задача 1.16 |
За заданим графіком швидкості тіла, що рухається з початку координат уздовж осі OX
побудувати графіки:
а) проєкції прискорення тіла aх (t);
б) координати x(t);
и) пройденого шляху s(t).
Розв'язання
а) Із рис. 16-1а випливає, що рух тіла складається з двох ділянок, на яких його прискорення \({{\vec{a}}_{1}}\) і \({{\vec{a}}_{2}}\) є сталими і мають проєкції на вісь ОХ складають: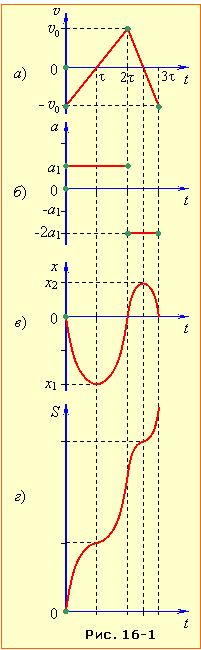
\( {a}_{1}=\frac{v_{0}-(-v_{0})}{2\tau}=\frac{v_{0}}{\tau}\),
\( {a_{2}=\frac{-v_{0}-v_{0}}{3\tau-2\tau}}=-\frac{2v_{0}}{\tau}\).
Отже, \( {a_{2}}=-2a_{1}\), і графік прискорення має вигляд рис. 16-б .
б) Перейдемо тепер до аналізу графіка координати x(t). Із рівняння (1.16), випливає, що він складається з ділянок двох парабол, причому, з урахуванням знаків прискорень (рис. 16-1б), вершина першої орієнтована донизу, а другої – догори. Вершини парабол відповідають точкам повороту, в яких змінюється напрям руху та знак проєкції швидкості, а сама швидкість проходить через нульове значення. За умовою задачі (див. рис. 16-1а) це відбувається в моменти часу t1 = τ і t2 = 2,5τ. До того ж, з рис. 16-1а видно, що сумарна площа під графіками (алгебраїчна величина!), котра визначає переміщення на кожній з ділянок, дорівнює нулю. Це означає, що в кінці кожного відтинку руху тіло повертається у вихідне положення х = 0.
На завершення з рівняння (1.18) визначимо координати точок повороту х1, х2, підставивши відповідні значення швидкостей та знайдені раніше величини а1 і а2:
\({{x}_{1}}=-\frac{{{v}_{0}}\tau }{2}\) \({{x}_{2}}=\frac{{{v}_{0}}\tau }{4}\)
Графік координати x(t), побудований за наведеними розрахунками, показано на рис. 1.16в.
в) Для побудови графіка шляху S(t) візьмемо до уваги, що при прямолінійному русі пройдений тілом шлях дорівнює сумі модулів його переміщень. Відтак графік S(t) легко отримати з рис. 16-1в, віддзеркаливши спадні ділянки від осі абсцис, як показано на рис. 16-1г.
| Задача 1.17 |
| Задача 1.17 |
На перегоні довжиною S = 4 км між двома станціями метро потяг рухається з середньою швидкістю \( \langle{v}\rangle \) = 68,4 км/год. На розгін та гальмування зі сталим прискоренням потяг витрачає по \( \tau=20 \) c, а решту часу рухається рівномірно.
Визначити
максимальну швидкість потяга v0.
|
Дано: |
|
v0 - ? |
Розв'язання
Для розв'язування задачі скористаємось графіком швидкості потяга, який, відповідно до умови, 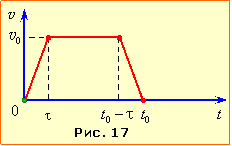 зображується рівнобічною трапецією (рис. 17). Шлях потяга S чисельно дорівнює площі цієї трапеції:
зображується рівнобічною трапецією (рис. 17). Шлях потяга S чисельно дорівнює площі цієї трапеції:
\( {s}=\frac{1}{2}(t_{0}+(t_{0}-2\tau{))}v_{0}=(t_{0}-\tau)v_{0}\).
Підставивши вираз повного часу руху потяга \( {t}_{0}=s/\langle{v}\rangle \), отримаємо відповідь:
\( {s}=\left(\frac{s}{\langle{v}\rangle}-\tau\right)v_{0}\) \( \Rightarrow \)
\( {v}_{0}=\frac{s\langle{v}\rangle}{s-\langle{v}\rangle\tau} \) ≈19,8 м/с ≈ 71,3 км/год.
| Задача 1.18 |
| Задача 1.18 |
Від потяга, що рухається рівномірно, відчіплюють останній вагон, який, рівномірно сповільнюючись, проходить до до зупинки шлях S.
Визначити
шлях S1, який пройде за цей час потяг.
Розв'язання
|
Дано: S |
|
S1 - ? |
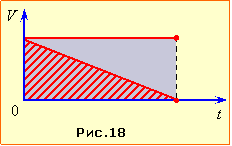 Графік швидкості вагона зображується нахиленим відрізком, а потяга – горизонтальним відрізком прямої (рис. 18). Позаяк площа під графіком швидкості чисельно дорівнює пройденому шляху, очевидно, що шлях потяга є вдвічі більший:
Графік швидкості вагона зображується нахиленим відрізком, а потяга – горизонтальним відрізком прямої (рис. 18). Позаяк площа під графіком швидкості чисельно дорівнює пройденому шляху, очевидно, що шлях потяга є вдвічі більший:
\( {S}_{1}=2{S}\).
| Задача 1.18 |
| Задача 1.19 |
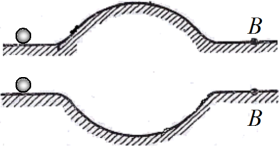
Дві кульки, що рухаються без тертя з однаковою швидкістю, одночасно підходять до викривлених симетричних профілів, перша – до опуклого, друга – до угнутого, рис. 19.
Обґрунтувати,
яка з кульок раніше потрапить у точку B.
Розв'язання
Поставлене питання можна вирішити, аналізуючи І – пройдені шляхи, або ІІ – середні швидкості кульок.
І. В теоретичних відомостях (п. 1.4) було показано, що при всякому русі площа S під заданою ділянкою графіка швидкості тіла v(t) чисельно дорівнює пройденому за відповідний час шляхові. Через симетрію профілів руху шляхи кульок і вказані площі S1 і S2 є однакові, тож із схематичних графіків швидкості рис. 19-1 видно, що t2 < t1, тобто друга кулька "прийде до фінішу" раніше.
ІІ. При проходженні профілів швидкість першої кульки на першій половині шляху зменшується, а потім збільшується до початкової величини, тоді як для другої кульки все відбувається з точністю до навпаки. Очевидно, що за таких умов середня швидкість першої кульки на всьому шляху є меншою, ніж у другої, тож вона випередить першу (час проходження дистанції t2 < t1).
Рух тіла, що кинуте під кутом до горизонту
Задача 1.20. Тіло кинули з висоти h над землею вгору під кутом α до горизонту з початковою швидкістю \( {v}_{0}\). Визначити: а) рівняння траєкторії y = f(x); б) час підйому до найвищої точки траєкторії tm; в) найбільшу висоту підйому тіла над горизонтом H; г) горизонтальну дальність польоту тіла L; д) кут кидання \( \alpha_{m}\), що відповідає є найбільшій дальності польоту.
Задача 1.21. Тіло кинули з поверхні землі з початковою швидкістю \( {v}_{0}\) = 10 м/с так, що за перші t = 0,5 c руху швидкість тіла зменшилася до величини \( {v}\) = 7 м/с. Визначити максимальну висоту підйому тіла H
Задача 1.22. Кулька, що вільно падає з висоти h = 80 см, пружно відбивається від похилої площини з кутом нахилу до горизонту α = 30°. Визначити: а) через який час τ і на якій відстані L від точки падіння кулька вперше знов зіткнеться з площиною; б) величину та напрям швидкості відскоку.
| Задача 1.20 |
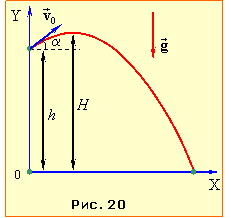
| Задача 1.20 |
Тіло кинули з висоти h над землею вгору під кутом \( \alpha \) до горизонту з початковою швидкістю \( {v}_{0}\).
Визначити:
а) рівняння траєкторії y = f(x);
б) час підйому до найвищої точки траєкторії th;
в) найбільшу висоту підйому тіла над горизонтом H;
г) горизонтальну дальність польоту тіла L;
д) кут кидання \( \alpha_{m}\), що відповідає є найбільшій дальності польоту.
|
Дано: h, α, v0 |
|
y = f(x) - ?
tm - ?
H - ?
L - ?
αm - ?
|
Розв'язання
Рух тіла відбувається зі сталим прискоренням \( \vec{g}\) і описується рівняннями (1.16). Оберемо систему координат із початком на землі під місцем кидання тіла (рис. 20). Тоді за умовою
|
|
|
|
|
|
|
|
|
|
|
|
і рівняння (1.16) мають вигляд:
| \( {x}=v_{0}t\cos\alpha \), | (1) |
| \( {v}_{x}=v_{0}\cos\alpha \), | (2) |
| \( {y}=h+v_{0}t\sin\alpha-\frac{gt^{2}}{2}\), | (3) |
| \( {v}_{y}=v_{0}\sin\alpha-{gt}\), | (4) |
а) Рівняння траєкторії тіла визначає його координату y як функцію координати x: y(x). Її можна знайти, виключивши з рівнянь координат час t. Для цього виразимо його з рівняння (1) і після підстановки в рівняння (3) та елементарних викладок отримаємо:
\( {t}=\frac{x}{v_{0}\cos\alpha}\) $\Rightarrow $
|
$y=h+x\operatorname{tg}\alpha -\frac{g}{2v_{0}^{2}{{\cos }^{2}}\alpha }{{x}^{2}}$ |
(5) |
Це є рівняння параболи з гілками, спрямованими донизу (рис. 1.19).
б) Вектор швидкості є дотичним до траєкторії й у верхній точці спрямований горизонтально. Отже,
\( {v}_{y}(t_{m})=v_{0y}-gt_{m}={0}\),
де \( {t}_{m}\) – час підйому тіла до верхньої точки траєкторії.
З цього рівняння маємо:
\( {t}_{m}=\frac{v_{0y}}{g}=\frac{v_{0}\sin\alpha}{g}\).
в) Найбільша висота підйому тіла над землею дорівнює координаті y на момент часу \( {t}_{m}\):
| \( {H}=y(t_{m})=h+v_{0y}t_{m}-\frac{gt_{m}^{2}}{2}=h+\frac{v_{0}^{2}\sin^{2}\alpha}{2g}\). | (6) |
г) Горизонтальна дальність польоту тіла L дорівнює координаті x точки перетину траєкторії з віссю OX (рис. 20), тобто при y = 0. Тож із рівняння (5) маємо:
| \( {0}=h+L\mathrm{tg}\alpha-\frac{g}{2v_{0}^{2}\cos^{2}\alpha}L^{2}\), | (7) |
звідки
| \( {L}=\frac{v_{0}^{2}\sin\alpha\cos\alpha+v_{0}\cos\alpha\sqrt{v_{0}^{2}\sin^{2}\alpha+2gh}}{g}\). | (8) |
(Від'ємний корінь не має фізичного змісту).
Звичайно, для визначення дальності польоту можна було би спочатку визначити повний час руху тіла t0 з рівняння (3), поклавши y = 0, а потім, підставивши його в рівняння (1), знайти x(t0) = L. Але такий шлях є більш громіздкий.
Зауважимо також, що в окремому випадку, коли тіло кидають з поверхні землі (h = 0), для дальності польоту виходить
| \( {L}=\frac{2v_{0}^{2}\sin\alpha\cos\alpha}{g}=\frac{v_{0}^{2}\sin{2}\alpha}{g}\) | (8a) |
д) Кут кидання, при якому дальність польоту тіла є найбільшою, логічно було би визначати стандартним методом вищої математики, дослідивши на максимум функцію L(α), що визначається виразом (8). Одначе це можна зробити й алгебраїчно . А саме. Зробивши в рівнянні (7) заміну \( \cos^{2}\alpha=1/(\mathrm{tg}\alpha+1) \), дістанемо:
\({h}+L\mathrm{tg}\alpha-\frac{gL^{2}}{2v_{0}{2}}(\mathrm{tg}^{2}\alpha+1) \) \( \Rightarrow \) \( \mathrm{tg}^{2}\alpha-\frac{2v_{0}^{2}}{gL}\mathrm{tg}\alpha-\left(\frac{2hv_{0}^{2}}{gL}-1\right)={0}\).
Корені отриманого рівняння
| \( \mathrm{tg}\alpha=\frac{v_{0}^{2}}{gL}\left(1\pm\sqrt{1+\frac{2gh}{v_{0}^{2}}-\left(\frac{gL}{v_{0}^{2}}\right)^{2}}\right) \) | (9) |
мають фізичний зміст лише за умови
\( {1}+\frac{2gh}{v_{0}^{2}}-\left(\frac{gL}{v_{0}^{2}}\right)^{2}\ge{0}\),
тобто, коли \( {L}\le\frac{v_{0}\sqrt{v_{0}^{2}+2gh}}{g}\). Отже, максимальна можлива дальність польоту тіла складає
\( {L}_{m}=\frac{v_{0}\sqrt{v_{0}^{2}+2gh}}{g}\).
Відтак підставимо це значення у формулу (9) і одержимо для кута кидання αm, що відповідає найбільшій дальності польоту, наступний вираз:
\( \mathrm{tg}\alpha_{m}=\frac{v_{0}^{2}}{gL_{m}}=\frac{v_{0}}{\sqrt{v_{0}^{2}+2gh}}\).
Принагідно відмітимо, що при киданні з поверхні землі (h = 0) для αm виходить tgαm = 1, тобто дальність польоту є максимальна при куті кидання 45°. Такого висновку можна дійти й на основі виразу (8а), позаяк максимальне значення \( \sin{2\alpha}={1}\).
| Задача 1.21 |
Тіло кинули з поверхні землі з початковою швидкістю \( {v}_{0}\) = 10 м/с так, що за перші t = 0,5 c руху швидкість тіла зменшилася до величини \( {v}\) = 7 м/с.
Визначити
максимальну висоту підйому тіла H.
Розв'язання
|
Дано: v0 = 10 м/с
t = 0,5 с
v = 7 м/с |
|
H - ?
|
Позаяк в умові не вказано напрям вектора ${{\vec{v}}_{0}}$, можна подумати, що тіло кинули вертикальною. Але це не так, інакше б його швидкість через 0,5 с, згідно з відповідним рівнянням (1.16), складала б v0 – gt = 5 м/с. Отже, тіло кинуто під кутом до горизонту.
Розмістимо початок координат у точці кидання, тож початкова координата y0 = 0, а в найвищій точці y = H, і вертикальна складова швидкості vy = 0. Отже, згідно з рівнянням (1.18),
| \( {H}=\frac{v_{0y}^{2}}{2g}\). | (1) |
Для визначення вертикальної складової початкової швидкості \( {v}_{0y}\) скористаємося рівняннями (1.16):
\( {v}_{x}=v_{0x}\),
\( {v}_{y}=v_{0y}-{gt}\).
З цих рівнянь можна отримати \( {v}_{0y}\), якщо піднести їх до квадрата та додати:
\( {v}_{x}^{2}+v_{y}^{2}=v_{0x}^{2}+(v_{0y}^{2}-gt)^{2}=v_{0x}^{2}+v_{0y}^{2}-2v_{0y}gt+g^{2}t^{2}\) \( \Rightarrow \)
\( {v}^{2}=v_{0}^{2}-2gtv_{0y}+g^{2}t^{2}\).
Звідси маємо
\( {v_{0y}=\frac{v_{0}^{2}-v^{2}+g^{2}t^{2}}{2gt}}\).
Відтак підставимо цей результат у вираз (1) і отримаємо відповідь:
\( {H}=\frac{(v_{0}^{2}-v^{2}+g^{2}t^{2})^{2}}{8g^{3}t^{2}}\) = 2,9 м.
| Задача 1.21 |
| Задача 1.22 |
Кулька, що вільно падає з висоти h = 80 см, пружно відбивається від похилої площини з кутом нахилу до горизонту α = 30°.
Визначити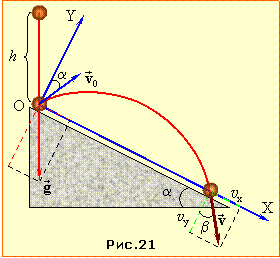
а) через який час τ і на якій відстані L від точки падіння кулька вперше знов зіткнеться з площиною; б) величину та напрям швидкості відскоку \(\vec{v}\).
Розв'язання
|
Дано: h = 20 см
α = 30°
|
|
τ-?, L-?, v -?, β-? |
При пружному зіткненні кулька дзеркально відбивається під кутом β0 = 60° до площини (рис. 21) із швидкістю падіння, що за формулою (1.19) дорівнює
| \( {v}_{0}=\sqrt{2gh}\) . |
(1) |
Тож у показаній на рис. 21 системі координат ХOY вирази проєкцій прискорення та рівняння проєкцій швидкості й координат кульки (1.16) мають вигляд:
|
\(\ {{a}_{x}}=g\cos {{\beta }_{0}}\) \(\ {{a}_{y}}=-g\sin {{\beta }_{0}}\) |
(2) |
|
\({{v}_{x}}=\left( {{v}_{0}}+gt \right)\cos {{\beta }_{0}}\) \({{v}_{y}}=\left( {{v}_{0}}-gt \right)\sin {{\beta }_{0}}\) |
(3) |
|
\(x=\left( {{v}_{0}}t+\frac{g{{t}^{2}}}{2} \right)\cos {{\beta }_{0}}\) \(y=\left( {{v}_{0}}t-\frac{g{{t}^{2}}}{2} \right)\sin {{\beta }_{0}}\). |
(4) |
Тепер перейдемо до пошуку означених в умові величин. На момент відскоку координати кульки дорівнюють нулю, тож, поклавши в рівняннях (4) y = 0, знайдемо час руху кульки t = τ між першим і другим зіткненням:
| \(\left( {{v}_{0}}\tau -\frac{g{{\tau }^{2}}}{2} \right)=0\) \(\Rightarrow \) \(\tau =\frac{2{{v}_{0}}}{g}\) | (5) |
Відтак, підставивши цей вираз у рівняння для х, визначимо відстань L = x(τ), на якій відбувається другий відскок:
|
\(L=\left( {{v}_{0}}\tau +\frac{g{{\tau }^{2}}}{2} \right)\cos {{\beta }_{0}}\) |
(6) |
Так само з рівнянь (3) знайдемо проєкції швидкості кульки на момент другого відскоку:
|
\({{v}_{x}}=\left( {{v}_{0}}+g\tau \right)\cos {{\beta }_{0}}=3{{v}_{0}}\cos {{\beta }_{0}}\) \({{v}_{y}}=\left( {{v}_{0}}-g\tau \right)\sin {{\beta }_{0}}=-{{v}_{0}}\sin {{\beta }_{0}}\) |
та її модуль і напрям β :
|
\(v={{v}_{0}}\sqrt{9{{\cos }^{2}}{{\beta }_{0}}+{{\sin }^{2}}{{\beta }_{0}}}\) tgβ = –\(\frac{\cos {{\beta }_{0}}}{\sin {{\beta }_{0}}}\) |
(7) |
(Примітка. Знак “–” в останньому виразі пояснюється тим, що в рівняннях (3) фігурує швидкість підльоту кульки до точки удару, а не швидкість відскоку).
Числові відповіді дістанемо з формул (5), (6), (7), підставивши значення β0 = 60° і, згідно з формулою (1) v0 = 4 м/с:
τ = 4 с
L = 3,2 м
v = 6,9 м/с
βв = 30°.
Наостанку зауважимо, що задачу можна розв'язувати і в “звичній” системі координат із горизонтальною і вертикальною осями, проте розв'язок буде більш громіздкий.
Рух двох тіл
Задача 1.23. Двоє байкерів рухаються однією прямою дорогою відповідно до рівнянь: \( {x}_{1}={8t} \) і \( {x}_{2}=14+0,5t^{2}\). 1. Проаналізувати рух і показати графіки координат байкерів x(t). 2. Визначити: а) час t та місце зустрічі байкерів (відстань L від початку координат); б) час τ, за який байкери подолають однаковий шлях і знайти його величину S.
Задача 1.24. Два тіла з однакової висоті над землею кинуто горизонтально у протилежних напрямах зі швидкостями \( {v}_{01}={4} \) м/с і \( {v}_{02}={9}\) м/с. Визначити, через який час t вектори швидкостей тіл стануть взаємно перпендикулярними.
Задача 1.25. З однієї точки одночасно і з однаковою швидкістю \( {v}\) = 20 м/с кидають вгору два тіла: одне вертикально, а інше – під кутом \( \alpha=50^{\circ}\) до горизонту. Визначити відстань L між тілами через час t = 0,5 c після початку руху.
| Задача 1.22 |
| Задача 1.23 |
Двоє байкерів рухаються однією прямою дорогою відповідно до рівнянь: \( {x}_{1}={8t} \) і \( {x}_{2}=14+0,5t^{2}\).
1. Проаналізувати рух і показати графіки координат байкерів x(t).
2. Визначити:
а) час t та місце зустрічі байкерів (відстань L від початку координат);
б) час τ, за який байкери подолають однаковий шлях і знайти його величину S.
|
Дано: x1 = 8t
x2 = 14 + 0,5t2
|
|
t - ? L - ? τ - ? |
Розв'язання
1. З умови випливає, що перший байкер рухається із сталою швидкістю v1 = 8 м/с і при t = 0 знаходиться в початку координат. Одночасно другий байкер, перебуваючи попереду на відстані x20 = 14 м, починає рухатись у тому самому напрямі з прискоренням a2 = 1 м/с2.
Для аналізу подальшого руху байкерів випишемо у загальному вигляді рівняння їхніх координат (1.16):
$\begin{align} & {{x}_{1}}={{v}_{1}}t \\ & {{x}_{2}}={{x}_{20}}+\frac{{{a}_{2}}{{t}^{2}}}{2} \\\end{align}$
Відтак, наклавши умову x2 = x1, отримаємо рівняння, що визначає можливі моменти зустрічі байкерів:
| ${{x}_{20}}+\frac{{{a}_{2}}{{t}^{2}}}{2}$ =${{v}_{1}}t$ $\Rightarrow $ ${{a}_{2}}{{t}^{2}}-2{{v}_{1}}t+2{{x}_{20}}=0$ | (1) |
Із виразу коренів цього рівняння
$ t=\frac{{{v}_{1}}\pm \sqrt{v_{1}^{2}-2{{a}_{2}}{{x}_{20}}}}{{{a}_{2}}}$
випливає, що на загал є три можливості:
1) $v_{1}^{2}<2{{a}_{2}}{{x}_{20}}$ корені не існують, тобто байкери взагалі не зустрінуться;
2) $v_{1}^{2}=2{{a}_{2}}{{x}_{20}}$ – байкери зустрінуться в момент t0 = v1/a2;
3) $v_{1}^{2}>2{{a}_{2}}{{x}_{20}}$ – відбудеться дві зустрічі.
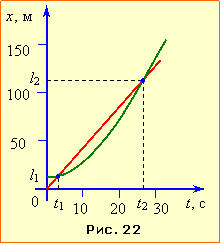
Сказане ілюструє рис. 22, на якому зображено графік x2(t), що являє гілку параболи з вершиною в очці х20 та три промені – графіки x1(t) для випадків 1), 2) і 3), відповідно.
Проаналізуємо за графіками рух байкерів у кожному з наведених випадків, узявши до уваги, що відстань між байкерами визначається різницею ординат х, а швидкість руху – нахилом графіків до осі абсцис t (див. п. 1.4). Тож, як видно, в кожному випадку перший байкер спочатку наздоганяє другого, а від моменту, коли їхні швидкості порівнюються, – відстає. При цьому:
– за малої швидкості v1 (випадок 1) перший байкер починає відставати, ще не діставшись точки старту другого, тож ніколи його не наздожене;
– у випадку 2 перший байкер у момент t0 і в точці х0 наздоганяє другого, але відразу починає відставати;
– при великій швидкості (випадок 3) перший байкер у момент t1 (перша зустріч) має більшу швидкість і починає випереджати другого. Але потім другий, поступово нарощуючи швидкість, у момент t2 (друга зустріч) наздоганяє й уже назавжди випереджає першого.2а. При заданих значеннях v1 = 8 м/с, x20 = 14 м і a2 = 1 м/с2 виконується умова 3), і корені рівняння (1) становлять t1 = 2 c, t2 = 14 c. Отже, байкери зустрічаються двічі – через 2 с та 14 с після старту другого і, згідно із заданими в умові рівняннями, на відстані L1 = 16 м і L2 = 112 м від початку координат.
2б. Пройдений кожним байкером шлях дорівнює зміні його координати. Тож, поклавши в заданих умовою задачі рівняннях х1 = х2 = S і t = τ , отримаємо:
$\left\{ \begin{align} & S=8\tau \\ & S=0,5{{\tau }^{2}} \\\end{align} \right.\quad \Rightarrow \quad \tau =16\text{ c;}\quad S=128\text{ }\text{м.}$
| Задача 1.23 |
| Задача 1.24 |
Два тіла з однакової висоті над землею кинуто горизонтально у протилежних напрямах зі швидкостями \( {v}_{01}={4} \) м/с і \( {v}_{02}={9}\) м/с.
Визначити,
через який час t вектори швидкостей тіл стануть взаємно перпендикулярними.
|
Дано: v01 = 4 м/c
v02 = 9 м/c
g = 10 м/с2
|
|
t - ? |
Розв'язання
Умова задачі містить інформацію про початкові та кінцеві швидкості двох тіл, які одночасно починають рух із однаковим прискоренням \( \vec{g}\). Тож шуканий час можна знайти за допомогою рівнянь (1.14):
\( \vec{v}_{1}(t)=\vec{v}_{01}+\vec{g}{t}\),
\( \vec{v}_{2}(t)=\vec{v}_{02}+\vec{g}{t}\)
одним із двох способів.
І спосіб. Згадаємо, що скалярний добуток векторів \( \vec{b}\) і \( \vec{c}\) визначається як \( \vec{b}\cdot\vec{c}=b{c}\cos\alpha \), де \( \alpha \) – кут між векторами. Для взаємно перпендикулярних векторів він дорівнює нулю, отже:
\( \vec{v}_{1}(t)\vec{v}_{2}(t)=\left(\vec{v}_{01}+\vec{g}t\right)\left(\vec{v}_{02}+\vec{g}t\right){=}\)
\( {=}\vec{v}_{01}\vec{v}_{02}+\vec{v}_{01}\vec{g}t+\vec{v}_{02}\vec{g}t+\vec{g}t\vec{g}{t}={0}\).
За умовою задачі кут між векторами \( \vec{v}_{01}\) та \( \vec{v}_{02}\) дорівнює \( {\pi}\). Отже, 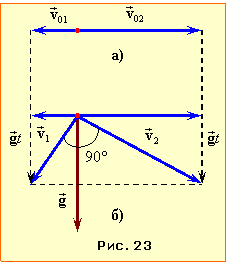
\( \vec{v}_{01}\vec{v}_{02}=-v_{01}{v}_{02}\).
При цьому кути між векторами \( \vec{v}_{01}\) і \( \vec{g}\) та \( \vec{v}_{02}\) і \( \vec{g}\) дорівнюють \( \pi{/2}\), тому\( \vec{v}_{01}\vec{g}=\vec{v}_{02}\vec{g}={0}\).
Крім того, скалярний добуток вектора самого на себе дорівнює квадрату його модуля: \( \vec{g}\cdot\vec{g}=g^{2}\). Таким чином,
\( \vec{v}_{1}\vec{v}_{2}=-v_{01}{v}_{02}+g^{2}t^{2}={0}\),
і
\( {t}=\frac{\sqrt{v_{01}v_{02}}}{g}={0,6}\) c.
ІІ спосіб. Оскільки вектори \( \vec{v}_{01},\,\vec{v}_{02}\) (див. рис. 23) є перпендикулярні до вектора \( \vec{g}\), то для швидкостей тіл у будь-який момент часу (див. рис. 23) можна записати:
| \( {v}_{1}^{2}=v_{01}^{2}+(gt)^{2}\), \( {v}_{2}^{2}=v_{02}^{2}+(gt)^{2}\). | (1) |
З іншого боку, позаяк за умовою вектори \( \vec{v}_{1}\) і \( \vec{v}_{2} \) (рис. 23б) є взаємно перпендикулярні, то
\( {v}_{1}^{2}+v_{2}^{2}=(v_{01}+v_{02})^{2}\).
Підставивши сюди вирази (1), дістанемо:
\( {v}_{01}^{2}+2(gt)^{2}+v_{02}^{2}=v_{01}^{2}+2v_{01}v_{01}+v_{02}^{2}\) \( \Rightarrow \)
\( {gt}=\sqrt{v_{01}v_{02}}\) \( \Rightarrow \) \( {t}=\frac{\sqrt{v_{01}v_{02}}}{g}={0,6}\) c.
| Задача 1.24 |
| Задача 1.25 |
З однієї точки одночасно і з однаковою швидкістю \( {v}\) = 20 м/с кидають вгору два тіла: одне вертикально, а інше – під кутом \( \alpha=50^{\circ}\) до горизонту.
Визначити
відстань L між тілами через час t = 0,5 c після початку руху.
|
Дано: v = 20 м/с
α = 50°
t = 0,5 с
|
|
L - ? |
Розв'язання
Залежно від вибору системи відліку, задачу можна розв'язати двома способами.
І спосіб. Оберемо координатну систему XOY з початком у точці кидання (рис. 24), в якій початкові координати обох тіл дорівнюють нулю, а проєкції початкових швидкостей \( {v}_{1x}={0}\), \( {v}_{1y}={v}\) і \( {v}_{2x}=v\cos\alpha\), \( {v}_{2y}=v\sin\alpha \). Координати тіл на момент часу t визначаються рівняннями (1.16а):
|
\( {x}_{1}={0}\), \( {x}_{2}=vt\cos\alpha \); \( {y}_{1}=vt-\frac{gt^{2}}{2}\), \( {y}_{2}=vt\sin\alpha-\frac{gt^{2}}{2}\). |
(1) |
Відстань між двома точками через їхні координати виражається формулою:
\( {L}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\).
Тож, підставивши сюди вирази (1) для координат, після простих перетворень отримаємо:
$L=vt\sqrt{{{\cos }^{2}}\alpha +{{\left( \sin \alpha -1 \right)}^{2}}}=vt\sqrt{2\left( 1-\sin \alpha \right)}$
Обчислення дають
L = 6,84 м.
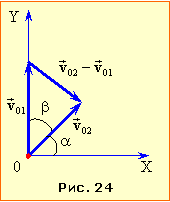
ІІ спосіб. Пов'яжемо з першим тілом рухому систему відліку, швидкість V якої відносно нерухомої (земна поверхня) складає \( \vec{V}\) = \( \vec{v}_{1}\). Тоді швидкість другого тіла відносно першого (швидкість в рухомій системі відліку) визначається формулою (1.11а):
| \( \vec{u}=\vec{v}_{2}-\vec{v}_{1}=(\vec{v}_{02}+\vec{g}t)-(\vec{v}_{01}+\vec{g}t)=\vec{v}_{02}-\vec{v}_{01}=\mathrm{const}\). |
Отже, позаяк прискорення тіл однакові, їхній відносний рух є рівномірним прямолінійним, і відстань між ними змінюється з часом, як
| \( {L}=ut=\left|\vec{v}_{02}-\vec{v}_{01}\right|{t}\). |
Величину $u=\left| {{{\vec{v}}}_{02}}-{{{\vec{v}}}_{01}} \right|$ знайдемо за теоремою косинусів (див. рис. 24):
\( {u}=\sqrt{v^{2}+v^{2}-2vv\cos^{2}\beta}\) = v\(\sqrt{2\left( 1-\cos \beta \right)}\) = \( {L}=vt\sqrt{2(1-\sin\alpha)}\).
Обертовий рух. Кочення.
Задача 1.26. Авто рухається по колу радіуса R = 250 м зі сталою швидкістю v = 36 км/год. Визначити залежність від часу: 1. Модуля переміщення та побудувати графік \(\left| \Delta \vec{r}\left( t \right) \right|\); 2. Координат x(t), y(t); 3. Проєкцій швидкості vx(t), vy(t) і прискорення ax(t), ay(t) та обчислити їхні модулі.
Задача 1.27. Диск рівномірно обертається навколо своєї осі, котра рухається горизонтально зі сталою швидкістю v0 = 2 м/с. Визначити швидкість v2 заданої точки 2 диска, якщо швидкість заданої точки 1 дорівнює v1 = 1 м/с.
Задача 1.28. Колесо радіуса R котиться горизонтальною площиною без ковзання зі швидкістю \( {v}_{0}\). Визначити швидкість v та прискорення \( {a}\) указаної точки на ободі, якщо її радіус обертання складає кут \( \alpha \) із вертикаллю.
Задача 1.29. Котушка радіуса R із шаром ниток радіусом r лежить на шорсткій горизонтальній поверхні. Визначити, в якому напрямі та з якою швидкістю u покотиться котушка, якщо нитку горизонтально потягнути за вільний кінець із швидкістю \( {v}\).
Задача 1.30. Із указаної точки на ободі колеса радіуса R, яке котиться горизонтальною площиною без ковзання, відлітає кусочок бруду. Визначити найменшу швидкість u колеса, при якій бруд знов потрапить у ту саму точку колеса при такому самому її розташуванні відносно осі.
Задача 1.31. Два тягарці різної маси, що з'єднані ниткою, перекинутою через нерухомий блок радіуса R, спочатку утримують на одному рівні, а потім вивільнюють. Відтак вони без ковзання нитки за час τ = 1 с розійшлися на відстань nR один від одного. Визначити кут повороту блоку \( \varphi \) та набуте за цей час прискорення \( \vec{a}\) указаною точкою, якщо R = 10 см і n = 3.
| Задача 1.25 |
| Задача 1.26. |
Авто рухається по колу радіуса R = 250 м зі сталою швидкістю v = 36 км/год.
Визначити залежність від часу:
1. Модуля переміщення та побудувати графік \(\left| \Delta \vec{r}\left( t \right) \right|\) ;
2. Координат x(t), y(t);
3. Проєкцій швидкості vx(t), vy(t) і прискорення ax(t), ay(t) та обчислити їхні модулі.
|
Дано: R = 250 м
v = 10 м/с
\(\alpha=60^{\circ}\)
|
|
\(\left| \Delta \vec{r}(t)\right|\) - ?
x(t), y(t) - ?
vx(t), vy(t), v - ?
ax(t), ay(t), a - ?
|
Розв’язання:
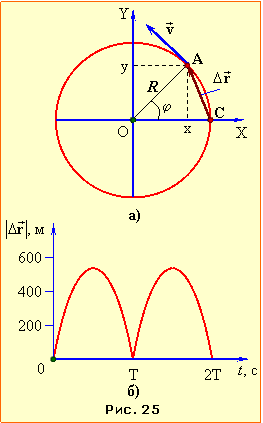
Умову задачі відображає рис. 25a.
1. Величину переміщення знайдемо за теоремою косинусів із трикутника AOC:
\(\left| \Delta \vec{r} \right|=\sqrt{{{R}^{2}}+{{R}^{2}}-2{{R}^{2}}\cos \varphi }=2R\cdot \left| \sin \frac{\varphi }{2} \right|\ .\)
Із геометрії відомо, що центральний кут φ = SR (рад), де S – довжина дуги кола між точками А і С, тобто пройдений шлях. Позаяк рух авто є рівномірним, то S = vt, і
|
\(\varphi =\frac{vt}{R}.\) |
(1) |
Тоді
\(\left| \Delta \vec{r} \right|=2R\left| \sin \left( \frac{vt}{2R} \right) \right|=500\left| \sin (0,02t) \right|.\)
Графік переміщення за час двох повних обертів руху 2T показано на рис. 25б.
2. З рис. 1.26а видно, що координати авто визначаються, як
\(x=R\cos \varphi ,\ \ y=R\sin \varphi \ .\)
Зробивши в цих виразах заміну (1), дістанемо:
|
\(x=R\cos \left( \frac{vt}{R} \right)=250\cos \left( 0,04t \right),\ \ \ \ \ y=R\sin \left( \frac{vt}{R} \right)=250\sin \left( 0,04t \right)\ .\) |
Звідси, відповідно до виразів (1.7а) і (1.7б), знайдемо:
\(v_{x}= x'(t)=-v\sin \left( \frac{vt}{R} \right)=-10\sin \left( 0,04t \right)\ ;\)
\(v_{y}= y'(t)=-v\cos \left( \frac{vt}{R} \right)=10\cos \left( 0,04t \right)\ .\)
3. проєкції вектора прискорення визначаються аналогічно з виразів (17) і (1.8) :
\(a_{x}= v{{'}_{\text{x}}}=x''(t)=-v\sin \left( \frac{vt}{R} \right)=-0,4\cos \left( 0,04t \right)\ ;\)
\(a_{y}= v{{'}_{\text{y}}}=y''(t)=v\cos \left( \frac{vt}{R} \right)=-0,4\sin \left( 0,04t \right)\ .\)
Модуль прискорення
|
\(a=\sqrt{a_{\text{x}}^{2}+a_{\text{y}}^{2}}=\frac{{{v}^{2}}}{R}\) = 0,4 м/с2. |
Зауважимо, що отриманий результат є цілком передбачуваним – адже при рівномірному русі по колу прискорення тіла є доцентровим і визначається формулою (1.28).
| Задача 1.26 |
| Задача 1.27 |
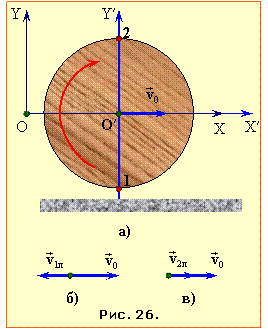 Диск рівномірно обертається навколо своєї осі, котра рухається горизонтально зі сталою швидкістю v0 = 2 м/с, рис. 26а.
Диск рівномірно обертається навколо своєї осі, котра рухається горизонтально зі сталою швидкістю v0 = 2 м/с, рис. 26а.
Визначити
швидкість v2 заданої точки 2 диска, якщо швидкість точки 1 дорівнює v1 =1м/с.
|
Дано: v1 = 1 м/с
v0 = 2 м/с
|
|
v2 - ?
|
Розв’язання:
Точки диска обертаються навколо осі й рухаються разом з нею. Тож для аналізу їхнього руху крім нерухомої системи відліку ХОY (рис. 1.27а), введемо й зв'язану з віссю диска рухому систему відліку X'O'Y', що має відносно нерухомої швидкість v0 і в якій швидкості точок диска ${\vec{v}}'$ є лінійними швидкостями їхнього обертального руху (див. п. 1.5). Тож за законом додавання швидкостей (1.10) для будь-якої точки диска можна записати:
|
$\vec{v}$ = ${\vec{v}}'$ + ${{\vec{v}}_{0}}$ $\Rightarrow $ ${{v}_{x}}={{{v}'}_{x}}+{{v}_{0}}$ |
(1) |
За умовою швидкість т. 1 в нерухомій системі відліку v1 < v0, що означає, що вектор ${{\vec{{v}'}}_{1}}$ є антипаралельним до \(\vec{v}_{0}\) (рис. 26б). Отже, диск обертається за годинниковою стрілкою, і в точці 2 вектори${{\vec{{v}'}}_{2}}$ і \({{\vec{v}}_{0}}\) є збіжні за напрямом (рис. 26в). Тому для проєкцій маємо: v0x = v0, ${{{v}'}_{1x}}$ = – v′, v2х = v2, і для кожної з точок формула (1) у проєкціях виглядає, як
\(v_{2}=v′+v_{0}\)
\(v_{1x}=-v′+v_{0}\)
Звідси випливає наступний результат:
|
\( {{v}_{2}}=-{{v}_{1x}}+2{{v}_{0}} .\) |
|
В умові задачі напрям руху точки 1 в нерухомій системі відліку ХОY не вказано. Тому, залежно від швидкості обертання диска і величини u, є можливі два випадки: 1) точка 1 відносно нерухомої системи відліку рухається праворуч, тоді v1x = v1, і 2) точка 1 рухається ліворуч, тож v1x = –v1. Тож задача має дві відповіді:
|
${{v}_{2}}=-{{v}_{1}}+2{{v}_{0}}$ = 3 м/с, і \({{v}_{2}}=v+2{{v}_{0}}=5\ \text{м/с}\ .\) |
| Задача 1.27 |
| Задача 1.28 |
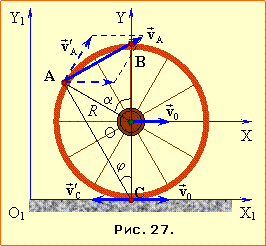 Колесо радіуса R котиться горизонтальною площиною без ковзання зі швидкістю \( {v}_{0}\).
Колесо радіуса R котиться горизонтальною площиною без ковзання зі швидкістю \( {v}_{0}\).
Визначити
швидкість v та прискорення а указаної точки на ободі, якщо її радіус обертання складає кут \( \alpha \) із вертикаллю.
|
Дано: \( {v}_{0}\) |
|
vА - ? а - ? |
Розв’язання
Пов'яжемо нерухому систему відліку XOY із площиною, а рухому X′O′Y′ – із віссю колеса, рис. 27. В такому разі швидкість осі колеса \( \vec{v}_{0}\) є швидкістю рухомої системи відліку, а лінійна швидкість обертання точки А навколо осі О′ \({{{\vec{v}}'}_{A}}\) – відносною швидкістю цієї точки. Тоді, згідно із законом додавання швидкостей (1.10), швидкість точки А відносно площини складає
\({{\vec{v}}_{A}}={{{\vec{v}}'}_{A}}+{{\vec{v}}_{0}}\).
Із паралелограма векторів на рис. 1.27, який відображає записану рівність, видно, що кут між векторами \( \vec{v}_{0}\) та \( \vec{v}_{A}^{\prime}\) дорівнює заданому кутові \( \alpha \). Тож за теоремою косинусів
\( {v}_{A}=\sqrt{(v^{\prime})^{2}+v_{0}^{2}+2v^{\prime}v_{0}\cos\alpha}\).
Позаяк кочення відбувається без ковзання, кожна точка колеса, що дотикається до площини, є відносно неї нерухомою:
\(\vec{v}_{с}=\vec{v}_{0}+\vec{v}_{с}^{\prime}\) = 0.
Отже,
\({{\vec{v}'}_{c}}\) = –\( \vec{v}_{0}\) \(\Rightarrow \) vс′ = v0.
Зрозуміло, що величина швидкості точки А є такою самою:
vА′ = v0.
Прискорення а′ точок колеса відносно його осі є доцентровим (формула (1.28)), отже на ободі його величина складає
\( {a}^{\prime}=\frac{v^{\prime{2}}}{R}=\frac{v_{0}^{2}}{R}\).
Відносно площини величина прискорення а така сама, позаяк вісь колеса відносно площини рухається без прискорення (див. п. 1.2).
| Задача 1.28 |
| Задача 1.29 |
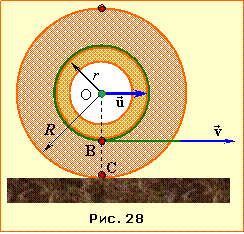 Котушка радіуса R із шаром ниток радіусом r лежить на шорсткій горизонтальній поверхні, рис. 28.
Котушка радіуса R із шаром ниток радіусом r лежить на шорсткій горизонтальній поверхні, рис. 28.
Визначити,
в якому напрямі і з якою швидкістю u покотиться котушка, якщо нитку горизонтально потягнути за вільний кінець із швидкістю \( {v}\).
|
Дано: R, r
\( {v}\)
|
|
\( {u}\) - ? |
Розв’язання
За умовою поверхня є шорсткою, тож котушка котитиметься по ній без ковзання. Це означає, що кожна точка котушки, що дотикається, на мить стає нерухомою відносно площини, ніби "пришпиленою" до неї. Тож при коченні без ковзання котушка в кожен момент часу лишень обертається навколо осі С, яка через це називається миттєвою віссю. При цьому очевидно, що напрям обертання котушки навколо миттєвої осі збігається із напрямом прикладеної до нитки сили. Отже, котушка буде рухатися праворуч, намотуючись на нитку (що без наведеного аналізу може здатися неочікуваним).
Швидкість \( {v}\), з якою тягнуть нитку, і шукана швидкість \( {u}\) осі О є лінійними швидкостями їхнього обертання навколо миттєвої осі С. Тому, позаяк кутова швидкість є однакова для усіх точок обертового тіла,то згідно з формулою (1.26) маємо:
\( \frac{v}{R-r}\) = \( \frac{u}{R}\) \(\Rightarrow \) \(u=\frac{R}{R-r}v\).
Наостанку зауважимо, що миттєва вісь існує не лише при коченні без ковзання, а й при деяких інших рухах тіл, що спрощує розв'язування відповідних задач механіки твердого тіла.
| Задача 1.29 |
| Задача 1.30 |
Із указаної точки на ободі колеса радіуса R, яке котиться горизонтальною площиною без ковзання, відлітає кусочок бруду.
Визначити
найменшу швидкість u колеса, при якій бруд знов потрапить у ту саму точку колеса при такому самому її розташуванні відносно осі.
|
Дано: R |
|
\( {u}\)-? |
Розв’язання
 На рис. 29 показано початкове та кінцеве положення колеса, що задовольняє умову задачі. При цьому за час t між відривом і потраплянням бруду на колесо воно має здійснити щонайменше один повний оберт і пройти відстань \( {S}=2\pi{R}\). Отже, необхідна швидкість колеса складає
На рис. 29 показано початкове та кінцеве положення колеса, що задовольняє умову задачі. При цьому за час t між відривом і потраплянням бруду на колесо воно має здійснити щонайменше один повний оберт і пройти відстань \( {S}=2\pi{R}\). Отже, необхідна швидкість колеса складає
| \( {u}=\frac{2\pi{R}}{t}\). | (1) |
Для визначення часу t перейдемо в систему відліку колеса ХOY, в якій бруд відлітає й рухається далі вертикально із початковою величиною швидкості u та прискорення g . При цьому через половину часу польоту він опиняється в найвищій точці й має нульову миттєву швидкість. Отже,
\(u=\frac{gt}{2}\quad \Rightarrow \quad t=\frac{2u}{g}\).
Підставивши це значення t у вираз (1), отримаємо відповідь:
\(u=\frac{\pi Rп}{u}\) \( \Rightarrow \) \( u=\sqrt{\pi{gR}}\).
| Задача 1.30 |
| Задача 1.31 |
Два тягарці різної маси, що з'єднані ниткою, перекинутою через нерухомий блок радіуса R, спочатку утримують на одному рівні, а потім вивільнюють. Відтак вони без ковзання нитки за час τ = 1 с розійшлися на відстань nR один від одного.
Визначити
кут повороту блоку \( \varphi \) та набуте за цей час прискорення \( \vec{a}\) указаною точкою, якщо R = 10 см і n = 3.
|
Дано: R= 10 см n=3 t = 1 с, |
|
\(\varphi\) -? \(\vec{a}\) -? |
Розв’язання
За відсутності ковзання точки на ободі блоку та кожен із тягарців за вказаний час проходять однакові шляхи
|
$S=\frac{nR}{2}.$ |
(1) |
Отже, кут повороту блоку складає
|
\( \varphi=\frac{S}{R}=\frac{n}{2}\) (рад) = 86°. |
 Далі визначаємо прискорення \(\vec{a}\) точок на ободі. Через різну вагу, тягарці рухаються прискорено, тож точки блоку змінюють не лише напрям, а й величину швидкості. Через це вони, крім доцентрового прискорення \({{\vec{a}}_{дц}}\) (див. п. 1.5), мають лінійне прискорення \({{\vec{a}}_{л}}\), котре показує, як швидко розганяється блок. Воно визначається приростом величини швидкості точки за одиницю часу і спрямоване по дотичній до блоку, як показано на рис. 30, і збігається з прискоренням тягарців.
Далі визначаємо прискорення \(\vec{a}\) точок на ободі. Через різну вагу, тягарці рухаються прискорено, тож точки блоку змінюють не лише напрям, а й величину швидкості. Через це вони, крім доцентрового прискорення \({{\vec{a}}_{дц}}\) (див. п. 1.5), мають лінійне прискорення \({{\vec{a}}_{л}}\), котре показує, як швидко розганяється блок. Воно визначається приростом величини швидкості точки за одиницю часу і спрямоване по дотичній до блоку, як показано на рис. 30, і збігається з прискоренням тягарців.
Таким чином, зміна вектора швидкості точок блоку визначається вектором повного прискорення
|
$\vec{a}={{\vec{a}}_{\text{л}}}+{{\vec{a}}_{\text{дц}}}$. |
Його модуль дорівнює
|
$ {a}=\sqrt{a_{дц}^{2}+a_{л}^{2}} $, |
(2) |
а напрям складає з ниткою кут α, що визначається співвідношенням:
|
$ \mathrm{tg}{\alpha}=\frac{a_{дц}}{{a}_{л}}$. |
(3) |
За відсутності ковзання нитки лінійне прискорення та швидкість точки на ободі блоку збігаються з прискоренням і швидкістю тягарців, які визначаються рівняннями кінематики (п. 1.3). Зокрема, враховуючи вираз (1), з рівняння (1.16) знаходимо:
| $ {{a}_{л}}=\frac{nR}{t^{2}}$. | (4) |
Далі з рівняння швидкості (1.16) визначаємо кінцеву швидкість тягарця
v = aлt = $ \frac{nR}{t}$
та за формулою (1.28) – величину доцентрового прискорення:
| aдц = \({{\left( \frac{nR}{t} \right)}^{2}}\cdot \frac{1}{R}\) = naл. | (5) |
Відтак за формулами (2), (4) і (5) знаходимо модуль вектора повного прискорення:
${{a}_{\text{л}}}\sqrt{{{n}^{2}}+1}$ = $\frac{R}{{{t}^{2}}}n\sqrt{{{n}^{2}}+1}$,
і за формулою (3) – його напрям:
α = arctg(n).
Обчислення дають:
а = 0,95 м/с2, α = 71,6°.
Задачі для самостійної роботи
Вивчаючи умови та розв'язуючи задачі кінематики, слід пам'ятати, що в текстах за умовчанням прийнято такі умови:
1. За відсутності обертання рухомі тіла розглядаються як матеріальні точки;
2. Нитки й мотузки, що зв'язують тіла, вважаються нерозтяжними;
3. У рівняннях, що наводяться в умовах задач, числові параметри виражаються в основних одиницях системи СІ.
Пропоновані для самостійного розв'язування задачі стосуються наступних тем:
Кінематика руху з постійним прискоренням
Графіки руху та їхнє використання
Рух тіла кинутого під кутом до горизонту
У наведених відповідях для прискорення вільного падіння прийнято значення g = 10 м/с2.
Кінематика рівномірного руху
Рівень А
|
1.32. |
При підйомі повітряної кулі на висоту 800 м її віднесло вітром по горизонталі на 600 м. Яке переміщення здійснила куля? [1 км] |
|
1.33. |
Тіло, що рухається колом радіуса 10 м, здійснило 3/4 оберту. Чому дорівнює переміщення тіла та пройдений ним шлях? [14,1 м; 47,1 м] |
|
1.34. |
Визначити шлях і переміщення точки на краю диска радіуса R, котрий здійснив: а) чверть, б) половину та в) повний оберт. [а) \(0,5\pi{R}\), \(R\sqrt{2}\); б) \(\pi{R}\), \(2R\); в) \(2\pi{R}\), \(0\) ] |
|
1.35. |
За час 10 с точка пройшла пів кола радіуса 100 см. Визначити: 1) шляхову швидкість точки; 2) модуль і напрям вектора її середньої швидкості за вказаний час. [1) 31,4 см/с; 2) 20 см/с, уздовж діаметра] |
|
1.36. |
Потяг метро проходить відстань 6,0 км за час 8 хв. Визначити середню швидкість потяга на цьому шляху в м/с і км/год. [12,5 м/с = 45 км/год] |
|
1.37. |
Тіло одночасно бере участь у двох рухах із однаковими швидкостями v1 = v2 = v, що напрямлені під кутом α = 120° одна до одної. Визначити величину та напрям швидкості v0 результуючого руху тіла. [v0 = v, вздовж бісектриси кута α] |
|
1.38. |
Розв'язати попередню задачу для кута 60°. [v0 = \(v\sqrt{3}\), вздовж бісектриси кута α] |
|
1.39. |
Ящик ковзає зі сталою швидкістю 1,0 м/с по похилій площині з кутом нахилу до горизонту 30°. Визначити, з якими швидкостями змінюються вертикальна та горизонтальна координати ящика. [0,5 м/с; ≈0,87 м/с] |
|
1.40. |
Літак відривається від злітної смуги під кутом 20° до горизонту зі швидкістю 216 км/год. Визначити, з якою швидкістю він: а) набирає висоту та б) віддаляється від летовища по горизонталі. [а) ≈ 73 км/год; б) ≈ 200 км/год] |
|
1.41. |
Човен рухається річкою із швидкістю течії 1,5 м/с. Визначити швидкість човна відносно берега, коли він рухається: а) за течією та б) проти течії, якщо відносно води його швидкість дорівнює 2,0 м/с. [а) 3,5 м/с; б) 0,5 м/с] |
Рівень Б
|
1.42. |
Визначити рівняння траєкторій руху y = f(x) тіла, координати якого змінюються з часом за законом: а) x = 2t + 3, y = 3t; б) x = 2t – 3, y = 3t – 2t2, в) \(x=2\cos(\pi{t}/2\), \(y=2\sin(\pi{t}/2)\) (всі числа подано в основних одиницях CІ). [ а) y = 1,5x – 4,5; б) y = 1,5x – x2; в) x2 + y2= 4 ] |
|
1.43. |
Одну половину часу велосипедист рухався зі швидкістю 10 км/год, а іншу – 30 км/год. Визначити середню швидкість велосипедиста за весь час. [20 км/год] |
|
1.44. |
Першу половину дистанції велосипедист пройшов із швидкістю 10 км/год, а другу – 30 км/год. Визначити середню швидкість велосипедиста на всій дистанції. [15 км/год] |
|
1.45. |
Мотоцикліст проїхав 40% шляху між двома містами зі швидкістю 72 км/год, а решту – зі швидкістю 54 км/год. Визначити середню швидкість мотоцикліста на всьому шляху. [60 км/год] |
|
1.46. |
Тіло послідовно здійснює два переміщення однакові величини. Перше – зі швидкістю v1 = 20 м/с під кутом α = 60°, а друге – зі швидкістю v2 = 40 м/с під кутом β = 120° до напрямку осі OX. Визначити модуль і напрям середньої швидкості переміщення тіла на всьому шляху. [23,1 м/с, вдовж осі OY] |
|
1.47. |
З катера, що йде за течією річки, випав рятувальний круг. Через 45 хв це виявили й повернули назад. Визначити швидкість течії, якщо круг зустріли на відстані 3 км нижче місця, де загубили. [2 км/год] |
|
1.48. |
Корабель пливе вздовж екватора курсом на схід зі швидкістю 30 км/год при південно-східному вітрі з напрямком 60° до екватора та швидкістю 15 км/год. Яка швидкість вітру фіксується на борту та який кут до курсу вказує флюгер? [з9,7 км/год; 19°] |
|
1.49. |
Швидкість теплохода відносно берега при русі рікою за течією складає 20 км/год, а проти течії – 18 км/год. Визначити: а) швидкість теплохода відносно води та б) швидкість течії. [а) 19 км/год; б) 1 км/год] |
|
1.50. |
Відстань 24 км між пристанями на ріці на катер за течією проходить за 2 год, а проти – за 4 год. Визначити: а) швидкість течії та б) швидкість катера відносно води. [а) 3 км/год; б) 9 км/год] |
|
1.51. |
Через ріку переправляється човен, який править упоперек течії. Швидкість човна відносно води 1,4 м/с, швидкість течії 0,7 м/с, ширина ріки 300 м. Визначити час переправи та знесення човна течією? [≈3,6 хв; 150 м] |
|
1.52. |
Човен пливе рікою зі швидкістю 3 м/с відносно води під кутом 60° до течії, швидкість якої складає 4 м/с. Визначити: а) величину й напрям швидкості човна відносно берега та б) його переміщення за 30 с руху. [а) 5 м/с; ≈37°; б) 150 м;] |
|
1.53. |
Коли спостерігач за звуком відчуває літак над собою, він бачить його під кутом 60° до горизонту. Визначити швидкість літака. [196 м/с] |
Рівень В
|
1.54. |
При куті нахилу ескалатора метро до горизонту 30° і швидкості 0,8 м/с людина, що стоїть на ньому, спускається на перон за 2,5 хв. На якій глибині залягає тунель метро? [60 м] |
|
1.55. |
Пряма, що є перпендикулярна до бісектриси прямого кута, рухається вздовж бісектриси із швидкістю 2 м/с. З якою швидкістю переміщуються точки перетину прямої зі сторонами кута? [≈2,8 м/с] |
|
1.56. |
Трактор кожну з трьох однакових ділянок шляху проходив із швидкістю 2 км/год, 4 км/год і 6 км/год, відповідно. Визначити середню швидкість трактора на всьому шляху. [3,27 км/год] |
|
1.57. |
Точка, розташована на осі ОХ, переміщується спочатку на S1 = 3,0 м під кутом \(\alpha\) = 30° до осі, а потім на S2 = 1,73 м так, що знов опиняється на осі ОХ. Визначити модуль вектора \(\vec{S}\) результуючого переміщення точки та кут між векторами \(\vec{S}_{1}\) і \(\vec{S}_{2}\). [ 3,46 м і 90°або 1,73 м і 150° ] |
|
1.58. |
Два тіла рухаються вздовж однієї прямої із заданими швидкостями v1 і v2. Визначити величину та напрям швидкості руху точки, що весь час знаходиться посередині між тілами. [\({\left| {{v}_{1}}\pm {{v}_{2}} \right|}/{2}\;\), напрям руху швидшого тіла] |
|
1.59. |
У метро спуск пасажира ескалатором займає 50 с, якщо він стоїть, і 30 с – коли йде по сходах. За який час він спуститься нерухомим ескалатором? [75 с] |
|
1.60. |
Потяг довжиною 120 м виїжджає зі швидкістю 18 км/год на міст довжини 480 м. За який час він його пройде? Чи можна в цій задачі вважати потяг матеріальною точкою? Чому? [2 хв; ні] |
|
1.61. |
Паралельними коліями рівномірно рухаються два потяги: вантажний довжиною 630 м зі швидкістю 48 км/год та пасажирський довжиною 120 м зі швидкістю 102 км/год. Визначити: а) відносну швидкість потягів, якщо вони рухаються в одному та в протилежних напрямах; б) час, протягом якого один потяг проходить повз іншого в обох випадках. [а) 54 км/год, 150 км/год; б) 50 с, 18 с] |
|
1.62. |
Скутер, який має швидкість 90 км/год, за відсутності течії проходить від корми до носа пароплава й назад за 37,5 с. Визначити швидкість пароплава, якщо його довжина дорівнює 300 м . [54 км/год] |
Кінематика руху з постійним прискоренням
Рівень А
|
1.63. |
Які з наведених рівнянь описують рух тіла зі сталим прискоренням? 1) vx = 5 – 5t; 2) ax = 0,25t; 3) x = 2t2; 4) vx = –8t +7; 5) vx = 0,8t; 6) x = 12 – 4t + 0,2t2; 7) x = 2t3 – 8t; 8) \(a_{x}=\sqrt{4t}\). [1); 3); 4); 6)] |
|
1.64. |
За час 1 мс швидкість ракети збільшилася на 5 см/с. Визначити прискорення ракети. [50 м/с2] |
|
1.65. |
На фініші дистанції велосипедист за 5 c збільшив швидкість від 27 км/год до 36 км/год. Визначити прискорення велосипедиста. [0,5 м/с2] |
|
1.66. |
Потяг починає рух із прискоренням 0,2 м/с2. Визначити його швидкість через t1 = 0,5 хв та t2 = 1,0 хв. [6 м/с; 12 м/с] |
|
1.67. |
Вагонетка починає рухатися з прискоренням 25 см/с2. Визначити швидкість вагонетки через 10 с після початку руху та її середню швидкість за цей час. [2,5 м/с; 1,25 м/с] |
|
1.68. |
Потяг починає гальмування із прискоренням –0,3 м/с2 і зупиняється через 1 хв. Визначити початкову швидкість потяга. [65 км/год] |
|
1.69. |
Куля, що котиться підлогою зі швидкістю 0,64 м/с, починає сповільнюватися з прискоренням –6 см/с2. Визначити час руху та пройдений кулею шлях до зупинки. [4 с; 1,28 м] |
|
1.70. |
Куля, що скочується похилим жолобом, за 5 c проходить шлях 75 см. Знайти прискорення кулі. [6 см/с2] |
|
1.71. |
Космічна ракета стартує з навколоземної орбіти при швидкості 7,9 км/с і на шляху 3000 км розганяється до швидкості 11,2 км/с. Визначити прискорення та час розгону ракети. [10,5 м/с2; 5,24 хв] |
|
1.72. |
Трасу швидкісного спуску довжиною 1000 м гірськолижник долає за 60 с. Визначити його швидкість на фініші та середню швидкість на дистанції, вважаючи рух рівноприскореним. [120 км/год; 60 км/год] |
|
1.73. |
При швидкості v = 43,2 км/год гальмівний шлях автобуса дорівнює S = 54 м. Визначити час екстреного гальмування автобуса при вказаній швидкості. [9 с] |
|
1.74. |
На підході до світлофора тепловоз протягом 10 с зменшив швидкість від 90 км/год до 36 км/год. Визначити, на якій відстані від світлофора та з яким прискоренням почав гальмування тепловоз. [175 м; –1,5 м/с2] |
|
1.75. |
Камінь, що падає з прямовисного урвища на березі річки, досягає води за 3 c. Зайти висоту урвища та швидкість каменя на момент падінні у воду. [45 м; 30 м/с] |
|
1.76. |
М'яч, кинутий вертикально вгору, впав на землю через 3 c. Визначити початкову швидкість м'яча. [15 м/с] |
|
1.77. |
Парашутист у стрибку з висоти 200 м розкриває парашут із затримкою 5 с. Визначити швидкість парашутиста та відстань до землі на момент розкриття парашута. [ 50 м/с; 75 м] |
|
1.78. |
Моторний човен спочатку протягом 10 c рухався рівномірно зі швидкістю 5 м/с, а потім ще 5 с – із прискоренням 1,0 м/с2. Який шлях пройшов човен за весь час? [87,5 м]. |
|
1.79. |
Моторолер починає розганятися з місця з прискоренням 1,0 м/с2. Якої швидкості він набуде на шляху 200 м? [72 км/год] |
|
1.80. |
На якому шляху авто, маючи прискорення 2,0 м/с2, розженеться від швидкості 36 км/год до 108 км/год? [200 м] |
|
1.81. |
Авто, рухаючись з прискоренням 2,0 м/с2, за час 5 c пройшло шлях 125 м. Визначити його початкову швидкість. [20 м/с] |
|
1.82. |
З яким прискоренням має рухатися локомотив, аби на шляху 500 м збільшити швидкість від 18 км/год до 36 км/год? [7,5 см/с2] |
|
1.83. |
При забиванні палі молот вільно падає на неї з висоти 5 м. Визначити швидкість молота на момент удару. [10 м/с] |
|
1.84. |
Яструб, який полює здобич, у вільному падінні наздоганяє її, маючи швидкість 100 м/с. З якої висоти він почав атаку? [0,5 км] |
|
1.85. |
У скільки разів треба збільшити початкову швидкість кинутого вгору м'яча, аби збільшити у два рази: а) час його повернення; б) висоту підйому ? [2; $\sqrt{2}$] |
Рівень Б
| 1.86. |
Чи можна сказати, що коли відстань між двома рухомими тілами залишається незмінною, то вони рухаються: а) рівномірно; б) з однаковою за величиною швидкістю; в) з однаковою за напрямом швидкістю? [а) так; б) ні; в) так] |
|
1.87. |
За наведеними рівняннями координати х(t) визначити прискорення ax(t) та там, де не задано, рівняння швидкості vx(t) для тих точок, які здійснюють рівнозмінний рух: а) x = –2 + 2t – 4t2; б) v = 3 + 4t2; в) vх = 1 + 2t – 3t2; г) vх = 1 – 0,01t; д) x = 2t2. [а) –8 м/с2, vх = 2 – 8t; г) –0,01 м/с2; д) vх = 4t; 4 м/с2] |
|
1.88. |
Рівняння руху тіла вздовж осі OX має вигляд: x = 5+ 12t – 4t2. Визначити: а) швидкість тіла на момент t0 = 3 c; б) момент, коли тіло змінює напрям руху; в) момент повернення тіла в точку x = 0; г) швидкість тіла в точці x = 0. [а) –12 м/с; б) 1,5 с; в) 3,375 с; г) –15 м/с] |
|
1.89. |
Куля, що летить зі швидкістю 400 м/с, ударяє в земляний вал і заглиблюється в нього на 36 см. Визначити: а) час руху кулі у землі; б) прискорення кулі; в) швидкість кулі на глибині 18 см; г) глибину, на якій швидкість кулі буде втричі менша за початкову. [а) 1,8 мс; б) –221 км/с2; в) 282 м/с; г) 32 см] |
|
1.90. |
Швидкість літака при посадці складає 270 км/год, шлях пробігу – 1,0 км. Визначити прискорення та час гальмування літака. [≈ –2,8 м/с2; ≈ 27 c] |
|
1.91. |
Потяг починає гальмування при швидкості 72 км/год і проходить до зупинки 1 км. Визначити: а) прискорення потяга; б) час гальмування; в) швидкість потяга біля світлофора, встановленого на середні гальмівного шляху. [а) –0,2 м/с2; б) ≈1,7 c; в) 14 м/с] |
|
1.92. |
Тіло, що починає рухатись із сталим прискоренням, за восьму секунду проходить відстань 30 м. Знайти величину прискорення тіла та відстань, яку воно проходить за п'ятнадцяту секунду руху. [4 м/с2, 58 м] |
|
1.93. |
Тіло починає рухатися прискорено й за шосту секунду проходить відстань 12 м. Визначити прискорення тіла та шлях, який воно подолає за 6 с. [≈2,2 м/с2; ≈39 м] |
|
1.94. |
Кинуте вгору тіло через 10 с падає зі швидкістю 20 м/с. Визначити швидкість кидка. [80 м/с] |
|
1.95. |
З даху будинку висотою 28 м кинули вгору камінь зі швидкістю 8 м/с. Визначити, з якою швидкістю камінь упаде на землю. [25 м/с] |
|
1.96. |
З гелікоптера, що завис, з інтервалом 1 с скинули без початкової швидкості два вантажі. Визначити відстань між вантажами через t1 = 2 c та t2 = 4 c після початку падіння першого вантажу. [15 м; 35 м] |
|
1.97. |
Людина, котра з краю прямовисного урвища відпустила камінь, почула звук падіння через 6 c. Визначити глибину урвища, прийнявши швидкість звуку 330 м/с. [≈150 м] |
|
1.98. |
З повітряної кулі, що опускається зі швидкістю 2 м/с, кинули вгору камінь зі швидкістю 18 м/с відносно землі. Визначити: а) відстань між каменем та кулею на момент, коли камінь підніметься на максимальну висоту над землею; б) через який час після кидка камінь пролетить повз кулю. [≈20 м; 4 с] |
|
1.99. |
З аеростата, що підійматися із землі з прискоренням 2 м/с2, через 5 c після початку підйому скинули баласт без початкової швидкості відносно аеростата. Через який час після скидання баласт впаде на землю? [3,2 c] |
|
1.100. |
Тіло кинули із землі вертикально вгору з початковою швидкістю 30 м/с. Через який час воно опиниться на висоті 25 м? [1 c, 5 c] |
|
1.101. |
У вертикальній площині розташовано дротяне кільце діаметра d із спицями,на які нанизано намистинки, що можуть ковзати без тертя з т. А (рис. 1.101). Визначити, які з них зісковзнуть найшвидше? за який час τ? [всі за однаковий час τ =\(\sqrt{2d/g}\) ]
|
Рівень В
|
1.102. |
Тіло рухається за законом \(\vec{r}=\vec{b}t(1-ct)\), де \(\vec{b}\) – радіус-вектор, \(\vec{b}\) і c – задані сталі. Визначити пройдений тілом шлях S та його середню швидкість за час від початкового моменту до повернення у вихідне положення. [S = (b/2c); $\left\langle v \right\rangle $ = b/2] |
|
1.103. |
За час \(\tau\) тіло пройшло шлях S, збільшивши за цей час швидкість у n разів. Визначити прискорення тіла. $\left[ a=\frac{n-1}{n+1}\cdot \frac{2S}{{{\tau }^{2}}} \right]$ |
|
1.104. |
Перший вагон потяга, що рухається рівносповільнено, проходить повз спостерігача на пероні за 1 c, а другий – за 1,5 c. Визначити прискорення та початкову швидкість потяга, якщо |
|
1.105. |
Тіло, що вільно падає, останні 30 м шляху проходить за 0,5 c. Знайти: а) висоту падіння тіла; б) час проходження першого та останнього метра шляху; в) шлях, пройдений за першу та за останню секунду руху; г) середню швидкість на другій половині шляху. [а) ≈195 м; б) ≈0,45 с; 0,016 с; в) 50 м; 57,5 м; г) 53,3 м/с] |
|
1.106. |
Сигнальна ракета, вертикальна запущено із землі, за час згоряння заряду протягом 2 с набула прискорення a = 2g. Визначити: а) максимальну висоту і час підйому ракети та б) час її падіння на землю. [а) 120 м, 6 с; б) 4,9 с] |
|
1.107. |
Тіло, яке кинуто вертикально вгору, на висоті h = 10 м побувало двічі з інтервалом \(\tau=1,5\) c. Визначити: а) початкову швидкість тіла; б) тривалість руху. [16 м/с; 3,2 с] |
|
1.108. |
Авто рівномірно проходить відстань 450 м, а потім гальмує до зупинки із прискоренням –2 м/с2. Визначити: а) швидкість рівномірного руху, при якій загальний час руху буде найменшим; б) його величину; в) шлях, пройдений під час гальмування. [30 м/с; 30 с; 225 м] |
|
1.109. |
При якому нахилі даху будинку дощова вода стікає з нього якнайшвидше? Тертя не враховувати. [ \(45^{\circ}\) ] |
|
1.110. |
По гладкій площині, що нахилена під кутом \(\alpha=45^{\circ}\) (рис.1.110), під таким самим кутом до ребра пускають кульку з початковою швидкістю v. На якій відстані від початкового положення кулька знов опиниться на ребрі? [ \(\sqrt{2}v^{2}/g\) ]
|
Графіки руху
Рівень А
|
1.111. |
За графіком швидкості точки (рис. 1.111) визначити модуль її переміщення за S за 10 c та накреслити графік залежності S(t). [150 м]
|
|
1.112. |
За графіком координати тіла (рис. 1.112) визначити його швидкість [36 км/год]
|
|
1.113. |
На графіку рис. 1.113 зображено ділянку траєкторії кульки (мірило: 1 поділка – 3,0 м), що рухається із швидкістю v = 50 см/с. Визначити: а) координати точок А і В; б) проекції Sx, Sy, та модулі переміщення S і швидкості v кульки; в) час проходження нею ділянки АВ. [а) xA = 3 м, yA = 6 м, xB = 13,5 м, yB = 9 м; б) Sх = 10,5, Sy = 3 м, S = 10,9 м; в) vх = 21,8 с, vy = 0,137 м/с]
|
|
1.114. |
На рис. 1.114 зображено графік руху катера в стоячій воді (1) та графік руху плота (2), що сплавляється по ріці. а) Побудувати графіки руху катера за та проти течії в цій ріці при тих самих обертах гвинта; б) за отриманими графіками знайти швидкість руху катера за та проти течії. [25 км/год; 15 км/год]
|
|
1.115. |
За графіком шляху (рис.1.115) визначити середні швидкості руху тіла протягом першої та шостої і за всі 6 секунд руху. [5 м/с; 2,5 м/с; ≈4,2 м/с]
|
|
1.116. |
Побудувати графіки швидкості тіла на проміжку часу 5 с, якщо початкова швидкість v0 і прискорення a складають, відповідно: 1) 10 см/с, 0; 2) 10 см/с, 2 см/с2; 3) 0, 4 см/с2; 4) 10 см/с, –2,5 см/с2. |
|
1.117. |
Графік прискорення тіла має вигляд рис. 1.117. Зобразити графік швидкості цього тіла та описати його рух.
|
|
1.118. |
За час 20 c від початку рівноприскореного руху точки її швидкість набула величини v = 8 м/с. Побудувати графік шляху точки S(t) на вказаному проміжку часу. |
|
1.119. |
На проміжку часу 10 с тіло рухалось уздовж осі OX відповідно до рис. 1.119. Визначити за графіком шлях та переміщення тіла за половину та за весь час. [5 м, 5 м; 10 м, 0 м]
|
|
1.120. |
На рис. 1.120 показано графіки швидкості двох тіл. За кожним із них: 1) описати рух тіл; 2) порівняти їхні прискорення; 3) визначити шляхи за час 5 с. [ 3): а) 37,5 м, 31,25 м; б) 125 м, 11 м; в) 25 м, 11,25 м; г) 18,75 м, 10 м; д) 37,5 м, 20 м; е) 37,5 м, 42,5 м]
|
|
1.121. |
Побудувати графік швидкості тіла, якщо його початкова швидкість v0 = –3 м/с, і прискорення a = 0,4 м/с2. Визначити за графіком шлях тіла за 5 c. [10 м] |
Рівень Б
|
1.122. |
Вантаж підіймають вгору з поверхні землі так, що перші 2 c він рухається з прискоренням 0,5 м/с2, наступні 11 c – рівномірно й останні 2 c – сповільнено з прискоренням –0,5 м/с2. Побудувати графік швидкості та визначити за ним висоту підйому вантажу. [13 м] |
|
1.123. |
На рис. 1.123 наведені графіки а) і б) швидкості vх(t) двох тіл, які рухаються вздовж однієї прямої ОХ. За наведеними графіками для кожного з тіл: 1) визначити прискорення ах на кожній ділянці; 2) прийнявши х0 = 0, побудувати графіки координати х(t) та шляху S(t) і визначити за ними шляхи S і переміщення Δх за 10 c руху. [ а) 1) 2 м/с2, –1 м/с2; 2) 34 м, –2 м. б): 1) –2 м/с2, 0, 1,33 м/с2; 2) 39 м, –27 м ]
|
|
1.124. |
Тіло рухається з точки x0 = –3 м із початковою швидкістю v0х = 2 м/с відповідно до заданого графіка прискорення ах(t), рис. 1.124. Побудувати графіки швидкості, координати та пройденого тілом шляху.
|
|
1.125. |
Велосипедист починає рух по прямій із сталим прискоренням 2 м/с2 і, досягнувши швидкості 6 м/с, деякий час рухається рівномірно, а в кінці гальмує з прискоренням –3 м/с2. Визначити час руху велосипедиста, якщо від старту до зупинки він пройшов шлях 120 м. [22,5 с] |
|
1.126. |
За графіком прискорення тіла (рис.1.126) визначити його швидкість на моменти t2 = 4 c і t3 = 15 c , якщо в момент t1 = 1 c вона складала 3 м/с. [7 м/с; 36 м/с]
|
Рух тіла, що кинуте під кутом до горизонту
Рівень А
|
1.127. |
Два тіла кинуто з однієї точки з однаковою швидкістю під кутами \(30^{\circ}\) і \(60^{\circ}\) до горизонту. Визначити відношення максимальних висот підйому та дальностей польоту тіл. [3; 1] |
|
1.128. |
М'яч, який кинуто горизонтально з висоти 2 м над землею, упав на землю на відстані 7 м по горизонталі. Визначити 1) початкову і 2) кінцеву швидкості м'яча. [ 1) ≈11 м/с; 2) ≈13 м/с] |
|
1.129. |
При якій швидкості v0 у точці A (рис. 1.129) мотоцикліст перелетить у точку В при L = 3 м і h = 1,125 м? [6 м/с]
|
|
1.130. |
Тіло кинули із землі під кутом \(30^{\circ}\) до горизонту з початковою швидкістю 100 м/с. Через який час тіло опиниться на на висоті 50 м? [≈1 с; ≈9 c] |
Рівень Б
|
1.131. |
М'яч кинули з землі під кутом \(30^{\circ}\) до горизонту з початковою швидкістю 10 м/с. Визначити: а) горизонтальну та вертикальну складові початкової швидкості м'яча; б) час його руху; в) висоту підйому і дальність польоту. [ а) \(\approx{8,7}\) м/с, 5 м/с; б) 1 с; в) \(\approx{1,3}\) м, \(\approx{8,7}\) м] |
|
1.132. |
Тіло кинули з поверхні землі під кутом \(60^{\circ}\) до горизонту з початковою швидкістю 20 м/с. Визначити наступні характеристики руху тіла: а) рівняння траєкторії y(x); б) час руху; в) найбільшу висоту підйому; г) дальність польоту; д) напрям його руху через 1 c після кидка. [a) y = 1,73x – 0,05x2; б) 3,46 с; в) 15 м; г) с; д) 34,6 м; е) \(47^{\circ}\) до до горизонту] |
|
1.133. |
Двоє хлопчиків перекидаються м'ячем. Якою є максимальна висота підйому м'яча над точкою кидання, якщо він перебуває в польоті 2 c? [5 м] |
|
1.134. |
Тіло з висоти 30 м кинули вниз під кутом \(30^{\circ}\) до горизонту зі швидкістю 10 м/с. Визначити: а) час польоту; б) горизонтальну дальність польоту; в) величину та напрям швидкості тіла на момент падіння. [а) 2 с; б) 17,3 м; в) ≈26,5 м/с, \(71^{\circ}\) до горизонту] |
|
1.135. |
Камінь, який кинуто горизонтально зі швидкістю 15 м/с, впав на землю під кутом \(60^{\circ}\) до горизонту. З якої висоти було кинуто камінь та на якій відстані по горизонталі від точки кидання він впав на землю? [≈34 м; ≈40 м] |
|
1.136. |
Снаряд, випущений під кутом \(30^{\circ}\) до горизонту, побував на деякій висоті двічі: через 3 c і 5 c з моменту пострілу. Визначити початкову швидкість та максимальну висоту підйому снаряда. [80 м/с; 80 м] |
|
1.137. |
Хлопчик, який стоїть на схилі гори з кутом нахилу до горизонту \(30^{\circ}\), кидає в напрямку вершини камінь під кутом \(60^{\circ}\) до горизонту. На якій відстані від хлопчика камінь впаде на схил при швидкості кидка 10 м/с? [≈7 м] |
|
1.138. |
Тіло кинуто з поверхні землі з початковою швидкістю 10 м/с. На якій відстані тіло впаде якщо за 0,5 c від початку руху його швидкість зменшилася до 7 м/с. [≈10 м] |
Рівень В
|
1.139. |
Частинка рухається по траєкторії y = 1,732x – 2x2 із прискоренням, проєкції котрого складають aх = 0 і ay = –10 м/с2. Визначити, з якою швидкістю частинка пройшла початок координат. [4,47 м/с] |
|
1.140. |
З якою мінімальною швидкістю v0, під яким кутом α та з якої відстані L слід кидати камінь, аби він перелетів через будівлю, профіль якої подано на рис. 1.140.[ v0 = \(\sqrt{g\left(\frac{l^{2}}{2(H-h)}\right)}\); α = \(\mathrm{arctg}\left(\frac{\sqrt{4H(H-h)}}{l}\right)\); L = \(l\sqrt{H/(H-h)}\)].
|
|
1.141. |
На кинуту з землі під кутом \(\varphi\) до горизонту легку кульку, діє вітер, який надає їй сталого горизонтального прискорення а. На скільки η% він змінить дальність польоту кульки? [η = (a·tgφ/g)·100%] |
|
1.142. |
Зі шланга, що лежить на землі, неперервно б'є струмінь води під кутом 45° до горизонту. Яка маса води знаходиться в повітрі, якщо швидкість вильоту води 10 м/с і площа перерізу шланга 5 см2? [7 кг] |
|
1.143. |
Унаслідок зіткнень із стінкою, кулька перескакує від одного до іншого боку півсферичної лунки (рис.1.143). Зіткнення відбуваються на одному рівні й абсолютно пружно (без утрати швидкості). Визначити радіус лунки, якщо час перельоту кульки від стінки до стінки в один бік складає T1, а в інший − T2. $\left[ \ \frac{g{{T}_{1}}{{T}_{2}}}{2\sqrt{2}}\ \right]$
|
Рух двох тіл
|
1.144. |
З пунктів А і В, розташованих на прямій трасі на відстані 100 км, одночасно починають рухатися два авто: з А зі швидкістю 50 км/год, а з В — 30 км/год. Через який час і на якій відстані від п. А вони зустрінуться, якщо рухатимуться: а) назустріч і б) одне авто наздоганятиме інше? [а) 1 год 15 хв, 62,5 км від п. А; б) 5 год, 250 км від п. А] |
|
1.145. |
З пунктів 1 і 2 розташованих на одній трасі на відстані 100 км виїхали назустріч автобуси: з першого о – 9 год із швидкістю 40 км/год, а з другого – о 9 год 30 хв із швидкістю 60 км/год. За допомогою рівнянь та за допомогою графіків руху автобусів знайти час і місце зустрічі автобусів. [10 год 30 хв, посередині] |
|
1.146. |
О 8-й ранку над пунктом А в напряку пункту В зі швидкістю 300 км/год пролетів літак. Відтак через 1 год у тому самому напрямі зі швидкістю 400 км/год пролетів другий літак. Визначити алгебраїчно та графічно, коли кожен із літаків прибуде в пункт В, якщо відстань між пунктами складає 1200 км. [одночасно о 12-й годині] |
|
1.147. |
По прямих автотрасах, які перетинаються під кутом \(\alpha=45^{\circ}\) рухаються два автомобілі зі швидкостями 50 км/год і 80 км/год. З якою швидкістю та під яким кутом рухається автомобілі один відносно одного? [120,7 км/год; 163°, або 57 км/год; 83,4°] |
|
1.148. |
Водій легкового автомобіля помітив, що краплі дощу не залишають слідів на задньому склі при швидкості, більшій за 60 км/год. Визначити швидкість крапель відносно землі, якщо вітру немає й скло нахилене під кутом 48° до горизонту. [18,5 м/с] |
|
1.149. |
Два тіла вільно падають з однієї точки з інтервалом 2 c. Через який час після початку руху першого тіла відстань між тілами буде в n = 3 рази більшою, ніж вона була на момент початку руху другого тіла? [4 c] |
|
1.150. |
На графіках швидкості двох тіл (рис. 1.150), що рухаються з однієї точки і в одному напрямі, величини t1 = 5 c і t2 = 9 c. В який момент часу t3 тіла зустрінуться? [t3 = 15 c]
|
|
1.151. |
З однієї точки з інтервалом часу τ кинуто два тіла під одним кутом до горизонту і з однаковими початковими швидкостями. Визначити швидкість першого тіла відносно другого. [$\vec{v}=-\vec{g}\tau $ ] |
|
1.152. |
Балістична ракета стартує вертикально з прискоренням 6,2 м/с2. Під яким кутом до горизонту необхідно одночасно зробити постріл з гармати, яку розташовано за 5 км від місця старту, аби поцілити в ракету при початковій швидкості снаряду 400 м/с? [\(15^{\circ}\) ] |
|
1.153. |
Хлопець кинув камінь із швидкістю v0 під кутом \(\varphi\) до горизонту точно в напрямку іграшкового коптера, шо рухається горизонтально зі сталою швидкістю u. Знайти висоту Н траєкторії коптера, якщо хлопець все ж таки влучив у нього, попри принципово хибне прицілювання? $\left[ H=\frac{2u\left( {{v}_{0}}\cos \varphi -u \right){{\operatorname{tg}}^{2}}\varphi }{g} \right]$
|
Розділ ІІ. ДИНАМІКА
Динаміка – це розділ механіки, в якому вивчається зв'язок між характеристиками руху тіла, (форма траєкторії, швидкість, прискорення) та його взаємодією з іншими тілами. Тут розглянуто основні закони класичної динаміки, що були сформульовані Ньютоном. Ці закони виконуються тільки при порівняно повільних рухах тіл і втрачають чинність для елементарних частинок і швидкостей, що є сумірні зі швидкістю світла у вакуумі c = 3·108 м/с.
Далі представлено такий навчальний матеріал.
2.1. Теоретичні відомості. Основні поняття динаміки
Основними величинами динаміки матеріальної точки є: маса, імпульс, сила.
2.2. Закони динаміки
|
Основними законами класичної динаміки є три закони Ньютона (перший, другий і третій), які були встановлені на основі результатів спостережень і дослідів. |
Цей закон виконується не в усіх, а тільки у так званих інерціальних системах відліку. (Примітка. Терміни "інерціальна система відліку" та "закон інерції" пояснюються тим, що рух вільних тіл, якими можна вважати зірки, називається рухом "за інерцією"). Експериментально встановлено, що інерціальними є системи відліку, котрі пов’язані з зірками. Такою є й геліоцентрична система відліку, в якій початок координат розміщується в центрі нашого Сонця, а осі спрямовані на віддалені зірки. Доведено також, що всяка система відліку, котра рухається поступально, рівномірно та прямолінійно відносно заданої інерціальної системи, також є інерціальною. Системи відліку, які мають прискорення відносно інерціальних, називаються неінерціальними. Очевидно, що в них закон інерції не виконується. Строго говорячи, це стосується й систем відліку, пов'язаних із Землею, бо вона має прискорення відносно Сонця, зумовлене добовим обертанням та орбітальним рухом. Але це прискорення не перевищує 3,5 см/с2, тоді як сама Земля надає тілам прискорення g = 9,8 м/с2. Тому в більшості випадків систему відліку пов'язану із Землею можна вважати інерціальною. |
В цьому рівнянні \( \Delta\vec{p}=\vec{p}_{2}-\vec{p}_{1}\) – зміна імпульсу за заданий проміжок часу Δt, \( \vec{F}\) – рівнодійна всіх сил, які прикладено до тіла. Формулу (2.3) можна також записати як
Вектор \( \vec{I}\) = \( \vec{F}\)Δt називається імпульсом сили. Отже,
Це інше, але рівносильне до попереднього, формулювання ІІ закону Ньютона. (Примітка. У виразах (2.3), (2.4) передбачається, що сила є сталою: \( \vec{F}\) = const. Натомість вираз (2.4а) є загальним. При цьому імпульс \(\vec{I}\) залежної від часу сили \(\vec{F}\left( t \right)\) обчислюється методами вищої математики). Наведені формулювання ІІ закону є найбільш загальними, зокрема вони є чинні навіть для тіл, маса котрих змінюється під час руху, як, до прикладу, у космічної ракети під час роботи двигуна. Якщо ж маса тіла лишається сталою, то \( \Delta\vec{p}=m\vec{v}_{2}-m\vec{v}_{1}=m(\vec{v}_{2}-\vec{v}_{1})=m\Delta\vec{v}\), і рівняння (2.3) набуває вигляду:
У такому разі можна дати ще одне формулювання ІІ закону Ньютона:
Якщо закони взаємодії даного тіла з іншими тілами (закони сил) є відомі, то з рівняння (2.5) можна визначити прискорення, а відтак і всі інші характеристики руху в довільний момент часу, тобто повністю визначити рух тіла. Саме тому другий закон Ньютона називають основним законом механіки. З рівняння (2.5) видно, що коли \( \vec{F}={0}\), то \( \vec{a}={0}\) і \(\vec{v}=const\), як того вимагає закон інерції. Це свідчить про те, що другий закон Ньютона виконується в інерціальних системах відліку, (а не про те, що І закон Ньютона є наслідком другого, як іноді помилково вважають). |
||||||||||
Третій закон Ньютона відображує той факт, що в природі не існує відокремленої дії – дія одних тіл на інші завжди є взаємною. Як і другий, він виконується тільки в інерціальних системах відліку. В довільній системі тіл ІІІ закон Ньютона виконується для всіх тіл попарно, причому для кожної пари сили взаємодії мають однакову фізичну природу. Варто також пам'ятати, що хоча сума сил взаємодії між двома тілами дорівнює нулю, їх не можна розглядати як компенсовані, бо вони прикладені до різних тіл. |
2.3. Сили в механіці
|
Для визначення прискорення тіла за другим законом Ньютона (2.5) треба знати сили, що його створюють. У традиційних задачах механіки це сили гравітації, пружні сили і сили сухого тертя та опору. |
Гравітаційні сили діють між всіма тілами і визначаються законом всесвітнього тяжіння Ньютона, за яким
де коефіцієнт G = 6,67·10-11 м3/(кг·с2) визначає "силу" гравітаційної взаємодії і називається гравітаційною сталою. |
(Примітка. Вираз (2.6) є чинним, якщо тіла можна вважати матеріальними точками, або вони є однорідними і мають кулясту форму).
|
Силу гравітаційного притягання порівняно невеликих тіл до планети називають силою тяжіння і, згідно з другим законом Ньютона, записують у вигляді:
де m – маса тіла, \( \vec{g}\) – вектор прискорення сили тяжіння, що є спрямований до центра планети (вертикально вниз) і має модуль
де M, R – маса і радіус планети, r – відстань від тіла до центра планети, h – його висота над поверхнею планети. |
|
\( {g}=G\frac{M}{R^{2}}=\mathrm{const}\). |
(2.9) |
Для Землі воно в середньому складає g = 9,8 м/с2 і зазвичай називається прискоренням вільного падіння. Але це не зовсім точно, бо, як говорилося, пов'язана з поверхнею Землі система відліку не є строго інерціальною.
|
Із гравітацією пов’язане поняття ваги тіла. Вага – це сила, з якою тіло тисне на горизонтальну опору або розтягує вертикальний підвіс унаслідок притягання до планети. Отже, вага тіла прикладена не до нього, а до опори, або підвісу, які його утримують. При цьому, коли опора (підвіс) не має прискорення відносно планети, то вага тіла дорівнює силі тяжіння:
Якщо ж опора (підвіс) рухається з прискоренням \( \vec{a}\) , то вага тіла
Зокрема, при \( \vec{a}=\vec{g}\) , вага тіла \( \vec{P}={0}\) і настає невагомість — стан, при якому тіло перестає тиснути на опору чи розтягувати підвіс. Варто акцентувати, що невагомість – це стан, у якому на тіло діє тільки сила тяжіння, а не “коли на тіло не діє сила тяжіння”, як іноді помилково твердять учні. |
|
Пружні сили виникають при пружних деформаціях тіла. Вони з'являються при дії на тіло якихось інших сил і зникають при припиненні їхньої дії. Загальні властивості пружніх сил визначаються законом Гука:
Для поздовжніх деформацій (стиснення або видовження) закон Гука записується у вигляді:
де F – проєкція сили пружності на вісь, що напрямлена в бік видовження тіла, (\( {x}=l-l_{0}\) – деформація, тобто різниця довжин деформованого та недеформованого тіла (x – алгебраїчна величина, при стисненні x < 0 ). Коефіцієнт k називається жорсткістю тіла. Для суцільного твердого тіла закон Гука записують також у вигляді:
де ε = \( \left|\frac{l-l_{0}}{l_{0}}\right| \) – відносна деформація, \( \sigma=F/S \) – механічна напруга, тобто відношення деформуючої сили до площі поперечного перерізу тіла (вимірюється в паскалях, 1 Па = 1 Н/м2). Величина \( {E}\) називається модулем пружності (або модулем Юнґа). Вона є характеристикою пружних властивостей даного матеріалу. Значення \( {E}\) можна знайти у довідкових таблицях. |
|
Сили тертя виникають при відносному русі, або спробі такого руху тіл, які перебувають у контакті. Тертя між твердими тілами називається сухим тертям, а між шарами рідини – в'язкістю (“мокрим” тертям). При русі тіла в рідині чи газі зазвичай говорять про силу опору середовища. Причиною тертя є зачеплення між мікроскопічними нерівностями поверхонь тіл при їх притисканні, що створює перешкоду рухові тіл одне відносно іншого. При цьому сили сухого тертя можуть до певної межі компенсувати прикладені зовнішні сили, так що тіла лишаються нерухомими одне відносно одного. В такому разі говорять про тертя спокою. Позаяк сила тертя спокою \( \vec{F}_{т}\) утримує тіло від руху, вона компенсує суму всіх інших прикладених до нього сил \( \vec{F}_{ін}\), тобто має такий самий модуль і протилежний напрям:
Для кожної пари тіл існує граничне (максимально можливе) значення сили тертя спокою
де \( \mu \) – коефіцієнт тертя, \( {N}\) – сила нормального тиску, що діє між цими тілами. Слід зауважити, що коефіцієнт тертя для кожної пари тіл, окрім матеріалу, залежить від багатьох інших факторів, як от чистота (гладкість) поверхонь, фізичні та хімічні забруднення, тощо. З цієї причини коефіцієнт тертя неможливо заздалегідь розрахувати. Тому в задачах при потребі його наводять в умові, а в техніці визначають дослідним шляхом. Якщо рівнодійна всіх інших сил перевищує деяке значення Fт max
, то починається рух тіл одне відносно одного, і тертя спокою переходить у тертя ковзання.
сила тертя ковзання є сталою і дорівнює максимальній силі тертя спокою і визначається формулою (2.14). Відповідно, графік залежності сили сухого тертя від величини прикладеної до тіла зовнішньої сили має вигляд рис.2.1. |
|
При русі в середовищі на тверде тіло діє сила опору, спрямована проти швидкості його руху відносно середовища. Сила опору має складні властивості. Зокрема, вона суттєво залежать від величини та форми поверхні тіла та швидкості його руху. При малих швидкостях силу опору можна вважати прямо пропорційною величині швидкості:
а при великих – її квадратові:
де \( \beta_{1},\,\beta_{2}\) – коефіцієнти опору, які залежать від властивостей середовища, розмірів і форми тіла та ін. |
2.4. Динаміка рівномірного руху по колу
|
При криволінійному русі сила, що діє на тіло, на загал, змінює і модуль, і напрям його швидкості. Але, коли вона весь час лишається перпендикулярною до напрямку руху, змінюється лише напрям швидкості, й тіло здійснює рівномірний криволінійний рух. Прикладом може бути рух штучного супутника Землі по коловій орбіті, або тягарця на нитці, що здійснює коловий рух у горизонтальній площині. В таких випадках рушійна сила та прискорення весь час спрямовані до центра кола й називаються доцентровою силою та доцентровим прискоренням. Доцентрове прискорення тіла (матеріальної точки) визначається формулами (1.28):
Відповідно, за ІІ законом Ньютона (2.5) формули доцентрової сили мають вигляд:
або
|
|
Зауважимо, що термін "доцентрова сила" не означає якусь спеціальну силу, що створює обертовий рух. За відповідних умов доцентровою може стати будь-яка сила або рівнодійна декількох сил. Зокрема, коловий рух штучних супутників Землі є зумовлений дією сили тяжіння (2.6), і, відповідно до виразу (2.17), відбувається зі швидкістю
Отже, аби вивести тіло на низьку орбіту супутника планети, де радіус траєкторії r практично збігається з радіусом планети R, йому необхідно надати швидкості
яку називають першою космічною швидкістю. Для Землі вона складає \( {v}_{1}={7,9}\) км/с. |
Приклади розв’язування задач
Розв'язування задач динаміки проводять за певною схемою, що викладена у рекомендаціях до розділу, враховуючи поради по оформленню розв'язку задач (див. "Етапи розв'язування задач"). При цьому по умовчанню тіла вважаються матеріальними точками, нитки невагомими й нерозтяжними, опір середовища відсутнім.
Далі наведено задачі за темами:
Прямолінійний рух одного тіла та зв'язаних тіл
Зв'язок між імпульсом та силою
При обчисленнях прийнято g = 10 м/с2.
Прямолінійний рух одного тіла та зв'язаних тіл
Задача 2.1. Ваговик рухається прямою дорогою зі швидкістю v0 = 36 км/год. Визначити: а) відстань S від місця розвантаження, на якій водій має вимкнути двигун, аби вчасно зупинитися без використання гальм; б) час руху t до зупинки із вимкненим двигуном при коефіцієнті опору (відношенні сили опору до ваги ваговика) μ = 0,5.
Задача 2.2. На горизонтальному столі знаходяться зв'язані ниткою бруски масами m1 і m2. Визначити прискорення брусків a та сила натягу нитки T, якщо коефіцієнти тертя між ними та столом, відповідно, складають \( \mu_{1}\) і \( \mu_{2}\), і до першого прикладено горизонтальну силу F.
Задача 2.3. Горизонтальну дошку, на якій лежить шайба маси m, починають підіймати за один кінець. Визначити та побудувати графік залежності сили тертя F, що діє на шайбу, від кута нахилу дошки до горизонту α при заданому коефіцієнті тертя μ.
Задача 2.4. Підлогою тягнуть за мотузку ящик масою m = 100 кг, прикладаючи силу під кутом до горизонту. Коефіцієнт тертя між ящиком та підлогою μ = 0,5. Визначити найменшу силу \({{\vec{F}}_{\min }}\), якою можна рухати ящик.
Задача 2.5. Брусок знаходиться на похилій площині, кут нахилу якої до горизонту α можна змінювати за допомогою вертикального штока (упора). Знайти величину кута α0, при якій брусок із стану спокою найшвидше спуститься від упора до основи при коефіцієнті тертя μ = 0,14.
Задача 2.6. Два тягарці масою M кожен, які зв'язані перекинутою через нерухомий блок ниткою, спочатку утримують на одному рівні. Потім до одного підвішують важок масою m і вивільняють систему. Визначити: а) прискорення a тягарців та час t, за який вони розійдуться на відстань H за відсутності ковзання нитки; б) силу натягу нитки \( {T}_{0}\), на якій підвішено важок, та силу тиску \( {F}\) на вісь блока.
Задача 2.7. На початку підйому та спуску ліфт має однакове прискорення. Визначити його величину a, якщо вага тіл у ліфті при підйомі в n = 1,5 рази перевищує вагу при спуску.
Задача 2.8. Повітряна куля загальною масою M = 1000 кг опускається зі сталою швидкістю. Визначити масу баласту m, яку треба скинути, аби куля почала підійматися з тою самою швидкістю. Піднімальна (архімедова) сила, що діє на кулю, F = 9700 H.
| Задача 2.1 |
| Задача 2.1 |
Ваговик рухається прямою дорогою зі швидкістю v0 = 36км/год.
Визначити:
а) відстань S від місця розвантаження, на якій водій має вимкнути двигун, аби вчасно зупинитися без використання гальм;
б) час руху t до зупинки із вимкненим двигуном при коефіцієнті опору (відношенні сили опору до ваги ваговика) μ = 0,5.
|
Дано: v0 = 36 км/год
\( \mu={0{,}5}\)
|
|
S - ? t - ? |
Розв'язання
а) При вимкненому двигуні на ваговик діють три сили: тяжіння \( {m}\vec{g}\), нормальна реакція опори \( \vec{N}\) та сила опору \( \vec{F}_{0}\) (рис. 2.1). Зрозуміло, що вертикальні сили є компенсовані:
\( {m}\vec{g}+\vec{N}\) = 0.
Отже,
\( {m}\vec{a}=\vec{F}_{0}\),
або у проекціях на напрям руху (вісь OX)
\( {m}a_{x}=-F_{0}\).
Знак мінус стоїть тому, що вектор \( \vec{a}\) є протилежним до напрямку руху. Сила опору визначається, як \( {F}_{0}=\mu{mg}\), отже
\( {a}_{x}=-\mu{g}\).
Відтак за формулою (1.19) знаходимо шлях ваговика до зупинки:
\( {S}=\frac{v_{0}^{2}}{2\mu{g}}\) ≈ 100 м.
б) Для визначення часу руху ваговика до зупинки використаємо рівняння швидкості \( {v}_{x}\) (1.16), звідки з урахуванням знаків проєкцій отримуємо:
\( {v}_{0}-\mu{mgt}={0}\) \( \Rightarrow \) \( {t}=\frac{v_{0}}{\mu{g}} = 20{,}4\) c.
Величину t також можна знайти і з рівняння ІІ закону Ньютона (2.4), згідно з яким зміна імпульсу ваговика \( \Delta{\vec{p}}=-m\vec{v}_{0}\) дорівнює імпульсові сили опору за час руху до зупинки \( \vec{F}_{0}{t}\). Позаяк ці вектори мають однаковий напрям, то
\( {mv}_{0}=F\Delta{t}\) \( \Rightarrow \) \( \Delta{t}=\frac{mv_{0}}{F}=\frac{mv_{0}}{\mu{mg}}=\frac{v_{0}}{\mu{g}}\),
що, природньо, збігається з раніше отриманим результатом.
| Задача 2.3 |
| Задача 2.2 |
На горизонтальному столі знаходяться зв'язані ниткою бруски масами m1 і m2.
Визначити
прискорення брусків a та сила натягу нитки T, якщо коефіцієнти тертя між ними та столом, відповідно, складають \( \mu_{1}\) і \( \mu_{2}\), і до першого прикладено горизонтальну силу F.
|
Дано: m1, m2
μ1, μ2
|
|
a - ? T - ? |
Розв'язання
На бруски діють сили тяжіння \( {m}_{1}\vec{g}\), \( {m}_{2}\vec{g}\), реакції опори \( \vec{N}_{1}\), \( \vec{N}_{2}\), тертя \( \vec{F}_{т1}\), \( \vec{F}_{т2}\), прикладена сила \( \vec{F}\) та сили натягу нитки \( \vec{T}_{1}\) і \( \vec{T}_{2}\) = –\( \vec{T}_{1}\), рис. 2.2.
Позаяк прискорення тіл однакові, і сили тяжіння та реакції опори компенсовані, то рівняння руху (2.5) брусків мають вигляд:
|
\( \vec{F}+\vec{F}_{т1}+\vec{T}_{1}=m_{1}\vec{a}\), \( \vec{T}_{2}+\vec{F}_{т2}=m_{2}\vec{a}\). |
Для розрахунків перепишемо їх через проєкції векторів на напрям руху (вісь ОХ), врахувавши, що Т1 = Т2 =Т, Fт1 = μ1m1g і Fт2 = μ2m2g:
|
F – μ1m1g – Т =m1a, Т – μ2m2g = m2a. |
(1) |
Далі, додавши праві та ліві частини рівнянь (1), знайдемо прискорення брусків:
|
\( {F}-(\mu_{1}m_{1}+\mu_{2}m_{2})g=(m_{1}+m_{2}){a}\) \( \Rightarrow \) \( {a}=\frac{{F}-(\mu_{1}m_{1}+\mu_{2}m_{2})g}{m_{1}+m_{2}}\). |
(2) |
Відтак, підставивши вираз прискорення (2) у будь-яке з рівнянь (1), для сили натягу нитки отримаємо:
\({T}=\frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\left[ F+\left( {{\mu }_{2}}-{{\mu }_{1}} \right){{m}_{1}}g \right] \).
Отже, сила натягу нитки, що з'єднує бруски, визначається різницею коефіцієнтів тертя. Тож μ1 = μ2 наявність тертя на неї взагалі не впливає.
Наостанку зауважимо, що вираз прискорення (2) за змістом є настільки очевидний, що його можна було би записати одразу. Але попередні міркування і викладки були наведені як ілюстрація загального алгоритму застосування другого закону Ньютона.
| Задача 2.4 |
| Задача 2.3 |
Горизонтальну дошку, на якій лежить шайба маси m, починають підіймати за один кінець.
Визначити та побудувати графік
залежності сили тертя F, що діє на шайбу, від кута нахилу дошки до горизонту α при заданому коефіцієнті тертя μ.
|
Дано m μ |
|
|
Розв'язання
На шайбу діють сили: тяжіння \( {m}\vec{g}\) і нормальної реакції площини \( \vec{N}\) та тертя \( \vec{F}\). При порівняно невеликих кутах нахилу, поки не почалося ковзання тіла, \(\vec{F}\) – це сила тертя спокою. Згідно з формулою (2.13) вона зрівноважує рівнодійну решти сил $\vec{R}=m\vec{g}+\vec{N}$ (рис. 2.3), модуль якої R = mgsinα. Отже, при невеликих \( \alpha \) сила тертя залежить від кутах нахилу площини за законом
| \( {F}=mg\sin\alpha \). | (1) |
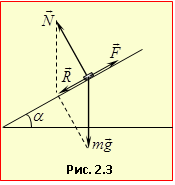 При збільшенні кута \( \alpha \) сила тертя спокою F зростає і при певному куті \( \alpha_{0}\), який називають "кутом тертя", досягає максимально можливого значення μN (формула (2.14)). Сила N компенсує нормальну до площини складову сили тяжіння, тож максимальна сила тертя спокою Fm = μmgcosα0. Відтак, враховуючи вираз (1), маємо:
При збільшенні кута \( \alpha \) сила тертя спокою F зростає і при певному куті \( \alpha_{0}\), який називають "кутом тертя", досягає максимально можливого значення μN (формула (2.14)). Сила N компенсує нормальну до площини складову сили тяжіння, тож максимальна сила тертя спокою Fm = μmgcosα0. Відтак, враховуючи вираз (1), маємо:
mgsinα0 = μmgcosα0, → α0= arctgμ.
При кутах нахилу площини α > α0, коли шайба рухається, на неї діє сила тертя ковзання
\({F}=\mu{mg}\cos\alpha \).
Таким чином, сила тертя між шайбою та площиною в залежності від кута нахилу площини виражається однією з формул: 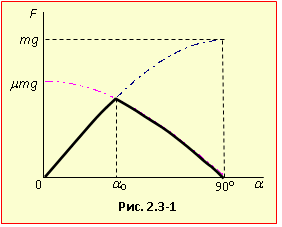
1. \( {F}=mg\sin\alpha \) при \( {0}\le\alpha\le\alpha_{0}\);
2. \( {F}=\mu{mg}\cos\alpha \) при \( \alpha_{0}<\alpha\le{90}^{\circ}\).
(\( \alpha_{0}=\mathrm{arctg}\mu \)).
Отже, графік \( {F}(\alpha) \), рис. 2.3-1, складається з відрізка синусоїди (1) і відрізка косинусоїди (2).
| Задача 2.2 |
| Задача 2.4 |
Підлогою тягнуть за мотузку ящик масою m = 100 кг, прикладаючи силу під кутом до горизонту. Коефіцієнт тертя між ящиком та підлогою μ = 0,5.
Визначити
найменшу силу \({{\vec{F}}_{\min }}\), якою можна рухати ящик.
|
Дано: m = 100 кг μ = 0,5 |
|
αmin - ? Fmin - ? |
Розв'язання
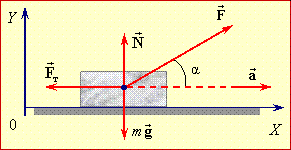
На ящик діють сили тяжіння \( {m\vec{g}}\), нормальної реакції опори \( \vec{N}\), тертя \( \vec{F}_{т}\) та натягу мотузки \( \vec{F}\), що дорівнює прикладеній силі (рис. 2.4).
За ІІ законом Ньютона (2.5) рівняння руху ящика має вигляд
\( \vec{F}+m\vec{g}+\vec{N}+\vec{F}_{\mathrm{т}}=m\vec{a}\).
Ящик рухається горизонтально (ay = 0, ax = a), тож у проекціях на осі координат маємо
OX: \( {F}\cos\alpha-F_{т}={ma}\),
OY: \( {F}\sin\alpha+N-mg={0}\).
Урахувавши, що сила тертя \( {F}_{\mathrm{т}}=\mu{N}\), отримуємо систему рівнянь
\(\left\{ \begin{matrix} F\cos \alpha -\mu N=ma, \\ F\sin \alpha +N-mg=0 \\ \end{matrix} \right.\),
з якої знайдемо прикладену натягу мотузки, при якій ящик рухається із прискоренням а:
|
\( {F}=\frac{\mu{mg}+ma}{\cos\alpha+\mu\sin\alpha}\). |
Її мінімальна величина, потрібна для руху ящика, відповідає умові a = 0 і складає
|
\( {F}_{0}=\frac{\mu{mg}}{\cos\alpha+\mu\sin\alpha}\). |
(1) |
З умови задачі випливає, що сила F при певному значенні кута α є найменшою, тобто тягти ящик найлегше. Чому це так, можна зрозуміти, проаналізувавши залежність F0(α) при малих та при великих значеннях α. Справді, при малих кутах косинус є близький до одиниці і майже не змінюється при збільшенні кута, тоді як синус швидко зростає. Тому знаменника у виразі (1) зростає, а величина F0 зменшується. При великих кутах все відбувається навпаки – косинус стрімко зменшується, тоді як синус майже не змінюється, і F0 збільшується. Тож при певному значенні кута α = αmin знаменник у виразі (1)
|
\( {f}(\alpha)=\cos\alpha+\mu\sin\alpha \) |
(2) |
буде максимальним, а необхідна для пересування ящика сила F0 – мінімальною.
Для визначення величини αmin уведемо позначення \( \mu=\mathrm{tg}\varphi \). Тоді формула (2) набуває вигляду
\( f(\alpha)=\cos\alpha+\frac{\sin\varphi}{\cos\varphi}\sin\alpha=\frac{\cos{(\alpha-\varphi)}}{\cos\varphi}\).
Кут \( \varphi \) є незмінним, тож функція \( {f}(\alpha)\) досягає максимуму за умови \( \cos{(\alpha-\varphi)}={1}\), тобто при \( \alpha_{\mathrm{min}}=\varphi \). Отже натяг мотузки мінімальний при
| \( \mathrm{tg}\alpha_{\mathrm{min}}=\mu\) \( \Rightarrow \) \( \alpha_{\mathrm{min}}=\mathrm{arctg}\mu \) = 26,6°. |
(3) |
Примітка. Якщо ви з математики вже знаєте похідні, відповідь можна знайти простіше, взявши та прирівнявши до нуля похідну функції (2):
\( {f}^{\prime}(\alpha)=-\sin\alpha+\mu\cos\alpha \) \( \Rightarrow \)
\( -\sin\alpha_{\mathrm{min}}+\mu\cos\alpha_{\mathrm{min}}=0\),
звідки
\( \alpha_{\mathrm{min}}=\mathrm{arctg}\mu \).
що, збігається з (3).
Урахувавши отриманий для tgα вираз (3) і замінивши за відомими формулами cosα i sinα у виразі (1) через tgα, після елементарних спрощень отримаємо другу відповідь:
${{F}_{\min }}=\frac{\mu mg}{\sqrt{1+{{\mu }^{2}}}}$ ≈ 450 Н.
| Задача 2.5 |
| Задача 2.5 |
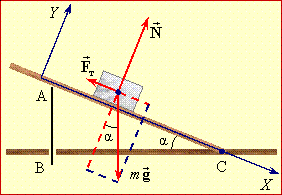
Брусок знаходиться на дошці із закріпленим кінцем, кут нахилу якої до горизонту α можна змінювати за допомогою вертикального упора (штока)на рис. 2.5.
Знайти,
при якій величині кута α0 брусок із стану спокою найшвидше спуститься від упора до точки кріплення дошки при коефіцієнті тертя μ = 0,14.
|
Дано: \( \mu={0{,}14}\) |
|
\( \alpha_{m}\)-? |
Розв'язання
Очевидно, що, аби отримати відповідь, спочатку треба встановити залежність t(α) часу спуску бруска від кута нахилу дошки.
Умову задачі ілюструє рис. 2.5. На брусок діють сили тяжіння \( {m\vec{g}}\), реакції опори \( \vec{N}\) та тертя \( \vec{F}_{т}\), отже, рівняння руху (2.5) має вигляд:
| \( {m}\vec{g}+\vec{N}+\vec{F}_{т}=m\vec{a}\), |
і в проєкціях на осі координат:
|
OX: \( {mg}\sin\alpha-F_{т}=ma \), OY: \( {N}-mg\cos\alpha={0} \) \(\Rightarrow \) \( {N}=mg\cos\alpha \) |
(1) |
Відтак, урахувавши, що Fт = μN = μmgcosα, з першого рівняння системи (1) визначимо прискорення бруска
\( {a}=g(\sin\alpha-\mu\cos\alpha)\),
і, за рівнянням (1.16), час проходження рим відстані l між точками А і С:
| \( {t}=\sqrt{\frac{2l}{g(\sin\alpha-\mu\cos\alpha)}}\). | (2) |
Згідно з отриманим виразом, цей час руху бруска формально залежить від двох величин – α і l. Але l = l0/cosα, де відстань між точками В і С l0 = const. Тож величина t виражається, як
$t\left( \alpha \right)$ = $\sqrt{\frac{2{{l}_{0}}}{g\cos \alpha \left( \sin \alpha -\mu \cos \alpha \right)}}$,
і залежить тільки від кута α. Характер цієї залежності визначається поведінкою функції в знаменнику
| \( {f}(\alpha)=\cos\alpha (\sin\alpha-\mu\cos\alpha )\), | (3) |
котру не важко якісно проаналізувати так, як у попередній задачі. При малих кутах збільшення α спричинює зростання f(α) і зменшенням часу спуску. А в області великих кутів при збільшенні α функція f(α) спадає, і час спуску збільшується. Отже, при деякому куті α = αm функція f(α) має максимум, і час спуску бруска є найменшим.
За канонами математики, щоби визначити величину αm, треба знайти й прирівняти до нуля похідну f′(α):
\( {f}^{\prime}(\alpha)=-\sin\alpha (\sin\alpha-\mu\cos\alpha )+\cos\alpha (\cos\alpha+\mu\sin\alpha){=}\)
\( {=}\sin^{2}\alpha+\cos^{2}\alpha+2\mu\sin\alpha\cos\alpha=\cos{2}\alpha+\mu\sin{2\alpha}\), отже,
\( \cos{2\alpha_{m}}+\mu\sin{2\alpha_{m}}={0}\), \(\Rightarrow \) $\operatorname{tg}2\alpha =-\frac{1}{\mu }$.
Звідси при μ = 0,14 шуканий оптимальний кут нахилу площини до горизонту складає 41°.
Примітка. Безпосередньо з отриманого виразу виходить αm = –41°. Це пояснюється тим, що кут між віссю ОХ і напрямком руху бруска, котрий фігурує в рівняннях (1), є від'ємним.
| Задача 2.7 |
| Задача 2.6 |
Два тягарці масою M кожен, зв'язані перекинутою через нерухомий блок ниткою, спочатку утримують на одному рівні. Потім до одного підвішують важок масою m і вивільняють систему.
Визначити:
а) прискорення a тягарців та час t, за який вони розійдуться на відстань H за відсутності ковзання нитки;
б) силу натягу нитки \( {T}_{0}\), на якій підвішено важок і силу тиску \( {F}\) на вісь блока.
|
Дано: M, m |
|
a - ? t - ? T - ? F - ? |
Розв'язання
Сили, що діють на кожне з тіл задачі, показані на рис. 2.6. Правий тягарець M взаємодіє з Землею (сила \( {M}\vec{g}\)) та з ниткою (сила \( \vec{T}_{1}\)). Так само на важок m діють сили \( {m}\vec{g}\) і \( \vec{T}_{0}\). Лівий тягарець M взаємодіє із Землею (сила \( {M}\vec{g}\)) та двома нитками (сили \( \vec{T}_{2}^{\prime},\,\vec{T}_{0}^{\prime}\) ). На блок з боку ниток діють сили \( \vec{T}_{1}^{\prime},\,\vec{T}_{2}^{\prime}\). Ця дія передається на вісь блока, створюючи силу \( \vec{F}=\vec{T}_{1}^{\prime}+\vec{T}_{2}^{\prime}\).
а) Прискорення кожного з трьох тіл визначається ІІ законом Ньютона (2.5):
| \( {M}\vec{g}+\vec{T}_{1}=M\vec{a}_{1}\), |
| \( M\vec{g}+\vec{T}_{0}+\vec{T}_{2}=M\vec{a}_{2}\), | (1) |
| \( {m}\vec{g}+\vec{T}_{0}=m\vec{a}_{2}\). |
При цьому, позаяк блок є невагомий, і ковзання нитки відсутнє, прискорення і сили натягу кожної ниток однакові: \( {T}_{1}=T_{1}^{\prime}=T_{2}=T_{2}^{\prime}={T}\), \( {T}_{0}=T_{0}^{\prime}\) і \( {a}_{1}=a_{2}={a}\). Врахувавши це, запишемо рівняння (1) у проєкціях на напрямлену вертикально вниз вісь OY нерухому відносно осі блока :
| \( {M}g-T=-M{a}\), |
| \( Mg+T_{0}-T=M{a}\), | (2) |
| \( mg-T_{0}=m{a}\). |
Для визначення величини а додамо ліві та праві частини рівнянь (2), попередньо помноживши перше на (-1):
| \( {mg}=(2M+m){a}\) \( \Rightarrow \) \( {a}=\frac{m}{2M+m}{g}\). | (3) |
Тягарці рухаються в протилежних напрямках без початкової швидкості та з однаковим прискоренням а. Тож за шуканий час кожен пройде однаковий шлях \( {l}=H/2 \). Тому, згідно з рівняннями (1.16),
\( \frac{H}{2}=\frac{at^{2}}{2}\) \( \Rightarrow \) \( t=\sqrt{\frac{H}{a}}\).
Підставивши сюди вираз (3), отримуємо шуканий час:
| \( {t}=\sqrt{\frac{2M+m}{m}\cdot\frac{H}{g}}\). | (4) |
б) Силу натягу T0 нитки, що з'єднує тягарець M із важком m, знайдемо з останнього рівняння (2), підставивши вираз (3):
\( {T}_{0}=m(g-a)=Mg\left(1+\frac{m}{2M+m}\right) \) \( \Rightarrow \) \( {T}_{0}=\frac{2Mg}{2M+m}{g} \).
Отже, сила тиску на вісь блока
\( {F}=T_{1}^{\prime}+T_{2}^{\prime}=2{T}\).
Величину T знайдемо з першого рівняння (2), підставивши вираз (3):
\( {T}=M(g+a)=Mg\left(1+\frac{m}{2M+m}\right) \) \( \Rightarrow \) \( {T}=\frac{2M(M+m)}{2M+m}{g}\).
Таким чином, шукана сила тиску на вісь блока дорівнює
\( {F}=\frac{4M(M+m)}{2M+m}{g}\).
| Задача 2.8 |
| Задача 2.7 |
На початку підйому та спуску ліфт має однакове прискорення.
Визначити
його величину a, якщо вага тіл у ліфті при підйомі в n = 1,5 рази перевищує вагу при спуску.
|
Дано: n = 1,5 |
|
a - ? |
Розв'язання
На тіло діють сила тяжіння \( {m}\vec{g}\) та нормальна реакція опори (підлоги ліфта) \( \vec{N}\) (рис. 2.7). За означенням вага тіла \( \vec{P}\) – то є сила, з якою воно діє на підлогу ліфта. Отже, за третім законом Ньютона
| \( \vec{P}=-\vec{N}\). | (1) |
Згідно з другим законом Ньютона (2.5), для кожного випадку маємо:
| \( \vec{N}_{1}+m\vec{g}=m\vec{a}_{1}\), | (2) | |
| \( \vec{N}_{2}+m\vec{g}=m\vec{a}_{2}\). |
Переписавши рівняння (2) у проекціях на напрям руху ліфта і врахувавши, що \( {a}_{1}=a_{2}={a}\), і P = N, отримаємо:
\( {P}_{1}=m(g+a)\) \( {P}_{2}=m(g-a)\) \( \Rightarrow \) \( \frac{P_{1}}{P_{2}}=\frac{g+a}{g-a}\).
Звідси, згідно з умовою \( \frac{P_{1}}{P_{2}}={n}\), дістанемо відповідь:
\( \frac{g+a}{g-a}={n}\) \( \Rightarrow \) \( {a}=\frac{n-1}{n+1}g= 2 м/с2.
| Задача 2.9 |
| Задача 2.8 |
Повітряна куля загальною масою M = 1000 кг опускається зі сталою швидкістю.
Визначити
масу баласту m, який треба скинути, аби куля почала підійматися з такою самою швидкістю, якщо архімедова сила, що діє на кулю, F = 9700 H.
|
Дано: M = 1000 кг
F = 9800 Н
|
|
m -? |
Розв'язання
За умовою, попри те, що сила тяжіння \(M\vec{g}\)
та архімедова сила $\vec{F}$, що діють на кулю, не однакові, підйом є рівномірним. Отже, їхня різниця компенсується силою опору повітря ${{\vec{F}}_{01}}$, рис. 2.8а. Це стосується й сили опору ${{\vec{F}}_{02}}$ (рис. 2.8б), що діє на кулю після скидання баласту. При цьому, через рівність швидкостей підйому та спуску, сили опору за величиною теж однакові: ${F}_{01}$ = ${F}_{02}$. Піднімальну силу \){F}\( теж можна вважати однаковою, позаяк об'єм викинутог о баласту є набагато менший за об'єм кулі. Різняться тільки сили тяжіння: \(M\vec{g}\) при опусканні та \){(M-m)}\vec{g}$$ при підйомі. При цьому в обох випадках прискорення відсутнє, отже сили є компенсовані:\(\left\{ \begin{align} & Mg\quad \quad \ \ =F+{{F}_{0}} \\ & Mg-mg=F-{{F}_{0}} \\\end{align} \right.\).
Звідси після додавання лівих і правих частини рівнянь знайдемо відповідь:
$m=\frac{2\left( Mg-F \right)}{g}=60\text{ }\text{кг.}$
Зв'язок між імпульсом і силою
|
Типовим завданням у таких задачах є визначення сил через зміну імпульсу тіла за певний проміжок часу. Тому слід пам'ятати, що зміна імпульсу тіла визначається не окремими силами, а рівнодійною всіх сил, що прикладені до нього. Досить часто розглядані сили є змінними. В такому разі зміна імпульсу тіла визначається середнім за час дії імпульсом сили, який чисельно дорівнює площі під відповідною ділянкою графіка сили F(t). |
Задача 2.9. Кулька масою m = 200г, яка падає вертикально, на момент удару об підлогу має швидкість v = 5 м/с. Після удару кулька підскакує на висоту h =80 см. Визначити зміну модуля імпульсу та модуль зміни імпульсу кульки при ударі.
Задача 2.10. Кинута вертикально вгору пластилінова кулька масою m = 100 г прилипає до стелі, маючи перед ударом швидкість v = 5 м/с. Визначити середню силу тиску F кульки на стелю, якщо час удару \( \tau \) = 0,18 с. (Примітка. Часом удару називають тривалість взаємодії тіл при зіткненні. В даній задачі це час сплющування кульки від моменту дотику до припинення руху всіх її частин).
Задача 2.11. На кульки масами m1 і m2 = 2m1, що рухались у взаємно перпендикулярних напрямах із імпульсами однакової величини р, подіяла однакова сила, котра змінила напрям руху першої кульки на протилежний без зміни величини швидкості. Визначити величину та напрям кінцевої швидкості другої кульки, якщо початкова дорівнювала v.
Задача 2.12. Ракета з початковою масою M при старті на деякий час зависає над землею. Визначити, скільки палива за одиницю часу \( \mu \) вона при цьому витрачає, якщо швидкість витоку газів відносно ракети дорівнює u.
Задача 2.13. Пучок молекул налітає перпендикулярно на закріплену пластину й пружньо (без утрати швидкості) відбивається. Концентрація молекул у пучку n = 2,5·1019см–3, маса молекули m = 3,3·10–27кг, швидкість v = 1000 м/с . Визначити тиск P пучка на пластину.
Задача 2.14. Пружна кулька, що рухається горизонтально, вдаряє у вертикальну стінку під кутом α до нормалі. Визначити, під яким кутом β відскочить кулька, якщо стінка: а) гладка; б) шорстка й має коефіцієнт тертя μ.
Задача 2.15. На вагон маси m = 50 т, який рухається за інерцією зі швидкістю \( {v}_{0}={10}\) м/с, починає діяти гальмівна сила, що змінюється з часом за законом \( {F}=\alpha{t}\), де \( \alpha={100}\) Н/с. Визначити час \( \tau \) руху вагона до зупинки.
| Задача 2.10 |
| Задача 2.9 |
зміну модуля імпульсу та модуль зміни імпульсу кульки при ударі.
|
Дано:
m=200г=0,2кг
v1 = 5 м/c
h = 46 см |
|
Δp -? \(\left| \Delta \vec{p} \right|\)-? |
Розв’язання
На рис. 2.9 показані вектори імпульсу кульки в момент падіння ${{\vec{p}}_{1}}$ = $m{{\vec{v}}_{1}}$ і відскоку ${{\vec{p}}_{2}}$ = $m{{\vec{v}}_{2}}$ та зміни імпульсу $\left| \Delta \vec{p} \right|$ = $m\left|{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}} \right|$. При цьому, згідно з формулою (1.19),
${{v}_{2}}=\sqrt{2gh}=4\text{ м/с}$.
Отже, маємо наступні відповіді:
Δp = m(v2 – v1) = –0,2 кг·м/с;
$\left| \Delta \vec{p} \right|$ = $m\left({{{{v}}}_{2}}+{{{{v}}}_{1}} \right)$ = 1,8 кг·м/с.
| Задача 2.10 |
| Задача 2.10 |
Кинута вертикально вгору пластилінова кулька масою m = 100 г, прилипає до стелі, маючи перед ударом швидкість v = 4,9 м/с.
Визначити
середню силу тиску F кульки на стелю, якщо час удару \( \tau \) = 0,18 с.
|
Дано: m=100г=0,1кг
v = 5 м/c
τ = 0,18 c
|
|
F -? |
Розв’язання
Прилипання є складним процесом пластичної деформації із невідомою залежністю від часу сил, які діють на кульку та на стелю. Але середню силу тиску кульки на стелю легко визначити за допомогою основних законів динаміки.
Під час удару на кульку діють сили тяжіння \( {m}\vec{g}\) та реакції опори (стелі) \( \vec{N}\), рис. 2.10. Отже, за другим законом Ньютона (5.4),
| $m\vec{g}+\vec{N}=\frac{\Delta \vec{p}}{\tau }\quad \Rightarrow \quad mg+N=\frac{\left| \Delta \vec{p} \right|}{\tau }$. | (1) |
За третім законом Ньютона шукана сила тиску кульки на стелю дорівнює реакції опори: F = N. Крім того, за час удару кулька втрачає увесь імпульс, отже,
${\left| \Delta \vec{p} \right|}$ = p = mv.
Зробивши такі підстановки в рівняння (1), знайдемо нвступну відповідь:
\( {F}=m\left(\frac{v}{\tau}-g\right) \) ≈ 1,7 Н.
| Задача 2.11 |
| Задача 2.11 |
На кульки масами m1 і m2 = 2m1, що рухались у взаємно перпендикулярних напрямах із імпульсами однакової величини р, подіяла однакова сила, котра змінила напрям руху першої кульки на протилежний без зміни величини швидкості.
Визначити
величину та напрям кінцевої швидкості другої кульки, якщо початкова дорівнювала v.
|
Дано: m2 = 2m1 v2 = v |
|
\({\vec{v}'_{2}}\)-? |
Розв'язання
Умову задачі відображує рис. 2.11-1а.
Згідно з умовою та ІІ законом Ньютона (2.4), прикладена сила спричинила однакову зміну імпульсів кульок:
\( \Delta\vec{p}_{1}=\Delta\vec{p}_{2}\),
тобто
| \({\vec{p}'_{1}}\) – \({\vec{p}_{1}}\)=\({\vec{p}'_{2}}\) – \({\vec{p}_{2}}\), |
де кінцеві величини позначені штрихом. Виразивши в цьому рівнянні імпульси через швидкості й маси, отримаємо:
| \({\vec{v}'_{1}}\) – \({\vec{v}_{1}}\)=2(\({\vec{v}'_{2}}\) – \({\vec{v}_{2}}\)). |
Звідси визначаємо вектор шуканої швидкості \({\vec{v}'_{2}}\), врахувавши, що за умовою \({\vec{p}'_{1}}\) = –\({\vec{p}_{1}}\), тож \({\vec{v}'_{1}}\) = –\({\vec{v}_{1}}\):
| \({\vec{v}'_{2}}\) = – \({\vec{v}_{1}}\) + \({\vec{v}_{2}}\). | (1) |
Модуль і напрям (кут α) вектора \({\vec{v}'_{2}}\) знайдемо із рис. 2.11-1б, який відображає вираз (1):
\({{v}'_{2}}\) = \(\sqrt{v_{1}^{2}+v_{2}^{2}}\), \(\operatorname{tg}\alpha =\frac{{{v}_{2}}}{{{v}_{1}}}\).
Отже,
\({{v}'_{2}}\) = v\(\sqrt{5}\) і α = 26,6°.
Зауважимо, що відповідь можна отримати й алгебраїчно, записавши рівняння (1) у проєкціях на осі координат:
|
v′2x = –2v, v′2y = v \( \Rightarrow \) \({{{v}'}_{2}}=\sqrt{{{\left( {{{{v}'}}_{2x}} \right)}^{2}}+{{\left( {{{{v}'}}_{2y}} \right)}^{2}}}=v\sqrt{5};\quad \alpha =\left| \operatorname{arctg}\frac{{{{{v}'}}_{2y}}}{{{{{v}'}}_{2x}}} \right|=26,6{}^\circ \). |
| Задача 2.12 |
| Задача 2.12 |
Ракета з початковою масою M при старті на деякий час "зависає" над землею.
Визначити,
скільки палива за одиницю часу \( \mu \) вона при цьому витрачає, якщо швидкість витоку газів відносно ракети дорівнює u.
|
Дано: M, u |
|
μ -? |
Розв'язання
Сила, що утримує ракету від падіння, є зумовлена тиском на стінкки камери двигуна газів, який створюють продукти згорянні палива, що схематично показано на рис. 2.12. У герметичній порожнині, як приміром у гранаті перед розривом, вказані сили є компенсовані. Проте в нижній стінкці камери згоряння двигуна ракети (рис. 2.12а) є отвір (сопло), тож її площа менша, ніж площа верхньої стінкки. Відповідно, меншою є й сила тиску газів на нижню стінкку. Як наслідок, виникає спрямована вгору реактивна сила тяги F (рис. 2.12б) рівна силі F′, яка діє на гази, що вилітають із сопла.
Нехай за невеликий проміжок часу\( \Delta{t}\) із сопла під дією сили \( {F}^{\prime}\) зі швидкістю u викидається порція газів \( масою\Delta{m}\). Тоді за другим законом Ньютона (2.3)
\( {F}^{\prime}=\frac{\Delta{mu}}{\Delta{t}}\) \( \Rightarrow \) \( {F}^{\prime}=\mu{u}\),
де \( \mu \) – витрата палива за одиницю часу.
За умовою реактивна сила \( {F}=F^{\prime}\) зрівноважує силу тяжіння, що діє на ракету, отже,
\( {M}g=\mu{u}\) \( \Rightarrow \) \( \mu=\frac{Mg}{u}\).
Примітка. Витрата пального \( \mu \) реально є досить велика, і маса ракети M стрімко зменшується. Тому в отриманій формулі величини \( \mu \) і M слід розглядати як миттєві. При цьому для забезпечення тривалого зависання ракети витрата пального має зменшуватися з часом відповідно до зменшення маси ракети. Але розрахунок залежності μ(t) і M(t) виходить за межі елементарної фізики.
| Задача 2.13 |
| Задача 2.13 |
Пучок молекул налітає перпендикулярно на закріплену пластину й пружно (без утрати швидкості) відбивається. Концентрація молекул у пучку n = 2,5·1019см–3, маса молекули m = 3,3·10–27кг, швидкість v = 1000 м/с .
Визначити
тиск P пучка на пластину.
|
Дано: m = 3,3·10-27кг v = 1000 м/с n = 2,5·1019см-3 |
|
P - ? |
Розв’язання
 При зіткненні з пластиною окрема молекула створює мікроскопічний імпульс сили типу "уколу". Але через дуже велику щільність молекул у пучку ці уколи відбуваються так часто й густо, що створюють сталу й рівномірно розподілену по поверхні силу тиску.
При зіткненні з пластиною окрема молекула створює мікроскопічний імпульс сили типу "уколу". Але через дуже велику щільність молекул у пучку ці уколи відбуваються так часто й густо, що створюють сталу й рівномірно розподілену по поверхні силу тиску.
Для її визначення виділимо на стінці ділянку площею S (рис. 2.13). Імпульс сили, що діє на пластину під час зіткнення однієї молекули, за третім законом Ньютона дорівнює імпульсу сили, що діє з боку пластини на молекулу, отже
\( {f}\Delta{t}=\left|\Delta\vec{p}\right| \),
де f – середнє значення сили взаємодії між молекулою та пластиною, \( \Delta{t}\) – тривалість зіткнення, \( \left|\Delta\vec{p}\right| \) – модуль зміни імпульсу молекули за час зіткнення. Імпульс сумарної сили F, що діє на ділянку S протягом часу \( \tau \), запишеться як
\( {F}\tau=N\left|\Delta\vec{p}\right| \),
де N – кількість зіткнень молекул з ділянкою за час \( \tau \). Звідси маємо:
| \( {F}=\frac{N}{\tau}\left|\Delta\vec{p}\right|=n_{з}\left|\Delta\vec{p}\right| \), | (1) |
де \( {n}_{з}\) –кількість зіткнень за одиницю часу.
При цьому, позаяк зіткнення відбуваються без утрати швидкості, \( \Delta\vec{p}=-2\vec{p}\) (рис. 2.13), і
| \( \left|\Delta\vec{p}\right|=2p=2{mv}\). | (2) |
Відтак лишається визначити величину \( {n}_{з}\). Для цього на площинці S як на основі побудуємо циліндр висотою \( \Delta{l}\). Усі \( {N}=nS\Delta{l}\) молекул (n – концентрація), що містяться в ньому, стикаються з площинкою S за час \( \tau=\frac{\Delta{l}}{v}\) (\( {v}\) – швидкість руху молекул). Тож кількість зіткнень за одиницю часу складає
\( {n}_{з}=\frac{N}{\tau}=\frac{nS\Delta{l}}{(\Delta{l}/v)}={nSv}\).
Підставивши цей вираз і вираз (2) у формулу (1), дістанемо:
\( {F}=2nmv^{2}{S}\).
Відтак, поділивши силу F на площу S, отримаємо відповідь:
\( {P}=2nmv^{2}=1,65\cdot{10^{5}}\) Па.
Пружна кулька, що рухається горизонтально, вдаряє у вертикальну стінку під кутом α до нормалі.
Визначити,
під яким кутом β відскочить кулька, якщо стінка:
а) гладка;
б) шорстка й має коефіцієнт тертя μ.
|
Дано: μ α |
|
β – ? |
Розв'язання
При косому ударі кульки в стінку, строго говорячи, завжди є присутнє тертя. Тому сила \( \vec{R}\) (рис. 2.14), з якою стінка діє на кульку, складається із сили нормального тиску \( \vec{N}\) та сили тертя $\vec{F}$:
\( \vec{R}\) = \( \vec{N}\) + $\vec{F}$.
Відповідно, за другим законом Ньютона (2.4) зміна імпульсу кульки $\vec{p}=m\vec{v}$ за час удару \(\tau \) визначається рівнянням:
|
$\vec{N}+\vec{F}=m\left( {{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}} \right)$. |
Отже, поклавши F = μN, отримаємо наступну систему рівнянь для проєкцій на горизонтальні осі (рис. 2.14):
|
OX: Nτ = m(v2cosβ + v1cosα) OY: –μNτ = m(v2sinβ – v1sinα), |
(1) |
і після почленного ділення
|
$\mu =\frac{{{v}_{1}}\sin \alpha -{{v}_{2}}\sin \beta }{{{v}_{1}}\cos \alpha +{{v}_{2}}\cos \beta }$. |
(2) |
Позаяк кулька є пружньою, процеси її стискання та відновлення форми, що зумовлені силою \( \vec{N}\), є віддзеркаленням один одного. Через це нормальні складові її швидкостей підльоту та відскоку збігаються:
|
v1cosα = v2cosβ \(\Rightarrow \) \( {v}_{2}=v_{1}\frac{\cos\alpha}{\cos\beta}\). |
(3) |
Зробивши таку заміну у виразі (2), після елементарних перетворень дістанемо:
|
$\mu =\frac{tg\alpha -tg\beta }{2}$, |
і загальний вираз, який визначає кут відбивання кульки від стінки:
| \( \mathrm{tg}\beta=\mathrm{tg}\alpha-2\mu \). | (4) |
а). Якщо стінка є гладка, то μ = 0 і, як випливає з виразів (4) і (3), β = α і v2 = v1. Отже, за відсутності тертя пружна кулька від нерухомої стінки відбивається дзеркально – під таким самим кутом і з такою самою швидкістю, що й падає. (До речі, такого висновку можна дійти й “без математики”, спираючись на закон збереження енергії).
б). При μ ≠ 0 ті ж таки співвідношення (3) і (4) дають v2 < v1 і β < α, тобто від шорсткої стінки кулька відбивається з меншою швидкістю і під меншим кутом, аніж падає. Це пояснюється тим, що на самому початку для сили тертя було взято звичну величину F = μN, при якій в процесі зіткнення кулька ковзає по стінці (див. п. 2.3), тож і гальмується. При цьому сила тертя зменшує тільки паралельну до стінки складову швидкості, що призводить до зменшення кута відскоку β. Але звертає на себе увагу наступне. При tgα < 2μ вираз (4) втрачає зміст, хоча є очевидним, що кут α може мати будь-яку величину в інтервалі 0 ≤ α ≤ 90°. Проте цей "парадокс" теж має пояснення. При зменшенні кута α сила нормального тиску N = Rcosα та гальмівна сила F = μN зростають, так що при tgα = 2μ кулька перед відривом перестає ковзати (v2sinα = 0) і відлітає по нормалі до стінки (β = 0).
Таким чином, при відбиванні кульки від шорсткої стіни відповідь задачі є подвійною:
β =arctg(tgα – 2μ), tgα > 2μ;
β = 0, tgα ≤ 2μ.
| Задача 2.15 |
| Задача 2.15 |
На вагон маси m = 50 т, який рухається за інерцією зі швидкістю \( {v}_{0}={10}\) м/с, починає діяти гальмівна сила, що змінюється з часом за законом \( {F}=\alpha{t}\), де \( \alpha={100}\) Н/с.
Визначити
час \( \tau \)руху вагона до зупинки.
|
Дано: m = 50 т v0 = 10 м/с F =αt α = 100 Н/с |
|
\( \tau \)-? |
Розв'язання
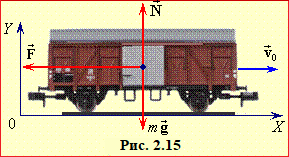
На вагон діють компенсовані сили тяжіння \(m\vec{g}\) і реакції опори \(m\vec{N}\) та гальмівна сила \(\vec{F}\) (рис. 2.15), яка й визначає його рух.
В умові по суті задано зміну імпульсу вагона, що за рівнянням (2.4а) дорівнює імпульсові діючих на нього сил:
| mv0 = І. | (1) |
Отже, треба встановити зв'язок між величиною І та часом руху τ вагона до зупинки. Але знайти його прямо без застосування вищої математики не можна, бо сила F є змінною. Проте це можна зробити за допомогою графіка залежності F(t), (рис. 2.15-1). Для цього подумки поділимо весь час τ на малі інтервали Δti, і приймемо, що в межах кожного сила має сталу величину Fi. Тоді імпульс сили за один інтервал Δti наближено визначається площею відповідної смужки
ΔIi ≈ Fi·Δti,
а за весь час τ – сумарною площею всіх смужок:
| I ≈ \(\sum{{{F}_{i}}}\Delta {{t}_{i}}\). | (2) |
Зрозуміло, що цей вираз буде тим точнішим, чим вужчими будуть смужки, і стане математично точним, коли смужки стануть гранично вузькими (Δti → 0). При цьому утворені при поділі сходинки зникнуть, і величина (2) стане рівною площі утвореного графіком F(t) трикутника:
\(I=\frac{1}{2}\alpha \tau \cdot \tau \).
Підставивши отримане значення I у вираз (1), знайдемо відповідь:
\( \tau=\sqrt{\frac{2mv_{0}}{\alpha}}={100}\) c.
Рівномірний рух по колу
У задачах на рівномірний рух по колу одним з найважливіших етапів розв'язування є аналіз того, які взаємодії даного тіла з іншими створюють "доцентрову силу", та складання рівняння руху за другим законом Ньютона.
При рівномірному русі тіла по колу напрямки сил, що діють на нього, прискорень та швидкостей неперервно змінюються. Тому використовувати при розв'язуванні нерухому систему відліку із фіксованим напрямком координатних осей є незручно. Набагато краще розглядати рух в кожен момент у проєкціях на радіус колової траєкторії та (при необхідності) на якийсь інший зручний напрямок, приміром, дотичну до траєкторії.
Задача 2.16. Літак виконує "мертву петлю", рухаючись зі сталою швидкістю у вертикальній площині по коловій траєкторії радіуса R = 1 км. Визначити швидкість v літака, якщо в ньому максимальна вага пілота в \( \eta={3}\) рази перевищує мінімальну.
Задача 2.17. На трасі мотокросу спортсмен долає пагорб у вигляді сферичного купола радіусом R = 40 м. Визначити, при якій найменшій швидкості \( {v}_{min}\) мотоцикл на вершині пагорба відірветься від землі.
Задача 2.18. Маленьку кульку, підвішену на нитці довжини l, рівномірно обертають у горизонтальній площині по колу радіусом R << l. Визначити період обертання кульки T.
Задача 2.19. Байкер рухається по коловому треку з кутом нахилу полотна до горизонту α = 15°. Максимальний радіус треку R = 50 м, коефіцієнт тертя між колесами та покриттям треку μ = 0,6. Визначити: 1. Максимальну швидкість \( {v}_{m}\), яку може розвинути байкер. 2. Кут \( \vartheta \), на який він має відхилятися від вертикалі, аби не впасти.
Задача 2.20. Вага тіла на полюсі планети є на η = 5% більша, ніж на екваторі. Визначити середню густину речовина планети ρ, якщо тривалість доби на ній складає T = 10 год.
| Задача 2.16 |
| Задача 2.16 |
Літак виконує "мертву петлю", рухаючись зі сталою швидкістю у вертикальній площині по коловій траєкторії радіуса R = 1 км.
Визначити
швидкість v літака, якщо в ньому максимальна вага пілота в \( \eta={3}\) рази перевищує
мінімальну.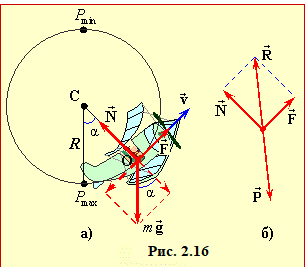
|
Дано: R = 1 км η = 3 |
|
v - ? |
Розв'язання
На рис. 2.16а схематично показано сили, що діють на пілота в літаку: сила тяжіння \( {m}\vec{g}\) та спрямована до центра траєкторії сила тиску сидіння \( \vec{N}\) і перпендикулярна до неї сила тиску спинки крісла \( \vec{F}\), що разом створюють силу реакції опори \(\vec{F}_{\text{оп}} = \vec{N} + \vec{F}\), рис. 2.16б. За третім законом Ньютона вага пілота (сила тиску на крісло) \(\vec{P} = – \vec{F}_{\text{оп}}\) і має модуль
| \( {P}=\sqrt{N^{2}+F^{2}}\). | (1) |
Далі, аби врахувати задану величину η, слід визначити сили N і F. Для цього запишемо другий закон Ньютона (2.5)
| \( {m}\vec{g}+\vec{N}+\vec{F}=m\vec{a}\) | (2) |
і врахуємо, що швидкість літака v = const, тож прискорення \( \vec{a}\) є доцентровим, тобто спрямоване радіально і має величину \( {a}=\frac{v^{2}}{R}\). В такому разі, записавши рівняння (2) у проєкціях на радіус та на дотичну до траєкторії, отримаємо:
| \( {N}=\frac{mv^{2}}{R}+mg\cos\alpha \), | ||
| \( {F}=mg\sin\alpha \). |
Звідси, згідно з (1), маємо:
| \( {P}=\sqrt{{{\left( \frac{m{{v}^{2}}}{R}+mg\cos \alpha \right)}^{2}}+{{\left( mg\sin \alpha \right)}^{2}}}\) |
і, після розкриття дужок,:
\( {P}=\sqrt{\left(\frac{mv^{2}}{R}\right)^{2}+(mg)^{2}+2\frac{m^{2}gv^{2}}{R}\cos\alpha}\).
Максимальній та мінімальній вазі пілота відповідають значення cosα = ±1 (нижня та верхня точки траєкторії) і величини:
| \(\left\{ \begin{matrix} {{P}_{\max }}=\frac{m{{v}^{2}}}{R}+mg, \\ {{P}_{\min }}=\frac{m{{v}^{2}}}{R}-mg. \\\end{matrix} \right.\) | (3) |
Відтак, поділивши праві та ліві частини цих виразів і врахувавши умову \( {P}_{max}/P_{min}=\eta \), після нескладних перетворень знайдемо:
\( {v}=\sqrt{\frac{\eta+1}{\eta-1}gR}= {504}\) км/год.
Із другого рівняння (3) випливає, що при швидкості літака
| \( {v}=\sqrt{gR}\) = 360 км/год, | (4) |
вага пілота у верхній точці траєкторії дорівнює нулю, тобто він перебуває в стані невагомості.
| Задача 2.17 |
| Задача 2.17 |
На трасі мотокросу спортсмен долає пагорб у вигляді сферичного купола радіусом R = 40 м.
Визначити,
при якій найменшій швидкості \( {v}_{min}\) мотоцикл на вершині пагорба відірветься від землі.
|
Дано: R = 40 м |
|
vmin - ? |
Розв'язання
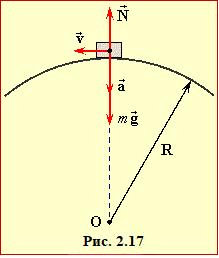
Вершину пагорба мотоцикліст проходить із доцентровим прискоренням a = (v2/R), що створюється силою тяжіння \( {m}\vec{g}\) та протилежно спрямованою реакцією опори \( \vec{N}\) (рис. 2.17). Тож за другим законом Ньютона (2.5)
| \( {mg}-N=\frac{mv^{2}}{R}\). | (1) |
Звідси випливає, що при збільшенні швидкості сила N, тож і сила тиску на пагорб (вага мотоцикла зі спортсменом), зменшуються і при певній величині vmin набувають нульового значення. А це означає, що мотоцикл відривається від землі. Таким чином, поклавши N = 0 в рівнянні (1), отримаємо
\( {mg}=\frac{mv_{min}^{2}}{R}\) \( \Rightarrow \)
|
${{v}_{\min }}=\sqrt{gR}$ |
(2) |
Обчислення дає:
vmin= 20 м/с = 72 км/год.
У момент відриву мотоцикл із мотоциклістом перестають тиснути на опору, тобто переходять у стан невагомості, як і пілот у попередній задачі при проходженні верхньої точки траєкторії.
| Задача 2.18 |
| Задача 2.18 |
Маленьку кульку, підвішену на нитці заданої довжини l, рівномірно обертають у горизонтальній площині по колу радіусом R<<l.
Визначити
період обертання кульки T.
|
Дано: l |
|
Т - ? |
Розв'язання
При рівномірному русі кульки із швидкістю v по колу радіуса R період обертання дорівнює
| \( {T}=\frac{2\pi{R}}{v}\), | (1) |
Кулька рухається під дією сил тяжіння \( {m}\vec{g}\) та натягу нитки \( \vec{F}_{\text{н}}\), рівнодійна яких \(\vec{F}\) має модуль F = mgtgφ (рис. 2.18) і створює прискорення a = gtgφ. Це прискорення є доцентровим і визначається формулою (1.28), отже
| g·tgφ = \( \frac{v^{2}}{R}\). | (2) | |
Позаяк за умовою R<<l, кут φ є малим, тож у виразі (2) можна покласти tgφ = (R/l). Тоді
\(\frac{gR}{l}=\frac{{{v}^{2}}}{R}\) \( \Rightarrow \) \(v=R\sqrt{\frac{g}{l}}\),
І з виразу (1) випливає наступна відповідь:
|
\(T=2\pi \sqrt{\frac{l}{g}}\). |
Отриманий вираз збігається з формулою періоду малих коливань математичного маятника, а нитка описує конус. Тому кульку на нитці, що обертається по колу в горизонтальній площині, називають конічним маятником.
| Задача 2.19 |
| Задача 2.19 |
Байкер рухається по коловому треку з кутом нахилу полотна до горизонту α = 15°. Максимальний радіус треку R = 50 м, коефіцієнт тертя між колесами та покриттям треку μ = 0,6.
Визначити:
1. Максимальну швидкість \( {v}_{m}\), яку може розвинути байкер.
2. Кут \( \vartheta \), на який він має відхилитися від вертикалі, аби не впасти.
|
Дано: α = 15° μ = 0,6 R = 50 м |
|
vm - ? η - ? |
Розв'язання
1. На байк діють сили тяжіння \( {m}\vec{g}\) (m – сумарна маса) і нормальної реакції опори \( \vec{N}\) та поперечна сила тертя\( \vec{F}\), що утримує його на коловій траєкторії, рис. 2.19a. (Діє ще й не показана поздовжня сила тертя, що є силою тяги і для розв'язування задачі не потрібна).
Під дією вказаних сил байк в горизонтальній площині по колу з доцентровим прискоренням \( \vec{a}\), модуль якого визначається швидкістю байка та радіусом траєкторії, як \( {a}=v^{2}/r\), (Розділ 1, ф-ла (1.28)). Отже, за ІІ законом Ньютона
\( {m}\vec{g}+\vec{N}+\vec{F}=m\vec{a}\),
і в проєкціях на осі координат
| \(\left\{ \begin{matrix} N\sin \alpha +{{F}}\cos \alpha =\dfrac{m{{v}^{2}}}{r},\ \ \ \ \ \\ -mg-{{F}}\sin \alpha +N\cos \alpha =0. \\\end{matrix} \right.\) | (1) |
Із першого рівняння системи випливає, що максимальна можлива швидкість руху байка без зісковзування vm відповідає радіусу траєкторії r = R і максимальній можливій силі тертя спокою F = μN (див. п. 2.3). Підставивши ці вирази в рівняння (1), отримаємо:
\(\left\{ \begin{matrix} N\left( \sin \alpha +\mu \cos \alpha \right)=\dfrac{mv_{m}^{2}}{R} \\ N\left( \cos \alpha -\mu \sin \alpha \right)=mg.\ \ \ \\\end{matrix} \right.\),
Звідси після нескладних перетворень знайдемо:
| \( {v}_{m}=\sqrt{gR\frac{\mathrm{tg}\alpha+\mu}{1-\mu\mathrm{tg}\alpha}}\). | (2) |
Обчислення дають:
vm = 22,75 м/с ≈ 82 км/год.
2. При знайденій швидкості байк буде рухатися без проковзування. Але лише лише цього для стійкого положення байкера на траєкторії є замало. З рис. 19б видно, що відносно центра ваги системи О сили \( \vec{N}\) і \( \vec{F}\) створюють обертові моменти протилежного знаку (див. Розділ 5). Тому при довільному куті відхилення від вертикалі байкера буде "завалювати" в той, чи інший бік. Тож він, аби не впасти, має відхилятися від вертикалі на такий кут \( \vartheta \) = α + φ, при якому вказані моменти мають однакову величину, отже,
| Nl1 = Fl2 \( \Rightarrow \) $\frac{F}{N}=\dfrac{{{l}_{1}}}{{{l}_{2}}}=\operatorname{tg}\varphi $ |
Позаяк при швидкості vm сила F = μN, то tgφ = μ, і необхідний кут відхилення байкера від вертикалі при максимальній швидкості руху складає:
| \( \vartheta=\alpha+\varphi=\alpha+\mathrm{arctg}\mu \). |
(3) |
Обчислення дають:
\( \vartheta=15^{\circ}+\mathrm{arctg}0,6=46^{\circ}\).
Таким чином, одночасне виконання умов (2) і (3) забезпечує рух байкера без падіння, а максимальна можлива швидкість визначається параметрами треку та коефіцієнтом тертя μ між шинами байка та полотном треку. При цьому існує два граничні випадки:
а). Полотно треку горизонтальне (\( \alpha={0}\)). В такому разі максимальна швидкість складає \( {v}_{m}=\sqrt{\mu{gR}}={17}\) м/с і суттєво поступається знайденій вище величині. Саме тому для покращення швидкісних характеристик треку полотно роблять похилим.
б). Коли величина \( \mu\mathrm{tg}\alpha \) у формулі (2) наближається до одиниці, а кут \( \alpha \) — до значення \( \alpha=\mathrm{arctg}(1/\mu)=\mathrm{arcctg}{\mu}\), максимальна можлива швидкість спортсмена необмежено зростає. Отже, поперечного проковзування коліс не буде ні в за якому разі. При цьому, як видно з формули (3),
\( \vartheta=\mathrm{arcctg}\mu+\mathrm{arctg}\mu=\frac{\pi}{2}\),
тобто спортсмен з байком будуть розташовані в горизонтальній площині. В давнину це демонстрували в цирках шапіто в атракціоні під назвою "Перегони по вертикальній стіні".
| Задача 2.20 |
| Задача 2.20 |
Вага тіла на полюсі планети є на η = 5% більша, ніж на екваторі; тривалість доби T = 10 год.
Визначити
середню густину речовина планети ρ.
|
Дано: T = 10 год η = 5% |
|
ρ – ? |
Розв'язання
Насамперед згадаймо, що вага \( \vec{P}\) є силою тиску тіла на горизонтальну опору внаслідок гравітації. Відповідно, на саме тіло діють сили всесвітнього тяжіння \( \vec{F}\) та реакції опори \( \vec{N}\), рис. 2.20. При цьому за третім законом Ньютона P = N.

Розглянемо вказані сили в інерціальній системі відліку, пов'язаній з центром планети. На полюсі тіло перебуває в спокої, отже, \( \vec{F}\) + \( \vec{N}\) = 0, і вага тіла
|
Pп = F |
(1) |
На екваторі тіло через добове обертання планети рухається по колу і має доцентрове прискорення \( \vec{a}\). Тож
| \( {F}-{P}_{е}=m{a}\) \( \Rightarrow \) \({{P}_{\operatorname{e}}}=F-ma\), |
(2) |
тобто добове обертання планети є причиною зменшення ваги тіла на екваторі.
Позаяк за умовою Pп – Pe =ηPп, то з рівнянь (1) і (2) маємо:
ηF = ma,
де величини F і а визначаються формулами (2.6) і (1.28), відповідно. Отже,
\(\eta \frac{GM}{{{R}^{2}}}={{\omega }^{2}}R\).
Звідси, виразивши масу планети через густину ρ, як M=(4/3)πR3 ρ , та кутову швидкість через тривалість доби, як ω = 2π/Т , отримаємо відповідь:
\( \rho=\frac{3\pi}{\eta{GT^{2}}}\) ≈ 2,2·1о3 кг/м3.
Нагадування. При обчисленнях не забувайте всі величини виражати в основних одиницях.
Задачі для самостійної роботи
Запропоновані задачі стосуються тем:
- Прямолінійний рух одного тіла та зв'язаних тіл
- Зв'язок між імпульсом і силою
- Динаміка рівномірного руху по колу
У наведених відповідях прийнято g = 10 м/с2.
Прямолінійний рух одного тіла та зв'язаних тіл
Рівень А
|
2.21. |
Двоє хлопчиків тягнуть за динамометр у протилежні боки із силою F = 100 Н кожен. Що показує динамометр? [100 Н] |
|
2.22. |
Через блок перекинуто нитку з прив'язаними гирями масою по 0,5 кг . Визначити силу натягу нитки.[5 Н] |
|
2.23. |
З якою силою притягаються один до одного два штучні супутники Землі масою 2,5 т кожен при наближенні один до одного на відстань 100 м? [≈42 нН] |
|
2.24. |
Визначити масу гирі, яку треба підвісити до пружини, аби вона розтяглася на 3 см. Жорсткість пружини 900 Н/м. [2,7 кг] |
|
2.25. |
Маса легковика m1 = 1 т, а вантажівки m2 = 8 т. Визначити відношення їхніх прискорень a1/a2, якщо сила тяги двигуна у вантажівки вдвічі більша, ніж у легковика. [4] |
|
2.26. |
Після того, як дві заряджені кульки поклали на гладку горизонтальну поверхню й відпустили, вони почали розлітатись із прискореннями a1 = 1 см/с2 і a2 = 1 м/с2. Як співвідносяться їхні маси? [(m1/m2) = 100] |
|
2.27. |
Яка сила має діяти на тіло масою 5 кг, аби воно рухалося вертикально вниз з прискоренням 3 м/с2? [35 Н] |
|
2.28. |
Під дією деякої сили одне тіло рухається з прискоренням 2,0 м/с2 , а інше — 3,0 м/с2. З яким прискоренням рухатимуться тіла під дією цієї сили, якщо їх з'єднати? [1,2 м/с2] |
|
2.29. |
Яким буде прискорення автомобіля на горизонтальній дорозі після вимикання двигуна при коефіцієнті опору μ ? [–µg ] |
|
2.30. |
Брусок рівномірно тягнуть за мотузку по горизонтальній дошці, прикладаючи поздовжню силу 1,5 Н. Визначити вагу бруска, якщо коефіцієнт тертя між ним і дошкою дорівнює 0,3. [5 Н] |
|
2.31. |
Авто рухається з прискоренням 0,6 м/с2. Визначити, яким воно стане після вимикання двигуна, якщо середня сила опору складає 25% сили тяги двигуна. [–0,2 м/с2] |
|
2.32. |
Тіло вільно ковзає з прискоренням 25 см/с2 по гладкій похилій площині. Знайти її кут нахилу до горизонту. [14,5°] |
|
2.33. |
Під яким кутом до горизонту встановиться поверхня води у відрі на візку, коли він почне рухатися горизонтально з прискоренням 1,5 м/с2?[\(\approx{8,5}^{\circ}\)] |
|
2.34. |
Знайти величину та напрям прискорення літака масою 20 т при злеті, якщо на мить відриву від злітної смуги підйомна сила крил дорівнювала 207 кН, а сили тяги двигуна та опору, відповідно, 20 кН і 10 кН. [≈0,6 м/с2; 35° до горизонту] |
Рівень Б
|
2.35. |
Через блок перекинули нитку з двома гирями масою по 200 г на кінцях. Яку вертикальну силу треба прикласти до однієї з гир, аби вона почала рухатись з прискоренням 50 см/с2? [0,2 Н] |
|
2.36. |
Два тягарці масою по 120 г висять на одному рівні на нитці, що перекинута через блок. Знайти відстань, на яку вони розійдуться та якої швидкості набудуть протягом 2 с, якщо за один потягти вниз із сталою 48 мН. [80 см; 40 см/с] |
|
2.36. |
Людина жердиною відштовхує від причалу баржу масою 300 т, прикладаючи протягом 30 c зусилля 400 Н. На яку відстань від причалу відійде баржа за цей час ? [0,6 м] |
|
2.37. |
Тіло масою 2 кг рухається з прискоренням 15 см/с2 по горизонтальній поверхні з коефіцієнтом тертя 0,05. Знати прикладену до тіла силу, коли вона діє: а) горизонтально; б) вгору під кутом 30° до горизонту? [1,3 H; 1,46 H] |
|
2.38. |
Тілу, що лежить на горизонтальній поверхні, поштовхом надали швидкості 3 м/c. Визначити коефіцієнт тертя між тілом та поверхнею, якщо воно пройшло до зупинки шлях 3 м. [0,15] |
|
2.39. |
Аби магніт масою 50 г, що "прилип" до вертикальної сталевої плити, рівномірно ковзав униз, до нього треба прикласти вздовж плити силу 1,5 H. Визначити: а) силу тиску магніту на плиту; б) силу, потрібну для рівномірного пересування магніту вгору. Коефіцієнт тертя між магнітом і плитою 0,2. [10 H; 2,5 H] |
|
2.40. |
Автомобіль рухається з незмінною швидкістю 72 км/год спочатку за, а потім проти вітру, швидкість якого дорівнює 15 м/с. У скільки разів сила опору повітря на зворотньому шляху є більшою, якщо вона лінійно залежить від швидкості автомобіля відносно повітря. [49] |
|
2.41. |
Вантаж масою 1,0 кг лежить на похилій площині. Яка сила тертя діє на нього, якщо нормальна реакція площини складає 6,0 Н. [8 Н] |
|
2.42. |
По похилій площині, нахиленій під кутом \(\alpha\) до горизонту, тіло ковзає рівномірно. За який час t воно зісковзне з висоти h, рухаючись по такій самій площині нахиленій до горизонту під кутом \(\beta\) ? $\left[ t=\sqrt{\frac{2h}{g}\cdot \frac{\cos \alpha }{\sin \beta \sin \left( \beta -\alpha \right)}},\quad \beta >\alpha \right]$ |
|
2.43. |
Визначити, за який час тіло зісковзує з гірки з кутом нахилу до горизонту 45° і висотою h = 2 м, якщо граничний кут нахилу, при якому тіло ще перебуває в рівновазі, складає 30°. [≈1,4 c] |
|
2.44. |
Тіло зісковзує без тертя з вершини похилої площини. При цьому його середня швидкість за перші 0,5 с є на 2,45 м/с менша, ніж за перші 1,5 c. Знайти кут нахилу площини до горизонту. [30°] |
| 2.45. |
Аби утримувати сани на схилі гори з ухилом 0,2, треба прикладати вздовж схилу силу 50 Н, а щоби рухати їх угору, її необхідно збільшити на 100 H. З яким прискоренням почнуть спускатися сани, якщо їх вивільнити? [0,1 м/с2] |
| 2.46. |
Тіло лежить на довгій дошці, нахиленій під кутом \(4^{\circ}\) до горизонту. Визначити: а) граничне значенні коефіцієнта тертя, при якому тіло почне ковзати по площині; б) прискорення тіла та час проходження ним відстані 10 м при коефіцієнті тертя 0,03; в) швидкість тіла наприкінці спуску. [а) 0,07; б) 0,39 м/с2, 22,6 с; в) 2,8 м/с] |
| 2.47 |
|
|
2.48. |
До одного з двох з'єднаних ниткою брусків масами 2 кг і 3 кг, які знаходяться на горизонтальній поверхні з коефіцієнтом тертя 0,4, прикладено силу 40 H під кутом \(30^{\circ}\) до горизонту. Визначити прискорення брусків і натяг нитки, якщо силу прикладено: а) до першого; б) до другого бруска. [а) 4,5 м/с2, 25,5 Н; б) 4,5 м/с2, 17,0 Н] |
|
2.49 |
Через блок перекинуто нитку з прикріпленими до кінців важками. Знайти відношення мас важків, якщо вони рухаються з прискоренням a = 0,2g (g – прискорення вільного падіння). [2 : 3] |
|
2.50. |
Мідний (ρ = 9 г/см3) брусок довжиною L = 50 см горизонтально рухається у поздовжньому напрямі з прискоренням a = 2 м/с2 . Знайти механічну напругу σ, що виникає в бруску на відстані l = 30 см від переднього кінця. [σ = ρ(L – l)a = 3,6 кПа] |
|
2.51. |
На початку підйому та спуску ліфт має однакове прискорення. Знайти його величину, якщо вага людини при цьому відрізняється в 3 рази? [4,9 м/с2] |
|
2.52. |
До стелі ліфта, що рухається рівноприскорено, на мотузці підвішено тіло масою 1 кг, з'єднане ниткою з тілом маси 2 кг. Знайти натяг мотузки, якщо натяг нитки складає 10 H. [15 H] |
Рівень В
|
2.53. |
М’яч вільно падає з великої висоти на горизонтальну поверхню й пружно (без утрати швидкості) відбивається. Знайти прискорення м’яча одразу після відскоку. [$2\vec{g}$] |
|
2.54. |
Спринтер прискорюється тільки на перших 20 м стометрівки. При якому коефіцієнті зчеплення (тертя) k взуття з біговою доріжкою він не зможе подолати дистанцію краще, ніж за 12 с? [k < 0,14] |
|
2.55. |
По похилій площині з кутом нахилу \(20^{\circ}\) до горизонту пускають вгору кульку масою 100 г. Визначити силу опору, що діє на кульку, якщо час її спуску є вдвічі більший, ніж час підйому. [6 H] |
|
2.56. |
На похилій площині з кутом нахилу \(\alpha\) до горизонту і коефіцієнтом тертя \(\mu\) лежить ящик маси m. Яку величину має мати і під яким кутом β до площини бути спрямована найменша сила Fmin , потрібна для пересування ящика вгору? $\left[ {{F}_{\min }}=\frac{mg\left( \sin \alpha +\mu \cos \alpha \right)}{\sqrt{1+{{\mu }^{2}}}};\quad \beta =\operatorname{arctg}\mu \right]$
|
|
2.57. |
Бруски з масами m1 = 1 кг і m2 = 1,5 кг знаходяться на горизонтальній поверхні (рис. 2.57). Коефіцієнт тертя між брусками \(\mu_{1}=0,4\), а між бруском m2 і поверхнею \(\mu_{2}=0,1\). З яким прискореннями рухатимуться бруски під дією сили F = 5 H, яка є прикладена під кутом $\vartheta $ = 30° до горизонту? [1,33 м/с2; 0,33 м/с2;] . |
|
2.58. |
Два бруски лежать один на одному. Маса верхнього бруска 2 кг, нижнього – 1 кг. Коефіцієнт тертя між брусками 0,25, а між нижнім поверхнею 0,5. З яким прискоренням верхній брусок буде рухатись відносно нижнього та відносно поверхні стола, якщо до нижнього прикласти горизонтальну силу 20 H.? [2,5 м/с2; 7,4 м/с2] |
|
2.59. |
На краю дошки масою 1 кг, яка лежить на гладкій горизонтальній поверхні, знаходиться брусок маси 200 г. Яку силу необхідно прикласти до бруска вздовж дошки, аби він зіскочив на момент, коли дошка переміститься на чотири довжини? Коефіцієнт тертя між бруском і дошкою 0,6. [1,5 H] |
|
2.60. |
Аби зрушити ящик масою M, людина масою m тягне його на себе під кутом до горизонту. Коефіцієнти тертя між підлогою та ящиком і між людиною та підлогою однакові й становлять \(\mu\). Яку силу має прикладати людина, аби тягти ящик? $\left[ F\ge \left( {g}/{2}\; \right)\sqrt{{{\mu }^{2}}{{\left( M+m \right)}^{2}}+{{\left( M-m \right)}^{2}}} \right]$ |
|
2.61. |
|
|
2.62. |
$\left[ {{a}_{1}}=\frac{\left| 2{{m}_{1}}-{{m}_{2}} \right|}{2{{m}_{1}}+\left( {{{m}_{2}}}/{2}\; \right)}g;\quad {{a}_{2}}=\frac{{{a}_{1}}}{2} \right]$
|
|
2.63. |
$\left[ \frac{4{{m}_{1}}{{m}_{2}}+{{m}_{0}}\left( {{m}_{1}}-{{m}_{2}} \right)}{{{m}_{1}}{{m}_{2}}+{{m}_{0}}\left( {{m}_{1}}+{{m}_{2}} \right)} \right]$g
|
|
2.64. |
На двох зіставлених похилих площинах із кутами нахилу 45° і 30° до горизонту знаходяться два однакові тягарці масою по 1 кг, які зв'язані ниткою, що перекинута через блок у вершині площин. Коефіцієнт тертя між тягарцями та площинами складає 0,1. Визначити: а) прискорення тягарців; б) силу натягу нитки; в) сила реакції осі блока. [а) 0,25 м/с2; б) 6 Н; в) 7,5 Н] |
Зв'язок між імпульсом і силою
Рівень А
|
2.65. |
Кулька масою 100 г, що рухається рівномірно, за час 0,5 хв обходить рівносторонній трикутник, долаючи шлях 4,5 м. Знайти величину (модуль) зміни імпульсу кульки та зміну його величини за час руху. [1,5·10–2 кг·м/с; 0] |
|
2.66. |
Футболіст, що б'є по нерухомому м'ячу масою 0,5 кг, надає йому швидкості 20 м/с. Знайти середню силу удару, якщо він триває 0,25 с. [40 H] |
|
2.67. |
Кулька маси 5 г, що летіла зі швидкістю 5 м/с, перпендикулярно вдарила у вертикальну стінку й пружно (без зміни швидкості) відбилася. Визначити середню силу удару, якщо контакт кульки зі стінкою тривав 50 мc. [1 H] |
|
2.68. |
Дві кульки масою по 20 г, які рухаються із однаковою швидкістю 10 м/с, пружно (без зміни швидкості) стикаються й розлітаються в протилежних напрямках. Знайти силу взаємодії кульок, якщо контакт між ними тривав о,02 с. [20 Н] |
|
2.69. |
Потяг масою 500 т, що мав швидкість 54 км/год, після припинення тяги зупинився через 0,5 хв. Визначити силу опору рухові потяга. [0,25 МН] |
Рівень Б-В
|
2.70. |
Тіло масою 2 кг описується рівнянням: x(t)=5 – 8t+4t2 (м). Визначити імпульс тіла через t1 = 2 c та t2 = 4 c після початку руху та силу, що діяла на тіло впродовж цього інтервалу часу. [16 кг·м/с, 48 кг·м/с; 16 Н] |
|
2.71. |
Модуль зміни імпульсу \(\left| \Delta \vec{p} \right|\) тіла масою 1 кг, яке кинули під кутом 30° до горизонту, за час польоту склав 10 кг·м/с. Визначити максимальну висоту підйому тіла. [1,25 м] |
|
2.72. |
Тіло масою 100 г, кинуте вгору зі швидкістю 30 м/с, піднімалося протягом 2,5 с. Визначити середню силу опору повітря, що діяла на тіло. [0,2 Н] |
|
2.73. |
М'яч масою 150 г пружно (без утрати швидкості) вдаряє в гладку вертикальну стіну зі швидкістю 10 м/с під кутом 30° до неї. Якою є сила удару, якщо його тривалість складає 0,1 c? [15 H] |
|
2.74. |
Дві однакові кульки з однаковою швидкістю налітають на вертикальну стіну: перша перпендикулярно, а друга під кутом 30° до стіни. Знайти співвідношення F1 : F2 між силами, що діють на стіну під час удару, коли кульки а) відбиваються пружно (без утрати швидкості); б) непружно (прилипають до стіни). [а) 2 : 1; б) 1 : 1] |
|
2.75 |
Визначити середню силу віддачі на плече при стрільбі з автомата чергами по 300 пострілів за хвилину, якщо маса кулі дорівнює 10 г і швидкість вильоту зі ствола – 300 м/с. [15 H] |
|
2.76. |
Кулька масою 40 г вільно падає з висоти 1,25 м на пружну горизонтальну плиту й відбивається без утрати швидкості. Визначити середню силу, з якою кулька діяла на плиту під час удару, якщо його тривалість склала 0,4 с. [1,4 Н] |
|
2.77. |
Визначити силу горизонтального удару тенісної ракетки по нерухомому в момент подачі м'ячу маси 100 г, якщо удар тривав 0,05 c і швидкість подачі була 216 км/год. [240 Н] |
|
2.78. |
Футболіст б'є по нерухомому м'ячу масою 400 г. Залежність від часу сили, що діє на м'яч при ударі, показана на рис.2.78. Визначити швидкість м'яча одразу після удару. [25 м/с] |
|
2.79. |
Струмінь води перерізом 6 см2 із швидкістю 12 м/с б'є в стіну під кутом 60° до нормалі і пружно (без утрати швидкості) відбивається. Знайти силу тиску на стіну. [86,4 Н] |
|
2.80. |
Космічна ракета з площею лобового перерізу 2 м2 при швидкості 1 Мм/с налітає на хмару космічного пилу з густиною 10 мкг/м3. Яку силу тяги має розвинути двигун ракети, аби її швидкість лишилася незмінною? Вважати, що частинки пилу стикаються з ракетою непружно. [20 МН] |
Динаміка рівномірного руху по колу
Рівень А
|
2.81. |
На якій максимальній відстані від центра горизонтального диска, що обертається навколо своєї осі з частотою 33 об/хв, може лежати шайба при коефіцієнті тертя між нею й диском 0,2? [≈17 см] |
|
2.82. |
Байкер рухається по опуклому мосту круглого профілю радіусом 100 м. При якій найменшій швидкості байк на вершині мосту перестане тиснути на нього? [≈98,5 км/год] |
|
2.83. |
По опуклому мосту з радіусом кривини 50 м зі швидкістю 36 км/год рухається авто масою 1 т. З якою силою воно тисне на середину мосту? [8 кH] |
|
2.84. |
Авто маси 2 т рухається зі швидкістю 36 км/год угнутим мостом із радіусом кривини 100 м. З якою максимальною силою авто тисне на міст? [22 кH] |
|
2.85. |
Лижник із сталою швидкістю 10 м/с рухається прямою трасою спочатку по опуклій, а потім по угнутій ділянках однакового радіуса кривини 20 м. У скільки разів відрізняється вага лижника у найвищій та найнижчій точках шляху? [3] |
|
2.86. |
Кулю, що прикріплена до кінця легкого стрижня, рівномірно обертають у вертикальній площині. Визначити масу кулі, якщо різниця сил натягу стрижня при його вертикальному розташуванні складає 20 Н. [1 кг] |
|
2.87. |
Кулю, прикріплену до кінця легкого стрижня довжиною 80 см, рівномірно обертають у вертикальній площині. Знайти максимальну можливу частоту обертання (об/с), якщо стрижень витримує потрійну вагу кулі. [0,8 об/с] |
|
2.88. |
Гирю масою 500 г, прив'язану до мотузки довжиною 1 м, обертають у вертикальній площині з частотою 3 об/с. Визначити силу натягу мотузки у найнижчій та найвищій точках траєкторії. [183 H; 173 H] |
|
2.89. |
Кульку на нитці довжиною l = 1 м обертають по колу в горизонтальній площині так, що нитка утворює кут 45° із вертикаллю. Знайти швидкість і період обертання кульки. [2,6 м/с; 1,7 с] |
|
2.90. |
З якою максимальною швидкістю можна обертати в горизонтальній площині кулю масою 2 кг на нитці завдовжки 1 м, яка витримує навантаження до 100 H? [7 м/с] |
Рівень Б
|
2.91. |
Горизонтальний диск, на якому на відстані 16 см від осі лежить тіло масою 250 г, починають розкручувати з прискоренням 0,5 рад/с2. А) визначити, при якій кутовій швидкості обертання та через який час тіло почне ковзати по диску; Б) побудувати графік залежності радіальної складової сили тертя, що діє на тіло, від його кутової швидкості. [А) 5 рад/с; Б) натисніть ліву кнопку "миші"] |
|
2.92. |
Порожнисту кулю із внутрішнім радіусом 2 м обертають навколо вертикальної осі з частотою n = 30 об/хв. На якій висоті від дна встановилася вміщена в кулю кулька, що обертається разом з нею? [1 м] |
|
2.93. |
По опуклому мосту радіусом кривини 90 м зі швидкістю 54 км/год рухається авто масою 2 т. У точці мосту, напрям від якої до центра кривини мосту складає кут \(\alpha\) з вертикаллю, авто тисне на міст із силою 14,4 кH. Визначити величину \(\alpha\). [\(8,2^{\circ}\)] |
|
2.94. |
Швидкість байка 54 км/год, коефіцієнті тертя між шинами та покриттям автодрому 0,3. Якого найменшого радіуса віраж може закласти байкер та на який кут від вертикалі він має при цьому нахилитись? [76,5 м; ≈17°] |
|
2.95. |
Потяг рухається зі швидкістю 72 км/год колією ширини 1,5 м. Визначити, на скільки зовнішня рейка має бути розташована вище за внутрішню на закругленні радіусом 800 м, аби колеса не чинили бічного тиску на рейки. [7,65 см] |
|
2.96. |
Байкер рухається по вертикальній циліндричній стіні діаметром d = 10 м. Якою має бути найменша швидкість байка, аби він не впав при коефіцієнті тертя між колесами та стіною 0,3? [65,7 км/год] |
|
2.97. |
|
|
2.98. |
|
|
2.99. |
Радіус Місяця приблизно в 3,7 рази, а маса у 81 разів є менші, ніж у Землі. Визначити прискорення вільного падіння на Місяці. [1,66 м/с2] |
|
2.100. |
Яку тривалість мала би доба на Землі, якби тіла на екваторі були би невагомі? [1,41 год] |
|
2.101. |
Чому дорівнює перша космічна швидкість для планети, маса і радіус якої є вдвічі більші, ніж у Землі. [16,8 км/год] |
|
2.102. |
Чому дорівнює висота орбіти штучного супутника Землі, якщо його орбітальна швидкість складає 7,5 км/с? [700 км] |
|
2.103. |
Визначити першу космічну швидкість для планети з такою густиною, як у Землі, але з удвоє меншим радіусом. [≈4 км/с] |
|
2.104. |
Обчислити першу космічну швидкість для Місяця, якщо на ньому прискорення вільного падіння є в 6 разів менше за земне. Радіус Місяця є в 3,7 рази менший за радіус Землі. [1,68 км/с] |
|
2.105. |
Визначити висоту орбіти та лінійну швидкість геостаціонарного штучного супутника, тобто такого, що рухається в екваторіальній площині без зміни положення відносно поверхні Землі. [≈36,6 тис. км; 3,1 км/с] |
|
2.106. |
Визначити середню густину планети радіусом 10000 км, якщо швидкість її супутника на коловій орбіті радіусом 105 км дорівнює 4,1 км/с. [6 г/см3] |
Рівень В
|
2.107. |
У вагоні потяга, що рухається зі швидкістю 72 км/год по закругленню радіусом 200 м, зважують на пружинних вагах вантаж масою 5 кг. Якої відносної похибки (%) при цьому припускаються? [2%] |
|
2.108. |
$\left[ F=\frac{{{m}_{1}}{{m}_{2}}{{v}^{2}}}{\left( {{m}_{1}}+{{m}_{2}} \right)l} \right]$ |
|
2.109. |
Підвішена до стелі на гумовій нитці кулька маси m рухається в горизонтальній площині по колу так, що нитка утворює з вертикаллю заданий кут \(\alpha\). Чому дорівнює кутова швидкість ω кульки, якщо довжина не розтягненої нитки та її жорсткість складають l0 і k, відповідно. $\left[ \omega =\sqrt{\frac{kg}{mg+k{{l}_{0}}\cos \alpha }} \right]$ |
Розділ ІІІ. ЗАКОН ЗБЕРЕЖЕННЯ ІМПУЛЬСУ
У теорії та на практиці доводиться мати справу не лише з окремими тілами, а й з їхніми сукупностями – механічними системами. При цьому рух системи як цілого визначається не траєкторіями, швидкостями та прискореннями окремих тіл, а величиною що називається імпульсом і має важливу властивість за відповідних умов зберігатися.
Далі подано такий матеріал.
3.1. Теоретичні відомості. Механічна система
Механічною системою називається виділена сукупність тіл, які взаємодіють між собою та з не включеними в систему зовнішніми тілами. Відповідно, сили взаємодії між тілами системи називаються внутрішніми силами, а сили, що діють на тіла системи з боку не включених у систему тіл, називаються зовнішніми силами.
За відсутності взаємодії тіл системи із зовнішніми тілами вона називається замкненою або ізольованою, а при наявності —незамкненою.
Склад системи не є наперед визначеним і диктується змістом поставленої задачі.
3.2. Теоретичні відомості. Закон збереження імпульсу
|
Для ізольованих систем є характерним збереження деяких важливих фізичних величин. Зокрема це стосується імпульсу. |
Стан руху окремих тіл системи визначається їхніми імпульсами
(Примітка. Система може складатися як із маленькими частинок, так і з великих тіл. Але будь-яке тіло за необхідності теж можна розглядати як систему, що складається з маленьких частинок-матеріальних точок. Тому далі терміни "частинка","матеріальна точка" та "тіло" змістовно не розрізняються). Стан руху системи як цілого теж визначається імпульсом системи, що дорівнює сумі імпульсів окремих тіл:
При цьому за ІІ законом Ньютона (2.3) зміна імпульсу кожного тіла системи визначається рівнодійною всіх прикладених до нього сил, як зовнішніх, так і внутрішніх. Але сили взаємодії між будь-якою парою тіл системи є однакові за величиною і протилежні за напрямом (ІІІ закон Ньютона) і спричинюють рівні за модулем і протилежні за напрямом зміни їхніх імпульсів. Через це
де ${{\vec{F}}_{зов}}=\sum{{{{\vec{F}}}_{i зов\,}}}$ – сумарна зовнішня сила. В ізольованій системі зовнішніх сил немає, отже, \( {{{\vec{F}}}_{\text{зов}}}=0.\) В такому разі \(\Delta{\vec{P}}=0 \), тобто
Формула (3.3) виражає закон збереження імпульсу:
Це означає, що сумарний імпульс усіх тіл ізольованої системи є однаковим у будь-які два моменти часу попри те, що імпульс кожного окремого тіла змінюється під дією інших тіл системи. Тож закон збереження можна подати у формі рівняння балансу імпульсів:
де ліва та права частини відповідають довільно вибраним"початковому" та "кінцевому" моментам часу. Наостанку необхідно сказати, що закон збереження імпульсу є одним з універсальних законів природи і виконується не лише в механічних, а й у всіх фізичних системах. |
||||||||||||||||||||||||
3.3. Теоретичні відомості. Збереження імпульсу в незамкнених системах
Закон збереження імпульсу має велику не лише теоретичну, а й практичну цінність. Це зумовлено тим, що за відповідних умов він виконується і в незамкнених системах. Так буває в наступних випадках.
1. Зовнішні сили є компенсовані, тобто
${{\vec{F}}_{i}}\ne 0$, але $\sum{{{{\vec{F}}}_{i}}}=0$
Таким прикладом є зіткнення тіл, що рухаються без тертя по горизонтальній поверхні, коли сили тяжіння компенсуються силами нормальної реакції опори.
2. У незамкненій системі короткочасно діють великі внутрішні сили, так що на час їхньої дії можна знехтувати порівняно малими некомпенсованими зовнішніми силами, приміром, як при розриві снаряда під дією сил тиску порохових газів. В такому випадку \( {{{\vec{F}}}_{\text{зов}}} \Delta t\approx 0 \), і, згідно з рівнянням (2.4), можна покласти
|
\( \Delta {\vec{P}}=0\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ {\vec{P}}=\text{const}.\) |
|
3. Зовнішні сили мають незмінний напрям. В такій ситуації повний імпульс системи не зберігається (\({\vec{P}}\ne \text{const}\)), проте зберігається його проекція на будь-яку вісь, перпендикулярну до напряму сумарної зовнішньої сили. Це випливає з рівняння (3.2) в проекціях на таку вісь:
|
${{F}_{x}}=0$ $\Rightarrow $ $\Delta {{p}_{x}}=0$ $\Rightarrow$ $\sum{{{p}_{ix}}}=\sum{{{m}_{i}}}{{v}_{ix}}=\text{const}$
|
(3.5) |
3.4. Теоретичні відомості. Центр мас
|
Швидкості та імпульси окремих тіл системи можуть суттєво відрізнятись як за модулем, так і за напрямом. Тому вираз імпульсу системи (3.1) не дає наочного уявлення про її рух як цілого. Проте таке уявлення дає рух деякої точки, що називається центром мас (або центром інерції) системи. Її положення визначається радіусом-вектором (див. п.1.1) |
де mi, ${{\vec{r}}_{i}}$ – маси та радіуси-вектори окремих тіл системи; величина $m=\sum{{{m}_{i}}}$ – загальна маса системи. Координати центра мас обчислюються за формулами:
Можна показати, що імпульс системи дорівнює добутку її загальної маси на вектор швидкості центра мас \( {{{\vec{V}}}_{\text{c}}}\):
Цей вираз дозволяє інакше записати рівняння (3.2):
де \( \vec{a}_{\text{c}}\) – прискорення центра мас. Отже, можна сказати, що
Це твердження називають теоремою про рух центра мас. За відсутності зовнішніх сил (ізольована система), або при їхній компенсації прискорення \( \vec{a}_{\text{c}}=0 \), тож швидкість центра мас \( \vec{V}_{\text{c}}=\text{const}\). Отже, внутрішні сили не впливають на положення та рух центра мас системи. |
Приклади розв'язування задач
У системах із невеликої кількості тіл (зазвичай двох) закон збереження імпульсу дозволяє ''автоматично'' визначати швидкості тіл після взаємодії через їхні значення до взаємодії. Це може бути самостійним завданням, або етапом розв'язування більш складної задачі.
Задача 3.1. Дві пластилінові кульки масами m1= 40 г та m2= 60 г, які рухаються гладкою горизонтальною поверхнею зі швидкостями v1= 0,3 м/с і v2= 0,4 м/с під кутом \( \alpha=60^{\circ}\) одна до одної, після зіткнення злипаються й рухаються далі, як одне ціле. Визначити швидкість v утвореного складеного тіла.
Задача 3.2. Граната, кинута під кутом \(\alpha \) = 60° до горизонту зі швидкістю v0 = 10 м/с, розривається на два однакові осколки так, що один відлітає вертикально вгору, а другий – під кутом \( \beta=45^{\circ}\) до горизонту. Визначити швидкість v2 відльоту другого осколка.
Задача 3.3. Коли два човни, що рухаються паралельними зустрічними курсами, порівнялись із першого в другий на ходу обережно переклали вантаж маси m = 25 кг. Відтак другий човен зупинився, а перший продовжив рух зі швидкістю u = 4 м/с. Визначити швидкості човнів v1 та v2 до перекладання вантажу, якщо маса другого човна M = 200 кг.
Задача 3.4. Двоє хлопців однакової маси горизонтально стрибають із нерухомого візка з однаковою швидкістю u щодо нього. Відношення мас візка та хлопця η = (М/m). Визначити швидкість відкочування візка v, якщо хлопці зістрибують: 1) одночасно і 2) поспіль один за одним.
Задача 3.5. Хлопець маси m, який стоїть на краю рухомого візка маси M, стрибає по ходу під кутом \( \alpha \) до горизонту зі швидкістю u відносно візка. Визначити величину та напрям швидкості візка ${{\vec{V}}_{1}}$ після стрибка, якщо до того її модуль складав V.
Задача 3.6. На кінці дошки масою M = 1,4 кг і довжиною l = 1 м, яка стоїть на плаву в ставку, сидить жаба маси m = 100 г. Жаба стрибає під кутом \( \alpha=30^{\circ}\) до поверхні дошки так, що опиняється на протилежному кінці. Визначити швидкість v0 стрибка жаби відносно води.
Задача 3.7. Випущена з поверхні землі граната у верхній точці траєкторії на висоті H = 45 м і відстані S0 = 300 м розривається на два однакові осколки так, що один падає на під точкою розриву через τ = 1 с. Визначити, на якій відстані S від нього впаде другий.
Задача 3.8. Рибалка масою m перейшов з корми на ніс човна маси M і довжини L, який стоїть на плаву в ставку. Нехтуючи опором води, визначити переміщення \( \vec{S}\), що його здійснив при цьому човен.
Задача 3.9. Кульки масами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг і m4 =4 кг, які в певний момент послідовно займають вершини квадрата, рухаються кожна в напрямку наступної із швидкостями v1 = 4 м/с, v2 = 3 м/с, v3 = 2 м/с, v4 = 1 м/с. Визначити швидкість \( \vec{V}\) центра мас кульок у цей момент.
Задача 3.10. Тягарці масами m1 = 1 кг і m2 = 2 кг, що з'єднані ниткою перекинутою через блок, утримують на одному рівні. Визначити, з яким прискоренням aс почне рухатися центр мас системи, якщо тягарці відпустити.
| Задача 3.1 |
| Задача 3.1 |
Дві пластилінові кульки масами m1= 40 г та m2= 60 г, які рухаються гладкою горизонтальною поверхнею зі швидкостями v1= 0,3 м/с і v2= 0,4 м/с під кутом \( \alpha=60^{\circ}\) одна до одної, після зіткнення злипаються й рухаються далі, як одне ціле
Визначити
швидкість v утвореного складеного тіла.
|
Дано: m1 = 40 г
m2 = 60 г
v1 = 0,3 м/с
v2 = 0,4 м/с
\( \alpha=60^{\circ}\) |
|
v - ? |
Розв'язання
Зовнішні сили (тяжіння та реакції поверхні), що діють на кульки, є компенсовані, тож імпульс системи зберігається:
| \( {m}_{1}\vec{v}_{1}+m_{2}\vec{v}_{2}=(m_{1}+m_{2})\vec{v}\) |
|
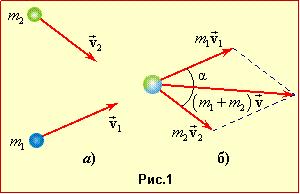
З побудованого за цим рівнянням паралелограма імпульсів (рис. 1) за допомогою теореми косинусів знаходимо відповідь:
\( {v}=\frac{\sqrt{(m_{1}v_{1})^{2}+(m_{2}v_{2})^{2}+2m_{1}m_{2}v_{1}v_{2}\cos\alpha}}{m_{1}+m_{2}}\) ≈ 0,3 м/с.
| Задача 3.2 |
| Задача 3.2 |
Граната, яку кинули під кутом \(\alpha \) = 60° до горизонту зі швидкістю v0 = 10 м/с, розривається на два однакові осколки. Один із них відлітає вертикально вгору, а другий – під кутом \( \beta=45^{\circ}\) до горизонту.
Визначити
швидкість v2 відльоту другого осколка.
|
Дано: v0 = 10 м/с
\( \alpha=60^{\circ}\)
\( \beta=45^{\circ}\)
|
|
v2 - ? |
Розв'язання
Система "граната-уламки" не є ізольованою, оскільки на тіла діє некомпенсована зовнішня сила тяжіння. Але на короткий час вибуху, коли діють дуже великі внутрішні сили тиску порохових газів, силою тяжіння можна знехтувати і вважати, що розрив гранати відбувається із збереженням імпульсу:
| \( \vec{p}=\vec{p}_{1}+\vec{p}_{2}\), |
де \( \vec{p}\) – імпульс гранати безпосередньо перед розривом, \( \vec{p}_{1}\) та \( \vec{p}_{2}\) – імпульси уламків одразу після розриву (рис. 2).
У проекціях на вісь OX записане рівняння має вигляд:
| \( {p}_{x}=p_{2x}\cos\beta \) \( \Rightarrow \) \( {m}v_{x}=\frac{m}{2}v_{2}\cos\beta \). | (1) |
 Складова імпульсу гранати вздовж осі OX залишається незмінною від моменту кидання до моменту розриву, оскільки проекція сили тяжіння на цей напрямок дорівнює нулю:
Складова імпульсу гранати вздовж осі OX залишається незмінною від моменту кидання до моменту розриву, оскільки проекція сили тяжіння на цей напрямок дорівнює нулю:
| \( {m}v_{x}=mv_{0}\cos\alpha\). | (2) |
Прирівнявши праві частини виразів (1) та (2), дістанемо:
| \( {m}v_{0}\cos\alpha=\frac{m}{2}v_{2}\cos\beta \) \( \Rightarrow \) \( {v}_{2}=v_{0}\frac{2\cos\alpha}{\cos\beta}={14,1}\) м/с. |
| Задача 3.3 |
| Задача 3.3 |
Коли два човни, що рухаються паралельними зустрічними курсами, порівнялись, із першого в другий на ходу обережно переклали вантаж маси m = 25 кг. Відтак другий човен зупинився, а перший продовжив рух зі швидкістю u = 4 м/с.
Визначити
швидкості човнів v1 та v2 до перекладання вантажу, якщо маса другого човна M2 = 200 кг.
|
Дано: m = 25 кг
u = 4 м/с
M2 = 200 кг
|
|
v1 - ? v2 - ? |
Розв'язання
Зовнішні сили (тяжіння та архімедова), що діють на човни є компенсовані, тож човни можна розглядати як замкнену систему. Тому при перекладанні вантажу імпульс першого човна зменшується, а другого збільшується на величину \( m\vec{v}_{1}\) без зміни сумарного імпульсу системи. Позаяк величина кінцевої швидкості першого човна u відома, то в проєкціях на напрям його руху можна записати:
| $\left( {{M}_{1}}+m \right){{v}_{1}}-m{{v}_{1}}={{M}_{1}}u$ \( \Rightarrow \) v1 = u = 4 м/с. |
У цьому результаті немає нічого дивного, бо при перекладанні вантажу на човни ніякі сили вздовж напряму руху не діють, тож причиною зміни імпульсу першого човна є тільки втрата маси.
Другий човен, який рухається назустріч, отримує імпульс перекладеного вантажу й зупиняється. Отже, його початковий імпульс мав таку саму величину:
|
\( {M_{2}}v_{2}=mv_{1}\) \( \Rightarrow \) ${{v}_{2}}=\frac{m}{{{M}_{2}}}u$ = 0,5 м/с. |
| Задача 3.4 |
| Задача 3.4 |
Двоє хлопців однакової маси горизонтально стрибають із нерухомого візка з однаковою швидкістю u щодо нього. Відношення мас візка та хлопця η = (М/m).
Визначити
швидкість відкочування візка v, якщо хлопці зістрибують:
1) одночасно;
2) поспіль один за одним.
|
Дано: (M/m) = η
u
|
|
V1 -? V2 -? |
Розв'язання
Система "візок-хлопці" на загал не є ізольованою, бо в ній діють зовнішні сили тяжіння та нормальної реакції поверхні, на якій стоїть візок. Але при горизонтальному відштовхуванні хлопців від візка ці сили лишаються компенсованими, тому імпульс системи зберігається.
1. Хлопці стрибають одночасно.
Позаяк до стрибка візок був нерухомий, сумарний імпульс візка та хлопців після стрибка
$M{{\vec{V}}_{1}}+2m{{\vec{v}}_{1}}=0$,
де ${{\vec{V}}_{1}}$ i ${{\vec{v}}_{1}}$ – швидкість візка та швидкість хлопців відносно землі.
Звідси, враховуючи співвідношення M = ηm і закон додавання швидкостей (1.11) ${{\vec{v}}_{1}}=\vec{u}+{{\vec{V}}_{1}}$, отримаємо швидкість візка після одночасного зістрибування хлопців:
| $\left( \eta +2 \right){{\vec{V}}_{1}}+2\vec{u}=0$, $ \Rightarrow $ ${{\vec{V}}_{1}}=-\frac{2}{\eta +2}\vec{u}$ |
Знак "–" указує на те, що візок відкочується в протилежному до стрибка напрямі.
2. Хлопці стрибають почергово.
У цьому випадку після першого стрибка візок набуває проміжного імпульсу ${\vec{P}}'$ і швидкості ${\vec{V}}'$, які знаходяться аналогічно до попереднього. А саме:
$\left( M+m \right){\vec{V}}'$ + $m{\vec{v}}'$ = 0.
Далі, позаяк M = ηm, і ${\vec{v}}'$ = $\vec{u}+{\vec{V}}'$, маємо:
| $\left( \eta +1 \right){\vec{V}}'+\left( \vec{u}+{\vec{V}}' \right)=0$ $ \Rightarrow $ ${\vec{V}}'=-\frac{1}{\eta +2}\vec{u}$ | (1) |
Збереження імпульсу при другому стрибку виражається рівнянням
$\left( M+m \right){\vec{V}}'=M{{\vec{V}}_{2}}+m{{\vec{v}}_{2}}$,
звідки, підставивши M = ηm і ${{\vec{v}}_{2}}=\vec{u}+{{\vec{V}}_{2}}$, дістанемо:
|
${{\vec{V}}_{2}}={\vec{V}}'-\frac{1}{\eta +1}\vec{u}$. |
Звідси, врахувавши вираз (1), після нескладних перетворень отримаємо кінцеву швидкість візка:
${{\vec{V}}_{2}}=-\frac{2\eta +3}{\left( \eta +1 \right)\left( \eta +2 \right)}\vec{u}$
| Задача 3.5 |
Хлопець маси m, який стоїть на краю рухомого візка маси M, стрибає по ходу під кутом \( \alpha \) до горизонту зі швидкістю u відносно візка.
Визначити
величину та напрям швидкості візка ${{\vec{V}}_{1}}$ після стрибка, якщо до її модуль складав V.
|
Дано: M, m
α
u
|
|
V1 - ? |
Розв'язання
Ця задача нагадує попередню. Але в даному випадку повний імпульс системи "візок-хлопець" не зберігається, в чому можна переконатися безпосередньо, зобразивши вектори імпульсу системи перед стрибком \( \vec{P}_{п}=(M+m)\vec{V}\) та після стрибка хлопця \( \vec{P}_{к}=M\vec{V}_{1}+m\vec{v}\) (рис. 5).
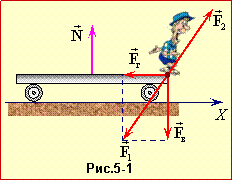
Очевидно, що вектори кінцевого та початкового імпульсу системи мають різний напрям. Тож за будь-яких умов
\( \vec{P}_{п}\ne\vec{P}_{к}\) \( \Rightarrow \) $\Delta \vec{P}\ne 0$.
Сказане може здатися неочікуваним – адже до стрибка зовнішні сили тяжіння та реакції опори були компенсовані. Це справді так і є, але під час стрибка компенсація даних сил порушується, позаяк сила відштовхування хлопця \( \vec{F}_{1}\) та протилежно спрямована реакція візка \( \vec{F}_{2}=-\vec{F}_{1}\) діють під кутом до горизонту (рис. 5-1). Ці сили є внутрішніми й самі по собі не здатні змінити імпульс системи хлопець-візок. Але сила \( \vec{F}_{1}\) не лише змінює швидкість візка завдяки складовій \( \vec{F}_{г}\), а й притискає його до землі, викликаючи додаткову реакцію опори \( \vec{N}=-\vec{F}_{в}\), яка є зовнішньою силою й змінює імпульс \( \vec{P}\) системи "візок-хлопець". При цьому, позаяк \( {N}_{x}={0}\), горизонтальна проєкція імпульсу системи Px не змінюється. Отже,
| \( {(M+m)}V=MV_{1x}+mv_{x}\). | (1) |
У цьому рівнянні vx – горизонтальна складова швидкості хлопця відносно землі \( \vec{v}\), котра пов'язана з його швидкістю відносно візка \( \vec{u}\) законом додавання швидкостей (1.19):
\( \vec{v}=\vec{u}+\vec{V}_{1}\) \( \Rightarrow \) \( {v}_{x}=u\cos\alpha+V_{1x}\).
(Зверніть увагу на те, що в рівняння входить швидкість візка після, а не до стрибка, адже на момент відриву ніг хлопця від опори візок уже набув кінцевої швидкості).
Підставивши отриманий вираз vx у рівняння (1) знайдемо:
\( {V}_{1x}=\frac{(M+m)V-mu\cos\alpha}{M+m}\).
У відповідності до отриманого результату можливі три різні випадки руху візка після стрибка хлопця:
1. При \( {(M+m)}V>mu\cos\alpha \), то \( {V}_{1x}>{0}\), отже, візок продовжує рухатись у тому самому напрямі, але з меншою швидкістю;
2. При \( {(M+m)}V<mu\cos\alpha \), то \( {V}_{1x}<{0}\), тобто візок змінює напрям руху;
3. При \( {(M+m)}V=mu\cos\alpha \), то \( {V}_{1x}={0}\), і візок зупиняється.
| Задача 3.6. |
| Задача 3.6. |
На кінці дошки масою M = 1,4 кг і довжиною l = 1 м, яка стоїть на плаву в ставку, сидить жаба маси m = 100 г. Жаба стрибає під кутом \( \alpha=30^{\circ}\) до поверхні дошки так, що опиняється на протилежному кінці.
Визначити
швидкість v0 стрибка жаби відносно води.
|
Дано: M = 1,4 кг
l = 1 м
m = 100 г
\( \alpha=30^{\circ}\)
|
|
v0 - ? |
Розв'язання
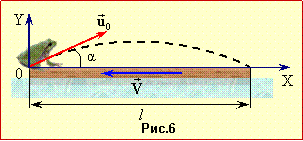 Розглянемо задачу спочатку в рухомій системі відліку дошки (рис. 6), занотувавши, що горизонтальне та вертикальне переміщення жаби за час стрибка складають Δx = l і Δy = 0, а проєкції прискорення ax = 0 і ay = –g. Відтак за допомогою рівнянь кінематики (1.16) визначимо модуль і проєкції швидкості $\vec{u}$ стрибка жаби відносно дошки:
Розглянемо задачу спочатку в рухомій системі відліку дошки (рис. 6), занотувавши, що горизонтальне та вертикальне переміщення жаби за час стрибка складають Δx = l і Δy = 0, а проєкції прискорення ax = 0 і ay = –g. Відтак за допомогою рівнянь кінематики (1.16) визначимо модуль і проєкції швидкості $\vec{u}$ стрибка жаби відносно дошки:
\(\left. \begin{matrix} l={{u}_{0}}t\cos \alpha \\ 0={{u}_{0}}t\sin \alpha -\frac{g{{t}^{2}}}{2} \\\end{matrix} \right\}\ \ \ \ \ \ \Rightarrow \ \ \ \ \ {{u}_{0}}=\sqrt{\frac{gl}{2\sin \alpha \cdot \cos \alpha }}.\)
| \( {u}_{0x}=u_{0}\cos\alpha=\sqrt{\frac{gl\cos^{2}\alpha}{2\sin\alpha{\cos\alpha}}}=\sqrt{\frac{gl}{2}\mathrm{ctg}\alpha}\), | (1) |
\( {u}_{0y}=u_{0}\sin\alpha=\sqrt{\frac{gl\sin^{2}\alpha}{2\sin\alpha\cos\alpha}}=\sqrt{\frac{gl}{2}\mathrm{tg}\alpha}\).
Унаслідок віддачі при стрибку жаби, дошка почне рухатись у зворотньому напрямі зі швидкістю \( \vec{V}\) відносно води (нерухома система відліку). При цьому за законом додавання швидкостей (1.19)
\( \vec{v}_{0}=\vec{u}_{0}+\vec{V}\),
а в проекціях на осі OX та OY
| \( {v}_{0x}=u_{0x}-{V}\), | (2) |
| \( {v}_{0y}=u_{0y}\). | (3) |
Тож, аби визначити швидкість стрибка жаби відносно води v0, треба спочатку знайти швидкість V, отриману дошкою. Це завдання є аналогічним до попередньої Задачі 3.5. А саме. Під час стрибка жаба трохи притоплює дошку, через що виникає некомпенсована додаткова архімедова сила, котра змінює імпульс системи. Але, позаяк ця сила спрямоване вертикально, горизонтальна складова імпульсу лишається незмінною:
\( {-M}V+mv_{0x}={0}\) \( \Rightarrow \) \( {V}=\frac{m}{M}v_{0x}\).
Підставивши цей вираз у рівняння (2), отримаємо
\( {v}_{0x}=u_{0x}-\frac{m}{M}v_{0x}\) \( \Rightarrow \) \( {v}_{0x}=\frac{M}{M+m}u_{0x}\).
Відтак, врахувавши рівняння (3) і вираз (1), знайдемо відповідь:
\( {v}_{0x}=\frac{M}{M+m}\sqrt{\frac{gl}{2}\mathrm{ctg}\alpha }\),
\( {v}_{0}=\sqrt{v_{0x}^{2}+v_{oy}^{2}}=\sqrt{\left(\frac{M}{m+M}\right)^{2}\frac{gl}{2}\mathrm{ctg}\alpha+\frac{gl}{2}\mathrm{tg}\alpha}\) =
= \(\sqrt{\frac{gl}{2}\left(\left(\frac{M}{M+m}\right)^{2}\mathrm{ctg\alpha}+\mathrm{tg}\alpha\right)}\).
Обчислення дають
v0 = 3,2 м/с.
| Задача 3.7 |
| Задача 3.7 |
Випущена з поверхні землі граната у верхній точці траєкторії на висоті H = 45 м і горизонтальній відстані S0 = 300 м розривається на два однакові осколки так, що один падає на під точкою розриву через τ = 1 с.
Визначити,
на якій відстані S від нього впаде другий
.
|
Дано: Н = 45 м
S0 = 300 м
τ = 1 с
|
|
S - ? |
Розв'язання
Процес розриву снаряда є швидкоплинний і відбувається без утрати його імпульсу, як показано на рис. 7:
| \( \vec{p}=\vec{p}_{1}+\vec{p}_{2}\). |
Це дозволяє взнати швидкість відльоту другого осколка \(\vec{v}_{2}\), що визначає шукану відстань S.
За умовою m1 = m2 = (m/2), отже,
|
\( {m}\vec{v}=\frac{1}{2}m\vec{v}_{1}+\frac{1}{2}m\vec{v}_{2}\) \( \Rightarrow \) \( \vec{v}_{2}=2\vec{v}-\vec{v}_{1}\). |
Звідси, враховуючи напрямки швидкостей снаряда й першого осколка, для проєкцій початкової швидкості другого осколка маємо:
|
${{v}_{2x}}=2{{v}_{0x}}$, \({v}_{2y}=v_{1}\). |
(1) |
Граната та осколки рухаються із прискоренням \( \vec{g}\), тож gх = 0, і шукана відстань
| S = v2xt2 = 2v0xt2. | (2) |
Таким чином, задача зводиться до визначення горизонтальної проєкції початкової швидкості гранати та часу руху другого осколка, які можна знайти з рівнянь кінематики через задані значення S0, H і t1. Зокрема, якщо позначити як t0 час руху гранати до розриву, то, за рівнянням (1.16)
| ${{v}_{0x}}=\frac{{{S}_{0}}}{{{t}_{0}}}$. |
За час t0 по вертикалі граната проходить відстань H і зменшує швидкість від v0y до 0, тож, згідно з рівняннями (1.16) і (1.18),
${{t}_{0}}=\frac{{{v}_{0y}}}{g}, {{v}_{0y}}=\sqrt{2gH}$ \( \Rightarrow \) ${{t}_{0}}=\sqrt{\frac{2H}{g}}$.
Отже,
|
${{v}_{0x}}={{S}_{0}}\sqrt{\frac{g}{2H}}$, |
і згідно з (2),
|
$S=2{{S}_{0}}\sqrt{\frac{g}{2H}}\cdot {{t}_{2}}$. |
(3) |
Відтак належить знайти час руху t2 другого осколка. Це можна зробити за допомогою рівнянь (1.16) через задані початкову y20 = H і кінцеву y2 = 0 координати та знайдену вертикальну складову початкової швидкості \({v}_{2y}=v_{1}\). Але зручніше окремо розглянути час ${{{t}'}_{2}}$ проходження ділянки АВ траєкторії та ${{{t}''}_{2}}$ – завершальної ділянки ВС. На першій ділянці швидкість спочатку зменшується від v1 до 0, а потім до такої ж величини зростає, тож ${{{t}'}_{2}}$ = (2v1/g). З цієї ж причини t2″= τ , отже,
|
${{t}_{2}}=\frac{2{{v}_{1}}}{g}+\tau $. |
(4) |
Таким чином, для визначення часу руху другого осколка необхідно мати величину v1. Її знайдемо з рівняння (1.16) для першого осколка, поклавши y1 = H i y10 = 0:
$0=H-{{v}_{1}}\tau -\frac{g{{\tau }^{2}}}{2}\quad \Rightarrow \quad \frac{2{{v}_{1}}}{g}=\frac{2H}{g\tau }-\tau $.
Урахувавши цей результат, із виразу (4) отримаємо
${{t}_{2}}=\frac{2H}{g}$,
і після підстановки у вираз (3) – відповідь задачі:
$S=\frac{4{{S}_{0}}}{\tau }\sqrt{\frac{H}{2g}}$ = 1,8 км.
Задача 3.8.
Рибалка масою m перейшов з корми на ніс човна маси M і довжини L, який стоїть на плаву в ставку. Нехтуючи опором води,
визначити
переміщення \( \vec{S}\), що його здійснив при цьому човен.
|
Дано: M, m
L
|
|
\(\vec{S}\)-? |
Розв’язання
Задачу можна розв'язати двома способами.
І спосіб. У системі ''рибалка-човен'' сили взаємодії між тілами є внутрішніми і не надають їй ніякого сумарного імпульсу. Тому при переміщенні рибалки з якоюсь швидкістю \( \vec{v}\) човен рухається в протилежному напрямку із таким самим величиною імпульсом і відповідною швидкістю \(\vec{V}\), тож
| $M\vec{V}=-m\vec{v}$ | (1) |
Відтак, виразивши швидкості через переміщення, отримаємо:
| \( {M}\vec{S}\) = –\( {m}\vec{s}\) | (2) |
На перший погляд отримане співвідношення по суті є розв'язком задачі, позаяк відстань між кормою та носом човна L є задана. Але таке міркування є хибним, бо рівняння (1) і (2) пов'язують швидкості та переміщення рибалки й човна відносно води, тоді як довжина човна L є переміщенням s′ рибалки відносно човна. А відносно води воно, згідно з формулою (1.9а), з урахуванням напрямків (див. рис. 3.8), дорінює
${s}={{s}}'–{S}$.
Підставивши цей вираз в рівняння (2) і, врахувавши, що s′ = L, після елементарних викладок отримаємо остаточну відповідь:
| $S=\frac{m}{M+m}L$. | (3) |
ІІ спосіб. Згідно з теорією ( п. 3.4, ф-ла (3.7)) імпульс системи "човен-рибалка" дорівнює добутку її сумарної маси на швидкість центра мас: ${{\vec{P}}_{\Sigma }}=\left( M+m \right){{V}_{с}}$. Тож, позаяк при переході рибалки ${{\vec{P}}_{\Sigma }}$ = 0, положення (радіус-вектор, п. 1.1) центра мас системи не змінюється. Тож, прирівнявши вирази (3.6) радіус-вектора \({{\vec{r}}_{с}}\) початкового та кінцевого положення рибалки (\( \vec{r}_{1р},\,\,\vec{r}_{2р}\)) та човна (\( \vec{r}_{1ч},\,\,\vec{r}_{2ч}\)), отримаємо:
\( M{{\vec{r}}_{1ч}}+m{{\vec{r}}_{1р}}=M{{\vec{r}}_{2ч}}+m{{\vec{r}}_{2р}}\ \ \Rightarrow \ \ \ M({{\vec{r}}_{1ч}}-{{\vec{r}}_{2ч}})=m({{\vec{r}}_{2р}}-{{\vec{r}}_{1р}}).\)
Приріст радіус-вектора точки є її переміщенням (ф-ла (1.1)), отже
| \( {M}\vec{S}\) = –\( {m}\vec{s}\), |
що збігається з виразом (2) і дає ту саму відповідь (3).
Задача 3.9.
Кульки масами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг і m4 =4 кг в певний момент послідовно займають вершини квадрата і рухаються кожна в напрямку наступної із швидкостями v1 = 4 м/с, v2 = 3 м/с, v3 = 2 м/с, v4 = 1 м/с.
Визначити
швидкість \( \vec{V}\) центра мас кульок у цей момент.
|
Дано: m1 = 1 кг, v1 = 4 м/с; m2 = 2 кг, v2 = 3 м/с; m3 = 3 кг, v3 = 2 м/с; m4 = 4 кг, v4 = 1 м/с. |
|
${\vec{V}}$-? |
Розв’язання
Згідно з формулами (1.5а) і (3.6а), проєкції швидкості центра мас Vx , Vy на осі координат визначаються відношенням суми добутків мас кульок на проєкції їхніх швидкості до сумарної маси системи. Тож, обравши для обчислень систему координат ХOY, як показано на рис. 3.9 і врахувавши напрямки векторів швидкості, отримаємо:
${{V}_{x}}=\frac{{{m}_{2}}{{v}_{2}}-{{m}_{4}}{{v}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ = 0,2 м/с;
${{V}_{y}}=\frac{{{m}_{1}}{{v}_{1}}-{{m}_{3}}{{v}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ = –0,2 м/с.
Таким чином, у вказаний момент центр мас кульок рухається із швидкістю
$V=\sqrt{V_{x}^{2}+V_{y}^{2}}\approx 0,3\text{м/с}$
праворуч і вниз під кутом 45° до осей координат. Аби визначити точку прикладання вектора \( \vec{V}\), треба за формулами (3.6а) обчислити координати центра мас кульок. Але в даній задачі це можна зробити і без обчислень, скориставшись їхнім сприятливим розташуванням. А саме. Позаяк сумарна маса двох горизонтальних пар кульок 2-3 і 1-4 (рис. 3.9) однакова, то очевидно, що центр мас С знаходиться на горизонталі аb, що проходить посередині. А сама точка С ділить відрізок аb у відношенні оберненому до відношення мас вертикальних пар кульок 1-2 і 3-4, тобто, як 7 : 3. Відповідно до цього на рис. 3.9 й показано вектор \( \vec{V}\).
Задача 3.10.
Тягарці масами m1 = 1 кг і m2 = 2 кг, що з'єднані ниткою, перекинутою через блок, утримують на одному рівні.
Визначити,
з яким прискоренням ас почне рухатися центр мас системи, якщо тягарці відпустити.
|
Дано: m1 = 1 кг, m2 = 2 кг |
|
aс - ? |
Розв’язання
Тягарці на нитці утворюють зв'язану систему тіл, в якій діють зовнішні сили тяжіння ${{m}_{1}}\vec{g}$, ${{m}_{2}}\vec{g}$ і реакція осі блока $\vec{R}$ та внутрішні сили натягу нитки $\vec{T}$, ${\vec{T}}'$, рис. 3.10. (Формально система включає ще й блок, але за умовчанням він є невагомим і ніяк не впливає на характеристики руху тягарців).
На загал величину а можна знайти за теоремою про рух центра мас та другим законом Ньютона. Але простіше це зробити, виходячи з того, що прискорення точки визначається другими похідними її координат по часу (розділ 1. вирази (1.8)). Тож, згідно з формулою (3.6а), можна записати:
\({{a}_{\operatorname{c}x}}=\frac{{{m}_{1}}{{x}_{1}}^{\prime \prime }+{{m}_{2}}{{x}_{2}}^{\prime \prime }}{{{m}_{1}}+{{m}_{2}}}\quad \Rightarrow \quad {{a}_{\operatorname{c}x}}=\frac{{{m}_{1}}{{a}_{1}}_{x}+{{m}_{2}}{{a}_{2}}_{x}}{{{m}_{1}}+{{m}_{2}}}\),
або, враховуючи, що прискорення тягарців мають однакову величину а,
| ${{a}_{\operatorname{c}x}}=\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)a$. | (1) |
Величину прискорення тягарців а легко знайти за другим законом Ньютона (2.5) з урахуванням напрямків руху:
$\left\{ \begin{align} & {{m}_{1}}g-T={{m}_{1}}a \\ & T-{{m}_{2}}g={{m}_{2}}a \\\end{align} \right.\quad \Rightarrow \quad a=\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)g$.
Відтак підставивши це значення у вираз (1), отримуємо відповідь:
$ {a}={{\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)}^{2}}g$.
Задачі для самостійної роботи
При складанні рівняння балансу імпульсів і обчисленнях не слід забувати, що імпульс є вектором, тож величина (модуль) сумарного імпульсу системи тіл не завжди дорівнює сумі величин імпульсів окремих тіл.
При визначенні координат центра мас складеного тіла чи системи тіл варто використовувати загальні формули, що наведені в п. 3.4, а не конструювати якісь геометричні побудови, як інколи роблять учні.
Нагадаємо, що відповіді до запропонованих далі задач передбачають значення g = 10 м/с2.
|
3.11. |
Знайти імпульс диска масою 5 кг і діаметром 1 м, який обертається із частотою 90 об/хв навколо перпендикулярної до нього осі, розташованої на відстані 20 см від центра. [≈14 кг·м/с] |
|
3.12. |
Із не закріпленої гармати масою 3 т, ствол якої є жорстко зв'язаний з лафетом, роблять горизонтальний постріл снарядом масою 15 кг. З якою швидкістю почне відкочуватися гармата при швидкості вильоту снаряда 650 м/с? [3,25 м/с] |
|
3.13. |
Снаряд масою 20 кг, що летить уздовж залізничної колії, знижуючися влучає влучає під кутом 45° зі швидкістю 500 м/с у нерухому платформу з піском масою 50 т. З якою швидкістю почне рухатись платформа? [0,14 м/с] |
|
3.14. |
З катера масою 750 т зроблено проти ходу постріл під кутом 60° до горизонту. Швидкість снаряда 1,0 км/с, маса снаряда 30 кг. Визначити, на скільки змінилася швидкість катера? [2 cм/c] |
|
3.15. |
З рухомої реактивної установки масою 5 т, яка перебуває у спокої, в горизонтальному напрямі роблять поспіль два постріли снарядами маси 25 кг. Визначити швидкість відкочування установки після другого пострілу при швидкості вильоту снарядів 1 км/с відносно установки. [10 м/с] |
|
3.16. |
Космонавт масою 80 кг, який знаходиться на поверхні сферичного астероїда з радіусом 1 км і середньою густиною речовини 5 г/см3, кидає камінь масою 4 кг. При якій найменшій швидкості каменя відносно астероїда космонавт може стати штучним супутником астероїда? [23,6 м/с] |
|
3.17. |
Космонавт масою 100 кг, що знаходиться на відстані 150 м від ракети масою 100 т, починає вибирати фал, котрим є прикріплений до неї. На яку відстань зміститься ракета вздовж фала за час переміщення космонавта до шлюзу? [15 см] |
|
3.18. |
Двоє рибалок масами 60 кг і 80 кг розташувалися по краях не заякореного човна довжиною 4 м і масою 200 кг, який стоїть у тихій воді. На скільки зміститься човен відносно берега, якщо рибалки поміняються місцями? [2 м] |
| 3.19. |
Космонавт, який перебуває на поверхні космічної станції у формі циліндра з діаметром D, починає обходити її навколо осі. По яких траєкторіях рухатимуться станція та космонавт при відношенні їхніх мас рівному η? [По колах радіуса \(\frac{D}{2\left( \eta +1 \right)}\) і \(\frac{\eta D}{2\left( \eta +1 \right)}\) навколо спільної осі].
|
Розділ ІV. РОБОТА ТА ЕНЕРГІЯ
Терміном "робота" у повсякденному житті характеризують діяльність людини та функціонування механізмів, а під енергією розуміють те, без чого виконання роботи є неможливим. Але як наукові поняття енергія та робота мають більш глибокий і чітко визначений зміст.
Задачі для самостійної роботи
4.1. Робота сили
|
Якщо на рухоме тіло діє сила, то вона виконує механічну роботу. За означенням роботою A сталої сили \( \vec{F}\) на переміщенні \( \vec{S}\) називається величина, що дорівнює скалярному добутку цих векторів (рис. 4.1):
|
|
При дії довільної сили на тіло, що рухається по довільній траєкторії, величина F та кут α у процесі руху змінюються. При цьому, позаяк загальне переміщення тіла між двома точками (рис. 4.2) складається з переміщень $\Delta {{\vec{S}}_{k}}$ на окремих ділянках, робота змінної сили на заданому шляху дорівнює сумі робіт ΔAk на всіх його ділянках:
Обчислення роботи змінної сили виконуються за допомогою методів вищої математики. Але при якісному аналізі, а інколи й у розрахунках, може стати в пригоді графік залежності проєкції сили Fs від пройденого шляху S, рис. 4.3. А саме. Якщо всю траєкторію подумки розбити на дуже малі ділянки, так, щоби силу
F та кут
α
можна було вважати незмінними, то на кожній ділянці елементарна робота ΔAk ≈ Fs·Sk чисельно дорівнюватиме площі відповідної смужки на графіку, і згідно з виразом (4.2а), вся робота наближено дорівнює площі площі зафарбованої уступчастої фігури на рис. 4.3.
Аби отриманий у такий спосіб результат був точним, смужки мають бути гранично вузькими (\(\Delta{S}_{k}\to{0}\)). В такому разі ламана на рис. 4.3 зливається з графіком FS = f(S) , тож робота змінної сили на заданому шляху чисельно дорівнює площі під відповідною ділянкою графіка сили. Проте слід зауважити, що точне обчислення цієї площі, знову таки вимагає застосування вищої математики і взагалі не завжди є можливим. Виняток становить тільки лінійна залежність FS(S), коли задана ділянка графіка разом з осями утворює звичайну трапецію чи трикутник.
|
4.2. Кінетична та потенціальна енергія
|
Робота сили в загальному випадку супроводжується зміною положення в просторі й швидкості тіла і є пов'язана із зміною механічної енергії. Існують два види механічної енергії – кінетична та потенціальна. |
|
Кінетична енергія – це "енергія руху". Вона визначається формулами
де m – маса, v – швидкість руху, p = mv – імпульс тіла. Кінетична енергія є адитивною величиною, тобто кінетична енергія системи тіл дорівнює сумі кінетичних енергій окремих тіл, які складають систему:
Між кінетичною енергією та роботою існує універсальний зв'язок, згідно з яким
де Wк1 і Wк2 – початкове та кінцеве значення кінетичної енергії. Із співвідношення (4.4) видно, що енергія, як і робота, вимірюється в джоулях (Дж).
|
|
Серед різноманітних сил існують такі, робота котрих не залежить від форми траєкторії тіла та пройденого шляху, а визначається тільки його початковим і кінцевим положенням. Такі сили називаються консервативними силами й вирізняються з проміж інших тим, що залежать тільки від розташування тіла, на яке діють. За рахунок консервативних сил тіло при зміні положення в просторі може виконувати роботу навіть тоді, коли його швидкість не змінюється. При цьому для кожної з консервативних сил існує фізична величина, що називається потенціальною енергією й визначає вказану роботу, згідно із співвідношенням
де Wп1, Wп2 – початкове та кінцеве значення потенціальної енергії, ΔWп = Wп2 – Wп1 – її приріст (зміна), а "–ΔWп" – спад. Отже,
Із незалежності роботи консервативних сил від траєкторії випливає також, що
Потенціальна енергія як один із видів механічної енергії має важливу особливість. Вираз (4.5) є подібним до виразу (4.4), що визначає роботу через кінетичну енергію тіла в заданих точках. Але на відміну від кінетичної, для потенціальної енергії не існує жодного способу встановити її значення в кожній із точок окремо. Інакше говорячи, потенціальна енергія в точці не є заданою, подібно до того, як не є заданим положення тіла в просторі доки не обрано відповідну систему відліку. Тож, аби надавати потенціальній енергії певних числових значень, треба спочатку вибрати "нульову точку" (початок відліку), тобто вказати положення тіла, в якому його потенціальна енергія приймається рівною нулю. Відтак можна дати наступне означення: . потенціальною енергією тіла в даній точці називається величина, що дорівнює роботі консервативних сил при переміщенні його в нульову точку. При цьому нульову точку можна вибирати довільно, в кожному випадку керуючись лише міркуваннями зручності. (Зауваження. Така можливість пояснюється тим, що в будь-якій задачі результат залежить тільки від зміни потенціальної енергії, а не від її значення в кожній точці окремо). Консервативна сила, як і будь-яка інша, є проявом взаємодії між тілами. Тож потенціальна енергія є їхньою "спільною власністю". Але часто тіла, що взаємодіють, дуже відрізняються за відповідними характеристиками, так що взаємодія помітно змінює стан лише одного з них. Тоді говорять про потенціальну енергію саме цього тіла. До прикладу, ми говоримо про потенціальну енергію тіла, піднятого над Землею, а не про ''потенціальну енергію системи "тіло-Земля''. |
|
Консервативні сили можуть бути різними за фізичною природою та конкретними властивостями, і в кожному випадку потенціальна енергія розраховується за своєю формулою. До прикладу, серед механічних сил консервативними є сили тяжіння (гравітаційні сили) та сили пружності. Відповідно, розрізняють гравітаційну та пружну потенціальну енергію. Для гравітаційних сил із закону всесвітнього тяжіння (2.6) і виразу (4.5) випливає наступна загальна формула гравітаційної потенціальної енергії (енергії тяжіння) Wт :
де G – гравітаційна стала, M, m, відповідно, – маса планети та даного тіла, r – відстань від центра планети до тіла. Для тіла, що перебуває на малій відстані від поверхні планети, цю формулу можна подати (див. Задачу 4.10 )) більш зручно:
де m – маса, g – прискорення вільного падіння і h – висота центра мас тіла відносно нульового рівня, за який приймається будь-яка горизонтальна площина. (Зауваження. Якщо тіло знаходиться нижче нульового рівня, то "висота" h має знак "–", і енергія Wп є від'ємною). |
|
Пружна потенціальна енергія тіла Wпр приймається рівною нулю за відсутності деформацій, що є природньо та зручно, хоча формально й не обов'язково. Зокрема, при деформаціях стиску-розтягу
де k –
жорсткість тіла, x –
величина деформації.
|
|
Згідно з виразами (4.5) – (4.8), робота сил тяжіння та пружності через потенціальну енергію виражається формулами:
|
4.3. Закон збереження механічної енергії
|
Кінетична та потенціальна енергія є складовими повної механічної енергії. Механічна енергія довільної системи, що на загал змінюється з часом, має здатність зберігатися за відповідних умов, які визначаються законом збереження механічної енергії. Отже. |
|
Повною механічною енергією тіла або системи тіл називається сума потенціальної та кінетичної енергії :
(Примітка. "Повною" часто опускають). |
|
Якщо в системі діють лише консервативні сили, то, згідно зі співвідношеннями (4.4) і (4.5), для будь-якого проміжку часу
Цей результат складає зміст закону збереження механічної енергії:
Можна сказати, що в такому разі механічна енергія є "законсервована". Це пояснює термін "консервативні сили". |
|
При наявності неконсервативних сил механічна енергія системи змінюється згідно з універсальним співвідношенням між енергією та роботою:
Неконсервативні сили в механічній системі – то практично завжди є ті чи інші сили тертя та опору. Тому математично закон зміни механічної енергії зазвичай записують у вигляді:
де W1, W2 – початкова та кінцева механічна енергія, Aт – робота всіх внутрішніх сил тертя та опору, що діють між тілами системи, Aзов – робота всіх зовнішніх неконсервативних сил. Якщо система є замкнена (ізольована), то Aзов = 0, і зміна енергії визначається тільки внутрішніми силами тертя та опору
У довільній системі сумарна робота сил тертя та опору може бути й додатньою, як до прикладу, для авто з увімкненим двигуном. Але в замкненій системі завжди Ат < 0, і ΔW < 0. Тобто за наявності тертя та опору середовища механічна енергія ізольованої системи зменшується з часом. Тож важливо пам'ятати, що на відміну від імпульсу, задля збереження механічної енергії однієї лише замкненості системи є недостатньо, необхідна ще й відсутність будь-яких сил тертя та опору. Так само, якщо від'ємна робота внутрішніх сил тертя та опору "компенсується" роботою зовнішніх сил, так що Aт + Aз = 0, то механічна енергія зберігається і в незамкненій системі. Подивившись анімацію і поекспериментувавши з нею, ви зможете краще зрозуміти процеси перетворення енергії. |
4.4. Потужність. ККД механізмів
|
Практична діяльність людини є нерозривно пов'язана з використанням різноманітних двигунів – пристроїв для отримання механічної енергії та виконання роботи за рахунок якихось інших видів енергії, найчастіше хімічної або електричної. Експлуатаційні характеристики двигуна визначаються не просто можливістю виконати якусь роботу, а здатністю виконувати задану роботу за заданий час, тобто – працювати з потрібною інтенсивністю або потужністю. Утворення в двигунах механічної енергії з інших видів завжди відбувається із втратами. Тому ще однією робочою характеристикою двигуна є коефіцієнт корисної дії (ККД). Нагадаємо означення згаданих величин. |
|
Середньою потужністю \( \langle{P}\rangle \) за проміжок часу t називається робота, що припадає на одиницю часу:
Потужність вимірюється у ватах (Вт): 1 Вт = 1 Дж/с – потужність, при якій за 1 с виконується робота 1 Дж. |
|
При стаціонарному режимі роботи вираз (4.15) визначає потужність не лише на загал, а й у будь-який момент. Але коли робота виконується не рівномірно, вона в кожен момент часу характеризується миттєвою потужністю
У техніці потужність механізмів виражається додатніми числами. Але для теорії потужність, є алгебраїчною величиною, знак якої визначається знаком роботи, тобто напрямками сили \( \vec{F}\), що діє на тіло, та його швидкості \( \vec{v}\). За означенням (4.1) \( \Delta{A}=\vec{F}\Delta\vec{S}\), отже, миттєва потужність
де \( \alpha \) – кут між векторами сили та швидкості. Знак потужності сили несе ту саму інформацію, що й знак роботи. |
Як говорилося, у будь-якому механізмі перетворення затраченої енергії Wз (потужності Pз) за рахунок виконаної роботи Аз на потрібну (корисну) енергію Wк (потужність Рк) й виконання корисної роботи Ак завжди супроводжується втратами. Ефективність функціонування механізму, або процесу перетворення енергії характеризується коефіцієнтом корисної дії (ККД) η:
ККД виражають або натуральним числом, або у відсотках (%).
|
4.5. Загальний закон збереження енергії
|
Крім механічної, розглядають й інші види енергії – внутрішню (теплову), електричну, хімічну, ядерну, тощо, – які істотно відрізняються за природою та властивостями. Але визначальною спільною властивістю всіх видів енергії є здатність до взаємних перетворень, у відповідності до загального закону збереження енергії, згідно з яким
Це означає, що
Отже, можна сказати, що
Усякий фізичний процес супроводжується перетвореннями одних видів енергії на інші. Зокрема, відповідно до співвідношень (4.4), (4.5), (4.12), (4.13), (4.14),
При цьому робота консервативних сил визначає взаємоперетворення різновидів механічної енергії. Так само робота неконсервативних сил визначає перетворення механічної енергії на інші види. Зокрема, робота сил тертя та опору визначає перетворення механічної енергії на внутрішню (теплову) енергію. |
4.6. Зіткнення
У механіці зіткненнями називають контактну взаємодію між рухомими тілами за відсутності або компенсації зовнішніх сил. Через це при зіткненнях завжди виконується закон збереження імпульсу. Що ж до механічної енергії, то в загальному випадку вона частково переходить у внутрішню (теплову) енергію тіл. Тож у теорії розглядають два крайні випадки – абсолютно пружні та абсолютно непружні зіткнення.
При абсолютно пружньому зіткненні в тілах виникають тільки пружні деформації при яких на першій стадії (стиснення) кінетична енергія переходить у потенціальну енергію пружної деформації, а на другій (розліт) відбувається відновлення форми тіл та повернення їхньої сумарної кінетичної енергії до початкової величини. Отже,
|
абсолютно пружні зіткнення є підпорядковані законам збереження імпульсу та кінетичної енергії:
\(\sum{{{{\vec{p}}}_{i}}}=\sum{{{{{p}'}}_{i}}}\); \(\sum{{{W}_{ki}}=}\sum{{{{{W}'}}_{ki}}}\). |
(4.18) |
При абсолютно непружному зіткненні виникають тільки пластичні деформації, через що тіла "склеюються", утворюючи одне складене тіло з іншим взаємним розташуванням молекул, аніж у вихідних тілах, отож і з іншою внутрішньою енергією. Тому
|
при непружному зіткненні імпульс системи зберігається, але частина кінетичної енергії втрачається – переходить у внутрішню (теплову) енергію: \(\sum{{{{\vec{p}}}_{i}}}=\sum{{{{{p}'}}_{i}}}\); \(\sum{{{W}_{ki}}=}\sum{{{{{W}'}}_{ki}}}\) + Q. |
(4.19) |
Сказане стосується й зворотніх процесів, коли одне тіло під дією внутрішніх сил розпадається на окремі фрагменти, що супроводжується частковим перетворенням внутрішньої енергії на кінетичну.
Приклади розв'язування задач
При розв’язуванні задач цього розділу, крім найпростіших, треба починати не з пошуків "потрібної формули", а з аналізу складу системи та сил, які діють на кожне тіло, з подальшим складанням рівняння енергетичного балансу на основі загального співвідношення (4.13) між механічною енергією та роботою.
Далі наведено приклади розв'язування задач із наступних тем:
Визначення роботи через силу
Задача 4.1. Брусок маси m повільно тягнуть горизонтальною поверхнею за мотузку, прикладаючи силу під кутом \( \alpha=45^{\circ}\) до горизонту. Визначити роботу A, яку при цьому виконують на шляху S = 6 м при коефіцієнті тертя між бруском і поверхнею \( \mu={0,5}\).
Задача 4.2. По дошці довжиною L, яка лежить на гладкій підлозі, з одного краю на інший пересувають брусок маси m і довжини l. Коефіцієнт тертя між тілами складає μ. Визначити сумарну роботу сили тертя за час пересування бруска.
Задача 4.3. Канат масою m = 6 кг і довжиною l = 5 м лежить на підлозі тренажерної зали з висотою стелі H = 6 м. Визначити роботу, яку треба виконати, аби підвісити канат до стелі.
| Задача 4.1 |
| Задача 4.1 |
Брусок маси m повільно тягнуть по горизонтальною поверхнею за мотузку, прикладаючи силу під кутом \( \alpha=45^{\circ}\) до горизонту.
Визначити
роботу A, яку при цьому виконують на шляху S = 6 м при коефіцієнті тертя між бруском і поверхнею \( \mu={0,5}\).
|
Дано: α = 45°
S = 6 м
μ = 0,5
|
|
A - ? |
Розв’язування
Сили, що діють на брусок, показано на рис. 1. За означенням (1) робота прикладеної до мотузки сили \( \vec{F}\) (рис.1) на шляху S дорівнює
| \( {A}=FS\cos\alpha \). | (1) |
 Позаяк брусок рухається без прискорення, рівнодійна сил \( \vec{F}\), тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\) та тертя \( \vec{F}_{т}\) (рис. 4.1) дорівнює нулю:
Позаяк брусок рухається без прискорення, рівнодійна сил \( \vec{F}\), тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\) та тертя \( \vec{F}_{т}\) (рис. 4.1) дорівнює нулю:
\( \vec{F}+\vec{F}_{т}+m\vec{g}+\vec{N}={0}\),
або в проекціях на осі координат
|
OX: \( {F}\cos\alpha-F_{т}={0}\), OY: \( {F}\sin\alpha+N-mg={0}\). |
Звідси, врахувавши, що \( {F}_{т}=\mu{N}\), дістанемо
\( {F}=\frac{\mu{mg}}{\cos\alpha+\mu\sin\alpha}\)
Відтак підставимо цей вираз у формулу (1) і знайдемо відповідь:
\( {A}=\frac{\mu{mg}S}{\cos\alpha+\mu\sin\alpha}\cdot\cos\alpha \) \( \Rightarrow \) \( {A}=\frac{\mu{mg}S}{1+\mu\mathrm{tg}\alpha}={19,6}\) Дж.
| Задача 4.2 |
| Задача 4.2 |
По дошці довжиною L, яка лежить на гладкій підлозі, з одного краю на інший пересувають брусок маси m і довжини l. Коефіцієнт тертя між тілами складає μ.
Визначити
сумарну роботу сили тертя за час пересування бруска.
|
Дано: m, l L μ |
|
А - ? |
Розв’язування
Між дошкою та бруском діють сили тертя \( \vec{F}_{1}\) = –\( \vec{F}_{2}\) (рис. 2) з модулем F = μmg, сумарна робота котрих
ККК
A = А1 + А2 = –μmgS1 + μmgS2 = –μmg( S1 – S2),
де S1 і S2 – модулі переміщення бруска і дошки відносно підлоги.
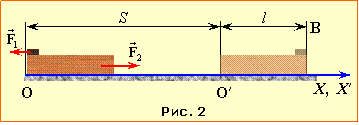
З рис. 2 видно, що ( S1 – S2) = (L – l), тож відповідь:
| A = – μmg(L – l). | (1) |
Ця задача є дуже простою й сама по собі не становить великого інтересу. Але, позаяк у системі сили взаємодії між парами тіл є незалежні, а самі сили є рівні за модулем і протилежні за напрямом (див. Розділ 2, п.п. 2.1, 2.2), отриманий результат відображує загальні властивості роботи сил тертя та опору:
1. Робота сили тертя, що діяла на дошку, А2 = μmgS2 > 0, проте повна робота А < 0. Це вказує на те, що
Повна робота внутрішніх сил тертя та опору в будь-якій системі завжди є від'ємна.
2. Величина (L – l) – це модуль переміщення ${{\vec{s}}_{12}}$ бруска відносно дошки та дошки відносно бруска ${{\vec{s}}_{21}}$ = – ${{\vec{s}}_{12}}$. Отже, в загальному вигляді відповідь (1) можна подати як
А = \( \vec{F}_{1}\)${{\vec{s}}_{12}}$ = \( \vec{F}_{2}\)${{\vec{s}}_{21}}$
і зробити наступний висновок:
сумарна робота сил тертя між двома тілами \( \vec{F}_{1}\) = –\( \vec{F}_{2}\) дорівнює добутку сили, що діє на одне з тіл на його переміщення відносно іншого.
Задача 4.3. Канат масою m = 6 кг і довжиною l = 5 м лежить на підлозі тренажерної зали висотою стелі H = 6 м.
роботу, яку треба виконати, аби підвісити канат до стелі.
|
Дано: |
|
А - ? |
Розв'язання
На початку підйому, доки переміщення кінця каната h є меншим за його довжину l, мінімальна потрібна сила F дорівнює вазі частини довжиною х, що звисає:
$F=\frac{mg}{l}h$,
а потім – вазі всього каната
F = mg.
Таким чином, маємо визначати роботу змінної сили, що найпростіше зробити, обчисливши площу під графіком сили рис. 3 (див. п. 4.1), тобто площу трапеції з основами H і (H – l) та висотою mg. Отже,
$A=\frac{1}{2}mg\left( 2H-l \right)$ = 210 Дж.
Визначення роботи через механічну енергію
Задача 4.4. Однорідний циліндричний стовб масою m і довжиною l лежить на землі. Визначити роботу A, яку треба виконати, аби поставити його вертикально.
Задача 4.5. При розтяганні недеформованої пружини виконано роботу A1 = 5 Дж. Визначити роботу A2, яку додатково слід виконати, аби видовжити пружину ще на η = 20% початкового розтягу.
Задача 4.6. Циліндричний колодязь діаметром d = 1,5 м та глибиною H = 20 м наполовину заповнено водою (\( \rho={1}\) г/см3). Визначити роботу A, яку має виконати електрична помпа, аби викачати всю воду з колодязя. Кінетичну енергією води та втрати в помпі не рахувати.
Задача 4.7. Авто масою m = 1 т спускається з вимкненим двигуном із вершини гори висотою h = 100 м і, пройшовши якийсь шлях по горизонталі, зупиняється. Визначити роботу A, що її має виконати двигун, аби авто повернулося назад шляхом спуску.
Задача 4.8. Кульку масою m = 10 г, яка висить на нитці довжиною l = 1 м, розкручують у горизонтальній площині так, що нитка відхиляється від вертикалі на кут φ = 10°. Визначити роботу A по розкручуванню кульки.
Задача 4.9. Прийнявши радіус Землі R = 6400 км, знайти відношення робіт (A2/A1) необхідних, аби підняти тіло на висоту h = 3200 км над поверхнею Землі (A1) та вивести його на колову орбіту такої самої висоти (A2).
Задача 4.10. Довести, що формула потенціальної енергії тіла біля поверхні планети (Wп = mgh) є:
1) окремим випадком загальної формули (4.6);
2) придатною для тіла довільних розмірів і форми, де h – висота розташування його центра мас.
| дача 4.3 |
| Задача 4.4 |
Однорідний циліндричний стовб масою m і довжиною l лежить на землі.
Визначити
роботу A, яку треба виконати, аби поставити його вертикально.
|
Дано: m, l |
|
A - ? |
Розв'язання
Ця задача змістовно є подібною до задачі 4.3. Але розв'язувати її через пряме обчислення немає потреби, позаяк робота проти сили тяжіння при підніманні стовба дорівнює зміні його потенціальної енергії (див. п.п. 4.1, 4.2). Тож, прийнявши її в початковому положенні стовба за нуль і врахувавши, що його центр мас знаходиться посередині, одразу дістанемо відповідь:
\( {A}=\frac{1}{2}{mgl}\).
Зверніть увагу на ефективність і простоту "енергетичного" способу розв'язання, при якому задача фактично є усною.
| Задача 4.4 |
| Задача 4.5 |
При розтяганні недеформованої пружини виконано роботу A1 = 5 Дж.
Визначити
роботу A2, яку додатково слід виконати, аби розтягти пружину ще на η = 20% від початкового видовження.
|
Дано: A1 = 4 Дж η = 20% |
|
А2 - ? |
Розв'язання
Робота по розтяганню пружини йде на зміну її потенціальної енергії. Тож, оскільки потенціальна енергія не розтягненої пружини Wп0 = 0, початкова робота, згідно з виразами (4.5) і (4.8), дорівнює
|
\( {A}_{1}=W_{п1}=\frac{kx_{1}^{2}}{2}\), |
(1) |
де k – жорсткість пружини, x1 – її початковий розтяг.
Робота, потрібна для додаткового розтягання пружини, дорівнює:
|
\( {A}_{2}=W_{п2}-W_{п1}\) = $\frac{k}{2}\left( x_{2}^{2}-x_{1}^{2} \right)$, |
(2) |
де кінцеве видовження пружини за умовою складає
х2 = х1 +ηх1 = (1 + η)х1.
Відтак підставивши цю величину у вираз (2) і врахувавши вираз (1), після елементарних викладок отримаємо наступну відповідь:
А2 = 2(2 + η)А1 = 2,2 Дж.
| Задача 4.5 |
| Задача 4.6 |
Циліндричний колодязь діаметром d = 1,5 м та глибиною H = 20 м наполовину заповнено водою (\( \rho={1}\) г/см3).
Визначити
роботу A, яку має виконати електрична помпа, аби викачати всю воду з колодязя. Кінетичну енергією води та втрати в помпі не рахувати
|
Дано: d = 1,5 м
H = 20 м
\( \rho={1}\) г/м3
|
|
A - ? |
Розв'язання
 Робота помпи йде на збільшення потенціальної енергії води:
Робота помпи йде на збільшення потенціальної енергії води:
A = Wп2 – Wп1.
Приймемо за нульовий рівень горизонтальну площину, що проходить через центр мас води перед початком відкачування (т. 1 на рис. 6), тоді Wп1 = 0. У процесі відкачування помпа кожну частинку, тож і всю воду, підіймає до рівня 2, що розташований на висоті \( {h}=\frac{3H}{4}\) від початкового положення центра мас води і надає їй потенціальної енергії Wп2 = mgh. Отже,
\( {A}=\frac{3mgH}{4}\).
Маса води в колодязі \( {m}=\frac{\rho{S}H}{2}=\frac{\pi{d}^{2}\rho{H}}{8}\), таким чином корисна робота насоса, котру треба знайти, дорівнює
\( {A}=\frac{3\pi{d^{2}}\rho{g}H^{2}}{32}\) = 2,6 МДж.
| Задача 4.6 |
| Задача 4.7 |
Авто масою m = 1 т спускається з вимкненим двигуном із вершини гори висотою h = 100 м, і пройшовши якийсь шлях по горизонталі, зупиняється.
Визначити
роботу A, що її має виконати двигун, аби авто повернулося назад шляхом спуску.
|
Дано: m = 1000 кг
h = 100 м
|
|
A - ? |
Розв'язання
На спуску авто за рахунок своєї потенціальної енергії виконує роботу А′ проти сил тертя та опору, отже
А′ = mgh.
Ту саму роботу проти сил тертя та опору на підйомі має виконати двигун. Але він має ще й надати автомобілю потенціальної енергії W = mgh. Отже, повна робота двигуна складає
А = 2mgh.
| Задача 4.7 |
| Задача 4.8 |
Кульку масою m = 10 г, яка висить на нитці довжиною l = 1 м, розкручують у горизонтальній площині так, що нитка відхиляється від вертикалі на кут φ = 10°.
Визначити
роботу A по розкручуванню кульки.
|
Дано: m = 10 г l = 1 м φ = 10°
|
|
A - ? |
Розв’язання
При розкручуванні кулька піднімається на деяку висоту h над початковим рівнем і набуває певної швидкості v, рис. 8. При цьому змінюються її кінетична Wк, потенціальна Wп та повна механічна енергія W. Згідно із виразом (4.13), зміна повної енергії кульки \( \Delta{W}\) дорівнює роботі по розкручуванню:
| \( {A}=\Delta{W}=\Delta{W}_{п}+\Delta{W}_{к}=mgh+\frac{mv^{2}}{2}\) | (1) |
Таким чином, задача зводиться до визначення швидкості кульки v та висоти підйому h .
З рис. 4.8 видно, що
\( {h=AB-OB}=l-l\cos\varphi=2l\sin^{2}\left(\frac{\varphi}{2}\right) \).
Для малих кутів (виражених в радіанах) sinφ = φ, тож
|
$h=\frac{l{{\varphi }^{2}}}{2}$. |
(2) |
Рух кульки по коловій траєкторії відбувається під дією рівнодійної сил тяжіння \( {m}\vec{g}\) та натягу нитки ${{\vec{F}}_{н}}$, що визначається, як
\( {F}=mg\mathrm{tg}\varphi=mg{\varphi}\).
З іншого боку, ${{F}_{\text{н}}}=\frac{m{{v}^{2}}}{r}$ (формули (2.5) та (1.28)), отже
| \( {m}g\varphi=\frac{mv^{2}}{r}\); \( \Rightarrow \) \( {v}^{2}=gr\varphi \). | (3) |
Із рис. 4.8 видно, що \( {r}=l\sin\varphi=l\varphi \), тож
\( {v}^{2}=gl\varphi^{2}\).
Відтак підставивши вирази h (2) і v2 (3) у формулу (1), визначимо роботу розкручування:
\( {A}=mg\frac{l\varphi^{2}}{2}+mg\frac{l\varphi^{2}}{2}=mgl\varphi^{2}\),
і, (виразивши величину φ в радіанах), знайдемо числову відповідь:
А = 0,003 Дж = 3 мДж.
| Задача 4.9. |
| Задача 4.9 |
Прийнявши радіус Землі R = 6400 км,
визначити
відношення робіт (A2/A1), які треба виконати, аби підняти тіло на висоту h = 3200 км над поверхнею Землі (A1) та вивести його на колову орбіту такої самої висоти (A2).
|
Дано: h = 3200 км
R = 6400 км
|
|
(A2/A1) - ? |
Розв'язання
Мінімальна робота, потрібна для підйому тіла на якусь висоту, дорівнює зміні його потенціальної енергії: A = Wп2 – Wп1. При підйомі на вказану в умові висоту сила тяжіння та прискорення g помітно змінюються. Тож зміна потенціальної енергії тіла маси m визначається формулою (4.10):
\( {A}=G\frac{Mm}{r_{1}}-G\frac{Mm}{r_{2}}\),
де M – маса Землі, а r – відстань від тіла до центра Землі. У вихідному положенні тіло знаходилось на поверхні Землі, тому r1 = R. У кінцевому положенні r2 = R + h. Отже,
| \( {A}_{1}=GMm\left(\frac{1}{R}-\frac{1}{R+h}\right)=GMm\frac{h}{R(R+h)}\). | (1) |
При виведенні на колову орбіту тілу, крім зміни потенціальної енергії, треба надати необхідну орбітальну швидкість і кінетичну енергію. Тож робота по виведенню тіла на орбіту складає
| \( {A}_{2}=A_{1}+\frac{mv^{2}}{2}\). | (2) |
Орбітальну швидкість супутника визначимо за допомогою другого закону Ньютона \( {F}=ma \), де \( {F}=G\frac{Mm}{(R+h)^{2}}\) , і \( {a}=\frac{v^{2}}{R+h}\) – доцентрове прискорення на орбіті радіуса r2 = R + h. Отже,
\( {G}\frac{Mm}{(R+h)^{2}}=\frac{mv^{2}}{(R+h)}\) \( \Rightarrow \) \( {m}v^{2}=G\frac{Mm}{R+h}\).
Підставивши це значення в формулу (2), отримаємо:
\( {A}_{2}=A_{1}+\frac{FMm}{2(R+h)}\),
а для відношення робіт
\( \frac{A_{2}}{A_{1}}=1+\frac{GMm}{2(R+h)A_{1}}\)
і, підставивши вираз (1), знайдемо відповідь:
\( \frac{A_{2}}{A_{1}}=1+\frac{R}{2h}={2}\).
| Задача 4.10. |
|||
| Задача 4.10. | |||
|
Довести, що формула потенціальної енергії тіла біля поверхні планети (Wп = mgh) є: 1) окремим випадком загальної формули (4.6); 2) придатною для тіла довільних розмірів і форми, де h – висота розташування його центра мас.
Доведення 1). При піднятті тіла масою m з поверхні планети маси M і радіуса R на висоту h зміна його потенціальної енергії згідно з виразом (4.6) складає Wп – Wп0 = $GmM\left( \frac{1}{R}-\frac{1}{R+h} \right)=\frac{GMmh}{R\left( R+h \right)}$ і не залежить від положення нульового рівня потенціальної енергії (див. п. 4.2). Але, позаяк при його виборі на поверхні планети Wп0 = 0, отриманий вираз визначає саму потенціальну енергію тіла на висоті h. Перепишемо його у вигляді
і, врахувавши вираз (2.9) та те, що біля поверхні планети величина h у формулі (1) є неістотною, отримаємо ${{W}_{п}}=mgh$, що й було треба. 2). Потенціальна енергія довільного тіла у полі сил тяжіння складається з потенціальних енергій всіх його частин: ${{W}_{\text{}}}=\sum{\Delta {{W}_{i}}}$. Тому, якщо тіло подумки поділити на гранично вузькі горизонтальні смужки масами Δmi, (одну з них показано на рис. 4.10), то ${{W}_{\text{п}}}=g\sum{{{m}_{i}}{{h}_{i}}}$, де hi – висота розташування смужки відносно нульового рівня. Відтак помноживши й поділивши цей вираз на масу всього тіла, отримаємо: ${{W}_{\text{п}}}=mg\frac{\sum{{{m}_{i}}{{h}_{i}}}}{m}$, або, з урахуванням виразу (3.6а), ${{W}_{\text{п}}}=mgh$, де h = Yс – вертикальна координата центра мас тіла.
|
Визначення потужності та ККД
Задача 4.11. На ділянці траси з ухилом \(\alpha=5^{\circ}\) авто має швидкість v1 = 36 км/год на підйомі і v2 = 54 км/год – на спуску. Визначити швидкість авта v3 при русі горизонтальною ділянкою тієї самої траси, якщо двигун у всіх випадках розвиває однакову потужність.
Задача 4.12. Легкомоторний літак масою m = 1 т розганяється із сталим прискоренням до швидкості v = 30 м/с злітною смугою довжини S = 300 м . Визначити середню потужність \( \langle{P}\rangle \) двигуна літака на злеті, якщо коефіцієнт опору \( \mu={0,3}\).
Задача 4.13. Вантаж піднімають похилою площиною з кутом нахилу α до горизонту, прикладаючи силу вздовж площини. Визначити ККД η площини, якщо її коефіцієнт тертя із вантажем становить \( \mu \).
Задача 4.14. Вантаж маси M = 50 кг повільно підіймають за допомогою системи з рухомого та нерухомого блоків, прикладаючи силу до вільного кінця мотузки. Маса рухомого блока m = 5 кг. Визначити ККД \( \eta \) механізму. Маса мотузки та тертя в осях є неістотні.
На ділянці траси з ухилом \(\alpha=5^{\circ}\) авто має швидкість v1 = 36 км/год на підйомі і v2 = 54 км/год – на спуску.
Визначити
швидкість авта v3 при русі горизонтальною ділянкою тієї самої траси, якщо двигун у всіх випадках розвиває однакову потужність.
|
Дано: v1 = 36 км/год
v2 = 54 км/год
\( \alpha=5^{\circ}\)
|
|
v3 - ? |
Розв’язування
Відповідно до формули (4.16) шукана швидкість авта визначається, як
| \(v=\frac{P}{F}\), | (1) |
але потрібні для цього робоча потужність двигуна P і сила тяги F3 в умові задачі не вказано. Проте однаковість потужності двигуна в усіх випадках дозволяє знайти швидкість v3 через її порівняння із заданими величинами v1 і v2.
Авто в кожному випадку рухається із сталою швидкістю, тож сили тяги двигуна \( \vec{F}\), тяжіння \( {m}\vec{g}\), нормальної реакції дороги \( \vec{N}\) та опору \( \vec{F}_{оп}\) (рис. 4.11) є компенсовані:
| \( \vec{F}+\vec{N}+m\vec{g}+\vec{F}_{оп}={0}\). | (2) | |
 |
Запишемо умову (2) в проєкціях на напрям руху авто для кожного випадку. При цьому, взявши до уваги малість кута α, покладемо cosα = 1 i sinα = α(рад). Тоді N = mg, проєкція \( {m}\vec{g}\) на напрям руху на похилій ділянці складає mgα, тож умови (2) набувають вигляду:
| \( {F}_{1}-mg\alpha-F_{оп}={0}\), | (3) | |
| \( {F}_{2}+mg\alpha-F_{оп}={0}\), | (4) | |
| \( {F}_{3}-F_{оп}={0}\) |
(5) |
Далі додавши рівняння (3) та (4) і врахувавши, що згідно з (5) Fоп = F3, отримаємо співвідношення між силами тяги двигуна:
F1 + F2 – 2F3 = 0 \( \Rightarrow \) F1 + F2 = 2F3.
Нарешті, виразивши в отриманому рівнянні сили через відношення потужності до швидкості, дістанемо відповідь:
\( \frac{P}{v}_{1}+\frac{P}{v_{2}}=2\frac{P}{v}_{3}\) \( \Rightarrow \) \( \frac{1}{v_{1}}+\frac{1}{v_{2}}=\frac{2}{v_{3}}\) \( \Rightarrow \) \( {v}_{3}=\frac{2v_{1}v_{2}}{v_{1}+v_{2}}\).
Обчислення дають
v3 = 43 км/год.
Легкомоторний літак масою m = 1 т розганяється із сталим прискоренням до швидкості v = 30 м/с злітною смугою довжини S = 300 м .
Визначити
середню потужність \( \langle{P}\rangle \) двигуна літака на злеті, якщо коефіцієнт опору \( \mu={0,3}\).
|
Дано: m = 1 т
S = 300 м
v = 30 м/с
\( \mu=0,3 \)
|
|
\( \langle{P}\rangle\) - ? |
Розв’язування
Середня потужність дорівнює відношенню зробленої роботи до часу її виконання:
| \( \langle{P}\rangle=\frac{A}{t}\). | (1) |
Згідно з виразом (4.4), кінетична енергія, отримана літаком за час розгону, дорівнює сумі роботи двигуна А та роботи сил опору Аоп. Отже,
A = Wк – Aоп = \(\frac{mv^{2}}{2}\) + μmgS,
де враховано вираз сили опору та те, що Aоп < 0.
Час розгону визначимо через відстань S та кінцеву швидкість v з рівнянь кінематики (1.16):
\( \left. \begin{matrix} S=\frac{a{{t}^{2}}}{2} \\ v=at \\\end{matrix} \right\}\ \ \ \ \ \Rightarrow \ \ \ \ \ \frac{S}{v}=\frac{t}{2}\ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ t=\frac{2S}{v}\).
Підставивши отримані вирази А та t у формулу (1), знайдемо відповідь:
\( \langle{P}\rangle=\frac{mv}{2}\left(\frac{v^{2}}{2S}+\mu{g}\right)={66,6}\) кВт.
Вантаж піднімають похилою площиною з кутом нахилу α до горизонту (рис. 4.13), прикладаючи силу вздовж площини.
Визначити
ККД η похилої площини, якщо її коефіцієнт тертя із вантажем становить μ.
|
Дано: \( \alpha\)
\( \mu \)
|
|
\( \eta \) - ? |
Розв’язування
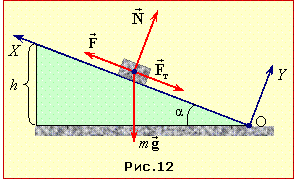
ККД похилої площини дорівнює відношенню потенціальної енергії піднятого вантажу W до роботи А прикладеної сили \( \vec{F}\), рис. 4.13:
| η = \(\frac{W}{A}\) = \(\frac{mgh}{FS}\). | (1) |
де m – маса вантажу, h – висота підйому, S – пройдений шлях.
Сила F долає "скочувальну" складову сили тяжіння mg·sinα та силу тертя Fт = μN = μmg·cosα і має величину
F = mg·sinα + μmg·cosα = mg(sinα + μcosα).
Шлях вантажу
|
$S=\frac{h}{\sin \alpha }$ |
Підставивши значення F i S у вираз (1), після елементарних перетворень отримаємо наступну відповідь:
$\eta =\frac{1}{1+\operatorname{ctg}\alpha }$.
Вантаж маси M = 50 кг повільно підіймають за допомогою системи з рухомого та нерухомого блоків (рис. 4.14), прикладаючи певну силу до вільного кінця мотузки. Маса рухомого блока m = 5 кг.
Визначити
ККД \( \eta \) механізму.
|
Дано: M = 50 кг
m = 5 кг
|
|
\( \eta \) -? |
Розв’язування
 Рухомий блок і вантаж можна розглядати як одне тіло маси (M+m), на яке діють сила тяжіння \( {(M+m)}\vec{g}\) та дві сили натягу мотузки \( \vec{T}\), рис. 4.14.
Рухомий блок і вантаж можна розглядати як одне тіло маси (M+m), на яке діють сила тяжіння \( {(M+m)}\vec{g}\) та дві сили натягу мотузки \( \vec{T}\), рис. 4.14.
Вантаж піднімають повільно, тож сили є зрівноважені:
(M +m)g = 2T.
Так само зрівноважені є й прикладена сила та сила натягу мотузки: T = F. Отже,
\( {(M+m)}g={2F}\) \( \Rightarrow \) \( {F}=\frac{(M+m)g}{2}\).
Цей результат ілюструє функціональне призначення блокових механізмів – піднімання вантажів силою, меншою за їхню вагу.
При піднятті вантажу разом із блоком на висоту h кінець мотузки переміщується на відстань \( {l}={2h}\), і робота сили F (затрачена робота)
\( {A}=Fl=\frac{(M+m)g}{2}\cdot{2h}=(M+m){gh}\).
Але корисною є робота тільки по підйому вантажу \( {A}_{к}=Mgh \), тож ККД цієї системи блоків дорівнює:
\( \eta=\frac{A_{к}}{A}=\frac{M}{M+m}\) = 91 %.
Зауважимо, що задачу можна розв’язати і без прямого визначення роботи, використовуючи зв’язок між нею та механічною енергією. Справді, затрачена робота дорівнює зміні потенціальної енергії всієї системи, тоді як корисна — тільки вантажу. Отже,
\( {A}=(M+m)gh \), \( {A}_{к}={Mgh}\),
і
\( \eta=\frac{A_{к}}{A}=\frac{Mgh}{(M+m)gh}=\frac{M}{M+m}\),
що, природньо, збігається з отриманим раніше результатом.
Робота та зміна механічного стану системи
Задача 4.15. Завантажений самоскид рухається прямою горизонтальною дорогою зі швидкістю v = 36 км/год при коефіцієнті опору μ = 0,05. Визначити, на якій відстані S від місця розвантаження водій має вимкнути двигун, аби дістатися туди без використання гальм, і який час Δt для цього знадобиться?
Задача 4.16. Куля перпендикулярно вдаряє в стос міцно закріплених одна за одною однакових дощок. Визначити, в якій за ліком дошці застрягне куля, якщо в першій вона втрачає \(\eta={10}\) % швидкості? Силу опору в дошках уважати незалежною від швидкості кулі.
Задача 4.17. Кулька для пінг-понгу маси m = 20 г вільно падає на підлогу з висоти H = 2 м і пружно (без утрати швидкості) відскакує на висоту h = 1,6 м. Визначити силу опору повітря F, що діє на кульку, вважаючи її сталою.
Задача 4.18. Кульку для пінг-понгу радіуса R = 1,5 см та маси m = 10 г занурили у воду на глибину H = 1м і відпустили. Визначити висоту h, на яку підскочить кулька після спливання. Сили опору (в'язкість) та поверхневий натяг не враховувати. Густина води \( \rho \) = 1 г/см3.
Задача 4.19. Іграшковий електровоз із моторчиком рухається зі швидкістю v горизонтальною коловою колією радіуса R. Визначити, кількість обертів N, яку він зробить по колу до зупинки після вимикання двигуна при коефіцієнті опору μ.
Задача 4.20. Санки довжиною l = 1 м, що рухалися горизонтальною заледенілою дорогою зі швидкістю v = 5 м/с, потрапили на очищену ділянку й зупинилися, коли передній край пройшов по ній шлях S = 2,5 м. Визначити коефіцієнт тертя μ санок об очищену дорогу.
Задача 4.21. Шприц площею перерізу S = 2 см2 і довжиною l = 5 см повністю заповнено водою. Площа перерізу отвору голки S0 = 0,5 мм2. Визначити час τ, за який із шприца випорсне вся вода при прикладанні до поршня сили F = 1,6 Н, уважаючи швидкість струменя сталою. Густина води \( \rho=\) 1 г/см3.
Завантажений самоскид рухається прямою горизонтальною дорогою зі швидкістю v = 36 км/год при коефіцієнті опору μ = 0,05Н.
Визначити,
на якій відстані S від місця розвантаження водій має вимкнути двигун, аби дістатися туди без використання гальм, і який час Δt для цього знадобиться?
|
Дано: v = 36 км/год
μ = 0,05
|
|
S - ? Δt - ? |
Розв'язання
Після вимкнення двигун самоскида на шляху S до місця розвантаження виконує роботу проти сили опору F (рис. 4.15), що дорівнює його початковій кінетичній енергії:
\(8FS=\frac{m{{v}^{2}}}{2}\quad \Rightarrow \quad S=\frac{m{{v}^{2}}}{2S}\).
Коефіцієнтом опору називається відношення сили опору до ваги самоскида, тож величина його прискорення при гальмуванні a = μg, і шлях до зупинки
\( {S}=\frac{v^{2}}{2\mu{g}}\) = 100 м.
Час руху до зупинки визначаємо за другим законом Ньютона (2.3):
\(\vec{F}=\frac{\Delta \vec{p}}{\Delta t}\quad \Rightarrow \quad \Delta t=\frac{v}{\mu g}=20\text{ c}\text{.}\)
Куля перпендикулярно вдаряє в стос міцно закріплених одна за одною однакових дощок.
Визначити,
в якій за ліком дошці застрягне куля, якщо в першій вона втрачає \( \eta={10}\) % швидкості? Силу опору в дошках уважати незалежною від швидкості кулі.
|
Дано: η=10% |
|
N - ? |
Розв'язання
За умовою дошки мають однакову товщину, і в кожній на кулю діє однакова сила опору. Тому при пробиванні будь-якої дошки куля втрачає таку саму енергію \( \Delta{W}\), як і в першій дошці:
\( \Delta{W}=\frac{m_{0}^{2}}{2}-\frac{m_{1}^{2}}{2}\),
де m – маса кулі, v0, v1 – швидкість кулі на вльоті та на вильоті з першої дошки, рис. 4.16. Згідно з умовою \( {v}_{1}=(1-\eta)v_{0}\), тому
\( \Delta{W}=\frac{mv_{0}^{2}}{2}\left(1-(1-\eta^{2})\right)\) \( \Rightarrow \) \( \Delta{W}=W_{0}\eta(2-\eta) \),
де \( {W}_{0}\) – початкова кінетична енергія кулі.
Таким чином, кількість пробитих дощок
\( {n}=\frac{W_{0}}{\Delta{W}}=\frac{1}{\eta{(2-\eta)}}\) = 5,26.
Отже, номер дошки, в якій застряне куля,
N = 6.
Кулька для пінг-понгу маси m = 20 г вільно падає на підлогу з висоти H = 2 м і пружно (без утрати швидкості) відскакує на висоту h = 1,6 м.
Визначити
силу опору повітря F, що діє на кульку, вважаючи її сталою.
|
Дано: m = 20 г = 0,02 кг
H = 2 м
h = 1,6 м
|
|
F - ? |
Розв'язання
Унаслідок дії сили опору повітря механічна енергія кульки змінюється на величину роботи цієї сили. В початковому та кінцевому положеннях кулька перебуває в спокої і має лише потенціальну енергію. Тож, прийнявши її рівною нулю на підлозі, маємо:
A = mgh – mgH = mg(h – H).
На від початкового до кінцевого положення кульки S = H + h сила опру виконує роботу A = –F(H + h), отже,
\( {m}g(H-h)=F(H+h)\) \( \Rightarrow \) \( F=\frac{H-h}{H+h}{mg}\) ≈ 2,2 Н.
Кульку для пінг-понгу радіуса R = 1,5 см та маси m = 10 г занурили у воду на глибину H = 1 м і відпустили.
Визначити
висоту h, на яку підскочить кулька після спливання. Сили опору (в'язкість) та поверхневий натяг не враховувати. Густина води \( \rho \) = 1 г/см3.
|
Дано: R = 1,5 см
m = 10 г
H = 1 м = 100 см
\( \rho \) = 1 г/см3
|
|
h - ? |
Розв'язання
На кульку при спливанні, крім сили тяжіння, на шляху H діє неконсервативна архімедова сила \( \vec{F}\) (рис. 4.18). Згідно із співвідношенням (4.13), її робота на шляху H дорівнює зміні механічної енергії кульки при піднятті на на висоту H + h:
mg(H + h) = FH.
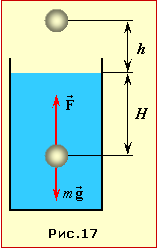 Виразивши архімедову силу за формулою (6.8) через густину води та радіус кульки, як
Виразивши архімедову силу за формулою (6.8) через густину води та радіус кульки, як
\( {F}=\rho{gV}=\rho\frac{4}{3}\pi{R^{3}}{g}\),
отримаємо:
\( {m}(H+h)=\frac{4\pi{R^{3}\rho{H}}}{3}\) \( \Rightarrow \) \( {h}=H\left(\frac{4\pi{R^{3}\rho}}{3m}-1\right) \) ≈ 41 см.
| Задача 4.18 |
| Задача 4.19 |
Іграшковий електровоз із моторчиком рухається зі швидкістю v горизонтальною коловою колією радіуса R.
Визначити,
кількість обертів N, яку він зробить по колу до зупинки після вимикання двигуна при коефіцієнті опору μ.
|
Дано: v
R
μ
|
|
N - ? |
Розв'язання
На початку гальмування вагончик мав кінетичну енергію \( {W}_{1}=\frac{mv^{2}}{2}\), яка надалі зменшилася до нуля (\( {W}_{1}={0}\)) за рахунок роботи A сили опору. Позаяк при русі горизонтальною поверхнею потенціальна енергія вагончика не змінюється, то
\( \Delta{W}=-\frac{mv^{2}}{2}=-F\cdot{S}\) \( \Rightarrow \) \( \frac{mv^{2}}{2}={FS}\),
де F - сила опору, S - пройдений вагончиком шлях, який пов'язаний з кількістю обертів по колу очевидним співвідношенням \( {S}=2\pi{RN}\). Таким чином,
\( {N}=\frac{mv^{2}}{4\pi{RF}}\).
Сила опору \( {F}=\mu{N}=\mu{mg}\), отже
\( {N}=\frac{v^{2}}{4\pi\mu{Rg}}\).
Задача 4.20.
Санки довжиною l = 1 м, що рухалися горизонтальною заледенілою дорогою зі швидкістю v = 5 м/с, потрапили на очищену ділянку й зупинилися, коли передній край пройшов по ній шлях S = 2,5 м. Визначити
коефіцієнт тертя μ санок об очищену дорогу.
|
Дано: \( {l}\)=1 м
v = 5 м/с
S = 2,5 м
|
|
\( \mu \) - ? |
Розв'язання
Крім сили тертя на санки діють сила тяжіння та сила нормальної реакції дороги Однак останні дві сили роботи не виконують, тому зміна кінетичної енергії санок при гальмуванні на асфальті зумовлена тільки роботою сили тертя:
| \( \Delta{W}_{к}=A_{т}\) \( \Rightarrow \) \( {-}\frac{mv^{2}}{2}=A_{т}\) \( \Rightarrow \) \( \frac{mv^{2}}{2}=|A_{т}| \) | (1) |
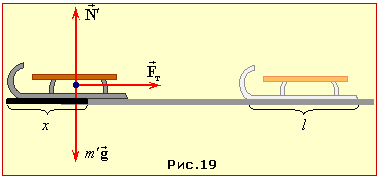 У процесі гальмування, доки санки не повністю виїхали на асфальт, сила тертя є змінною, позаяк частина санок, яка знаходиться на асфальті, поступово збільшується. Величина сили тертя \( {F}_{т}=\mu{N}=\mu{m^{\prime}}g\), де \( \mu \) – шуканий коефіцієнт тертя, а \( {m^{\prime}}\) – маса частини санок, що вже виїхала на асфальт (рис. 4.20). Очевидно, що \( {m}^{\prime}=(m/l){x}\), де \( {l}\) – довжина санок, а x - довжина їхньої частини, що знаходиться на асфальті. Отже \( {F}_{т}(x)=\frac{\mu{mg}x}{l}\), \( {x}\le{l}\).
У процесі гальмування, доки санки не повністю виїхали на асфальт, сила тертя є змінною, позаяк частина санок, яка знаходиться на асфальті, поступово збільшується. Величина сили тертя \( {F}_{т}=\mu{N}=\mu{m^{\prime}}g\), де \( \mu \) – шуканий коефіцієнт тертя, а \( {m^{\prime}}\) – маса частини санок, що вже виїхала на асфальт (рис. 4.20). Очевидно, що \( {m}^{\prime}=(m/l){x}\), де \( {l}\) – довжина санок, а x - довжина їхньої частини, що знаходиться на асфальті. Отже \( {F}_{т}(x)=\frac{\mu{mg}x}{l}\), \( {x}\le{l}\).
Після того, як санки повністю виїдуть на асфальт (\( {x}\ge{l}\)), сила тертя стає рівною \( \mu{mg}\) і надалі не змінюється. Отже графік сили тертя має вигляд рис. 4.20-1. Як сказано в теорії (п. 4.1), площа під ним чисельно дорівнює модулю роботи сили тертя:
\( {|A_{т}|}=\frac{1}{2}(S+S-l)\mu{mg}=\frac{\mu{mg}(2S-l)}{2}\).
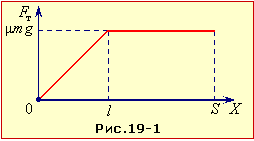 Підставивши цей вираз у формулу (1), дістанемо
Підставивши цей вираз у формулу (1), дістанемо
\( \mu=\frac{v^{2}}{g(2S-l)}={0,64}\).
| Задача 4.20 |
| Задача 4.21 |
Шприц площею перерізу S = 2 см2 і довжиною l = 5 см повністю заповнено водою. Площа перерізу отвору голки S0 = 0,5 мм2.
Визначити
час τ, за який із шприца випорсне вся вода при прикладанні до поршня сили F = 1,6 Н, уважаючи швидкість струменя сталою. Густина води \( \rho=\) 1 г/см3.
|
Дано: S = 2 см2
l = 5 см
S0 = 0,5 мм2
F = 1,6 Н
ρ = 1 г/см3
|
|
τ–? |
Розв'язання
Початковий об'єм води у шприці V = lS. Якщо позначити об'єм води, що виходить із шприца за одиницю часу, як v, то час витікання всієї води
|
$\tau =\frac{V}{v}$. |
(1) |
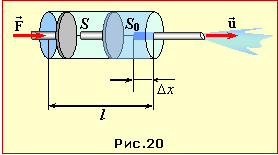 Для визначення величини v виділимо тонкий шар води об'ємом \( \Delta{V}=S_{0}\Delta{x}\), що прилягає до отвору голки, рис. 4.21. Ця вода при швидкості руху частинок u пройде крізь отвір за час
Для визначення величини v виділимо тонкий шар води об'ємом \( \Delta{V}=S_{0}\Delta{x}\), що прилягає до отвору голки, рис. 4.21. Ця вода при швидкості руху частинок u пройде крізь отвір за час
$\Delta t=\frac{\Delta x}{u}$,
отже,
$v=\frac{\Delta V}{\Delta t}={{S}_{0}}u$
Підставивши цей вираз у формулу (1), отримаємо
| \( \tau=\frac{lS}{S_{0}u}\). | (2) |
Відтак задача зводиться до визначення швидкості струменя u, яку легко знайти за допомогою енергетичних міркувань. А саме. Кожна частинка води набуває швидкості u і відповідної кінетичної енергії завдяки роботі сили тиску F на поршень та воду. Тож за теоремою про кінетичну енергію (4.4)
\( {Fl}=\frac{mu^{2}}{2}\),
де m – початкова маса води в шприці. Позаяк \( {m}=\rho{lS}\), то
\( {Fl}=\frac{\rho{S}lu^{2}}{2}\) \( \Rightarrow \) \( {u}=\sqrt{\frac{2F}{\rho{S}}}\).
Підставивши цей результат у вираз (2), отримуємо відповідь:
\( \tau=\frac{lS}{S_{0}}\sqrt{\frac{\rho{S}}{2F}}\) τ = 5 с.
.
Збереження механічної енергії
Задача 4.22. Визначити, під яким кутом α до горизонту зроблено постріл з гармати, якщо в найвищій точці траєкторії кінетична енергія снаряда є на k = 25 % менша за початкову.
Задача 4.23. Визначити, при яких кутах стрільби \( \alpha\) на траєкторії снаряда існують точки, де його кінетична енергія у k = 3 рази перевищує потенціальну.
Задача 4.24. Тягарець на нитці відхиляють на кут \( \alpha=60^{\circ}\) від вертикалі й відпускають. Визначити кут \( \beta \), на який відхилиться нитка по інший бік, якщо під точкою підвісу посередині вбито цвях.
Задача 4.25. Маленька шайба починає зісковзувати без тертя з вершини закріпленої півсфери радіуса R. Визначити, на якій висоті h від основи півсфери шайба відірветься.
Задача 4.26. Через гладкий горизонтальний штир перекинуто м'який канат довжини \( {l=10}\) м так, що його кінці розташовані на одному рівні. Після незначного поштовху канат починає зісковзувати. Визначити його швидкість на момент сходу зі штиря.
Задача 4.27. Підвішений на пружині тягарець, який розтягає її на задану величину х0, підіймають до положення, коли пружина не деформована, й відпускають. Визначити: 1) максимальний розтяг хm пружини; 2) максимальну швидкість тягарця vm.
Визначити,
під яким кутом α до горизонту зроблено постріл з гармати, якщо в найвищій точці траєкторії кінетична енергія снаряда на k = 25 % менша за початкову.
|
Дано: k = 25 % = 0,25 |
|
α - ? |
Розв’язання
Позаяк на снаряд діє лише консервативна сила тяжіння, його повна механічна енергія не змінюється, й можна записати:
| \(\frac{mv_{0}^{2}}{2}=\frac{m{{v}^{2}}}{2}+mgh\) $\Rightarrow $ \(\frac{mv_{0}^{2}}{2}-\frac{m{{v}^{2}}}{2}=mgh\), | (1) |
де \( {m} \) – маса снаряда, \( {{v}_{0}}\), \( v \) – швидкості в точці пострілу та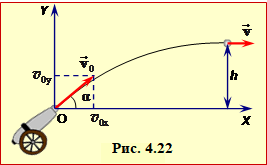 найвищій точці траєкторії, \( {h} \) – максимальна висота підйому відносно точки пострілу (рис. 4.22).
найвищій точці траєкторії, \( {h} \) – максимальна висота підйому відносно точки пострілу (рис. 4.22).
За умовою
\(\frac{mv_{0}^{2}}{2}-\frac{m{{v}^{2}}}{2}=k\frac{mv_{0}^{2}}{2},\)
отже,
| \(mgh=k\frac{mv_{0}^{2}}{2}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ 2gh=kv_{0}^{2}.\) | (2) |
З іншого боку, за рівнянням (1.18)
| \( 2gh=v_{0\text{y}}^{2}=v_{0}^{2}{{\sin }^{2}}\text{ }\!\!\alpha\!\!\text{ }.\) | (3) |
Тож порівнявши вирази (2) і (3), знайдемо відповідь:
\(\sin \text{ }\!\!\alpha\!\!\text{ }=\sqrt{k}=\frac{1}{2}\ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \text{ }\!\!\alpha\!\!\text{ }=30{}^\circ .\)
Визначити,
при яких кутах стрільби \( \alpha\) на траєкторії снаряда існують точки, де його кінетична енергія у k = 3 рази перевищує потенціальну.
|
Дано: k = 3 |
|
α - ? |
Розв’язання
На снаряд у польоті діє тільки консервативна сила тяжіння, тож його механічна енергія зберігається, і в будь-якій точці траєкторії (рис. 23)
| \(\frac{mv_{0}^{2}}{2}=\frac{m{{v}^{2}}}{2}+mgh,\) |
де \({{v}_{0}}\) – початкова швидкість снаряда, \( {v} \) – його швидкість на висоті h.
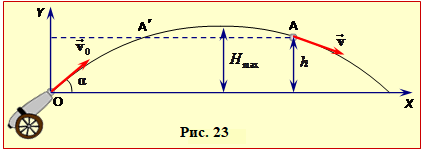
Згідно з умовою, \(\frac{m{{v}^{2}}}{2}=kmgh\), отже,
| \(\frac{mv_{0}^{2}}{2}=\left( k+1 \right)mgh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ h=\frac{v_{0}^{2}}{2\left( k+1 \right)g}.\) |
|
При цьому максимальна висота підйому снаряда за рівнянням (1.18) складає
| \(H=\frac{v_{0}^{2}{{\sin }^{2}}\text{ }\!\!\alpha\!\!\text{ }}{2g}.\) |
|
Отже, позаяк \( {h\le H} \),
\(\frac{v_{0}^{2}}{2\left( k+1 \right)g}\le \frac{v_{0}^{2}{{\sin }^{2}}\text{ }\!\!\alpha\!\!\text{ }}{2g}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \sin \text{ }\!\!\alpha\!\!\text{ }\ge \frac{1}{\sqrt{k+1}}.\)
Таким чином, вказані точки існують при кутах кидання
\(\text{ }\!\!\alpha\!\!\text{ }\ge \arcsin \left( \frac{1}{\sqrt{k+1}} \right).\)
При всіх можливих значеннях α, крім найменшого, це дві точки на гілках траєкторії (рис. 4.23), а при найменшому одна – її вершина.
Згідно з умовою k = 3, тож числова відповідь складає
α ≥ 30°.
Тягарець, який підвішено на нитці, відхиляють на кут \( \alpha=60^{\circ}\) від вертикалі й відпускають.
Визначити
кут \( \beta \), на який відхилиться нитка по інший бік, якщо під точкою підвісу посередині вбито цвях.
|
Дано: α = 60° |
|
\( \beta \) - ? |
Розв’язання
На тягарець, окрім консервативної сили тяжіння, діє тільки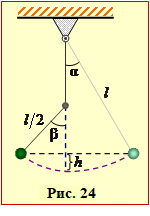 поперечна до руху сила натягу нитки, що не виконує роботи. Тому повна механічна енергія тягарця зберігається, і в крайніх точках він розташовується на одній висоті h відносно початкового положення, рис. 4.24, і, позначивши довжину нитки як l, можна записати:
поперечна до руху сила натягу нитки, що не виконує роботи. Тому повна механічна енергія тягарця зберігається, і в крайніх точках він розташовується на одній висоті h відносно початкового положення, рис. 4.24, і, позначивши довжину нитки як l, можна записати:
\( \cos\alpha=\frac{l-h}{l} \) = $1-\frac{h}{l}$,
\( \cos\beta=\frac{\left( l/2 \right)-h}{\left( l/2 \right)}=1-2\frac{h}{l}\)
звідки, виключивши відношення \( {h/l}\), отримати відповідь:
\( \cos\beta=2\cos\alpha-1 \) \( \Rightarrow \) \( \beta=\mathrm{arccos}(2\cos\alpha-1) \) = 90°.
Маленька шайба починає зісковзувати без тертя з вершини закріпленої півсфери радіуса R.
Визначити,
на якій висоті h від основи півсфери шайба відірветься від неї.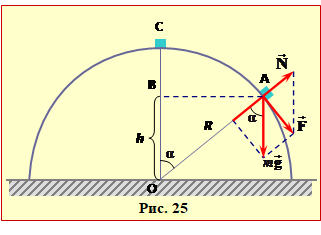
|
Дано: R |
|
h - ? |
Розв’язання
До відриву шайба під дією сил тяжіння та нормальної реакції опори (рис. 25. рухається по колу радіуса R з прискоренням, яке визначається рівнянням
\(m\vec{g}+\vec{N}=m\vec{a}\)
При цьому проєкція вектора \( {\vec{a}}\) на дотичну до кола визначає зміну величини швидкості шайби. Відповідно, його проєкція на радіус визначає зміну напрямку швидкості і є доцентровим прискоренням, котре виражається формулою (1.28). Отже, за другим законом Ньютона (2.5)
|
\(mg\cos \text{ }\!\!\alpha\!\!\text{ }-N=\frac{m{{v}^{2}}}{R}.\) |
(1) |
При зісковзуванні швидкість шайби v і кут α з часом зростають. Через це, як легко бачити з рівняння (1), реакція опори N поступово зменшується і на певній висоті h взагалі зникає, що означає відрив шайби від півсфери. Тож, поклавши в рівнянні (1) N = 0 i врахувавши вираз cosα = (h/R), знайдемо, що в точці відриву
|
${{v}^{2}}=gh$. |
(2) |
Величину ${{v}^{2}}$ не важко визначити із закону збереження енергії. У верхній точці півсфери шайба має тільки потенціальну енергію \( {{W}_{1}}=mgR \), а в точці відриву її енергія при тій самій величині W2 = W1 складається з кінетичної та потенціальної:
|
\({{W}_{2}}=\frac{m{{v}^{2}}}{2}+mgh.\) |
|
Отже,
|
\(mgR=\frac{m{{v}^{2}}}{2}+mgh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ R=\frac{{{v}^{2}}}{2g}+h.\) |
|
Відтак, замінивши v2, згідно з виразом (2), отримаємо відповідь:
|
\(h=\frac{2}{3}R=40\) см. |
|
Через гладкий горизонтальний штир перекинуто м'який канат довжини \( {l=10}\) м так, що його кінці розташовані на одному рівні, (рис. 26а). Після незначного поштовху канат починає зісковзувати.
Визначити
його швидкість на момент сходу зі штиря, (рис. 26б).
|
Дано: l = 10 м |
|
v - ? |
Розв’язання
За умовою на канат діють лише консервативна сила тяжіння реакція штиря, котра не виконує роботи, бо через відсутність тертя є перпендикулярною до переміщення каната. В такому разі повна механічна енергія каната зберігається, тож набута ним кінетична енергія дорівнює спадові потенціальної енергії:
$\frac{m{{v}^{2}}}{2}=mg{{h}_{1}}-mg{{h}_{2}}$ $\Rightarrow $ $v=\sqrt{2g\left( {{h}_{1}}-{{h}_{2}} \right)}$,
де (h1 – h2) – відстань між початковим і кінцевим положенням центра мас каната, котра, як видно з рис. 26, дорівнює (l/4). Отже, шукана швидкість каната дорівнює
\( v=\sqrt{\frac{gl}{2}}\) = 7 м/с.
|
|
| Задача 4.27ЗАЗадача 4.26 |
| Задача 4.27 |
Підвішений на пружині тягарець, який розтягає її на задану величину х0, підіймають до положення, в якому пружина не деформована, й відпускають.
Визначити:
1) максимальний розтяг хm пружини;
2) максимальну швидкість тягарця vm.
|
Дано: х0 |
|
хm - ? vm - ? |
Розв’язання
У системі "тягарець-пружина" діють тільки консервативні сили тяжіння та пружності, тож її механічна енергія зберігається.
1) Будемо відраховувати потенціальну енергію тягарця від найнижчого положення (т. 2 на рис. 27б), де деформація пружини xm є найбільшою. Тоді в момент вивільнення тягарця (т. 1) енергія системи складається лише з потенціальної енергії тягарця mgxm, а в найнижчому (т. 2) – тільки з такої самої за величиною потенціальної енергії розтягнутої пружини \(\left( {kx_{m}^{2}}/{2}\; \right)\). Отже,
|
\( {mg}{{x}_{{m}}}=\frac{kx_{{m}}^{2}}{2}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ {{x}_{{m}}}=\frac{2mg}{k} \), |
(1) |
де m – маса тягарця, k – жорсткість пружини.
Відношення (m/k) визначимо з умови рівноваги підвішеного тягарця через задану величину статичного розтягу пружини x0 (рис. 27а) :
|
mg = kx0 $\Rightarrow $ $\frac{m}{k}$ = $\frac{{{x}_{0}}}{g}$ |
(2) |
Відтак
| xm = 2x0. |
(3) |
2) Для визначення максимальної швидкості тягарця врахуємо, що коли він знаходиться вище положення рівноваги (розтяг пружини \( {x}\lt{{x}_{0}}\)), рівнодійна сил тяжіння та пружності напрямлена донизу, і швидкість тягарця зростає. Якщо ж \( {x}\gt{{x}_{0}}\), то рівнодійна напрямлена вгору, і швидкість тягарця зменшується. Тож максимальну швидкість тягарець має при проходженні положення рівноваги (т. 3 на рис. 27б). При цьому механічна енергія системи
|
\({{W}_{3}}=\frac{mv_{{m}}^{2}}{2}+\frac{kx_{0}^{2}}{2}+mg{{x}_{0}}.\) |
|
Згідно із законом збереження \( {{W}_{1}}={{W}_{2}}\) (або \( {{W}_{3}}={{W}_{2}}\)), отже
|
\(\frac{mv_{{m}}^{2}}{2}+\frac{kx_{0}^{2}}{2}+mg{{x}_{0}}=mg{{x}_{{m}}}.\) |
|
З цього рівняння, врахувавши співвідношення (2) та результат (3), знайдемо
|
\({{v}_{{m}}}=\sqrt{g{{x}_{0}}}.\) |
|
Величину vm можна знайти більш прямо, визначивши за законом збереження енергії та проаналізувавши на максимум залежність v(х) швидкості тягарця від координати (відстані від т. 2). Але для цього треба знати відповідні положення вищої математики.
Збереження механічної енергії та імпульсу
Задача 4.28. Рухома шайба непружно стикається з нерухомою шайбою в k = 2 рази більшої маси. Визначити, яка частина η кінетичної енергії шайби перетворюється на тепло.
Задача 4.29. Дві кулі масами m1 і m2, що рухаються вздовж осі OX зі швидкостями \( \vec{v}_{1}\) і \( \vec{v}_{2} \), абсолютно пружно стикаються в лоб. Визначити швидкості куль u1 та u2 після зіткнення.
Задача 4.30. Куля, що мала швидкість \({{v}_{1}}=3\,\mathrm{м/с}\), після пружного зіткнення з нерухомою кулею продовжила рух у тому самому напрямі зі швидкістю \({{u}_{1}}=2\,\mathrm{м/с}\). Визначити відношення мас куль (m1/m2) та швидкість другої кулі u2 після зіткнення.
Задача 4.31. Дві однакові кульки, що рухались із швидкостями \( \vec{v}_{1}\) та \( \vec{v}_{2}\) під кутом \( \alpha \) одна до одної, після пружного удару розлетілись із швидкостями \( \vec{u}_{1}\) та \( \vec{u}_{2}\). Визначити кут розльоту кульок \( \beta \).
Задача 4.32. Куля масою m = 10 г, що горизонтально летить зі швидкістю v = 1000 м/с, вдаряє в центр підвішеного на шнурі дерев'яного куба, й застряє, заглибившись на d = 10 см. Відстань від точки підвісу до центра куба l = 1,5 м, його маса M = 5 кг. Визначити: 1. Максимальний кут відхилення α шнура від вертикалі та відстань S, яку при цьому проходить куб. 2. Силу F і тривалість удару τ, та відстань s, яку проходить за цей час куля.
Задача 4.33. Шматок м'якої глини масою m = 0,5 кг падає зі швидкістю v = 5 м/с на горизонтальну плиту масою M = 1 кг, що розташована на закріпленій вертикальній пружині жорсткістю k = 980 Н/м. Визначити максимальне стиснення хт пружини внаслідок удару.
Задача 4.34. Із закріпленої на залізничній платформі гармати роблять постріл удовж колії під кутом α = 60° до горизонту. Визначити відстань S, на яку відкотиться платформа, якщо коефіцієнт опору k = 0,5, відношення маси снаряду до маси платформи з гарматою η = 10–3 і швидкість вильоту снаряду v = 600 м/с.
Задача 4.35. Маленька шайба, що без тертя зісковзує з гірки висотою h = 90 см, плавно виїжджає на довгу дошку, котра лежить на гладкій горизонтальній поверхні. Визначити, на якій відстані S від краю дошки шайба зупиниться, якщо коефіцієнт тертя між нею й дошкою μ = 0,5 і відношення мас шайби й дошки η = 0,2.
Задача 4.36. Протон з кінетичною енергією W0 = 1,7·10-17 Дж при лобовому зіткненні з нерухомим атомом відбивається назад і переводить його в збуджений стан, утрачаючи при цьому η = 75% енергії. Визначити енергію збудження атома U, якщо відношення його маси M до маси протона m складає k = 4.
Задача 4.28
Рухома шайба непружно стикається з нерухомою шайбою в k = 2 рази більшої маси.
Визначити,
яка частина η кінетичної енергії шайби перетворюється на тепло.
|
Дано: (m2/m1) = k = 2 |
|
η - ? |
Розв’язання
При непружному зіткненні тіла пластично деформуються і далі рухаються як одне ціле. При цьому їхня кінетична енергія не зберігається, позаяк при пластичній деформації вона частково перетворюється на внутрішню енергію (див. п.4.6, (4.19)). Тож
|
\({{W}_{1}}={{W}_{2}}+Q,\) $\Rightarrow $ $Q={{W}_{1}}-{{W}_{2}}$, |
де \( {{W}_{1}}\), \( {{W}_{2}}\) – початкова та кінцева кінетична енергія шайб, Q – кількість тепла, що виділяється при зіткненні.
Якщо позначити як v початкову швидкість рухомої шайби, u – спільну швидкість шайб після зіткнення і врахувати задане відношення мас k, то шукана втрата кінетичної енергії
|
$\eta =\frac{Q}{{{W}_{1}}}=1-\left( k+1 \right){{\left( \frac{u}{v} \right)}^{2}}$ |
(1) |
Відношення швидкостей визначається із закону збереження імпульсу:
|
${{m}_{1}}v=\left( {{m}_{1}}+{{m}_{2}} \right)u\quad \Rightarrow \quad \frac{u}{v}=\frac{1}{k+1}$ |
Відтак, урахувавши цей результат у вираз (1), отримаємо відповідь:
|
\(\text{ }\!\!\eta\!\!\text{ }=1-\frac{\left( k+1 \right){{v}^{2}}}{{{\left( k+1 \right)}^{2}}{{v}^{2}}} \ \ \ \ \ \Rightarrow \ \ \ \ \ \text{ }\!\!\eta\!\!\text{ }=\frac{k}{k+1}=\frac{2}{3}.\) |
Варто звернути увагу на те, що частина втраченої кінетичної енергії зростає при збільшенні маси нерухомого тіла.
Дві кулі з масами m1 і m2, що рухаються вздовж осі OX зі швидкостями \( \vec{v}_{1}\) і \( \vec{v}_{2} \), абсолютно пружно стикаються в лоб.
Визначити
швидкості куль u1 та u2 після зіткнення.
|
Дано: m1, m2, \( \vec{v}_{1},\ \ \vec{v}_{2} \) |
|
u1, u2 - ? |
Розв’язання
 При абсолютно пружному зіткненні тіла, не втрачають ані сумарного імпульсу, ані сумарної кінетичної енергії (рівняння (4.18)). За умовою зіткнення куль є лобовим, тобто вони рухаються по одній прямій, рис. 29. Отже, для проєкцій на вісь ОХ маємо:
При абсолютно пружному зіткненні тіла, не втрачають ані сумарного імпульсу, ані сумарної кінетичної енергії (рівняння (4.18)). За умовою зіткнення куль є лобовим, тобто вони рухаються по одній прямій, рис. 29. Отже, для проєкцій на вісь ОХ маємо:
|
\({{m}_{1}}{{v}_{1\text{x}}}+{{m}_{2}}{{v}_{\text{2x}}}={{m}_{1}}{{u}_{1\text{x}}}+{{m}_{2}}{{u}_{\text{2x}}},\) |
(1) |
|
\(\frac{{{m}_{1}}v_{1\text{x}}^{2}}{2}+\frac{{{m}_{2}}v_{\text{2x}}^{2}}{2}=\frac{{{m}_{1}}u_{1\text{x}}^{2}}{2}+\frac{{{m}_{2}}u_{\text{2x}}^{2}}{2}.\) |
(2) |
Далі перегрупуємо ці вирази, як
|
\({{m}_{1}}\left( {{v}_{1\text{x}}}-{{u}_{1\text{x}}} \right)={{m}_{2}}\left( {{u}_{\text{2x}}}-{{v}_{\text{2x}}} \right),\) |
(1а) |
|
\({{m}_{1}}\left( v_{1\text{x}}^{2}-u_{1\text{x}}^{2} \right)={{m}_{2}}\left( u_{\text{2x}}^{2}-v_{\text{2x}}^{2} \right)\) |
(2а) |
та, згадавши формулу різниці квадратів і, поділивши рівняння (2а) на (1а), отримаємо:
|
|
\({{v}_{1\text{x}}}+{{u}_{1\text{x}}}={{u}_{\text{2x}}}+{{v}_{\text{2x}}}.\) |
|
Відтак об'єднаємо цей результат і рівняння (1а) в систему
|
\( \left\{ \begin{align} & {v_{1x}+u_{1x}=u_{2x}+v_{2x}} \\ & {m_{1}(v_{1x}-u_{1x})=m_{2}(v_{2x}-u_{2x})} \\ \end{align} \right.\), |
|
з якої знайдемо наступні вирази швидкостей куль після зіткнення:
|
\({{u}_{1\text{x}}}=\frac{2{{m}_{2}}{{v}_{\text{2x}}}+\left( {{m}_{1}}-{{m}_{2}} \right){{v}_{1\text{x}}}}{{{m}_{1}}+{{m}_{2}}},\) |
(3) |
|
\({{u}_{\text{2x}}}=\frac{2{{m}_{1}}{{v}_{\text{1x}}}+\left( {{m}_{2}}-{{m}_{1}} \right){{v}_{\text{2x}}}}{{{m}_{1}}+{{m}_{2}}}.\) |
(4) |
Ці формули, на загал, відображають очевидне: величини та напрями швидкостей куль після зіткнення визначаються співвідношенням їхніх мас та величиною й напрямком початкових швидкостей. А от якими саме будуть швидкості, залежить від конкретних умов задачі.
Для прикладу розглянемо випадок, коли v2 = 0, тобто перше тіло налітає на нерухоме друге. В такому разі вирази (3) і (4) набувають вигляду:
| \({{u}_{\text{1x}}}=\frac{\left( {{m}_{1}}-{{m}_{2}} \right){{v}_{\text{1x}}}}{{{m}_{1}}+{{m}_{2}}};\ \ \ \ \ \ {{u}_{\text{2x}}}=\frac{2{{m}_{1}}{{v}_{\text{1x}}}}{{{m}_{1}}+{{m}_{2}}}.\) |
(5) |
Тож маємо очевидне: u2х > 0, тобто друга куля відскочить в напрямку руху першої. Але напрям руху першої кулі після удару не є однозначним і залежить від співвідношення мас. Якщо перша куля є масивнішою (\({{m}_{1}}>{{m}_{2}}\)), то \({{u}_{\text{1x}}}>0\), тобто вона продовжить рух у тому самому напрямі, проте з меншою швидкістю. Відповідно, при \( {{m}_{1}}<{{m}_{2}} \) перша куля після удару відскочить у зворотньому напрямі (\({{u}_{\text{1x}}}<0\)).
Наведені наслідки сприймаються як очевидні і пояснюються лобовим характером зіткнення. А ось при рівних масах куль (m1 = m2) із формул (3) і (4) випливає нетривіальний результат:
|
\({{u}_{\text{1x}}}={{v}_{\text{2x}}},\ \ \ \ \ \ {{u}_{\text{2x}}}={{v}_{\text{1x}}}.\) |
|
Отже, однакові пружні кулі при лобовому зіткненні обмінюються імпульсами та кінетичними енергіями. Зокрема, якщо одна з куль до зіткнення є нерухомою, то вона перебирає на себе увесь імпульс і енергію першої, а та зупиняється.
Куля, що мала швидкість \({{v}_{1}}=3\,\mathrm{м/с}\), після пружного зіткнення з нерухомою кулею продовжила рух у тому самому напрямі зі швидкістю \({{u}_{1}}=2 \,\mathrm{м/с}\).
Визначити
відношення мас куль m1/m2 та швидкість другої кулі u2 після зіткнення.
|
Дано: v1 = 3 м/с u1 = 2 м/с |
|
m1/m2 - ? u2 - ? |
Розв’язання
Позаяк напрям першої кулі після зіткнення не змінився, воно є центральним (лобовим), і дана задача по суті є окремим випадком попередньо. Тож, увівши позначення m1/m2 = k і зробивши заміну m1 = km2, з першій формули (5) задачі 4.29 отримаємо:
|
\({{u}_{\text{1}}}=\frac{\left( k-1 \right){{v}_{\text{1}}}}{k+1}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ k=\frac{{{v}_{\text{1}}}+{{u}_{1}}}{{{v}_{\text{1}}}-{{u}_{1}}}=5.\) |
|
Відтак із другої формули знайдемо швидкість:
|
\({{u}_{2}}=\frac{2k{{v}_{\text{1}}}}{k+1}=5\) м/с. |
|
Дві однакові кульки, що рухались із швидкостями \( \vec{v}_{1}\) та \( \vec{v}_{2}\) під кутом \( \alpha \) одна до одної, після пружного удару розлетілись із швидкостями \( \vec{u}_{1}\) та \( \vec{u}_{2}\).
Визначити
кут розльоту кульок \( \beta \).
|
Дано: \( \vec{v}_{1}\), \(\vec{v}_{2}\), \( \vec{u}_{1}\), \( \vec{u}_{2}\), \( \alpha \)
|
|
\( \beta \) - ? |
Розв’язання
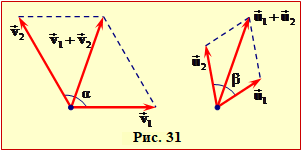
Пружне зіткнення кульок відбувається із збереженням імпульсу та кінетичної енергії відповідно до рівнянь (4.18):
|
\( \left\{ \begin{align} & {m\vec{v}_{1}+m\vec{v}_{2}=m\vec{u}_{1}+m\vec{u}_{2},} \\ & {\frac{mv_{1}^{2}}{2}+\frac{mv_{2}^{2}}{2}=\frac{mu_{1}^{2}}{2}+\frac{mu_{2}^{2}}{2}}; \\ \end{align} \right.\) \( \Rightarrow \) \( \left\{ \begin{align} & {\vec{v}_{1}+\vec{v}_{2}=\vec{u}_{1}+\vec{u}_{2},} \\ & {v_{1}^{2}+v_{2}^{2}=u_{1}^{2}+u_{2}^{2}.} \\ \end{align} \right.\) |
(1) |
Вектори \( \vec{v}_{1}+\vec{v}_{2} \) та \(\vec{u}_{1}+\vec{u}_{2}\) являють собою діагоналі паралелограмів швидкостей (рис. 31), причому \(\vec{v}_{1}+\vec{v}_{2}=\vec{u}_{1}+\vec{u}_{2}\). Отже, за теоремою косинусів маємо
|
\(v_{1}^{2}+v_{2}^{2}+2{{v}_{1}}{{v}_{2}}\cos \text{ }\!\!\alpha\!\!\text{ }=u_{1}^{2}+u_{2}^{2}+2{{u}_{1}}{{u}_{2}}\cos \text{ }\!\!\beta\!\!\text{ }\text{.}\) |
|
Врахувавши друге рівняння системи (1), дістанемо:
|
\({{v}_{1}}{{v}_{2}}\cos \text{ }\!\!\alpha\!\!\text{ }={{u}_{1}}{{u}_{2}}\cos \text{ }\!\!\beta\!\!\text{ }\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \cos \text{ }\!\!\beta\!\!\text{ }=\frac{{{v}_{1}}{{v}_{2}}}{{{u}_{1}}{{u}_{2}}}\cos \text{ }\!\!\alpha\!\!\text{ }\ \text{.}\) |
|
В окремому випадку, коли одна з кульок (до прикладу, друга) перебуває в спокої, то \( \cos \text{ }\!\!\beta\!\!\text{ }=0 \) і \( \text{ }\!\!\beta\!\!\text{ }=90{}^\circ \), тобто кульки розлітаються під прямим кутом.
Куля масою m = 10 г, що горизонтально летить зі швидкістю v = 1000 м/с, вдаряє в центр підвішеного на шнурі дерев'яного куба, й застряє, заглибившись на d = 10 см. Відстань від точки підвісу до центра куба l = 1,5 м, його маса M = 5 кг.
Визначити:
1. Максимальний кут відхилення α шнура від вертикалі та відстань S, яку при цьому проходить куб.
2. Силу F і тривалість удару τ, та відстань s, яку проходить за цей час куля.
Дано:
|
m = 10 г
v = 1000 м/с
d = 10 см
l = 1,5 м
M = 5 кг
|
|
α - ?, S - ?; F - ?, τ - ?, s - ? |
Розв’язання
1. Куб відхиляється за рахунок енергії та імпульсу, отриманих при влучанні кулі. При цьому через масивність куба та велику силу опору, що діє на кулю, удар (заглиблення кулі в куб) триває дуже короткий проміжок часу, протягом якого імпульс системи куля-куб лишається практично незмінним:
|
\(mv=\left( m+M \right)u,\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{mv}{m+M},\) |
|
де u – початкова швидкість руху куба з кулею після удару.
За умовою m << M, отже, вираз u без утрати точності (похибка 0,2%) можна спростити, відкинувши у знаменнику величину m:
|
$u=\frac{m}{M}v$ = 2 м/с. |
(1) |
Подальший рух куба з кулею відбувається під дією сили тяжіння та поперечної сили натягу мотузки, що не виконує роботи. Тож відхилення куба відбувається без утрати механічної енергії, і максимальна висота h його підняття над початковим рівнем (рис. 4.32) визначається рівнянням
|
\(\frac{\left( m+M \right){{u}^{2}}}{2}=\left( m+M \right)gh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ h=\frac{{{u}^{2}}}{2g},\) |
|
або з урахуванням виразу (1),
|
h = ${{\left( \frac{m}{M} \right)}^{2}}\frac{{{v}^{2}}}{2g}$ |
(2) |
Відтак можна визначити максимальний кут відхилення куба α. А саме, як зрозуміло з рис. 31,
| \( {h}=l(1-cos\alpha)=2l\sin^{2}\frac{\alpha}{2}\), | (3) |
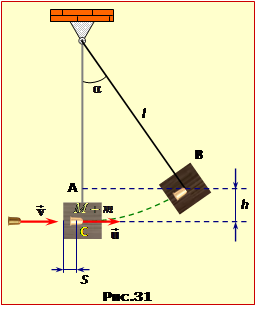 тож прирівнявши вирази (2) і (3), знайдемо:
тож прирівнявши вирази (2) і (3), знайдемо:
|
\(\sin \frac{\text{ }\!\!\alpha\!\!\text{ }}{2}= \frac{mv}{2M\sqrt{gl}}.\) |
Обчислення дають:
\(\sin \frac{\text{ }\!\!\alpha\!\!\text{ }}{2}=0,258 \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \text{ }\!\!\alpha\!\!\text{ }=30{}^\circ .\)
Пройдений при цьому кубом шлях складає:
S = lα = $\frac{\pi l}{6}$ = 78,5 см.
2. Силу удару знайдемо через сумарну роботу А сил тертя між кубом і кулею, котра (див. задачу 4.2) визначається добутком сили тертя, що діє лише на кулю, та її переміщення відносно бруса:
| \({A}=-Fd\). |
|
Згідно з (4.4), ця робота дорівнює зміні кінетичної енергії системи, отже,
|
$\frac{\left( M+m \right){{u}^{2}}}{2}-\frac{m{{v}^{2}}}{2}$ = \(-Fd\) |
|
Підставивши вираз u з формули (1), після перетворень дістанемо наступний практично точний результат:
|
F = \( \frac{m{{v}^{2}}}{2d}=5\cdot {{10}^{4}}\ \mathrm{H}\) |
|
Отже, сила удару є дуже велика: вона дорівнює силі тиску на горизонтальну опору вантажу масою 5 т.
Тривалість удару τ теж легко оцінити, позаяк за час руху всередині куба куля майже повністю втрачає швидкість (формула (1)), так що середня швидкість кулі за час удару складає <v> = (v/2).
Отже, тривалість удару
$\tau =\frac{2d}{v}$ = 2·10–4 c = 0,2 мс.
При цьому куб, рухаючись із середньою швидкістю (u/2), за час τ проходить шлях
${s}=\frac{u\tau }{2}=0,2 \text{мм }$.
Насамкінець відмітимо, що отримані значення τ і s переконливо доводять зроблене на початку припущення про "миттєвий" характер зіткнень тіл.
 Шматок м'якої глини масою m = 0,5 кг падає зі швидкістю v = 5 м/с на горизонтальну плиту масою M = 1 кг, що розташована на закріпленій вертикальній пружині жорсткістю k = 980 Н/м.
Шматок м'якої глини масою m = 0,5 кг падає зі швидкістю v = 5 м/с на горизонтальну плиту масою M = 1 кг, що розташована на закріпленій вертикальній пружині жорсткістю k = 980 Н/м.
Визначити
максимальне стиснення х пружини внаслідок удару.
|
Дано: m = 0,5 кг
M = 1 кг
k = 980 Н/м
v = 5 м/с
|
|
xm - ? |
Розв’язання
Змістовно й за алгоритмом розв'язування ця задача є аналогом попередньої. Отже, можна вважати, що прилипання глини до пластини відбувається без зміни імпульсу системи й задовольняє рівняння:
|
\(mv=\left( m+M \right)u,\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{mv}{m+M},\) |
(1) |
де u – швидкість руху плити разом з глиною одразу після.
Те саме можна сказати й про енергію: позаяк за умовою сили тертя не враховуються, в процесі стискання пружини відбувається лише перетворення кінетичної енергії на потенціальну без зміни загальної кількості.
Для наступних викладок є логічним обрати нульовий рівень гравітаційної потенціальної енергії в початковому положенні пластини (рис. 4.33), а для пружини – коли вона ще не була навантажена плитою. В такому разі початкова енергія системи W1 складається з кінетичної енергії пластини з глиною та потенціальної енергії пружини, що деформована вагою пластини на певну величину x0 = (mg/k). Тоді, врахувавши вираз (1), маємо:
|
\({{W}_{1}}=\frac{{{m}^{2}}{{v}^{2}}}{2\left( m+M \right)}+\frac{{{\left( Mg \right)}^{2}}}{2k}.\) |
(2) |
В кінцевому (найнижчому) положенні енергія системи W2 складається тільки з потенціальних енергій пружини, деформованої на максимальну величину xm = x0 + x, та пластини з глиною масою M+m, що опустилися на відстань х від нульового рівня:
|
\({{W}_{2}}=\frac{k{{\left( x+{{x}_{0}} \right)}^{2}}}{2}-\left( m+M \right)gx.\) |
(3) |
(Знак "–" стоїть тому, що кінцева потенціальна енергія тіл є від'ємна).
За законом збереження енергії W1 = W2, тож, прирівнявши вирази (2) та (3) після спрощень отримаємо:
|
\(k{{x}^{2}}-2mgx-\frac{{{\left( mv \right)}^{2}}}{m+M}=0.\) |
|
З цього рівняння визначаємо додаткове
|
\(x=\frac{mg+\sqrt{{{\left( mg \right)}^{2}}+\frac{k{{\left( mv \right)}^{2}}}{m+M}}}{k}\) |
|
і повне \( {x}_{m}={x}_{0}+{x}\) стиснення пружини:
|
\({{x}_{\text{m}}}=\frac{1}{k}\left( \left( m+M \right)g+\sqrt{{{\left( mg \right)}^{2}}+\frac{k{{\left( mv \right)}^{2}}}{m+M}} \right).\) |
|
Обчислення дають:
хт = 8 см.
Із закріпленої на залізничній платформі гармати роблять постріл удовж колії під кутом α = 60° до горизонту.
Визначити
відстань S, на яку відкотиться платформа, якщо коефіцієнт опору μ = 0,5, відношення маси снаряду до маси платформи з гарматою η = 10–3 і швидкість вильоту снаряду v = 600 м/с.
|
Дано: α = 60° |
|
S - ? |
Розв’язання
При пострілі під кутом повний імпульс системи "платформа-снаряд" не зберігається, проте зберігається його проекція на напрям копії ОХ (див. задачу 3.5). Отже,
|
\(-Mu+mv\cos \text{ }\!\!\alpha\!\!\text{ }=0\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=nv\cos \text{ }\!\!\alpha\!\!\text{ },\) |
(1) |
де u – початкова швидкість відкочування платформи після пострілу, M і m – маси платформи з гарматою та снаряда.
Унаслідок пострілу платформа отримує кінетичну енергію \( {W}=\frac{M{{u}^{2}}}{2}\), яку потім витрачає на роботу проти сили опору \( {F}=\mu{mg}\) на шляху S. Отже:
|
\(\frac{M{{u}^{2}}}{2}=\text{ }\!\!\mu\!\!\text{ }mgS\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ S=\frac{{{u}^{2}}}{2\text{ }\!\!\mu\!\!\text{ }g}.\) |
|
Врахувавши вираз (1), отримуємо відповідь:
|
\(S=\frac{{{\left( nv\cos \text{ }\!\!\alpha\!\!\text{ } \right)}^{2}}}{2\text{ }\!\!\mu\!\!\text{ }g}\) = 9 см. |
|
Маленька шайба, що без тертя зісковзує з гірки висотою h = 90 см, плавно виїжджає на довгу дошку, котра лежить на гладкій горизонтальній поверхні.
Визначити,
на якій відстані S від краю дошки шайба зупиниться, якщо коефіцієнт тертя між нею й дошкою μ = 0,5 і відношення мас шайби й дошки η = 0,2.
|
Дано: h = 0,9 м
μ = 0,5
η = 0,2
|
|
S - ? |
Розв’язання
За умовою шайба зісковзує без тертя, отже без втрат механічної енергії. Тому,
|
\(\frac{m{{v}^{2}}}{2}\ =mgh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ v=\sqrt{2gh}\text{,}\) |
(1) |
де v – швидкість шайби в момент виходу на дошку.
Ковзаючи далі по дошці, шайба під дією сили тертя гальмується, а дошка, навпаки, прискорюється. Внаслідок цього через певний час їхні швидкості зрівняються, і ковзання шайби по дошці припиниться. Рух шайби й дошки відбувається із збереженням імпульсу системи, позаяк зовнішні сили тяжіння та реакції опори є компенсовані. Це дозволяє визначити кінцеву швидкість дошки з шайбою u:
|
\(mv=\left( m+M \right)u\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{mv}{m+M}\ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{nv}{1+n}.\) |
(2) |
Ковзання шайби по дошці супроводжується зміною кінетичної енергії системи, рівною сумарній роботі сил тертя:
|
\(\frac{\left( m+M \right){{u}^{2}}}{2}-\ \frac{m{{v}^{2}}}{2}={{A}_{\text{т}}}.\) |
(3) |
Згідно з результатом задачі 4.2,(формула (2)), ця сумарна робота дорівнює добутку сили тертя, що діє на шайбу, на її переміщення відносно дошки: \({{A}_{\text{т}}}=-\text{ }\!\!\mu\!\!\text{ }mg\). Після підстановки цього виразу й виразу (2) в рівняння (3) та елементарних перетворень отримаємо:
|
\(S=\frac{{{v}^{2}}}{2\left( 1+n \right)\text{ }\!\!\mu\!\!\text{ }g},\) |
|
або, з урахуванням виразу (1),
|
\(S=\frac{h}{\left( 1+n \right)\text{ }\!\!\mu\!\!\text{ }}=1,5\ \text{м}\text{.}\) |
|
Протон з кінетичною енергією W0 = 1,7·10-17 Дж при лобовому зіткненні з нерухомим атомом відбивається назад і переводить його в збуджений стан, утрачаючи при цьому η = 75% енергії.
Визначити
енергію збудження атома U, якщо відношення його маси M до маси протона m складає k = 4.
|
Дано: W0 = 1,7·10-17 Дж
η = 75%
k = 4
|
|
U - ? |
Розв’язання
 При зіткненні втрачена протоном енергія
При зіткненні втрачена протоном енергія
\(W=\eta{W}_{0}\)
передається атому у формі кінетичної енергії Wа, а решта переходить у внутрішню енергію атома (енергію збудження U):
ηW0 = Wа + U $\Rightarrow $ U = ηW0 – Wа.
Зіткнення протона з атомом відбувається із збереженням імпульсу. Тому в записаному співвідношенні величину Wа є доцільно виразити через імпульс pa і масу M атома:
| $U=\eta {{W}_{0}}-\frac{p_{a}^{2}}{2M}$ |
(1) |
За законом збереження імпульсу (3.3) з урахуванням напрямків (рис. 36)
p0 = –p + ра $\Rightarrow $ ${{p}_{a}}=\frac{3}{2}{{p}_{0}}$,
де взято до уваги, що кінцевий імпульс протона р дорівнює половині початкового, бо за умовою після зіткнення у нього лишається чверть початкової кінетичної енергії. В такому разі, згідно з виразом (1) і заданим співвідношенням мас M = km, після елементарних перетворень отримуємо наступну відповідь:
$U=\left( \eta -\frac{9}{4k} \right){{W}_{0}}\approx 3,2\cdot {{10}^{-18}}\text{Дж}$.
Задачі для самостійної роботи.
Далі пропонуються для розв'язування задачі з наступних тем:
Робота та зміна стану механічної системи
Збереження механічної енергії та імпульсу
У наведених відповідях передбачається значення g = 10 м/с2.
Робота, потужність, ККД
При розв'язуванні задач із даної теми слід пам'ятати, що робота й потужність є алгебраїчними величини, залежними не тільки від величини сил і швидкостей, а й від їхніх напрямів.
При визначенні ККД важливо уважно проаналізувати процеси перетворень енергії, з'ясувати канали втрат механічної енергії та встановити, яка робота (енергія, потужність) є корисною, а яка – затраченою.
Наведені відповіді передбачають g = 10 м/с2.
Рівень А
|
Рівень Б
|
Рівень В
|
Робота та зміна стану механічної системи
В багатьох задачах робота неконсервативних сил є заданою, або може бути прямо визначена за умовою. В такому разі, склавши рівняння енергетичного балансу (4.13), можна визначити положення й швидкості тіл та інші відомості про механічний стан системи.
Наведені відповіді отримано при g = 10 м/с2.
Рівень А
|
4.62. |
Тіло маси 2 кг, якому поштовхом уздовж похилої площини надали швидкості 5 м/с, зупинилося на висоті 0,5 м. Визначити кількість теплоти, що виділилося під час руху тіла. [15 Дж] |
|
4.63. |
При розтягуванні пружини на 4 мм виконано роботу A = 20 мДж. Яку роботу треба виконати, аби стиснути пружину на 4 см? [2 Дж] |
|
4.64. |
При стисканні пружини на 1 см хлопчик виконав роботу 2 Дж. Яку роботу він має виконати, аби стиснути пружину ще на 2 см? [16 Дж] |
|
4.65. |
Куля при влучанні в стіну проникає на глибину 10 см. На яку глибину ввійде в стіну така сама куля при вдвічі більшій швидкості руху? [40 см] |
|
4.66. |
З глибини 500 м качають нафту насосом із потужністю 10 кВт і коефіцієнтом корисної дії 80 %. Яку масу нафти піднімають за 5 год роботи насоса? [29 т] |
|
4.67. |
Куля маси 10 г, яку випущено з гвинтівки вертикально вгору зі швидкістю 1000 м/с, впала на землю зі швидкістю 500 м/с. Визначити роботу сили опору повітря за час польоту кулі. [ –3,75 кДж] |
|
4.68. |
Кулька масою 20 г падає з висоти 1 м на горизонтальну плиту і після відбивання підскакує на висоту 80 см. Яка кількість теплоти, виділяється при цьому? [40 мДж] |
|
4.69. |
Пластилінова кулька масою 10 г вдаряє в стіну зі швидкістю v = 10 м/с та прилипає. Яка кількість тепла виділяється при цьому? [0,5 Дж] |
|
4.70. |
Тіло масою 4 кг починають підіймати з поверхні землі, прикладаючи силу 50 H. Визначити кінетичну енергію тіла на висоті 10 м. [100 Дж] |
Рівень Б
| 4.71. |
Горизонтальна сила 20 H за 10 мс тілу, що лежить на гладкій горизонтальній поверхні, надає кінетичної енергії 3 Дж. Яку енергію воно отримало б, якби на початок дії сили рухалося б у її напрямку зі швидкістю 10 м/с? [5 Дж] |
|
4.72. |
Куля масою 10 г, яка має швидкість 600 м/с, пробиває дошку завтовшки 4 см і вилітає зі швидкістю 400 м/с. Визначити середню силу опору, що діяла на кулю у дошці. [25 кН] |
|
4.73. |
По гладкому столу зі швидкістю u рухається чорна дошка. Якої довжини слід залишить на дошці шматочок крейди, який пустили по ній впоперек руху зі швидкістю v, якщо коефіцієнт тертя між крейдою та дошкою дорівнює\(\mu\). [\((v^{2}+u^{2})/(2\mu{g})\)] |
|
4.74. |
При повільному підніманні тіла по похилій площині з кутом нахилу \(\varphi\) виконали роботу A. Яка її частка η пішла на нагрівання тіла й площини при коефіцієнті тертя між ними μ? $\left[ \eta =\frac{\mu }{\operatorname{tg}\varphi +\mu } \right]$ |
|
4.75. |
Чому дорівнює ККД похилої площин довжиною 1 м і висотою 0,6 м при підніманні тіла при коефіцієнті тертя 0,1? [88%] |
|
4.76. |
При підійманні бруска масою 1 кг по похилій площині з ККД η = 80% виконали роботу 10 Дж. З якою швидкістю брусок повернеться у вихідне положення, якщо його відпустити? [4 м/с] |
|
4.77. |
Сани, що разом з людиною мають масу 100 кг, з’їжджають з гори висотою 8 м і довжиною 100 м. Визначити середню силу опору рухові саней, якщо вкінці спуску їхня швидкість склала 10 м/с. [30 Н] |
|
4.78. |
Санки, що з'їжджають з плоскої гірки висотою 2 м і довжиною основи 5 м, зупиняються, пройшовши відстань S = 35 м по горизонталі. Визначити, з яким коефіцієнтом тертя рухалися санки, вважаючи його однаковим на всьому шляху. [0,05] |
|
4.79. |
Невеличкий брусок масою 10 г зісковзує з висоти 1,2 м по жолобу, що плавно переходить у вертикальну петлю радіусом 40 см. Знайти роботу сили тертя на шляху від вершини гірки до найвищої точки петлі, якщо брусок, не втрачаючи контакту, перестає тиснути на неї. [20 мДж] |
|
4.80. |
Дві пружини з жорсткостями k1 і k2 з'єднано послідовно. Яку роботу треба виконати, аби розтягнути їх на задану величину x? [\((k_{1}k_{2}x^{2})/2(k_{1}+k_{2})\)] |
|
4.81. |
Куб переміщують на деяку відстань один раз тягнучи по горизонтальній поверхні, а інший – кантуванням, тобто, перекидаючи через ребро. При якому коефіцієнті тертя між кубом і поверхнею в обох випадках виконають однакову роботу? [≈0,21] |
|
4.82. |
Яку найменшу роботу необхідно виконати, щоб поставити вертикально стовп масою m і довжиною l, який лежить на землі? [mgl/2] |
|
4.83. |
Воду із ущент заповненого циліндричного резервуару з площею основи 2 м3 і глибиною 50 см перекачують у високий циліндр усемеро меншого діаметра за допомогою насоса з потужністю 0,5 кВт і ККД 80% . За який час буде перекачано всю воду? [5 хв]. |
|
4.84. |
Колодязь, який має площу дна 1 м2 і глибину 10 м, до половини заповнено водою. Яку потужність має мати насос з ККД 86%, аби відкачати всю воду за 100 c по трубі з площею перерізу 0,01 м2? [50 кВт] |
|
4.85. |
Вантажний кран за 7 год роботи підіймає 3000 т будівельних матеріалів на висоту 10 м. Яку потужність має двигун крана, якщо його ККД 0,6? [20 кВт] |
|
4.86. |
Транспортер підіймає 200 кг піску на автомашину за 1 с. Довжина стрічки транспортера 3 м, кут нахилу до горизонту 30°. Визначити потужність двигуна транспортера, якщо його ККД складає 85%. [3,46 кВт] |
|
4.87. |
Потужність гідростанції 73,5 МВт. Визначити об'ємні витрати води, якщо ККД станції дорівнює 75 %, а спад рівня води за греблею складає 10 м. [1000 м3/с] |
|
4.88. |
Тіло масою 1 кг кинули вертикально вгору з початковою швидкістю 1 м/с. Визначити потужність сили тяжіння на момент, коли кінетична енергія тіла зменшилася вдвічі. [\(\pm{7}\) Вт] |
|
4.89. |
Тіло масою m кинули під кутом \(\varphi\) до горизонту з початковою швидкістю v0. Визначити: А) середню потужність \(\langle{P}\rangle\) сили тяжіння за весь час руху тіла; Б) залежність миттєвої потужності сили тяжіння від часу. [0; \(mg(gt-v_{0}\sin\varphi)\)] |
|
4.90. |
Брускові масою 1 кг, який лежить на горизонтальній поверхні з коефіцієнтом тертя 0,27, поштовхом уздовж площини надають швидкість 1,5 м/с. Визначити середню потужність сили тертя за час подальшого руху бруска. [≈ 2 ВтЇ |
|
4.91. |
Коробка із сірниками масою 50 г лежить на відстані 30 см від краю стола. Кулька масою 1 г, що летить горизонтально з швидкістю 150 м/с, пробиває коробку і вилітає зі швидкістю 75 м/с. При якому найменшому коефіцієнті тертя коробка не злетить зі стола? [0,38] |
|
4.92. |
Автомобіль масою 1000 кг, який рушає з місця зі сталим прискоренням, за перші 2 c проходить шлях 20 м. Визначити: А) потужність двигуна автомобіля у кінці другої секунди; Б) середню потужність двигуна на вказаному шляху. ККД двигуна дорівнює 50 %. [400 кВт; 200 кВт] |
|
4.93. |
Два зв'язані перекинутою через нерухомий блок ниткою важки m1 і m2 (m1 > m2) утримують так, що важок m1 знаходиться на висоті h над підлогою, а потім без поштовху відпускають. Яка кількість теплоти виділиться при непружному ударі важка об підлогу? [\(m_{1}gh(m_{1}-m_{2})/(m_{1}+m_{2})\)] |
|
4.94. |
Тілу масою 1 кг, що лежить на горизонтальному столі висотою 1 м, поштовхом надають швидкість 2 м/с, через що воно, пройшовши по столу 2 м, впало на підлогу. Яка кількість тепла виділилася при непружному ударі тіла об підлогу, якщо коефіцієнт тертя між ним та поверхнею стола дорівнював 0,1? [10 Дж] |
|
4.95. |
Після кожного удару копра паля заглиблюється у землю на 1 см. Маса копра 500 кг, швидкість перед ударом 10 м/с. Знайти силу опору рухові палі у ґрунті, вважаючи її сталою. Масою палі знехтувати. [2,5 МН] |
|
4.96. |
Палю масою 1000 кг забивають за допомогою копра масою 400 кг. Копер вільно падає з висоти 5 м, і при кожному ударі заглиблює палю на 5 см. Визначити силу опору ґрунту при забиванні палі, якщо її вважати сталою. [127,5 кН] |
|
4.97. |
Яку мінімальну швидкість необхідно надати тілу на поверхні Землі, аби воно могло покинути Сонячну систему? [ \(\sqrt{2gR}\) ] |
| 4.98. | Яку роботу необхідно виконати для виведення штучного супутника масою 500 кг на низьку колову орбіту? [\(1,6\cdot{10}^{10}\) Дж] |
Рівень В
|
4.99. |
Камінь масою 200 г, який кинули з поверхні землі під кутом до горизонту, через 1,2 c впав на відстані 5 м . Яку роботу було виконано при киданні каменя? [5,2 Дж] |
|
4.100. |
Камінь масою 1,5 кг кинули під певним кутом до горизонту з поверхні землі. Визначити мінімальну роботу, що має бути виконана при киданні, щоб камінь впав на відстані 20 м. [150 Дж] |
|
4.101. |
 До бруска масою 12 кг, який лежить на горизонтальній поверхні з коефіцієнтом тертя 0,4, прикріплено пружину жорсткістю 300 Н/м, рис. 4.101. Яку роботу треба виконати, аби повільно перемістити тіло на 40 см, прикладаючи до пружини силу під кутом \(30^{\circ}\) до горизонту?[27,3 Дж] До бруска масою 12 кг, який лежить на горизонтальній поверхні з коефіцієнтом тертя 0,4, прикріплено пружину жорсткістю 300 Н/м, рис. 4.101. Яку роботу треба виконати, аби повільно перемістити тіло на 40 см, прикладаючи до пружини силу під кутом \(30^{\circ}\) до горизонту?[27,3 Дж] |
|
4.102. |
М'яч, який вільно падає з висоти50 см, при ударі об підлогу втрачає 40 % енергії. Скільки разів (теоретично) підстрибне м'яч? Чому дорівнює весь шлях пройдений м'ячем? [ $\infty $; ≈1,2 м] |
|
4.103. |
Тенісний м'яч, масою 100 г горизонтально летить зі швидкістю v1 = 15 м/с. Ударом ракетки його відбивають у протилежному напрямку при швидкості ракетки в момент удару v2 = 15 м/с. Уважаючи удар абсолютно пружним, знайти виконану при ударі роботу. [90 Дж] |
|
4104. |
Тіло масою 2 кг ковзає з гірки висотою 4,4 м, яка плавно переходить у циліндричну поверхню радіусом 2 м. При русі з вихідного положення до вищої точки циліндричної поверхні сила тертя виконала роботу A = 40 Дж. Визначити силу тиску тіла на циліндричну поверхню у її верхній точці . [10 Н] |
Збереження механічної енергії
Рівень А
|
4.105. |
Тіло кинули з поверхні землі вертикально вгору зі швидкістю 20 м/с. На якій висоті його кінетична енергія тіла дорівнюватиме потенціальній? [10 м] |
|
4.106. |
Тіло, кинуте вертикально вгору, піднялося на максимальну висоту 20 м. Якою була його швидкість на половині висоти підйому? [14 м/с] |
|
4.107. |
Кульку на нитці довжиною 62,5 см відвели на кут \(60^{\circ}\) від вертикалі й відпустили. Якою буде її найбільша швидкість? [2,5 м/с] |
|
4.108. |
Із пружинного пістолета стріляють вгору кулькою маси 10 г. На яку висоту підніметься кулька, якщо при заряджанні пружину пістолета жорсткістю 100 Н/м було стиснуто на 10 см? [5 м] |
Рівень Б
|
4.109. |
Камінь масою 300 г горизонтально кинуто з башти. Яку кінетичну енергію він має через 1 с, якщо при цьому рухається під кутом 30° до горизонту? [60 Дж] |
|
4.110. |
Під яким кутом до горизонту кулю масою 20 г випущено із гвинтівки зі швидкістю 600 м/с, якщо в найвищій точці траєкторії її кінетична енергія дорівнює 900 Дж? [\(60^{\circ}\)] |
|
4.111. |
З якої висоти тіло маси 1 кг впало на чашку ваг із жорсткістю пружин k = 250 Н/мм, якщо максимальна деформація пружини склала 1 см. [1,25 м] |
|
4.112. |
На відстані двох третин довжини нитки з підвішеною до неї кулькою маси m у стіну вбито гвіздок. Кульку відвели до горизонтального положення й відпустили. Якою буде сила натягу нитки на момент, коли вона займе горизонтальне положення? [4mg/3] |
|
4.113. |
Кульку масою 100 г обертають на нитці у вертикальній площині. Яку мінімальну міцність на розрив має мати нитка? [6 Н] |
|
4.114. |
Кульку математичного маятника довжини l прикріплено один раз до нитки, а інший – до невагомого стрижня. Якої найменшої швидкості слід поштовхом надати кульці в кожному випадку, аби вона здійснила повний оберт у вертикальній площині? [\(\sqrt{5gl}\); \(2\sqrt{gl}\)] |
|
4.115. |
Шматок каната довжиною 1 м і масою 0,5 кг із прикріпленою до нього гирею маси 1 кг утримують на гладкому столі так, що гиря ледь звисає. В якийсь момент канат вивільняють, і гиря починає падати. Якої швидкості вона набуде на момент сходу каната зі столу? [≈4 м/с] |
Рівень В
|
4.116. |
|
|
4.117. |
Невагомий стрижень з двома однаковими кульками на кінцях може вільно обертатися навколо закріпленої осі, що ділить його довжину у відношенні 1:3. Стрижень спочатку утримують у горизонтальному положенні, а потім відпускають. Якої максимальної кутової швидкості він набуде? [4 рад/с] |
|
4.118. |
Підвішене на нитці тіло маси 1 кг відвели до горизонтального положення й відпустили. Визначити силу натягу нитки на момент, коли вертикальна складова швидкості тіла сягне максимуму. [≈14 Н] |
|
4.119. |
На шляху обруча, що котиться без ковзання зі швидкістю v = 5 м/с, трапляється гірка довільного профілю. На яку максимальну висоту h зможе піднятися центр обруча? $\left[ h=\frac{{{v}^{2}}}{g}=2,5\text{м} \right]$
|
Збереження механічної енергії та імпульсу
Рівень Б
|
4.120. |
Куля, що летить горизонтально зі швидкістю v = 800 м/с, влучає й застряє в підвішеному на міцній мотузці довжиною l = 1,6 м брусі в η = 200 разів більшої маси. Знайти, на який кут α від вертикалі відкинеться брус. $\left[ \alpha =\arccos \left( 1-\frac{{{v}^{2}}}{2gl{{\eta }^{2}}} \right)=60{}^\circ \right]$ |
|
4.121. |
Ковзаняр масою 60 кг, який стоїть на льоду, горизонтально кинув камінь маси 5 кг із швидкістю 12 м/с відносно льоду. Яку роботу він при цьому виконав? [390 Дж] |
|
4.122. |
Ковзаняр масою 60 кг кидає у горизонтальному напрямі камінь масою 1 кг з висоти 1,8 м. Камінь падає на лід на відстані 9 м від точки кидання. Визначити відстань, на яку відкотиться ковзаняр після кидання, якщо коефіцієнт тертя дорівнює 0,01? [0,3 м] |
|
4.123. |
|
|
4.124. |
Куля масою 10 г горизонтально вдаряє зі швидкістю 500 м/с у підвішений на мотузці дерев'яний брус масою 20 кг і застряє, заглибившись на 20 см. Визначити середню силу опору рухові кулі в бруску. [6,25 кН] |
|
4.125. |
Брусок маси M, що ковзає по гладкій горизонтальній поверхні, непружно вдаряє в невагому пластину на кінці двох з'єднаних пружини жорсткістю k1 і k2, як показано на рис. 4.125. Визначити початкову швидкість бруска, якщо при максимальному стисканні енергія пружини 2 становить W. $\left[ v=\sqrt{\frac{2W}{M}\left( 1+\frac{{{k}_{2}}}{{{k}_{1}}} \right)} \right]$ |
|
4.126. |
Футболіст приймає на ногу м'яч, який летить із швидкістю 10 м/с. З якою швидкістю футболіст має відвести ногу в момент дотику м'яча, аби зупинити його? Уважати удар абсолютно пружним, а масу м'яча значно меншою за масу ноги. [5 м/с] |
|
4.127. |
Шайба, що рухається по гладкій горизонтальній поверхні, налітає й пружно відскакує назад від нерухомої шайби вдвічі більшої маси. Яку частку (%) своєї енергії перша шайба передає другій при ударі? [≈67%] |
|
4.128. |
Рухома куля пружно, але не в лоб, стикається з такою самою нерухомою шайбою. Під яким кутом вони розлетяться? [\(90^{\circ}\)] |
|
4.129. |
Рухома частинка 1 пружно стикається з нерухомою 2 так, що вони розлітаються під заданим кутом 2φ симетрично відносно початкового напрямку руху частинки 1. Визначити відношення мас частинок η = (m1/m2). [η = ctg2φ] |
|
4.130. |
Брускові масою 1 кг, розташованому на дошці масою 2 кг, яка лежить на гладкій горизонтальній поверхні, поштовхом надають швидкості 2 м/с. Який шлях пройде та яку швидкість матиме дошка на момент припинення ковзання бруска при коефіцієнті тертя 0,2. [≈23 см; ≈0,7 м/с] |
Рівень В
|
4.131 |
Кулька масою m1, яка рухається зі швидкістю v, налітає на нерухому кульку масою m2. Визначити швидкості кульок після центрального абсолютно пружного зіткнення? $\left[ {{v}_{1}}=\frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}v;\quad {{v}_{2}}=\frac{2{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}v \right]$ |
|
4.132. |
Куля перпендикулярно вдаряє в стос закріплених вертикальних пластин з однакового матеріалу й однакової товщини. В якій за ліком пластині застрягне куля, якщо в першій вона втрачає 5% швидкості? [ В одинадцятій ] |
|
4.133. |
Шайба маси 90 г, яка рухається зі швидкістю 1,35 м/с, після пружного зіткнення з іншою, доти нерухомою, шайбою відлітає під прямим кутом із удвічі меншою швидкістю. Визначити масу другої шайби та отриману нею швидкість. [150 г; 2,0 м/с] |
|
4.134. |
Рухома шайба, що має кінетичну енергію W, налітає на якусь іншу шайбу, що була нерухома. Визначити, за якої умови та якої максимальної величини кінетичну енергію отримає ця шайба від першої при центрального абсолютно пружному удар? [ W ] |
|
4.135. |
Дві маленькі пружні кульки масами 8 г і 20 г підвішено в дотик на нитках довжиною, відповідно, 10 см і 6 см. Потім першу відводять на кут \(\varphi=60^{\circ}\) і відпускають. Визначити максимальні кути відхилення ниток після зіткнення кульок. [φ1 ≈25°; φ2 ≈74°] |
Розділ V. СТАТИКА
Статика – це розділ механіки, в якому вивчаються умови механічної рівноваги тіл.
Механічною рівновагою називають стан спокою тіла, що знаходиться під дією сил. Ураховуючи відносність руху та спокою, формально в стані рівноваги перебуває й усяке тіло, що рухається без прискорення в інерціальній системі відліку. Але таке уточнення для задач статики є не істотним.
Далі представлено такий навчальний матеріал.
5.1. Основні поняття статики
|
Існує три види рівноваги твердого тіла: стійка, нестійка і байдужа. Рівновага називається стійкою, якщо при малих зміщеннях тіла з положення рівноваги виникають сили, що намагаються повернути його у вихідне положення. Важливою ознакою є те, що в стані стійкої рівноваги тіло має мінімальну можливу потенціальну енергію. Рівновага є нестійкою, якщо при малих зміщеннях тіла з положення рівноваги виникають сили, що віддаляють його від вихідного положення. У стані нестійкої рівноваги тіло має максимальну потенціальну енергію. У випадку байдужої рівноваги при зміщенні тіла ніякі сили не виникають, і його потенціальна енергія не змінюється. |
|
Зрівноважене тіло контактує з іншими тілами, що обмежують його рух. Такі тіла називаються в'язями, а сили, що діють на дане тіло з боку в'язей, – силами реакції в'язей. Типовими в'язями є опори та підвіси. Силою реакції підвісу є сила натягу, а силу реакції опори зручно розглядати як сукупність двох сил – нормальної реакції опори та сили тертя. |
|
За наявності в'язей прикладені сили можуть спричинювати не лише поступальний, а й обертальний рух тіла (до прикладу, як при скочуванні циліндра з похилої площини). При поступальному русі істотними є лише величина та напрям сили, що діє на тіло. Але при обертанні тіла важливим є ще й розташуванням лінії дії сили відносно осі обертання. При цьому мірою обертальної дії сили є момент сили. В елементарній фізиці розглядають лише обертання навколо осі незмінного напряму під дією сил, що є перпендикулярні до неї. В такому випадку момент сили дорівнює добутку сили на її плече:
а плечем сили називають найкоротшу відстань між лінією дії сили та віссю обертання (рис. 5.1), тобто – довжину їхнього спільного перпендикуляра.
Позаяк плече визначається лінією дії, а не точкою прикладання сили, то задля зручності вектор сили можна довільно переносити вздовж лінії дії. Сила може обертати тіло навколо даної осі в одному з двох можливих напрямків. Тому момент сили розглядають як алгебраїчну величину і приписують йому знак "плюс" або "мінус". Який саме, не має принципового значення. Треба лише, щоби в одній задачі всі моменти з одним напрямком дії мали однаковий знак. При дії декількох сил, які лежать в одній площині, результуючий момент дорівнює алгебраїчній сумі моментів окремих сил:
|
||||
|
Досить часто трапляються випадки, коли на тіло діє пара сил – однакові антипаралельні сили ${{\vec{F}}_{1}}=-{{\vec{F}}_{2}}$, лінії дії котрих не збігаються (рис. 5.2).
Обертальна дія (момент) пари сил теж визначається формулою (5.1), в якій F – модуль однієї із сил, а l – відстань між їхніми лініями дії, котра називається плечем пари. Особливістю пари сил є те, що її момент не залежить від положення осі обертання. |
5.2. Рівновага твердого тіла, центр ваги
|
Статична рівновага тіла означає нерухомість його центра мас і відсутність обертання. Тому для забезпечення рівноваги довільного тіла мають бути виконані дві вимоги, що в сукупності складають загальні умови рівноваги твердого тіла. |
|
Перша умова рівноваги твердого тіла є умовою рівноваги центра мас і гласить:
або у проекціях на координатні осі
Друга умова рівноваги твердого тіла є умовою відсутності обертання і називається правилом моментів:
Це правило треба розуміти так, що при складанні рівняння (5.4) для зрівноваженого тіла віртуальну вісь обертання можна обирати, як зручно, а не обов'язково в точці дотику до опори чи в точці кріплення підвісу. При розв'язуванні деяких задач статики використання обох умов рівноваги не є необхідним. Так буває у двох випадках: 1. Моменти реакцій в'язей гарантовано компенсують моменти всіх інших сил. У такому разі тіло може рухатися тільки поступально, і достатньою умовою рівноваги є (5.3). При цьому всі сили можна вважати прикладеними в одній точці, до прикладу, в центрі мас. 2. Якщо тіло має закріплену вісь обертання, то умова (5.3) виконується автоматично. В такому випадку достатньо скористатися тільки правилом моментів (5.4). |
||||||||||
|
Одним із важливих понять статики є центр ваги – точка прикладання рівнодійної сил тяжіння, що діють на всі частини тіла. Отже, при підвішуванні тіла за будь-яку точку центр ваги встановлюється з нею на одній вертикалі. На цьому ґрунтується простий лабораторний спосіб визначення центра ваги плоскої пластини. А саме, її підвішують послідовно за дві різні точки, проводять через них вертикалі й на їхньому перетині дістають положення центра ваги. При підвішуванні (чи підпиранні) тіла в центрі ваги рівновага є байдужою, тобто не залежить від орієнтації тіла в просторі. Це дозволяє з умов рівноваги тіла із закріпленою віссю обертання (5.4) вивести загальні формули для обчислення положення центра ваги пластини. Для цього подумки підвісимо пластину в центрі ваги С і розмістимо в її площині жорстко зв'язану систему координат так, аби осі ОX і OY мали звичну орієнтацію. В такому разі момент сили тяжіння відносно осі ОZ визначиться формулою M = mgХс, де Хс – координата центра ваги, яка є плечем сили тяжіння. З іншого боку, цей момент складається з моментів сил тяжіння, що діють на всі частинки пластини з масами mi й координатами xi. Отже,
і
Відтак подумки повернувши тіло разом із системою координат на 90°, отримаємо подібну формулу для координати Y:
(Примітка. Конкретний розрахунок за цим алгоритмом наведено в розділі ''Статика. Приклади розв'язування задач, Задача 5.18). В наведених міркуваннях пластина по умовчанню вважалася тонкою. Проте для товстої пластини третя координата Zс визначається аналогічною формулою, позаяк між осями ОХ і OZ немає жодної фізичної відміни. Зрозуміло також, що отримані формули є чинними не лише для пластини, а й для тіла довільної форми. Наостанку зауважимо, що наведені формули збігаються із формулами (3.6а), отже, центр ваги тіла збігається з його центром мас.
|
СТАТИКА. Приклади розв'язування задач
Наведені далі приклади задач згруповано по темах:
Рівновага тіла, що не може обертатися
Рівновага тіла із закріпленою віссю обертання
Визначення положення центра ваги (центра тяжіння)
У всіх умовах по умовчанню блоки вважаються невагомими, тертя в осях відсутнім, а мотузки й троси – невагомими й нерозтяжними. Крім того, при обчисленнях прийнято g = 1о м/с2.
Рівновага тіла, що не може обертатися
Відповіді наведено для \(g=10\ ,м/с^2\) .
Задача 5.1. Вантаж маси M підвісили до стелі на канаті довжиною l і масою m. Визначити та показати на графіку залежність сили натягу каната Т від відстані x до точки кріплення вантажу.
Задача 5.2. Через два паралельні гладкі стрижні, що закріплені в одній горизонтальній площині на відстані 2l = 50 см, перекинуто нитку з двома тягарями однакової маси m1 = m2 = m, розташованими на одному рівні. Визначити: 1. На яку висоту h піднімуться тягарі, якщо посередині між стрижнями підвісити й повільно опустити до положення рівноваги гирю масою m0 = km, де k = 1,2. 2. Чи буде ця рівновага стійкою?
Задача 5.3. Визначити, за якого мінімального коефіцієнта тертя μ клин із кутом α при забиванні в колоду не вислизатиме назад. Вагою клина знехтувати.
Задача 5.4. Дві невагомі пружини однакової довжини мають коефіцієнти жорсткості k1 та k2. Знайти жорсткість k складеної пружини, яка утвориться при з'єднанні цих пружин: 1) паралельно впритул і 2) послідовно.
Задача 5.5. Із двох однакових тонкостінних порожнистих півкуль радіуса R = 10 см, які щільно дотикаються одна до одної, відкачали повітря до тиску P = 80 кПа й підвісили їх до стелі так, аби лінія дотику була горизонтальна. Визначити найбільшу масу m тягаря, який можна підвісити до нижньої півкулі, аби вона не відірвалася при атмосферному тиску P0 = 100 кПа. Товщиною стінок і масою півкуль знехтувати.
Вантаж маси M підвісили до стелі на канаті довжиною l і масою m.
Визначити та показати на графіку
залежність T(x) сили натягу каната Т від відстані x від точки кріплення вантажу.
Дано:
| M, m, l |
|
T(x) - ? |
Розв’язання
Натяг каната створюється не лише підвішеного вагою вантажу, а й вагою самого каната, що є рівномірно розподілена по його довжині. Тож у певній точці каната сила натягу дорівнює
T = (M + m′)g,
де m′ – маса частини каната між цією точкою та точкою кріплення вантажу, рис. 1а.
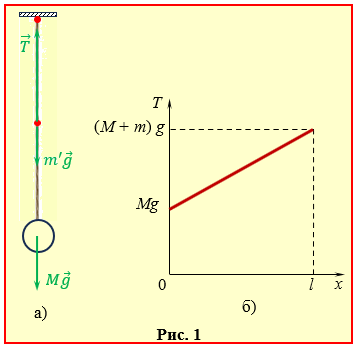
Очевидно, що
${m}'=m\frac{x}{l} $,
де m – маса всього каната, х – відстань від даної точки каната до точки кріплення вантажу.
Отже, відповідь задачі:
|
T(x) =$\left( M+m\frac{x}{l} \right)$g |
(1) |
Графік залежності T(x) наведено на рис. 1б.
Зауважимо, що при m = 0 сила натягу T = Mg не залежить від відстані х. Тож вираз (1) формально доводить положення, котре в задачах динаміки приймається по умовчанню: в невагомих нитках (мотузках, тощо) сила натягу є скрізь однакова.
Через два паралельні гладкі стрижні, що закріплені в одній горизонтальній площині на відстані 2l = 50 см, перекинуто нитку з двома тягарями однакової маси m, розташованими на одному рівні.
Визначити
1. На яку висоту h піднімуться тягарі, якщо посередині між стрижнями підвісити й повільно опустити до положення рівноваги гирю масою m0 = km, де k = 1,2.
2. Чи буде ця рівновага стійкою?
Дано:
|
2l = 50 см m0 = km k = 1,2 |
|
h - ? |
Розв’язання
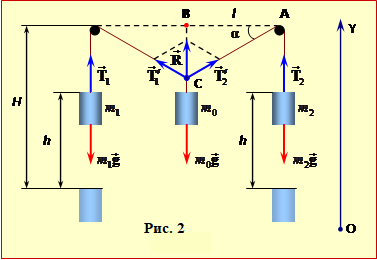
На рис. 2 схематично показано початкове та кінцеве положення тіл і сили, що діють на них.
Після підвішування в т А гиря опускається до т. А′, а тягарі підіймаються на шукану висоту h. При цьому відстань від точки кріплення гирі до кожного стрижня збільшується від заданого значення l до величини
${{l}_{1}}=\frac{l}{\cos \alpha }$.
Отже,
|
\(h=l\left( \frac{1}{\cos \alpha }-1 \right)\) |
(1) |
Таким чином, задача зводиться до визначення кута провисання нитки α, котрий залежить від співвідношення k мас гирі та тягарів. Величину α легко знайти з першої умови рівноваги твердого тіла (5.3), позаяк модулі всіх сил натягу однакові (для ниток, які утримують тягарі, це очевидно, а для тих, що утримують гирю, випливає з відсутності тертя в стрижнях):
|
${T}'={T}''=T$. |
(2) |
Справді, тягарі зрівноважуються натягом ниток
T = mg,
а гиря – рівнодійною $\vec{R}$ = ${\vec{T}}'$ + ${\vec{T}}''$, модуль якої складає (див. рис. 2)
|
\(R=2T\sin \alpha \) = \(2mg\sin \alpha \) |
(3) |
і дорівнює m0g. Отже, порівнюючи величини R і T, дістанемо
${{m}_{0}}=2m\sin \alpha $
і, врахувавши співвідношення m0 = km, –
| \(\sin \alpha =\frac{k}{2}\) \(\Rightarrow \) \(\cos \alpha =\sqrt{1-{{\left( {k}/{2}\; \right)}^{2}}}\). |
|
Відтак із виразу (1) отримаємо відповідь:
\( {h}=l\left(\frac{1}{\sqrt{1-{{\left( {k}/{2}\; \right)}^{2}}}}-1 \right)\) = 6,25 см.
Формальна відповідь на запитання, чи є рівновага стійкою, випливає з виразу (3). Дійсно, якщо гирю подумки трохи підняти (опустити) то сила R стане меншою (більшою) за m0g, і після вивільнення гиря повернеться у вихідне положення. Отже, рівновага є стійкою.
На завершення з'ясуємо, чому в тексті наголошено на повільному опускання гирі. Справа в тому, що рівновага, або відсутність сил, які діють тіло, означає відсутність у нього прискорення, проте не швидкості. Тож, якщо після підвішування гирю просто відпустити, то, розігнавшись при вільному опусканні, вона за інерцією проскочить положення рівноваги, тож у момент зупинки величина R перевищуватиме m0g. Відтак гиря почне прискорено підійматися, і все повториться у зворотньому порядку. Іншими словами, гиря буде здійснювати коливання, і поставлене в задачі запитання не матиме однозначної відповіді. Саме через це за умовою рух гирі не є вільним.
Визначити,
за якого мінімального коефіцієнта тертя μ клин із кутом α при забиванні в колоду не вислизатиме назад. Вагою клина знехтувати.
|
Дано: α = 30° |
| μmin - ? |
Розв’язання
На забитий в колоду клин діють сили нормальної реакції \( \vec{N}_{1}\), \( \vec{N}_{2}\), які виштовхують його, та сили тертя \( \vec{F}_{1}\), \( \vec{F}_{2}\), що утримують (рис. 2а). Очевидно, що клин не може обертатися, тож задля зручності будемо вважати, що всі сили є прикладені в одній точці (рис. 2б).
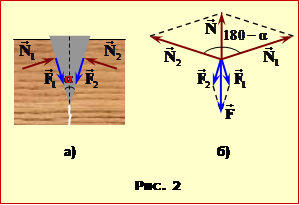 |
Аби клин не вислизав, рівнодійні сил тиску \( \vec{N}=\vec{N}_{1}+\vec{N}_{2}\) та тертя \( \vec{F}=\vec{F}_{1}+\vec{F}_{2}\) мають бути зрівноважені:
|
\( \vec{N}+\vec{F}=0\ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ {F=N.}\) |
(1) |
Із міркувань симетрії випливає, що \( {{N}_{1}}={{N}_{2}}\) і \( {{F}_{1}}={{F}_{2}}\). Тож (див. рис. 2б) умова рівноваги (1) набуває вигляду:
|
\( 2{{N}_{1}} \cos \left( 90{}^\circ -\frac{\alpha }{2} \right)\) = \(2{{F}_{1}} \cos \frac{\alpha }{2}\) $\Rightarrow $ $\frac{{{F}_{1}}}{{{N}_{1}}}=\operatorname{tg}\frac{\alpha }{2}$ |
|
Звідси, позаяк сила тертя спокою ${{F}_{1}}\le \mu {{N}_{1}}$ (див. розділ 2, п. 2.4), отримуємо відповідь:
\( \mu\ge\mathrm{tg}\frac{\alpha }{2}\) $\Rightarrow $ μmin = 0,27.
Дві невагомі пружини однакової довжини мають коефіцієнти жорсткості k1 та k2.
Знайти
жорсткість k складеної пружини, яка утвориться при з'єднанні цих пружин: 1) паралельно впритул; 2) послідовно.
|
Дано: k1, k2 |
|
k - ? |
Розв’язання
Згідно із законом Гука (2.11) жорсткість пружини дорівнює відношенню прикладеної сили до видовження:
|
$k=\frac{F}{x}$. |
(1) |
У цьому й полягає задача.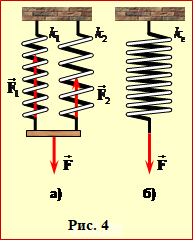
1) При навантаженні паралельно з'єднаних впритул пружин різної жорсткості (рис. 4a) перекосом перетинки можна нехтувати. В такому разі видовження кожної пружини збігається з видовженням системи: х1 = х2 = х, і за законом Гука (2.11) сили пружності в них складають:
\( {F}_{1}={k}_{1}x,\ \ \ {F}_{2}={k}_{2}x \).
Ці сили зрівноважують прикладену до системи силу F, отже,
|
\( {k}_{1}x\ + \ {k}_{2}x \) = \( {k}x \) $\Rightarrow $ $k={{k}_{1}}+{{k}_{2}}$ |
Одержана відповідь очевидно узагальнюється й на випадок паралельного з'єднання довільної кількості пружин:
|
\(k=\sum{{{k}_{i}}}\) |
|
2) Розглянемо тепер умову рівноваги системи послідовно з'єднаних пружин, до якої прикладено силу \( \vec{F}\) (рис. 3-1). Безпосередньо вона прикладається до першої пружини і зрівноважується тільки силою \( \vec{F}_{1}\):
|
\({{F}_{1}}=F.\) |
|
Відповідно, на нижній кінець другої пружини (точка О) безпосередньо діє лише перша пружина із силою ${{\vec{F}}_{1}}^{\prime }$, котра зрівноважується силою натягу другої пружини ${{\vec{F}}_{2}}$:Отже,
|
\(F_{2}=F^{\prime}_{1}\). |
|
Сили \( \vec{F}_{1}\) і \(\vec{F}_{1}^{\prime}\) визначаються деформацією однієї пружини, тож
|
\(F^{\prime}_{1}=F_{1}\). |
|
Відтак із записаних рівностей випливає, що
|
\( {F}={{F}_{1}}={{F}_{2}}.\) |
(2) |
Загальне видовження послідовно з'єднаних пружин дорівнює сумі видовжень кожної з них:
|
\( {x}={{x}_{1}}+{{x}_{2}}.\) |
|
Отже, згідно з виразом (1),
|
$\frac{F}{k}$ = \(\frac{{{F}_{1}}}{{{k}_{1}}}+\frac{{{F}_{2}}}{{{k}_{2}}}=F\left( \frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}} \right)\), |
|
і, враховуючи співвідношення (2), отримуємо:
|
\(\frac{1}{k}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\) \(\Rightarrow \) $k=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}$ |
|
Для довільної кількості послідовно з'єднаних пружин розрахункова формула має наступний вигляд:
|
\( \frac{1}{k}=\sum\frac{1}{{{k}_{i}}}. \) |
|
Із двох однакових тонкостінних порожнистих півкуль радіуса R = 10 см, які щільно дотикаються одна до одної, відкачали повітря до тиску P = 80 кПа й підвісили їх до стелі так, аби лінія дотику була горизонтальна.
Визначити
найбільшу масу m тягаря, який можна підвісити до нижньої півкулі, щоби вона не відірвалася при атмосферному тиску P0 = 100 кПа. Товщиною стінок і масою півкуль знехтувати.
|
Дано: R = 10 см
P = 80 кПа
P0= 100 кПа |
|
m0 - ?
|
Розв’язання
Невагома за умовою нижня півкуля утримується від падіння силою атмосферного тиску \(\vec{F}_{0}\), яка долає вагу гирі $m\vec{g}$, силу залишкового тиску повітря всередині \(\vec{F}\) і силу \(\vec{N}\) (рис. 5а), з якою верхня півкуля діє на нижню. При цьому, за третім законом Ньютона (розділ ІІ, п. 2.2) з такою самою за величиною силою нижня півкуля притискається до верхньої. Тож, позаяк за умовою рівноваги
\(\vec{F}_{0}\) + $m\vec{g}$ + \(\vec{F}\) + \(\vec{N}\) = 0,
сила, з якою півкулі притискаються одна до одної, дорівнює
|
N = F0 – F – mg |
(1) |
Зрозуміло, що при збільшенні ваги тягаря притискання між півкулями буде зменшуватись і врешті зникне. Тож, шукану критичну масу тягаря m0, котру можна розглядати як максимально допустиму при утриманні нижньої півкулі, або як мінімальну, необхідну для її відриву, знайдемо, поклавши в рівності (1) N= 0:
|
m0g = F0 – F |
(2) |
Далі визначимо величини F0 і F, для чого на поверхні нижньої півкулі виділимо тонку горизонтальну смужку і подумки розчленуємо її на однакові малі діаметральні ділянки \( \Delta{S}\) (рис.7-1б). Тоді, позаяк сила тиску є перпендикулярна до поверхні, на кожну пару таких ділянок діють рівні за модулем сили \(\vec{F}_{01}\) і \(\vec{F}_{02}\), які лежать в одній вертикальній площині й зустрічно спрямовані під однаковими кутами \( \alpha \) до горизонту. Тож їхні горизонтальні складові є компенсовані, й рівнодійна напрямлена вертикально вгору. З таких парних ділянок складається вся смужка, а зі смужок – вся півкуля. Тому сила атмосферного тиску F0, що діє на нижню півкулю, дорівнює сумі \( \Delta {{F}_{0B}}\) вертикальних складових сил тиску на кожну ділянку \( \Delta S \). Як видно з рис. 5б, їхня величина визначається, як
$\Delta {{F}_{B}}=\Delta {{F}_{0}}\sin \alpha $
а через атмосферний тиск P0 – як
$\Delta {{F}_{B}}={{P}_{0}}\Delta S\sin \alpha ={{P}_{0}}\Delta {S}'$
де \( \Delta {S}'\) – площа проєкції ділянки \( \Delta{S}\) на горизонтальну площину. Отже, модуль сили атмосферного тиску на всю поверхню
|
\( {{F}_{0}}=\sum{{{F}_{0B}}={{P}_{0}}{S}',}\) |
|
де \( {S}'=\pi {{R}^{2}}\) – площа проєкції на горизонтальну площину всієї нижньої півсфери, котра являє собою круг радіуса R. Урахувавши це, маємо:
|
\( {{F}_{0}}=\pi {{R}^{2}}{{P}_{0}}. \) |
|
Аналогічно знаходимо й силу F залишкового тиску повітря всередині півкуль:
|
\( {F}=\pi {{R}^{2}}P. \) |
|
Відтак, підставивши отримані значення вирази F0 і F у вираз (1), дістанемо відповідь:
\( {{m}_{0}}=\frac{({{P}_{0}}-{{P}_{1}})\pi {{R}^{2}}}{g}\) ≈ 63 кг.
Рівновага тіла з закріпленою віссю обертання
Задача 5.6. Конічна колода знаходиться в рівновазі на підпірці, що встановлена на третині довжини колоди від товщого кінця. Якщо підпірку розмістити посередині, а на тонший край посадити людину масою m = 70 кг, то колода знову буде зрівноважена. Визначити масу колоди M.
Задача 5.7. Стрижень масою m = 2 кг і довжиною l = 50 см, який шарнірно прикріплено одним кінцем до вертикальної стіни, за інший кінець утримується під кутом α = 30° до вертикалі горизонтальною ниткою. Визначити силу натягу цієї нитки, якщо до кінця стрижня підвішено тягар масою m1 = 4 кг.
Задача 5.8. Прут, зігнутий у формі прямого кута з нерівними сторонами, шарнірно підвішено за коротший край. Визначити відношення n довжин сторін кута, якщо менша утворює з вертикаллю кут \(\vartheta =50^{\circ} \).
Конічна колода знаходиться в рівновазі на підпірці, що встановлена на третині довжини колоди від товщого кінця. Якщо підпірку розмістити посередині, а на тонший край посадити людину масою m = 70 кг, то колода знову буде зрівноважена.
Визначити
масу колоди M.
|
Дано: m = 70 кг |
|
M - ? |
Розв’язання
З умови зрозуміло, що в першому випадку підпірка розташована під центром ваги колоди С, (рис. 6а). У другому випадку за умовою рівноваги (5.4) моменти сил
тяжіння \( {M}\vec{g}\) і \( {m}\vec{g}\), що діють на колоду та на людину (рис.6б) відносно осі О мають бути однакові. Плечі цих сил дорівнюють \({{h}_{1}}={l}/{2}\;-{l}/{3}\;={l}/{6}\; \) і \( {{h}_{2}}={l}/{2}\;\), відповідно. Отже,
\( {Mgl}/{6}={mgl}/{2}\); \( \Rightarrow \) \( {M}=3m\) = 210кг.
Стрижень масою m = 2 кг і довжиною l = 50 см, який шарнірно прикріплено одним кінцем до вертикальної стіни, за інший кінець утримується під кутом α = 30° до вертикалі горизонтальною ниткою.
Визначити
силу натягу цієї нитки, якщо до кінця стрижня підвішено тягар масою m1 = 4 кг.
|
Дано: m = 2 кг
l = 0,5 м
α =30°
m1 = 4 кг
|
|
F - ? |
Розв’язання
 Стрижень має закріплену вісь обертання в точці О (рис. 7), тож згідно з правилом моментів (5.4),
Стрижень має закріплену вісь обертання в точці О (рис. 7), тож згідно з правилом моментів (5.4),
|
M1 + M2 + M3 = 0, |
(1) |
де M1, M2, M3 – моменти відносно осі О наступних сил: 1) натягу горизонтальної нитки \( \vec{F}\), 2) ваги (сили тяжіння) стрижня \({m}\vec{g}\) і 3) натягу підвісу тягаря \({\vec{T}}\) = ${{m}_{1}}\vec{g}$. Плечі цих сил ОС, ВС і АС (рис. 5) дорівнюють: 1) h1 = l·cosα, h2 = (l/2)·sinα і h3 = l·sinα, відповідно. Тож, підставивши указані величини сил і пліч в рівняння (1) і, врахувавши знаки моментів, дістанемо відповідь:
|
\( {l}T\sin\alpha+\frac{l}{2}mg\sin\alpha-lF\cos\alpha={0}\) \( \Rightarrow \) \(F=\left(\frac{m}{2}+{m}_{1}\right)g\mathrm{tg}\alpha \), |
|
і після обчислень
F = 28,3 H.
Прут, зігнутий у формі прямого кута з нерівними сторонами, шарнірно підвішено за короткий кінець.
Визначити
відношення n довжин сторін кута, якщо менша утворює з вертикаллю кут \(\vartheta =50^{\circ} \).
|
Дано: \(\vartheta =50^{\circ} \) |
|
n - ? |
Розв’язання
Згідно умовою (5.4) при рівновазі прута моменти сил тяжіння, що діють на частини прута, відносно осі О (рис. 6) мають мати однакову величину:
M1 = M2.
Позначимо для їхнього визначення довжину та масу короткої сторони прута як l і m. Тоді для довгої матимемо nl і nm і для сил тяжіння – mg і nmg, відповідно. Ці сили є прикладені в центрах ваги (посередині) сторін (рис. 6), отже, їхні плечі дорівнюють:
\({{h}_{1}}=\frac{l}{2}\sin\vartheta \),
\({{h}_{2}}=\frac{nl}{2}\cos\vartheta -l\sin\vartheta\),
а моменти
\( {{M}_{1}}=\frac{mgl}{2}\sin \vartheta \),
\({M}_{2}=nmgl\left(\frac{n}{2}\cos\vartheta -\sin\vartheta\right)\).
${{n}^{2}}-2n\operatorname{tg}\vartheta -{{\operatorname{tg}}}\vartheta $ = 0,
з якого знайдемо відповідь (від'ємний корінь не має змісту):
Загальні умови рівноваги тіла
Задача 5.9. Однорідну балку масою m = 500 кг і довжиною l = 5 м підвішено горизонтально на двох паралельних тросах так, що один розташовано скраю, а інший – на відстані a = 1 м від протилежного кінця балки Визначити сили натягу тросів T1 і T2.
Задача 5.10. Кулю підвішено на короткій нитці до вертикальної стіни. Визначити: 1) при якому коефіцієнті тертя μ між кулею та стіною точка кріплення нитки до кулі та її центр можуть бути розташовані на одній вертикалі? 2) як розміститься куля за відсутності тертя?
Задача 5.11. На похилій площині з кутом нахилу до горизонту α лежить прикріплена до стіни за кінець нитки котушка з ободом радіуса R і шаром ниток радіусом r. Визначити найменший можливий коефіцієнт тертя μ0 між котушкою та площиною, коли не намотаний кінець нитки є паралельним до площини.
Задача 5.12. На похилій площині із заданим кутом нахилу до горизонту α стоїть циліндр заданої висоти h і діаметра d. Визначити: 1. Відстань l між віссю циліндра та лінією дії сили нормальної реакції опори; 2. Максимальний кут нахилу площини αm , при якому циліндр ще не перекинеться.
Задача 5.13. На підлозі стоїть куб масою m = 50 кг. Визначити: 1) найменшу силу F0, котрою можна перекинути куб через ребро; 2) мінімальний необхідний для цього коефіцієнт тертя μ0 між кубом і підлогою.
Задача 5.14. Визначити, під яким найменшим кутом до горизонту ${{\theta }_{\min }}$ може встояти приставлена до стіни драбина при однаковому коефіцієнті її тертя зі стіною та підлогою, що дорівнює 0,3?
Задача 5.15. На горизонтальному столі лежить дошка масою M = 6 кг, котра на третину виступає за його край. До кінця дошки на нитці підвішено тягар, який відводять до горизонтального положення й відпускають. Визначити масу тягаря m, якщо при його проходженні через найнижче положення протилежний край дошки відривається від стола.
Задача 5.16. Тонкий гладенький стрижень уміщують у напівсферичну лунку з гладкою поверхнею. Визначити, під яким кутом α до горизонту встановиться стрижень, якщо відношення його довжини до діаметра лунки складає задану величину (l/d) = η.
Однорідна балку масою m = 500 кг і довжиною l = 5 м підвішено горизонтально на двох паралельних тросах так, що один розташовано скраю, а інший – на відстані a = 1 м від протилежного кінця балки.
Визначити
сили натягу тросівT1 і T2.
|
Дано: m = 500 кг
l = 5 м
a = 1 м
|
|
T1, T2 - ? |
Розв’язання
На балку діють показані на рис. 9 сила тяжіння \( {m}\vec{g}\), прикладена у центрі ваги С посередині, та сили натягу тросів \( \vec{T}_{1}\) і \( \vec{T}_{2}\), котрі її зрівноважують:
\( {mg}={{T}_{1}}+{{T}_{2}}.\)
Записана рівність визначає сумарну силу натягу тросів, але не кожну із них окремо. Тож використаємо ще й другу умову рівноваги – правило моментів. Для цього запишемо рівняння (5.4) для осей А і В, що проходять через точки підвішування балки, приймаючи в кожному випадку момент сили тяжіння додатнім.
Відносно осі A моменти створюють сила тяжіння mg з плечем h′ = (l/2) і сила натягу другого троса T2, плече котрої h2 =(l – a). Отже,
\( {mg}\frac{l}{2}-{{T}_{2}}\left( l-a \right)=0\), \(\Rightarrow\) \( {{T}_{2}}=\frac{mg}{2}\cdot \frac{l}{l-a}.\)
Силу натягу першого троса Т1 визначимо аналогічно, склавши рівняння моментів відносно осі В, для якої плече сили mg складає h″ = ((l/2) – a):
\( {mg}\left( \frac{l}{2}-a \right)-{{T}_{1}}\left( l-a \right)=0\ \ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ {{T}_{1}}=\frac{mg}{2}\cdot \frac{l-2a}{l-a}. \)
Обчислення дають:
Т1 = 1875 Н, Т2 = 3125 Н.
З приводу наведеного розв'язку варто нагадати, що вибір віртуальних осей при складанні рівнянь (5.4) є довільним. До прикладу, замість осей А і В можна було би взяти вісь 1 посередині між точками А і С та вісь 2 на вільному кінці балки. Тоді рівняння моментів мали би вигляд:
|
$(1)\quad \ {{T}_{1}}l+mgl-\ \ {{T}_{2}}\left( 3l-4a \right)=0$, $( 2)\quad 2{{T}_{1}}l-mgl+2{{T}_{2}}a$. |
Корені цієї системи, звичайно, збігаються із раніше знайденими значеннями Т1, Т2 (радимо переконатися в цьому самостійно), але розв'язання є суттєво громіздкішим. Тож має сенс вибирати осі так, аби кожна перетинала лінію якоїсь із шуканих сил.
Кулю підвішено на короткій нитці до вертикальної стіни (рис. 10).
Визначити:
1) при якому коефіцієнті тертя μ між кулею та стіною точка кріплення нитки до кулі та її центр можуть бути розташовані на одній вертикалі?
2) як розміститься куля за відсутності тертя?
Розв’язання
При рівновазі довільного тіла дорівнюють нулю векторна сума всіх сил, які діють на нього, та алгебраїчна сума їхніх моментів відносно довільної осі.
1) Почнемо з моментів. На рис. 10-2 показано потрібне розташування точки кріплення нитки С і діючі на кулю сили тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\), тертя \( \vec{F}\) та натягу нитки \( \vec{T}\). Позаяк за умовою задачі силу натягу нитки визначати не треба, для складання рівняння моментів доцільно вибрати віртуальну вісь, що проходить через точку С, відносно котрої моменти створюють лише сили \( \vec{F}\) та \( \vec{N}\). З рис.10-2 видно, що їхні плечі однакові, тож згідно з умовою (5.4), однакові й самі сили:
| \( {F}={N.}\) |
(1) |
При рівновазі на кулю діє сила тертя спокою F ≤ μN (див. розділ 2, п. 2.3). Тож із співвідношення (1) випливає:
μN ≥ N \( \Rightarrow \) μ ≥ 1.
2) За відсутності тертя (F = 0) на кулю діють тільки сили \( {m}\vec{g}\), \( \vec{N}\) та \( \vec{T}\), причому алгебраїчна сума їхніх моментів має дорівнювати нулю відносно будь-якої осі, зокрема, осі О, що проходить через центр кулі. При цьому позаяк моменти сили тяжіння та нормальної реакції стіни є нульовими, таким має бути й момент сили натягу нитки. Отже, куля встановиться в положенні, при якому продовження нитки проходить через центр кулі.
Відмітимо, що, як і в попередній задачі, раціональний вибір віртуальних осей обертання дозволив отримати відповіді за допомогою однієї умови рівноваги тіла – правила моментів (5.4). Але слід зауважити, що в даній задачі відповіді можна отримати й за допомогою лише першої умов рівноваги (5.3а), проте розв'язування буде більш громіздким.
Задача 5.11
На похилій площині з кутом нахилу до горизонту α лежить прикріплена до стіни за кінець нитки котушка з ободом радіуса R і шаром ниток радіусом r, рис. 11.
Визначити
найменший можливий коефіцієнт тертя μ0 між котушкою та площиною, коли не намотаний кінець нитки є паралельним до площини.
 |
 |
|
Дано: α, R, r |
|
μ0 - ? |
Розв’язання
Згідно із загальними умовами (5.3) і (5.4), для рівноваги котушки рівнодійна та сумарний момент прикладених до неї сил мають бути нульовими.
Сили, що діють на котушку (тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\), тертя \( \vec{F}\) та натягу нитки \( \vec{T}\)) разом із системою координат ХOY показано на рис. рис. 9-1. Відповідно,перша умова (5.3а) в проєкціях на площину має вигляд:
|
\( \begin{align} & \mathrm{OX:}\ \ \ mg\sin\alpha-F -T=0 \\ & \mathrm{OY:}\ \ \ N-mg\cos\alpha=0 \\ \end{align} \). |
|
Звідси після елементарних перетворень отримаємо:
|
$\frac{F+T}{N}=\operatorname{tg}\alpha $ |
(1) |
Коефіцієнт тертя визначає зв'язок між силою тертя F та силою нормального тиску N. Його можна знайти з рівняння (1), виключивши величину T за допомогою другої умови рівноваги (5.4). Для цього запишемо рівняння моментів відносно осі котушки С:
|
\(FR-Tr=0.\) \( \Rightarrow \) $T=F\frac{R}{r}$, |
(2) |
і, зробивши таку підстановку в рівнянні (1), дістанемо:
| $\frac{F}{N}=\frac{r}{R+r} \operatorname{tg}\alpha $. |
(3) |
Сила тертя спокою F задовольняє умову F ≤ μN (див. розділ 2., п. 2.3), тож відповідно до виразу (3) можна записати:
|
$\mu \ge \frac{r}{R+r} \operatorname{tg}\alpha $. |
|
Отже, найменше значення коефіцієнта тертя необхідне, аби котушка не ковзала, складає
|
\( \mu_{0 }=\frac{r}{R+r}\mathrm{tg}{\alpha.}\) |
На похилій площині із заданим кутом нахилу до горизонту α стоїть суцільний однорідний циліндр заданої висоти h і діаметра d.
Визначити:
1. Відстань l, від лінії дії сили нормальної реакції опори до осі циліндра;
2. Максимальний кут нахилу площини αm , при якому циліндр ще не перекинеться.
|
Дано: α, h, d |
| l-?, αm-? |
Розв’язання
У задачах динаміки по умовчанню приймається, що тіло, котре перебуває на якійсь поверхні (опорі), під час руху не може перекинутись. Тому задля зручності всі сили вважаються прикладеними в одній точці (зазвичай в центрі мас тіла). Але в багатьох задачах статики так міркувати не можна, і належить ураховувати не лише самі сили, а й їхні моменти. Прикладом є дана задача.
На циліндр діють сили тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\) та тертя \( \vec{F}\) (рис. 12). При цьому відносно центра ваги циліндра C сила \( \vec{F}\) створює обертовий момент, який прагне перекинути циліндр. Але при рівновазі він компенсується зворотнім моментом сили \( \vec{N}\), лінія котрої проходить праворуч від осі циліндра на шуканій відстані l.
\( {l}=\frac{h}{2}\text{tg}\alpha \).
2. Для рівноваги циліндра моменти сил тертя та тяжіння відносно осі О1 мають бути компенсовані, що є можливо лише коли вона знаходиться всередині основи циліндра. А це означає, що максимальна відстань ОО1 дорівнює його радіусові r = (d/2). Отже, як видно з рис.12, максимальний можливий кут нахилу площини до горизонту складає
αm = $\operatorname{arctg}\left( \frac{d}{h} \right)$
.
На підлозі стоїть куб масою m = 50 кг.
Визначити:
1) найменшу силу F0, котрою можна перекинути куб через ребро;
2) мінімальний необхідний для цього коефіцієнті тертя μ0 між кубом і підлогою.
|
Дано: m = 5 кг |
|
F0 - ? μ0 - ? |
Розв’язання
1) Аби перекинути куб було найлегше, момент прикладеної сили відносно опорного ребра має бути найбільшим із усіх можливих. Тому шукану силу ${{\vec{F}}_{0}}$ слід прикладати посередині протилежного ребра перпендикулярно до фронтальної діагоналі куба, тож під кутом α = 45° до горизонту, як показано в перерізі на рис. 5-11. При цьому за величиною вказаний момент має дорівнювати моментові сили тяжіння відносно того самого ребра:
|
${{F}_{0}}\cdot a\sqrt{2}=mg\cdot \frac{a}{2}$, |
|
де a – ребро куба.
Отже, величина F0 складає
|
\( {{F}_{0 }}=\frac{mg}{2\sqrt{2}}\) = 177 Н. |
(1) |
2) Сила \( \vec{F}_{0}\) має горизонтальну складову
|
Fгор = ${{F}_{0}}\cos \alpha =\left( {{F}_{0}}/\sqrt{2} \right)$, |
(2) |
котра при недостатньому терті може спричинити не перекидання, а ковзання куба по підлозі. Аби цього не сталося, гранична сила тертя спокою (див. розділ 2, п. 2.3) Fсп = μN, яка забезпечує нерухомість нижнього ребра куба, має бути не меншою, ніж Fгор:
|
$\mu N\ge \frac{{{F}_{0}}}{\sqrt{2}}$, |
(3) |
де нормальна реакція опори N та вертикальна складова F0sinα прикладеної сили зрівноважують силу тяжіння, що діє на куб. Отже,
N + F0sinα = mg.
Звідси, врахувавши вираз (1) і значення sinα = $\left( {1}/{\sqrt{2}}\; \right)$, отримаємо
N = \(\frac{3mg}{4}\)
і, відтак розв'язавши нерівність (3), дістанемо відповідь:
${{\mu }_{0}}=\frac{1}{3}$.
Визначити,
під яким найменшим кутом до горизонту ${{\theta }_{\min }}$ може встояти приставлена до стіни драбина при однаковому коефіцієнті її тертя зі стіною та підлогою, що дорівнює 0,3?
|
Дано: μ = 0,3 |
|
θmin - ? |
Розв’язання
На драбину діють: сила тяжіння \( {m}\vec{g}\), сили нормальної реакції опор (підлоги \(\vec{N}_{1}\) і стіни \(\vec{N}_{2}\)), та сили тертя між драбиною і підлогою \( \vec{F}_{1}\) та стіною \( \vec{F}_{2}\), які утримують драбину від зісковзування під дією сили тяжіння, рис. 12.
Для рівноваги драбини вказані сили та їхні моменти відносно довільної осі мають бути компенсовані. Отже, за умовою (5.3)
|
N2 = F1, F2 + N1 = mg. |
(1) |
Для складання рівняння моментів (5.4) виберемо віртуальну вісь С, відносно якої моменти створюють лише сили \( {m}\vec{g}\), \( \vec{F}_{1}\) і \( \vec{F}_{2}\), плечі котрих при куті нахилу драбини θ складають, відповідно:
h = (l/2)·cosθ, h1 = l·sinθ, h2 = l·cosθ.
Тоді
\( {-mg}\frac{l}{2}\cos\theta+{F}_{1}l\sin\theta+{F}_{2}l\cos\theta=0. \)
З цього рівняння після елементарних перетворень дістанемо:
|
$tg\theta =\frac{mg-2{{F}_{2}}}{2{{F}_{1}}}$, |
|
і, врахувавши співвідношення (1),
|
$\operatorname{tg}\theta =\frac{{{N}_{1}}-{{F}_{2}}}{2{{F}_{1}}}$. |
(2) |
Загальний зміст отриманого результату є самоочевидним – рівновагу приставленої до стіни драбини забезпечують сили тертя спокою між нею та підлогою й стіною, величина яких залежить від кута нахилу драбини. Але, позаяк сила тертя спокою не може перевищувати певного граничного значення, існує відповідний найменший можливий кут нахилу драбини до підлоги ${{\theta }_{\min }}$, при якому вона ще не зісковзує.
Величину ${{\theta }_{\min }}$ можна знайти із виразу (2), врахувавши, що за співвідношенням (1) N2 = F1, та підставивши граничні значення сил тертя F1 = μ1N1 і F2 = μ2N2 (див. розділ 2, формула (2.14)). Відтак отримаємо наступну загальну відповідь:
|
$\operatorname{tg}{{\theta }_{\min }}$ = $\frac{1-{{\mu }_{1}}{{\mu }_{2}}}{2{{\mu }_{1}}}$ |
|
У даній задачі μ1 = μ2 = 0,3, отже,
$\operatorname{tg}{{\theta }_{\min }}$ = 1,52 \( \Rightarrow \) ${{\theta }_{\min }}$ ≈ 57°.
Наостанок розглянемо деякі можливі окремі випадки:
1. Стіна гладка (μ2 = 0). В такому разі
$\operatorname{tg}{{\theta }_{\min }}$ = $\frac{1}{2{{\mu }_{1}}}$ \( \Rightarrow \) θ = 59°.
Таким чином, тертя між драбиною та стіною не спричинює суттєвого впливу на її критичне рівноважне положення.
2. Підлога гладка (μ1 = 0). В такому випадку θmin = 90°, тобто, драбина теоретично може перебувати в рівновазі лише, коли її щільно приставити до стіни, причому рівновага буде нестійкою.
3. Коефіцієнти тертя між драбиною та стіною й підлогою такі, що μ1μ2 = 1. В такому разі θ = 0, і драбина не буде зісковзувати в жодному положенні.
На горизонтальному столі лежить дошка масою M = 6 кг, котра на третину виступає за його край. До кінця дошки на нитці підвішено тягар, який відводять до горизонтального положення й відпускають.
Визначити
масу тягаряm, якщо при його проходженні через найнижче положення протилежний край дошки відривається від стола.
|
Дано: M = 6 кг
η = (1/3)
|
|
m - ? |
Розв’язання
Із початком руху тягаря в мотузці з'являється сила натягу \( \vec{F}\), що намагається повернути дошку навколо осі О (рис. 15), а тягар примушує рухатися по колу. Проте спочатку вона є невелика, й сила тяжіння ${{M}}\vec{g}$ утримує дошку в спокої. Але через зростання швидкості тягаря сила F поступово збільшується й стає здатною подолати вагу дошки Mg й вивести її з рівноваги. Це відбувається, коли зрівнюються моменти указаних сил (п. 5.1). За умовою задачі в момент відриву дошки мотузка розташована вертикально, тож, як видно з рис. 13, плече сили \( \vec{F}\) дорівнює (l/3), а плече сили ${{M}}\vec{g}$ весь час складає (l/6), де l – довжина дошки. Отже, в момент відриву F (l/3) = Mg(l/6), і сила натягу мотузки| F = $\frac{Mg}{2}$. |
(1) |
Сила натягу мотузки не лише діє на дошку, а й примушує тягар рухатися по колу з відповідним доцентровим прискоренням, яке визначається законами динаміки. Тому, знаючи величину F, можна знайти й масу тягаря m. А саме. Доцентрове прискорення тягаря за формулою (1.28) визначається його швидкістю v та радіусом траєкторії (довжиною мотузки) r, як
$a=\frac{{{v}^{2}}}{{{r}}}$.
Тож у момент проходження тягарем найнижчого положення і відриву дошки, згідно з другим законом Ньютона (2.5), маємо:
| F – mg = m$\frac{{{v}^{2}}}{{{r}}}$ \( \Rightarrow \) F= mg + m$\frac{{{v}^{2}}}{{{r}}}$ |
|
Величину v в цьому виразі можна знайти за законом збереження енергії, згідно з яким набута тягарем у нижній точці кінетична енергія дорівнює спадові його потенціальної енергії при опусканні по вертикалі на відстань r:
$\frac{m{{v}^{2}}}{2}=mg{{r}}\quad \Rightarrow \quad {{v}^{2}}=2g{{r}}$ ,
отже F = 3mg.
Підставивши отриманий вираз F у співвідношення (1), знайдемо відповідь задачі:
| 3mg = \( \frac{{{M}g}}{6}\) \( \Rightarrow \) m = $\frac{M}{6}$ = 1 кг. |
(5) |
Корисне запитання. Поміркуйте, як слід було би змінити умову задачі при дещо більшій масі тягаря?
Тонкий гладенький стрижень уміщують у напівсферичну лунку з гладкою поверхнею.
Визначити,
під яким кутом α до горизонту встановиться стрижень, якщо відношення його довжини до діаметра лунки складає задану величину (l/d) = η.
|
Дано: (l/d) = η |
|
α - ? |
Розв’язання
Перед початком розв'язування задачі відразу вкажемо, що її нетривіальні розв'язки існують лише за умови η > 1, тобто, коли довжина стрижня перевищує поперечник лунки, як показано на рис. 16. Справді, за умовами рівноваги (5.3) і (5.4) лінія рівнодійної сил, з якими стінки лунки діють на стрижень, має бути спрямована по вертикалі, що проходить через його середину (центр ваги). Очевидно, що для короткого (l < d) стрижня так може бути лише при його горизонтальному розташуванні.
Рівноважну орієнтацію (кут α) стрижня при (l > d) можна знайти, як звично, склавши та розв'язавши систему рівнянь (5.3а) – (5.4). Але набагато легше зробити це через потенціальну енергію стрижня, використавши те, що положенні стійкої рівноваги вона для всякого тіла має мінімум. Це не важко зрозуміти. Якщо стрижень у довільній орієнтації опустити в лунку й відпустити, то, переміщуючи його в рівноважне положення, сила тяжіння виконуватиме додатню роботу. При цьому, згідно із співвідношенням (4.5), потенціальна енергія стрижня буде спадати до найменшого можливого значення.
Для подальших обчислень оберемо за нульовий рівень (початок відліку) потенціальної енергії горизонтальну площину, дотичну до дна лунки, рис. 14-1.
Тоді потенціальна енергія стрижня
\( {{W}_{\text{}}}=mgh\),
де h = h′ + h″ – висота його центра ваги С відносно нульового рівня. З рисунка зрозуміло, що
|
${h}'=\frac{l}{2}\sin \alpha $ і ${h}''=\frac{d}{2}\left( 1-\sin 2\alpha \right)$, |
|
і, позаяк за умовою l = ηd,
$h=\frac{d}{2}\left( \eta \sin \alpha -\sin 2\alpha +1 \right)$.
Таким чином, потенціальній енергії стрижня в положенні рівноваги відповідає мінімум функції
f(α) = $\eta \sin \alpha -\sin 2\alpha +1 $.
Як відомо з математики, умовою мінімуму функції є рівність нулю її похідної: f′(α) = 0. Отже,
$\eta \cos \alpha -2\cos 2\alpha =0$.
Відтак, зробивши заміну cos2α = 2cos2α – 1, отримаємо
|
$4{{\cos }^{2}}\alpha -\eta \cos \alpha -2=0$ і $\cos \alpha =\frac{\eta +\sqrt{{{\eta }^{2}}+32}}{8}$. |
|
(Другий корінь не має змісту).
Проаналізуємо отриманий результат. По-перше, згадаємо, що його отримано за умови η > 1 і, по-друге, врахуємо, що cosα ≤ 1, тож
$\eta +\sqrt{{{\eta }^{2}}+32}\le 8$ $\Rightarrow $ $\eta \le 2$.
Це обмеження є цілком зрозумілим: при η ≥ 2 (l ≥ 2d) центр ваги є розташований за межами лунки, й стрижень за будь-яких умов займає горизонтальне положення. Зауважимо також, що у формально можливому випадку η = 1 (l = d) відповідь не існує, позаяк напрямки сил тиску на стрижень, які реально збігається із радіусами кривини ребра лунки, є невизначені.
Визначення положення центра ваги (центра тяжіння)
Задача 5.17. Дві маленькі кульки масами m1 = 100 г та m2 = 60 г з'єднані між собою тонким стрижнем масою m = 40 г і довжиною l = 20 см. Визначити, на якій відстані Хс від першої кульки знаходиться центр ваги системи.
Задача 5.18. Довести, що центр ваги трикутної пластини знаходиться на перетині медіан.
Задача 5.19. Визначити положення центра ваги пластини заданої (рис. 5. 18) конфігурації та розмірів.
Задача 5.20. В однорідній квадратній пластинці зі стороною a = 1 м зроблено отвір радіуса r = (a/4), як показано на рис. 5. 19. Визначити, на якій відстані R від центра квадрата знаходиться центр ваги пластинки.
|
|
|
|
|
|
Дві маленькі кульки масами m1 = 100 г та m2 = 60 г з'єднані між собою тонким стрижнем масою m = 40 г і довжиною l = 20 см.
Визначити,
на якій відстані Хс від першої кульки знаходиться центр ваги системи.
|
Дано: m1 = 100 г
m2 = 60 г
m = 40 г
l = 20 см
|
|
Хс - ? |
Розв’язання
Якщо стрижень підперти в центрі ваги системи О, (рис. 15), то система буде зрівноважена, тобто алгебраїчна сума моментів сил тяжіння \( {m}_{1}\vec{g}\), \( {m}_{2}\vec{g}\) і \( {m}\vec{g}\) відносно осі O дорівнюватиме нулю. Плечі цих сил показані на рис. 15 (враховано, що центр ваги стрижня знаходиться посередині). Отже маємо:
${{m}_{1}}g{{XR}_{c}}-mg\frac{l}{2}-{{m}_{2}}g\left( l-{{X}_{c}} \right)=0$,
звідки
Xc = $\frac{{{m}_{2}}+\left( {m}/{2}\; \right)}{m+{{m}_{1}}+{{m}_{2}}}l$ = 8 см.
Варто зауважити, що цей результат можна було б отримати одразу за загальною формулою (5.5а), підставивши задані маси m1, m2, m та координати кульок: х1 = 0, х2 = l – Хс 0, х = (l/2).
Довести,
що центр ваги трикутної пластини знаходиться на перетині медіан.
Розв’язання
Подумки розіб'ємо пластину на вузькі смужки паралельні до однієї із сторін трикутника. Очевидно, що центр ваги мужки знаходиться на її середині, а всього трикутника – на медіані даної сторони. Позаяк це стосується будь-якої зі сторін, то
центр ваги трикутника є розташований на перетині його медіан.
|
|
Визначити
координати центра ваги пластини заданої конфігурації та розмірів (рис. 16) .
Розв’язання
Жорстко зв'яжемо з пластиною систему координат XOY й подумки підвісимо її за удаваний центр ваги С один раз, як показано на рис. 16-1, а другий – як на рис.16-2. При цьому, позаяк в обох положеннях пластина є зрівноваженою, координати центра ваги можна знайти через рівняння моментів (5.4).
Для складання цих рівнянь поділимо пластину на два прямокутники 1, 2 та прямокутний трикутник 3, як показано штриховими лініями, і врахуємо, що центри ваги прямокутників знаходяться на перетині діагоналей, а трикутника – на перетині медіан. У такому разі при першій орієнтації для кожної частини пластини плече сили тяжіння відносно осі С через координати її центра ваги x1, x2, x3 та центра ваги всієї пластини Xc виражаються як h1 = Xc – x1, h2 = x2– Xc, h3 = x3– Xc, відповідно. Відтак, приписавши в рівнянні (5.4) знак "+" моментам, які діють за годинниковою стрілкою, отримаємо:
\(-{{m}_{1}}\left( {{X}_{\text{c}}}-{{x}_{1}} \right)+{{m}_{2}}\left( {{x}_{2}}-{{X}_{\text{c}}} \right)+{{m}_{3}}\left( {{x}_{3}}-{{X}_{\text{c}}} \right)=0. \)
Звідси для координати центра ваги пластини хс маємо:
|
\( {X}_ {c}=\frac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}. \) |
(1) |
Координату Yс центра ваги знайдемо, аналогічно визначивши плечі сил і записавши рівняння (5.4) для другої орієнтації пластини:
|
\( {{Y}_{\text{c}}}=\frac{{{m}_{1}}{{y}_{1}}+{{m}_{2}}{{y}_{2}}+{{m}_{3}}{{y}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}. \) |
(2) |
Варто зауважити, що формули (1) і (2) збігаються з виразами (5.5а) і 5.5б) так, ніби кожен фрагмент пластини є матеріальною точкою відповідної маси, розміщеною в його центрі ваги.
Перейдемо до обчислень. Позначимо як m масу квадрата зі стороною a. Тоді, як зрозуміло з умови задачі, маси частин пластини складають
m1 = m2 = 2m, m3 = m/4.
При цьому координати "х" точок 1, 2, 3 дорівнюють:
\( {{x}_{1}}=\frac{a}{2};\ \ \ \ \ \ \ {{x}_{2}}=2a;\ \ \ \ \ \ \ \ {{x}_{3}}=3a+\frac{a}{6}=\frac{19a}{6}\)
(враховано, що точка перетину медіан трикутника ділить їх відношення 1 : 2).
Аналогічно для координат "y" маємо:
\( {{y}_{1}}=a;\ \ \ \ \ \ \ {{y}_{2}}={{y}_{3}}=\frac{a}{2}. \)
Підставивши знайдені величини у формули (1) і (2), отримаємо відповідь:
\({{X}_{\text{c}}}=\frac{139a}{102}\approx 1,36a\)
і
\( {{Y}_{\text{c}}}=\frac{25a}{34}\approx 0,74a. \)
 В однорідній квадратній пластинці зі стороною a = 10 см (рис. 17) зробили отвір радіуса r =(a/4), як показано на .
В однорідній квадратній пластинці зі стороною a = 10 см (рис. 17) зробили отвір радіуса r =(a/4), як показано на .
Визначити,
на якій відстані Х від центра квадрата знаходиться центр ваги пластинки.
|
Дано: a = 1 м
r = a/4
|
|
Хс - ? |
Розв’язання
Якщо подумки ''вставити на місце'' видалену частину, (рис.17-1), то утвориться суцільний квадрат, який при підвішуванні в геометричному центрі O буде зрівноважений. Це означає, що сили тяжіння, котрі діють на пластинку з отвором \( {m}\vec{g}\) та на "вставку" \( {m}_{1}\vec{g}\), відносно осі О створюють моменти однакової величини. Отже,
|
mgХс = m1gl $\Rightarrow $ Хс = $\frac{{{m}_{1}}}{m}l$, |
(1) |
де Хс = ОС – шукане плече сили тяжіння, що діє на пластинку з отвором, а l = ОС1– плече сили тяжіння, що діє на "вставку".
Відношення мас і величина l легко знаходяться з рис. 5.19-1 і складають
$\frac{{{m}_{1}}}{m}$ = $\frac{{{S}_{1}}}{{{S}_{0}}-{{S}_{1}}}$ = $\frac{\pi }{16-\pi }$,
де S1 = π(a/4)2 – площа отвору, S0 = a2 – площа суцільного квадрата, та
l = $\frac{a\sqrt{2}}{4}$,
Відтак підставивши отримані величини у вираз (1), після обчислень 
отримаємо відповідь:
R = 8,6 см.
Задачі для самостійної роботи
Наведені далі задачі для самостійного розв'язування згруповано по темах:
- Рівновага тіла, що не може обертатися
- Рівновага тіла із закріпленою віссю обертання
- Рівновага довільного тіла
- Визначення положення центра тяжіння
У всіх умовах задач по умовчанню блоки вважаються невагомими, тертя в осях відсутнім, а мотузки й троси – невагомими й нерозтяжними.
Наведені відповіді отримані при значенні g = 1о м/с2.
Рівновага тіла, що не може обертатися
Рівень А
|
5.20. |
Два хлопці, перетягаючи канат, прикладають до його кінців протилежно спрямовані сили величиною F і 1,5F . Чому дорівнює сила натягу каната? [F] |
|
5.21. |
Тіло на горизонтальній поверхні перебуває в спокої, коли прикладена до нього горизонтальна сила не перевищує 1 H. Коефіцієнт тертя між тілом та поверхнею \(\mu=0,1\). Визначити вагу тіла. [10 H] |
|
5.22. |
Через прикріплений до стелі блок перекинули мотузку, один кінець якої закріплено на підлозі, а до іншого прив'язано тягар масою 10 кг. Визначити силу, з якою блок діє на стелю. [200 H] |
|
5.23. |
До середини мотузки, кінці котрої закріплено на однаковій висоті, підвісили тягар масою 15 кг. Визначити силу натягу мотузки, якщо провис її частин складає 30° до горизонту. [150 H] |
|
5.24. |
Довести, що ніяку мотузку чи трос неможливо натягнути строго горизонтально. |
|
5.25. |
Канат, який лежить на столі, частково звисає. Визначити коефіцієнт тертя між канатом і столом, якщо при звисанні на 25% довжини він починає зісковзувати. [1/3] |
|
5.26. |
Дошку, на якій лежить брусок, підіймають за один кінець. При якому куті нахилу дошки до горизонту брусок почне ковзати, якщо при коефіцієнт тертя складає 0,25? [\(14^{\circ}\)]. |
|
5.27. |
З якою найменшою горизонтальною силою треба притискати брусок маси 5 кг до вертикальної стіни, аби запобігти його зісковзуванню при коефіцієнті тертя 0,1? [500 H] |
|
5.28. |
На похилу площину поклали два бруски (рис. 5.18) масами m1 = 1 кг і m2 = 0,6 кг. Коефіцієнти тертя між брусками та поверхнею \(\mu_{1}=0,3\) і \(\mu_{2}=0,1\). Визначити максимальний кут нахилу площини, при якому бруски ще не будить ковзати. [\(\alpha=12,7^{\circ}\)]
|
|
5.29. |
Підвішені на нитках тягарці А і В з'єднали горизонтальною нитяною перетинкою, як показано на рис. 5.19. Кути складають: \(\alpha=60^{\circ}\), \(\beta=30^{\circ}\). Знайти масу тягаря В, якщо маса тягаря А дорівнює 3 кг. [2 кг]
|
Рівень Б
|
5.30. |
Вантажі m1 = 2 кг і m2 = 1 кг з'єднані ниткою, перекинутою через блок на краю стола (рис. 5.9) і перебувають у рівновазі. Визначити: а) силу тертя, що діє на вантаж m1 і б) силу реакції осі, що діє на блок. [10 Н; 14 Н]
|
|
5.31. |
Сила тертя, що діє на тіло маси 1 кг, яке лежить на похилій площині, дорівнює 6 H. Визначити силу нормальної реакції опори, що діє на нього. [8 H] |
|
5.32. |
На тіло, що лежить на столі, діють спрямовані під кутом \(120^{\circ}\) одна до одної горизонтальні сили F1 = 1,0 H, F2 = 2,0 H і F3 = 3,0 H. Визначити величину та напрям сили тертя, котра діє на тіло. [1,73 H, \(30^{\circ}\) до напрямку F1] |
|
5.33. |
Посередині вулиці треба підвісити на тросі ліхтар маси 10 кг так, аби його висота над землею була не меншою, ніж 5 м при висоті стовпів 6 м і відстані між ними 10 м. Якої мінімальної міцності трос для цього можна взяти? [250 H]. |
|
5.34. |
Якою горизонтальною силою F треба притискати брусок масою 1 кг до похилої площини з кутом нахилу до горизонту \(\alpha=30^{\circ}\), аби він перебував у рівновазі при коефіцієнті тертя о,1? [4,8 H ≤ F ≤ 6,8 Н] |
|
5.35. |
|
|
5.36. |
|
|
5.37. |
|
|
5.38. |
Циліндр маси m утримують у рівновазі на похилій площині з кутом нахилу \(\varphi\) паралельною до неї силою $\vec{F}$, рис. 5.17. Визначити: а) мінімальний коефіцієнт тертя, при якому це є можливо, і б) величину F . [а) \(\mu\ge(1/2)\mathrm{tg}\varphi\)]; б) \((mg/2)\sin\varphi\)
|
|
5.39. |
Визначити відношення жорсткостей пружин, якщо жорсткості їхнього паралельного та послідовного з'єднань відносяться, як 4,5 : 1. [2] |
|
5.40. |
Циліндр маси M за кінець намотаної на нього нитки утримують на горизонтальній підставці. Підставку прибирають і одночасно починають тягти вгору за нитку так, що циліндр лишається на незмінній висоті. Визначити силу натягу нитки і чи буде вона зрівноважувати силу тяжіння. [Mg, ні] |
|
5.41. |
Куля масою 5 кг спирається на дві гладкі похилі площини з кутами нахилу 35° і 20° до горизонту. З якою силою вона тисне на кожну з площин? [20 H; 34 H] |
|
5.42. |
Балку масою 1000 кг і довжиною 2 м горизонтально підвісили на двох тросах однакової довжини, один з яких закріплено за кінець балки, а інший – на відстані a = 25 см від її протилежного краю. Знайти натяг кожного троса. [5,5 кН; 4,2 кН] |
|
5.43. |
До гладкої вертикальної стіни на нитці довжиною 4 см підвішено кулю масою 300 г і радіусом 2,5 см. Визначити силу тиску кулі на стіну. [1,25 Н] |
Рівень B
|
5.44. |
Дошка знаходиться між двома горизонтальними стрижнями А і Б, рис. 5.26. Кут α = 30°, a = 10 см, b = 15 см (т. С – центр ваги). При якій величині коефіцієнта тертя μ між стрижнями та дошкою вона перебуватиме в спокої? [ μ ≥ 0,143]
|
|
5.45. |
Людина масою m тягне на себе за мотузку ящик масою M, який лежить на підлозі. Коефіцієнт тертя між людиною з ящиком та підлогою дорівнює μ. Яку мінімальну силу має прикладати людина, аби тягти ящик? [\(0,5g\sqrt{(M-m)^{2}+\mu(M+m)^{2}}\)] |
Рівновага тіла із закріпленою віссю обертання
Рівень А
|
5.46. |
Циліндричний стовб масою 500 кг лежить на землі. Яку найменшу силу треба прикласти, аби відірвати його кінець від землі?[2,5 кН] |
|
5.47. |
|
|
5.48. |
До кінця легкого стрижня довжиною 3,2 м, який може вільно обертатися навколо горизонтальної осі, що проходить через його середину, підвісили тягар масою 30 кг. Де слід підвісити інший тягар масою 40 кг, аби стрижень був зрівноважений? [на відстані 1,2 м від осі] |
|
5.49. |
|
Рівень Б
|
5.50. |
Дошку поклали на стіл так, що чверть її довжини виступає за край. Визначити масу дошки, якщо, аби її підважити, до вільного кінця довелося прикласти силу 200 H. [20 кг] |
|
5.51. |
Аби зрівноважити нерівноплечі терези з тілом на одній чашці, на другу поклали гирі масою 2,2 кг. Коли ж тіло переклали на іншу чашку, то для зрівноважування терезів знадобилися гирі масою 3,8 кг. Чому дорівнює маса тіла. [2,89 кг] |
|
5.52. |
Прут, зігнутий під прямим кутом у відношенні 1 : 2, шарнірно підвішено за край короткого плеча. Який кут воно утворює з вертикаллю? [\(33,7^{\circ}\)] |
|
5.53. |
Визначити маси вантажів, що є зрівноважені на важелі при плечах 500 мм і 700 мм, якщо вони тиснуть на опору із силою 78,0 H. [455 г; 325 г] |
|
5.54. |
Конічна колода перебуває в рівновазі, якщо її підперти на відстані 1/3 довжини від товстого кінця. Якщо опору розмістити посередині, а на тонкий кінець посадити людину масою 70 кг, то колода знову буде зрівноважена. Визначити силу тиску на опору в обох випадках. [2100 H; 2800 H] |
|
5.55. |
Перед сходинкою висотою 20 см лежить коток масою 30 кг і радіусом 50 см. Визначити мінімальну горизонтальну силу, що треба прикласти до осі котка, аби викотити його на сходинку за відсутності ковзання. [1,2 кH] |
|
5.56. |
Перед сходинкою висотою 20 см лежить бочка масою 100 кг і радіусом 50 см. Визначити, якою найменшою силою її можна закотити на сходинку за відсутності ковзання. [800 H] |
Рівновага довільного тіла
Рівень Б
|
5.57. |
Під яким найменшим кутом до горизонту може стояти драбина, приставлена до гладенької вертикальної стіни, якщо коефіцієнт тертя драбини по підлозі дорівнює \(\mu\)? Вважати, що центр ваги знаходиться посередині драбини. [\(\mathrm{arctg}(2\mu)\)] |
|
5.58. |
Людина масою 60 кг підіймається легкою драбиною довжиною 4 м, що приставлена до гладенької стіни під кутом \(\alpha=30^{\circ}\). На яку висоту може піднятися людина, якщо максимальна сила тертя спокою між драбиною і підлогою дорівнює 200 Н? [2 м] |
|
5.59. |
Куб маси m стоїть на горизонтальній площині. При якому мінімальному коефіцієнті тертя куб можна перекинути через ребро горизонтальною силою, перпендикулярною до ребра? Чому вона дорівнює? [0,5; mg/2] |
|
5.60. |
Якою найменшою силою та при якому найменшому коефіцієнті тертя можна перекинути через ребро куб маси 50 кг, що лежить на горизонтальній площині? [177 H; 1/3] |
|
5.61. |
Однорідний стрижень маси m, шарнірно закріплений одним кінцем, іншим спирається на візок, утворюючи з вертикаллю кут \(\alpha\), рис. 61. Якою найменшою горизонтальною силою візок можна зрушити при коефіцієнт тертя між ним і стрижнем \(\mu\): а) ліворуч; б) праворуч? $\left[ a)\frac{\mu mg}{2\left( 1+\mu \operatorname{ctg}\alpha \right)}; б)\frac{\mu mg}{2\left( 1-\mu \operatorname{ctg}\alpha \right)},\mu <\operatorname{tg}\alpha \right]$
|
|
5.62. |
|
|
5.63. |
Котушку з мотком ниток, яка лежить на шорсткому столі, починають горизонтально тягти за довгий вільний кінець нитки. Як поведеться котушка: буде намотуватися на нитку, чи розмотуватись? |
|
5.64. |
Котушку тягнуть за нитку по столу зі сталою швидкістю так, що вона не обертається. Вказані на рис. 64 розміри котушки є задані. 1. Який кут \(\varphi\) утворює нитка з горизонтом? 2. Чому дорівнює сила натягу нитки F при масі котушки з нитками m і коефіцієнті тертя ковзання котушки \(\mu\)? $\left[ \varphi =\arccos \frac{r}{R};\quad F=\frac{mg}{\mu +\operatorname{ctg}\varphi } \right]$
|
Рівень B
|
5.65. |
|
|
5.66. |
|
|
5.67. |
|
Визначення положення центра ваги
Рівень A
|
5.68. |
Дві маленькі кульки масами 0,2 кг і 0,3 кг закріплено на кінцях невагомого стрижня довжиною 0,5 м. Визначити, на якій відстані від легшої кульки є розташований центр ваги системи. [0,3 м] |
|
5.69. |
Горизонтальну шорстку дошку, на якій стоять важкий і легкий суцільні циліндри однакової висоти й діаметра основи, починають підіймати за кінець. Який циліндр перекинеться раніше? [обидва одночасно] |
|
5.70. |
Суцільні 1) циліндр і 2) конус із відношенням висоти до діаметра основи рівним 2 стоять на шорсткій горизонтальній дошці, котру поступово піднімають за край. При якому найбільшому куті нахилу φ дошки до горизонту кожне з тіл ще не перекинеться? [φ1 = 26,6°; φ1 = 36,9°] |
|
5.71. |
Дві однакові дротини завдовжки по 10 см скріпили у формі літери T. Визначити положення центра мас утвореного каркасу. [2,5 см від точки кріплення] |
Рівень Б
|
5.72. |
Десять намистин (кульок з отворами) масами 1, 2, 3, …, 10 г закріплені на невагомій спиці так, що відстань між центрами сусідніх кульок дорівнює a = 10 см. На якій відстані від найлегшої кульки знаходиться центр ваги системи? [30 см] |
|
5.73. |
Визначити положення центр мас тонкого диска радіусом R, в якому зроблено круглий отвір удвоє меншого радіуса і з центром посередині радіуса диска. [на відстані R/6 від центра диска] |
|
5.74. |
Де розташовано центри ваги тіл, що зображені на рис. 74? [На осі симетрії на відстані від вершини: [а) ≈0,64a ; б) ≈0,6a; в) ≈0,8a]
|
|
|
|
Розділ VI. ГІДРО-АЕРОСТАТИКА
У цьому розділі механіки вивчають сили статичного тиску на занурені в рідину чи газ тіла та на дно й стінки посудини з рідиною, або газом. При цьому середовище розглядається як суцільне, тобто без урахування його атомно-молекулярної будови. Тому співвідношення й закони гідроаеростатики є спільними як для рідин, так і для газів. Через це для позначення рідкого та газоподібного середовища часто вживають спільний термін – "рідина".
Молекули рідин та газів мають велику рухливість, через що в них відсутні сили тертя спокою. Це означає, (див. (п. 2.3), що в стані рівноваги сили взаємодії між шарами рідини та між зануреним тілом та рідиною завжди є спрямовані по нормалі до поверхонь дотику. Крім того, рідина є практично нестисливою, тобто її об'єм не змінюється під дією зовнішніх сил.
На вказаних властивостях рідин і газів ґрунтуються всі основні положення гідро-аеростатики.
6.1. Теоретичні відомості. Закон Паскаля, гідростатичний тиск
|
Через велику рухливість молекул в рідині сила, що діє на неї, є не зосереджена в певній точці, а неперервно розподілена по поверхні дотику рідини зі стінкою посудини чи прилеглим шаром. Тому кількісною мірою силової взаємодії в кожній точці середовища є не сама сила, а тиск, тобто відношення перпендикулярної складової сили, що припадає на гранично малу ділянку поверхні в околі даної точки, до її площі:
При рівновазі сила тиску в рідині є скрізь перпендикулярною до поверхні, на яку діє. Тому, якщо вона рівномірно розподілена по поверхні S, то тиск
де F – сила, що діє на всю поверхню. Тиск вимірюють у паскалях (Па): 1 Па = 1 Н/м2. Використовуються також позасистемні одиниці: міліметр ртутного стовпчика (1 мм.рт.ст. = 133,4 Па) та атмосфера (1 атм = 760 мм.рт.ст. = 1,013·105 Па). |
|
При натисканні на поставлений на опору твердий циліндр відстані між його молекулами трохи зменшуються в напрямку прикладеної сили, і виникає пружна сила протилежного напрямку. Але якщо натиснути поршнем на поверхню рідини, то через рухливість молекул відстань між ними однаково зміниться по всіх напрямах. Тож і сили, що виникнуть при цьому, теж будуть діяти по всіх напрямах однаково. Це відображає закон Паскаля: в рідинах і газах тиск передається по всіх напрямках однаково. Це твердження слід розуміти так, що тиск, який діє в рідині чи газі на невеличку площадку, не залежить від її просторової орієнтації. До прикладу, якщо занурити в рідину маленький кубик (рис.6.1), то при будь-яких його поворотах сили тиску на грані лишатимуться незмінними. Закон Паскаля є основним законом гідростатики. |
|
де \( \rho \) – густина рідини, g – прискорення вільного падіння. При наявності зовнішнього тиску P0, тобто тиску на вільну поверхню рідини (найчастіше це атмосферний тиск), повний тиск у рідині на глибині h дорівнює сумі зовнішнього та гідростатичного тисків:
|
|
На законі Паскаля та нестисливості рідини ґрунтується робота гідравлічного преса та підйомника, пристроїв, які по суті є двома сполученими циліндрами з різною площею перерізу, що заповнені рідиною і щільно закриті поршнями (рис.6.3). Дія зовнішньої сили F1 на перший поршень створює у рідині тиск, який, за законом Паскаля без зміни передається на другий. Гідростатичним тиском при цьому зазвичай можна знехтувати, так що
Отже, якщо S1 << S2, то F2 >> F1, тобто малою силою, прикладеною до меншого поршня, можна створити значно більшу силу, що діє на більший поршень. На цьому ґрунтується робота гідравлічного підйомника – пристрою, що дозволяє малою силою підіймати великі вантажі. Якщо великий циліндр над поршнем наглухо перекрити міцною ''стелею'', то підйомник перетвориться на гідравлічний прес. Варто зауважити, що переміщення великого поршня (підіймальної платформи) є набагато меншим за переміщення (хід) малого поршня:
При цьому з формул (6.4) і (6.5) випливає, що F1l1 = F2l2, тобто роботи сил \( \vec{F}_{1}\) та \( \vec{F}_{2}\) є однакові, тож виграючи в силі, ми так само програємо у відстані. Це стосується й інших простих механізмів і складає відкрите ще в давнину "золоте правило механіки", котре є відображенням установленого на віки пізніше закону збереження енергії. |
|
У різних гідравлічних механізмах широко використовуються сполучені посудини – дві (або більше) посудини, що є з'єднані між собою у нижній частині і заповнені рідиною (рис.6.4). Умовою рівноваги рідин у сполучених посудинах є рівність тисків у всіх точках трубки, що з'єднує посудини. Тому, згідно з формулою (6.3), однорідна рідина в сполучених посудинах встановлюється на одному рівні незалежно від форми та площ перерізу посудин (рис.6.4а). (Примітка. Це не стосується капілярів, тобто трубок дуже малого діаметра.)
Якщо у колінах сполучених посудин знаходяться дві різні незмішувані рідини (рис.6.4б), то відраховані від рівня поділу висоти стовпів рідин є обернено пропорційні до їхніх густин:
|
6.2. Теоретичні відомості. Сила Архімеда
|
При зануренні тіла в рідину чи газ гідростатичні тиск (6.2) на верхню частину поверхні тіла є меншим, ніж на нижню. Через це виникає виштовхувальна сила, що визначається законом Архімеда: |
на тіло в рідині (газі) діє виштовхувальна (архімедова) сила, рівна вазі рідини в об'ємі зануреної частини тіла.
У нерухомій посудині з рідиною величина архімедової сили
|
${{F}_{A}}=\rho Vg$, |
(6.7) |
а в посудині, що має прискорення \( \vec{a}\), відповідно до означення ваги (2.10),
|
${\vec{F}_{A}}=\rho V\left( \vec{a}-\vec{g} \right)$, |
(6.7а) |
де \( \rho \) – густина рідини, V – об'єм зануреної в рідину або газ частини тіла.
Архімедова сила є рівнодійною сил тиску, з якими рідина (газ) діє на всі точки зануреного тіла. Вона завжди є прикладена в центрі ваги тієї рідини, місце якої зайняло дане тіло.
Якщо тіло повністю занурити в рідину й відпустити, то, залежно від величини сили тяжіння FТ та архімедової сили FA, можливі три випадки, як відображено на рис. 6.5 а), б), в):
а) FA ≤ FТ – тіло тоне (опускається на дно);
б) FA = FТ – тіло плаває, тобто є зважене (перебуває всередині рідини в стані байдужої рівноваги);
в) FA ≥ FТ – тіло спливає (піднімється на поверхню).
В останньому випадку архімедова сила, що зрівноважує силу тяжіння, визначається об'ємом тільки зануреної частини тіла \( {V}^{\prime}\) (рис.6.5 г). Але в процесі спливання та при плаванні обидві сили визначаються об'ємом всього тіла та густинами речовини тіла ρт і рідини ρ. Тому із співвідношень б), в) маємо наступну умову плавання:
| ρт ≤ ρ. |
(6.8) |
Зауважимо, що умова (6.8) стосується лише суцільних тіл. Порожнисті тіла можуть плавати та спливати й тоді, коли густина їхньої речовини є більшою за густину рідини. На цьому ґрунтується судноплавство та повітроплавання.
Приклади розв’язування задач
Далі розглянуто приклади розв'язування задач із наступних тем:
Всі обчислення виконано при g = 10 м/с2.
Гідростатичний тиск. Сполучені посудини. Гідравлічні механізми
Задача 6.1. Циліндричне й два конічні відра однакового об'єму й висоти є вщент заповнені водою заданої маси m. Визначити силу тиску води на дно кожного відра, якщо радіуси отвору та основи в конічних відрах відрізняються вдвічі.
Задача 6.2. Визначити глибину h водойми, якщо тиск на невелике тіло на дні є в k = 3 рази більший ніж на поверхні. Атмосферний тиск P0 = 100 кПа, густина води ρ = 1 г/см3.
Задача 6.3. Довгу запаяну з одного боку й відкачану скляну трубку занурили відкритим кінцем у посудину зі ртуттю під кутом $\alpha=30{}^\circ$ до вертикалі . Визначити довжину l стовпчика ртуті в трубці при атмосферному тиску Р0 = 750 мм. рт. ст.
Задача 6.4. Кубічний акваріум об'ємом 150 л ущент заповнено водою (ρ = 1 г/см3). Визначити силу гідростатичного тиску на стінку акваріума.
Задача 6.5. Циліндри гідравлічного підйомника (див. п. 6.1) площею перерізу S1 = 1 м2 та S2 =25 см2 містять технічну олію (ρ = 0,8 г/см3). Нехтуючи вагою поршнів і тертям, визначити висоту h2, на яку підніметься малий поршень, якщо на платформу (великий поршень) покласти вантаж масою m = 200 кг.
Задача 6.6. В одне коліно сполучених посудин із ртуттю (ρр = 13,6 г/см3) наливають шар машинної олії (ρ0 = 0,75 г/см3) товщиною h0 = 40 см, а в інше – воду (ρв = 1 г/см3) до рівня олії. Визначити товщину шару води hв.
Задача 6.7. Для заміни колеса автівку масою 1 т її хочуть підважити за передній бампер гідравлічним домкратом із відношенням площ поршнів (S/S1) = 250 і ККД η = 80%. Визначити, яку силу для цього треба прикладати до малого поршня, якщо відстань від переднього бампера до центра ваги автівки складає п'яту частину його відстані до задньої осі.
Задача 6.1.
Циліндричне й два конічні відра однакового об'єму й висоти є вщент заповнені водою заданої маси m. Визначити
силу тиску води на дно кожного відра, якщо радіуси отвору та основи в конічних відрах відрізняються вдвічі.
|
Дано: m R2 = 2R1 |
|
F0, F1 F2 - ? |
Розв’язання
Профілі та розміри відер показано на рис. 1-1.
Сила гідростатичного тиску (6.2) на дно кожного відра визначається, як
| F = ρghS = πρghR2 |
(1) |
Для циліндричного відра величина hS = V – об'єм налитої води, отже, сила тиску на дно дорівнює її вазі:
| F = mg. |
|
У конічних відрах сили тиску на дно теж визначаються формулою (1):
| F1 = πρghR12; F2 = πρghR22. |
|
Тож вони є не однаковими й відрізняються від ваги води так, що
| ${{F}_{1}}=mg\frac{R_{1}^{2}}{{{R}^{2}}};\quad {{F}_{2}}=mg\frac{R_{2}^{2}}{{{R}^{2}}}$ |
|
Тому, врахувавши, що висота та місткість відер за умовою є однакові й R2 = 2R1, за формулами об'єму циліндра $V=h\pi R_{0}^{2}$ та зрізаного конуса \( {V}=\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }h \left( {{R}^{2}}+R_{1}^{2}+R{{R}_{1}} \right) \) після елементарних викладок (зробіть самостійно!) знайдемо наступні значення шуканих сил:
${{F}_{1}}=\frac{3}{7}mg;\quad {{F}_{2}}=\frac{12}{7}mg$.
Як видно, сила тиску на дно в розширеному догори відрі є менша, а в звуженому – більша, ніж вага налитої води. Останній ефект, який називають "гідростатичним парадоксом", 
може здатися дивним, але має просте пояснення. Справа в тому, що вода у відрі взаємодіє не лише із дном, а й зі стінкою, причому сили тиску скрізь діють по нормалі до поверхні (рис. 1-2). Тож у циліндричному відрі вони є горизонтальними й не впливають на силу тиску на дно. В конічному відрі з розширеним верхом бічні сили спрямовані під деяким кутом до горизонту вгору і частково компенсують силу притягання mg води до землі, тим самим зменшуючи силу тиску на дно. А ось у звуженому догори відрі бічні сили, навпаки, створюють додатковий тиск на дно, що й пояснює гідростатичний парадокс.
Задача 6.2.
Визначити,
на якій глибині h в озері тиск, який діє на занурене тіло, буде у k = 3 рази більший за тиск на поверхні. Атмосферний тиск P0 = 100 кПа, густина води ρ = 1 г/см3.
|
Дано: k = 3
P0 = 100 кПа
ρ = 1 г/см3
|
|
h - ? |
Розв’язання
Тиск на тіло, що занурене в рідину з відкритою поверхнею, складається з атмосферного тиску P0 та гідростатичного тиску (6.2) на глибині занурення:
P = P0 + ρgh.
За умовою задачі P = kP0, отже,
Задача 6.3. Довгу запаяну з одного боку й відкачану скляну трубку занурили відкритим кінцем у посудину зі ртуттю під кутом $\alpha=30{}^\circ$ до вертикалі .
Визначити
довжину l стовпчика ртуті в трубці при атмосферному тиску Р0 = 750 мм.рт.ст.
|
Дано: α =30°
Р0 = 750 мм.рт.ст.
|
|
l - ? |
Розв’язання
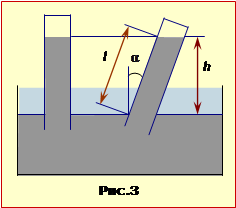 Історично склалося так, що на практиці атмосферний тиск вимірюють не в паскалях (Па), а в позасистемних одиницях – міліметрах ртутного стовпа, причому за означенням 1 мм.рт.ст. дорівнює гідростатичному тискові стовпчика ртуті висотою 1 мм.
Історично склалося так, що на практиці атмосферний тиск вимірюють не в паскалях (Па), а в позасистемних одиницях – міліметрах ртутного стовпа, причому за означенням 1 мм.рт.ст. дорівнює гідростатичному тискові стовпчика ртуті висотою 1 мм.
При зануренні ртуть у трубці під дією атмосферного тиску підніметься над рівнем у посудині на висоту h (див. рис. 3), при якій гідростатичний тиск (6.2) стовпчика зрівняється з атмосферним. Отже, за умовою, h = 750 мм. Тож очевидно, що шукана довжина стовпчика ртуті
$ {l}=\frac{h}{\cos \text{ }\!\!\alpha\!\!\text{ }} $ = 86,6 см.
Задача 6.4. Кубічний акваріум об'ємом 150 л ущент заповнено водою (ρ = 1 г/см3).
Визначити
силу гідростатичного тиску на стінку акваріума.
|
m = 150 кг |
|
F - ? |
Розв’язання
Якщо позначити ребро куба як а, то за формулою (6.2) тиск води на стінку при переміщенні вглиб лінійно зростає від нуля на поверхні до величини Р = ρga на дні, як показано на рис. 4-1. Тому для підрахунку сили тиску води на всю стінку подумки розділимо її на вузькі горизонтальні смужки шириною Δhi і площею ΔSi = а·Δhі, одну з яких показано на рис. 4-1. Тоді тиск Pi і сила тиску ΔFi на стінку в межах смужки
Pi ≈ ρghі, ΔFi ≈ Pi·ΔSi = аPiΔhі.
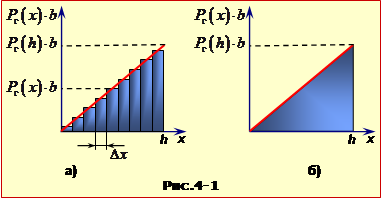
Відповідно, сила тиску на всю стінку
| $F\approx a\sum{{{P}_{i}}\Delta {{h}_{i}}}$ = aS |
(1) |
Записаний вираз є наближеним, бо в межах кожної смужки тиск на різних рівнях все ж не є однаковим. Але, якщо смужки поступово звужувати, вказана похибка буде зменшуватись, і в границі взагалі зникне. При цьому ''сходинки'' на графіку зіллються у відрізок прямої, й величина S у виразі (1) стане чисельно рівною площі трикутника, утвореного графіком P(h):
$S=\frac{1}{2}P(a)\cdot a$.
Отже, сила тиску води на стінку акваріума дорівнює
$F=\frac{1}{2}\rho g{{a}^{3}}$ $\Rightarrow $ ${F=\frac{mg}{2}}$.
У числах
F = 750 Н.
На завершення варто зауважити наступне. Сила тиску на кожну з чотирьох стінок складає (mg/2) – половину ваги всієї води. Тож може виникнути думка, що сила тиску на 4 стінки дорівнює 2mg, тобто вдвічі перевищує вагу всієї налитої води. Але такий "парадокс" є фейком, бо сума модулів векторів різного напрямку не дорівнює модулю їхньої суми. Тож насправді величина (модуль) сумарної сили тиску води на стінки акваріума дорівнює нулю.
Задача 6.5
Циліндри гідравлічного підйомника (див. п. 6.1) площею перерізу S1 = 1 м2 та S2 =25 см2 містять технічну олію (ρ = 0,8 г/см3). Нехтуючи вагою поршнів і тертям,
визначити
висоту h2, на яку підніметься малий поршень, якщо на платформу (великий поршень) покласти вантаж масою m = 200 кг.
|
Дано: S1 = 1 м2
S2 = 25 см2
m = 200 кг
ρ = 0,8 г/см3 |
|
h2 - ? |
Розв’язання
Рівноважне положення невагомих поршнів визначається рівністю тисків на основи циліндрів, які створюються атмосферою, стовпами рідини та покладеним вантажем. Але про атмосферний тиск не має сенсу говорити, бо він однаково діє на обидва поршні.
Згідно з виразом (6.2), платформа й малий поршень спочатку розташовуються на одному рівні, рис. 5а. Але після вміщення вантажу (рис. 5б) платформа опускається на певну відстань h1, а поршень піднімається на відповідну відстань h2, доки створювані вантажем і надлишковим стовпом води тиски P1 = (mg/S1) і P2 = ρg(h1+h2) не зрівняються.
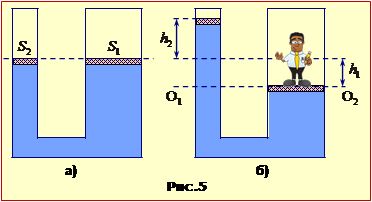 |
Отже,
|
\(\frac{m}{{{S}_{1}}}=\text{ }\!\!\rho\!\!\text{ }\left( {{h}_{1}}+{{h}_{2}} \right).\) |
(1) |
При цьому зміна об'ємів рідини в циліндрах є однакова, тож
|
\({{S}_{1}}{{h}_{1}}={{S}_{2}}{{h}_{2}}\) $\Rightarrow \quad {{h}_{1}}=\frac{{{S}_{2}}}{{{S}_{1}}}{{h}_{2}}$. |
(2) |
Підставивши отриманий вираз h1 у рівняння (1), після елементарних перетворень знайдемо наступну точну відповідь:
|
|
${{h}_{2}}=\frac{m}{{\rho }{\left( {{S}_{1}}+{{S}_{2}} \right)}}$. |
|
Але, позаяк за умовою величина S2 складає всього 0,25% від S1, відповідь можна без утрати точності записати більш лаконічно:
${{h}_{2}}=\frac{m}{\rho {{S}_{1}}}=25\text{см}$.
|
|
Задача 6.6. В одне коліно сполучених посудин із ртуттю (ρр = 13,6 г/см3) наливають шар машинної олії (ρ0 = 0,75 г/см3) товщиною h0 = 40 см, а в інше – воду (ρв = 1 г/см3) до рівня олії.
Визначити
товщину шару води hв.
|
Дано: h0 = 40 см
ρ0 = 0,75 г/см3
ρв = 1,0 г/см3
ρр = 13,6 г/см3
|
|
hв - ? |
Розв’язання
Оскільки \(\rho_{в}>\rho_{o}\), то межа поділу ртуті з водою O1- O2 проходить нижче, ніж для ртуті з олією, рис. 6-1.
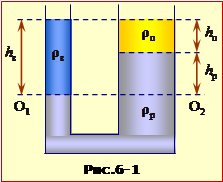 |
Тож, позаяк гідростатичний тиск (6.2) стовпа води висотою hв зрівноважується сумарним тиском стовпів олії (h0) та витісненої ртуті (hр), маємо:
ρвhв = ρ0h0 + ρрhр.
Відтак, зробивши очевидну заміну hр = hв – h0, отримаємо відповідь:
\({{h}_{\text{в}}}=40,8\ \text{см}.\)
Для заміни колеса автівку масою m = 1 т її хочуть підважити за передній бампер гідравлічним домкратом із відношенням площ поршнів (S/S1) = 250 і ККД η = 80%.
яку силу F1 для цього треба прикладати до малого поршня, якщо відстань l1 від переднього бампера до центра ваги автівки складає п'яту частину його відстані l до задньої осі.
|
Дано: m = 1 т l1 = 0,2 l |
|
F1 - ? |
Розв'язання
Для відриву передніх коліс автівки від землі (підважування), прикладена до бампера сила F має створювати відносно задньої осі (точніше – точок дотику коліс до землі) момент М1 = F1′l, який здатен подолати момент сили тяжіння М2 = mg(l–l1), див. рис. 6.7. За умовою М1 = М2, і
${{F}}=\frac{l-{{l}_{1}}}{l}mg=0,8mg$.
У такому разі шукана сила, згідно із співвідношення (6.4), мала би складати F1′ = (S1/S)F. Але через утрати енергії, які відображує ККД домкрата, реально до малого поршня треба прикласти силу F1 = F1′/η. Отже,
${{F}_{1}}=\frac{0,8mg}{\eta \left( {S}/{{{S}_{1}}}\; \right)}=40$ Н
Сила Архімеда. Плавання тіл
Розв’язання
На занурений у воду палець діє виштовхувальна сила з боку води. Рівна за модулем і протилежна за напрямком сила діє на воду і через неї передається до дна посудини. Тож терези вийдуть із рівноваги. Іншими словами те саме можна пояснити, як наслідок збільшенням гідростатичного тиску води на дно посудини через підняття її рівня при зануренні пальця.
Таким чином, правильна відповідь – "ТАК".
|
Дано: h = 5 см
\( \rho_{\text{ст}}=7,8\ {\text{г}}/{\text{м}}^{3} \)
\( \rho_{\text{в}}=1\ \text{г}/\text{м}^{3}\)
\( \rho_{\text{р}}=13,6\ {\text{г}}/{\text{м}}^{3}\)
|
|
h′ - ? |
Розв’язання
Позаяк циліндр плаває, сила тяжіння \( {m}\vec{g}\) і сумарна архімедова сила, $\vec{F}={{\vec{F}}_{\text{}}}+{{\vec{F}}_{\text{}}}$, що створюється ртуттю та водою (рис. 9, є компенсовані:
| Fр + Fв = mg. |
|
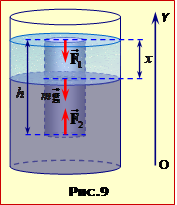
Виразивши архімедову силу в кожній з рідин за формулою (6.8), а її масу через густину та об'єм, після елементарних перетворень отримаємо відповідь:
${{\rho }_{\text{}}}{h}'+{{\rho }_{\text{}}}\left( h-{h}' \right)={{\rho }_{\text{}}}h$
\(\Rightarrow \)
\({h}'=\frac{{{\rho }_{\text{}}}-{{\rho }_{\text{}}}}{{{\rho }_{\text{}}}-{{\rho }_{\text{}}}}h\) = 2,3 см.
|
Дано: m = 5 кг
\( \rho_{\text{в}}=1000\ {\text{кг}}/{\text{м}}^{3}\)
\( \rho_{\text{ст}}=7800\ {\text{кг}}/{\text{м}}^{3}\)
|
|
V0 - ? |
Розв’язання
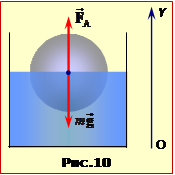
Об'єм порожнини
| V0 = V – Vст, |
(1) |
де V – об'єм кулі, Vст – об'єм сталі, з якої вона складається.
Позаяк куля плаває, її вага mg є компенсована архімедовою силою (6.8), рис. 10. Отже ,
|
$mg={{\rho }_{\text{в}}}\left( \frac{V}{2} \right)g\quad \Rightarrow \quad V=\frac{2m}{{{\rho }_{\text{в}}}}$. |
|
Відповідно, об'єм речовини кулі
|
${{V}_{\text{ст}}}=\frac{m}{{{\rho }_{\text{ст}}}}$. |
(2) |
Відтак, підставивши визначені величини об'ємів у вираз (1), знайдемо відповідь:
${{V}_{0}}=m\left( \frac{2}{{{\rho }_{\text{в}}}}-\frac{1}{{{\rho }_{\text{ст}}}} \right)$ = 93,6 см3
Кусочок сплаву золота з міддю важить у повітрі Q1 = 0,5 H, а у воді – Q2 = 0,456 H.
Визначити
маси золота mз та міді mм у сплаві. Густина золота ρз = 19,3 г/см3, міді ρм = 8,9 г/см3, води ρв = 1 г/см3.
|
Дано: Q1 = 0,5 Н
Q2 = 0,456 Н
ρз = 19,3 г/см3
ρм = 8,9 г/см3
ρв = 1 г/см3
|
|
mз, mм - ?
|
Розв’язання
За означенням вага тіла – це сила, з якою воно тисне на опору або розтягає вертикальний підвіс унаслідок гравітації. При цьому вага визначається як силою тяжіння, так і архімедовою силою, що створюється середовищем, в якому знаходиться тіло.
У повітрі архімедова сила є неістотною, тож вага сплаву
|
Q1 = (mз + mм)g, |
(1) |
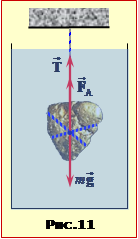
де mз і mм – маси золота та міді. Але, коли кусочок сплаву прив'язати до нитки й опустити у воду (рис. 11), то його вага Q2 (сила натягу нитки), згідно із формулою (6.8), зменшиться на величину Q1 – Q2 = ρвVg . Враховуючи, що об'єм сплаву V дорівнює сумі об'ємів золота Vз = (mз/ρз) та міді Vм = (mM/ρM), що входять до його складу, маємо:
| Q1 – Q2 = ${{\rho }_{\text{в}}}g\left( \frac{{{m}_{\text{з}}}}{{{\rho }_{\text{з}}}}+\frac{{{m}_{\text{м}}}}{{{\rho }_{\text{м}}}} \right)$. |
(2) |
Відтак з рівнянь (1) і (2) після простих, але дещо громіздких викладок отримаємо відповіді:
\( {{m}_{\text{з}}}=\frac{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}}}{\left( {{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}-{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}} \right)g}\left( \frac{{{Q}_{1}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}}}-\frac{{{Q}_{1}}-{{Q}_{2}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{в}}}} \right), \)
\( {{m}_{\text{м}}}=\frac{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}}}{\left( {{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}-{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}} \right)g}\left( \frac{{{Q}_{1}}-{{Q}_{2}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{в}}}}-\frac{{{Q}_{1}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}} \right). \)
Обчислення дають:
\( {m}_{з}=20,3\) г,
\( {m}_{\text{м}}=29,7\) г.
Звідси маса зразка m = 50 г, що, природньо, дорівнює (Q1/g).
Тонка паличка з густиною ρ = 3,6 г/см3 одним кінцем закріплена шарнірно, а іншим опущена у воду (ρв = 1 г/см3) без дотику до дна та стінок посудини.|
Дано: ρ = 360 кг/м3 ρв = 1 г/см3 |
|
k - ?
|
Розв’язання
Уведемо позначення: для довжини палички l, кута її нахилу до горизонту α і довжини зануреної частини x (рис. 12.)
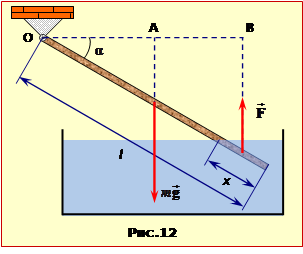
На паличку діють сила тяжіння \( {m}\vec{g}\), прикладена посередині, та сила Архімеда $\vec{F}=-{{\rho }_{\text{}}}{V}'\vec{g}$ (V′ – об'єм зануреної частини палички), що прикладена посередині зануреної частини. Умовою рівноваги палички є рівність величин моментів цих сил відносно осі О (розділ 5, п. 5.2). Як видно з рисунка, їхні плечі складають
$\frac{l}{2} \cos \alpha $ і $\left( l-\frac{x}{2} \right) \cos \alpha $,
отже, умова (5.4) рівноваги палички має вигляд:
$mg\frac{l}{2}$ = F$\left( l-\frac{x}{2} \right)$.
Тож після підстановок m = ρlS i F = ρвxSg отримаємо рівняння${{\left( \frac{x}{l} \right)}^{2}}-2\frac{x}{l}+\frac{\text{ }\!\!\rho\!\!\text{ }}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{в}}}}=0$,
Задачі для самостійної роботи
Пропоновані задачі згруповано за темами:
1. Гідростатичний тиск. Сполучені посудини.
2. Cила Архімеда. Плавання тіл
Наведені відповіді отримано при значенні g = 10 м/с2.
Гідростатичний тиск. Сполучені посудини
| Рівень А | |
|
6.13. |
Визначити гідростатичний тиск на стінку на відстані 10 см від дна циліндричного відра внутрішнім діаметром 25 см, в якому міститься 12 л води (густина 1 г/см3). [1,4 кПа] |
|
6.14. |
У циліндричну посудину площею дна 100 см2, налили шар води (густина 1 г/см3) та шар машинного масла (густина 0,75 г/см3) завтовшки по 10 см. Визначити загальний тиск на дно посудини при атмосферному тиску 100 кПа. [101,75 кПа] |
|
6.15. |
У циліндричній посудині з однаковою масою води та ртуті загальна висота рівня рідин складає 143 см. Визначити гідростатичний тиск на дно посудини. [≈26,6 кПа] |
|
6.16. |
У коліна однакових сполучених посудин із ртуттю наливають в одне воду , а в інше бензин так, що їхні верхні рівні зрівнюються. Визначити різницю рівнів ртуті в колінах, якщо висота стовпчика води складає 21,5 см? Густина бензину 0,7 г/см3. [4,5 мм] |
|
6.17 |
У циліндричних сполучених посудинах із внутрішніми діаметрами 3 см і 7 см міститься вода. Знайти, на скільки понизиться рівень води у вужчому коліні, якщо в нього налити 80 г олії. [≈9,6 см] |
|
6.18. |
При опусканні малого поршня гідравлічного преса на 20 см платформа (великий поршень) підіймається на 1 см. Визначити силу тиску на вміщену в прес деталь при прикладанні до малого поршня сили 500 Н. [10 МН] |
|
6.19. |
При підніманні вантажу масою 2 т гідравлічним підйомником за 10 ходів малого поршня виконали роботу 40 Дж. Визначити відношення площ його поршнів, якщо робочий хід малого поршня складає 10 см. [500] |
|
6.20. |
У вертикальний циліндр із водою (густина 1 г/см3), що має дно площею 100 см2, повільно опускають до встановлення рівноваги поршень масою 2,4 кг із вертикальною трубкою перерізом 20 см2. Визначити, на яку висоту підніметься вода в трубці за відсутності тертя. [30 см] |
|
6.21. |
Визначити товщину шару технічної олії (густина 800 кг/м3), який треба залити в одне коліно U-подібної трубки із ртуттю (густина 13,6 г/см3), аби її рівень в іншому піднявся 1,6 см? [27,2 см] |
|
6.22. |
У циліндричних сполучених посудинах, внутрішні радіуси котрих відрізняються вдвічі, міститься вода (густина 1 г/см3). Визначити зміну рівня води у ширшому коліні після того, як у вужче залили шар гасу (густина 800 кг/м3) товщиною 20 см. [3,2 см] |
| 6.23. |
В одне коліно U-подібної трубки зі ртуттю наливають шар гасу товщини 20 см, а в інше — шар води товщини 10 см. Визначити різницю рівнів ртуті в трубці. Густини: вода 1 г/см3, гас 0,8 г/см3, ртуть 13,6 г/см3. [4,4 мм] |
|
|
|
| Рівень Б |
|
| 6.24. | Визначити силу, з якою вода тисне на ворота шлюзу шириною 20 м, якщо рівень води у камері шлюзу становить 10 м. [1 МН] |
| 6.25.
|
На столі стоїть тонкостінна циліндрична посудина з діаметром 8 см і масою 1 кг. Визначити, якої висоти шар води слід залити в посудину воду, аби тиск на стіл дорівнював 4 кПа.[20 см]
|
| 6.26. |
Визначити, з якої найбільшої глибини можна відкачувати воду поршневим насосом при атмосферному тиску 100 кПа. [10 м] |
| 6.27. |
У два сполучені циліндри з однаковою площею поперечного перерізу S залили рідину густиною ρ. Визначити зміну Δh рівнів рідини в посудинах, коли в одне з колін помістити брусок маси m, який не тоне. [Δh = (m/ρS)] |
|
6.28. |
У водоймі закріплено вертикальну трубу з поршнем площею 5 дм2 і масою 2 кг, який торкається поверхні води. Визначити, яку роботу слід виконати, аби підняти поршень на висоту 15 м при атмосферному тиску 100 кПа. [50,3 кДж] |
| 6.29. |
Висота стовпа рідини у циліндричній посудині дорівнює 10 см. Визначити діаметр дна посудини, якщо рідина з однаковою силою тисне на її дно та бічну поверхню. [20 см] |
| 6.30. |
У відкриту трубку перерізом 2 см2, занурену одним кінцем у воду (густина 1000 кг/м3), налили 72 г олії (густина 900 кг/м3). Визначити відстань між вільними поверхнями рідин. [4 см] |
|
6.31. |
В одну з трьох однакових сполучених посудин із водою (густина 1 г/см3) доливають шар гасу (густина 0,8 г/см3) завтовшки 30 см. На скільки підніметься рівень води в інших посудинах? [8см] |
Cила Архімеда. Плавання тіл
Рівень А
|
6.32. |
На гладкому горизонтальному дні посудини лежить гладенький дерев'яний кубик. Що відбудеться з кубиком, якщо, притримуючи його рукою, заповнити посудину водою, а потім відпустити? [Нічого] |
|
6.33. |
Визначити вантажопідйомність дерев'яного плота об'ємом 12 м3, який на плаву є наполовину занурений у воду (густина 1 г/см3). [600 кг] |
|
6.34. |
Визначити густину речовини тіла, що плаває на воді, занурившись на чверть об’єму. [250 кг/м3] |
|
6.35. |
Визначити товщину залізної пластинки 25 см2, яка у воді важить 195 мH. [1 мм] |
|
6.36. |
Знайти мінімальну силу, що треба прикладати до каменя масою 40 кг і об’ємом 10 дм3, аби підняти його з дна водойми. Густина води 1 г/м3. [300 Н] |
|
6.37. |
Колода довжиною якої 3 м і діаметром 30 см плаває на воді. Визначити найбільшу масу, при якій людина може стояти на колоді, не замочивши ніг? Густина дерева 670 кг/м3 . [70 кг] |
|
6.38. |
Знайти, який мінімальний об’єм має мати наповнена воднем (густина 90 г/м3) повітряна куля, аби підіймати людину масою 72 кг? Густина повітря 1,29 кг/м3, вага оболонки не істотна. [60 м3] |
|
6.39. |
Корок (густина 0,25 г/см3) масою 20 г прикріплено на нитці до дна посудини з водою так, що він є на три чверті об'єму занурений у воду. Знайти силу натягу нитки. [ 0,4 Н] |
|
6.40 |
Прямокутна тонкостінна коробочка масою 76 г із площею дна 38 см2 і висотою 6 см плаває у воді. Визначити висоту надводної частини коробочки. [4 см] |
Рівень Б
|
6.41. |
Визначити, яку найбільшу глибину можна виміряти корабельним лотом – гирею, прикріпленою до сталевого (густина 7800 кг/м3) тросу, – якщо межа міцності сталі складає 500 МПа. [7,35 км] |
|
6.42. |
Бульбашка газу об'ємом 1 см3 спливає з дна озера зі сталою швидкістю. Визначити силу опору води. [10 мН] |
|
6.43. |
У посудину зі ртуттю (густина 13,6 г/см3), в якій плаває сталевий (густина 7,8 г/см3) кубик із ребром 10 см, наливають до рівня верхньої грані воду (густина 1 г/см3). Визначити: а) товщину шару води; б) тиск на нижню грань кубика. [4,6 см; 7,8 кПа] |
|
6.44. |
При повному зануренні у воду (густина 1 г/см3) порожнистої алюмінієвої (густина 2,7 г/см3) кулі масою 350 г на неї діє архімедова сила 1,8 Н. Визначити об’єм порожнини. [50 см3] |
|
6.45. |
Сталева (густина 7,8 г/см3) сферична оболонка радіусом 10 см плаває у воді (густина 1 г/см3), занурившись рівно наполовину. Визначити товщину оболонки. [≈2 мм] |
|
6.46. |
Порожниста алюмінієва (ρа = 2,7 г/см3) куля із зовнішнім радіусом на η = 9% більшим за внутрішній, яку утримують під водою (ρв = 1 г/см3), при вивільненні спливає. Визначити густину ρ речовини, якою слід заповнити порожнину, аби куля плавала під водою. [ρ = ρа – (ρа– ρв)(1+η)3 = 0,5 г/см3] |
|
6.47. |
Коли порожнисту кулю радіусом 10 см і масою 0,5 кг із підвішеною до неї свинцевою (густина 11,3 г/см3) кулькою опустили у воду, вона занурилася рівно наполовину. Знайти діаметр свинцевої кульки. [≈6,7 см] |
|
6.48. |
Тіло, підвішене до пружини динамометра, в повітрі розтягає її на 22 мм, а при повному зануренні у воду (густина 1 г/см3) – на 14 мм. Визначити об’єм тіла та його густину. [82 см3; 2,7 г/см3] |
|
6.49. |
Вага тіла у воді є в 3 рази менша, ніж у повітрі. Визначити густину матеріалу тіла. [1,5 г/см3] |
|
6.50. |
Якщо в посудину з водою (густина 1 г/см3) без дотику до дна занурити підвішене до динамометра тіло, то покази динамометра зміняться на 0,5 H, а рівень води – на 5 см. Визначити площу дна посудини. [10 см2] |
|
6.51. |
Унаслідок того, що в посудину з водою (густина 1 г/см3) опустили донизу дном відкриту залізну (густина 7,8 г/см3) коробочку, рівень води піднявся на 2 см. Визначити, як і на скільки він зміниться після затоплення коробочки. [Знизиться на 1,74 см] |
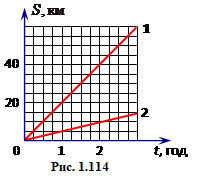
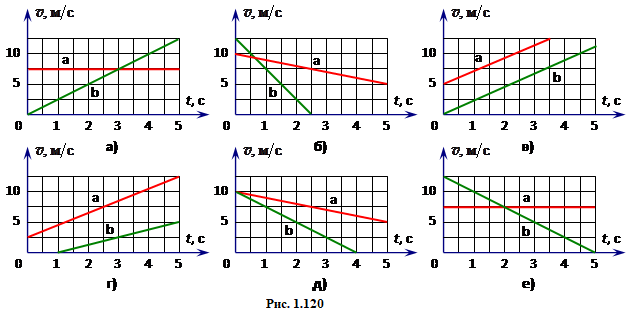
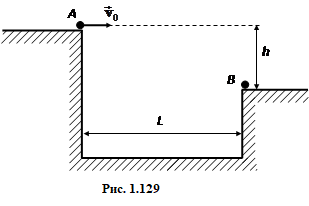
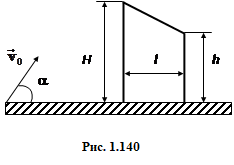
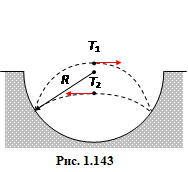
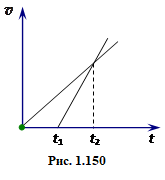
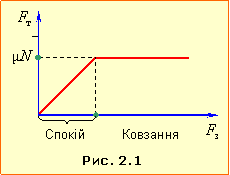 При переході тіла до ковзання та в подальшому русі сила тертя складно
При переході тіла до ковзання та в подальшому русі сила тертя складно  Два зв'язані ниткою тягарці
Два зв'язані ниткою тягарці 
 Визначити прискорення вантажів m1 і m2 у системі блоків рис. 2.
Визначити прискорення вантажів m1 і m2 у системі блоків рис. 2.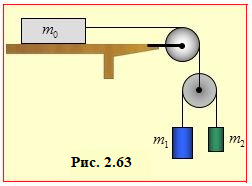 У системі, що показана на рис. 2.
У системі, що показана на рис. 2. Дві кульки маси m1 = 50 г і m2 = 100 г
Дві кульки маси m1 = 50 г і m2 = 100 г  Намистинки (матеріальні точки) масами m1 і m2 = 2m1 нанизали на горизонтальну спицю,
Намистинки (матеріальні точки) масами m1 і m2 = 2m1 нанизали на горизонтальну спицю,  Дві кулі масами
Дві кулі масами 
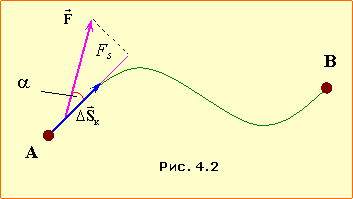
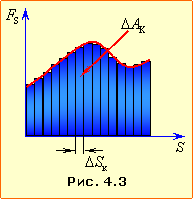
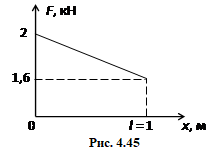
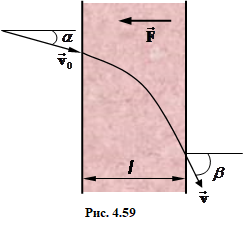 Частинка маси m влітає зі швидкістю
Частинка маси m влітає зі швидкістю  Лижник масою 70 кг починає спуск з вершини гори висотою H =
Лижник масою 70 кг починає спуск з вершини гори висотою H =  На шляху тіла, яке ковзає горизонтально по поверхні, знаходиться незакріплена гірка висотою h = 2 м (рис. 4.123). При якій мінімальній швидкості тіло зможе подолати гірку, якщо воно в 5 разів легше за гірку? Тертя відсутнє. [≈7 м/с]
На шляху тіла, яке ковзає горизонтально по поверхні, знаходиться незакріплена гірка висотою h = 2 м (рис. 4.123). При якій мінімальній швидкості тіло зможе подолати гірку, якщо воно в 5 разів легше за гірку? Тертя відсутнє. [≈7 м/с]
 Ліхтар вагою P = 50 H закріплено двома шнурами, як показано на рис. 5.
Ліхтар вагою P = 50 H закріплено двома шнурами, як показано на рис. 5. Ліхтар вагою P = 50H на горизонтальному шарнірному упорі АВ
Ліхтар вагою P = 50H на горизонтальному шарнірному упорі АВ  На кронштейні (рис. 5.16) висить вантаж масою m = 100 кг. Визначити сили, що діють на стрижні AB і BC, якщо вони утворюють кут
На кронштейні (рис. 5.16) висить вантаж масою m = 100 кг. Визначити сили, що діють на стрижні AB і BC, якщо вони утворюють кут 
 До бруска масою 10 кг, що стоїть на шорсткій опорі, прикладають
До бруска масою 10 кг, що стоїть на шорсткій опорі, прикладають  Вантаж вагою 100 H
Вантаж вагою 100 H 
 Котушка з нитками, підвішена до стіни (рис. 62), перебуває в рівновазі. При якому найменшому коефіцієнті тертя між котушкою й стіною це є можливо, якщо кут між ниткою й стіною
Котушка з нитками, підвішена до стіни (рис. 62), перебуває в рівновазі. При якому найменшому коефіцієнті тертя між котушкою й стіною це є можливо, якщо кут між ниткою й стіною 
 На дві однакові колоди, що впритул
На дві однакові колоди, що впритул  Однорідний стрижень
Однорідний стрижень  Куля радіусом R = 30 см і масою m = 7 кг , яку підвішено д
Куля радіусом R = 30 см і масою m = 7 кг , яку підвішено д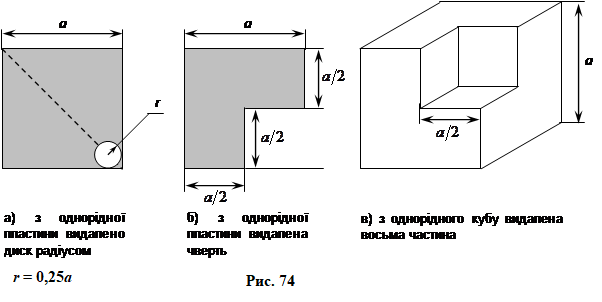
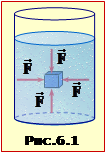
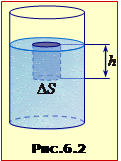 Тиск, який створюється в рідині завдяки силі тяжіння, називається
Тиск, який створюється в рідині завдяки силі тяжіння, називається