ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Рух двох тіл
Задача 1.23. Двоє байкерів рухаються однією прямою дорогою відповідно до рівнянь: \( {x}_{1}={8t} \) і \( {x}_{2}=14+0,5t^{2}\). 1. Проаналізувати рух і показати графіки координат байкерів x(t). 2. Визначити: а) час t та місце зустрічі байкерів (відстань L від початку координат); б) час τ, за який байкери подолають однаковий шлях і знайти його величину S.
Задача 1.24. Два тіла з однакової висоті над землею кинуто горизонтально у протилежних напрямах зі швидкостями \( {v}_{01}={4} \) м/с і \( {v}_{02}={9}\) м/с. Визначити, через який час t вектори швидкостей тіл стануть взаємно перпендикулярними.
Задача 1.25. З однієї точки одночасно і з однаковою швидкістю \( {v}\) = 20 м/с кидають вгору два тіла: одне вертикально, а інше – під кутом \( \alpha=50^{\circ}\) до горизонту. Визначити відстань L між тілами через час t = 0,5 c після початку руху.
| Задача 1.22 |
| Задача 1.23 |
Двоє байкерів рухаються однією прямою дорогою відповідно до рівнянь: \( {x}_{1}={8t} \) і \( {x}_{2}=14+0,5t^{2}\).
1. Проаналізувати рух і показати графіки координат байкерів x(t).
2. Визначити:
а) час t та місце зустрічі байкерів (відстань L від початку координат);
б) час τ, за який байкери подолають однаковий шлях і знайти його величину S.
|
Дано: x1 = 8t
x2 = 14 + 0,5t2
|
|
t - ? L - ? τ - ? |
Розв'язання
1. З умови випливає, що перший байкер рухається із сталою швидкістю v1 = 8 м/с і при t = 0 знаходиться в початку координат. Одночасно другий байкер, перебуваючи попереду на відстані x20 = 14 м, починає рухатись у тому самому напрямі з прискоренням a2 = 1 м/с2.
Для аналізу подальшого руху байкерів випишемо у загальному вигляді рівняння їхніх координат (1.16):
$\begin{align} & {{x}_{1}}={{v}_{1}}t \\ & {{x}_{2}}={{x}_{20}}+\frac{{{a}_{2}}{{t}^{2}}}{2} \\\end{align}$
Відтак, наклавши умову x2 = x1, отримаємо рівняння, що визначає можливі моменти зустрічі байкерів:
| ${{x}_{20}}+\frac{{{a}_{2}}{{t}^{2}}}{2}$ =${{v}_{1}}t$ $\Rightarrow $ ${{a}_{2}}{{t}^{2}}-2{{v}_{1}}t+2{{x}_{20}}=0$ | (1) |
Із виразу коренів цього рівняння
$ t=\frac{{{v}_{1}}\pm \sqrt{v_{1}^{2}-2{{a}_{2}}{{x}_{20}}}}{{{a}_{2}}}$
випливає, що на загал є три можливості:
1) $v_{1}^{2}<2{{a}_{2}}{{x}_{20}}$ корені не існують, тобто байкери взагалі не зустрінуться;
2) $v_{1}^{2}=2{{a}_{2}}{{x}_{20}}$ – байкери зустрінуться в момент t0 = v1/a2;
3) $v_{1}^{2}>2{{a}_{2}}{{x}_{20}}$ – відбудеться дві зустрічі.
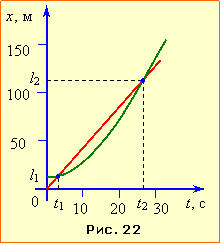
Сказане ілюструє рис. 22, на якому зображено графік x2(t), що являє гілку параболи з вершиною в очці х20 та три промені – графіки x1(t) для випадків 1), 2) і 3), відповідно.
Проаналізуємо за графіками рух байкерів у кожному з наведених випадків, узявши до уваги, що відстань між байкерами визначається різницею ординат х, а швидкість руху – нахилом графіків до осі абсцис t (див. п. 1.4). Тож, як видно, в кожному випадку перший байкер спочатку наздоганяє другого, а від моменту, коли їхні швидкості порівнюються, – відстає. При цьому:
– за малої швидкості v1 (випадок 1) перший байкер починає відставати, ще не діставшись точки старту другого, тож ніколи його не наздожене;
– у випадку 2 перший байкер у момент t0 і в точці х0 наздоганяє другого, але відразу починає відставати;
– при великій швидкості (випадок 3) перший байкер у момент t1 (перша зустріч) має більшу швидкість і починає випереджати другого. Але потім другий, поступово нарощуючи швидкість, у момент t2 (друга зустріч) наздоганяє й уже назавжди випереджає першого.2а. При заданих значеннях v1 = 8 м/с, x20 = 14 м і a2 = 1 м/с2 виконується умова 3), і корені рівняння (1) становлять t1 = 2 c, t2 = 14 c. Отже, байкери зустрічаються двічі – через 2 с та 14 с після старту другого і, згідно із заданими в умові рівняннями, на відстані L1 = 16 м і L2 = 112 м від початку координат.
2б. Пройдений кожним байкером шлях дорівнює зміні його координати. Тож, поклавши в заданих умовою задачі рівняннях х1 = х2 = S і t = τ , отримаємо:
$\left\{ \begin{align} & S=8\tau \\ & S=0,5{{\tau }^{2}} \\\end{align} \right.\quad \Rightarrow \quad \tau =16\text{ c;}\quad S=128\text{ }\text{м.}$
| Задача 1.23 |
| Задача 1.24 |
Два тіла з однакової висоті над землею кинуто горизонтально у протилежних напрямах зі швидкостями \( {v}_{01}={4} \) м/с і \( {v}_{02}={9}\) м/с.
Визначити,
через який час t вектори швидкостей тіл стануть взаємно перпендикулярними.
|
Дано: v01 = 4 м/c
v02 = 9 м/c
g = 10 м/с2
|
|
t - ? |
Розв'язання
Умова задачі містить інформацію про початкові та кінцеві швидкості двох тіл, які одночасно починають рух із однаковим прискоренням \( \vec{g}\). Тож шуканий час можна знайти за допомогою рівнянь (1.14):
\( \vec{v}_{1}(t)=\vec{v}_{01}+\vec{g}{t}\),
\( \vec{v}_{2}(t)=\vec{v}_{02}+\vec{g}{t}\)
одним із двох способів.
І спосіб. Згадаємо, що скалярний добуток векторів \( \vec{b}\) і \( \vec{c}\) визначається як \( \vec{b}\cdot\vec{c}=b{c}\cos\alpha \), де \( \alpha \) – кут між векторами. Для взаємно перпендикулярних векторів він дорівнює нулю, отже:
\( \vec{v}_{1}(t)\vec{v}_{2}(t)=\left(\vec{v}_{01}+\vec{g}t\right)\left(\vec{v}_{02}+\vec{g}t\right){=}\)
\( {=}\vec{v}_{01}\vec{v}_{02}+\vec{v}_{01}\vec{g}t+\vec{v}_{02}\vec{g}t+\vec{g}t\vec{g}{t}={0}\).
За умовою задачі кут між векторами \( \vec{v}_{01}\) та \( \vec{v}_{02}\) дорівнює \( {\pi}\). Отже, 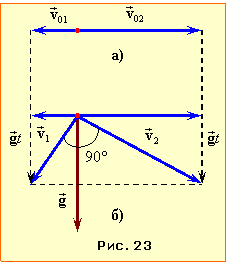
\( \vec{v}_{01}\vec{v}_{02}=-v_{01}{v}_{02}\).
При цьому кути між векторами \( \vec{v}_{01}\) і \( \vec{g}\) та \( \vec{v}_{02}\) і \( \vec{g}\) дорівнюють \( \pi{/2}\), тому\( \vec{v}_{01}\vec{g}=\vec{v}_{02}\vec{g}={0}\).
Крім того, скалярний добуток вектора самого на себе дорівнює квадрату його модуля: \( \vec{g}\cdot\vec{g}=g^{2}\). Таким чином,
\( \vec{v}_{1}\vec{v}_{2}=-v_{01}{v}_{02}+g^{2}t^{2}={0}\),
і
\( {t}=\frac{\sqrt{v_{01}v_{02}}}{g}={0,6}\) c.
ІІ спосіб. Оскільки вектори \( \vec{v}_{01},\,\vec{v}_{02}\) (див. рис. 23) є перпендикулярні до вектора \( \vec{g}\), то для швидкостей тіл у будь-який момент часу (див. рис. 23) можна записати:
| \( {v}_{1}^{2}=v_{01}^{2}+(gt)^{2}\), \( {v}_{2}^{2}=v_{02}^{2}+(gt)^{2}\). | (1) |
З іншого боку, позаяк за умовою вектори \( \vec{v}_{1}\) і \( \vec{v}_{2} \) (рис. 23б) є взаємно перпендикулярні, то
\( {v}_{1}^{2}+v_{2}^{2}=(v_{01}+v_{02})^{2}\).
Підставивши сюди вирази (1), дістанемо:
\( {v}_{01}^{2}+2(gt)^{2}+v_{02}^{2}=v_{01}^{2}+2v_{01}v_{01}+v_{02}^{2}\) \( \Rightarrow \)
\( {gt}=\sqrt{v_{01}v_{02}}\) \( \Rightarrow \) \( {t}=\frac{\sqrt{v_{01}v_{02}}}{g}={0,6}\) c.
| Задача 1.24 |
| Задача 1.25 |
З однієї точки одночасно і з однаковою швидкістю \( {v}\) = 20 м/с кидають вгору два тіла: одне вертикально, а інше – під кутом \( \alpha=50^{\circ}\) до горизонту.
Визначити
відстань L між тілами через час t = 0,5 c після початку руху.
|
Дано: v = 20 м/с
α = 50°
t = 0,5 с
|
|
L - ? |
Розв'язання
Залежно від вибору системи відліку, задачу можна розв'язати двома способами.
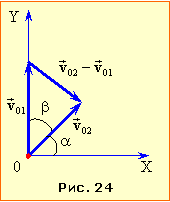
І спосіб. Оберемо координатну систему XOY з початком у точці кидання (рис. 24), в якій початкові координати обох тіл дорівнюють нулю, а проєкції початкових швидкостей \( {v}_{1x}={0}\), \( {v}_{1y}={v}\) і \( {v}_{2x}=v\cos\alpha\), \( {v}_{2y}=v\sin\alpha \). Координати тіл на момент часу t визначаються рівняннями (1.16а):
|
\( {x}_{1}={0}\), \( {x}_{2}=vt\cos\alpha \); \( {y}_{1}=vt-\frac{gt^{2}}{2}\), \( {y}_{2}=vt\sin\alpha-\frac{gt^{2}}{2}\). |
(1) |
Відстань між двома точками через їхні координати виражається формулою:
\( {L}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\).
Тож, підставивши сюди вирази (1) для координат, після простих перетворень отримаємо:
$L=vt\sqrt{{{\cos }^{2}}\alpha +{{\left( \sin \alpha -1 \right)}^{2}}}=vt\sqrt{2\left( 1-\sin \alpha \right)}$
Обчислення дають
L = 6,84 м.
ІІ спосіб. Пов'яжемо з першим тілом рухому систему відліку, швидкість V якої відносно нерухомої (земна поверхня) складає \( \vec{V}\) = \( \vec{v}_{1}\). Тоді швидкість другого тіла відносно першого (швидкість в рухомій системі відліку) визначається формулою (1.11а):
| \( \vec{u}=\vec{v}_{2}-\vec{v}_{1}=(\vec{v}_{02}+\vec{g}t)-(\vec{v}_{01}+\vec{g}t)=\vec{v}_{02}-\vec{v}_{01}=\mathrm{const}\). |
Отже, позаяк прискорення тіл однакові, їхній відносний рух є рівномірним прямолінійним, і відстань між ними змінюється з часом, як
| \( {L}=ut=\left|\vec{v}_{02}-\vec{v}_{01}\right|{t}\). |
Величину $u=\left| {{{\vec{v}}}_{02}}-{{{\vec{v}}}_{01}} \right|$ знайдемо за теоремою косинусів (див. рис. 24):
\( {u}=\sqrt{v^{2}+v^{2}-2vv\cos^{2}\beta}\) = v\(\sqrt{2\left( 1-\cos \beta \right)}\) = \( {L}=vt\sqrt{2(1-\sin\alpha)}\).