physics.zfftt.kpi.ua

Явище електромагнітної індукції свідчить про те, що електричне поле породжується не лише зарядами, а й магнітними полями. Але Максвелл також установив, що й магнітне поле створюється не тільки рухомими зарядами (струмами), а й електричними полями. Відтак стало можливим відобразити загальні властивості електромагнітного поля в чотирьох рівняннях, які складають фундамент усієї класичної електродинаміки.

Далі розглядаються наступні питання:

2.1. Струм зміщення

До думки про здатність електричного поля створювати магнітне поле можна дійти, до прикладу, аналізуючи процес заряджання конденсатора. При підключенні конденсатора до джерела у просторі виникне магнітне поле, створене струмом заряджання. При цьому, якщо охопити якимось контуром \(L\) провідник, що підходить до обкладки конденсатора (рис. 2.1а), то, відповідно до теореми про циркуляцію магнітного поля ((3.9), розділ IV), можна записати:

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}, \tag{2.1} \end{equation}

де \(S_{1}\) — поверхня, що спирається на контур \(L\), \( \vec{j}\) — густина струму на цій поверхні.

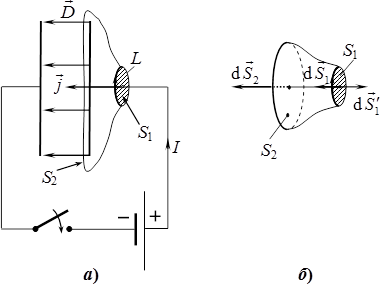
Інтеграл у правій частині (2.1) визначає сумарний струм, який охоплюється контуром \(L\), тож не залежить від розмірів та форми поверхні \(S_{1}\). Отже, можна взяти якусь іншу поверхню, скажімо у формі “глечика”, що охоплює одну обкладку конденсатора, як схематично показано на рис. 2.1. Ніякі струми цю поверхню не перетинають, і на ній скрізь \( \vec{j}=0 \). Тому рівняння (2.1) мало би виглядати як

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=0 . \tag{2.1а} \end{equation}

Але цього не може бути бо йдеться про циркуляцію того самого поля \( \vec{H}\) по тому самому контуру \(L\). Тож логічно припустити, що циркуляцію нестаціонарного магнітного поля, крім струму провідності, визначає ще якийсь фактор. Його вірогідну природу можна відшукати на основі закону збереження електричного заряду, який для нестаціонарних процесів виражається рівнянням неперервності (розділ III, п. 1.2):

\begin{equation} \oint\limits_{S}{\vec{j}\,\mathrm{d}\vec{S}}=-\int\limits_{V}{\frac{\partial \rho }{\partial t}\mathrm{d}V}, \tag{2.2} \end{equation}

яке засвідчує, що зміна величини заряду в об’ємі \(V\) за будь-який проміжок часу в точності дорівнює кількості заряду, що проходить за той самий час крізь замкнену поверхню \(S\), що обмежує цей об’єм.

Для вибраної замкненої поверхні (рис. 2.1а) підінтегральна функція \(\vec{j}\) в рівнянні (2.2) відмінна від 0 тільки на “кришці” \(S_{1}\) (рис. 2.1б), отже, його можна подати як

\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{\vec{S}}}{}_{1}^{\prime }}=-\int\limits_{V}{\frac{\partial \rho }{\partial t}\mathrm{d}V}. \tag{2.2а} \end{equation}

Урахуємо також, що при обчисленні потоку крізь замкнену поверхню вектори елементарних площинок спрямовують по зовнішніх нормалях, а при обчисленні циркуляції за рівнянням (2.1) узгоджують із напрямком обходу контуру \(L\) за правилом правого гвинта. В такому разі \( \mathrm{d}{{\vec{S}}'_{1}} = - \mathrm{d}{{\vec{S}}_{1}}\), і попередній вираз набуває вигляду:

\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}=\int\limits_{V}{\frac{\partial \rho }{\partial t}\,\mathrm{d}V}. \tag{2.2б} \end{equation}

Інтеграл в лівій частині визначає струм, який проходить через поверхню \(S_{1}\), тож

\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}=\frac{\text{d}q}{\text{d}t}, \end{equation}

де \(\mathrm{d}q\) — заряд, який заходить всередину “глечика” і осідає на пластині конденсатора за час \(\mathrm{d}t\), а похідна визначає швидкість зміни заряду пластини \(q\). Цей заряд створює електричне поле, в якому за теоремою Гаусса ((2.9а), розділ II) потік вектора \( \vec{D}\) крізь будь-яку замкнену поверхню

\begin{equation} \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}=q , \end{equation}

де \(q\) — вільний заряд всередині поверхні \(S\), який в нашому випадку зосереджений на пластині конденсатора. Тому поле є лише між пластинами, і потік \( \vec{D}\) створюється тільки через дно “глечика” \(S_{2}\), так що

\begin{equation} q=\int\limits_{{{S}_{2}}}{\vec{D}\,\mathrm{d}{{{\vec{S}}}_{2}}} . \end{equation}

Відповідно, швидкість зміни заряду

\begin{equation} \frac{\text{d}q}{\text{d}t}=\int\limits_{{{S}_{2}}}{\frac{\partial \vec{D}}{\partial t}\mathrm{d}{{{\vec{S}}}_{2}}} . \end{equation}

Порівнюючи цей вираз із (2.2б), доходимо висновку, що

\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}=\int\limits_{{{S}_{2}}}{\frac{\partial \vec{D}}{\partial t}\mathrm{d}{{{\vec{S}}}_{2}}}. \tag{2.3} \end{equation}

Це й вирішує “парадокс” рівняння (2.1а): якщо його записати у вигляді

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{{{S}_{2}}}{\frac{\partial \vec{D}}{\partial t}\mathrm{d}{{{\vec{S}}}_{2}}}, \tag{2.4} \end{equation}

то результат обчислення циркуляції \( \vec{H}\) за виразами (2.1) і (2.4) буде однаковий, незалежно від вибору поверхні. При цьому в одному випадку поверхню перетинає тільки струм, а в іншому — тільки електричне поле. Тому вирази (2.1) і (2.4) можна об’єднати в одне загальне рівняння

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\left( \vec{j}+\frac{\partial \vec{D}}{\partial t} \right)\mathrm{d}\vec{S}}, \tag{2.5} \end{equation}

що є чинним при будь-якій формі поверхні \(S\), обмеженої контуром \(L\).

Треба сказати, що цей результат сам по собі має лише формальний зміст. Він отриманий тільки для окремого випадку — магнітного поля струму заряджання конденсатора — і пояснюється тим, що між струмом заряджання та електричним полем конденсатора є прямий зв’язок. По закінченню заряджання рівняння (2.5) втрачає зміст, бо струм припиняється (\( \vec{j}={0}\)), електричне поле у конденсаторі стає постійним (\( {\partial \vec{D}}/{\partial t}=0 \)), і магнітне поле зникає. Але Максвелл дійшов висновку, що рівняння (2.5) є чинним завжди, не втрачаючи змісту і при \( \vec{j}=0 \). Якщо так, то при \( ( {\partial \vec{D}}/{\partial t})\ne 0 \)

\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\frac{\partial \vec{D}}{\partial t}\,\mathrm{d}\vec{S}}\ne 0\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \vec{H}\ne 0. \end{aligned} \tag{2.5а}\end{equation}

Тим самим Максвелл постулював, що

магнітне поле створюється не лише струмами провідності (рухом заряджених частинок), а й змінними електричними полями.

Слід зауважити, що розглянуті міркування і викладки не доводять із необхідністю такий умовивід, а тільки вказують на його вірогідність. Але його істинність, як і інші фундаментальні відкриття Максвела, незаперечно підтверджується дослідом і всім розвитком класичної електродинаміки.

Похідна \( {\partial \vec{D}}/{\partial t}\), яка фігурує в рівняннях (2.5), (2.5а), як і густина струму провідності \(\vec{j}\), має розмірність [\(\text{А/м}^2\)] і по аналогії називається “густиною струму зміщення” позначається таким самим символом:

\begin{equation} {{\vec{j}}_{\text{зм}}}=\frac{\partial \vec{D}}{\partial t}. \tag{2.6} \end{equation}

Але цю термінологію і символіку не слід розуміти буквально, бо

струм зміщення є мірою швидкості зміни електричного поля

і в загальному випадку не пов’язаний із рухом зарядів-носіїв струму.

Уведення струму зміщення дозволяє зручно записувати і формулювати закон (2.5):

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\bigl( \vec{j}+{{{\vec{j}}}_{\text{зм}}} \bigr)\mathrm{d}\vec{S}}, \tag{2.7} \end{equation}

або

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{{{{\vec{j}}}_{\text{повн}}}\,\mathrm{d}\vec{S}}, \tag{2.7а} \end{equation}

де величина

\begin{equation} {{\vec{j}}_{\text{повн}}}=\vec{j}+{{\vec{j}}_{\text{зм}}}=\vec{j}+\frac{\partial \vec{D}}{\partial t} \tag{2.8} \end{equation}

називається густиною повного струму. Відповідно, рівняння (2.7а) інколи називають законом повного струму.

Поняття струму зміщення дозволяє також інакше подати співвідношення (2.2б), що випливає з рівняння неперервності (2.2):

\begin{equation} \begin{aligned} &\oint\limits_{S}{\vec{j}\,\mathrm{d}\vec{S}}=-\oint\limits_{S}{{{{\vec{j}}}_{\text{зм}}}\,\mathrm{d}\vec{S}}\quad \Rightarrow {}\\ &\quad {}\Rightarrow\quad \oint\limits_{S}{( \vec{j}+{{{\vec{j}}}_{\text{зм}}} )\mathrm{d}\vec{S}}=0\quad \Rightarrow {}\\ &\quad {}\Rightarrow\quad \oint\limits_{S}{{{{\vec{j}}}_{\text{повн}}}\mathrm{d}\vec{S}}=0. \end{aligned} \end{equation}

Це означає, що лінії повного струму є завжди неперервні — в точках розриву провідності кожна лінія струму провідності (лінія вектора \( \vec{j}\)), продовжується лінією струму зміщення (лінією вектора \( {\partial \vec{D}}/{\partial t}\)) і навпаки. (У розглянутому прикладі це відбувається на обкладках конденсатора.) Саме з цієї причини рівняння (2.6), розділ III, й називається рівнянням неперервності.

2.2. Рівняння Максвелла в інтегральній формі

Відкриття вихрового електричного поля та струму зміщення як джерела магнітного поля лягло в основу створеної Максвеллом класичної електродинаміки — теорії, що трактує макроскопічні електромагнітні явища при нерелятивістських (\(v \ll c\)) швидкостях руху зарядів.

Фундаментальні рівняння. Найбільш загальні властивості електромагнітного поля відображаються системою фундаментальних рівнянь електромагнітного поля, або рівнянь Максвелла. Вони є найбільш загальними виразами розглянутих у попередніх розділах теорем про циркуляції та потоки електричного і магнітного полів і мають вигляд:

\begin{equation} \begin{aligned} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}&=-\int\limits_{S}{\frac{\partial \vec{B}}{\partial t}\,\mathrm{d}\vec{S}}; \\ \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}&=\int\limits_{S}{\left( \vec{j}+\frac{\partial \vec{D}}{\partial t} \right)\mathrm{d}\vec{S}};\\ \oint\limits_{S}\vec{D}\,\mathrm{d}\vec{S}&=\int\limits_{V}{\rho \,\mathrm{d}V};\\ \oint\limits_{S}{\vec{B}\,\mathrm{d}\vec{S}}&=0. \end{aligned} \tag{2.9} \end{equation}

Зауважимо, що ця система не включає рівняння неперервності, яке виражає закон збереження електричного заряду. Але його неявно відображає неперервність ліній повного струму, про що говорилося вище.

У випадку стаціонарних полів, для яких \( ( {\partial \vec{D}}/{\partial t} )=( {\partial \vec{B}}/{\partial t} )=0 \), система (2.9) розпадається на дві пари незалежних рівнянь електростатики та магнітостатики, котрі визначають найголовніші властивості стаціонарних полів:

\begin{equation} \begin{aligned} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}&=0;\\ \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}&=\int\limits_{V}{\rho \,\mathrm{d}V}, \end{aligned} \end{equation}

і

\begin{equation} \begin{aligned} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}&=\int\limits_{S}{\vec{j}\,\mathrm{d}\vec{S}};\\ \oint\limits_{S}{\vec{B}\,\mathrm{d}\vec{S}}&=0. \end{aligned} \end{equation}

Перша пара відображає той факт, що статичні електричні поля створюються зарядженими частинками і є потенціальними, а друга — що статичні магнітні поля створюються тільки струмами провідності (рухом зарядів) і є непотенціальними (вихровими).

У випадку нестатичних (змінних у часі) полів із загальної системи фундаментальних рівнянь випливає, що джерелом якогось одного поля є не лише заряди або струми, а й інше поле. Тож нестаціонарні електричне і магнітне поля є органічно взаємопов’язані, й одне не може існувати без іншого. Змінне електричне поле породжує магнітне, котре в свою чергу породжує електричне, а воно — знов магнітне, і т.д. При цьому, як показав Максвелл, із рівнянь (2.9) випливає, що цей процес має хвильовий характер і поширюється у просторі зі швидкістю світла. Тим самим Максвелл теоретично відкрив існування електромагнітних хвиль та електромагнітну природу світла, що потім було підтверджено експериментально.

Матеріальні рівняння. Рівняння Максвелла виконуються за будь-яких умов, на те вони й фундаментальні. Але в математичному сенсі система рівнянь (2.9) є неповною. Вона містить два векторні рівняння для циркуляцій і два скалярні для потоків. При записі в проекціях це дає 8 рівнянь, тоді як навіть при заданих функціях \( \rho \) і \(\vec{j}\) для визначення чотирьох векторів полів треба мати 12 рівнянь.

Причина такої недостатньості фундаментальних рівнянь полягає в тому, що вони не містять електричних і магнітних характеристик середовища, котрі саме й визначають перебіг електромагнітних процесів у кожному конкретному випадку. Тому фундаментальні рівняння мають бути доповнені матеріальними рівняннями — співвідношеннями, що відображають зв’язки між різними електричними та магнітними характеристиками поля в речовині (“матеріалі”). Ці співвідношення істотно відрізняються для різних класів речовин, тому для кожного є свої матеріальні рівняння. Для ізотропних лінійних речовин, які є найбільш поширені і вживані на практиці, матеріальні рівняння мають знайомий з попередніх розділів вигляд:

\begin{equation} \begin{aligned} \vec{D}&={{\varepsilon }_{0}}\varepsilon \vec{E};\\ \vec{B}&={{\mu }_{0}}\mu \vec{H};\\ \vec{j}&=\sigma \vec{E}, \end{aligned} \end{equation}

де \(\varepsilon \), \(\mu \) — діелектрична та магнітна проникності, а \(\sigma\) — питома електропровідність речовини.

Фундаментальні рівняння разом із матеріальними співвідношеннями утворюють повну систему рівнянь електромагнітного поля в нерухомому середовищі, котра в кожному випадку принципово дозволяє дослідити будь-яке електромагнітне явище.

2.3 Диференціальні характеристики поля

Розглянуті інтегральні рівняння (2.9) встановлюють зв’язок між джерелами і характеристиками електромагнітного поля через потоки й циркуляції, тож відображують його властивості не в кожній точці (локально), а лише інтегрально — на заданій лінії або поверхні. Через це вони не дають принципової відповіді на деякі важливі запитання. До прикладу, нульова величина циркуляції напруженості заданого електричного поля по обраному контуру \(L\) не може бути доказом його потенціальності, бо не виключає існування в цьому полі інших контурів, для котрих

\begin{equation} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}\ne 0. \end{equation}

Так само, коли сума струмів, які охоплює даний замкнений контур \(L\), дорівнює нулю, то за відсутності змінного електричного поля з другого рівняння (2.9) випливає, що

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=0. \end{equation}

Та це зовсім не означає, що магнітне поле є потенціальним.

Але такі питання, у принципі, не виникають при використанні рівнянь Максвелла в диференціальній формі, котрі встановлюють зв’язок між джерелами та характеристиками поля локально, тобто в кожній точці. Ці рівняння оперують величинами, що визначають не саме поле, а його поведінку в кожній точці. Їхній зміст , розглянуто в питаннях:

2.3.1. Дивергенція поля

2.3.2. Ротор поля

2.3.1. Дивергенція поля

Ця величина принципово вирішує задачу визначення розподілу зарядів і струмів за заданими характеристиками створюваного ними поля, що є важливим і в теорії, і на практиці. Як це робиться, розглянемо на прикладі електричного поля.

Третє рівняння Максвелла (2.9) дозволяє знайти сумарний електричний заряд у будь-якій області простору за відомим електричним зміщенням \( \vec{D}( {\vec{r}} ) \). Але так, у принципі, можна визначити не лише величину заряду в заданій області, а й його просторовий розподіл. Для цього будемо діяти за наступною логічною схемою.

Розчленуємо подумки все поле на маленькі комірки і підрахуємо потік вектора \( \vec{D}\) крізь кожну. Тоді там, де він дорівнює нулю, заряду немає, а в комірках із ненульовим потоком заряд є, причому його величина дорівнює величині потоку. Тому, зменшуючи розміри комірок, у такий спосіб можна врешті решт отримати достатньо точну інформацію про заряд, зосереджений у кожній точці поля.

Запропонована позірна схема може здатися практично нездійсненою через гранично велику необхідну кількість указаних комірок. Але насправді вона досить просто реалізується методами вищої математики.

Визначимо потік вектора \( \vec{D}\) крізь якусь одну комірку у формі невеликого паралелепіпеда з ребрами \( \Delta{x}\), \( \Delta{y}\), \( \Delta{z}\) , паралельними до осей координат, як показано на рис. 2.2.

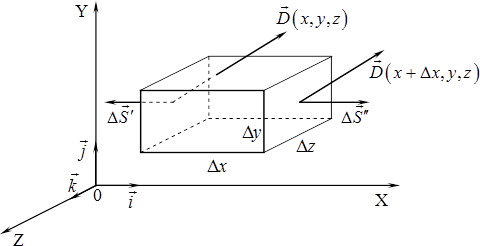
Для цього подамо його як суму потоків крізь пари паралельних граней:

\begin{equation} \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}={{\Phi }_{1}}+{{\Phi }_{2}}+{{\Phi }_{3}}. \end{equation}

При малих розмірах комірок величину \( \vec{D}\) в усіх точках заданої грані можна наближено вважати однаковою. Тоді потік крізь одну грань

\begin{equation} \Delta \Phi \approx \vec{D}\,\Delta \vec{S}, \end{equation}

де \(\Delta S\) — площа грані.

Відповідно, для потоку крізь пару граней з координатами \(x\) і \( {x}+\Delta{x}\) матимемо:

\begin{equation} {{\Phi }_{1}}\approx \vec{D}( x,y,z )\Delta {{\vec{S}}'_{1}}+\vec{D}( x+\Delta x,y,z )\Delta {{\vec{S}}''_{1}}. \end{equation}

Вектори площинок

\begin{equation} \Delta {\vec{S}}{}_{1}^{\prime }=-\vec{i}\,\Delta y\,\Delta z\qquad \text{i}\qquad \Delta {\vec{S}}{}_{1}^{\prime \prime }=\vec{i}\,\Delta y\,\Delta z, \end{equation}

отож,

\begin{equation} \begin{aligned} &{{\Phi }_{1}}\approx \bigl( -{{D}_{x}}( x,y,z )+{{D}_{x}}( x+\Delta x,y,z ) \bigr)\Delta y\,\Delta z={}\\ &\quad{}= \Delta {{D}_{x}}\,\Delta y\,\Delta z. \end{aligned} \end{equation}

Величина \( \Delta {{D}_{x}}\) визначається відомим з математики виразом

\begin{equation} \Delta {{D}_{x}}\approx \frac{\partial {{D}_{x}}}{\partial x}\Delta{x}. \end{equation}

Примітка. Частинна похідна стоїть тому, що зміна вектора зміщення зумовлена зміною тільки координати \(x\).

Відтак для потоку крізь дану пару граней маємо

\begin{equation} \begin{aligned} &{{\Phi }_{1}}\approx \frac{\partial {{D}_{x}}}{\partial x}\Delta x\,\Delta y\,\Delta z\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {{\Phi }_{1}}\approx \frac{\partial {{D}_{x}}}{\partial x}\Delta V, \end{aligned} \end{equation}

де \( \Delta{V}\) — об’єм комірки.

Очевидно, що аналогічно виражаються потоки і крізь дві інші пари граней:

\begin{equation} {{\Phi }_{2}}\approx \frac{\partial {{D}_{y}}}{\partial y}\Delta V,\qquad {{\Phi }_{3}}\approx \frac{\partial {{D}_{z}}}{\partial z}\Delta V. \end{equation}

Отже, потік крізь усю поверхню комірки наближено виражається формулою:

\begin{equation} \begin{aligned} &\oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}\approx{}\\ &\quad{}\approx \left( \frac{\partial {{D}_{x}}}{\partial x}+\frac{\partial {{D}_{y}}}{\partial y}+\frac{\partial {{D}_{z}}}{\partial z} \right)\Delta V. \end{aligned} \tag{2.11}\end{equation}

Вираз у дужках часто стрічається у різних задачах математики та фізики. Тому він має спеціальну назву “дивергенція” поля і позначення “div”. Отже,

\begin{equation} \operatorname{div}\vec{D}=\left( \frac{\partial {{D}_{x}}}{\partial x}+\frac{\partial {{D}_{y}}}{\partial y}+\frac{\partial {{D}_{z}}}{\partial z} \right) . \tag{2.12} \end{equation}

Зауважимо, що залежно від симетрії поля можуть виявитися зручнішими сферичні або циліндричні координати, в яких формули дивергенції при збереженні загальної структури відрізняються від виразу (2.12). Тому він є не означенням, а тільки формулою для обчислення дивергенції в декартових координатах. А інваріантне означення, що висвітлює фізичний зміст дивергенції, випливає з виразу (2.11) при переході до границі \( \Delta V\to{0}\) шляхом стягання комірки в точку:

\begin{equation} \begin{aligned} &\oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}\approx \operatorname{div}\vec{D}\cdot \Delta V\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \operatorname{div}\vec{D}=\lim\limits_{\Delta{V}\to{0}}\frac{\oint\limits{\vec{D}\,\mathrm{d}\vec{S}}}{\Delta{V}}. \end{aligned} \tag{2.13}\end{equation}

Таким чином,

дивергенцією векторного поля в заданій точці називається границя відношення потоку поля крізь замкнену поверхню до обмеженого нею об’єму при стяганні поверхні в задану точку.

Ураховуючи формулу (2.12) і теорему Гаусса для вектора \(\vec{D}\) (розділ II, (4.9а)), вираз (2.11) можна подати, як

\begin{equation} \operatorname{div}\vec{D}\cdot \Delta V\approx q=\langle \rho \rangle \Delta V, \end{equation}

де \( \langle \rho \rangle \) — середня густина заряду в об’ємі \( \Delta{V}\). Очевидно, що при \( \Delta{V}\to{0}\) ця рівність стане точною. Таким чином, у кожній точці поля

\begin{equation} \operatorname{div}\vec{D}=\rho . \tag{2.14} \end{equation}

Позаяк цей результат випливає з інтегральної теореми Гаусса, рівняння (2.14) називається теоремою Гаусса в диференціальній формі. Воно встановлює локальний (у кожній точці) зв’язок між полем і його джерелами, й вирішує проблему визначення розподілу заряду \( \rho ( x,y,z ) \), яким створюється задане поле. Для цього достатньо провести в (2.14) необхідне диференціювання заданої функції \( \vec{D}( x,y,z ) \).

Якщо в рівнянні ((4.9), розділ II) зробити заміну (2.14), то отримаємо вираз математичної теореми Остроградського — Гаусса

\begin{equation} \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}=\int\limits_{V}{\operatorname{div}\vec{D}\cdot \mathrm{d}V} . \tag{2.15} \end{equation}

А саме,

потік векторного поля крізь довільну замкнену поверхню дорівнює інтегралу від дивергенції цього поля по об’єму обмеженому даною поверхнею.

Формула (2.15) є чинною для будь-якого векторного поля, зокрема, для магнітного. Тож

\begin{equation} \oint\limits_{S}{\vec{B}\,\mathrm{d}\vec{S}}=\int\limits_{V}{\operatorname{div}\vec{B}\cdot \mathrm{d}V}. \end{equation}

Але, згідно з інтегральною теоремою Гаусса (10.1), ліва частина записаного рівняння дорівнює нулю при будь-яких розмірах і формі замкненої поверхні \(S\). Тож і права частина дорівнює нулю при будь-якій величині \(V\), а це можливо тільки за умови, що

в будь-якій точці магнітного поля дивергенція вектора \(\vec{B}\) дорівнює нулю:

\begin{equation} \operatorname{div}\vec{B}=0. \tag{2.16} \end{equation}

Це твердження виражає теорему Гаусса для магнітного поля в диференціальній (локальній) формі.

2.3.2. Ротор поля

Теорему про циркуляцію векторного поля теж можна виразити в диференціальній формі. Покажемо це на прикладі магнітного поля струмів провідності.

Нехай магнітне поле \( \vec{H}( x,y,z ) \) створюється заданим розподілом струмів провідності \(\vec{J}( x,y,z )\).

Примітка. Позначення густини струму збігається з позначенням одного з ортів декартової системи координат. Тому, аби запобігти плутанині, далі до кінця п. 2.3 густина струму позначається як \(\vec{J}\).

Виберемо невеликий прямокутний контур із сторонами \( \Delta{x}\) і \( \Delta{y}\), розташований у площині \(\mathrm{XOY}\), як показано на рис. 2.3,

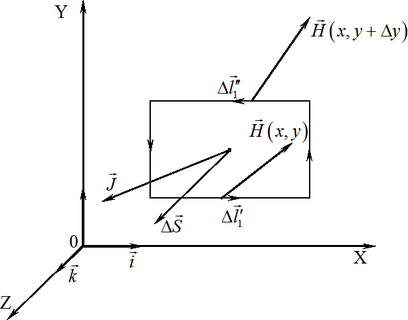
і запишемо для нього наближений вираз теореми про циркуляцію вектора \( \vec{H}\), взявши до уваги, що орт нормалі \( \vec{n}\) збігається з ортом \( \vec{k}\) координатної системи:

\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}\approx \vec{J}\,\Delta \vec{S}={{J}_{n}}\,\Delta S={}\\ &\quad{}= {{J}_{z}}\,\Delta x\,\Delta y. \end{aligned} \tag{2.17}\end{equation}

Циркуляція по вказаному контуру складається із внесків від усіх сторін прямокутника. Ці внески не важко визначити. Розглянемо для прикладу внесок \(C_{1}\) від горизонтальних сторін, обходячи контур проти годинникової стрілки (у додатному напрямі відносно вектора \(\vec{J}\)). При малих розмірах прямокутника можна нехтувати зміною поля на переміщенні вздовж кожної із сторін і наближено записати:

\begin{equation} \begin{aligned} &{{C}_{1}}\approx \vec{H}( x,y )\Delta {{\vec{l}}}{}_{1}^{\prime }+\vec{H}( x,y+\Delta y )\Delta {{\vec{l}}}{}_{1}^{\prime \prime }={}\\ &\quad{}=\bigl( \vec{H}( x,y )\vec{i}-\vec{H}( x,y+\Delta y )\vec{i} \bigr)\Delta x={}\\ &\quad{}=-{{( \Delta {{H}_{x}} )}_{y}}\Delta x. \end{aligned} \end{equation}

Тут ураховано, що \(\Delta {{\vec{{l}}}}{}_{1}^{\prime }=\vec{i}\Delta x\), \(\Delta {{{l}}}{}_{1}^{\prime \prime }=-\vec{i}\Delta x\) і, що скалярний добуток вектора на орт є проекцією цього вектора на відповідну вісь. У такому разі величина \( {{( \Delta {{H}_{x}} )}_{y}}\) є частинним приростом величини \( {{H}_{x}}\) при зміні координати \(y\) при переході до верхньої сторони контуру. За правилами диференціального числення

\begin{equation} {{( \Delta {{H}_{x}} )}_{y}}\approx \frac{\partial {{H}_{x}}}{\partial y}\Delta y , \end{equation}

отже, розглянутий внесок у циркуляцію складає

\begin{equation} {{C}_{1}}\approx -\frac{\partial {{H}_{x}}}{\partial y}\Delta x\,\Delta y. \end{equation}

Аналогічно можна показати, що вклад від іншої пари сторін

\begin{equation} \begin{aligned} &{{C}_{2}}\approx \bigl( \vec{H}( x+\Delta x,y )\vec{j}-\vec{H}( x,y )\vec{j} \bigr)\Delta y={}\\ &\quad{}= {{( \Delta {{H}_{y}} )}_{x}}\Delta y\approx \frac{\partial {{H}_{y}}}{\partial x}\Delta x\,\Delta y . \end{aligned} \end{equation}

Відповідно, циркуляція по всьому контуру \(C = C_{1} + C_{2}\) дорівнює

\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}\approx {}\\ &\quad{}\approx\left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\Delta y\,\Delta x={}\\ &\quad{}=\left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\Delta S . \end{aligned} \tag{2.17а} \end{equation}

Порівнюючи цей вираз із (2.17), бачимо, що

\begin{equation} \left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\Delta S\approx {{J}_{z}}\,\Delta S. \end{equation}

Отримана рівність є наближеною, тому що в ній не врахована зміна проекцій поля \(H_{x}\) і \(H_{y}\) при переміщенні вздовж сторін прямокутника в процесі інтегрування, а також не визначене точне положення точки, в якій береться величина \(\vec{J}\). Але в границі \( \Delta S\to 0 \) при стяганні прямокутника в задану точку рівність стає точною:

\begin{equation} \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y}={{J}_{z}}. \end{equation}

Вибравши в околі тієї ж точки ще два контури, паралельні іншим координатним площинам, аналогічно отримаємо:

\begin{equation} \frac{\partial {{H}_{z}}}{\partial y}-\frac{\partial {{H}_{y}}}{\partial z}={{J}_{x}}, \end{equation} \begin{equation} \frac{\partial {{H}_{x}}}{\partial z}-\frac{\partial {{H}_{z}}}{\partial x}={{J}_{y}}. \end{equation}

Вектор \(\vec{J}\) через проекції та орти зображується, як

\begin{equation} \vec{J}={{J}_{x}}\cdot \vec{i}+{{J}_{y}}\cdot \vec{j}+{{J}_{z}}\cdot \vec{k}. \end{equation}

Тож маємо наступний вираз, який визначає вектор густини струму \(\vec{J}\) в будь-якій точці заданого поля \( \vec{H}( x,y,z ) \):

\begin{equation} \begin{aligned} &\vec{J}=\left( \frac{\partial {{H}_{z}}}{\partial y}-\frac{\partial {{H}_{y}}}{\partial z} \right)\vec{i}+{}\\ &\quad{}+\left( \frac{\partial {{H}_{x}}}{\partial z}-\frac{\partial {{H}_{z}}}{\partial x} \right)\vec{j}+{}\\ &\quad{}+ \left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\vec{k}. \end{aligned} \end{equation}

Подібний громіздкий набір операцій доводиться виконувати в багатьох задачах математики і фізики. Тому права частина даного виразу має спеціальне позначення “\(\operatorname{rot}\)” і назву “ротор” поля. Отже,

\begin{equation} \begin{aligned} &\operatorname{rot}\vec{H}=\left( \frac{\partial {{H}_{z}}}{\partial y}-\frac{\partial {{H}_{y}}}{\partial z} \right)\vec{i}+{}\\ &\quad{}+\left( \frac{\partial {{H}_{x}}}{\partial z}-\frac{\partial {{H}_{z}}}{\partial x} \right)\vec{j}+{}\\ &\quad{}+\left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\vec{k}. \end{aligned} \tag{2.18} \end{equation}

Відтак зв’язок між векторами \( \vec{H}\) і \(\vec{J}\) згорнуто записується у вигляді:

\begin{equation} \operatorname{rot}\vec{H}=\vec{J}. \tag{2.19} \end{equation}

За цим рівнянням для визначення розподілу струмів \(\vec{J}( x,y,z )\), які створюють задане магнітне поле, треба лише виконати необхідні диференціювання заданої функції \( \vec{H}( x,y,z ) \). За допомогою рівняння (2.19), у принципі, можна визначити й поле, створене заданим розподілом струмів. Але така математична задача є досить складною і має точні розв’язки тільки в найпростіших випадках.

Зауважимо, що рівняння (2.19) є чинним і в інших системах координат, але формула ротора в кожній з них має свій вигляд. Тому вираз (2.18) є не означенням, а тільки формулою для обчислення ротора в декартових координатах. Аби дати незалежне від координатної системи означення ротора, звернемо увагу на те, що в наведених викладках орти \( ( \vec{i}, \vec{j}, \vec{k} ) \) є й одиничними векторами нормалей \( \vec{n}\) до поверхонь розглянутих контурів. Тож у (2.18) множники при ортах є проекціями вектора \(\operatorname{rot}\vec{H}\) на нормалі до елементарних контурів розміщених у координатних площинах. Враховуючи це, вираз (2.17а) можна переписати, як

\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}\approx {{\operatorname{rot}}_{n}}\vec{H}\cdot \Delta S\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {{\operatorname{rot}}_{n}}\vec{H}\approx \frac{\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}}{\Delta S}. \end{aligned} \end{equation}

Стягаючи контур у задану точку, отримаємо точний вираз:

\begin{equation} {{\operatorname{rot}}_{n}}\vec{H}=\underset{\Delta{S}\to{0}}\lim\limits \frac{\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}}{\Delta S}, \end{equation}

який по суті є означенням поняття “ротор векторного поля”.

Якщо магнітне поле створюється не лише струмами провідності, а й змінним електричним полем, у рівняння (2.19) додасться ще й густина струму зміщення (2.6):

\begin{equation} \operatorname{rot}\vec{H}=\vec{j}+\frac{\partial \vec{D}}{\partial t}. \tag{2.20} \end{equation}

Це рівняння випливає з інтегральної теореми про циркуляцію магнітного поля і є загальним виразом цієї теореми в диференціальній (локальній) формі.

Підставивши вираз (2.20) у рівняння (2.9), отримаємо математичну теорему Стокса

\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\operatorname{rot}\vec{H}\cdot \,\mathrm{d}\vec{S}}, \tag{2.21} \end{equation}

згідно з якою

циркуляція векторного поля по довільному замкненому контуру дорівнює потокові ротора цього поля крізь довільну поверхню обмежену цим контуром.

Теорема Стокса є чинною для будь-якого векторного поля, тож і для електричного:

\begin{equation} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\operatorname{rot}\vec{E}\cdot \mathrm{d}\vec{S}}. \end{equation}

Порівнюючи цей вираз із (12.17а), отримуємо рівняння

\begin{equation} \operatorname{rot}\vec{E}=-\frac{\partial \vec{B}}{\partial t}, \tag{2.22} \end{equation}

яке виражає теорему про циркуляцію електричного поля в диференціальній (локальній) формі.

У випадку, коли електричне поле створюється тільки зарядами і є потенціальним, циркуляція вектора по будь-якому контуру дорівнює нулю (розділ І, п. 5.1). Тому, згідно з формулою Стокса, в усіх точках

\begin{equation} \operatorname{rot}\vec{E}=0 . \tag{2.23} \end{equation}

Цей вираз є диференціальним (локальним) критерієм потенціальності поля. Відповідно до нього потенціальні поля є безвихровими.

Локальний критерій (2.23) є дуже зручним: за ним потенціальність заданого поля \( \vec{E}( x,y,z ) \) однозначно встановлюється за допомогою не складної операції диференціювання.

2.4. Рівняння Максвелла в локальній формі

Розглянуті результати дозволяють описати фундаментальні властивості електромагнітного поля не лише інтегральними рівняннями Максвелла (2.9), а й відповідною системою диференціальних рівнянь, які відображають локальні (в кожній точці) властивості поля. Далі розглядаються:

Диференціальні рівняння Максвелла

Оператор \( \vec{\nabla }\)

Операторна форма рівнянь Максвелла

Диференціальні рівняння Максвелла. З використанням понять “дивергенція” і “ротор” основні рівняння електромагнітного поля мають вигляд:

\begin{equation} \begin{aligned} \operatorname{rot}\vec{E}&=-\frac{\partial \vec{B}}{\partial t};\\ \operatorname{rot}\vec{H}&=\vec{j}+\frac{\partial \vec{D}}{\partial t};\\ \operatorname{div}\vec{D}&=\rho ;\\ \operatorname{div}\vec{B}&=0. \end{aligned} \end{equation}

Відповідно, рівняння електростатики та магнітостатики (коли поля не залежать від часу) в диференціальній формі мають вигляд:

\begin{eqnarray} \operatorname{rot}\vec{E}=0, &\qquad \operatorname{rot}\vec{H}=\vec{j},\\ \operatorname{div}\vec{D}=\rho , &\qquad \operatorname{div}\vec{B}=0. \end{eqnarray}

Оператор \( \vec{\nabla }\). Дивергенція і ротор векторів \( \vec{E}\) і \(\vec{H}\), а також розглянутий раніше (розділ І, п. 3) градієнт потенціалу \( \varphi \), характеризують у кожній точці не саме поле, а його поведінку при переміщенні в прилеглі точки. Тому для визначення цих величин, над заданою функцією (\( \varphi \), \(\vec{E}\), \(\vec{H}\), або ін.) треба виконати відповідний набір математичних дій або “операцій” ((3.4), розділ І), (2.12), або (2.18). Самі по собі вони не є складним, але при необхідності виконання комбінованих операцій, на кшталт \( \operatorname{div}( \operatorname{rot}\vec{B} ) \) чи \( \operatorname{rot}( \operatorname{rot}\vec{E} )\), прямі викладки є трудомісткими. Проте існує дуже ефективний уніфікований непрямий спосіб обчислень за допомогою векторного диференціального оператора набла \( \vec{\nabla }\), інакше — оператора Гамільтона.

На загал, термін “оператор” має різні сенси. Тут це символ, яким позначають дію (“операцію”) чи набір дій, які належить виконати над однією функцією, аби перетворити її на деяку іншу функцію. Оператори дозволяють не лише лаконічно записувати громіздкі математичні вирази, як приміром (2.12) чи (2.18), а й значно скорочують і полегшують математичні перетворення. Це можна проілюструвати на прикладі обчислення градієнта та дивергенції. Для обчислення градієнта потенціалу електричного поля за формулою (розділ І, (3.4)) треба:

— взяти похідні по координатах від заданої функції \( \varphi ( x,y,z ) \);

— помножити їх на орти \( ( \vec{i},\vec{j},\vec{k} ) \);

— додати утворені складові вектори.

Ця стандартна послідовність математичних операції являє собою оператор градієнта і позначається символом \( \operatorname{grad}\). Аналогічно можна деталізувати й сукупність операції, які складають оператор дивергенції і шифруються символом \( \operatorname{div}\). До прикладу, для визначення дивергенції вектора \( \vec{D}\) електричного поля треба за формулою (3.12) виконати наступну послідовність операцій:

— взяти похідні по координатах від відповідних проекцій заданої функції \( \vec{D}( x,y,z ) \);

— додати їх.

Але, як виявляється, необхідні для визначення обох цих величин дії можна виконувати за допомогою одного оператора, який позначається символом \( \vec{\nabla}\). Це можна побачити, якщо у виразах градієнта та дивергенції дещо інакше записати частинні похідні по координатах, увівши “оператори диференціювання” \( {\partial }/{\partial x}\), \({\partial }/{\partial y}\), \({\partial }/{\partial z}\):

\begin{equation} \operatorname{grad}\varphi =\vec{i}\frac{\partial }{\partial x}\varphi +\vec{j}\frac{\partial }{\partial y}\varphi +\vec{k}\frac{\partial }{\partial z}\varphi \end{equation}

і

\begin{equation} \operatorname{div}\vec{D}=\frac{\partial }{\partial x}{{D}_{x}}+\frac{\partial }{\partial y}{{D}_{y}}+\frac{\partial }{\partial z}{{D}_{z}}. \end{equation}

При цьому перша формула виглядає, як вираз деякого вектора \( \vec{G}\), що є добутком вектора \( \vec{A}\) на скаляр \( {B}\):

\begin{equation} \vec{G}=\vec{A}\cdot B=( \vec{i}{{A}_{x}} )B+( \vec{j}{{A}_{y}} )B+( \vec{k}{{A}_{z}} )B. \end{equation}

Відповідно, формула для дивергенції нагадує скалярний добуток \(S\) якихось векторів \( \vec{A}\) і \( \vec{C}\):

\begin{equation} {S}=\vec{A}\cdot \vec{C}={{A}_{x}}{{C}_{x}}+{{A}_{y}}{{C}_{y}}+{{A}_{z}}{{C}_{z}}. \end{equation}

Це дозволяє увести оператор \( \vec{\nabla }\) у вигляді символічного вектора

\begin{equation} \vec{\nabla }=\vec{i}\frac{\partial }{\partial x}+\vec{j}\frac{\partial }{\partial y}+\vec{k}\frac{\partial }{\partial z}, \tag{2.25} \end{equation}

і розглядати градієнт як результат символічного множення (тобто дії) “вектора” \( \vec{\nabla }\) на скалярну функцію координат \( \varphi \):

\begin{equation} \operatorname{grad}\varphi \equiv \vec{\nabla }\varphi . \tag{2.26} \end{equation}

Аналогічно, дивергенцію можна трактувати як скалярний добуток векторів \( \vec{\nabla }\) і \( \vec{D}\):

\begin{equation} \operatorname{div}\vec{D}\equiv \vec{\nabla }\cdot \vec{D}. \tag{2.27} \end{equation}

Можна показати, що й ротор (2.18) можна трактувати як символічний векторний добуток:

\begin{equation} \operatorname{rot}\vec{H}\equiv [ \vec{\nabla }\,\vec{H} ]. \tag{2.28} \end{equation}

У цьому легко переконатись, якщо розкрити вираз (2.28) за допомогою визначника:

\begin{equation} [ \vec{\nabla }\vec{H} ]=\left| \begin{matrix} \vec{i} &\vec{j} &\vec{k} \\ ( {\partial }/{\partial x} ) &( {\partial }/{\partial y} ) & ( {\partial }/{\partial z} ) \\ {{H}_{x}} & {{H}_{y}} & {{H}_{z}} \end{matrix} \right|, \end{equation}

як це робиться у векторній алгебрі.

Таким чином, всі основні диференціальні операції теорії поля можна зображувати і виконувати за допомогою одного диференціального векторного оператора \( \vec{\nabla }\), властивості котрого одночасно задовольняють і основні правила диференціювання, і аксіоми векторної алгебри. Тому використання оператора \( \vec{\nabla}\) є дуже продуктивним, позаяк значно спрощує проведення громіздких диференціальних перетворень скалярних і векторних функцій координат, якими зокрема є характеристики електромагнітного поля.

Операторна форма рівнянь Максвелла. На завершення зведемо в одну систему фундаментальні рівняння електромагнітного поля (рівняння Максвелла), виражені в операторній формі через оператор \( \vec \nabla \):

\begin{equation} \begin{aligned} &[ {\vec \nabla \vec E} ] = - \frac{{\partial \vec B}}{{\partial t}}, \\ &[ {\vec \nabla \vec H} ] = \vec j + \frac{{\partial \vec D}}{{\partial t}}, \\ &\vec \nabla \cdot \vec D = \rho , \\ &\vec \nabla \cdot \vec B = 0. \end{aligned} \tag{2.29} \end{equation}

У такому вигляді вони найбільш зручні для проведення різноманітних викладок. Для ілюстрації наведемо два приклади.

Приклад 1. Рівняння Пуассона. Електричні поля зарядів (кулонівські поля) є потенціальними, тому вектор напруженості \( \vec E \) можна визначати не тільки через заряди, а й через скалярну величину — потенціал \( \varphi \). Тому так само, як у випадку напруженості, важливо знати зв’язок між розподілом заряду та потенціалом поля в кожній точці. З інтегральних рівнянь Максвелла (2.9) цей зв’язок безпосередньо не випливає. Але, враховуючи, що

\begin{equation} \vec E = - \operatorname{grad} \varphi \equiv - \vec \nabla \varphi , \end{equation}

його не складно отримати з диференціальних рівнянь (2.24) чи (2.29), принаймні, для ізотропних однорідних середовищ, в яких

\begin{equation} \vec D = {\varepsilon _0}\varepsilon \vec E. \end{equation}

Справді, зробивши наведені підстановки в треті рівняння (2.24), або (2.29), отримаємо: \( \operatorname{div} \vec D = \rho \),

\begin{equation} \operatorname{div} ( {\operatorname{grad} \varphi } ) = - \frac{\rho }{{{\varepsilon _1}\varepsilon }}, \end{equation}

або

\begin{equation} \vec \nabla ( {\vec \nabla \varphi } ) = - \frac{\rho }{{{\varepsilon _0}\varepsilon }}. \end{equation}

Ліву частину цього рівняння легко перетворити, згадавши, що до оператора \( \vec \nabla \) можна застосовувати правило скалярного множення векторів і записати:

\begin{equation} \vec \nabla ( {\vec \nabla \varphi } ) = \nabla _x^2\varphi + \nabla _y^2\varphi + \nabla _z^2\varphi , \end{equation}

де за правилами операторного множення

\begin{equation} \begin{aligned} \nabla_x^2\varphi&=\frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}\varphi\right)=\frac{\partial ^2}{\partial x^2}\varphi ,\\ \nabla_y^2\varphi&=\frac{\partial^2}{\partial y^2}\varphi ,\\ \nabla_z^2\varphi&=\frac{\partial^2}{\partial z^2}\varphi . \end{aligned} \end{equation}

Отже,

\begin{equation} \frac{\partial^2\varphi}{\partial x^2}+\frac{\partial^2\varphi}{\partial y^2}+\frac{\partial^2\varphi}{\partial z^2}=-\frac{\rho}{\varepsilon_0}\varepsilon . \tag{2.30} \end{equation}

Це рівняння називається рівнянням Пуассона, і відіграє важливу роль в теорії електричного поля.

Рівняння Пуассона можна записати в операторній формі через оператор \( {\nabla ^2} \) (набла квадрат) або, як його ще називають, оператор Лапласа і позначають також символом \( \Delta \) (дельта):

\begin{equation} {\nabla ^2} \equiv \Delta = \frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}}. \end{equation}

Множення (тобто дія) цього оператора на функцію полягає у взятті та додаванні її других частинних похідних по координатах. Відтак рівняння Лапласа в операторній формі згорнуто записується, як

\begin{equation} \nabla^2 \varphi=-\frac{\rho}{\varepsilon_0\varepsilon}, \quad \text{або} \quad \delta \varphi=-\frac{\rho}{\varepsilon_0\varepsilon}. \tag{2.30а} \end{equation}

Приклад 2. Рівняння неперервності. Це рівняння встановлює зв’язок між густиною струму на замкненій поверхні та зарядом носіїв всередині неї і є узагальненим виразом закону збереження електричного заряду. В інтегральній формі воно має вигляд ((1.6), розділ III):

\begin{equation} \oint\limits_S {\vec j\,\mathrm{d} \vec S} = - \int\limits_V {\frac{{\partial \rho }}{{\partial t}}\mathrm{d} V} . \end{equation}

Рівняння неперервності в диференціальній формі визначає указаний зв’язок локально (в кожній точці) і дає детальну інформацію про структуру ліній струму. Таку форму рівняння неперервності можна отримати із наведеного інтегрального рівняння за допомогою формули Остроградського — Гаусса (2.15), відповідно до якої

\begin{equation} \oint\limits_S {\vec j\,\mathrm{d} \vec S} = \int\limits_V {\operatorname{div} \vec j \cdot \mathrm{d} V} . \end{equation}

Отже,

\begin{equation} \int\limits_V {\operatorname{div} \vec j \cdot \mathrm{d} V} = - \int\limits_V {\frac{{\partial \rho }}{{\partial t}}\mathrm{d} V} . \end{equation}

Позаяк вихідні рівняння є чинними для довільної замкненої поверхні \(S\), записана рівність виконується при будь-якому значенні об’єму \(V\), що можливо лише коли в обох інтегралах значення підінтегральних функцій збігаються у кожній точці. Отже,

\begin{equation} \operatorname{div} \vec j = - \frac{{\partial \rho }}{{\partial t}}. \tag{2.31} \end{equation}

Це і є рівняння неперервності в диференціальній формі. З нього випливає, що в тих точках, де \( ({\partial \rho }/{\partial t} ) < 0 \), \( \operatorname{div} \vec j > 0 \), і навпаки. Згідно з (2.13) і домовленістю про напрям електричного струму, це означає, що лінії струму виходять із точок, з яких витікає додатній заряд, і закінчуються в точках, до яких він стікається. Тому в математиці точки, де дивергенція додатня, називаються витоками, а точки з від’ємною дивергенцією — стоками поля.

Рівняння (2.31) можна отримати і безпосередньо з рівнянь Максвелла в диференціальній формі. Для цього достатньо взяти дивергенцію від лівої та правої частини другого рівняння системи (2.24):

\begin{equation} \operatorname{div}\operatorname{rot} \vec H = \operatorname{div} \vec j + \operatorname{div} \frac{{\partial \vec D}}{{\partial t}}. \end{equation}

Безпосереднє розкриття лівої частини потребує громіздких перетворень, але за допомогою оператора \( \vec \nabla \) це робиться досить легко. А саме,

\begin{equation} \operatorname{div}\, \operatorname{rot} \vec H = \vec \nabla [ {\vec \nabla \vec H} ]. \end{equation}

У лівій частині маємо символічний мішаний добуток векторів, який за законами векторної алгебри є інваріантним відносно циклічної перестановки множників. Тож можна записати:

\begin{equation} \vec \nabla [ {\vec \nabla \vec H} ] = [ {\vec \nabla ,\vec \nabla } ]\vec H \equiv 0. \end{equation}

Відтак маємо:

\begin{equation} \operatorname{div} \vec j + \operatorname{div} \frac{{\partial \vec D}}{{\partial t}} = 0. \end{equation}

Послідовність диференціювання по незалежних змінних (час і координати) є довільною, тож, урахувавши третє рівняння (2.9), отримуємо рівняння неперервності (2.31):

\begin{equation} \begin{aligned} &\operatorname{div}\vec j=-\operatorname{div}\frac{\partial\vec D}{\partial t}=-\frac{\partial}{\partial t}(\operatorname{div}\vec D)\quad\Rightarrow{}\\ &\quad{}\Rightarrow \quad\operatorname{div}\vec j=-\frac{\partial\rho}{\partial t}. \end{aligned} \end{equation}

В операторній формі воно має вигляд

\begin{equation} \vec \nabla \cdot \vec j = - \frac{{\partial \rho }}{{\partial t}}. \tag{2.31а} \end{equation}