ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 03:17 |
Оглавление
ВСТУП
Електричний заряд і електромагнітне поле
Фундаментальні взаємодії. Вивчаючи механіку, можна переконатися, що зміни стану системи зумовлюються силами — величинами, які визначають взаємодію частинок між собою та із зовнішніми тілами. При цьому спостерігається багато різних сил: сили тяжіння, пружності, тертя та опору середовища, сили натягу нитки або троса, магнітні та електричні сили, тощо. Але всі ці сили є проявом всього чотирьох фундаментальних[1] взаємодій — гравітаційної, електромагнітної, слабкої та сильної[2].
Властивості фундаментальних взаємодій суттєво відрізняються. Зокрема, гравітаційні та електромагнітні сили теоретично існують при будь-якій відстані між взаємодіючими частинками і є далекодіючими. Натомість сильна та слабка взаємодії є короткодіючими вони існують тільки на відстанях порядку розмірів атомного ядра і менше. Тому всі процеси в навколишньому світі, крім процесів в атомних ядрах та надрах зірок, зумовлені тільки гравітаційною та електромагнітною взаємодіями. При цьому гравітаційна взаємодія є гранично слабкою,[3] вона помітна лише при дуже великій (астрономічній) масі хоча б одного із взаємодіючих тіл. Тому, за винятком тяжіння всі процеси, які ми спостерігаємо навколо себе, мають електромагнітну природу.
Електричний заряд. Гравітаційна взаємодія є властивою для всіх без винятку частинок матерії. Але до електромагнітної взаємодії є здатними лише деякі з них. Так, протони й електрони беруть участь в електромагнітній взаємодії, а нейтрони і фотони — ні. До електромагнітної взаємодії здатними є тільки частинки з певною внутрішньою властивістю, що називається електричним зарядом. При цьому, будучи внутрішньою властивістю частинки, заряд є невіддільним від неї і не може бути повністю чи частково переданий іншій частинці, як, скажімо, імпульс або енергія. Тому словом “заряд” задля зручності позначають і саму таку частинку. До прикладу, говорять не “рух частинок, які мають заряд”, а “рух зарядів”.
Природа електричного заряду ще остаточно не встановлена, але його властивості вивчені достатньо повно. Нагадаємо їх.
1. Заряд усіх заряджених елементарних частинок, які можуть існувати у вільному стані, має однакову величину \(e = 1,6\cdot10^{-19}\ \text{Кл}\), яка називається елементарним зарядом. Отже, в природі існує найменша порція або квант електричного заряду, тобто він є дискретною величиною на відміну, скажімо, від маси, яка може бути якою завгодно.
2. У природі існує два типи електричного заряду, названі позитивним “+” та негативним “–”. Із добре знайомих частинок носієм негативного заряду –е є електрон, а позитивного +е — протон. Наявність двох типів заряду випливає з того факту, що між зарядженими частинками спостерігаються як сили притягання, так і сили відштовхування.
3. Заряд є величиною, що зберігається: в природі діє закон збереження електричного заряду, який гласить:
алгебраїчна сума зарядів усіх частинок електрично ізольованої системи[4] зберігається, тобто не змінюється ні при яких процесах у ній.
Цей закон може здатися тривіальним наслідком збереження кількості частинок в ізольованій системі. Але елементарні частинки здатні до взаємних перетворень: одні частинки можуть зникати і натомість з’являтися інші, у тому числі й заряджені. Тож кількість частинок в замкненій системі може змінюватись, але її електричний заряд лишається незмінним. А це означає, що електрично заряджені частинки можуть зникати й народжуватися не поодинці, а тільки парами протилежно заряджених частинок. Як приклад можна навести народження електрон-позитронної пари (\(e^-\), \(e^+\)) при розпаді електрично нейтральної елементарної частинки — \(\gamma\)-кванта, що є носієм електромагнітного випромінювання. Тому закон збереження електричного заряду є одним з важливих законів, які “керують” процесами в мікросвіті.
4. Електричний заряд є інваріантною величиною, тобто не змінюється при переході від однієї системи відліку до іншої. Це природньо, адже заряд є не характеристикою стану, а внутрішньою властивістю частинки.
Електромагнітне поле. За сучасними уявленнями будь-яка силова взаємодія між частинками здійснюється не безпосередньо, а за допомогою відповідного поля. Зокрема, електромагнітна взаємодія між зарядженими частинками забезпечується електромагнітним полем за схемою “заряд — поле — заряд”: кожна заряджена частинка чи тіло створює у просторі електромагнітне поле, в якому на будь-яку іншу заряджену частинку чи тіло діє відповідна сила. Тому можна вказати на ще одну, первісну, властивість електричного заряду:
електричний заряд є джерелом електромагнітного поля.
На загал властивості електромагнітного поля крім величини зарядів, які його створюють, визначаються просторовим розташуванням і станом руху зарядів. Але в окремому випадку один із указаних факторів може виявитися не істотним. Приміром, якщо поле створюється нерухомими зарядженими тілами, то на його властивості в навколишньому просторі не впливають мікроскопічні теплові рухи зарядів всередині тіла. У такому разі говорять, що в просторі створюється електричне поле, і на вміщені в нього заряди діють електричні сили. А ось будь-яка ділянка провідника із постійним струмом є електрично нейтральною. Тому характеристики поля поза провідником визначаються тільки рухом його зарядів. У такому випадку говорять про магнітне поле та магнітні сили. Отож можна говорити, що електромагнітне поле складається з електричного та магнітного полів. Але електричне і магнітне поля не є двома різними фізичними полями — це два різні прояви єдиного електромагнітного поля. В цьому можна переконатися на такому простому прикладі. Досліджуючи поле, створене нерухомою зарядженою кулькою, ми побачимо, що воно є чисто електричним. Але якщо спостерігати поле тієї ж кульки з візка, що проїжджає повз неї, то буде виявлено як електричне, так і магнітне поле. Це показує, що поділ поля на електричне та магнітне є відносним і залежить від системи відліку, в якій воно розглядається. При цьому у випадку змінних полів електричне та магнітне поля не можуть існувати окремо одне від одного. Ці та інші факти переконують, що у природі існує єдине електромагнітне поле, котре поряд з речовиною є окремим видом матерії, а не просто зручним способом розгляду взаємодії між зарядами.
Навчальний матеріал, який розглядається в даному розділі курсу, розподілено по таких темах:
II. ЕЛЕКТРИЧНЕ ПОЛЕ В РЕЧОВИНІ
[1] Фундаментальною називається взаємодія, що не зводиться ні до якої іншої.
[2] Слід зауважити, що за сучасними уявленнями електромагнітна та слабка взаємодії є проявами єдиної електрослабкої взаємодії. Але за конкретними властивостями ці взаємодії настільки різні, що їх розглядають окремо.
[3] Для прикладу, сила гравітаційного притягання між двома протонами приблизно в \(10^{36}\) разів менша за силу їхнього електричного відштовхування.
[4] Мається на увазі система, в яку не можуть заходити та виходити з неї заряджені частинки.
І. ЕЛЕКТРИЧНЕ ПОЛЕ У ВАКУУМІ
Як говорилося вище, переважна більшість явищ, які ми спостерігаємо, має електромагнітну природу і визначається властивостями електричного та магнітного полів.
Далі розглядаються характеристики електричного поля у вакуумі. При цьому реально йдеться і про повітря, позаяк гази при невеликому тиску мають відносно невелику концентрацію молекул і практично не впливають на характеристики поля. Розглянуто наступні питання:
1. Напруженість електричного поля
1. Напруженість електричного поля
Електромагнітне поле ніяк не впливає на органи чуття людини, тому його властивості можна встановити лише опосередковано через властивості сил, які воно створює. При цьому електричні сили і поле досліджують за допомогою “пробних зарядів” — заряджених частинок з малими розмірами та величиною електричного заряду. Через малі розміри такі частинки відображають властивості електричного поля локально (в точці), а завдяки малій величині заряду не спотворюють його. Цей параграф присвячено основній величині, що характеризує електричне поле — напруженості. Розглянуто такі питання:
1.1. Вектор \(\vec{E}\)
Експериментальні дослідження сил, які діють на пробні заряди в електричному полі, свідчать про таке:
1. У даній точці поля вектор сили \( \vec{F} \), що діє на пробний заряд \(q\), завжди напрямлений вздовж однієї й тієї ж прямій в той чи інший бік, залежно від знаку заряду. Це означає, що електричне поле в кожній точці має визначений напрям.
2. Величина сили, з якою поле діє на пробний заряд, є прямо пропорційною до величини цього заряду:
\begin{equation} {F}\sim|q| . \end{equation}
Це означає, що відношення
\begin{equation} {E}=\frac{F}{|q|} \end{equation}
не залежить від заряду і є мірою “потужності” самого поля. Воно називається напруженістю електричного поля і, аби відображало ще й напрям поля, розглядається як вектор:
\begin{equation} \vec{E}=\frac{\vec{F}}{q} . \tag{1.1} \end{equation}
Сказане ілюструє рис. 1.1.
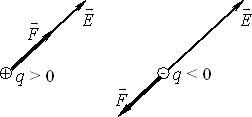
Рис. 1.1
Таким чином, вектор напруженості \( \vec{E} \) є силовою характеристикою (силовим вектором) електричного поля. За модулем і напрямом він збігається із силою, що діє на одиничний позитивний заряд вміщений в дану точку поля.
За одиницю напруженості природньо було би прийняти \(1\ \text{Н/Кл}\), тобто напруженість такого електричного поля, в якому на одиничний заряд діє одинична сила. Але в міжнародній системі одиниць (СІ) одиниця напруженості уводиться інакше і називається “один вольт-на-метр” (\(1\ \text{В/м}\)). Про це буде сказано далі (п. 2.4), а тут лише зауважимо, що \(1\ \text{В/м}\) = \(1\ \text{Н/Кл}\), тобто при Е = \(1\ \text{В/м}\) на заряд \(1\ \text{Кл}\) діє сила \(1\ \text{Н}\).
З означення (1.1) випливає загальна формула сили, що діє в електричному полі на точковий заряд:
\begin{equation} \vec{F}=q\vec{E} . \tag{1.2} \end{equation}
Із цієї формули, зокрема, випливає, що сила, яка діє в полі на позитивний заряд, за напрямком є збіжною, а на негативний — антипаралельною з напрямом поля, як показано на рис. 1.1.
Формула (1.2) є однією з основних у теорії електричного поля, оскільки дозволяє обчислювати силу і відтак визначати рух заряджених частинок в електричних полях. Але для цього треба вміти знаходити напруженість поля незалежно від означення (1.1), тобто без вимірювання сил. Тому встановлення способів визначення напруженості є однією з основних задач теорії електричного поля.
1.2. Напруженість поля точкового заряду
Можливість теоретичного розрахунку напруженості різних електричних полів ґрунтується на двох основних законах, які встановлені на досліді — законі Кулона та принципі суперпозиції.
Закон Кулона. Цей закон був установлений ще до виникнення концепції поля і визначає електричну взаємодію точкових зарядів. Він твердить, що
сили взаємодії між двома точковими зарядами є прямо пропорційні величинам цих зарядів і обернено пропорційні квадратові відстані між ними.
Ці сили задовольняють третій закон Ньютона: вони рівні по модулю і діють у протилежних напрямах уздовж прямої, що проходить через заряди, рис. 1.2.
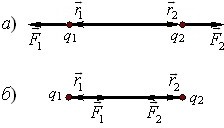
У векторній формі ці сили виражаються, як
\begin{equation} \vec{F}_1=k\frac{q_1 q_2}{r^2}\vec{e}_{12} ,\quad \vec{F}_2=k\frac{q_1 q_2}{r^2}\vec{e}_{21} , \tag{1.3} \end{equation}
або
\begin{equation} \vec{F}_1=k\frac{q_1 q_2}{r^3}\vec{r}_{1} , \quad \vec{F}_2=k\frac{q_1 q_2}{r^3} \vec{r}_{2} , \tag{1.3а} \end{equation}
де \( \vec{e}_{12}=(\vec{r}_1/{r_1})\) і \( \vec{e}_{21}=(\vec{r}_2 / r_2) \) — одиничні вектори, а \( \vec{r}_{1} \) та \( \vec{r}_{2} \) — радіуси-вектори точки розташування заряду, на який діє сила з боку поля, що створюється в цій точці іншим зарядом; \({r}=|\vec{r}_1|=|\vec{r}_{2}| \) — відстань між зарядами; k — коефіцієнт пропорційності.
Позаяк \(\vec{r}_1 = -\vec{r}_{2} \), напрямки цих сил протилежні, а модулі однакові і дорівнюють
\begin{equation} {F}=k\frac{|q_1|\cdot |q_2|}{r^2} . \tag{1.3б} \end{equation}
Отже, сили кулонівської взаємодії між зарядами задовольняють третій закон Ньютона. Векторні вирази (1.3а) відображають також і характер взаємодії зарядів. Справді, якщо заряди однойменні, то \(q_{1}\cdot q_{2} > 0\), і вектори \(\vec{F}_{1}\) і \(\vec{F}_{2}\) мають напрямки радіусів-векторів \(\vec{r}_{1}\) і \(\vec{r}_{2}\), що відображає відштовхування однойменних зарядів (рис. 1.2а). Для різнойменних зарядів \(q_{1}\cdot q_{2} < 0\), що відповідає притяганню між ними (рис. 1.2б).
Розмірний коефіцієнт \(k\) визначається силою взаємодії між двома одиничними зарядами у вакуумі при одиничній відстані між ними. Його числове значення залежить від системи одиниць і в СІ складає \(k = 9\cdot 10^9\ \text{м/Ф}\) (\(\text{Ф}\) — одиниця електричної ємності “фарад”). Зауважимо, що розмірність \([\text{м/Ф}]\) є рівносильною розмірності \([\text{Н}\cdot \text{м/Кл}^2]\), яка випливає з формули (1.3а). Число \(k\) є зручним для обчислень, але в літературі формули прийнято записувати через електричну сталу \(\varepsilon_{0} \), що визначається як
\begin{equation} \varepsilon_{0}=\frac{1}{4\pi{k}}=8{,}85\cdot{10^{-12}}\ \frac{\text{Ф}}{\text{м}}. \end{equation}
Тому розгорнуто вирази (1.3а), (1.3б) записуються, як
\begin{equation} \begin{aligned} \vec{F}_{1}&=\frac{q_1 q_2\mathstrut}{4\pi\varepsilon_{0}r^3\mathstrut}\vec{r}_{1}, \\ \vec{F}_{2}&=\frac{q_2 q_1\mathstrut}{4\pi\varepsilon_{0}r^{3}\mathstrut}\vec{r}_{2}, \\ {F}&=\frac{|q_1|\cdot{|q_2|}\mathstrut}{4\pi\varepsilon_{0}r^2\mathstrut}. \end{aligned} \tag{1.3в} \end{equation}
Напруженість поля точкового заряду. Сили (1.3в) зумовлені дією на кожен із двох зарядів з боку електричного поля, створеного іншим. Тому відповідно до означення (1.1), поділивши вектор сили, що діє на будь-який із зарядів на його величину, отримаємо загальний вираз вектора напруженості поля точкового заряду:
\begin{equation} \vec{E}=\frac{q}{4\pi\varepsilon_{0}r^{3}}\vec{r}, \tag{1.4} \end{equation}
де \(q\) — алгебраїчна величина заряду, що створює поле, \(\vec{r}\) — радіус-вектор точки, в якій визначається його напруженість (рис. 1.3).
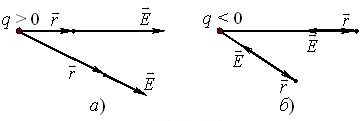
Як видно з формули (1.4) і рис. 1.3, поле точкового заряду є центральним — воно скрізь напрямлене радіально від заряду, якщо \(q > 0\), і до заряду при \(q < 0\), та має модуль
\begin{equation} {E}=\frac{|q|}{4\pi\varepsilon_{0}r^2}, \quad \text{або} \quad {E}=\frac{k|q|}{r^2}. \tag{1.4а} \end{equation}
Зауважимо також, що формули (1.4) і (1.4а) по суті виражають закон Кулона в польовій формі.
1.3. Принцип суперпозиції
Поле системи зарядів. Принцип суперпозиції. Уявімо, що вимірюють напруженість поля системи з двох зарядів у досліді, який складається з наступному трьох частин.
1. Спочатку у вільному просторі в якусь точку 1 вміщують заряд \(q_{1}\) і за допомогою пробного заряду \(q\) та формули (1.1) визначають напруженість поля \(\vec{E}_{1}\) у вибраній точці P (рис. 1.4а).
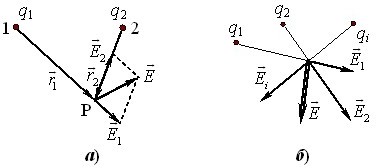
2. Заряд \(q_{1}\) прибирають, а в точку 2 вносять заряд \(q_{2}\) і аналогічно визначають у точці P напруженість \(\vec{E}_{2}\).
3. Не прибираючи заряду \(q_{2}\), в точку 1 повертають заряд \(q_{1}\) і визначають напруженість поля \(\vec{E}\) в точці P, коли присутні обидва заряди.
Цей дослід, проведений реально, дає
\begin{equation} \vec{E}=\vec{E}_{1}+\vec{E}_{2}. \end{equation}
А це означає, що характеристики поля одного заряду не змінюються в присутності іншого. Такий самий результат виходить і при довільній кількості зарядів. Отже, можна зробити висновок, що
електричні поля діють на заряди, але не діють одне на одного.
Указану незалежність полів відображає принцип суперпозиції, який гласить:
вектор напруженості електричного поля, створеного заданою системою зарядів, в будь-якій точці дорівнює сумі векторів напруженості полів, які створюються в цій точці кожним із зарядів системи окремо (тобто за відсутності інших).
Математично принцип суперпозиції виражається загальною формулою
\begin{equation} \begin{aligned} &\vec{E}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}+\cdots +{{\vec{E}}_{i}}+\cdots ={}\\ &\quad{}=\sum{{{\vec{E}}}_{i}}\quad \Rightarrow \quad \vec{E}=\sum{{{{\vec{E}}}_{i}}}. \end{aligned} \tag{1.5} \end{equation}
Згідно з формулою (1.4), для поля системи точкових зарядів \(q_i\) (рис. 1.4б) можна записати:
\begin{equation} \vec{E}=\frac{1}{4\pi {{\varepsilon }_{0}}}\sum{\frac{{{q}_{i}}}{r_{i}^{3}}}{{\vec{r}}_{i}}. \tag{1.6} \end{equation}
Щодо наведеного формулювання принципу суперпозиції слід зауважити таке. Весь ряд доданків у сумі (1.5) можна згрупувати в декілька окремих блоків (наприклад, у два) і спочатку аналогічно обчислити напруженості \(\vec{E}_{\textrm{I}}\) і \(\vec{E}_{\textrm{II}}\) поля кожного блока. Тоді напруженість поля всієї системи виразиться, як
\begin{equation} \vec{E}=\vec{E}_{\textrm{I}}+\vec{E}_{\textrm{II}}. \end{equation}
Це означає, що
напруженість електричного поля довільної системи зарядів дорівнює сумі напруженостей полів будь-яких (не обов’язково точкових) частин цієї системи.
Тому при обчисленні поля за принципом суперпозиції систему можна поділяти на окремі області так, як це найбільш зручно.
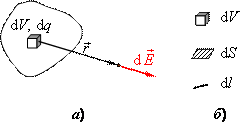
Поле неперервного розподілу заряду. За принципом суперпозиції можна розрахувати і поля, створені неточковими тілами, в яких заряд розподілений неперервно. Для цього тіло слід подумки розділити на елементарні області, кожна з яких містить гранично малий заряд \(\mathrm{d}q\) і створює в заданій точці гранично слабке поле \( \mathrm{d}\vec{E}\) (рис. 1.5а).
Тоді поле, створюване всім тілом,
\begin{equation} \vec{E}=\int\limits{\mathrm{d}\vec{E}}. \end{equation}
Якщо елементарні області точкові, то поля \(\mathrm{d}\vec{E}\) визначаються кулонівською формулою (1.4):
\begin{equation} \mathrm{d}\vec{E}=\frac{k\,\mathrm{d}q}{r^3}\vec{r}. \end{equation}
У такому разі
\begin{equation} \vec{E}=\int\limits\frac{k\,\mathrm{d}q}{r^3}\vec{r}=\frac{1}{4\pi\varepsilon_0}\int\limits\frac{\mathrm{d}q}{r^3}\vec{r}. \tag{1.7} \end{equation}
Ця інтегральна формула, яка є узагальненим виразом принципу суперпозиції, дає алгоритм розрахунку електричного поля створеного будь-яким заданим розподілом електричного заряду.
На практиці окремо розрізняють об’ємний, поверхневий і лінійний розподіли заряду і розділяють область його локалізації на елементарні об’ємчики \(\mathrm{d}V\), площинки \(\mathrm{d}S\), або відрізки \(\mathrm{d}l\) (рис. 1.5б).
Об’ємний розподіл. При розподілі заряду по об’єму тіла величина \(\mathrm{d}q\) у виразі (1.7) у кожній ділянці об’єму \(\mathrm{d}V\) визначається, як \(\mathrm{d}q={\rho}(\vec{r})\mathrm{d}{V}\), через об’ємну густину заряду
\begin{equation} \rho{(\vec{r})}=\frac{\mathrm{d}q}{\mathrm{d}V}\Biggl(\frac{\text{Кл}}{\text{м}^{3}}\Biggr). \end{equation}
У такому разі
\begin{equation} \begin{aligned} &\vec{E}=k\int\limits_{V}\frac{\rho(\vec{r})\vec{r}}{r^3}\mathrm{d}{V}={}\\ &\quad{}=\frac{1}{4\pi\varepsilon_{0}}\int\limits_{V}\frac{\rho(\vec{r}) \vec{r}}{r^3}\mathrm{d}{V}, \end{aligned} \tag{1.8} \end{equation}
де інтегрування проводиться по всьому об’єму зарядженого тіла.
Поверхневий розподіл. Аналогічно, якщо поле створюється зарядженою поверхнею, то заряд її довільної елементарної ділянки \(\mathrm{d}S\) \(\mathrm{d}q=\sigma(\vec{r})\mathrm{d}{S}\), де
\begin{equation} \sigma =\frac{ \d q}{\d s} \ \Biggl(\frac{\text{Кл}}{\text{м}^2}\Biggr) \end{equation}
— поверхнева густина заряду в заданій точці. Тоді
\begin{equation} \begin{aligned} &\vec{E}=k\int\limits_{S}\frac{\sigma\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{S}={}\\ &\quad{}=\frac{q}{4\pi\varepsilon_{0}}\int\limits_{S}\frac{\sigma\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{S}, \end{aligned} \tag{1.8а} \end{equation}
де інтегрування ведеться по всій зарядженій поверхні.
Лінійний розподіл. Нарешті, коли заряд розподілений по заданій лінії («нитці»), то \(\mathrm{d}q=\lambda(\vec{r})\mathrm{d}{l}\), де
\begin{equation} \lambda{(\vec{r})}=\frac{\mathrm{d}q}{\mathrm{d}l}\ \left(\frac{\text{Кл}}{\text{м}}\right) \end{equation}
— лінійна густина заряду. В цьому випадку напруженість визначається через криволінійний інтеграл
\begin{equation} \begin{aligned} &\vec{E}=k\int\limits_{l}\frac{\lambda\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{l}={}\\ &\quad{}=\frac{1}{4\pi\varepsilon_{0}}\int\limits_{l}\frac{\lambda\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{l}. \end{aligned} \tag{1.8б} \end{equation}
Інтегральні вирази (1.8)—(1.8б) випливають із загальної формули (1.7), в основі якої лежить закон Кулона. Тому електричні поля, створювані не лише точковими, а й неперервно розподіленими зарядами, називаються кулонівськими полями.
Принагідно зазначимо, що з усіх наведених формул найбільш загальною є формула (1.8) для об’ємного розподілу заряду, бо поверхневий і лінійний розподіли є просто виродженими випадками об’ємного. Дійсно, заряджена поверхня є не поверхнею в математичному сенсі, а тонкою пластиною із якоюсь товщиною \(h = \mathrm{const}\), тож \(\mathrm{d}q=\rho h\,\mathrm{d}S\). Тому розподіл заряду замість об’ємної густини \(\rho\) зручніше задавати поверхневою густиною \(\sigma=\rho h\) (\(\text{Кл/м}^2\)), яка визначає заряд одиниці поверхні пластинки. Так само нитка являє собою прямий чи викривлений тонкий стержень сталого перерізу \(S\), об’єм елементарної ділянки котрого \(\mathrm{d}V = S\,\mathrm{d}l\). Тоді \(\mathrm{d}q=\rho S\,\mathrm{d}l\), або \(\mathrm{d}q = \lambda\,\mathrm{d}l\), де \(\lambda=\rho S\) — лінійна густина заряду (Кл/м). Нарешті, формула (1.8) вбирає і дискретний розподіл, тобто систему заряджених “кульок” малого об’єму \(\Delta V_i\). У такому разі при інтегруванні у виразі (1.8) в місцях локалізації заряду матимемо \(\rho_i\,\Delta V_i=q_i\), а скрізь у решті об’єму \(\rho\,\mathrm{d}V = 0\). Відтак інтеграл (1.8) вироджується в дискретну суму (1.6).
Що до практичних розрахунків, то способи обчислення наведених інтегралів розглядаються у вищій математиці. Проте в простих випадках достатньо розуміти фізичний зміст виразів (1.8), (1.8а) і (1.8б). У складних випадках, коли задача взагалі не має аналітичних (формульних) розв’язків, використовують комп’ютерні розрахунки. Але принципово використання закону Кулона та принципу суперпозиції є універсальним алгоритмом, який дозволяє розрахувати будь-яке кулонівське електричне поле.
1.4. Лінії напруженості
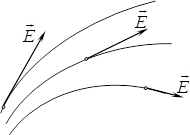
Поля безпосередньо не впливають на наші органи чуття. Тому, задля отримання наочного уявлення про поле, його в той чи інший спосіб зображують на папері чи екрані монітора. Одним із способів візуалізації поля є лінії напруженості (лінії поля, силові лінії, лінії вектора \(\vec{E}\)), тобто
лінії, в кожній точці яких дотична збігається з вектором напруженості в цій точці (рис. 1.6).
Лінії поля відображають конфігурацію поля, тобто його напрям в різних точках, як це ілюструє рис. 1.7 для полів поодиноких зарядів і пари неподалік один від одного розташованих різнойменних зарядів.
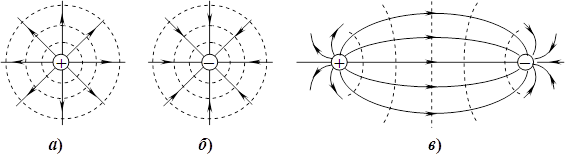
Конфігурація полів інших систем зарядів є складнішою, але їхні силові лінії мають певні спільні властивості. А саме.
Лінії напруженості кулонівського електричного поля є незамкненими; вони виходять із позитивних і сходяться на негативних зарядах.
Також, позаяк в одній точці поле не може мати два різні напрями,
лінії поля не можуть перетинатися.
Окрім того, силові лінії відображають і величину напруженості поля в різних місцях. Як видно з наведених на рис. 1.7 прикладів, поблизу зарядів, де поле є більш сильним, силові лінії розташовані щільніше, ніж на віддаленні. Отже, між лініями поля та величиною напруженості є певний зв’язок. Його легко встановити для поля точкового заряду, яке в усіх рівновіддалених на відстань \(r\) точках має однакову напруженість
\begin{equation} {E}=\frac{q}{4\pi\varepsilon_0{r^2}} \end{equation}
і радіальні силові лінії (рис. 1.7а, б). Тож, якщо для зображення цього поля використати N ліній, то крізь поверхню концентричної сфери з радіусом \(r\) вони будуть проходити з однаковою щільністю
\begin{equation} {n}=\frac{N}{S}=\frac{N}{4\pi{r^2}}. \end{equation}
Якщо в цьому виразі на основі формули (1.4а) зробити заміну
\begin{equation} {4\pi{r^2}}=\frac{q}{\varepsilon_0{E}}, \end{equation}
то отримаємо:
\begin{equation} {E=\frac{q}{\varepsilon_0{N}}n} \quad \Rightarrow \quad {E\sim{n}}. \end{equation}
Тобто на будь-якій відстані від точкового заряду напруженість його поля є прямо пропорційною щільності силових ліній на цій відстані. Такий зв’язок зберігається й для більш складних полів. При цьому щільність ліній \(n\) в кожній точці визначається як
\begin{equation} {n}=\frac{\mathrm{d}N}{\mathrm{d}S_{\bot}}, \end{equation}
де \(\mathrm{d}N\) — кількість ліній поля, що перетинають площадку \(\mathrm{d}S_{\bot}\), перпендикулярну до напрямку поля.
Через будь-яку точку поля можна провести відповідну силову лінію, тож при зображенні поля кількість силових ліній можна вибирати на свій розсуд. Тому домовились уважати, що
в кожній точці щільність ліній поля дорівнює числовому значенню його напруженості:
\begin{equation} E = n. \tag{1.9} \end{equation}
Відтак можна вважати, що кількість силових ліній \(\mathrm{d}N\), які перетинають перпендикулярну до поля елементарну площадку \({\mathrm{d}S_{\bot}}\), дорівнює
\begin{equation} \mathrm{d}N=E\,\mathrm{d}{S}_{\bot}. \tag{1.10} \end{equation}
Така домовленість у деяких ситуаціях виявляється вельми зручною.
Контрольні запитання
1. Що таке фундаментальні взаємодії? Перелічіть їх.
2. Що є схожого і що відмінного між електромагнітною та гравітаційною взаємодією?
3. Що таке електричний заряд і які його основні властивості?
4. Опишіть польовий механізм взаємодій. Чим визначаються загальні властивості електромагнітного поля та його складових — електричного і магнітного полів?
5. Перелічіть загальні властивості електричних сил.
6. Що називається напруженістю електричного поля?
7. Сформулюйте та запишіть у векторній формі закон Кулона. Чи виконується він для довільних заряджених тіл?
8. Якою формулою визначається та як напрямлений вектор напруженості електричного поля точкового заряду?
9. Як записується та який фізичний зміст має принцип суперпозиції електричних полів?
10. Запишіть і поясніть загальний зміст виразів напруженості електричного поля, що створюється зарядженими не точковими тілами при різних типах розподілу заряду.
11. Чи може модуль напруженості поля системи з двох точкових зарядів дорівнювати: 1) сумі модулів і 2) модулю різниці модулів напруженості поля кожного із зарядів? Якщо так, то коли? Окремо розглянути випадки, коли заряди: а) однойменні і б) різнойменні
12. Запишіть вираз напруженості електричного поля посередині між двома однаковими точковими зарядами \(q\) розміщеними не відстані \({l}\) один від одного, коли заряди: а) різнойменні і б) однойменні.
13. Чому дорівнює напруженість електричного поля в центрі правильного трикутника, якщо в його вершинах розміщені однойменні заряди однакової величини.
14. Електричне поле створюється системою з чотирьох однакових зарядів \(q\) розміщених у вершинах квадрата зі стороною \(a\). Чому дорівнює напруженість цього поля на відстані \(r \gg a\) від центра квадрата?
15. Чи можна говорити, що силові лінії збігаються з траєкторіями руху заряджених частинок в електричному полі? Чому?
16. Як за картиною силових ліній електричного поля встановити, де воно сильніше?
17. Чи можуть перетинатися або дотикатися силові лінії електричного поля? Чому?
2. Потенціал
У вступі говорилося, що в природі існує єдине електромагнітне поле, яке “складається” з електричного та магнітного полів. Але ці поля не є двома окремими полями і за відповідних умов можуть породжувати (індукувати) одне одного. Через це в природі є два види електричних полів: “кулонівські”, що безпосередньо створюються зарядженими частинками, і так звані “вихрові”, які породжуються магнітними полями. Силова дія обох полів, зокрема, їхня робота при переміщенні зарядів визначається вектором напруженості. Але кулонівське поле до того ж є потенціальним, тобто його робота не залежить від траєкторії руху зарядженої частинки та пройденого нею шляху. Тому кулонівське поле, крім напруженості, характеризується ще й скалярною величиною — потенціалом.
Далі розглядаються такі питання:
2.1. Потенціальність електричного поля зарядів
2.2. Різниця потенціалів і потенціал
2.1. Потенціальність електричного поля зарядів
У потенціальності електричного поля зарядів можна переконатися прямими розрахунками. Розглянемо спочатку роботу поля точкового заряду \(q\) при переміщенні іншого точкового заряду \(q'\) вздовж довільної траєкторії між заданими точками 1 і 2 (рис. 2.1).
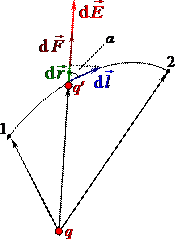
На гранично малому переміщенні \(\mathrm{d}\vec{l}\) поле виконує елементарну роботу \(\delta{A}=\vec{F}\,\mathrm{d}\vec{l}=q'\vec{E}\,\mathrm{d}\vec{l}\). Робота на всьому шляху складається з усіх елементарних робіт \(\delta{A}\) і визначається криволінійним інтегралом по траєкторії:
\begin{equation} {A}=\int\limits_{1\to{2}}E\,|\mathrm{d}\vec{l}|\cos\alpha . \tag{2.1} \end{equation}
З рис. 2.1 видно, що величина \(|\mathrm{d}\vec{l}|\cos\alpha=\mathrm{d}{r}\) є приростом відстані \(r\) при переміщенні \(\mathrm{d}\vec{l}\). Тому, врахувавши формулу (1.4а), отримаємо:
\begin{equation} \begin{aligned} &{A}=\frac{q{'}q}{4\pi\varepsilon_0}\int\limits_{r_1}^{r_2}{\frac{\mathrm{d}r}{r^2}} \quad \Rightarrow\quad {A}={}\\ &\quad= q{'}\left(\frac{q}{4\pi\varepsilon_0{r_1}}-\frac{q}{4\pi\varepsilon_0{r_2}}\right) . \end{aligned} \tag{2.2} \end{equation}
Очевидно, знайдена робота залежить тільки від відстаней \(r_1\) і \(r_2\) від заряду \(q'\) до \(q\), а не від форми траєкторії та пройденого ним шляху. Це вірно і для поля створеного довільною системою зарядів \(q_i\). Дійсно, напруженість поля системи \(\vec{E}=\sum\limits_{i}{\vec{E}_i}\), тому
\begin{equation} \begin{aligned} &{A}=\int\limits_{1\to{2}}q{'}\left(\sum\limits_{i}\vec{E}_i\right)\mathrm{d}\vec{l}={}\\ &\quad{}=\sum\limits_{i}\Biggl(\,\int\limits_{1\to{2}}q{'}\vec{E}_i\,\mathrm{d}\vec{l}\Biggr)= \sum\limits_{i}{A_i}, \end{aligned} \end{equation}
де роботи \(A_i\) складових полів \(\vec{E}_{i}\) визначаються виразом (2.2). Тож
\begin{equation} {A}=q{'}\left(\sum\limits_{i}\frac{q_i}{4\pi\varepsilon_0{r_{i1}}}-\sum\limits_{i}\frac{q_i}{4\pi\varepsilon_0{r_{i2}}}\right) , \tag{2.2а} \end{equation}
де \(r_{i1}\) і \(r_{i2}\) — відстані від початкової та кінцевої точок переміщення заряду \(q_i\) до \(i\)-го заряду системи.
Таким чином, при переміщенні заряду в будь-якому кулонівському полі робота поля не залежить від траєкторії. Отже,
електричне поле, створене зарядженими частинками (кулонівське поле), є потенціальним полем.
Слід зауважити, що це не так для електричних полів, які породжується не зарядами, а змінним магнітним полем.
2.2. Різниця потенціалів і потенціал
Означення. У виразах (2.2) і (2.2a) величина в дужках не залежить від заряду \(q'\) і визначається тільки величиною поля у початковій та кінцевій точках переміщення. Тому вираз роботи поля при переміщенні заряду \(q\) між заданими двома точками по будь-якому шляху можна подати, як
\begin{equation} {A}=q(\varphi_1-\varphi_2)=-q\,\Delta{\varphi} , \tag{2.3} \end{equation}
а при нескінченно малому переміщенні — як
\begin{equation} \delta{A}=-q\,\mathrm{d}{\varphi}. \tag{2.3а} \end{equation}
Величина
\begin{equation} {U}=\varphi_1-\varphi_2 \tag{2.4} \end{equation}
є однією з характеристик електричного поля і називається різницею потенціалів або напругою. Отже:
різницею потенціалів (напругою) між заданими двома точками називається величина, що чисельно дорівнює роботі поля при перенесенні між цими точками одиничного позитивного заряду.
Відтак формулу (2.3) можна записати і як
\begin{equation} {A=qU}. \tag{2.5} \end{equation}
Напруга вимірюється у вольтах (В), причому різниця потенціалів (напруга) двома між точками дорівнює \(1\ \text{В} = 1\ \text{Дж/Кл}\), якщо при перенесенні між ними заряду \(1\) Кл поле виконує роботу \(1\) Дж.
Таким чином, потенціальне поле визначається на лише силовою характеристикою — вектором напруженості \(\vec{E}\), а й скалярною алгебраїчною величиною — потенціалом \(\varphi\), який є енергетичною характеристикою поля. Але вираз (2.4) визначає тільки різницю потенціалів у двох точках. Що ж до потенціалу \(\varphi\), то він сам по собі не є однозначно визначеним — якщо в усіх точках поля до величини \(\varphi\) додати будь-яке задане число, то це ніяк не вплине ні на результати обчислень роботи за формулою (2.3), ні на значення напруженості поля. Тому, аби потенціал у всіх точках був визначений однозначно, треба спочатку вибрати так звану нульову точку (або нульовий рівень) потенціалу — якусь точку \(P_0\) (або множину точок), де потенціал за домовленістю приймається рівним нулю: \(\varphi(P_0)=0\). У такому разі формула (2.3) для роботи поля \(A_0\) при переміщенні заряду з довільної точки \(P\) у нульову точку \(P_0\) запишеться, як
\begin{equation} {A_0}=q\varphi , \end{equation}
і
\begin{equation} {\varphi}=\frac{A_0}{q}. \tag{2.6} \end{equation}
Цей вираз по суті є означенням потенціалу:
потенціал електричного поля є визначеним тільки по відношенню до вибраної нульової точки і чисельно дорівнює роботі поля при перенесенні одиничного позитивного заряду з даної точки в нульову точку.
Слід зазначити, що вибір нульової точки, в принципі, є довільним і лімітується лише міркуваннями зручності. Наприклад, у випадку окремої зарядженої частинки чи системи зарядів обмежених розмірів поле послаблюється з відстанню, тому у фізиці нульову точку потенціалу вибирають “на нескінченності”, тобто в довільній точці віддаленій від системи на необмежено велику відстань. Виняток становлять тільки ідеалізовані поля необмежених розподілів заряду, таких, як нескінченна зарядженою площина, або нескінченний заряджений циліндр, тощо.
На практиці корпуси вузлові (“нульові”) точки схем електричних приладів сполучають із корпусом, а сам корпус із міркувань техніки безпеки “заземлюють”, тобто з’єднують із земною поверхнею. Тому в електротехніці за нуль приймається потенціал Землі.
При виборі нульової точки на нескінченності з виразів (2.2), (2.2а) і (2.3) випливають такі формули потенціалу поля окремого точкового заряду \(q\) та системи зарядів \(q_i\):
\begin{align} \varphi&=\frac{q\mathstrut}{4\pi\varepsilon_0{r}}, \tag{2.7}\\ \varphi&=\sum\limits_{i}\frac{q_i\mathstrut}{4\pi\varepsilon_0{r_i}}. \tag{2.7а} \end{align}
Остання формула показує, що потенціал, як і напруженість поля, задовольняє принцип суперпозиції:
\begin{equation} \varphi=\sum\limits_{i}\varphi_{i}. \tag{2.8} \end{equation}
Це дозволяє розраховувати і потенціали полів неперервно розподілених зарядів за тою самою схемою, що й для напруженості (п. 1.3). А саме, весь заряд поділяють на окремі точкові ділянки \(\mathrm{d}q\), потім за формулою (2.7) записують потенціал поля окремої ділянки \(\mathrm{d}\varphi = k\,\mathrm{d}q/r\), і у виразі (2.8) дискретне додавання замінюють інтегруванням:
\begin{equation} \varphi=k\int\limits{\frac{\mathrm{d}q}{r}} . \tag{2.9} \end{equation}
Відтак, записавши \(\mathrm{d}q\) через густину заряду та розміри ділянки, отримуємо наступні інтегральні формули для обчислення потенціалу при кожному можливому типі розподілу:
\begin{align} \varphi&=k\int\limits_V{\frac{\rho{(\vec{r})}}{r}}\mathrm{d} V = \frac{1}{4\pi\varepsilon_0}\int\limits_{V}\frac{\rho{(\vec{r})}}{r}\mathrm{d}{V} . \tag{2.9а}\\ \varphi&=k\int\limits_{S}{\frac{\sigma{(\vec{r})}}{r}}\mathrm{d}S =\frac{1}{4\pi {{\varepsilon }_{0}}}\int\limits_{S}{\frac{\sigma ( {\vec{r}} )}{r}\mathrm{d}S}, \tag{2.9б}\\ \varphi&=k\int\limits_{L}{\frac{\lambda ( {\vec{r}} )}{r}\mathrm{d}\vec{l}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\int\limits_{L}{\frac{\lambda ( {\vec{r}} )}{r}\mathrm{d}\vec{l}}, \tag{2.9в}\\ \end{align}
де \(\rho{(\vec{r})}\), \(\sigma{(\vec{r})}\) та \(\lambda{(\vec{r})}\) — функція об’ємної, поверхневої та лінійної густини заряду.
Наостанок згадаємо про таке. З механіки відомо, що при переміщенні тіла в потенціальному полі будь-якої природи робота сил поля дорівнює спаду потенціальної енергії тіла:
\begin{equation} {A}=-\Delta{W}=W_1-W_2 . \tag{2.10} \end{equation}
Тож, зваживши на формулу (2.3), маємо такий загальний вираз потенціальної енергії зарядженої частинки в електричному полі:
\begin{equation} W =q\varphi. \tag{2.10а} \end{equation}
2.3. Еквіпотенціальні поверхні
Наочне уявлення про розподіл потенціал поля в просторі можна скласти за допомогою еквіпотенціальних поверхонь, тобто таких,
для кожної з яких потенціал поля в усіх точках однаковий: \(\varphi= \textrm{const}\).
Форма еквіпотенціальних поверхонь визначається видом залежності потенціалу від координат і для кожного значення потенціалу \(\varphi_0\) встановлюється з рівняння \(\varphi(\vec{r})=\varphi_{0}\). Зокрема, для поля точкового заряду, згідно з виразом (2.7), виходить:
\begin{equation} \frac{q}{4\pi\varepsilon_0{r}}=\varphi_{0} \quad\Rightarrow \quad{r}=\frac{q}{4\pi\varepsilon_0\varphi_{0}}=\mathrm{const}. \end{equation}
Отже, еквіпотенціальними поверхнями такого поля є сфери з центром у заряді, як показано штриховими лініями на рис. 1.7а,б (п. 1.4). (Зрозуміло, що на папері зображуються не самі еквіпотенціальні поверхні, а лінії їхнього перетину із площиною рисунка.)
Аби за допомогою еквіпотенціальних поверхонь наочно показати не тільки розподіл, а й зміну потенціалу при переміщенні в полі від точки до точки, їх (поверхні) проводять з однаковим кроком \(\Delta\varphi=\mathrm{const}\). У такому разі чим швидше змінюється потенціал, тим ближче одна до одної розташовуються еквіпотенціальні поверхні. Це стосується як поля точкового заряду, так і інших полів, наприклад, поля двох різнойменних зарядів:
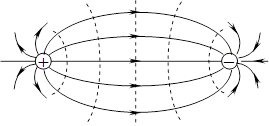
Форма еквіпотенціальних поверхонь, як і форма ліній поля, в загальному випадку є складною і може взагалі не виражатись якимось рівнянням. Але за будь-яких умов у всіх точках
силові лінії та еквіпотенціальні поверхні є взаємно ортогональними,
тобто в точці перетину дотична до силової лінії (напрям \({\vec{E}}\)) і площина, дотична до еквіпотенціальної поверхні, є взаємно перпендикулярними. Це випливає з того, що при будь-якому переміщенні \(\mathrm{d}\vec{l}\) заряду \(q\) по еквіпотенціальній поверхні, згідно з (2.3а), робота поля \(\delta A=q\vec{E}\,\mathrm{d}\vec{l}=-q\,\mathrm{d}\varphi =0\), отже кут між векторами \(\vec{E}\) і \(\mathrm{d}\vec{l}\) дорівнює \(90^\circ\).
Контрольні запитання
1. Що свідчить про потенціальність електричного поля зарядів?
2. Що називається різницею потенціалів у двох точках електричного поля? Потенціалом у заданій точці?
3. Потенціал у деякій точці електричного поля дорівнює \(1\ \text{кВ}\). Що це означає?
4. Запишіть формулу потенціалу поля точкового заряду відносно землі, якщо земна поверхня має потенціал \(\varphi_0\) відносно нескінченності.
5. Електричне поле нескінченної рівномірно зарядженої площини є однорідним (скрізь однаковим). Чи можна записати для нього формулу потенціалу? Чому?
6. Електричне поле створюється двома закріпленими однаковими різнойменними зарядами. Яку форму має і що собою являє еквіпотенціальна поверхня, котра проходить через середину відрізка, що з’єднує заряди?
7. Як, маючи картину еквіпотенціальних поверхонь електричного поля, можна показати вигляд його силових ліній?
3. Зв’язок між напруженістю та потенціалом
Із механіки відомо, що при переміщенні частинки в потенціальному полі роботу поля можна визначити як через силу, так і через потенціальну енергію. Тому роботу при переміщенні заряду в кулонівському електричному полі можна знайти як через напруженість поля, так і через потенціал. Отже, між напруженістю і потенціалом є органічний зв’язок, що дозволяє визначати одну з цих величин за відомою іншою. Далі розглянуто:
3.1. Визначення потенціалу поля через напруженість
3.1. Визначення потенціалу поля через напруженість
Задачу про зв’язок між напруженістю та потенціалом можна розглядати двояко: як установлення способу визначення потенціалу поля \(\varphi(\vec{r}) \) через задану напруженість \(\vec{E}{(\vec{r})}\), та як установлення способу визначення напруженості поля \(\vec{E}{(\vec{r})}\) через заданий потенціал \(\varphi{(\vec{r})}\).
Перша задача по суті вже була розглянута в п. 2.2. Справді, підставляючи у формулу (2.3) вираз роботи поля (2.1), отримуємо загальний вираз різниці потенціалів між заданими точками 1 і 2 через напруженість поля:
\begin{equation} \varphi_1-\varphi_2=\int\limits_{1\to{2}}{\vec{E}\,\mathrm{d}\vec{l}}. \tag{3.1} \end{equation}
Так само, попередньо обравши нульову точку \(P_0\), за формулою (2.6) можна знайти й потенціал в будь-якій точці \(P\):
\begin{equation} \varphi =\int\limits_{P\to {{P}_{0}}}{\vec{E}\,\mathrm{d}\vec{l}}, \tag{3.2} \end{equation}
Як було показано раніше (п. 2.1), ці інтеграли не залежать від траєкторії, що дозволяє при розрахунках обирати найзручніший шлях інтегрування. Часто це силова лінія поля.
3.2. Визначення напруженості поля через потенціал
Проекція напруженості \(\vec{E}\) на заданий напрям. Розглянемо роботу поля \(\Delta{A}\) при невеликому переміщенні \(\Delta{\vec{l}}\) заряду \(q\) у заданому напрямку між точками з потенціалами \(\varphi\) та \(\varphi+\Delta\varphi\) (рис. 3.1).
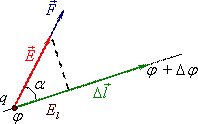
Згідно з (2.3), ця робота складає
\begin{equation} \Delta{A}=-q\,\Delta{\varphi}. \end{equation}
На невеликому переміщенні зміни напруженості поля \({\vec{E}}\) та сили \(\vec{F}=q\vec{E}\), що діє на заряд є незначними. Тому, вказану роботу можна наближено визначити через напруженість в початковій точці:
\begin{equation} \Delta{A}\approx{q}\vec{E}\cdot\Delta\vec{l}. \end{equation}
Прирівнюючи обидва вирази роботи і враховуючи, що \(\vec{E}\,\Delta\vec{l}=E\,\Delta{l}\cos\alpha=E_{l}\,\Delta{l}\) (див. рис. 3.1), отримаємо для проекції вектора \(\vec{E}\) на напрям переміщення заряду \(q\):
\begin{equation} {E_l}\approx-\frac{\Delta\varphi}{\Delta{l}}. \end{equation}
При зменшенні відстані \(\Delta{l}\) похибка буде зменшуватись, і в границі \(\Delta{l}\to{0}\) цей вираз стане точним. Отже,
\begin{equation} E_{l}=-\lim\limits_{\Delta{l}\to{0}}\frac{\Delta{\varphi}}{\Delta{l}}. \end{equation}
Границя у правій частині — то є швидкість зміни величини \(\varphi\) при переміщенні в заданому напрямку \(\vec{l}\). Вона позначається як \(\partial \varphi /\partial l\) і називається похідною функції \( \varphi \) за напрямом \(\vec{l}\):
\begin{equation}\frac{\partial\varphi}{\partial{l}}=\lim\limits_{\Delta{l}\to{0}}\frac{\Delta{\varphi}}{\Delta{l}}.\end{equation}
Таким чином,
\begin{equation} {E_l}=-\frac{\partial{\varphi}}{\partial{l}}, \tag{3.3} \end{equation}
тобто
проекція вектора напруженості електричного поля на заданий напрям дорівнює взятій із зворотнім знаком похідній потенціалу в цьому напрямі.
Зв’язок між \(\vec{E}\) та φ. Попри схожість в означенні та позначенні, похідна за напрямом не є звичною похідною, і в (3.3) символ \(\partial l\) означає не приріст якогось аргументу \(l\), а величину нескінченно малого переміщення у напрямі \(l\). Виняток становить рух уздовж координатних осей, коли елементарні переміщення \(\mathrm{d}x\), \(\mathrm{d}y\), \(\mathrm{d}{z}\) є приростами аргументів \(x\), \(y\), \(z\) функції \(\varphi(x,y,z)\). У такому випадку похідні у напрямках координатних осей вироджуються в частинні похідні по відповідних координатах, і згідно з (3.3)
\begin{equation} \begin{aligned} &{E_x}=-\frac{\partial{\varphi}}{\partial{x}}, \quad {E_y}=-\frac{\partial{\varphi}}{\partial{y}} \quad \text{і} \\ &\quad {E_z}=-\frac{\partial\varphi}{\partial{z}}. \end{aligned} \end{equation}
Це дозволяє виразити через потенціал і вектор напруженості \(\vec{E}=E_x\vec{i}+E_y\vec{j}+e_z\vec{k}\):
\begin{equation} \vec{E}=-\left(\frac{\partial\varphi}{\partial{x}}\vec{i}+\frac{\partial\varphi}{\partial{y}}\vec{j}+\frac{\partial\varphi}{\partial{z}}\vec{k}\right) . \end{equation}
Величина в дужках називається градієнтом потенціалу і позначається як \(\operatorname{grad} \varphi\):
\begin{equation} \operatorname{grad}\varphi=\frac{\partial\varphi}{\partial{x}}\vec{i}+\frac{\partial\varphi}{\partial{y}}\vec{j}+\frac{\partial\varphi}{\partial{z}}\vec{k}. \tag{3.4} \end{equation}
Отже,
\begin{equation} \vec{E}=-\operatorname{grad}\varphi . \tag{3.5} \end{equation}
Вектор напруженості електричного поля в кожній точці дорівнює взятому з протилежним знаком градієнту потенціалу в цій точці.
Ще раз наголосимо, що йдеться тільки про потенціальне (кулонівське) поле.
3.3. Градієнт
Вирази (3.4) і (3.5) показують, як слід обчислювати напруженість поля через потенціал, заданий в декартових координатах, і не дають наочного уявлення про зв’язок напруженості з потенціалом та зміст поняття “градієнт”. Аби висвітлити його, згадаймо, що в кожній точці вектор напруженості \(\vec{E}\) напрямлений уздовж нормалі \(\vec{n}\) до еквіпотенціальної поверхні, і, згідно з (3.3), проекція \(E_n\) і модуль \(E\) напруженості поля визначаються похідною вздовж нормалі:
\begin{equation} {E_n}=\frac{\partial\varphi}{\partial{n}} \qquad \text{і} \qquad {E}=\left|\frac{\partial\varphi}{\partial{n}}\right| . \tag{3.6} \end{equation}
У випадку однорідного поля (\(\vec{E}=\mathrm{const}\)), потенціал у будь-якому напрямку змінюється лінійно, тому
\begin{equation} {E}=\frac{U}{d}, \tag{3.6а} \end{equation}
де \(U=\varphi_1-\varphi_2\) — різниця потенціалів (напруга) між двома точками, розміщеними одна від одної на відстані \(d\) у напрямку поля. На основі цієї формули встановлена одиниця напруженості поля “вольт-на-метр” (В/м):
\(1\ \text{В/м}\) — це напруженість однорідного електричного поля, в якому між точками, розташованими на відстані \(1\ \text{м}\) у напрямку поля, напруга становить \(1\ \text{В}\).
Відповідно до співвідношень (3.6) вектор \(\vec{E}\) виражається, як
\begin{equation} \vec{E}=-\frac{\partial\varphi}{\partial{n}}\vec{n}, \end{equation}
де \(\vec{n}\) — орт (одиничний вектор) нормалі до еквіпотенціальної поверхні, напрямлений в бік зростання потенціалу.
Зіставляючи цей вираз із виразом (3.5), бачимо, що
\begin{equation} \operatorname{grad}\varphi=\frac{\partial\varphi}{\partial{n}}\vec{n}. \tag{3.7} \end{equation}
Цей результат можна розглядати як інваріантне (не залежне від системи координат) означення поняття градієнта потенціалу. Аби зрозуміти його зміст, згадаймо, що модуль вектора більший за модуль його проекції на будь-який інший напрям: \(|\vec{E}|\gt |E| \). Це означає, що \(\left|\frac{\partial\varphi}{\partial{n}}\right|\gt\left|\frac{\partial\varphi}{\partial{l}}\right|\), тобто напрям градієнта є напрямом найшвидшої зміни \(\varphi\). Відтак можна дати наступне формулювання:
градієнтом потенціалу у заданій точці називається вектор, який спрямований в бік найшвидшого зростання потенціалу і має модуль, рівний швидкості його зміни в цьому напрямі.
Примітка. У математиці градієнт трактують як указану міру швидкості зміни будь-якої функції координат.
Відповідно, позаяк у виразі (3.5) фігурує знак “\(-\)”, вектор напруженості електричного поля у кожній точці напрямлений в бік найшвидшого зменшення потенціалу.
Контрольні запитання
1. Яка відміна існує між похідною за напрямом і частинною похідною?
2. Що є спільним і що відмінним у поняттях “похідна за напрямом” і “градієнт”?
3. Як відрізняється похідна потенціалу у напрямку силової лінії поля від похідної в якомусь іншому напрямку?
4. Чому не можна сказати, що вектор напруженості електричного поля є похідною потенціалу в напрямку силової лінії?
5. Часто в репортажі про велоперегони коментатори вживають вислів “градієнт траси”. Що вони мають на увазі і чи відповідає це математичному означенню поняття “градієнт”?
6. Як за картиною еквіпотенціальних поверхонь узнати, де поле сильніше, а де слабше?
7. Електричне поле створюється двома паралельними нескінченними площинами, що різноіменно заряджені з однаковими густинами заряду \(\sigma\) і \(-\sigma\). Що можна сказати про напруженість і потенціал поля поза площинами?
4. Електричний диполь
Електричним диполем (двополюсником) називаються два різнойменні заряди (полюси) \(+q\) і \(-q\) однакової величини, що розміщені на малій відстані \(l\) один від одного, рис. 4.1а.
Диполь у цілому є електронейтральним, але через рознесеність полюсів у просторі він створює власне електричне поле та зазнає дії зовнішніх полів. При цьому власне поле диполя та його поведінка у зовнішньому полі визначаються не безпосередньо зарядом полюса, а електричним (дипольним) моментом \(\vec{p}\) — величиною, що визначається як
\begin{equation} \vec{p}=q\vec{l}, \tag{4.1} \end{equation}
де \(q > 0\) — заряд диполя, а вектор \(\vec{l}\), проведений від негативного до позитивного полюса, називається плечем диполя.
Варто завважити, що розглянута система з двох заряджених кульок майже не має прямого практичного застосування. Але диполь є цінною моделлю, що використовується в різних розділах електродинаміки. Зокрема, уявлення про електричний диполь є базовим у теорії електричного поля в діелектриках. Далі розглядаються такі питання:
4.1. Електричне поле диполя
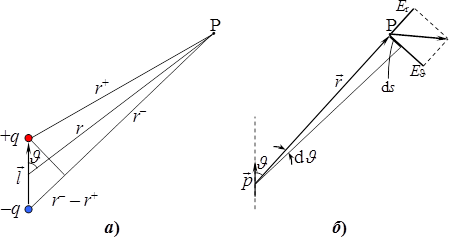
Розглянемо електричне поле, що створюється диполем із моментом \(\vec{p}\) на відстанях \( r\gg l\) від його центра (у так званій дипольній зоні). Очевидно, що це поле має осьову симетрію: його характеристики однакові у всіх точках кола з центром на осі диполя й перпендикулярного до неї. Тому напруженість і потенціал поля диполя у будь-якій точці P залежать тільки від відстані \(r\) та кута \(\vartheta\) (рис. 4.1а):
\begin{equation} \vec{E}=\vec{E}(r,\vartheta) ,\qquad \varphi=\varphi(r,\vartheta) . \end{equation}
Потенціал поля диполя. Розрахунок поля диполя почнемо з потенціалу, який за принципом суперпозиції дорівнює
\begin{equation} \varphi=\varphi_{-}+\varphi_{+}, \end{equation}
де потенціали \(\varphi_-\) і \(\varphi_+\) полів кожного з полюсів визначаються формулою (2.7). Отже,
\begin{equation} \begin{aligned} &\varphi=\frac{-q}{4\pi\varepsilon_0{r_{-}}}+\frac{q}{4\pi\varepsilon_0{r_{+}}} ={}\\ &\quad{}= \frac{q}{4\pi\varepsilon_0}\left(\frac{1}{r_{+}}-\frac{1}{r_{-}}\right) = \frac{q}{4\pi\varepsilon_0}\cdot\frac{r_{-}-r_{+}}{r_{+}r_{-}}. \end{aligned} \end{equation}
Оскільки за умовою \({r}\gg{l}\), різниця довжин відрізків \(r_-\) і \(r_+\) та кут між ними є малими (рис. 4.1), можна прийняти \({r_{-}}-r_{+}=l\cos\vartheta \) і \({r_{+}r_{-}}=r^2 \). Тоді
\begin{equation} \varphi(r,\vartheta)=\frac{p\cos\vartheta}{4\pi\varepsilon_0{r^2}}. \tag{4.2} \end{equation}
Отже, як і говорилося, потенціал поля диполя визначається не окремо величиною зарядів і відстанню між ними, а дипольним моментом.
Напруженість поля диполя. Вектор напруженості теж можна знайти за принципом суперпозиції як \(\vec{E}=\vec{E}_{+}+\vec{E}_{-}\). Але корисніше зробити це за допомогою функції потенціалу (4.2) через проекції \({E_r}\) на радіус-вектор \(\vec{r}\) точки P і \({E}_{\vartheta}\) — на дотичну до кола радіуса \(r\) із центром у центрі диполя (рис. 4.1б). Ці проекції, відповідно до формули (3.3), визначаються як
\begin{equation} {E_r}=-\frac{\partial\varphi}{\partial{r}}, \qquad {E_{\vartheta}=-\frac{\partial\varphi}{\partial{s}}}=-\frac{\partial\varphi}{r\,\partial\vartheta}. \end{equation}
Тут враховано, що елементарне переміщення \(\d s\) у напрямку дотичної збігається з дугою кола: \(\mathrm{d}s=r\,\mathrm{d}{\vartheta}\). Відтак, після указаних диференціювань функції (4.2), отримуємо:
\begin{equation} \left\{ \begin{aligned} E_{r}&=\frac{1}{4\pi\varepsilon_{0}}\frac{2p\cos\vartheta}{r^{3}}, \\ E_{\vartheta}&=\frac{1}{4\pi\varepsilon_{0}}\frac{p\sin\vartheta}{r^{3}}. \\ \end{aligned} \right. \tag{4.3} \end{equation}
Звідси для модуля напруженості \({E}=\sqrt{E_r^2+E_{\vartheta}^2}\) маємо:
\begin{equation} {E}=\frac{p}{4\pi\varepsilon_0{r^3}}\sqrt{1+3\cos^2{\vartheta}}. \tag{4.4} \end{equation}
Напрям вектора \(\vec{E}\) задамо кутом \(\alpha\) між ним і радіусом-вектором \(\vec{r}\) точки P (рис. 4.1б). Тоді, згідно з (4.3),
\begin{equation} \operatorname{tg}\alpha=\frac{1}{2}\operatorname{tg}\vartheta . \tag{4.5} \end{equation}
Формули (2.23) і (2.24) повністю визначають вектор \(\vec{E}\) у будь-якій точці дипольної зони (\({r}\gg{l}\)), хоч і не є дуже наочними. Але для точок на осі диполя та на перпендикулярі до осі, що проходить через центр диполя, вектор напруженості можна визначити однією формулою. В першому випадку кут \(\vartheta\) складає або \(0\), або \(\pi\), тож відповідно до (4.5), такі самі значення має і кут \(\alpha\). Це означає, що на осі напрям поля скрізь збігається з напрямком електричного моменту диполя \(\vec{p}\). Врахувавши це та підставивши в (4.4) значення \(\cos^2\vartheta=1 \), отримуємо:
\begin{equation} {{\vec{E}}_{\parallel }}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{2\vec{p}}{r^3}. \tag{4.6} \end{equation}
Прийнявши \(\vartheta=\pi/2 \), так само одержимо вираз вектора напруженості в другому випадку:
\begin{equation} {{\vec{E}}_{\perp }}=-\frac{1}{4\pi {{\varepsilon }_{0}}}\cdot \frac{{\vec{p}}}{{{r}^{3}}}. \tag{4.7} \end{equation}
З приводу цього виразу корисно зауважити, що в усіх таких точках \(\cos\vartheta={0}\), тож відповідно до (4.2), \(\varphi={0}\). Це наочно ілюструє специфіку зв’язку між напруженістю та потенціалом електричного поля (формула (3.5)). А саме, відсутність потенціалу в заданій точці ще не означає відсутності самого поля. Про відсутність поля свідчить не величина потенціалу, а його незмінність при зміщенні з даної в будь-яку сусідню точку.
Підводячи підсумок, зазначимо, що в цілому електрично нейтральна система зарядів, якою є диполь, навіть на великих порівняно з її розмірами відстанях створює електричне поле. Але його потенціал і напруженість змінюються з відстанню швидше, ніж у випадку поля точкового заряду. Це є характерним і для полів мультиполів — нейтральних систем зарядів складнішої конфігурації. Причому, чим складніша конфігурація, тим сильніша залежність поля від відстані. Тому електричні поля таких систем, як атоми та молекули, існують практично тільки на відстанях порядку розмірів цих частинок.
4.2. Диполь у зовнішньому електричному полі
Момент сил, що діють на диполь. Якщо диполь із зарядом \(q\) і плечем \(\vec{l}\) вміщено в однорідне електричне полі \(\vec{E}= \textrm{const}\), то на полюси діють протилежно напрямлені сили \(\vec{F}_{+}\) і \(\vec{F}_{-}\) (рис. 4.2а), які намагаються повернути диполь за годинниковою стрілкою.
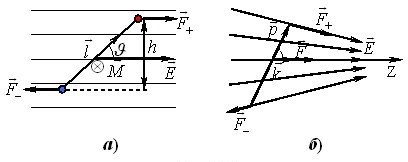
Обертальна дія сил визначається вектором моменту сил \(\vec{M}\). У нашому випадку його легко розрахувати, позаяк сили є однакові за величиною та протилежні за напрямом, тож утворюють так звану “пару сил”. А з механіки відомо, що модуль моменту \(\vec{M}\) пари дорівнює
\begin{equation} {M=Fh}, \end{equation}
де відстань між лініями дії сил, яка називається “плечем” пари.
Напрям вектора моменту сил визначається за правилом правого гвинта. Тут це напрям “від нас”.
(На рис. 4.2а це позначено як \(\otimes \). Аналогічно, напрям “до нас” позначають як \(\odot \).)
З рисунка видно, що \( {h}=l\sin\vartheta \), отже
\begin{equation} {M}=qEl\sin\vartheta=pE\sin{\vartheta}, \tag{4.8} \end{equation}
де \({p=ql}\) — модуль електричного моменту диполя.
З урахуванням напрямків момент сил визначається векторним добуток векторів \(\vec{p}\) і \(\vec{E}\):
\begin{equation} \vec{M}=\bigl[\vec{p}\vec{E}\bigr] . \tag{4.9} \end{equation}
У неоднорідному полі \(\vec{E}\ne\mathrm{const}\) сили \(\vec{F}_{+}\), \(\vec{F}_{-}\) не утворюють пари (див. рис. 4.2б), і формула (4.9) строго є не дійсною. Але для елементарного (із дуже малим плечем) диполя вона зберігає чинність, бо в межах диполя поле лишається практично однорідним. Тому можна сказати, що
будь-яке електричне поле намагається зорієнтувати елементарний диполь так, аби напрям дипольного моменту збігався із напрямом поля.
Сила, що діє на диполь у неоднорідному полі. В однорідному полі результуюча сила, що діє на диполь, \(\vec{F}=\vec{F}_{+}+\vec{F}_{-}={0}\). Тому поле лише повертає диполь навколо нерухомого центра мас. Але в неоднорідному полі (рис. 4.2б) \(\vec{F}_{+}\ne -\vec{F}_{-}\), і на диполь діє ще й деяка результуюча сила \(\vec{F}_{+}+\vec{F}_{-}\ne{0}\). Тому вільний диполь буде не лише повертатися навколо центра мас, а й рухатись як ціле.
Указана сила визначається величиною та орієнтацією електричного моменту диполя \(\vec{p}\) і конфігурацією та ступенем неоднорідності зовнішнього поля. Її загальний вираз легко знайти:
\begin{equation} \vec{F}=\vec{F}_{+}+\vec{F}_{-}=q\bigl(\vec{E}_{+}-\vec{E}_{-}\bigr)=q\,\Delta\vec{E}. \tag{4.10} \end{equation}
де \(\Delta\vec{E}\) — зміна напруженості поля при переміщенні на відстань \(l\) у напрямку плеча диполя. При малій величині \(l\) зміна поля є незначною, тож можна записати:
\begin{equation} \Delta \vec{E}=\frac{\partial \vec{E}}{\partial l}l, \end{equation}
де \(\partial\vec{E}/\partial{l}\) — похідна вектора \(\vec{E}\) у напрямку \({\vec{l}}\), яка визначає швидкість зміни напруженості поля в напрямку плеча диполя. Відтак вираз (4.10) набуває вигляду:
\begin{equation} \vec{F}=p\frac{\partial\vec{E}}{\partial{l}}, \tag{4.11} \end{equation}
де \({p=ql}\) — електричний момент диполя.
Слід зауважити, що попри позірну простоту формули (4.11), властивості сили \(\vec{F}\) у деталях є досить складними. Але ситуація спрощується у випадку елементарного диполя в осесиметричному неоднорідному полі, напруженість якого змінюється тільки у напрямку самого поля, як схематично показано на рис. 4.2б. В такому випадку якщо спрямувати координатну вісь \(\mathrm{Z}\) (орт \(\vec{k}\)) у напрямку поля, то \(\vec{E}=E\vec{k}\), а елементарне переміщення вздовж осі диполя, що фігурує у виразі (4.11), \(\partial{l}=(\partial{z}/\cos\vartheta) \). Отже,
\begin{equation} \vec{F}=p_z\frac{\partial{E}}{\partial{z}}\vec{k}, \tag{4.12} \end{equation}
де \({{p}_{z}}=p\cos \vartheta \) — проекція моменту диполя на напрям поля, а вектор \((\partial{E}/\partial{z})\vec{k}\) — градієнт напруженості поля, в якому знаходиться диполь.
За вказаних умов вектор сили \(\vec{F}\) є колінеарним до осі \(\mathrm{Z}\), тож вираз сили зручно записати через проекцію \({F_z}=\pm{F}\)
\begin{equation} {F_z}=p_z\frac{\partial{E}}{\partial{z}}. \tag{4.13} \end{equation}
Оскільки вісь \(\mathrm{Z}\) на рис. 4.2 спрямована в бік підсилення поля, то у виразах (4.12) і (4.13) \(\partial{E}/\partial{z}\gt{0}\). Це означає, що при орієнтації по полю \(\vartheta\lt{90^{\circ}}\) диполь втягується в область сильнішого поля, а при протилежній орієнтації \((\vartheta\gt{90^{\circ}}) \) — виштовхується в бік слабшого поля. Якщо ж у неоднорідне поле внести диполь у довільній орієнтації та вивільнити, то він почне одночасно повертатися і рухатись у той чи інший бік, але врешті зорієнтується по полю і рухатиметься в бік зростання напруженості.
Енергія диполя в зовнішньому полі. Електричне поле діє не на диполь як ціле, а на кожен заряд окремо. Тому, попри електричну нейтральність, диполь у зовнішньому полі має відповідну потенціальну енергію, яку можна визначити через роботу поля при зміні орієнтації диполя.
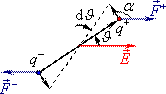
Нехай диполь із зарядом \(q\) і плечем \(\vec{l}\) є зорієнтований під кутом \(\vartheta \) до напрямку електричного поля \(\vec{E}\), рис. 4.3. Тоді при повороті диполя проти годинникової стрілки на елементарний кут \({\mathrm{d}}\vartheta \) заряди диполя переміщуються на відстань \(\mathrm{d}s\), а сили поля \(F=qE\) виконують сумарну роботу \(\delta A=2F\cos \vartheta \,\mathrm{d}s \). Із рис. 4.3 видно, що \(\mathrm{d}s=(l/2)\,\mathrm{d}\vartheta \), і \(\alpha=90^{\circ}-\vartheta \). Отже, \(\cos \alpha =-\sin \vartheta \), і
\begin{equation} \delta{A}=-qEl\sin\vartheta\cdot\mathrm{d}\vartheta=-pE\sin\vartheta\cdot\mathrm{d}\vartheta, \end{equation}
де \({p}={ql}\) — модуль електричного моменту диполя.
Звідси, згідно із співвідношенням (2.10), можна знайти приріст потенціальної енергії диполя при заданій зміні кута \(\vartheta \) від \(\vartheta_1 \) до \(\vartheta_{2}\):
\begin{equation} \begin{aligned} &{W_2-W_1}=-A=pE\int\limits_{\vartheta_{1}}^{\vartheta_{2}}\sin\vartheta\cdot\mathrm{d}\vartheta={}\\ &\quad{}= pE\bigl(\cos\vartheta_{1}-\cos\vartheta_{2}\bigr) . \end{aligned} \end{equation}
Переписавши цей вираз як
\begin{equation} {W_2-W_1}=\bigl(-pE\cos\vartheta_{2}\bigr)-\bigl(-pE\cos\vartheta_{1}\bigr) , \end{equation}
бачимо, що потенціальна енергія диполя у зовнішньому полі визначається формулою
\begin{equation} {W}=-pE\cos\vartheta , \tag{4.14} \end{equation}
або
\begin{equation} {W}=-\vec{p}\vec{E}. \tag{4.14а} \end{equation}
При цьому \(W = 0\), коли \(\cos{\vartheta}={0}\), тобто за нульовий рівень енергії приймається енергія диполя в положенні коли його вісь перпендикулярна до напрямку поля. Відповідно, при \(\vartheta=0{}^{\circ}\) енергія диполя є мінімальною і складає \({W}_{\textrm{min}}=-pE \), а при \(\vartheta=180{}^{\circ}\) вона максимальна і дорівнює \({W}_{\textrm{max}}={pE}\). У відповідності до законів механіки в обох цих положеннях диполь перебуває в рівновазі, але в першому вона є стійкою, тоді як в другому — нестійкою.
5. Циркуляція і потік електричного поля
Окрім напруженості \(\vec{E}\), що визначає електричне поле локально (в кожній точці), існують ще й інтегральні величини, котрі характеризують його не в точці, а на заданій лінії або поверхні. Ці величини називаються “циркуляцією” та “потоком” поля і розглядаються в наступних питаннях:
5.1. Циркуляція потенціального електричного поля
5.2. Електростатична теорема Гаусса
5.1. Циркуляція потенціального електричного поля
Співвідношення (3.5) дозволяє розраховувати напруженість не прямо, а через потенціал. Це може спростити задачу, бо визначати скалярні інтеграли (2.9) зазвичай легше, ніж векторні (1.7). Але такий шлях є прийнятним тільки для потенціальних полів. Тому треба мати формальний (математичний) критерій, який дозволяє розрізняти потенціальні та непотенціальні поля.
Для встановлення такого критерію розглянемо роботу \(A_{12}\) кулонівського поля при переміщенні заряду з точки 1 у точку 2 по двох різних траєкторіях I і II, рис. 5.1.
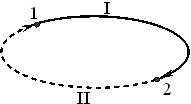
Позаяк таке поле є потенціальним, то за означенням ці роботи однакові:
\begin{equation} {A_{12}^{\mathrm{(I)}}}={A_{12}^{\mathrm{(II)}}}. \end{equation}
Тому, якщо заряд перемістити з точки 1 в точку 2 по шляху (I) і потім повертати назад по шляху (II), то на зворотньому шляху робота \( A_{21}^{( \text{II} )} \) буде відрізнятися від величини \( A_{12}^{( \text{I} )} \) тільки знаком. Отже, на всьому замкненому шляху робота поля
\begin{equation} {A_0}=A_{12}^{\mathrm{(I)}}+A_{21}^{\mathrm{(II)}}={0}. \tag{5.1} \end{equation}
Із механіки відомо, що робота сили \( \vec{F} \) на заданій замкненій траєкторії \(L\) виражається криволінійним інтегралом по цій траєкторії від скалярного добутку сили на переміщення:
\begin{equation} {A_0}=\oint\limits_L\vec{F}\,\mathrm{d}\vec{l}. \end{equation}
В електричному полі \(\vec{F}=q\vec{E}\), отже, враховуючи вираз (5.1), для потенціального (кулонівського) електричного поля маємо:
\begin{equation} \oint\limits_L\vec{E}\,\mathrm{d}\vec{l}=\oint\limits_L{E_l}\,\mathrm{d}{l}={0}, \tag{5.2} \end{equation}
де \({E_l}\) — проекція напруженості на напрям обходу траєкторії інтегрування.
Інтеграл
\begin{equation} {C}=\oint\limits_L\vec{E}\,\mathrm{d}\vec{l}=\oint\limits_L{E_l}\,\mathrm{d}{l} \tag{5.2а} \end{equation}
має спеціальну назву — циркуляція. Тобто,
криволінійний інтеграл від скалярного добутку вектора напруженості поля на вектор елементарного переміщення вздовж заданого замкненого контуру називається циркуляцією поля по цьому контуру.
Можна сказати, що циркуляція дорівнює роботі поля при переміщенні по замкненому контуру одиничного заряду.
Поняття циркуляції і рівність (5.2) дозволяють сформулювати наступний інтегральний критерій потенціальності поля:
умовою потенціальності поля є нульова величина його циркуляції по будь-якому замкненому контуру, що повністю розташований у полі.
Саме таким є кулонівське поле — електричне поле, що створюється зарядженими частинками.
Зауважимо також, що, позаяк циркуляція по суті є питомою роботою поля на замкненому контурі, вона може мати той чи інший знак залежно від обраного напрямку обходу контуру при інтегруванні.
5.2. Електростатична теорема Гаусса
Зміст, властивості та значення другої з інтегральних характеристик електричного поля — потоку розглядаються далі в наступних питаннях:
5.2.1. Потік електричного поля
5.2.1. Потік електричного поля
Поняття та означення потоку походить із механіки суцільних середовищ.
Потік рідини. У повсякденному вжитку слово “потік” означає характерний рух рідини чи газу, скажімо, гірський чи повітряний потік. Але в науковій і технічній лексиці цим терміном позначають також кількісну міру різних процесів переносу: перенесення рідини, газу, чи сипучої речовини при транспортуванні трубопроводами, тощо.
Нехай в якійсь області простору переноситься речовина, приміром, тече вода в річці. Кількісна міра перенесення води через вибрану на її шляху задану поверхню називається потоком крізь цю поверхню і визначається як об’єм води, що проходить крізь неї за одиницю часу (\(\text{м}^3\!/\text{c}\)):
\begin{equation} \Phi=\frac{\mathrm{d}V}{\mathrm{d}t}. \tag{5.3} \end{equation}
Зрозуміло, що потік рідини залежить від швидкості течії та характеристик поверхні. Аби з’ясувати, як саме, виділимо на вибраній поверхні \(S\) (рис. 5.2а) довільну елементарну площинку \(\mathrm{d}S\) і покажемо орт (одиничний вектор) нормалі до неї \(\vec{n}\) та вектор швидкості течії \(\vec{v}\) в цьому місці.
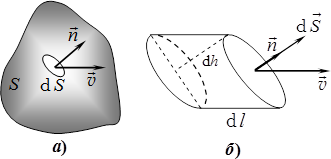
Відтак побудуємо на площинці \(\mathrm{d}S\) як на основі косий циліндрик із твірною \(\mathrm{d}{l}\) та об’ємом \(\mathrm{d}V=\mathrm{d}S\cdot\mathrm{d}h=\mathrm{d}S\cdot\mathrm{d}l\cos\alpha \), як показано на рис. 5.2б. Очевидно, що вся рідина в об’ємі циліндрика проходить крізь площинку \(\mathrm{d}S\) за час \(\mathrm{d}t={\mathrm{d}l}/v \). Тому, згідно з (5.3), елементарний потік \(\mathrm{d}\Phi\) крізь площинку \(\mathrm{d}S\) дорівнює
\begin{equation} \mathrm{d}\Phi=v\,\mathrm{d}S\cos\alpha . \tag{5.4} \end{equation}
Потік \(\Phi\) крізь поверхню \(S\) складається з елементарних потоків \(\mathrm{d}\Phi\) через усі її ділянки: \(\Phi=\int\limits_S\mathrm{d}{\Phi}\), отже
\begin{equation} \Phi=\int\limits_S{v}\,\mathrm{d}S\cos\alpha , \tag{5.4а} \end{equation}
де індекс \(S\) показує, що інтегрування проводиться по всій поверхні \(S\).
Як бачимо, потік крізь задану поверхню визначається як її величиною, так і орієнтацією її ділянок відносно напрямку перенесення рідини. Тому в теорії елементарну площинку трактують як вектор \(\mathrm{d}\vec{S}=\vec{n}\,\mathrm{d}{S}\). Тим самим вектор \(\mathrm{d}\vec{S}\) відображає як величину, так і орієнтацію площинки в просторі. Це дозволяє лаконічно записати вирази (5.4) і (5.4а) у векторній формі:
\begin{equation} \mathrm{d}\Phi=\vec{v}\,\mathrm{d}\vec{S} \end{equation}
і
\begin{equation} \Phi=\int\limits_S\vec{v}\,\mathrm{d}\vec{S}. \tag{5.5} \end{equation}
Швидкість руху частинок \(\vec{v}\) є скрізь визначеною і такою, що закономірно змінюється від точки до точки, тобто є заданою функцією координат: \(\vec{v}=\vec{v}(\vec{r}) \). У математиці векторну функцію координат, визначену в заданій області простору, називають полем вектора, або векторним полем. Отже, мовою математики об’єм рідини, що проходить крізь задану поверхню за одиницю часу, дорівнює потокові поля вектора швидкості течії крізь цю поверхню, або коротко — потокові вектора \(\vec{v}\).
Потік електричного поля. Поняття потоку і означення (5.4) і (5.4а) або (5.5) зберігають чинність та корисність і для векторних полів будь-якої іншої природи. Зокрема,
інтеграл по заданій поверхні \(S\) від скалярного добутку вектора напруженості електричного поля \(\vec{E}\) на вектор елемента поверхні \(\mathrm{d}\vec{S}\) називається потоком напруженості (або потоком поля) крізь цю поверхню:
\begin{equation} \Phi=\int\limits_{S}\vec{E}\,\mathrm{d}\vec{S}. \tag{5.6} \end{equation}
Підінтегральний вираз \(\mathrm{d}\Phi =\vec{E}\,\mathrm{d}\vec{S}\), що визначає потік напруженості крізь довільну елементарну ділянку \(\mathrm{d}S\) поверхні \(S\), можна записати й інакше, розкривши скалярний добуток:
\begin{equation} \begin{aligned} &\mathrm{d}\Phi =\vec{E}\,\mathrm{d}\vec{S}=E\,\mathrm{d}S\cos \alpha ={}\\ &\quad{}={{E}_{n}}\,\mathrm{d}S=E\,\mathrm{d}{{S}_{\bot }}, \end{aligned} \tag{5.7} \end{equation}
де \(E\) і \(\mathrm{d}S\) — модулі векторів \(\vec{E}\) і \(\mathrm{d}\vec{S}\), \(E_n\) — проекція \(\vec{E}\) на нормаль до поверхні, і \(\mathrm{d}{{S}_{\bot }}\) — проекція площинки \(\mathrm{d}\vec{S}\) на площину перпендикулярну до напрямку поля (рис. 5.3).
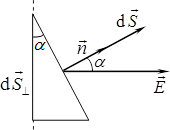
Відповідно, потік поля крізь усю поверхню теж можна подати в різний спосіб:
\begin{equation} \begin{aligned} &\Phi =\int\limits_{S}{\vec{E}\,\mathrm{d}\vec{S}}=\int\limits_{S}E\,\mathrm{d}S\cos\alpha ={}\\ &\quad{}=\int\limits_{S}{{E}_{n}}\,\mathrm{d}S=\int\limits_{S}{E\,\mathrm{d}{{S}_{\bot }}}. \end{aligned} \tag{5.7а} \end{equation}
Говорячи про потік поля, слід зауважити таке. Потік є алгебраїчною величиною і, залежно від кута \(\alpha\) між векторами \(\vec{E}\) і \(\mathrm{d}\vec{S}\), може бути додатнім чи від’ємним. З іншого боку, напрям векторів \(\mathrm{d}\vec{S}\), відтак і знак \(\Phi\), є невизначеними, позаяк орти \(\vec{n}\) можна провести як по один, так і по інший бік поверхні, причому для незамкнених поверхонь — все одно як. Проте у випадку замкнених поверхонь знак потоку набуває суттєвого змісту, тому за домовленістю в усіх точках замкненої поверхні вектори \(\mathrm{d}\vec{S}\) напрямляють назовні (рис. 5.4).
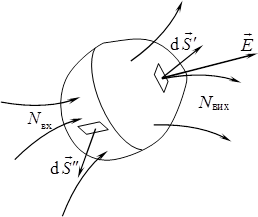
Геометрична інтерпретація потоку. Раніше (п. 1.4) говорилося, що електричне поле можна зображувати за допомогою ліній вектора \(\vec{E}\) (силових ліній), і що такі лінії відображають не лише конфігурацію, а й величину поля в різних областях простору. При цьому за умовою (1.9а) \(E\,\mathrm{d}{{S}_{\bot }} = \mathrm{d}n\). Отже, відповідно до означень (5.7), (5.7а), виконуються числові рівності:
\begin{equation} \left|\mathrm{d}\Phi\right|=\mathrm{d}N\quad \Rightarrow \quad \left|\Phi\right|=N, \tag{5.8} \end{equation}
тобто, можна вважати, що
чисельно потік поля крізь задану поверхню дорівнює кількості ліній поля, що її перетинають.
У випадку замкненої поверхні (оболонки) лінії поля в одних точках заходять усередину, а в інших виходять назовні (рис. 5.4). При цьому в першому випадку \(\alpha>90^\circ\) і створюється від’ємний потік, а в другому \(\alpha<90^\circ\) і потік є додатнім. Тому згідно з (3.6) потік крізь замкнену поверхню \(\Phi_0=\Phi_1+\Phi_2\) можна подати, як
\begin{equation} \Phi_0=N_{\text{вих}}-N_{\text{вх}}, \tag{5.8а} \end{equation}
де \(N_{\text{вих}}\) — кількість ліній поля, що виходять із поверхні назовні, а \(N_{\text{вх}}\) — тих, які входять усередину.
Таке геометричне трактування потоку є зручним у багатьох випадках.
5.2.2. Теорема Гаусса
Потік є важливою характеристикою поля, котра разом із циркуляцією відображає специфічні риси ("обличчя") кожного силового поля. Теорема Гаусса трактує про властивості потоку електричного поля крізь замкнену поверхню.
Потік поля точкового заряду. Визначимо потік \(\Phi\) напруженості крізь довільну замкнену поверхню \(S\) для поля точкового заряду \(q\) у вакуумі (рис. 5.5а).
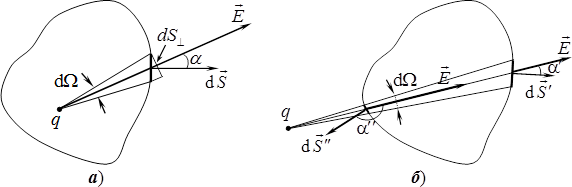
Згідно з виразами (5.7а),
\begin{equation} \Phi =\oint\limits_{S}{E\,\mathrm{d}S\cos \alpha }=\oint\limits_{S}{E\,\mathrm{d}{{S}_{\bot }}}, \end{equation}
де \(\mathrm{d}S\) — площа якоїсь елементарної ділянки замкненої поверхні \(S\).
Проекцію цієї ділянки на площину, перпендикулярну до напрямку поля, можна розглядати як елементарну площадку на поверхні сфери радіуса \(r\) і виразити величину \(\mathrm{d}{{S}_{\bot}}=\mathrm{d}S\cos \alpha \) через відповідний тілесний кут \(\mathrm{d}\Omega\):
\begin{equation} \mathrm{d}{{S}_{\bot }}={{r}^{2}}\,\mathrm{d}\Omega . \tag{5.9} \end{equation}
Довідка. Плоский кут \(\varphi\) визначає частину простору між двома променями, які починаються в одній точці — вершині кута. Його мірою є довжина дуги \(s\), що вирізається сторонами кута на колі заданого радіуса \(r\) із центром у вершині кута. Одиниця плоского кута називається “радіан” (\(\text{рад}\)) і дорівнює кутові, для якого \((s/r) = 1\). За цим означенням усій площині відповідає плоский кут \(\varphi_0=(2\pi r/r)=2\pi\ \text{рад}\). Окрім радіанної, використовують й інші міри, зокрема градусну, де з усією площиною (або довжиною кола) зіставляють кут \(360^\circ\). Тілесний або просторовий кут \(\Omega\) — це частина простору, обмежена певною незамкненою конічною поверхнею. Його мірою є площа сегмента, що вирізається конічною поверхнею на сфері заданого радіуса \(r\) із центром у вершині кута. Одиницею тілесного кута є стерадіан (\(1\ \text{ср}\)) — тілесний кут, для якого \((S/r^2)=1\). Відповідно, всьому тривимірному простору відповідає тілесний кут \({{\Omega }_{0}}=( {4\pi {{r}^{2}}}/{{{r}^{2}}} )=4\pi\ \text{ср} \).
З іншого боку, величина \(E\) визначається формулою (1.4а), тому
\begin{equation} \begin{aligned} &\oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\oint\limits_{S}{\frac{q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}{{r}^{2}}\,\mathrm{d}\Omega }={}\\ &\quad{}=\frac{q}{4\pi {{\varepsilon }_{0}}}\oint\limits_{S}{\mathrm{d}\Omega }. \end{aligned} \end{equation}
Останній інтеграл виражає тілесний кут усього простору і дорівнює \(4\pi \ \text{ср}\), отже,
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{q}{{{\varepsilon }_{0}}}. \tag{5.10} \end{equation}
Тепер розглянемо другий можливий випадок, коли заряд \(q\) знаходиться поза поверхнею \(S\) (рис. 5.5б). В такому разі конічні промені, спрямовані від усіх точок контуру якоїсь площадки \(\mathrm{d}S'\) до заряду й утворюють тілесний кут \(\mathrm{d}\Omega\), виріжуть на протилежному боці відповідну площадку \(\mathrm{d}S''\) з тим самим тілесним кутом. Тому, врахувавши формули (5.9) і (1.4а) та те, що \(\cos\alpha<0\), для потоків крізь указану пару ділянок отримаємо:
\begin{equation} \mathrm{d}\Phi''=-\mathrm{d}\Phi' \quad \Rightarrow \quad \mathrm{d}\Phi'+\mathrm{d}\Phi''=0. \end{equation}
Очевидно, що в такий спосіб можна розчленувати всю замкнену поверхню. Тож сумарний потік крізь замкнену поверхню, що не охоплює заряд,
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=0. \tag{5.10а} \end{equation}
Такого висновку можна дійти і на основі геометричної інтерпретації потоку (5.8а), позаяк у даному випадку кількості ліній поля, що входять усередину поверхні та виходять назовні є однакові.
Відтак, об’єднуючи вирази (5.10) і (5.10а), маємо:
\begin{equation} \oint\limits_{S}\vec{E}\mathrm{d}\vec{S} = \left\{ \begin{aligned} &\frac{q}{\varepsilon_{0}}&&(q\ всередині\ S); \\ &0&&(q\ назовні\ S) .\\ \end{aligned} \right. \tag{5.11} \end{equation}
Теорема Гаусса. Отриманий результат легко узагальнити і на поле, створене довільною системою зарядів (рис. 5.6а).
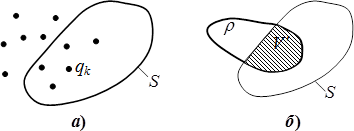
За принципом суперпозиції напруженість поля системи в будь-якій точці
\begin{equation} \vec{E}=\sum\limits_{i}{{{{\vec{E}}}_{i}}}. \end{equation}
Тому потік результуючого поля крізь довільну замкнену поверхню дорівнює сумі потоків полів кожного із зарядів системи:
\begin{equation} \begin{aligned} &\oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\oint\limits_{S}\left( \sum\limits_{i}{{{{\vec{E}}}_{i}}} \right)\mathrm{d}\vec{S}={}\\ &\quad{}=\sum\limits_{i}{\oint\limits_{S}{{{{\vec{E}}}_{i}}\,\mathrm{d}\vec{S}}}. \end{aligned} \end{equation}
Але згідно з (5.11) потік створюють лише заряди, що знаходяться всередині вибраної поверхні. Тому, позначивши такі заряди індексом \(k\), можемо записати:
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{1}{{{\varepsilon }_{0}}}\sum\limits_{k}{{q}_{k}}, \end{equation}
або
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{q}{{{\varepsilon }_{0}}}, \tag{5.12} \end{equation}
де \({q}=\sum\limits_{k}{q}_{k}\).
Це рівняння й виражає інтегральну теорему Гаусса для електричного поля у вакуумі:
потік напруженості електричного поля у вакуумі крізь довільну замкнену поверхню дорівнює сумарному зарядові, що знаходиться всередині цієї поверхні, діленому на \(\varphi_0\).
Рівняння (5.12) є чинним і для заряджених тіл, тобто для полів створених неперервним розподілом заряду в заданому об’ємі (рис. 5.5б). Тільки й того, що величина \(q\) визначається не додаванням зарядів , а інтегруванням заданої густини заряду \(\rho\) по об’єму \(V'\), який займають заряди всередині поверхні \(S\). Але область інтегрування формально поширюють на весь об’єм \(V\) обмежений замкненою поверхнею і записують
\begin{equation} {q}=\int\limits_{V}{\rho \,\mathrm{d}V}. \tag{5.13} \end{equation}
Таким чином,
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{1}{{{\varepsilon }_{0}}}\int\limits_{V}{\rho \,\mathrm{d}V}. \tag{5.14} \end{equation}
Це рівняння є найбільш загальним виразом теореми Гаусса, оскільки інтеграл у правій частині включає як окремі випадки і поверхневий, і лінійний, і дискретний розподіли заряду (див. п. 1.3).
Фізичний зміст теореми Гаусса. Переходячи до аналізу отриманих результатів, одразу звернемо увагу на те, що при незмінній величині заряду всередині замкненої поверхні потік поля крізь неї, тобто значення інтеграла (5.7), не залежить від форми та розмірів поверхні, тим самим і від величини та напрямку напруженості \(\vec{E}\) в різних точках поверхні. Це означає, що на практиці
при визначенні потоку крізь задану складну поверхню можна замінити її зручнішою для обчислень простою поверхнею, що охоплює ті самі заряди.
Друга особливість полягає в тому, що потік поля крізь замкнену поверхню визначається не всіма зарядами, що створюють це поле, а тільки тими з них, які опинилися всередині поверхні. Тому, якщо всередині поверхні зарядів немає, або їхня сума дорівнює нулю, то потік \(\Phi = 0\). Це може спровокувати на хибний висновок, що й напруженість поля \(\vec{E}=0\). Але відсутність потоку ще не означає відсутності поля. Просто в такій ситуації крізь різні ділянки замкненої поверхні створюються потоки різного знаку і такої величини, що сумарний потік виявляється нульовим. Очевидним прикладом є однорідне поле \(\vec{E}=\mathrm{const}\), потік якого крізь будь-яку замкнену поверхню дорівнює нулю.
Походження вказаних особливостей теореми Гаусса можна зрозуміти, повернувшись до її виведення. При цьому легко бачити, що вже у викладці, що передує виразу (5.10), щезає змінна \(r\), яка визначається положенням точок на вибраній поверхні, тож залежить від її розмірів і форми. Це стається через закон Кулона, згідно з яким поле точкового заряду \( E\sim ( {1}/{{{r}^{2}}} )\). При будь-якій іншій залежності \(E(r)\) потік був би залежним від \(r\). За праву частину рівняння (5.12) чи (5.14) “відповідальним” є принцип суперпозиції, який відображає незалежність електричних полів. Завдяки цьому заряди, розташовані назовні замкненої поверхні, не впливають на поле внутрішніх зарядів, отже, й на потік крізь цю поверхню.
Таким чином, теорема Гаусса органічно об’єднує обидва основні закони теорії електричного поля — закон Кулона і принцип суперпозиції. Тому в класичній теоретичній електродинаміці теорема Гаусса розглядається як один із вихідних постулатів (основних законів), а закон Кулона — як один із його наслідків.
Теорема Ірншоу. Позаяк між зарядами спостерігається і притягання, і відштовхування, то можна так підібрати величину та розташування зарядів у системі, що вона буде перебувати в стані механічної рівноваги. Прикладом може слугувати система з двох однакових зарядів \(q\) і розташованого посередині між ними заряду \(q'=-q/4\). Прямим обчисленням можна переконатися, що за таких умов рівнодійна сила, котра діє на кожен заряд з боку двох інших, дорівнює нулю, отже всі заряди перебувають в рівновазі. Але ця рівновага є нестійкою, і зміна положення будь-якого із зарядів призведе до її руйнації. Це відображає теорема Ірншоу, згідно з якою жодна система частинок, між якими діють тільки кулонівські сили, принципово не може перебувати в стані стійкої рівноваги.
Справедливість цього твердження прямо випливає з теореми Гаусса. Доведемо це від зворотнього, припустивши, що якийсь заряд \(-q\) (знак не істотний) системи знаходиться в положенні стійкої рівноваги. Тоді при всякому його зміщенні має з’являтися напрямлена до положення рівноваги сила \(\vec{F}=-q\vec{E}\) (рис. 5.7), що створюється полем \(\vec{E}\) решти зарядів.
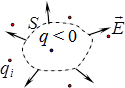
Тому, якщо охопити заряд маленькою замкненою поверхнею так, аби всі інші заряди опинилися поза нею, то вектори \(\vec{E}\) на цій поверхні скрізь мають бути напрямлені назовні і створювати крізь неї потік \(\Phi >0\). Але так не може бути, бо це суперечить теоремі Гаусса: всередині \(S\) немає жодного із зарядів, які створюють указане поле \(\vec{E}\), отже \(\Phi = 0\). Таким чином, стійка рівновага зарядів під дією тільки кулонівських сил є неможливою.
5.3. Обчислення полів за допомогою теореми Гаусса
Напруженість електричного поля, створеного будь-якою заданою системою зарядів, принципово завжди можна прямо розрахувати на основі закону Кулона і принципу суперпозиції, хоча такий розрахунок може виявитися досить трудомістким. Але для високосиметричних полів задачу можна розв’язати набагато легше за допомогою теореми Гаусса. Далі розглянуто декілька прикладів такого розрахунку для полів, що створюються однорідно (із сталою густиною) розподіленим зарядом.
Приклад 4. Циліндрична поверхня
Поле однорідно зарядженої кулі. Поставимо таку задачу: розрахувати напруженість \(\vec{E}(\vec{r})\) поля, що створюється у вакуумі зарядом розподіленим із густиною \(\rho(\vec{r})=\mathrm{const}\) по об’єму кулі радіуса \(R\) (рис. 5.8).
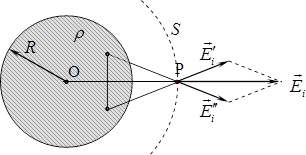
Приступаючи до обчислень, найперше встановимо симетрію поля — проаналізуємо, який воно має напрям і від чого залежить його величина в довільній точці \(P\). Це можна зробити за допомогою закону Кулона та принципу суперпозиції наступним чином. Якщо провести через точку \(P\) радіальну вісь, то при \(\rho=\textrm{const}\) всю кулю можна поділити на пари однакових малих ділянок із зарядами \(q_{i}\), розташованих симетрично до цієї осі. Поля цих зарядів \(\vec{E}{}_i'\) і \(\vec{E}{}_i''\) симетрично орієнтовані і однакові за модулем. Тож зрозуміло, що сумарне поле кожної пари зарядів \(\vec{E}_i=\vec{E}{}_i'+\vec{E}{}_i''\) і поле всієї кулі \(\vec{E}=\sum\limits\vec{E}_{i}\) скрізь мають радіальний напрям і однаковий модуль у рівновіддалених від центра кулі точках.
Таким чином, шукане поле є сферично симетричним (центральним): його лінії напруженості \(\vec{E}\) є радіальними променями, які починаються (або закінчуються) в центрі зарядженої кулі. Тому на концентричній сферичній поверхні довільного радіуса \(r\) проекція напруженості \({E}_n = \textrm{const}\). Через це інтеграл потоку (5.7) крізь таку поверхню легко обчислюється:
\begin{equation} \Phi=\oint\limits_S{E_n\,\mathrm{d}S}=E_n\oint\limits_S{\mathrm{d}S}, \end{equation}
або
\begin{equation} \Phi=E_n S, \tag{5.15} \end{equation}
де \({S}=\oint\limits_S\,\mathrm{d}{S}\) — площа всієї поверхні, крізь яку обчислюється потік.
З іншого боку за теоремою Гаусса потік крізь усяку замкнену поверхню визначається рівнянням (5.14). Тому підставивши в нього вираз (5.13), отримаємо:
\begin{equation} {{E}_{n}}=\frac{q}{{{\varepsilon}_{0}}S}, \tag{5.16} \end{equation}
де \(q\) — величина заряду всередині сфери.
Зауважимо, що позаяк вектор \(\vec{E}\) напрямлений по нормалі до поверхні \(S\), вона є однією з еквіпотенціальних поверхонь поля (див. п. 3.3). Тому зрозуміло, що формула (5.16) годиться не лише для центрального, а й для всякого іншого симетричного поля, що має еквіпотенціальні поверхні простої форми, на яких \(E_n=\textrm{const}\). Що ж до поля кулі, то у формулах (5.15) і (5.16) \(S = 4\pi r^2\), отже
\begin{equation} {E_n}=\frac{q}{4\pi\varepsilon_0{r^2}}. \tag{5.17} \end{equation}
Таким чином, для визначення напруженості поля \(E_n(r)\) треба лишень обчислити заряд зосереджений всередині сфери радіуса \(r\). В загальному випадку він визначається інтегралом (5.11), але при \(\rho=\textrm{const}\)
\begin{equation} q = \rho V', \end{equation}
де \(V'\) — частина об’єму всередині сферичної поверхні, що заповнена зарядом.
Об’єм \(V'\) залежить від того, охоплює сферична поверхня всю заряджену кулю, чи тільки її частину. Тому для визначення напруженості всередині кулі та поза нею розрахунок величини \(q\) треба проводити нарізно.
Поле всередині кулі (\(0\leqslant r \leqslant R\)). У цьому випадку весь обмежений сферичною поверхнею об’єм є заповнений зарядом, і
\begin{equation} {q}=\rho\frac{4}{3}\pi{r^3}. \end{equation}
Отже, згідно з формулою (5.14), всередині зарядженої кулі напруженість електричного поля
\begin{equation} {E_n}=\frac{\rho{r}}{3\varepsilon_0}, \tag{5.18} \end{equation}
або у векторному вигляді
\begin{equation} \vec{E}=\frac{\rho\vec{r}}{3\varepsilon_0}. \tag{5.18а} \end{equation}
Поле назовні кулі (\(r > R\)). За такої умови всередині сферичної поверхні незалежно від її радіуса \(r\) знаходиться весь заряд кулі
\begin{equation} {q}=\rho\frac{4}{3}\pi{R^3}. \end{equation}
Відповідно, напруженість електричного поля у зовнішній області простору
\begin{equation} {E_n}=\frac{\rho{R^3}}{3\varepsilon_0{r^2}}. \tag{5.19} \end{equation}
Аби записати цей вираз у векторній формі, помножимо праву частину на одиничний вектор \((\vec{r}/{r}) \). Тоді
\begin{equation} \vec{E}=\frac{\rho{R^3}}{3\varepsilon_0{r^3}}\vec{r}. \tag{5.19а} \end{equation}
Отримані формули (5.18) і (5.19) показують, що заряджена куля поділяє простір на дві області, в кожній з яких електричне поле залежить від відстані \(r\) до центра кулі за своїм законом. Графік залежності \(E(r)\) показано на рис. 5.9а.
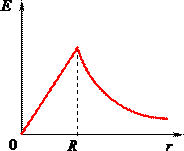
Зауважимо також, що коли у формулі (5.18а) виразити величину \(\rho\) через заряд всієї кулі, як \(\rho=q/(4/3)\pi{R^3}\), то вийде:
\begin{equation} \vec{E}(\vec{r})=\frac{q}{4\pi\varepsilon_0{r^3}}\vec{r}. \tag{5.19б} \end{equation}
Отже, поле назовні рівномірно зарядженої кулі збігається з полем точкового заряду такої самої величини, що розміщений у центрі кулі, рис. 5.9а.
Так виходить і при неоднорідному, але сферично симетричному розподілі заряду \(\rho(r)\).
Поле однорідно зарядженої сфери. Розрахуємо далі поле, що створюється сферичною оболонкою радіуса \(R\), зарядженою з поверхневою густиною заряду \(\sigma=\textrm{const}\). Це поле теж є сферично симетричним, тому його обчислення не відрізняється від попереднього. Відміна лише в тому, що всередині сферичної “гаусової” поверхні при \(r < R\) у формулі (5.16) \(q=0\), а при \(r\geqslant R\) \(q=\sigma\cdot 4\pi r^2\). Тому всередині зарядженої сфери (\(r < R\)) електричного поля немає:
\begin{equation} \vec{E}={0}. \end{equation}
Відповідно, назовні зарядженої сфери (\(r\geqslant R\)) напруженість електричного поля дорівнює
\begin{equation} {E(r)}=\frac{\sigma{R^2}}{\varepsilon_0{r^2}}, \quad \vec{E}(\vec{r})=\frac{\sigma{R^2}}{\varepsilon_0{r^3}}\vec{e}, \tag{5.20} \end{equation}
і, як говорилося, збігається з напруженістю поля точкового заряду \(q=\sigma\cdot 4\pi r^2\). Графік залежності \(E(r)\) показаний на рис. 5.9б.
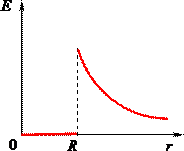
Поле однорідно зарядженого циліндра. Тепер знайдемо електричне поле, що створюється зарядом розподіленим із об’ємною густиною \(\rho=\textrm{const}\) по нескінченному циліндру радіуса \(R\) (рис. 5.10).
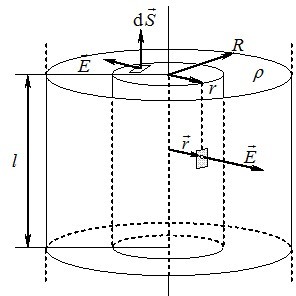
Міркуючи, як раніше, встановлюємо, що шукане має осьову симетрію : в будь-якій точці вектор \(\vec{E}\) напрямлений радіально, і його модуль залежить тільки від відстані до осі циліндра. Отже, якщо охопити частину заряду коаксіальною циліндричною поверхнею довільного радіуса \(r\) і висоти \(l\), то на його основах \(E_n = 0\). Тому потік створюється тільки через бічну поверхню \(S_{\text{біч}}=2\pi rl\), на якій скрізь \(E_n=\textrm{const}\). Відтак
\begin{equation} \Phi=\oint\limits_{S}E_{n}\,\mathrm{d}S=E_{n}\oint\limits_{S_{\text{біч}}}\,\mathrm{d}S=E_{n}\cdot{2}\pi{rl}. \end{equation}
Тож за формулою (5.14) для проекції напруженості на радіальний напрям маємо:
\begin{equation} {E_r}=\frac{q}{2\pi{l}\varepsilon_0{r}}. \tag{5.21} \end{equation}
Далі, як і в попередніх прикладах, обчислення величини \(q\) виконуємо нарізно для областей всередині та назовні зарядженого циліндра.
Поле всередині циліндра (\(r < R\)). У цьому випадку вся замкнена циліндрична поверхня радіуса \(r\) і висоти \({l}\) заповнена зарядом. Тому
\begin{equation} {q}=\rho\pi{r^2}{l}, \end{equation}
і, згідно з формулою (5.19),
\begin{equation} {E_r}=\frac{\rho{r}}{2\varepsilon_0}, \tag{5.22} \end{equation}
а у векторному вигляді
\begin{equation} \vec{E}=\frac{\rho\vec{r}}{2\varepsilon_0}. \tag{5.22а} \end{equation}
Поле назовні циліндра (\(r > R\)). За такої умови всередині замкненої поверхні незалежно від її радіуса \(r\) зосереджений весь заряд охопленої частини циліндра:
\begin{equation} {q}=\rho\pi{R^2}{l}. \end{equation}
Відповідно, формула (5.19):
\begin{equation} {E_r}=\frac{\rho{R^2}}{2\varepsilon_0{r}}. \tag{5.23} \end{equation}
Помноживши праву частину цієї формули на одиничний вектор \({(\vec{r}/r)}\), отримаємо вираз для вектора напруженості:
\begin{equation} \vec{E}=\frac{\rho{R^2}}{2\varepsilon{r^2}}\vec{r}. \tag{5.23а} \end{equation}
Порівнюючи вирази (5.22а) і (5.18а) та (5.23а) і (5.19а), бачимо, що залежності \(\vec{E}(\vec{r}) \) для поля циліндра та кулі є схожими. Відповідно, і графік залежності \(E(r)\) для поля циліндра якісно є таким, як на рис. 5.9а.
Поле однорідно зарядженої циліндричної поверхні. Якщо заряд розподілений із густиною \(\sigma=\textrm{const}\) по нескінченній циліндричній поверхні радіуса \(R\), то, як і у випадку сфери, для точок всередині у формулі (5.21) \(q=0\). Тому всередині зарядженої циліндричної поверхні (\(r < 0\)) поля немає:
\begin{equation} \vec{E}={0}; \end{equation}
Назовні (\(r \geqslant R\)) \( {q}=\sigma\cdot 2\pi{Rl} \), тож
\begin{equation} {E_r}=\frac{\sigma{R}}{\varepsilon_0{r}} \tag{5.24} \end{equation}
і
\begin{equation} \vec{E}=\frac{\sigma{R}} {\varepsilon_0{r^2}}\vec{r}. \tag{5.24а} \end{equation}
Графік залежності \(E(r)\) має вигляд рис. 5.9б.
Поле однорідно зарядженої нитки. Нитку будемо розглядати як нескінченний циліндр гранично малого радіуса, заряджений з лінійною густиною \(\lambda=\textrm{const}\). Тому напруженість поля визначається формулою (5.21), в якій \({q}=\lambda{l}\). Отже,
\begin{equation} {E_r}=\frac{\lambda}{2\pi\varepsilon_0{r}}. \tag{5.25} \end{equation}
У векторній формі
\begin{equation} \vec{E}=\frac{\lambda}{2\pi\varepsilon_0{r^2}}\vec{r}. \tag{5.25а} \end{equation}
Графік \(E(r)\) наведено на рис. 5.11.
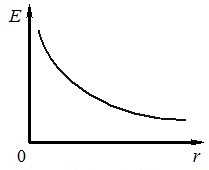
Поле однорідно зарядженої площини. Нарешті визначимо напруженість електричного поля, що створюється нескінченною плоскою поверхнею, зарядженою з поверхневою густиною заряду \(\sigma=\textrm{const}\).
Для встановлення симетрії поля теж можна скористатися законом Кулона та принцип суперпозиції. Але симетрію як цього так і розглянутих полів можна з’ясувати й на основі загальних логічних міркувань, які спираються на однорідність та ізотропність простору. А саме. Уявімо, що вектор \(\vec{E}\) має певний напрям, що складає з площиною кут \(\alpha\ne 90^\circ\). Але тоді виникає запитання, на яке немає відповіді: а чому в такому разі вектор \(\vec{E}\) не може бути спрямований в будь-якому іншому з безлічі напрямків під тим самим кутом \(\alpha\) до площини, адже всі вони є фізично еквівалентними (рівноправними). У той же час подібне запитання не виникає щодо перпендикулярного (\(\alpha=90^\circ\)) до площини напрямку, бо він є один. Отже, у випадку нескінченної однорідно зарядженої площини вектор \(\vec{E}\) скрізь напрямлений перпендикулярно до неї в той чи інший бік залежно від знаку заряду. З таких самих міркувань очевидно, що фізично еквівалентними є і всі точки будь-якої площини паралельної до тієї, що створює поле. Тому на такій площині не тільки напрям, а й модуль напруженості \(E\) скрізь однаковий, тож \(\vec{E}=\textrm{const}\). Іншими словами, дане поле є плоско симетричним і однорідним.
Зауваження. Наведені міркування є придатними для аналізу симетрії будь-якої задачі і мають таку саму доказову силу, як і аналітичні викладки. Але до подібного аналізу слід підходити з уважністю. Наприклад, поле однорідно зарядженої плоскої поверхні у формі диска теж симетричне, але його симетрія не є плоскою. Зокрема, перпендикулярно до площини диска воно напрямлене тільки на осі. Модуль напруженості теж однаковий не скрізь, а тільки на колі з центром на осі й площиною паралельною до площини диска.
Завдяки високій симетрії поле площини теж легко розраховується за допомогою теореми Гаусса. Для цього оточимо частину площини якоюсь замкненою поверхнею, до прикладу, прямим циліндром із паралельними до площини і рівновіддаленими від неї основами, рис. 5.12а.
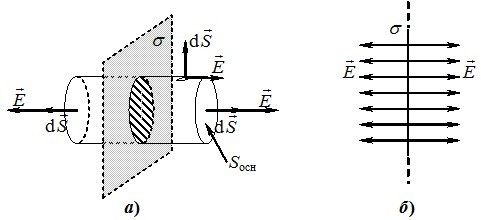
У такому випадку вектори \(\vec{E}\) на основах циліндра мають однакову величину \(E_n=\textrm{const}\), а на бічній поверхні поле є скрізь паралельним до неї і не створює потоку. За таких умов інтеграл потоку (5.5) крізь увесь замкнений циліндр виражається як
\begin{equation} \Phi=2E_{n}\int\limits_{S_{\text{осн}}}\,\mathrm{d}S=2E_{n}S_{\text{осн}}. \end{equation}
При цьому заряд всередині циліндра \(q = \sigma S_{\text{осн}}\). Отже, з рівняння (5.10) маємо:
\begin{equation} {E_n}=\frac{\sigma}{2\varepsilon_0}. \tag{5.26} \end{equation}
У векторному вигляді
\begin{equation} \vec{E}=\frac{\sigma}{2\varepsilon_0}\vec{n}, \tag{5.26а} \end{equation}
де \(\vec{n}\) — орт зовнішньої нормалі до площини.
Таким чином, заряджена з густиною \(\sigma=\textrm{const}\) нескінченна площина створює по обидва боки однорідне електричне поле, що напрямлене від площини при \(\sigma > 0\) і до неї при \(\sigma < 0\). Лінії такого поля являють систему паралельних променів, які розміщені на однаковій відстані один від одного (рис. 5.12б).
Контрольні запитання
1. Що називається циркуляцією силового поля \(\vec{F}\) по заданому контуру \(L\). Який фізичний зміст має ця величина та від чого залежить її знак для заданого контуру?
2. Яку ознаку поля відображає його циркуляція по довільному контуру? Чому вона дорівнює для електричного поля зарядів?
3. Поміркуйте, в яких одиницях вимірюється та що собою являє потік електричного заряду через поверхню поперечного перерізу провідника, по якому тече електричний струм.
4. Потік електричного поля крізь задану замкнену поверхню дорівнює нулю. Чи означає це, що всередині неї немає поля? Немає зарядів?
5. Чому потік поля точкового заряду \(q\) крізь якусь замкнену поверхню дорівнює нулю, коли заряд перебуває поза нею, і не дорівнює нулю, коли він знаходиться всередині?
6. Електричне поле створюється двома паралельними площинами, що різноіменно заряджені з однаковою густиною заряду \(\sigma\) (\(\text{Кл/м}^2\)). Визначте потік електричного поля крізь якусь замкнену поверхню, що розташована: а) поза площинами; б) між площинами. Що спричинює кожну відповідь?
7. Електричне поле створюється двома паралельними площинами, що заряджені з однаковою густиною заряду \(\sigma\) (\(\text{Кл/м}^2\)). Визначте потік електричного поля крізь внутрішню та зовнішню частину поверхні невеликої сфери радіуса \(R\) із центром на одній з пластин, якщо площини заряджені: а) різнойменно і б) однойменно.
8. Із теореми Гаусса випливає, що всередині будь-якої зарядженої провідної оболонки (замкненої поверхні) електричне поле відсутнє. Як це довести?
ІІ. ЕЛЕКТРИЧНЕ ПОЛЕ В РЕЧОВИНІ
Добре відомо, що середовище істотно впливає на електричне поле. Це пояснюється тим, що всяка речовина є сукупністю великої кількості атомів, що складаються із заряджених частинок – ядер та електронів, які створюють мікроскопічне електричне поле (“мікрополе”) атома \(\vec{E}_{\text{мікро}}\). Через загальну електричну нейтральність атома та швидкий рух зарядів, мікрополе має помітну величину лише в околі атома і хаотично змінюється в часі внаслідок теплового руху атомів. Тому при описі поля в речовині використовують усереднене мікроскопічне поле \({\vec E}{}'=\langle E_{\text{мікро}}\rangle\), яке називають внутрішнім або власним макроскопічним полем (макрополем) речовини. При цьому, аби величина \({\vec E}{}'\) визначала поле локально (в кожній точці середовища), усереднення проводиться по так званому фізично нескінченно малому об’єму — ділянці, яка за розмірами практично є точковою, але містить макроскопічну кількість атомів. При такому усередненні згладжуються всі нерегулярності та швидкі зміни поля на відстанях порядку міжатомних, але зберігаються плавні зміни макроскопічного поля.
Через хаотичність теплового руху атомів, мікрополя зазвичай є компенсованими, і власне макроскопічне поле в речовині є відсутнім. Але при вміщенні зразка речовини в зовнішнє електричне поле воно спричинює переміщення негативних і позитивних зарядів атомів у взаємно протилежних напрямках, що порушує компенсацію мікрополів. Як наслідок, у речовині виникне власне макроскопічне поле, що разом із зовнішнім утворює результуюче поле з іншою напруженістю.
Описане переміщення зарядів під дією поля відбувається в усіх речовинах, але його особливості і ступінь впливу на поле істотно залежить від внутрішньої будови речовини. З огляду на це всі речовини поділяються на два класи — діелектрики і провідники. За електричними властивостями розрізняють іще один клас речовин — напівпровідники. Але за характером впливу на електричне поле вони є просто недосконалими діелектриками.
Електричні властивості діелектриків і провідників та їхній вплив на електричне поле розглядаються в наступних розділах:
1. Електричне поле в діелектриках
Вплив діелектриків на характеристики електричного поля розглядається в наступних питаннях:
1.2. Теорема Гаусса для діелектриків. Вектор \(\vec{D}\)
1.3. Діелектричні сприйнятливість і проникність
1.1. Поляризація діелектриків
Полярні та неполярні молекули. Діелектриками називаються речовини, в молекулах яких усі електрони сильно зв’язані з ядрами так, що навіть у сильних електричних полях вони ледь зміщуються відносно ядер. Через це в діелектрику є неможливим електричний струм, тобто переміщення зарядів по всьому об’єму. З цієї причини суцільна діелектрична оболонка ізолює область, яку оточує, від проникнення в неї зарядів. Тому діелектрики інакше називаються “ізоляторами”.
В атомах і молекулах електрони рухаються так швидко, що ядра є немов оточені суцільною хмаринкою від’ємного заряду, або вкриті “електронною оболонкою”. При цьому, залежно від конфігурації електронних оболонок, молекули і діелектричні речовини поділяють на неполярні та полярні. У молекулах неполярних діелектриків, прикладами яких є гелій \(\textrm{He}\) та молекулярний водень \(\textrm{H}_2\), “центри ваги” зарядів електронів і ядер збігаються, як можна зрозуміти із схематичного на рис. 1.1а.
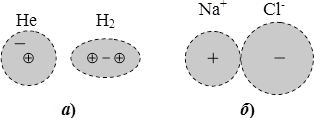
Тому неполярні молекули самі по собі не мають електричного моменту і не створюють власного електричного поля. В молекулах полярних діелектриків, таких як \(\textrm{NaCl}\), заряди електронів і ядер рознесені у просторі (рис. 1.1б) й утворюють елементарні диполі з відповідним власним електричним моментом. Тому в околі полярної молекули існує власне мікрополе \(\vec{E}_{\text{мікро}}\).
Нижче ви можете бачити анімацію, як демонструє поведінку різних молекул в електричному полі.
Поляризація і поляризованість. Унаслідок теплового руху молекул їхні мікрополя в полярному діелектрику орієнтовані хаотично, так що середня величина \(\langle\vec{E}_{\text{мікро}}\rangle=0\). Тому не тільки в неполярних, а й у полярних діелектриках зазвичай ніякого макроскопічного поля немає. Але при внесенні діелектрика в зовнішнє електричне поле \(\vec{E}_{0}\) ситуація змінюється внаслідок поляризації.
Сутність цього явища з’ясуємо на прикладі діелектрика з неполярними молекулами, які будемо розглядати як нейтральні кульки. На перший погляд такі молекули через високий ступінь просторової компенсації зарядів узагалі не мають реагувати на зовнішнє електричне поле. Але поле діє не на молекулу як ціле, а на електрони і на ядра окремо. Через це відбувається деформація електронних оболонок — електрони зміщуються відносно ядер і в кожної молекули з’являється так званий індукований (або наведений) електричний момент \(\vec{p}_{i}\), орієнтований у напрямку електричного поля (рис. 1.2а).
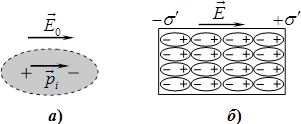
Рознесення негативних і позитивних зарядів частинок діелектрика у взаємно протилежних напрямках під дією електричного поля називається поляризацією.
Примітка. У деяких діелектриках, які називаються п’єзоелектриками, поляризація спостерігається і при механічних деформаціях.
У полярних діелектриках головну роль при поляризації відіграє не деформація електронних оболонок молекул, а переорієнтація їхніх власних електричних моментів під дією поля. Відповідно, поляризацію неполярних діелектриків називають деформаційною, а полярних — орієнтаційною. Слід відмітити, що власні моменти полярних молекул є значно більшими, ніж індуковані. Але через їхню хаотичну орієнтацію та інтенсивний тепловий рух молекул при орієнтаційній поляризації відбувається лише часткове впорядкування власних моментів, так що в обох цих типах діелектриків здатність до поляризації є приблизно однаковою.
При будь-якому виді поляризації молекули під дією електричного поля утворюють систему елементарних диполів із частково впорядкованими (ефетивними) моментами \(\vec{p}_{i}\), фспрямованими по полю, як на рис. 1.2. Тому кожна область діелектрика набуває електричного моменту \(\sum\limits\vec{p}_{i}\ne{0}\). Як наслідок порушується компенсація мікроскопічних полів молекул і в діелектрику виникає внутрішнє (власне) макроскопічне поле \(\vec{E}{'}\). Це поле разом із зовнішнім полем \(\vec{E}_{0}\) формує результуюче макроскопічне поле в діелектрику:
\begin{equation} \vec{E}=\vec{E}_0+\vec{E}{'}. \tag{1.1} \end{equation}
Зрозуміло, що чим сильніша поляризація, тим більша величина \( \sum\limits{\vec{p}_i} \). Тому її використовують для кількісної характеристики ступеня поляризації діелектрика в кожній точці. Відповідна фізична величина називається поляризованістю або вектором поляризації \( \vec{P} \). За означенням
\begin{equation} \vec{P}=\frac{1}{\Delta{V}}\sum\limits\vec{p}_{i}, \tag{1.2} \end{equation}
де \(\Delta V\) — фізично нескінченно малий об’єм діелектрика в околі даної точки, \( \vec{p}_{i} \) — електричні моменти окремих молекул у цьому об’ємі.
Примітка. Як говорилося на початку, фізично нескінченно малим об’ємом називається область у речовині, яка може вважатися точковою, але вміщує макроскопічну кількість молекул. Такі вимоги не є суперечливими через гранично малі розміри молекул. Наприклад, у кубику твердої речовини з ребром \(10^{-6}\) м міститься \(10^{10}\div10^{11}\) молекул.
Отже, можна сказати, що
поляризованість \(\vec{P}\) дорівнює електричному моменту одиниці об’єму поляризованого діелектрика.
Одиницею поляризованості є \(1~\text{Кл/м}^2\), що збігається (і не випадково) з одиницею поверхневої густини заряду.
В однорідному неполярному діелектрику індуковані дипольні моменти всіх молекул однакові, і вираз (1.2) можна записати у вигляді:
\begin{equation} \vec{P}=n\vec{p}, \tag{1.2а} \end{equation}
де \(n\) (\(1/\text{м}^3\)) — концентрація молекул (кількість в одиниці об’єму), \(\vec{p}\) — дипольний момент однієї молекули. Якщо ж вираз (1.2) помножити і поділити на кількість молекул в об’ємі \(\Delta V\), то таким робом можна виразити і поляризованість неоднорідного діелектрика:
\begin{equation} \vec{P}=\frac{N}{\Delta{V}}\cdot\frac{\sum\limits{\vec{p}_{i}}}{N}\quad \Rightarrow \quad \vec{P}=n\langle{\vec{p}_{i}}\rangle, \tag{1.2б} \end{equation}
де \(\langle{\vec{p}_{i}}\rangle \) — дипольний момент, який у середньому припадає на одну молекулу в об’ємі \(\Delta V\).
Поляризаційні та сторонні заряди. В усіх діелектриках поляризація супроводжується появою макроскопічних поляризаційних зарядів.
Механізм виникнення поляризаційних зарядів в однорідному неполярному діелектрику, вміщеному в однорідне електричне поле, ілюструє рис. 1.2б. Унаслідок деформації електронних оболонок молекул електрична нейтральність діелектрика в цілому не порушується, але на його поверхнях з’являються макроскопічні заряди протилежного знаку, що розподіляються з деякою густиною \(\sigma '\) і \(-\sigma '\) і тому називаються поверхневими поляризаційними зарядами. В той же час всередині різнойменні заряди сусідніх молекул розміщені щільно, і в об’ємі діелектрик лишається електрично нейтральним у кожній точці. У полярних діелектриках поверхневі поляризаційні заряди виникають унаслідок повороту дипольних моментів молекул у напрямку поля.
У неоднорідних діелектриках, а також при вміщенні діелектриків у неоднорідне електричне поле, крім поверхневих, виникають і об’ємні поляризаційні заряди, розподілені з деякою об’ємною густиною \(\rho'\). Це легко зрозуміти на прикладі поляризації умовного неоднорідного діелектрика, в якому концентрація молекул зростає в напрямку зовнішнього поля. В такому разі на поверхню зразка, що орієнтована по полю, вийде більше «плюсів» ніж вийде «мінусів» на протилежну поверхню (рис. 1.3)
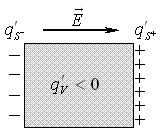
Тож на поверхнях з’явиться сумарний поляризаційний заряд \((q'_{s^+}+q'_{s^-}) > 0\). Тому, враховуючи загальну нейтральність зразка, в об’єм теж стане зарядженим:
\begin{equation} q'_{s^+}+q'_{s^-}+q'_{V}=0 \quad \Rightarrow \quad q'_V=-(q'_{s^+}+q'_{s^-}) < 0 . \end{equation}
Цей об’ємний поляризаційний заряд, розподіляється з відповідною об’ємною густиною \(\rho' < 0\). Зрозуміло, що при зміні напрямку поля на протилежний зміниться і знак \(\rho'\).
При поляризації електрони в молекулах діелектрика зміщуються тільки на дуже малу відстань, лишаючись зв’язаними із своїми ядрами. Тому поляризаційні заряди не можна відокремити один від одного і перемістити в інше місце. Приміром, якщо зразок поляризованого діелектрика розрізати навпіл, то обидві частини лишаться електрично нейтральними і поляризованими так само, як вихідний зразок. Тому поляризаційні заряди інакше називають зв’язаними зарядами.
Принагідно зазначимо, що в теорії електричного поля в діелектриках оперують також поняттям вільних зарядів. Так називають заряди, що, в принципі, можуть довільно розташовуватися і переміщуватися. Вони не належать атомам середовища, тому ще називаються сторонніми зарядами. Такі заряди створюють зовнішнє поле \(\vec{E}_{0}\), яке є першопричиною поляризації. Прикладом сторонніх зарядів можуть бути заряди заряджених кульок, вміщених у діелектричну рідину, або протилежні за знаком заряди на пластинах зарядженого конденсатора, між якими знаходиться діелектрик.
Зв’язок між поляризованістю та поляризаційними зарядами. Із сказаного вище зрозуміло, що величина і розподіл поляризаційних зарядів у діелектрику залежать від ступеня та характеру поляризації.
Установимо спочатку зв’язок між поляризованістю \(\vec P\) і густиною поверхневих поляризаційних зарядів \(\sigma '\). Для цього в шарі однорідно поляризованого діелектрика (\(\vec P = \text{const} \)) товщиною \(h\) виділимо ділянку у вигляді косого циліндра із твірною \(l\) та основами \(\Delta S\), як показано на рис. 1.4.
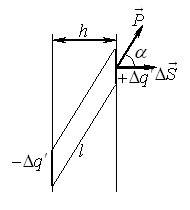
На основах циліндра зосереджені різнойменні поляризаційні заряди однакової величини \(q = \sigma '\Delta S\), отже, він є диполем із плечем \(l = h/\cos \alpha\) і величиною електричного моменту
\begin{equation} p={\sigma }'\Delta Sl= {{\sigma }'\Delta S}\frac{h}{\cos \alpha }. \end{equation}
Поділивши цю величину на об’єм циліндра \(\Delta V = \Delta S h = \Delta S l\cos \alpha \) згідно з означенням (1.2), отримаємо для поляризованості:
\begin{equation} P = \frac{{\sigma '}}{{\cos \alpha }}\quad \Rightarrow \quad P\cos \alpha = \sigma ', \end{equation}
або
\begin{equation} {P_n} = \sigma ', \tag{1.3} \end{equation}
де \({P_n} = P\cos \alpha \) — нормальна до площадки \(\Delta S\) складова поляризованості.
Такий самий результат дістанемо і при неоднорідній поляризації, взявши такі малі значення \(h\) і \(\Delta S\), аби в межах \(\Delta V\) неоднорідність була не істотною. Тому формула (1.3) є загальною й означає, що
на поверхні діелектрика нормальна складова поляризованості в будь-якій точці дорівнює поверхневій густині зв’язаних зарядів у цій точці.
Зокрема, в прямому циліндрі з діелектрика, що однорідно поляризований уздовж осі, поверхнева густина зв’язаних зарядів на основах \(\sigma ' = P\), а повна величина заряду \({q'_s} = PS\) (\(S\) — площа основи). На бічній поверхні \({P_n} = 0\), отже, \(\sigma ' = 0\) і \({q'_S} = 0\).
У загальному випадку зв’язаний заряд на якійсь поверхні \(S\) (рис. 1.5а) визначається інтегруванням зарядів \({\text{d}}q' = \sigma '{\,\text{d}}S\) на всіх її елементарних ділянках:
\begin{equation} {q'_S} = \int\limits_S {{P_n}\,\text{d} S = } \int\limits_S {P\,\text{d} S\cos\alpha = } \int\limits_S {\vec P\,\text{d} \vec S} . \end{equation}
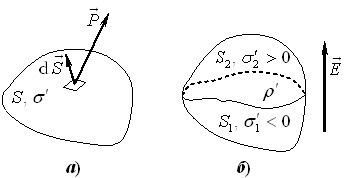
Іншими словами,
поляризаційний заряд на поверхні діелектрика дорівнює потокові вектора \(\vec P\) крізь цю поверхню.
За допомогою виразу (1.3) можна знайти зв’язок і між поляризованістю та об’ємними поляризаційними зарядами. Для цього розглянемо потік вектора \(\vec P\) крізь довільну замкнену поверхню \(S\) (рис. 1.5б). Подумки поділимо її на дві частини \({S_1}\) і \({S_2}\). Тоді потік крізь усю поверхню
\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = \int\limits_{{S_1}} {\vec P\,\text{d} \vec S} + \int\limits_{{S_2}} {\vec P\,\text{d} \vec S} , \end{equation}
і, враховуючи (1.3),
\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = \int\limits_{{S_1}} {{{\sigma '}_1}\,\text{d} S} + \int\limits_{{S_2}} {{{\sigma '}_2}\,\text{d} S} = {q'_{S1}} + {q'_{S2}} = {q'_S}, \tag{1.4} \end{equation}
де \({q'_S} = {q'_{S1}} + {q'_{S2}}\) — поляризаційний заряд на всій замкненій поверхні \(S\).
При однорідній поляризації \({q'_{S1}}\) і \({q'_{S2}}\) відрізняються тільки знаком, так що \({q'_S} = 0\). Але в неоднорідно поляризованому діелектрику \(| {{q'_{S1}}} | \ne {q'_{S2}}\), тож при його загальній електричній нейтральності зразка заряд на всій поверхні \({q'_S} \ne 0\). Це означає, що при неоднорідній поляризації в об’ємі теж виникає поляризаційний заряд \({q'_V} = - {q'_S}\). Відтак вираз (1.4) можна подати у вигляді:
\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = - {q'_V}. \tag{1.5} \end{equation}
або
\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = - \int\limits_V {\rho '\,\text{d} V} , \tag{1.5а} \end{equation}
де \(\rho '\) — об’ємна густина поляризаційного заряду.
Рівняння (1.5), (1.5а) встановлюють загальний зв’язок між поляризованістю та поляризаційними зарядами в діелектрику і по суті виражають теорему Гаусса для вектора \(\vec P\):
потік вектора поляризованості крізь довільну замкнену поверхню в діелектрику дорівнює величині поляризаційного заряду всередині цієї поверхні взятому з протилежним знаком.
1.2. Теорема Гаусса для діелектриків. Вектор \(\vec D\)
Як говорилося на початку, поле в діелектрику складається з поля сторонніх зарядів \({\vec E_0}\) і внутрішнього макроскопічного поля \(\vec E'\):
\begin{equation} \vec E = {\vec E_0} + \vec E'. \end{equation}
При цьому внутрішнє макроскопічне поле \(\vec E'\) є усередненим мікроскопічним полем всіх молекул поляризованого діелектрика. Але речовина діелектрика скрізь, окрім місць розташування поляризаційного заряду, лишається електрично нейтральною і як така участі у створенні поля \(\vec E'\) не бере. Тому при розгляді поля в діелектрику можна вважати, що поляризаційні заряди, як і сторонні, розташовані у вакуумі. Відтак на основі теореми Гаусса ((5.14), розділ І) для результуючого поля \(\vec E\) можна записати:
\begin{equation} \oint\limits_S {\vec E\,\text{d} \vec S = } \frac{1}{{{\varepsilon _0}}}\int\limits_V {( {\rho + \rho '} )\,\text{d} V} , \tag{1.6} \end{equation}
де \(\rho\) i \(\rho '\) — об’ємна густина сторонніх і поляризаційних зарядів, відповідно.
Рівняння (1.6) є подібним до ((5.14), розділ І) але трактувати його як вираз теореми Гаусса для поля в діелектриках не можна, бо воно містить невідомий параметр \(\rho '\), який не визначає поле \(\vec E\), а сам залежить від нього. Тому з огляду на теорію рівняння (1.6) не виражає фундаментальних (загальних) властивостей поля в діелектриках, і не може трактуватись як самодостатній фізичний закон. Воно лише відображає той тривіальний факт, що у створенні електричного поля в діелектрику окрім сторонніх зарядів беруть участь і заряди самого діелектрика. Практичної цінності рівняння (1.6) теж не має, бо шукати з нього невідоме поле \(\vec E\) можна було би тільки знаючи розподіл поляризаційних зарядів \(\rho '\), який визначається тим таки невідомим полем \(\vec E\).
Але вихід з цього хибного логічного кола існує, позаяк поляризаційні заряди є пов’язані з поляризованістю. Розкривши у виразі (1.6) дужки та зробивши заміну (1.5а) матимаемо:
\begin{equation} \oint\limits_{S}{\vec{E}\,\text{d}\vec{S}} = \int\limits_{V}{\rho \,\text{d}V} - \oint\limits_{S}{\vec{P}\,\text{d}\vec{S}}\quad \Rightarrow \quad \oint\limits_{S}{( {{\varepsilon }_{0}}\vec{E}+\vec{P} )\,\text{d}\vec{S}} = \int\limits_{V}{\rho \,\text{d}V}. \tag{1.7} \end{equation}
Величина в дужках, як і напруженість \(\vec E\), є визначеною в усіх точках простору і утворює відповідне векторне поле. Тому вона позначається одним символом \(\vec D\) і називається “вектором \(\vec D\)” або “вектором електричного зміщення”. Таким чином, за означенням
вектором електричного зміщення називається вектор
\begin{equation} \vec D = {\varepsilon _0}\vec E + \vec P. \tag{1.8} \end{equation}
Відтак рівняння (1.7) набуває вигляду:
\begin{equation} \oint\limits_S {\vec D\,\text{d} \vec S = } \int\limits_V {\rho \,\text{d} V} \tag{1.9} \end{equation}
або
\begin{equation} \oint\limits_S {\vec D\,\text{d} \vec S = } q \tag{1.9а} \end{equation}
і виражає теорему Гаусса для електричного поля в діелектриках:
потік вектора \(\vec D\) крізь довільну замкнену поверхню дорівнює сумарній величині вільного заряду всередині цієї поверхні.
Рівняння (1.9), на відміну від (1.7), не містить невідомих параметрів і є чинним як для всіх діелектриків, так і для вакууму. Справді, у вакуумі через відсутності речовини \(\rho ' = 0\), тож \(\vec D = {\varepsilon _0}\vec E\), і рівняння (1.9) трансформується в рівняння (5.14) теореми Гаусса для поля у вакуумі:
\begin{equation} \oint\limits_S {{\varepsilon _0}\vec E\,\text{d} \vec S = } \int\limits_V {\rho \,\text{d} V} \quad \Rightarrow \quad \oint\limits_S {\vec E\,\text{d} \vec S = } \frac{1}{{{\varepsilon _0}}}\int\limits_V {\rho \,\text{d} V} . \end{equation}
Теорема Гаусса виконується і в нестаціонарних полях при не надто швидкій їхній зміні з часом. Тому рівняння (1.9) є одним з основних інтегральних рівнянь класичної теорії електромагнітного поля, створеної Максвеллом. Разом із тим слід усвідомити, що вектор \(\vec D\) є синтетичним утворенням і не має прямого фізичного змісту, як, скажімо, вектор \(\vec E\). Справді, згідно з означенням (1.8), вектор \(\vec D\) є комбінацією двох різних за змістом векторів: вектора \({\varepsilon _0}\vec E\), що визначається станом поля, та вектора \(\vec P\), який відображає стан речовини. Тому
вектор \(\vec D\) не є польовим вектором,
тобто кількісною характеристикою електричного поля.
1.3. Діелектричні сприйнятливість і проникність
Уведення вектора \(\vec D\) є доцільним і в практичному сенсі, бо часто полегшує обчислення електричного поля в діелектриках. Це зумовлено тим, що в деяких випадках поле вектора \(\vec D\) можна розрахувати, знаючи розподіл тільки сторонніх зарядів. З іншого боку, за поляризацію відповідає повне поле в діелектрику, тож поляризованість \(\vec P\) є функцією напруженості \(\vec E: \vec P = \vec P( {\vec E} )\). Тому при відомому зміщенні, вираз (1.8) із означення перетворюється на функціональне рівняння
\begin{equation} \vec{D}( {\vec{r}} )={{\varepsilon }_{0}}\vec{E}( {\vec{r}} )+\vec{P}( \vec{E}( {\vec{r}} ) ) \tag{1.10} \end{equation}
з якого можна визначити напруженість поля, створеного в діелектрику заданим розподілом сторонніх зарядів \(\rho ( {\vec r} )\).
Такий розрахунок включає два етапи:
— визначення допоміжного вектора \(\vec D( {\vec r} )\) через заданий розподіл сторонніх зарядів \(\rho ( {\vec r} )\);
— визначення основного вектора поля \(\vec E( {\vec r} )\) за допомогою рівняння (1.10).
У загальному випадку це може бути не простою задачею через складну залежність поляризованості від напруженості поля \(\vec P = \vec P( {\vec E} )\). Але ізоляційні матеріали, що використовуються в електротехніці та електроніці, є ізотропними діелектриками, і залежність \(\vec P( {\vec E} )\) в них має простий вигляд:
\begin{equation} \vec P=\varepsilon_0\varkappa\vec E, \tag{1.11} \end{equation}
де безрозмірне число \(\varkappa\) називається діелектричною сприйнятливістю діелектрика. Ця величина показує, наскільки сильно, чи слабко поляризується діелектрик в полі заданої напруженості, тобто дійсно характеризує його сприйнятливість до впливу електричного поля.
Підставивши співвідношення (1.11) у рівняння (1.10), отримаємо:
\begin{equation} \vec D=\varepsilon_0(1+\varkappa)\vec E. \tag{1.12} \end{equation}
У цьому виразі число в дужках має той самий, що й \(\varkappa \), загальний зміст. Тому його позначають одним символом \(\varepsilon \) і називають діелектричною проникністю речовини. Отже, за означенням
\begin{equation} \varepsilon=1+\varkappa. \tag{1.13} \end{equation}
Діелектрична проникність є табличною характеристикою речовини і для звичайних діелектриків складає декілька одиниць за винятком води, для якої \(\varepsilon = 81\). Але існують також тверді діелектрики, що звуться сегнетоелектриками, і мають аномально високу (до \( \sim 104\)) проникність. Це зумовлено особливостями їхньої внутрішньої будови.
Із виразів (1.12) і (1.13) випливає важлива формула, що напряму пов’язує вектори \(\vec D\) і \(\vec E\) в ізотропному діелектрику:
\begin{equation} \vec D = {\varepsilon _0}\varepsilon \vec E. \tag{1.14} \end{equation}
1.4. Умови на межі двох діелектриків
Співвідношення (1.14) пов’язує напруженість \(\vec E\) поля в діелектрику з допоміжною величиною \(\vec D\). Але реально напруженість поля в заданому діелектрику визначається полем сторонніх зарядів \({\vec E_0}\), в яке він уміщений і яке є першопричиною його поляризації. Аби встановити зв’язок між векторами \(\vec E\) і \({\vec E_0}\), для початку розглянемо поле у плоскопаралельній пластині однорідного ізотропного діелектрика з проникністю \(\varepsilon \), яка вміщена в однорідне зовнішнє поле \({\vec E_0} = \text{const}\), що перпендикулярне до її поверхонь, рис. 1.6а.
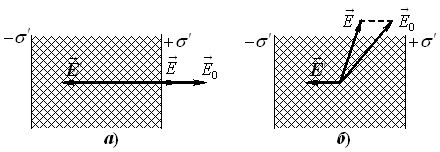
За таких умов внутрішнє поле \(\vec E'\) можна розглядати як поле двох заряджених з густиною заряду \(\sigma'\) і \(-\sigma'\) паралельних площин (поверхонь діелектрика). Воно напрямлене протилежно до зовнішнього поля \({\vec E_0}\) і, згідно з принципом суперпозиції і формулою ((5.23), розділ І), має величину
\begin{equation} E' = \frac{{\sigma '}}{{{\varepsilon _0}}}. \end{equation}
Тому модуль напруженості результуючого поля в діелектрику, відповідно до (1.1), дорівнює
\begin{equation} E = {E_0} - \frac{{\sigma '}}{{{\varepsilon _0}}}. \end{equation}
Звідси, врахувавши співвідношення (1.3) і (1.11), знаходимо зв’язок між полями:
\begin{equation} E=E_0-\varkappa E \quad \Rightarrow \quad (1+\varkappa) E = E_0 \quad \Rightarrow \quad \varepsilon E=E_0\Rightarrow\vec E=\frac{\vec E_0}{\varepsilon} . \tag{1.15} \end{equation}
Отже, пластина послаблює поле в \(\varepsilon \) разів без зміни його напрямку. Тому може здатися, що проникність зразка діелектрика \(\varepsilon \) — то є просто коефіцієнт послаблення ним електричного поля. Але насправді діелектрична проникність не має такого прозорого змісту, а простота виразу (1.15) зумовлена не властивостями речовини діелектрика, а формою та орієнтацією його поверхонь. Це стає зрозумілим, якщо розглянути ту саму пластину вміщену в електричне поле, що спрямоване навкіс, як на рис. 1.6б. Очевидно, що тепер вектори \({\vec E_0}, \vec E'\) і \(\vec E\) вже не є колінеарними, тож і \(\vec E \ne ( \vec E_0/\varepsilon )\). Тому формула (1.15) без застережень виконується лише в абстрактному ізотропному діелектрику, що не має поверхонь, тобто займає увесь безмежний простір. Що ж до обмеженого діелектрика, що має певні розміри та поверхню, співвідношення (1.15) виконується тільки у відповідних випадках, які визначаються так званими умовами на межі — співвідношеннями між векторами \({\vec D_1}\) і \({\vec D_2}\) та \({\vec E_1}\) і \({\vec E_2}\) на поверхні поділу двох діелектриків.
Визначимо указані співвідношення для двох ізотропних діелектриків з проникностями \({\varepsilon _1}\) і \({\varepsilon _2}\) у випадку, коли на межі поділу немає сторонніх зарядів. Для цього спочатку розглянемо потік вектора \(\vec D\) крізь поверхню невеликого замкненого циліндра з паралельними до межі поділу основами \(\Delta S\) і висотою \(h\), рис. 1.7а.
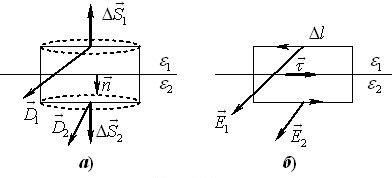
Цей потік складається з потоків через основи циліндра \(\Delta {\Phi _1}, \Delta {\Phi _2}\) і бічну поверхню \(\Delta \Phi '\) і, згідно з теоремою Гаусса (1.9), за відсутності сторонніх зарядів дорівнює нулю:
\begin{equation} \Delta {\Phi _1} + \Delta {\Phi _2} + \Delta \Phi ' = 0. \end{equation}
Позаяк циліндр малий, потоки через основи можна наближено записати як \(\Delta {\Phi _1} \approx - {D_{1n}}\Delta S\) і \(\Delta {\Phi _2} \approx {D_{2n}}\Delta S\), спроектувавши вектори на спільну нормаль \(\vec n\) до межі поділу. Тоді виходить:
\begin{equation} - {D_{1n}}\Delta S + {D_{2n}}\Delta S + \Delta \Phi ' \approx 0. \end{equation}
Неточність цієї рівності зумовлена тим, що в кожному з діелектриків у різних точках площинки \(\Delta S\) величина \({D_n}\) не однакова. Тому для отримання точного виразу треба перейти до границі, “стягнувши” циліндр у якусь точку на межі поділу. Задля більшої прозорості зробимо це в два етапи. Спочатку будемо подумки зменшувати висоту циліндра, поступово наближаючи основи до межі поділу. Тоді у границі \(h \to 0\) зникне потік крізь бічну поверхню:
\begin{equation} - {D_{1n}}\Delta S + {D_{2n}}\Delta S \approx 0\quad \Rightarrow \quad {D_{1n}}\Delta S \approx {D_{2n}}\Delta S. \end{equation}
А тепер будемо зменшувати основи, зменшуючи й похибку в отриманій рівності, аж поки в границі \(\Delta S \to 0\) вона не стане математично точною:
\begin{equation} {D_{1n}} = {D_{2n}}. \tag{1.16а} \end{equation}
Відтак за допомогою співвідношення (1.14) встановлюємо зв’язок між нормальними складовими для векторів напруженості поля:
\begin{equation} {\varepsilon _1}{E_{1n}} = {\varepsilon _2}{E_{2n}}\quad \Rightarrow \quad \frac{{{E_{1n}}}}{{{E_{2n}}}} = \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}}. \tag{1.16б} \end{equation}
Далі за допомогою теореми про циркуляцію ((5.2), розділ І) і формули (1.14) встановимо межові умови для тангенціальних складових векторів. Для цього розглянемо циркуляцію \(C\) вектора \(\vec E\) по малому прямокутнику, що охоплює деяку точку на межі поділу діелектриків і орієнтований так, як показано на рис. 1.7б. Ураховуючи малість контуру, інтеграл у рівнянні ((5.2), розділ І) наближено виразимо через вклади окремих сторін:
\begin{equation} -{{E}_{1\tau }}+{{E}_{2\tau }}+\Delta C\approx 0. \end{equation}
де \(\Delta C\) — спільний вклад від поперечних сторін, а проекції векторів поля на напрям переміщення вздовж поздовжніх сторін записані через спільний орт \(\vec \tau \) дотичної до межі поділу.
Далі, стягаючи спочатку поперечні, а потім поздовжні сторони прямокутника в вибрану точку на межі поділу діелектриків, отримаємо в границі точні співвідношення для напруженості
\begin{equation} {E_{1\tau }} = {E_{2\tau }} \tag{1.17а} \end{equation}
і, за допомогою формули (1.14), — для електричного зміщення.
\begin{equation} \frac{{{D_{1\tau }}}}{{{\varepsilon _1}}} = \frac{{{D_{2\tau }}}}{{{\varepsilon _2}}}. \tag{1.17б} \end{equation}
Зведемо всі отримані результати, які й складають умови на межі двох діелектриків:
\begin{equation} \begin{aligned} {{D}_{1n}}={{D}_{2n}},& \qquad \frac{{{E}_{1n}}}{{{E}_{2n}}}=\frac{{{\varepsilon }_{2}}}{{{\varepsilon }_{1}}};\\\frac{{{D}_{1\tau }}}{{{D}_{2\tau }}}=\frac{{{\varepsilon }_{1}}}{{{\varepsilon }_{2}}},& \qquad {{E}_{1\tau }}={{E}_{2\tau }}. \end{aligned} \tag{1.18} \end{equation}
З умов (1.18) випливає, що при переході через межу поділу діелектриків змінюються не тільки модулі, а й напрямки векторів \(\vec D\) і \(\vec E\). При цьому напрямки векторів змінюються однаково, а модулі — ні. Це наочно ілюструє рис. 1.8: коли \({\varepsilon _2} < {\varepsilon _1}\) (рис. 1.8а)), то \({D_2} < {D_1}\), а \({E_2} > {E_1}\), тоді як при \({\varepsilon _2} > {\varepsilon _1}\) (рис. 1.8б)) навпаки \({D_2} > {D_1}\), а \({E_2} < {E_1}\).
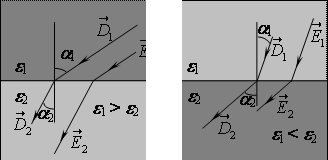
Для межі поділу вакууму (\( {{\varepsilon _1} = 1} \)) і діелектрика (\( {{\varepsilon _2} = \varepsilon } \)) умови (1.18) мають вигляд:
\begin{equation} \begin{aligned} {{D}_{n}}={{D}_{0n}},& \qquad \frac{{{D}_{\tau }}}{{{D}_{0\tau }}}=\varepsilon ;\\ \frac{{{E}_{n}}}{{{E}_{0n}}}=\frac{1}{\varepsilon },& \qquad {{E}_{\tau }}={{E}_{0\tau }}. \end{aligned} \tag{1.18а} \end{equation}
Звідси випливає, що \(E = \sqrt {( E_{0n}/\varepsilon )^2 + E^2_{0\tau }} \). Отже, на загал \(E \ne ( E_0/E_0\varepsilon )\), як і говорилося на початку. Виняток становить тільки випадок, коли поле напрямлене по нормалі до поверхні діелектрика. Тоді \({E_\tau } = {E_{0\tau }} = 0\), і поверхня діелектрика співпадає з однією з еквіпотенціальних поверхонь поля (див. розділ І, п. 2). У такому разі нормальні проекції векторів напруженості збігаються з модулями, і поле в діелектрику
\begin{equation} E = \frac{{{E_0}}}{\varepsilon } \tag{1.19} \end{equation}
так, немов він є безмежним. Відповідно, для двох діелектриків, межа поділу яких є еквіпотенціальною,
\begin{equation} \frac{{{E_1}}}{{{E_2}}} = \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}}. \tag{1.20} \end{equation}
У загальному випадку при переході з одного діелектрика в інший змінюється і напрямок поля. Через це на межі поділу спостерігається ефект заломлення ліній векторів \(\vec D\) і \(\vec E\), рис. 1.9
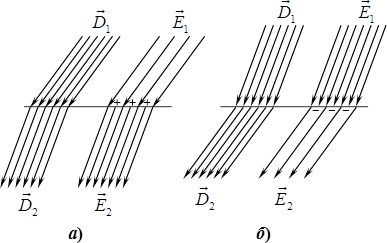
При цьому з умов (1.18) випливає наступний “закон заломлення”:
\begin{equation} \frac{{\operatorname{tg} {\alpha _1}}}{{\operatorname{tg} {\alpha _2}}} = \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}}. \tag{1.21} \end{equation}
Прийнявши \({\varepsilon _1} = 1\) і \({\varepsilon _2} = \varepsilon \) та відповідно позначивши кути як \({\alpha _0}\) і \(\alpha \), отримаємо зв’язок між напрямками векторів на межі вакууму і діелектрика з проникністю \(\varepsilon \):
\begin{equation} \frac{{\operatorname{tg} {\alpha _0}}}{{\operatorname{tg} \alpha }} = \frac{1}{\varepsilon }. \tag{1.21а} \end{equation}
Зрозуміло, що лінії векторів \(\vec D\) і \(\vec E\) заломлюються однаково, але в їхній поведінці є й істотна відмінність. Якщо розглянути потоки цих векторів крізь замкнену поверхнею у формі диска з основами \(\Delta S\), що прилягають до поверхні поділу діелектриків, як на рис. 1.7, то згідно з (1.18) отримаємо: \({D_{1n}}\Delta S = {D_{2n}}\Delta S\). З урахуванням геометричного змісту потоку це означає, що при переході через межу поділу кількість ліній вектора \(\vec D\) не змінюється, тобто вони є неперервними. Натомість для напруженості \({E_{1n}}\Delta S \ne {E_{2n}}\Delta S\), і лінії вектора \(\vec E\) терплять розрив, як показано на рис. 1.9.
Це не важко пояснити. Через різну проникність діелектриків їхня поляризованість не однакова, і поляризаційні заряди протилежного знаку, що виникають на прилеглих поверхнях мають різну величину. Через це на поверхні дотику існують некомпенсовані зв’язані заряди того, чи іншого знаку. Якщо \({\varepsilon _2} > {\varepsilon _1}\), то ці заряди від’ємні, і на них певна кількість ліній \(\vec E\) закінчується, як на рис. 1.9а. При \({\varepsilon _1} > {\varepsilon _2}\) указані заряди мають знак «\(+\)», і на межі поділу виникають додаткові лінії напруженості, рис. 1.9б.
Наостанку вкажемо наступний корисний для практики висновок, що випливає з проведеного розгляду. Позаяк у безмежному діелектричному середовищі та в діелектрику, обмеженому еквіпотенціальними поверхнями, електричне поле порівняно з вакуумом просто ослаблюється в \(\varepsilon \) разів без зміни напрямку, то будь-яку необхідну формулу можна отримати з відповідної формули для вакууму заміною \({\varepsilon _0}\) на \({\varepsilon _0}\varepsilon \). До прикладу, при наявності діелектрика замість формул (1.4) чи (5.26) з розділу І маємо:
\begin{equation} E = \frac{q}{{4\pi \varepsilon {\varepsilon _0}{r^2}}}, \tag{1.22} \end{equation}
та
\begin{equation} E = \frac{\sigma }{{{\varepsilon _0}\varepsilon }}. \tag{1.23} \end{equation}
Контрольні запитання
1. Які речовини називаються діелектриками та як вони впливають на електричне поле?
2. Що таке внутрішнє (власне) макроскопічне поле в діелектрику? Як воно виникає та від чого залежить?
3. Що таке поляризація та поляризованість діелектрика?
4. Як утворюються поляризаційні заряди. Яка відміна існує між ними та сторонніми зарядами?
5. Який зв’язок існує між поляризаційними зарядами та поляризованістю діелектрика?
6. Як формулюється теорема Гаусса для електричного поля в діелектрику? Чи можна вважати, що вектор \(\vec D\) визначається тільки розподілом сторонніх зарядів?
7. Чи можна вважати \(\vec D\) вектором електричного поля в діелектрику?
8. Який зв’язок існує між поляризованістю та напруженістю поля в ізотропних діелектриках?
9. Установіть зв’язок між вектором \(\vec D\) та напруженістю поля \(\vec E\) в ізотропному діелектрику.
10. Чи можна трактувати діелектричну проникність \(\varepsilon \) як коефіцієнт послаблення напруженості поля в ізотропному діелектрику?
11. Запишіть умови на межі двох ізотропних діелектриків за відсутності на межі сторонніх зарядів. У якому випадку поле в діелектрику просто послаблюється в \(\varepsilon \) разів порівняно з вакуумом?
12. У якому випадку при переході з одного діелектрика в інший лінії векторів \(\vec D\) і \(\vec E\) відхиляються до межі поділу діелектриків, а в якому від неї? Покажіть картину ліній цих векторів у випадку однорідного поля.
13. Поясніть, як змінюється щільність ліній векторів \(\vec E\) і \(\vec D\) при переході з одного діелектрика в інший, якщо вектори напрямлені а) по нормалі і б) під кутом до межі поділу діелектриків.
2. Провідники в електричному полі
Провідниками називаються речовини, що мають у своєму складі багато вільних заряджених частинок, які здатні рухатися по всьому об’єму зразка. Через це вони за впливом на електричне поле дуже відрізняються від діелектриків. Далі розглядаються властивості та поведінка провідників у статичних електричних полях. А саме:
2.1. Електростатичні властивості провідників
2.2. Електрична ємність. Конденсатори
2.1. Електростатичні властивості провідників
Електростатична індукція. Класичними провідниками є метали — речовини, в атомах яких валентні електрони є слабко зв’язані з ядром. Тому при об’єднанні атомів у твердий метал валентні електрони взагалі вивільняються від “своїх” ядер і поводяться подібно до частинок газу в посудині, утворюючи “електронний газ”. Але при внесенні металу в якесь електричне поле \(\vec{E}_{0}\) вільні електрони, окрім хаотичного теплового руху, починають зміщуватися проти напрямку поля під дією сили \(\vec{F}=-e\vec{E}_{0}\). Як наслідок, на поверхні зразка з одного боку з’являється не компенсований негативний заряд –qi, а з протилежного — такий самий позитивний заряд qi, рис. 2.1.
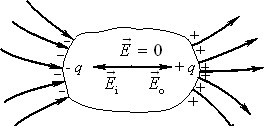
Виникнення макроскопічних зарядів на поверхні незарядженого провідника під дією електричного поля називається електростатичною індукцією, а самі заряди — індукованими зарядами.
Індуковані заряди створюють у провіднику власне поле \(\vec{E}_{i}\), яке напрямлене протилежно до зовнішнього поля \(\vec{E}_{0}\), що нагадує ситуацію в діелектриках. Але, коли в діелектрику на поверхню здатні виходити лише електрони молекул поверхневого шару, то в металі це можуть робити всі вільні електрони, кількість яких є сумірною із кількістю атомів у зразку. Тому можлива величина індукованих зарядів у провіднику по суті є нічим не обмеженою, і їхнє накопичення триває, доки напруженість внутрішнього поля не досягне величини \({{\vec{E}}_{i}}=-{{\vec{E}}_{0}}\), а напруженість результуючого поля — значення \(\vec{E}=\vec{E}_0+\vec{E}_{i}=0\). Відтак переміщення електронів припиняється і в провіднику встановлюється такий рівноважний розподіл зарядів, при якому електричне поле існує тільки на поверхні провідника та поза ним. При цьому поле в кожній точці поверхні спрямоване по нормалі (рис. 2.1), бо інакше вільні заряди продовжували би рухатися по поверхні.
Через кулонівське відштовхування так само поводяться й сторонні (надлишкові) заряди в провіднику: вони виходять на поверхню і розміщуються так, що всередині провідника поля відсутнє, а на поверхні воно напрямлене по нормалі.
Із сказаного випливає загальний висновок про те, що
всередині провідника існування статичного електричного поля є неможливим.
Наостанку зазначимо, що описаний тут розгорнуто в часі процес зникнення поля в провіднику насправді відбувається практично миттєво.
Еквіпотенціальність провідника. Вектор напруженості електричного поля пов’язаний з потенціалом співвідношенням ((3.5), розділ І). Тому відсутність статичного електричного поля в провіднику означає, що
\begin{equation} \mathop{\mathrm{grad}} \varphi = 0 \quad \Rightarrow \quad \varphi = \mathrm{const}, \end{equation}
тобто, всі точки в об’ємі провідника мають однаковий потенціал \(\varphi\). Такий самий потенціал мають і всі точки поверхні. Це теж випливає із співвідношення ((3.5), розділ І), за яким функція потенціалу не може мати розривів, інакше на поверхні було би \(E\to\infty\).
Таким чином,
при рівновазі зарядів усі точки об’єму та поверхні провідника мають однаковий потенціал.
Тому можна говорити про потенціал усього провідника, тоді як в діелектрику — лише про потенціал заданої точки.
Зауваження. Еквіпотенціальність є важливою властивістю провідників, про яку не можна забувати, розв’язуючи задачі. Приміром, при з’єднанні між собою заряджених металевих куль перерозподіл зарядів на них буде тривати до вирівнювання їхніх потенціалів, а не величини зарядів.
Поле біля поверхні провідника. Вістря. Характеристики електричного поля на поверхні провідника визначаються розподілом індукованих і сторонніх зарядів, який задається поверхневою густиною заряду \(\sigma\). Для визначення напруженості \(\vec{E}\) поля провідника оточимо якусь точку на поверхні невеликою замкненою циліндричною оболонкою, як показано на рис. 2.2.
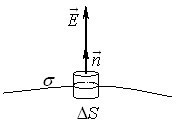
Позаяк поля всередині провідника немає, потік напруженості створюється тільки крізь зовнішню основу циліндрика і наближено дорівнює
\begin{equation} \Delta \Phi\approx E\,\Delta S. \end{equation}
Тому, згідно з теоремою Гаусса (розділ І, п. 5.2.2), можна записати:
\begin{equation} {E}\,\Delta{S}\approx\frac{1}{\varepsilon_0}\sigma\,\Delta{S}, \end{equation}
де \(\sigma\,\Delta{S}=\Delta q\) — заряд ділянки провідника, що охоплена циліндриком. Стягнувши його у вибрану точку на поверхні провідника, отримаємо точний вираз:
\begin{equation} {E}=\frac{\sigma}{\varepsilon_0}, \quad \text{або} \quad \vec{E}=\frac{\sigma}{\varepsilon_0}\vec{n}, \tag{2.1} \end{equation}
де \(\vec{n}\) — орт зовнішньої нормалі до поверхні провідника.
Якщо провідник оточений ізотропним діелектриком з проникністю \(\varepsilon\), то напруженість на поверхні виражається формулою
\begin{equation} \vec{E}=\frac{\sigma}{\varepsilon_0\varepsilon}\vec{n}. \tag{2.1a} \end{equation}
Оскільки напруженість в кожній точці поверхні визначається густиною заряду, з’ясуємо, від чого залежить величина \(\sigma\) в різних точках поверхні. Для цього розглянемо провідник, який складається з двох металевих кульок із радіусами \(R_1\) і \(R_2\), що з’єднані довгою тонкою дротиною (рис. 2.3).
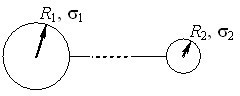
За таких умов кулонівська взаємодія між кульками та заряд, який осідає на дротині, є незначними і можна вважати, що кульки заряджені рівномірно з деякими густинами \(\sigma_1\) і \(\sigma_2\).
Кульки є частинами єдиного провідника і мають однакові потенціали \(\varphi_1=\varphi_2\). Тож згідно з формулою ((2.7), розділ І),
\begin{equation} \frac{q_1}{4\pi\varepsilon_0{R_1}}=\frac{q_2}{4\pi\varepsilon_0{R_2}}. \end{equation}
Підставивши сюди вирази заряду \(q=\sigma S\) і площі поверхні кулі \(S=4\pi R^2\), отримаємо:
\begin{equation} \sigma_1{R_1}=\sigma_2{R_2} \quad \Rightarrow \quad \frac{\sigma_1}{\sigma_2}=\frac{R_2}{R_1}. \tag{2.2} \end{equation}
Таким чином, поверхнева густина зарядів на кульках є обернено пропорційною радіусам, які визначають кривизну \(K=1/R\) їхніх поверхонь.
Для провідника довільної форми співвідношення (2.2), звісно, точно не виконується. Але воно відображає загальну тенденцію:
сторонні заряди у провіднику розподіляються відповідно до форми його поверхні так, що поверхнева густина заряду в кожній точці є тим більшою, чим більша кривизна поверхні в цій точці.
З цієї причини біля вістер і гострих виступів або ребер на поверхні зарядженого провідника електричне поле може виявитися настільки сильним, що викличе електричний пробій у прилеглому шарі діелектрика. Тому в електричному устаткуванні поверхні елементів, що знаходяться під високою напругою, як скажімо ізолятори повітряних ліній передач, роблять гладенькими і закругленими.
Але накопичення зарядів на нерівностях поверхні провідника має і корисні застосування. Одним із прикладів є громовідвід — простий і ефективний пристрій для захисту споруд чи устаткування від ураження блискавкою. Громовідвід являє собою загострений металевий штир, який встановлюється на даху будівлі чи поруч із обладнанням і з’єднується металевою шиною із закопаним у землю листом металу. Громовідвід “працює” так. Перед і під час грози в хмарах і повітрі накопичується багато заряджених частинок — іонів, які й спричинюють блискавки, тобто гігантські іскрові розряди між хмарами та наземними об’єктами. Частина вказаних зарядів осідає на загостреному кінці громовідводу і створює навколо нього сильне неоднорідне поле. Під його дією інші атмосферні заряди притягаються до вістря і далі стікають у землю. Внаслідок цього повітря навколо громовідводу стає збідненим на заряди, і ймовірність потрапляння блискавки в споруду значно зменшується. Тож усупереч поширеній думці, громовідвід не приймає блискавку на себе, хоча таке інколи й трапляється, а “відводить” її від споруди.
На властивостях вістря ґрунтується і робота іонного проектора — надпотужного мікроскопа, який дозволяє спостерігати навіть розташування окремих атомів у металі. Проектор, спрощена схема якого наведена на рис. 2.4, складається із скляного балона та дуже гострої голки з досліджуваного металу, яка є одним з електродів.

Внутрішня поверхня балона вкрита тонким шаром провідної люмінесцентної речовини, що є другим електродом. Балон відкачують і натомість впускають невелику кількість атомарного газу (зазвичай гелію).
Прилад працює так. При подаванні на електроди високої напруги навколо вістря створюється дуже сильне неоднорідне електричне поле, в якому атоми газу поляризуються (див. п. 1.1) і починають рухатися до вістря (див. розділ І, п. 4.2). Радіус кривизни кінчика добре заточеної голки може складати всього 0,1 мкм, а напруженість поля досягати \(\sim 5\cdot 10^7\) В/м. У такому надсильному полі атоми газу біля вістря іонізуються — розділяються на електрони та іони. Електрони падають на голку, а іони відбиваються і рухаються по силових лініях до балона, де вдаряючи в покриття, викликають його свічення, як у телевізійній трубці. Поверхня вістря складається з окремих атомів і є зернистою, тому у місцях виходу атомів напруженість і щільність ліній поля вища, ніж у проміжках між атомами. Відповідно, до таких точок підлітає і відбивається відносно більша кількість іонів, і на поверхні колби утворюється система світлих цяток, положення яких відображає розташування атомів на поверхні вістря.
Із властивостями вістер пов’язані й інші ефекти, зокрема, електризація тертям.
Електростатичне екранування. Якщо провідник є порожнистим, то статичного електричного поля не може бути не лише в самому провіднику, а й у порожнині. Це легко довести. Якщо суцільний провідник зарядити або внести у зовнішнє поле, то заряди розташуються на поверхні, але в об’ємі речовина лишиться електрично нейтральною в кожній точці. Тож, якщо з об’єму видалити частину речовини, утворивши порожнину, то це не призведе до зміни розподілу зарядів на поверхні та появи в порожнині поля. Звідси, до речі, випливає, що у порожнистому провіднику за відсутності зарядів у порожнині сторонні заряди розміщуються тільки на зовнішній поверхні.
Таким чином, ніякі заряди, розміщені на поверхні провідної оболонки чи поза нею, не можуть створити електричного поля всередині. Тому провідна оболонка забезпечує повний захист (екранування) всього, що знаходиться всередині, від впливу будь-яких зовнішніх електростатичних полів. Це широко використовується на практиці. Зокрема, в електроніці задля захисту чутливих елементів схеми їх вміщують у закриті металеві корпуси, а проводи — в металеву обплітку.
Провідна оболонка “працює” і в зворотному напрямку. Наприклад, якщо в порожнині розмістити точковий заряд \(q\) (рис. 2.5а), то його електричне поле індукує на поверхнях провідника заряди \({q}_i^{+}={q}\) і \({q}_i^{-}=-{q}\), які компенсують поле в самому провіднику.
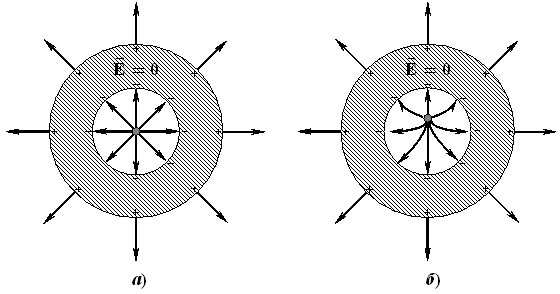
Тому поле назовні провідника буде визначатися тільки величиною та розподілом заряду \({q}_i^{+}\) на зовнішній поверхні, причому зміна поля всередині внаслідок зміщення заряду \(q\) і перерозподіл заряду \({q}_i^{-}\) на внутрішній поверхні порожнини ніяк не вплине на зовнішнє поле (рис. 2.5б). Якщо зовнішню поверхню оболонки заземлити, то ніякого поля назовні взагалі не буде. Таким чином,
замкнена провідна оболонка поділяє весь простір на дві електрично незалежні області.
Фундаментальна причина цього полягає в тому, що у випадку провідної оболонки на шляху із середини назовні обов’язково трапиться область (сама оболонка), в якій немає електричного поля — “передавача” взаємодії між зарядами, розташованими всередині та назовні оболонки.
2.2. Електрична ємність. Конденсатори
Ємність відокремленого провідника. Напруженість електричного поля на поверхні зарядженого провідника в кожній точці визначається густиною заряду (формула (2.1а)) і має різну величину та напрям. Натомість потенціал провідника є скрізь однаковий, тож у кожній точці визначається не густиною заряду в цій точці, а зарядом усього провідника. При цьому дослід свідчить, що потенціал провідника є прямо пропорційним до його заряду:
\begin{equation} \varphi=\frac{1}{C}{q} \quad \text{або} \quad {q=C\varphi}. \end{equation}
Величина
\begin{equation} C=\frac{q}{\varphi } \tag{2.3} \end{equation}
називається електричною ємністю провідника, електроємністю, або просто ємністю.
Одиницею ємності є фарад (Ф). Згідно з (2.3) можна сказати, що
фарад дорівнює ємності провідника, котрому для збільшення потенціалу на \(1\ \text{В}\) треба надати заряд \(1\ \text{Кл}\). Отже, \(1\ \text{Ф} = 1\ \text{Кл/В}\).
Ємність не залежить ані від заряду, ані від потенціалу і для відокремленого провідника визначається тільки його геометричною конфігурацією та властивостями діелектричного середовища, в якому він знаходиться.
Примітка. Відокремленим називається провідник, який є єдиним у всьому просторі. Звичайно, це ідеалізація. Реально провідник можна вважати відокремленим, якщо вплив на нього з боку інших тіл є неістотним.
Задля ілюстрації визначимо ємність провідної кулі радіуса \(R\), що знаходиться в безмежному однорідному ізотропному діелектрику з проникністю \(\varepsilon\). За таких умов заряд розподіляється по поверхні кулі рівномірно, і її електричне поле збігається з полем точкового заряду (1.22). Тож потенціал
\begin{equation} \varphi=\frac{q}{4\pi\varepsilon_0\varepsilon{R}}. \end{equation}
Тоді за означенням (2.3) ємність кулі
\begin{equation} {C}=4\pi\varepsilon_0\varepsilon{R}, \tag{2.4} \end{equation}
як і сказано, визначається тільки геометрією та властивостями середовища, в якому вона знаходиться.
Конденсатори, ємність конденсатора. Електрична ємність як фізична властивість провідників має важливі застосування в електротехніці та електроніці. Але окремі провідники в цьому сенсі мають принципові вади. По-перше, ємність окремо взятого провідника є дуже малою. Наприклад, згідно з формулою (2.4), ємність провідної кулі з розмірами Землі (\(R\approx 6400\) км) у вакуумі складає всього біля \(7\cdot 10^{-4}\) Ф. А по-друге, в реальних умовах ємність окремого провідника не має визначеної величини, бо істотно залежить від оточення. Справді, якщо заряджена металева куля є відокремленою (рис. 2.6а), то її заряд \(q\) розподілений рівномірно, і вона має відповідний потенціал \(\varphi_0\) та ємність \(C_0=q/\varphi_0\). Але коли наблизити до кулі якесь тіло, наприклад, незаряджений кусок металу, то під дією поля кулі на його поверхні з’являться індуковані заряди \({q}_i^{-}\) і \({q}_i^{+}\), як показано на рис. 2.6б. Це призведе до зміщення зарядів кулі ближче до металу, бо індуковані заряди \({q}_i^{-}\) будуть притягати заряди кулі сильніше, ніж заряди \({q}_i^{+}\) — відштовхувати їх. Такий перерозподіл заряду кулі \(q\) змінить її потенціал \(\varphi\), тож і ємність \(C=q/\varphi\). При цьому, як показує глибший аналіз, присутність інших тіл завжди зменшує потенціал і збільшує ємність даного тіла. Крім того, ємність буде змінюватися при будь-якій зміні взаємного розташування кулі та сусіднього тіла.

Указана нестабільність може негативно впливати на роботу апаратури і вимагає спеціального захисту (екранування) чутливих вузлів електронних пристроїв. Але оточення практично не впливає на системи провідників, які називаються конденсаторами. Найпростіший і найуживаніший плоский конденсатор складається з двох паралельних металевих пластин — обкладок, простір між якими заповнений діелектриком, зокрема, повітрям (рис. 2.7).
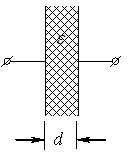
Обкладки розміщують близько одна від одної, тому електричне поле в конденсаторі, за винятком країв пластин, є однорідним, як у випадку нескінченних площин. Спотворення поля на краях пластин (так званий “крайовий ефект”) є незначними, тому в теорії ними нехтують і розглядають конденсатор як ідеальний.
Нечутливість конденсаторів до впливу зовнішніх тіл і полів пояснюється ефектом електростатичного екранування. Це неважко зрозуміти. При підключенні конденсатора до полюсів джерела напруги частина електронів з однієї обкладки переміщується на іншу, й на них з’являться різнойменні заряди однакової величини \(q\) і \(-q\) та відповідна різниця потенціалів \(U=\varphi_+-\varphi_-\).
(Принагідно зазначимо, що величина \(q > 0\) називається зарядом, а \(U\) — напругою конденсатора.)
Заряди в конденсаторі через кулонівське притягання розміщуються на внутрішніх поверхнях пластин. Тож створюване між ними електричне поле є відокремлене від зовнішнього простору самими пластинами, бо всередині них електричного поля не може бути (див. п. 2.1, електростатичне екранування). Тому поле конденсатора не може вийти за його межі, а зовнішнє поле не може потрапити всередину. З цієї причини зовнішні тіла та поля не можуть впливати на конденсатор, а він — на них.
Іншою цінною властивістю конденсаторів є те, що вони при невеликих розмірах можуть мати велику ємність і акумулювати значну кількість електричної енергії. Тому конденсатори мають практичне застосування як накопичувачі електричної енергії.
Типи конденсаторів. Електрична ємність конденсатора визначається відношенням його заряду до напруги:
\begin{equation} {C}=\frac{q}{U}. \tag{2.5} \end{equation}
Тому, аби визначити ємність конденсатора, треба за допомогою відомих методів розрахувати напругу \(U\) на конденсаторі при заданій величині заряду \(q\) і скористатися формулою (2.5). Проілюструємо це на прикладі ідеального плоского конденсатора з площею пластин \(S\), відстанню між ними \(d\) і проникністю діелектрика \(\varepsilon\). Напруженість поля в такому конденсаторі визначається формулою (1.23):
\begin{equation} {E}=\frac{\sigma}{\varepsilon_0\varepsilon}=\frac{q}{\varepsilon_0\varepsilon{S}}. \end{equation}
Це поле є однорідним, тому відповідно до п. 3.1, розділ І, напруга на конденсаторі
\begin{equation} {U}=Ed=\frac{qd}{\varepsilon_0\varepsilon{S}}, \end{equation}
і, згідно з означенням (3.5), ємність плоского конденсатора визначається формулою:
\begin{equation} {C}=\frac{\varepsilon_0\varepsilon{S}}{d}. \tag{2.6} \end{equation}
Отже, чим більша проникність діелектрика та площа обкладок і менша відстань між ними, тим більша ємність конденсатора. У цьому зв’язку слід зазначити, що сучасні технології дозволяють виготовляти конденсатори ємністю \(\sim 1\) Ф розмірами з монету.
На практиці використовують переважно плоскі конденсатори. Але в теорії розглядають ще два типи простих конденсаторів — сферичні та циліндричні. Обкладками сферичного конденсатора є дві концентричні металеві оболонки з якимись радіусами \(R_1\) і \(R_2\) (рис. 2.8а), а циліндричного — коаксіальні циліндри з радіусами \(R_1\) і \(R_2\) і довжиною \(l\) (рис. 2.8б).
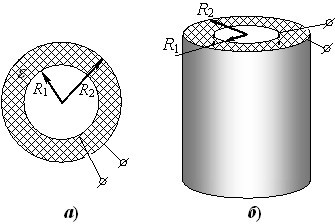
Формули ємності таких конденсаторів розраховуються так само, як для плоского, і мають вигляд:
\begin{equation} C_{\text{сфер}} = \frac{4\pi\varepsilon_0\varepsilon{R_1}{R_2}}{R_2-R_1}, \tag{2.7} \end{equation} \begin{equation} C_{\text{цил}}=\frac{2\pi\varepsilon_0\varepsilon{l}}{\ln(R_2/R_1)}. \tag{2.8} \end{equation}
З’єднання конденсаторів. В електричних колах окрім поодиноких конденсаторів використовують з’єднання (батареї) декількох певним чином сполучених між собою конденсаторів. Виведемо формули ємності найпростіших паралельного та послідовного з’єднань, виходячи з того, що ємність з’єднання, як і одного конденсатора, визначається формулою (2.5) через сумарний заряд батареї та подану на неї напругу.
Паралельне з’єднання. При паралельному з’єднанні всі конденсатори безпосередньо сполучаються між собою, як показано на рис. 2.9а.
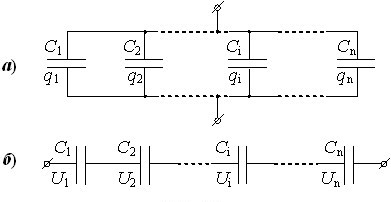
Усі з’єднані обкладки утворюють єдиний провідник і за будь-яких умов мають однаковий потенціал. Тому, якщо подати на батарею напругу \(U\), то напруги \(U_i\) всіх конденсаторів будуть такими самими: \(U_i=U\). Також є очевидним, що заряд батареї дорівнює сумі зарядів усіх з’єднаних конденсаторів: \({q}=\sum\limits{q_i}\). Отже, ємність з’єднання
\begin{equation} \begin{aligned} &C_{\text{пар}}=\frac{q}{U}=\frac{\sum\limits{q_i}}{U}=\sum\limits_i{\frac{q_i}{U_i}}\quad\Rightarrow{}\\ &\quad{}\Rightarrow \quad C_{\text{пар}} = \sum\limits{C_i}. \end{aligned} \tag{2.9} \end{equation}
Таким чином,
при паралельному сполученні конденсаторів ємність з’єднання дорівнює сумі ємностей всіх сполучених конденсаторів.
Зокрема, при паралельному з’єднанні \(n\) конденсаторів однакової ємності \(C\) загальна ємність
\begin{equation} C_{\text{пар}} = nC. \tag{2.9а} \end{equation}
Послідовне з’єднання. В цьому випадку конденсатори утворюють ланцюг, у кожній ланці котрого безпосередньо з’єднуються тільки два конденсатори, як показано на рис.2.9б. При такому сполученні питання про ємність з’єднання не є таким очевидним, як при паралельному, тому проаналізуємо сам процес заряджання послідовного ланцюга конденсаторів. У момент приєднання до джерела заряди \(q\) і \(-q\) подаються тільки на зовнішні пластини першого і останнього конденсаторів \(C_1\) і \(C_n\). Але під дією поля, що виникає, тієї ж миті на всіх з’єднаних між собою парах пластин з’являються індуковані заряди однакової величини \(q_i\) і \(-q_i\), і всі конденсатори виявляються зарядженими. При цьому напруга на ланцюгу дорівнює сумі напруг на окремих конденсаторах: \(U=\sum\limits U_i\), а заряди всіх конденсаторів \(q_i\) однакові і дорівнюють заряду всього ланцюга: \(q_i=q\). Це легко зрозуміти на прикладі ідеальних плоских конденсаторів. У момент підключення до джерела між крайніми пластинами ланцюга виникає однорідне електричне поле \(\vec{E}\). Але всередині з’єднаних пластин поля бути не може, тому індуковані заряди на з’єднаних пластинах мають створювати внутрішнє поле \(\vec{E}_i=-\vec{E}\). А для цього величина індукованих зарядів \(q_i\) повинна дорівнювати величин поданих на ланцюг сторонніх зарядів \(q\).
Таким чином, ємність послідовного з’єднання конденсаторів
\begin{equation} C_{\text{пос}} = \frac{q}{U}=\frac{q}{\sum\limits{U_i}}, \end{equation}
де
\begin{equation} {U_i}=\frac{q_i}{C_i}=\frac{q}{C_i}. \end{equation}
Після такої підстановки виходить наступна формула для розрахунку ємності послідовного з’єднання конденсаторів:
\begin{equation} \frac{1}{C_{\text{пос}}}=\sum\limits\frac{1}{C_i}. \tag{2.10} \end{equation}
Отже,
при послідовному з’єднанні конденсаторів додаються не ємності, а їхні обернені величини.
Із загального виразу (2.10) випливають прості формули прямого розрахунку ємності послідовного з’єднання двох конденсаторів з ємностями \(C_1\) і \(C_2\):
\begin{equation} C_{\text{пос}} = \frac{C_1 C_2}{C_1+C_2} \tag{2.10а} \end{equation}
та \(n\) конденсаторів однакової ємності \(C\):
\begin{equation} C_{\text{пос}} = \frac{C}{n}. \tag{2.10б} \end{equation}
Формули (2.9) і (2.10) дозволяють розраховувати й більш складні комбіновані з’єднання, які можна розчленувати на окремі паралельні та послідовні ділянки.
2.3. Енергія електричного поля
Енергія та її трансформації є універсальними чинниками, що визначають стан будь-якої фізичної системи і процеси в ній. Згадаймо хоча би про механічну енергію та її роль в механічних процесах. Електростатична система, тобто сукупність заряджених частинок або тіл, має відповідний запас електричної енергії. Її походження неважко збагнути. Сили кулонівської взаємодії завжди намагаються звести докупи і нейтралізувати різнойменні заряди та розкидати на нескінченність однойменні. Тому при створенні заданої конфігурації зарядів треба виконувати роботу по подоланню кулонівських сил, тим самим надаючи системі відповідного запасу електростатичної енергії. Позаяк кулонівські сили є консервативними, ця енергія є різновидом потенціальної енергії і, як усяка енергія, може переходити в інші форми. Наприклад, в кінетичну, якщо зарядам системи дозволити рухатися під дією сил кулонівської взаємодії між ними.
Енергія взаємодії системи точкових зарядів. Розглянемо гіпотетичний процес утворення системи з трьох точкових зарядів шляхом перенесення їх з нескінченності, де потенціал поля \(\varphi=0\), в задані точки 1, 2, 3 (рис. 2.10):
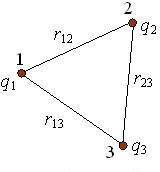
Переміщення першого заряду \(q_1\) в точку 1 відбувається вільно, але наступний заряд \(q_2\) вже рухається в полі заряду \(q_1\) і для його переміщення в точку 2 треба виконати деяку роботу \(A'\) проти сил поля. Ця робота дорівнює взятій з протилежним знаком роботі \(A\) самого поля і визначає потенціальну енергію \(W_{12}\) заряду \(q_2\) в полі заряду \(q_1\). Тож, відповідно до формул ((2.10а) і (2.7), розділ І),
\begin{equation} {W}_{12}=k\frac{q_1 q_2}{r_{12}}. \tag{2.11} \end{equation}
Але, якщо спочатку розташувати заряд \(q_2\) в точці 2, а потім перенести в точку 1 заряд \(q_1\), то нічого не зміниться крім того, що вираз (2.11) буде трактуватись як потенціальна енергію заряду \(q_1\) в полі заряду \(q_2\). Тому величина \(W_{12}\) є “спільним надбанням” обох зарядів і визначає енергію їхньої електричної взаємодії.
При включенні в систему заряду \(q_3\) додасться ще й енергія його взаємодії з першим та другим зарядами, котра виражається аналогічно. Отже, енергія системи з трьох зарядів
\begin{equation} \begin{aligned} &{W}=W_{21}+W_{31}+W_{32}={}\\ &\quad{}=k\frac{q_2 q_1}{r_{12}}+k\frac{q_3 q_1}{r_{13}}+k\frac{q_3 q_2}{r_{23}}. \end{aligned} \end{equation}
Позаяк у кожній парі заряди є рівноправними партнерами взаємодії, перепишемо цей вираз симетрично, як
\begin{equation} \begin{aligned} &{W}=\frac{1}{2}\left(q_1{k}\frac{q_2}{r_{12}}+q_2{k}\frac{q_1}{r_{12}}+q_2{k}\frac{q_3}{r_{23}}+{}\right.\\ &\qquad\left.{}+q_3{k}\frac{q_2}{r_{23}}+q_3{k\frac{q_1}{r_{13}}}+q_1{k}\frac{q_3}{r{13}}\right), \end{aligned} \end{equation}
або, після перегрупування,
\begin{equation} \begin{aligned} &{W}=\frac{1}{2}\left( q_1\left({k}\frac{q_2}{r_{12}}+{k}\frac{q_3}{r_{13}}\right)+{}\right.\\ &\qquad{}\left.{} +q_2\left({k}\frac{q_1}{r_{12}}+{k}\frac{q_3}{r_{23}}\right)+{}\right.\\ &\qquad{}\left.{}+q_3\left({k}\frac{q_1}{r_{13}}+{k}\frac{q_2}{r_{23}}\right) \right). \end{aligned} \end{equation}
Згідно з формулою ((2.7а), розділ І), вираз у кожній малій дужці визначає потенціал поля, що створюється в місці розташування відповідного заряду двома іншими.
Зрозуміло, що при додаванні наступних зарядів нічого принципово не зміниться. Тому електростатична енергія взаємодії довільної системи точкових зарядів виражається загальною формулою
\begin{equation} {W}=\frac{1}{2}\sum\limits{q_i \varphi_i}, \tag{2.12} \end{equation}
де \(\varphi_i\) — потенціали полів, що створюються в місцях розташування зарядів \(q_i\) всіма іншими зарядами системи.
Енергія зарядженого діелектрика та провідника. В протяжних тілах заряд розподіляється в просторі неперервно. Тому для підрахунку електростатичної енергії в зарядженому діелектрику увесь заряд треба подумки розчленувати на елементарні точкові порції \(\mathrm{d}q\) і замінити у виразі (2.12) дискретне додавання на інтегрування по всій зарядженій області:
\begin{equation} {W}=\frac{1}{2}\int\limits{\varphi\,\mathrm{d}q}. \tag{2.13} \end{equation}
Якщо заряд розподілений по об’єму з густиною \(\rho (\vec{r}) \), то \(\mathrm{d}q=\rho\,\mathrm{d}V\), і
\begin{equation} {W}=\frac{1}{2}\int\limits_V{\varphi\rho}\,\mathrm{d}{V}. \tag{2.14} \end{equation}
При розподілі заряду по поверхні з густиною \(\sigma(\vec{r}) \) або по тонкому стержню з лінійною густиною \(\lambda(\vec{r}) \) електростатична енергія виражається, відповідно, як
\begin{equation} {W}=\frac{1}{2}\int\limits_S{\varphi\sigma}\,\mathrm{d}{S} \tag{2.14а} \end{equation}
і
\begin{equation} {W}=\frac{1}{2}\int\limits_{L}\varphi\lambda\,\mathrm{d}{l}. \tag{2.14б} \end{equation}
Провідники в електростатичному стані є еквіпотенціальними. Тому у виразі (2.13) \(\varphi=\text{const}\), і електростатична енергія провідника визначається формулою
\begin{equation} {W}=\frac{1}{2}q\varphi. \tag{2.15} \end{equation}
Стосовно отриманих результатів необхідно зробити важливе зауваження. Хоча вирази (2.12) і (2.13) —(2.15) за загальним змістом видаються ідентичними, між ними є принципова відміна. Це стає зрозумілим, якщо згадати, що точкові заряди є абстракцією. Реально “точкові” заряди є частинками скінченних розмірів, тож заряди в них теж є рознесені в просторі і взаємодіють між собою. З цією взаємодією пов’язана відповідна власна електростатична енергія зарядів, не відображена у формулі (2.12). Напроти, формули (2.13) —(2.15) враховують взаємодію всіх зарядів тіла і визначають власну електростатичну енергію. А ось в електростатичну енергію системи тіл окрім власної енергії \(W_{\text{вл}}=\sum\limits{W_i}\), яка дорівнює сумі енергій всіх тіл, входить іще й енергія взаємодії \(W_{\text{вз}}\) кожного з кожним:
\begin{equation} W=W_{\text{вл}}+W_{\text{вз}}. \end{equation}
Таким чином, електростатична енергія довільної системи не дорівнює сумі енергій окремих її частин (тіл), тобто не є адитивною величиною. Тому в загальному випадку при підрахунках не можна забувати про енергію електростатичної взаємодії \(W_{\text{вз}}\), яка визначається конфігурацією системи — взаємним розташуванням заряджених тіл. Але для точкових заряджених тіл через їхні дуже малі розміри зміна взаємного розташування зарядів в них практично не впливає на власну електростатичну енергію, тож \(W_{\text{вл}}=\text{const}\). Тому власна енергія системи точкових зарядів ніяк не впливає на процеси в ній і може бути відкинута. Отже, хоча формула (2.12) принципово є неповною, фактично вона дає всю необхідну інформацію про електростатичну енергію системи точкових зарядів.
Енергія зарядженого конденсатора. Ця енергія дорівнює роботі по заряджанню конденсатора. Для її підрахунку будемо вважати, що конденсатор заряджається шляхом перенесення нескінченно малих порцій заряду з однієї обкладки на іншу (як це й відбувається в дійсності). Тоді, якщо при напрузі на конденсаторі \(u\) перенести з однієї обкладки на іншу порцію заряду \(\mathrm{d}q\), виконавши роботу \(\delta A'\), то енергія конденсатора збільшиться на величину виконаної роботи:
\begin{equation} \mathrm{d}W=\delta A'=u\,\mathrm{d}q. \end{equation}
Виразивши за формулою (2.5) перенесений заряд через ємність конденсатора та приріст напруги як \(\mathrm{d}q=C\,\mathrm{d}u\), і проінтегрувавши вираз \(\mathrm{d}W\) у границях від \(0\) до кінцевої напруги \(U\), одержимо наступну формулу енергії зарядженого конденсатора:
\begin{equation} {W}=\frac{CU^2}{2}, \tag{2.16} \end{equation}
або рівнозначні формули
\begin{equation} {W}=\frac{q^2}{2C} \tag{2.16а} \end{equation}
і
\begin{equation} {W}=\frac{1}{2}q{U}. \tag{2.16б} \end{equation}
Енергія електричного поля. Всі отримані вище формули виражають електростатичну енергію через характеристики тіл — заряди, потенціали та ємності. Але її можна подати й інакше. Якщо для плоского конденсатора у формулі (2.16) ємність виразити за формулою (2.6), а напругу — за формулою ((3.6а), розділ І), то вийде
\begin{equation} {W}=\frac{\varepsilon_0\varepsilon{E^2}}{2}{V}, \tag{2.17} \end{equation}
де \(Sd=V\) — об’єм області простору між пластинами.
В об’ємі \(V\) зосереджене все поле конденсатора, тож формула (2.17) виражає енергію конденсатора вже не через характеристики пластин, а тільки через характеристики електричного поля між ними. Це наводить на думку, що саме в полі, а не на пластинах, зосереджена електростатична енергія конденсатора. Якщо так, то величина
\begin{equation} {w_e}=\frac{\varepsilon_{0}\varepsilon{E^2}}{2} \tag{2.18} \end{equation}
визначає об’ємну густину енергії електричного поля в ізотропному середовищі, тобто енергію, зосереджену в одиниці об’єму поля.
Слід зауважити, що в електростатиці таке припущення неможливо ані довести, ані спростувати. Але в електродинаміці, де досліджуються явища в нестаціонарних (змінних) полях, теорія й експеримент однозначно доводять, що
електричне поле має енергію, яка в ізотропному середовищі розподілена з об’ємною густиною (2.18).
Об’ємну густину енергії електричного поля можна виразити ще двома рівнозначними формулами, врахувавши зв’язок між векторами \(\vec{E}\) і \(\vec{D}\), а саме:
\begin{equation} {w_{e}}=\frac{D^2}{2\varepsilon_0\varepsilon} \tag{2.18а} \end{equation}
і
\begin{equation} {w_{e}}=\frac{ED}{2}. \tag{2.18б} \end{equation}
У неоднорідному полі об’ємна густина характеризує концентрацію енергії в кожній точці і визначається як
\begin{equation} {w}=\frac{\mathrm{d}W}{\mathrm{d}V}. \tag{2.19} \end{equation}
У цьому випадку енергія поля в заданій області \(V\) є інтегралом (сумою) енергій \(\mathrm{d}W=w\mathrm{V}\) в усіх елементарних областях \(\mathrm{d}V\):
\begin{equation} {W}=\int\limits_{V}w\,\mathrm{d}{V}. \end{equation}
Отже, згідно з формулами (2.18) маємо наступні вирази для обчислення енергії електричного поля в заданому об’ємі:
\begin{equation} {W}=\int\limits_{V}\frac{\varepsilon_0\varepsilon{E^2}}{2}\mathrm{d}{V}; \tag{2.20} \end{equation} \begin{equation} {W}=\int\limits_{V}\frac{D^2}{2\varepsilon_0\varepsilon}\mathrm{d}{V}; \tag{2.20а} \end{equation} \begin{equation} {W}=\int\limits_{V}\frac{ED}{2}\mathrm{d}{V}. \tag{2.20б} \end{equation}
На завершення зазначимо, що всі результати, отримані тут для статичних полів, зберігають чинність і для залежних від часу (нестаціонарних) полів.
Контрольні запитання
1. Чому всередині діелектрика електростатичне поле лише послаблюється, а в провіднику повністю зникає?
2. Що таке електростатична індукція? Як розподіляються в провіднику індуковані заряди?
3. У чому полягає причина еквіпотенціальності провідника? Чому потенціали об’єму та поверхні провідника не можуть бути різними?
4. Якою формулою визначається напруженість електричного поля біля поверхні провідника? Поміркуйте, чому напруженість біля поверхні провідника вдвічі більша, ніж біля поверхні зарядженої площини з такою самою густиною заряду (формула (3.2), розділ І)).
5. Від чого залежить поверхнева густина заряду в різних точках поверхні провідника?
6. Які особливості має електричне поле вістер? Чому натертий об чисте волосся гребінець притягає до себе мілкі незаряджені клаптики паперу?
7. Поясніть принцип дії громовідводу. Що й куди він“відводить”?
8. Чому ніякі зовнішні заряди та електричні поля не діють на заряди вміщені всередину провідної оболонки?
9. Знайдіть формулу напруженості електричного поля назовні незарядженої металевої сферичної оболонки, в центрі якої знаходиться точковий заряд \(q\). Чим створюється це поле?
10. Заряд \(q\) знаходиться у порожнині в куску металу. Поясніть, що відбуватиметься в порожнині й назовні з напруженістю поля та з розподілом індукованих зарядів на поверхнях провідника при переміщенні заряду \(q\) у порожнині.
11. Дайте означення електричної ємності відокремленого провідника та конденсатора.
12. В яких одиницях вимірюється електрична ємність? Чому не можна дати означення одиниці ємності безпосередньо з формули (2.3) для ємності відокремленого провідника?
13. Поясніть, чому ємність відокремленого провідника залежить від зовнішніх тіл і полів, а ємність конденсатора — ні.
14. Запишіть формули для обчислення ємності паралельного та послідовного з’єднань конденсаторів і покажіть, що у випадку послідовного з’єднання загальна ємність є завжди меншою за найменшу із ємностей, що входять до з’єднання.
15. Поясніть походження електростатичної енергії в системи заряджених частинок чи тіл.
16. Поясніть, як буде змінюватись електростатична енергія системи закріплених зарядів, якщо всі, або частину зарядів вивільнити.
ІІІ. ЕЛЕКТРИЧНИЙ СТРУМ
Значна частина електромагнітних явищ, які знаходять широке практичне застосування, пов’язана з електричним струмом — упорядкованим рухом частинок, який супроводжується перенесенням електричного заряду.
У цьому розділі розглянуті такі питання:
1. Загальні закони електричного струму
1. Загальні закони електричного струму
Електричним струмом називається напрямлений рух заряджених частинок — носіїв струму. Носіями струму можуть бути всякі заряджені частинки. В металах і сплавах це електрони провідності — вивільнені при об’єднанні атомів у тверду речовину валентні електрони, які можуть переміщуватися по всьому об’єму зразка. У рідких провідниках (електролітах) носіями струму є іони, а в газах — і те, й інше. Потоки заряджених частинок у вакуумі теж створюють електричний струм.
Кількісні характеристики та загальні закони струму розглядаються далі в наступних питаннях:
1.3. Дрейф носіїв струму. Закон Ома в локальній формі
1.1. Сила та густина струму
Сутність явища електричного струму полягає в перенесенні в просторі електричного заряду, а його кількісною характеристикою є сила струму, або величина струму, котра визначається кількістю заряду, що переноситься через задану поверхню за одиницю часу. У випадку стаціонарного (постійного) струму сила струму
\begin{equation} {I=\frac{q}{t}}. \tag{1.1} \end{equation}
Для нестаціонарного (залежного від часу) струму величина (1.1) визначає середню силу струму за час \(t\), а його точна (миттєва) величина в кожен момент часу визначається відношенням елементарної порції перенесеного заряду \(\mathrm{d}q\) до відповідного елементарного проміжку часу \(\mathrm{d}t\):
\begin{equation} {I}=\frac{\mathrm{d}q}{\mathrm{d}t}. \tag{1.1а} \end{equation}
Одиниця сили струму називається ампер (\(\text{А}\)). Вона визначається через магнітну взаємодію струмів і прийнята як одна з основних одиниць міжнародної системи (SІ). Відтак одиниці всіх інших електричних і магнітних величин у кінцевому підсумку визначаються через ампер. Зокрема, одиниця заряду \(1\ \text{Kл}\) = \(1\ \text{А}\cdot \text{с}\) — то є заряд, який проходить через поперечний переріз провідника за одиницю часу при силі струму \(1\ \text{А}\).
Сила струму є скалярною величиною, проте струм як процес має напрям, який визначається напрямом перенесення носіями електричного заряду. При цьому, позаяк існує два знаки заряду, за домовленістю
напрям струму прийнято напрям перенесення позитивного заряду.
Отже в металах, де носіями є електрони, напрям струму є протилежним до напрямку впорядкованого руху носіїв.
У тонких провідниках струм є спрямований уздовж провідника й рівномірно розподілений по перерізу. Але в провідному середовищі маємо справу з об’ємними струмами, котрі в різних точках можуть мати різну величину та напрям. Тому крім інтегральної характеристики — сили струму \(I\) використовують іще й локальну величину — вектор густини струму \(\vec{j}\), який задає інтенсивність і напрям перенесення заряду в кожній точці. Розглянемо, чим визначається вектор \(\vec{j}\) у провідному середовищі з носіями одного сорту. Для цього підрахуємо струм \(\mathrm{d}I=\mathrm{d}q/\mathrm{d}{t}\), який протікає через елементарну ділянку \(\mathrm{d}\vec{S}\) якоїсь поверхні \(S\) (рис. 1.1а).
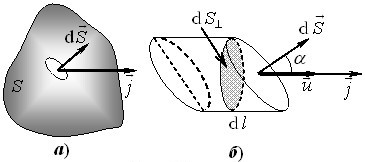
За час \(\mathrm{d}t\) крізь указану ділянку пройдуть усі носії, що знаходилися всередині косого циліндрика (рис. 1.1б) з основою \(\mathrm{d}S\) і твірною \(\mathrm{d}l=u\,\mathrm{d}{t}\), паралельною до швидкості \(\vec{u}\) їхнього упорядкованого руху. Заряд цих носіїв
\begin{equation} \mathrm{d}q=enV\,\mathrm{d}V=enu\,\mathrm{d}t\,\mathrm{d}S\cos\alpha , \end{equation}
де \(e\) — заряд одного носія, \(n\) — їхня концентрація. Отже величина струму через площинку \(\mathrm{d}S\) дорівнює
\begin{equation} \mathrm{d}I=enu\,\mathrm{d}S\cos\alpha=enu\,\mathrm{d}{S}_{\bot}, \tag{1.2} \end{equation}
де \(\mathrm{d}S_{\bot}=\mathrm{d}S\cos\alpha \) — площа проекції ділянки \(\mathrm{d}S\) на площину перпендикулярну до напрямку руху носіїв. Величина
\begin{equation} {j}=\frac{\mathrm{d}I}{\mathrm{d}S_{\bot}}=enu , \end{equation}
яка в кожній точці визначає струм, що припадає на одиницю площі поверхні, перпендикулярної до його напрямку, називається густиною струму і вимірюється в \(\text{А/м}^2\). Аби величина \(j\) відображала ще й напрям струму, її розглядають як вектор:
\begin{equation} \vec{j}=en\vec{u}. \tag{1.3} \end{equation}
У металах і сплавах носіями струму є електрони, але в інших середовищах у створенні струму можуть брати участь різні частинки-носії, кожна із своєю величиною заряду \(q_i\) концентрацію \(n_i\) та швидкістю упорядкованого руху \(\vec{u}_{i}\). Тоді
\begin{equation} \vec{j}=\sum\limits{{{q}_{i}}{{n}_{i}}{{{\vec{u}}}_{i}}}. \tag{1.3а} \end{equation}
Через вектор густини струму можна згорнуто виразити силу струму крізь елементарну площинку \(\mathrm{d}S\) (формула (1.2)) та через довільну поверхню \(S\):
\begin{equation} \mathrm{d}I=\vec{j}\,\mathrm{d}\vec{S}, \tag{1.4} \end{equation} \begin{equation} {I}=\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S}. \tag{1.4а} \end{equation}
Отже, силу струму можна трактувати як потік вектора густини струму через задану поверхню і при необхідності зображувати розподіл струму у просторі лініями вектора \(\vec{j}\) (лініями струму).
Якщо струм по площі поперечного перерізу провідника розподіляється рівномірно, то
\begin{equation} {I}={jS}. \tag{1.4б} \end{equation}
1.2. Рівняння неперервності
Розглянуті характеристики струму дозволяють подати загальній математичний вираз одного із фундаментальних фізичних законів — закону збереження електричного заряду. Якщо виділити в просторі довільну замкнену поверхню, то згідно з означенням (1.1а) і виразом (1.4а) можна записати:
\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}=\frac{\mathrm{d}q_{S}}{\mathrm{d}{t}}, \tag{1.5} \end{equation}
де \(\mathrm{d}q_{s}/\mathrm{d}{t}\) — заряд, який проходить за одиницю часу крізь поверхню \(S\) назовні. Але позаяк заряд не виникає з нічого і не зникає безслідно, ця похідна в точності дорівнює швидкості зменшення величини заряду в об’ємі, що обмежений даною поверхнею. Отже:
\begin{equation} \begin{aligned} &\frac{\mathrm{d}q_{S}}{\mathrm{d}t} =- \frac{\mathrm{d}q_{V}}{\mathrm{d}t}=-\frac{\mathrm{d}}{\mathrm{d}t}\int\limits_{V}\rho\,\mathrm{d}{V}={}\\ &\quad{}= - \int\limits_{V}\frac{\partial \rho }{\partial t}\mathrm{d}{V}, \end{aligned} \end{equation}
де \(\rho\) — об’ємна густина заряду.
Примітка. Під знаком інтеграла стоїть частинна похідна, тому що об’єм V є обмежений фіксованою (нерухомою) поверхнею, і похідна визначається тільки явною залежністю заряду в об’ємі від часу, а не, скажімо, рухом стінок поверхні.
Підставивши цей вираз у (1.5), отримуємо:
\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}=-\int\limits_{V}\frac{\partial \rho }{\partial t}\mathrm{d}{V}. \tag{1.6} \end{equation}
Рівняння (1.6) називається рівнянням неперервності і є загальним виразом закону збереження електричного заряду. Воно, зокрема, вбирає й закон збереження заряду в електрично ізольованій системі, про який говорилося в електростатиці. Справді, крізь будь-яку замкнену поверхню, що відділяє таку систему від оточення, не проходять заряджені частинки, і в усіх її точках \(\vec{j}={0}\). Отже, згідно з (1.6),
\begin{equation} \begin{aligned} &\int\limits_{V}\frac{\partial\rho}{\partial{t}}={0} \quad \Rightarrow \quad \frac{\partial\rho}{\partial{t}}=0 \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {q(t)}=\mathrm{const}, \end{aligned} \end{equation}
тобто повний заряд системи не змінюється з часом (зберігається).
Із рівняння неперервності випливають також деякі загальні висновки щодо умов існування електричного струму. Зокрема, це висновок про те, що постійний струм може існувати лишень у замкнених провідних контурах. Дійсно, при постійному струмі розподіл потенціалів і зарядів у провідному середовищі не змінюється з часом, отже, в рівнянні (1.6) похідна \(\partial\rho / \partial{t}=0\) в усіх точках. Тому для будь-якої замкненої поверхні
\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}={0}. \end{equation}
а це означає, що кількість ліній струму (ліній вектора \(\vec{j}\)), які заходять усередину поверхні та виходять назовні є завжди однаковою. Інакше говорячи, лінії стаціонарного струму є неперервними (замкненими) — вони ніде не починаються і ніде не закінчуються. Це одна з причин, чому рівняння (1.6) називають рівнянням неперервності. З нього випливає той загальновідомий факт, що
постійний струм може протікати тільки по замкненому провідному контуру.
Але з рівняння неперервності випливає й зовсім не самоочевидний висновок про те, що
залежний від часу струм може існувати і в незамкнених контурах,
як от у колах із конденсаторами. При цьому в точках розриву контуру (на пластинах конденсатора) відбувається накопичення зарядів того чи іншого знаку, і в них \( (\partial\rho{/}\partial{t})\ne{0}\). Тому відповідно до рівняння (1.6), потік \(\vec{j}\) крізь малу замкнену поверхню, що охоплює таку точку,
\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S} > {0}\quad \text{при} \ \frac{\partial\rho}{\partial{t}}<{0} \end{equation}
і
\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}<{0}\quad \text{при} \ \frac{\partial\rho}{\partial{t}}>{0}. \end{equation}
Згідно з геометричним змістом потоку ці вирази означають, що лінії змінного струму мають початки і кінці: вони починаються в одних точках і закінчуються в інших. (Чому, попри це, рівняння (1.6) називається рівнянням неперервності, див. розділ V, п. 2.) Отже, рівняння неперервності не заперечує можливості існування електричного струму в незамкненому контурі. Але через обмежену кількість носіїв у провіднику, вони не можуть в точках розриву накопичуватися весь час. Тому в незамкненому провіднику довготривалий нестаціонарний струм може існувати лише за умови, що його напрям періодично змінюється на протилежний. Саме такі струми означає термін “змінний струм”.
1.3. Закон Ома в локальній формі
Дрейф носіїв струму. Розглянемо механізм електричного струму в металевому провіднику на основі уявлень класичної фізики, за якими електрони провідності в металі утворюють “електронний газ” і здійснюють інтенсивний тепловий рух. Його усереднену швидкість \({v}\) можна оцінити з відомих формул молекулярної фізики:
\begin{equation} \frac{m\left\langle {{v}^{2}} \right\rangle }{2}=\frac{3}{2}kT \quad \Rightarrow \quad {v}=\sqrt{\frac{3kT}{m}}. \end{equation}
Підставивши значення маси електрона \(m = 9{,}1\cdot10^{-31}\ \text{кг}\), сталої Больцмана \(k = 1{,}38\cdot 10^{-23}\ \text{Дж/К}\) і прийнявши \(T=293\ \text{К}\) (\(20^\circ \,\text{C}\)), отримаємо:
\begin{equation} {v}=\sqrt{\frac{3\cdot{1{,}38\cdot{10^{-23}}}\cdot 293}{9{,}1\cdot{10^{-31}}}}\approx 10^{5}\ \text{м/с}. \end{equation}
Отже, електрони здійснюють дуже інтенсивний тепловий рух. Але він є безладним і не спричинює перенесення заряду, тобто електричного струму. Струм створюється впорядкованим рухом носіїв, і саме його швидкість \(u\), відповідно до формули (1.3), визначає густину струму. Задля кращого уявлення про цей рух оцінимо величину \(u\) в мідному провіднику при густині струму \(j = 10\ \text{А/мм}^2 = 10^7\ \text{А/м}^2\), прийнявши концентрацію носіїв рівною концентрації атомів \(n = 8{,}5\cdot10^{28}\ 1/\text{м}^3\):
\begin{equation} \begin{aligned} &{u}=\frac{j}{en}=\frac{10^7}{1{,}6\cdot{10^{-19}}\cdot{8{,}5}\cdot{10^{28}}}\approx{}\\ &\quad{}\approx 10^{-3}\ \text{м/с} = 1\ \text{мм/с}. \end{aligned} \end{equation}
Це складає всього \(10^{-8}\) від теплової швидкості, й упорядкований рух окремого електрона на тлі хаотичного теплового руху взагалі не можна розрізнити. Тож величина \(u\) визначає не рух окремого електрона, а рух сукупності носіїв струму в цілому. Такий колективний рух називається дрейфом, а швидкість \(u\) — дрейфовою швидкістю носіїв. Дрейф носіїв нагадує знесення (дрейф) рою комах “товкунців” слабким вітерцем.
Закон Ома. Мала величина дрейфової швидкості пояснюється тим, що в металі електрони провідності на своєму шляху натикаються на іони кристалічної ґратки, що перешкоджає їхньому впорядкованому рухові вздовж провідника. Між іонами та електронами діють сили притягання. Через це при зустрічі з масивними іонами електрони повністю втрачають швидкість упорядкованого руху, подібно до того, як пластилінова кулька втрачає швидкість при зіткненні зі стіною. Це й перешкоджає дрейфові носіїв. Тому для створення та підтримання струму в провіднику має існувати електричне поле. Це не суперечить твердженню про неможливість в провідниках електричного поля, про що говорилося раніше (розділ II, п. 2), бо в провіднику із струмом заряди-носії не перебувають у рівновазі, й указане поле не є електростатичним.
Зауваження. Вільні електрони, звісно, стикаються й між собою. Але ці зіткнення є пружними і, згідно із законом збереження імпульсу, не впливають на сумарний імпульс, тож і на дрейфову швидкість електронів-носіїв струму. Тому зіткнення між електронами не перешкоджає струмові.
Таким чином, через непружні зіткнення з іонами носії вільно рухаються тільки від зіткнення до зіткнення, проходячи в середньому деяку відстань \(\langle\lambda\rangle \), яка називається середньою довжиною вільного пробігу. При цьому середній проміжок часу між двома послідовними зіткненнями електрона з іонами \(\langle\tau{\rangle}\), який називається середнім часом вільного пробігу, складає
\begin{equation} \langle\tau\rangle = \frac{\lambda}{v}, \tag{1.7} \end{equation}
де \({v}\) — швидкість теплового руху електрона.
Атоми в твердих тілах розміщені дуже щільно, майже впритул, Тому величина \(\langle\lambda{\rangle}\) має бути близькою до відстані між атомами в провіднику. Ця відстань для більшості металів складає \((3\div 5)\cdot 10^{-10}\ \text{м}\), а теплова швидкість \({v}\approx{10^5}\ \text{м/с}\). За таких умов час вільного пробігу виявляється настільки малим, що електрони під дією поля не встигають помітно розігнатися, чим пояснюється мала величина дрейфової швидкості носіїв.
Розглянутий класичний механізм руху електронів провідності в металі дозволяє теоретично встановити один з основних законів електричного струму — закон Ома в локальній (інакше диференціальній) формі, який визначає зв’язок між струмом та електричним полем у кожній точці металевого провідника. За час між двома послідовними зіткненнями з іонами кожен електрон під дією поля збільшує швидкість руху уздовж провідника від \(0\) до певної максимальної величини \(\vec{u}_{m}\), яка в середньому дорівнює
\begin{equation} \langle\vec{u}_{m}\rangle=\vec{a}\cdot\langle\tau\rangle=\frac{\vec{F}}{m}\langle\tau\rangle=\frac{e\vec{E}}{m}\langle\tau{\rangle}, \tag{1.8} \end{equation}
де \(\vec{a}\) — прискорення електрона, \(e\) і \(m\) — його заряд і маса, \(\vec{E}\) — напруженість електричного поля в провіднику і \(\langle\tau{\rangle}\) — середній час вільного пробігу електрона.
Дрейфова швидкість носіїв дорівнює половині величини \(u_m\):
\begin{equation} \vec{u}=\frac{1}{2}\langle\vec{u}_{m}\rangle=\frac{e\vec{E}}{2m}\langle\tau{\rangle}. \end{equation}
У такому разі для густини струму відповідно до формули (1.2) маємо:
\begin{equation} \vec{j}=\frac{e^2 n\langle\tau\rangle}{2m}\vec{E}, \end{equation}
або, враховуючи вираз (1.7),
\begin{equation} \vec{j}=\frac{e^2 n\langle\lambda\rangle}{2mv}\vec{E}. \end{equation}
Згорнуто ці формули записують у вигляді
\begin{equation} \vec{j}=\sigma\vec{E} \tag{1.9} \end{equation}
або
\begin{equation} \vec{j}=\frac{\vec{E}}{\rho}. \tag{1.9а} \end{equation}
Величина
| \(\sigma=\frac{e^2 n\langle\tau\rangle}{2m}=\frac{e^2 n\langle\lambda\rangle}{2mv}\) | (1.10) |
показує, наскільки добре дана речовина проводить струм і називається питомою електропровідністю. Відповідно, обернена величина
\begin{equation} \rho=\frac{1}{\sigma}=\frac{2m}{e^2 n\langle\lambda\rangle} \tag{1.10а} \end{equation}
називається питомим опором речовини.
Формули (1.10), (1.10а) виражають один з основних законів електричного струму — закон Ома в локальній формі:
густина електричного струму в кожній точці провідника є прямо пропорційною напруженості поля в цій точці.
Одразу зазначимо, що закон Ома не є загальним. Він виконується тільки в лінійних провідниках — таких, в яких електропровідність не залежить від напруженості поля, тож і від напруги на їхніх кінцях. Окрім металів і сплавів, лінійними є однорідні напівпровідники та електроліти (рідкі провідники) — середовища, в яких концентрація носіїв струму \(n\), відтак і електропровідність \(\sigma\), не залежать від напруженості поля \(E\). А ось гази та контакти різних напівпровідників або напівпровідників із металами є нелінійними провідниками. Тому в газорозрядних і вакуумних лампах, а також у напівпровідникових електронних приладах закон Ома не виконується.
1.4. Питома потужність струму
Стикаючись із іонами металу, електрони провідності передають їм імпульс та енергію, набуті в дрейфовому русі. Ця енергія називається енергією електричного струму і далі перетворюється на ті чи інші види. Наприклад, у газорозрядній лампі частина цієї енергії трансформується в енергію збудження атомів газу і по тому — в енергію світлового випромінювання, а в електричному двигуні майже вся енергія струму перетворюється на кінетичну енергію обертання ротора. При цьому в усіх випадках та чи інша частка енергії струму переходить у внутрішню (теплову) енергію провідників. Зокрема, в нерухомих рідких і твердих провідниках із постійним струмом на тепло перетворюється вся енергія струму.
Кількісною характеристикою перетворень енергії струму на тепло в кожній точці провідника є питома потужність струму (\(\text{Вт/м}^3\)), яка дорівнює енергії, що передається провіднику носіями в одиниці об’єму за одиницю часу
\begin{equation} {w}=\frac{\mathrm{d}W}{\mathrm{d}t\,\mathrm{d}V}. \tag{1.11} \end{equation}
Величину \({w}\) можна визначити, прямо підрахувавши енергію \(\mathrm{d}W\), що виділяється в об’ємі провідника \(\mathrm{d}V\) за час \(\mathrm{d}t\), як
\begin{equation} \mathrm{d}W=\langle{K_1}\rangle\mathrm{d}N\,\mathrm{d}{Z_1}, \end{equation}
де \(\langle{K_1}{\rangle}\) — середня величина кінетичної енергії дрейфового руху одного електрона на момент зіткнення з іоном металу, \(\mathrm{d}N\) — кількість електронів провідності в об’ємі \(\mathrm{d}V\), і \(\mathrm{d}Z_{1}\) — кількість зіткнень з іонами, які відбуває один електрон за час \(\mathrm{d}t\).
Але зручніше у виразі (6.12) величину \(\mathrm{d}W /\mathrm{d}V \) розглядати як роботу, а \(\mathrm{d}W/(\mathrm{d}t\cdot\!\mathrm{d}V) \) — як потужність сил, що діють на всі носії в одиниці об’єму провідника. Тоді, враховуючи відому з механіки формулу \(p=Fu\) для потужності сили \(F\), що діє на частинку при швидкості руху \(u\), можна записати:
\begin{equation} {w}=np={nuF}, \end{equation}
де \(n\) — кількість носіїв в одиниці об’єму. Відтак, урахувавши вираз (1.3), отримаємо:
\begin{equation} {w}=j\frac{F}{e}. \tag{1.12} \end{equation}
Формула (1.12) не пов’язана з природою сил, які діють на носії струму, тож є найбільш загальним виразом питомої потужності струму. Але зазвичай \(F=eE\), де \(E\) — напруженість електричного поля в провіднику із струмом. Тоді
\begin{equation} {w}={jE}, \tag{1.13} \end{equation}
а з урахуванням закону Ома (1.9)
\begin{equation} {w}=\rho{j^2}, \tag{1.13а} \end{equation}
або
\begin{equation} {w}=\sigma{E^2}=\frac{E^2}{\rho}. \tag{1.13б} \end{equation}
У випадку постійного струму всі ці формули є рівносильними і виражають закон Джоуля в локальній (“диференціальній”) формі:
кількість теплоти, що виділяється за одиницю часу (теплова потужність) в одиниці об’єму однорідного провідника із струмом, в кожній точці є прямо пропорційною квадратові густини струму або квадратові напруженості електричного поля в цій точці.
1.5. Обмеженість класичної теорії електропровідності
Отримані в класичній теорії висновки про лінійну залежність густини струму від напруженості електричного поля (закон Ома) та квадратичну залежність потужності струму від напруженості електричного поля (закон Джоуля) в однорідних лінійних провідниках підтверджуються на досліді. Але низка її кількісних передбачень не справджується, тож класична теорія електропровідності металів є неповною. А саме.
Відомо, що концентрація вільних електронів у міді \(n = 8{,}5\cdot10^{28} \text{м}^{-3}\), і питомий опір \(\rho = 1{,}7\cdot 10^{-8}\ \text{Ом}\cdot \text{м}\) при \(t=20^\circ \,\text{C}\). Якщо підставити ці величини, отриману раніше величину теплової швидкості електронів \({v}\approx 10^{5}\ \text{м/с}\), та заряд і масу електрона у формулу (1.10а), то для середньої довжини вільного пробігу електрона виходить \(\langle\lambda\rangle\approx 5{\cdot}{10^{-9}}\ \text{м}\). Позаяк відстань між атомами в міді \(d = 3{,}6\cdot 10^{-10}\ \text{м}\), то виходить, що електрон без зіткнень проходить у середньому півтора десятка іонів, які трапляються на його шляху. В класичній концепції електронного газу цього не можна збагнути, адже атоми в твердому тілі розміщені дуже щільно, практично впритул. Істотні розбіжності між класичною теорією та дослідом існують і щодо температурної залежності опору металевих провідників \(\rho(T)\). Згідно з формулами (1.10а) і (1.7) питомий опір має бути прямо пропорційним величині \(\sqrt{T}\), але насправді в широкому температурному інтервалі залежність \(\rho(T)\) є лінійною. Крім того класична теорія взагалі не здатна пояснити існування явища надпровідності — повного зникнення електричного опору в деяких металах і сплавах при наднизьких температурах.
Обмеженість класичної теорії електропровідності пояснюється тим, що електрони в металі не можна розглядати як матеріальні точки, підпорядковані законам класичної фізики. Як з’ясувалося, електрони мають складні квантові властивості, і їхній рух у твердому тілі радше нагадує не рух кульок, а поширення хвиль. При цьому виявляється, що перешкоду упорядкованому рухові електронів у провіднику, тобто опір, створюють не самі іони, а дефекти кристалічної структури — різні порушення строгої періодичності в розташуванні іонів у вузлах кристалічної ґратки. Такими можуть бути відсутність іонів у деяких вузлах ґратки, їх заміщення чужорідними атомами, розташування власних чи чужорідних атомів у міжвузіллях, з рештою, і тепловий рух атомів. В оптиці подібні дефекти середовища є причиною розсіяння світла (розсіяння фотонів). Відповідно, взаємодію носіїв із дефектами структури провідника називають розсіюванням носіїв струму.
Кількість дефектів у провіднику є набагато меншою за кількість власних атомів, а відстань між ними, відповідно, більшою. Це пояснює аномально велику як для класичної теорії, довжину вільного пробігу носіїв струму. Квантова теорія правильно пояснює й інші властивості провідників, зокрема передбачає лінійну залежність опору від температури і пояснює явище надпровідності. В цьому зв’язку те, що класична теорія при принципово хибних засадах дає правильні основні закони струму (1.9) і (1.13) може викликати подив. Але насправді нічого дивного в цьому немає, позаяк залежності (1.9) і (1.13) є наслідком лише того, що при заданій напруженості поля в провіднику встановлюється постійна швидкість дрейфу носіїв. А це пов’язано тільки із самим фактом розсіювання носіїв, а не з його механізмом.
Контрольні запитання
1. У рухомій металевій кульці її вільні електрони, що є носіями струму, теж напрямлено рухаються із швидкістю кульки. Поясніть, чи створює електричний струм цей рух.
2. Як пов’язаний напрям струму із напрямком руху носіїв, які його створюють?
3. По довгій прямій дротині протікає струм. Чи виявить струм у дротини спостерігач, який рухається вздовж неї із швидкістю дрейфу електронів? Якщо так, то якими будуть його величина та напрям?
4. Поясніть, яку властивість електричного заряду відображує рівняння неперервності.
5. Чи можна створити тривалий електричний струм у незамкненому провіднику? Якщо ні, то чому? Якщо так, то за яких умов?
6. Говорять, що струм у металі створюється напрямленим рухом вільних електронів. Якщо так, то чому швидкість цього руху є дуже малою?
7. В яких випадках закон Ома не виконується? Які провідники називаються лінійними і що є умовою лінійності провідника?
8. У чому полягає закон Джоуля в локальній формі? Чи завжди вся робота струму переходить у тепло?
9. У чому виявляється неповнота класичної теорії електропровідності металів та якою є її причина?
2. Електричне коло
Розглянуті локальні закони електричного струму дозволяють встановити зв’язки між характеристиками струму та електричного поля не лише в кожній точці провідника, а й на кожній ділянці електричного кола, або ланцюга, тобто з’єднаних між собою провідників, приладів і пристроїв, які утворюють систему провідних контурів для струму. Далі розглядаються найпростіші нерозгалужені кола, котрі включають тільки один контур.
Розглянуті такі питання:
2.1. Сторонні сили. ЕРС
Сторонні сили. Раніше говорилося, що для протікання стаціонарного електричного струму потрібний замкнений провідний контур. Але одного цього замало, бо крім носіїв струму в провіднику є й протилежно заряджені частинки, що своїм електричним полем перешкоджають вільному рухові носіїв по контуру. Тому для підтримування струму в провіднику на носії мають діяти якісь інші сили, що діють проти сил указаного електричного поля і здатні переміщувати носії вздовж провідника. Зрозуміло, що такі сили не можуть створюватися зарядами самого провідника і мають зовнішнє походження. Тому вони називаються сторонніми силами.
Через наявність у провіднику із струмом сторонніх сил у виразах закону Ома для густини струму (1.10) і (1.10а) має стояти сумарна напруженість поля кулонівських та сторонніх сил:
\begin{equation} \vec{j}=\sigma \bigl( {{{\vec{E}}}_{\text{к}}}+{{{\vec{E}}}_{\text{cт}}} \bigr). \tag{2.1} \end{equation}
Теоретично сторонні сили можна створити у різний спосіб. Зазвичай для цього в контур включають спеціальні пристрої — джерела струму. Дія джерел струму ґрунтується теж на різних принципах, але в приладах малої потужності найчастіше використовують хімічні джерела — “батарейки” і акумулятори.
Розглянемо, як діє найпростіше коло, що складається із внутрішньої ділянки (джерела) і зовнішньої ділянки у вигляді провідника, котрий через ключ К приєднаний до полюсів (вивідних контактів) джерела (рис. 2.1).
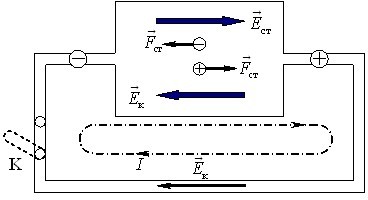
Всередині джерела під дією сторонніх сил певна кількість електронів (носіїв струму) переходить з одного полюса на інший, створюючи між ними відповідну різницю потенціалів і кулонівське електричне поле \(\vec{E}_{\text{к}}\) всередині джерела та на зовнішній ділянці. При розімкненому ключі це поле не спричинює струму, бо всередині джерела воно компенсується полем сторонніх сил, а назовні між полюсами для носіїв немає неперервного провідного шляху. Але після замикання ключа надлишкові електрони з негативного полюса під дією кулонівського поля починають рухатися по зовнішній ділянці і з’єднуватися з надлишковими зарядами на позитивному полюсі. Якби в джерелі на електрони не діяли сторонні сили, це призвело би до практично миттєвої нейтралізації полюсів і припинення руху носіїв по колу. Та насправді електрони, що приходять по зовнішній ділянці кола на позитивний полюс, підхоплюються сторонніми силами і, всупереч дії кулонівського поля всередині джерела, знову переміщуються на негативний полюс. Тож, доки діють сторонні сили, в колі зберігається електричне поле і напрямлений рух (дрейф) носіїв, тобто — електричний струм. Можна сказати, що джерело струму "переганяє" носії струму від одного полюса до іншого, долаючи кулонівське поле всередині джерела, подібно до насоса, котрий переганяє воду від вхідного до вихідного отвору, долаючи опір рухові води в трубопроводі.
Спад напруги та ЕРС. Через розсіювання носіїв у провіднику, вони втрачають енергію впорядкованого руху. Тому для підтримання струму ці втрати мають компенсуватися за рахунок роботи сил, які забезпечують струм. На довільній ділянці кола (рис. 2.2) це можуть бути і кулонівські \(\vec{F}_{\text{к}}\), і сторонні \(\vec{F}_{\text{ст}}\) сили.
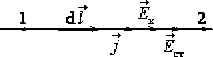
Отже, при елементарному переміщенні \(\mathrm{d}\vec{l}\) уздовж провідника над носіями із загальним зарядом \(q\) виконується робота
\begin{equation} \begin{aligned} &\delta A=\delta A_{\text{к}}+\delta A_{\text{ст}} = \vec F_{\text{к}} \,\mathrm{d}\vec l +\vec F_{\text{ст}}\,\mathrm{d} \vec l ={}\\ &\quad{}= q\vec E_{\text{к}} \,\mathrm{d}\vec l +q\vec E_{\text{ст}}\,\mathrm{d} \vec l. \end{aligned} \end{equation}
Для всієї ділянки між точками 1 і 2 маємо:
\begin{equation} \begin{aligned} &A=A_{\text{к}}+A_{\text{ст}} ={}\\ &\quad{}= q\int\limits_{1\to2}\vec E_{\text{к}} \,\mathrm{d}\vec l +q\int\limits_{1\to2}\vec E_{\text{ст}}\,\mathrm{d} \vec l. \end{aligned} \tag{2.2}\end{equation}
де інтегрування ведеться вздовж провідника.
Робота \(A\) є прямо пропорційною до перенесеного носіями заряду \(q\), тож відношення \(A/q\) не залежить від \(q\) і є характеристикою сумарного силового поля в провіднику. Воно позначається символом \(U\) і називається спадом напруги на заданій ділянці кола:
\begin{equation} {U}=\frac{A}{q}. \tag{2.3} \end{equation}
На елементарній ділянці спад напруги
\begin{equation} \mathrm{d}U=\frac{\delta{A}}{q}. \tag{2.3а} \end{equation}
Таким чином,
спадом напруги на заданій ділянці кола називається відношення роботи всіх сил, які діють на носії струму, до перенесеного по цій ділянці заряду.
Відповідно до даного означення і виразу (2.2),
\begin{equation} U= \int\limits_{1\to2}\vec E_{\text{к}} \,\mathrm{d}\vec l +\int\limits_{1\to2}\vec E_{\text{ст}}\,\mathrm{d} \vec l. \end{equation}
Кулонівське поле є потенціальним (див. розділ І, п. 2), тож перший доданок дорівнює різниці потенціалів на кінцях ділянки:
\begin{equation} \int\limits_{1\to{2}}\vec{E}\,\mathrm{d}\vec{l}=\varphi_1-{\varphi_2}. \tag{2.4} \end{equation}
Другий доданок характеризує поле сторонніх сил. Він позначається символом \(\mathscr{E}\) і називається електрорушійною силою (ЕРС) на даній ділянці кола:
\begin{equation} \mathscr{E}=\frac{{A}_{\text{ст}}}{q} =\int\limits_{1\to2}\vec E_{\text{ст}}\,\mathrm{d} \vec l. \tag{2.5} \end{equation}
Отже,
електрорушійною силою на даній ділянці кола називається відношення роботи сторонніх сил, які діють на носії струму, до перенесеного по цій ділянці заряду.
Ураховуючи означення (2.3) і (2.5), можна записати наступний загальний вираз для спаду напруги на ділянці кола:
\begin{equation} {U}=\varphi_{1}-\varphi_{2}+\mathscr{E}. \tag{2.6} \end{equation}
При цьому на однорідній ділянці, тобто такій, де відсутні сторонні сили, \(\mathscr{E}\) = 0, і спад напруги дорівнює різниці потенціалів на кінцях:
\begin{equation} {U}=\varphi_{1}-\varphi_{2}. \tag{2.6а} \end{equation}
Це означає, що на зовнішній ділянці кола робота по переміщенню зарядів дорівнює
\begin{equation} A=q(\varphi_{1}-\varphi_{2}) \end{equation}
і виконується тільки кулонівським електричним полем. Всередині джерела струму, де \(\mathscr{E}\ne0\), вказана робота виконується обома силовими полями і дорівнює
\begin{equation} {A}=qU=q(\varphi_{1}-\varphi_{2}+\mathscr{E}) . \end{equation}
А ось при обході замкненого контуру \(\varphi_{1}=\varphi_{2}\), і спад напруги у всьому контурі, тобто сума спадів напруги на всіх ділянках,
\begin{equation} {U}=\mathscr{E}. \tag{2.6б} \end{equation}
Отже, відповідно до (2.3), повна робота, що виконується над носіями струму в замкненому контурі дорівнює роботі тільки сторонніх сил:
\begin{equation} {A}=q\mathscr{E}. \tag{2.7} \end{equation}
Це пояснюється тим, що через потенціальність кулонівського поля сума його робіт на зовнішній \( {{A}'_{\text{к}}}=q( {{\varphi }_{1}}-{{\varphi }_{2}} ) \) та на внутрішній \( {{A}''_{\text{к}}}=q( {{\varphi }_{2}}-{{\varphi }_{1}} ) \) ділянках замкненого контуру дорівнює нулю. Тож одні лише кулонівські сили принципово не можуть забезпечити електричний струм. Відповідно,
електричний струм в колі існує виключно завдяки енергії, що надається носіям джерелом струму.
Тому роль сторонніх можуть виконувати тільки ті сили, робота і циркуляція поля котрих на даному провідному контурі є відмінною від нуля:
\begin{equation} \oint\limits\vec E_{\text{ст}}\,\mathrm{d} \vec l\ne0. \end{equation}
При цьому фізична природа та конкретне походження сторонніх сил не має принципового значення.
Що ж до кулонівського поля, то воно, хоч і не дає енергії для протікання струму, виконує в контурі важливу “диспетчерську” функцію — переносить енергію від джерела до інших ділянок.
Наостанок зробимо ще дві ремарки. По-перше, з означень (2.5) і (2.6) випливає, що ЕРС та спад напруги, як і різниця потенціалів, вимірюються у вольтах (\(\text{В}\)). І, по-друге, всі згадані величини є алгебраїчними; їхні знаки визначаються напрямками кулонівського поля та поля сторонніх сил відносно напрямку переміщення від початкової до кінцевої точки заданої ділянки кола. Детальніше про це говориться в п. 2.5.
2.2. Узагальнений закон Ома
Вище говорилося, що для практики важливо знати зв’язок між струмом і полем не лише в точці, а й на окремих ділянках і в усьому колі в цілому. Цей зв’язок визначається відомим законом Ома, який був установлений дослідним шляхом. Але, виходячи із співвідношень (2.2) і (2.3), указаний закон можна отримати й теоретично.
Розглянемо струм у тонкому провіднику, в якому струм рівномірно розподіляється по площі перерізу, так що густина струму
\begin{equation} {j}=\frac{I}{S}, \tag{2.8} \end{equation}
і вектори густини струму \(\vec{j}\) та полів \(\vec{E}_{\text{к}}\), \(\vec{E}_{\text{ст}}\) і \(\vec{E}=\vec{E}_{\text{к}}\) + \(\vec{E}_{\text{ст}}\) спрямовані вздовж провідника.
(Зауважимо, що в теорії термін “тонкий” означає не величину перерізу, а рівномірність розподілу по ньому струму, і на практиці цей критерій задовольняють всі електричні кола.)
На малій ділянці \(\mathrm{d}{l}\) провідника елементарна робота \(\delta A\), яку виконують над носіями всі сили, дорівнює
\begin{equation} \delta{A}=qE\,\mathrm{d}{l}, \end{equation}
або, відповідно до закону Ома (1.9а) і виразу (2.8),
\begin{equation} \delta{A}=q\rho{l}\frac{\mathrm{d}l}{S}. \end{equation}
З іншого боку, згідно з означенням (2.3а),
\begin{equation} \delta{A}=q\,\mathrm{d}{U}, \end{equation}
де \(\mathrm{d}{U}\) — спад напруги на ділянці \(\mathrm{d}{l}\). Отже,
\begin{equation} \mathrm{d}U=\rho{l}\frac{\mathrm{d}l}{S}. \end{equation}
Проінтегрувавши цей вираз по всій довжині провідника з урахуванням того, що для стаціонарного струму \({I}=\mathrm{const}\) по всій довжині, отримаємо:
\begin{equation} {U}=\int\limits_{l}I\rho\frac{\mathrm{d}l}{S}=I\int\limits_{l}\rho\frac{\mathrm{d}l}{S}. \tag{2.9} \end{equation}
У цьому виразі величина
\begin{equation} {R}=\int\limits_{l}\rho\frac{\mathrm{d}l}{S} \tag{2.10} \end{equation}
залежить тільки від розмірів і конфігурації (форми) провідника та властивостей його речовини і називається електричним опором.
Таким чином, струм і спад напруги на довільній ділянці кола пов’язані співвідношеннями
\begin{equation} {U=IR} \tag{2.11} \end{equation}
або
\begin{equation} {I}=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\mathscr{E}}{R}, \tag{2.11а} \end{equation}
які виражають узагальнений закон Ома:
сила струму в довільній ділянці електричного кола дорівнює відношенню спаду напруги на цій ділянці до її опору.
Закон Ома в такій редакції називається узагальненим, оскільки вираз (2.11а) є чинним як для неоднорідної ділянки кола, де на носії діють і кулонівські, і сторонні сили, так і для однорідної ділянки, де діють лише кулонівські сили. В останньому випадку в (2.11а) \(\mathscr{E}=0\), і
\begin{equation} {I}=\frac{\varphi_{1}-\varphi_{2}}{R}. \tag{2.12} \end{equation}
У підручниках з елементарної фізики цей вираз називають законом Ома для ділянки кола:
сила струму в (однорідній) ділянці кола дорівнює відношенню різниці потенціалів на кінцях ділянки до її опору.
Відповідно, при обході всього замкненого контуру \(\varphi_{1}=\varphi_{2}\) і
\begin{equation} {I}=\frac{\mathscr{E}}{R_{0}}, \end{equation}
або
\begin{equation} {I}=\frac{\mathscr{E}}{R+r}, \tag{2.13} \end{equation}
де \(R_{0} = R + r\) — опір всього кола, \(R\) — опір зовнішньої ділянки кола, або навантаження, і \(r\) — внутрішній опір джерела струму (рис. 2.3).
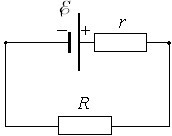
Цю формулу називають законом Ома для повного кола:
сила струму в замкненому колі дорівнює відношенню ЕРС, яка діє в ньому, до повного опору кола.
Формулу (2.13) можна переписати у вигляді
\begin{equation} {IR}+Ir=\mathscr{E}. \tag{2.13а} \end{equation}
Величини \(IR\) та \(Ir\) визначають спади напруги на однорідній зовнішній і неоднорідній внутрішній ділянці кола, відповідно. При цьому згідно з (2.12) \(IR = \varphi _{1}-\varphi _{2}\), тож
\begin{equation} \varphi_{1}-\varphi_{2}=\mathscr{E}-Ir . \tag{2.14} \end{equation}
Отже, різниця потенціалів на полюсах джерела не збігається з ЕРС. Так само не збігаються і спади напруги на цих двох ділянках, попри те, що вони мають спільні крайні точки — полюси джерела.
Зауважимо також, що, тоді як співвідношення (2.11а) виконується для будь-якої ділянки будь-якого кола, формула (2.13) є чинною тільки для найпростішого кола (рис. 2.3), що містить тільки один провідний контур.
2.3. Електричний опір
Опір однорідного провідника. Електричний опір спричинюється розсіюванням носіїв у провіднику із струмом і в загальному випадку визначається інтегральною формулою (2.10). Але на практиці зазвичай використовують однорідні провідники (\(\rho = \mathrm{const}\)) сталого поперечного перерізу (\(S = \mathrm{const}\)) по всій довжині \(l\). В такому разі
\begin{equation} {R}=\frac{\rho}{S}\int\limits_{l}\,\mathrm{d}{l}\quad \Rightarrow \quad {R}=\rho\frac{l}{S}. \tag{2.15} \end{equation}
У деяких випадках замість опору зручніше використовувати обернену величину \(\Lambda=(1/R) \), яка називається провідністю і визначається формулою
\begin{equation} \Lambda=\sigma\frac{S}{l}, \tag{2.15а} \end{equation}
де \(\sigma = (1/ \rho )\) — питома електропровідність речовини провідника.
Електричний опір вимірюється в омах (Ом), а провідність — у сіменсах (См), \(1\ \text{См} = 1\ \text{Ом}^{-1}\).
Опір провідника залежить не лише від його довжини та перерізу, а й від температури. Як показує дослід, при нагріванні опір металів зростає і в доволі широкому діапазоні температур виражається формулою:
\begin{equation} {R}=R_{0}(1+\alpha{t}) , \tag{2.16} \end{equation}
де \(t\) — температура за шкалою Цельсія, \(R_{0}\) — опір провідника при температурі \(0\)°C, і \(\alpha \) (\(1\)/K) — таблична константа, що називається температурним коефіцієнтом опору і показує відносну зміну опору провідника при зміні температури на \(1\) К.
Зростання опору металевих провідників при нагріванні пояснюється зростанням швидкості теплового руху \({v}\) і, згідно з (1.7), зменшенням часу вільного пробігу носіїв \(\langle{\tau}\rangle \). Через це збільшується питомий опір речовини \(\rho \) (1.10а), тож і опір провідника \(R\). В інших провідних середовищах — напівпровідниках і провідниках другого роду (електролітах) — опір теж залежить від температури, але на відміну від металів, при нагріванні зменшується. Це пояснюється тим, що в указаних речовинах при підвищенні температури суттєво зростає концентрація носіїв струму, так що зменшення їхнього часу вільного пробігу перестає бути визначальним.
З’єднання резисторів. Електричний опір є робочим параметром резисторів — найпростіших приладів, які присутні практично в усіх електричних схемах. Резистор по суті є просто зразком провідної речовини із заданим опором \(R\). Для резисторів використовують матеріали з малою електропровідністю, що дозволяє отримувати великі значення опору при малих розмірах резисторів.
В електричних і електронних схемах використовують як поодинокі резистори, так і різні з’єднання (комбінації) резисторів. Але при розрахунках часто буває зручно все з’єднання замінити одним еквівалентним резистором із опором, при якому струми в усіх інших ділянках кола лишаються незмінними. Тож опір еквівалентного резистора має бути таким, що напруга і струм у ньому збігаються з напругою та струмом на всьому з’єднанні.
Встановимо формули для розрахунку еквівалентного опору найпростіших з’єднань резисторів — послідовного та паралельного.
Послідовне з’єднання. В такому з’єднанні всі резистори сполучені в ланцюг так, як показано на рис. 2.4а.
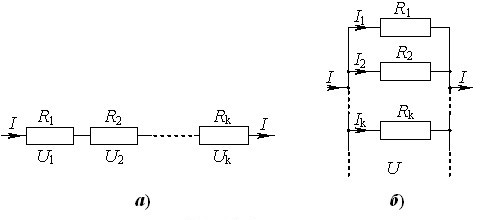
При цьому струм у всіх резисторах однаковий, а напруга на ланцюзі дорівнює сумі напруг на всіх з’єднаних резисторах:
\begin{equation} {I}_{k}={I},\qquad {U}=\sum\limits_{k}U_{k}. \end{equation}
Відповідно, опір з’єднання
\begin{equation} R_{\text{пос}} = \frac{U}{I}=\frac{1}{I}\sum\limits_{k}U_{k}=\sum\limits_{k}\frac{U_k}{I_k}, \end{equation}
тобто
\begin{equation} R_{\text{пос}} = \sum\limits_{k}R_{k}. \tag{2.17} \end{equation}
Отже,
еквівалентний опір послідовного з’єднання дорівнює сумі опорів усіх резисторів, які з’єднані.
Зокрема, коли послідовно з’єднані \(n\) однакових резисторів із опором \(R_{1}\) кожен, то опір з’єднання
\begin{equation} R_{\text{пос}} = nR_{1}. \tag{2.17а} \end{equation}
Паралельне з’єднання. Схема такого з’єднання показана на рис. 2.4б. Очевидно, що в цьому випадку напруга на всіх резисторах однакова і дорівнює напрузі на всьому з’єднанні, а величина струму, що проходить через з’єднання, згідно із законом збереження заряду, дорівнює сумі струмів у кожному із з’єднаних резисторів:
\begin{equation} {U_{k}}={U},\qquad {I}=\sum\limits_{k}{I_k}. \end{equation}
Тому для опору з’єднання маємо:
\begin{equation} \begin{aligned} &R_{\text{пар}}=\frac{U}{I}=\frac{U}{\sum\limits_k I_k} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \frac{1}{R_{\text{пар}}}=\frac{\sum\limits_k I_k} {U}=\sum\limits_k\frac{I_k}{U_k}. \end{aligned} \end{equation}
Звідси випливають такі розрахункові формули:
\begin{equation} \frac{1}{R_{\text{пар}}}=\sum\limits_k\frac{1}{R_k} \tag{2.18} \end{equation}
або
\begin{equation} \Lambda_{\text{пар}} = \sum\limits_{k}\Lambda_{k}. \tag{2.18а} \end{equation}
Отже,
еквівалентна провідність паралельного з’єднання резисторів дорівнює сумі провідностей всіх з’єднаних резисторів.
Якщо паралельно з’єднані \(n\) однакових резисторів опором \(R_{1}\) кожен, то згідно з формулою (2.18)
\begin{equation} R_{\text{пар}} = \frac{R_1}{n}. \tag{2.19а} \end{equation}
Для двох паралельно з’єднаних двох резисторів \(R_{1}\) і \(R_{2}\) також можна записати просту пряму формулу розрахунку еквівалентного опору:
\begin{equation} R_{\text{пар}} = \frac{R_{1}R_{2}}{R_1+R_2}. \tag{2.19б} \end{equation}
Отримані формули дозволяють розраховувати й опори більш складних комбінованих з’єднань резисторів, які можна“розбити” на окремі послідовні та паралельні ланцюжки, що в свою чергу, з’єднані між собою послідовно та паралельно.
2.4. З’єднання джерел струму
Хімічне джерело струму має невелику ЕРС і запас енергії (енергоємність). Тому на практиці крім поодиноких елементів живлення використовують батареї, що складаються з декількох з’єднаних між собою елементів. Параметри батареї — ЕРС \(\mathscr{E}\) і внутрішній опір \(r\) — так само, як і опір з’єднань резисторів, можна розрахувати на основі закону збереження заряду та закону Ома.
Послідовне з’єднання джерел (рис. 2.5).

В цьому випадку величина струму в усіх з’єднаних джерелах (\( {{E}_{k}}\), \({{r}_{k}} \)) однакова:
\begin{equation} {I_{k}}={I}, \end{equation}
а різниці потенціалів на полюсах кожного джерела, згідно з (2.14), дорівнюють
\begin{equation} \varphi_{1k}-\varphi_{2k}=\mathscr{E}_{k}-Ir_{k}. \end{equation}
Додавши всі ці вирази, одержимо різницю потенціалів на полюсах батареї:
\begin{equation} \varphi_{1}-\varphi_{2}=\sum\limits\mathscr{E}_{k}-I\sum\limits{r}_{k}. \end{equation}
З іншого боку, для еквівалентного джерела
\begin{equation} \varphi_{1}-\varphi_{2}=\mathscr{E}-{Ir}. \end{equation}
Отже, доходимо висновку, що ЕРС \(\mathscr{E}\) і внутрішній опір \(r\) батареї послідовно з’єднаних елементів визначаються формулами
\begin{equation} \mathscr{E}=\sum\limits\mathscr{E}_{k}, \qquad {r}=\sum\limits{r}_{k}. \tag{2.20} \end{equation}
Зокрема, при узгодженому з’єднанні \(n\) однакових елементів, коли знаки всіх \(\mathscr{E}_i\) однакові,
\begin{equation} \mathscr{E}=n\mathscr{E}_{1}, \qquad {r}=nr_{1}. \tag{2.20а} \end{equation}
У такий спосіб отримують джерела живлення з необхідною величиною ЕРС.
Із приводу з’єднання джерел слід зауважити наступне. На практиці при використанні з’єднань (батарей) джерела завжди сполучають узгоджено. Але в навчальних завданнях свідомо використовуються і неузгодженні з’єднання. Тому при розв’язуванні задач треба пам’ятати, що електрорушійна сила є алгебраїчною величиною, і враховувати не тільки її модуль, а й знак.
Паралельне з’єднання джерел (рис. 2.6).
При паралельному з’єднанні різниці потенціалів на полюсах кожного джерела і всієї батареї однакові, а величина струму через батарею відповідно до закону збереження заряду дорівнює сумі струмів у всіх джерелах:
\begin{equation} \varphi _{1k} - \varphi _{2k} = \varphi _{1} - \varphi _{2},\qquad {I}=\sum\limits{I}_{k} . \end{equation}
Згідно із законом Ома (2.11а), для струмів через окремі джерела можна записати:
\begin{equation} {I}_{k}=\frac{1}{r_{k}}(\varphi_{1}-\varphi_{2})+\frac{\mathscr{E}_{k}}{r_{k}}. \end{equation}
Додавши всі струми \({I_{k}}\), отримаємо струм через батарею:
\begin{equation} {I}=(\varphi_{1}-\varphi_{2})\sum\limits\frac{1}{r_{k}}+\sum\limits\frac{\mathscr{E}_{k}}{r_{k}}. \end{equation}
Аналогічно виражається цей струм і через ЕРС \( \mathscr{E}\) та внутрішній опір \(r\) еквівалентного джерела:
\begin{equation} {I}=\frac{1}{r}(\varphi_{1}-\varphi_{2})+\frac{\mathscr{E}}{r}. \end{equation}
Порівнюючи обидва вирази, бачимо, що
при паралельному з’єднанні джерел внутрішній опір \(r\) і ЕРС \( \mathscr{E}\) батареї визначаються формулами:
\begin{equation} \frac{1}{r}=\sum\limits\frac{1}{r_{k}},\qquad \mathscr{E}=r\sum\limits\frac{\mathscr{E}_{k}}{r_{k}}. \tag{2.21} \end{equation}
При узгодженому з’єднанні \(n\) однакових елементів (\( \mathscr{E}_{1}\), \(r_{1}\)) маємо:
\begin{equation} \mathscr{E}=\mathscr{E}_{1},\qquad {r}=\frac{r_{1}}{n}. \tag{2.21а} \end{equation}
Тож при паралельному з’єднанні однакових елементів у джерелі живлення його ЕРС не збільшується, але збільшується запас енергії та потужність, яку джерело може віддавати в навантаження.
Таким чином, комбінуючи послідовні та паралельні з’єднання низьковольтних малопотужних елементів, можна отримувати джерела живлення з потрібною величиною ЕРС і великою енергоємністю. Яскравим свідченням цього є акумуляторні батареї для електромобілів, які забезпечують пробіг у сотні кілометрів без дозарядки.
2.5. Розгалужене коло
Найпростіше електричне коло, приміром, електрична лампа ввімкнена в мережу, складається з одного провідного контуру, що включає одне джерело струму. Але широко використовуються і більш складні розгалужені кола. Характерною ознакою таких кіл є наявність декількох вузлів, гілок і контурів. Вузлом називається точка, в якій сходиться більше, ніж два провідники. Гілкою (або віткою) називають ділянку кола, що з’єднує два вузли. Відповідно, під контуром розуміють сукупність гілок, яка дозволяє носіям рухатися замкненим шляхом, не відгалужуючись.
Для кожної гілки, звичайно, виконується узагальнений закон Ома (2.11а), але потенціали вузлів визначаються не лише “власним” джерелом, а й джерелами, ввімкненими в усі інші гілки кола. Тому струми в різних частинах одного контуру не однакові, і визначити їх безпосередньо за законом Ома неможливо. Для розгалужених кіл використовують спеціальні методи розрахунку, розроблені в теорії електричних кіл. Із них найпрозорішим є метод розрахунку за допомогою двох правил Кірхґофа, що безпосередньо випливають із основних законів електричного струму.
Перше правило Кірхґофа. Це правило стосується струмів у вузлах розгалуженого кола і є прямим наслідком закону збереження електричного заряду. У випадку постійного струму потенціали вузлів не змінюються з часом, отже, в них не відбувається накопичення зарядів. Це означає, що заряд, який підходить до вузла за одиницю часу, точно дорівнює зарядові, що виходить із нього. Іншими словами, сума струмів, які входить у вузол, дорівнює сумі струмів, які виходять із нього. Цю умову прийнято записувати у вигляді
\begin{equation} \sum\limits_{k}I_{k}={0}, \tag{2.22} \end{equation}
розглядаючи величини \(I_k\) як алгебраїчні і приписуючи струмам, які виходять з вузла один знак, наприклад додатній, а тим, що входять — протилежний.
Таким чином, перше правило Кірхґофа твердить, що
алгебраїчна сума струмів, які сходяться в довільному вузлі розгалуженого кола, дорівнює нулю.
Друге правило Кірхґофа. Згідно із узагальненим законом Ома (2.11а), струм у довільній ділянці (гілці) кола із заданим опором визначається різницею потенціалів на її кінцях та електрорушійною силою, що діє на цій ділянці:
\begin{equation} {I}_{k}R_{k}=\varphi_{1k}-\varphi_{2k}+\mathscr{E}_{k}. \end{equation}
Якщо вибрати в розгалуженому колі якийсь замкнений контур і обходити його в заданому напрямку, то кінцева точка \(k\)-ї гілки буде початковою точкою наступної \((k + 1)\)-ої гілки. Тому при додаванні указаних рівнянь для всіх гілок контуру потенціали скоротяться і вийде:
\begin{equation} \sum\limits_{k}I_{k}R_{k}=\sum\limits_{k}\mathscr{E}_{k}. \tag{2.23} \end{equation}
Це рівняння виражає друге правило Кірхґофа, що по суті є узагальненням закону Ома на розгалужене коло. Воно гласить:
алгебраїчна сума добутків сил струму на опори всіх гілок довільного контуру розгалуженого кола дорівнює алгебраїчній сумі ЕРС, які діють у цьому контурі.
Знаки величин \(I_{k}\) і \( \mathscr{E}_{k}\) є умовними, але мають бути узгодженими. Тому вони визначаються за наступними правилами. Якщо даний струм \(I_k\) за напрямом збігається з напрямом обходу контуру, обраним при складанні рівнянь (2.23), то \(I_k > 0\). Знак ЕРС збігається зі знаком роботи сторонніх сил у джерелі при переміщенні позитивних носіїв у напрямку обходу контуру. Це означає, що \( \mathscr{E}_{k}>{0}\), якщо при обході контуру ми потрапляємо на від’ємний полюс (коротку жирну риску на зображенні джерела на схемі кола). Ці правила ілюструються наступними рівняннями для вузла (рис. 2.7а) та контуру (рис. 2.7б) якогось розгалуженого кола:
\begin{equation} {I}_{1}-I_{2}-I_{3}+I_{4}+I_{5}-I_{6}={0}; \end{equation}
\begin{equation} \begin{aligned} &{I}_{1}R_{1}-I_{2}R_{2}-I_{3}R_{3}-I_{4}R_{4}={}\\ &\quad{}= \mathscr{E}_{1}-\mathscr{E}_{2}+\mathscr{E}_{4}. \end{aligned} \end{equation}
Зауважимо, що величини \(R_k\) в рівнянні (2.23) включають і внутрішні опори джерел \(r_k\). Тому для нерозгалуженого кола, котре можна розглядати як контур із двох гілок з опорами \(R\) і \(r\) та однаковою величиною струму, рівняння (2.23) вироджується в рівняння закону Ома:
\begin{equation} {IR}+Ir=\mathscr{E} \quad \Rightarrow \quad {I}=\frac{\mathscr{E}}{R+r}. \end{equation}
У такому контексті закон Ома можна трактувати як окремий випадок другого правила Кірхґофа.
Порядок розрахунку розгалуженого кола. Склавши та розв’язавши систему рівнянь (2.22) і (2.23), можна розрахувати розгалужене коло, тобто визначити величини та напрями всіх струмів у колі через усі наявні в ньому опори \(R_k\) та ЕРС \( \mathscr{E}_{k}\). Розрахунок варто проводити в такому порядку.
1. Довільно вибрати й позначити на схемі напрямки струмів \(I_k\) у всіх гілках кола;
2. Скласти максимально можливу кількість незалежних рівнянь (2.22) для вузлів, дотримуючись обраного правила знаків.
Примітки. 1) Максимальна кількість рівнянь для вузлів є не обов’язковою, але доцільною, зважаючи на їхню простоту; 2) Аби рівняння були незалежними, кожен наступний вибраний вузол має включати хоча б одну нову гілку. За такої умови максимальна кількість рівнянь (2.22) дорівнює \(N - 1\), де \(N\) — повна кількість вузлів кола.
3. Скласти решту необхідних рівнянь за другим правилом Кірхґофа (2.23) для замкнених контурів. При цьому конфігурацію та напрями обходу контурів можна вибирати довільно, але так, аби кожен наступний включав хоча б одну нову гілку.
4. Розв’язати отриману систему рівнянь. При цьому корені \(I_k\) системи покажуть не тільки величини, а й напрями всіх струмів. А саме, коли \(I_k > 0\), то прийнятий в п. 1 при складанні рівнянь напрям даного струму є правильним. Якщо ж \(I_k < 0\), то дійсний напрям даного струму є протилежним до вибраного при складанні рівнянь.
Контрольні запитання
1. Відомо, що на однорідній ділянці кола носії струму рухаються під дією електричного поля, створюваного зарядженими частинками провідника. Тоді для чого потрібні ще й сторонні сили?
2. Що таке сторонні сили? Чи можуть вони мати неелектричну природу?
3. Який фізичний зміст мають різниця потенціалів, електрорушійна сила та спад напруги на заданій ділянці кола?
4. Чи може в нерозгалуженому електричному ланцюзі різниця потенціалів на полюсах джерела струму бути рівною ЕРС?
5. Поясніть природу електричного опору провідників.
6. Поясніть, чому опір провідника зростає при збільшенні його довжини і зменшується при збільшенні площі перерізу.
7. Поясніть, чому опір металів зростає при нагріванні?
8. Покажіть, що при паралельному з’єднанні резисторів опір з’єднання є завжди меншим за найменший з опорів сполучених резисторів.
9. Поясніть, чи може ЕРС послідовного з’єднання елементів живлення бути меншою за суму ЕРС усіх з’єднаних елементів?
10. Поясніть, чи може ЕРС паралельного з’єднання елементів живлення бути: а) меншою і б) більшою за суму ЕРС усіх з’єднаних елементів?
11. Як із однакових елементів з ЕРС \(1{,}5\) В можна зібрати батарею з ЕРС \(15\) В і п’ятикратним запасом енергії?
12. Які характерні ознаки має розгалужене електричне коло? Чи може бути розгалуженим коло, в яке включено всього одне джерело ЕРС?
13. При розрахунку розгалуженого кола напрямки струму в гілках є невідомі. В такому разі, як вони враховуються при складанні рівнянь за правилами Кірхґофа?
14. Як визначаються напрямки струму в гілках розгалуженого кола за результатами розрахунку за правилами Кірхґофа?
15. Чим визначається необхідна кількість рівнянь при розрахунку розгалуженого кола за правилами Кірхґофа?
3. Струм у колі з конденсатором
Стаціонарні (постійні у часі) струми можуть існувати тільки в замкнених провідних контурах. Але з рівняння неперервності (1.6) випливає, що нестаціонарні (залежні від часу) струми можуть існувати і в незамкнених контурах. Про це свідчить широке використання в колах змінного струму конденсаторів — схемних елементів, які створюють розриви провідності у відповідних гілках електричного кола. Нижче на прикладі найпростішого такого кола показана можливість застосування до залежних від часу струмів загальних законів стаціонарного струму, які були отримані вище в пп. 1, 2.
Далі розглядаються такі питання:
3.1. Квазістаціонарні струми
Те, що нестаціонарні (змінні) струми можуть існувати не тільки в замкнених, а й у незамкнених контурах, ставить природнє запитання, чи виконуються для них розглянуті вище закони електричного струму.
Аби отримати відповідь, згадаймо (див. п. 1.3), що час \(\tau \) і довжина \(\lambda \) вільного пробігу носіїв у провіднику є гранично малими, отже, вони між зіткненнями рухаються в практично постійному полі \(\vec{E}\), як і при стаціонарному струмі. Тому в кожну мить і в кожній точці провідника густина нестаціонарного струму \(\vec{j}(t) \) і напруженість поля \(\vec{E}(t) \) задовольняють закон Ома в локальній формі (1.9), як і при стаціонарному струмі. Так само лишається чинним і локальний закон Джоуля (1.13).
Але для всього кола чи його ділянки ситуація ускладнюється, позаяк електричне поле поширюється вздовж провідника не миттєво. Через це виникає ефект запізнення: струм у віддалених від джерела точках кола в даний момент часу \(t\) визначається напругою, що була створена на вході в якийсь попередній момент \(t - \Delta t\). При цьому “час запізнення” \(\Delta t\) визначається швидкістю поширення поля \(c\) та відстанню \(l\) від джерела до даної точки кола:
\begin{equation} \Delta{t}=\frac{l}{c}. \end{equation}
Отже, миттєва сила нестаціонарного струму в різних точках кола строго є не однаковою. Тому у виразі (2.9) величину струму \(I\) не можна винести з під знаку інтеграла і отримати співвідношення (2.11) і (2.11а). Це означає, що на загал у колах нестаціонарного струму інтегральний закон Ома не виконується. Проте, якщо за час \(\Delta t\) напруга на вході кола не встигає помітно змінитися, то ефект запізнення буде неістотним і закон Ома в кожен момент часу виконуватиметься практично точно для будь-якої ділянки кола. Такі "повільні" струми називаються квазістаціонарними. Тож
для миттєвих значень квазістаціонарних струмів виконуються ті самі основні закони, що й для постійних струмів.
Умову (критерій) квазістаціонарності можна записати так:
\begin{equation} \Delta{t}\ll \tau \qquad \text{або} \qquad \frac{l}{c}\ll \tau , \tag{3.1} \end{equation}
де \(\Delta t\) — час запізнення на довжині кола \(l\), \(c\) — швидкість поширення поля в провідниках, \(\tau \) — характерний для даного струму час суттєвої зміни.
Слід зауважити, що позаяк \(c\sim 3\cdot10^{8}\) м/с, умова (8.4) не є жорсткою і в теорії електричних кіл має радше теоретичне значення. Наприклад, для промислового струму частота складає \(\nu = 50\) Гц, а період \(T = 0{,}02\) c. Тому, прийнявши \(\tau\sim{T}\), для граничних розмірів кола \(L\), в якому такий струм є квазістаціонарним, з умови (8.4) отримаємо:
\begin{equation} {L}\sim{cT}=6\cdot{10^6}\ \text{м}. \end{equation}
Аналогічно отримаємо оцінку максимальної частоти, при якій виконується умова квазістаціонарності для різних електронних пристроїв, розміри яких зазвичай не перевищують \({l}\sim{1}\) м:
\begin{equation} \nu\sim\frac{c}{l}=300\ \text{МГц}, \end{equation}
що перекриває весь радіочастотний діапазон, включно з УКХ і FM.
Таким чином, змінні струми в широкому діапазоні частот і розмірів кіл є квазістаціонарними, і для них виконуються ті самі основні закони, що й для постійного струму.
3.2. Струм зарядки конденсатора
Як приклад аналізу квазістаціонарних струмів, розглянемо процес заряджання та розряджання конденсатора ємності \(C\) що сполучений з резистором \(R\) і через ключ може підключатися (чи відключатися) до ідеального (\(r = 0\)) джерела з ЕРС (рис. 3.1).
Нехай в момент \(t = 0\) ключ переводять у позицію 1, приєднуючи до джерела незаряджений (\(q (0) = 0\), \(U(0) = 0\)) конденсатор \(C\). Після замикання електрони під дією джерела відразу почнуть переходити з однієї обкладки конденсатора на іншу, і через резистор та джерело потече струм, який будемо вважати квазістаціонарним. Тоді для миттєвих значень на основі узагальненого закону Ома (2.11а) можна записати:
\begin{equation} \begin{aligned} &IR = \varphi _{-} - \varphi _{+} + U_{0}\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad IR + U = U_{0}. \end{aligned} \end{equation}
де \(U = \varphi _{+} - \varphi _{-}\) — напруга на обкладках конденсатора. Виражаючи величину \(U\) через заряд і ємність конденсатора (ф-ла (2.3), розділ II), отримаємо:
\begin{equation} {IR}+\frac{q}{C}=U_{0}. \tag{3.2} \end{equation}
У це рівняння входять дві невідомі величини — струм \(I\) у резисторі та заряд конденсатора \(q\). Аби лишити тільки одне, врахуємо, що заряд, який проходить через резистор, дорівнює зміні заряду конденсатора. Отже, миттєва сила струму через резистор \(I = (\mathrm{d}q/\mathrm{d}t)\) дорівнює швидкості зміни заряду конденсатора, і рівняння (3.2) набуває вигляду:
\begin{equation} \begin{aligned} &\frac{\mathrm{d}q}{\mathrm{d}t}R+\frac{q}{C}=U_{0} \quad \Rightarrow {}\\ &\quad{}\Rightarrow\quad \frac{\mathrm{d}q}{\mathrm{d}t}= -\frac{q}{\tau}+\frac{U_{0}}{R}, \end{aligned} \tag{3.2а}\end{equation}
де введено позначення
\begin{equation} \tau={RC}. \tag{3.3} \end{equation}
Диференціальне рівняння (3.2а) легко розв’язати. Для цього задля зручності введемо нову змінну
\begin{equation} {z}=\frac{U_{0}}{R}-\frac{q}{\tau}, \tag{3.4} \end{equation}
і зробимо наступні підстановки в рівняння (3.2а):
\begin{equation} {-\frac{q}{\tau}}=z-\frac{U_{0}}{R},\qquad \frac{\mathrm{d}q}{\mathrm{d}t}=-\tau\frac{\mathrm{d}z}{\mathrm{d}t}. \end{equation}
Відтак рівняння набуває вигляду
\begin{equation} \tau=\frac{\mathrm{d}z}{\mathrm{d}t}=-{z}, \end{equation}
і його можна переписати як
\begin{equation} \frac{\mathrm{d}z}{z}=-\frac{\mathrm{d}t}{\tau}. \tag{3.5} \end{equation}
Примітка. Таке перетворення обґрунтовується в теорії диференціальних рівнянь і називається відокремленням змінних.
Після цього, інтегруючи праву частину від \(t = 0\) до довільного моменту часу \(t\), а ліву — від початкового значення змінної \(z_{0}\) до значення \(z\) в момент \(t\), дістанемо:
\begin{equation} \begin{aligned} &\int\limits_{z_{0}}^{z}\frac{\mathrm{d}z}{z}=-\frac{1}{\tau}\int\limits_{0}^{t}\,\mathrm{d}{t} \quad \Rightarrow {}\\ &\quad{}\Rightarrow \quad \ln\frac{z}{z_0}=-\frac{t}{\tau} \quad \Rightarrow\quad {z}=z_{0}e^{-\frac{t}{\tau}}. \end{aligned} \tag{3.5а}\end{equation}
Зробивши зворотню заміну (3.4) і врахувавши, що \(z_{0} = (U_{0} / R)\) і \(\tau={RC}\), отримаємо остаточний результат:
\begin{equation} {q}=q_{m}(1-e^{-t/\tau}), \tag{3.6} \end{equation}
де величина
\begin{equation} {q}_{m}=CU_{0} \tag{3.7} \end{equation}
дорівнює максимальному заряду, що може бути накопичений на конденсаторі при заряджанні.
Поділивши \(q\) на \(C\), отримаємо залежність від часу напруги на конденсаторі:
\begin{equation} {U}=U_{0}(1-e^{-t/\tau}), \tag{3.8} \end{equation}
де максимальна напруга
\begin{equation} {U}_{0}=\frac{q_{m}}{C}, \end{equation}
природньо, дорівнює ЕРС джерела.
Диференціюючи рівняння (3.6) за часом, знайдемо закон зміни струму заряджання:
\begin{equation} {I}=I_{0}e^{-t/\tau}, \tag{3.9} \end{equation}
де \({I_{0}}=(q_{m}/\tau)={I(0)}\) — струм у резисторі в момент замикання ключа. Якщо сюди підставити вирази (3.3) і (3.7), то вийде
\begin{equation} {I}_{0}=\frac{U_{0}}{R}. \end{equation}
Вираз (3.9) можна отримати й за законом Ома, врахувавши, що напруга на конденсаторі має зустрічну до джерела полярність (“\(+\)” до “\(+\)” і “\(-\)” до “\(-\)”), отже напруга на опорі
\begin{equation} {U}_{R}=U_{0}-U=U_{0}e^{-t/\tau}, \end{equation}
і струм в колі
\begin{equation} {I}=\frac{U_{R}}{R}=\frac{U_{0}}{R}e^{-t/\tau}. \end{equation}
Графіки залежностей \(U ( t)\) і \(I ( t)\) показані на рис. 3.2а.
Впадає в око стрибок струму від \(0\) до \(I_{0}\) в момент замикання ключа, немов конденсатора взагалі немає. Але це цілком природньо, адже в першу мить після замикання напруга на конденсаторі \(U(0) = 0\), і він ще ніяк не перешкоджає рухові зарядів.
3.3. Струм розрядки конденсатора
Якщо після повного заряджання конденсатора перемкнути ключ у позицію 2, то конденсатор почне розряджатися через резистор. При цьому в будь-яку мить напруга (різниця потенціалів) на резисторі та на конденсаторі однакова, тому \({IR}=q/{C}\). Сила струму при розряджанні дорівнює швидкості спаду заряду конденсатора: \({I}=-(\mathrm{d}q/\mathrm{d}t) \), отже,
\begin{equation} {R}\frac{\mathrm{d}q}{\mathrm{d}t}=-\frac{q}{C} \quad \Rightarrow \quad \frac{\mathrm{d}q}{\tau}. \end{equation}
Відокремивши змінні, як раніше, та проінтегрувавши по тому отримане рівняння, дістанемо:
\begin{equation} {q}=q_{0}e^{-t/\tau}, \end{equation}
де \(q_{0} = CU_{0}\) — початковий заряд на конденсаторі. Відповідно, напруга на конденсаторі \(U = q / C\) і струм розряджання \(I = U / R\) змінюються за законом:
\begin{equation} {U}=U_{0}e^{-t/\tau}, \tag{3.10} \end{equation} \begin{equation} {I}=I_{0}e^{-t/\tau}, \tag{3.11} \end{equation}
де \({I}_{0}=U_{0}/{R}\). Графіки залежностей \(U ( t)\) і \(I ( t)\) при розряджанні конденсатора показані на рис. 3.2б.
Стосовно отриманих тут і в попередньому пункті результатів треба зробити наступні зауваження. Залежності (3.5)—(3.11) є асимптотичними, тому однозначно вказати час повної зарядки чи розрядки конденсатора неможливо. Можна говорити лише про швидкість процесу, мірою якої є параметр \({\tau}\). Ця величина називається часом релаксації або сталою часу RC-ланцюжка і визначається формулою (3.3).
Час релаксації має прозорий зміст: згідно з формулами (3.10), (3.11), на момент \({t=\tau}\) напруга на конденсаторі \({U}(\tau)=U_{0}/{e}\) і струм уколі \({I}(\tau)=I_{0}/{\tau}\). Отже,
час релаксації — то є проміжок часу, протягом якого напруга та струм при розряджанні конденсатора зменшуються в \({e}\approx{2{,}7}\) разів.
Що ж до повної зарядки або розрядки конденсатора, то теоретично вона взагалі не настає ніколи, бо потребує нескінченно великого часу \({t}\to\infty \). Але такий висновок є абстрактним. Через хаотичність теплового руху частинок у макроскопічних системах неперервно відбуваються так звані флуктуації — неконтрольовані мікроскопічні зміни параметрів системи. У нашому випадку це стосується густини потоку носіїв, а отже сили струму в провідниках і заряду та напруги на конденсаторі. Тому величини \({q}\), \(u\), \(i \) реально змінюються, лише доки їхня відміна від асимптотичних (граничних) значень не досягне величини флуктуацій. Відтак настає повна розрядка (або зарядка) конденсатора, при якій величини \({q}\), \(u\), \(i \) будуть здійснювати тільки мікроскопічні флуктуації навколо граничних значень. Причому, такий стан настає достатньо швидко — за час у декілька \(\tau \).
При наведених розрахунках уважалося, що струми зарядки і розрядки конденсатора є квазістаціонарними. З’ясуємо, наскільки таке припущення є обґрунтованим. В \(RC\)-ланцюжках потужних електричних і електронних кіл використовують конденсатори з ємністю щонайменше в декілька мікрофарад і резистори в десятки й більше омів. За таких умов час релаксації \({\tau}={RC}\), що є мірою суттєвої зміни струму, складає \(\geqslant 10^{-5}\) c. Розміри таких ланцюжків можуть досягати \({l}\approx{10}\) см, що відповідає часові запізнення \(\Delta{t}=(l/c)\approx{10^{-10}}\) c. Отже, \({\Delta{t}}/\tau\approx{10^{-4}}\) і критерій квазістаціонарності (3.1) виконується з великим запасом. Тим більше в мікроелектроніці, де розміри схемних елементів і часи запізнення є на порядки менші.
Контрольні запитання
1. Чи є можливим електричний струм у незамкненому контурі? Якщо ні, то чому? Якщо так, то коли?
2. У чому полягає відміна між нестаціонарним і стаціонарним струмом? Нестаціонарним і квазістаціонарним? Сформулюйте і запишіть критерій квазістаціонарності струму.
3. Чи виконуються закони Ома (1.9а) та (2.11а) для нестаціонарного та квазістаціонарного струму? Чому?
4. Чому, коли підключити до джерела конденсатор, напруга на ньому встановлюється не одразу, а поступово?
5. Від чого залежить швидкість заряджання конденсатора? Що таке час релаксації (стала часу) ланцюжка з конденсатором і що показує його числове значення?
6. Як змінюється з часом струм у колі з конденсатором а) при підключенні і б) відключенні від джерела напруги?
7. У скільки разів змінюється струм у колі з конденсатором за проміжок часу \(2\tau \) від \(t_{1} = 0\) до \(t_{2} = 2 \tau \) та від \(t_{3} = 4 \tau \) до \(t_{4} = 6 \tau \)?
8. Яка частка (%) енергії ідеального джерела (\(r = 0\)) йде на зарядку підключеного до нього через резистор \(R\) конденсатора? Як пояснити те, що вона не залежить від величини \(R\)?
4. Робота і потужність струму
Сили, що забезпечують дрейфовий рух носіїв у провіднику із струмом, виконують над ними роботу, яка називається роботою електричного струму. Ця робота виконується за рахунок енергії джерела струму і є мірою її перетворення в інші форми — теплову, механічну, світлову, тощо. Згідно з означенням (2.3), робота постійного струму (\(I = \textrm{const}\)) на довільній ділянці кола визначається добутком перенесеного заряду на спад напруги: \(A = qU\). При цьому заряд \(q = It\), отож
\begin{equation} {A}={IUt}. \tag{4.1} \end{equation}
З урахуванням закону Ома (2.11) роботу постійного струму можна також виразити формулами:
\begin{equation} {A}=I^{2}Rt \tag{4.1а} \end{equation}
і
\begin{equation} {A}=\frac{U^{2}}{R}{t}. \tag{4.1б} \end{equation}
У випадку квазістаціонарного струму спад напруги та сила струму змінюються з часом: \(u = u ( t)\) і \(i = i ( t)\). Тому за наведеними формулами можна виразити тільки елементарну роботу \(\delta A\) за нескінченно малий проміжок часу \(\mathrm{d} t\), а повна робота \(A\) за заданий час \(t\) визначається інтегруванням:
\begin{equation} \begin{aligned} &{A}=\int\limits{\delta{A}} \quad \Rightarrow \quad {A}=\int\limits{iu}\,\mathrm{d}t={}\\ &\quad {}=\int\limits{i^2}R\,\mathrm{d}t=\int\limits{\frac{u^2}{R}}\,\mathrm{d}{t}, \end{aligned} \tag{4.2} \end{equation}
де \(i\), \(u\) — миттєві значення струму та напруги.
Потужність струму \(P\), яка визначає роботу струму за одиницю часу, для постійного струму, відповідно до виразів (4.1), обчислюється за якоюсь із формул:
\begin{equation} {P}={IU}, \tag{4.3} \end{equation} \begin{equation} {P}={I^2{R}}, \tag{4.3а} \end{equation}
або
\begin{equation} {P}=\frac{U^2}{R}. \tag{4.3б} \end{equation}
У випадку квазістаціонарного струму при підстановці в ці формули миттєвих значень струму та спаду напруги \(u = u ( t)\) і \(i = i ( t)\) отримаємо миттєву потужність струму \(p(t)\) у відповідний момент часу.
Струм у провідниках завжди супроводжується виділенням тепла. При цьому теплова потужність стаціонарного струму, тобто кількість теплоти, що виділяється в провіднику із струмом за одиницю часу, в загальному випадку виражається формулою (4.3а). Відповідно, кількість теплоти \(Q\), що виділяється за час \(t\) в провіднику з опором \(R\) і силою струму \(I\), визначається формулою
\begin{equation} {Q}=I^{2}R{t}, \tag{4.4} \end{equation}
яка виражає відомий закон Джоуля.
Якщо провідники не рухаються і в них за рахунок електричної енергії не відбуваються хімічні перетворення, на тепло перетворюється вся енергія струму. В такому разі теплову потужність постійного струму можна обчислювати і за формулами (4.3) і (4.3б), а кількість теплоти — за формулами
\begin{equation} {Q}={IUt} \tag{4.4а} \end{equation}
та
\begin{equation} {Q}=\frac{U^2}{R}{t}. \tag{4.4б} \end{equation}
У випадку квазістаціонарного струму \(u = u ( t )\), \(i = i ( t)\) відповідні формули мають вигляд:
\begin{equation} {Q}=\int\limits{i^{2}R}\,\mathrm{d}{t}, \tag{4.5} \end{equation} \begin{equation} {Q}=\int\limits{iu}\,\mathrm{d}{t}, \tag{4.5а} \end{equation} \begin{equation} {Q}=\int\limits\frac{u^2}{R}\,\mathrm{d}{t}. \tag{4.5б} \end{equation}
Контрольні запитання
1. Що таке робота електричного струму? Яким є її безпосередній (на мікроскопічному рівні) результат?
2. Чи виконують роботу в колі із струмом сили кулонівського електричного поля? Якщо так, то за рахунок якої енергії?
3. В які види, крім теплової, може перетворюватись енергія електричного струму? Наведіть конкретні приклади.
4. За якою із наведених формул (4.4), (4.4а), (4.4б) найдоцільніше обчислювати час закипання води в електричному чайнику з відомим опором нагрівача?
5. Нагрівник електричної плитки складається з трьох однакових секцій, котрі можна використовувати окремо, або як завгодно з’єднавши між собою. За який найменший час можна закип’ятити воду в чайнику, якщо при ввімкненні однієї секції вона закипає за час \(\tau \)?
6. Електричний двигун працює при напрузі \(U\), опір дроту обмоток його ротора Чи можна за цими даними обчислити кількість теплоти, що виділяється в роторі за заданий час \(t\)? Чому?
IV. МАГНІТНЕ ПОЛЕ
Як говорилося на самому початку (Вступ), взаємодія між зарядами, що зумовлена їхнім рухом, називається магнітною і здійснюється через магнітне поле. Магнітні сили відіграють важливу роль у природі та техніці.
Цей розділ присвячено загальним властивостям магнітного поля та його дії на рухомі заряджені частинки й електричні струми. Розглянуто наступні питання:
1. Магнітна взаємодія
Між зарядженими частинками крім електричної спостерігається ще й магнітна взаємодія, яка зумовлена їхнім рухом і здійснюється за допомогою магнітного поля. У цьому можна переконатися на простому досліді. Якщо по двох паралельних дротинах пропустити струми, то вони або притягнуться одна до одної, або відштовхнуться залежно від напрямків струму. Позаяк струм не порушує електричної нейтральності провідників, указана взаємодія зумовлена саме рухом зарядів і здійснюється за польовою схемою: кожен із провідників створює своє магнітне поле, котре діє на інший. При цьому взаємодія припиняється при вимкненні струму в будь-якому з провідників. Це означає, що
магнітне поле створюється рухомими зарядами і діє лише на рухомі заряди.
(Принагідно зауважимо, що магнітні поля породжується також змінними електричними полями (див. розділ V).)
Нижче розглянуті наступні питання:
1.1. Вектор \( \vec{B} \)
Властивості магнітного поля і його кількісні характеристики можна встановити, вивчаючи на досліді магнітні сили, що діють на провідники або контури зі струмом. Але магнітне поле безпосередньо діє не на провідник як такий, а на носії струму, тому логічніше виходити із властивостей сил, які діють у магнітному полі на окремі рухомі заряди. Одразу зауважимо, що, позаяк магнітні сили визначаються не лише величиною заряду, а й величиною та напрямком швидкості його руху, вони мають більш складні властивості, ніж електричні.
Стосовно магнітних сил, які діють на рухомі заряди, дослід показує наступне.
1. У кожній точці магнітного поля серед безлічі напрямів є один такий, при русі зарядженої частинки вздовж котрого магнітне поле на неї не діє. Цей напрям прийнятий за напрям магнітного поля. Інакше говорячи,
при русі зарядженої частинки вздовж напряму магнітного поля магнітна сила на неї не діє.
2. Напрям магнітної сили завжди є перпендикулярним одночасно і до напрямку поля, і до напрямку руху зарядженої частинки, а її модуль \(F_{m}\) є прямо пропорційний величині заряду \(|q|\), його швидкості \({v}\) і синусу кута \(\alpha \) між напрямком швидкості та напрямком поля:
\begin{equation} {F_m}\sim |q|\cdot{v}\cdot\sin\alpha . \end{equation}
Інакше це можна записати як
\begin{equation} {F_m}=B\cdot |q|\cdot{v}\cdot\sin\alpha, \tag{1.1} \end{equation}
де величина
\begin{equation} {B}=\frac{F_m}{|q|\cdot{v}\cdot\sin\alpha} \tag{1.2} \end{equation}
не залежить від заряду та характеристик руху частинки і є силовою характеристикою самого поля. Вона називається індукцією магнітного поля або магнітною індукцією. Аби магнітна індукція вказувала також напрям магнітного поля, її розглядають як вектор \(\vec{B}\), так що формула (1.1) набуває вигляду:
\begin{equation} \vec{F}_{m}=q[\vec{v}\vec{B}], \tag{1.3} \end{equation}
де квадратні дужки означають векторний добуток. Отже, напрям сили, що діє на рухомий точковий заряд у магнітному полі, визначається правилом правого гвинта («свердлика») з урахуванням знаку заряду (рис. 1.1а):
якщо правий гвинт обертати від вектора швидкості заряду до вектора магнітної індукції найкоротшим шляхом, то він буде угвинчуватись у напрямку магнітної сили, що діє на додатній заряд.
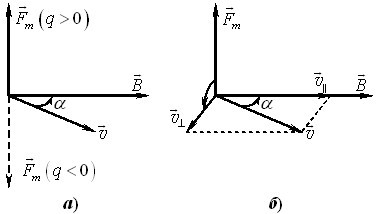
При зміні знаку заряду напрям магнітної сили змінюється на протилежний.
Варто зауважити, що магнітну силу (1.3) зазвичай називають “силою Лоренца”, що не зовсім точно, бо, строго говорячи, силою Лоренца називається повна сила, що діє на заряд в електромагнітному полі; вона складається з електричної та магнітної компонент:
\begin{equation} \vec{F}=\vec{F}_{e}+\vec{F}_{m}=q\bigl(\vec{E}+[\vec{v}\vec{B}]\bigr). \end{equation}
Формула (1.3) є однією з основних у теорії магнітного поля. Зокрема, вона дозволяє дати пряме означення вектора \(\vec{B}\). Якщо швидкість заряду розкласти на паралельну та перпендикулярну до напрямку поля складові так, що \(\vec{v}=\vec{v}_{\parallel}+\vec{v}_{\bot}\) (рис. 1.1б), то, враховуючи, що \({v}_{\bot}=v\sin\alpha \), з виразів (1.1)—(1.3) виходить:
\begin{equation} \vec{B}=\frac{[ \vec{F}{{{\vec{v}}}_{\bot }} ]}{qv_{\bot }^{2}}. \tag{1.4} \end{equation}
Таким чином,
індукція магнітного поля чисельно дорівнює силі, з якою воно діє на одиничний заряд, що рухається перпендикулярно до напрямку поля з одиничною швидкістю.
Одиниця індукції називається тесла (Тл). Її означення буде дано пізніше, а зараз укажемо, що в полі з індукцією \(B=1\) Тл на заряд \(q=1\) Кл при \({v}_{\bot} =1\) м/с діє сила \(F_{m}=1\) H.
1.2. Магнітне поле точкового заряду
Формула (1.3) дозволяє обчислити силу, що діє на заряджену частинку в кожній точці магнітного поля. Відтак за допомогою законів механіки можна знайти закон руху частинки в полі. Тому однією з основних задач теорії є встановлення способів розрахунку магнітних полів. Ці способи, як і у випадку електричного поля, ґрунтуються на виразі індукції магнітного поля окремого точкового заряду та принципі суперпозиції.
Із експериментальних даних установлено, що для поля заряду \(q\), що рухається з нерелятивістською швидкістю \( \vec{v}\) (рис. 1.2), індукція \(\vec{B}\) в будь-якій точці визначається формулою
\begin{equation} \vec{B}=k\frac{q[\vec{v}\vec{r}]}{r^3},\qquad B=k\frac{qv_{\bot}}{r^2}, \tag{1.5} \end{equation}
в якій \(\vec{r}\) — радіус-вектор даної точки поля відносно заряду і \({v}_{\bot}=v\sin\vartheta \) — перпендикулярна до \(\vec{r}\) складова швидкості заряду.
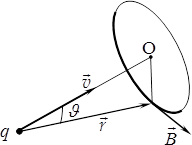
Коефіцієнт пропорційності \(k\) залежить від вибраної системи одиниць і в СІ дорівнює
\begin{equation} k = 10^{-7} Гн/м, \end{equation}
де Гн (генрі) — одиниця індуктивності (див. розділ V). Числове значення \(k\) є зручним для обчислень, але в літературі при записі формул використовують так звану магнітну сталу \(\mu _{0}=4\pi k\), і формули (1.5) записують у вигляді:
\begin{equation} \vec{B}=\frac{\mu_{0}}{4\pi}\frac{q\left[\vec{v}\vec{r}\right]}{r^3},\qquad B=\frac{\mu_0}{4\pi}\frac{qv_{\bot}}{r^2}. \tag{1.5а} \end{equation}
Згідно з цією формулою, вектор \(\vec{B}\) напрямлений перпендикулярно до площини векторів \(\vec{v}\) і \(\vec{r}\), тобто по дотичній до кола, що проходить в цій площині через задану точку і має центр О на лінії вектора \(\vec{v}\), як показано на рис. 1.2. Зауважимо, що, позаяк величина \(\vec{r}\) змінюється з часом, поле точкового заряду є нестаціонарним (залежним від часу): \(\vec{B}=\vec{B}(t) \).
Вирази (1.3) і (1.5а) дозволяють визначити силу \(\vec{F}_{m1}\), яка діє на заряд \(q_{1}\), що рухається із швидкістю \(\vec{v}_{1}\) у магнітному полі іншого заряду \(q_{2}\), який має швидкість \(\vec{v}_{2}\):
\begin{equation} \vec{F}_{m1}=q_{1}[\vec{v}_{1}\vec{B}_{2}],\quad \text{де} \quad \vec{B}_{2}=\frac{\mu_{0}}{4\pi}\frac{q_{2}[\vec{v}_{2}\vec{r}]}{r^{3}}. \end{equation}
Аналогічно можна виразити і силу \(\vec{F}_{m2}\), що діє на заряд \(q_{2}\) з боку поля заряду \(q_{1}\). Слід зазначити, що позаяк індукції полів і магнітні сили залежать не лише від взаємного розташування, а й від величин та напрямків швидкостей зарядів, магнітна взаємодія між ними є набагато складнішою, ніж електрична. Зокрема, магнітні сили на загал не задовольняють третій закон Ньютона. Виняток становить лише випадок, коли два заряди мають однакову за величиною й напрямом швидкість \({v}_{1}=v_{2}={v}\) і розташовані один проти одного (рис. 1.3).
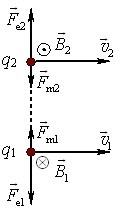
У цьому випадку \(\vec{F}_{m1}=-\vec{F}_{m2}\), причому
\begin{equation} {F}_{m1}=F_{m2}=\frac{\mu_0}{4\pi}\frac{q_1 q_2 v^2}{r^2}. \tag{1.6} \end{equation}
Між зарядами крім магнітних діють ще й електричні сили \(\vec{F}_{e2}=-\vec{F}_{e1}\), величина яких визначається законом Кулона:
\begin{equation} {F}_{e1}=F_{e2}=\frac{1}{4\pi\epsilon_{0}}\frac{q_{1}q_{2}}{r^2}. \tag{1.7} \end{equation}
У випадку, що розглядається, відношення сил магнітної та електричної взаємодії складає
\begin{equation} \frac{F_{m}}{F_{e}}=\mu_{0}\epsilon_{0}{v^2}. \end{equation}
Величина \(\mu _{0}=4\pi \cdot 10^{-7}\) Гн/м, а \(\varepsilon _{0}=9\cdot 10^{-9}/(4\pi )\) Ф/м (див. розділ I, п. 1.2), тож
\begin{equation} \mu_{0}\varepsilon_{0}=\frac{1}{9\cdot 10^{16}}\ \left(\frac{с}{м}\right)^2=\frac{1}{c^2}. \end{equation}
де \(c=3\cdot 10^{8}\) м/с — швидкість світла у вакуумі. Таким чином
\begin{equation} \frac{F_{m}}{F_{e}}=\frac{v^2}{c^2}. \tag{1.8} \end{equation}
1.3. Магнітне поле струмів
Із співвідношення (1.8) видно, що при нерелятивістських швидкостях руху магнітна взаємодія між зарядами є несумірно слабшою за електричну. Тому магнітні сили (1.3) є істотними і знаходять практичне застосування тільки за відсутності помітних електричних полів і тільки в потужних магнітних полях, які створюються не поодинокими зарядами, а інтенсивними потоками заряджених частинок, тобто макроскопічними електричними струмами. На практиці магнітні поля створюють, пропускаючи електричний струм по провідниках відповідної конфігурації, як от обмотки ротора електродвигуна або трансформатора чи електромагніта. Властивості магнітного поля струмів і його дія на заряди та інші струми розглядаються в наступних пунктах:
1.3.2. Розрахунок магнітного поля за законом Біо і Савара
1.3.1. Закон Біо і Савара
Індукцію магнітного поля провідника із струмом можна розрахувати на основі виразу (1.5) для поля точкового заряду та принципу суперпозиції, позаяк кожну елементарну ділянку \(\mathrm{d}\vec{l}\) провідника із струмом (рис. 1.4) можна розглядати як рухомий точковий заряд.
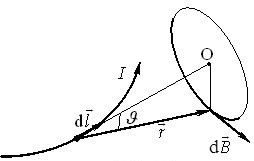
Його величина \(\d q\) дорівнює сумарному заряду зосереджених на цій ділянці носіїв струму, а швидкість руху збігається із їхньою дрейфовою швидкістю \(\vec{u}\). Отже, в заданій точці простору \(\vec{r}\) гранично мала ділянка струму створює елементарне магнітне поле
\begin{equation} \mathrm{d}\vec{B}=k\frac{\mathrm{d}q[\vec{u}\vec{r}]}{r^3}. \end{equation}
Зауважимо, що це поле, на відміну від поля (1.5), є стаціонарним \(\mathrm{d}\vec{B}=\mathrm{const}\), бо кожен носій, який виходить із ділянки \(\mathrm{d}\vec{l}\) тієї ж миті заміщується носієм, який входить в неї.
Величина \(\d q\) у ділянці \(\mathrm{d}\vec{l}\) дорівнює
\begin{equation} \mathrm{d}q=en\,\mathrm{d}V=enS\,\mathrm{d}{l}, \end{equation}
де \(e\), \(n\) — заряд і концентрація носіїв, \(S\) — площа перерізу провідника. Отже,
\begin{equation} \mathrm{d}\vec{B}=k\frac{Sen\,\mathrm{d}l\,[\vec{u},\vec{r}]}{r^3}=k\frac{S[en\,\mathrm{d}l\,\vec{u},\vec{r}]}{r^3}. \end{equation}
Вектори \(\mathrm{d}\vec{l}\) і \(\vec{u}\) мають однаковий напрям, тож \( \d l\, \vec{u}=u\,\mathrm{d}\vec{l}\), і можна записати:
\begin{equation} \mathrm{d}\vec{B}=k\frac{enuS[\mathrm{d}\vec{l},\vec{r}]}{r^3}. \end{equation}
Згідно з формулами (розділ III, (1.3), (1.4б)), \({enuS} ={I}\), отже
\begin{equation} \mathrm{d}\vec{B}=k\frac{I[\mathrm{d}\vec{l},\vec{r}]}{r^3}. \end{equation}
Урахувавши, що \(k = \mu _{0} /4 \pi \), отримуємо остаточні вирази:
\begin{equation} \mathrm{d}\vec{B}=\frac{\mu_{0}I[\mathrm{d}\vec{l},\vec{r}]}{4\pi{r^3}}, \tag{1.9} \end{equation} \begin{equation} \mathrm{d}B=\frac{\mu_{0}I\,\mathrm{d}{l}\sin\vartheta}{4\pi{r^2}}. \tag{1.9а} \end{equation}
Вирази (1.9), (1.9а) спочатку були встановлені на основі дослідних фактів і виражають закон Біо і Савара. Згідно з ними вектор \(\mathrm{d}\vec{B}\) напрямлений перпендикулярно до площини векторів \(\mathrm{d}\vec{l}\) і \(\vec{r}\) так само, як поле \(\vec{B}\) позитивного точкового заряду, що рухається в напрямку струму. Тобто,
напрям магнітного поля струму збігається із напрямом обертання правого гвинта (свердлика), що укручується в напрямку струму.
Зауважимо також, що для точок на напрямку струму на даній ділянці вектори \(\mathrm{d}\vec{l}\) і \(\vec{r}\) є колінеарними, і \(\mathrm{d}\vec{B}={0}\).
1.3.2. Розрахунок магнітного поля за законом Біо і Савара
Закон Біо і Савара разом із принципом суперпозиції дозволяє розрахувати індукцію магнітного поля будь-якого заданого провідника із струмом. Для цього треба знайти вираз (1.9) для довільної нескінченно малої ділянки провідника \(\mathrm{d}\vec{l}\) і проінтегрувати його по всій довжині провідника:
\begin{equation} \vec{B}=\int\limits_{L}\,\mathrm{d}\vec{B}. \tag{1.10} \end{equation}
Визначити індукцію у такий спосіб принципово можна завжди. Але розв’язати задачу аналітично і отримати формулу, що визначає поле в будь-якій точці, можна тільки в окремих випадках за сприятливої конфігурації струму. Розглянемо деякі з них:
1. Поле відрізка та нескінченного прямого струму
2. Поле на осі кільцевого струму. Магнітний момент
Поле відрізка прямого струму. Якщо струм \(I\) протікає по відрізку прямого провідника (рис. 1.5), то в будь-якій точці P, згідно із законом Біо і Савара (1.9), елементарні поля \(\mathrm{d}\vec{B}\) напрямлені перпендикулярно до площини, в якій лежить ця точка та відрізок струму (на рис. 1.5 “до нас”). Тож вектор \(\vec{B}\) результуючого поля напрямлений так само, і його модуль (1.10) визначається інтегралом уздовж відрізка
\begin{equation} {B}=\frac{\mu_{0}I}{4\pi}\int\limits_{1}^{2}\frac{\mathrm{d}{l}\sin\vartheta}{r^2} \tag{1.11} \end{equation}
від початкової точки 1 до кінцевої точки 2.
Для обчислень позначимо як \(R\) відстань від точки P до лінії струму і \(r\) — відстань від точки O до довільної точки на відрізку провідника. Тоді величина
\begin{equation} {l}=R\operatorname{ctg}\vartheta \end{equation}
є функцією \({l}(\vartheta) \) кута \({\vartheta}\) (див. рис. 1.5).
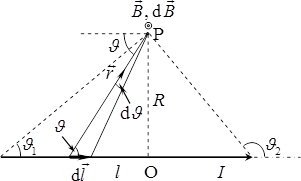
Тому величина \(\mathrm{d}{l}\) під інтегралом (1.11) є модулем приросту цієї функції і за правилами диференціального числення визначається через похідну:
\begin{equation} \mathrm{d}l=|l^{\prime}(\vartheta)\mathrm{d}{\vartheta}| \quad \Rightarrow \quad \mathrm{d}l=R\left(\frac{1}{\sin^2\vartheta}\right)\mathrm{d}{\vartheta}. \end{equation}
Урахуємо також, що \({r}=(R/\!\sin\vartheta) \), тоді
\begin{equation} {B}=\frac{\mu_{0}I}{4\pi{R}}\int\limits_{\vartheta_{1}}^{\vartheta_{2}}\sin\vartheta\,\mathrm{d}\vartheta, \end{equation}
і
\begin{equation} {B}=\frac{\mu_{0}I}{4\pi{R}}(\cos\vartheta_{1}-\cos\vartheta_{2}), \tag{1.12} \end{equation}
де кути \({\vartheta_{1}}\) і \(\vartheta_{2}\) визначають довжину відрізка та положення його кінців відносно заданої точки і відраховуються від напряму струму; \(R\) — відстань від точки до лінії струму.
Поле нескінченного прямого струму. При збільшенні довжини відрізка \({l}\) кут \(\vartheta_{1}\) буде зменшуватись, а \(\vartheta_{2}\) — зростати так, що при \({l}\to\infty\) \(\vartheta_{1}\to{0}\) і \(\vartheta_{2}\to\pi \). Отже, відповідно до виразу (1.12), індукція магнітного поля нескінченного прямого провідника із струмом визначається формулою
\begin{equation} {B}=\frac{\mu_{0}I}{2\pi{R}}. \tag{1.13} \end{equation}
Напрям вектора \(\vec{B}\), як завжди, пов’язаний із напрямом струму правилом правого гвинта.
Поле на осі кільцевого струму. Визначимо тепер індукцію \(\vec{B}\) поля на осі колового контуру (кільця) радіуса \(R\) із струмом \(I\) в залежності від відстані \(r\) до центра (рис. 1.6).
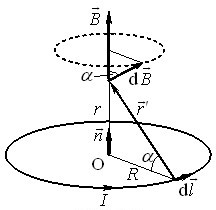
Приступаючи до обчислень за виразом (1.10) одразу врахуємо, що на осі кільця елементарні поля \(\mathrm{d}\vec{B}\) від усіх ділянок орієнтовані під однаковим кутом \(\alpha \) до осі. Тому перпендикулярні відносно осі складові всіх векторів \(\mathrm{d}\vec{B}\) є компенсованими, і результуючий вектор \(\vec{B}\) поля всього кільця напрямлений вздовж осі. Отже, для визначення величини \(B\) слід інтегрувати тільки осьові складові елементарних полів \(\mathrm{d}{{B}_{\parallel }}=\mathrm{d}B\cos \alpha \):
\begin{equation} {B}=\oint\limits\mathrm{d}B\cos\alpha. \tag{1.14} \end{equation}
(Кружальце на символі інтеграла означає, що інтегрування проводиться по замкненому контуру.)
Виражаючи \(\d B\) за формулою (1.9а) і враховуючи, що в ній для точок на осі \(\vartheta=90^{\circ}\) і \({r}=\mathrm{const}\), отримаємо:
\begin{equation} \begin{aligned} &{B}=\frac{\mu_{0}I\cos\alpha}{4\pi{r^{\prime 2}}}\oint\limits\,\mathrm{d}l=\frac{\mu_{0}I\cos\alpha}{4\pi{r^{\prime 2}}}2\pi{R} \quad \Rightarrow \\ &\quad\Rightarrow \quad {B}=\frac{\mu_{0}IR\cos\alpha}{2r^{\prime 2}}. \end{aligned} \end{equation}
Із рис. 1.5 видно, що \(\cos\alpha=R/r^{\prime} \) і \({r^{\prime}}=(r^2+R^2)^{1/2}\), отже,
\begin{equation} {B}=\frac{\mu_{0}IR^2}{2(r^2+R^2)^{3/2}}. \tag{1.15} \end{equation}
У векторному вигляді
\begin{equation} \vec{B}=\frac{\mu_{0}IR^2\vec{n}}{2(r^2+R^2)^{3/2}}, \tag{1.15а} \end{equation}
де \(\vec{n}\) — орт (одиничний вектор) додатньої нормалі до площини кільця, тобто нормалі, що пов’язана з напрямом струму правилом правого гвинта.
При \(r=0\) отримуємо формулу індукції магнітного поля в центрі кільцевого струму:
\begin{equation} \vec{B}=\frac{\mu_{0}I\vec{n}}{2R}. \tag{1.16} \end{equation}
Напрям магнітного поля на осі кільцевого струму теж визначається правилом правого гвинта, котре в даному випадку звучить так:
якщо правий гвинт обертати в напрямку струму в кільці, то він буде вкручуватись у напрямку магнітного поля, створюваного цим струмом на осі кільця.
Магнітний момент контуру зі струмом. Помноживши у формулі (1.15а) чисельник і знаменник на \(2\pi\), отримаємо:
\begin{equation} \vec{B}=\frac{\mu_{0}}{4\pi}\frac{2lS\vec{n}}{(r^2+R^2)^{3/2}}, \end{equation}
де \(S = \pi R^{2}\) — площа кільця.
Цей вираз показує, що індукція магнітного поля в заданій точці на осі кільця визначається не просто струмом \({I}\), а величиною
\begin{equation} \vec{p}=IS\vec{n}\qquad \text{або} \qquad\vec{p}=I\vec{S}, \tag{1.17} \end{equation}
де \(\vec{n}\) — орт (одиничний вектор) додатньої нормалі до поверхні контуру, а \(\vec{S}\) — «вектор поверхні» контуру. Це поняття можна узагальнити і на неплоскі контури.
Вектор (1.17) називається магнітним моментом контуру і є загальною характеристикою його магнітних властивостей. Вектор \(\vec{p}\) визначає магнітне поле кільця також і в інших точках та магнітні поля контурів іншої конфігурації. Дія зовнішнього поля на контур із струмом теж визначається його магнітним моментом. Одиницею магнітного моменту є \(1\ А\cdot м^{2}\).
З урахуванням сказаного формула індукції магнітного поля на осі кільцевого струму набуває вигляду:
\begin{equation} \vec{B}=\frac{\mu_0}{4\pi}\frac{2\vec{p}}{(r^2+R^2)^{3/2}}. \tag{1.18} \end{equation}
Окремий інтерес являють властивості поля на великих відстанях від кільця або при дуже малих його розмірах, коли \(r \gg R\). У такому разі, нехтуючи величиною \(R^{2}\), для поля на осі отримаємо формулу
\begin{equation} \vec{B}=\frac{\mu_0}{4\pi}\frac{2\vec{p}}{r^3}=k_{m}\frac{2\vec{p}}{r^3}, \tag{1.19} \end{equation}
яка є ідентичною до формули ((4.6), розділ I) для напруженості поля на осі електричного диполя. Так само й інші магнітні властивості малого контуру із струмом і відповідні електричні властивості електричного диполя виражаються ідентичними формулами. Тому малий контур із струмом називають магнітним диполем. Принагідно зауважимо, що через дуже малі розміри магнітного диполя форма контура, що його уособлює, не має значення.
1.4. Дія магнітного поля на провідники із струмом
Проходження струму не порушує електричної нейтральності провідників, тому на них не діє зовнішнє електричне поле. Але через дрейф (упорядкований рух) носіїв на провідники зі струмом діє магнітне поле. Далі розглядаються питання:
1.4.2. Контур із струмом у магнітному полі
1.4.1. Сила Ампера
Закон Ампера. Сила, що діє в магнітному полі на провідник із струмом, називається силою Ампера. Її походження не важко зрозуміти. За наявності струму електрони-носії дрейфують уздовж провідника, і на них діє відповідна усереднена магнітна сила (1.3), що визначається величиною дрейфової швидкості носіїв. Під дією цієї сили електрони на шляху вільного пробігу отримують поперечний імпульс, який відтак передають іонам кристалічної ґратки провідника при зіткненнях. Як наслідок, виникає сила, що діє на провідник як ціле, тобто — сила Ампера. Таким чином, магнітне поле діє на провідник із струмом опосередковано, через носії струму. Тож сила Ампера діє як на рухомі, так і на нерухомі провідники, і її величина дорівнює результуючій магнітній силі, що діє на всі носії струму в провіднику.
Визначимо згідно з описаним механізмом амперову силу \(\mathrm{d}\vec{F}\), яка діє на елементарну ділянку \(\mathrm{d}\vec{l}\) провідника із струмом \(I\), що вміщений у задане магнітне поле з індукцією \(\vec{B}\) (рис. 1.7).
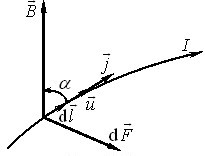
На зосереджені в ділянці носії із сумарним зарядом \(\d q\), що рухаються із дрейфовою швидкістю \(\vec{u}\), діє магнітна сила
\begin{equation} \mathrm{d}\vec{F}=\mathrm{d}q[\vec{u},\vec{B}]. \end{equation}
Якщо позначити заряд носія, їхню концентрацію та площу перерізу провідника відповідно як \(e\), \(n\) і \(S\), то
\begin{equation} \mathrm{d}q=en\,\mathrm{d}V=enS\,\mathrm{d}{l}. \end{equation}
Тут враховано, що для однаково напрямлених векторів \(\mathrm{d}\vec{l}\) і \(\vec{u}\) \(\mathrm{d}l\,\vec{u}\equiv{u}\,\mathrm{d}\vec{l}\). Множник перед векторним добутком, відповідно до формул (1.3) і (1.4б), розділ II, дорівнює силі струму в провіднику, отже,
\begin{equation} \begin{aligned} &\d\vec{F}=I[ \d\vec{l},\vec{B} ],\\ &\mathrm{d}F=IB\,\mathrm{d}l\sin\alpha. \end{aligned} \tag{1.20} \end{equation}
Формули (1.20) виражають закон Ампера, котрий визначає дію магнітного поля на елементарну ділянку струму.
Напрям сили Ампера визначається правилом правого гвинта (рис.1.7):
якщо правий гвинт обертати від напрямку струму в даній ділянці провідника до напрямку магнітного поля, то він буде укручуватись у напрямку сили Ампера, що діє на дану ділянку.
Зауважимо, що це правило є еквівалентним відомому із школи правилу лівої руки.
Сила Ампера, що діє на весь провідник, складається із сил, які діють на окремі його ділянки, і в загальному випадку визначається інтегруванням виразу (1.20) по всій довжині провідника:
\begin{equation} \begin{aligned} &\vec{F}=\int\limits\,\mathrm{d}\vec{F},\\ &\vec{F}=I\int\limits{[ \d\vec{l},\vec{B} ]}. \end{aligned} \tag{1.21} \end{equation}
В окремих випадках формула (1.21) спрощується. До прикладу, якщо довільний провідник знаходиться в однорідному полі \(\vec{B}=\mathrm{const}\), то вектор індукції можна винести з-під інтеграла, не змінюючи порядку множників у векторному добутку. Тоді вийде:
\begin{equation} \begin{aligned} &\vec{F}=I\left[\int\limits\,\mathrm{d}\vec{l},\vec{B}\right] \quad \Rightarrow \quad \vec{F}=I[\vec{l},\vec{B}],\\ &{F}=IlB\sin\alpha, \end{aligned} \tag{1.22} \end{equation}
де \( \int\limits\,\mathrm{d}\vec{l}=\vec{l} \) — вектор проведений від початкової до кінцевої точки провідника (рис. 1.8), \(l\) — відстань між цими точками, а для прямолінійного провідника — його довжина.
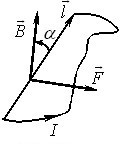
Найпростішою є ситуація, коли маємо прямолінійний провідник розташований перпендикулярно до напрямку однорідного поля. Тоді
\begin{equation} {F}={IBl}. \tag{1.23} \end{equation}
Відмітимо також, що при \(\alpha =0\) або \(\pi \) величина \(F=0\). Отже,
магнітне поле не діє на прямий провідник із струмом, якщо він орієнтований паралельно до напрямку поля.
1.4.2. Контур із струмом у магнітному полі
Вирази (1.20) і (1.21) визначають дію магнітного поля на якусь частину замкненого контуру із струмом. Проте зазвичай у полі перебуває весь контур, і при зміні його орієнтації та переміщенні в полі амперові сили виконують роботу. Тому контур із струмом має відповідну енергію у зовнішньому магнітному полі. Далі розглядаються наступні питання:
1) Момент сил, що діє на контур у магнітному полі.
2) Сила, що діє на магнітний диполь у неоднорідному полі.
3) Енергія магнітного диполя у зовнішньому полі.
Момент сил, що діє на контур. Аби знайти силу, що діє на контур із струмом \(I\) в зовнішньому магнітному полі \(\vec{B}\), інтегрування у виразі (1.21) треба провести по всьому цьому контуру:
\begin{equation} \vec{F}=I\oint\limits{[ d\vec{l},\vec{B} ]}. \end{equation}
При цьому, якщо поле однорідне (\(\vec{B}=\mathrm{const}\)), то
\begin{equation} \vec{F}=I\left[\oint\limits\,\mathrm{d}\vec{l},\vec{B}\right]={0}, \tag{1.24} \end{equation}
бо інтеграл у цьому виразі є сумою безлічі векторів \(\mathrm{d}\vec{l}\), які утворюють замкнену лінію.
Таким чином, в однорідному магнітному полі сила Ампера, що діє на будь-який замкнений контур як ціле, дорівнює нулю. Але це не означає, що поле ніяк не діє на контур, бо амперові сили, прикладені до окремих ділянок контуру, не є компенсованими. Аби в цьому переконатися, проаналізуємо дію однорідного поля \(\vec{B}\) на жорстку прямокутну рамку із струмом \(I\) і сторонами \(a\) і \(b\) (рис. 1.9а).
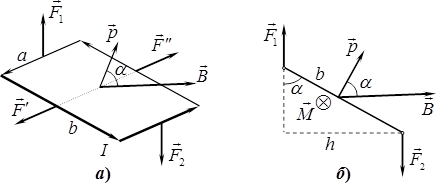
Поле є паралельним, а площина рамки перпендикулярною до площини рисунка (передня сторона рамки і сторона, де струм іде "від нас", наведені жирніше).
При \(\vec{B}=\mathrm{const}\) сили (1.22), прикладені до паралельних сторін рамки, мають однакові модулі і протилежні напрямки: \(\vec{F}{}'=-\vec{F}{}'' \) і \(\vec{F}_{1}=-\vec{F}_{2}\). При цьому перші дві сили діють по одній лінії в площині рамки і є компенсованими. Але дві інші не компенсовані, бо вони намагаються повернути рамку навколо осі \({F}'-{F}'' \) і утворюють так звану "пару сил". Обертальна дія пари сил відносно осі \( {F}'-{F}'' \) визначається вектором моменту пари \(\vec{M}\), який за правилом правого гвинта напрямлений "від нас" (рис. 1.9б) і має модуль \(M\) рівний добутку модуля однієї із сил \(F_{1} = F_{2} = F\) на плече пари (відстань \(h\) між лініями дії сил):
\begin{equation} M = Fh. \end{equation}
Із рис. 1.9б видно, що \( {h}=b\sin\alpha \), а за формулою (1.23) \( {F=IaB}\), отже,
\begin{equation} {M}=IabB\sin\alpha. \end{equation}
Величина \({Iab}=IS={p}\) є модулем магнітного моменту рамки, тож
\begin{equation} {M}=pB\sin\alpha\quad \Rightarrow \quad \vec{M}=[\vec{p},\vec{B}] . \tag{1.25} \end{equation}
Отриманий вираз показує, що магнітне поле намагається повернути рамку так, аби зорієнтувати її магнітний момент у напрямку поля (\(\alpha =0\)), а площину рамки — перпендикулярно до поля. В такому положенні рамки не лише сили \({F}' \) і \({F}'' \), а й \(\vec{F}_{1}\) та \(\vec{F}_{2}\) діють уздовж однієї прямої, тож момент \(\vec{M}={0}\), і контур перебуває у стані рівноваги. Ця рівновага є стійкою, позаяк при повороті рамки навколо осі, напрям якої не збігається з напрямом поля, виникає момент, що намагається повернути рамку у вихідне положення. При протилежній орієнтації (\(\alpha =180\)°) рамка теж буде перебувати в рівновазі, але нестійкій: при щонайменшій зміні орієнтації вона перевернеться у положення \(\alpha =0\).
Можна довести, що в однорідному полі формула (1.25) є правильною для контуру якої завгодно форми та розмірів. Але для довільного контуру в неоднорідному полі вона втрачає чинність. Виняток становить магнітний диполь (малий контур із струмом). У цьому випадку поле в усіх точках контуру можна вважати однаковим, тому для магнітного диполя формула (1.25) лишається придатною. Отже,
на контур із струмом у зовнішньому магнітному полі діє момент сил, який при малих розмірах контуру визначається виразом (1.25).
Сила, що діє на магнітний диполь у неоднорідному полі. В неоднорідному полі вектор \(\vec{B}\ne\mathrm{const}\), тому у виразі (1.22) його не можна винести з-під інтеграла і отримати результат (1.24). А це означає, що
в неоднорідному магнітному поліна на контур із струмом, окрім моменту, діє певна результуюча сила Ампера
\begin{equation} \vec{F}=I\int\limits{[ \d\vec{l},\vec{B} ]}\ne 0. \end{equation}
Це наочно ілюструє рис. 1.10, на якому зображено в профіль круглий контур із струмом (кільце), розміщений в осесиметричному неоднорідному магнітному полі.
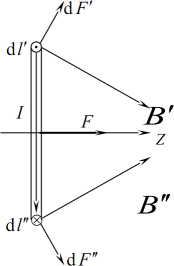
В показаному положенні на всі елементарні ділянки кільця діють однакові за модулем симетричні сили \(\mathrm{d}\vec{F}\), які створюють сумарну силу \(\vec{F}\), спрямовану вздовж осі Z. При іншій орієнтації контуру з’являється ще й момент сил, який намагається перевести контур у показане положення. Тому у неоднорідному полі вільний магнітний диполь під дією амперових сил буде й обертатися, і рухатися поступально. Так само поводиться електричний диполь у зовнішньому електричному полі (див. розділ І, п. 4). При цьому вирази крутних моментів і результуючих сил в обох випадках теж виявляються ідентичними. Зокрема, сила, що діє на магнітний диполь в осесиметричному неоднорідному полі визначається формулою:
\begin{equation} {F}_{z}=p_{z}\frac{\partial{B}}{\partial{z}}, \tag{1.26} \end{equation}
де \({{p}_{z}}=p\cos \alpha \) — проекція магнітного моменту диполя на напрям поля, а \( (\partial{B}/\partial{z}) \) — градієнт індукції, що є мірою неоднорідності поля.
Енергія магнітного диполя в зовнішньому полі. Вище було показано, що в однорідному зовнішньому полі вільний контур із струмом (магнітний диполь) розташовується у площині перпендикулярній до напрямку поля. Це є положення стійкої рівноваги, тож для зміни орієнтації контуру на нього має подіяти момент якихось сторонніх сил, аби подолати момент амперових сил, які утримують контур у положенні стійкої рівноваги. Згідно із законами механіки, робота цих сторонніх сил при повороті контуру йде на зміну його енергії:
\begin{equation} W_2-W_1=A_{стор}. \tag{1.24} \end{equation}
На загал енергія контуру складається із механічної енергії та енергії його взаємодії із зовнішнім полем. Але при повільному повороті навколо нерухомої осі механічна енергія контуру не змінюється, і робота, що виконується моментом прикладених сил, йде тільки на зміну магнітної енергії контуру у зовнішньому полі. З механіки відомо, що робота моменту сили при повороті тіла визначається загальним виразом
\begin{equation} {A}=\int\limits{M}\,\mathrm{d}{\alpha}, \end{equation}
де \(\mathrm{d}{\alpha}\) — елементарний кут повороту. Очевидно, що при повільному повороті контуру моменти сторонніх і амперових сил мають однаковий модуль (1.25). Тому при зміні кута \(\alpha \) від \(\alpha _{1}\) до \(\alpha _{2}\) зміна магнітної енергії контуру в зовнішньому полі складає:
\begin{equation} \begin{aligned} &{W_2}-W_{1}=pB\int\limits_{\alpha_1}^{\alpha_2}\sin\alpha\,\mathrm{d}\alpha \quad \Rightarrow {}\\ &\quad{}\Rightarrow\quad {W}_{2}-W_{1}=pB\cos\alpha_{1}-pB\cos\alpha_{2}. \end{aligned} \end{equation}
Цей результат передбачає, що поле однорідне (\(B = \const\)). Але для малого контуру (магнітного диполя) він зберігає чинність і в неоднорідному полі. Тому на основі отриманого виразу можна зробити висновок, що
магнітний диполь у зовнішньому магнітному полі має енергію, що визначається формулою:
\begin{equation} {W}=-\vec{p}\vec{B}, \tag{1.27} \end{equation}
або
\begin{equation} {W}=-p_{z}{B}, \tag{1.27а} \end{equation}
де \(p_{z}\) — проекція магнітного моменту диполя на напрям зовнішнього поля.
Робота сили Ампера. Сила Ампера здатна рухати провідник із струмом і виконувати над ним механічну роботу. На цьому принципі, зокрема, працюють електричні двигуни. Але провідник із постійним струмом завжди є частиною якогось провідного контуру. Тому не будемо зосереджуватися на окремому провіднику, а одразу розглянемо роботу сил Ампера при переміщенні в магнітному полі замкненого контуру із струмом. У загальному випадку різні точки контуру здійснюють різні переміщення і на них діють різні за величиною та напрямом амперові сили. Тому спочатку розглянемо роботу \({\delta}'A=I\vec{F}\,\mathrm{d}\vec{r}\), що виконується при елементарному переміщенні \(\mathrm{d}\vec{r}\) однієї елементарної ділянки контуру \(\mathrm{d}\vec{l}\) (рис. 1.11).
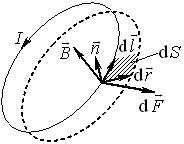
Згідно з виразом (1.20),
\begin{equation} {\delta }'A=I[\mathrm{d}\vec{l},\vec{B}]\cdot \mathrm{d}\vec{r}. \tag{1.28} \end{equation}
Отже, ця робота визначається векторно-скалярним (інакше — мішаним) добутком трьох векторів: \(\mathrm{d}\vec{l}\), \(\vec{B}\) і \(\mathrm{d}\vec{r}\). Властивості мішаного добутку трьох векторів \([\vec{a},\vec{b}]\cdot\vec{c}\) вивчаються у векторній алгебрі. При цьому доводиться, що при так званих циклічних перестановках множників добуток не змінюються, а саме, \([\vec{a},\vec{b}]\cdot\vec{c}\equiv[\vec{c},\vec{a}]\cdot\vec{b}\). Тому вираз (1.28) можна переписати як
\begin{equation} {\delta}'A =I[\mathrm{d}\vec{r},\mathrm{d}\vec{l}]\cdot\vec{B}. \end{equation}
У цьому виразі вектор \([\mathrm{d}\vec{r},\mathrm{d}\vec{l}]\) напрямлений по нормалі \(\vec{n}\) до площинки \(\d S\), а його модуль \(\mathrm{d}r\,\mathrm{d}l\sin\alpha=\mathrm{d}{S}\) дорівнює величині цієї площинки, тож
\begin{equation} [\mathrm{d}\vec{r},\mathrm{d}\vec{l}]=\vec{n}\,\mathrm{d}{S} \end{equation}
і
\begin{equation} \begin{aligned} &{\delta }'A = I\vec{B}\cdot\vec{n}\,\mathrm{d}S=IB_{n}\,\mathrm{d}S \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \delta А = I\d'\Phi, \end{aligned} \end{equation}
де \(\d'\Phi\) — магнітний потік крізь площадку \(\d S\).
Очевидно, що \(\d'\Phi\) є частиною приросту потоку \(\d\Phi\) крізь усю поверхню контуру при його елементарному переміщенні в полі, а \({\delta }'A\) — відповідною частиною повної елементарної роботи \(\delta A\), що виконується при цьому, отже,
\begin{equation} \delta A=I\d \Phi. \tag{1.29} \end{equation}
Повна робота при скінченному переміщенні контуру із струмом у магнітному полі дорівнює
\begin{equation} A=I\cdot\Delta\Phi=I(\Phi_2-\Phi_1). \tag{1.29а} \end{equation}
Таким чином,
при переміщенні контуру із струмом у магнітному полі сили Ампера виконують роботу рівну добутку сили струму в контурі на зміну магнітного потоку крізь поверхню, обмежену цим контуром.
Зауважимо, що коли знак роботи є істотним, при обчисленні потоків слід використовувати додатні нормалі до поверхні контуру, які є пов’язані з напрямом струму правилом правого гвинта.
У зв’язку з отриманим результатом виникає наступне питання. Позаяк амперові сили виконують роботу, вони можуть надавати провідникам із струмом кінетичної, а при наявності, крім магнітного, й інших полів — ще й потенціальної енергії. Але амперові сили є результатом дії на заряди магнітних лоренцових сил (1.3), які є поперечними і ні за яких умов роботи не виконують. То ж звідки береться енергія, за рахунок якої виконують роботу амперові сили? Відповідь полягає в тому, що коли контур із струмом починає рухатися в неоднорідному магнітному полі, то для збереження величини струму на початковому рівні в контурі мають з’явитися додаткові сторонні сили, за рахунок яких і виконується робота (1.29а). Детальніше це питання розглядається в розділі V.
Контрольні запитання
1. Що таке магнітна взаємодія? Чим вона є подібна і чим відмінна від електричної? Що прийнято за напрям магнітного поля?
2. Чи визначає напрям магнітного поля напрям сили, з якою воно діє на частинку із заданим зарядом? Чому?
3. І електричне, і магнітне поля змінюють характеристики руху зарядженої частинки. Чим принципово відрізняються ці зміни?
4. Що називається магнітною індукцією? Дайте формулювання і запишіть математичний вираз вектора \( \vec{B}\).
5. Як визначається величина та напрям магнітної сили, що діє на рухомий заряд?
6. Запишіть закон Біо — Савара. Як визначається напрям вектора \( \mathrm{d}\vec{B} \) поля елементарної ділянки струму \( \mathrm{d}\vec{l} \)? Чому дорівнює поле \( \mathrm{d}\vec{B} \) на напрямку \( \mathrm{d}\vec{l} \)?
7. Який напрям має магнітне поле нескінченного прямого струму та поле на осі кільцевого струму?
8. Запишіть математичний вираз закону Ампера. Як визначається напрям сили Ампера?
9. Від чого і як залежить сила Ампера, що діє на довільний провідник із струмом в однорідному магнітному полі?
10. Чому дорівнює сила Ампера, що діє в однорідному магнітному полі на довільний контур із струмом? Чи можна сказати, що в такому випадку дія магнітного поля на струм відсутня?
11. У чому полягає відміна дії однорідного та неоднорідного магнітного поля на контур із струмом?
12. Що таке магнітний момент контура із струмом? Невагому рамку із струмом, яку утримували в однорідному магнітному полі, відпускають. Як поведеться рамка, якщо її магнітний момент складав із напрямком поля кут а) \(30^\circ\) і б) \(60^\circ\)?
2. Потік і циркуляція магнітного поля
У розділі І було показано, що для електричного поля зарядів, окрім напруженості та потенціалу, які характеризують поле в кожній точці (локально), існують й інтегральні величини — потік і циркуляція, — котрі відображують “поведінку” поля на заданій поверхні чи лінії і містять важливу інформацію про його фундаментальні властивості. Нижче подібний аналіз проводиться для магнітного поля струмів у вакуумі. Розглядаються наступні питання:
2.1. Теорема Гаусса для магнітного поля
2.2. Теорема про циркуляцію магнітного поля струмів у вакуумі
2.3. Розрахунок магнітного поля струмів за допомогою теореми про циркуляцію
2.1. Теорема Гаусса для магнітного поля
Магнітне поле, як і електричне, задля наочності зображують за допомогою ліній вектора \( \vec{B}\) або ліній магнітної індукції. Ці лінії відображають напрям і величину магнітного поля, але не є "силовими" лініями, бо безпосередньо не вказують напрямок магнітних сил.
Дослід свідчить, що лінії магнітного поля є завжди замкненими, тож кожна лінія, що входить всередину якоїсь замкненої поверхні, обов’язково десь виходить назовні. Згідно з геометричною інтерпретацією потоку (розділ І, п. 5), це означає, що потоки на вході та на виході замкненої поверхні завжди мають однакову величину і протилежний знак. Тому
потік вектора індукції магнітного поля крізь довільну замкнену поверхню дорівнює нулю:
\begin{equation} \oint\limits_{S}\vec{B}\,\mathrm{d}\vec{S}={0}. \tag{2.1} \end{equation}
У цьому полягає теорема Гаусса для магнітного поля. Вона відображає фундаментальний дослідний факт — відсутність у природі "магнітних зарядів", тобто особливих частинок, які би самі по собі мали здатність створювати магнітне поле подібну до здатності електронів або протони створювати електричне поле. Тому рівняння (2.1) є одним з основних рівнянь класичної електромагнітної теорії.
Наостанок зауважимо, що рівняння (2.1) “завдячує” замкненості ліній магнітного поля, тож є чинним для поля із замкненими лініями, незалежно від його природи. Зокрема, це стосується електричних полів, котрі створюється не зарядами, а нестаціонарними магнітними полями. Картина ліній подібних полів нагадує завихрення, що інколи виникають у потоці води в річці та в повітрі. Тому поля із замкненими лініями називаються вихровими полями. Тож
магнітне поле є вихровим силовим полем.
2.2. Теорема про циркуляцію магнітного поля струмів у вакуумі
Розглянемо тепер другу інтегральну характеристику магнітного поля — циркуляцію вектора \( \vec{B}\), що за означенням (розділ І, ф-ла (5.2а)) визначається як
\begin{equation} {C}=\oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}. \end{equation}
Циркуляція поля прямого струму. Визначимо спочатку циркуляцію поля одного нескінченного прямого провідника із струмом \(I\) по довільному плоскому контуру \(L\), розташованому, як показано на рис. 2.1а.
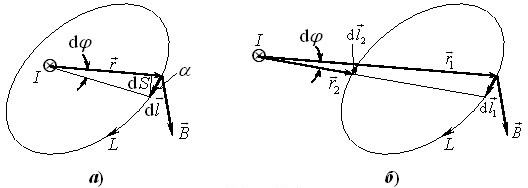
В цьому випадку задача не становить ніяких труднощів. Домовимось обходити контур за годинниковою стрілкою, тоді
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\oint\limits_{L}B\,\mathrm{d}l\cos\alpha, \tag{2.2} \end{equation}
а з рис. 2.1а зрозуміло, що
\begin{equation} \mathrm{d}l\cos\alpha=\mathrm{d}s=r\,\mathrm{d}{\varphi}. \end{equation}
Отже,
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\oint\limits_{L}Br\,\mathrm{d}{\varphi}. \end{equation}
Урахувавши, що індукція поля прямого струму визначається формулою (1.13), отримуємо:
\begin{equation} \begin{aligned} &\oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\frac{\mu_{0}I}{2\pi}\oint\limits_{L}\,\mathrm{d}\varphi \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}{I}. \end{aligned} \tag{2.3}\end{equation}
Для визначення циркуляції у випадку, коли струм не охоплюється контуром, розсічемо його радіальними променями на пари ділянок, як показано на рис. 2.1б. Тоді вклад в інтеграл (2.2) від кожної пари складе
\begin{equation} \begin{aligned} &{B_1}\,\mathrm{d}l_1\cos\alpha_1+B_2\,\mathrm{d}l_2\cos\alpha_2={}\\ &\quad{}=(B_{1}r_{1}-B_{2}r_{2})\mathrm{d}{\varphi}= {0}. \end{aligned} \end{equation}
Отже,
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}={0}. \tag{2.3а} \end{equation}
Теорема про циркуляцію. Отримані результати легко узагальнити на магнітне поле системи паралельних прямих струмів \(I_i\) (рис.2.2).
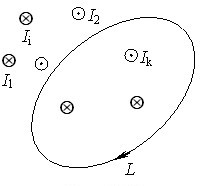
У такому випадку за принципом суперпозиції \( \vec{B}=\sum\limits_{i}\vec{B}_{i}\) і
\begin{equation} \oint\limits_{L}{\vec{B}\,\mathrm{d}\vec{l}} = \oint\limits_{L}{\sum\limits{{{{\vec{B}}}_{i}}\,\mathrm{d}\vec{l}}} = \sum\limits{\oint\limits_{L}{{{{\vec{B}}}_{i}}\,\mathrm{d}\vec{l}}}. \end{equation}
Кожен з інтегралів під знаком суми має значення або (2.3), або (2.3а) залежно від розташування струму \(I_i\) відносно контуру \(L\). Обидва ці випадки можна об’єднати, приписавши всім струмам, які охоплені контуром \(L\), окремий індекс \(k\). Тоді
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}\sum\limits_{k}I_{k}=\mu_{0}{I}, \tag{2.4} \end{equation}
де \(I\) — алгебраїчна сума струмів, які охоплені контуром інтегрування. При цьому знак “\(+\)” мають струми, напрямки яких пов’язані з обраним при інтегруванні напрямом обходу контуру правилом правого гвинта.
Можна довести, що отриманий результат є загальним. Він зберігає чинність і для провідників довільної форми та для об’ємних струмів, розподілених із заданою густиною \( \vec{j}\). Тож у загальному випадку сумарний струм \(I\) в рівнянні (2.4) визначається формулою:
\begin{equation} {I}=\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S}, \end{equation}
де \(S\) — довільна поверхня, що спирається на контур інтегрування \(L\). Відтак рівняння (2.4) набуває вигляду
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S} \tag{2.4а} \end{equation}
і є загальним виразом теореми про циркуляцію магнітного поля струмів у вакуумі:
циркуляція вектора індукції магнітного поля струмів у вакуумі по довільному замкненому контуру дорівнює сумарній силі струму, що охоплений цим контуром, помноженій на \(\mu_{0}\).
Таким чином, циркуляція магнітного поля по замкненому контуру на загал не дорівнює нулю. Відповідно до критерію потенціальності (розділ І, п. 5.1) це означає, що магнітне поле є непотенціальним полем, тобто, для нього не існує скалярної характеристики подібної до потенціалу \(\varphi \) кулонівського електричного поля.
2.3. Розрахунок магнітного поля струмів за допомогою теореми про циркуляцію
Практична значимість теореми про циркуляцію магнітного поля зумовлена тим, що вона спрощує розрахунки магнітних полів високої симетрії, подібно до теореми Гаусса у випадку електричних полів (розділ І, п. 5.2). Розглянемо декілька конкретних прикладів:
3. Поле циліндричного шару із струмом
Поле прямого струму. Перш за все продемонструємо переваги використання теореми про циркуляцію на прикладі поля нескінченного прямого провідника із струмом, для якого вже було отримано формулу індукції за допомогою закону Біо і Савара (п. 1.3).
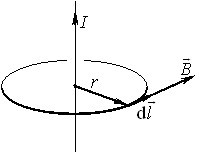
Позаяк індукція такого поля однакова по модулю і напрямлена по дотичній до кола з центром на провіднику, яке є лінією вектора \( \vec{B}\) (рис. 2.3), то
\begin{equation} \begin{aligned} &\oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=B\cdot{2\pi}r=\mu_{0}I \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {B}=\frac{\mu_{0}I}{2\pi{r}}, \end{aligned} \tag{2.5}\end{equation}
що збігається з формулою (1.14).
Поле циліндра із струмом. Розрахуємо тепер індукцію магнітного поля струму, що тече вздовж нескінченного суцільного циліндра радіуса \(R\) із немагнітної речовини. Будемо вважати, що в усіх точках перерізу циліндра (рис. 2.4) вектор густини струму \( \vec{j}=\mathrm{const}\) і напрямлений “до нас”.
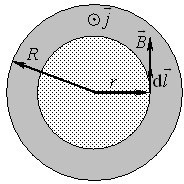
Очевидно, що таке поле, як і в попередньому прикладі, має осьову симетрію, і його індукція теж визначається виразом (2.5). Але тепер величина \(I\) залежить від розмірів контуру інтегрування \(L\) і має визначатися окремо для області всередині циліндра та поза ним.
Поле всередині циліндра (\( {r\le{R}}\)). У цьому випадку контур \(L\) (коло радіуса \(r\) на рис.2.4) охоплює частину всього струму, рівну
\begin{equation} {I}=j\cdot\pi{r^2}. \end{equation}
Отже, модуль індукції магнітного поля всередині циліндра дорівнює
\begin{equation} {B}=\frac{\mu_{0}jr}{2}, \tag{2.6} \end{equation}
вектор \( \vec{B}\) визначається, як
\begin{equation} \vec{B}=\frac{\mu_{0}[\vec{j},\vec{r}]}{2}. \tag{2.6а} \end{equation}
Поле поза циліндром (\( {r>R}\)). За такої умови при будь-якому радіусі контуру \(L\) проходить увесь струм
\begin{equation} {I}=j\cdot\pi{R^2}. \end{equation}
Тож індукція магнітного поля поза циліндром визначається формулою
\begin{equation} {B}=\frac{\mu_{0}jR^2}{2r}, \tag{2.7} \end{equation}
або
\begin{equation} \vec{B}=\frac{\mu_{0}R^2[\vec{j},\vec{r}]}{2r^2}. \tag{2.7а} \end{equation}
На рис. 2.5 показаний графік залежності \(B ( r)\) поля циліндра.
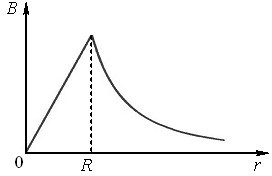
Поле циліндричного шару із струмом. Розглянемо ще й поле, що створюється поздовжнім струмом у циліндричному шарі (циліндрі з коаксіальною порожниною) із радіусами \(R_{1}\) і \(R_{2}\) (рис. 2.6), при рівномірному розподілі струму по перерізу із заданою густиною \( \vec{j}\).
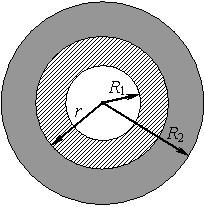
Це поле теж має осьову симетрію, і його розрахунок є аналогічним до попереднього, за винятком того, що він доповнюється розглядом поля в порожнині.
Поле в порожнині (\(r < R_1\)). При осьовій симетрії поля його індукція скрізь визначається загальним виразом (2.5). Але для будь-якого \(r < R_1\) величина \(I=0\), отже,
в порожнині поле відсутнє:
\begin{equation} \vec{B}={0}. \end{equation}
Поле всередині шару (\( {R_{1}}\le{r}\le{R_{2}}\)). У цьому випадку коло радіуса \(r\) охоплює частину всього струму, рівну
\begin{equation} {I}=l\cdot\pi{(r^2-R_{1}^{2})}. \end{equation}
Відповідно, індукція поля всередині циліндричного шару із струмом визначається формулою
\begin{equation} {B}=\frac{\mu_{0}j\left(r^2-R_{1}^{2}\right)}{2r}, \tag{2.8} \end{equation}
або
\begin{equation} \vec{B}=\frac{\mu_{0}[\vec{j},\vec{r}]}{2}\left(1-\frac{R_{1}^{2}}{r^2}\right). \tag{2.8а} \end{equation}
Поле назовні шару (\( {r > R_{2}}\)). Крізь будь-яке коло такого радіуса проходить увесь струм шару. Тому величина \(I\) не залежить від \(r\) і дорівнює
\begin{equation} {I}=j\cdot{\pi}\left(R_{2}^{2}-R_{1}^{2}\right) . \end{equation}
Отже, індукція поля назовні циліндричного шару із струмом визначається формулою
\begin{equation} {B}=\frac{\mu_{0}j\left(R_{2}^{2}-R_{1}^{2}\right)}{2r}, \tag{2.9} \end{equation}
або
\begin{equation} \vec{B}=\frac{\mu_{0}[\vec{j},\vec{r}]\left(R_{2}^{2}-R_{1}^{2}\right)}{2r^2}. \tag{2.9а} \end{equation}
Графік залежності \(B(r)\) наведено на рис. 2.7.
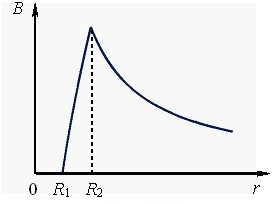
Варто звернути увагу на те, що поле суцільного циліндра і циліндричного шару назовні збігається із полем тонкого провідника розташованого на осі системи, по якому проходить увесь струм. Це ж вірно і для неоднорідного, але симетричного відносно осі розподілу густини струму \( \vec{j}(r)\).
Поле ідеального соленоїда. Ідеальним соленоїдом називається нескінченна циліндрична котушка, щільно намотана гранично тонким дротом в один шар (рис. 2.8а).
Примітка. Реальний соленоїд — це котушка, довжина котрої є сумірною із діаметром.
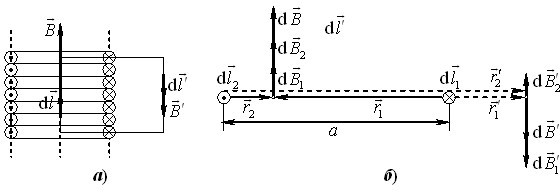
За допомогою закону Біо і Савара можна розрахувати магнітне поле тільки на осі соленоїда. А ось за допомогою теореми про циркуляцію поле ідеального соленоїда можна визначити в усьому просторі. Для цього проаналізуємо симетрію даного поля. Найперше констатуємо, що всі рівновіддалені від осі соленоїда точки є фізично еквівалентними, тож поле в них повинно мати однакову величину. Так само з міркувань симетрії випливає, що поле нескінченного соленоїда має осьовий напрямок, оскільки він є безальтернативним, тобто таким, для якого не існує інших рівноправних напрямів. Всередині соленоїда напрям \( \vec{B}\), як і для окремого витка, пов’язаний із струмом правилом правого гвинта, а назовні має бути протилежним. Це випливає із замкненості ліній \( \vec{B}\) і видно з рис. 2.8б, на якому показані вектори елементарних полів, створюваних парою діаметральних ділянок \( \mathrm{d}\vec{l}_{1}\) і \(\mathrm{d}\vec{l}_{2}\) одного витка всередині (\( {\mathrm{d}\vec{B}}\)) і назовні (\( {\mathrm{d}\vec{B}{}^{\,\prime }}\)). Крім того, поле \( \vec{B}{}^{\,\prime}\) має послаблюватися при віддаленні від соленоїда. Такий висновок випливає із закону Біо і Савара. Справді, відповідно до виразу (1.9а) модуль поля \( \mathrm{d}{B^{\,\prime}}\) двох показаних на рис. 2.8б ділянок дорівнює
\begin{equation} \begin{aligned} &\mathrm{d}B^{\,\prime}=\mathrm{d}B_{1}^{\,\prime}-\,\mathrm{d}B_{2}^{\,\prime} = \frac{\mu_{0}I\,\mathrm{d}l}{4\pi}\left(\frac{1}{r_{1}^{2}}-\frac{1}{r_{2}^{2}}\right)={}\\ &\quad{}=\frac{\mu_{0}I\,\mathrm{d}l}{4\pi}\cdot\frac{(r_{2}-r_{1})(r_{2}+r_{1})}{r_{1}^{2}r_{2}^{2}} . \end{aligned} \end{equation}
У цьому виразі \(r_{2} - r_{1} = d\) — діаметр витка, а \(r_{2} + r_{1} = 2 r\), де \(r\) — відстань від осі соленоїда до даної точки. Крім того, за винятком точок поблизу поверхні соленоїда, \(r_{1}r_{2}\approx r^2\). Отже,
\begin{equation} \mathrm{d}B^{\,\prime}\approx\frac{\mu_{0}Id\,\mathrm{d}l}{2\pi}\cdot\frac{1}{r^{3}}. \end{equation}
Зрозуміло, що так само мають спадати з відстанню поля й інших подібних парних ділянок, а отже й поле \( {B}^{\,\prime}\) всього соленоїда.
Для визначення поля за теоремою про циркуляцію виберемо прямокутний контур, який має бічну сторону \(l\) і розташований у площині діаметрального перерізу соленоїда, як показано на рис. 2.8а. При такій орієнтації контуру вектори індукції спрямовані паралельно до бічних і перпендикулярно до поперечних сторін контуру та на кожній бічній стороні мають незмінний модуль. В такому разі
\begin{equation} \oint\limits_{L}B_{l}\,\mathrm{d}l=Bl+B^{\,\prime}{l}, \end{equation}
і, згідно з теоремою про циркуляцію (2.4),
\begin{equation} \begin{aligned} &\left(B+B^{\,\prime}\right){l}=\mu_{0}NI \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {B}+B^{\,\prime} =\mu_{0}n{I}, \end{aligned} \tag{2.10}\end{equation}
де \(N\) — кількість витків соленоїда, що охоплені контуром, а \( {n}={N/l}\) — щільність намотки (кількість витків на одиницю довжини соленоїда).
Отриманий вираз означає, що при заданій величині \( {I}\) незалежно від розмірів прямокутника
\begin{equation} {B+B^{\,\prime} = \mathrm{const}}. \end{equation}
Але ця умова може виконуватися тільки при \( {B^{\,\prime}}={0}\), бо ця величина не може бути сталою, вона має зменшуватися при віддаленні від соленоїда.
Таким чином,
магнітне поле ідеального соленоїда існує тільки всередині, є однорідним і визначається формулою
\begin{equation} {B}=\mu_{0}{nI}. \tag{2.11} \end{equation}
Поле тороїда. Тороїдом називається дротяна котушка щільно намотана в один шар по всій поверхні тора (рис. 2.9), який будемо вважати немагнітним.

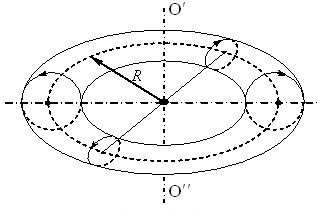
Примітка. Тор являє собою «математичний бублик», тобто тіло, утворене обертанням кола навколо осі, що розташована в площині кола поза його межами.
Розрахуємо поле тороїда з радіусами \(R_1\) і \(R_2\), кількістю витків \(N\), по якому тече струм \(I\).
Поле всередині тороїда. З міркувань симетрії очевидно, що всі точки кола з радіусом \(r\), яке проходить всередині тороїда (\(R_{1}\) < \(r\) < \(R_{2}\)) і має центр на осі системи \(\mathrm{O}'\mathrm{O}''\), є фізично еквівалентними. Тому в кожній з них вектор \( \vec{B}\) напрямлений перпендикулярно до площини витка і має однаковий модуль. Отже, циркуляція \( \vec{B}\) по такому колу
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=B\cdot{2\pi{r}}, \end{equation}
і за теоремою про циркуляцією (10.3)
\begin{equation} {B}=\frac{\mu_{0}NI}{2\pi{r}}, \tag{2.12} \end{equation}
де \(NI\) — повний струм, який охоплюється контуром інтегрування.
Цікаво, що поле всередині тороїда збігається із полем нескінченного прямого провідника із струмом \(I_{0} = NI\) розташованого на осі \(\mathrm{O}'\mathrm{O}''\) тороїда.
Формулу (10.11) можна також записати у вигляді
\begin{equation} {B}=\mu_{0}nI\frac{R_{0}}{r}, \tag{2.12а} \end{equation}
де
\begin{equation} {n}=\frac{N}{2\pi{R_0}} \end{equation}
— щільність витків, тобто кількість витків на одиницю довжини середньої лінії тороїда (кола з радіусом \(R_{0} =( R_{1} + R_{2})/2\)).
Поле поза тороїдом. Якщо коловий контур радіуса \(r\) розташований поза тороїдом, то при \(r < R_1\) струм узагалі не перетинає поверхню контуру, а при \(r > R_{2}\) струм від кожного витка перетинає її двічі і в протилежних напрямках. Тож в обох випадках
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=0\quad \Rightarrow \quad \vec{B}={0}. \end{equation}
Таким чином, як і в соленоїді,
за межами тороїда магнітне поле відсутнє.
Принагідно відмітимо, що з виразу (2.12а) можна отримати формулу індукції магнітного поля ідеального соленоїда, бо його можна формально трактувати як тороїд радіуса \( {R}_{0}\to\infty \). У такому разі \((R_{0} / r) = 1\), і вираз (2.12а) переходить у (2.11).
Наостанку нагадаємо, що в наведених прикладах соленоїд і тороїд розглядалися ідеалізовано, як сукупність щільно складених гранично тонких кілець із струмом. Але насправді кожна з котушок утворює гвинтову лінію. Через це при протіканні струму по витках існує й деяке перенесення заряду, тобто додатковий струм, уздовж осі соленоїда та вздовж середньої лінії тороїда. Тому поза соленоїдом є магнітне поле таке, як поза циліндром із струмом, а поза тороїдом є поле таке, як у кільця радіуса \(R_{0}\). Але, через те, що котушки зазвичай намотують тонким дротом, крок гвинтової лінії й указані поздовжні струми є дуже малими, тож створювані ними поля є неістотними.
Контрольні запитання
1. Як формулюється та про що свідчить теорема Гаусса для магнітного поля?
2. Яку принципову відміну мають потоки крізь замкнену поверхню у випадку магнітного та кулонівського електричного полів?
3. Як ви гадаєте, чому лінії магнітного поля є завжди замкнені, а лінії кулонівського електричного поля — ні?
4. Яку фундаментальну властивість магнітного поля відображує теорема про циркуляцію вектора \( \vec{B}\)?
5. Циркуляція електричного поля визначає його роботу при переміщенні одиничного заряду по заданій замкненій траєкторії. Чи можна аналогічно трактувати циркуляцію магнітного поля? Чому?
6. Коли магнітне поле заданого розподілу струму набагато легше розрахувати за допомогою теореми про циркуляцію, ніж за законом Біо — Савара?
3. Магнітне поле в речовині
Речовина змінює характеристики не лише електричного, а й магнітного поля. Загальною (але не єдиною) причиною цього є інтенсивний рух електронів у атомах, який створює в речовині власні мікроскопічні магнітні поля подібно до мікроскопічних електричних полів у діелектриках. При цьому одні речовини (діелектрики) лише послаблююсь статичне електричне поле, а інші (провідники) повністю його знищують. Але вплив різних речовин на магнітне поле так радикально не відрізняється, і тому всі вони є магнетиками.
Опис магнітного поля в речовині та загальні властивості різних типів магнетиків розглядаються далі в наступних питаннях:
3.2. Вектор \( \vec{H}\). Теорема про циркуляцію магнітного поля в речовині
3.3. Магнітні сприйнятливість і проникність
3.4. Умови на межі двох магнетиків
3.1. Намагнічування речовини
Намагніченість. Замкнений рух електронів в атомах навколо ядер створює мікроскопічні молекулярні струми. Тим самим атоми уподібнюються до мікроскопічних витків із струмом — магнітних диполів, які створюють в околі атомів мікроскопічні магнітні поля. За звичайних умов ці поля в більшості речовин орієнтовані хаотично і є компенсованими. Але при вміщенні магнетика у зовнішнє магнітне поле магнітні моменти і мікрополя атомів частково орієнтуються по зовнішньому полю і перестають бути компенсованими. Як наслідок, у речовині створюється внутрішнє макроскопічне магнітне поле. Цей процес називається намагнічуванням речовини. Він є аналогічним до поляризації діелектриків, при якій відбувається упорядкування електричних моментів молекул і в речовині виникає внутрішнє електричне поле. Подібно до діелектриків уводиться і кількісна характеристика ступеня намагніченості речовини в кожній точці — намагніченість або вектор намагнічування \(\vec{J}\):
\begin{equation} \vec{J}=\frac{1}{\Delta{V}}\sum\limits\vec{p}_{i}=\frac{\vec{p}_{\Sigma}}{\Delta{V}}, \tag{3.1} \end{equation}
де \(\Delta V\) — фізично нескінченно малий об’єм (див. розділ II, п. 1) в околі даної точки речовини, а \(\vec{p}_{\Sigma}=\sum\limits\vec{p}_{i}\) — сумарний магнітний момент атомів у цьому об’ємі. Помноживши і поділивши вираз (3.1) на кількість \(N\) атомів у об’ємі \(\Delta V\), намагніченість можна подати через концентрацію частинок речовини \(n = ( N / \Delta V)\) і середній магнітний момент однієї частинки \(\langle {\vec{p}} \rangle =\frac{1}{N}\sum\limits{{{{\vec{p}}}_{i}}}\):
\begin{equation} \vec{J}=n\langle\vec{p}\rangle. \tag{3.1а} \end{equation}
Струми намагнічування. Переважна орієнтація магнітних моментів атомів уздовж напрямку поля при намагнічуванні речовини означає, що електрони в атомах починають рухають узгоджено. Як наслідок, у намагніченій речовині виникають макроскопічні струми намагнічування. Це можна зрозуміти з рис. 3.1, де стрілками схематично показано циркуляцію заряду в атомах поверхневому шару намагніченого вздовж осі циліндричного зразка.
В об’ємі молекулярні струми сусідніх молекул спрямовані взаємно протилежно і є компенсованими, тоді як на поверхні всі молекулярні струми напрямлені однаково. Тому, хоч електрони й не переміщуються від атома до атома, на поверхні відбувається напрямлений рух електричного заряду. Таке своєрідне обтікання зарядом поверхні зразка називається поверхневим струмом намагнічування. Розподіл поверхневих струмів намагнічування визначається лінійною густиною струму намагнічування
\begin{equation} {i}_{m}=\frac{\mathrm{d}I_{m}}{\mathrm{d}l}\ (\text{А/м}), \tag{3.2} \end{equation}
тобто, струмом намагнічування, що припадає на одиницю довжини поверхні зразка в напрямку намагніченості (рис. 3.1).
У неоднорідному магнетику повної компенсації молекулярних струмів усередині зразка немає, тому при намагнічуванні виникають не лише поверхневі, а й об’ємні струми намагнічування, котрі, як і звичайні струми, характеризуються поверхневою густиною струму
\begin{equation} {j}_{m}=\frac{\mathrm{d}I_{m}}{\mathrm{d}S}\ (\text{А/м}^2), \tag{3.3} \end{equation}
яка визначає об’ємний струм намагнічування через одиничну площинку, перпендикулярну до напрямку перенесення заряду.
Ще раз наголосимо, що вказане перенесення заряду не пов’язане з рухом електронів (носіїв) по зразку магнетика. Тому для струмів намагнічування немає поняття електричного опору, вони не супроводжуються виділенням джоульового тепла або електрохімічними процесами і можуть існувати в будь-якому середовищі, а не лише в провідниках. Але струми намагнічування і струми провідності є однаковими щодо спроможності створювати магнітне поле. А саме,
магнітне поле струмів намагнічування нічим не відрізняється від магнітного поля струмів провідності такої самої величини та конфігурації.
Зв’язок між намагніченістю та струмами намагнічування. Уявлення про струми намагнічування дозволяє побудувати послідовну теорію макроскопічного магнітного поля в речовині. Це, зокрема, є зумовлене існуванням безпосереднього зв’язку між струмами намагнічування та намагніченістю. Аби його встановити, виділимо тонкий шар в однорідно намагніченому косому циліндрі з віссю, що складає кут \(\alpha \) з вектором \(\vec{J}\), і перпендикулярними до нього основами площею \(S\) (рис. 3.2).
Такий шар можна розглядати як контур із струмом
\begin{equation} {I}_{m}=i_{m}\,\Delta{l}, \end{equation}
де \({i}_{m}\) — лінійна густина поверхневого струму намагнічування, \(\Delta{l}\) — товщина шару уздовж осі циліндра. Тоді магнітний момент шару має величину \({p}=I_{m}{S}\), а намагніченість, згідно з означенням (3.1),
\begin{equation} J=\frac{{{I}_{m}}S}{\Delta V}=\frac{{{i}_{m}}\Delta lS}{\Delta V}. \tag{3.3а} \end{equation}
Звідси, врахувавши, що \(\Delta{V}=S\Delta{l}\cos\alpha \), маємо:
\begin{equation} {J}\cos\alpha={i_{m}}\qquad \text{або}\qquad {J_{l}}=i_{m}, \tag{3.4} \end{equation}
де \({J}_{l}\) — осьова складова намагніченості.
Цей результат дозволяє отримати важливий для теорії магнітного поля в речовині вираз циркуляції намагніченості \(\oint\limits_{L}\vec{J}\,\mathrm{d}\vec{l}=\oint\limits_{L}J_{l}\,\mathrm{d}{l}\) по довільному замкненому контуру \(L\) (рис. 3.3).
Якщо оточити контур \(L\) дуже тонкою циліндричною трубкою, то згідно з (3.4) на кожній ділянці \(\mathrm{d}{l}\) контуру
\begin{equation} {J}_{l}\,\mathrm{d}l=i_{m}\,\mathrm{d}l=\mathrm{d}{I_{m}}, \end{equation}
де \(\mathrm{d}I_{m}\) — струм намагнічування, що тече по відповідній ділянці поверхні трубки. Таким чином,
\begin{equation} \oint\limits_{L}\vec{J}\,\mathrm{d}\vec{l}=I_{m}, \tag{3.5} \end{equation}
тобто:
циркуляція вектора намагнічування по довільному замкненому контуру дорівнює струмові намагнічування, що охоплюється цим контуром (інакше — перетинає поверхню обмежену цим контуром).
Цей результат, який можна трактувати як теорему про циркуляцію вектора намагнічування, зберігає чинність і при неоднорідній намагніченості речовини.
3.2. Вектор \(\vec{H}\). Теорема про циркуляцію магнітного поля в речовині
При намагнічуванні у речовині створюється внутрішнє макроскопічне магнітне поле \(\vec{{B}}{}^{\,\prime}\), яке разом із зовнішнім полем \(\vec{B}_{0}\) визначає результуюче поле в магнетику
\begin{equation} \vec{B}=\vec{B}_{0}+\vec{B}{}^{\,\prime}. \end{equation}
Зовнішнє поле створюється макроскопічним рухом (дрейфом) електронів у провідниках, а внутрішнє — мікроскопічними рухами електронів навколо ядер в атомах магнетика. Але, як говорилося, ніякої різниці у загальних властивостях між цими полями немає. Тому так само, як поле \(\vec{B}_{0}\) визначається величиною та конфігурацією струмів провідності, поле \(\vec{{B}}{}^{\,\prime}\) визначається величиною та конфігурацією струмів намагнічування. Отже, на основі теореми про циркуляцію магнітного поля струмів у вакуумі (2.4), для поля в речовині можна записати
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}(I+I_{m}), \tag{3.6} \end{equation}
де \({I}\) та \({I}_{m}\) — сумарна величина струмів провідності та струмів намагнічування, що охоплюються контуром інтегрування.
Записаний вираз формально є подібним до рівняння (2.4). Проте трактувати його як теорему про циркуляцію магнітного поля в речовині по суті не можна, бо він визначає циркуляцію поля \(\vec{B}\) через величину \({I}_{m}\), яка сама залежить від \(\vec{B}\). Тому для опису магнітного поля в речовині, як і в теорії електричного поля в діелектриках, уводиться відповідний допоміжний вектор. Зважаючи на співвідношення (3.5), перетворимо вираз (3.6) наступним чином:
\begin{equation} \begin{aligned} &\oint\limits_{L}\frac{\vec{B}}{\mu_{0}}\,\mathrm{d}\vec{l}=I+\oint\limits_{L}\vec{J}\,\mathrm{d}\vec{l} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \oint\limits_{L}\left(\frac{\vec{B}}{\mu_{0}}-\vec{J}\right)\mathrm{d}\vec{l}={I} \end{aligned} \tag{3.7}\end{equation}
і введемо величину
\begin{equation} \vec{H}=\frac{\vec{B}}{\mu_{0}}-\vec{J}, \tag{3.8} \end{equation}
яку у фізиці зазвичай називають “вектором \(\vec{H}\)”, рідше — “напруженістю” магнітного поля, терміном, який є поширеним в електротехніці. Відтак рівняння (3.7) набуває вигляду
\begin{equation} \oint\limits_{L}\vec{H}\,\mathrm{d}\vec{l}={I} \tag{3.9} \end{equation}
і виражає теорему про циркуляцію магнітного поля струмів у речовині:
циркуляція вектора \(\vec{H}\) по довільному замкненому контуру дорівнює сумарному струмові провідності І, котрий проходить крізь довільну поверхню обмежену цим контуром.
Величина \(I\) залежить від розподілу струмів провідності у просторі і в загальному випадку визначається інтегральною формулою ((1.4а), розділ І). Тому розгорнуто рівняння (3.9) записується, як
\begin{equation} \oint\limits\vec{H}\,\mathrm{d}\vec{l}=\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S}. \tag{3.9а} \end{equation}
Слід сказати, що рівняння (3.9) і (3.9а) як окремий випадок вбирають і доведену раніше теорему про циркуляцію магнітного поля у вакуумі. У цьому легко переконатися, взявши до уваги, що у вакуумі \(\vec{J}={0}\), тож
\begin{equation} \vec{H}=\frac{\vec{B}}{\mu_{0}}. \end{equation}
Отже, рівняння (3.9а) відображує загальні властивості магнітного поля більш повно, ніж рівнянням (2.4а) для циркуляції вектора \(\vec{B}\). У той же час \(\vec{H}\) є допоміжним, а не основним (“польовим”) вектором, бо, згідно з (3.8), у кожній точці він визначається не лише станом поля, а й станом речовини. Але це не зменшує значимість вектора \(\vec{H}\), бо він дозволяє одним рівнянням (3.9а) виразити важливі властивості магнітного поля як у вакуумі, так і в будь-якому середовищі.
3.3. Магнітні сприйнятливість і проникність
Циркуляція вектора \(\vec{H}\) не залежить від струмів намагнічування, тож і від речовини магнетика. Але цього, звичайно, не можна сказати про сам вектор \(\vec{H}\), бо згідно з означенням (3.8) він через вектор \(\vec{J}\) є пов’язаний із струмами намагнічування. Проте в деяких випадках не тільки циркуляція, а й сам вектор \(\vec{H}\) виявляється прямо не залежним від струмів намагнічування, що дозволяє його визначити тільки через струми провідності. З іншого боку, у фізиці матеріалів установлені функціональні зв’язки \(\vec{J}{(\vec{H})}\) між намагніченістю \(\vec{J}\) та вектором \(\vec{H}\) у різних типах магнетиків. За такої умови означення (3.8) перетворюється на функціональне рівняння, з якого можна знайти індукцію \(\vec{B}\) магнітного поля, створеного в магнетику заданим розподілом струмів провідності:
\begin{equation} \begin{aligned} &\vec{H}=\frac{\vec{B}}{\mu_{0}}-\vec{J}(\vec{H}) \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \vec{B}={{\mu}_{0}}\bigl( \vec{H}+\vec{J}({\vec{H}}) \bigr). \end{aligned} \tag{3.10}\end{equation}
Такий розрахунок включає два етапи:
— визначення допоміжного вектора \(\vec{H}(\vec{r}) \) через розподіл сторонніх струмів провідності \(\vec{j}\left( {\vec{r}} \right)\),
— визначення вектора індукції поля \(\vec{B}(\vec{r}) \) за допомогою рівняння (3.10).
У загальному випадку розрахунок є складним через складну залежність \(\vec{J}( {\vec{H}} )\). Але майже всі технологічні магнітні матеріали є ізотропними, тобто їхні властивості не залежать від напрямку поля. А в таких речовинах зв’язок між векторами \( \vec{J} \) і \( \vec{H} \) є простим і має вигляд:
\begin{equation} \vec{J}=\chi\vec{H}, \tag{3.11} \end{equation}
де безрозмірне число \({\chi}\) (читається “хі”) називається магнітною сприйнятливістю і показує наскільки добре дана речовина намагнічується у заданому магнітному полі. Тож підставивши співвідношення (3.11) у рівняння (3.10), отримаємо:
\begin{equation} \vec{B}=\mu_{0}(1+\chi )\vec{H}. \tag{3.12} \end{equation}
Величину \({1+\chi}\) в цьому виразі позначають одним символом \({\mu}\) і називають магнітною проникністю речовини. Отже, за означенням
\begin{equation} \mu = 1+\chi. \tag{3.13} \end{equation}
Слід сказати, що для переважної більшості речовин \(\chi\approx{0}\) і \(\mu\approx{1}\), тобто вони майже не намагнічуються і не впливають на магнітне поле. Але деякі, як до прикладу залізо, є дуже сильними магнетиками, і для них величина \({\chi}\) сягає \(10^5\) і навіть більше.
Із виразів (3.12) і (3.13) випливає важлива формула, що напряму пов’язує вектори \(\vec{B}\) і \({\vec{H}}\) в ізотропному магнетику:
\begin{equation} \vec{B}=\mu_{0}\mu\vec{H}. \tag{3.14} \end{equation}
3.4. Умови на межі двох магнетиків
При переході через межу поділу намагнічених речовин характеристики магнітного поля закономірно змінюються. При цьому співвідношення між векторами \(\vec{B}_{1}\) і \(\vec{B}_{2}\) та \(\vec{H}_{1}\) і \(\vec{H}_{2}\) визначаються умовами на межі, котрі випливають із теорем про потік та про циркуляцію магнітного поля.
Спочатку встановимо зв’язок між нормальними складовими векторів у двох ізотропних магнетиках із проникностями \(\mu _1\) і \(\mu_2\) за відсутності на межі поділу струмів провідності. Для цього розглянемо потік вектора \(\vec{B}\) крізь маленький замкнений циліндр із висотою \(h\) і паралельними до межі поділу основами \(\Delta S\) (рис. 3.4а).
Він складається з потоків через основи циліндра \(\Delta \Phi_1\), \(\Delta \Phi_2\) та бічну поверхню \(\Delta \Phi'\) і за теоремою Гаусса (2.1) дорівнює нулю:
\begin{equation} \Delta \Phi_1+\Delta \Phi_2+\Delta \Phi'=0. \end{equation}
Циліндр малий, тому, спроектувавши вектори на спільну нормаль \(\vec{n}\) до межі поділу, потоки через основи можна наближено виразити, як \(\Delta \Phi_1\approx -B_{1n}\Delta S\) і \(\Delta \Phi_2\approx B_{2n}\Delta S\). Тоді
\begin{equation} -B_{1n}\Delta S + B_{2n}\Delta S + \Delta \Phi'\approx 0. \end{equation}
Неточність цього виразу зумовлена можливою відміною значень \(B_n\) у різних точках площинок \(\Delta S\). Тому для отримання точної рівності треба перейти до границі, “стягнувши” циліндр у якусь точку на межі поділу. Для цього спочатку будемо подумки зменшувати висоту циліндра, поступово наближаючи основи до межі поділу. Тоді у границі \({h}\to{0}\) зникне потік крізь бічну поверхню:
\begin{equation} \begin{aligned} &-B_{1n}\Delta S + B_{2n}\Delta S\approx 0 \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad B_{1n}\Delta S\approx B_{2n}\Delta S. \end{aligned} \end{equation}
При подальшому стяганні основ точність отриманої рівності буде підвищуватись, і в границі \(\Delta S\to 0\) отримаємо:
\begin{equation} B_{1n} = B_{2n}. \tag{3.15а} \end{equation}
Відтак за допомогою співвідношення (3.14) встановлюємо зв’язок між нормальними складовими для векторів \(\vec{H}\):
\begin{equation} \begin{aligned} &\mu_{1}H_{1n}=\mu_{2}H_{2n} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \frac{H_{1n}}{H_{2n}}=\frac{\mu_{2}}{\mu_{1}}. \end{aligned} \tag{3.15б}\end{equation}
Аналогічно за допомогою теореми про циркуляцію вектора \(\vec{H}\) (3.9) і формули (3.14) встановимо межові умови для тангенціальних складових векторів. Для цього розглянемо циркуляцію \(C\) вектора \(\vec{H}\) уздовж малого прямокутника, що охоплює деяку точку на межі поділу магнетиків і орієнтований так, як показано на рис. 3.4б. Ураховуючи малість контуру, інтеграл у рівнянні (2.4) наближено виразимо через вклади окремих сторін:
\begin{equation} {-H_{1\tau}}\Delta{l}+H_{2\tau}\Delta{l}+\Delta{C_{\text{п}}}\approx{0}, \end{equation}
де \(\Delta C_{\text{п}}\) — спільний вклад від поперечних сторін, а проекції векторів поля на напрям переміщення вздовж поздовжніх сторін записані через спільний орт \(\tau \) дотичної до межі поділу.
Далі, стягаючи прямокутник у вибрану точку на межі поділу магнетиків, отримаємо
\begin{equation} {H_{1\tau}}=H_{2\tau} \tag{3.16а} \end{equation}
і, за допомогою формули (3.14),
\begin{equation} \frac{B_{1\tau}}{\mu_{1}}=\frac{B_{2\tau}}{\mu_{2}}. \tag{3.16б} \end{equation}
Зведемо всі отримані результати, які складають умови на межі двох магнетиків за відсутності струмів провідності:
\begin{equation} \begin{gathered} {B_{1n}}=B_{2n},\qquad &\frac{B_{1\tau}}{B_{2\tau}}=\frac{\mu_1}{\mu_2};\\ \frac{H_{1n}}{H_{2n}}=\frac{\mu_2}{\mu_1},\qquad &H_{1\tau}=H_{2\tau}. \end{gathered} \tag{3.17} \end{equation}
Умови (3.17) визначають зв’язок як між модулями, так і між напрямками векторів \(\vec{B}\) і \(\vec{H}\) на межі ізотропних магнетиків. Зокрема, з них випливає, що напрямки цих векторів задовольняють наступний “закон заломлення” (рис. 3.5):
\begin{equation} \frac{\mathrm{tg}\alpha_1}{\mathrm{tg}\alpha_2}=\frac{\mu_1}{\mu_2}. \end{equation}
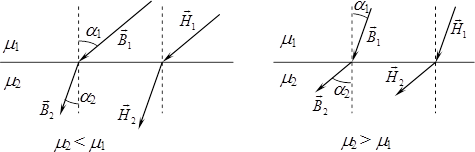
Наостанку зауважимо наступне. Умови на межі (3.17) і зв’язок між векторами магнітного поля (3.14) в ізотропних магнетиках є такий самий, як і в діелектриках ((2.18), (2.14), розділ II). Тож формули для характеристик магнітного поля в ізотропних середовищах, можна отримати з відповідних формул для поля у вакуумі заміною \(\mu_0\) на \(\mu_0\mu\). Зокрема, для поля ідеального соленоїда з ізотропним осердям це дає
\begin{equation} {B}=\mu_{0}\mu{nI} \tag{3.18} \end{equation}
та
\begin{equation} {H=nI}. \tag{3.19} \end{equation}
3.5. Магнетики (пара-, діа- і феромагнетики)
Усі речовини є магнетиками, тобто вони так, чи інакше змінюють характеристики магнітного поля. При цьому за ступенем та характером впливу на магнітне поле виділяють декілька типів магнетиків, серед яких найпоширенішими є парамагнетики, діамагнетики та феромагнетики.
Пара- і діамагнетики. До цих двох типів магнетиків належить переважна більшість речовин. Попри різний механізм намагнічування пара- та діамагнетики єднає те, що вони дуже слабко впливають на магнітне поле, їхня сприйнятливість \(\chi\approx 0\), а проникність \(\mu \approx 1\). При цьому парамагнетики трохи підсилюють, а діамагнетики трохи послаблюють магнітне поле.
Парамагнетиками є речовини, в яких власні магнітні моменти атомів зазвичай орієнтовані хаотично. При внесенні в зовнішнє магнітне поле напрямки магнітних моментів атомів парамагнетика впорядковуються, що зумовлює намагнічування у напрямку поля. Але цьому процесу перешкоджає тепловий рух атомів, отож ступінь упорядкованості моментів і магнітна сприйнятливість парамагнетиків є дуже слабкими і зменшуються при підвищенні температури.
До діамагнетиків належать речовини, в атомах яких магнітні моменти електронів є компенсованими. Тому атоми діамагнетика не мають власного магнітного моменту і, здавалося б, взагалі не повинні намагнічуватись. Але зовнішнє поле діє не на атом як ціле, а на кожен окремий електрон. При цьому рух електронів навколо ядра змінюється так, що у кожного електрона й атома в цілому з’являється індукований магнітний момент, напрямлений протилежно до зовнішнього поля. Тому в діамагнетиках вектори \(\vec{J}=\chi\vec{H}\) і \(\vec{H}\) є антипаралельними, тож \(\chi<{0}\) і \(\mu < 1\).
Ще однією особливістю діамагнетиків є незалежність магнітної сприйнятливості від температури. Це пояснюється тим, що тепловий рух атомів не спроможний впливати на рух електронів навколо ядра. Слід також зауважити, що зовнішнє магнітне поле створює індуковані моменти електронів у будь-яких атомах. Тому діамагнітна намагніченість є притаманною всім магнетикам. Але це практично не впливає на властивості інших видів магнетиків, оскільки діамагнітна намагніченість є значно слабшою, ніж парамагнітна.
Феромагнетики. До цього класу магнетиків належать атоми і деякі сполуки елементів групи заліза (Fe, Co, Ni) та деякі рідкоземельні елементи, а також сплави на їхній основі. Феромагнетики є сильними магнетиками (\({\mu\gg{1}}\)), що зумовлює їхнє практичне застосування в якості технологічних магнітних матеріалів.
Відміна феромагнетиків від слабких магнетиків зумовлена їхньою внутрішньою будовою. З причин, які пояснюються в квантовій фізиці, у феромагнетиках атоми об’єднуються в домени — окремі малі, але макроскопічні (розміром \((1\div 10)\) мкм і навіть більше) області, в яких магнітні моменти атомів є співнапрямленими. Тож домени є спонтанно (самі по собі) намагнічені до теоретичної границі. Наявність доменної структури саме й спричинює особливі магнітні властивості феромагнетиків.
Основна крива намагнічування. У розмагніченому феромагнетику магнітні моменти доменів орієнтовані хаотично, і в ньому, як і в слабких магнетиках, немає власного макроскопічного магнітного поля. Але, на відміну від них, намагнічування феромагнетика при вміщенні у зовнішнє поле зумовлюється упорядкуванням магнітних моментів не окремих атомів, а цілих доменів, і має складний характер. Його можна дослідити, вмістивши залізний сердечник всередину соленоїда із струмом. Оскільки поле соленоїда напрямлене уздовж осі, модулі напруженості в магнетику \(H\) та повітрі \(H_{0}\) збігаються з їхніми проекціями на поверхню сердечника, тож за умовами (3.17) \(H = H_{0}\). Відтак, узявши до уваги формули (2.10) і (3.14), отримуємо
\begin{equation} {H}={nI}. \end{equation}
Отже, величина \(H\) у сердечнику однозначно визначається силою струму в котушці. Тому, поступово збільшуючи величину струму, можна експериментально визначити залежність намагніченості \(J\) та індукції \(B\) від напруженості \(H\). Вигляд графіка \(J ( H)\), який називається основною кривою намагнічування феромагнетика, наведений на рис. 3.6а.
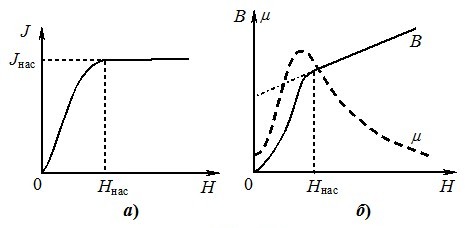
Ця крива наочно відображає особливості намагнічування феромагнетиків — нелінійність і ефект насичення: вже при порівняно невеликій величині \(H_{\text{нас}}\) в сердечнику намагніченість досягає максимального значення \(J_{\text{нас}}\) і далі не змінюється. Такий характер намагнічування пояснюється складними процесами впорядкування магнітних моментів доменів, яке завершується практично повною їхньою орієнтацією в напрямку поля. Тому намагніченість \(J_{\text{нас}}\) є дуже великою і близькою до теоретичного максимуму. Величина індукції \(B ( H)\), яка визначається виразом (3.10), при намагнічуванні теж спочатку зростає подібно до \(J ( H)\), рис. 3.6б, але на відміну індукція після насичення намагніченості продовжує потроху (значно повільніше, ніж зображено) зростати за лінійним законом:
\begin{equation} B(H)=B_m+\mu_0H,\qquad B_m=\mu_0J_{\text{нас}}. \end{equation}
Феромагнетики зазвичай мають полікристалічну структуру, тобто складаються з маленьких неупорядкованих кристалічних зерен — кристалітів. Тому макроскопічно феромагнітна речовина є ізотропним магнетиком, і формула (3.14) зберігає чинність. Але через нелінійність намагнічування проникність феромагнетика \(\mu\ne\textrm{const}\) і є не табличною характеристикою, а залежною від поля величиною
\begin{equation} \mu{(H)}=\frac{B(H)}{\mu_{0}H}. \end{equation}
Із кривої намагнічування випливає, що \(\mu(h)\) спочатку зростає, потім досягає максимуму поблизу насичення, і далі асимптотично спадає до одиниці, як показано на рис. 3.6б штриховою кривою.
Гістерезис. Ще однією особливістю феромагнетиків є часткова необоротність процесу намагнічування, яку ілюструє рис. 3.7.
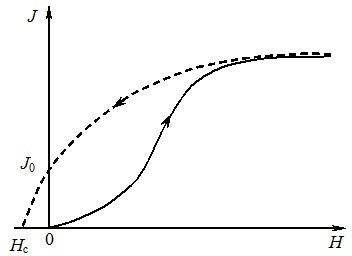
Якщо феромагнітний сердечник намагнітити по основній кривій до насичення (точка А), а потім почати зменшувати струм у котушці, то зміна \(J\) не буде поспівати за зміною \(H\), і феромагнетик буде розмагнічуватися не по шляху намагнічування А — \(0\), а по деякій кривій А — \(J_{0}\). Таке відставання намагніченості називається магнітним гістерезисом (“гістерезис” грецькою саме й означає відставання або спізнення). Через гістерезис при зменшенні напруженості \(H\) до \(0\) феромагнетик повністю не розмагнічується, в ньому зберігається деяка залишкова намагніченість \(J_0\). Тому для повного розмагнічування феромагнетика по котушці треба пропустити струм зворотнього напрямку, котрий створить необхідну для розмагнічування напруженість \(H_{\text{с}}\), яка називається коерцитивною силою.
Залежно від величини коерцитивної сили магнітні матеріали поділяють на магнітном’які та магнітнотверді. Перші мають малу величину \(H_{\text{с}}\), легко перемагнічуються змінним зовнішнім полем і за його відсутності є ненамагніченими. Із таких матеріалів виготовляють сердечники трансформаторів, електромагнітів та інших пристроїв. Напроти, магнітнотверді матеріали мають велику коерцитивну силу і тому зберігають намагніченість навіть у сильних розмагнічуючих полях. Вони, зокрема, використовуються для виготовлення постійних магнітів.
Унаслідок гістерезису при перемагнічуванні феромагнетика змінним струмом залежність \(B ( H)\) зображується на графіку замкненою кривою, що називається петлею гістерезису і виглядає, як на рис. 3.8а для магнітом’яких і на рис. 3.8б для магнітнотвердих матеріалів.
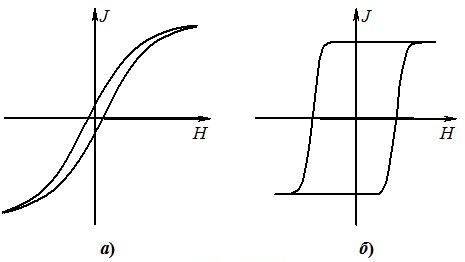
При цьому намагнічений магнітнотвердий феромагнетик фактично може перебувати тільки в якомусь із двох станів насичення, перехід між якими відбувається “стрибком”, тобто при дуже малій зміні напруженості в околі \(H_{\text{с}}\). Це зумовлює використання таких матеріалів у різноманітних логічних електронних схемах та накопичувачах інформації.
Доменна структура і спроможність до феромагнітного намагнічування є не у всіх кристалічних речовин і не при всіх температурах. У більшості феромагнетиків вона зменшується при нагріванні і зовсім зникає при характерній для кожного феромагнетика температурі, що називається точкою Кюрі. Це пояснюється тим, що в точці Кюрі змінюється взаємне розташування атомів (тип кристалічної ґратки) феромагнетика. Відтак існування доменів стає неможливим і феромагнетик перетворюється на звичайний парамагнетик. Але при охолодженні нижче точки Кюрі феромагнітні властивості речовини повністю відновлюються.
Контрольні запитання
1. Якою є загальна причина впливу речовини на магнітне поле?
2. Чим вплив речовини на магнітне поле відрізняється від впливу на електричне поле?
3. Що таке намагнічування та намагніченість речовини?
4. Що таке струми намагнічування? Чим вони відрізняються від “звичайних” струмів (струмів провідності)?
5. Чи придатні рівняння (2.1) і (2.4) для магнітного поля в речовині? Чому?
6. Запишіть і сформулюйте теорему про циркуляцію магнітного поля в речовині. Чи придатна вона для поля у вакуумі? Чому?
7. Чи є напруженість основним вектором магнітного поля? Чому?
8. Чи завжди виконується співвідношення (3.14)?
9. Що є спільного у впливі на магнітне поле між а) пара- та діамагнетиками і б) пара- та феромагнетиками?
10. У чому полягає та чим пояснюється відміна у впливі на магнітне поле між а) пара- та діамагнетиками і б) пара- та феромагнетиками?
V. ЕЛЕКТРОМАГНЕТИЗМ
У розглянутих досі явищах електричне і магнітне поля виявляють себе як незалежні поля. Але в дійсності вони є двома проявами єдиного електромагнітного поля. Це проявляється в нестаціонарних електромагнітних процесах, які спостерігаються в залежних від часу полях. Далі розглядаються:
1. Явище електромагнітної індукції
Органічний зв’язок між електричним і магнітним полями найбільш яскраво проявляється у їхній здатності до взаємних перетворень. Зокрема — у здатності нестаціонарного магнітного поля породжувати електричне поле. В цьому полягає глибинний зміст явища електромагнітної індукції (ЕМІ), яке розглядається далі в наступних питаннях:
1.3. Струм при замиканні та розмиканні кола з індуктивністю
1.1. Основний закон ЕМІ
Явище ЕМІ. Закон Фарадея. Раніше (розділ IV, п. 1.4) було показано, що при зміні магнітного потоку крізь поверхню контуру зі струмом при малому переміщення в магнітному полі виконується робота
\begin{equation} \delta{A}=I\,\mathrm{d}{\Phi}. \end{equation}
Але магнітні сили, що діють на носії струму в контурі, є поперечними і як такі роботи не виконують. Тоді за рахунок чого вона виконується?
Аби це з’ясувати, розглянемо такий дослід. Нехай у магнітному полі \(\vec{B}\) закріплено дві паралельні металеві рейки, кінці яких з одного боку замкнені на джерело струму із заданою ЕРС \(\E\), рис. 1.1.
По рейках може ковзати без тертя перетинка із струмом опором \(R\), яку спочатку утримують у фіксованому положенні.
Якщо задля простоти знехтувати опором джерела і рейок, то сила струму в перетинці дорівнює
\begin{equation} {I}_{0}=\frac{\E}{R}. \end{equation}
При цьому вся робота джерела йде на нагрівання провідників і за час \(\mathrm{d}t\) складає
\begin{equation} \delta{A}={\E}I_{0}\,\mathrm{d}t=I_{0}^{2}R\,\mathrm{d}{t}. \end{equation}
Але після звільнення перетинка почне рухатися під дією сили Ампера, і енергія джерела буде витрачатися вже не тільки на тепло, а й на виконання роботи по переміщенню перетинки в магнітному полі:
\begin{equation} {\E}I\,\mathrm{d}t=I^{2}R\,\mathrm{d}t+I\,\mathrm{d}\Phi. \end{equation}
У такому разі струм у колі зміниться і стане рівним
\begin{equation} {I}=\frac{{\E}-\mathrm{d}\Phi/\mathrm{d}t}{R}. \end{equation}
Отже, виходить, що під час руху перетинки в контурі крім ЕРС джерела \(\E\) діє ще одна ЕРС, яка дорівнює
\begin{equation} {\E}_{i}=-\frac{\mathrm{d}\Phi}{\mathrm{d}t}. \tag{1.1} \end{equation}
Відповідно, сила струму
\begin{equation} {I}=\frac{\E+\E_{i}}{R}. \end{equation}
Отриманий результат є одним із проявів відкритого М. Фарадеєм явища електромагнітної індукції (ЕМІ), котре полягає в тому, що
при зміні магнітного потоку крізь поверхню, обмежену провідним контуром, в ньому виникає електричний струм.
Такий струм називається індукційним струмом і створюється електрорушійною силою (ЕРС) індукції (1.1). Отже,
\begin{equation} {I}=\frac{\E}{R}=-\frac{1}{R}\cdot\frac{\mathrm{d}\Phi}{\mathrm{d}t}. \tag{1.2} \end{equation}
Важливою особливістю явища ЕМІ є його універсальність. Як показали досліди Фарадея, виникнення ЕРС індукції не залежить від причини та способу зміни потоку, причому величина \( {\E}_{i}\) в усіх випадках визначається виразом (1.1). Тому його називають основним законом електромагнітної індукції, або законом Фарадея.
Потік крізь контур можна змінювати багатьма конкретними способами, але є тільки дві різні причини його зміни. Це або рух контура чи його частини у магнітному полі, або зміна із часом (нестаціонарність) самого магнітного поля. Істотно й те, що ЕРС індукції визначається швидкістю зміни потоку, а не його величиною. Тому за відповідних умов у слабкому полі ЕРС \( {\E}_{i}\) може виявитися великою, а в сильному — незначною.
Зазначимо також, що в СІ на основі закону (1.1) встановлюється одиниця магнітного потоку вебер (Вб, \(1\ \text{Вб} = 1\ \text{В}\cdot\text{с}\)):
\(1\ \text{Вб}\) — то є магнітний потік, при рівномірній зміні котрого до нуля за час \(1\ \text{с}\) у зв’язаному з ним контурі індукується ЕРС \(1\ \text{В}\).
Відтак установлюються одиниці інших магнітних величин. Зокрема, одиниця індукції магнітного поля — тесла (\(1\ \text{Тл}\)) має наступне означення:
\(1\ \text{Тл}\) дорівнює індукції такого однорідного магнітного поля, в якому крізь перпендикулярну до нього плоску поверхню площею \(1\ \text{м}^2\) створюється магнітний потік \(1\ \text{Вб}\).
Отже, \(1\ \text{Тл} = 1\ \text{Вб}/\text{м}^2\).
Правило Ленца. Досліджуючи електромагнітну індукцію, Фарадей виявив, що напрям індукційного струму залежить від того, зростає потік крізь контур із часом, чи зменшується. Пізніше Ленц дослідним шляхом установив загальне правило, що носить його ім’я і дозволяє визначити напрям індукційного струму в кожному випадку. А саме,
індукційний струм у контурі завжди має такий напрям, при якому перешкоджає причині, що його породжує.
Конкретно це означає, що магнітне поле \({{\vec{B}}_{i}}\), яке створюється індукційним струмом і завжди пов’язане з ним правилом правого гвинта, має бути напрямлене так, аби власним потоком послаблювати зміну потоку поля, яка викликає індукційний струм. Приміром, якщо нерухоме дротяне кільце знаходиться в однорідному нестаціонарному магнітному полі \(\vec{B}( t )\), що послаблюється з часом (\(\mathrm{d}B/\mathrm{d}t < 0\)), то потік крізь кільце спадає. Тоді поле індукційного струму \({{\vec{B}}_{i}}\) має підживлювати поле \(\vec{B}\) й індукційний струм буде циркулювати за правим гвинтом відносно напряму \(\vec{B}\), як показано на рис. 1.2а.
Із тих самих міркувань при (\(\mathrm{d}B/\mathrm{d}t > 0\)) напрям індукційного струму є протилежним (рис. 1.2б). Так можна визначати напрям індукційного струму і в будь-якому іншому випадку. Але зручніше робити це безпосередньо за виразом (1.2), використовуючи наступне правило знаків (див. рис. 1.2а,б):
якщо за формулою (1.2) виходить \(I_i>0\), то індукційний струм пов’язаний із напрямом магнітного поля, що його породжує, правилом правого гвинта. При \(I_i < 0\) напрям струму протилежний.
До прикладу, коли кільце рухається в постійному неоднорідному полі показаному на рис. 1.2в,г, то при русі в напрямку поля \(\mathrm{d}\Phi /\mathrm{d}t < 0\), а в протилежному напрямку \(\mathrm{d}\Phi /\mathrm{d}t > 0\). Тому, у випадку в) індукційний струм \(I_i > 0\) і тече за годинниковою стрілкою, якщо дивитися вздовж напрямку поля, а у випадку г) \(I_i < 0\), і струм протікає в протилежному напрямку.
На завершення скажемо, що правило Ленца диктується законом збереження енергії і є одним із проявів загального принципу Ле Шательє — Брауна, за яким усякий зовнішній вплив, що намагається вивести систему із стійкої рівноваги, продукує в ній компенсаційні процеси, спрямовані на нівелювання цього впливу.
1.2. Самоіндукція
ЕРС у контурі може індукуватись як зовнішнім магнітним полем, так і власним полем, створюваним струмом у самому контурі. Останній випадок називається самоіндукцією.
Власний потік та індуктивність контуру. Магнітне поле струму, що протікає по замкненому контуру, створює відповідний потік крізь поверхню, обмежену цим контуром. В силу неперервності ліній магнітного поля, цей потік не залежить від площі та форми такої поверхні і називається власним потоком або потоком самоіндукції контуру.
За відсутності феромагнетиків величина індукції магнітного поля провідника із струмом у будь-якій точці простору є прямо пропорційною величині струму: \(B\sim I\). Це стосується й потоку поля крізь будь-яку задану поверхню, тож для власного потоку \(\Phi_{\text{с}}\) контуру із струмом \(I\) можна записати:
\begin{equation} \Phi_{\text{с}}={LI}, \tag{1.3} \end{equation}
де величина
\begin{equation} {L}=\frac{\Phi_{\text{с}}}{I} \tag{1.4} \end{equation}
називається індуктивністю або коефіцієнтом самоіндукції контуру.
Зауваження. Означення (1.4), строго говорячи, є неоднозначним, бо невідомо, як саме має проходити всередині провідника контур поверхні, через яку визначається величина \(\Phi_{\text{с}}\). Але, позаяк на практиці контури виготовляють із тонкого дроту, указана обставина є не істотною.
Одиницею індуктивності є генрі (Гн) — індуктивність контуру, власний потік якого складає \(1\ \text{Вб}\) при силі струму \(1\ \text{А}\):
\begin{equation} 1\ \text{Гн} = 1\ \text{Вб}/\text{А}. \end{equation}
Величина \(L\) не залежить від сили струму і визначається тільки конфігурацією контуру та магнітними властивостями середовища, в якому він знаходиться. У цьому легко переконатися на прикладі довгого соленоїда, в якому при струмі \(I\) створюється магнітна поле з індукцією, що визначається формулою (3.18), розділ IV:
\begin{equation} B=\mu_0\mu nI, \end{equation}
де \(n\) — кількість витків на одиницю довжини соленоїда.
В такому разі потік крізь один виток складає
\begin{equation} \Phi_1=\mu_0\mu nIS, \end{equation}
а власний потік усього соленоїда, котрий ще називається потокозчепленням, дорівнює
\begin{equation} \begin{aligned} &\Phi_{\text{с}}=N\mu_0\mu nIS=\mu_0\mu n^2ISl={}\\ &\quad{}= \mu_0\mu n^2IV, \end{aligned} \end{equation}
де \(N\) — повна кількість витків соленоїда, \(S\) — площа його перерізу, \(l\) — довжина і \(V\) — об’єм. Відтак за формулою (1.4) індуктивність соленоїда
\begin{equation} L=\mu_0\mu n^2V. \tag{1.5} \end{equation}
ЕРС і струм самоіндукції. При зміні з часом власного магнітного потоку контуру в ньому виникає ЕРС самоіндукції \({\E}_{\text{с}}\), яка, природньо, визначається законом Фарадея (1.1):
\begin{equation} {\E}_{\text{с}} = -\frac{\mathrm{d}\Phi }{\mathrm{d}t}= -\frac{\mathrm{d}( LI )}{\mathrm{d}t}. \end{equation}
Якщо контур є жорстким і знаходиться в діа- чи парамагнітному середовищі, то \(\mu = \textrm{const}\), \(L = \textrm{const}\), і величина \({{E}_{\text{с}}}\) визначається тільки швидкістю зміни струму в контурі:
\begin{equation} {\E}_{\text{с}} = -L\frac{\mathrm{d}I}{\mathrm{d}t}. \tag{1.6} \end{equation}
Але при деформації не жорсткого контуру чи зміні струму в котушці з феромагнітним осердям індуктивність теж змінюється з часом, і вираз \({\E}_{\text{с}}\) істотно ускладнюється:
\begin{equation} {\E}_{\text{с}} = -L\frac{\mathrm{d}I}{\mathrm{t}} - I\frac{\mathrm{d}L}{\mathrm{d}t}. \end{equation}
За таких умов чисто аналітичні розрахунки ланцюгів із індуктивностями стають неможливими, і використовуються інші методи аналізу.
ЕРС самоіндукції створює в контурі додатковий струм самоіндукції \(I_{\text{с}}\), напрям якого є підпорядкований правилу Ленца і встановлюється дуже просто:
напрям струму самоіндукції збігається з напрямом основного струму при його зменшенні і є протилежним до основного струму при його зростанні.
1.3. Струм при замиканні та розмиканні кола з індуктивністю
При замиканні та розмиканні кола, в якому є тільки резистори, струм установлюється і зникає практично миттєво. Але в колах із котушками індуктивності при комутаціях виникають індукційні струми, котрі за правилом Ленца уповільнюють зміну основних струмів. Тому при замиканні чи розмиканні кола з індуктивністю струм змінюється поступово.
Струм при замиканні кола. Розглянемо процес установлення струму в простому колі, що складається з котушки індуктивності \(L = \textrm{const}\), резистора \(R\), джерела з ЕРС \( {\E}\) та ключа К (рис. 1.3).
Будемо вважати, що опір дроту котушки включено в \(R\), а опір джерела дорівнює нулю. Також приймемо, що струм є квазістаціонарним (див. розділ III, п. 3.1).
Після замикання в момент \(t = 0\) ключа К у котушці виникне ЕРС самоіндукції \( {\E}_{\text{с}} \), так що струм у колі дорівнюватиме
\begin{equation} {I}=\frac{{\E}+{\E}_{\text{с}}}{R}. \end{equation}
Підставивши сюди вираз (1.6), отримаємо диференціальне рівняння
\begin{equation} \begin{aligned} &{IR}={\E}-L\frac{\mathrm{d}I}{\mathrm{d}t} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \frac{\mathrm{d}I}{\mathrm{d}t}=\frac{{\E}-IR}{L}, \end{aligned} \tag{1.7}\end{equation}
з якого можна знайти закон зміни струму \(I=I(t)\).
Рівняння (1.7) легко інтегрується методом відокремлення змінних. Але задля зручності спочатку введемо позначення :
\begin{equation} {V}={\E}-IR . \tag{1.7а} \end{equation}
Тоді
\begin{equation} \frac{\mathrm{d}I}{\mathrm{d}t} = - \frac{1}{R}\frac{\mathrm{d}V}{\mathrm{d}t} \end{equation}
і рівняння (1.7) набуває вигляду
\begin{equation} \begin{aligned} &\frac{\mathrm{d}V}{\mathrm{d}t}=-\frac{V}{\tau} \quad \Rightarrow \quad \frac{\mathrm{d}V}{V}=-\frac{\mathrm{d}t}{\tau},\\ &\tau= \frac{L}{R}. \end{aligned} \end{equation}
Проінтегрувавши це рівняння від \(t = 0\) до довільного моменту \(t\) і від \(V_{0}\) до \(V\), отримуємо:
\begin{equation} \begin{aligned} &\int\limits_{V_{0}}^{V}\frac{\mathrm{d}V}{V}=-\int\limits_{0}^{\tau}\frac{\mathrm{d}t}{\tau} \quad \Rightarrow {}\\ &\quad{}\Rightarrow\quad \ln\frac{V}{V_{0}}=-\frac{t}{\tau} \quad \Rightarrow \quad {V}=V_{0}e^{-\frac{t}{\tau}}. \end{aligned} \end{equation}
У момент замикання ключа \(t = 0\) струм у колі відсутній: \(I=0\). Отже, відповідно до (1.7а) маємо \( {V}_{0}={\E} \).
Відтак, зробивши зворотню заміну \( {V}={\E}-{IR}\), дістанемо:
\begin{equation} \begin{aligned} &{I}(t)=I_{m}\bigl(1-\mathrm{e}^{-t/\tau}\bigr),\\ &{I}_{m}=\frac{{\E}}{R} . \end{aligned} \tag{1.8}\end{equation}
Отриманий результат має прозорий зміст. А саме: струм у колі складається із двох частин
\begin{equation} {I}=I_{m}+{I^\prime}, \end{equation}
де \( {I}_{m}={\E}/{R} \) — струм, який створюється джерелом, а \( {I}'=-{{I}_{m}}{{e}^{-{t}/{\tau }}}\) — зустрічний струм самоіндукції, що виникає в котушці.
З часом зустрічний струм самоіндукції поступово зменшується, а повний струм \(I\) зростає і наближається до усталеного значення \(I_m\). Наскільки швидко це буде відбуватися, залежить від величини
\begin{equation} \tau=\frac{L}{R}, \tag{1.9} \end{equation}
яка називається часом установлення струму (сталою часу) \(RL\)-ланцюжка.
Зокрема, через час \(\tau \) після замикання ключа струм у колі досягає величини \({I}=I_{m}(1-e^{-1})=0{,}63I_{m}\). При цьому чим більша величина \(\tau \), тим повільніше наростає струм (рис. 1.4).
Струм при розмиканні кола. Розглянемо тепер поведінку струму в котушці, яка має індуктивність \(L\) і опір \(r\), після розмикання ключа К у колі рис. 1.5. Як і раніше, опір джерела дорівнює нулю.
Після розмикання ключа струм через котушку та резистор визначається тільки ЕРС самоіндукції і дорівнює
\begin{equation} {I}=\frac{{\E}_{\text{с}}}{R+r}=\frac{{\E}_{\text{с}}}{R_{0}}, \end{equation}
де \(R_{0} = R + r\) — повний опір кола.
Цей струм називається екстраструмом розмикання і відповідно до (1.6) задовольняє диференціальне рівняння
\begin{equation} \begin{aligned} &{I}=-\frac{L}{R_{0}}\frac{\mathrm{d}I}{\mathrm{d}t}\quad \Rightarrow \quad \frac{\mathrm{d}I}{\mathrm{d}t}=-\frac{I}{\tau},\\ &\tau= \frac{L}{R_{0}}, \end{aligned} \end{equation}
що, як і раніше, розв’язується методом відокремлення змінних:
\begin{equation} \begin{aligned} &\frac{\mathrm{d}I}{I}=-\frac{\mathrm{d}t}{\tau} \quad \Rightarrow \quad \int\limits_{I_{0}}^{I}\frac{\mathrm{d}I}{I}=-\int\limits_{0}^{t}\frac{\mathrm{d}t}{\tau} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \ln\frac{I}{I_{0}}=-\frac{t}{\tau}. \end{aligned} \end{equation}
Отже,
\begin{equation} {I}=I_{0}e^{-t/\tau}, \tag{1.10} \end{equation}
де величина \({I}_{0}=I{(0)}\) — струм, який створювався в котушці джерелом \( {\E}\) до розмикання ключа і дорівнював
\begin{equation} {I}_{0}=\frac{{\E}}{r}. \end{equation}
Таким чином, після відключення джерела в котушці виникає струм, що експоненціально спадає з часом як показано на рис. 1.6.
Цей струм тече і через резистор \(R\), тож між точками 1 і 2 створюється напруга
\begin{equation} {U}=IR=I_{0}R\mathrm{e}^{-t/\tau}=\frac{R}{r}{\E}\mathrm{e}^{-t/\tau}. \end{equation}
Позаяк опір котушки зазвичай малий \(r\ll R\), у момент розмикання ключа К створюється стрибок напруги \(U \gg {\E}\). Це може викликати електричний пробій ізоляції, тому в потужних колах з індуктивностями передбачають спеціальні системи захисту від екстраструмів розмикання.
1.4. Енергія магнітного поля
При встановленні струму в контурі з індуктивністю джерело виконує роботу по подоланню ЕРС самоіндукції. Тому його енергія витрачається не тільки на джоульове тепло, а й частково переходить в іншу форму, що називається магнітною енергією струму \(W_m\). Про це свідчить те, що після відключення джерела у колі з індуктивністю продовжує текти струм (1.10) і виділятися тепло. Очевидно, що це відбувається за рахунок магнітної енергії струму, адже ніяких інших джерел енергії в колі немає. З іншого боку, за умови квазістаціонарності струму немає й інших каналів перетворення магнітної енергії.
(Примітка. У випадку нестаціонарних, тобто швидкозмінних, струмів частина цієї енергії йде на електромагнітне випромінювання).
Тому \(W_m=Q\), де \(Q\) — кількість тепла, що виділяється при повному згасанні струму в контурі після відключення зовнішнього джерела. Це дозволяє розрахувати магнітну енергію \(W_m\) через силу струму \(I\) в контурі.
Якщо в колі на рис. 1.5 на момент розмиканні ключа К t = 0 струм у котушці індуктивності дорівнює I, то, згідно з (1.10), надалі він буде зменшуватися за законом \({i}=Ie^{-t/\tau}\). При цьому магнітна енергія котушки буде перетворюватися в тепло на повному опорі кола R0=R+r, згідно із законом Джоуля (розділ III, формула (4.2)). Формально цей процес триватиме необмежений час, тож кількість тепла, що виділиться за час до повного згасання струму, визначається, як:
\begin{equation} {Q}=R_{0}{{I}^{2}}\int\limits_{0}^{\infty }{{{e}^{-{2t}/{\tau }}}\,\mathrm{d}t}=\frac{\tau R_{0}{{I}^{2}}}{2}. \end{equation}
(Довідка. Інтеграли з нескінченними границями називаються невласними інтегралами і обчислюється через граничний перехід:
Але коли границя перехід є очевидною, із символом \({\infty}\) поводяться, як із звичайним числом.
Звідси, враховуючи, що \(W_m=Q\) і \(\tau = L / R_{0}\), отримуємо наступну формулу магнітної енергії струму:
\begin{equation} {W}_{m}=\frac{LI^2}{2}. \tag{1.11} \end{equation}
Вираз (1.11) показує, що крім величини струму магнітна енергія залежить від параметрів контуру. Наприклад, для соленоїда, зважаючи на формулу (1.5),
\begin{equation} {W}_{m}=\frac{\mu_{0}\mu{n^2}I^2}{2}{V}. \tag{1.11а} \end{equation}
Але для соленоїда nI = H — напруженість поля, тож
\begin{equation} {W}_{m}=\frac{\mu_{0}\mu{H^2}}{2}V. \tag{1.11б} \end{equation}
Отже, магнітну енергію соленоїда можна виразити не через конфігурацію контуру та величину струму ньому, а через характеристики магнітного поля в соленоїді та об’єм простору який воно займає. В об’ємі соленоїда зосереджене все його поле, тому отриманий результат дає підстави думати, що магнітна енергія зосереджена не в самій котушці із струмом, а в її магнітному полі. Інакше говорячи, магнітне поле має енергію. Такий висновок повністю підтверджується і теорією, і дослідом.
Магнітне поле ідеального соленоїда є однорідним, і його енергія розподілена у просторі рівномірно з об’ємною густиною
\begin{equation} {w}_{m}=\frac{W}{V}\ (\text{Дж}/\text{м}^3), \end{equation}
що, згідно з виразом (1.11б), визначається формулою
\begin{equation} {w}_{m}=\frac{\mu_{0}\mu{H^2}}{2}. \tag{1.12} \end{equation}
Урахувавши співвідношення B = μ0μH (див. розділ IV), можна записати й такі формули:
\begin{equation} {w}_{m}=\frac{B^2}{2\mu_{0}\mu} \tag{1.12а} \end{equation}
та
\begin{equation} {w}_{m}=\frac{BH}{2}. \tag{1.12б} \end{equation}
Таким чином, енергія заданого об’єму однорідного магнітного поля виражається, як
\begin{equation} {W}_{m}={wV}. \end{equation}
Формули (1.12), (1.12а) і (1.12б) зберігають чинність і для неоднорідного поля, але в такому разі об’ємна густина енергії не скрізь однакова і в кожній точці визначається як
\begin{equation} {w}_{m}=\frac{\mathrm{d}W}{\mathrm{d}V}. \end{equation}
Відповідно, енергія в заданому об’ємі \(V\) неоднорідного поля знаходиться інтегруванням енергій
\begin{equation} \mathrm{d}W_{m}=w\,\mathrm{d}{V}, \end{equation}
зосереджених у всіх елементарних ділянках цього об’єму:
\begin{equation} {W_{m}}=\int\limits_{V}w\,\mathrm{d}{V}. \tag{1.13} \end{equation}
1.5. Природа ЕМІ. Вихрове електричне поле
На початку розділу відзначалося, що є дві різні причини зміни магнітного потоку і виникнення ЕРС індукції та індукційного струму — рух провідників та зміна з часом магнітного поля, в якому знаходиться провідний контур, — але в обох випадках виконується один і той самий закон (1.1). Така універсальність є унікальною рисою явища ЕМІ, бо сторонні сили, що забезпечують рух електронів уздовж контуру, в кожному з указаних випадків мають різне походження.
Індукція в рухомих провідниках. Розглянемо виникнення індукційного струму в провідному контурі утвореному нерухомим металевим каркасом із рухомою дротяною перетинкою, який вміщений у перпендикулярне до його площини однорідне магнітне поле (рис.1.7а).
Якщо перетинку привести в рух, як показано, то внаслідок збільшення потоку крізь поверхню контуру, по ньому, відповідно до (1.2), потече індукційний струм \(I_0\), спрямований проти годинникової стрілки. Природа сторонньої сили, яка його створює, на перший погляд є очевидною. Адже з початком руху перетинки вздовж неї на носії струму починає діяти магнітна сила Лоренца \( \vec{F}_{m}\) (розділ IV, ф-ла (1.3)). Тож вона і є причиною переміщення (дрейфу) носіїв по перетинці та виникнення струму. Але в такому поясненні є протиріччя. При протіканні струму сторонні сили мають виконувати над носіями роботу по подоланню електричного опору, тоді як магнітна сила є поперечною і не може виконувати роботу. Пояснення цього "парадоксу" полягає в тому, що насправді швидкість носіїв відносно магнітного поля дорівнює не швидкості перетинки \(\vec{v}\), а величині \(\vec{v}_{e}=\vec{v}+\vec{u}\), де \(\vec{u}\) — дрейфова швидкість, тобто швидкість руху носіїв відносно перетинки. Тому магнітна сила, що діє на носії,
\begin{equation} \vec{F}_{m}=e\bigl[\vec{v}_{e},\vec{B}\bigr] , \tag{1.14} \end{equation}
напрямлена не вздовж перетинки, а під кутом, як показано на рис.1.7б (задля зручності заряд носіїв будемо вважати позитивним). Тому вона має дві складові:
\begin{equation} {{\vec{F}}_{m}}={{\vec{F}}_{\parallel }}+{{\vec{F}}_{\bot }}. \end{equation}
При цьому лише паралельна до перетинки складова
\begin{equation} {{\vec{F}}_{\parallel }}={{\vec{F}}_{\bot }}-{{\vec{F}}_{m}}. \end{equation}
безпосередньо рухає носії по перетинці. А інша складова \(\vec{F}_{\bot}\) гальмує перетинку (це є наочним проявом правила Ленца), і для підтримки руху до неї має бути прикладена якась зовнішня сила
\begin{equation} \vec{F}_{\text{зовн}} = - \vec{F}_{\bot}. \end{equation}
Таким чином, за сторонню силу, що створює струм і визначає ЕРС у контурі, править рівнодійна
\begin{equation} \vec{F}_{\text{стор}} = \vec{F}_{m} + \vec{F}_{\text{зовн}} = \vec{F_{\parallel}}. \end{equation}
При цьому, позаяк магнітна сила роботи не виконує, робота сторонньої сили збігається з роботою зовнішньої сили:
\begin{equation} {{A}_{\text{стор}}}={{A}_{\text{зовн}}}={{A}_{\parallel }} \end{equation}
і виконується за рахунок якогось зовнішнього джерела енергії.
Робота сторонніх сил над носіями струму визначає ЕРС, отже, констатуємо, що
ЕРС індукції в рухомих провідниках зумовлена сумісною дією на носії струму магнітного поля та зовнішніх сил, які підтримують рух. При цьому сили магнітного поля забезпечують дрейф носіїв, а зовнішні сили надають необхідну для цього енергію.
Описаний електронний механізм ЕМІ повністю узгоджується із законом Фарадея, в чому можна переконатися прямим розрахунком ЕРС індукції на основі означення ЕРС (див. розділ III, п. 2.1):
\begin{equation} {\E}=\frac{A_{\text{стор}}}{q}, \end{equation}
де \(A_{\text{стор}}\) — робота сторонньої сили при переміщенні заряду \(q\) по всій довжині перетинки \(l\). Вона дорівнює
\begin{equation} A_{\text{стор}}={F}_{\parallel}l=F_{m}\cos\alpha\cdot{l}. \end{equation}
З урахуванням виразу (1.14)
\begin{equation} A_{\text{стор}}=qBv_e\cos\alpha\cdot{l}=qBvl, \end{equation}
де \({v}\) — швидкість руху перетинки. Відтак для ЕРС індукції в рухомій перетинці отримуємо:
\begin{equation} {\E}_{i}={Blv}. \tag{1.15} \end{equation}
Якщо тепер узяти до уваги, що \( \mathrm{d}v=\mathrm{d}x/\mathrm{d}t \) і \( {l}\,\mathrm{d}x=\mathrm{d}{S}\) — зміна площі контуру за час \(\mathrm{d}t\), то для ЕРС індукції виходить
\begin{equation} {\E}_{i}=\frac{B\,\mathrm{d}S}{\mathrm{d}t}=\frac{\mathrm{d}\Phi}{\mathrm{d}t}, \end{equation}
у відповідності із законом Фарадея.
Наостанку вкажемо, що отримані результати зберігають чинність і при довільній орієнтації та напрямку руху прямого провідника в магнітному полі. При цьому в будь-який момент часу величина ЕРС індукції визначається, як
\begin{equation} {\E}_{i}=B_{\bot}lv_{\bot}, \tag{1.15а} \end{equation}
де \({v_\bot}\) — перпендикулярна до провідника складова його швидкості, а \({B_{\bot}}\) - складова вектора \(\vec{B}\), перпендикулярна до площини руху провідника в цей момент.
Вихрове електричне поле. Коли контур, який знаходиться в стаціонарному магнітному полі \(\vec{B}=\mathrm{const} \), не рухається, то потік крізь нього не змінюється з часом, і електромагнітна індукція не спостерігається. Але щойно магнітне поле починає змінюватись, у контурі з’являється ЕРС та індукційний струм у повній згоді з основним законом ЕМІ (1.1). Пояснити цей факт на основі розглянутого електронного механізму неможливо, бо через хаотичність теплового руху на носії в нерухомому контурі ніяка магнітна сила не діє: \( {{\vec{F}}_{m}} = 0\). Отже, стороння сила, що створює індукційний струм, має чисто електричне походження. А це означає, що в нерухомому контурі вміщеному у змінне магнітне поле з’являється електричне поле \(\vec{E}_{B}\), яке й створює сторонню силу
\begin{equation} \vec{F}=q\vec{E}_{B}, \tag{1.16} \end{equation}
відповідальну за індукційний струм. Такого висновку дійшов Максвелл, який сформулював наступне твердження:
всяке нестаціонарне магнітне поле генерує у просторі відповідне вихрове електричне поле.
На відміну від кулонівського, вихрове поле не створюється зарядами і має замкнені силові лінії. Тому воно не є потенціальним і здатне переміщувати носії струму по замкненому контуру, тобто створювати струм. Робота такого поля віднесена до одиниці перенесеного по контуру заряду — то і є ЕРС індукції. Це дозволяє на основі закону ЕМІ (1.1) і означення ЕРС встановити зв’язок між вихровим електричним полем \(\vec{E}_{B}\) та нестаціонарним магнітним полем \(\vec{B}=\vec{B}{(t)}\), яке його продукує. Згідно з означенням ЕРС,
\begin{equation} {\E}_{i}=\frac{1}{q}\oint\limits_{L}q\vec{E}_{B}\,\mathrm{d}\vec{l} \quad \Rightarrow \quad {\E}_{i}=\oint\limits_{L}\vec{E}_{B}\,\mathrm{d}\vec{l} . \end{equation}
А за основним законом ЕМІ (1.1) та означенням потоку (розділ І, п. 5.2.1) ЕРС індукції можна подати як
\begin{equation} {\E}_{i}=-\frac{\mathrm{d}}{\mathrm{d}t}=\int\limits_{S}\vec{B}\,\mathrm{d}\vec{S}=-\int\limits_{S}\frac{\partial{\vec{B}}}{\partial{t}}\,\mathrm{d}\vec{S}. \end{equation}
(Під інтегралом поставлено знак частинної похідної, позаяк при нерухомому контурі зміна потоку крізь поверхню S зумовлюється тільки явною залежністю індукції поля від часу.)
Таким чином,
\begin{equation} \oint\limits_{L}\vec{E}_{B}\,\mathrm{d}\vec{l}=-\int\limits_{S}\frac{\partial\vec{B}}{\partial{t}}\,\mathrm{d}\vec{S}. \tag{1.17} \end{equation}
Це встановлене Максвеллом рівняння означає, що
циркуляція напруженості вихрового електричного поля по довільному контуру дорівнює взятому з протилежним знаком потокові швидкості зміни індукції магнітного поля через довільну поверхню обмежену цим контуром.
При цьому напрям обходу контуру пов’язаний із векторами \(\mathrm{d}\vec{S}\) правилом правого гвинта, що випливає з правила Ленца. Максвелл також довів, що вектори \(\vec{E}_{B}\) і \(\vec{B}{(t)}\) є завжди взаємно перпендикулярні, тож якщо поле \(\vec{B}{(t)}\) однорідне, то лінії вектора \(\vec{E}_{B}\) лежать у площинах, перпендикулярних до \(\vec{B}{(t)}\) і напрямлені, як на рис. 1.8.
Фарадей трактував електромагнітну індукцію як виникнення струму у замкненому провіднику, вміщеному в магнітне поле. Але за Максвеллом сутність ЕМІ полягає не у виникненні струму в провідниках, а в створенні змінним магнітним полем електричного поля у просторі. А дротяний контур є лишень індикатором цього електричного поля, тому індукційні ефекти мають спостерігатись і в діелектриках та вакуумі. Такий висновок повністю підтверджується дослідом. Ілюстрацією може слугувати бетатрон — один із типів прискорювачів елементарних частинок, у якому електронні пучки у вакуумній камері, вміщеній у змінне магнітне поле, під дією індукованого вихрового електричного поля розганяються майже до швидкості світла.
Таким чином, за Максвеллом співвідношення (1.17) слід трактувати не як вираз ЕРС індукції в дротяному витку, а як рівняння циркуляції вихрового електричного поля по вибраній у просторі замкненій лінії. Але в природі існує ще й кулонівське електричне поле \(\vec{E}_{K}\), створюване зарядами. Тому в загальному випадку електричне поле є суперпозицією полів обох видів, і його напруженість
\begin{equation} \vec{E}=\vec{E}_{K}+\vec{E}_{B}. \end{equation}
При цьому кулонівське поле \(\vec{E}_{K}\) є потенціальним і не дає вкладу в циркуляцію (див. розділ І, п. 5.1). Тож будь-яке електричне поле \(\vec{E}\) задовольняє рівняння
\begin{equation} \oint\limits_{L}\vec{E}\,\mathrm{d}\vec{l}=-\int\limits_{S}\frac{\partial\vec{B}}{\partial{t}}\,\mathrm{d}\vec{S}, \tag{1.17а} \end{equation}
яке є загальним виразом теореми про циркуляцію електричного поля.
Відносність механізмів ЕМІ. Істотна відміна розглянутих умов виникнення індукційного струму в дротяному контурі може навести на думку, що індукційні ефекти пов’язані з двома окремими фізичними явищами. Але насправді це не так, бо однозначно розділити їх неможливо. Це наочно ілюструє наступний позірний дослід. Нехай один спостерігач знаходиться на візку 1 біля нерухомого штабового магніту, другий — на візку 2 із закріпленим дротяним витком, а третій — ще на одному візку 3, як схематично показано на рис. 1.9.
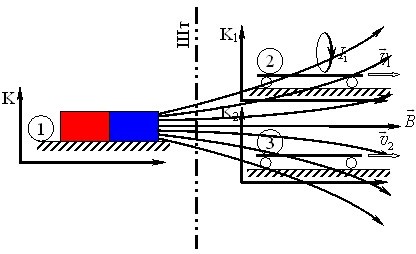
При цьому візки відділені від магніту шторкою Шт із тонованого скла, так що перший спостерігач бачить другого та третього, а вони його — ні. Іншими словами, спостерігачі знаходяться в трьох різних системах відліку \(\text{К}\), \(\text{К}_1\) і \(\text{К}_2\).
Уявімо, що кожен із спостерігачів може реєструвати струм у витку і вимірювати індукцію магнітного поля в місці свого розташування. Тоді, якщо візки 2 і 3 почнуть рухатись із різними швидкостями, всі троє спостерігачів зафіксують появу у витку індукційного струму. Проте вони розійдуться в поясненні причини його виникнення. Перший спостерігач пояснить це дією постійного магнітного поля на носії струму внаслідок руху витка. Другий буде спостерігати струм у нерухомому витку, і пов’яже його з вихровим електричним полем, оскільки виявить, що магнітне поле змінюється з часом. (Ця зміна зумовлена зменшенням величини В у напрямку руху візка з витком.) Третій спостерігач пояснить струм обома причинами, бо для нього й магнітне поле змінюється, й виток рухається. При цьому аргументи кожного спостерігача є неспростовними. Отже, відповідь на запитання, чому виникла ЕМІ і яка її частка зумовлена магнітним, а яка електричним полем, в кожному випадку залежить від умов спостереження, тобто від системи відліку. Це промовисто ілюструє тезу, висловлену ще у Вступі:
носієм електромагнітної взаємодії є єдине електромагнітне поле, поділ якого на електричне та магнітне поля є відносним, залежним від системи відліку.
Іншими словами, електричне та магнітне поля є не різними полями, а різними проявами одного поля, котрі в різній мірі виявляють себе в різних системах відліку. Відповідно, існують встановлені Лоренцом формули перетворень електричного та магнітного полів від однієї до іншої системи відліку, на яких не будемо тут зупинятись. Укажемо лише, що в окремих випадках можна знайти таку систему відліку, в якій існує тільки одне з полів (у розглянутому прикладі це система \(\text{К}_1\), де є лише магнітне поле), а в інших випадках, як, наприклад, для електромагнітних хвиль, таку систему знайти неможливо.
Контрольні запитання
1. У чому полягає відміна між термінами "магнітна індукція" та "електромагнітна індукція"?
2. Що є умовою виникнення в контурі ЕРС індукції та чим визначається її величина?
3. За якої умови в контурі, що рухається в магнітному полі, не буде індукуватись ЕРС? Наведіть приклади.
4. У чому полягає правило Ленца?
5. Поясніть, як визначається напрям індукційного струму в контурі через знак ЕРС індукції за формулою (1.1)?
6. Доведіть, що при будь-якій зміні магнітного потоку крізь дротяний виток унаслідок його руху, магнітне поле буде гальмувати цей рух.
7. Дротяна рамка може обертатися в магнітному полі навколо осі, що лежить у площині рамки і перпендикулярна до напрямку поля. Поясніть, чому рамку легше обертати, коли вона розімкнена.
8. Поясніть, як зміниться індуктивність котушки, щільно намотаної на циліндричне осердя, при її розтяганні в довжину.
9. Кругле дротяне кільце, приєднане через резистор до джерела струму, починають розтягати по діаметру в лінію. Як це вплине на величину струму в резисторі? Чому?
10. Паралельний ланцюжок складається з електричної лампочки та такої самої лампочки послідовно приєднаної до котушки з великою індуктивністю \(L\):
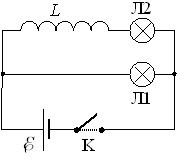
Опишіть та поясніть поведінку лампочок при замиканні та розмиканні ключа К.
11. Поясніть походження сторонніх сил, які є відповідальні за індукційний струм у рухомому та в нерухомому контурі.
2. Рівняння Максвелла
Явище електромагнітної індукції свідчить про те, що електричне поле породжується не лише зарядами, а й магнітними полями. Але Максвелл також установив, що й магнітне поле створюється не тільки рухомими зарядами (струмами), а й електричними полями. Відтак стало можливим відобразити загальні властивості електромагнітного поля в чотирьох рівняннях, які складають фундамент усієї класичної електродинаміки.
Далі розглядаються наступні питання:
2.2. Рівняння Максвелла в інтегральній формі
2.3. Диференціальні характеристики поля
2.1. Струм зміщення
До думки про здатність електричного поля створювати магнітне поле можна дійти, до прикладу, аналізуючи процес заряджання конденсатора. При підключенні конденсатора до джерела у просторі виникне магнітне поле, створене струмом заряджання. При цьому, якщо охопити якимось контуром \(L\) провідник, що підходить до обкладки конденсатора (рис. 2.1а), то, відповідно до теореми про циркуляцію магнітного поля ((3.9), розділ IV), можна записати:
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}, \tag{2.1} \end{equation}
де \(S_{1}\) — поверхня, що спирається на контур \(L\), \( \vec{j}\) — густина струму на цій поверхні.
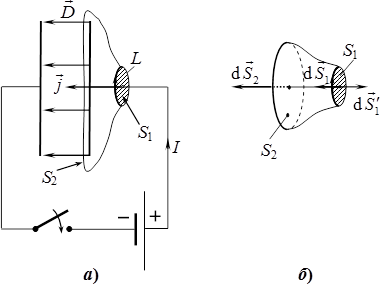
Інтеграл у правій частині (2.1) визначає сумарний струм, який охоплюється контуром \(L\), тож не залежить від розмірів та форми поверхні \(S_{1}\). Отже, можна взяти якусь іншу поверхню, скажімо у формі “глечика”, що охоплює одну обкладку конденсатора, як схематично показано на рис. 2.1. Ніякі струми цю поверхню не перетинають, і на ній скрізь \( \vec{j}=0 \). Тому рівняння (2.1) мало би виглядати як
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=0 . \tag{2.1а} \end{equation}
Але цього не може бути бо йдеться про циркуляцію того самого поля \( \vec{H}\) по тому самому контуру \(L\). Тож логічно припустити, що циркуляцію нестаціонарного магнітного поля, крім струму провідності, визначає ще якийсь фактор. Його вірогідну природу можна відшукати на основі закону збереження електричного заряду, який для нестаціонарних процесів виражається рівнянням неперервності (розділ III, п. 1.2):
\begin{equation} \oint\limits_{S}{\vec{j}\,\mathrm{d}\vec{S}}=-\int\limits_{V}{\frac{\partial \rho }{\partial t}\mathrm{d}V}, \tag{2.2} \end{equation}
яке засвідчує, що зміна величини заряду в об’ємі \(V\) за будь-який проміжок часу в точності дорівнює кількості заряду, що проходить за той самий час крізь замкнену поверхню \(S\), що обмежує цей об’єм.
Для вибраної замкненої поверхні (рис. 2.1а) підінтегральна функція \(\vec{j}\) в рівнянні (2.2) відмінна від 0 тільки на “кришці” \(S_{1}\) (рис. 2.1б), отже, його можна подати як
\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{\vec{S}}}{}_{1}^{\prime }}=-\int\limits_{V}{\frac{\partial \rho }{\partial t}\mathrm{d}V}. \tag{2.2а} \end{equation}
Урахуємо також, що при обчисленні потоку крізь замкнену поверхню вектори елементарних площинок спрямовують по зовнішніх нормалях, а при обчисленні циркуляції за рівнянням (2.1) узгоджують із напрямком обходу контуру \(L\) за правилом правого гвинта. В такому разі \( \mathrm{d}{{\vec{S}}'_{1}} = - \mathrm{d}{{\vec{S}}_{1}}\), і попередній вираз набуває вигляду:
\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}=\int\limits_{V}{\frac{\partial \rho }{\partial t}\,\mathrm{d}V}. \tag{2.2б} \end{equation}
Інтеграл в лівій частині визначає струм, який проходить через поверхню \(S_{1}\), тож
\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}=\frac{\text{d}q}{\text{d}t}, \end{equation}
де \(\mathrm{d}q\) — заряд, який заходить всередину “глечика” і осідає на пластині конденсатора за час \(\mathrm{d}t\), а похідна визначає швидкість зміни заряду пластини \(q\). Цей заряд створює електричне поле, в якому за теоремою Гаусса ((2.9а), розділ II) потік вектора \( \vec{D}\) крізь будь-яку замкнену поверхню
\begin{equation} \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}=q , \end{equation}
де \(q\) — вільний заряд всередині поверхні \(S\), який в нашому випадку зосереджений на пластині конденсатора. Тому поле є лише між пластинами, і потік \( \vec{D}\) створюється тільки через дно “глечика” \(S_{2}\), так що
\begin{equation} q=\int\limits_{{{S}_{2}}}{\vec{D}\,\mathrm{d}{{{\vec{S}}}_{2}}} . \end{equation}
Відповідно, швидкість зміни заряду
\begin{equation} \frac{\text{d}q}{\text{d}t}=\int\limits_{{{S}_{2}}}{\frac{\partial \vec{D}}{\partial t}\mathrm{d}{{{\vec{S}}}_{2}}} . \end{equation}
Порівнюючи цей вираз із (2.2б), доходимо висновку, що
\begin{equation} \int\limits_{{{S}_{1}}}{\vec{j}\,\mathrm{d}{{{\vec{S}}}_{1}}}=\int\limits_{{{S}_{2}}}{\frac{\partial \vec{D}}{\partial t}\mathrm{d}{{{\vec{S}}}_{2}}}. \tag{2.3} \end{equation}
Це й вирішує “парадокс” рівняння (2.1а): якщо його записати у вигляді
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{{{S}_{2}}}{\frac{\partial \vec{D}}{\partial t}\mathrm{d}{{{\vec{S}}}_{2}}}, \tag{2.4} \end{equation}
то результат обчислення циркуляції \( \vec{H}\) за виразами (2.1) і (2.4) буде однаковий, незалежно від вибору поверхні. При цьому в одному випадку поверхню перетинає тільки струм, а в іншому — тільки електричне поле. Тому вирази (2.1) і (2.4) можна об’єднати в одне загальне рівняння
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\left( \vec{j}+\frac{\partial \vec{D}}{\partial t} \right)\mathrm{d}\vec{S}}, \tag{2.5} \end{equation}
що є чинним при будь-якій формі поверхні \(S\), обмеженої контуром \(L\).
Треба сказати, що цей результат сам по собі має лише формальний зміст. Він отриманий тільки для окремого випадку — магнітного поля струму заряджання конденсатора — і пояснюється тим, що між струмом заряджання та електричним полем конденсатора є прямий зв’язок. По закінченню заряджання рівняння (2.5) втрачає зміст, бо струм припиняється (\( \vec{j}={0}\)), електричне поле у конденсаторі стає постійним (\( {\partial \vec{D}}/{\partial t}=0 \)), і магнітне поле зникає. Але Максвелл дійшов висновку, що рівняння (2.5) є чинним завжди, не втрачаючи змісту і при \( \vec{j}=0 \). Якщо так, то при \( ( {\partial \vec{D}}/{\partial t})\ne 0 \)
\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\frac{\partial \vec{D}}{\partial t}\,\mathrm{d}\vec{S}}\ne 0\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \vec{H}\ne 0. \end{aligned} \tag{2.5а}\end{equation}
Тим самим Максвелл постулював, що
магнітне поле створюється не лише струмами провідності (рухом заряджених частинок), а й змінними електричними полями.
Слід зауважити, що розглянуті міркування і викладки не доводять із необхідністю такий умовивід, а тільки вказують на його вірогідність. Але його істинність, як і інші фундаментальні відкриття Максвела, незаперечно підтверджується дослідом і всім розвитком класичної електродинаміки.
Похідна \( {\partial \vec{D}}/{\partial t}\), яка фігурує в рівняннях (2.5), (2.5а), як і густина струму провідності \(\vec{j}\), має розмірність [\(\text{А/м}^2\)] і по аналогії називається “густиною струму зміщення” позначається таким самим символом:
\begin{equation} {{\vec{j}}_{\text{зм}}}=\frac{\partial \vec{D}}{\partial t}. \tag{2.6} \end{equation}
Але цю термінологію і символіку не слід розуміти буквально, бо
струм зміщення є мірою швидкості зміни електричного поля
і в загальному випадку не пов’язаний із рухом зарядів-носіїв струму.
Уведення струму зміщення дозволяє зручно записувати і формулювати закон (2.5):
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\bigl( \vec{j}+{{{\vec{j}}}_{\text{зм}}} \bigr)\mathrm{d}\vec{S}}, \tag{2.7} \end{equation}
або
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{{{{\vec{j}}}_{\text{повн}}}\,\mathrm{d}\vec{S}}, \tag{2.7а} \end{equation}
де величина
\begin{equation} {{\vec{j}}_{\text{повн}}}=\vec{j}+{{\vec{j}}_{\text{зм}}}=\vec{j}+\frac{\partial \vec{D}}{\partial t} \tag{2.8} \end{equation}
називається густиною повного струму. Відповідно, рівняння (2.7а) інколи називають законом повного струму.
Поняття струму зміщення дозволяє також інакше подати співвідношення (2.2б), що випливає з рівняння неперервності (2.2):
\begin{equation} \begin{aligned} &\oint\limits_{S}{\vec{j}\,\mathrm{d}\vec{S}}=-\oint\limits_{S}{{{{\vec{j}}}_{\text{зм}}}\,\mathrm{d}\vec{S}}\quad \Rightarrow {}\\ &\quad {}\Rightarrow\quad \oint\limits_{S}{( \vec{j}+{{{\vec{j}}}_{\text{зм}}} )\mathrm{d}\vec{S}}=0\quad \Rightarrow {}\\ &\quad {}\Rightarrow\quad \oint\limits_{S}{{{{\vec{j}}}_{\text{повн}}}\mathrm{d}\vec{S}}=0. \end{aligned} \end{equation}
Це означає, що лінії повного струму є завжди неперервні — в точках розриву провідності кожна лінія струму провідності (лінія вектора \( \vec{j}\)), продовжується лінією струму зміщення (лінією вектора \( {\partial \vec{D}}/{\partial t}\)) і навпаки. (У розглянутому прикладі це відбувається на обкладках конденсатора.) Саме з цієї причини рівняння (2.6), розділ III, й називається рівнянням неперервності.
2.2. Рівняння Максвелла в інтегральній формі
Відкриття вихрового електричного поля та струму зміщення як джерела магнітного поля лягло в основу створеної Максвеллом класичної електродинаміки — теорії, що трактує макроскопічні електромагнітні явища при нерелятивістських (\(v \ll c\)) швидкостях руху зарядів.
Фундаментальні рівняння. Найбільш загальні властивості електромагнітного поля відображаються системою фундаментальних рівнянь електромагнітного поля, або рівнянь Максвелла. Вони є найбільш загальними виразами розглянутих у попередніх розділах теорем про циркуляції та потоки електричного і магнітного полів і мають вигляд:
\begin{equation} \begin{aligned} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}&=-\int\limits_{S}{\frac{\partial \vec{B}}{\partial t}\,\mathrm{d}\vec{S}}; \\ \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}&=\int\limits_{S}{\left( \vec{j}+\frac{\partial \vec{D}}{\partial t} \right)\mathrm{d}\vec{S}};\\ \oint\limits_{S}\vec{D}\,\mathrm{d}\vec{S}&=\int\limits_{V}{\rho \,\mathrm{d}V};\\ \oint\limits_{S}{\vec{B}\,\mathrm{d}\vec{S}}&=0. \end{aligned} \tag{2.9} \end{equation}
Зауважимо, що ця система не включає рівняння неперервності, яке виражає закон збереження електричного заряду. Але його неявно відображає неперервність ліній повного струму, про що говорилося вище.
У випадку стаціонарних полів, для яких \( ( {\partial \vec{D}}/{\partial t} )=( {\partial \vec{B}}/{\partial t} )=0 \), система (2.9) розпадається на дві пари незалежних рівнянь електростатики та магнітостатики, котрі визначають найголовніші властивості стаціонарних полів:
\begin{equation} \begin{aligned} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}&=0;\\ \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}&=\int\limits_{V}{\rho \,\mathrm{d}V}, \end{aligned} \end{equation}
і
\begin{equation} \begin{aligned} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}&=\int\limits_{S}{\vec{j}\,\mathrm{d}\vec{S}};\\ \oint\limits_{S}{\vec{B}\,\mathrm{d}\vec{S}}&=0. \end{aligned} \end{equation}
Перша пара відображає той факт, що статичні електричні поля створюються зарядженими частинками і є потенціальними, а друга — що статичні магнітні поля створюються тільки струмами провідності (рухом зарядів) і є непотенціальними (вихровими).
У випадку нестатичних (змінних у часі) полів із загальної системи фундаментальних рівнянь випливає, що джерелом якогось одного поля є не лише заряди або струми, а й інше поле. Тож нестаціонарні електричне і магнітне поля є органічно взаємопов’язані, й одне не може існувати без іншого. Змінне електричне поле породжує магнітне, котре в свою чергу породжує електричне, а воно — знов магнітне, і т.д. При цьому, як показав Максвелл, із рівнянь (2.9) випливає, що цей процес має хвильовий характер і поширюється у просторі зі швидкістю світла. Тим самим Максвелл теоретично відкрив існування електромагнітних хвиль та електромагнітну природу світла, що потім було підтверджено експериментально.
Матеріальні рівняння. Рівняння Максвелла виконуються за будь-яких умов, на те вони й фундаментальні. Але в математичному сенсі система рівнянь (2.9) є неповною. Вона містить два векторні рівняння для циркуляцій і два скалярні для потоків. При записі в проекціях це дає 8 рівнянь, тоді як навіть при заданих функціях \( \rho \) і \(\vec{j}\) для визначення чотирьох векторів полів треба мати 12 рівнянь.
Причина такої недостатньості фундаментальних рівнянь полягає в тому, що вони не містять електричних і магнітних характеристик середовища, котрі саме й визначають перебіг електромагнітних процесів у кожному конкретному випадку. Тому фундаментальні рівняння мають бути доповнені матеріальними рівняннями — співвідношеннями, що відображають зв’язки між різними електричними та магнітними характеристиками поля в речовині (“матеріалі”). Ці співвідношення істотно відрізняються для різних класів речовин, тому для кожного є свої матеріальні рівняння. Для ізотропних лінійних речовин, які є найбільш поширені і вживані на практиці, матеріальні рівняння мають знайомий з попередніх розділів вигляд:
\begin{equation} \begin{aligned} \vec{D}&={{\varepsilon }_{0}}\varepsilon \vec{E};\\ \vec{B}&={{\mu }_{0}}\mu \vec{H};\\ \vec{j}&=\sigma \vec{E}, \end{aligned} \end{equation}
де \(\varepsilon \), \(\mu \) — діелектрична та магнітна проникності, а \(\sigma\) — питома електропровідність речовини.
Фундаментальні рівняння разом із матеріальними співвідношеннями утворюють повну систему рівнянь електромагнітного поля в нерухомому середовищі, котра в кожному випадку принципово дозволяє дослідити будь-яке електромагнітне явище.
2.3 Диференціальні характеристики поля
Розглянуті інтегральні рівняння (2.9) встановлюють зв’язок між джерелами і характеристиками електромагнітного поля через потоки й циркуляції, тож відображують його властивості не в кожній точці (локально), а лише інтегрально — на заданій лінії або поверхні. Через це вони не дають принципової відповіді на деякі важливі запитання. До прикладу, нульова величина циркуляції напруженості заданого електричного поля по обраному контуру \(L\) не може бути доказом його потенціальності, бо не виключає існування в цьому полі інших контурів, для котрих
\begin{equation} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}\ne 0. \end{equation}
Так само, коли сума струмів, які охоплює даний замкнений контур \(L\), дорівнює нулю, то за відсутності змінного електричного поля з другого рівняння (2.9) випливає, що
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=0. \end{equation}
Та це зовсім не означає, що магнітне поле є потенціальним.
Але такі питання, у принципі, не виникають при використанні рівнянь Максвелла в диференціальній формі, котрі встановлюють зв’язок між джерелами та характеристиками поля локально, тобто в кожній точці. Ці рівняння оперують величинами, що визначають не саме поле, а його поведінку в кожній точці. Їхній зміст , розглянуто в питаннях:
2.3.1. Дивергенція поля
Ця величина принципово вирішує задачу визначення розподілу зарядів і струмів за заданими характеристиками створюваного ними поля, що є важливим і в теорії, і на практиці. Як це робиться, розглянемо на прикладі електричного поля.
Третє рівняння Максвелла (2.9) дозволяє знайти сумарний електричний заряд у будь-якій області простору за відомим електричним зміщенням \( \vec{D}( {\vec{r}} ) \). Але так, у принципі, можна визначити не лише величину заряду в заданій області, а й його просторовий розподіл. Для цього будемо діяти за наступною логічною схемою.
Розчленуємо подумки все поле на маленькі комірки і підрахуємо потік вектора \( \vec{D}\) крізь кожну. Тоді там, де він дорівнює нулю, заряду немає, а в комірках із ненульовим потоком заряд є, причому його величина дорівнює величині потоку. Тому, зменшуючи розміри комірок, у такий спосіб можна врешті решт отримати достатньо точну інформацію про заряд, зосереджений у кожній точці поля.
Запропонована позірна схема може здатися практично нездійсненою через гранично велику необхідну кількість указаних комірок. Але насправді вона досить просто реалізується методами вищої математики.
Визначимо потік вектора \( \vec{D}\) крізь якусь одну комірку у формі невеликого паралелепіпеда з ребрами \( \Delta{x}\), \( \Delta{y}\), \( \Delta{z}\) , паралельними до осей координат, як показано на рис. 2.2.
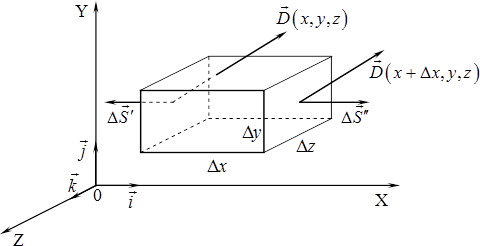
Для цього подамо його як суму потоків крізь пари паралельних граней:
\begin{equation} \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}={{\Phi }_{1}}+{{\Phi }_{2}}+{{\Phi }_{3}}. \end{equation}
При малих розмірах комірок величину \( \vec{D}\) в усіх точках заданої грані можна наближено вважати однаковою. Тоді потік крізь одну грань
\begin{equation} \Delta \Phi \approx \vec{D}\,\Delta \vec{S}, \end{equation}
де \(\Delta S\) — площа грані.
Відповідно, для потоку крізь пару граней з координатами \(x\) і \( {x}+\Delta{x}\) матимемо:
\begin{equation} {{\Phi }_{1}}\approx \vec{D}( x,y,z )\Delta {{\vec{S}}'_{1}}+\vec{D}( x+\Delta x,y,z )\Delta {{\vec{S}}''_{1}}. \end{equation}
Вектори площинок
\begin{equation} \Delta {\vec{S}}{}_{1}^{\prime }=-\vec{i}\,\Delta y\,\Delta z\qquad \text{i}\qquad \Delta {\vec{S}}{}_{1}^{\prime \prime }=\vec{i}\,\Delta y\,\Delta z, \end{equation}
отож,
\begin{equation} \begin{aligned} &{{\Phi }_{1}}\approx \bigl( -{{D}_{x}}( x,y,z )+{{D}_{x}}( x+\Delta x,y,z ) \bigr)\Delta y\,\Delta z={}\\ &\quad{}= \Delta {{D}_{x}}\,\Delta y\,\Delta z. \end{aligned} \end{equation}
Величина \( \Delta {{D}_{x}}\) визначається відомим з математики виразом
\begin{equation} \Delta {{D}_{x}}\approx \frac{\partial {{D}_{x}}}{\partial x}\Delta{x}. \end{equation}
Примітка. Частинна похідна стоїть тому, що зміна вектора зміщення зумовлена зміною тільки координати \(x\).
Відтак для потоку крізь дану пару граней маємо
\begin{equation} \begin{aligned} &{{\Phi }_{1}}\approx \frac{\partial {{D}_{x}}}{\partial x}\Delta x\,\Delta y\,\Delta z\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {{\Phi }_{1}}\approx \frac{\partial {{D}_{x}}}{\partial x}\Delta V, \end{aligned} \end{equation}
де \( \Delta{V}\) — об’єм комірки.
Очевидно, що аналогічно виражаються потоки і крізь дві інші пари граней:
\begin{equation} {{\Phi }_{2}}\approx \frac{\partial {{D}_{y}}}{\partial y}\Delta V,\qquad {{\Phi }_{3}}\approx \frac{\partial {{D}_{z}}}{\partial z}\Delta V. \end{equation}
Отже, потік крізь усю поверхню комірки наближено виражається формулою:
\begin{equation} \begin{aligned} &\oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}\approx{}\\ &\quad{}\approx \left( \frac{\partial {{D}_{x}}}{\partial x}+\frac{\partial {{D}_{y}}}{\partial y}+\frac{\partial {{D}_{z}}}{\partial z} \right)\Delta V. \end{aligned} \tag{2.11}\end{equation}
Вираз у дужках часто стрічається у різних задачах математики та фізики. Тому він має спеціальну назву “дивергенція” поля і позначення “div”. Отже,
\begin{equation} \operatorname{div}\vec{D}=\left( \frac{\partial {{D}_{x}}}{\partial x}+\frac{\partial {{D}_{y}}}{\partial y}+\frac{\partial {{D}_{z}}}{\partial z} \right) . \tag{2.12} \end{equation}
Зауважимо, що залежно від симетрії поля можуть виявитися зручнішими сферичні або циліндричні координати, в яких формули дивергенції при збереженні загальної структури відрізняються від виразу (2.12). Тому він є не означенням, а тільки формулою для обчислення дивергенції в декартових координатах. А інваріантне означення, що висвітлює фізичний зміст дивергенції, випливає з виразу (2.11) при переході до границі \( \Delta V\to{0}\) шляхом стягання комірки в точку:
\begin{equation} \begin{aligned} &\oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}\approx \operatorname{div}\vec{D}\cdot \Delta V\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \operatorname{div}\vec{D}=\lim\limits_{\Delta{V}\to{0}}\frac{\oint\limits{\vec{D}\,\mathrm{d}\vec{S}}}{\Delta{V}}. \end{aligned} \tag{2.13}\end{equation}
Таким чином,
дивергенцією векторного поля в заданій точці називається границя відношення потоку поля крізь замкнену поверхню до обмеженого нею об’єму при стяганні поверхні в задану точку.
Ураховуючи формулу (2.12) і теорему Гаусса для вектора \(\vec{D}\) (розділ II, (4.9а)), вираз (2.11) можна подати, як
\begin{equation} \operatorname{div}\vec{D}\cdot \Delta V\approx q=\langle \rho \rangle \Delta V, \end{equation}
де \( \langle \rho \rangle \) — середня густина заряду в об’ємі \( \Delta{V}\). Очевидно, що при \( \Delta{V}\to{0}\) ця рівність стане точною. Таким чином, у кожній точці поля
\begin{equation} \operatorname{div}\vec{D}=\rho . \tag{2.14} \end{equation}
Позаяк цей результат випливає з інтегральної теореми Гаусса, рівняння (2.14) називається теоремою Гаусса в диференціальній формі. Воно встановлює локальний (у кожній точці) зв’язок між полем і його джерелами, й вирішує проблему визначення розподілу заряду \( \rho ( x,y,z ) \), яким створюється задане поле. Для цього достатньо провести в (2.14) необхідне диференціювання заданої функції \( \vec{D}( x,y,z ) \).
Якщо в рівнянні ((4.9), розділ II) зробити заміну (2.14), то отримаємо вираз математичної теореми Остроградського — Гаусса
\begin{equation} \oint\limits_{S}{\vec{D}\,\mathrm{d}\vec{S}}=\int\limits_{V}{\operatorname{div}\vec{D}\cdot \mathrm{d}V} . \tag{2.15} \end{equation}
А саме,
потік векторного поля крізь довільну замкнену поверхню дорівнює інтегралу від дивергенції цього поля по об’єму обмеженому даною поверхнею.
Формула (2.15) є чинною для будь-якого векторного поля, зокрема, для магнітного. Тож
\begin{equation} \oint\limits_{S}{\vec{B}\,\mathrm{d}\vec{S}}=\int\limits_{V}{\operatorname{div}\vec{B}\cdot \mathrm{d}V}. \end{equation}
Але, згідно з інтегральною теоремою Гаусса (10.1), ліва частина записаного рівняння дорівнює нулю при будь-яких розмірах і формі замкненої поверхні \(S\). Тож і права частина дорівнює нулю при будь-якій величині \(V\), а це можливо тільки за умови, що
в будь-якій точці магнітного поля дивергенція вектора \(\vec{B}\) дорівнює нулю:
\begin{equation} \operatorname{div}\vec{B}=0. \tag{2.16} \end{equation}
Це твердження виражає теорему Гаусса для магнітного поля в диференціальній (локальній) формі.
2.3.2. Ротор поля
Теорему про циркуляцію векторного поля теж можна виразити в диференціальній формі. Покажемо це на прикладі магнітного поля струмів провідності.
Нехай магнітне поле \( \vec{H}( x,y,z ) \) створюється заданим розподілом струмів провідності \(\vec{J}( x,y,z )\).
Примітка. Позначення густини струму збігається з позначенням одного з ортів декартової системи координат. Тому, аби запобігти плутанині, далі до кінця п. 2.3 густина струму позначається як \(\vec{J}\).
Виберемо невеликий прямокутний контур із сторонами \( \Delta{x}\) і \( \Delta{y}\), розташований у площині \(\mathrm{XOY}\), як показано на рис. 2.3,
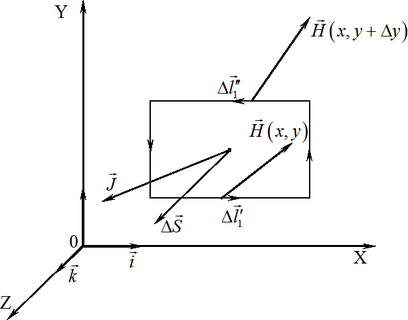
і запишемо для нього наближений вираз теореми про циркуляцію вектора \( \vec{H}\), взявши до уваги, що орт нормалі \( \vec{n}\) збігається з ортом \( \vec{k}\) координатної системи:
\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}\approx \vec{J}\,\Delta \vec{S}={{J}_{n}}\,\Delta S={}\\ &\quad{}= {{J}_{z}}\,\Delta x\,\Delta y. \end{aligned} \tag{2.17}\end{equation}
Циркуляція по вказаному контуру складається із внесків від усіх сторін прямокутника. Ці внески не важко визначити. Розглянемо для прикладу внесок \(C_{1}\) від горизонтальних сторін, обходячи контур проти годинникової стрілки (у додатному напрямі відносно вектора \(\vec{J}\)). При малих розмірах прямокутника можна нехтувати зміною поля на переміщенні вздовж кожної із сторін і наближено записати:
\begin{equation} \begin{aligned} &{{C}_{1}}\approx \vec{H}( x,y )\Delta {{\vec{l}}}{}_{1}^{\prime }+\vec{H}( x,y+\Delta y )\Delta {{\vec{l}}}{}_{1}^{\prime \prime }={}\\ &\quad{}=\bigl( \vec{H}( x,y )\vec{i}-\vec{H}( x,y+\Delta y )\vec{i} \bigr)\Delta x={}\\ &\quad{}=-{{( \Delta {{H}_{x}} )}_{y}}\Delta x. \end{aligned} \end{equation}
Тут ураховано, що \(\Delta {{\vec{{l}}}}{}_{1}^{\prime }=\vec{i}\Delta x\), \(\Delta {{{l}}}{}_{1}^{\prime \prime }=-\vec{i}\Delta x\) і, що скалярний добуток вектора на орт є проекцією цього вектора на відповідну вісь. У такому разі величина \( {{( \Delta {{H}_{x}} )}_{y}}\) є частинним приростом величини \( {{H}_{x}}\) при зміні координати \(y\) при переході до верхньої сторони контуру. За правилами диференціального числення
\begin{equation} {{( \Delta {{H}_{x}} )}_{y}}\approx \frac{\partial {{H}_{x}}}{\partial y}\Delta y , \end{equation}
отже, розглянутий внесок у циркуляцію складає
\begin{equation} {{C}_{1}}\approx -\frac{\partial {{H}_{x}}}{\partial y}\Delta x\,\Delta y. \end{equation}
Аналогічно можна показати, що вклад від іншої пари сторін
\begin{equation} \begin{aligned} &{{C}_{2}}\approx \bigl( \vec{H}( x+\Delta x,y )\vec{j}-\vec{H}( x,y )\vec{j} \bigr)\Delta y={}\\ &\quad{}= {{( \Delta {{H}_{y}} )}_{x}}\Delta y\approx \frac{\partial {{H}_{y}}}{\partial x}\Delta x\,\Delta y . \end{aligned} \end{equation}
Відповідно, циркуляція по всьому контуру \(C = C_{1} + C_{2}\) дорівнює
\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}\approx {}\\ &\quad{}\approx\left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\Delta y\,\Delta x={}\\ &\quad{}=\left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\Delta S . \end{aligned} \tag{2.17а} \end{equation}
Порівнюючи цей вираз із (2.17), бачимо, що
\begin{equation} \left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\Delta S\approx {{J}_{z}}\,\Delta S. \end{equation}
Отримана рівність є наближеною, тому що в ній не врахована зміна проекцій поля \(H_{x}\) і \(H_{y}\) при переміщенні вздовж сторін прямокутника в процесі інтегрування, а також не визначене точне положення точки, в якій береться величина \(\vec{J}\). Але в границі \( \Delta S\to 0 \) при стяганні прямокутника в задану точку рівність стає точною:
\begin{equation} \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y}={{J}_{z}}. \end{equation}
Вибравши в околі тієї ж точки ще два контури, паралельні іншим координатним площинам, аналогічно отримаємо:
\begin{equation} \frac{\partial {{H}_{z}}}{\partial y}-\frac{\partial {{H}_{y}}}{\partial z}={{J}_{x}}, \end{equation} \begin{equation} \frac{\partial {{H}_{x}}}{\partial z}-\frac{\partial {{H}_{z}}}{\partial x}={{J}_{y}}. \end{equation}
Вектор \(\vec{J}\) через проекції та орти зображується, як
\begin{equation} \vec{J}={{J}_{x}}\cdot \vec{i}+{{J}_{y}}\cdot \vec{j}+{{J}_{z}}\cdot \vec{k}. \end{equation}
Тож маємо наступний вираз, який визначає вектор густини струму \(\vec{J}\) в будь-якій точці заданого поля \( \vec{H}( x,y,z ) \):
\begin{equation} \begin{aligned} &\vec{J}=\left( \frac{\partial {{H}_{z}}}{\partial y}-\frac{\partial {{H}_{y}}}{\partial z} \right)\vec{i}+{}\\ &\quad{}+\left( \frac{\partial {{H}_{x}}}{\partial z}-\frac{\partial {{H}_{z}}}{\partial x} \right)\vec{j}+{}\\ &\quad{}+ \left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\vec{k}. \end{aligned} \end{equation}
Подібний громіздкий набір операцій доводиться виконувати в багатьох задачах математики і фізики. Тому права частина даного виразу має спеціальне позначення “\(\operatorname{rot}\)” і назву “ротор” поля. Отже,
\begin{equation} \begin{aligned} &\operatorname{rot}\vec{H}=\left( \frac{\partial {{H}_{z}}}{\partial y}-\frac{\partial {{H}_{y}}}{\partial z} \right)\vec{i}+{}\\ &\quad{}+\left( \frac{\partial {{H}_{x}}}{\partial z}-\frac{\partial {{H}_{z}}}{\partial x} \right)\vec{j}+{}\\ &\quad{}+\left( \frac{\partial {{H}_{y}}}{\partial x}-\frac{\partial {{H}_{x}}}{\partial y} \right)\vec{k}. \end{aligned} \tag{2.18} \end{equation}
Відтак зв’язок між векторами \( \vec{H}\) і \(\vec{J}\) згорнуто записується у вигляді:
\begin{equation} \operatorname{rot}\vec{H}=\vec{J}. \tag{2.19} \end{equation}
За цим рівнянням для визначення розподілу струмів \(\vec{J}( x,y,z )\), які створюють задане магнітне поле, треба лише виконати необхідні диференціювання заданої функції \( \vec{H}( x,y,z ) \). За допомогою рівняння (2.19), у принципі, можна визначити й поле, створене заданим розподілом струмів. Але така математична задача є досить складною і має точні розв’язки тільки в найпростіших випадках.
Зауважимо, що рівняння (2.19) є чинним і в інших системах координат, але формула ротора в кожній з них має свій вигляд. Тому вираз (2.18) є не означенням, а тільки формулою для обчислення ротора в декартових координатах. Аби дати незалежне від координатної системи означення ротора, звернемо увагу на те, що в наведених викладках орти \( ( \vec{i}, \vec{j}, \vec{k} ) \) є й одиничними векторами нормалей \( \vec{n}\) до поверхонь розглянутих контурів. Тож у (2.18) множники при ортах є проекціями вектора \(\operatorname{rot}\vec{H}\) на нормалі до елементарних контурів розміщених у координатних площинах. Враховуючи це, вираз (2.17а) можна переписати, як
\begin{equation} \begin{aligned} &\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}\approx {{\operatorname{rot}}_{n}}\vec{H}\cdot \Delta S\quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {{\operatorname{rot}}_{n}}\vec{H}\approx \frac{\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}}{\Delta S}. \end{aligned} \end{equation}
Стягаючи контур у задану точку, отримаємо точний вираз:
\begin{equation} {{\operatorname{rot}}_{n}}\vec{H}=\underset{\Delta{S}\to{0}}\lim\limits \frac{\oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}}{\Delta S}, \end{equation}
який по суті є означенням поняття “ротор векторного поля”.
Якщо магнітне поле створюється не лише струмами провідності, а й змінним електричним полем, у рівняння (2.19) додасться ще й густина струму зміщення (2.6):
\begin{equation} \operatorname{rot}\vec{H}=\vec{j}+\frac{\partial \vec{D}}{\partial t}. \tag{2.20} \end{equation}
Це рівняння випливає з інтегральної теореми про циркуляцію магнітного поля і є загальним виразом цієї теореми в диференціальній (локальній) формі.
Підставивши вираз (2.20) у рівняння (2.9), отримаємо математичну теорему Стокса
\begin{equation} \oint\limits_{L}{\vec{H}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\operatorname{rot}\vec{H}\cdot \,\mathrm{d}\vec{S}}, \tag{2.21} \end{equation}
згідно з якою
циркуляція векторного поля по довільному замкненому контуру дорівнює потокові ротора цього поля крізь довільну поверхню обмежену цим контуром.
Теорема Стокса є чинною для будь-якого векторного поля, тож і для електричного:
\begin{equation} \oint\limits_{L}{\vec{E}\,\mathrm{d}\vec{l}}=\int\limits_{S}{\operatorname{rot}\vec{E}\cdot \mathrm{d}\vec{S}}. \end{equation}
Порівнюючи цей вираз із (12.17а), отримуємо рівняння
\begin{equation} \operatorname{rot}\vec{E}=-\frac{\partial \vec{B}}{\partial t}, \tag{2.22} \end{equation}
яке виражає теорему про циркуляцію електричного поля в диференціальній (локальній) формі.
У випадку, коли електричне поле створюється тільки зарядами і є потенціальним, циркуляція вектора по будь-якому контуру дорівнює нулю (розділ І, п. 5.1). Тому, згідно з формулою Стокса, в усіх точках
\begin{equation} \operatorname{rot}\vec{E}=0 . \tag{2.23} \end{equation}
Цей вираз є диференціальним (локальним) критерієм потенціальності поля. Відповідно до нього потенціальні поля є безвихровими.
Локальний критерій (2.23) є дуже зручним: за ним потенціальність заданого поля \( \vec{E}( x,y,z ) \) однозначно встановлюється за допомогою не складної операції диференціювання.
2.4. Рівняння Максвелла в локальній формі
Розглянуті результати дозволяють описати фундаментальні властивості електромагнітного поля не лише інтегральними рівняннями Максвелла (2.9), а й відповідною системою диференціальних рівнянь, які відображають локальні (в кожній точці) властивості поля. Далі розглядаються:
Диференціальні рівняння Максвелла
Операторна форма рівнянь Максвелла
Диференціальні рівняння Максвелла. З використанням понять “дивергенція” і “ротор” основні рівняння електромагнітного поля мають вигляд:
\begin{equation} \begin{aligned} \operatorname{rot}\vec{E}&=-\frac{\partial \vec{B}}{\partial t};\\ \operatorname{rot}\vec{H}&=\vec{j}+\frac{\partial \vec{D}}{\partial t};\\ \operatorname{div}\vec{D}&=\rho ;\\ \operatorname{div}\vec{B}&=0. \end{aligned} \end{equation}
Відповідно, рівняння електростатики та магнітостатики (коли поля не залежать від часу) в диференціальній формі мають вигляд:
\begin{eqnarray} \operatorname{rot}\vec{E}=0, &\qquad \operatorname{rot}\vec{H}=\vec{j},\\ \operatorname{div}\vec{D}=\rho , &\qquad \operatorname{div}\vec{B}=0. \end{eqnarray}
Оператор \( \vec{\nabla }\). Дивергенція і ротор векторів \( \vec{E}\) і \(\vec{H}\), а також розглянутий раніше (розділ І, п. 3) градієнт потенціалу \( \varphi \), характеризують у кожній точці не саме поле, а його поведінку при переміщенні в прилеглі точки. Тому для визначення цих величин, над заданою функцією (\( \varphi \), \(\vec{E}\), \(\vec{H}\), або ін.) треба виконати відповідний набір математичних дій або “операцій” ((3.4), розділ І), (2.12), або (2.18). Самі по собі вони не є складним, але при необхідності виконання комбінованих операцій, на кшталт \( \operatorname{div}( \operatorname{rot}\vec{B} ) \) чи \( \operatorname{rot}( \operatorname{rot}\vec{E} )\), прямі викладки є трудомісткими. Проте існує дуже ефективний уніфікований непрямий спосіб обчислень за допомогою векторного диференціального оператора набла \( \vec{\nabla }\), інакше — оператора Гамільтона.
На загал, термін “оператор” має різні сенси. Тут це символ, яким позначають дію (“операцію”) чи набір дій, які належить виконати над однією функцією, аби перетворити її на деяку іншу функцію. Оператори дозволяють не лише лаконічно записувати громіздкі математичні вирази, як приміром (2.12) чи (2.18), а й значно скорочують і полегшують математичні перетворення. Це можна проілюструвати на прикладі обчислення градієнта та дивергенції. Для обчислення градієнта потенціалу електричного поля за формулою (розділ І, (3.4)) треба:
— взяти похідні по координатах від заданої функції \( \varphi ( x,y,z ) \);
— помножити їх на орти \( ( \vec{i},\vec{j},\vec{k} ) \);
— додати утворені складові вектори.
Ця стандартна послідовність математичних операції являє собою оператор градієнта і позначається символом \( \operatorname{grad}\). Аналогічно можна деталізувати й сукупність операції, які складають оператор дивергенції і шифруються символом \( \operatorname{div}\). До прикладу, для визначення дивергенції вектора \( \vec{D}\) електричного поля треба за формулою (3.12) виконати наступну послідовність операцій:
— взяти похідні по координатах від відповідних проекцій заданої функції \( \vec{D}( x,y,z ) \);
— додати їх.
Але, як виявляється, необхідні для визначення обох цих величин дії можна виконувати за допомогою одного оператора, який позначається символом \( \vec{\nabla}\). Це можна побачити, якщо у виразах градієнта та дивергенції дещо інакше записати частинні похідні по координатах, увівши “оператори диференціювання” \( {\partial }/{\partial x}\), \({\partial }/{\partial y}\), \({\partial }/{\partial z}\):
\begin{equation} \operatorname{grad}\varphi =\vec{i}\frac{\partial }{\partial x}\varphi +\vec{j}\frac{\partial }{\partial y}\varphi +\vec{k}\frac{\partial }{\partial z}\varphi \end{equation}
і
\begin{equation} \operatorname{div}\vec{D}=\frac{\partial }{\partial x}{{D}_{x}}+\frac{\partial }{\partial y}{{D}_{y}}+\frac{\partial }{\partial z}{{D}_{z}}. \end{equation}
При цьому перша формула виглядає, як вираз деякого вектора \( \vec{G}\), що є добутком вектора \( \vec{A}\) на скаляр \( {B}\):
\begin{equation} \vec{G}=\vec{A}\cdot B=( \vec{i}{{A}_{x}} )B+( \vec{j}{{A}_{y}} )B+( \vec{k}{{A}_{z}} )B. \end{equation}
Відповідно, формула для дивергенції нагадує скалярний добуток \(S\) якихось векторів \( \vec{A}\) і \( \vec{C}\):
\begin{equation} {S}=\vec{A}\cdot \vec{C}={{A}_{x}}{{C}_{x}}+{{A}_{y}}{{C}_{y}}+{{A}_{z}}{{C}_{z}}. \end{equation}
Це дозволяє увести оператор \( \vec{\nabla }\) у вигляді символічного вектора
\begin{equation} \vec{\nabla }=\vec{i}\frac{\partial }{\partial x}+\vec{j}\frac{\partial }{\partial y}+\vec{k}\frac{\partial }{\partial z}, \tag{2.25} \end{equation}
і розглядати градієнт як результат символічного множення (тобто дії) “вектора” \( \vec{\nabla }\) на скалярну функцію координат \( \varphi \):
\begin{equation} \operatorname{grad}\varphi \equiv \vec{\nabla }\varphi . \tag{2.26} \end{equation}
Аналогічно, дивергенцію можна трактувати як скалярний добуток векторів \( \vec{\nabla }\) і \( \vec{D}\):
\begin{equation} \operatorname{div}\vec{D}\equiv \vec{\nabla }\cdot \vec{D}. \tag{2.27} \end{equation}
Можна показати, що й ротор (2.18) можна трактувати як символічний векторний добуток:
\begin{equation} \operatorname{rot}\vec{H}\equiv [ \vec{\nabla }\,\vec{H} ]. \tag{2.28} \end{equation}
У цьому легко переконатись, якщо розкрити вираз (2.28) за допомогою визначника:
\begin{equation} [ \vec{\nabla }\vec{H} ]=\left| \begin{matrix} \vec{i} &\vec{j} &\vec{k} \\ ( {\partial }/{\partial x} ) &( {\partial }/{\partial y} ) & ( {\partial }/{\partial z} ) \\ {{H}_{x}} & {{H}_{y}} & {{H}_{z}} \end{matrix} \right|, \end{equation}
як це робиться у векторній алгебрі.
Таким чином, всі основні диференціальні операції теорії поля можна зображувати і виконувати за допомогою одного диференціального векторного оператора \( \vec{\nabla }\), властивості котрого одночасно задовольняють і основні правила диференціювання, і аксіоми векторної алгебри. Тому використання оператора \( \vec{\nabla}\) є дуже продуктивним, позаяк значно спрощує проведення громіздких диференціальних перетворень скалярних і векторних функцій координат, якими зокрема є характеристики електромагнітного поля.
Операторна форма рівнянь Максвелла. На завершення зведемо в одну систему фундаментальні рівняння електромагнітного поля (рівняння Максвелла), виражені в операторній формі через оператор \( \vec \nabla \):
\begin{equation} \begin{aligned} &[ {\vec \nabla \vec E} ] = - \frac{{\partial \vec B}}{{\partial t}}, \\ &[ {\vec \nabla \vec H} ] = \vec j + \frac{{\partial \vec D}}{{\partial t}}, \\ &\vec \nabla \cdot \vec D = \rho , \\ &\vec \nabla \cdot \vec B = 0. \end{aligned} \tag{2.29} \end{equation}
У такому вигляді вони найбільш зручні для проведення різноманітних викладок. Для ілюстрації наведемо два приклади.
Приклад 1. Рівняння Пуассона. Електричні поля зарядів (кулонівські поля) є потенціальними, тому вектор напруженості \( \vec E \) можна визначати не тільки через заряди, а й через скалярну величину — потенціал \( \varphi \). Тому так само, як у випадку напруженості, важливо знати зв’язок між розподілом заряду та потенціалом поля в кожній точці. З інтегральних рівнянь Максвелла (2.9) цей зв’язок безпосередньо не випливає. Але, враховуючи, що
\begin{equation} \vec E = - \operatorname{grad} \varphi \equiv - \vec \nabla \varphi , \end{equation}
його не складно отримати з диференціальних рівнянь (2.24) чи (2.29), принаймні, для ізотропних однорідних середовищ, в яких
\begin{equation} \vec D = {\varepsilon _0}\varepsilon \vec E. \end{equation}
Справді, зробивши наведені підстановки в треті рівняння (2.24), або (2.29), отримаємо: \( \operatorname{div} \vec D = \rho \),
\begin{equation} \operatorname{div} ( {\operatorname{grad} \varphi } ) = - \frac{\rho }{{{\varepsilon _1}\varepsilon }}, \end{equation}
або
\begin{equation} \vec \nabla ( {\vec \nabla \varphi } ) = - \frac{\rho }{{{\varepsilon _0}\varepsilon }}. \end{equation}
Ліву частину цього рівняння легко перетворити, згадавши, що до оператора \( \vec \nabla \) можна застосовувати правило скалярного множення векторів і записати:
\begin{equation} \vec \nabla ( {\vec \nabla \varphi } ) = \nabla _x^2\varphi + \nabla _y^2\varphi + \nabla _z^2\varphi , \end{equation}
де за правилами операторного множення
\begin{equation} \begin{aligned} \nabla_x^2\varphi&=\frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}\varphi\right)=\frac{\partial ^2}{\partial x^2}\varphi ,\\ \nabla_y^2\varphi&=\frac{\partial^2}{\partial y^2}\varphi ,\\ \nabla_z^2\varphi&=\frac{\partial^2}{\partial z^2}\varphi . \end{aligned} \end{equation}
Отже,
\begin{equation} \frac{\partial^2\varphi}{\partial x^2}+\frac{\partial^2\varphi}{\partial y^2}+\frac{\partial^2\varphi}{\partial z^2}=-\frac{\rho}{\varepsilon_0}\varepsilon . \tag{2.30} \end{equation}
Це рівняння називається рівнянням Пуассона, і відіграє важливу роль в теорії електричного поля.
Рівняння Пуассона можна записати в операторній формі через оператор \( {\nabla ^2} \) (набла квадрат) або, як його ще називають, оператор Лапласа і позначають також символом \( \Delta \) (дельта):
\begin{equation} {\nabla ^2} \equiv \Delta = \frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}}. \end{equation}
Множення (тобто дія) цього оператора на функцію полягає у взятті та додаванні її других частинних похідних по координатах. Відтак рівняння Лапласа в операторній формі згорнуто записується, як
\begin{equation} \nabla^2 \varphi=-\frac{\rho}{\varepsilon_0\varepsilon}, \quad \text{або} \quad \delta \varphi=-\frac{\rho}{\varepsilon_0\varepsilon}. \tag{2.30а} \end{equation}
Приклад 2. Рівняння неперервності. Це рівняння встановлює зв’язок між густиною струму на замкненій поверхні та зарядом носіїв всередині неї і є узагальненим виразом закону збереження електричного заряду. В інтегральній формі воно має вигляд ((1.6), розділ III):
\begin{equation} \oint\limits_S {\vec j\,\mathrm{d} \vec S} = - \int\limits_V {\frac{{\partial \rho }}{{\partial t}}\mathrm{d} V} . \end{equation}
Рівняння неперервності в диференціальній формі визначає указаний зв’язок локально (в кожній точці) і дає детальну інформацію про структуру ліній струму. Таку форму рівняння неперервності можна отримати із наведеного інтегрального рівняння за допомогою формули Остроградського — Гаусса (2.15), відповідно до якої
\begin{equation} \oint\limits_S {\vec j\,\mathrm{d} \vec S} = \int\limits_V {\operatorname{div} \vec j \cdot \mathrm{d} V} . \end{equation}
Отже,
\begin{equation} \int\limits_V {\operatorname{div} \vec j \cdot \mathrm{d} V} = - \int\limits_V {\frac{{\partial \rho }}{{\partial t}}\mathrm{d} V} . \end{equation}
Позаяк вихідні рівняння є чинними для довільної замкненої поверхні \(S\), записана рівність виконується при будь-якому значенні об’єму \(V\), що можливо лише коли в обох інтегралах значення підінтегральних функцій збігаються у кожній точці. Отже,
\begin{equation} \operatorname{div} \vec j = - \frac{{\partial \rho }}{{\partial t}}. \tag{2.31} \end{equation}
Це і є рівняння неперервності в диференціальній формі. З нього випливає, що в тих точках, де \( ({\partial \rho }/{\partial t} ) < 0 \), \( \operatorname{div} \vec j > 0 \), і навпаки. Згідно з (2.13) і домовленістю про напрям електричного струму, це означає, що лінії струму виходять із точок, з яких витікає додатній заряд, і закінчуються в точках, до яких він стікається. Тому в математиці точки, де дивергенція додатня, називаються витоками, а точки з від’ємною дивергенцією — стоками поля.
Рівняння (2.31) можна отримати і безпосередньо з рівнянь Максвелла в диференціальній формі. Для цього достатньо взяти дивергенцію від лівої та правої частини другого рівняння системи (2.24):
\begin{equation} \operatorname{div}\operatorname{rot} \vec H = \operatorname{div} \vec j + \operatorname{div} \frac{{\partial \vec D}}{{\partial t}}. \end{equation}
Безпосереднє розкриття лівої частини потребує громіздких перетворень, але за допомогою оператора \( \vec \nabla \) це робиться досить легко. А саме,
\begin{equation} \operatorname{div}\, \operatorname{rot} \vec H = \vec \nabla [ {\vec \nabla \vec H} ]. \end{equation}
У лівій частині маємо символічний мішаний добуток векторів, який за законами векторної алгебри є інваріантним відносно циклічної перестановки множників. Тож можна записати:
\begin{equation} \vec \nabla [ {\vec \nabla \vec H} ] = [ {\vec \nabla ,\vec \nabla } ]\vec H \equiv 0. \end{equation}
Відтак маємо:
\begin{equation} \operatorname{div} \vec j + \operatorname{div} \frac{{\partial \vec D}}{{\partial t}} = 0. \end{equation}
Послідовність диференціювання по незалежних змінних (час і координати) є довільною, тож, урахувавши третє рівняння (2.9), отримуємо рівняння неперервності (2.31):
\begin{equation} \begin{aligned} &\operatorname{div}\vec j=-\operatorname{div}\frac{\partial\vec D}{\partial t}=-\frac{\partial}{\partial t}(\operatorname{div}\vec D)\quad\Rightarrow{}\\ &\quad{}\Rightarrow \quad\operatorname{div}\vec j=-\frac{\partial\rho}{\partial t}. \end{aligned} \end{equation}
В операторній формі воно має вигляд
\begin{equation} \vec \nabla \cdot \vec j = - \frac{{\partial \rho }}{{\partial t}}. \tag{2.31а} \end{equation}
Контрольні запитання
1. Що свідчить про неповноту рівняння (2.1), яке виражає теорему про циркуляцію магнітного поля струмів провідності?
2. Що називається густиною струму зміщення? Чи може існувати струм зміщення у діелектрику та вакуумі?
3. У чому полягає закон повного струму?
4. В яких одиницях вимірюється густина струму зміщення \(j_{\text{зм}}\)? Якщо густина струму зміщення у вакуумі дорівнює \(1\ \text{нА/м}^2\), то що це означає?
5. Запишіть рівняння Максвелла для електромагнітного поля у вакуумі за відсутності заряджених частинок.
6. Чи є повною система рівнянь Максвелла? Чому?