ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Приклади розв'язування задач
Задача 17.2
На тонку плівку з показником заломлення n = 1,33 падає паралельний пучок білого світла під кутом \(\alpha=30^{\circ}\).
Визначити
мінімальну товщину плівки d, при якій відбите світло з довжиною хвилі \(\lambda_{1}=0,64\) мкм максимально підсилене внаслідок інтерференції, а з довжиною хвилі \(\lambda_{2}=0,40\) мкм – зовсім не відбивається. Врахувати, що при відбиванні від оптично більш густого середовища фаза відбитої хвилі стрибком змінюється на \(\delta=\pi\).
|
Дано: n = 1,33
\(\alpha=30^{\circ}\)
\(\lambda_{1}=0,64\) мкм
\(\lambda_{2}=0,40\) мкм
|
|
d - ?
|
Розв’язання
Світло, що падає на плівку, частково відбивається від її верхньої поверхні, частково входить у плівку, відбивається від її нижньої поверхні та виходить назовні. Хід одного з падаючих променів показаний на рис.2. Промені 1 та 2 є когерентними, оскільки утворені поділом одного падаючого променя. Якщо на шляху променів поставити лінзу, що збере їх в одну точку (такою лінзою може бути кришталик ока), то буде спостерігатись інтерференція. Як наслідок, інтенсивність відбитого світла в залежності від різниці фаз \(\delta\) може підсилюватися (при виконанні умови (17.7а)), або послаблятися (при виконанні умови (17.7б)).
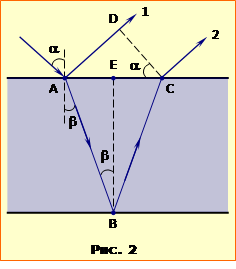
Різниця фаз залежить від різниці ходу променів (формула (17.5)). Визначимо геометричні довжини шляху променів 1 та 2 від точки падіння А до точок D та С (подальші шляхи променів до екрана однакові, тому їх не треба враховувати). Шлях променя 1 l1 = AD. З трикутника ACD:
l1 = AC\(\cdot\sin\alpha\)=2AE\(cdot\sin\alpha\).
З трикутника ABE: AE = \(d\cdot\mathrm{tg}\beta\), отже \(l_{1}=2d\cdot\frac{\sin\alpha\cdot\sin\beta}{\sqrt{1-\sin^{2}\beta}}\)
Підставивши вираз \(\sin\beta=\sin\alpha/n\) з закону заломлення світла (16.6), дістанемо:
|
|
\(l_{1}=2d\frac{\sin^{2}\alpha}{n\sqrt{1-\sin^{2}\alpha/n}}=\frac{2d\sin^{2}\alpha}{\sqrt{n^{2}-sin^{2}\alpha}}\). |
(1) |
Аналогічно визначаємо шлях променя 2 (див. рис.2):
|
|
\(l_{2}=AB+BC=2AB=\frac{2d}{\cos\beta}=\frac{2d}{\sqrt{1-\sin^{2}\beta}}=\frac{2dn}{\sqrt{n^{2}-\sin^{2}\alpha}}\). |
(2) |
В однорідному середовищі різниця фаз пов’язана з шляхами променів співвідношенням (17.5). Але в даній задачі промені поширюються в різних середовищах: промінь 1 у повітрі (n = 1), а промінь 2 у плівці (n = 1,33). Тоді довжини хвиль цих променів різні: у променя 1 задане в умові значення \(\lambda_{0}\), а у променя 2 \(\lambda=\lambda_{0}/n\) (див. формулу (16.4)), і формула (17.5) набуває вигляду:
\(\delta=\frac{2\pi{l_{2}}}{\lambda}-\frac{2\pi{l_{1}}}{\lambda_{0}}\) \(\Rightarrow\) \(\delta=\frac{2\pi}{\lambda}(l_{2}n-l_{1})\).
Підставивши в це співвідношення вирази (2) і (1), після спрощення отримаємо:
|
|
\(\delta=\frac{2\pi}{\lambda_{0}}\cdot{2d}\sqrt{1-\sin^{2}\alpha}\). |
(3) |
Для визначення результату інтерференції цих променів слід урахувати вказаний в умові ефект зміни фази на \(\delta_{0}=\pi\) променя 1, який відбивається від плівки (оптично більш густої, ніж повітря). Промінь 2 в точці В відбивається від повітря, тому його фаза не змінюється. Тому повна різниця фаз променів 1 і 2 \(\delta_{n}=\delta-\delta_{0}=\delta-\pi\). З урахуванням виразу (3), маємо:
|
|
\(\delta=\frac{2\pi}{\lambda_{0}}\cdot\left(2d\sqrt{n^{2}-\sin^{2}\alpha}-\frac{\lambda_{0}}{2}\right)\). |
(4) |
Максимум інтерференції для довжини хвилі \)\lambda_{0}=\lambda_{1}\) спостерігається при виконанні умови (17.7a), тобто
|
|
\(\frac{2\pi}{\lambda_{0}}\left(2d\sqrt{n^{2}-\sin^{2}\alpha}-\frac{\lambda_{0}}{2}\right)=2m_{1}\pi\) \(\Rightarrow\) \(\Rightarrow\) \(2d\sqrt{n^{2}-\sin^{2}\alpha}=(2m+1)\frac{\lambda_{0}}{2}\). |
(5) |
Мінімум інтерференції для довжини хвилі \(\lambda_{0}=\lambda\) спостерігається при виконанні умови (17.7б), тобто
|
|
\(\frac{2\pi}{\lambda_{0}}\left(2d\sqrt{n^{2}-\sin^{2}\alpha}-\frac{\lambda_{0}}{2}\right)=(2m_{2}+1)\pi\) \(\Rightarrow\) \(\Rightarrow\) \(2d\sqrt{n^{2}-\sin^{2}\alpha}=(m_{2}+1)\lambda_{0}\). |
(6) |
Порядки інтерференції (числа m1, m2) у формулах (5) та (6) є незалежними і, звичайно, можуть бути різними.
Оскільки умови (5) і (6) повинні виконуватись одночасно, то, прирівнюючи праві частини, дістанемо
\((2m_{1}+1)\frac{\lambda_{1}}{2}=(m_{2}+1)\lambda_{2}\) \(\Rightarrow\) \(\frac{2m_{2}+2}{2m_{1}+1}=\frac{\lambda_{1}}{\lambda_{2}}\)
Мінімальній можливій товщині плівки відповідають мінімальні значення цілих чисел m2 та m1, що з урахуванням значень \(\lambda_{1}\) та \(\lambda_{2}\) дає
\(\frac{2m_{2}+2}{2m_{1}+1}=\frac{8}{5}\) \(\Rightarrow\) \(\frac{m_{2}+1}{2m_{1}+1}=\frac{4}{5}\).
Звідси: m2 + 1 = 4; 2m1 + 1 =5.
Підставивши будь-яке з цих чисел у відповідну формулу ((6) або (5)), отримаємо відповідь. Наприклад:
\(d=\frac{(2m+1)\lambda}{4\sqrt{n^{2}-sin^{2}\alpha}}=\frac{5\cdot{0,64}\cdot{10^{-6}}}{4\sqrt{1,33^{2}-\sin^{2}30^{\circ}}}=6,49\cdot{10}^{-7}\) м \(\approx\) 0,65 мкм.