ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Розділ 16. Геометрична оптика
Теоретичні відомості. Дзеркала і лінзи
|
На законах геометричної оптики заснований принцип дії різноманітних оптичних приладів, призначених для одержання зображень. Основними елементами оптичних приборів є лінзи та дзеркала – прилади, які формують дійсні та уявні зображення. Загальна теорія зображень в оптичних приборах є складною. Тому в елементарній теорії світлові промені вважають параксіальними, а лінзи – тонкими. (Пояснення: "параксіальний" у перекладі означає "приосьовий". Параксіальний пучок створюється вузьким пучком променів, що падають на поверхню дзеркала або лінзи у області її оптичного центра). Найпростішим оптичними приладами є плоске дзеркало і сферичні дзеркала. Положення і характеристики зображень у дзеркалах визначаються формулою сферичного дзеркала. Для одержання зображень використовуються різні сферичні лінзи. Положення і характеристики зображень у лінзах визначаються формулою тонкої лінзи. |
Якщо промені, що попадають в оптичний пристрій – ОП (наприклад, лінзу), виходять з однієї точки (рис.16.4), тоді або самі промені, що пройшли через пристрій (рис.16.4а), або їхні продовження (рис.16.4б) також перетинаються в одній точці \(S^{\prime}\) (винятком є випадок, коли точка S знаходиться у фокусі збірної лінзи).
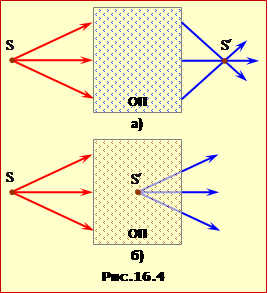
В першому випадку точка \(S^{\prime}\) називається дійсним, а в другому – уявним зображенням точки S. У точках дійсного зображення відбувається концентрація світлової енергії, і його можна спостерігати на екрані, розташованому в потрібному місці. Уявне зображення на екрані спостерігати неможливо. При візуальному спостереженні кришталик ока перетворює уявне зображення в дійсне на "екрані" – сітківці.
Зображення класифікують за:
- типом (дійсне або уявне);
- розміром (збільшене або зменшене);
- орієнтацією (пряме або перевернуте).
Одним з найпростіших приладів, що утворять зображення, є плоске дзеркало.
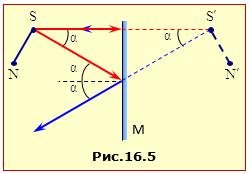
Рис.16.5 ілюструє утворення зображення точки S і предмета SN у плоскому дзеркалі M. На основі закону відбивання (16.5) легко збагнути, що продовження відбитих від дзеркала променів, які виходять з точки S, перетинаються в точці \(S^{\prime}\), розташованій симетрично точці S. Те ж саме стосується будь-якої іншої точки. Звідси випливає, що плоске дзеркало дає уявне пряме зображення \(S^{\prime}N^{\prime}\) предмета SN у натуральну величину, симетричне відносно дзеркала.
Сферичні дзеркала, на відміну від плоских, дають зображення різного типу, розміру та положення. Поверхня такого дзеркала має форму угнутого (рис.16.6а) або опуклого (рис.16.6б) сферичного сегмента.

Основні характеристики сферичного дзеркала (див. рис.16.6):
- оптичний центр С – геометричний центр сфери, частиною якої є дзеркало;
- полюс O – вершина сферичного сегмента, що утворює дзеркало;
- головна оптична вісь CO – пряма, що проходить через центр і полюс дзеркала;
- побічна вісь – будь-яка пряма, що проходить через оптичний центр дзеркала;
- головний фокус F – точка на головній оптичній осі, у якій перетинаються відбиті промені (угнуте дзеркало), або їхні продовження (опукле дзеркало), якщо падаючі промені паралельні головній оптичній осі (рис.16.6). Фокус угнутого дзеркала дійсний, а опуклого – уявний.
- головна фокусна відстань F = OF – відстань між полюсом і головним фокусом дзеркала. Вона дорівнює половині радіуса кривизни поверхні дзеркала:
|
|
\(F=\frac{R}{2}\) |
(16.8) |
- фокальна площина – площина, що проходить через головний фокус і перпендикулярна головній оптичній осі.
Фокальна площина угнутого дзеркала дійсна, а опуклого – уявна.
Збиральна властивість фокальної площини:
|
будь-які паралельні між собою промені після відбивання від дзеркала перетинаються (самі або їхні продовження) в одній точці фокальної площини. |
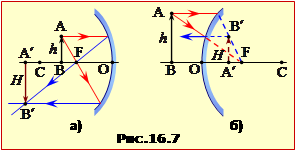
Положення предмета AB та його зображення A′B′ у дзеркалі (рис.16.7) пов'язані формулою сферичного дзеркала:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(16.9) |
де d = OA – відстань від предмета до дзеркала; f = OA′ – відстань від дзеркала до зображення; F = OF – головна фокусна відстань дзеркала.
Величини d, f, F, розглядаються як алгебраїчні. Для них чинне таке правило знаків:
|
відстані між полюсом дзеркала і дійсними точками беруть зі знаком "+", а між полюсом і уявними точками – зі знаком "–". |
(Дійсна точка – це точка, з якої промені виходять чи сходяться(перетинаються). Уявна точка – це точка перетину не самих променів, але їхніх продовжень).
Відношення висоти зображення H = A′B′ до висоти предмета h = AB називається поперечним збільшенням: Г = H/h. Для сферичного дзеркала
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\), |
(16.10) |
Знак Г визначає тип зображення: при Г > 0 зображення дійсне, а при Г < 0 – уявне. Виразивши f з рівняння (16.9) і підставивши його у формулу (16.10), можна одержати
|
|
\(\Gamma=\frac{F}{d-F}\), |
(16.10а) |
Збільшення зображення визначається положенням предмета, фокусною відстанню і типом дзеркала.
Для опуклого дзеркала F < 0 (фокус F – уявний), тому при будь-якому значенні d Г < 0 і |Г| < 1. Таким чином, незалежно від положення предмета, опукле дзеркало дає уявне зменшене зображення.
В увігнутому дзеркалі F > 0, і можливі різні ситуації:
1) якщо d > 2F, то 0 < Г < 1, зображення дійсне зменшене;
2) якщо d = 2F, то Г = 1, зображення дійсне в натуральну величину;
3) F < d, то Г > 1, зображення дійсне збільшене;
4) якщо d < F, то Г < 0 та |Г| > 1, зображення уявне збільшене;
5) якщо d = F маємо особливий випадок \(\Gamma\to\infty\) і, відповідно до формули (16.10), \(f\to\infty\), тобто відбиті промені ніде не перетинаються (йдуть паралельно), і зображення не існує.
Сферичні лінзи являють собою прозорі тіла, обмежені з двох боків сферичними поверхнями. В окремому випадку одна з поверхонь може бути плоскою. На рис.16.8 показані (у розрізі) різні типи лінз: двоопукла (а), плоскоопукла (б), двоввігнута (в), плосковігнута (г), опукловігнуті або меніски (д, е).
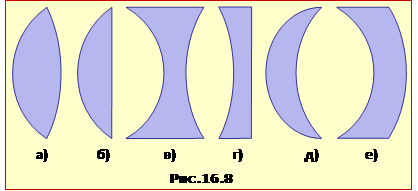
За характером дії на світлові промені лінзи поділяють на збиральні та розсіювальні. Збральна лінза перетворює паралельний пучок променів на збіжний, а розсіювальна – на розбіжний. Дія лінзи на промені визначається як формою поверхонь, так і співвідношенням між оптичними густинами лінзи і навколишнього середовища (див. нижче формулу (16.12)). Тому одна й та ж лінза в залежності від умов може бути як збиральною, так і розсіювальною. У повітрі лінзи типів а), б), д) є збиральними, а типів в), г), е) – розсіювальними. В оптично більш густому середовищі – навпаки.
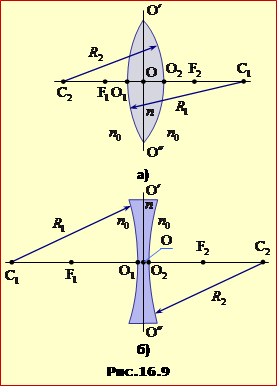 Лінзи характеризують наступними параметрами (див. рис.16.9):
Лінзи характеризують наступними параметрами (див. рис.16.9):
- радіуси кривизни R1, R2 сфер, що утворюють поверхні лінзи;
- головна оптична вісь C1C2 – пряма, що проходить через центри C1, C2 зазначених сфер;
- у тонкій лінзі можна вважати, що точки перетину O1, O2 поверхонь лінзи з головною оптичною віссю зливаються в одну точку O, яка називається оптичним центром лінзи;
- побічна вісь – будь-яка пряма, що проходить через оптичний центр лінзи;
- площина лінзи O′O″ – площина, що проходить через оптичний центр лінзи перпендикулярно до головної оптичній осі;
- фокуси F1, F2 – точки на головній оптичній осі, у яких перетинаються заломлені промені (збірна лінза) або їхні продовження (розсівна лінза), що падають на лінзу паралельно головній оптичної осі. У збірній лінзі фокуси дійсні, а в розсівній лінзі – уявні. У тонкій лінзі фокуси розташовані симетрично відносно площини лінзи, тобто на однакових відстанях від центра ;
- фокусна відстань F = OF1 = OF2 – відстань між головним фокусом і оптичним центром лінзи;
- оптична сила лінзи D – величина, обернена головній фокусній відстані:
|
|
\(D=\frac{1}{ F}\). |
(16.11) |
Одиницею оптичної сили є діоптрія (дптр). 1 дптр = 1 м-1 – оптична сила лінзи з головною фокусною відстанню 1 м. Оптична сила збиральної лінзи додатня, розсіювальної – від'ємна. Оптична сила тонкої лінзи визначається за формулою
|
|
\(D=\left(\frac{n}{n_{0}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\). |
(16.12) |
де n, n0 – показники заломлення речовини лінзи і навколишнього середовища; R1, R2 – радіуси кривизни передньої (відносно падаючого променя) і задньої поверхонь лінзи. Величини R1, R2 у формулі (16.12) розглядаються як алгебраїчні: радіус опуклої поверхні береться зі знаком "+", а увігнутої – зі знаком "–".
- фокальна площина – площина, що проходить через фокус перпендикулярно головній оптичній осі.
Фокальна площина збиральної лінзи дійсна, а розсіювальної– уявна.
Збиральна властивість фокальної площини:
|
будь–які паралельні між собою промені після проходження крізь лінзу перетинаються (самі або їхні продовження) в одній точці фокальної площини. |
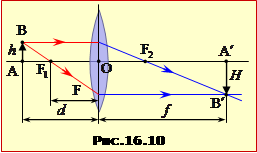
Положення предмета AB та його зображення A′B′ у лінзі (рис.16.10) пов'язані формулою тонкої лінзи:
|
|
\(\frac{1}{d}+\frac{1}{f}=\frac{1}{F}\). |
(16.13) |
де d = AO – відстань від предмета до лінзи; f = OA′ – відстань від лінзи до зображення; F = OF – фокусна відстань лінзи.
Величини d, f, F розглядаються як алгебраїчні відповідно до такого правила знаків:
|
відстані між центром лінзи і дійсними точками беруть із знаком "+", а відстані між центром лінзи і уявними точками беруть із знаком "–". |
Відношення розміру зображення H = A′B′ до розміру предмета h = AB: Г = H/h називається поперечним збільшенням. Воно визначається формулою
|
|
\(\Gamma=\frac{f}{d}\). |
(16.14) |
Визначивши відстань f з формули лінзи (16.13), одержимо ще один вираз для збільшення:
|
|
\(\Gamma=\frac{F}{d-F}\). |
(16.14а) |
Формули (16.13), (16.14) і (16.14а) ідентичні формулам (16.9), (16.10) і (16.10a) для сферичного дзеркала. Це означає, що властивості збиральної лінзи аналогічні властивостям увігнутого, а властивості розсіювальної лінзи – властивостям опуклого дзеркала. Тому наведений вище аналіз зображень у дзеркалах цілком придатний і для лінз.
На практиці в різних оптичних приладах використовують не окремі лінзи, а системи лінз. Найпростішою є система з двох складених разом тонких лінз. Такою ж системою можна вважати око людини, що "озброєне" окулярами. Оптична сила системи лінз, розташованих впритул одна до одної, дорівнює алгебраїчній сумі оптичних сил кожної з лінз:
|
|
D = D1 + D2. |
(16.15) |