ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Розділ 16. Геометрична оптика
Теоретичні відомості. Закони відбивання і заломлення світла
|
При падінні на межу поділу двох середовищ з різною оптичною густиною світлова хвиля поділяється на відбиту і заломлену. Відбита хвиля поширюється в першому середовищі, а заломлена – проходить у друге середовище. В ізотропних середовищах напрямки поширення відбитої і заломленої хвиль підпорядковані законам відбивання і заломлення світла. За відповідних умов на межі поділу двох прозорих речовин спостерігається явище повного відбивання. |
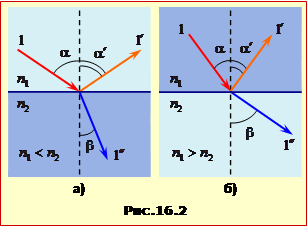
На межі поділу середовищ з різними показниками заломлення падаючий промінь 1 поділяється на відбитий промінь 1’ і заломлений промінь 1’’ (рис.16.2).
|
В ізотропних середовищах усі три промені – падаючий, відбитий і заломлений – лежать у площині падіння. |
Кути \(\alpha\), \(\alpha^{\prime}\), і \(\beta\) пов'язані законом відбивання і законом заломлення.
|
Закон відбивання світла Кут відбивання дорівнює куту падіння: |
|||
|
\(\alpha^{\prime}=\alpha\). |
(16.5) |
||
|
Закон заломлення світла Відношення синуса кута падіння до синуса кута заломлення дорівнює оберненому відношенню показників заломлення двох даних середовищ: |
|||
|
\(\frac{\sin\alpha}{\sin\beta}=\frac{n_{2}}{n_{1}}\) |
або |
\(n_{1}\sin\alpha=n_{2}\sin\beta\). |
(16.6) |
Закон заломлення відображає той факт, що
|
співвідношення між зазначеними кутами не залежить від кута падіння і визначається тільки оптичними густинами середовищ, |
тобто швидкостями поширення світла в них (див. формулу (16.2)).
З формул (16.6) видно, що напрям заломленого променя залежить від співвідношення між оптичними густинами.
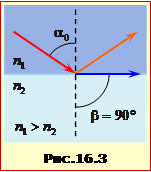
При переході світла із середовища, що має малу густину в середовище з більшою густиною (n1 < n2) заломлений промінь відхиляється до нормалі (рис.16.2а), а за умови n1 > n2 він відхиляється до границі розподілу (рис.16.2б). В останньому випадку, при певному значенні кута падіння \(\alpha_{0}\) кут заломлення набуває свого найбільш можливого значення \(\beta=90^{\circ}\) (рис.16.3). При цьому відповідно до закону (16.6)
|
|
\(\sin\alpha_{0}=\frac{n_{2}}{n_{1}}\), \(n_{2}\lt{n}_{1}\). |
(16.7) |
Кут \(\alpha_{0}\), що визначається умовою (16.7), називається граничним кутом для даних двох середовищ.
Зрозуміло, що при кутах падіння \(\alpha\gt\alpha_{0}\) рівняння (16.6) не виконується. Причина цього полягає в тому, що при кутах падіння \(\alpha\gt\alpha_{0}\) спостерігається явище повного відбивання. Енергія світла, що падає на прозору межу поділу середовищ, не проходить крізь неї, а повністю відбивається, як від ідеального дзеркала.
Таким чином повне відбивання спостерігається якщо:
1) світло падає на межу поділу з оптично більш густого середовища (n1 > n2);
2) кут падіння не менший за граничний кута для цих середовищ (\(\alpha\ge\alpha_{0}\)).