physics.zfftt.kpi.ua

Найпростішою за властивостями монохроматичною хвилею є плоска хвиля. У рівнянні плоскої монохроматичної хвилі міститься інформація про основні параметри монохроматичної хвилі: амплітуду, період (частоти), швидкість поширення і довжину хвилі (хвильове число). Крім того використовуються такі поняття: фаза, хвильові поверхні, промінь, різниця фаз та різниці ходу.

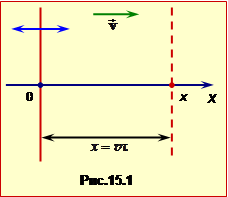Уявлення про плоску монохроматичну хвилю можна одержати, якщо уявити нескінченну площину-мембрану, яка здійснює гармонічні коливання в пружному середовищі (рис.15.1). Завдяки силам зчеплення між частинками середовища, ці коливання в усіх точках поширюються паралельно осі OX. Звичайно, коливання поширюються в обидва боки від мембрани. Але оскільки їхні властивості не залежать від напрямку, то надалі будемо вважати, що хвиля поширюється в додатному напрямку осі OX.

З огляду симетрії зрозуміло, що коливання всіх точок середовища в будь-якій площині, паралельній мембрані, повністю однакові. Тому така хвиля називається плоскою.

У пружному середовищі відсутнє поглинання енергії коливань. Тому коливання частинок середовища в плоскій хвилі мають однакову амплітуду і частоту. Але оскільки хвиля поширюється з кінцевою швидкістю, коливання у віддалених від джерела (мембрани) точках починаються з деяким запізненням.

Нехай мембрана і частинки середовища, що безпосередньо прилягають до неї, здійснюють коливання за законом

\(\xi(0,t)=\xi_{0}\cos\frac{2\pi}{t}t\),

де \(\xi\) – відхилення від положення рівноваги в момент часу t частинок середовища (у випадку немеханічної хвилі – це, відповідно, інша величина), розташованих в площині x = 0, \(\xi_{0}\) – амплітуда, T – період коливань.

Частинки, розташовані на відстані x від джерела, почнуть коливання з деяким запізненням \(\tau\). Отже, ці коливання описуються рівнянням

\(\xi(x,t)=\xi_{0}\cos\frac{2\pi}{T}(t-\tau)\).

Якщо хвиля поширюється зі швидкістю v, то \(\tau=x/v\) (див. рис.15.1), і

Рівняння (15.1) називається рівнянням плоскої монохроматичної хвилі, що поширюється уздовж осі OX.  Так само, як у випадку гармонічних коливань, існує кілька рівнозначних способів представлення рівняння монохроматичної хвилі, див. нижче. Рівняння (15.1) дає значення величини \(\xi\) у будь-якій точці простору і у будь-який момент часу.

Усі характеристики гармонічних коливань є також параметрами монохроматичної хвилі. Зокрема, – це амплітуда, період, циклічна або лінійна частота (див. розділ 13 ("Механічні коливання"), формули (13.1), (13.2), (13.3)).

Коливання в монохроматичній хвилі вимушені, вони створюються і підтримуються джерелом. Тому

Швидкість поширення хвилі характеризується швидкістю хвилі v, тобто відстанню, на яку поширюються коливання від джерела за одиницю часу.

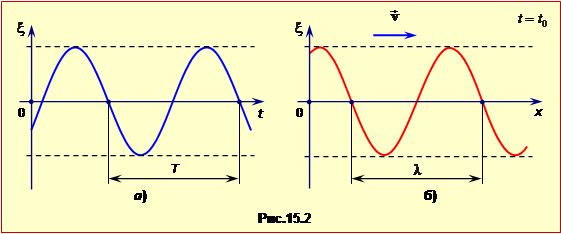
У будь-якій заданій точці x = x₀ відповідно до рівняння (15.1) збуджуються гармонічні коливання (рис.15.2а):

початкова фаза яких \(\varphi_{0}\) визначається положенням цієї точки:

Аналогічно в будь-який заданий момент часу t = t₀ значення \(\xi\) залежать від координати за законом:

де

Таким чином, величина \(\xi\) змінюється від точки до точки теж за гармонічним законом (рис.15.2б). При цьому значення \(\xi\) повністю повторюються на відстані \(\lambda\) (рис.15.2.б), яка називається довжиною хвилі. З рівняння (15.3) випливає, що

Можна сказати, що довжина хвилі – це відстань, на яку поширюється хвиля за час одного періоду коливань.

Очевидно також, що

Величину \(\lambda\) можливо також виражати через швидкість v і частоти \(\nu\) або \(\omega\) співвідношеннями:

З використанням \(\lambda\) рівняння хвилі (15.1) можна записати як

Замість періоду T використовують також частоту \(\omega=2\pi/T\), а замість довжини хвилі \(\lambda\) – так зване хвильове число:

При цьому рівняння монохроматичної хвилі записується найбільш компактно:

Коливання у хвилі в кожній точці в кожен момент часу визначаються фазою.

Фазою хвилі називається аргумент функції в рівнянні хвилі, наприклад у (15.7)

У будь-якій заданій точці фаза безперервно змінюється з часом, а в будь-який заданий момент часу вона безперервно змінюється від точки до точки. Для наочного уявлення про розподіл фаз у просторі використовують поняття хвильових поверхонь, а для характеристики напрямків поширення хвилі використовують поняття променів.

Хвильова поверхня (іноді її називають фронтом хвилі) – це поверхня, у всіх точках якої фаза хвилі має одне і теж значення в даний момент часу.

Форма хвильових поверхонь дає наочне уявлення про хвилю. Вона залежить від типу джерела і властивостей середовища. Рівняння хвильових поверхонь знаходять підстановкою фіксованих значень \(\varphi=\varphi_{0}\) та t = t₀ до рівняння фази. Для розглянутої тут хвилі з рівняння (15.8) виходить

\(\varphi_{0}=\omega{t}-kx\)     \(\Rightarrow\)     x = const.

Це означає, що хвильові поверхні являють собою площини, перпендикулярні осі OX, тобто напрямку поширення хвилі (рис.15.3а). Саме тому така хвиля називається плоскою.

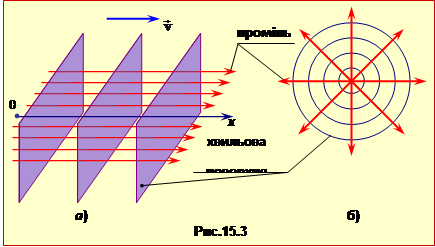
Іншим поширеним типом хвиль є сферична хвиля, що створюється точковим джерелом в однорідному ізотропному середовищі. Хвильові поверхні такої хвилі – сфери з центром у джерелі (рис.15.3б).

Промінь – це лінія, уздовж якої хвиля переносить енергію від джерела до даної точки.

У випадку однорідного та ізотропного середовища промені в кожній точці співпадають з напрямком швидкості хвилі і спрямовані уздовж нормалі до хвильової поверхні, що проходить через дану точку.

При розгляді різних хвильових явищ важливу роль відіграє різниця фаз хвилі \(\delta=\varphi_{2}-\varphi_{1}\) у двох точках в один і той же момент часу. Відповідно до рівняння (15.8) і формули (15.6)

де \(\Delta{x}=x_{2}-x_{1}\) – різниця відстаней від цих точок до джерела.

Формулою (15.9) визначається також

При цьому \(\Delta{x}\) – різниця відстаней від джерел до даної точки – називається різницею ходу хвиль (або променів).