ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
Розділ 14. Електромагнітні коливання. Змінний струм
Теоретичні відомості. Змінний струм
|
Змінним струмом називаються вимушені коливання в електричному колі, підключеному до генератора. В елементарній фізиці розглядаються тільки синусоїдальні змінні струми. Такі струми повсюди використовуються в силових електричних установках (двигуни, нагрівачі, освітлювачі й ін.). Але в електроніці широко застосовують різноманітні змінні струми інших видів. У загальному випадку коло змінного струму, крім генератора, включає резистори, конденсатори і котушки індуктивності. Кожний з цих елементів створює певний опір струмові. Розрізняють три види опорів змінному струмові: активний опір, реактивний ємнісний та реактивний індуктивний опори. Зв'язок між струмом і напругою (ЕРС) генератора залежить від повного опору кола і описується законом Ома для змінного струму. За певних умов у колах змінного струму спостерігається резонанс – явище, яке має важливі практичні застосування. Потужність змінного струму залежить не тільки від напруги і сили струму, але й від різниці фаз між коливаннями цих величин. Для перетворення напруги і сили змінного струму використовують трансформатори. |
Синусоїдальним називається змінний струм, при якому сила струму і напруги на ділянках кола здійснюють гармонічні коливання.
Синусоїдальний струм створюється генератором змінної напруги (ЕРС), яке залежить від часу за законом:
|
|
\(u=U_{m}\sin\omega{t}\), |
(14.17) |
де Um – амплітуда напруги генератора, \(\omega\) – циклічна частота. На практиці використовують лінійну частоту \(\nu\). Наприклад, на пристроях, що використовують промисловий змінний струм, вказують: \(\nu\) = 50 Гц. (Зауважимо, що зміна напруги з часом може описуватися і законом косинуса).
![]()
Генератор змінного струму на електричних схемах зображують так:
 Активним опором у колі (мається на увазі, що коло нерухоме, тобто відсутнє перетворення електричної енергії у механічну) змінного струму (рис.14.4) називають опір резисторів. Він має таку ж природу, що й при постійному струмі, тобто обумовлений гальмуванням носіїв струму іншими частинками провідника. Всі формули, співвідношення і закони постійного струму залишаються чинними і для змінного струму в резисторах. Зокрема, для них виконується закон Ома
Активним опором у колі (мається на увазі, що коло нерухоме, тобто відсутнє перетворення електричної енергії у механічну) змінного струму (рис.14.4) називають опір резисторів. Він має таку ж природу, що й при постійному струмі, тобто обумовлений гальмуванням носіїв струму іншими частинками провідника. Всі формули, співвідношення і закони постійного струму залишаються чинними і для змінного струму в резисторах. Зокрема, для них виконується закон Ома
|
|
\(i=\frac{u}{R}\), |
(14.18) |
де i, u – миттєві значення сили струму і напруги на резисторі, R – активний опір.
Якщо резистор підключити до генератора змінної напруги u (формула (14.17)), то сила струму у резисторі
|
|
\(i=I_{m}\sin\omega{t}\), |
(14.19) |
тобто коливання сили струму в резисторі відбуваються в однаковій фазі з коливаннями напруги і мають амплітуду
|
|
\(I_{m}=\frac{U_{m}}{R}\). |
(14.20) |
 Реактивним ємнісним опором називається опір, що створюється ідеальним конденсатором при протіканні змінного струму.
Реактивним ємнісним опором називається опір, що створюється ідеальним конденсатором при протіканні змінного струму.
Напруга на конденсаторі, підключеному до генератора (рис.14.5), дорівнює напрузі генератора (формула (14.17)): uC = u. Отже, заряд конденсатора неперервно змінюється за законом
|
|
\(q=Cu=CU_{m}\sin\omega{t}\). |
(14.21) |
При цьому через з'єднувальні провідники і генератор тече струм, який визначається формулою (14.2):
\(i=q^{\prime}(t)\).
У теорії змінного струму цю величину називають струмом конденсатора. (Струм конденсатора – абстрактне поняття, оскільки ніякого руху носіїв між обкладками немає. Струм в конденсаторі визначається не швидкістю носіїв, як звичайний струм, а швидкістю зміни в ньому електричного поля). Відповідно до рівняння (14.21) струм конденсатора
|
|
\(i=\omega{C}U_{m}\cos\omega{t}\), |
(14.22) |
або
|
|
\(i=I_{m}\sin\left(\omega{t}+\frac{\pi}{2}\right)\), |
(14.22a) |
де Im – амплітуда струму, яку можна записати як
\(I_{m}=\frac{U_{m}}{(1/\omega{C})}\).
Цей вираз і за виглядом, і за змістом аналогічний формулі (14.20). Отже, величина
|
|
\(X_{C}=\frac{1}{\omega{C}}=\frac{1}{2\pi\nu{C}}\) |
(14.23) |
описує опір конденсатора змінному струмові. Вона називається реактивним ємнісним опором.
Таким чином, для змінного струму в конденсаторі з'вязок між амплітудами сили струму Im і напруги Um аналогічний зв'язку між силою струму і напругою в колі постійного струму:
|
|
\(I_{m}=\frac{U_{m}}{X_{C}}\), |
(14.24) |
Але, як видно з рівнянь (14.22) і (14.17), \(i(t)\ne{u}(t)/X_{C}\), тобто
|
для миттєвих значень сили змінного струму і напруги на конденсаторі закон Ома не виконується. |
 Реактивним індуктивним опором називається опір змінному струмові, створюваний ідеальною котушкою індуктивності.
Реактивним індуктивним опором називається опір змінному струмові, створюваний ідеальною котушкою індуктивності.
Якщо до генератора підключити котушку з індуктивністю L і активним опором R (рис.14.6а), то відповідно до формули (11.15)
\(iR=u+\mathcal{E}_{с}\),
де i – сила струму, u – напруга (ЕРС) генератора, \(\mathcal{E}_{с}\) – ЕРС самоіндукції в котушці. Для ідеальної котушки R = 0 (рис.14.6б), отже
|
|
\(-\mathcal{E}_{с}=u\). |
(14.25) |
Оскільки котушка підключена до генератора прямо, то напруга на ній дорівнює напрузі генератора: uL = u. Тому, підставивши вирази u (14.17), та \(\mathcal{E}_{с}\) (12.14) у співвідношення (14.25), одержуємо
|
|
\(Li^{\prime}=U_{m}\sin\omega{t}\). |
(14.26) |
З цього рівняння випливає, що
|
|
\(i=I_{m}\sin\left(\omega{t}-\frac{\pi}{2}\right)\). |
(14.27) |
де амплітуда сили струму Im визначається виразом
\(I_{m}=\frac{U_{m}}{\omega{L}}\).
(Розв'язання рівняння (14.26) можна визначити або прямим інтегруванням, або підстановкою загального рівняння коливань струму \(i=I_{m}\sin(\omega{t}+\varphi_{0})\).
Порівняння цього виразу з формулами (14.20) і (14.23) показує, що котушка індуктивності створює для змінного струму опір
|
|
\(X_{L}=\omega{L}=2\pi\nu{L}\), |
(14.28) |
який називається реактивним індуктивним опором.
Індуктивний опір XL визначає зв'язок між амплітудами сили струму Im і напруги Um на котушці індуктивності в колі змінного струму:
|
|
\(I_{m}=\frac{U_{m}}{X_{L}}\). |
(14.29) |
Але для миттєвих значень (див. рівняння (14.27) та (14.17)) такого зв'язку немає: \(i\ne{u}/X_{L}\). Отже,
|
для миттєвих значень сили змінного струму і напруги на котушці індуктивності закон Ома не виконується. |
Прямо пропорційний зв'язок між амплітудою сили струму і амплітудою напруги зберігається в будь-якому колі змінного струму. У цьому полягає закон Ома для змінного струму:
|
амплітуда сили змінного струму в колі прямо пропорційна амплітуді напруги (ЕРС) генератора і обернено пропорційна повному опору кола: |
|
|
\(I_{m}=\frac{U_{m}}{Z}\). |
(14.30) |
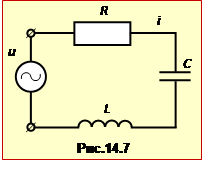 При цьому повний опір Z (його ще називають ще "імпедансом") визначається параметрами елементів кола (R, L, C) і способом їх з'єднання. Для найпростішого послідовного кола (рис.14.7)
При цьому повний опір Z (його ще називають ще "імпедансом") визначається параметрами елементів кола (R, L, C) і способом їх з'єднання. Для найпростішого послідовного кола (рис.14.7)
|
\(Z=\sqrt{R^{2}+(X_{L}-X_{C})^{2}}\), |
(14.31) |
або
|
\(Z=\sqrt{R^{2}+\left(\omega{L}-\frac{1}{\omega{C}}\right)^{2}}\). |
(14.31a) |
Закон Ома для змінного струму стосується амплітуд. Для миттєвих значень сили струму він не виконується, тобто сила струму в даний момент часу не дорівнює відношенню напруги в цей же момент часу до повного опору. (Це не суперечить співвідношенню (14.30), тому що сила струму і напруга здійснюють коливання зі зсувом фаз і досягають своїх максимальних значень Im і Um не одночасно).
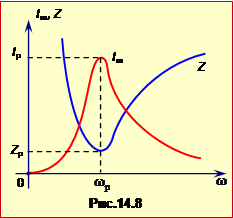 Згідно з формулами (14.23), (14.28) та (14.30), повний опір кола Z залежить від частоти. Відповідно, від частоти залежить і амплітуда сили струму Im. Вигляд цих залежностей для послідовного кола показаний на рис.14.8. На рисунку виразно простежується явище резонансу в електричному колі, яке полягає у різкому збільшенні амплітуди коливань при при наближенні частоти струму до резонансної частоти \(\omega_{р}\). Резонансна частота відповідає мінімуму повного опору і знаходиться з умови
Згідно з формулами (14.23), (14.28) та (14.30), повний опір кола Z залежить від частоти. Відповідно, від частоти залежить і амплітуда сили струму Im. Вигляд цих залежностей для послідовного кола показаний на рис.14.8. На рисунку виразно простежується явище резонансу в електричному колі, яке полягає у різкому збільшенні амплітуди коливань при при наближенні частоти струму до резонансної частоти \(\omega_{р}\). Резонансна частота відповідає мінімуму повного опору і знаходиться з умови
|
\(\omega_{р}L-\frac{1}{\omega_{р}C}\) \(\Rightarrow\) \(\omega_{р}=\frac{1}{\sqrt{LC}}\). |
(14.32) |
При \(\omega=\omega_{р}\) повний опір Zр і резонансна амплітуда сили струму Iр відповідно до формул (14.31a) та (14.30), дорівнюють
\(Z_{р}=R\),
\(I_{р}=\frac{U_{m}}{R}\).
Видно, що при резонансі відбувається компенсація ємнісного й індуктивного опорів. Це пояснюється тим, що коливання напруги на конденсаторі і на котушці протилежні по фазі і, отже, віднімаються. Тому при резонансі сумарний спад напруги на них дорівнює нулю.
Потужність змінного струму, що виділяється в колі у кожний момент часу, дорівнює добутку миттєвих значень сили струму і напруги. Ця миттєва потужність змінюється з великою частотою і її достатньо складно безпосередньо виміряти.
Тому потужністю змінного струму називають середнє значення добутку сили струму і напруги.
Повна потужність у колі змінного струму виражається формулою
|
|
\(P=\frac{1}{2}I_{m}U_{m}\cos\varphi\), |
(14.33) |
де Im, Um – амплітуди сили струму і напруги генератора, \(\varphi\) – різниця фаз між коливаннями струму і напруги генератора.
Величина \(\cos\varphi\) називається коефіцієнтом потужності і виражається через активний і повний опір кола формулою
|
|
\(\cos\varphi=\frac{R}{Z}\). |
(14.34) |
Якщо підставити цей вираз у формулу (14.33) і врахувати закон Ома (формула (14.30), то виходить
|
|
\(P=\frac{I_{m}^{2}}{2}R=\frac{U_{Rm}^{2}}{2R}\), |
(14.35) |
де URm = ImR – напруги на активному опорі кола.
Така ж потужність виділялася б у колі постійного струму з опором R при силі струму і напрузі
|
|
\(I=\frac{I_{m}}{\sqrt{2}}\), \(U=\frac{U_{m}}{\sqrt{2}}\). |
(14.34) |
Величини I та U, що визначаються формулами (14.36), називаються діючими, або ж ефективними значеннями сили струму і напруги.
Діючі значення є загальноприйнятими практичними характеристиками змінного струму. Зокрема, електровимірювальні прилади показують діючі значення, робочі величини струмів і напруг на різних побутових приладах теж вказують у діючих значеннях.
Із застосуванням діючих значень струму й напруги формули потужності (14.33) і (14.35) записуються у вигляді
|
|
\(P=IU\cos\varphi\), |
(14.37) |
та
|
|
\(P=I^{2}R=\frac{U_{m}^{2}}{R}\). |
(14.38) |
Остання формула показує, що споживана від генератора потужність змінного струму, виділяється тільки на активному опорі, а реактивні елементи – конденсатор і котушка індуктивності – енергії не споживають. Це пов'язано з тим, що при зарядці конденсатор поглинає відповідну енергію, а при розрядці – повністю повертає її в коло. Те ж саме відбувається і у котушці індуктивності при збільшенні і зменшенні сили струму.
Трансформатор – це пристрій для перетворення ("трансформації") величини напруги та сили змінного струму.
Робота трансформатора грунтується на явищі електромагнітної індукції.
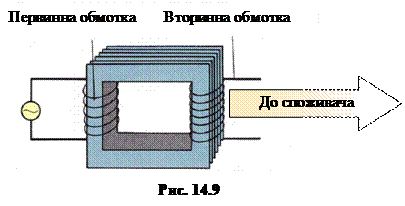
Трансформатор складається з двох (або більше) обмоток, надітих на спільне залізне осердя. Та обмотка, яка підключається до джерела живлення, называється первинною, а та, до якої підключають навантаження, – вторинною. Якщо напруга на вторинній обмотці u2 більша, ніж на первинній u1, трансформатор називають підвищувальним, інакше (u2 < u1) – знижувальним.
Роботу трансформатора якісно можна пояснити так. При протіканні в первинній обмотці змінного струму в залізному осерді виникає змінний магнітный потік, який пронизує обидві обмотки і створює в кожному витку однакову ЕРС індукції ei. Активний опір первинної обмотки малий порівняно з індуктивним. Тому спадом напруги на активному опорі можно нехтувати і вважати, що напруга на первинній обмотці
\(u_{1}=\mathcal{E}_{1}=Ne_{i}\),
де N1 – кількість витків у первинній обмотці.
При розімкненій вторинній обмотці (режим "холостого ходу") напруга на ній
\(u_{2}=\mathcal{E}_{2}=N_{2}e_{i}\),
де N2 – кількість витків у вторинній обмотці.
Отже, відношення напруг
|
|
\(k=\frac{U_{1}}{U_{2}}=\frac{\mathcal{E}_{1}}{\mathcal{E}_{2}}=\frac{N_{1}}{ N_{2}}\). |
(14.39) |
Величину k називають коефіцієнтом трансформації. Для знижувального трансформатора k > 1, для підвищувального k < 1. Однак на практиці коефіцієнт трансформації підвищувального трансформатора виражають числом \(k^{\prime}=\frac{1}{k}\), яке більше за одиницю. Наприклад, говорять: "підвищувальний трансформатор з коефіцієнтом трансформації 10".
В трансформаторі певна частка енергії електричного струму втрачається внаслідок виділення тепла на активних опорах обмоток та при перемагнічуванні осердя. Але ці втрати невеликі, і ККД трансформації близький до 1. Тому з достатньою точністю можна вважати, що потужності струму у обмотках однакові:
|
|
\(U_{1}I_{1}= U_{2}I_{2}\) \(\Rightarrow\) \(\frac{I_{2}}{I_{1}}=\frac{U_{1}}{U_{2}}=\frac{1}{k}\). |
(14.38) |
Отже, у скільки разів трансформатор змінює напругу, у стільки ж разів (тільки в зворотному напрямку) він змінює й силу струму.