ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
Розділ 14. Електромагнітні коливання. Змінний струм
Теоретичні відомості. Вільні коливання у контурі
|
Вільні електричні коливання спостерігаються у коливальному контурі, причому в ідеальному контурі вони є гармонічними. Повну інформацію про коливання містить диференціальне рівняння коливального контуру. Зокрема, з нього можна визначити частоту і період вільних коливань, одержати рівняння коливань заряду, напруги і сили струму в контурі. У коливальному контурі відбуваються перетворення електричної і магнітної енергії коливань. |
Коливальним контуром називається електричне коло, що складається з резистора (резистором у контурі часто є дроти), конденсатора і котушки індуктивності. При певних співвідношеннях між параметрами кола R, L, C, в ньому можливі вільні електричні коливання.
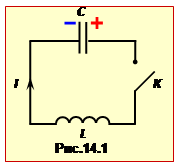У теорії електричних коливань базовою моделлю є ідеальний коливальний контур. Такий контур (рис.14.1) складається тільки з ідеальних конденсатора і котушки індуктивності і не має опору (R = 0). (Ідеальний конденсатор заповнений ідеальним діелектриком, і його електричне поле зосереджене тільки між обкладками. Ідеальна котушка не має опору (R = 0) , і її магнітне поле зосереджене тільки усередині котушки).
Вільні електричні коливання у контурі виникають так. Якщо зарядити конденсатор і замкнути ключ K, то конденсатор почне розряджатися через котушку, і в ній виникне струм, що змінюється за величиною. Цей струм створює ЕРС самоіндукції (див. формулу (12.14)), яка за правилом Ленца перешкоджає зміні струму. Як наслідок, після замикання ключа К сила струму розрядки конденсатора спочатку поступово збільшується, а потім поступово зменшується. При цьому за рахунок ЕРС самоіндукції на момент повної розрядки конденсатора (q, U = 0) струм не припиняється, а продовжує текти в тому ж напрямку, що призводить до перезаряджання конденсатора. Далі всі процеси повторюються у зворотному напрямку, тобто виникають коливання.
Диференціальне рівняння ідеального контуру виходить з тієї очевидної умови, що, оскільки котушка приєднана безпосередньо до конденсатора (рис.14.1), то в будь–який момент часу напруга на конденсаторі u дорівнює ЕРС самоіндукції \(\mathcal{E}_{с}\):
|
\(u=\mathcal{E}_{с}\). |
Величини u і \(\mathcal{E}_{с}\) визначаються формулами (10.23) і (12.14), отже
|
|
\(\frac{q}{C}=-Li^{\prime}\), |
(14.1) |
де q – заряд конденсатора, \(i^{\prime}\) – похідна сили струму по часу.
Струм у контурі створюється переміщенням заряду з однієї обкладки конденсатора на іншу. Тому заряд, що проходить протягом часу dt через переріз провідників контуру, дорівнює зміні заряду конденсатора dq протягом цього ж часу. Отже, сила струму
|
|
\(i=q^{\prime}\), |
(14.2) |
де \(a^{\prime}\) – похідна заряду конденсатора по часу, тобто
|
|
\(i^{\prime}=q^{\prime\prime}(t)\), |
(14.3) |
Після підстановки цього виразу до рівняння (14.1) маємо диференціальне рівняння ідеального контуру
|
|
\(q^{\prime\prime}=-\frac{1}{LC}q\). |
(14.4) |
Рівняння (14.4) ідентичне рівнянню (13.22). З цього випливають два висновки.
|
По–перше, вільні електричні коливання в ідеальному контурі є гармонічними. По–друге, |
|
|
\(\frac{1}{LC}=\omega^{2}\). |
(14.5) |
де \(\omega\) – циклічна частота коливань.
Частоти і період вільних коливань в ідеальному контурі виражаються наступними формулами.
Циклична частота
|
|
\(\omega=\frac{1}{\sqrt{LC}}\). |
(14.5a) |
Період коливань (див. формулу (13.3))
|
|
\(T=2\pi\sqrt{LC}\). |
(14.6) |
Останній вираз називається формулою Томсона.
Лінійна частота (див. формулу (13.2))
|
|
\(\nu=\frac{1}{2\pi\sqrt{LC}}\). |
(14.7) |
Рівняння коливань заряду конденсатора в ідеальному контурі можна одержати з рівняння механічних коливань (13.4) або (13.1), (13.1a), (13.4a), замінивши зміщення x на заряд q:
|
|
\(q=q_{m}\cos(\omega{t}+\varphi_{0})\), |
(14.8) |
де qm – амплітуда заряду, \(\omega\) – циклічна частота (формула (14.5)) і \(\varphi_{0}\) – початкова фаза коливань.
Напруга на конденсаторі \(u=q/C\) (формула (10.23)), тому рівняння коливань напруги на конденсаторі ідеального контуру має вигляд:
|
|
\(u=U_{m}\cos(\omega{t}+\varphi_{0})\), |
(14.9) |
де Um – амплітуда напруги, що визначається як
|
|
\(U_{m}=\frac{q_{m}}{C}\). |
(14.10) |
Оскільки сила струму в контурі \(i=q^{\prime}(t)\), то сила струму в ідеальному контурі:
|
|
\(i=-\omega{q}_{m}\sin(\omega{t}+\varphi_{0})\) |
(14.11) |
|
|
\(i=I_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\), |
(14.11a) |
де амплітуда сили струму
|
|
\(I_{m}=\omega{q}_{m}\). |
(14.12) |
З рівнянь (14.9) і (14.11а) видно, що в ідеальному контурі коливання сили струму випереджають по фазі коливання напруги на конденсаторі на \(\pi/2\) або на ¼ періоду (рис.14.2).
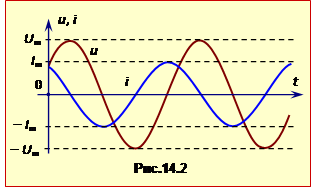
(Коливання заряду на конденсаторі завжди мають таку ж фазу, як і коливання напруги (див. рівняння (14.8) та (14.9)). Тому графік q(t) на рисунку не показаний).
Енергія коливань в ідеальному контурі складається з енергії електричного поля конденсатора WE та енергії магнітного поля котушки індуктивності WB:
|
|
W = WE + WB. |
(14.13) |
Відповідно до формул (10.32), (12.15) і рівнянь (14.9), (14.11а)
|
|
\(W_{Е}=\frac{q_{m}^{2}}{2C}\cos^{2}(\omega{t}+\varphi_{0})\) =\(\frac{q_{m}^{2}}{4C}\left(1+cos(2\omega{t}+2\varphi_{0})\right)\), |
(14.14) |
|
|
\(W_{В}=\frac{LI_{m}^{2}}{2}\sin^{2}(\omega{t}+\varphi_{0})=\frac{LI_{m}^{2}}{2}\left(1-\cos(2\omega{t}+2\varphi_{0})\right)\). |
(14.15) |
З виразів (14.12) та (14.5) виходить:
\(LI_{m}^{2}=L\omega^{2}q_{m}^{2}\) \(\Rightarrow\) \(LI_{m}^{2}=\frac{q_{m}^{2}}{C}\).
Тому з виразів (14.13), (14.14) і (14.15) очевидно, що
|
|
\(W=\frac{q_{m}^{2}}{2C}=\frac{LI_{m}^{2}}{2}\) = const. |
(14.13) |
Таким чином,
|
повна енергія вільних коливань в ідеальному контурі не залежить від часу, тобто зберігається. |
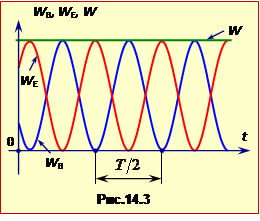На рис.14.3 зображені графіки залежності від часу електричної WE, магнітної WB і повної енергії коливань W в ідеальному контурі.
Ці графіки наочно показують, що при вільних коливаннях в ідеальному контурі відбуваються неперервні взаємні перетворення електричного та магнітного полів без втрати енергії. Крім того, з рівнянь (14.14) і (14.15) випливає, що коливання енергії кожного з полів відбуваються з подвоєною частотою \(\omega^{\prime}\) відносно коливань напруги і струму:
|
\(\omega^{\prime}=2\omega\) |
або |
\(T^{\prime}=\frac{T}{2}\). |
Порівняння формул (14.16) і (13.21) показує їх математичну ідентичність. При цьому для контуру величини 1/C і L виконують ту ж саму роль, що й жорсткість пружини k та маса вантажу m у випадку пружинного маятника.