ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв’язування задач
Сила Архімеда. Плавання тіл
Розв’язання
На занурений у воду палець діє виштовхувальна сила з боку води. Рівна за модулем і протилежна за напрямком сила діє на воду і через неї передається до дна посудини. Тож терези вийдуть із рівноваги. Іншими словами те саме можна пояснити, як наслідок збільшенням гідростатичного тиску води на дно посудини через підняття її рівня при зануренні пальця.
Таким чином, правильна відповідь – "ТАК".
|
Дано: h = 5 см
\( \rho_{\text{ст}}=7,8\ {\text{г}}/{\text{м}}^{3} \)
\( \rho_{\text{в}}=1\ \text{г}/\text{м}^{3}\)
\( \rho_{\text{р}}=13,6\ {\text{г}}/{\text{м}}^{3}\)
|
|
h′ - ? |
Розв’язання
Позаяк циліндр плаває, сила тяжіння \( {m}\vec{g}\) і сумарна архімедова сила, $\vec{F}={{\vec{F}}_{\text{}}}+{{\vec{F}}_{\text{}}}$, що створюється ртуттю та водою (рис. 9, є компенсовані:
| Fр + Fв = mg. |
|
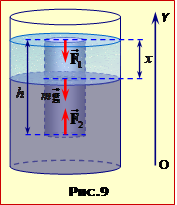
Виразивши архімедову силу в кожній з рідин за формулою (6.8), а її масу через густину та об'єм, після елементарних перетворень отримаємо відповідь:
${{\rho }_{\text{}}}{h}'+{{\rho }_{\text{}}}\left( h-{h}' \right)={{\rho }_{\text{}}}h$
\(\Rightarrow \)
\({h}'=\frac{{{\rho }_{\text{}}}-{{\rho }_{\text{}}}}{{{\rho }_{\text{}}}-{{\rho }_{\text{}}}}h\) = 2,3 см.
|
Дано: m = 5 кг
\( \rho_{\text{в}}=1000\ {\text{кг}}/{\text{м}}^{3}\)
\( \rho_{\text{ст}}=7800\ {\text{кг}}/{\text{м}}^{3}\)
|
|
V0 - ? |
Розв’язання
Об'єм порожнини
| V0 = V – Vст, |
(1) |
де V – об'єм кулі, Vст – об'єм сталі, з якої вона складається.
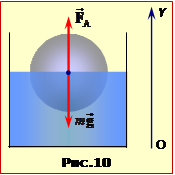
Позаяк куля плаває, її вага mg є компенсована архімедовою силою (6.8), рис. 10. Отже ,
|
$mg={{\rho }_{\text{в}}}\left( \frac{V}{2} \right)g\quad \Rightarrow \quad V=\frac{2m}{{{\rho }_{\text{в}}}}$. |
|
Відповідно, об'єм речовини кулі
|
${{V}_{\text{ст}}}=\frac{m}{{{\rho }_{\text{ст}}}}$. |
(2) |
Відтак, підставивши визначені величини об'ємів у вираз (1), знайдемо відповідь:
${{V}_{0}}=m\left( \frac{2}{{{\rho }_{\text{в}}}}-\frac{1}{{{\rho }_{\text{ст}}}} \right)$ = 93,6 см3
Кусочок сплаву золота з міддю важить у повітрі Q1 = 0,5 H, а у воді – Q2 = 0,456 H.
Визначити
маси золота mз та міді mм у сплаві. Густина золота ρз = 19,3 г/см3, міді ρм = 8,9 г/см3, води ρв = 1 г/см3.
|
Дано: Q1 = 0,5 Н
Q2 = 0,456 Н
ρз = 19,3 г/см3
ρм = 8,9 г/см3
ρв = 1 г/см3
|
|
mз, mм - ?
|
Розв’язання
За означенням вага тіла – це сила, з якою воно тисне на опору або розтягає вертикальний підвіс унаслідок гравітації. При цьому вага визначається як силою тяжіння, так і архімедовою силою, що створюється середовищем, в якому знаходиться тіло.
У повітрі архімедова сила є неістотною, тож вага сплаву
|
Q1 = (mз + mм)g, |
(1) |
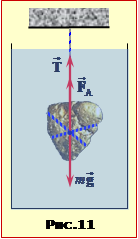
де mз і mм – маси золота та міді. Але, коли кусочок сплаву прив'язати до нитки й опустити у воду (рис. 11), то його вага Q2 (сила натягу нитки), згідно із формулою (6.8), зменшиться на величину Q1 – Q2 = ρвVg . Враховуючи, що об'єм сплаву V дорівнює сумі об'ємів золота Vз = (mз/ρз) та міді Vм = (mM/ρM), що входять до його складу, маємо:
| Q1 – Q2 = ${{\rho }_{\text{в}}}g\left( \frac{{{m}_{\text{з}}}}{{{\rho }_{\text{з}}}}+\frac{{{m}_{\text{м}}}}{{{\rho }_{\text{м}}}} \right)$. |
(2) |
Відтак з рівнянь (1) і (2) після простих, але дещо громіздких викладок отримаємо відповіді:
\( {{m}_{\text{з}}}=\frac{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}}}{\left( {{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}-{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}} \right)g}\left( \frac{{{Q}_{1}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}}}-\frac{{{Q}_{1}}-{{Q}_{2}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{в}}}} \right), \)
\( {{m}_{\text{м}}}=\frac{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}}}{\left( {{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}-{{\text{ }\!\!\rho\!\!\text{ }}_{\text{м}}} \right)g}\left( \frac{{{Q}_{1}}-{{Q}_{2}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{в}}}}-\frac{{{Q}_{1}}}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{з}}}} \right). \)
Обчислення дають:
\( {m}_{з}=20,3\) г,
\( {m}_{\text{м}}=29,7\) г.
Звідси маса зразка m = 50 г, що, природньо, дорівнює (Q1/g).
Тонка паличка з густиною ρ = 3,6 г/см3 одним кінцем закріплена шарнірно, а іншим опущена у воду (ρв = 1 г/см3) без дотику до дна та стінок посудини.|
Дано: ρ = 360 кг/м3 ρв = 1 г/см3 |
|
k - ?
|
Розв’язання
Уведемо позначення: для довжини палички l, кута її нахилу до горизонту α і довжини зануреної частини x (рис. 12.)
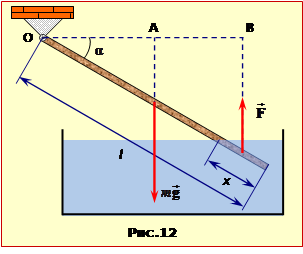
На паличку діють сила тяжіння \( {m}\vec{g}\), прикладена посередині, та сила Архімеда $\vec{F}=-{{\rho }_{\text{}}}{V}'\vec{g}$ (V′ – об'єм зануреної частини палички), що прикладена посередині зануреної частини. Умовою рівноваги палички є рівність величин моментів цих сил відносно осі О (розділ 5, п. 5.2). Як видно з рисунка, їхні плечі складають
$\frac{l}{2} \cos \alpha $ і $\left( l-\frac{x}{2} \right) \cos \alpha $,
отже, умова (5.4) рівноваги палички має вигляд:
$mg\frac{l}{2}$ = F$\left( l-\frac{x}{2} \right)$.
Тож після підстановок m = ρlS i F = ρвxSg отримаємо рівняння${{\left( \frac{x}{l} \right)}^{2}}-2\frac{x}{l}+\frac{\text{ }\!\!\rho\!\!\text{ }}{{{\text{ }\!\!\rho\!\!\text{ }}_{\text{в}}}}=0$,