ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
СТАТИКА. Приклади розв'язування задач
Загальні умови рівноваги тіла
Задача 5.9. Однорідну балку масою m = 500 кг і довжиною l = 5 м підвішено горизонтально на двох паралельних тросах так, що один розташовано скраю, а інший – на відстані a = 1 м від протилежного кінця балки Визначити сили натягу тросів T1 і T2.
Задача 5.10. Кулю підвішено на короткій нитці до вертикальної стіни. Визначити: 1) при якому коефіцієнті тертя μ між кулею та стіною точка кріплення нитки до кулі та її центр можуть бути розташовані на одній вертикалі? 2) як розміститься куля за відсутності тертя?
Задача 5.11. На похилій площині з кутом нахилу до горизонту α лежить прикріплена до стіни за кінець нитки котушка з ободом радіуса R і шаром ниток радіусом r. Визначити найменший можливий коефіцієнт тертя μ0 між котушкою та площиною, коли не намотаний кінець нитки є паралельним до площини.
Задача 5.12. На похилій площині із заданим кутом нахилу до горизонту α стоїть циліндр заданої висоти h і діаметра d. Визначити: 1. Відстань l між віссю циліндра та лінією дії сили нормальної реакції опори; 2. Максимальний кут нахилу площини αm , при якому циліндр ще не перекинеться.
Задача 5.13. На підлозі стоїть куб масою m = 50 кг. Визначити: 1) найменшу силу F0, котрою можна перекинути куб через ребро; 2) мінімальний необхідний для цього коефіцієнт тертя μ0 між кубом і підлогою.
Задача 5.14. Визначити, під яким найменшим кутом до горизонту ${{\theta }_{\min }}$ може встояти приставлена до стіни драбина при однаковому коефіцієнті її тертя зі стіною та підлогою, що дорівнює 0,3?
Задача 5.15. На горизонтальному столі лежить дошка масою M = 6 кг, котра на третину виступає за його край. До кінця дошки на нитці підвішено тягар, який відводять до горизонтального положення й відпускають. Визначити масу тягаря m, якщо при його проходженні через найнижче положення протилежний край дошки відривається від стола.
Задача 5.16. Тонкий гладенький стрижень уміщують у напівсферичну лунку з гладкою поверхнею. Визначити, під яким кутом α до горизонту встановиться стрижень, якщо відношення його довжини до діаметра лунки складає задану величину (l/d) = η.
Однорідна балку масою m = 500 кг і довжиною l = 5 м підвішено горизонтально на двох паралельних тросах так, що один розташовано скраю, а інший – на відстані a = 1 м від протилежного кінця балки.
Визначити
сили натягу тросівT1 і T2.
|
Дано: m = 500 кг
l = 5 м
a = 1 м
|
|
T1, T2 - ? |
Розв’язання
На балку діють показані на рис. 9 сила тяжіння \( {m}\vec{g}\), прикладена у центрі ваги С посередині, та сили натягу тросів \( \vec{T}_{1}\) і \( \vec{T}_{2}\), котрі її зрівноважують:
\( {mg}={{T}_{1}}+{{T}_{2}}.\)
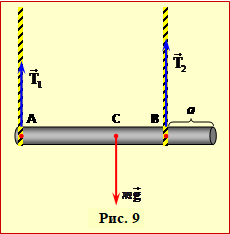
Записана рівність визначає сумарну силу натягу тросів, але не кожну із них окремо. Тож використаємо ще й другу умову рівноваги – правило моментів. Для цього запишемо рівняння (5.4) для осей А і В, що проходять через точки підвішування балки, приймаючи в кожному випадку момент сили тяжіння додатнім.
Відносно осі A моменти створюють сила тяжіння mg з плечем h′ = (l/2) і сила натягу другого троса T2, плече котрої h2 =(l – a). Отже,
\( {mg}\frac{l}{2}-{{T}_{2}}\left( l-a \right)=0\), \(\Rightarrow\) \( {{T}_{2}}=\frac{mg}{2}\cdot \frac{l}{l-a}.\)
Силу натягу першого троса Т1 визначимо аналогічно, склавши рівняння моментів відносно осі В, для якої плече сили mg складає h″ = ((l/2) – a):
\( {mg}\left( \frac{l}{2}-a \right)-{{T}_{1}}\left( l-a \right)=0\ \ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ {{T}_{1}}=\frac{mg}{2}\cdot \frac{l-2a}{l-a}. \)
Обчислення дають:
Т1 = 1875 Н, Т2 = 3125 Н.
З приводу наведеного розв'язку варто нагадати, що вибір віртуальних осей при складанні рівнянь (5.4) є довільним. До прикладу, замість осей А і В можна було би взяти вісь 1 посередині між точками А і С та вісь 2 на вільному кінці балки. Тоді рівняння моментів мали би вигляд:
|
$(1)\quad \ {{T}_{1}}l+mgl-\ \ {{T}_{2}}\left( 3l-4a \right)=0$, $( 2)\quad 2{{T}_{1}}l-mgl+2{{T}_{2}}a$. |
Корені цієї системи, звичайно, збігаються із раніше знайденими значеннями Т1, Т2 (радимо переконатися в цьому самостійно), але розв'язання є суттєво громіздкішим. Тож має сенс вибирати осі так, аби кожна перетинала лінію якоїсь із шуканих сил.
Кулю підвішено на короткій нитці до вертикальної стіни (рис. 10).
Визначити:
1) при якому коефіцієнті тертя μ між кулею та стіною точка кріплення нитки до кулі та її центр можуть бути розташовані на одній вертикалі?
2) як розміститься куля за відсутності тертя?
Розв’язання
При рівновазі довільного тіла дорівнюють нулю векторна сума всіх сил, які діють на нього, та алгебраїчна сума їхніх моментів відносно довільної осі.
1) Почнемо з моментів. На рис. 10-2 показано потрібне розташування точки кріплення нитки С і діючі на кулю сили тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\), тертя \( \vec{F}\) та натягу нитки \( \vec{T}\). Позаяк за умовою задачі силу натягу нитки визначати не треба, для складання рівняння моментів доцільно вибрати віртуальну вісь, що проходить через точку С, відносно котрої моменти створюють лише сили \( \vec{F}\) та \( \vec{N}\). З рис.10-2 видно, що їхні плечі однакові, тож згідно з умовою (5.4), однакові й самі сили:
| \( {F}={N.}\) |
(1) |
При рівновазі на кулю діє сила тертя спокою F ≤ μN (див. розділ 2, п. 2.3). Тож із співвідношення (1) випливає:
μN ≥ N \( \Rightarrow \) μ ≥ 1.
2) За відсутності тертя (F = 0) на кулю діють тільки сили \( {m}\vec{g}\), \( \vec{N}\) та \( \vec{T}\), причому алгебраїчна сума їхніх моментів має дорівнювати нулю відносно будь-якої осі, зокрема, осі О, що проходить через центр кулі. При цьому позаяк моменти сили тяжіння та нормальної реакції стіни є нульовими, таким має бути й момент сили натягу нитки. Отже, куля встановиться в положенні, при якому продовження нитки проходить через центр кулі.
Відмітимо, що, як і в попередній задачі, раціональний вибір віртуальних осей обертання дозволив отримати відповіді за допомогою однієї умови рівноваги тіла – правила моментів (5.4). Але слід зауважити, що в даній задачі відповіді можна отримати й за допомогою лише першої умов рівноваги (5.3а), проте розв'язування буде більш громіздким.
Задача 5.11
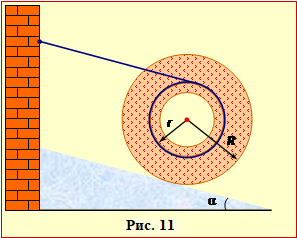
На похилій площині з кутом нахилу до горизонту α лежить прикріплена до стіни за кінець нитки котушка з ободом радіуса R і шаром ниток радіусом r, рис. 11.
Визначити
найменший можливий коефіцієнт тертя μ0 між котушкою та площиною, коли не намотаний кінець нитки є паралельним до площини.
 |
 |
|
Дано: α, R, r |
|
μ0 - ? |
Розв’язання
Згідно із загальними умовами (5.3) і (5.4), для рівноваги котушки рівнодійна та сумарний момент прикладених до неї сил мають бути нульовими.
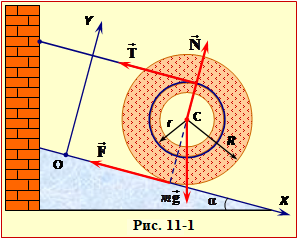
Сили, що діють на котушку (тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\), тертя \( \vec{F}\) та натягу нитки \( \vec{T}\)) разом із системою координат ХOY показано на рис. рис. 9-1. Відповідно,перша умова (5.3а) в проєкціях на площину має вигляд:
|
\( \begin{align} & \mathrm{OX:}\ \ \ mg\sin\alpha-F -T=0 \\ & \mathrm{OY:}\ \ \ N-mg\cos\alpha=0 \\ \end{align} \). |
|
Звідси після елементарних перетворень отримаємо:
|
$\frac{F+T}{N}=\operatorname{tg}\alpha $ |
(1) |
Коефіцієнт тертя визначає зв'язок між силою тертя F та силою нормального тиску N. Його можна знайти з рівняння (1), виключивши величину T за допомогою другої умови рівноваги (5.4). Для цього запишемо рівняння моментів відносно осі котушки С:
|
\(FR-Tr=0.\) \( \Rightarrow \) $T=F\frac{R}{r}$, |
(2) |
і, зробивши таку підстановку в рівнянні (1), дістанемо:
| $\frac{F}{N}=\frac{r}{R+r} \operatorname{tg}\alpha $. |
(3) |
Сила тертя спокою F задовольняє умову F ≤ μN (див. розділ 2., п. 2.3), тож відповідно до виразу (3) можна записати:
|
$\mu \ge \frac{r}{R+r} \operatorname{tg}\alpha $. |
|
Отже, найменше значення коефіцієнта тертя необхідне, аби котушка не ковзала, складає
|
\( \mu_{0 }=\frac{r}{R+r}\mathrm{tg}{\alpha.}\) |
На похилій площині із заданим кутом нахилу до горизонту α стоїть суцільний однорідний циліндр заданої висоти h і діаметра d.
Визначити:
1. Відстань l, від лінії дії сили нормальної реакції опори до осі циліндра;
2. Максимальний кут нахилу площини αm , при якому циліндр ще не перекинеться.
|
Дано: α, h, d |
| l-?, αm-? |
Розв’язання
У задачах динаміки по умовчанню приймається, що тіло, котре перебуває на якійсь поверхні (опорі), під час руху не може перекинутись. Тому задля зручності всі сили вважаються прикладеними в одній точці (зазвичай в центрі мас тіла). Але в багатьох задачах статики так міркувати не можна, і належить ураховувати не лише самі сили, а й їхні моменти. Прикладом є дана задача.
На циліндр діють сили тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\) та тертя \( \vec{F}\) (рис. 12). При цьому відносно центра ваги циліндра C сила \( \vec{F}\) створює обертовий момент, який прагне перекинути циліндр. Але при рівновазі він компенсується зворотнім моментом сили \( \vec{N}\), лінія котрої проходить праворуч від осі циліндра на шуканій відстані l.
\( {l}=\frac{h}{2}\text{tg}\alpha \).
2. Для рівноваги циліндра моменти сил тертя та тяжіння відносно осі О1 мають бути компенсовані, що є можливо лише коли вона знаходиться всередині основи циліндра. А це означає, що максимальна відстань ОО1 дорівнює його радіусові r = (d/2). Отже, як видно з рис.12, максимальний можливий кут нахилу площини до горизонту складає
αm = $\operatorname{arctg}\left( \frac{d}{h} \right)$
.
На підлозі стоїть куб масою m = 50 кг.
Визначити:
1) найменшу силу F0, котрою можна перекинути куб через ребро;
2) мінімальний необхідний для цього коефіцієнті тертя μ0 між кубом і підлогою.
|
Дано: m = 5 кг |
|
F0 - ? μ0 - ? |
Розв’язання
1) Аби перекинути куб було найлегше, момент прикладеної сили відносно опорного ребра має бути найбільшим із усіх можливих. Тому шукану силу ${{\vec{F}}_{0}}$ слід прикладати посередині протилежного ребра перпендикулярно до фронтальної діагоналі куба, тож під кутом α = 45° до горизонту, як показано в перерізі на рис. 5-11. При цьому за величиною вказаний момент має дорівнювати моментові сили тяжіння відносно того самого ребра:
|
${{F}_{0}}\cdot a\sqrt{2}=mg\cdot \frac{a}{2}$, |
|
де a – ребро куба.
Отже, величина F0 складає
|
\( {{F}_{0 }}=\frac{mg}{2\sqrt{2}}\) = 177 Н. |
(1) |
2) Сила \( \vec{F}_{0}\) має горизонтальну складову
|
Fгор = ${{F}_{0}}\cos \alpha =\left( {{F}_{0}}/\sqrt{2} \right)$, |
(2) |
котра при недостатньому терті може спричинити не перекидання, а ковзання куба по підлозі. Аби цього не сталося, гранична сила тертя спокою (див. розділ 2, п. 2.3) Fсп = μN, яка забезпечує нерухомість нижнього ребра куба, має бути не меншою, ніж Fгор:
|
$\mu N\ge \frac{{{F}_{0}}}{\sqrt{2}}$, |
(3) |
де нормальна реакція опори N та вертикальна складова F0sinα прикладеної сили зрівноважують силу тяжіння, що діє на куб. Отже,
N + F0sinα = mg.
Звідси, врахувавши вираз (1) і значення sinα = $\left( {1}/{\sqrt{2}}\; \right)$, отримаємо
N = \(\frac{3mg}{4}\)
і, відтак розв'язавши нерівність (3), дістанемо відповідь:
${{\mu }_{0}}=\frac{1}{3}$.
Визначити,
під яким найменшим кутом до горизонту ${{\theta }_{\min }}$ може встояти приставлена до стіни драбина при однаковому коефіцієнті її тертя зі стіною та підлогою, що дорівнює 0,3?
|
Дано: μ = 0,3 |
|
θmin - ? |
Розв’язання
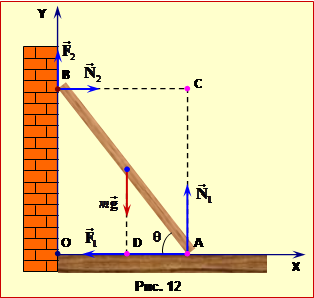
На драбину діють: сила тяжіння \( {m}\vec{g}\), сили нормальної реакції опор (підлоги \(\vec{N}_{1}\) і стіни \(\vec{N}_{2}\)), та сили тертя між драбиною і підлогою \( \vec{F}_{1}\) та стіною \( \vec{F}_{2}\), які утримують драбину від зісковзування під дією сили тяжіння, рис. 12.
Для рівноваги драбини вказані сили та їхні моменти відносно довільної осі мають бути компенсовані. Отже, за умовою (5.3)
|
N2 = F1, F2 + N1 = mg. |
(1) |
Для складання рівняння моментів (5.4) виберемо віртуальну вісь С, відносно якої моменти створюють лише сили \( {m}\vec{g}\), \( \vec{F}_{1}\) і \( \vec{F}_{2}\), плечі котрих при куті нахилу драбини θ складають, відповідно:
h = (l/2)·cosθ, h1 = l·sinθ, h2 = l·cosθ.
Тоді
\( {-mg}\frac{l}{2}\cos\theta+{F}_{1}l\sin\theta+{F}_{2}l\cos\theta=0. \)
З цього рівняння після елементарних перетворень дістанемо:
|
$tg\theta =\frac{mg-2{{F}_{2}}}{2{{F}_{1}}}$, |
|
і, врахувавши співвідношення (1),
|
$\operatorname{tg}\theta =\frac{{{N}_{1}}-{{F}_{2}}}{2{{F}_{1}}}$. |
(2) |
Загальний зміст отриманого результату є самоочевидним – рівновагу приставленої до стіни драбини забезпечують сили тертя спокою між нею та підлогою й стіною, величина яких залежить від кута нахилу драбини. Але, позаяк сила тертя спокою не може перевищувати певного граничного значення, існує відповідний найменший можливий кут нахилу драбини до підлоги ${{\theta }_{\min }}$, при якому вона ще не зісковзує.
Величину ${{\theta }_{\min }}$ можна знайти із виразу (2), врахувавши, що за співвідношенням (1) N2 = F1, та підставивши граничні значення сил тертя F1 = μ1N1 і F2 = μ2N2 (див. розділ 2, формула (2.14)). Відтак отримаємо наступну загальну відповідь:
|
$\operatorname{tg}{{\theta }_{\min }}$ = $\frac{1-{{\mu }_{1}}{{\mu }_{2}}}{2{{\mu }_{1}}}$ |
|
У даній задачі μ1 = μ2 = 0,3, отже,
$\operatorname{tg}{{\theta }_{\min }}$ = 1,52 \( \Rightarrow \) ${{\theta }_{\min }}$ ≈ 57°.
Наостанок розглянемо деякі можливі окремі випадки:
1. Стіна гладка (μ2 = 0). В такому разі
$\operatorname{tg}{{\theta }_{\min }}$ = $\frac{1}{2{{\mu }_{1}}}$ \( \Rightarrow \) θ = 59°.
Таким чином, тертя між драбиною та стіною не спричинює суттєвого впливу на її критичне рівноважне положення.
2. Підлога гладка (μ1 = 0). В такому випадку θmin = 90°, тобто, драбина теоретично може перебувати в рівновазі лише, коли її щільно приставити до стіни, причому рівновага буде нестійкою.
3. Коефіцієнти тертя між драбиною та стіною й підлогою такі, що μ1μ2 = 1. В такому разі θ = 0, і драбина не буде зісковзувати в жодному положенні.
На горизонтальному столі лежить дошка масою M = 6 кг, котра на третину виступає за його край. До кінця дошки на нитці підвішено тягар, який відводять до горизонтального положення й відпускають.
Визначити
масу тягаряm, якщо при його проходженні через найнижче положення протилежний край дошки відривається від стола.
|
Дано: M = 6 кг
η = (1/3)
|
|
m - ? |
Розв’язання
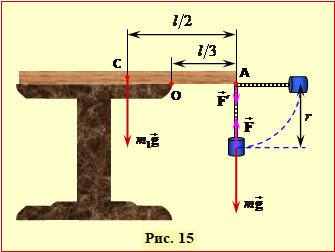
Із початком руху тягаря в мотузці з'являється сила натягу \( \vec{F}\), що намагається повернути дошку навколо осі О (рис. 15), а тягар примушує рухатися по колу. Проте спочатку вона є невелика, й сила тяжіння ${{M}}\vec{g}$ утримує дошку в спокої. Але через зростання швидкості тягаря сила F поступово збільшується й стає здатною подолати вагу дошки Mg й вивести її з рівноваги. Це відбувається, коли зрівнюються моменти указаних сил (п. 5.1). За умовою задачі в момент відриву дошки мотузка розташована вертикально, тож, як видно з рис. 13, плече сили \( \vec{F}\) дорівнює (l/3), а плече сили ${{M}}\vec{g}$ весь час складає (l/6), де l – довжина дошки. Отже, в момент відриву F (l/3) = Mg(l/6), і сила натягу мотузки| F = $\frac{Mg}{2}$. |
(1) |
Сила натягу мотузки не лише діє на дошку, а й примушує тягар рухатися по колу з відповідним доцентровим прискоренням, яке визначається законами динаміки. Тому, знаючи величину F, можна знайти й масу тягаря m. А саме. Доцентрове прискорення тягаря за формулою (1.28) визначається його швидкістю v та радіусом траєкторії (довжиною мотузки) r, як
$a=\frac{{{v}^{2}}}{{{r}}}$.
Тож у момент проходження тягарем найнижчого положення і відриву дошки, згідно з другим законом Ньютона (2.5), маємо:
| F – mg = m$\frac{{{v}^{2}}}{{{r}}}$ \( \Rightarrow \) F= mg + m$\frac{{{v}^{2}}}{{{r}}}$ |
|
Величину v в цьому виразі можна знайти за законом збереження енергії, згідно з яким набута тягарем у нижній точці кінетична енергія дорівнює спадові його потенціальної енергії при опусканні по вертикалі на відстань r:
$\frac{m{{v}^{2}}}{2}=mg{{r}}\quad \Rightarrow \quad {{v}^{2}}=2g{{r}}$ ,
отже F = 3mg.
Підставивши отриманий вираз F у співвідношення (1), знайдемо відповідь задачі:
| 3mg = \( \frac{{{M}g}}{6}\) \( \Rightarrow \) m = $\frac{M}{6}$ = 1 кг. |
(5) |
Корисне запитання. Поміркуйте, як слід було би змінити умову задачі при дещо більшій масі тягаря?
Тонкий гладенький стрижень уміщують у напівсферичну лунку з гладкою поверхнею.
Визначити,
під яким кутом α до горизонту встановиться стрижень, якщо відношення його довжини до діаметра лунки складає задану величину (l/d) = η.
|
Дано: (l/d) = η |
|
α - ? |
Розв’язання
Перед початком розв'язування задачі відразу вкажемо, що її нетривіальні розв'язки існують лише за умови η > 1, тобто, коли довжина стрижня перевищує поперечник лунки, як показано на рис. 16. Справді, за умовами рівноваги (5.3) і (5.4) лінія рівнодійної сил, з якими стінки лунки діють на стрижень, має бути спрямована по вертикалі, що проходить через його середину (центр ваги). Очевидно, що для короткого (l < d) стрижня так може бути лише при його горизонтальному розташуванні.
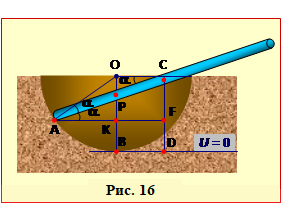
Рівноважну орієнтацію (кут α) стрижня при (l > d) можна знайти, як звично, склавши та розв'язавши систему рівнянь (5.3а) – (5.4). Але набагато легше зробити це через потенціальну енергію стрижня, використавши те, що положенні стійкої рівноваги вона для всякого тіла має мінімум. Це не важко зрозуміти. Якщо стрижень у довільній орієнтації опустити в лунку й відпустити, то, переміщуючи його в рівноважне положення, сила тяжіння виконуватиме додатню роботу. При цьому, згідно із співвідношенням (4.5), потенціальна енергія стрижня буде спадати до найменшого можливого значення.
Для подальших обчислень оберемо за нульовий рівень (початок відліку) потенціальної енергії горизонтальну площину, дотичну до дна лунки, рис. 14-1.
Тоді потенціальна енергія стрижня
\( {{W}_{\text{}}}=mgh\),
де h = h′ + h″ – висота його центра ваги С відносно нульового рівня. З рисунка зрозуміло, що
|
${h}'=\frac{l}{2}\sin \alpha $ і ${h}''=\frac{d}{2}\left( 1-\sin 2\alpha \right)$, |
|
і, позаяк за умовою l = ηd,
$h=\frac{d}{2}\left( \eta \sin \alpha -\sin 2\alpha +1 \right)$.
Таким чином, потенціальній енергії стрижня в положенні рівноваги відповідає мінімум функції
f(α) = $\eta \sin \alpha -\sin 2\alpha +1 $.
Як відомо з математики, умовою мінімуму функції є рівність нулю її похідної: f′(α) = 0. Отже,
$\eta \cos \alpha -2\cos 2\alpha =0$.
Відтак, зробивши заміну cos2α = 2cos2α – 1, отримаємо
|
$4{{\cos }^{2}}\alpha -\eta \cos \alpha -2=0$ і $\cos \alpha =\frac{\eta +\sqrt{{{\eta }^{2}}+32}}{8}$. |
|
(Другий корінь не має змісту).
Проаналізуємо отриманий результат. По-перше, згадаємо, що його отримано за умови η > 1 і, по-друге, врахуємо, що cosα ≤ 1, тож
$\eta +\sqrt{{{\eta }^{2}}+32}\le 8$ $\Rightarrow $ $\eta \le 2$.
Це обмеження є цілком зрозумілим: при η ≥ 2 (l ≥ 2d) центр ваги є розташований за межами лунки, й стрижень за будь-яких умов займає горизонтальне положення. Зауважимо також, що у формально можливому випадку η = 1 (l = d) відповідь не існує, позаяк напрямки сил тиску на стрижень, які реально збігається із радіусами кривини ребра лунки, є невизначені.