ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Збереження механічної енергії та імпульсу
Задача 4.28. Рухома шайба непружно стикається з нерухомою шайбою в k = 2 рази більшої маси. Визначити, яка частина η кінетичної енергії шайби перетворюється на тепло.
Задача 4.29. Дві кулі масами m1 і m2, що рухаються вздовж осі OX зі швидкостями \( \vec{v}_{1}\) і \( \vec{v}_{2} \), абсолютно пружно стикаються в лоб. Визначити швидкості куль u1 та u2 після зіткнення.
Задача 4.30. Куля, що мала швидкість \({{v}_{1}}=3\,\mathrm{м/с}\), після пружного зіткнення з нерухомою кулею продовжила рух у тому самому напрямі зі швидкістю \({{u}_{1}}=2\,\mathrm{м/с}\). Визначити відношення мас куль (m1/m2) та швидкість другої кулі u2 після зіткнення.
Задача 4.31. Дві однакові кульки, що рухались із швидкостями \( \vec{v}_{1}\) та \( \vec{v}_{2}\) під кутом \( \alpha \) одна до одної, після пружного удару розлетілись із швидкостями \( \vec{u}_{1}\) та \( \vec{u}_{2}\). Визначити кут розльоту кульок \( \beta \).
Задача 4.32. Куля масою m = 10 г, що горизонтально летить зі швидкістю v = 1000 м/с, вдаряє в центр підвішеного на шнурі дерев'яного куба, й застряє, заглибившись на d = 10 см. Відстань від точки підвісу до центра куба l = 1,5 м, його маса M = 5 кг. Визначити: 1. Максимальний кут відхилення α шнура від вертикалі та відстань S, яку при цьому проходить куб. 2. Силу F і тривалість удару τ, та відстань s, яку проходить за цей час куля.
Задача 4.33. Шматок м'якої глини масою m = 0,5 кг падає зі швидкістю v = 5 м/с на горизонтальну плиту масою M = 1 кг, що розташована на закріпленій вертикальній пружині жорсткістю k = 980 Н/м. Визначити максимальне стиснення хт пружини внаслідок удару.
Задача 4.34. Із закріпленої на залізничній платформі гармати роблять постріл удовж колії під кутом α = 60° до горизонту. Визначити відстань S, на яку відкотиться платформа, якщо коефіцієнт опору k = 0,5, відношення маси снаряду до маси платформи з гарматою η = 10–3 і швидкість вильоту снаряду v = 600 м/с.
Задача 4.35. Маленька шайба, що без тертя зісковзує з гірки висотою h = 90 см, плавно виїжджає на довгу дошку, котра лежить на гладкій горизонтальній поверхні. Визначити, на якій відстані S від краю дошки шайба зупиниться, якщо коефіцієнт тертя між нею й дошкою μ = 0,5 і відношення мас шайби й дошки η = 0,2.
Задача 4.36. Протон з кінетичною енергією W0 = 1,7·10-17 Дж при лобовому зіткненні з нерухомим атомом відбивається назад і переводить його в збуджений стан, утрачаючи при цьому η = 75% енергії. Визначити енергію збудження атома U, якщо відношення його маси M до маси протона m складає k = 4.
Задача 4.28
Рухома шайба непружно стикається з нерухомою шайбою в k = 2 рази більшої маси.
Визначити,
яка частина η кінетичної енергії шайби перетворюється на тепло.
|
Дано: (m2/m1) = k = 2 |
|
η - ? |
Розв’язання
При непружному зіткненні тіла пластично деформуються і далі рухаються як одне ціле. При цьому їхня кінетична енергія не зберігається, позаяк при пластичній деформації вона частково перетворюється на внутрішню енергію (див. п.4.6, (4.19)). Тож
|
\({{W}_{1}}={{W}_{2}}+Q,\) $\Rightarrow $ $Q={{W}_{1}}-{{W}_{2}}$, |
де \( {{W}_{1}}\), \( {{W}_{2}}\) – початкова та кінцева кінетична енергія шайб, Q – кількість тепла, що виділяється при зіткненні.
Якщо позначити як v початкову швидкість рухомої шайби, u – спільну швидкість шайб після зіткнення і врахувати задане відношення мас k, то шукана втрата кінетичної енергії
|
$\eta =\frac{Q}{{{W}_{1}}}=1-\left( k+1 \right){{\left( \frac{u}{v} \right)}^{2}}$ |
(1) |
Відношення швидкостей визначається із закону збереження імпульсу:
|
${{m}_{1}}v=\left( {{m}_{1}}+{{m}_{2}} \right)u\quad \Rightarrow \quad \frac{u}{v}=\frac{1}{k+1}$ |
Відтак, урахувавши цей результат у вираз (1), отримаємо відповідь:
|
\(\text{ }\!\!\eta\!\!\text{ }=1-\frac{\left( k+1 \right){{v}^{2}}}{{{\left( k+1 \right)}^{2}}{{v}^{2}}} \ \ \ \ \ \Rightarrow \ \ \ \ \ \text{ }\!\!\eta\!\!\text{ }=\frac{k}{k+1}=\frac{2}{3}.\) |
Варто звернути увагу на те, що частина втраченої кінетичної енергії зростає при збільшенні маси нерухомого тіла.
Дві кулі з масами m1 і m2, що рухаються вздовж осі OX зі швидкостями \( \vec{v}_{1}\) і \( \vec{v}_{2} \), абсолютно пружно стикаються в лоб.
Визначити
швидкості куль u1 та u2 після зіткнення.
|
Дано: m1, m2, \( \vec{v}_{1},\ \ \vec{v}_{2} \) |
|
u1, u2 - ? |
Розв’язання
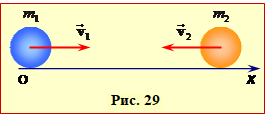 При абсолютно пружному зіткненні тіла, не втрачають ані сумарного імпульсу, ані сумарної кінетичної енергії (рівняння (4.18)). За умовою зіткнення куль є лобовим, тобто вони рухаються по одній прямій, рис. 29. Отже, для проєкцій на вісь ОХ маємо:
При абсолютно пружному зіткненні тіла, не втрачають ані сумарного імпульсу, ані сумарної кінетичної енергії (рівняння (4.18)). За умовою зіткнення куль є лобовим, тобто вони рухаються по одній прямій, рис. 29. Отже, для проєкцій на вісь ОХ маємо:
|
\({{m}_{1}}{{v}_{1\text{x}}}+{{m}_{2}}{{v}_{\text{2x}}}={{m}_{1}}{{u}_{1\text{x}}}+{{m}_{2}}{{u}_{\text{2x}}},\) |
(1) |
|
\(\frac{{{m}_{1}}v_{1\text{x}}^{2}}{2}+\frac{{{m}_{2}}v_{\text{2x}}^{2}}{2}=\frac{{{m}_{1}}u_{1\text{x}}^{2}}{2}+\frac{{{m}_{2}}u_{\text{2x}}^{2}}{2}.\) |
(2) |
Далі перегрупуємо ці вирази, як
|
\({{m}_{1}}\left( {{v}_{1\text{x}}}-{{u}_{1\text{x}}} \right)={{m}_{2}}\left( {{u}_{\text{2x}}}-{{v}_{\text{2x}}} \right),\) |
(1а) |
|
\({{m}_{1}}\left( v_{1\text{x}}^{2}-u_{1\text{x}}^{2} \right)={{m}_{2}}\left( u_{\text{2x}}^{2}-v_{\text{2x}}^{2} \right)\) |
(2а) |
та, згадавши формулу різниці квадратів і, поділивши рівняння (2а) на (1а), отримаємо:
|
|
\({{v}_{1\text{x}}}+{{u}_{1\text{x}}}={{u}_{\text{2x}}}+{{v}_{\text{2x}}}.\) |
|
Відтак об'єднаємо цей результат і рівняння (1а) в систему
|
\( \left\{ \begin{align} & {v_{1x}+u_{1x}=u_{2x}+v_{2x}} \\ & {m_{1}(v_{1x}-u_{1x})=m_{2}(v_{2x}-u_{2x})} \\ \end{align} \right.\), |
|
з якої знайдемо наступні вирази швидкостей куль після зіткнення:
|
\({{u}_{1\text{x}}}=\frac{2{{m}_{2}}{{v}_{\text{2x}}}+\left( {{m}_{1}}-{{m}_{2}} \right){{v}_{1\text{x}}}}{{{m}_{1}}+{{m}_{2}}},\) |
(3) |
|
\({{u}_{\text{2x}}}=\frac{2{{m}_{1}}{{v}_{\text{1x}}}+\left( {{m}_{2}}-{{m}_{1}} \right){{v}_{\text{2x}}}}{{{m}_{1}}+{{m}_{2}}}.\) |
(4) |
Ці формули, на загал, відображають очевидне: величини та напрями швидкостей куль після зіткнення визначаються співвідношенням їхніх мас та величиною й напрямком початкових швидкостей. А от якими саме будуть швидкості, залежить від конкретних умов задачі.
Для прикладу розглянемо випадок, коли v2 = 0, тобто перше тіло налітає на нерухоме друге. В такому разі вирази (3) і (4) набувають вигляду:
| \({{u}_{\text{1x}}}=\frac{\left( {{m}_{1}}-{{m}_{2}} \right){{v}_{\text{1x}}}}{{{m}_{1}}+{{m}_{2}}};\ \ \ \ \ \ {{u}_{\text{2x}}}=\frac{2{{m}_{1}}{{v}_{\text{1x}}}}{{{m}_{1}}+{{m}_{2}}}.\) |
(5) |
Тож маємо очевидне: u2х > 0, тобто друга куля відскочить в напрямку руху першої. Але напрям руху першої кулі після удару не є однозначним і залежить від співвідношення мас. Якщо перша куля є масивнішою (\({{m}_{1}}>{{m}_{2}}\)), то \({{u}_{\text{1x}}}>0\), тобто вона продовжить рух у тому самому напрямі, проте з меншою швидкістю. Відповідно, при \( {{m}_{1}}<{{m}_{2}} \) перша куля після удару відскочить у зворотньому напрямі (\({{u}_{\text{1x}}}<0\)).
Наведені наслідки сприймаються як очевидні і пояснюються лобовим характером зіткнення. А ось при рівних масах куль (m1 = m2) із формул (3) і (4) випливає нетривіальний результат:
|
\({{u}_{\text{1x}}}={{v}_{\text{2x}}},\ \ \ \ \ \ {{u}_{\text{2x}}}={{v}_{\text{1x}}}.\) |
|
Отже, однакові пружні кулі при лобовому зіткненні обмінюються імпульсами та кінетичними енергіями. Зокрема, якщо одна з куль до зіткнення є нерухомою, то вона перебирає на себе увесь імпульс і енергію першої, а та зупиняється.
Куля, що мала швидкість \({{v}_{1}}=3\,\mathrm{м/с}\), після пружного зіткнення з нерухомою кулею продовжила рух у тому самому напрямі зі швидкістю \({{u}_{1}}=2 \,\mathrm{м/с}\).
Визначити
відношення мас куль m1/m2 та швидкість другої кулі u2 після зіткнення.
|
Дано: v1 = 3 м/с u1 = 2 м/с |
|
m1/m2 - ? u2 - ? |
Розв’язання
Позаяк напрям першої кулі після зіткнення не змінився, воно є центральним (лобовим), і дана задача по суті є окремим випадком попередньо. Тож, увівши позначення m1/m2 = k і зробивши заміну m1 = km2, з першій формули (5) задачі 4.29 отримаємо:
|
\({{u}_{\text{1}}}=\frac{\left( k-1 \right){{v}_{\text{1}}}}{k+1}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ k=\frac{{{v}_{\text{1}}}+{{u}_{1}}}{{{v}_{\text{1}}}-{{u}_{1}}}=5.\) |
|
Відтак із другої формули знайдемо швидкість:
|
\({{u}_{2}}=\frac{2k{{v}_{\text{1}}}}{k+1}=5\) м/с. |
|
Дві однакові кульки, що рухались із швидкостями \( \vec{v}_{1}\) та \( \vec{v}_{2}\) під кутом \( \alpha \) одна до одної, після пружного удару розлетілись із швидкостями \( \vec{u}_{1}\) та \( \vec{u}_{2}\).
Визначити
кут розльоту кульок \( \beta \).
|
Дано: \( \vec{v}_{1}\), \(\vec{v}_{2}\), \( \vec{u}_{1}\), \( \vec{u}_{2}\), \( \alpha \)
|
|
\( \beta \) - ? |
Розв’язання
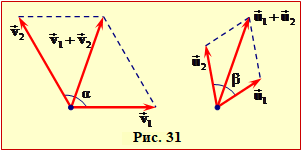
Пружне зіткнення кульок відбувається із збереженням імпульсу та кінетичної енергії відповідно до рівнянь (4.18):
|
\( \left\{ \begin{align} & {m\vec{v}_{1}+m\vec{v}_{2}=m\vec{u}_{1}+m\vec{u}_{2},} \\ & {\frac{mv_{1}^{2}}{2}+\frac{mv_{2}^{2}}{2}=\frac{mu_{1}^{2}}{2}+\frac{mu_{2}^{2}}{2}}; \\ \end{align} \right.\) \( \Rightarrow \) \( \left\{ \begin{align} & {\vec{v}_{1}+\vec{v}_{2}=\vec{u}_{1}+\vec{u}_{2},} \\ & {v_{1}^{2}+v_{2}^{2}=u_{1}^{2}+u_{2}^{2}.} \\ \end{align} \right.\) |
(1) |
Вектори \( \vec{v}_{1}+\vec{v}_{2} \) та \(\vec{u}_{1}+\vec{u}_{2}\) являють собою діагоналі паралелограмів швидкостей (рис. 31), причому \(\vec{v}_{1}+\vec{v}_{2}=\vec{u}_{1}+\vec{u}_{2}\). Отже, за теоремою косинусів маємо
|
\(v_{1}^{2}+v_{2}^{2}+2{{v}_{1}}{{v}_{2}}\cos \text{ }\!\!\alpha\!\!\text{ }=u_{1}^{2}+u_{2}^{2}+2{{u}_{1}}{{u}_{2}}\cos \text{ }\!\!\beta\!\!\text{ }\text{.}\) |
|
Врахувавши друге рівняння системи (1), дістанемо:
|
\({{v}_{1}}{{v}_{2}}\cos \text{ }\!\!\alpha\!\!\text{ }={{u}_{1}}{{u}_{2}}\cos \text{ }\!\!\beta\!\!\text{ }\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \cos \text{ }\!\!\beta\!\!\text{ }=\frac{{{v}_{1}}{{v}_{2}}}{{{u}_{1}}{{u}_{2}}}\cos \text{ }\!\!\alpha\!\!\text{ }\ \text{.}\) |
|
В окремому випадку, коли одна з кульок (до прикладу, друга) перебуває в спокої, то \( \cos \text{ }\!\!\beta\!\!\text{ }=0 \) і \( \text{ }\!\!\beta\!\!\text{ }=90{}^\circ \), тобто кульки розлітаються під прямим кутом.
Куля масою m = 10 г, що горизонтально летить зі швидкістю v = 1000 м/с, вдаряє в центр підвішеного на шнурі дерев'яного куба, й застряє, заглибившись на d = 10 см. Відстань від точки підвісу до центра куба l = 1,5 м, його маса M = 5 кг.
Визначити:
1. Максимальний кут відхилення α шнура від вертикалі та відстань S, яку при цьому проходить куб.
2. Силу F і тривалість удару τ, та відстань s, яку проходить за цей час куля.
Дано:
|
m = 10 г
v = 1000 м/с
d = 10 см
l = 1,5 м
M = 5 кг
|
|
α - ?, S - ?; F - ?, τ - ?, s - ? |
Розв’язання
1. Куб відхиляється за рахунок енергії та імпульсу, отриманих при влучанні кулі. При цьому через масивність куба та велику силу опору, що діє на кулю, удар (заглиблення кулі в куб) триває дуже короткий проміжок часу, протягом якого імпульс системи куля-куб лишається практично незмінним:
|
\(mv=\left( m+M \right)u,\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{mv}{m+M},\) |
|
де u – початкова швидкість руху куба з кулею після удару.
За умовою m << M, отже, вираз u без утрати точності (похибка 0,2%) можна спростити, відкинувши у знаменнику величину m:
|
$u=\frac{m}{M}v$ = 2 м/с. |
(1) |
Подальший рух куба з кулею відбувається під дією сили тяжіння та поперечної сили натягу мотузки, що не виконує роботи. Тож відхилення куба відбувається без утрати механічної енергії, і максимальна висота h його підняття над початковим рівнем (рис. 4.32) визначається рівнянням
|
\(\frac{\left( m+M \right){{u}^{2}}}{2}=\left( m+M \right)gh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ h=\frac{{{u}^{2}}}{2g},\) |
|
або з урахуванням виразу (1),
|
h = ${{\left( \frac{m}{M} \right)}^{2}}\frac{{{v}^{2}}}{2g}$ |
(2) |
Відтак можна визначити максимальний кут відхилення куба α. А саме, як зрозуміло з рис. 31,
| \( {h}=l(1-cos\alpha)=2l\sin^{2}\frac{\alpha}{2}\), | (3) |
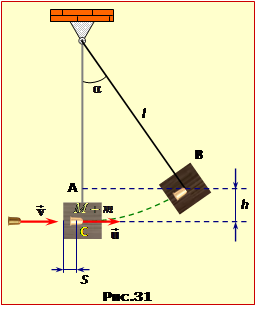 тож прирівнявши вирази (2) і (3), знайдемо:
тож прирівнявши вирази (2) і (3), знайдемо:
|
\(\sin \frac{\text{ }\!\!\alpha\!\!\text{ }}{2}= \frac{mv}{2M\sqrt{gl}}.\) |
Обчислення дають:
\(\sin \frac{\text{ }\!\!\alpha\!\!\text{ }}{2}=0,258 \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \text{ }\!\!\alpha\!\!\text{ }=30{}^\circ .\)
Пройдений при цьому кубом шлях складає:
S = lα = $\frac{\pi l}{6}$ = 78,5 см.
2. Силу удару знайдемо через сумарну роботу А сил тертя між кубом і кулею, котра (див. задачу 4.2) визначається добутком сили тертя, що діє лише на кулю, та її переміщення відносно бруса:
| \({A}=-Fd\). |
|
Згідно з (4.4), ця робота дорівнює зміні кінетичної енергії системи, отже,
|
$\frac{\left( M+m \right){{u}^{2}}}{2}-\frac{m{{v}^{2}}}{2}$ = \(-Fd\) |
|
Підставивши вираз u з формули (1), після перетворень дістанемо наступний практично точний результат:
|
F = \( \frac{m{{v}^{2}}}{2d}=5\cdot {{10}^{4}}\ \mathrm{H}\) |
|
Отже, сила удару є дуже велика: вона дорівнює силі тиску на горизонтальну опору вантажу масою 5 т.
Тривалість удару τ теж легко оцінити, позаяк за час руху всередині куба куля майже повністю втрачає швидкість (формула (1)), так що середня швидкість кулі за час удару складає <v> = (v/2).
Отже, тривалість удару
$\tau =\frac{2d}{v}$ = 2·10–4 c = 0,2 мс.
При цьому куб, рухаючись із середньою швидкістю (u/2), за час τ проходить шлях
${s}=\frac{u\tau }{2}=0,2 \text{мм }$.
Насамкінець відмітимо, що отримані значення τ і s переконливо доводять зроблене на початку припущення про "миттєвий" характер зіткнень тіл.
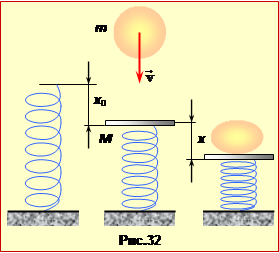 Шматок м'якої глини масою m = 0,5 кг падає зі швидкістю v = 5 м/с на горизонтальну плиту масою M = 1 кг, що розташована на закріпленій вертикальній пружині жорсткістю k = 980 Н/м.
Шматок м'якої глини масою m = 0,5 кг падає зі швидкістю v = 5 м/с на горизонтальну плиту масою M = 1 кг, що розташована на закріпленій вертикальній пружині жорсткістю k = 980 Н/м.
Визначити
максимальне стиснення х пружини внаслідок удару.
|
Дано: m = 0,5 кг
M = 1 кг
k = 980 Н/м
v = 5 м/с
|
|
xm - ? |
Розв’язання
Змістовно й за алгоритмом розв'язування ця задача є аналогом попередньої. Отже, можна вважати, що прилипання глини до пластини відбувається без зміни імпульсу системи й задовольняє рівняння:
|
\(mv=\left( m+M \right)u,\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{mv}{m+M},\) |
(1) |
де u – швидкість руху плити разом з глиною одразу після.
Те саме можна сказати й про енергію: позаяк за умовою сили тертя не враховуються, в процесі стискання пружини відбувається лише перетворення кінетичної енергії на потенціальну без зміни загальної кількості.
Для наступних викладок є логічним обрати нульовий рівень гравітаційної потенціальної енергії в початковому положенні пластини (рис. 4.33), а для пружини – коли вона ще не була навантажена плитою. В такому разі початкова енергія системи W1 складається з кінетичної енергії пластини з глиною та потенціальної енергії пружини, що деформована вагою пластини на певну величину x0 = (mg/k). Тоді, врахувавши вираз (1), маємо:
|
\({{W}_{1}}=\frac{{{m}^{2}}{{v}^{2}}}{2\left( m+M \right)}+\frac{{{\left( Mg \right)}^{2}}}{2k}.\) |
(2) |
В кінцевому (найнижчому) положенні енергія системи W2 складається тільки з потенціальних енергій пружини, деформованої на максимальну величину xm = x0 + x, та пластини з глиною масою M+m, що опустилися на відстань х від нульового рівня:
|
\({{W}_{2}}=\frac{k{{\left( x+{{x}_{0}} \right)}^{2}}}{2}-\left( m+M \right)gx.\) |
(3) |
(Знак "–" стоїть тому, що кінцева потенціальна енергія тіл є від'ємна).
За законом збереження енергії W1 = W2, тож, прирівнявши вирази (2) та (3) після спрощень отримаємо:
|
\(k{{x}^{2}}-2mgx-\frac{{{\left( mv \right)}^{2}}}{m+M}=0.\) |
|
З цього рівняння визначаємо додаткове
|
\(x=\frac{mg+\sqrt{{{\left( mg \right)}^{2}}+\frac{k{{\left( mv \right)}^{2}}}{m+M}}}{k}\) |
|
і повне \( {x}_{m}={x}_{0}+{x}\) стиснення пружини:
|
\({{x}_{\text{m}}}=\frac{1}{k}\left( \left( m+M \right)g+\sqrt{{{\left( mg \right)}^{2}}+\frac{k{{\left( mv \right)}^{2}}}{m+M}} \right).\) |
|
Обчислення дають:
хт = 8 см.
Із закріпленої на залізничній платформі гармати роблять постріл удовж колії під кутом α = 60° до горизонту.
Визначити
відстань S, на яку відкотиться платформа, якщо коефіцієнт опору μ = 0,5, відношення маси снаряду до маси платформи з гарматою η = 10–3 і швидкість вильоту снаряду v = 600 м/с.
|
Дано: α = 60° |
|
S - ? |
Розв’язання
При пострілі під кутом повний імпульс системи "платформа-снаряд" не зберігається, проте зберігається його проекція на напрям копії ОХ (див. задачу 3.5). Отже,
|
\(-Mu+mv\cos \text{ }\!\!\alpha\!\!\text{ }=0\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=nv\cos \text{ }\!\!\alpha\!\!\text{ },\) |
(1) |
де u – початкова швидкість відкочування платформи після пострілу, M і m – маси платформи з гарматою та снаряда.
Унаслідок пострілу платформа отримує кінетичну енергію \( {W}=\frac{M{{u}^{2}}}{2}\), яку потім витрачає на роботу проти сили опору \( {F}=\mu{mg}\) на шляху S. Отже:
|
\(\frac{M{{u}^{2}}}{2}=\text{ }\!\!\mu\!\!\text{ }mgS\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ S=\frac{{{u}^{2}}}{2\text{ }\!\!\mu\!\!\text{ }g}.\) |
|
Врахувавши вираз (1), отримуємо відповідь:
|
\(S=\frac{{{\left( nv\cos \text{ }\!\!\alpha\!\!\text{ } \right)}^{2}}}{2\text{ }\!\!\mu\!\!\text{ }g}\) = 9 см. |
|
Маленька шайба, що без тертя зісковзує з гірки висотою h = 90 см, плавно виїжджає на довгу дошку, котра лежить на гладкій горизонтальній поверхні.
Визначити,
на якій відстані S від краю дошки шайба зупиниться, якщо коефіцієнт тертя між нею й дошкою μ = 0,5 і відношення мас шайби й дошки η = 0,2.
|
Дано: h = 0,9 м
μ = 0,5
η = 0,2
|
|
S - ? |
Розв’язання
За умовою шайба зісковзує без тертя, отже без втрат механічної енергії. Тому,
|
\(\frac{m{{v}^{2}}}{2}\ =mgh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ v=\sqrt{2gh}\text{,}\) |
(1) |
де v – швидкість шайби в момент виходу на дошку.
Ковзаючи далі по дошці, шайба під дією сили тертя гальмується, а дошка, навпаки, прискорюється. Внаслідок цього через певний час їхні швидкості зрівняються, і ковзання шайби по дошці припиниться. Рух шайби й дошки відбувається із збереженням імпульсу системи, позаяк зовнішні сили тяжіння та реакції опори є компенсовані. Це дозволяє визначити кінцеву швидкість дошки з шайбою u:
|
\(mv=\left( m+M \right)u\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{mv}{m+M}\ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ u=\frac{nv}{1+n}.\) |
(2) |
Ковзання шайби по дошці супроводжується зміною кінетичної енергії системи, рівною сумарній роботі сил тертя:
|
\(\frac{\left( m+M \right){{u}^{2}}}{2}-\ \frac{m{{v}^{2}}}{2}={{A}_{\text{т}}}.\) |
(3) |
Згідно з результатом задачі 4.2,(формула (2)), ця сумарна робота дорівнює добутку сили тертя, що діє на шайбу, на її переміщення відносно дошки: \({{A}_{\text{т}}}=-\text{ }\!\!\mu\!\!\text{ }mg\). Після підстановки цього виразу й виразу (2) в рівняння (3) та елементарних перетворень отримаємо:
|
\(S=\frac{{{v}^{2}}}{2\left( 1+n \right)\text{ }\!\!\mu\!\!\text{ }g},\) |
|
або, з урахуванням виразу (1),
|
\(S=\frac{h}{\left( 1+n \right)\text{ }\!\!\mu\!\!\text{ }}=1,5\ \text{м}\text{.}\) |
|
Протон з кінетичною енергією W0 = 1,7·10-17 Дж при лобовому зіткненні з нерухомим атомом відбивається назад і переводить його в збуджений стан, утрачаючи при цьому η = 75% енергії.
Визначити
енергію збудження атома U, якщо відношення його маси M до маси протона m складає k = 4.
|
Дано: W0 = 1,7·10-17 Дж
η = 75%
k = 4
|
|
U - ? |
Розв’язання
 При зіткненні втрачена протоном енергія
При зіткненні втрачена протоном енергія
\(W=\eta{W}_{0}\)
передається атому у формі кінетичної енергії Wа, а решта переходить у внутрішню енергію атома (енергію збудження U):
ηW0 = Wа + U $\Rightarrow $ U = ηW0 – Wа.
Зіткнення протона з атомом відбувається із збереженням імпульсу. Тому в записаному співвідношенні величину Wа є доцільно виразити через імпульс pa і масу M атома:
| $U=\eta {{W}_{0}}-\frac{p_{a}^{2}}{2M}$ |
(1) |
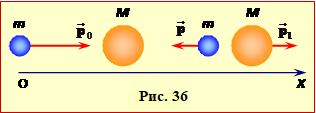
За законом збереження імпульсу (3.3) з урахуванням напрямків (рис. 36)
p0 = –p + ра $\Rightarrow $ ${{p}_{a}}=\frac{3}{2}{{p}_{0}}$,
де взято до уваги, що кінцевий імпульс протона р дорівнює половині початкового, бо за умовою після зіткнення у нього лишається чверть початкової кінетичної енергії. В такому разі, згідно з виразом (1) і заданим співвідношенням мас M = km, після елементарних перетворень отримуємо наступну відповідь:
$U=\left( \eta -\frac{9}{4k} \right){{W}_{0}}\approx 3,2\cdot {{10}^{-18}}\text{Дж}$.