ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Збереження механічної енергії
Задача 4.22. Визначити, під яким кутом α до горизонту зроблено постріл з гармати, якщо в найвищій точці траєкторії кінетична енергія снаряда є на k = 25 % менша за початкову.
Задача 4.23. Визначити, при яких кутах стрільби \( \alpha\) на траєкторії снаряда існують точки, де його кінетична енергія у k = 3 рази перевищує потенціальну.
Задача 4.24. Тягарець на нитці відхиляють на кут \( \alpha=60^{\circ}\) від вертикалі й відпускають. Визначити кут \( \beta \), на який відхилиться нитка по інший бік, якщо під точкою підвісу посередині вбито цвях.
Задача 4.25. Маленька шайба починає зісковзувати без тертя з вершини закріпленої півсфери радіуса R. Визначити, на якій висоті h від основи півсфери шайба відірветься.
Задача 4.26. Через гладкий горизонтальний штир перекинуто м'який канат довжини \( {l=10}\) м так, що його кінці розташовані на одному рівні. Після незначного поштовху канат починає зісковзувати. Визначити його швидкість на момент сходу зі штиря.
Задача 4.27. Підвішений на пружині тягарець, який розтягає її на задану величину х0, підіймають до положення, коли пружина не деформована, й відпускають. Визначити: 1) максимальний розтяг хm пружини; 2) максимальну швидкість тягарця vm.
Визначити,
під яким кутом α до горизонту зроблено постріл з гармати, якщо в найвищій точці траєкторії кінетична енергія снаряда на k = 25 % менша за початкову.
|
Дано: k = 25 % = 0,25 |
|
α - ? |
Розв’язання
Позаяк на снаряд діє лише консервативна сила тяжіння, його повна механічна енергія не змінюється, й можна записати:
| \(\frac{mv_{0}^{2}}{2}=\frac{m{{v}^{2}}}{2}+mgh\) $\Rightarrow $ \(\frac{mv_{0}^{2}}{2}-\frac{m{{v}^{2}}}{2}=mgh\), | (1) |
де \( {m} \) – маса снаряда, \( {{v}_{0}}\), \( v \) – швидкості в точці пострілу та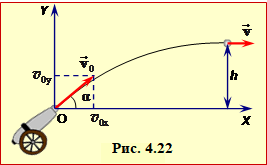 найвищій точці траєкторії, \( {h} \) – максимальна висота підйому відносно точки пострілу (рис. 4.22).
найвищій точці траєкторії, \( {h} \) – максимальна висота підйому відносно точки пострілу (рис. 4.22).
За умовою
\(\frac{mv_{0}^{2}}{2}-\frac{m{{v}^{2}}}{2}=k\frac{mv_{0}^{2}}{2},\)
отже,
| \(mgh=k\frac{mv_{0}^{2}}{2}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ 2gh=kv_{0}^{2}.\) | (2) |
З іншого боку, за рівнянням (1.18)
| \( 2gh=v_{0\text{y}}^{2}=v_{0}^{2}{{\sin }^{2}}\text{ }\!\!\alpha\!\!\text{ }.\) | (3) |
Тож порівнявши вирази (2) і (3), знайдемо відповідь:
\(\sin \text{ }\!\!\alpha\!\!\text{ }=\sqrt{k}=\frac{1}{2}\ \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \text{ }\!\!\alpha\!\!\text{ }=30{}^\circ .\)
Визначити,
при яких кутах стрільби \( \alpha\) на траєкторії снаряда існують точки, де його кінетична енергія у k = 3 рази перевищує потенціальну.
|
Дано: k = 3 |
|
α - ? |
Розв’язання
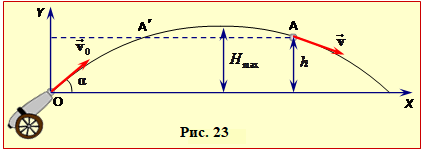
На снаряд у польоті діє тільки консервативна сила тяжіння, тож його механічна енергія зберігається, і в будь-якій точці траєкторії (рис. 23)
| \(\frac{mv_{0}^{2}}{2}=\frac{m{{v}^{2}}}{2}+mgh,\) |
де \({{v}_{0}}\) – початкова швидкість снаряда, \( {v} \) – його швидкість на висоті h.
Згідно з умовою, \(\frac{m{{v}^{2}}}{2}=kmgh\), отже,
| \(\frac{mv_{0}^{2}}{2}=\left( k+1 \right)mgh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ h=\frac{v_{0}^{2}}{2\left( k+1 \right)g}.\) |
|
При цьому максимальна висота підйому снаряда за рівнянням (1.18) складає
| \(H=\frac{v_{0}^{2}{{\sin }^{2}}\text{ }\!\!\alpha\!\!\text{ }}{2g}.\) |
|
Отже, позаяк \( {h\le H} \),
\(\frac{v_{0}^{2}}{2\left( k+1 \right)g}\le \frac{v_{0}^{2}{{\sin }^{2}}\text{ }\!\!\alpha\!\!\text{ }}{2g}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \sin \text{ }\!\!\alpha\!\!\text{ }\ge \frac{1}{\sqrt{k+1}}.\)
Таким чином, вказані точки існують при кутах кидання
\(\text{ }\!\!\alpha\!\!\text{ }\ge \arcsin \left( \frac{1}{\sqrt{k+1}} \right).\)
При всіх можливих значеннях α, крім найменшого, це дві точки на гілках траєкторії (рис. 4.23), а при найменшому одна – її вершина.
Згідно з умовою k = 3, тож числова відповідь складає
α ≥ 30°.
Тягарець, який підвішено на нитці, відхиляють на кут \( \alpha=60^{\circ}\) від вертикалі й відпускають.
Визначити
кут \( \beta \), на який відхилиться нитка по інший бік, якщо під точкою підвісу посередині вбито цвях.
|
Дано: α = 60° |
|
\( \beta \) - ? |
Розв’язання
На тягарець, окрім консервативної сили тяжіння, діє тільки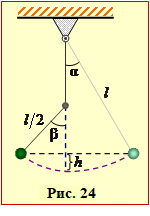 поперечна до руху сила натягу нитки, що не виконує роботи. Тому повна механічна енергія тягарця зберігається, і в крайніх точках він розташовується на одній висоті h відносно початкового положення, рис. 4.24, і, позначивши довжину нитки як l, можна записати:
поперечна до руху сила натягу нитки, що не виконує роботи. Тому повна механічна енергія тягарця зберігається, і в крайніх точках він розташовується на одній висоті h відносно початкового положення, рис. 4.24, і, позначивши довжину нитки як l, можна записати:
\( \cos\alpha=\frac{l-h}{l} \) = $1-\frac{h}{l}$,
\( \cos\beta=\frac{\left( l/2 \right)-h}{\left( l/2 \right)}=1-2\frac{h}{l}\)
звідки, виключивши відношення \( {h/l}\), отримати відповідь:
\( \cos\beta=2\cos\alpha-1 \) \( \Rightarrow \) \( \beta=\mathrm{arccos}(2\cos\alpha-1) \) = 90°.
Маленька шайба починає зісковзувати без тертя з вершини закріпленої півсфери радіуса R.
Визначити,
на якій висоті h від основи півсфери шайба відірветься від неї.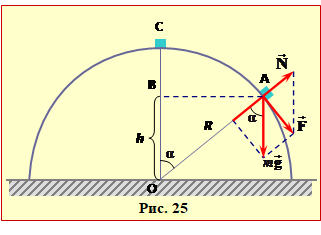
|
Дано: R |
|
h - ? |
Розв’язання
До відриву шайба під дією сил тяжіння та нормальної реакції опори (рис. 25. рухається по колу радіуса R з прискоренням, яке визначається рівнянням
\(m\vec{g}+\vec{N}=m\vec{a}\)
При цьому проєкція вектора \( {\vec{a}}\) на дотичну до кола визначає зміну величини швидкості шайби. Відповідно, його проєкція на радіус визначає зміну напрямку швидкості і є доцентровим прискоренням, котре виражається формулою (1.28). Отже, за другим законом Ньютона (2.5)
|
\(mg\cos \text{ }\!\!\alpha\!\!\text{ }-N=\frac{m{{v}^{2}}}{R}.\) |
(1) |
При зісковзуванні швидкість шайби v і кут α з часом зростають. Через це, як легко бачити з рівняння (1), реакція опори N поступово зменшується і на певній висоті h взагалі зникає, що означає відрив шайби від півсфери. Тож, поклавши в рівнянні (1) N = 0 i врахувавши вираз cosα = (h/R), знайдемо, що в точці відриву
|
${{v}^{2}}=gh$. |
(2) |
Величину ${{v}^{2}}$ не важко визначити із закону збереження енергії. У верхній точці півсфери шайба має тільки потенціальну енергію \( {{W}_{1}}=mgR \), а в точці відриву її енергія при тій самій величині W2 = W1 складається з кінетичної та потенціальної:
|
\({{W}_{2}}=\frac{m{{v}^{2}}}{2}+mgh.\) |
|
Отже,
|
\(mgR=\frac{m{{v}^{2}}}{2}+mgh\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ R=\frac{{{v}^{2}}}{2g}+h.\) |
|
Відтак, замінивши v2, згідно з виразом (2), отримаємо відповідь:
|
\(h=\frac{2}{3}R=40\) см. |
|
Через гладкий горизонтальний штир перекинуто м'який канат довжини \( {l=10}\) м так, що його кінці розташовані на одному рівні, (рис. 26а). Після незначного поштовху канат починає зісковзувати.
Визначити
його швидкість на момент сходу зі штиря, (рис. 26б).
|
Дано: l = 10 м |
|
v - ? |
Розв’язання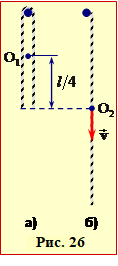
За умовою на канат діють лише консервативна сила тяжіння реакція штиря, котра не виконує роботи, бо через відсутність тертя є перпендикулярною до переміщення каната. В такому разі повна механічна енергія каната зберігається, тож набута ним кінетична енергія дорівнює спадові потенціальної енергії:
$\frac{m{{v}^{2}}}{2}=mg{{h}_{1}}-mg{{h}_{2}}$ $\Rightarrow $ $v=\sqrt{2g\left( {{h}_{1}}-{{h}_{2}} \right)}$,
де (h1 – h2) – відстань між початковим і кінцевим положенням центра мас каната, котра, як видно з рис. 26, дорівнює (l/4). Отже, шукана швидкість каната дорівнює
\( v=\sqrt{\frac{gl}{2}}\) = 7 м/с.
|
|
| Задача 4.27ЗАЗадача 4.26 |
| Задача 4.27 |
Підвішений на пружині тягарець, який розтягає її на задану величину х0, підіймають до положення, в якому пружина не деформована, й відпускають.
Визначити:
1) максимальний розтяг хm пружини;
2) максимальну швидкість тягарця vm.
|
Дано: х0 |
|
хm - ? vm - ? |
Розв’язання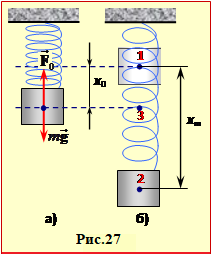
У системі "тягарець-пружина" діють тільки консервативні сили тяжіння та пружності, тож її механічна енергія зберігається.
1) Будемо відраховувати потенціальну енергію тягарця від найнижчого положення (т. 2 на рис. 27б), де деформація пружини xm є найбільшою. Тоді в момент вивільнення тягарця (т. 1) енергія системи складається лише з потенціальної енергії тягарця mgxm, а в найнижчому (т. 2) – тільки з такої самої за величиною потенціальної енергії розтягнутої пружини \(\left( {kx_{m}^{2}}/{2}\; \right)\). Отже,
|
\( {mg}{{x}_{{m}}}=\frac{kx_{{m}}^{2}}{2}\ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \ {{x}_{{m}}}=\frac{2mg}{k} \), |
(1) |
де m – маса тягарця, k – жорсткість пружини.
Відношення (m/k) визначимо з умови рівноваги підвішеного тягарця через задану величину статичного розтягу пружини x0 (рис. 27а) :
|
mg = kx0 $\Rightarrow $ $\frac{m}{k}$ = $\frac{{{x}_{0}}}{g}$ |
(2) |
Відтак
| xm = 2x0. |
(3) |
2) Для визначення максимальної швидкості тягарця врахуємо, що коли він знаходиться вище положення рівноваги (розтяг пружини \( {x}\lt{{x}_{0}}\)), рівнодійна сил тяжіння та пружності напрямлена донизу, і швидкість тягарця зростає. Якщо ж \( {x}\gt{{x}_{0}}\), то рівнодійна напрямлена вгору, і швидкість тягарця зменшується. Тож максимальну швидкість тягарець має при проходженні положення рівноваги (т. 3 на рис. 27б). При цьому механічна енергія системи
|
\({{W}_{3}}=\frac{mv_{{m}}^{2}}{2}+\frac{kx_{0}^{2}}{2}+mg{{x}_{0}}.\) |
|
Згідно із законом збереження \( {{W}_{1}}={{W}_{2}}\) (або \( {{W}_{3}}={{W}_{2}}\)), отже
|
\(\frac{mv_{{m}}^{2}}{2}+\frac{kx_{0}^{2}}{2}+mg{{x}_{0}}=mg{{x}_{{m}}}.\) |
|
З цього рівняння, врахувавши співвідношення (2) та результат (3), знайдемо
|
\({{v}_{{m}}}=\sqrt{g{{x}_{0}}}.\) |
|
Величину vm можна знайти більш прямо, визначивши за законом збереження енергії та проаналізувавши на максимум залежність v(х) швидкості тягарця від координати (відстані від т. 2). Але для цього треба знати відповідні положення вищої математики.