ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
У системах із невеликої кількості тіл (зазвичай двох) закон збереження імпульсу дозволяє ''автоматично'' визначати швидкості тіл після взаємодії через їхні значення до взаємодії. Це може бути самостійним завданням, або етапом розв'язування більш складної задачі.
Задача 3.1. Дві пластилінові кульки масами m1= 40 г та m2= 60 г, які рухаються гладкою горизонтальною поверхнею зі швидкостями v1= 0,3 м/с і v2= 0,4 м/с під кутом \( \alpha=60^{\circ}\) одна до одної, після зіткнення злипаються й рухаються далі, як одне ціле. Визначити швидкість v утвореного складеного тіла.
Задача 3.2. Граната, кинута під кутом \(\alpha \) = 60° до горизонту зі швидкістю v0 = 10 м/с, розривається на два однакові осколки так, що один відлітає вертикально вгору, а другий – під кутом \( \beta=45^{\circ}\) до горизонту. Визначити швидкість v2 відльоту другого осколка.
Задача 3.3. Коли два човни, що рухаються паралельними зустрічними курсами, порівнялись із першого в другий на ходу обережно переклали вантаж маси m = 25 кг. Відтак другий човен зупинився, а перший продовжив рух зі швидкістю u = 4 м/с. Визначити швидкості човнів v1 та v2 до перекладання вантажу, якщо маса другого човна M = 200 кг.
Задача 3.4. Двоє хлопців однакової маси горизонтально стрибають із нерухомого візка з однаковою швидкістю u щодо нього. Відношення мас візка та хлопця η = (М/m). Визначити швидкість відкочування візка v, якщо хлопці зістрибують: 1) одночасно і 2) поспіль один за одним.
Задача 3.5. Хлопець маси m, який стоїть на краю рухомого візка маси M, стрибає по ходу під кутом \( \alpha \) до горизонту зі швидкістю u відносно візка. Визначити величину та напрям швидкості візка ${{\vec{V}}_{1}}$ після стрибка, якщо до того її модуль складав V.
Задача 3.6. На кінці дошки масою M = 1,4 кг і довжиною l = 1 м, яка стоїть на плаву в ставку, сидить жаба маси m = 100 г. Жаба стрибає під кутом \( \alpha=30^{\circ}\) до поверхні дошки так, що опиняється на протилежному кінці. Визначити швидкість v0 стрибка жаби відносно води.
Задача 3.7. Випущена з поверхні землі граната у верхній точці траєкторії на висоті H = 45 м і відстані S0 = 300 м розривається на два однакові осколки так, що один падає на під точкою розриву через τ = 1 с. Визначити, на якій відстані S від нього впаде другий.
Задача 3.8. Рибалка масою m перейшов з корми на ніс човна маси M і довжини L, який стоїть на плаву в ставку. Нехтуючи опором води, визначити переміщення \( \vec{S}\), що його здійснив при цьому човен.
Задача 3.9. Кульки масами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг і m4 =4 кг, які в певний момент послідовно займають вершини квадрата, рухаються кожна в напрямку наступної із швидкостями v1 = 4 м/с, v2 = 3 м/с, v3 = 2 м/с, v4 = 1 м/с. Визначити швидкість \( \vec{V}\) центра мас кульок у цей момент.
Задача 3.10. Тягарці масами m1 = 1 кг і m2 = 2 кг, що з'єднані ниткою перекинутою через блок, утримують на одному рівні. Визначити, з яким прискоренням aс почне рухатися центр мас системи, якщо тягарці відпустити.
| Задача 3.1 |
| Задача 3.1 |
Дві пластилінові кульки масами m1= 40 г та m2= 60 г, які рухаються гладкою горизонтальною поверхнею зі швидкостями v1= 0,3 м/с і v2= 0,4 м/с під кутом \( \alpha=60^{\circ}\) одна до одної, після зіткнення злипаються й рухаються далі, як одне ціле
Визначити
швидкість v утвореного складеного тіла.
|
Дано: m1 = 40 г
m2 = 60 г
v1 = 0,3 м/с
v2 = 0,4 м/с
\( \alpha=60^{\circ}\) |
|
v - ? |
Розв'язання
Зовнішні сили (тяжіння та реакції поверхні), що діють на кульки, є компенсовані, тож імпульс системи зберігається:
| \( {m}_{1}\vec{v}_{1}+m_{2}\vec{v}_{2}=(m_{1}+m_{2})\vec{v}\) |
|
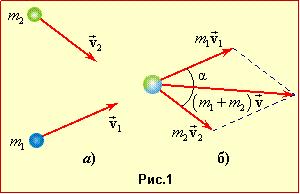
З побудованого за цим рівнянням паралелограма імпульсів (рис. 1) за допомогою теореми косинусів знаходимо відповідь:
\( {v}=\frac{\sqrt{(m_{1}v_{1})^{2}+(m_{2}v_{2})^{2}+2m_{1}m_{2}v_{1}v_{2}\cos\alpha}}{m_{1}+m_{2}}\) ≈ 0,3 м/с.
| Задача 3.2 |
| Задача 3.2 |
Граната, яку кинули під кутом \(\alpha \) = 60° до горизонту зі швидкістю v0 = 10 м/с, розривається на два однакові осколки. Один із них відлітає вертикально вгору, а другий – під кутом \( \beta=45^{\circ}\) до горизонту.
Визначити
швидкість v2 відльоту другого осколка.
|
Дано: v0 = 10 м/с
\( \alpha=60^{\circ}\)
\( \beta=45^{\circ}\)
|
|
v2 - ? |
Розв'язання
Система "граната-уламки" не є ізольованою, оскільки на тіла діє некомпенсована зовнішня сила тяжіння. Але на короткий час вибуху, коли діють дуже великі внутрішні сили тиску порохових газів, силою тяжіння можна знехтувати і вважати, що розрив гранати відбувається із збереженням імпульсу:
| \( \vec{p}=\vec{p}_{1}+\vec{p}_{2}\), |
де \( \vec{p}\) – імпульс гранати безпосередньо перед розривом, \( \vec{p}_{1}\) та \( \vec{p}_{2}\) – імпульси уламків одразу після розриву (рис. 2).
У проекціях на вісь OX записане рівняння має вигляд:
| \( {p}_{x}=p_{2x}\cos\beta \) \( \Rightarrow \) \( {m}v_{x}=\frac{m}{2}v_{2}\cos\beta \). | (1) |
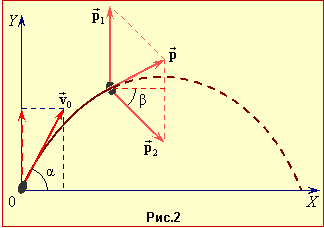 Складова імпульсу гранати вздовж осі OX залишається незмінною від моменту кидання до моменту розриву, оскільки проекція сили тяжіння на цей напрямок дорівнює нулю:
Складова імпульсу гранати вздовж осі OX залишається незмінною від моменту кидання до моменту розриву, оскільки проекція сили тяжіння на цей напрямок дорівнює нулю:
| \( {m}v_{x}=mv_{0}\cos\alpha\). | (2) |
Прирівнявши праві частини виразів (1) та (2), дістанемо:
| \( {m}v_{0}\cos\alpha=\frac{m}{2}v_{2}\cos\beta \) \( \Rightarrow \) \( {v}_{2}=v_{0}\frac{2\cos\alpha}{\cos\beta}={14,1}\) м/с. |
| Задача 3.3 |
| Задача 3.3 |
Коли два човни, що рухаються паралельними зустрічними курсами, порівнялись, із першого в другий на ходу обережно переклали вантаж маси m = 25 кг. Відтак другий човен зупинився, а перший продовжив рух зі швидкістю u = 4 м/с.
Визначити
швидкості човнів v1 та v2 до перекладання вантажу, якщо маса другого човна M2 = 200 кг.
|
Дано: m = 25 кг
u = 4 м/с
M2 = 200 кг
|
|
v1 - ? v2 - ? |
Розв'язання
Зовнішні сили (тяжіння та архімедова), що діють на човни є компенсовані, тож човни можна розглядати як замкнену систему. Тому при перекладанні вантажу імпульс першого човна зменшується, а другого збільшується на величину \( m\vec{v}_{1}\) без зміни сумарного імпульсу системи. Позаяк величина кінцевої швидкості першого човна u відома, то в проєкціях на напрям його руху можна записати:
| $\left( {{M}_{1}}+m \right){{v}_{1}}-m{{v}_{1}}={{M}_{1}}u$ \( \Rightarrow \) v1 = u = 4 м/с. |
У цьому результаті немає нічого дивного, бо при перекладанні вантажу на човни ніякі сили вздовж напряму руху не діють, тож причиною зміни імпульсу першого човна є тільки втрата маси.
Другий човен, який рухається назустріч, отримує імпульс перекладеного вантажу й зупиняється. Отже, його початковий імпульс мав таку саму величину:
|
\( {M_{2}}v_{2}=mv_{1}\) \( \Rightarrow \) ${{v}_{2}}=\frac{m}{{{M}_{2}}}u$ = 0,5 м/с. |
| Задача 3.4 |
| Задача 3.4 |
Двоє хлопців однакової маси горизонтально стрибають із нерухомого візка з однаковою швидкістю u щодо нього. Відношення мас візка та хлопця η = (М/m).
Визначити
швидкість відкочування візка v, якщо хлопці зістрибують:
1) одночасно;
2) поспіль один за одним.
|
Дано: (M/m) = η
u
|
|
V1 -? V2 -? |
Розв'язання
Система "візок-хлопці" на загал не є ізольованою, бо в ній діють зовнішні сили тяжіння та нормальної реакції поверхні, на якій стоїть візок. Але при горизонтальному відштовхуванні хлопців від візка ці сили лишаються компенсованими, тому імпульс системи зберігається.
1. Хлопці стрибають одночасно.
Позаяк до стрибка візок був нерухомий, сумарний імпульс візка та хлопців після стрибка
$M{{\vec{V}}_{1}}+2m{{\vec{v}}_{1}}=0$,
де ${{\vec{V}}_{1}}$ i ${{\vec{v}}_{1}}$ – швидкість візка та швидкість хлопців відносно землі.
Звідси, враховуючи співвідношення M = ηm і закон додавання швидкостей (1.11) ${{\vec{v}}_{1}}=\vec{u}+{{\vec{V}}_{1}}$, отримаємо швидкість візка після одночасного зістрибування хлопців:
| $\left( \eta +2 \right){{\vec{V}}_{1}}+2\vec{u}=0$, $ \Rightarrow $ ${{\vec{V}}_{1}}=-\frac{2}{\eta +2}\vec{u}$ |
Знак "–" указує на те, що візок відкочується в протилежному до стрибка напрямі.
2. Хлопці стрибають почергово.
У цьому випадку після першого стрибка візок набуває проміжного імпульсу ${\vec{P}}'$ і швидкості ${\vec{V}}'$, які знаходяться аналогічно до попереднього. А саме:
$\left( M+m \right){\vec{V}}'$ + $m{\vec{v}}'$ = 0.
Далі, позаяк M = ηm, і ${\vec{v}}'$ = $\vec{u}+{\vec{V}}'$, маємо:
| $\left( \eta +1 \right){\vec{V}}'+\left( \vec{u}+{\vec{V}}' \right)=0$ $ \Rightarrow $ ${\vec{V}}'=-\frac{1}{\eta +2}\vec{u}$ | (1) |
Збереження імпульсу при другому стрибку виражається рівнянням
$\left( M+m \right){\vec{V}}'=M{{\vec{V}}_{2}}+m{{\vec{v}}_{2}}$,
звідки, підставивши M = ηm і ${{\vec{v}}_{2}}=\vec{u}+{{\vec{V}}_{2}}$, дістанемо:
|
${{\vec{V}}_{2}}={\vec{V}}'-\frac{1}{\eta +1}\vec{u}$. |
Звідси, врахувавши вираз (1), після нескладних перетворень отримаємо кінцеву швидкість візка:
${{\vec{V}}_{2}}=-\frac{2\eta +3}{\left( \eta +1 \right)\left( \eta +2 \right)}\vec{u}$
| Задача 3.5 |
Хлопець маси m, який стоїть на краю рухомого візка маси M, стрибає по ходу під кутом \( \alpha \) до горизонту зі швидкістю u відносно візка.
Визначити
величину та напрям швидкості візка ${{\vec{V}}_{1}}$ після стрибка, якщо до її модуль складав V.
|
Дано: M, m
α
u
|
|
V1 - ? |
Розв'язання
Ця задача нагадує попередню. Але в даному випадку повний імпульс системи "візок-хлопець" не зберігається, в чому можна переконатися безпосередньо, зобразивши вектори імпульсу системи перед стрибком \( \vec{P}_{п}=(M+m)\vec{V}\) та після стрибка хлопця \( \vec{P}_{к}=M\vec{V}_{1}+m\vec{v}\) (рис. 5).
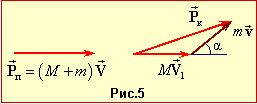
Очевидно, що вектори кінцевого та початкового імпульсу системи мають різний напрям. Тож за будь-яких умов
\( \vec{P}_{п}\ne\vec{P}_{к}\) \( \Rightarrow \) $\Delta \vec{P}\ne 0$.
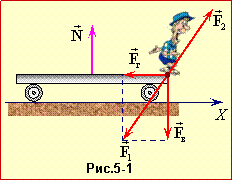
Сказане може здатися неочікуваним – адже до стрибка зовнішні сили тяжіння та реакції опори були компенсовані. Це справді так і є, але під час стрибка компенсація даних сил порушується, позаяк сила відштовхування хлопця \( \vec{F}_{1}\) та протилежно спрямована реакція візка \( \vec{F}_{2}=-\vec{F}_{1}\) діють під кутом до горизонту (рис. 5-1). Ці сили є внутрішніми й самі по собі не здатні змінити імпульс системи хлопець-візок. Але сила \( \vec{F}_{1}\) не лише змінює швидкість візка завдяки складовій \( \vec{F}_{г}\), а й притискає його до землі, викликаючи додаткову реакцію опори \( \vec{N}=-\vec{F}_{в}\), яка є зовнішньою силою й змінює імпульс \( \vec{P}\) системи "візок-хлопець". При цьому, позаяк \( {N}_{x}={0}\), горизонтальна проєкція імпульсу системи Px не змінюється. Отже,
| \( {(M+m)}V=MV_{1x}+mv_{x}\). | (1) |
У цьому рівнянні vx – горизонтальна складова швидкості хлопця відносно землі \( \vec{v}\), котра пов'язана з його швидкістю відносно візка \( \vec{u}\) законом додавання швидкостей (1.19):
\( \vec{v}=\vec{u}+\vec{V}_{1}\) \( \Rightarrow \) \( {v}_{x}=u\cos\alpha+V_{1x}\).
(Зверніть увагу на те, що в рівняння входить швидкість візка після, а не до стрибка, адже на момент відриву ніг хлопця від опори візок уже набув кінцевої швидкості).
Підставивши отриманий вираз vx у рівняння (1) знайдемо:
\( {V}_{1x}=\frac{(M+m)V-mu\cos\alpha}{M+m}\).
У відповідності до отриманого результату можливі три різні випадки руху візка після стрибка хлопця:
1. При \( {(M+m)}V>mu\cos\alpha \), то \( {V}_{1x}>{0}\), отже, візок продовжує рухатись у тому самому напрямі, але з меншою швидкістю;
2. При \( {(M+m)}V<mu\cos\alpha \), то \( {V}_{1x}<{0}\), тобто візок змінює напрям руху;
3. При \( {(M+m)}V=mu\cos\alpha \), то \( {V}_{1x}={0}\), і візок зупиняється.
| Задача 3.6. |
| Задача 3.6. |
На кінці дошки масою M = 1,4 кг і довжиною l = 1 м, яка стоїть на плаву в ставку, сидить жаба маси m = 100 г. Жаба стрибає під кутом \( \alpha=30^{\circ}\) до поверхні дошки так, що опиняється на протилежному кінці.
Визначити
швидкість v0 стрибка жаби відносно води.
|
Дано: M = 1,4 кг
l = 1 м
m = 100 г
\( \alpha=30^{\circ}\)
|
|
v0 - ? |
Розв'язання
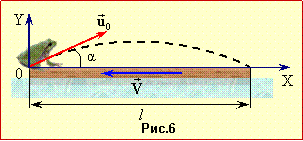 Розглянемо задачу спочатку в рухомій системі відліку дошки (рис. 6), занотувавши, що горизонтальне та вертикальне переміщення жаби за час стрибка складають Δx = l і Δy = 0, а проєкції прискорення ax = 0 і ay = –g. Відтак за допомогою рівнянь кінематики (1.16) визначимо модуль і проєкції швидкості $\vec{u}$ стрибка жаби відносно дошки:
Розглянемо задачу спочатку в рухомій системі відліку дошки (рис. 6), занотувавши, що горизонтальне та вертикальне переміщення жаби за час стрибка складають Δx = l і Δy = 0, а проєкції прискорення ax = 0 і ay = –g. Відтак за допомогою рівнянь кінематики (1.16) визначимо модуль і проєкції швидкості $\vec{u}$ стрибка жаби відносно дошки:
\(\left. \begin{matrix} l={{u}_{0}}t\cos \alpha \\ 0={{u}_{0}}t\sin \alpha -\frac{g{{t}^{2}}}{2} \\\end{matrix} \right\}\ \ \ \ \ \ \Rightarrow \ \ \ \ \ {{u}_{0}}=\sqrt{\frac{gl}{2\sin \alpha \cdot \cos \alpha }}.\)
| \( {u}_{0x}=u_{0}\cos\alpha=\sqrt{\frac{gl\cos^{2}\alpha}{2\sin\alpha{\cos\alpha}}}=\sqrt{\frac{gl}{2}\mathrm{ctg}\alpha}\), | (1) |
\( {u}_{0y}=u_{0}\sin\alpha=\sqrt{\frac{gl\sin^{2}\alpha}{2\sin\alpha\cos\alpha}}=\sqrt{\frac{gl}{2}\mathrm{tg}\alpha}\).
Унаслідок віддачі при стрибку жаби, дошка почне рухатись у зворотньому напрямі зі швидкістю \( \vec{V}\) відносно води (нерухома система відліку). При цьому за законом додавання швидкостей (1.19)
\( \vec{v}_{0}=\vec{u}_{0}+\vec{V}\),
а в проекціях на осі OX та OY
| \( {v}_{0x}=u_{0x}-{V}\), | (2) |
| \( {v}_{0y}=u_{0y}\). | (3) |
Тож, аби визначити швидкість стрибка жаби відносно води v0, треба спочатку знайти швидкість V, отриману дошкою. Це завдання є аналогічним до попередньої Задачі 3.5. А саме. Під час стрибка жаба трохи притоплює дошку, через що виникає некомпенсована додаткова архімедова сила, котра змінює імпульс системи. Але, позаяк ця сила спрямоване вертикально, горизонтальна складова імпульсу лишається незмінною:
\( {-M}V+mv_{0x}={0}\) \( \Rightarrow \) \( {V}=\frac{m}{M}v_{0x}\).
Підставивши цей вираз у рівняння (2), отримаємо
\( {v}_{0x}=u_{0x}-\frac{m}{M}v_{0x}\) \( \Rightarrow \) \( {v}_{0x}=\frac{M}{M+m}u_{0x}\).
Відтак, врахувавши рівняння (3) і вираз (1), знайдемо відповідь:
\( {v}_{0x}=\frac{M}{M+m}\sqrt{\frac{gl}{2}\mathrm{ctg}\alpha }\),
\( {v}_{0}=\sqrt{v_{0x}^{2}+v_{oy}^{2}}=\sqrt{\left(\frac{M}{m+M}\right)^{2}\frac{gl}{2}\mathrm{ctg}\alpha+\frac{gl}{2}\mathrm{tg}\alpha}\) =
= \(\sqrt{\frac{gl}{2}\left(\left(\frac{M}{M+m}\right)^{2}\mathrm{ctg\alpha}+\mathrm{tg}\alpha\right)}\).
Обчислення дають
v0 = 3,2 м/с.
| Задача 3.7 |
| Задача 3.7 |
Випущена з поверхні землі граната у верхній точці траєкторії на висоті H = 45 м і горизонтальній відстані S0 = 300 м розривається на два однакові осколки так, що один падає на під точкою розриву через τ = 1 с.
Визначити,
на якій відстані S від нього впаде другий
.
|
Дано: Н = 45 м
S0 = 300 м
τ = 1 с
|
|
S - ? |
Розв'язання
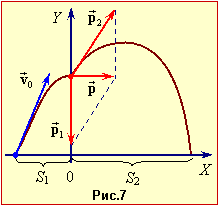
Процес розриву снаряда є швидкоплинний і відбувається без утрати його імпульсу, як показано на рис. 7:
| \( \vec{p}=\vec{p}_{1}+\vec{p}_{2}\). |
Це дозволяє взнати швидкість відльоту другого осколка \(\vec{v}_{2}\), що визначає шукану відстань S.
За умовою m1 = m2 = (m/2), отже,
|
\( {m}\vec{v}=\frac{1}{2}m\vec{v}_{1}+\frac{1}{2}m\vec{v}_{2}\) \( \Rightarrow \) \( \vec{v}_{2}=2\vec{v}-\vec{v}_{1}\). |
Звідси, враховуючи напрямки швидкостей снаряда й першого осколка, для проєкцій початкової швидкості другого осколка маємо:
|
${{v}_{2x}}=2{{v}_{0x}}$, \({v}_{2y}=v_{1}\). |
(1) |
Граната та осколки рухаються із прискоренням \( \vec{g}\), тож gх = 0, і шукана відстань
| S = v2xt2 = 2v0xt2. | (2) |
Таким чином, задача зводиться до визначення горизонтальної проєкції початкової швидкості гранати та часу руху другого осколка, які можна знайти з рівнянь кінематики через задані значення S0, H і t1. Зокрема, якщо позначити як t0 час руху гранати до розриву, то, за рівнянням (1.16)
| ${{v}_{0x}}=\frac{{{S}_{0}}}{{{t}_{0}}}$. |
За час t0 по вертикалі граната проходить відстань H і зменшує швидкість від v0y до 0, тож, згідно з рівняннями (1.16) і (1.18),
${{t}_{0}}=\frac{{{v}_{0y}}}{g}, {{v}_{0y}}=\sqrt{2gH}$ \( \Rightarrow \) ${{t}_{0}}=\sqrt{\frac{2H}{g}}$.
Отже,
|
${{v}_{0x}}={{S}_{0}}\sqrt{\frac{g}{2H}}$, |
і згідно з (2),
|
$S=2{{S}_{0}}\sqrt{\frac{g}{2H}}\cdot {{t}_{2}}$. |
(3) |
Відтак належить знайти час руху t2 другого осколка. Це можна зробити за допомогою рівнянь (1.16) через задані початкову y20 = H і кінцеву y2 = 0 координати та знайдену вертикальну складову початкової швидкості \({v}_{2y}=v_{1}\). Але зручніше окремо розглянути час ${{{t}'}_{2}}$ проходження ділянки АВ траєкторії та ${{{t}''}_{2}}$ – завершальної ділянки ВС. На першій ділянці швидкість спочатку зменшується від v1 до 0, а потім до такої ж величини зростає, тож ${{{t}'}_{2}}$ = (2v1/g). З цієї ж причини t2″= τ , отже,
|
${{t}_{2}}=\frac{2{{v}_{1}}}{g}+\tau $. |
(4) |
Таким чином, для визначення часу руху другого осколка необхідно мати величину v1. Її знайдемо з рівняння (1.16) для першого осколка, поклавши y1 = H i y10 = 0:
$0=H-{{v}_{1}}\tau -\frac{g{{\tau }^{2}}}{2}\quad \Rightarrow \quad \frac{2{{v}_{1}}}{g}=\frac{2H}{g\tau }-\tau $.
Урахувавши цей результат, із виразу (4) отримаємо
${{t}_{2}}=\frac{2H}{g}$,
і після підстановки у вираз (3) – відповідь задачі:
$S=\frac{4{{S}_{0}}}{\tau }\sqrt{\frac{H}{2g}}$ = 1,8 км.
Задача 3.8.
Рибалка масою m перейшов з корми на ніс човна маси M і довжини L, який стоїть на плаву в ставку. Нехтуючи опором води,
визначити
переміщення \( \vec{S}\), що його здійснив при цьому човен.
|
Дано: M, m
L
|
|
\(\vec{S}\)-? |
Розв’язання
Задачу можна розв'язати двома способами.
І спосіб. У системі ''рибалка-човен'' сили взаємодії між тілами є внутрішніми і не надають їй ніякого сумарного імпульсу. Тому при переміщенні рибалки з якоюсь швидкістю \( \vec{v}\) човен рухається в протилежному напрямку із таким самим величиною імпульсом і відповідною швидкістю \(\vec{V}\), тож
| $M\vec{V}=-m\vec{v}$ | (1) |
Відтак, виразивши швидкості через переміщення, отримаємо:
| \( {M}\vec{S}\) = –\( {m}\vec{s}\) | (2) |
На перший погляд отримане співвідношення по суті є розв'язком задачі, позаяк відстань між кормою та носом човна L є задана. Але таке міркування є хибним, бо рівняння (1) і (2) пов'язують швидкості та переміщення рибалки й човна відносно води, тоді як довжина човна L є переміщенням s′ рибалки відносно човна. А відносно води воно, згідно з формулою (1.9а), з урахуванням напрямків (див. рис. 3.8), дорінює
${s}={{s}}'–{S}$.
Підставивши цей вираз в рівняння (2) і, врахувавши, що s′ = L, після елементарних викладок отримаємо остаточну відповідь:
| $S=\frac{m}{M+m}L$. | (3) |
ІІ спосіб. Згідно з теорією ( п. 3.4, ф-ла (3.7)) імпульс системи "човен-рибалка" дорівнює добутку її сумарної маси на швидкість центра мас: ${{\vec{P}}_{\Sigma }}=\left( M+m \right){{V}_{с}}$. Тож, позаяк при переході рибалки ${{\vec{P}}_{\Sigma }}$ = 0, положення (радіус-вектор, п. 1.1) центра мас системи не змінюється. Тож, прирівнявши вирази (3.6) радіус-вектора \({{\vec{r}}_{с}}\) початкового та кінцевого положення рибалки (\( \vec{r}_{1р},\,\,\vec{r}_{2р}\)) та човна (\( \vec{r}_{1ч},\,\,\vec{r}_{2ч}\)), отримаємо:
\( M{{\vec{r}}_{1ч}}+m{{\vec{r}}_{1р}}=M{{\vec{r}}_{2ч}}+m{{\vec{r}}_{2р}}\ \ \Rightarrow \ \ \ M({{\vec{r}}_{1ч}}-{{\vec{r}}_{2ч}})=m({{\vec{r}}_{2р}}-{{\vec{r}}_{1р}}).\)
Приріст радіус-вектора точки є її переміщенням (ф-ла (1.1)), отже
| \( {M}\vec{S}\) = –\( {m}\vec{s}\), |
що збігається з виразом (2) і дає ту саму відповідь (3).
Задача 3.9.
Кульки масами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг і m4 =4 кг в певний момент послідовно займають вершини квадрата і рухаються кожна в напрямку наступної із швидкостями v1 = 4 м/с, v2 = 3 м/с, v3 = 2 м/с, v4 = 1 м/с.
Визначити
швидкість \( \vec{V}\) центра мас кульок у цей момент.
|
Дано: m1 = 1 кг, v1 = 4 м/с; m2 = 2 кг, v2 = 3 м/с; m3 = 3 кг, v3 = 2 м/с; m4 = 4 кг, v4 = 1 м/с. |
|
${\vec{V}}$-? |
Розв’язання
Згідно з формулами (1.5а) і (3.6а), проєкції швидкості центра мас Vx , Vy на осі координат визначаються відношенням суми добутків мас кульок на проєкції їхніх швидкості до сумарної маси системи. Тож, обравши для обчислень систему координат ХOY, як показано на рис. 3.9 і врахувавши напрямки векторів швидкості, отримаємо:
${{V}_{x}}=\frac{{{m}_{2}}{{v}_{2}}-{{m}_{4}}{{v}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ = 0,2 м/с;
${{V}_{y}}=\frac{{{m}_{1}}{{v}_{1}}-{{m}_{3}}{{v}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ = –0,2 м/с.
Таким чином, у вказаний момент центр мас кульок рухається із швидкістю
$V=\sqrt{V_{x}^{2}+V_{y}^{2}}\approx 0,3\text{м/с}$
праворуч і вниз під кутом 45° до осей координат. Аби визначити точку прикладання вектора \( \vec{V}\), треба за формулами (3.6а) обчислити координати центра мас кульок. Але в даній задачі це можна зробити і без обчислень, скориставшись їхнім сприятливим розташуванням. А саме. Позаяк сумарна маса двох горизонтальних пар кульок 2-3 і 1-4 (рис. 3.9) однакова, то очевидно, що центр мас С знаходиться на горизонталі аb, що проходить посередині. А сама точка С ділить відрізок аb у відношенні оберненому до відношення мас вертикальних пар кульок 1-2 і 3-4, тобто, як 7 : 3. Відповідно до цього на рис. 3.9 й показано вектор \( \vec{V}\).
Задача 3.10.
Тягарці масами m1 = 1 кг і m2 = 2 кг, що з'єднані ниткою, перекинутою через блок, утримують на одному рівні.
Визначити,
з яким прискоренням ас почне рухатися центр мас системи, якщо тягарці відпустити.
|
Дано: m1 = 1 кг, m2 = 2 кг |
|
aс - ? |
Розв’язання
Тягарці на нитці утворюють зв'язану систему тіл, в якій діють зовнішні сили тяжіння ${{m}_{1}}\vec{g}$, ${{m}_{2}}\vec{g}$ і реакція осі блока $\vec{R}$ та внутрішні сили натягу нитки $\vec{T}$, ${\vec{T}}'$, рис. 3.10. (Формально система включає ще й блок, але за умовчанням він є невагомим і ніяк не впливає на характеристики руху тягарців).
На загал величину а можна знайти за теоремою про рух центра мас та другим законом Ньютона. Але простіше це зробити, виходячи з того, що прискорення точки визначається другими похідними її координат по часу (розділ 1. вирази (1.8)). Тож, згідно з формулою (3.6а), можна записати:
\({{a}_{\operatorname{c}x}}=\frac{{{m}_{1}}{{x}_{1}}^{\prime \prime }+{{m}_{2}}{{x}_{2}}^{\prime \prime }}{{{m}_{1}}+{{m}_{2}}}\quad \Rightarrow \quad {{a}_{\operatorname{c}x}}=\frac{{{m}_{1}}{{a}_{1}}_{x}+{{m}_{2}}{{a}_{2}}_{x}}{{{m}_{1}}+{{m}_{2}}}\),
або, враховуючи, що прискорення тягарців мають однакову величину а,
| ${{a}_{\operatorname{c}x}}=\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)a$. | (1) |
Величину прискорення тягарців а легко знайти за другим законом Ньютона (2.5) з урахуванням напрямків руху:
$\left\{ \begin{align} & {{m}_{1}}g-T={{m}_{1}}a \\ & T-{{m}_{2}}g={{m}_{2}}a \\\end{align} \right.\quad \Rightarrow \quad a=\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)g$.
Відтак підставивши це значення у вираз (1), отримуємо відповідь:
$ {a}={{\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)}^{2}}g$.