ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв’язування задач
Зв'язок між імпульсом і силою
|
Типовим завданням у таких задачах є визначення сил через зміну імпульсу тіла за певний проміжок часу. Тому слід пам'ятати, що зміна імпульсу тіла визначається не окремими силами, а рівнодійною всіх сил, що прикладені до нього. Досить часто розглядані сили є змінними. В такому разі зміна імпульсу тіла визначається середнім за час дії імпульсом сили, який чисельно дорівнює площі під відповідною ділянкою графіка сили F(t). |
Задача 2.9. Кулька масою m = 200г, яка падає вертикально, на момент удару об підлогу має швидкість v = 5 м/с. Після удару кулька підскакує на висоту h =80 см. Визначити зміну модуля імпульсу та модуль зміни імпульсу кульки при ударі.
Задача 2.10. Кинута вертикально вгору пластилінова кулька масою m = 100 г прилипає до стелі, маючи перед ударом швидкість v = 5 м/с. Визначити середню силу тиску F кульки на стелю, якщо час удару \( \tau \) = 0,18 с. (Примітка. Часом удару називають тривалість взаємодії тіл при зіткненні. В даній задачі це час сплющування кульки від моменту дотику до припинення руху всіх її частин).
Задача 2.11. На кульки масами m1 і m2 = 2m1, що рухались у взаємно перпендикулярних напрямах із імпульсами однакової величини р, подіяла однакова сила, котра змінила напрям руху першої кульки на протилежний без зміни величини швидкості. Визначити величину та напрям кінцевої швидкості другої кульки, якщо початкова дорівнювала v.
Задача 2.12. Ракета з початковою масою M при старті на деякий час зависає над землею. Визначити, скільки палива за одиницю часу \( \mu \) вона при цьому витрачає, якщо швидкість витоку газів відносно ракети дорівнює u.
Задача 2.13. Пучок молекул налітає перпендикулярно на закріплену пластину й пружньо (без утрати швидкості) відбивається. Концентрація молекул у пучку n = 2,5·1019см–3, маса молекули m = 3,3·10–27кг, швидкість v = 1000 м/с . Визначити тиск P пучка на пластину.
Задача 2.14. Пружна кулька, що рухається горизонтально, вдаряє у вертикальну стінку під кутом α до нормалі. Визначити, під яким кутом β відскочить кулька, якщо стінка: а) гладка; б) шорстка й має коефіцієнт тертя μ.
Задача 2.15. На вагон маси m = 50 т, який рухається за інерцією зі швидкістю \( {v}_{0}={10}\) м/с, починає діяти гальмівна сила, що змінюється з часом за законом \( {F}=\alpha{t}\), де \( \alpha={100}\) Н/с. Визначити час \( \tau \) руху вагона до зупинки.
| Задача 2.10 |
| Задача 2.9 |
зміну модуля імпульсу та модуль зміни імпульсу кульки при ударі.
|
Дано:
m=200г=0,2кг
v1 = 5 м/c
h = 46 см |
|
Δp -? \(\left| \Delta \vec{p} \right|\)-? |
Розв’язання
На рис. 2.9 показані вектори імпульсу кульки в момент падіння ${{\vec{p}}_{1}}$ = $m{{\vec{v}}_{1}}$ і відскоку ${{\vec{p}}_{2}}$ = $m{{\vec{v}}_{2}}$ та зміни імпульсу $\left| \Delta \vec{p} \right|$ = $m\left|{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}} \right|$. При цьому, згідно з формулою (1.19),
${{v}_{2}}=\sqrt{2gh}=4\text{ м/с}$.
Отже, маємо наступні відповіді:
Δp = m(v2 – v1) = –0,2 кг·м/с;
$\left| \Delta \vec{p} \right|$ = $m\left({{{{v}}}_{2}}+{{{{v}}}_{1}} \right)$ = 1,8 кг·м/с.
| Задача 2.10 |
| Задача 2.10 |
Кинута вертикально вгору пластилінова кулька масою m = 100 г, прилипає до стелі, маючи перед ударом швидкість v = 4,9 м/с.
Визначити
середню силу тиску F кульки на стелю, якщо час удару \( \tau \) = 0,18 с.
|
Дано: m=100г=0,1кг
v = 5 м/c
τ = 0,18 c
|
|
F -? |
Розв’язання
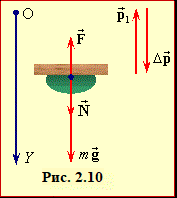
Прилипання є складним процесом пластичної деформації із невідомою залежністю від часу сил, які діють на кульку та на стелю. Але середню силу тиску кульки на стелю легко визначити за допомогою основних законів динаміки.
Під час удару на кульку діють сили тяжіння \( {m}\vec{g}\) та реакції опори (стелі) \( \vec{N}\), рис. 2.10. Отже, за другим законом Ньютона (5.4),
| $m\vec{g}+\vec{N}=\frac{\Delta \vec{p}}{\tau }\quad \Rightarrow \quad mg+N=\frac{\left| \Delta \vec{p} \right|}{\tau }$. | (1) |
За третім законом Ньютона шукана сила тиску кульки на стелю дорівнює реакції опори: F = N. Крім того, за час удару кулька втрачає увесь імпульс, отже,
${\left| \Delta \vec{p} \right|}$ = p = mv.
Зробивши такі підстановки в рівняння (1), знайдемо нвступну відповідь:
\( {F}=m\left(\frac{v}{\tau}-g\right) \) ≈ 1,7 Н.
| Задача 2.11 |
| Задача 2.11 |
На кульки масами m1 і m2 = 2m1, що рухались у взаємно перпендикулярних напрямах із імпульсами однакової величини р, подіяла однакова сила, котра змінила напрям руху першої кульки на протилежний без зміни величини швидкості.
Визначити
величину та напрям кінцевої швидкості другої кульки, якщо початкова дорівнювала v.
|
Дано: m2 = 2m1 v2 = v |
|
\({\vec{v}'_{2}}\)-? |
Розв'язання
Умову задачі відображує рис. 2.11-1а.
Згідно з умовою та ІІ законом Ньютона (2.4), прикладена сила спричинила однакову зміну імпульсів кульок:
\( \Delta\vec{p}_{1}=\Delta\vec{p}_{2}\),
тобто
| \({\vec{p}'_{1}}\) – \({\vec{p}_{1}}\)=\({\vec{p}'_{2}}\) – \({\vec{p}_{2}}\), |
де кінцеві величини позначені штрихом. Виразивши в цьому рівнянні імпульси через швидкості й маси, отримаємо:
| \({\vec{v}'_{1}}\) – \({\vec{v}_{1}}\)=2(\({\vec{v}'_{2}}\) – \({\vec{v}_{2}}\)). |
Звідси визначаємо вектор шуканої швидкості \({\vec{v}'_{2}}\), врахувавши, що за умовою \({\vec{p}'_{1}}\) = –\({\vec{p}_{1}}\), тож \({\vec{v}'_{1}}\) = –\({\vec{v}_{1}}\):
| \({\vec{v}'_{2}}\) = – \({\vec{v}_{1}}\) + \({\vec{v}_{2}}\). | (1) |
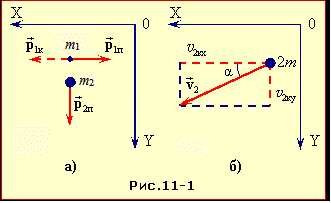
Модуль і напрям (кут α) вектора \({\vec{v}'_{2}}\) знайдемо із рис. 2.11-1б, який відображає вираз (1):
\({{v}'_{2}}\) = \(\sqrt{v_{1}^{2}+v_{2}^{2}}\), \(\operatorname{tg}\alpha =\frac{{{v}_{2}}}{{{v}_{1}}}\).
Отже,
\({{v}'_{2}}\) = v\(\sqrt{5}\) і α = 26,6°.
Зауважимо, що відповідь можна отримати й алгебраїчно, записавши рівняння (1) у проєкціях на осі координат:
|
v′2x = –2v, v′2y = v \( \Rightarrow \) \({{{v}'}_{2}}=\sqrt{{{\left( {{{{v}'}}_{2x}} \right)}^{2}}+{{\left( {{{{v}'}}_{2y}} \right)}^{2}}}=v\sqrt{5};\quad \alpha =\left| \operatorname{arctg}\frac{{{{{v}'}}_{2y}}}{{{{{v}'}}_{2x}}} \right|=26,6{}^\circ \). |
| Задача 2.12 |
| Задача 2.12 |
Ракета з початковою масою M при старті на деякий час "зависає" над землею.
Визначити,
скільки палива за одиницю часу \( \mu \) вона при цьому витрачає, якщо швидкість витоку газів відносно ракети дорівнює u.
|
Дано: M, u |
|
μ -? |
Розв'язання
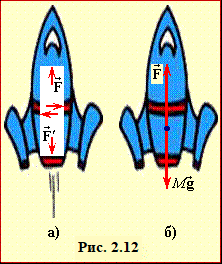
Сила, що утримує ракету від падіння, є зумовлена тиском на стінкки камери двигуна газів, який створюють продукти згорянні палива, що схематично показано на рис. 2.12. У герметичній порожнині, як приміром у гранаті перед розривом, вказані сили є компенсовані. Проте в нижній стінкці камери згоряння двигуна ракети (рис. 2.12а) є отвір (сопло), тож її площа менша, ніж площа верхньої стінкки. Відповідно, меншою є й сила тиску газів на нижню стінкку. Як наслідок, виникає спрямована вгору реактивна сила тяги F (рис. 2.12б) рівна силі F′, яка діє на гази, що вилітають із сопла.
Нехай за невеликий проміжок часу\( \Delta{t}\) із сопла під дією сили \( {F}^{\prime}\) зі швидкістю u викидається порція газів \( масою\Delta{m}\). Тоді за другим законом Ньютона (2.3)
\( {F}^{\prime}=\frac{\Delta{mu}}{\Delta{t}}\) \( \Rightarrow \) \( {F}^{\prime}=\mu{u}\),
де \( \mu \) – витрата палива за одиницю часу.
За умовою реактивна сила \( {F}=F^{\prime}\) зрівноважує силу тяжіння, що діє на ракету, отже,
\( {M}g=\mu{u}\) \( \Rightarrow \) \( \mu=\frac{Mg}{u}\).
Примітка. Витрата пального \( \mu \) реально є досить велика, і маса ракети M стрімко зменшується. Тому в отриманій формулі величини \( \mu \) і M слід розглядати як миттєві. При цьому для забезпечення тривалого зависання ракети витрата пального має зменшуватися з часом відповідно до зменшення маси ракети. Але розрахунок залежності μ(t) і M(t) виходить за межі елементарної фізики.
| Задача 2.13 |
| Задача 2.13 |
Пучок молекул налітає перпендикулярно на закріплену пластину й пружно (без утрати швидкості) відбивається. Концентрація молекул у пучку n = 2,5·1019см–3, маса молекули m = 3,3·10–27кг, швидкість v = 1000 м/с .
Визначити
тиск P пучка на пластину.
|
Дано: m = 3,3·10-27кг v = 1000 м/с n = 2,5·1019см-3 |
|
P - ? |
Розв’язання
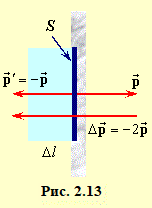 При зіткненні з пластиною окрема молекула створює мікроскопічний імпульс сили типу "уколу". Але через дуже велику щільність молекул у пучку ці уколи відбуваються так часто й густо, що створюють сталу й рівномірно розподілену по поверхні силу тиску.
При зіткненні з пластиною окрема молекула створює мікроскопічний імпульс сили типу "уколу". Але через дуже велику щільність молекул у пучку ці уколи відбуваються так часто й густо, що створюють сталу й рівномірно розподілену по поверхні силу тиску.
Для її визначення виділимо на стінці ділянку площею S (рис. 2.13). Імпульс сили, що діє на пластину під час зіткнення однієї молекули, за третім законом Ньютона дорівнює імпульсу сили, що діє з боку пластини на молекулу, отже
\( {f}\Delta{t}=\left|\Delta\vec{p}\right| \),
де f – середнє значення сили взаємодії між молекулою та пластиною, \( \Delta{t}\) – тривалість зіткнення, \( \left|\Delta\vec{p}\right| \) – модуль зміни імпульсу молекули за час зіткнення. Імпульс сумарної сили F, що діє на ділянку S протягом часу \( \tau \), запишеться як
\( {F}\tau=N\left|\Delta\vec{p}\right| \),
де N – кількість зіткнень молекул з ділянкою за час \( \tau \). Звідси маємо:
| \( {F}=\frac{N}{\tau}\left|\Delta\vec{p}\right|=n_{з}\left|\Delta\vec{p}\right| \), | (1) |
де \( {n}_{з}\) –кількість зіткнень за одиницю часу.
При цьому, позаяк зіткнення відбуваються без утрати швидкості, \( \Delta\vec{p}=-2\vec{p}\) (рис. 2.13), і
| \( \left|\Delta\vec{p}\right|=2p=2{mv}\). | (2) |
Відтак лишається визначити величину \( {n}_{з}\). Для цього на площинці S як на основі побудуємо циліндр висотою \( \Delta{l}\). Усі \( {N}=nS\Delta{l}\) молекул (n – концентрація), що містяться в ньому, стикаються з площинкою S за час \( \tau=\frac{\Delta{l}}{v}\) (\( {v}\) – швидкість руху молекул). Тож кількість зіткнень за одиницю часу складає
\( {n}_{з}=\frac{N}{\tau}=\frac{nS\Delta{l}}{(\Delta{l}/v)}={nSv}\).
Підставивши цей вираз і вираз (2) у формулу (1), дістанемо:
\( {F}=2nmv^{2}{S}\).
Відтак, поділивши силу F на площу S, отримаємо відповідь:
\( {P}=2nmv^{2}=1,65\cdot{10^{5}}\) Па.
Пружна кулька, що рухається горизонтально, вдаряє у вертикальну стінку під кутом α до нормалі.
Визначити,
під яким кутом β відскочить кулька, якщо стінка:
а) гладка;
б) шорстка й має коефіцієнт тертя μ.
|
Дано: μ α |
|
β – ? |
Розв'язання
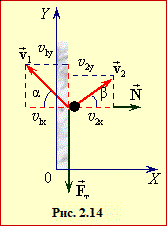
При косому ударі кульки в стінку, строго говорячи, завжди є присутнє тертя. Тому сила \( \vec{R}\) (рис. 2.14), з якою стінка діє на кульку, складається із сили нормального тиску \( \vec{N}\) та сили тертя $\vec{F}$:
\( \vec{R}\) = \( \vec{N}\) + $\vec{F}$.
Відповідно, за другим законом Ньютона (2.4) зміна імпульсу кульки $\vec{p}=m\vec{v}$ за час удару \(\tau \) визначається рівнянням:
|
$\vec{N}+\vec{F}=m\left( {{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}} \right)$. |
Отже, поклавши F = μN, отримаємо наступну систему рівнянь для проєкцій на горизонтальні осі (рис. 2.14):
|
OX: Nτ = m(v2cosβ + v1cosα) OY: –μNτ = m(v2sinβ – v1sinα), |
(1) |
і після почленного ділення
|
$\mu =\frac{{{v}_{1}}\sin \alpha -{{v}_{2}}\sin \beta }{{{v}_{1}}\cos \alpha +{{v}_{2}}\cos \beta }$. |
(2) |
Позаяк кулька є пружньою, процеси її стискання та відновлення форми, що зумовлені силою \( \vec{N}\), є віддзеркаленням один одного. Через це нормальні складові її швидкостей підльоту та відскоку збігаються:
|
v1cosα = v2cosβ \(\Rightarrow \) \( {v}_{2}=v_{1}\frac{\cos\alpha}{\cos\beta}\). |
(3) |
Зробивши таку заміну у виразі (2), після елементарних перетворень дістанемо:
|
$\mu =\frac{tg\alpha -tg\beta }{2}$, |
і загальний вираз, який визначає кут відбивання кульки від стінки:
| \( \mathrm{tg}\beta=\mathrm{tg}\alpha-2\mu \). | (4) |
а). Якщо стінка є гладка, то μ = 0 і, як випливає з виразів (4) і (3), β = α і v2 = v1. Отже, за відсутності тертя пружна кулька від нерухомої стінки відбивається дзеркально – під таким самим кутом і з такою самою швидкістю, що й падає. (До речі, такого висновку можна дійти й “без математики”, спираючись на закон збереження енергії).
б). При μ ≠ 0 ті ж таки співвідношення (3) і (4) дають v2 < v1 і β < α, тобто від шорсткої стінки кулька відбивається з меншою швидкістю і під меншим кутом, аніж падає. Це пояснюється тим, що на самому початку для сили тертя було взято звичну величину F = μN, при якій в процесі зіткнення кулька ковзає по стінці (див. п. 2.3), тож і гальмується. При цьому сила тертя зменшує тільки паралельну до стінки складову швидкості, що призводить до зменшення кута відскоку β. Але звертає на себе увагу наступне. При tgα < 2μ вираз (4) втрачає зміст, хоча є очевидним, що кут α може мати будь-яку величину в інтервалі 0 ≤ α ≤ 90°. Проте цей "парадокс" теж має пояснення. При зменшенні кута α сила нормального тиску N = Rcosα та гальмівна сила F = μN зростають, так що при tgα = 2μ кулька перед відривом перестає ковзати (v2sinα = 0) і відлітає по нормалі до стінки (β = 0).
Таким чином, при відбиванні кульки від шорсткої стіни відповідь задачі є подвійною:
β =arctg(tgα – 2μ), tgα > 2μ;
β = 0, tgα ≤ 2μ.
| Задача 2.15 |
| Задача 2.15 |
На вагон маси m = 50 т, який рухається за інерцією зі швидкістю \( {v}_{0}={10}\) м/с, починає діяти гальмівна сила, що змінюється з часом за законом \( {F}=\alpha{t}\), де \( \alpha={100}\) Н/с.
Визначити
час \( \tau \)руху вагона до зупинки.
|
Дано: m = 50 т v0 = 10 м/с F =αt α = 100 Н/с |
|
\( \tau \)-? |
Розв'язання
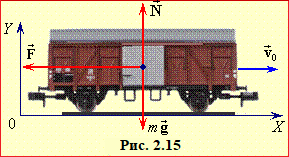
На вагон діють компенсовані сили тяжіння \(m\vec{g}\) і реакції опори \(m\vec{N}\) та гальмівна сила \(\vec{F}\) (рис. 2.15), яка й визначає його рух.
В умові по суті задано зміну імпульсу вагона, що за рівнянням (2.4а) дорівнює імпульсові діючих на нього сил:
| mv0 = І. | (1) |
Отже, треба встановити зв'язок між величиною І та часом руху τ вагона до зупинки. Але знайти його прямо без застосування вищої математики не можна, бо сила F є змінною. Проте це можна зробити за допомогою графіка залежності F(t), (рис. 2.15-1). Для цього подумки поділимо весь час τ на малі інтервали Δti, і приймемо, що в межах кожного сила має сталу величину Fi. Тоді імпульс сили за один інтервал Δti наближено визначається площею відповідної смужки
ΔIi ≈ Fi·Δti,
а за весь час τ – сумарною площею всіх смужок:
| I ≈ \(\sum{{{F}_{i}}}\Delta {{t}_{i}}\). | (2) |
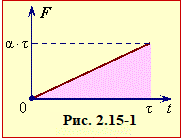
Зрозуміло, що цей вираз буде тим точнішим, чим вужчими будуть смужки, і стане математично точним, коли смужки стануть гранично вузькими (Δti → 0). При цьому утворені при поділі сходинки зникнуть, і величина (2) стане рівною площі утвореного графіком F(t) трикутника:
\(I=\frac{1}{2}\alpha \tau \cdot \tau \).
Підставивши отримане значення I у вираз (1), знайдемо відповідь:
\( \tau=\sqrt{\frac{2mv_{0}}{\alpha}}={100}\) c.