ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Розділ ІІ. ДИНАМІКА
2.3. Сили в механіці
|
Для визначення прискорення тіла за другим законом Ньютона (2.5) треба знати сили, що його створюють. У традиційних задачах механіки це сили гравітації, пружні сили і сили сухого тертя та опору. |
Гравітаційні сили діють між всіма тілами і визначаються законом всесвітнього тяжіння Ньютона, за яким
де коефіцієнт G = 6,67·10-11 м3/(кг·с2) визначає "силу" гравітаційної взаємодії і називається гравітаційною сталою. |
(Примітка. Вираз (2.6) є чинним, якщо тіла можна вважати матеріальними точками, або вони є однорідними і мають кулясту форму).
|
\( {g}=G\frac{M}{R^{2}}=\mathrm{const}\). |
(2.9) |
Для Землі воно в середньому складає g = 9,8 м/с2 і зазвичай називається прискоренням вільного падіння. Але це не зовсім точно, бо, як говорилося, пов'язана з поверхнею Землі система відліку не є строго інерціальною.
|
Із гравітацією пов’язане поняття ваги тіла. Вага – це сила, з якою тіло тисне на горизонтальну опору або розтягує вертикальний підвіс унаслідок притягання до планети. Отже, вага тіла прикладена не до нього, а до опори, або підвісу, які його утримують. При цьому, коли опора (підвіс) не має прискорення відносно планети, то вага тіла дорівнює силі тяжіння:
Якщо ж опора (підвіс) рухається з прискоренням \( \vec{a}\) , то вага тіла
Зокрема, при \( \vec{a}=\vec{g}\) , вага тіла \( \vec{P}={0}\) і настає невагомість — стан, при якому тіло перестає тиснути на опору чи розтягувати підвіс. Варто акцентувати, що невагомість – це стан, у якому на тіло діє тільки сила тяжіння, а не “коли на тіло не діє сила тяжіння”, як іноді помилково твердять учні. |
|
Пружні сили виникають при пружних деформаціях тіла. Вони з'являються при дії на тіло якихось інших сил і зникають при припиненні їхньої дії. Загальні властивості пружніх сил визначаються законом Гука:
Для поздовжніх деформацій (стиснення або видовження) закон Гука записується у вигляді:
де F – проєкція сили пружності на вісь, що напрямлена в бік видовження тіла, (\( {x}=l-l_{0}\) – деформація, тобто різниця довжин деформованого та недеформованого тіла (x – алгебраїчна величина, при стисненні x < 0 ). Коефіцієнт k називається жорсткістю тіла. Для суцільного твердого тіла закон Гука записують також у вигляді:
де ε = \( \left|\frac{l-l_{0}}{l_{0}}\right| \) – відносна деформація, \( \sigma=F/S \) – механічна напруга, тобто відношення деформуючої сили до площі поперечного перерізу тіла (вимірюється в паскалях, 1 Па = 1 Н/м2). Величина \( {E}\) називається модулем пружності (або модулем Юнґа). Вона є характеристикою пружних властивостей даного матеріалу. Значення \( {E}\) можна знайти у довідкових таблицях. |
|
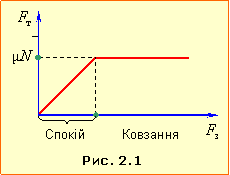
Сили тертя виникають при відносному русі, або спробі такого руху тіл, які перебувають у контакті. Тертя між твердими тілами називається сухим тертям, а між шарами рідини – в'язкістю (“мокрим” тертям). При русі тіла в рідині чи газі зазвичай говорять про силу опору середовища. Причиною тертя є зачеплення між мікроскопічними нерівностями поверхонь тіл при їх притисканні, що створює перешкоду рухові тіл одне відносно іншого. При цьому сили сухого тертя можуть до певної межі компенсувати прикладені зовнішні сили, так що тіла лишаються нерухомими одне відносно одного. В такому разі говорять про тертя спокою. Позаяк сила тертя спокою \( \vec{F}_{т}\) утримує тіло від руху, вона компенсує суму всіх інших прикладених до нього сил \( \vec{F}_{ін}\), тобто має такий самий модуль і протилежний напрям:
Для кожної пари тіл існує граничне (максимально можливе) значення сили тертя спокою
де \( \mu \) – коефіцієнт тертя, \( {N}\) – сила нормального тиску, що діє між цими тілами. Слід зауважити, що коефіцієнт тертя для кожної пари тіл, окрім матеріалу, залежить від багатьох інших факторів, як от чистота (гладкість) поверхонь, фізичні та хімічні забруднення, тощо. З цієї причини коефіцієнт тертя неможливо заздалегідь розрахувати. Тому в задачах при потребі його наводять в умові, а в техніці визначають дослідним шляхом. Якщо рівнодійна всіх інших сил перевищує деяке значення Fт max
, то починається рух тіл одне відносно одного, і тертя спокою переходить у тертя ковзання.
сила тертя ковзання є сталою і дорівнює максимальній силі тертя спокою і визначається формулою (2.14). Відповідно, графік залежності сили сухого тертя від величини прикладеної до тіла зовнішньої сили має вигляд рис.2.1. |
|
При русі в середовищі на тверде тіло діє сила опору, спрямована проти швидкості його руху відносно середовища. Сила опору має складні властивості. Зокрема, вона суттєво залежать від величини та форми поверхні тіла та швидкості його руху. При малих швидкостях силу опору можна вважати прямо пропорційною величині швидкості:
а при великих – її квадратові:
де \( \beta_{1},\,\beta_{2}\) – коефіцієнти опору, які залежать від властивостей середовища, розмірів і форми тіла та ін. |
 При переході тіла до ковзання та в подальшому русі сила тертя складно
При переході тіла до ковзання та в подальшому русі сила тертя складно