ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Рух тіла, що кинуте під кутом до горизонту
Задача 1.20. Тіло кинули з висоти h над землею вгору під кутом α до горизонту з початковою швидкістю \( {v}_{0}\). Визначити: а) рівняння траєкторії y = f(x); б) час підйому до найвищої точки траєкторії tm; в) найбільшу висоту підйому тіла над горизонтом H; г) горизонтальну дальність польоту тіла L; д) кут кидання \( \alpha_{m}\), що відповідає є найбільшій дальності польоту.
Задача 1.21. Тіло кинули з поверхні землі з початковою швидкістю \( {v}_{0}\) = 10 м/с так, що за перші t = 0,5 c руху швидкість тіла зменшилася до величини \( {v}\) = 7 м/с. Визначити максимальну висоту підйому тіла H
Задача 1.22. Кулька, що вільно падає з висоти h = 80 см, пружно відбивається від похилої площини з кутом нахилу до горизонту α = 30°. Визначити: а) через який час τ і на якій відстані L від точки падіння кулька вперше знов зіткнеться з площиною; б) величину та напрям швидкості відскоку.
| Задача 1.20 |
| Задача 1.20 |
Тіло кинули з висоти h над землею вгору під кутом \( \alpha \) до горизонту з початковою швидкістю \( {v}_{0}\).
Визначити:
а) рівняння траєкторії y = f(x);
б) час підйому до найвищої точки траєкторії th;
в) найбільшу висоту підйому тіла над горизонтом H;
г) горизонтальну дальність польоту тіла L;
д) кут кидання \( \alpha_{m}\), що відповідає є найбільшій дальності польоту.
|
Дано: h, α, v0 |
|
y = f(x) - ?
tm - ?
H - ?
L - ?
αm - ?
|
Розв'язання
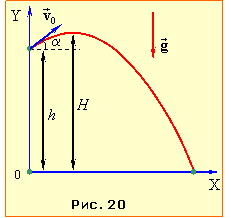
Рух тіла відбувається зі сталим прискоренням \( \vec{g}\) і описується рівняннями (1.16). Оберемо систему координат із початком на землі під місцем кидання тіла (рис. 20). Тоді за умовою
|
|
|
|
|
|
|
|
|
|
|
|
і рівняння (1.16) мають вигляд:
| \( {x}=v_{0}t\cos\alpha \), | (1) |
| \( {v}_{x}=v_{0}\cos\alpha \), | (2) |
| \( {y}=h+v_{0}t\sin\alpha-\frac{gt^{2}}{2}\), | (3) |
| \( {v}_{y}=v_{0}\sin\alpha-{gt}\), | (4) |
а) Рівняння траєкторії тіла визначає його координату y як функцію координати x: y(x). Її можна знайти, виключивши з рівнянь координат час t. Для цього виразимо його з рівняння (1) і після підстановки в рівняння (3) та елементарних викладок отримаємо:
\( {t}=\frac{x}{v_{0}\cos\alpha}\) $\Rightarrow $
|
$y=h+x\operatorname{tg}\alpha -\frac{g}{2v_{0}^{2}{{\cos }^{2}}\alpha }{{x}^{2}}$ |
(5) |
Це є рівняння параболи з гілками, спрямованими донизу (рис. 1.19).
б) Вектор швидкості є дотичним до траєкторії й у верхній точці спрямований горизонтально. Отже,
\( {v}_{y}(t_{m})=v_{0y}-gt_{m}={0}\),
де \( {t}_{m}\) – час підйому тіла до верхньої точки траєкторії.
З цього рівняння маємо:
\( {t}_{m}=\frac{v_{0y}}{g}=\frac{v_{0}\sin\alpha}{g}\).
в) Найбільша висота підйому тіла над землею дорівнює координаті y на момент часу \( {t}_{m}\):
| \( {H}=y(t_{m})=h+v_{0y}t_{m}-\frac{gt_{m}^{2}}{2}=h+\frac{v_{0}^{2}\sin^{2}\alpha}{2g}\). | (6) |
г) Горизонтальна дальність польоту тіла L дорівнює координаті x точки перетину траєкторії з віссю OX (рис. 20), тобто при y = 0. Тож із рівняння (5) маємо:
| \( {0}=h+L\mathrm{tg}\alpha-\frac{g}{2v_{0}^{2}\cos^{2}\alpha}L^{2}\), | (7) |
звідки
| \( {L}=\frac{v_{0}^{2}\sin\alpha\cos\alpha+v_{0}\cos\alpha\sqrt{v_{0}^{2}\sin^{2}\alpha+2gh}}{g}\). | (8) |
(Від'ємний корінь не має фізичного змісту).
Звичайно, для визначення дальності польоту можна було би спочатку визначити повний час руху тіла t0 з рівняння (3), поклавши y = 0, а потім, підставивши його в рівняння (1), знайти x(t0) = L. Але такий шлях є більш громіздкий.
Зауважимо також, що в окремому випадку, коли тіло кидають з поверхні землі (h = 0), для дальності польоту виходить
| \( {L}=\frac{2v_{0}^{2}\sin\alpha\cos\alpha}{g}=\frac{v_{0}^{2}\sin{2}\alpha}{g}\) | (8a) |
д) Кут кидання, при якому дальність польоту тіла є найбільшою, логічно було би визначати стандартним методом вищої математики, дослідивши на максимум функцію L(α), що визначається виразом (8). Одначе це можна зробити й алгебраїчно . А саме. Зробивши в рівнянні (7) заміну \( \cos^{2}\alpha=1/(\mathrm{tg}\alpha+1) \), дістанемо:
\({h}+L\mathrm{tg}\alpha-\frac{gL^{2}}{2v_{0}{2}}(\mathrm{tg}^{2}\alpha+1) \) \( \Rightarrow \) \( \mathrm{tg}^{2}\alpha-\frac{2v_{0}^{2}}{gL}\mathrm{tg}\alpha-\left(\frac{2hv_{0}^{2}}{gL}-1\right)={0}\).
Корені отриманого рівняння
| \( \mathrm{tg}\alpha=\frac{v_{0}^{2}}{gL}\left(1\pm\sqrt{1+\frac{2gh}{v_{0}^{2}}-\left(\frac{gL}{v_{0}^{2}}\right)^{2}}\right) \) | (9) |
мають фізичний зміст лише за умови
\( {1}+\frac{2gh}{v_{0}^{2}}-\left(\frac{gL}{v_{0}^{2}}\right)^{2}\ge{0}\),
тобто, коли \( {L}\le\frac{v_{0}\sqrt{v_{0}^{2}+2gh}}{g}\). Отже, максимальна можлива дальність польоту тіла складає
\( {L}_{m}=\frac{v_{0}\sqrt{v_{0}^{2}+2gh}}{g}\).
Відтак підставимо це значення у формулу (9) і одержимо для кута кидання αm, що відповідає найбільшій дальності польоту, наступний вираз:
\( \mathrm{tg}\alpha_{m}=\frac{v_{0}^{2}}{gL_{m}}=\frac{v_{0}}{\sqrt{v_{0}^{2}+2gh}}\).
Принагідно відмітимо, що при киданні з поверхні землі (h = 0) для αm виходить tgαm = 1, тобто дальність польоту є максимальна при куті кидання 45°. Такого висновку можна дійти й на основі виразу (8а), позаяк максимальне значення \( \sin{2\alpha}={1}\).
| Задача 1.21 |
Тіло кинули з поверхні землі з початковою швидкістю \( {v}_{0}\) = 10 м/с так, що за перші t = 0,5 c руху швидкість тіла зменшилася до величини \( {v}\) = 7 м/с.
Визначити
максимальну висоту підйому тіла H.
Розв'язання
|
Дано: v0 = 10 м/с
t = 0,5 с
v = 7 м/с |
|
H - ?
|
Позаяк в умові не вказано напрям вектора ${{\vec{v}}_{0}}$, можна подумати, що тіло кинули вертикальною. Але це не так, інакше б його швидкість через 0,5 с, згідно з відповідним рівнянням (1.16), складала б v0 – gt = 5 м/с. Отже, тіло кинуто під кутом до горизонту.
Розмістимо початок координат у точці кидання, тож початкова координата y0 = 0, а в найвищій точці y = H, і вертикальна складова швидкості vy = 0. Отже, згідно з рівнянням (1.18),
| \( {H}=\frac{v_{0y}^{2}}{2g}\). | (1) |
Для визначення вертикальної складової початкової швидкості \( {v}_{0y}\) скористаємося рівняннями (1.16):
\( {v}_{x}=v_{0x}\),
\( {v}_{y}=v_{0y}-{gt}\).
З цих рівнянь можна отримати \( {v}_{0y}\), якщо піднести їх до квадрата та додати:
\( {v}_{x}^{2}+v_{y}^{2}=v_{0x}^{2}+(v_{0y}^{2}-gt)^{2}=v_{0x}^{2}+v_{0y}^{2}-2v_{0y}gt+g^{2}t^{2}\) \( \Rightarrow \)
\( {v}^{2}=v_{0}^{2}-2gtv_{0y}+g^{2}t^{2}\).
Звідси маємо
\( {v_{0y}=\frac{v_{0}^{2}-v^{2}+g^{2}t^{2}}{2gt}}\).
Відтак підставимо цей результат у вираз (1) і отримаємо відповідь:
\( {H}=\frac{(v_{0}^{2}-v^{2}+g^{2}t^{2})^{2}}{8g^{3}t^{2}}\) = 2,9 м.
| Задача 1.21 |
| Задача 1.22 |
Кулька, що вільно падає з висоти h = 80 см, пружно відбивається від похилої площини з кутом нахилу до горизонту α = 30°.
Визначити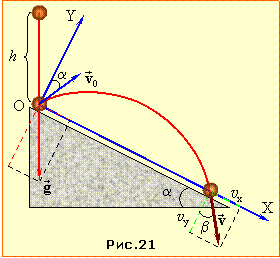
а) через який час τ і на якій відстані L від точки падіння кулька вперше знов зіткнеться з площиною; б) величину та напрям швидкості відскоку \(\vec{v}\).
Розв'язання
|
Дано: h = 20 см
α = 30°
|
|
τ-?, L-?, v -?, β-? |
При пружному зіткненні кулька дзеркально відбивається під кутом β0 = 60° до площини (рис. 21) із швидкістю падіння, що за формулою (1.19) дорівнює
| \( {v}_{0}=\sqrt{2gh}\) . |
(1) |
Тож у показаній на рис. 21 системі координат ХOY вирази проєкцій прискорення та рівняння проєкцій швидкості й координат кульки (1.16) мають вигляд:
|
\(\ {{a}_{x}}=g\cos {{\beta }_{0}}\) \(\ {{a}_{y}}=-g\sin {{\beta }_{0}}\) |
(2) |
|
\({{v}_{x}}=\left( {{v}_{0}}+gt \right)\cos {{\beta }_{0}}\) \({{v}_{y}}=\left( {{v}_{0}}-gt \right)\sin {{\beta }_{0}}\) |
(3) |
|
\(x=\left( {{v}_{0}}t+\frac{g{{t}^{2}}}{2} \right)\cos {{\beta }_{0}}\) \(y=\left( {{v}_{0}}t-\frac{g{{t}^{2}}}{2} \right)\sin {{\beta }_{0}}\). |
(4) |
Тепер перейдемо до пошуку означених в умові величин. На момент відскоку координати кульки дорівнюють нулю, тож, поклавши в рівняннях (4) y = 0, знайдемо час руху кульки t = τ між першим і другим зіткненням:
| \(\left( {{v}_{0}}\tau -\frac{g{{\tau }^{2}}}{2} \right)=0\) \(\Rightarrow \) \(\tau =\frac{2{{v}_{0}}}{g}\) | (5) |
Відтак, підставивши цей вираз у рівняння для х, визначимо відстань L = x(τ), на якій відбувається другий відскок:
|
\(L=\left( {{v}_{0}}\tau +\frac{g{{\tau }^{2}}}{2} \right)\cos {{\beta }_{0}}\) |
(6) |
Так само з рівнянь (3) знайдемо проєкції швидкості кульки на момент другого відскоку:
|
\({{v}_{x}}=\left( {{v}_{0}}+g\tau \right)\cos {{\beta }_{0}}=3{{v}_{0}}\cos {{\beta }_{0}}\) \({{v}_{y}}=\left( {{v}_{0}}-g\tau \right)\sin {{\beta }_{0}}=-{{v}_{0}}\sin {{\beta }_{0}}\) |
та її модуль і напрям β :
|
\(v={{v}_{0}}\sqrt{9{{\cos }^{2}}{{\beta }_{0}}+{{\sin }^{2}}{{\beta }_{0}}}\) tgβ = –\(\frac{\cos {{\beta }_{0}}}{\sin {{\beta }_{0}}}\) |
(7) |
(Примітка. Знак “–” в останньому виразі пояснюється тим, що в рівняннях (3) фігурує швидкість підльоту кульки до точки удару, а не швидкість відскоку).
Числові відповіді дістанемо з формул (5), (6), (7), підставивши значення β0 = 60° і, згідно з формулою (1) v0 = 4 м/с:
τ = 4 с
L = 3,2 м
v = 6,9 м/с
βв = 30°.
Наостанку зауважимо, що задачу можна розв'язувати і в “звичній” системі координат із горизонтальною і вертикальною осями, проте розв'язок буде більш громіздкий.