ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Графіки руху та їхнє використання
Задача 1.15. Тіло рухається з початку координат у напрямку осі ОХ перші 5 с рівномірно зі швидкістю v0 = 10 м/с, а наступні 15 c – із протилежно напрямленим прискоренням a = 2 м/с2. Побудувати графіки: а) проєкції швидкості \( {v}_{x}(t) \) та б) координати x(t) тіла.
Задача 1.16. За заданим графіком швидкості тіла, що рухається з початку координат уздовж осі OX побудувати графіки: прискорення тіла ax(t), його координати x(t) і пройденого шляху s(t).
Задача 1.17. На перегоні між двома станціями метро довжиною s = 4 км потяг рухається з середньою швидкістю \( \langle{v}\rangle \) = 68,4 км/год. На розгін та гальмування з однаковим прискоренням він витрачає по \( \tau=20 \) c, а решту часу рухається рівномірно. Визначити максимальну швидкість потяга v0.
Задача 1.18. Від потяга, що рухається рівномірно, відчіплюють останній вагон, який, рівномірно сповільнюючись, проходить до до зупинки шлях S. Визначити шлях S1, який пройде за цей час потяг.
Задача 1.19. Дві кульки, що рухаються без тертя з однаковою швидкістю, одночасно підходять до викривлених симетричних профілів, перша – до опуклого, друга – до угнутого. Обґрунтувати, яка з кульок раніше пройде свій профіль.
| Задача 1.15 | |
|
Задача 1.15 |
Тіло рухається з початку координат у напрямку осі ОХ перші 5 с рівномірно зі швидкістю v0 = 10 м/с, а наступні 15 c – із протилежно напрямленим прискоренням a = 2 м/с2.
Побудувати графіки
а) проєкції швидкості \( {v}_{x}(t) \);
б) координати x(t) тіла.
|
Дано: v0 = 10 м/с
a = 2 м/c2
τ1 = 5 c
τ2 = 15 c
x0 = 0
|
|
\( {v}_{x}(t) \)?, x(t)? |
Розв'язання
а) На першому відтинку часу (від 0 до t=τ1) швидкість тіла vх = v0 = const, тож графік \( {v}_{x}{(t)}\) є відрізком прямої, паралельної до осі t, рис. 1.15, а.
На другому проміжку часу тривалістю τ2 тіло рухається з прискоренням, проєкція котрого ax = –a. Отже, згідно з рівняннями швидкості (1.16), графік \( {v}_{x}{(t)}\) зображується відрізком спадної прямої, рис. 15, а. При цьому в точці перетину графіка з віссю t величина vх змінює знак, тобто тіло змінює напрям руху на протилежний. 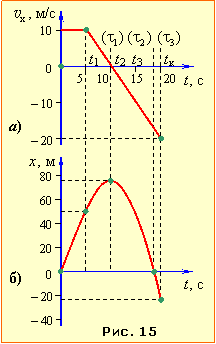
б) Розглянемо тепер графік координати х(t). На першому проміжку часу (від t = 0 до t = t1) координата змінюється за законом x = v0t, а на другому – згідно з рівнянням координати х (1.16), яке зручно записати у вигляді:
|
\(x={{x}_{1}}+{{v}_{0}}\tau -\frac{a{{\tau }^{2}}}{2}\), |
(1) |
де х1 – початкова координата тіла і τ = (t – τ1) – поточний час на другому інтервалі руху. Відповідно, графік х(t) зображується відрізками прямої та параболи, що мають бути спряжені (плавно переходити один в один, як на рис. 15, б), бо їхній нахил до осі часу визначає одну й ту саму величину v0. При цьому вершина параболи орієнтована догори (ax < 0) і визначає точку повороту, тобто точку максимального віддалення тіла від початкового положення й зміни напрямку руху.
Відтак для коректного відображення на рисунку умов задачі знайдемо числові значення необхідних параметрів графіків. А саме:
– координату тіла в момент t1
х1 = v0τ1 = 50 м;
– проєкцію кінцевої швидкості
vк = v0 – aτ2 = –20 м/с;
– координати вершини параболи, які визначають момент повороту tп і координату xп точки, в якій він відбувається. Обидві величини легко визначаються з рівнянь (1.16) і (1.18). Позаяк у момент tп швидкість тіла v = 0, то
tп = τ1 + \(\frac{v_{0}}{a}\) = 10 c,
і
|
\(v_{0}^{2}=2a\left( {x}_{п}-{{x}_{1}} \right)\) \(\Rightarrow \) \({{x}_{\text{п}}}={{x}_{1}}+\frac{v_{0}^{2}}{2a}\); |
– кінцеву координату тіла хк :
xк = \({{x}_{1}}+{{v}_{0}}{{\tau }_{2}}-\frac{a\tau _{2}^{2}}{2}\) = –25 м;
– час повернення тіла в початкове положення x0 = 0, який дорівнює t0 = τ1 + τ0, де величина τ0 є коренем рівняння:
\( {x}_{1}+v_{0}\tau_{0}-\frac{a\tau^{0}}{2}={0}\) \( \Rightarrow \) τ0 ≈ 13,7 с \( \Rightarrow \) τ0 ≈ 18,7 с.
(Другий корінь не задовольняє умову задачі).
Згідно з обчисленнями, відмічаємо на графіку всі розраховані точки і проводимо через них відрізок прямої та відрізок параболи, як показано на рис. 15, б).
| Задача 1.16 |
| Задача 1.16 |
За заданим графіком швидкості тіла, що рухається з початку координат уздовж осі OX
побудувати графіки:
а) проєкції прискорення тіла aх (t);
б) координати x(t);
и) пройденого шляху s(t).
Розв'язання
а) Із рис. 16-1а випливає, що рух тіла складається з двох ділянок, на яких його прискорення \({{\vec{a}}_{1}}\) і \({{\vec{a}}_{2}}\) є сталими і мають проєкції на вісь ОХ складають: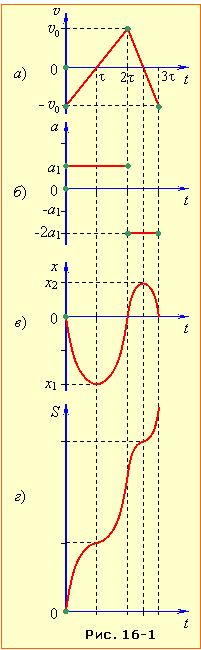
\( {a}_{1}=\frac{v_{0}-(-v_{0})}{2\tau}=\frac{v_{0}}{\tau}\),
\( {a_{2}=\frac{-v_{0}-v_{0}}{3\tau-2\tau}}=-\frac{2v_{0}}{\tau}\).
Отже, \( {a_{2}}=-2a_{1}\), і графік прискорення має вигляд рис. 16-б .
б) Перейдемо тепер до аналізу графіка координати x(t). Із рівняння (1.16), випливає, що він складається з ділянок двох парабол, причому, з урахуванням знаків прискорень (рис. 16-1б), вершина першої орієнтована донизу, а другої – догори. Вершини парабол відповідають точкам повороту, в яких змінюється напрям руху та знак проєкції швидкості, а сама швидкість проходить через нульове значення. За умовою задачі (див. рис. 16-1а) це відбувається в моменти часу t1 = τ і t2 = 2,5τ. До того ж, з рис. 16-1а видно, що сумарна площа під графіками (алгебраїчна величина!), котра визначає переміщення на кожній з ділянок, дорівнює нулю. Це означає, що в кінці кожного відтинку руху тіло повертається у вихідне положення х = 0.
На завершення з рівняння (1.18) визначимо координати точок повороту х1, х2, підставивши відповідні значення швидкостей та знайдені раніше величини а1 і а2:
\({{x}_{1}}=-\frac{{{v}_{0}}\tau }{2}\) \({{x}_{2}}=\frac{{{v}_{0}}\tau }{4}\)
Графік координати x(t), побудований за наведеними розрахунками, показано на рис. 1.16в.
в) Для побудови графіка шляху S(t) візьмемо до уваги, що при прямолінійному русі пройдений тілом шлях дорівнює сумі модулів його переміщень. Відтак графік S(t) легко отримати з рис. 16-1в, віддзеркаливши спадні ділянки від осі абсцис, як показано на рис. 16-1г.
| Задача 1.17 |
| Задача 1.17 |
На перегоні довжиною S = 4 км між двома станціями метро потяг рухається з середньою швидкістю \( \langle{v}\rangle \) = 68,4 км/год. На розгін та гальмування зі сталим прискоренням потяг витрачає по \( \tau=20 \) c, а решту часу рухається рівномірно.
Визначити
максимальну швидкість потяга v0.
|
Дано: |
|
v0 - ? |
Розв'язання
Для розв'язування задачі скористаємось графіком швидкості потяга, який, відповідно до умови, 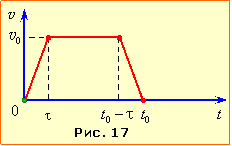 зображується рівнобічною трапецією (рис. 17). Шлях потяга S чисельно дорівнює площі цієї трапеції:
зображується рівнобічною трапецією (рис. 17). Шлях потяга S чисельно дорівнює площі цієї трапеції:
\( {s}=\frac{1}{2}(t_{0}+(t_{0}-2\tau{))}v_{0}=(t_{0}-\tau)v_{0}\).
Підставивши вираз повного часу руху потяга \( {t}_{0}=s/\langle{v}\rangle \), отримаємо відповідь:
\( {s}=\left(\frac{s}{\langle{v}\rangle}-\tau\right)v_{0}\) \( \Rightarrow \)
\( {v}_{0}=\frac{s\langle{v}\rangle}{s-\langle{v}\rangle\tau} \) ≈19,8 м/с ≈ 71,3 км/год.
| Задача 1.18 |
| Задача 1.18 |
Від потяга, що рухається рівномірно, відчіплюють останній вагон, який, рівномірно сповільнюючись, проходить до до зупинки шлях S.
Визначити
шлях S1, який пройде за цей час потяг.
Розв'язання
|
Дано: S |
|
S1 - ? |
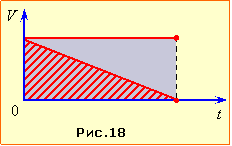 Графік швидкості вагона зображується нахиленим відрізком, а потяга – горизонтальним відрізком прямої (рис. 18). Позаяк площа під графіком швидкості чисельно дорівнює пройденому шляху, очевидно, що шлях потяга є вдвічі більший:
Графік швидкості вагона зображується нахиленим відрізком, а потяга – горизонтальним відрізком прямої (рис. 18). Позаяк площа під графіком швидкості чисельно дорівнює пройденому шляху, очевидно, що шлях потяга є вдвічі більший:
\( {S}_{1}=2{S}\).
| Задача 1.18 |
| Задача 1.19 |
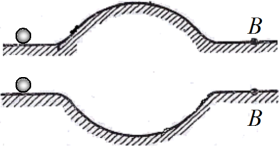
Дві кульки, що рухаються без тертя з однаковою швидкістю, одночасно підходять до викривлених симетричних профілів, перша – до опуклого, друга – до угнутого, рис. 19.
Обґрунтувати,
яка з кульок раніше потрапить у точку B.
Розв'язання
Поставлене питання можна вирішити, аналізуючи І – пройдені шляхи, або ІІ – середні швидкості кульок.
І. В теоретичних відомостях (п. 1.4) було показано, що при всякому русі площа S під заданою ділянкою графіка швидкості тіла v(t) чисельно дорівнює пройденому за відповідний час шляхові. Через симетрію профілів руху шляхи кульок і вказані площі S1 і S2 є однакові, тож із схематичних графіків швидкості рис. 19-1 видно, що t2 < t1, тобто друга кулька "прийде до фінішу" раніше.
ІІ. При проходженні профілів швидкість першої кульки на першій половині шляху зменшується, а потім збільшується до початкової величини, тоді як для другої кульки все відбувається з точністю до навпаки. Очевидно, що за таких умов середня швидкість першої кульки на всьому шляху є меншою, ніж у другої, тож вона випередить першу (час проходження дистанції t2 < t1).