ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Розділ І. КІНЕМАТИКА
1.4. Графіки руху
Графіками руху називають графіки залежності від часу кінематичних величин: проєкцій та модулів прискорення, швидкості, переміщення, а також координати й шляху. Графіки руху наочно відображають його властивості і в багатьох випадках полегшують розв'язування задачі.
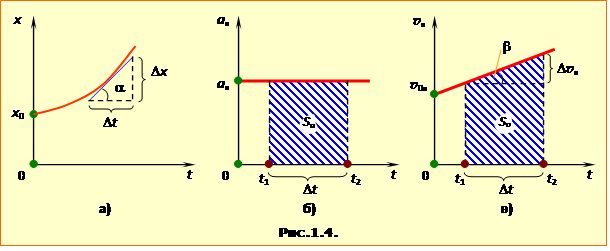
Згідно з рівняннями (1.16), для руху зі сталим прискоренням графіки прискорення та швидкості зображуються відрізками прямої, а переміщення, координати та шляху – відрізками параболи, як, до прикладу, на рис.1.4.
 |
Графіки руху мають певні загальні властивості, що дозволяють за графіком якоїсь величини отримати інформацію не лише про неї, а й про інші кінематичні величини. Конкретно:
1. Тангенс кута нахилу графіка проєкції швидкості (рис.1.4в) чисельно дорівнює проєкції прискорення на ту саму вісь:
| \( \mathrm{tg}\beta=\frac{\Delta{v}_{x}}{\Delta{t}}=a_{x} \) | (1.20) |
2. Тангенс кута нахилу дотичної до графіка координати (рис.1.4а) чисельно дорівнює проєкції миттєвої швидкості тіла на дану координатну вісь:
| \( \mathrm{tg}\alpha=\frac{\Delta{x}}{\Delta{t}}=v_{x} \). | (1.20а) |
(Примітка. Позаяк на графіку дотичну до кривої точно провести не можна, на практиці tgα визначається через відношення малого приросту координати до відповідного проміжку часу).
3. Площа під заданою ділянкою графіка проєкції швидкості на вісь (заштрихована на рис.1.4в) чисельно дорівнює проєкції на цю вісь переміщення (зміні координати) тіла за відповідний проміжок часу.
| \( {S}_{v}=\Delta{x}\) |
4. Шлях чисельно дорівнює площі під відповідною ділянкою графіка модуля швидкості.
5. Площа під ділянкою графіка проєкції прискорення (заштрихована на рис.1.4б) чисельно дорівнює зміні проєкції швидкості на цю вісь за відповідний проміжок часу:
| \( {S}_{a}=\Delta{v}_{x} \) |
На завершення, як приклад застосування графіків руху при розв'язуванні задач, визначимо формулу середньої швидкості у випадку руху із сталим прискоренням. Графік швидкості такого руху (рис. 1.4в) зображується відрізком прямої, а його виділена ділянка має форму трапеції. Отже, на проміжку часу Δt, за який швидкість тіла змінюється від v1 до v2, пройдений тілом шлях дорівнює
$S=\frac{1}{2}\left( ~{{v}_{1}}+{{v}_{2}} \right)\Delta t$,
і середня швидкість
|
$\left\langle v \right\rangle =\frac{{{v}_{1}}+{{v}_{2}}}{2}$. |
(1.21) |
Примітка. Ця формула відповідає нашому інтуїтивному уявленню про середнє значення змінної величини і може здатися самоочевидною. Але це не так, і середні швидкості для різних змінних рухів визначаються різними формулами.