ФІЗИКА ДЛЯ БАКАЛАВРІВ. КОЛИВАННЯ І ХВИЛІ
Частина І. КОЛИВАННЯ
2. Механічні гармонічні коливання
Найбільш наочними й зручними для вивчення є механічні коливання – рух тіла (матеріальної точки), при якому його положення у просторі та інші характеристики руху з плином часу періодично повторюються.
Характер руху всякого тіла визначається властивостями діючих на нього сил. Зокрема, якщо прикладена “спонукальна” сила періодично змінює свій напрям на протилежний і здатна подолати сили тертя та опору, то тіло здійснює вимушені коливання. Вільні механічні коливання тіла спостерігаються, коли рівнодійна прикладених сил весь час намагається повернути його в положення рівноваги. Таку силу інколи називають “повертаючою силою”. Але слід пам’ятати, що цей термін є умовним. У природі не існує ніякої спеціальної повертаючої сили — вона створюється сумісною дією якихось інших сил. До прикладу, при вільних коливаннях кульки на нитці повертаюча сила є рівнодійною сил тяжіння та натягу нитки.
Далі розглянуто:
2.1. Координата, швидкість, прискорення
2.2. Умова існування механічних гармонічних коливань
2.4. Енергія механічних гармонічних коливань
1.1. Координата, швидкість, прискорення
|
\( {x(t)}=x_{m}\cos{(}\omega{t}+\varphi_{0}{)}\), |
(2.1) |
де xm – амплітуда коливань (максимальне відхилення тіла від положення рівноваги).
Рівняння швидкості. Швидкість і напрям руху тіла визначається проєкцією вектора швидкості на вісь ОХ, тобто похідною координати по часу: \( {v}=\mathrm{d}x/\mathrm{d}{t}\). Отже, згідно з (2.1), рівняння швидкості тіла при гармонічних коливаннях має вигляд:
|
\( {v(t)}=-v_{m}\omega\sin{(}\omega{t}+\varphi_{0}{)}\) або \( {v(t)}=v_{m}\cos{(}\omega{t}+\varphi_{0}+\frac{\pi}{2}{)}\), |
(2.2) |
де \( {v_{m}}\) – амплітуда (максимальне значення) швидкості пов’язана з амплітудою коливань співвідношенням
|
\( {v_{m}}=x_{m}{\omega}\). |
(2.2а) |
Примітка. В рівнянні (2.2) мається на увазі проєкція вектора швидкості, але, позаяк рух відбувається вздовж однієї осі, індекс проєкції не вказують. Це стосується і всіх інших векторних величин, які використовуються далі для характеристики гармонічних коливань.
З рівняння (2.2) видно, що коливання швидкості за фазою випереджають коливання координати на π/2 або на чверть періоду.
Рівняння прискорення отримаємо аналогічно з (2.1) або (2.2), врахувавши, що прискорення є першою похідною по часу від швидкості або другою похідною від координати:
|
\( {a(t)}=-A\omega^{2}\cos{(}\omega{t}+\varphi_{0}{)}\) або \( {a(t)}=a_{m}\cos{(}\omega{t}+\varphi_{0}+\pi{)}\). |
(2.3) |
Амплітуда прискорення
|
\( {a_{m}}=x_{m}\omega^{2}=v_{m}{\omega}\). |
(2.3а) |
Із рівняння (2.3) випливає, що коливання прискорення випереджають (або відстають) коливання координати на π. Інакше говорячи, коливання прискорення відбуваються у протифазі до коливань координати.
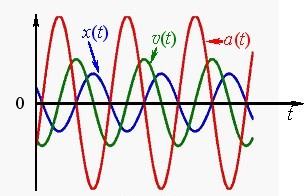
На рис. 2.1 зображені графіки координати x(t) швидкості \({v(t)}\) і прискорення \( {a(t)}\) тіла при гармонічних коливаннях, які наочно показують фазові співвідношення між цими величинами.
 |
2.2. Умова існування механічних гармонічних коливань
Із рівнянь (2.1) і (2.3) випливає, що при гармонічних коливаннях прискорення тіла в будь-який момент часу є прямо пропорційним до координати (зміщення з положення рівноваги):
|
\( {a}=-\omega^2{x}\). |
(2.4) |
Тому за другим законом Ньютона проєкцію на вісь ОХ рівнодійної сили, що прикладена до тіла, можна записати, як
|
\( {F}=-{kx}\), |
(2.5) |
де
|
\( {k}=m{\omega^{2}}\). |
(2.6) |
Із (2.5) видно, що при x > 0 проєкція сили F < 0 і навпаки. Отже, будь-якої миті сила F напрямлена до положення рівноваги і є прямо пропорційною величині відхилення. Таку властивість має сила пружності. Але в загальному випадку рівнодійна F може створюватись і силами, які за природою не є пружними. Тому її називають квазіпружною силою.
Сказане дозволяє сформулювати критерій (достатню умову) механічних гармонічних коливань:
якщо тіло перебуває під дією пружної або квазіпружної сили, то воно здійснює гармонічні коливання.
Частота ω і період T гармонічних коливань визначаються коефіцієнтом пропорційності k у виразі сили (2.5) і масою тіла m, згідно з формулами:
|
\( \omega=\sqrt{\frac{k}{m}}\), |
(2.7) |
|
|
\( {T}=2\pi\sqrt{\frac{m}{k}}\). |
(2.8) |
Відмітимо також, що, відповідно до (2.5), сила, яка зумовлює гармонічні коливання (2.1), сама змінюється за гармонічним законом:
\( {F}=-F_{m}\cos{(}\omega{t}+\varphi_{0}{)}\),
де амплітуда сили \( {F_{m}}=mx_{m}{\omega^{2}}\).
2.3. Маятники
Практичне значення розглянутої умови гармонічних коливань (2.5) і співвідношення (2.6) полягає в тому, що, визначивши рівнодійну прикладених до тіла сил, можна не лишень установити, чи здійснює воно гармонічні коливання, а й знайти їхню основну характеристику – частоту або період. Проілюструємо це на прикладі маятника – тіла, що підвішене на пружині чи нитці, або знаходиться на осі, навколо якої може здійснювати вільні коливання.
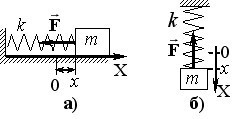
Пружинний маятник являє собою невеликий тягарець маси m, з’єднаний з невагомою пружиною жорсткості k із закріпленим іншим кінцем і може рухатися або горизонтально (рис.2.2а), або вертикально (рис.2.2б). Будемо вважати, що сили тертя та опору відсутні. Тоді, якщо координату x відраховувати від положення рівноваги тягарця, то прикладена до нього рівнодійна сила в обох випадках дорівнює тільки силі пружності \( \vec{F} \), що виникає внаслідок зміщення маятника з положення рівноваги (сили тяжіння та реакція опори у випадку а) і сила тяжіння та статична сила пружності при x = 0 у випадку б) є компенсованими і на рисунку не показані):
\( {F}=-{kx}\),
де x – координата маятника.
 |
Оскільки сила F задовольняє умову (2.5), маятник (тягарець на пружині), виведений з положення рівноваги і наданий самий собі, в обох випадках здійснює гармонічні коливання з циклічною частотою та періодом, які визначаються жорсткістю пружини k і масою тягарця m, відповідно до формул (2.7) і (2.8).
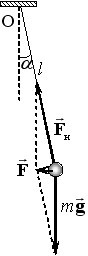
Математичний маятник. У строгому розумінні математичним маятником називається матеріальна точка, підвішена на невагомій нерозтяжній нитці. Реально – це кулька певної маси m підвішена на довгій тонкій сталевій дротині (струні) довжини l, масою котрої можна нехтувати (рис. 2.3). Силу тертя в точці кріплення та силу опору повітря також можна вважати не істотними.
Коли маятник перебуває в рівновазі, сили тяжіння та натягу нитки є компенсованими. Але, якщо кульку відвести й відпустити, з’явиться рівнодійна \(\vec{F}=m\vec{g}+\vec{F}\)н, напрямлена до положення рівноваги (рис. 2.3). Відтак маятник буде здійснювати вільні коливання. Рух маятника можна розглядати як рух матеріальної точки маси m по колу радіуса \({l}\) навколо горизонтальної осі Z, що проходить через точку кріплення нитки (т. О на рис. 2.3). Тому, відповідно до відомого з механіки рівнянням моментів відносно осі (див. МЕХАНІКА. Розділ 7, п. 7.3), можемо записати:
|
\({M_{z}}={I\beta_{z}}\), |
(2.9) |
де \( {M_{z}},~I,~\beta_{z}\) – сумарний момент сил, момент інерції кульки відносно осі О та кутове прискорення, відповідно.
Оскільки напрям сили натягу \(\vec{F}\)н проходить через вісь Z, момент відносно неї створює тільки сила тяжіння: \({M_{z}}=-mgl\sin\alpha \), де α - кут відхилення нитки маятника від вертикалі. Знак "–" у виразі стоїть тому, що кут α відраховують проти годинникової стрілки, а момент сили тяжіння діє за годинниковою стрілкою, тобто у від’ємному напрямку. Крім того \(\beta_{z}=\mathrm{d}^{2}\alpha /\mathrm{d}{t}^{2}\). Відтак можемо записати:
\({-mgl}\sin\alpha=I\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}~~~~\Rightarrow~~~~\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}+\frac{mgl}{I}\sin\alpha ={0}\),
Підставивши в (2.9) вираз моменту інерції матеріальної точки \({I}={ml^{2}}\), отримаємо диференціальне рівняння руху математичного маятника:
|
\(\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}+\frac{g}{l}\sin\alpha = {0}\). |
(2.9а) |
Диференціальне рівняння (2.9а) є доволі складним – воно не збігається з рівнянням гармонічних коливань (1.18) і не має розв’язків у елементарних функціях. Це означає, що коливання маятника не є гармонічними. Але при малих амплітудах максимальний кут відхилення нитки маятника від вертикалі малий (αm << 1), і рівнянні (2.9а) можна з достатньою точністю покласти \(\sin\alpha =\alpha \). Тоді
|
\(\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}+\omega^{2}\alpha={0},~~~\omega^{2}=\frac{g}{l}\). |
(2.9б) |
Отримане спрощене рівняння (2.9б) не відрізняється від загального диференціального рівняння гармонічних коливань (1.18), отже, кут відхилення нитки маятника від вертикалі змінюється за законом (1.4):
|
\(\alpha{(t)}=\alpha_{m}\cos{(\omega{t}+\varphi_{0})}\). |
(2.10) |
Оскільки при малих кутах дуга практично співпадає з хордою, можна вважати, що кулька маятника рухається вздовж горизонтальної осі, і її координата \({x=l\alpha}\) змінюється за законом:
\({x(t)}=x_{m}\cos{(\omega{t}+\varphi_{0})}\),
де амплітуда визначається довжиною та максимальним кутом відхилення маятника від вертикалі: \({x}_{m}={l\alpha_{m}}\).
Таким чином, при малих амплітудах математичний маятник здійснює вільні гармонічні коливання з циклічною частотою
|
\(\omega=\sqrt{\frac{g}{l}}\) |
(2.11) |
і періодом
|
\({T}=2\pi\sqrt{\frac{l}{g}}\). |
(2.11а) |
Останній вираз називається формулою Гюйґенса.
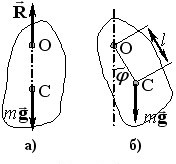
Фізичний маятник. Фізичним маятником називають протяжне тверде тіло, яке може вільно коливатися навколо закріпленої осі О, що не проходить через його центр мас С, (рис. 2.4). У положенні рівноваги центр мас маятника знаходиться на одній вертикалі з точкою підвісу (рис. 2.4а), тому сили тяжіння \({m\vec{g}}\) та реакції осі \(\vec{R}\) є компенсованими. Але після відхилення тіла на деякий кут φ (рис. 2.4б) так само, як у випадку математичного маятника, виникає момент сили тяжіння \( {M}=-mgl\sin\varphi \) (\({l}\) – відстань між точкою підвісу та центром мас) відносно осі О, який намагається повернути маятник у положення рівноваги. Тому, якщо маятник надати самому собі, він почне коливатися згідно із рівнянням (2.9а), яке не є диференціальним рівнянням гармонічних коливань. Але, як і раніше, при малих кутах відхилення воно спрощується і набуває вигляду (2.9б):
\( \frac{\mathrm{d}^{2}\varphi}{\mathrm{d}t^{2}}+\omega^{2}\varphi = {0}\), \( \omega^{2}=\frac{mgl}{I}\).
Це означає, що при малих кутах відхилення \({\varphi_{m}}\ll{1}\), вільні коливання фізичного маятника є гармонічними і здійснюються за законом:
|
\( \varphi{(t)}=\varphi_{m}\cos{(\omega{t}+\phi_{0})}\) |
(2.12) |
із циклічною частотою
|
\( \omega =\sqrt{\frac{mdl}{I}}\), |
(2.13) |
чи періодом
|
\( {T}=2\pi\sqrt{\frac{I}{mgl}}\). |
(2.13а) |
При розгляді коливань фізичного маятника часто використовують поняття зведеної довжини фізичного маятника:
|
\( {l}\)зв = \(\frac{I}{ml}\). |
(2.14) |
У такому разі формули (2.13) і (2.13а) трансформуються в
|
\( \omega=\sqrt{g/l_{зв}}\) |
(2.15) |
|
|
\( {T}=2\pi\sqrt{l_{зв}/g}\), |
(2.15а) |
які збігаються з відповідними формулами для математичного маятника. Тому можна сказати, що
зведена довжина фізичного маятника дорівнює довжині математичного маятника з таким самим періодом вільних коливань.
2.4. Енергія гармонічних коливань
При зміні швидкості та координати тіла, що здійснює гармонічні коливання, відповідно змінюється і його кінетична та потенціальнв енергія.
Кінетична енергія гармонічних коливань (2.1) у довільний момент часу, з урахуванням виразів (2.2), (2.2а) і (2.6), визначається, як:
|
\( {K}=\frac{mv^{2}}{2}=\frac{1}{2}mx_{m}^{2}\omega^{2}\sin^{2}(\omega{t}+\varphi_{0})=\frac{1}{2}kx_{m}^{2}\sin^{2}{(\omega{t}+\varphi_{0})}\). |
(2.16) |
Максимальна величина кінетичної енергії
|
\({K}_{m}=\frac{1}{2}mx_{m}^{2}\omega^{2}=\frac{1}{2}kx_{m}^{2}\). |
(2.16а) |
Гармонічні коливаннях тіла відбуваються під дією квазіпружної сили (2.5), котра, як і пружна, є консервативною. Тому, з урахуванням виразу (2.1), потенціальна енергія гармонічних коливань у довільний момент часу визначається виразом
|
\({U}=\frac{kx^{2}}{2}=\frac{kx_{m}^{2}}{2}\cos^{2}(\omega{t}+\varphi_{0}) \). |
(2.17) |
Максимальне значення потенціальної енергії
|
\({U}_{m}=\frac{kx_{m}^{2}}{2}\). |
(2.17а) |
Із виразів (2.16а) та (2.17а) видно, що
при гармонічних коливаннях максимальні значення кінетичної та потенціальної енергій тіла збігаються:
|
\({K}_{m}=U_{m}=W_{0}\). |
(2.18) |
Відтак для повної енергії гармонічних коливань у довільний момент часу, урахувавши (2.16), (2.17) і (2.18), отримуємо:
|
\({W}=K+U=W_{0}\sin^{2}{(\omega{t}+\varphi_{0})}+W_{0}\cos^{2}{(\omega{t}+\varphi_{0})}={W_{0}}\). |
(2.19) |
Таким чином,
при гармонічних коливаннях повна енергія коливань зберігається, тобто не залежить від часу.
Це означає, що при вільних гармонічних коливаннях механічна енергія не переходить в інші форми, зокрема, в тепло. Тому такі коливання можливі лише за відсутності сил тертя та опору, які насправді в механічних системах завжди є. Отже, реально
вільні коливання ніколи не бувають строго гармонічними.
Але це не стосується вимушених коливань, позаяк у цьому випадку втрати механічної енергії на тертя та опір можуть компенсуватися за рахунок роботи спонукальної сили.
Відмітимо також, що згідно з (2.16а), (2.17) і (2.18),
повна енергія гармонічних коливань є прямо пропорційною квадратові амплітуди.
Наостаок зауважимо, що вирази (2.16) і (2.17) можна записати, як
\(K=\frac{1}{2}{{K}_{m}}\left( 1-\cos \left( 2\omega +2{{\varphi }_{0}} \right) \right)\)
та
\(U=\frac{1}{2}{{U}_{m}}\left( 1+\cos \left( 2\omega +2{{\varphi }_{0}} \right) \right)\),
звідки видно, що
при гармонічних коливаннях кінетична та потенціальна енергії змінюються з подвоєною частотою по відношенню до частоти самих коливань.
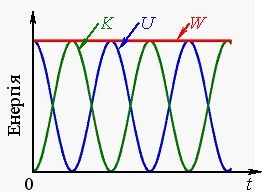
На рис. 2.5 показані графіки кінетичної K, потенціальної U та повної W енергій тіла, що здійснює гармонічні коливання. З них видно, що кінетична та потенціальна енергії змінюються в протифазі. Це пояснює, чому максимальне значення кожної з них дорівнює повній енергії коливань.