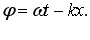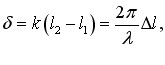ФІЗИКА ДЛЯ БАКАЛАВРІВ. КОЛИВАННЯ І ХВИЛІ
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА ДЛЯ БАКАЛАВРІВ. КОЛИВАННЯ І ХВИЛІ |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 16:09 |
Національний технічний університет України
"Київський політехнічний інститут імені Ігоря Сікорського"
Вступ
Коливаннями називаються процеси, які багаторазово точно, або наближено повторюються у часі. Приклади таких процесів легко знайти і в природі, і в техніці. Коливальні процеси можуть мати різне походження. Зокрема, важливими типами коливань, які часто спостерігаються в природі і використовуються в техніці, є механічні та електромагнітні коливання. Механічними коливаннями, зокрема, зумовлений звук, а електромагнітними – світло. Як приклади коливань можна навести також добові чи сезонні зміни температури повітря, зміни видимої площі освітленої поверхні Місяця, тощо. Але незалежно від природи коливальні процеси мають спільні загальні властивості, й описуються аналогічними математичними рівняннями та співвідношеннями. Тому теорія коливальних і хвильових процесів різної природи становить єдиний самостійний розділ фізики – фізику коливань.
Загальні властивості коливань визначаються умовами виникнення та законом зміни їхніх характеристик у часі. При цьому всі коливання поділяють на вільні та вимушені. Вільні коливання виникають після одноразового виведення системи із рівноважного стану і далі існують самостійно. Вільні коливання можливі тільки в так званих коливальних системах або осциляторах, в яких при відхиленні від рівноважного стану виникають внутрішні процеси, що спричинюють періодичні зміни фізичних характеристик системи. Натомість вимушені коливання створюються постійним зовнішнім впливом і тому можливі в будь-якій системі.
Що до змін у часі, то найпростішими є гармонічні коливання — процеси, в яких зміна їхніх характеристик у часі визначається гармонічними функціями (синус і косинус).
Усе сказане стосується й хвиль — процесів поширення коливань у просторі з плином часу.
Загальні властивості гармонічних коливальних і хвильових процесів розглядаються в наступних частинах:
Частина І. КОЛИВАННЯ
У цій частині посібника розглядаються гармонічні коливання. Важливість вивчення саме таких процесів зумовлена двома обставинами. По-перше, вони зустрічаються в природі й використовуються на практиці. А по-друге, як доводить математика, будь-який складний коливальний процес можна розглядати як суперпозицію (сукупність) гармонічних коливань, що є важливим для теорії.
Далі розглянуто так питання:
2. Механічні гармонічні коливання
3. Загасаючі та вимушені механічні коливання
4. Вільні електромагнітні коливання
І. Гармонічні коливання
Серед періодичних коливань для науки і практики найважливішими є гармонічні коливання, які описуються гармонічними функціями і мають прості властивості. Важливість саме таких процесів зумовлена двома обставинами. По-перше, реальні коливання і хвилі, з якими доводиться мати справу, часто є близькими до гармонічних. По-друге, будь-який складний коливальний процес, як доводить математика, можна розглядати як суперпозицію (сукупність) гармонічних коливань. Тому в цей розділ присвячено саме таким процесам. Далі розглянуто:
1. Рівняння гармонічних коливань
2. Зображення гармонічних функцій
3. Додавання гармонічних коливань
4. Диференціальне рівняння гармонічних коливань
1. Рівняння гармонічних коливань
Як було сказано, гармонічні коливання якоїсь величини ξ відбуваються за законом синуса або косинуса, тож визначаються рівнянням:
|
\( \xi (t)=A\cos\left(\frac{2\pi}{T}t+\varphi_{0}\right) \) або \( \xi (t)=A\sin\left(\frac{2\pi}{T}t+\phi_{0}\right) \), де \( \varphi_{0}=\phi_{0}+\frac{\pi}{2}\), |
(1.1) |
і визначаються трьома параметрами — амплітудою, періодом (або частотою) і фазою.
Амплітуда A — додатнє число, що дорівнює максимальному значенню коливної величини \( \xi \), так що всі її можливі значення лежать в інтервалі \(\pm A \). Іншими словами, амплітуда задає “розмах” коливань.
За рівнянням (1.1), величина ξ задовольняє умову \( \xi(t+nT)=\xi{(t)}\), отже
період коливань T є найменшим проміжком часу, через який значення величини ξ та характер її зміни повністю повторюються.
Окрім періоду, повторюваність коливального процесу у часі характеризують іще й частотою. При цьому розрізняють лінійну та циклічну (колову) частоту.
Лінійна частота \(\nu \) є величиною оберненою до періоду:
|
\( \nu=\frac{1}{T}\) |
(1.2) |
Вона дорівнює кількості коливань, які здійснюються за одну секунду і вимірюється в герцах (Гц). При частоті 1 Гц = 1 с-1 за одну секунду здійснюється одне повне коливання.
Циклічна (колова) частота ω пов’язана з лінійною частотою та періодом співвідношеннями
|
\(\omega=2\pi\nu=\frac{2\pi}{T}\) |
(1.3) |
і вимірюється в рад/с. (Часто пишуть 1/с або с-1).
Використання частоти, замість періоду, дозволяє записати рівняння коливань більш компактно:
|
\( \xi (t)=A\cos (2\pi\nu{t}+\varphi_{0}) \) або \(\xi (t)=\cos (\omega{t}+\varphi_{0}) \). |
(1.4) |
Якщо коливання описуються функцією синуса, то
|
\( \xi (t)=A\sin (2\pi\nu{t}+\phi_{0}) \) або \( \xi (t)=A\sin (\omega{t}+\phi_{0}) \). |
(1.4а) |
Задля зручності в теорії найчастіше використовують частоту ω і відповідні рівняння (1.4) або (1.4а).
З рівнянь гармонічних коливань також видно, що при заданій амплітуді A величина ξ(t) у кожен момент часу визначається аргументом гармонічної функції, що називається фазою коливань φ. Отже,
|
\( \varphi (t)=\omega{t}+\varphi_{0}\) |
(1.5) |
Відповідно, величина \( \varphi_{0} \) називається початковою фазою. Одиницею фази є радіан (1 рад).
Слід зауважити, що термін “фаза” вживається не лишень у вказаному формальному сенсі, а й для словесної характеристики стадії коливального процесу або узгодженості коливань – згадаймо такі знайомі вислови, як “фази Місяця” або “коливання відбуваються в однакових (чи протилежних) фазах”.
2. Зображення гармонічних функцій
При розгляді декількох гармонічних коливань, які відбуваються одночасно, доводиться додавати відповідну кількість гармонічних функцій вигляду. Це потребує громіздких перетворень, а при великій кількості коливань може стати технічно нездійсненним без використання комп’ютера. Тому при аналізі коливань часто використовують штучні математичні прийоми, а саме:
2.1. Векторне зображення гармонічних функцій
2.2. Комплексне зображення гармонічних функцій
2.1. Векторне зображення гармонічних функцій
Цей спосіб ґрунтується на існуванні відповідності між гармонічними коливаннями та обертальним рухом. Нехай маємо вектор з модулем A, який обертається з кутовою швидкістю ω навколо свого початку (рис. 1.1) Якщо в початковий момент часу цей вектор складає з деякою віссю ОХ кут \(\varphi_{0}\), то в довільний момент t кут між ним і віссю буде рівним
\(\varphi (t)=\omega{t}+\varphi_{0}\).
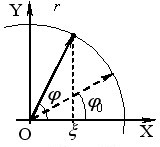 |
Відповідно, якщо проекцію такого обертового вектора Аx = Acosφ на вісь ОХ позначити як ξ, то отримаємо:
\(\xi (t)=A\cos (\omega{t}+\varphi_{0}) \),
що збігається з (1.4), а спроєктувавши цей вектор на вісь OY, отримаємо рівняння (1.4а). Таким чином,
кожному гармонічному коливанню можна поставити у відповідність вектор із модулем, рівним амплітуді коливань А, який обертається з кутовою швидкістю, рівною циклічній частоті коливань ω, і в початковий момент часу складає з вибраною віссю кут, рівний початковій фазі коливань φ0.
Доречі, саме через збіг величини ω із швидкістю обертання вказаного вектора вона й має назву “циклічної”, або “колової” частоти коливань.
Таким чином, гармонічні коливання можна зображувати відповідними векторами на рисунку, який називається векторною діаграмою, і оперувати не безпосередньо гармонічними функціями, а векторами, що їх зображують.
2.2. Комплексне зображення гармонічних функцій
З математики відомо, що комплексне число z = a + ib \(\left(i=\sqrt{-1}\right) \) можна записати або в показниковій формі, як \({z}=Ae^{i\varphi}\), або в тригонометричній формі у вигляді
|
\({z}=A\cos\varphi+iA\sin\varphi \), |
(1.6) |
де модуль A та аргумент \( \varphi \) комплексного числа визначаються співвідношеннями
\({A}=\sqrt{a^2+b^2}\) і \(\cos\varphi=\frac{a}{A}\), \( \sin\varphi=\frac{b}{A}\).
Тому, згідно з (1.6) і (1.4), рівняння гармонічних коливань ξ(t) можна розглядати як дійсну частину комплексної функції
|
\( \tilde{\xi }=A{{e}^{\omega t+{{\varphi }_{0}}}}=\tilde{A}{{e}^{\omega t}}\) \( \Rightarrow \) \( \xi \left( t \right) = {Re}\left( \tilde{\xi }\left( t \right) \right) \). |
(1.7) |
При цьому комплексне число \( \tilde{A}=Ae^{i\varphi_{0}}\) називається комплексною амплітудою коливань. Дійсна (істинна) амплітуда визначається через квадрат модуля комплексної амплітуди на основі тотожності
|
\( {A^2}=\left|\tilde{A}^{2}\right|=\tilde{A}\cdot {{\tilde{A}}^{*}}=Ae^{i\varphi}\cdot Ae^{-i\varphi}\). |
(1.8) |
(Нагадаємо, що спряженою до комплексної величини z називається величина z*, що створюється заміною уявної одиниці і у виразі z на –i.)
Указана відповідність (1.7) зберігається для всіх лінійних математичних операцій: множення на константу, додавання або віднімання, диференціювання, інтегрування. У цьому легко переконатися прямими обчисленнями. Через це розглянутий підхід є дуже продуктивним, оскільки оперувати з експонентами набагато зручніше, ніж із тригонометричними функціями. Зокрема, поширена задача про накладання декількох коливань однакової частоти та напрямку зводиться просто до додавання комплексних чисел (комплексних амплітуд).
3. Додавання гармонічних коливань
На початку говорилося про те, що складні коливальні процеси можна трактувати як суперпозицію (накладання), гармонічних коливань. Цей прийом широко застосовується в оптиці, техніці передачі сигналів та інших областях для аналізу та формування сигналів необхідної форми. Розглянемо найпростіші випадки — додавання двох гармонічних коливань, які відбуваються в одному та у взаємно перпендикулярних напрямках.
3.1. Додавання коливань одного напрямку
3.2. Додавання взаємно перпендикулярних коливань
3.1. Додавання коливань одного напрямку
Розглянемо рух тіла (матеріальної точки), яке бере участь одночасно у двох гармонічних коливаннях одного напрямку. Прикладом можуть бути вертикальні коливання кульки на пружині, прикріпленій до стелі салону автомобіля, який теж коливається на ресорах у вертикальному напрямку. Рух кульки відносно землі складається з коливань відносно автомобіля та коливань автомобіля відносно землі. Відповідно, закон руху кульки буде визначатися сумою рівнянь цих двох коливань. Аналіз показує, що результат такого додавання суттєво залежить від того, однакові чи ні частоти складових коливань.
Частоти однакові. Нехай точка бере участь у двох рухах уздовж однієї осі ОХ відповідно до рівнянь:
|
\( {x}_{1}(t)=A_{1}\cos (\omega{t}+\alpha_{1}) \), \( {x}_{2}(t)=A_{2}\cos (\omega{t}+\alpha_{2}) \). |
(1.9) |
Для визначення рівняння результуючого руху \( {x}(t)=x_{1}(t)+x_{2}(t) \) скористаємося векторним способом зображення гармонічних функцій (1.9). Для цього зобразимо їх в момент t = 0 за допомогою векторів \( \vec{A}_{1}\) і \( \vec{A}_{2}\), що обертаються навколо осі О з кутовою швидкістю ω, як це описано в п. 2.1. На отриманій векторній діаграмі
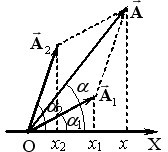 |
(рис. 1.2) результуючий рух точки зображується вектором \(\vec{A}=\vec{A}_{1}+\vec{A}_{2}\), модуль якого за теоремою косинусів задається виразом:
|
\({A^2}=A_{1}^{2}+A_{2}^{2}+2A_{1}A_{2}\cos{(\alpha_{2}-\alpha_{1})}\), |
(1.10) |
а кут з віссю ОХ, як випливає з рисунка:
|
\(\mathrm{tg}\alpha =\frac{A_{1}\sin\alpha_{1}+A_{2}\sin\alpha_{2}}{A_{1}\cos\alpha_{1}+A_{2}\cos\alpha_{2}}\). |
(1.11) |
Таким чином, результатом додавання двох гармонічних коливань однакової частоти та напрямку є гармонічні коливання тієї самої частоти, амплітуда A та початкова фаза α яких визначаються виразами (1.10) і (1.11). Слід зауважити, що при цьому амплітуда результуючих коливань не дорівнює сумі амплітуд коливань, які додаються. Залежно від початкових фаз α1 і α2 вона може мати будь-яке значення в межах від A1 + A2 до |A1 – A2|.
Частоти різні. Розглянемо тепер випадок, коли точка бере участь у двох коливаннях однакового напрямку, але різної частоти ω1 і ω2. Якщо для спрощення викладок прийняти A1 = A2 і α1 = α2 = 0, то рівняння цих коливань мають вигляд:
|
\({x}_{1}=A_{1}\cos\omega_{1}{t}\), \( {x}_{2}=A_{1}\cos\omega_{1}{t}\). |
(1.12) |
Рівняння результуючого руху точки \({x}_{1}(t)+x_{2}(t) \) запишемо, скориставшися відомою формулою тригонометрії:
|
\({x}(t)=2A\cos\left(\frac{\omega_{1}-\omega_{2}}{2}t\right)\cos\left(\frac{\omega_{1}+\omega_{2}}{2}t\right) \). |
(1.13) |
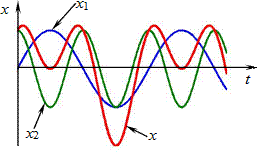
Це рівняння описує складний коливальний процес, наочне уявлення про який можна отримати, побудувавши графік функції (1.13), або шляхом безпосереднього графічного додавання функцій (1.12). На рис. 1.3 показано результат такого додавання для випадку α = 0 функцій
\({x}_{1}=A_{1}\cos\left(\omega{t}-\frac{\pi}{2}\right) \), \( x_{2}=A_{1}\cos{2}\omega{t}\).
 |
Як для теорії, так і для практики окремий інтерес являє випадок, коли частоти ω1 і ω2 є близькими й відрізняються від певного значення ω на величину Δω << ω так, що ω1 = ω + Δω і ω2 = ω - Δω. У такому разі рівняння (1.13) набуває вигляду:
|
\( {x}(t)=\left( 2A_{1}\cos\Delta\omega{t}\right)\cos\omega{t}\). |
(1.14) |
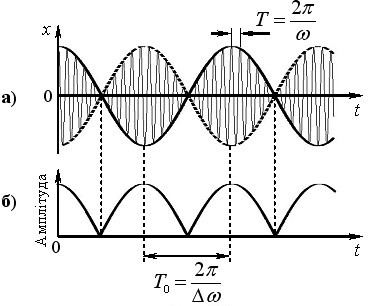
У цьому рівнянні величина cosΔωt змінюється з періодом \( {T}=2\pi /\Delta\omega \), тобто в \( \omega{/}\Delta\omega \) разів повільніше, ніж величина \(\cos\omega{t}\), період зміни якої \({T}=2\pi/\omega \). При Δω << ω за час T0 відбувається багато коливань величини x з частотою ω, як показано на рис. 1.4а для випадку Δω = ω/10. Тому в (1.14) вираз у дужках можна трактувати як залежну від часу амплітуду A(t) і розглядати рух точки як гармонічні коливання з частотою ω, амплітуда яких змінюється теж за гармонічним законом із частотою Δω :
|
\({x}(t)=A(t)\cos\omega{t}\), \( {A}(t)=2A|\cos\Delta\omega{t}|\). |
(1.14а) |
Графік A(t) показаний на рис. 1.4б.
 |
Розглянуті коливання називають биттями. При накладанні акустичних коливань з близькими частотами ω1 і ω2 биття створюють відчуття (не завжди приємне) звукових пульсацій, які повторюються з частотою |ω1 - ω2|. Биття за відповідних умов виникають і при накладанні коливань не механічної природи, зокрема — напруг і струмів у електричних або електронних пристроях.
3.2. Додавання взаємно перпендикулярних коливань
Якщо точка одночасно здійснює гармонічні коливання у двох взаємно перпендикулярних напрямках, то на загал її рух не є коливальним і відбувається по складній траєкторії. Зокрема, траєкторія може виявитися незамкненою і ніколи не проходити через одну точку двічі. Проте, коли відношення частот коливань виражається відношенням цілих чисел, тіло рухається по замкненій траєкторії, форма котрої визначається співвідношенням частот, амплітуд і початкових фаз складових коливань.
Частоти однакові. Найпростішим є випадок додавання взаємно перпендикулярних коливань однієї частоти. Якщо коливання точки відбуваються вздовж координатних осей ОХ і OY, то їх можна описати рівняннями:
|
\({x}=a\cos\omega{t}\), \( {y}=b\cos (\omega{t}+\alpha) \), |
(1.15) |
де початкова фаза коливань координати x вважається нульовою. Ото ж α по суті є різницею фаз цих двох коливань. Аби одержати рівняння траєкторії точки, тобто залежність y(x), з рівнянь (1.15) треба виключити час. Для цього за допомогою відомих формул тригонометрії перетворимо друге рівняння (1.15) наступним чином:
\(\frac{y}{b}=(\cos\omega{t}\cos\alpha-\sin\omega{t}\sin\alpha ) \) \( \Rightarrow \) \( \frac{y}{b}\left(\cos\omega{t}\cos\alpha-\sqrt{1-\cos^2\omega{t}}\cdot\sin\alpha\right) \).
Підставивши сюди вираз \(\cos\omega{t}=x/a \), який випливає з першого рівняння (1.15), отримаємо:
\(\frac{y}{b}=\frac{x}{a}\cos\alpha-\sin\alpha\cdot\sqrt{1-\left(\frac{x}{a}\right)^2}\).
Після піднесення до квадрату і нескладних перетворень одержимо шукане рівняння траєкторії:
|
\( \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{2xy}{ab}\cos\alpha=\sin^2{\alpha}\). |
(1.16) |
З математики відомо, що рівняння (1.16) є рівнянням еліпса. Отже, на загал точка рухається по еліптичній траєкторії, параметри та просторова орієнтація котрої залежать від амплітуд а, b і різниці фаз α складових коливань. Розглянемо деякі окремі випадки.
1) α = 0. З (1.16) випливає, що
\( {y}=\frac{b}{a}{x}\),
тобто еліпс вироджується у відрізок прямої. Отже, точка здійснює гармонічні коливання, напрямок яких пролягає в першій і третій чвертях і визначається відношенням амплітуд складових коливань.
2) α = π. У цьому випадку ситуація подібна — з (1.16) маємо:
\( {y}=-\frac{b}{a}{x}\).
Тож у такому випадку точка теж здійснює гармонічні коливання, але вздовж лінії, що лежить у другій та четвертій чвертях.
Отримані результати дозволяють розглядати гармонічні коливання вздовж певного напрямку як суму (суперпозицію) двох гармонічних коливань тієї самої частоти, котрі відбуваються у взаємно перпендикулярних напрямках і мають різницю фаз α, або π. Такий підхід плідно використовується, зокрема, в оптиці.
3) α = π/2. При такій різниці фаз рівняння (1.16) набуває вигляду:
\( \frac{x^2}{a^2}+\frac{y^2}{b^2}={1}\).
Це означає, що при не однакових амплітудах складових коливань точка рухається по еліпсу, осі котрого орієнтовані вздовж осей координат. При а = b еліпс вироджується в коло з центром у початку координат. Знак різниці фаз α визначає один з двох можливих напрямів руху точки по траєкторії.
Фігури Ліссажу. Якщо точка здійснює взаємно перпендикулярні коливання з різними частотами, що співвідносяться, як цілі числа, траєкторіями руху є складні замкнені криві, що називаються фігурами Ліссажу.
У простих випадках рівняння фігур Ліссажу можна отримати за формулами тригонометрії. Наприклад, нехай складові коливання описуються рівняннями x = Asinωt та y = Asin2ωt. Тоді
y = 2Asinωt·cosωt = 2Asinωt\( \sqrt{1-{{\sin }^{2}}\omega t}\),
де sinωt = х/А. Зробивши таку заміну, дістанемо рівняння траєкторії точки:
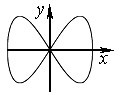
\( {y}=2x\sqrt{1-{{\left( {x}/{A}\; \right)}^{2}}}\).
Її вигляд показує рис. 1.5.
 |
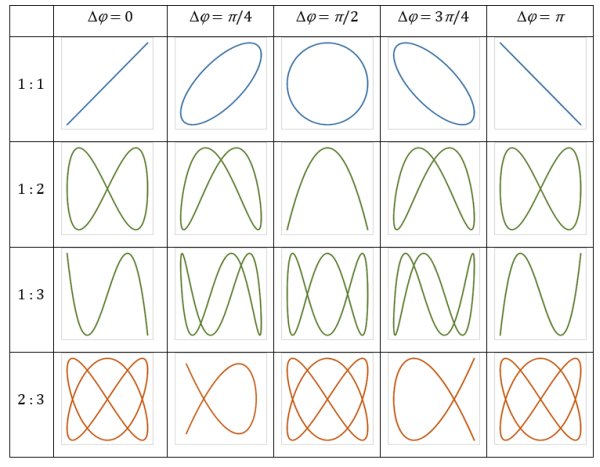 |
Фігури Ліссажу для деяких інших співвідношень частот і зсувів фаз Δφ коливань представлені на рис. 1.6. Зазначимо, що фігури Ліссажу при додаванні електричних коливань легко спостерігати на екрані осцилографа. Це використовують на практиці для вимірювання та налаштовування частот електричних сигналів.
4. Диференціальне рівняння гармонічних коливань
Незалежно від умов і фізичної природи величини ξ(t) рівняння гармонічних коливань (1.4) є розв’язком єдиного диференціального рівняння. Його можна установити, знайшовши першу та другу похідні функції ξ(t):
\(\frac{\mathrm{d}\xi}{\mathrm{d}t}=-\omega{A}\sin(\omega{t}+\varphi_{0}) \) \( \Rightarrow \) \( \frac{\mathrm{d}^2\xi}{\mathrm{d}t^2}=-\omega^{2}A\cos (\omega{t}+\varphi_{0}) \).
Як видно, вираз другої похідної містить вихідну функцію (1.4), отже,
|
\( \frac{\mathrm{d}^{2}\xi}{\mathrm{d}t^{2}}=-\omega^{2}\xi \). |
(1.17) |
Отримане співвідношення є критерієм (достатньою умовою) гармонічних коливань:
якщо в будь-який момент часу друга похідна даної величини по часу виявляється прямо пропорційною самій величині і має протилежний знак, то ця величина здійснює гармонічні коливання, а коефіцієнт пропорційності дорівнює квадратові циклічної частоти коливань.
Мовою математики вираз (1.17) є звичайним однорідним диференціальним рівнянням другого порядку із постійними коефіцієнтами, яке прийнято записувати у вигляді:
|
\(\frac{\mathrm{d}^{2}\xi}{\mathrm{d}t^2}+\omega^2\xi={0}\). |
(1.18) |
У математиці доводиться, що розв’язками такого рівняння можуть бути тільки гармонічні функції. Тому рівняння (1.18) є диференціальним рівнянням гармонічних коливань.
Контрольні запитання
1. Які фізичні процеси називаються коливаннями? За якими ознаками класифікують коливання?
2. Назвіть умови існування вільних і вимушених коливань. Чи може однорідний диск, який закріплений на осі, що проходить через його центр, здійснювати вільні коливання? Вимушені коливання?
3. Які коливання називаються гармонічними та якими величинами вони характеризуються?
4. Що визначає амплітуда коливань? Чи може вона бути від’ємною?
5. Які величини визначають повторюваність коливального процесу в часі? Який вони мають зміст і як пов’язані між собою?
6. Чи можна довільні періодичні коливання характеризувати періодом T? Лінійною частотою ν? Циклічною частотою ω?
7. Чому гармонічні коливання можна зображувати векторами? Як у цьому способі відображається амплітуда коливань? Початкова та поточна фаза?
8. Чому гармонічні коливання можна зображувати комплексними експонентами?
9. Що таке комплексна амплітуда коливань? Яку інформацію вона містить?
10. Коли використання векторного або комплексного способів зображення гармонічних коливань є продуктивним?
11. Що таке биття? За якої умови вони спостерігаються?
12. Що таке фігури Лісажу? За якої умови вони спостерігаються?
13. Сформулюйте критерій гармонічних коливань і запишіть його математичний вираз.
2. Механічні гармонічні коливання
Найбільш наочними й зручними для вивчення є механічні коливання – рух тіла (матеріальної точки), при якому його положення у просторі та інші характеристики руху з плином часу періодично повторюються.
Характер руху всякого тіла визначається властивостями діючих на нього сил. Зокрема, якщо прикладена “спонукальна” сила періодично змінює свій напрям на протилежний і здатна подолати сили тертя та опору, то тіло здійснює вимушені коливання. Вільні механічні коливання тіла спостерігаються, коли рівнодійна прикладених сил весь час намагається повернути його в положення рівноваги. Таку силу інколи називають “повертаючою силою”. Але слід пам’ятати, що цей термін є умовним. У природі не існує ніякої спеціальної повертаючої сили — вона створюється сумісною дією якихось інших сил. До прикладу, при вільних коливаннях кульки на нитці повертаюча сила є рівнодійною сил тяжіння та натягу нитки.
Далі розглянуто:
2.1. Координата, швидкість, прискорення
2.2. Умова існування механічних гармонічних коливань
2.4. Енергія механічних гармонічних коливань
1.1. Координата, швидкість, прискорення
|
\( {x(t)}=x_{m}\cos{(}\omega{t}+\varphi_{0}{)}\), |
(2.1) |
де xm – амплітуда коливань (максимальне відхилення тіла від положення рівноваги).
Рівняння швидкості. Швидкість і напрям руху тіла визначається проєкцією вектора швидкості на вісь ОХ, тобто похідною координати по часу: \( {v}=\mathrm{d}x/\mathrm{d}{t}\). Отже, згідно з (2.1), рівняння швидкості тіла при гармонічних коливаннях має вигляд:
|
\( {v(t)}=-v_{m}\omega\sin{(}\omega{t}+\varphi_{0}{)}\) або \( {v(t)}=v_{m}\cos{(}\omega{t}+\varphi_{0}+\frac{\pi}{2}{)}\), |
(2.2) |
де \( {v_{m}}\) – амплітуда (максимальне значення) швидкості пов’язана з амплітудою коливань співвідношенням
|
\( {v_{m}}=x_{m}{\omega}\). |
(2.2а) |
Примітка. В рівнянні (2.2) мається на увазі проєкція вектора швидкості, але, позаяк рух відбувається вздовж однієї осі, індекс проєкції не вказують. Це стосується і всіх інших векторних величин, які використовуються далі для характеристики гармонічних коливань.
З рівняння (2.2) видно, що коливання швидкості за фазою випереджають коливання координати на π/2 або на чверть періоду.
Рівняння прискорення отримаємо аналогічно з (2.1) або (2.2), врахувавши, що прискорення є першою похідною по часу від швидкості або другою похідною від координати:
|
\( {a(t)}=-A\omega^{2}\cos{(}\omega{t}+\varphi_{0}{)}\) або \( {a(t)}=a_{m}\cos{(}\omega{t}+\varphi_{0}+\pi{)}\). |
(2.3) |
Амплітуда прискорення
|
\( {a_{m}}=x_{m}\omega^{2}=v_{m}{\omega}\). |
(2.3а) |
Із рівняння (2.3) випливає, що коливання прискорення випереджають (або відстають) коливання координати на π. Інакше говорячи, коливання прискорення відбуваються у протифазі до коливань координати.
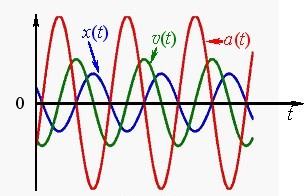
На рис. 2.1 зображені графіки координати x(t) швидкості \({v(t)}\) і прискорення \( {a(t)}\) тіла при гармонічних коливаннях, які наочно показують фазові співвідношення між цими величинами.
 |
2.2. Умова існування механічних гармонічних коливань
Із рівнянь (2.1) і (2.3) випливає, що при гармонічних коливаннях прискорення тіла в будь-який момент часу є прямо пропорційним до координати (зміщення з положення рівноваги):
|
\( {a}=-\omega^2{x}\). |
(2.4) |
Тому за другим законом Ньютона проєкцію на вісь ОХ рівнодійної сили, що прикладена до тіла, можна записати, як
|
\( {F}=-{kx}\), |
(2.5) |
де
|
\( {k}=m{\omega^{2}}\). |
(2.6) |
Із (2.5) видно, що при x > 0 проєкція сили F < 0 і навпаки. Отже, будь-якої миті сила F напрямлена до положення рівноваги і є прямо пропорційною величині відхилення. Таку властивість має сила пружності. Але в загальному випадку рівнодійна F може створюватись і силами, які за природою не є пружними. Тому її називають квазіпружною силою.
Сказане дозволяє сформулювати критерій (достатню умову) механічних гармонічних коливань:
якщо тіло перебуває під дією пружної або квазіпружної сили, то воно здійснює гармонічні коливання.
Частота ω і період T гармонічних коливань визначаються коефіцієнтом пропорційності k у виразі сили (2.5) і масою тіла m, згідно з формулами:
|
\( \omega=\sqrt{\frac{k}{m}}\), |
(2.7) |
|
|
\( {T}=2\pi\sqrt{\frac{m}{k}}\). |
(2.8) |
Відмітимо також, що, відповідно до (2.5), сила, яка зумовлює гармонічні коливання (2.1), сама змінюється за гармонічним законом:
\( {F}=-F_{m}\cos{(}\omega{t}+\varphi_{0}{)}\),
де амплітуда сили \( {F_{m}}=mx_{m}{\omega^{2}}\).
2.3. Маятники
Практичне значення розглянутої умови гармонічних коливань (2.5) і співвідношення (2.6) полягає в тому, що, визначивши рівнодійну прикладених до тіла сил, можна не лишень установити, чи здійснює воно гармонічні коливання, а й знайти їхню основну характеристику – частоту або період. Проілюструємо це на прикладі маятника – тіла, що підвішене на пружині чи нитці, або знаходиться на осі, навколо якої може здійснювати вільні коливання.
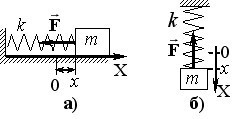
Пружинний маятник являє собою невеликий тягарець маси m, з’єднаний з невагомою пружиною жорсткості k із закріпленим іншим кінцем і може рухатися або горизонтально (рис.2.2а), або вертикально (рис.2.2б). Будемо вважати, що сили тертя та опору відсутні. Тоді, якщо координату x відраховувати від положення рівноваги тягарця, то прикладена до нього рівнодійна сила в обох випадках дорівнює тільки силі пружності \( \vec{F} \), що виникає внаслідок зміщення маятника з положення рівноваги (сили тяжіння та реакція опори у випадку а) і сила тяжіння та статична сила пружності при x = 0 у випадку б) є компенсованими і на рисунку не показані):
\( {F}=-{kx}\),
де x – координата маятника.
 |
Оскільки сила F задовольняє умову (2.5), маятник (тягарець на пружині), виведений з положення рівноваги і наданий самий собі, в обох випадках здійснює гармонічні коливання з циклічною частотою та періодом, які визначаються жорсткістю пружини k і масою тягарця m, відповідно до формул (2.7) і (2.8).
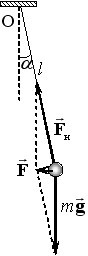
Математичний маятник. У строгому розумінні математичним маятником називається матеріальна точка, підвішена на невагомій нерозтяжній нитці. Реально – це кулька певної маси m підвішена на довгій тонкій сталевій дротині (струні) довжини l, масою котрої можна нехтувати (рис. 2.3). Силу тертя в точці кріплення та силу опору повітря також можна вважати не істотними.
Коли маятник перебуває в рівновазі, сили тяжіння та натягу нитки є компенсованими. Але, якщо кульку відвести й відпустити, з’явиться рівнодійна \(\vec{F}=m\vec{g}+\vec{F}\)н, напрямлена до положення рівноваги (рис. 2.3). Відтак маятник буде здійснювати вільні коливання. Рух маятника можна розглядати як рух матеріальної точки маси m по колу радіуса \({l}\) навколо горизонтальної осі Z, що проходить через точку кріплення нитки (т. О на рис. 2.3). Тому, відповідно до відомого з механіки рівнянням моментів відносно осі (див. МЕХАНІКА. Розділ 7, п. 7.3), можемо записати:
|
\({M_{z}}={I\beta_{z}}\), |
(2.9) |
де \( {M_{z}},~I,~\beta_{z}\) – сумарний момент сил, момент інерції кульки відносно осі О та кутове прискорення, відповідно.
Оскільки напрям сили натягу \(\vec{F}\)н проходить через вісь Z, момент відносно неї створює тільки сила тяжіння: \({M_{z}}=-mgl\sin\alpha \), де α - кут відхилення нитки маятника від вертикалі. Знак "–" у виразі стоїть тому, що кут α відраховують проти годинникової стрілки, а момент сили тяжіння діє за годинниковою стрілкою, тобто у від’ємному напрямку. Крім того \(\beta_{z}=\mathrm{d}^{2}\alpha /\mathrm{d}{t}^{2}\). Відтак можемо записати:
\({-mgl}\sin\alpha=I\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}~~~~\Rightarrow~~~~\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}+\frac{mgl}{I}\sin\alpha ={0}\),
Підставивши в (2.9) вираз моменту інерції матеріальної точки \({I}={ml^{2}}\), отримаємо диференціальне рівняння руху математичного маятника:
|
\(\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}+\frac{g}{l}\sin\alpha = {0}\). |
(2.9а) |
Диференціальне рівняння (2.9а) є доволі складним – воно не збігається з рівнянням гармонічних коливань (1.18) і не має розв’язків у елементарних функціях. Це означає, що коливання маятника не є гармонічними. Але при малих амплітудах максимальний кут відхилення нитки маятника від вертикалі малий (αm << 1), і рівнянні (2.9а) можна з достатньою точністю покласти \(\sin\alpha =\alpha \). Тоді
|
\(\frac{\mathrm{d}^{2}\alpha}{\mathrm{d}t^{2}}+\omega^{2}\alpha={0},~~~\omega^{2}=\frac{g}{l}\). |
(2.9б) |
Отримане спрощене рівняння (2.9б) не відрізняється від загального диференціального рівняння гармонічних коливань (1.18), отже, кут відхилення нитки маятника від вертикалі змінюється за законом (1.4):
|
\(\alpha{(t)}=\alpha_{m}\cos{(\omega{t}+\varphi_{0})}\). |
(2.10) |
Оскільки при малих кутах дуга практично співпадає з хордою, можна вважати, що кулька маятника рухається вздовж горизонтальної осі, і її координата \({x=l\alpha}\) змінюється за законом:
\({x(t)}=x_{m}\cos{(\omega{t}+\varphi_{0})}\),
де амплітуда визначається довжиною та максимальним кутом відхилення маятника від вертикалі: \({x}_{m}={l\alpha_{m}}\).
Таким чином, при малих амплітудах математичний маятник здійснює вільні гармонічні коливання з циклічною частотою
|
\(\omega=\sqrt{\frac{g}{l}}\) |
(2.11) |
і періодом
|
\({T}=2\pi\sqrt{\frac{l}{g}}\). |
(2.11а) |
Останній вираз називається формулою Гюйґенса.
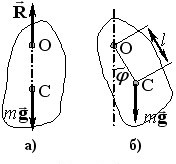
Фізичний маятник. Фізичним маятником називають протяжне тверде тіло, яке може вільно коливатися навколо закріпленої осі О, що не проходить через його центр мас С, (рис. 2.4). У положенні рівноваги центр мас маятника знаходиться на одній вертикалі з точкою підвісу (рис. 2.4а), тому сили тяжіння \({m\vec{g}}\) та реакції осі \(\vec{R}\) є компенсованими. Але після відхилення тіла на деякий кут φ (рис. 2.4б) так само, як у випадку математичного маятника, виникає момент сили тяжіння \( {M}=-mgl\sin\varphi \) (\({l}\) – відстань між точкою підвісу та центром мас) відносно осі О, який намагається повернути маятник у положення рівноваги. Тому, якщо маятник надати самому собі, він почне коливатися згідно із рівнянням (2.9а), яке не є диференціальним рівнянням гармонічних коливань. Але, як і раніше, при малих кутах відхилення воно спрощується і набуває вигляду (2.9б):
\( \frac{\mathrm{d}^{2}\varphi}{\mathrm{d}t^{2}}+\omega^{2}\varphi = {0}\), \( \omega^{2}=\frac{mgl}{I}\).
Це означає, що при малих кутах відхилення \({\varphi_{m}}\ll{1}\), вільні коливання фізичного маятника є гармонічними і здійснюються за законом:
|
\( \varphi{(t)}=\varphi_{m}\cos{(\omega{t}+\phi_{0})}\) |
(2.12) |
із циклічною частотою
|
\( \omega =\sqrt{\frac{mdl}{I}}\), |
(2.13) |
чи періодом
|
\( {T}=2\pi\sqrt{\frac{I}{mgl}}\). |
(2.13а) |
При розгляді коливань фізичного маятника часто використовують поняття зведеної довжини фізичного маятника:
|
\( {l}\)зв = \(\frac{I}{ml}\). |
(2.14) |
У такому разі формули (2.13) і (2.13а) трансформуються в
|
\( \omega=\sqrt{g/l_{зв}}\) |
(2.15) |
|
|
\( {T}=2\pi\sqrt{l_{зв}/g}\), |
(2.15а) |
які збігаються з відповідними формулами для математичного маятника. Тому можна сказати, що
зведена довжина фізичного маятника дорівнює довжині математичного маятника з таким самим періодом вільних коливань.
2.4. Енергія гармонічних коливань
При зміні швидкості та координати тіла, що здійснює гармонічні коливання, відповідно змінюється і його кінетична та потенціальнв енергія.
Кінетична енергія гармонічних коливань (2.1) у довільний момент часу, з урахуванням виразів (2.2), (2.2а) і (2.6), визначається, як:
|
\( {K}=\frac{mv^{2}}{2}=\frac{1}{2}mx_{m}^{2}\omega^{2}\sin^{2}(\omega{t}+\varphi_{0})=\frac{1}{2}kx_{m}^{2}\sin^{2}{(\omega{t}+\varphi_{0})}\). |
(2.16) |
Максимальна величина кінетичної енергії
|
\({K}_{m}=\frac{1}{2}mx_{m}^{2}\omega^{2}=\frac{1}{2}kx_{m}^{2}\). |
(2.16а) |
Гармонічні коливаннях тіла відбуваються під дією квазіпружної сили (2.5), котра, як і пружна, є консервативною. Тому, з урахуванням виразу (2.1), потенціальна енергія гармонічних коливань у довільний момент часу визначається виразом
|
\({U}=\frac{kx^{2}}{2}=\frac{kx_{m}^{2}}{2}\cos^{2}(\omega{t}+\varphi_{0}) \). |
(2.17) |
Максимальне значення потенціальної енергії
|
\({U}_{m}=\frac{kx_{m}^{2}}{2}\). |
(2.17а) |
Із виразів (2.16а) та (2.17а) видно, що
при гармонічних коливаннях максимальні значення кінетичної та потенціальної енергій тіла збігаються:
|
\({K}_{m}=U_{m}=W_{0}\). |
(2.18) |
Відтак для повної енергії гармонічних коливань у довільний момент часу, урахувавши (2.16), (2.17) і (2.18), отримуємо:
|
\({W}=K+U=W_{0}\sin^{2}{(\omega{t}+\varphi_{0})}+W_{0}\cos^{2}{(\omega{t}+\varphi_{0})}={W_{0}}\). |
(2.19) |
Таким чином,
при гармонічних коливаннях повна енергія коливань зберігається, тобто не залежить від часу.
Це означає, що при вільних гармонічних коливаннях механічна енергія не переходить в інші форми, зокрема, в тепло. Тому такі коливання можливі лише за відсутності сил тертя та опору, які насправді в механічних системах завжди є. Отже, реально
вільні коливання ніколи не бувають строго гармонічними.
Але це не стосується вимушених коливань, позаяк у цьому випадку втрати механічної енергії на тертя та опір можуть компенсуватися за рахунок роботи спонукальної сили.
Відмітимо також, що згідно з (2.16а), (2.17) і (2.18),
повна енергія гармонічних коливань є прямо пропорційною квадратові амплітуди.
Наостаок зауважимо, що вирази (2.16) і (2.17) можна записати, як
\(K=\frac{1}{2}{{K}_{m}}\left( 1-\cos \left( 2\omega +2{{\varphi }_{0}} \right) \right)\)
та
\(U=\frac{1}{2}{{U}_{m}}\left( 1+\cos \left( 2\omega +2{{\varphi }_{0}} \right) \right)\),
звідки видно, що
при гармонічних коливаннях кінетична та потенціальна енергії змінюються з подвоєною частотою по відношенню до частоти самих коливань.
На рис. 2.5 показані графіки кінетичної K, потенціальної U та повної W енергій тіла, що здійснює гармонічні коливання. З них видно, що кінетична та потенціальна енергії змінюються в протифазі. Це пояснює, чому максимальне значення кожної з них дорівнює повній енергії коливань.
3. Загасаючі та вимушені механічні коливання
Незагасаючі вільні коливання є ідеалізацією. В реальній коливальній системі завжди присутні різноманітні сили тертя і опору, які призводять до втрат енергії коливань. Тому в дійсності вільні коливання є загасаючими – їхня амплітуда невпинно зменшується від початкового значення аж до нуля. Основні властивості таких коливань розглянуті нижче у наступних питаннях:
3.1. Рівняння вільних загасаючих коливань
3.2. Параметри загасання вільних коливань
3.3. Вимушені механічні коливання. Резонанс
3.1. Рівняння вільних загасаючих коливань
Fоп = \( {-\alpha{v}}=-\alpha\frac{\mathrm{d}x}{\mathrm{d}t} \),
де \( {\alpha} \) – стала, яку називають коефіцієнтом опору. Знак “–” зумовлений тим, що сила опору напрямлена протилежно до вектора швидкості. В такому разі, згідно з другим законом Ньютона, рух тіла визначається рівнянням
\( {m}\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} \) \( =-kx-\alpha\frac{\mathrm{d}x}{\mathrm{d}t}\) \( \Rightarrow \) \( \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+\frac{\alpha}{m}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{k}{m}x={0}\).
Уведемо співвідношення \(\left( {\alpha }/{m}\; \right)=2\beta, \) в якому \({\beta}\) називається коефіцієнтом загасання. Врахуємо також, що згідно з (2.6) і (2.7) \({k/m}=\omega_{0}^{2}\), де \({\omega_{0}}\) – частота вільних гармонічних коливань під дією квазіпружної сили. Її називають власною частотою коливальної системи. Після таких замін отримуємо диференціальне рівняння загасаючих коливань:
|
\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+2\beta\frac{\mathrm{d}x}{\mathrm{d}t}+\omega_{0}^{2}x={0}\). |
(3.1) |
З математики відомо, що загальні розв’язки цього рівняння, отже й рух тіла, залежать від співвідношення між параметрами β і ω0. Зокрема, за умови β < ω0 рух тіла має коливальний характер. Це зрозуміло, бо за такої умови домінує квазіпружна сила, що спричинює коливання. А от при \(\beta\ge\omega_{0}\) сили опору є настільки великими, що рух тіла після виведенні з рівноваги є аперіодичним: на шляху від крайнього до середнього положення тіло втрачає практично всю свою механічну енергію і зупиняється. Аналіз такого руху не становить інтересу для теми лекції, тому далі розглядається лише випадок β < ω0. У цьому разі з (3.1) випливає наступне загальне рівняння координати тіла при загасаючих коливаннях:
|
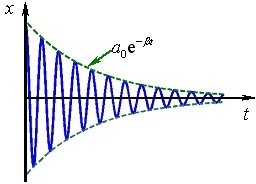
\( {x}{t}=A_{0}\mathrm{e}^{-\beta{t}}\cos{(\omega{t}+\varphi)}\), |
(3.2) |
Графік функції (3.2) показаний на рис. 3.1 (штрихові лінії визначають межі, в яких знаходиться зміщення х тіла з положення рівноваги).
 |
Циклічна частота загасаючих коливань дорівнює
| \( \omega = \sqrt{\omega_{0}^{2}-\beta^{2}}\). | (3.3) |
Відповідно, період
| \( {T}=\frac{2\pi}{\sqrt{\omega_{0}^{2}-\beta^{2}}}\). | (3.3а) |
|
\( {x(t)}=A(t)\cos (\omega{t}+\varphi) \). |
(3.4) |
де
|
\( {A}(t)={{A}_{0}}{{e}^{-\beta{t}}}\), |
(3.5) |
вільні коливання можливі лише за умови \( \beta<\omega_{0}\).
3.2. Параметри загасання вільних коливань
Для кількісної характеристики загасання коливань використовують декілька величин. Одна з них – коефіцієнт загасання β – фігурує безпосередньо в рівнянні (3.2). Що більша величина β, тим швидше спадає амплітуда коливань (рис. 3.2). Використовують також інші параметри загасання: час релаксації, логарифмічний декремент загасання та добротність.
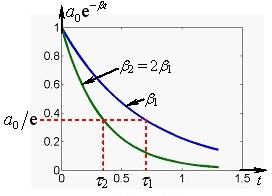 |
Часом релаксації τ — то є проміжок часу, за який амплітуда коливань зменшується в e ≈ 2,72 разів. Тож узявши до уваги вираз (3.4), отримаємо:
|
\( \frac{a_{0}e^{-\beta{t}}}{a_{0}e^{-\beta{(t+\tau)}}}={e} \) \( \Rightarrow \) \( e^{\beta\tau}=e \) \( \Rightarrow \) \( \tau=\frac{1}{\beta} \), |
(3.6) |
Таким чином, час релаксації є величиною оберненою до коефіцієнта загасання і показує наскільки повільно загасають коливання.
Логарифмічний декремент загасання λ – це логарифм відношення двох амплітуд, які відділені проміжком часу в один період:
|
\( \lambda =\ln\frac{A(t)}{A(t+T)}=\ln\frac{a_{0}e^{-\beta{t}}}{a_{0}e^{-\beta (t+T)}} \) \( \Rightarrow \) \( \lambda=\beta{T}=\frac{2\pi\beta}{\omega}\). |
(3.7) |
З урахуванням (3.6) можна також записати:
|
\( \lambda=\frac{T}{\tau}\). |
(3.7а) |
|
\( {N}_{e}=\frac{\tau}{T}=\frac{1}{\lambda}\). |
(3.8) |
Що більша величина Ne, тим довше в коливальній системі зберігаються вільні коливання, тобто тим якіснішою вона є. Але зазвичай якість коливальної системи характеризують не безпосередньо числом Ne, а добротністю Q – величиною, котра пов’язана з Ne або з декрементом загасання λ співвідношеннями:
|
\( {Q}=\pi{N}_{e}=\frac{\pi}{\lambda}\). |
(3.9) |
Згідно з (3.7) і (3.7а), добротність можна виразити через частоту та коефіцієнт загасання або через час релаксації та період вільних коливань:
|
\( {Q}=\frac{\omega}{2\beta}\), |
(3.9а) |
|
|
\( {Q}=\pi\frac{\tau}{T}\). |
(3.9б) |
Добротність характеризує також втрати енергії коливань унаслідок загасання. Можна показати, що при слабкому загасанні (β << ω0)
|
\( {Q}=\frac{2\pi{W}}{|\Delta{W}|}\), |
(3.10) |
де W – енергія вільних коливань у даний момент часу, а |ΔW| – утрата енергії коливань за один період, починаючи від цього моменту.
3.3. Вимушені механічні коливання. Резонанс
Коливання різної природи широко використовуються в технічних пристроях і машинах, тому вони мають бути незагасаючими. Для цього до системи треба весь час підводити енергію, аби компенсувати завжди наявні втрати енергії коливань. Отже, незагасаючими можуть бути лише вимушені коливання, що створюються і підтримуються завдяки постійному періодичному зовнішньому впливу на систему.
Рівняння вимушених коливань. Вимушені механічні коливання відбуваються під дією періодичної зовнішньої спонукальної (змушуючої) сили, властивості якої й визначають характер коливань. Найпростішими є вимушені коливання тіла, на яке, крім квазіпружної сили Fпр = –kx та сили опору \( {F}_{оп}=-\alpha{v}\), діє гармонічна спонукальна сила
\( {F}=F_{0}\cos\omega{t} \).
У такому разі для тіла маси m рівняння руху (другий закон Ньютона) має вигляд:
\( {m}\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-kx-\alpha\frac{\mathrm{d}x}{\mathrm{d}t}+F_{0}\cos\omega{t}\).
Увівши стандартні параметри \(\alpha /m=2\beta \), \({k/m}=\omega_{0}^{2}\) і позначення \( {f_{0}}=F_{0}/{m}\), це рівняння можна переписати у загально прийнятому вигляді диференціального рівняння вимушених коливань під дією гармонічної спонукальної сили:
|
\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+2\beta\frac{\mathrm{d}x}{\mathrm{d}t}+\omega_{0}^{2}x=f_{0}\cos\omega{t}\). |
(3.11) |
У такому вигляді воно є чинним не лише для координати, а й для будь якої іншої фізичної величини.
Із математики відомо, що загальний розв’язок диференціального рівняння такого виду складається з двох доданків:
\( {x}(t)=a_{0}e^{-\beta{t}}\cos{(}\omega^{\prime}{t} + \varphi)+A\cos{(}\omega{t}-\varphi_{0}{)}\),
де величина \( \omega\prime = \sqrt{\omega_{0}^{2}-\beta^{2}}\) збігається з частотою вільних загасаючих коливань (3.3). Отже, можна говорити, що тіло бере участь у двох рухах: 1) загасаючих коливаннях із частотою і 2) незагасаючих коливаннях із частотою спонукальної сили ω. Але внесок від першого доданку з плином часу зменшується, тому амплітуда коливань поступово наближається до незмінної величини A, як показано на рис. 3.3.
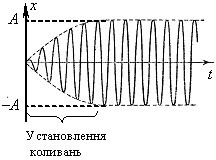 |
Це відбувається за певний час установлення, що є сумірним із часом релаксації \({\tau}\) вільних загасаючих коливань. Наприклад, за час \( {t}=5\tau \) амплітуда вимушених коливань досягає величини 99,5% від усталеної величини A. Відтак установлюються гармонічні стаціонарні вимушені коливання, що відбуваються за законом:
|
\( {x(t)}=A\cos{(}\omega{t}-\varphi_{0}{)}\). |
(3.12) |
Амплітуду A та початкову фазу φ0 вимушених коливань можна визначити різними способами. Наприклад, підставивши функцію (3.12) в рівняння (3.11) і побудувавши відповідну векторну діаграму (див. Розділ І, п. 1.2). Відповідні розрахунки дають:
|
\( {A}=\frac{f_{0}}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2}+4\beta^{2}\omega^{2}}}\), |
(3.13) |
і
|
\( \mathrm{tg}\varphi_{0}=\frac{2\beta\omega}{\omega_{0}^{2}-\omega^{2}}\). |
(3.14) |
Ці вирази указують на суттєві відмінності між вимушеними та вільними коливаннями:
1. У той час, як частота вільних коливань визначається параметрами коливальної системи, частота вимушених коливань від них ніяк не залежить і повністю визначається частотою спонукальної сили;
2. Амплітуда і початкова фаза вимушених коливань залежать як від властивостей спонукальної сили (амплітуди F0 та частоти ω, так і від властивостей коливальної системи (власної частоти ω0 та коефіцієнта загасання β). У той же час амплітуда та початкова фаза вільних коливань “ні від чого не залежать” і визначаються тільки способом виведення системі із стану рівноваги – величиною початкового відхилення, або початкової швидкості тіла;
3. Амплітуда вимушених коливань є функцією частоти: A = A(ω).
Резонанс. Проаналізуємо характер залежності амплітуди вимушених коливань від частоти, задля чого будемо подумки поступово збільшувати величину ω у виразі (3.13). Відтак при наближенні величини ω до ω0 перший доданок під коренем у (3.13) буде швидко зменшуватися, наближаючись до нуля, а по тому – так само швидко збільшуватись. Відповідно, амплітуда A спочатку буде зростати, а потім спадати, проходячи при певному значенні частоти ω = ωр через максимум. Таке зростання амплітуди вимушених коливань при наближенні частоти спонукальної сили до певної величини ωр називається резонансом, а частота ωр — резонансною частотою. Резонансну частоту можна знайти, дослідивши підкорінну функцію в (3.13) на мінімум. Відповідний розрахунок дає
|
\( \omega_{p}=\sqrt{\omega_{0}^2-2\beta^{2}}\). |
(3.15) |
Підставивши цей вираз у (3.13), визначимо резонансну амплітуду:
|
\( {A_{p}}=\frac{f_{0}}{2\beta\sqrt{\omega_{0}^{2}-\beta^{2}}}\). |
(3.16) |
Отримані вирази показують, що резонансна частота та резонансна амплітуда залежать від коефіцієнта загасання коливальної системи β. При його зменшенні резонансна частота ωр наближається до власної частоти ω0, а резонансна амплітуда Ар зростає, як показано на рис. 3.4.
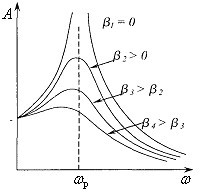
При β = 0 формула (3.15) дає ωр = ω0, а (3.16) – \( {A}_{p}\to\infty \). Але повністю позбутися загасання неможливо, можна лише зробити його слабким, так, що β << ω0. При цьому резонансна частота практично збігається із власною частотою системи ωр = ω0, але резонансна амплітуда коливань лишається скінченною.
Резонанс є важливим явищем, яке широко використовується в техніці. Приміром, на явищі резонансу ґрунтується дія язичкового частотоміра. Використовують це явище і в резонансних машинах, які призначені для випробування матеріалів на міцність. Широко використовують резонанс в акустиці, електро- та радіотехніці, тощо. Але явище резонансу може бути і шкідливим. До прикладу, відомо, що в масивних обертових вузлах машини при недостатньо точній збалансованості мас під час роботи виникають великі періодичні сили, що діють на підшипники, опору машини, корпус корабля, тощо. Частота таких сил, яка дорівнює частоті обертання валу, може збігтися з власною частотою коливань певної частини машини. При цьому виникнуть сильні резонансні коливання, що може призвести до поломки валу або руйнування фундаменту. Так само через недоліки в конструкції літака при певній швидкості польоту можуть виникнути руйнівні коливання крил. Тому при розробці подібних машин і пристроїв приділяють велику увагу запобіганню можливості виникнення резонансних коливань або, принаймні, їхньому послабленню до безпечного рівня.
Контрольні запитання
1. Чи можливі вільні гармонічні коливання в реальній механічній системі? Чому?
2. Якщо тіло маси m здійснює коливання в середовищі, де на нього діє сила опору
F = – \(\alpha{v}\), то чому дорівнює коефіцієнт загасання коливань?
3. Чи є вільні загасаючі коливання гармонічними? Строго періодичними?
4. Чому частота вільних загасаючих коливань маятника менша, ніж його власна частота?
5. Назвіть ті величини, що визначають швидкість загасання коливань і ті, що характеризують їхню тривалість
6. Що показує час релаксації коливань?
7. Що називається логарифмічним декрементом загасання? Як він пов’язаний з часом релаксації?
8. Яку кількість вільних коливань здійснює точка за час релаксації при логарифмічному декременті загасання λ?
9. Що таке добротність коливальної системи? Як вона виражається через циклічну частоту та коефіцієнт загасання?
10. Який зв’язок існує між втратами енергії загасаючих коливань і добротністю системи?
11. Від чого залежать частота стаціонарних вимушених коливань і частота вільних коливань?
12. Від чого залежать амплітуда стаціонарних вимушених коливань і амплітуда вільних коливань?
13. У чому полягає явище резонансу? Від чого і як залежить резонансна частота вимушених гармонічних коливань точки?
5. Вимушені гармонічні коливання в контурі
Загасаючі коливання становлять інтерес для теорії. А на практиці щонайширше застосування мають незагасаючі електричні коливання – від промислового змінного струму і до найрізноманітніших радіоелектронних приладів і пристроїв. Для створення незагасаючих коливань у контурі необхідно весь час компенсувати втрати електричної енергії на опорі R. Це роблять, включаючи в контур зовнішнє джерело (генератор) змінної напруги, яке створює та підтримує незагасаючі коливання.
Далі розглянуті наступні питання:
5.1. Амплітуда та фаза коливань заряду
5.2. Коливання напруг і струму. Резонанс
5.1. Амплітуда та фаза коливань заряду
Схема контура для дослідження вимушених коливань була наведена в п. 4.1 і має вигляд:
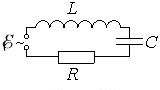
Там же було встановлено й загальне диференціальне рівняння (4.7) послідовного контура:
\( \frac{\mathrm{d}^{2}q}{\mathrm{d}t^{2}}+2\beta\frac{\mathrm{d}q}{\mathrm{d}t}+\omega_{0}^{2}q=\frac{\mathcal{E}}{L}\),
Розглянемо контур, в який включено зовнішній генератор із ЕРС, що змінюється за гармонічним законом \(E={{E}_{0}}\cos \omega t\). У такому разі наведене рівняння контура має вигляд:
|
\(\frac{\mathrm{d}^{2}q}{\mathrm{d}t^{2}}+2\beta\frac{\mathrm{d}q}{\mathrm{d}t}+\omega_{0}^{2}q=\frac{\mathcal{E}_{0}}{L}\cos\omega{t}\). |
(5.1) |
|
де β = R/2L – загасання, і ω0 = \({1}/{\sqrt{LC}}\;\) – власна частота контура.
Із теорії диференціальних рівнянь відомо, що загальні розв’язки цього рівняння можна записати, як
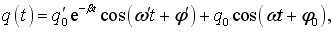
де \( \omega^{\prime} =\sqrt{\omega_{0}^{2}-\beta^{2}}\), що збігається з частотою вільних коливань у контурі, а ω — частота генератора.
Така структура функцій q(t) має просте фізичне обґрунтування. В момент увімкнення генератор виводить контур з рівноважного стану. Відтак у ньому крім вимушених коливань, які створюються й підтримуються генератором і визначаються другим доданком у виразі q(t), збуджуються й вільні загасаючі коливання (перший доданок). Але останні через якийсь час практично повністю загасають, і в контурі встановлюються стаціонарні вимушені коливання заряду на конденсаторі, що визначаються рівнянням:
|
|
(5.2) |
За своїми властивостями такі коливання суттєво відрізняються від вільних. Приміром, частота вимушених коливань зовсім не залежить від параметрів контура і задається генератором. Також, на відміну від вільних коливань, у яких амплітуда та початкова фаза не залежать від параметрів контура і “задаються” умовами створення, амплітуда й фаза вимушених коливань визначаються не тільки генератором, а й параметрами контура.
Мовою математики амплітуда q0 і початкова фаза φ0 є сталими інтегрування рівняння (5.1), які визначаються шляхом підстановки розв’язку у вихідне рівняння. Тож знайдемо з (5.2) похідні dq/dt та d2q/dt2 і підставимо їх у (5.1):
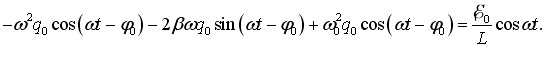
Далі зробимо заміну
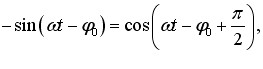
і після елементарних викладок дістанемо:
|
|
(5.3) |
|
|
|
Хоча в рівняння (5.3) входять дві невідомі величини – амплітуда заряду q0 і початкова фаза φ0, – з нього за допомогою векторного зображення гармонічних коливань (розділ 1, п. 1.2) можна визначити обидва параметри. При цьому ліва частина рівняння (5.3) зображується двома взаємно перпендикулярними векторами, а права – вектором, який є їхньою сумою, як показано на рис. 5.1. Вектори на цій діаграмі утворюють прямокутний трикутник, з якого легко отримати вирази для амплітуди та початкової фази заряду на конденсаторі контура:
|
|
(5.4) |
і
|
|
(5.5) |
5.2. Коливання напруг і струму. Резонанс
Вимушені коливання струму та напруг. Вимушені гармонічні коливання в контурі відбуваються за таким самим законом, як і вільні коливання в ідеальному контурі. Тому струм та напруги на конденсаторі і котушці індуктивності визначаються рівняннями й співвідношеннями, що є аналогічними до (4.11), (4.13), (4.15). Тож, увівши в них позначення
|
|
(5.6) |
отримаємо:
|
|
(5.7) |
|
|
|
(5.8) |
|
|
|
(5.9) |
Початкова фаза коливань струму, згідно з (5.5) і (5.6), визначається, як
|
|
(5.10) |
За фазою коливання напруги на конденсаторі (5.8) відстають, а на котушці індуктивності (5.9) випереджають коливання струму на π/2. Отже, фазові співвідношення при вимушених коливаннях в контурі такі самі, як і при вільних незагасаючих коливаннях.
Резонанс. Як і при механічних коливаннях (розділ 3, п. 3.3), амплітуди вимушених коливань у контурі залежать від частоти. Ці залежності називають амплітудними (або резонансними) характеристиками контура. Відповідно до (5.4) і (4.11а), (4.12а), та (4.15а), вони визначаються такими виразами:
|
|
(5.11) |
|
|
|
(5.12) |
|
|
|
(5.13) |
Із цих виразів випливає, що для напруг на конденсаторі й котушці та струму в контурі можливе явище резонансу – проходження амплітуди вимушених коливань через максимум при певній резонансній частоті ω = ωр.
Резонансну частоту для кожної з указаних величин можна знайти за стандартним алгоритмом, визначивши та прирівнявши до нуля її похідну. Такі обчислення показують, що резонансна частота стуму збігається із власною частотою контура:
|
\( \omega_{I}=\omega_{0}=\frac{1}{\sqrt{LC}}\). |
(5.14) |
А от резонансні частоти напруг на конденсаторі ωс і котушці індуктивності ωL залежать від загасання β і визначаються виразами:
|
\( \omega_{C}=\sqrt{\omega_{0}^{2}-2\beta^{2}} \), |
(5.15) |
|
|
\( \omega_{L}=\frac{\omega_{0}^{2}}{\sqrt{\omega_{0}^{2}-2\beta^{2}}}\). |
(5.16) |
Як видно, ці частоти пов’язані співвідношенням:
\( \omega_{C}\cdot\omega_{L}=\omega_{0}^{2} \)
Підстановка резонансних частот (5.14) – (5.16) у вирази амплітуд (5.11) – (5.13) дає:
|
|
(5.17) |
|
|
|
(5.18) |
При слабкому загасанні величиною \( \beta^{2} \) під коренем можна знехтувати і, урахувавши (4.34), отримати:
|
|
(5.19) |
Ці вирази дають простий спосіб вимірювання добротності та показують ще одне “обличчя” цієї важливої характеристики контура:
добротність можна трактувати як коефіцієнт підсилення напруги на ємності або індуктивності контура при резонансі.
Головні особливості резонансу в коливальному контурі наочно відображають рис. 5.2 і 5.3.
|
|
На рис. 5.2 показані резонансні криві напруги на конденсаторі та на котушці індуктивності при заданій ЕРС генератора в контурі з малою добротністю й заданим загасанням, а на рис. 5.3 – резонансні криві струму в контурі при різних загасаннях і однаковій ЕРС генератора. Видно, що при зменшенні загасання і збільшенні добротності резонанс стає гострішим: криві \( {I}_{m}(\omega)\) стають вищими та вужчими. Можна довести, що при слабкому загасанні добротність контура
|
\( {Q}=\frac{\omega_{0}}{\Delta\omega} \), |
(5.20) |
де ω0 – резонансна частота струму (5.14), а Δω = |ω1 - ω2| ширина резонансної кривої, визначена на рівні
|
\( {I}_{m}= \frac{I_{p}}{\sqrt{2}} \), |
(5.21) |
як показано на рис. 5.3.
Велика гострота резонансу в контурі з високою добротністю зумовлює широке практичне застосування коливальних контурів у царині радіотехніки та телекомунікацій, позаяк дозволяє здійснювати селекцію сигналів. Ставлячи на вході приймального пристрою коливальний контур і налаштовуючи його на відповідну резонансну частоту, можна з широкого спектру частот, які приходять з ефіру чи лінії передач, виділяти і далі опрацьовувати сигнали тільки з потрібною частотою. При цьому що вища добротність контура, тим краще він виділяє сигнал заданої частоти. Отже,
добротність виступає ще і як міра селективності контура.
Контрольні запитання
1. Що треба зробити, аби в реальному коливальному контурі створити гармонічні коливання?
2. Від чого залежить частота стаціонарних вимушених коливань у контурі?
3. Зобразіть приблизний вигляд графіка залежності від часу амплітуди вимушених коливань у контурі.
4. Чому дорівнює зсув фаз між коливаннями напруги генератора та заряду конденсатора контура? За якої умови коливання заряду за фазою: а) відстають від коливань напруги генератора; б) випереджають їх?
5. Відстають чи випереджають за фазою вимушені коливання напруги на конденсаторі контура коливання струму? На скільки?
6. Відстають чи випереджають за фазою вимушені коливання напруги на коушці контура коливання струму? На скільки?
7. Відстають чи випереджають за фазою вимушені коливання напруги на конденсаторі контура коливання напруги на котушці? На скільки?
8. За якої умови вимушені коливання струму в контурі за фазою: а) відстають від коливань напруги генератора; б) випереджають коливання напруги генератора; в) збігаються з коливаннями напруги генератора?
9. При якій частоті амплітуда вимушених коливань струму в контурі є максимальною?
10. При якій частоті амплітуда вимушених коливань напруги на конденсаторі контура є максимальною?
11. Чому дорівнює резонансна амплітуда напруги на конденсаторі контура при слабкому загасанні?
12. При якій частоті амплітуда вимушених коливань напруги на котушці контура є максимальною?
13. Чому дорівнює резонансна амплітуда напруги на котушці контура при слабкому загасанні?
6. Змінний струм
‹
Одним із важливих для практики видів вимушених електричних коливань є змінний струм. У широкому значенні змінним струмом називають будь-які періодичні вимушені коливання струму та напруги в електричному колі. Але зазвичай під змінним струмом розуміють синусоїдальний струм, який змінюється за гармонічним законом. Це пояснюється тим, що саме за таким законом змінюється з часом ЕРС потужних індукційних генераторів на електростанціях, які дають більшу частину всієї споживаної людством електричної енергії. Далі розглядаються такі питання:
6.1. Закон Ома для змінного струму
6.2. Резонанс у колі змінного струму
6.3. Потужність у колі змінного струму
6.1. Закон Ома для змінного струм
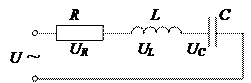 |
Найпростішим повним за складом колом змінного струму є послідовний контур, який включає резистор R, конденсатор C і котушку індуктивності L (див. схему), на які подається гармонічна напруга
|
u = U0cosωt. |
(6.1) |
Але на відміну від коливального контура, в загальному випадку наявність у колі всіх полічених елементів не є обов’язковою. Зокрема це стосується котушки індуктивності. Тому в теорії змінного струму вона розглядається не як джерело ЕРС самоіндукції, а як пасивний елемент кола, що разом з іншими живиться від генератора змінної напруги.
Раніше (ЕЛЕКТРИКА І МАГНЕТИЗМ, частина ІІІ) було показано, що змінні струми практично завжди є квазістаціонарними. Тому, відповідно до другого правила Кірхґофа, для миттєвих значень напруг на ділянках послідовного кола можна записати:
|
uR + uC + uL = U0cosωt. |
(6.2) |
При цьому струм у всіх ділянках кола в кожен момент часу однаковий, і виражається загальним рівнянням
|
|
(6.3) |
У випадку стаціонарного (постійного) струму зв’язок між струмом та напругою, що подається на послідовне коло, визначається законом Ома. Чи це так і для змінного струму, не є очевидним і потребує спеціального розгляду. Спочатку проаналізуємо зв’язок між струмом і напругою для кожної ділянки кола окремо.
Резистор у колі змінного струму. Активний опір. Резистор по суті – то є просто провідник із певним опором R , для якого в кожну мить виконується закон Ома u = iR . Отже, рівняння коливань напруги на опорі R, згідно з (6.3), має вигляд:
|
|
(6.4) |
Відмітимо, що струм і напруга на опорі R змінюються синфазно, і їхні амплітуди пов’язані співвідношенням:
|
|
(6.5) |
У колах змінного струму крім резисторів фігурують і котушки індуктивності та конденсатори, які теж чинять опір протіканню струму. Тому в теорії змінного струму опір R, що зумовлений розсіюванням носіїв струму і є причиною виділення у провіднику джоульового тепла, називають активним опором.
Котушка індуктивності та конденсатор у колі змінного струму. Реактивні опори. При протіканні змінного струму по котушці індуктивності напруга на ній визначається як:
\( {U}_{L}=L\frac{\mathrm{d}I}{\mathrm{d}t}\).
Тому, згідно з (6.3), напруга на котушці змінюється за законом:
|
|
(6.6) |
Отже,
коливання напруги на котушці за фазою випереджають коливання струму на π/2, або чверть періоду,
і їхні амплітуди пов’язані співвідношенням:
|
\( {U}_{L0}=I_{0}\omega{L}\) або \( {I}_{0}=\frac{U_{L0}}{X_{L}}\), |
(6.7) |
де уведено позначення
|
\( {X}_{L}=\omega{L} \). |
(6.8) |
Установимо тепер зв’язок між струмом i у колі та напругою uс на конденсаторі. При протіканні струму в колі з конденсатором заряд, який проходить по провідниках, потрапляє на обкладку конденсатора. Тому кожної миті сила струму в колі дорівнює швидкості зміни заряду конденсатора: і = dq/dt, тож
\( dq=idt\quad \Rightarrow \quad q=\int{idt}\).
Відповідно, напруга на конденсаторі uС = q/С визначається, як|
\( {{u}_{c}}={{U}_{C0}}\cos \left( \omega t-\varphi -\frac{\pi }{2} \right)\). |
(6.9) |
Таким чином,
коливання напруги на конденсаторі за фазою відстають від коливань струму на π/2, або чверть періоду.
При цьому їхні амплітуди пов’язані співвідношенням:
|
\( {U}_{C0}=I_{0}X_{C}\) або \( {I}_{0}=\frac{U_{C0}}{X_{C}} \), |
(6.10) |
де уведено позначення
|
\( {X}_{C}=\frac{1}{\omega{C}}\). |
(6.11) |
Порівняння виразів (6.7), (6.10) із (6.5) показує, що котушка індуктивності та конденсатор обмежують амплітуду струму при заданій амплітуді напруги, аналогічно до того, як це робить резистор. Тому можна говорити, що індуктивність і ємність теж створюють опір для протікання змінного електричного струму. Відповідно, величина XL, яка визначається формулою (6.8), називається реактивним індуктивним опором, а величина ХС (формула (6.11)) — реактивним ємнісним опором.
Отримані співвідношення (6.5), (6.7) і (6.10) показують, що на кожному опорі амплітуди струму та напруги пов’язані між собою законом Ома. Але для миттєвих значень він не виконується. Справді, з рівнянь (6.3), (6.6) і (6.9) випливає, що
|
|
(6.12) |
і
|
|
(6.12а) |
тобто
миттєва величина струму не є прямо пропорційною напрузі,
як того вимагає закон Ома. Відповідно, реактивний опір, на відміну від активного, не можна трактувати як коефіцієнт пропорційності між напругою та струмом на котушці або на конденсаторі.
Властивості реактивних опорів є доволі специфічними. З одного боку реактивний опір, подібно до активного, залежить від параметрів відповідного пристрою – котушки індуктивності чи конденсатора. Але на відміну від активного,
реактивні опори (6.8), (6.11) залежать від частоти струму.
Тому, якщо на коло подати постійну напругу (ω = 0), то реактивні опори ХL = 0 і XC → ∞. Це абсолютно природньо: адже для постійного струму котушка являє собою просто шматок дроту, а конденсатор – розрив кола. Якщо котушки в колі взагалі немає, то знову маємо L = 0, і ХL = 0. Зрозуміло, що за відсутності конденсатора так само ХС = 0, але з (6.11) при цьому випливає досить дивний формальний висновок: C → ∞. Цей “парадокс” має просте пояснення. Відсутність конденсатора означає відсутність у колі розриву провідності, отже, “викидаючи” з кола конденсатор, ми з’єднуємо провідники на місці його розташування. Тому формальний перехід до випадку “коло без конденсатора” можна здійснити, подумки наближаючи пластини конденсатора аж до дотику. При цьому відстань між пластинами конденсатора d = 0, і “все стає на місця”: ємність C = ∞, і опір XC = 0.
З ємнісним опором пов’язано ще одне питання. Опір ХС ми трактуємо як величину, що пов’язує амплітуди напруги та струму в конденсаторі, тоді як заряджені частинки-носії струму рухатися в діелектрику між пластинами конденсатора не можуть. І дійсно, стаціонарний струм може протікати тільки по замкнених провідниках. Але змінний струм можливий і при розриві провідності, як от у колі з конденсатором. При цьому із загальних рівнянь електродинаміки (ЕЛЕКТРИКА І МАГНЕТИЗМ, V, п. 2) випливає, що лінії струму провідності, які розриваються на пластинах конденсатора, замикаються всередині лініями струму зміщення, котрий є мірою швидкості зміни електричного поля всередині конденсатора. Отже
струм конденсатора – то є струм зміщення,
котрий в кожен момент часу збігається із струмом провідності в провідниках, які підходять до обкладок.
Імпеданс. Закон Ома для змінного струму. Встановимо тепер, як струм у колі пов’язаний з напругою на вході (напругою генератора). Вище вже говорилося, що в послідовному колі за умови квазістаціонарності напруга на вході дорівнює сумі напруг на всіх ділянках кола, а струм скрізь однаковий, так само, як у випадку стаціонарного (постійного) струму. Тому може здатися, що величина змінного струму, як і у випадку постійного, дорівнює відношенню напруги на вході до суми опорів усіх ділянок кола. Але насправді це не так, оскільки напруги на різних ділянках кола мають різні фази (див. рівняння (6.1),(6.4), (6.6) і (6.9)).
Для встановлення зв’язку між змінним струмом та напругою побудуємо векторну діаграму кола так, як це робилося при розгляді вимушених коливань у контурі (п. 5, рис. 5.1). При цьому врахуємо, що фаза напруги на індуктивному опорі випереджає, а на ємнісному – відстає від фази струму на π/2. З отриманої векторної діаграми, котра показана на рис. 6.1, випливає, що
|
\( {U}_{0}^{2}=U_{R}^{2}\left(U_{L}^{2}-U_{C}^{2}\right) \). |
(6.13) |
|
|
|
Відтак, урахувавши (6.5), (6.9) і (6.10), одержимо
|
\( {U}_{0}=I_{0}\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\). |
(6.14) |
Величина
|
X = XL - XC |
(6.15) |
називається реактивним опором, а величина
|
\( {Z}=\sqrt{R^{2}+X^{2}} \) |
(6.16) |
називається повним опором, або імпедансом послідовного кола змінного струму. Тож співвідношення (6.14) між амплітудами напруги та струму набуває вигляду:
|
\( {U}_{0}=I_{0}Z \), або \( {I}_{0}=\frac{U_{0}}{Z}\) |
(6.17) |
і є подібним до співвідношення між напругою та силою постійного струму. Тому воно називається законом Ома для змінного струму. З урахуванням (6.8), (6.11) і (6.15), імпеданс послідовного кола та закон Ома в розгорнутому вигляді записуються, як
|
\( {Z}=\sqrt{R^{2}+\left(\omega{L}-\frac{1}{\omega{C}}\right)^{2}} \), |
(6.18) |
|
|
\( {I}_{0}=\frac{U_{0}}{\sqrt{R^{2}+(\omega{L}-\frac{1}{\omega{C}}})^{2}}\). |
(6.19) |
Із векторної діаграми рис. 6.1 також випливає, що зсув фаз φ між струмом і напругою на вході кола визначається виразом:
|
|
(6.20) |
Стосовно закону Ома для змінного струму необхідно зробити наступні зауваження:
1. Поняття реактивних опорів й імпедансу та їхні вирази введені для гармонічних (синусоїдальних) струмів. Тому всі розглянуті співвідношення включно із законом Ома стосуються тільки таких струмів.
2. Закон Ома (6.17) виконується для амплітудних і не виконується для миттєвих значень струму та напруги. Це випливає з рівнянь (6.1), (6.3) і виразу (6.17):
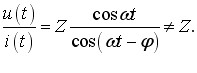
Така “невідповідність” пояснюється зсувом фаз φ між струмом і напругою, через що вони набувають своїх амплітудних значень у різні моменти часу. Тому кожної миті напруга і струм складають не однакові й не фіксовані частки від амплітудних значень. Через це за великим рахунком змінний струм не не задовольняє закон Ома, позаяк сила струму не є прямо пропорційною напрузі. Але для практики це нічого не вартує, бо, через швидку зміну, значущими є лишень усереднені характеристики змінного струму, що залежать тільки від амплітуд і тому підпорядковуються законові Ома.
6.2. Резонанс у колі змінного струму
Реактивні опори (6.8), (6.11) та імпеданс (6.18) залежать від частоти, як показано на рис. 6.2а. При зростанні частоти індуктивний опір збільшується, а ємнісний зменшується. Тому, коли опори ХL і ХС зрівнюються, то реактивний опір ХL – ХС, = 0 й імпеданс, згідно з (6.18), має мінімальне можливе значення Z = R . Відповідно, амплітуда струму (6.19) набуває максимального можливого при заданій амплітуді напруги на вході значення
|
\( {I}_{p}=\frac{U_{0}}{R}\) |
(6.21) |
і надалі спадає (рис. 6.2б). Тобто, в колі змінного струму спостерігається резонанс. Резонансна частота ωp визначається умовою XL = XC, отже згідно з (6.8) і (6.11),
|
\( \omega_{p}L=\frac{1}{\omega_{p}C} \) \(\Rightarrow \) \( \omega_{p}=\frac{1}{\sqrt{LC}}=\omega_{0} \). |
(6.22) |
|
|
При резонансі напруга на активному опорі кола має найбільше можливе значення, рівне напрузі генератора, а сумарна напруга на реактивних опорах дрпівнює нулю. Але напруги окремо на котушці індуктивності UL = IpXL та на конденсаторі UC = IpXC не дорівнюють нулеві. Згідно з (6.8), (6.11), (6.21), і (6.22), вони визначаються, як
|
\( {U}_{L}=U_{C}=\frac{U_{0}}{R}\sqrt{\frac{L}{C}}\), |
(6.23) |
і можуть виявитися набагато вищими, ніж амплітуда напруги генератора. Це має враховуватися, бо при резонансі може виникнути загроза електричного пробою ізоляції провідників.
Як видно з (6.22), резонансна частота струму в колі збігається із власною частотою коливального контура (4.10), що має такі самі індуктивність і ємність. Всі інші розглянуті співвідношення для кола змінного струму теж збігаються з аналогічними співвідношеннями, що характеризують коливальний контур. У цьому не важко переконатися, зробивши у відповідних виразах для контура заміни:
\( {\omega_{0}}=\frac{1}{\sqrt{LC}}\), \( {\omega{L}}=X_{L} \) і \( \frac{1}{\omega{C}}=X_{C} \).
Указаний збіг є цілком природнім, адже коливальний контур принципово не відрізняється від повного кола змінного струму. Відміна полягає тільки у співвідношенні параметрів: активний опір R у реальних коливальних контурах є дуже малим, а в силових електричних колах змінного струму, напроти, великим.
6.3. Потужність у колі змінного струму
Можливості отримання корисної енергії в тому чи іншому електричному пристрої визначаються роботою та потужністю електричного струму в колах цього пристрою. Розглянемо, від чого залежить потужність на окремих ділянках та в усьому колі змінного струму.
Потужність на активному опорі. Діючі значення напруги та струму. Спочатку розглянемо потужність струму, що виділяється на резисторі. Миттєва потужність на будь-якій ділянці кола дорівнює добутку миттєвих значень струму та напруги. Відповідно, на резисторі вона, згідно з (6.3) і (6.4), визначається виразом:
|
\( {P}_{R}=iu_{R}=I_{0}U_{R0}\cos^{2}(\omega{t}-\varphi{)}\). |
(6.24) |
Але, позаяк змінні струми мають високу частоту, практично значимою є тільки середня потужність \( {P}=\langle{p}\rangle \), тобто величина
|
\( {P}_{R}=I_{0}U_{R0}\langle\cos^{2}(\omega{t}-\varphi{)}=\frac{I_{0}U_{R0}}{2}\langle{1}+\cos{(2}(\omega{t}-\varphi{)})\rangle \). |
(6.24а) |
Середнє значення функцій косинус і синус дорівнює нулеві, тому, з урахуванням (6.5),
|
\( {P}_{R}=\frac{I_{0}U_{R0}}{2}=\frac{I_{0}^{2}R}{2}=\frac{U_{0}^{2}}{2R}\). |
(6.25) |
Ці формули можна записати зручніше, увівши так звані “діючі” (або “ефективні”) значення струму та напруги, котрі виражаються через амплітуди як
|
\( {I}=\frac{I_{0}}{\sqrt{2}}\) і \( {U}=\frac{U_{0}}{\sqrt{2}}\). |
(6.26) |
Відтак формули (6.25) набувають вигляду:
|
\( {P}_{R}=IU_{R}=I^{2}R=\frac{U_{R}^{2}}{R}\), |
(6.27) |
і стають такими самими, як і для постійного струму. Отже, можна сказати, що
діючі значення напруги та сили змінного струму – це такі величини напруги та сили постійного струму, при яких у провіднику виділяється така сама потужність, як і при заданому змінному струмі.
Іншими словами, діючі значення дорівнюють характеристикам постійного струму, котрий є енергетично еквівалентним даному змінному струмові.
Із означень (6.26) випливає, що всі співвідношення, в які входять амплітуди струму й напруги, зберігаються і для діючих значень. Зокрема, це стосується співвідношень, які виражають закон Ома для всього кола (6.17) та окремих ділянок (6.5), (6.7), (6.10):
|
U = IZ, UR =IR, UL = IXL, UC = IXC. |
(6.28) |
Діючі значення є дуже зручними і тому загально прийнятими на практиці. Зокрема, всі вимірювальні прилади змінного струму проградуйовані в діючих значеннях. Тому в техніці та побуті, коли мова йде про величину змінного струму чи напруги, терміни “діючі значення” спеціально не вживають, і слова “напруга в мережі дорівнює 220 В” або напис на вилці чи розетці “220 В, 6 А” по замовчуванню означають саме діючі значення. Що ж до амплітуди напруги в освітлювальній мережі, то вона складає \( {U}_{0}=220\cdot\sqrt{2}\approx{311}\) В. Ще одне зауваження про терміни. Діючі значення були уведені через потужність змінного струму, що виділяється на резисторі R. На відміну від котушки індуктивності та конденсатора, ця потужність виділяється при будь-якому напрямку і фазі φ струму. Можна сказати, що резистор "активно" споживає енергію джерела струму, тому опір R називають активним опором. Слід також зауважити, що активний опір в колі змінного струму не є тотожнім до опору в колі постійного струму. Ці величини збігаються тільки в нерухомих колах, де опір R зумовлюється виключно розсіюванням ("гальмуванням") носіїв струму при зіткненнях із іншими частинками провідника і є фактором необоротного перетворення енергії електричного струму на тепло. Але, до прикладу, в електричних двигунах споживана енергія струму переходить не тільки в тепло, а й, головно, в механічну роботу. Тому активний опір працюючого двигуна є набагато більшим, ніж нерухомого.
Потужність на котушці індуктивності та на конденсаторі. Суттєва відмінність між реактивними опорами XL і XC та активним опором R виявляється в процесах перетворення енергії в колі змінного струму. Аби в цьому переконатися, знайдемо миттєву та середню потужності струму на індуктивності та на ємності. Вказані миттєві потужності визначаються добутком миттєвих значень струму (6.3) та відповідної миттєвої напруги (6.6) і (6.9):
|
pL = –\(\frac{1}{2}{{I}_{0}}{{U}_{L0}}\sin \left( 2\omega t-2\varphi \right)\) = –\(I{{U}_{L}}\sin \left( 2\omega t-2\varphi \right)\)
|
(6.29) |
|
|
pC = \(\frac{1}{2}{{I}_{0}}{{U}_{C0}}\sin \left( 2\omega t-2\varphi \right)\) =\(I{{U}_{C}}\sin \left( 2\omega t-2\varphi \right)\). |
(6.29а) |
І, позаяк середня величина \( \langle\sin{(}2\omega{t}-2\varphi{)}\rangle={0}\), середні потужності на котушці та на конденсаторі
|
PL = PC = 0. |
(6.30) |
Цей, можливо, неочікуваний результат має просте пояснення. Ані в котушці індуктивності, ані в конденсаторі не відбувається ніяких перетворень електричної енергії в інші форми, наприклад у тепло. Через це магнітна енергія, яка накопичується в котушці під час збільшення струму від нуля до амплітудного значення, при подальшому зменшенні струму до нуля повністю повертається до генератора чи інших частин кола. Подібні процеси відбуваються й при збільшенні та зменшенні напруги на конденсаторі. Тому, на відміну від активного опору, стосовно індуктивності та ємності слід говорити не про споживання енергії від генератора, а тільки про енергообмін між ними та генератором. Саме з цієї причини котушку індуктивності та конденсатор називають реактивними елементами кола, а величини XL і XC – реактивними опорами.
Повна потужність у колі змінного струму. Згідно з (6.1) і (6.3), миттєва потужність струму у всьому колі
\( {p}=iu=I_{0}U_{0}\cos{(}\omega{t}-\varphi{)}\cos\omega{t}\).
За допомогою відомої формули тригонометрії цей вираз можна записати, як
|
|
(6.31) |
|
|
|
Звідси видно, що миттєва потужність, яка виділяється в колі, коливається навколо рівня 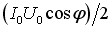 з подвоєною частотою струму. Можливий вигляд графіка p(t), згідно з (6.31), показаний на рис. 6.3. Наявність на графіку ділянок із p < 0 може видатися несподіваною, але легко пояснюється присутністю в колі реактивних опорів. Раніше вже говорилося про те, що, на відміну від резистора, котушка індуктивності та конденсатор не перетворюють енергію струму на інші форми, а лише періодично накопичують, а потім повністю повертають її в коло (див. (6.29), (6.29а)). Причому ці процеси відбувається не синхронно. Тому може статися, що протягом певних частин періоду енергія, яку віддають реактивні елементи перевищує ту, що поглинається на активному опорі. В такому разі “зайву” енергію коло віддає в генератор, а формальною мовою це означає, що воно споживає від’ємну потужність.
з подвоєною частотою струму. Можливий вигляд графіка p(t), згідно з (6.31), показаний на рис. 6.3. Наявність на графіку ділянок із p < 0 може видатися несподіваною, але легко пояснюється присутністю в колі реактивних опорів. Раніше вже говорилося про те, що, на відміну від резистора, котушка індуктивності та конденсатор не перетворюють енергію струму на інші форми, а лише періодично накопичують, а потім повністю повертають її в коло (див. (6.29), (6.29а)). Причому ці процеси відбувається не синхронно. Тому може статися, що протягом певних частин періоду енергія, яку віддають реактивні елементи перевищує ту, що поглинається на активному опорі. В такому разі “зайву” енергію коло віддає в генератор, а формальною мовою це означає, що воно споживає від’ємну потужність.
Розглянутий аналіз процесів перетворення енергії в колі є важливими для теорії, але практичне значення має лише середня потужність струму \( {P}=\langle{p}\rangle \), яку споживає коло. Тому на практиці під потужністю змінного струмурозуміють саме середнє значення величини (6.31):
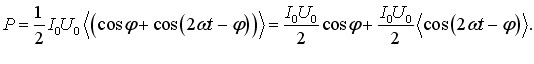
Урахувавши, що 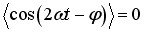 , і перейшовши від амплітуд до діючих значень, отримуємо:
, і перейшовши від амплітуд до діючих значень, отримуємо:
|
|
(6.32) |
Отже, потужність, яка виділяється в колі змінного струму, залежить не тільки від сили струму та напруги, а й від зсуву фаз між ними. Відповідно, величина cosφ називається коефіцієнтом потужності (в інженерній практиці — “косинусом фі”. Його вираз можна знайти безпосередньо з векторної діаграми (рис. 6.1) як UR/U0, або через формулу (6.20):
|
|
(6.33) |
Коефіцієнт потужності відіграє важливу роль в електротехніці, оскільки визначає ефективність використання електричної енергії. Справді, якщо cosφ << 1, то навіть при великому струмі та напрузі коло майже не споживає енергії з мережі живлення. При цьому генератор працює вхолосту, і необхідні для генерації струму енергетичні ресурси витрачаються марно. Тому коефіцієнт потужності завжди необхідно максимально підвищувати. Для цього треба наближати імпеданс до активного опору, тобто зменшувати реактивну складову імпедансу. З цією метою в коло з великою індуктивністю, яку мають, скажімо, обмотки електричного двигуна, включають компенсуючі конденсатори. Аналогічно в коло з великою ємністю включають додаткові котушки індуктивності. Таким чином, хоча середня потужність на реактивних опорах дорівнює нулеві, ці опори відіграють суттєву роль в енергетиці кола змінного струму. Тому в електротехніці крім потужності (6.32), яку називають активною потужністю, розглядають так звану реактивну потужність Q, яку вимірюють не у ватах, а у “варах” (скорочення від "вольт-ампер реактивний") і визначають за формулою Q = IUsinφ. Але детально це питання розглядають не в загальній фізиці, а в електротехніці.
Контрольні запитання
1. Що таке ємнісний опір? Якою формулою він визначається?
2. Що таке індуктивний опір? Якою формулою він визначається?
3. Якою формулою визначається повний реактивний опір кола?
4. Якою формулою визначається імпеданс (повний опір) послідовного кола?
5. Якою формулою визначається імпеданс (повний опір) послідовного кола, в якому немає конденсатора?
6. Якою формулою визначається імпеданс (повний опір) послідовного кола, в якому немає котушки індуктивності?
7. Якою формулою визначається імпеданс (повний опір) ідеального коливального контура?
8. Сформулюйте та запишіть закон Ома для змінного струму.
9. Чи справджується закон Ома для миттєвих значень змінного струму та напруги? Дайте обґрунтовану відповідь.
10. В якому випадку коливання струму в послідовному колі за фазою випереджають коливання напруги генератора?
11. В якому випадку коливання струму в послідовному колі за фазою відстають від коливань напруги генератора?
12. В якому випадку коливання струму в послідовному колі відбуваються в одній фазі з коливаннями напруги генератора?
13. Чи можуть коливання струму за фазою випереджати коливання напруги генератора в колі без конденсатора?
14. Чи можуть коливання струму за фазою відставати від коливань напруги генератора в колі без котушки індуктивності?
15. При якій частоті амплітуда струму в послідовному колі з параметрами R,L,C буде максимальною?
16. Від чого та як залежить максимальна можлива амплітуда змінного струму в колі?
17. Отримайте вирази (6.23).
18. Якими формулами визначаються діючі значення змінного струму та напруги та який фізичний зміст вони мають?
19. Чому дорівнює середня потужність змінного струму, що виділяється на активному опорі? Ємнісному опорі? Індуктивному опорі?
20. Якими формулами визначається повна потужність у колі змінного струму?
21. Чи може в колі змінного струму бути від’ємною: а) миттєва потужність струму; б) середня потужність струму?
22. Що таке коефіцієнт потужності та як його можна змінювати для підвищення потужності, що виділяється в колі змінного струму?
Частина II. ХВИЛІ
Коливання як такі є локальним процесом, місце протікання якого обмежується розташуванням і розмірами коливальної системи, до прикладу, маятника чи коливального контура. Але за відповідних умов коливання та інші збурення від місця виникнення поширюються по всіх доступних напрямках, охоплюючи все більшу область простору.
Поширення збурень у просторі з плином часу називається хвильовим процесом, або просто хвилею.
(Примітка. Збуреннями називаються різкі локальні відхилення системи від рівноважного тану).
Визначальною властивістю хвиль є їхня здатність переносити енергію. Достатньо вказати, що цій властивості ми завдячуємо самим своїм існуванням. В усьому іншому хвилі мають багато спільного з локальними коливаннями. Зокрема, хвилі різної природи мають спільні загальні властивості й описуються за допомогою єдиного математичного апарату. Далі розглядаються такі питання:
1. Загальні властивості гармонічних хвиль
При єдності загальних властивостей хвилі можуть мати істотні відмінності, пов'язані з їхнім походженням і фізикою процесів, які в них відбуваються. Тому в теорії хвилі класифікуються за відповідними ознаками. До прикладу, окремо розглядають механічні хвилі, з якими, зокрема, пов'язаний звук, та електромагнітні хвилі, що є відповідальні за світло. Крім того, властивості хвиль істотно залежать від умов поширення і можуть бути складними. В даному посібнику розглядаються хвилі в ізотропних середовищах, де характеристики хвиль не залежать від напрямку поширення.
Далі розглядається:
1.1. Поперечні та поздовжні хвилі
1.2. Характеристики та рівняння гармонічних хвиль
1.1. Поперечні та поздовжні хвилі
Одним з класифікаторів хвилі є напрям коливань, що відбуваються в ній. За цією ознакою хвилі поділяють на поздовжні та поперечні. При цьому
в поздовжній хвилі коливання в кожній точці відбуваються вздовж напрямку поширення.
Відповідно,
в поперечній хвилі коливання відбуваються перпендикулярно до напрямку поширення.
Теорія і дослід свідчать, що електромагнітні хвилі можуть існувати і в речовині, й у вакуумі, і завжди є поперечними. Натомість механічні хвилі, котрі є можливі тільки в речовині, можуть бути як поперечними, так і поздовжніми. При цьому тип хвиль, які можуть виникати, залежить від взаємодії між молекулами середовища. У твердому тілі, де сили зв'язку між атомами є пружними, виникають хвилі обох типів. Проте в об'ємі рідини, де сили взаємодії між молекулами ними є непружними, та в газі, де їх практично немає, можуть існувати лише поздовжні хвилі. Але на поверхні рідини між молекулами діють споріднені з пружними сили поверхневого натягу. Через це на поверхні рідини виникають і поперечні хвилі, які кожен бачив на водоймах.
Нижче наведена “жива картинка”, що схематично зображує поздовжню та поперечну хвилю в середовищі. Якщо уважно до неї придивитися, можна помітити важливу деталь: точки-частинки середовища, не рухаються в напрямку поширення хвилі, а лише здійснюють коливання навколо фіксованих положень. Отже,
у хвилі відбувається не перенесення речовини, а перенесення коливань.
 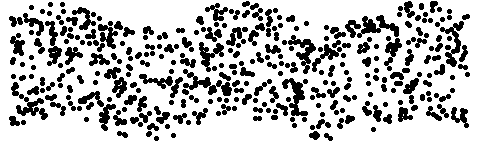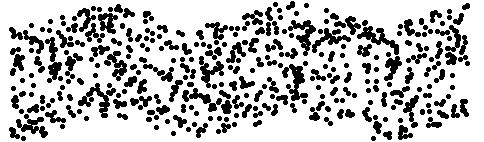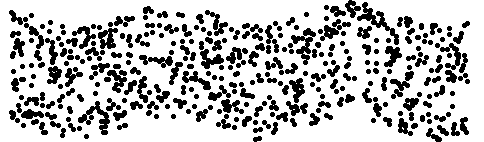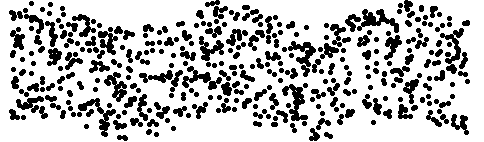 |
1.2. Характеристики та рівняння гармонічних хвиль
Вище говорилося, що хвилі різної природи мають спільні загальні властивості й описуються за допомогою єдиного математичного апарату. При цьому найпростішими і найважливішими є гармонічні хвилі, що являють собою поширення у просторі гармонічних коливань.
Рівняння плоскої гармонічної хвилі. Уявімо, що в однорідному пружному середовищі розміщена нескінченна площина-мембрана. Якщо вона почне коливатися, то через сили зчеплення частинки прилеглого шару середовища будуть утягувати в рух сусідній шар, він – наступний, і так далі. Як наслідок, коливання від джерела будуть поширюватись, охоплюючи все більшу область простору, тобто, утвориться хвиля. З міркувань симетрії зрозуміло, що в будь-якій площині паралельній до мембрани всі точки середовища будуть рухатись однаково, тому така хвиля називається плоскою.
Нехай мембрана й прилеглі частинки середовища здійснюють коливання вздовж осі ОХ (рис. 1.1) за законом
\( \xi{(0,t)}=\xi_{0}\cos\frac{2\pi}{T}t \),
де ξ – зміщення з положення рівноваги, ξ0 – амплітуда, T - період коливань.
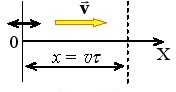 |
У пружному середовищі відсутні сили тертя, тому з такою самою амплітудою та періодом коливатимуться частинки і в будь-якому іншому шарі. Але, позаяк хвиля поширюється з кінцевою швидкістю, у віддалених шарах частинки почнуть коливатись із деяким запізненням τ , відповідно до рівняння
\( \xi =\xi_{0}\cos\frac{2\pi}{T}(t-\tau) \).
Час запізнення дорівнює \( \tau=x/v \), де \( {v}\) – швидкість поширення хвилі, x – відстань від джерела до даної точки (див. рис 1.1). Тому зміщення ξ є функцією двох змінних — координати й часу:
\( \xi(x,t)=\xi_{0}\cos\frac{2\pi}{T}\left(t-\frac{x}{v}\right) \) або \( \xi(x,t)=\xi_{0}\cos\left(\frac{2\pi}{T}t-\frac{2\pi}{vT}x\right) \).
Це рівняння можна переписати зручніше у вигляді
|
\( \xi(x,t)=\xi_{0}\left(\frac{2\pi}{T}t-\frac{2\pi}{\lambda}x\right) \), |
(1.1) |
або
|
\( \xi (x,t)=\xi_{0}\cos (\omega{t}-kx) \), |
(1.2) |
де враховано співвідношення ω = 2π/T та введено величини λ і k , які називаються відповідно довжиною хвилі та хвильовим числом і визначаються співвідношеннями:
|
\( \lambda={vT}\), |
(1.3) |
|
|
\( {k}=\frac{\omega}{v}=\frac{2\pi}{\lambda} \). |
(1.4) |
Вираз (1.2) (або (1.1)) є рівнянням плоскої гармонічної хвилі. Воно визначає зміщення ξ частинок середовища у будь-якій точці простору і в будь-який момент часу.
(Примітка. Для хвилі іншої природи під “зміщенням” слід розуміти збурення тієї фізичної величини, що визначає природу хвилі).
Розглянута хвиля утворюється праворуч від мембрани й поширюється в додатньому напрямку осі ОХ. По інший бік мембрани утворюється така сама хвиля, що поширюється в протилежному напрямі. Її рівняння отримаємо з (1.2) заміною \( {v}\) на \( {-v}\):
|
\( \xi (x,t)=\xi_{0}\cos\left(\omega{t}+\frac{\omega}{v}x\right)=\xi_{0}\cos\left(\omega{t}+\frac{2\pi}{\lambda}x\right)=\xi_{0}\cos{(\omega{t}+kx)} \). |
(1.5) |
Характеристики гармонічної хвилі. Зрозуміло, що всі характеристики гармонічних коливань одночасно є характеристиками й гармонічної хвилі. Це амплітуда ξ0, період T, циклічна ω або лінійна ν частота та фаза (аргумент гармонічної функції у рівнянні хвилі). У цьому зв’язку одразу зауважимо, що коливання в гармонічній хвилі створюються й підтримуються певним джерелом, тобто є вимушеними. Тому
період (частота) хвилі визначається тільки джерелом і не залежить від властивостей середовища.
Дві інші величини – λ і k – є специфічними саме для хвилі й пов’язані з її поширенням у просторі. Зокрема із (1.3) видно, що
довжина хвилі дорівнює відстані, на яку поширюється хвиля за час одного періоду коливань.
Для кращого розуміння особливостей хвильового процесу розглянемо залежність величини ξ від часу ξ(t) в заданій точці простору x = x0 та від координати ξ(х) в заданий момент часу t = t0. Згідно з (1.1), ці залежності мають вигляд:
|
|
(1.6) |
|
|
|
(1.6а) |
Графіки ξ(t) та ξ(x) показані на рис. 1.2.
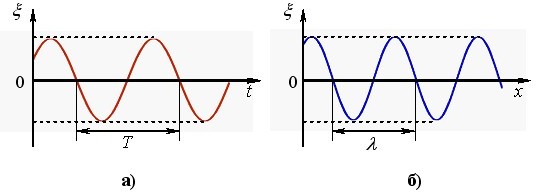
Рис. 1.2а показує, що в будь-якій точці простору відбуваються гармонічні коливання величини ξ з періодом T і частотою ω = 2π/T, а з рис. 1.2б видно, що в будь-який момент часу значення ξ розподілені у просторі теж за гармонічним законом. При цьому величина λ дорівнює найменшій відстані у напрямку поширення хвилі між точками, в яких коливання відбуваються в однаковій фазі.
(Примітка. Формально зсув фаз складає 2π, але, позаяк частинки в таких точках рухаються однаково, говорять, що вони коливаються в однаковій фазі, або синфазно).
Отже, можна сказати, що
довжина хвилі є просторовим періодом хвилі.
Як і для локальних коливань,
аргумент гармонічної функції в рівняннях (1.1), (1.2) називається фазою хвилі.
Згідно з (1.2), фаза хвилі через частоту та хвильове число визначається, як
|
|
(1.7) |
Фаза визначає і величину ξ, і характер її зміни в різних точках і в різні моменти часу. Тому різниця фаз δ = φ1 - φ2 в двох точках простору характеризує узгодженість коливань, які збуджуються хвилею в цих точках. Для хвилі в однорідному ізотропному середовищі різниця фаз у двох точках в заданий момент часу дорівнює
|
|
(1.7а) |
де літерою l позначено відстань від джерела до даної точки й ураховано зв’вязок (1.4) між хвильовим числом і довжиною хвилі. Співвідношення (1.7а) визначає також і різницю фаз двох різних хвиль у даній точці простору за умови, що вони мають однакові частоти і початкові фази. В цьому випадку величина Δl називається різницею ходу хвиль; вона є зручною при аналізі різних хвильових явищ.
Хвильові поверхні та фазова швидкість. Фаза хвилі є функцією координат і часу. В даній точці простору вона змінюється з часом. Так само, в даний момент часу фаза змінюється при переході від однієї точки до іншої. При цьому задане значення фази хвиля має не в одній, а в цілій множині точок, які утворюють відповідну “хвильову поверхню”. Отже,
хвильовою поверхнею називається множина точок у просторі хвилі, в яких у фіксований момент часу фаза хвилі має однакове значення.
В однорідному й ізотропному середовищі, як випливає з (1.7), всі точки хвильової поверхні є рівновіддаленими від джерела. Справді, при заданих величинах φ = φ0 і t = t0
|
\( {x}=\frac{\omega{t}_{0}-\varphi_{0}}{k}=\mathrm{const} \). |
(1.8) |
Через кожну точку з будь-якою координатою x проходить хвильова поверхня із відповідною фазою
φ0 = ωt0 - kx,
отож у просторі хвилі існує нескінченна множина хвильових поверхонь.
Гармонічна хвиля, що тут розглядається, є ідеалізацією: вона займає увесь нескінченний простір і ніяк не обмежена у часі, позаяк у рівнянні (1.2) величини x і t можуть бути якими завгодно. Але реальна хвиля за час від моменту виникнення до заданої миті досягає точок, які віддалені від джерела на певну скінченну відстань. Тому існує хвильова поверхня, що відокремлює область простору, в якій хвиля є, від тієї, куди вона ще не дісталась. Така межова поверхня називається фронтом хвилі.
Із рівнянь (1.7) і (1.8) випливає також, що хвильові поверхні рухаються. Рівняння руху хвильової поверхні отримаємо з (1.8), увівши замість заданого моменту t0 поточний час t:
\( {x}=-\frac{\varphi_{0}}{k}+\frac{\omega}{k}{t} \) \( \Rightarrow \) \( {v}=\frac{\omega}{k}\).
Отже, хвильові поверхні рухаються із швидкістю
|
\( {v}=\frac{\omega}{k}\), |
(1.9) |
яка називається фазовою швидкістю.
Зіставлення цього виразу з (1.4) показує, що саме з такою швидкістю поширюється гармонічна хвиля. Тому визначник “фазова” може здатися зайвим. Але в теорії він є необхідним, оскільки реальні хвилі не є строго гармонічними і поширюються з іншою, так званою груповою швидкістю, що збігається фазовою лише в окремих випадках.
Плоскі, циліндричні та сферичні хвилі. Оскільки в однорідному й ізотропному середовищі всі точки хвильової поверхні є рівновіддаленими від джерела, їхня форма визначається геометричною конфігурацією джерела і може бути складною. Але в теорії та практиці найчастіше розглядаються три найпростіші типи хвиль – плоскі, циліндричні та сферичні.
Плоскою хвилею називається така, що має плоскі хвильові поверхні. Саме тому розглянута вище хвиля (1.2), що створюється джерелом у формі нескінченної площини і в усіх точках поширюється в одному напрямку ОХ, називається плоскою. Відповідно до (1.8), координати точок довільної хвильової поверхні хвилі (1.2) визначаються загальним рівнянням x = const, яке є рівнянням площини, перпендикулярної до осі ОХ. Отже, хвильові поверхні плоскої хвилі (1.2) складають множину площин, які орієнтовані перпендикулярно до напрямку поширення хвилі (рис. 1.3а ).
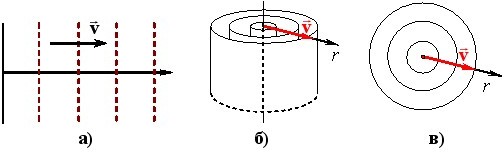 |
Розглянемо тепер хвилю, що створюється джерелом у вигляді нескінченної прямої пульсуючої нитки. З міркувань симетрії зрозуміло, що така хвиля в однорідному ізотропному просторі поширюється від нитки радіально по всіх напрямках і з однаковою швидкістю. Відповідно, хвильові поверхні такої хвилі являють собою множину коаксіальних циліндрів (рис. 1.3б), через що вона й називається циліндричною хвилею.
Рівняння циліндричної хвилі можна з відповідними корекціями отримати з (1.2). По-перше, циліндрична хвиля поширюється по всіх радіальних напрямках, тому координату x в (1.2) треба замінити на відстань r від даної точки хвилі до нитки:
ξ(r,t) = ξ0cos(ωt - kr).
І, по-друге, слід урахувати залежність амплітуди циліндричної хвилі від відстані r до джерела. Джерело має певну потужність і створює у просторі відповідний потік енергії. Тому в середовищі без поглинання крізь будь-яку хвильову поверхню щосекунди проходить однакова енергія Φ0 .
(Примітка. В ідеальній циліндричній хвилі лінійне джерело вважається нескінченним. Тому під Φ0 слід розуміти потік енергії, що проходить крізь ділянку циліндричної хвильової поверхні заданої довжини).
Енергія коливань розподіляється по хвильовій поверхні S із поверхневою густиною
\( {j}=\frac{\Phi_{0}}{S} \).
Величина j визначає концентрацію енергії, тож і амплітуду коливань у кожній точці хвильової поверхні. Енергія коливань є прямо пропорційною квадратові амплітуди (див. Частина І, п. 2.4), отже
|
\( {j}\sim\xi_{0}^{2}\) \( \Rightarrow \) \( \xi_{0}\sim\sqrt{j}\sim\frac{1}{\sqrt{S}}\). |
(1.10) |
У циліндричній хвилі площа ділянки хвильової поверхні довжини \( {l} \) і радіуса r дорівнює \( {S} = 2\pi{rl} \), Тому можна записати
|
\( \xi_{0}=\frac{a}{\sqrt{r}} \), |
(1.10а) |
де a – амплітудний множник залежний від потужності джерела.
Відтак рівняння циліндричної хвилі набуває вигляду:
|
\( \xi{(r,t)}=\frac{a}{\sqrt{r}}\cos{(\omega{t}-kr)}\). |
(1.11) |
Третя з названих простих є сферична хвиля. Вона створюється в однорідному ізотропному середовищі точковим джерелом і має хвильові поверхні у формі сфер із центром у джерелі (рис.1.3в). Очевидно, що миттєві значення величини ξ(r, t) зменшуються при віддаленні від джерела, тому рівняння сферичної хвилі є подібним до рівняння циліндричної хвилі. Відміна полягає тільки в залежності амплітуди ξ0 від відстані r до джерела. В сферичній хвилі на відстані r від джерела потік енергії Φ0 рівномірно розподіляється по поверхні сфери площею S = 4πr2, тож густина потоку є обернено пропорційна квадратові відстані: j ~ (1/r2). Отже, згідно з (1.10) і (1.11),
|
\( \xi_{0}=\frac{a}{r}\), |
(1.12) |
і рівняння сферичної хвилі має вигляд
|
\( \xi{(r,t)}=\frac{a}{r}\cos{(\omega{t}-kr)}\). |
(1.13) |
Стосовно отриманих результатів слід зробити деякі зауваження. По-перше, можливі значення координат і часу в рівняннях (1.2), (1.11) і (1.13) формально є нічим не обмежені. Тож вони описують абстрактні хвилі, що охоплюють увесь простір і ніяк не обмежені в часі. Реальні ж хвилі десь і колись починаються та закінчуються і тому мають складніші властивості, зокрема, характеризуються двома швидкостями – фазовою та груповою. Крім того плоске та лінійне джерело не можуть бути нескінченними, тому створити плоску або циліндричну хвилю в усьому просторі є принципово неможливо.
(Правда, за допомогою відповідних технічних засобів їх можна створити в обмеженій області простору. До прикладу, в оптиці це роблять за допомогою лінз або дзеркал).
Неможливим є й необмежене зростання амплітуди (\( \xi_{0}\to\infty\)) циліндричної та сферичної хвиль при наближенні до джерела (\( {r}\to{0}\)), яке випливає з рівнянь (1.11) і (1.13), оскільки в дійсності лінійне (нитка) та точкове (кулька) джерело мають певний скінченний радіус r0. Тому рівняння (1.11) і (1.13) реально виконуються тільки хвильовій зоні — на відстанях r, які суттєво перевищують r0.
Хвильовий вектор. Для однієї плоскої хвилі завжди можна вибрати систему координат так, аби хвиля поширювалась уздовж осі ОХ і описувалася рівнянням (1.2). Але при одночасному розгляді декількох хвиль, які поширюються в різних напрямках, це неможливо. Тому треба встановити загальне рівняння хвилі, тобто визначити функцію \( \xi{(\vec{r}t)}\) у довільній точці з радіусом-вектором \( \vec{r}\). Для зручності розглянемо хвилю, що поширюється перпендикулярно до осі OZ у довільному напрямку. Покажемо цей напрямок на рис. 1.4 одиничним вектором (ортом) \( \vec{n} \) і проведемо в напрямку \(\vec{n}\) допоміжну координатну вісь ОХ′.
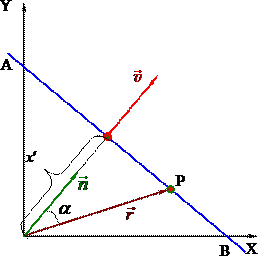
Виберемо тепер якусь точку \( \mathrm{P}(\vec{r}) \) із радіусом-вектором \( \vec{r} \) і проведемо через неї відрізок АВ перпендикулярно до осі ОХ′, який зображує хвильову поверхню, що проходить через точку Р і перетинається з віссю ОХ′ в точці Р′. Оскільки обидві точки лежать на одній хвильовій поверхні, коливання в них однакові і, згідно з (1.2), записуються, як:
\( \xi = \xi_{0}\cos{(\omega{t}-kx^{\prime})} \).
Із рис. 1.4 видно, що \( {x}^{\prime}=r\cos\alpha =\vec{n}\cdot\vec{r} \). То ж рівняння коливань в точці \( {P}(\vec{r}) \) має вигляд
\( \xi{(r,t)}=\xi_{0}\cos{(\omega{t}-kr\cos\alpha )}=\xi_{0}\cos{(\omega{t}-k\vec{n}\cdot\vec{r})}\).
Це рівняння є чинним для будь-якої точки та будь-якого напрямку поширення плоскої хвилі й по суті є її загальним рівнянням. Але його можна подати краще, увівши замість хвильового числа k = 2π/λ хвильовий вектор
|
\( \vec{k}=\frac{2\pi}{\lambda}\vec{n}\), |
(1.14) |
який визначає не лише довжину хвилі λ, а й напрям її поширення. Тому загальне рівняння плоскої гармонічної хвилі у векторній формі записується як
|
\( \xi{(r,t)}=\xi_{0}\cos{(\omega{t}-\vec{k}\cdot\vec{r})}\). |
(1.15) |
У декартовій системі координат
|
\( \xi{(x,y,z,t)}=\xi_{o}\cos{(\omega{t}-k_{x}x-k_{y}y-k_{z}z)} \). |
(1.15а) |
При поширенні плоскої хвилі вздовж осі OX ky = kz =0, kx = k, і рівняння (1.15а) трансформується в розглянуте раніше рівняння (1.2). Також, з урахуванням виразів (1.10а) і (1.12), рівняння (1.15) можна застосовувати й для циліндричних та сферичних хвиль.
Загасаючі хвилі. Досі розглядалися хвилі в абсолютно пружному середовищі, де відсутні втрати енергії коливань. Якщо ж середовище поглинає енергію хвилі, то це призводить до додаткового зменшення амплітуди із віддаленням від джерела, і хвиля є загасаючою. Як свідчить дослід, зменшення амплітуди через поглинання відбувається за експоненціальним законом \( \xi=\xi_{0}\mathrm{e}^{-\gamma{x}}\). Тому рівняння плоскої, сферичної та циліндричної хвиль у середовищі із загасанням, відповідно, мають вигляд:
\( \xi=\xi_{0}\mathrm{e}^{-\eta{x}}\cos{(\omega{t}-kx)}\),
\( \xi=\frac{A}{r}\mathrm{e}^{-\eta{r}}\cos{(\omega{t}-kr)} \),
\( \xi=\frac{A}{\sqrt{r}}\mathrm{e}^{-\eta{r}}\cos{(\omega{t}-kr)} \).
1.3. Хвильове рівняння
На початку відмічалося, що всі хвильові процеси мають низку спільних властивостей. Це виявляється в тому, що хвильова функція ξ будь-якої хвилі є розв’язком єдиного диференціального рівняння, що називається хвильовим рівнянням. Знайдемо хвильове рівняння незагасаючої хвилі на прикладі плоскої гармонічної хвилі (1.15а). Для цього визначимо другі частинні похідні по часу та по координатах від функції ξ(x,y,z,t):
|
\( \frac{\partial^{2}\xi}{\partial{t}^{2}}=-\xi_{0}\omega^{2}\cos{(\omega{t}-k_{x}x-k_{y}y-k_{z}z)}=-\omega^{2}\xi \) \( \Rightarrow \) \( \xi=-\frac{1}{\omega^{2}}\frac{\partial^{2}\xi}{\partial{t}^{2}}\) |
(1.16) |
\( \frac{\partial^{2}\xi}{\partial{x}^{2}}=-\xi_{0}k_{x}^{2}\cos{(\omega{t}-k_{x}x-k_{y}y-k_{z}z)}=-k_{x}^{2}\xi \).
Аналогічно отримаємо:
\( \frac{\partial^{2}\xi}{\partial{y}^{2}}=-k_{y}^{2}\xi \), \( \frac{\partial^{2}\xi}{\partial{z}^{2}}=-k_{z}^{2}\xi \).
Додавши координатні похідні і врахувавши, що \( {k}_{x}^{2}+k_{y}^{2}+k_{z}^{2}=k^{2}\), одержимо:
|
\(\frac{\partial^{2}\xi}{\partial{x}^{2}}+\frac{\partial^{2}\xi}{\partial{y}^{2}}+\frac{\partial^{2}\xi}{\partial{z}^{2}}=-k^{2}\xi \) \( \Rightarrow \) \( \xi=-\frac{1}{k^{2}}\left(\frac{\partial^{2}\xi}{\partial{x}^{2}}+\frac{\partial^{2}\xi}{\partial{y}^{2}}+\frac{\partial^{2}\xi}{\partial{z}^{2}}\right)\). |
(1.17) |
Вираз в дужках записують скорочено, як
| \( \frac{\partial^{2}\xi}{\partial{x}^{2}}+\frac{\partial^{2}\xi}{\partial{y}^{2}}+\frac{\partial^{2}\xi}{\partial{z}^{2}}=\Delta{\xi}=\nabla^{2}\xi{}\), | (1.18) |
де символи \( \Delta \) або \( \nabla^{2}\) позначають оператор Лапласа.
(Довідка. У математиці терміном “оператор” і відповідним символом позначають задану послідовність математичних дій (операцій), які належить виконати над тою чи іншою функцією. Зокрема, в декартових координатах (1.17) оператор Лапласа передбачає взяття других похідних по координатах від заданої функції \( \xi{(x,y,z,t)}\) вираз буде іншим.
З урахуванням цього вираз (1.17) можна переписати, як
\( \xi=-\frac{1}{k^{2}}\nabla^{2}\xi\).
Відтак, порівнюючи його з виразом (1.16), отримуємо:
\( \frac{1}{k^{2}}\nabla^{2}\xi=\frac{1}{\omega^{2}}\frac{\partial^{2}\xi}{\partial{t}^{2}}\).
Звідси випливає хвильове рівняння:
|
\( \Delta\xi=\frac{1}{v^{2}}\cdot\frac{\partial^{2}\xi}{\partial{t}^{2}}\) або \( \nabla^{2}\xi=\frac{1}{v^{2}}\cdot\frac{\partial^{2}\xi}{\partial{t}^{2}}\), |
(1.19) |
в якому параметр \( {v}=(\omega{/k}) \) є фазовою швидкістю хвилі.
Можна довести, що це диференціальне рівняння виконується не лише для плоскої гармонічної хвилі (1.15а), а й для незагасаючої хвилі будь-якого виду та природи.
1.4 Стоячі хвилі
При накладанні хвиль, які поширюються в зустрічних напрямах, за відповідних умов виникає специфічний коливальний процес, відомий як стояча хвиля. Розглянемо утворення стоячої хвилі при накладанні двох плоских гармонічних хвиль, які поширюються у протилежних напрямах осі ОХ (див. анімацію) і в яких коливання відбуваються вздовж одного напрямку з однаковою амплітудою ξ0 і частотою ω, але з певним зсувом фаз α.
Відповідно до (1.2) і (1.5), запишемо рівняння указаних хвиль у вигляді:
|
\( \xi_{1}=\xi_{0}\cos{(\omega{t}-kx)}\), \( \xi_{2}=\xi_{0}\cos{(\omega{t}+kx+\alpha)}\). |
(1.20) |
Відомо, що хвилі задовольняють принцип суперпозиції. Тому при накладанні даних двох хвиль результуючі коливання в кожній точці й у кожен момент часу визначаються як ξ = ξ1 + ξ2, або розгорнуто:
|
\( \xi=\xi_{0}\left(\cos{(\omega{t}-kx)}+\cos{(\omega{t}+kx+\alpha)}\right)= \) \( =2\xi_{0}\cos\left(kx+\frac{\alpha}{2}\right)\cos\left(\omega{t}+\frac{\alpha}{2}\right)\). |
(1.21) |
Це рівняння можна переписати у вигляді
|
\( \xi=A\cos\left(\omega{t}\frac{\alpha}{2}\right)\), |
(1.22) |
де
|
\( {A}=2\xi_{0}\left|\cos\left(kx+\frac{\alpha}{2}\right)\right|\). |
(1.23) |
Отже, при накладанні указаних зустрічних хвиль у кожній точці простору виникають гармонічні коливання з частотою ω та залежною від координати амплітудою A(x). Згідно з (1.23), амплітуда коливань періодично змінюється так, що вздовж осі ОХ утворюється низка пучностей — точок із максимальною амплітудою Aп = 2ξ0 та вузлів — точок, у яких амплітуда Aв = 0, тобто, коливання відсутні. Визначимо координати таких точок, узявши до уваги, що k = (2π/ λ). Для пучностей маємо:
|
\( \cos\left(kx+\frac{\alpha}{2}\right)=\pm{1}\) \( \Rightarrow \) \( {kx}\)п + \( \frac{\alpha}{2}=n\pi\) \( \Rightarrow \) xп = \(\frac{\lambda}{2}\left(n-\frac{\alpha}{2\pi}\right)\), n = 1, 2, 3, ... |
(1.24) |
Виходячи з умови cos(kx - (α/2)) = 0, аналогічно отримаємо координати вузлів:
|
\( x_{в}= \frac{\lambda}{2}\left(n+\frac{1}{2}-\frac{\alpha}{2\pi}\right)\), n = 0, 1, 2, ... |
(1.24а) |
Координати пучностей і вузлів не залежать від часу. Це означає, що утворені при накладанні зустрічних хвиль коливання (1.22) не поширюються в просторі. Тому такий коливальний процес називається стоячою хвилею. Відповідно, рівняння (1.21) є рівнянням плоскої стоячої хвилі. У цьому контексті хвилю, що поширюється, називають біжучою хвилею. Краще уявити характер коливань у стоячій хвилі та її відміну від біжучої допоможе рис. 1.5, на якому показано графіки ξ(x) при α = – π для моментів часу t1 < t2 < t3 у випадку біжучої (а) та стоячої (б) хвиль.
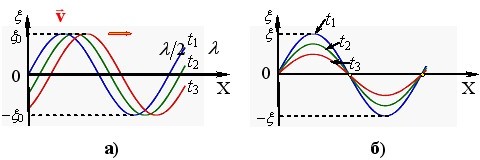
Видно, що в біжучій хвилі коливання зміщуються в напрямку поширення хвилі, а в стоячій хвилі вони не переміщуються в просторі й мають характер пульсацій. Як наслідок, енергія в стоячій хвилі виявляється запертою в областях між вузлами й не переноситься в просторі.
Положення вузлів та пучностей залежить від зсуву фаз α в (1.23), який для двох абстрактних хвиль може бути довільним. Але практично зустрічні хвилі (1.20) утворюють, спрямовуючи плоску хвилю по нормалі на плоску поверхню, що відбиває падаючу хвилю у зворотньому напрямку. В такому разі величина α може дорівнювати тільки 0, або π, залежно від умов відбивання. При відбиванні від більш густого середовища (див. анімацію), як, наприклад, при відбиванні звукової хвилі в повітрі від твердої стінки, фаза в точці відбивання змінюється на протилежну, тож α = π. А при відбиванні від менш густого середовища (див. анімацію), приміром, як у випадку звукової хвилі, що поширюється всередині твердого стержня й відбивається від його торців, фаза не змінюється, і α = 0. Тому, відповідно до (1.24) і (1.24а), координати пучностей та вузлів стоячої хвилі у першому випадку визначаються, як
|
\( {x}_{п}= \frac{\lambda}{2}\left(n+\frac{1}{2}\right) \), n = 0, 1, 2, ... \( {x}_{в}=\frac{\lambda}{2}n \), n = 0, 1, 2, ... |
(1.25) |
а в другому – як
|
\( {x}_{п}= \frac{\lambda}{2}n \), n = 0, 1, 2, ... \( {x}_{в}= \frac{\lambda}{2}\left(n+\frac{1}{2}\right) \), n = 0,1,2,... |
(1.25а) |
Із цих виразів випливає, що в точці відбивання (x = 0) при відбиванні від більш густого середовища утворюється вузол, а при відбиванні від менш густого середовища – пучність стоячої хвилі. Але за будь-яких умов відстань Δx між сусідніми вузлами або пучностями стоячої хвилі дорівнює
|
\( \Delta{x}=\frac{\lambda}{2}=\frac{\pi}{k}\). |
(1.26) |
Реально стоячі хвилі утворюються в обмеженому об’ємі, наприклад, при відбиванні від основ пружного стержня. При цьому на обох основах утворюються або вузли, або пучності, тому на довжині стержня вкладається ціла кількість вузлів або пучностей. Це означає, що між двома відбиваючими поверхнями, розміщеними одна від одної на відстані l, можуть утворюватися лише стоячі хвилі з дискретними наборами довжин хвилі λп і хвильових чисел kп, які задовольняють умови:
|
\( {l}=n\frac{\lambda_{n}}{2}\) \( \Rightarrow \) \( \lambda_{n}=\frac{2l}{n}\), \( {k}_{n}=\frac{\pi}{l}n \), n = 0, 1, 2, ... |
(1.27) |
Частоти таких хвиль, які інакше називають власними частотами, мають значення
|
\( \omega_{n}=\frac{\pi{v}}{l}n \), n = 0, 1, 2, ... |
(1.27а) |
де \( {v}\) – фазова швидкість хвилі.
Як наслідок, при збудженні й поширенні в обмеженому просторі багатьох коливань із будь-якими можливими частотами, в ньому утворюються система стоячих хвиль із відповідним дискретним набором (спектром) власних частот і довжин хвилі. При цьому частотний спектр стоячих хвиль залежить від форми та розмірів області простору, в якій вони утворюються і у випадку звукових хвиль визначає характерне "забарвлення" або тембр звуку.
Контрольні запитання
1. Що таке хвиля? Наведіть приклади хвиль різної природи.
2. Які хвилі називаються гармонічними?
3. Що таке довжина хвилі та хвильове число?
4. Як пов’язані між собою довжина хвилі, період коливань і швидкість поширення хвилі? Від чого залежить кожна з цих величин?
5. Що називається фазою хвилі? Чи можна сказати, чому дорівнює фаза хвилі із заданою частотою та довжиною хвилі: а) у даній точці простору ; б) у даний момент часу?
6. Що називається хвильовою поверхнею? Фронтом хвилі?
7. З якою швидкістю рухаються хвильові поверхні? Як ця швидкість називається?
8. Чи визначає фазова швидкість механічної хвилі рух частинок середовища? А групова?
9. Яка відміна існує між термінами “рівняння хвилі” та “хвильове рівняння”? Запишіть хвильове рівняння та загальне рівняння плоскої гармонічної хвилі.
10. Що таке стояча хвиля та за яких умов вона утворюється?
11. Плоска звукова хвиля падає по нормалі на плоску стінку й відбивається. Запишіть координати вузлів та пучностей стоячої хвилі, що утворюється.
2. Пружні хвилі
Поширення механічних коливань на значну відстань від джерела можливе тільки в пружному середовищі, де відсутнє (або є не істотним) перетворення механічної енергії в тепло. Тому механічні хвилі називають пружними хвилями. Пружні хвилі в тілі супроводжуються деформаціями стискання-розтягу або зсуву. При деформаціях першого типу хвилі можуть існувати в будь-якій речовині – твердій, рідкій, чи газоподібній і є поздовжніми. Натомість пружні деформації зсуву можуть виникати тільки в тілах, які мають “пружність форми”, тобто здатність зберігати та перешкоджати зміні своєї форми. Така властивість є у твердих тіл, тому в них можливі як поздовжні, так і поперечні хвилі. Рідини, на загал, не зберігають форму, але внаслідок поверхневого натягу таку здатність має їхня вільна поверхня. Тому хвилі в об'ємі рідини є поздовжніми, а на поверхні – поперечними. Що ж до газів, то в них можливі тільки поздовжні хвилі.
Далі розглядаються такі питання:
2.2. Енергія та інтенсивність пружних хвиль
2.1. Швидкість пружних хвиль.
У пружній хвилі переносяться механічні коливання частинок середовища. Але самі частинки не рухаються разом із хвилею, а лише здійснюють коливання навколо фіксованих положень рівноваги. Тому швидкість поширення хвилі в середовищі та швидкість руху його частинок – це різні речі.
У рівнянні механічної хвилі функція ξ визначає зміщення частинок середовища з положення рівноваги, тобто, їхні миттєві положення. Тому швидкість руху частинок середовища можна визначити з рівняння (1.15) шляхом диференціювання по часу:
|
\( {u}=\frac{d\xi }{dt}=-{{\xi }_{0}}\omega \sin \left( \omega t-\vec{k}\vec{r} \right)\), |
(2.1) |
Частинки середовища у хвилі здійснюють вимушені коливання, частота яких задається джерелом хвилі. Тож і швидкість руху частинок середовища визначається тільки джерелом. Натомість швидкість поширення хвилі (1.9), тобто швидкість передачі коливань частинок середовища від шару до шару, визначається силою пружної взаємодії між частинками та їхньою масою. Тому швидкість поширення хвилі виявляється залежною від властивостей середовища та типу хвилі. Це прямо відображують формули фазової швидкості, які наводимо без доведення.
У твердому тілі фазова швидкість поздовжніх хвиль визначається, як
|
\( {{v}_{1}}=\sqrt{\frac{E}{\rho }}\), |
(2.2) |
де під коренем стоять табличні константами речовини: – густина і модуль Юнга, який визначає пружні властивості тіла при деформаціях стискання-розтягу. Відповідні розрахунки та вимірювання показують, що для переважної більшості металів і мінералів ця величина потрапляє в інтервал v1 = (3÷ 6)×103 м/с.
Поперечні хвилі в твердих тілах поширюються із швидкістю
|
\( {{v}_{2}}=\sqrt{\frac{G}{\rho }},\) |
(2.2а) |
де G — модуль зсуву, що визначає пружні властивості тіла при деформаціях зсуву. Швидкість поперечних хвиль для вказаної вище групи твердих тіл складає v2 = (2 ÷ 3)×103 м/с.
Рідини та гази не зберігають форму, але мають об’ємну пружність, тобто чинять опір зміні об’єму при зміні тиску. При малих деформаціях між зміною тиску dP та відносною зміною об’єму dV/V існує прямо пропорційний зв’язок :
|
\( \mathrm{d}P=-\kappa \frac{\mathrm{d}V}{V}\). |
(2.3) |
Величина \(\kappa \) називається модулем об’ємної пружності. Саме модуль об'ємної пружності разом із густиною визначають швидкість пружних хвиль у рідинах і газах, відповідно до формули:
|
\( {v}=\sqrt{\frac{\kappa }{\rho }}\). |
(2.4) |
Модуль об'ємної пружності залежить від виду процесу стискання та розширення речовини. При цьому для ідеального газу (газ можна вважати ідеальним при не дуже високих тисках і не наднизьких температурах) його можна визначити теоретично з рівняння процесу. Зокрема, при малій частоті, коли частинки газу рухаються з невеликою швидкістю, процес можна вважати ізотермічним. У такому разі
|
\( {PV}=\mathrm{const}\) \( \Rightarrow \) \( {V}\mathrm{d}P+P\mathrm{d}V=0 \) \( \Rightarrow \) \( \mathrm{d}P=-P\frac{\mathrm{d}V}{V}\). |
Порівнюючи цей вираз із (2.3), маємо \( \kappa =P \). При великій частоті хвилі й, відповідно, швидкій зміні тиску процес іде адіабатично. Тому з рівняння адіабати \( PV^{\gamma}=\mathrm{const}\) аналогічно виходить \( \kappa =\gamma{P}\), де \( \gamma={{{C}_{P}}}/{{{C}_{V}}}\). Урахувавши ці результати та вираз густини ідеального газу \( \rho ={PM}/{RT}\) через тиск \( {P}\), температуру \( {T}\) та молярну масу \( {M}\), отримаємо для швидкості поширення низькочастотних \( {v}_{1}\) та високочастотних хвиль у газі:
|
\( {{v}_{1}}=\sqrt{\frac{RT}{M}}\) \( {{v}_{2}}=\sqrt{\frac{\gamma{RT}}{M}}\) |
(2.4а) |
Звукові хвилі мають велику частоту. Тому швидкість звуку в газах визначає друга формула. Зокрема, для звуку в повітрі (\( {M}=29\cdot{{10}^{-3}}\)кг/моль і \( \gamma=1,4 \)) при температурі \( {t}=17{}^{\circ}{С}\) вона дає 340 м/с, що узгоджується із результатами вимірів. Швидкість звуку в інших газах, за винятком дуже легкого водню, має подібні значення. Рідини порівняно з газами мають великі модулі об’ємної пружності й, відповідно, більші швидкості поширення пружних хвиль. Так, швидкість звуку у воді становить приблизно 1,5·103 м/с. В інших рідинах вона лежить в інтервалі (1÷2)·103 м/с.
2.2. Енергія та інтенсивність пружної хвилі
Об’ємна густина енергії хвилі. Винятково важливою властивістю хвиль є те, що вони переносять енергію від джерела до віддалених точок простору. Достатньо сказати, що практично всі процеси на Землі, включно із самим життям, відбуваються завдяки енергії, що переноситься від Сонця електромагнітними хвилями. Енергія пружної хвилі складається з кінетичної енергії коливального руху частинок К і потенціальної енергії їхньої взаємодії U у формі енергії пружної деформації середовища, в якому поширюється хвиля.
Розподіл енергії хвилі в просторі визначається об’ємною густиною енергії, тобто, відношенням енергії \( \mathrm{d}W \) в елементарному об’ємі \( \mathrm{d}{V}\) до його величини:
|
\( {w}=\frac{\mathrm{d}W}{\mathrm{d}V}=\frac{\mathrm{d}K+\mathrm{d}U}{\mathrm{d}V}\). |
Знайдемо величину \( {w}\) на прикладі поздовжньої пружної хвилі. Кінетична енергія \( \mathrm{d}{K}\) в об’ємі \( \mathrm{d}V \) визначається швидкістю коливального руху частинок u та їхньою загальною масою \( \mathrm{d}m=\rho \mathrm{d}{V}\), де \( \rho \) – густина середовища:
|
\( \mathrm{d}K=\frac{{{u}^{2}}\mathrm{d}m}{2}=\frac{\rho {{u}^{2}}}{2}\mathrm{d}{V}\). |
Для плоскої гармонічної хвилі швидкість u дається виразом (2.1), отже
|
\( \mathrm{d}K=\frac{\rho \xi _{0}^{2}{{\omega }^{2}}\text{d}V}{2}{{\sin }^{2}}(\omega{t}-kx)\). |
(2.5) |
Потенціальна енергію dU в об’ємі dV при пружних деформаціях стиску-розтягу, як відомо з механіки, визначається виразом
|
\( \mathrm{d}U=\frac{E{{\varepsilon}^{2}}}{2}\mathrm{d}{V}\), |
(2.6) |
де \( {E}\) – модуль пружності (модуль Юнга) і \( \varepsilon \) – відносна деформація. Для визначення величини \( \varepsilon \) подумки виділимо в деякій точці \( {x}\) середовища елементарний циліндричний шар із товщиною \( \mathrm{d}x\) і основами площею S, які перпендикулярні до напрямку поширення хвилі (рис. 2.1).
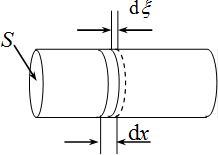
Об’єм цього шару \( \mathrm{d}V=S\mathrm{d}{x}\). Відповідно до рівняння хвилі (1.2), зміщення частинок із положень рівноваги на основах шару будь-якої миті відрізняються на величину
|
\( {|}\mathrm{d}\xi{|}=|\frac{\partial\xi}{\partial{x}} |\mathrm{d}x={{\xi }_{0}}k\sin{(}\omega{t}-kx)\mathrm{d}x\), |
яка є величиною деформації шару. Тоді відносна деформація \( \varepsilon ={|}\mathrm{d}\xi{|}/{\mathrm{d}x}\) визначається, як
|
\( \varepsilon =\frac{\partial\xi}{\partial{x}}=\xi_{0}k\sin{(}\omega{t}-kx{)}\). |
Підставляючи цей результат у (2.6), отримуємо:
|
\( \varepsilon =\frac{\partial\xi}{\partial x}\), |
|||
|
\( \mathrm{d}U=\frac{E\xi_{0}^{2}{{k}^{2}}\mathrm{d}V}{2}{{\sin }^{2}}(\omega{t}-kx) \). |
(2.7) |
||
Виразивши хвильове число як \( {k}={\omega}/{v}\), і взявши для \( {v}\) формулу (2.2) отримаємо для потенціальної енергії:
|
\( \mathrm{d}U=\frac{\rho\xi_{0}^{2}{{\omega }^{2}}\mathrm{d}V}{2}{{\sin}^{2}}(\omega{t}-kx).\) |
(2.7а) |
Відтак повна енергія хвилі в об’ємі \( \mathrm{d}{V}\)
|
\( \mathrm{d}W=\mathrm{d}K+\mathrm{d}U=\rho \xi _{0}^{2}{{\omega }^{2}}\mathrm{d}V{{\sin }^{2}}(\omega{t}-kx) \), |
а об’ємна густина енергії
|
\( {w}=\frac{\mathrm{d}W}{\mathrm{d}V}=\rho \xi _{0}^{2}{{\omega }^{2}}{{\sin }^{2}}(\omega{t}-kx) \). |
(2.8) |
Густина потоку енергії та інтенсивність хвилі. Із виразу (2.8) видно, що енергія хвилі в будь-який заданий момент часу неоднорідно розподілена в просторі й у будь-якій точці змінюється з часом. При цьому координата точки із заданим значенням густини енергії \( {w}=\mathrm{const}\) задовольняє рівняння
|
\( \omega{t}-kx=\mathrm{const}\) \( \Rightarrow \) \( {x}=vt-\mathrm{const}\) \( {v}=\frac{\omega }{k}\). |
Це означає, що в ідеальній гармонічній хвилі швидкість перенесення енергії від джерела до віддалених точок збігається із фазовою швидкістю (1.9). (Але в реальних хвилях, як говорилося раніше, енергія переноситься з груповою швидкістю, відмінною від фазової).
Енергія, що переноситься хвилею через задану поверхню за заданий проміжок часу залежить як від площі цієї поверхні, так і від величини проміжку часу. Тому кількісною мірою самого процесу перенесення в кожній точці є густина потоку енергії
|
\( {j}=\frac{\mathrm{d}W}{\mathrm{d}t\mathrm{d}{{S}_{\bot }}}\). |
(2.9) |
Можна сказати, що
густина потоку дорівнює енергії, котра переноситься за одиницю часу через одинцю площі поверхні, перпендикулярної до напрямку перенесення.
Якщо хвиля поширюється із швидкістю \(v\), то за час \( \mathrm{d}{t}\) енергія переноситься на відстань \( \mathrm{d}l=v\mathrm{d}{t}\). Тому при об’ємній густині енергії w через якусь площадку \( \mathrm{d}{{S}_{\bot }}\) за час \( \mathrm{d}{t}\) проходить енергія \( \mathrm{d}W=w\mathrm{d}{{S}_{\bot}}\mathrm{d}l=w\mathrm{d}{{S}_{\bot }}v\mathrm{d}{t}\). Відповідно, величина густини потоку енергії дорівнює
|
\( {j}=wv \). |
(2.10) |
В кожній точці енергія переноситься у напрямку вектора швидкості поширення хвилі \( \vec{v}\). Аби це відобразити у формулі, густину потоку енергії трактують як вектор
|
\( \vec{j}=w\vec{v}\). |
(2.11) |
Розгорнуто він, згідно з (2.8), записується у вигляді:
|
\( \vec{j}=\rho\xi_{0}^{2}{{\omega}^{2}}\vec{v}{{\sin}^{2}}{(}\omega{t}-kx)\). |
(2.12) |
Вираз \( \vec{j} \) можна подати інакше, використавши тотожність \( {2}{{\sin }^{2}}\alpha=(1-\cos{2}\alpha{)}\):
|
\( \vec{j}=\frac{\rho \xi_{0}^{2}{{\omega }^{2}}\vec{v}}{2} (1-\cos{2}(\omega{t}-kx)) \). |
(2.12а) |
Із отриманих виразів випливає, що напрям вектора \( \vec{j}\) лишається незмінним, а модуль змінюється з подвоєною частотою хвилі \( {2}\omega \), тобто перенесення енергії має пульсуючий характер. Але частота хвиль переважно є досить високою, тому реально перенесення енергії визначається
середньою величиною густини потоку енергії, яка називається інтенсивністю хвилі \( {I}\):
|
\( {I}=\langle{j} \rangle \). |
(2.13) |
Згідно з (2.12а), інтенсивність пружної хвилі
|
\( {I}=\frac{\rho\xi _{0}^{2}\omega^{2}v}{2}\langle{1}-\cos{2}(\omega{t}-kx) \rangle =\frac{\rho\xi_{0}^{2}\omega ^{2}v}{2}(1- \langle\cos{2}(\omega{t}-kx)\rangle{)} \). |
На інтервалі одного періоду кожному додатньому значенню функції косинус відповідає таке саме по модулю від’ємне значення, тому її середня величина за період дорівнює нулю.
(Зауважимо, що цей результат є чинним і для будь-якої іншої періодичної знакозмінної функції, графік якої є симетричним відносно осі абсцис).
Отже, в наведеному виразі другий доданок у дужках дорівнює нулю, й інтенсивність гармонічної хвилі виражається, як
|
\( {I}=\frac{1}{2}\rho\xi_{0}^{2}{{\omega}^{2}}{v}\). |
(2.14) |
В однорідному середовищі величини \(\rho \) і \( {v}\) скрізь однакові, тому в будь-якій точці інтенсивність хвилі заданої частоти \(\omega \) визначається тільки квадратом амплітуди:
|
\( {I}\sim\xi_{0}^{2}\). |
(2.14а) |
Тому, коли треба знати не саму інтенсивність, а лише характер її розподілу в просторі, замість величини I (2.14), оперують квадратом амплітуди \( \xi_{0}^{2}\).
2.3. Звукові хвилі
Характеристики звуку. Пружні хвилі певних частот створюють у людини та інших істот специфічне відчуття звуку й називаються звуковими хвилями. Діапазон частот звукових хвиль, який сприймається людським вухом, складає \( (16\div{20000})\,{Гц}\). Пружні хвилі з частотами меншими за 16 Гц і більшими, ніж 20 кГц називаються інфразвуком та ультразвуком, відповідно.
Суб’єктивне сприйняття звуку залежить від спектрального складу (набору частот) та інтенсивності пружної хвилі, що потрапляє у вухо. Залежно від спектрального складу розрізняють музичні звуки та шуми. Музичні звуки створюються хвилями з упорядкованим набором частот. Характерною ознакою музичного звуку є висота тону – суб’єктивне відчуття, завдяки якому ми, до прикладу, легко розрізняємо дзижчання комара та джмеля. За висоту тону є відповідальною частота коливань у звуковій хвилі: чим вона більша, тим вищим є звук. Але й при однаковій висоті тону звуки, що створюються різними джерелами, приміром, голосом чи музичними інструментами, легко пізнаються, бо мають характерне “забарвлення”, або тембр. Природа тембру така. При видобуванні звуку, скажімо в скрипці або роялі, через обмежену довжину струн в них виникають власні коливання з різними частотами, які збуджують у порожнині інструменту (резонаторі) відповідні звукові хвилі. Далі при відбиванні від стінок резонатора й накладанні одні з цих хвиль підсилюються, а інші послаблюються. Відтак у резонаторі встановлюється та випромінюється в простір система звукових хвиль із характерним для даного інструменту (джерела звуку) спектром, тобто, розподілом по частотах та амплітудах. При цьому коливання найнижчої частоти, які називаються основним тоном, мають найбільшу амплітуду й визначають наше сприйняття висоти звуку. Всі інші частоти називаються обертонами, або гармоніками. Набір гармонік і їхній розподіл по амплітудах саме і визначає тембр звуку. Треба зазначити, що хоча людина розрізняє з частотою лише до 20 кГц, більш високочастотні обертони все ж впливають на темброве забарвлення звуку. Тому в пристроях для звукозапису та відтворення звуку намагаються отримати весь діапазон коливань, який дає джерело звуку.
Поряд із музичними звуками існують шуми – звуки з невпорядкованим, переважно неперервним частотним спектром. Такими, зокрема, є звук працюючого двигуна авто чи літака, аплодисменти, приголосні звуки мови, тощо. Шуми сприймаються як беззмістовні звуки, що не мають ані певної висоти, ані тембру. Але суб’єктивне сприйняття шуму все ж таки залежить від характеру розподілу енергії звуку по частотах, подібно до того, як від спектрального складу залежить кольорова гама світла, що сприймається оком. Тому в акустиці, по аналогії з оптикою, шумам умовно приписують різні “кольори”. Так, якщо енергія коливань рівномірно розподілена по всьому звуковому діапазону, шум називається білим. Натомість у “рожевому” шумі більш інтенсивними є низькочастотні коливання, а в “блакитному” – високочастотні.
Гучність звуку. Усі звуки характеризуються гучністю – величиною, що пов’язана з інтенсивністю звукової хвилі , яка потрапляє у вухо. Вухо є дуже чутливим приймачем звуку і характеризується порогом чутності – інтенсивністю найтихішого звуку, який воно здатне сприймати. Для вуха людини поріг чутності складає всього \( {I}_{0}={10}^{-12}\,{Вт/м^{2}}\). Із ростом інтенсивності звуку зростає і гучність. Але відчуття гучності звуку підсилюється значно повільніше, ніж зростає інтенсивність, так що зв’язок між ними є нелінійним і близьким до логарифмічного. Тому для адекватної характеристики гучності використовують логарифмічну величину, що називається рівнем інтенсивності звуку L і визначається як
|
\( {L}=\lg\frac{I}{{{I}_{0}}}\). |
Вимірюється величина L у белах (Б): при L = 1 Б інтенсивність звуку перевищує поріг чутності в 10 разів. Це досить велика різниця, тому на практиці використовують частинну одиницю децибел, котра складає 0,1 бела. То ж
|
\( {L} ({дБ})=10\lg \frac{I}{{{I}_{0}}}\). |
(2.15) |
У цій шкалі рівень інтенсивності звуку, що створюється при тихій розмові на відстані
Таким чином, діапазон рівнів інтенсивності звуку, що його сприймає людина, простягається від 10–12 Вт/м2 до 1 Вт/м2, тобто складає дванадцять порядків. Ця цифра вражає. Для порівняння зазначимо, що коли б ми мали фантастичну лінійку з таким діапазоном вимірювань, то могли би нею визначати відстані, починаючи від розмірів атома (~ 10–10 м) й аж до розмірів футбольного поля (~ 100 м).
Рівень інтенсивності є об’єктивною характеристикою сили звуку. Але суб’єктивне сприйняття гучності залежить не тільки від рівня інтенсивності, а й від частоти звуку так, що чутливість вуха є максимальною на частоті приблизно 1000 Гц і помітно зменшується на низьких та на високих частотах. Наприклад, звук із рівнем інтенсивності 30 дБ, який людина добре розрізняє на частоті 1000 Гц, на частоті 100 Гц є вже не чутним. Тому для кількісної характеристики суб’єктивного сприйняття гучності звуку вводять одиницю фон. При цьому приймається, що на частоті 1000 Гц гучність звуку у фонах дорівнює рівню його інтенсивності в децибелах. У такому разі звук з рівнем інтенсивності, скажімо, 60 дБ, на частоті 1000 Гц має гучність 60 фон. Але при такому самому рівні інтенсивності гучність звуку з частотою 50 Гц буде складати вже тільки біля 25 фон.
Відбивання звуку. Пружні хвилі, як і будь-які інші, мають здатність відбиватися від перешкод на своєму шляху й повертатися до місця випромінювання. Цей ефект, який називається луною, у випадку звукових хвиль сприймається як послаблений повторний звук. В однорідному середовищі, такому, як повітря чи вода, швидкість звуку є сталою. Тому, знаючи величину і вимірюючи час повернення τ відбитого сигналу (відлуння), можна знайти відстань l від джерела звуку до предмета, від якого він відбивається:
|
\( {l}=\frac{1}{2}v\tau \). |
(2.16) |
На цьому ґрунтується ехолокація – спосіб виявлення різних цілей та визначення їхнього положення в просторі за допомогою відбивання ультразвуку.
При відбиванні звуку від декількох перешкод, відстані від яких до джерела суттєво відрізняються, спостерігається декілька послідовних загасаючих лун. Цей ефект створює своєрідний емоційний вплив на слухача й використовується в музичній акустиці шляхом створення в звуковідтворюючій апаратурі послідовності штучних загасаючих сигналів-копій. У приміщеннях, унаслідок многократного відбивання звуку від стін та різних предметів, утворюється велика кількість лун, які розділені дуже малими проміжками часу – (0,01 ÷ 1) мс. Тому вони сприймаються купно, створюючи характерний звуковий шлейф, або відгомін, який називається реверберацією. Завдяки цьому, після припинення дії джерела звук відчувається ще протягом певного часу реверберації. Реверберація впливає на суб’єктивне сприйняття звуку, створюючи ефект глибини простору. При цьому суттєву роль відіграє час реверберації. Якщо він занадто великий, то послідовні звуки “наповзають” один на одного, що утруднює сприйняття музики й, особливо, мови. Аналогічно, при малому часі реверберації звук стає “сухим” і “тусклим”. При цьому кожен різновид звуку має свій оптимальний час реверберації. Наприклад, для камерної та оркестрової музики це приблизно (1÷2) мс, а для органа – набагато більше. Час реверберації залежить від розмірів і конфігурації приміщення та від матеріалу стін і предметів, які знаходяться в ньому. Тому великі приміщення при проектуванні розраховують на оптимальний час реверберації, залежно від їхнього функціонального призначення.
2.4. Ефект Допплера
Раніше відмічалося, що швидкість поширення пружних, зокрема звукових, хвиль визначається тільки властивостями середовища (див. (1.18) - (1.20)), а частота задається джерелом, яке генерує хвилю. При цьому передбачалося, що джерело та приймач (спостерігач) не рухаються відносно середовища. Але коли джерело або приймач перебувають у русі, частота звуку ν, яку реєструє приймач, на загал, відрізняється від частоти ν0, яку генерує джерело. Мабуть кожен спостерігав різке пониження висоти звуку сирени локомотива потяга в момент проходження повз спостерігача на великій швидкості (див. відео та аудіо трек).
Зміна частоти звуку, яку фіксує приймач, унаслідок його руху відносно джерела, чи джерела відносно нього, називається ефектом Допплера.
Ефект Допплера існує як для звукових, так і для інших, до прикладу, електромагнітних хвиль. Розглянемо теорію класичного ефекту Допплера, коли рух джерела та приймача відбувається з нерелятивістською швидкістю.
Нехай маємо розміщені на осі ОХ нерухомі приймач Пр і джерело Дж, яке випромінює звукову хвилю у вигляді коротких імпульсів із частотою повторення ν0 і періодом T0 і поширюються відносно середовища із заданою швидкістю \( {v}\). В такому разі відстань між двома послідовними імпульсами (довжина хвилі) складає \( \lambda_{0}=vT_{0}=v/\nu_{0}\), як схематично показано на рис. 2.2.
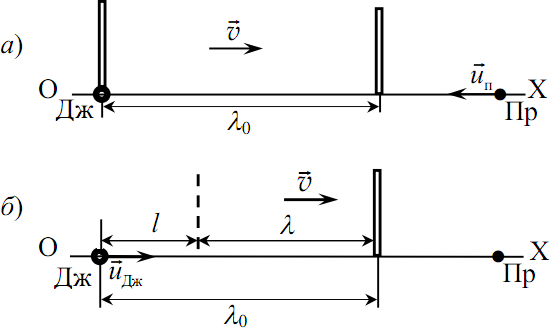
Проаналізуємо, яку частоту звуку буде реєструвати приймач, якщо він і джерело рухаються вздовж осі ОХ. Розглянемо спочатку окремі випадки.
Випадок 1: рухається тільки приймач . Нехай приймач наближається до нерухомого джерела із швидкістю \( {u}_{п}\). У такому разі його швидкість відносно імпульсів дорівнює \( {u}^{\prime}_{п}={u}_{п}+{v}\), і відстань λ0 між послідовними імпульсами приймач долає за час
|
T = \(\frac{{{\lambda }_{0}}}{{{{{u}'}}_{\text{п}}}}\) = \(\frac{v{{T}_{0}}}{v+{{u}_{\text{п}}}}\). |
Цей час є періодом повторення звукових імпульсів, які приходять на приймач, тож частота звуку, яку він реєструє становить
|
\( \nu =\frac{v+u_{п}}{v}\nu_{0}\). |
(2.17) |
Випадок 2: рухається тільки джерело (рис. 2.2б). Нехай тепер джерело рухається в бік нерухомого приймача із швидкістю uд, і випускає імпульс 1 у момент t1. Тоді на момент випускання наступного імпульсу t2 = t1 + T0 перший пройде в середовищі відстань \( {{\lambda }_{0}}=v{{T}_{0}}\), а джерело переміститься в тому самому напрямі на відстань \( {l}=u_{д}T_{0}=u_{д}/\nu_{0}\). Тож відстань між імпульсами (довжина хвилі) складатиме \( \lambda =\lambda_{0}-l=(v-{u}_{д})/\nu_{0}\). Позаяк відносно нерухомого приймача швидкість переміщення імпульсів дорівнює \( {v}\), вони потраплятимуть на нього з інтервалом часу (періодом)
|
\( {T}=\frac{\lambda}{v}=\frac{v-{v}_{д}}{v}T_{0}\). |
Отже, приймач реєструватиме звук із частотою
|
\( \nu =\frac{v}{(v-u_{д})}\nu_{0}\). |
(2.18) |
Загальний випадок. Якщо рухаються і приймач, і джерело, то на частоту ν, що реєструється приймачем, впливають обидва фактори. Тому можна записати загальний вираз ν, який вбирає обидві формули (2.17) і (2.18):
|
\( \nu =\frac{v\mathsf{+}{u}_{п}}{v-u_{д}}\nu_{0}\). |
(2.19) |
В обох розглянутих випадках частота звуку, що реєструється приймачем, є більша за частоту звукових імпульсів, які створюються в джерелі. Не важко збагнути, що це зумовлено тим, що в обох випадках відносний рух джерела і приймача був зустрічним. При русі джерела або приймача в протилежному напрямку, у виразах (2.17) – (2.19) треба змінити знак перед відповідною швидкістю. Але цим можна не спеціально не перейматися в кожному окремому випадку, якщо в указаних виразах модулі швидкостей приймача та джерела замінити їхніми проекціями на напрям поширення імпульсів (вісь ОХ ):
|
\( \nu =\frac{v+u_{пx}}{v-u_{дx}}\nu_{0}\). |
(2.20) |
У проведеному аналізі задля більшої наочності розглядалась умовна хвиля у вигляді послідовності імпульсів. Але отримані результати є чинними для хвиль будь-якого вигляду, зокрема для гармонічних хвиль, у яких такими імпульсами слугують “горби”, або “впадини”. Проте слід зазначити, що вираз (2.20) не є загальним, позаяк отриманий лише для випадку, коли джерело та приймач рухаються вздовж однієї прямої. Якщо це не так, зв’язок між частотами є більш складним. Але при не дуже великій відстані між джерелом і приймачем і малій (порівняно із звуковою) швидкості їхнього руху формула (2.20) з достатньою точністю справджується й при довільних напрямах руху джерела чи приймача.
Контрольні запитання
3. Електромагнітні хвилі
Із класичної електродинаміки Максвела відомо, що змінні електричне та магнітне поля мають здатність до взаємного перетворення. А саме, якщо в певному місці створити змінне електричне поле, то одразу ж виникне й відповідне змінне магнітне поле, котре створить нове електричне поле, воно — нове магнітне і так далі. Тож змінні електричне та магнітне поля є нерозривно пов’язані між собою й утворюють єдине електромагнітне поле, котре може існувати автономно, незалежно від зарядів або струмів, які були його першоджерелом. При цьому описаний процес взаємоперетворень полів не лишається локалізованим в околі джерела, а охоплює з часом все більшу й більшу область простору, тобто є хвильовим процесом. Отже, за Максвелом, змінне електромагнітне поле існує у формі електромагнітних хвиль (ЕМХ).
Зауваження. Таке уявлення є неповним. У дійсності електромагнітна енергія переноситься не неперервною хвилею, а потоком особливих елементарних частинок — квантів, які мають і хвильові, і корпускулярні властивості, (див. ЕЛЕМЕНТИ КВАНТОВОЇ ФІЗИКИ). Тут лише зазначимо, що прояви одних або інших властивостей залежать від частоти випромінювання. Зокрема, радіохвилі практично не показують ознак частинок, а гамма-промені — ознак хвиль. А ось випромінювання оптичного та рентгенівського діапазону в різних явищах проявляє як хвильові, так і квантові властивості.
Експериментально існування електромагнітних хвиль підтвердив Герц, який першим спостерігав електромагнітні хвилі радіочастотного діапазону, що виникали під час іскрового газового розряду. Електромагнітні хвилі утворюються також і в інших процесах й охоплюють дуже великий інтервал частот, який поділяють на декілька діапазонів, рис. 3.1.Не зрозуміло, треба продовжити шкалу
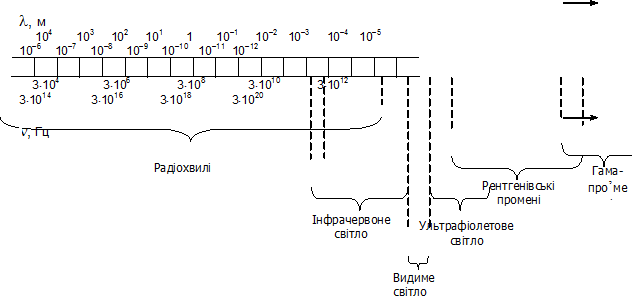
Далі розглядаються наступні питання:
3.1. Характеристики електромагнітних хвиль
3.2. Енергія електромагнітної хвилі
3.3. Властивості електромагнітних хвиль. Додаток
3.1. Характеристики електромагнітних хвиль
Всі властивості електромагнітних хвиль (ЕМХ) випливають із загальних рівнянь електромагнітного поля, але їхній теоретичний аналіз потребує серйозної математичної підготовки. Тому далі основні властивості ЕМХ розглядаються без доведення, а деякі необхідні для формального обґрунтування викладки наводяться в п. 3.3.
Швидкість поширення ЕМХ. У провідному середовищі електричне поле створює електричний струм, енергія якого перетворюється на тепло. Через це коливання електромагнітного поля швидко загасають, тож
електромагнітні хвилі реально можуть існувати тільки в діелектриках і вакуумі.
В цьому випадку з рівнянь Максвелла випливає, що за відсутності вільних зарядів вектори напруженості електричного \(\vec E\) та магнітного \(\vec H\) полів задовольняють диференціальні рівняння:
| \({\nabla ^2}\vec E = \varepsilon {\varepsilon _0}\mu {\mu _0}\frac{{{\partial ^2}\vec E}}{{\partial {t^2}}},\) | (3.1) |
| \({\nabla ^2}\vec H = \varepsilon {\varepsilon _0}\mu {\mu _0}\frac{{{\partial ^2}\vec H}}{{\partial {t^2}}},\) | (3.1а) |
де \({\varepsilon _0}\), \({\mu _0}\) — електрична та магнітна сталі, \(\varepsilon\), \(\mu \) — діелектрична та магнітна проникності середовища. Ці рівняння, подібно до (1.4), є хвильовими рівняннями електромагнітного поля. Загальний розв’язок кожного з них \(\vec{E}( \vec{r},t )\) або \(\vec{H}( \vec{r},t )\) у випадку змінних полів являє собою рівняння відповідної хвилі. Але позаяк електричне та магнітне поля є органічно взаємопов’язані, рівняння (3.1) і (3.1а) в сукупності описують єдину електромагнітну хвилю.
У хвильовому рівнянні (1.4) коефіцієнт при часовій похідній дорівнює оберненому квадрату швидкості, отже у загальному випадку швидкість поширення електромагнітні хвилі
| \(v = \frac{1}{{\sqrt {\varepsilon {\varepsilon _0}\mu {\mu _0}} }},\) | (3.2) |
а у вакуумі (\(\varepsilon = 1\), \(\mu = 1\))
| \({{v}_{\text{вак}}}=c=\frac{1}{\sqrt{{{\varepsilon }_{0}}{{\mu }_{0}}}}.\) | (3.3) |
Підстановка у формулу (3.3) значень \(\varepsilon _{0}\) та \(\mu _{0}\) дає \(c=3\cdot {{10}^{8}}\) м/с, що збігається із швидкістю світла у вакуумі. Отже, із хвильових рівнянь (3.1) і (3.1а) випливає, що світло має електромагнітну природу. Це теоретичне відкриття Максвелла надалі було підтверджено всім розвитком фізичної оптики.
Враховуючи формулу (3.3), швидкість поширення електромагнітної хвилі у середовищі можна виразити як
| \(v = \frac{c}{{\sqrt {\varepsilon \mu } }}.\) | (3.4) |
Раніше відмічалося, що електромагнітні хвилі можуть існувати лишень у вакуумі та діелектриках, які переважно є немагнітними середовищами (\(\mu = 1\)). Тому швидкість електромагнітних хвиль у речовині реально визначається формулою
| \(v = \frac{c}{{\sqrt \varepsilon }}.\) | (3.4а) |
Поперечність ЕМХ і зв’язок між полями. В електромагнітній хвилі коливання напруженостей електричного \(\vec E\) та магнітного \(\vec H\) полів відбуваються у взаємно перпендикулярних напрямках, які в той же час є перпендикулярними й до напрямку поширення хвилі (до напрямку вектора \(\vec v\)). Отже,
електромагнітні хвилі є поперечними хвилями.
При цьому вказані вектори утворюють праву трійку, тобто в кожній з послідовностей \(( \vec{E},\vec{H},\vec{v} )\), \(( \vec{H},\vec{v},\vec{E} )\) або \(( \vec{v},\vec{E},\vec{H} )\) останній вектор є спрямований за правим гвинтом відносно перших двох, як показано на рис. 3.2 (вектори, які зображені косо, напрямлені “до нас”).
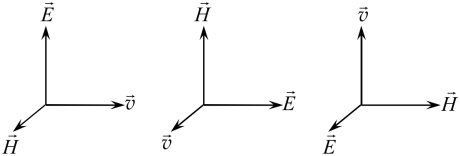
Поперечність електромагнітних хвиль виявляє себе в низці так званих поляризаційних ефектів, які знаходять широке практичне застосування.
Не лише напрямки, а й величини полів в електромагнітній хвилі не є довільними. Величина одного поля однозначно визначає величину іншого так, що за будь-яких умов амплітуди електричного \(E_0\) і магнітного \(H_0\) полів є пов’язані співвідношенням
| \(\sqrt {\varepsilon {\varepsilon _0}} {E_0} = \sqrt {\mu {\mu _0}} {H_0}.\) | (3.5) |
А у вільній хвилі ця умова виконується і для миттєвих значень проекцій напруженостей в кожній точці простору:
| \(\sqrt {\varepsilon {\varepsilon _0}} E( {\vec r,t} ) = \sqrt {\mu {\mu _0}} H( {\vec r,t} ).\) | (3.5а) |
Примітка. Під вільною мається на увазі хвиля, що поширюється у вільному просторі без відбивання від якихось “стінок”.
Це означає, що у вільній електромагнітній хвилі коливання електричного та магнітного полів є синфазними й описуються ідентичними рівняннями. Зокрема, гармонічна електромагнітна хвиля стандартно описується парою рівнянь:
| \(\left\{ \begin{gathered} \vec E( {\vec r,t} ) = {{\vec E}_0}\cos ( {\omega t - \vec k\vec r} ),\\ \vec H( {\vec r,t} ) = {{\vec H}_0}\cos ( {\omega t - \vec k\vec r} ). \end{gathered} \right.\) | (3.6) |
Описаний зв’язок між полями ілюструє рис. 3.3, на якому показано розподіл напруженостей полів у якийсь момент часу в напрямку поширення плоскій електромагнітної хвилі, що поширюється в напрямі осі \(\mathrm{OX}\).
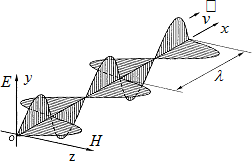
Зауважимо, що завдяки співвідношенню (3.5а), кожне з рівнянь (3.6) по суті містить повну інформацію про електромагнітну хвилю. Тому у багатьох задачах можна оперувати лишень одним із них.
3.2. Енергія електромагнітної хвилі
Вектор Пойнтінґа. Електромагнітна хвиля являє собою поширення у просторі змінного електромагнітного поля і тому переносить енергію, що складається з енергії електричного та магнітного полів хвилі. Цей процес у кожній точці простору й у кожен момент часу, як і в механічній хвилі, визначається вектором густини потоку енергії (2.11), який дорівнює добутку об’ємної густини енергії \(w\) хвилі та вектора її швидкості \(\vec v\). Із електродинаміки випливає, що
| \(w = {w_E} + {w_H} = \frac{{\varepsilon {\varepsilon _0}{E^2}}}{2} + \frac{{\mu {\mu _0}{H^2}}}{2},\) | (3.7) |
де враховані відомі вирази об’ємної густини енергії електричного та магнітного полів. За допомогою співвідношення (3.5а) цей вираз можна записати згорнуто:
| \(w = \varepsilon {\varepsilon _0}{E^2} = \mu {\mu _0}{H^2} = \sqrt {\mu {\mu _0}\varepsilon {\varepsilon _0}} EH.\) | (3.7а) |
Звідси, з урахуванням (3.2), виходить, що
| \(w = \frac{1}{v}EH.\) | (3.7б) |
Відтак величина густини потоку енергії (2.11), яку для електромагнітного поля позначимо літерою \(\Pi\), визначається, як
| \(\Pi=EH.\) | (3.8) |
Напрям перенесення енергії співпадає з напрямом вектора швидкості поширення хвилі \(\vec v\), який пов’язаний із напрямками векторів \(\vec E\) і \(\vec H\) правилом правого гвинта (рис. 3.2). Тому вектор густини потоку енергії електромагнітної хвилі \(\vec \Pi\), який називається вектором Пойнтінґа, визначається векторним добутком векторів полів:
| \(\vec{\Pi}=[ \vec{E}\vec{H} ].\) | (3.8а) |
Інтенсивність електромагнітної хвилі. У випадку гармонічної хвилі (3.6) модуль вектора Пойнтінґа дорівнює
| \(\Pi={{E}_{0}}{{H}_{0}}{{\cos }^{2}}( \omega t-\vec{k}\vec{r} ),\) | (3.9) |
або, з урахуванням (3.5),
| \(\Pi=\sqrt{\frac{{{\varepsilon }_{0}}\varepsilon }{{{\mu }_{0}}\mu }}E_{0}^{2}{{\cos }^{2}}( \omega t-\vec{k}\vec{r} ).\) | (3.9а) |
Частота електромагнітних хвиль, які знаходять застосування, \(\omega \geqslant {10^4}\ \text{c}^{ - 1}\), тож густина потоку енергії дуже швидко змінюється. Тому перенесення електромагнітної енергії в кожній точці простору реально визначається
середньою за період величиною густини потоку, яка називається інтенсивністю хвилі \(I\).
Отже, за означенням \(I=\langle\Pi \rangle \) і, згідно з (3.9),
\(I = {E_0}{H_0}\bigl\langle {{{\cos }^2}( {\omega t - \vec k\vec r} )} \bigr\rangle = \frac{1}{2}{E_0}{H_0}\bigl\langle {1 + \cos \bigl( {2(\omega t - \vec k\vec r)} \bigr)} \bigr\rangle.\)
Оскільки величина
\(\bigl\langle {1 + \cos \bigl( {2(\omega t - \vec k\vec r)} \bigr)} \bigr\rangle = 1 + \bigl\langle {\cos \bigl( {2(\omega t - \vec k\vec r)} \bigr)} \bigr\rangle = 1,\)
то для інтенсивності електромагнітної хвилі маємо:
| \(I = \frac{1}{2}{E_0}{H_0}.\) | (3.10) |
Аналогічно з (3.9а):
| \(I = \frac{1}{2}\sqrt {\frac{{\varepsilon {\varepsilon _0}}}{{\mu {\mu _0}}}} E_0^2.\) | (3.11) |
Позаяк для вакууму або однорідного середовища величина радикала в усіх точках є однаковою, розподіл інтенсивності в просторі повністю визначається квадратом амплітуди поля:
\(I \sim E_0^2.\)
Це дозволяє в багатьох випадках замість інтенсивності \(I\) оперувати величиною \(E_0^2\).
Формула (3.11) дозволяє визначити інтенсивність електромагнітної хвилі тільки через величину електричного поля. Ця обставина широко використовується в оптиці, де більшість ефектів зумовлена саме електричним полем світлової хвилі. Але за допомогою співвідношення (3.5) інтенсивність хвилі при необхідності можна виразити й через амплітуду магнітного поля:
| \(I = \frac{1}{2}\sqrt {\frac{{\mu {\mu _0}}}{{\varepsilon {\varepsilon _0}}}} H_0^2.\) | (3.11а) |
3.3. Властивості електромагнітних хвиль. Додаток
Хвильові рівняння. Існування і загальні властивості електромагнітних хвиль (ЕМХ) можна теоретично довести за допомогою основних рівнянь електромагнітного поля (рівнянь Максвела) в операторній формі (див. ЕЛЕКТРИКА І МАГНЕТИЗМ, частина V, п. 2.4.3). У випадку однорідного ізотропного діелектрика за відсутності вільних зарядів ці рівняння мають вигляд:
| \( [ {\vec \nabla \vec E} ] = - {\mu _0}\mu \frac{{\partial \vec H}}{{\partial t}}, \) | (3.12) |
| \( \vec \nabla \cdot \vec E = 0; \) | (3.13) |
| \( [ {\vec \nabla \vec H} ] = \varepsilon {\varepsilon _0}\frac{{\partial \vec E}}{{\partial t}}, \) | (3.14) |
| \( \vec \nabla \cdot \vec H = 0. \) | (3.15) |
Наведені рівняння містять тільки перші похідні, тоді як загальне хвильове рівняння (розділ ІІ, п. 1.3) пов’язує другі координатні та часові похідні відповідної характеристики хвилі. Тому спочатку “продиференціюємо по координатах” рівняння (3.12), взявши ротор від лівої та правої частин :
\( \bigl[ {\vec \nabla [ {\vec \nabla \vec E} ]} \bigr] = - {\mu _0}\mu \left[ {\vec \nabla,\frac{{\partial \vec H}}{{\partial t}}} \right]\quad \Rightarrow \quad \bigl[ {\vec \nabla [ {\vec \nabla \vec E} ]} \bigr] = - {\mu _0}\mu \frac{\partial }{{\partial t}}[ {\vec \nabla \vec H} ]. \)
(У правій частині використано те, що диференціювання по незалежних змінних можна проводити в довільному порядку.)
Далі, врахувавши рівняння (3.14), запишемо:
| \( \bigl[ {\vec \nabla [ {\vec \nabla \vec E} ]} \bigr] = - {\mu _0}\mu \frac{{{\partial ^2}\vec E}}{{\partial {t^2}}}. \) | (3.16) |
І нарешті розкриємо ліву частину за відомим правилом “бац мінус цаб” для подвійного векторного добутку: \(\bigl[ {\vec {a}[ {\vec {b}\vec {c}} ]} \bigr] = \vec {b}( {\vec {a}\vec {c}} ) - \vec {c}( {\vec {a}\vec {b}} )\). Відтак отримаємо:
\( \bigl[ {\vec \nabla [ {\vec \nabla \vec E} ]} \bigr] = \vec \nabla ( {\vec \nabla \vec E} ) - ( {\vec \nabla \vec \nabla } )\vec E. \)
Урахувавши, що в цьому виразі \((\vec \nabla \vec E) = 0\), згідно з (3.13), і \(( {\vec \nabla \vec \nabla } ) = {\nabla ^2}\) — оператор Лапласа, отримуємо з (3.16) хвильове рівняння (3.1) для вектора \(\vec E\):
\( {\nabla ^2}\vec E = {\varepsilon _0}\varepsilon {\mu _0}\mu \frac{{{\partial ^2}\vec E}}{{\partial {t^2}}}. \)
Так само виводиться й рівняння (3.1а) для магнітного вектора електромагнітної хвилі.
Поперечність ЕМХ. Для спрощення викладок розглянемо довільну плоску хвилю, що поширюється в напрямку координатної осі ОХ і, отже, має плоскі хвильові поверхні перпендикулярні до вказаної осі. Тому поля \(\vec E\) і \(\vec H\) залежать тільки від координати \(x\) і їхні похідні по \(y\) та по \(z\) дорівнюють нулю. Тоді наведені рівняння спрощуються і в координатній формі записуються, як:
| \( - {\vec e_y}\frac{{\partial {E_z}}}{{\partial x}} + {\vec e_z}\frac{{\partial {E_y}}}{{\partial x}} = - {\mu _0}\mu \left( {{{\vec e}_x}\frac{{\partial {H_x}}}{{\partial t}} + {{\vec e}_y}\frac{{\partial {H_y}}}{{\partial t}} + {{\vec e}_z}\frac{{\partial {H_z}}}{{\partial t}}} \right), \) | (3.17) |
| \( \frac{{\partial {E_x}}}{{\partial x}} = 0, \) | (3.18) |
| \( - {\vec e_y}\frac{{\partial {H_z}}}{{\partial x}} + {\vec e_z}\frac{{\partial {H_y}}}{{\partial x}} = {\varepsilon _0}\varepsilon \left( {{{\vec e}_x}\frac{{\partial {E_x}}}{{\partial t}} + {{\vec e}_y}\frac{{\partial {E_y}}}{{\partial t}} + {{\vec e}_z}\frac{{\partial {E_z}}}{{\partial t}}} \right), \) | (3.19) |
| \(\frac{{\partial {H_x}}}{{\partial x}} = 0\), | (3.20) |
де \({\vec e_x}\), \({\vec e_y}\), \({\vec e_z}\) — орти (одиничні вектори) координатних осей.
Проаналізуємо ці рівняння. Вектори в лівих частинах рівнянь (3.17) і (3.19) не мають \(x\)-компонент, отже, не мають їх і вектори в правих частинах. Тому \((\partial {H_x} / {\partial t}) = ( \partial {E_x} / {\partial t}) = 0\), і, врахувавши (3.18) і (3.20), маємо:
\(\left\{ \begin{gathered} \frac{{\partial {E_x}}}{{\partial x\mathstrut}} = 0,\qquad \frac{{\partial {E_x}}}{{\partial t}} = 0; \hfill \\ \frac{{\partial {H_x}}}{{\partial x}} = 0,\qquad \frac{{\partial {H_x}}}{{\partial t}} = 0. \hfill \\ \end{gathered} \right.\)
Це означає, що \({E_x}( {x,t} ) = \textrm{const}\) і \({H_x}( {x,t} ) = \textrm{const}\), тобто складові в напрямку осі \(\mathrm{OX}\) можуть мати лишень однорідні та стаціонарні (статичні) електричне й магнітне поля. Поля в електромагнітній хвилі такими не є, отже, в електромагнітній хвилі, що розглядається,
\(\left\{ \begin{gathered} {E_x} = 0\quad \Rightarrow \quad \vec E \bot {{\vec e}_x}, \hfill \\ {H_x} = 0\quad \Rightarrow \quad \vec H \bot {{\vec e}_x}. \hfill \\ \end{gathered} \right.\)
Таким чином, обидва поля є перпендикулярними до напрямку поширення електромагнітної хвилі, тобто, вона є поперечною.
Аби з’ясувати взаємну орієнтацію векторів \(\vec E\) і \(\vec H\), уявімо, що електричне поле хвилі напрямлене вздовж осі \(\mathrm{OY}\): \(\vec E = {\vec e_y}{E_y}\), тож \({E_x} = {E_z} = 0\). Тоді рівняння (3.17) і (3.19) набувають вигляду:
| \(\left\{ \begin{gathered} {\vec e_z}\frac{{\partial {E_y}}}{{\partial x}} = - {\mu _0}\mu \left( {{{\vec e}_y}\frac{{\partial {H_y}}}{{\partial t}} + {{\vec e}_z}\frac{{\partial {H_z}}}{{\partial t}}} \right), \\ {}- {\vec e_y}\frac{{\partial {H_z}}}{{\partial x}} + {\vec e_z}\frac{{\partial {H_y}}}{{\partial x}} = {\varepsilon _0}\varepsilon {\vec e_y}\frac{{\partial {E_y}}}{{\partial t}}. \end{gathered} \right.\) | (3.21) |
Оскільки у векторному рівнянні напрямки векторів у лівій та правій частинах мають бути однакові, робимо висновок, що в (3.21)
\({H_y} = 0 \quad \Rightarrow \quad \vec H = {\vec e_z}{H_z}.\)
Отже, якщо \(\vec E = {\vec e_y}{E_y}\), то \(\vec H = {\vec e_z}{H_z}\). Таким чином, вектори \(\vec E\) і \(\vec H\) є взаємно перпендикулярними та перпендикулярними до напрямку поширення хвилі й утворюють праву трійку, як показано на рис. 3.2.
Хвильові рівняння і швидкість поширення. У щойно розглянутому випадку рівняння (3.21) набувають вигляду:
| \(\left\{ \begin{gathered} \frac{{\partial {E_y}}}{{\partial x\mathstrut}} = - {\mu _0}\mu \frac{{\partial {H_z}}}{{\partial t}}, \hfill \\ - \frac{{\partial {H_z}}}{{\partial x}} = {\varepsilon _0}\varepsilon \frac{{\partial {E_y}}}{{\partial t}}. \hfill \\ \end{gathered} \right.\) | (3.21а) |
Продиференціювавши перше рівняння по координаті, а друге по часу, дістанемо:
\( \left\{ \begin{gathered} \frac{{{\partial ^2}{E_y}}}{{\partial {x^2}}} = - {\mu _0}\mu \frac{{{\partial ^2}{H_z}}}{{\partial x\partial t\mathstrut}}, \hfill \\ - \frac{{{\partial ^2}{H_z}}}{{\partial x\partial t}} = {\varepsilon _0}\varepsilon \frac{{{\partial ^2}{E_y}}}{{\partial {t^2}}} \hfill \\ \end{gathered} \right.\quad \Rightarrow \quad \frac{{{\partial ^2}{E_y}}}{{\partial {x^2}}} = {\varepsilon _0}\varepsilon {\mu _0}\mu \frac{{{\partial ^2}{E_y}}}{{\partial {t^2}}}, \)
а це є хвильове рівняння для електричної компоненти електромагнітної хвилі. Аналогічно отримується й хвильове рівняння для магнітної компоненти електромагнітної хвилі:
\( \frac{{{\partial ^2}{H_z}}}{{\partial {x^2}}} = {\varepsilon _0}\varepsilon {\mu _0}\mu \frac{{{\partial ^2}{H_z}}}{{\partial {t^2}}}, \)
При цьому для фазової швидкості виходить вираз (3.2):
\(v = \frac{1}{{\sqrt {\varepsilon {\varepsilon _0}\mu {\mu _0}} }}.\)
Зв’язок між полями. Наостанку на прикладі гармонічної хвилі знайдемо зв’язок між величиною полів \(E\) та \(H\). Нехай електричне поле хвилі визначається, як
\( {E_y}( {x,t} ) = {E_0}\cos (\omega t - kx). \)
Тоді з першого рівняння (3.15а) маємо:
\(\frac{{\partial {H_z}}}{{\partial t}} = \frac{{k{E_0}}}{{{\mu _0}\mu }}\sin (\omega t - kx).\)
Отже, коливання магнітного поля в якійсь заданій точці \(x = {x_0}\) задовольняють рівняння:
\(\frac{{\operatorname{d}\! {H_z}}}{{\operatorname{d}\! t}} = \frac{{k{E_0}}}{{{\mu _0}\mu }}\sin (\omega t - {\varphi _0}),\qquad {\varphi _0} = k{x_0}.\)
Проінтегрувавши це рівняння, знайдемо залежність магнітного поля хвилі від часу:
\({H_z}( {t,{x_0}} ) = \frac{{k{E_0}}}{{{\mu _0}\mu }}\int {\sin ( {\omega t - {\varphi _0}} )\operatorname{d}\! t} = \frac{k}{{{\mu _0}\mu \omega }}{E_0}\cos ( {\omega t - {\varphi _0}} ) = \frac{k}{{{\mu _0}\mu \omega }}{E_y}( {t,{x_0}} ).\)
Із виразів (1.4) і (3.2) випливає, що
\(\frac{k}{{{\mu _0}\mu \omega }} = \sqrt {\frac{{{\varepsilon _0}\varepsilon }}{{{\mu _0}\mu }}},\)
отже,
| \({H_z}( {t,{x_0}} ) = \sqrt {\frac{{{\varepsilon _0}\varepsilon }}{{{\mu _0}\mu }}} {E_y}( {t,{x_0}} ).\) | (3.22) |
Даний результат є чинним при будь-яких значеннях \({x_0}\), тому в будь-якій точці простору й у будь-яку мить між величинами електричного та магнітного полів у гармонічній існує співвідношення (3.15а):
\(\sqrt {\varepsilon {\varepsilon _0}} E( {x,t} ) = \sqrt {\mu {\mu _0}} H( {x,t} ).\)
Звернімо увагу й на те, що знаки проекцій \({E_y}\) і \({H_z}\) у (3.22) завжди однакові. А це означає, що у вільній електромагнітній хвилі коливання полів відбуваються в однаковій фазі.
На завершення вкажемо, що такі самі результати можна отримати й для вільної хвилі і з довільним законом коливань \(E = f\left( {\omega t - kx} \right)\).
Контрольні запитання
- Від чого залежить швидкість електромагнітних хвиль? Скориставшись довідковими даними, обчисліть швидкість поширення електромагнітних хвиль у вакуумі.
- До якого типу належать електромагнітні хвилі? Яка взаємна орієнтація векторів полів \(\vec E\), \(\vec H\) і швидкості поширення \(\vec v\) в електромагнітній хвилі?
- Запишіть співвідношення між амплітудами електричного та магнітного поля електромагнітної хвилі. Чи завжди воно виконується?
- Запишіть співвідношення між миттєвими значеннями електричного та магнітного поля електромагнітної хвилі. Чи завжди воно виконується?
- Який зміст має вектор Пойнтінґа та як він визначається? Що таке інтенсивність електромагнітної хвилі?
- Запишіть вираз інтенсивності електромагнітної хвилі через амплітуду напруженості електричного поля хвилі. Знайдіть величину та розмірність числового коефіцієнта в цьому виразі.
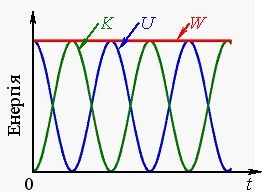
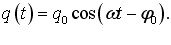
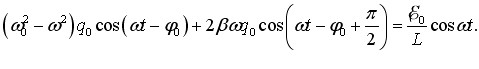
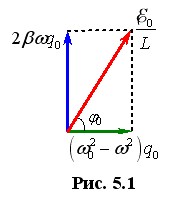
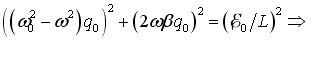
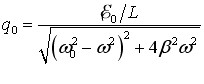
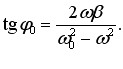
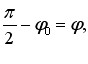
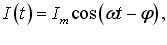
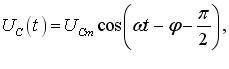
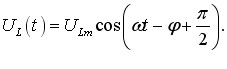
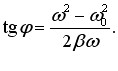
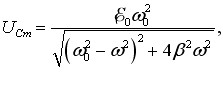
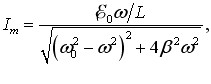
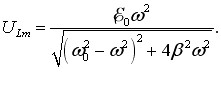
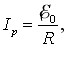
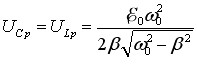
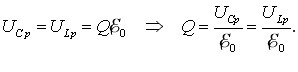
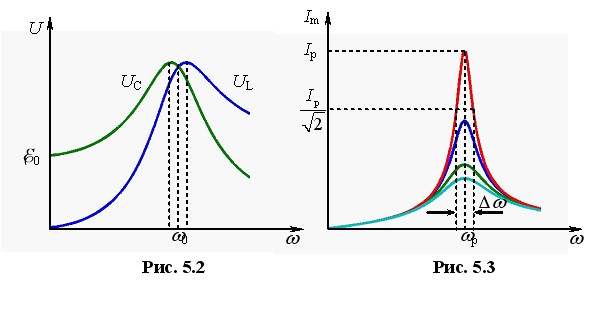
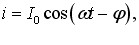
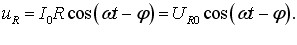
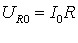 або
або 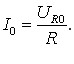
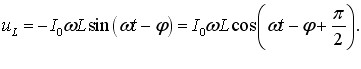
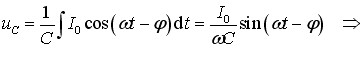
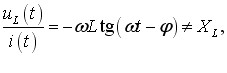
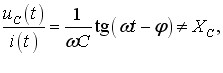
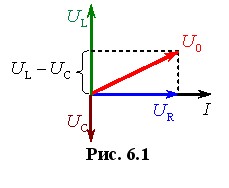
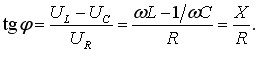
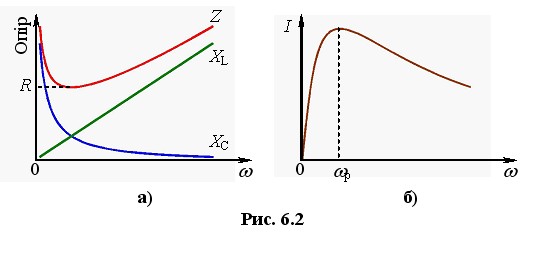
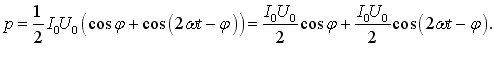
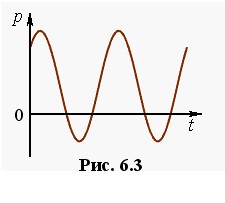
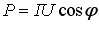 .
.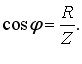
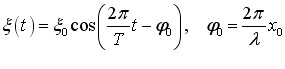 ,
,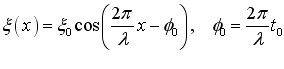 .
.