ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ
V. ЕЛЕКТРОМАГНЕТИЗМ
1. Явище електромагнітної індукції
Органічний зв’язок між електричним і магнітним полями найбільш яскраво проявляється у їхній здатності до взаємних перетворень. Зокрема — у здатності нестаціонарного магнітного поля породжувати електричне поле. В цьому полягає глибинний зміст явища електромагнітної індукції (ЕМІ), яке розглядається далі в наступних питаннях:
1.3. Струм при замиканні та розмиканні кола з індуктивністю
1.1. Основний закон ЕМІ
Явище ЕМІ. Закон Фарадея. Раніше (розділ IV, п. 1.4) було показано, що при зміні магнітного потоку крізь поверхню контуру зі струмом при малому переміщення в магнітному полі виконується робота
\begin{equation} \delta{A}=I\,\mathrm{d}{\Phi}. \end{equation}
Але магнітні сили, що діють на носії струму в контурі, є поперечними і як такі роботи не виконують. Тоді за рахунок чого вона виконується?
Аби це з’ясувати, розглянемо такий дослід. Нехай у магнітному полі \(\vec{B}\) закріплено дві паралельні металеві рейки, кінці яких з одного боку замкнені на джерело струму із заданою ЕРС \(\E\), рис. 1.1.
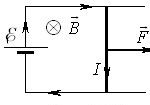
По рейках може ковзати без тертя перетинка із струмом опором \(R\), яку спочатку утримують у фіксованому положенні.
Якщо задля простоти знехтувати опором джерела і рейок, то сила струму в перетинці дорівнює
\begin{equation} {I}_{0}=\frac{\E}{R}. \end{equation}
При цьому вся робота джерела йде на нагрівання провідників і за час \(\mathrm{d}t\) складає
\begin{equation} \delta{A}={\E}I_{0}\,\mathrm{d}t=I_{0}^{2}R\,\mathrm{d}{t}. \end{equation}
Але після звільнення перетинка почне рухатися під дією сили Ампера, і енергія джерела буде витрачатися вже не тільки на тепло, а й на виконання роботи по переміщенню перетинки в магнітному полі:
\begin{equation} {\E}I\,\mathrm{d}t=I^{2}R\,\mathrm{d}t+I\,\mathrm{d}\Phi. \end{equation}
У такому разі струм у колі зміниться і стане рівним
\begin{equation} {I}=\frac{{\E}-\mathrm{d}\Phi/\mathrm{d}t}{R}. \end{equation}
Отже, виходить, що під час руху перетинки в контурі крім ЕРС джерела \(\E\) діє ще одна ЕРС, яка дорівнює
\begin{equation} {\E}_{i}=-\frac{\mathrm{d}\Phi}{\mathrm{d}t}. \tag{1.1} \end{equation}
Відповідно, сила струму
\begin{equation} {I}=\frac{\E+\E_{i}}{R}. \end{equation}
Отриманий результат є одним із проявів відкритого М. Фарадеєм явища електромагнітної індукції (ЕМІ), котре полягає в тому, що
при зміні магнітного потоку крізь поверхню, обмежену провідним контуром, в ньому виникає електричний струм.
Такий струм називається індукційним струмом і створюється електрорушійною силою (ЕРС) індукції (1.1). Отже,
\begin{equation} {I}=\frac{\E}{R}=-\frac{1}{R}\cdot\frac{\mathrm{d}\Phi}{\mathrm{d}t}. \tag{1.2} \end{equation}
Важливою особливістю явища ЕМІ є його універсальність. Як показали досліди Фарадея, виникнення ЕРС індукції не залежить від причини та способу зміни потоку, причому величина \( {\E}_{i}\) в усіх випадках визначається виразом (1.1). Тому його називають основним законом електромагнітної індукції, або законом Фарадея.
Потік крізь контур можна змінювати багатьма конкретними способами, але є тільки дві різні причини його зміни. Це або рух контура чи його частини у магнітному полі, або зміна із часом (нестаціонарність) самого магнітного поля. Істотно й те, що ЕРС індукції визначається швидкістю зміни потоку, а не його величиною. Тому за відповідних умов у слабкому полі ЕРС \( {\E}_{i}\) може виявитися великою, а в сильному — незначною.
Зазначимо також, що в СІ на основі закону (1.1) встановлюється одиниця магнітного потоку вебер (Вб, \(1\ \text{Вб} = 1\ \text{В}\cdot\text{с}\)):
\(1\ \text{Вб}\) — то є магнітний потік, при рівномірній зміні котрого до нуля за час \(1\ \text{с}\) у зв’язаному з ним контурі індукується ЕРС \(1\ \text{В}\).
Відтак установлюються одиниці інших магнітних величин. Зокрема, одиниця індукції магнітного поля — тесла (\(1\ \text{Тл}\)) має наступне означення:
\(1\ \text{Тл}\) дорівнює індукції такого однорідного магнітного поля, в якому крізь перпендикулярну до нього плоску поверхню площею \(1\ \text{м}^2\) створюється магнітний потік \(1\ \text{Вб}\).
Отже, \(1\ \text{Тл} = 1\ \text{Вб}/\text{м}^2\).
Правило Ленца. Досліджуючи електромагнітну індукцію, Фарадей виявив, що напрям індукційного струму залежить від того, зростає потік крізь контур із часом, чи зменшується. Пізніше Ленц дослідним шляхом установив загальне правило, що носить його ім’я і дозволяє визначити напрям індукційного струму в кожному випадку. А саме,
індукційний струм у контурі завжди має такий напрям, при якому перешкоджає причині, що його породжує.
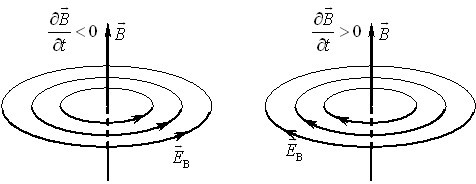
Конкретно це означає, що магнітне поле \({{\vec{B}}_{i}}\), яке створюється індукційним струмом і завжди пов’язане з ним правилом правого гвинта, має бути напрямлене так, аби власним потоком послаблювати зміну потоку поля, яка викликає індукційний струм. Приміром, якщо нерухоме дротяне кільце знаходиться в однорідному нестаціонарному магнітному полі \(\vec{B}( t )\), що послаблюється з часом (\(\mathrm{d}B/\mathrm{d}t < 0\)), то потік крізь кільце спадає. Тоді поле індукційного струму \({{\vec{B}}_{i}}\) має підживлювати поле \(\vec{B}\) й індукційний струм буде циркулювати за правим гвинтом відносно напряму \(\vec{B}\), як показано на рис. 1.2а.
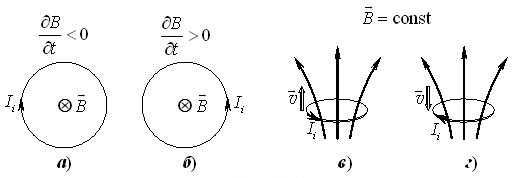
Із тих самих міркувань при (\(\mathrm{d}B/\mathrm{d}t > 0\)) напрям індукційного струму є протилежним (рис. 1.2б). Так можна визначати напрям індукційного струму і в будь-якому іншому випадку. Але зручніше робити це безпосередньо за виразом (1.2), використовуючи наступне правило знаків (див. рис. 1.2а,б):
якщо за формулою (1.2) виходить \(I_i>0\), то індукційний струм пов’язаний із напрямом магнітного поля, що його породжує, правилом правого гвинта. При \(I_i < 0\) напрям струму протилежний.
До прикладу, коли кільце рухається в постійному неоднорідному полі показаному на рис. 1.2в,г, то при русі в напрямку поля \(\mathrm{d}\Phi /\mathrm{d}t < 0\), а в протилежному напрямку \(\mathrm{d}\Phi /\mathrm{d}t > 0\). Тому, у випадку в) індукційний струм \(I_i > 0\) і тече за годинниковою стрілкою, якщо дивитися вздовж напрямку поля, а у випадку г) \(I_i < 0\), і струм протікає в протилежному напрямку.
На завершення скажемо, що правило Ленца диктується законом збереження енергії і є одним із проявів загального принципу Ле Шательє — Брауна, за яким усякий зовнішній вплив, що намагається вивести систему із стійкої рівноваги, продукує в ній компенсаційні процеси, спрямовані на нівелювання цього впливу.
1.2. Самоіндукція
ЕРС у контурі може індукуватись як зовнішнім магнітним полем, так і власним полем, створюваним струмом у самому контурі. Останній випадок називається самоіндукцією.
Власний потік та індуктивність контуру. Магнітне поле струму, що протікає по замкненому контуру, створює відповідний потік крізь поверхню, обмежену цим контуром. В силу неперервності ліній магнітного поля, цей потік не залежить від площі та форми такої поверхні і називається власним потоком або потоком самоіндукції контуру.
За відсутності феромагнетиків величина індукції магнітного поля провідника із струмом у будь-якій точці простору є прямо пропорційною величині струму: \(B\sim I\). Це стосується й потоку поля крізь будь-яку задану поверхню, тож для власного потоку \(\Phi_{\text{с}}\) контуру із струмом \(I\) можна записати:
\begin{equation} \Phi_{\text{с}}={LI}, \tag{1.3} \end{equation}
де величина
\begin{equation} {L}=\frac{\Phi_{\text{с}}}{I} \tag{1.4} \end{equation}
називається індуктивністю або коефіцієнтом самоіндукції контуру.
Зауваження. Означення (1.4), строго говорячи, є неоднозначним, бо невідомо, як саме має проходити всередині провідника контур поверхні, через яку визначається величина \(\Phi_{\text{с}}\). Але, позаяк на практиці контури виготовляють із тонкого дроту, указана обставина є не істотною.
Одиницею індуктивності є генрі (Гн) — індуктивність контуру, власний потік якого складає \(1\ \text{Вб}\) при силі струму \(1\ \text{А}\):
\begin{equation} 1\ \text{Гн} = 1\ \text{Вб}/\text{А}. \end{equation}
Величина \(L\) не залежить від сили струму і визначається тільки конфігурацією контуру та магнітними властивостями середовища, в якому він знаходиться. У цьому легко переконатися на прикладі довгого соленоїда, в якому при струмі \(I\) створюється магнітна поле з індукцією, що визначається формулою (3.18), розділ IV:
\begin{equation} B=\mu_0\mu nI, \end{equation}
де \(n\) — кількість витків на одиницю довжини соленоїда.
В такому разі потік крізь один виток складає
\begin{equation} \Phi_1=\mu_0\mu nIS, \end{equation}
а власний потік усього соленоїда, котрий ще називається потокозчепленням, дорівнює
\begin{equation} \begin{aligned} &\Phi_{\text{с}}=N\mu_0\mu nIS=\mu_0\mu n^2ISl={}\\ &\quad{}= \mu_0\mu n^2IV, \end{aligned} \end{equation}
де \(N\) — повна кількість витків соленоїда, \(S\) — площа його перерізу, \(l\) — довжина і \(V\) — об’єм. Відтак за формулою (1.4) індуктивність соленоїда
\begin{equation} L=\mu_0\mu n^2V. \tag{1.5} \end{equation}
ЕРС і струм самоіндукції. При зміні з часом власного магнітного потоку контуру в ньому виникає ЕРС самоіндукції \({\E}_{\text{с}}\), яка, природньо, визначається законом Фарадея (1.1):
\begin{equation} {\E}_{\text{с}} = -\frac{\mathrm{d}\Phi }{\mathrm{d}t}= -\frac{\mathrm{d}( LI )}{\mathrm{d}t}. \end{equation}
Якщо контур є жорстким і знаходиться в діа- чи парамагнітному середовищі, то \(\mu = \textrm{const}\), \(L = \textrm{const}\), і величина \({{E}_{\text{с}}}\) визначається тільки швидкістю зміни струму в контурі:
\begin{equation} {\E}_{\text{с}} = -L\frac{\mathrm{d}I}{\mathrm{d}t}. \tag{1.6} \end{equation}
Але при деформації не жорсткого контуру чи зміні струму в котушці з феромагнітним осердям індуктивність теж змінюється з часом, і вираз \({\E}_{\text{с}}\) істотно ускладнюється:
\begin{equation} {\E}_{\text{с}} = -L\frac{\mathrm{d}I}{\mathrm{t}} - I\frac{\mathrm{d}L}{\mathrm{d}t}. \end{equation}
За таких умов чисто аналітичні розрахунки ланцюгів із індуктивностями стають неможливими, і використовуються інші методи аналізу.
ЕРС самоіндукції створює в контурі додатковий струм самоіндукції \(I_{\text{с}}\), напрям якого є підпорядкований правилу Ленца і встановлюється дуже просто:
напрям струму самоіндукції збігається з напрямом основного струму при його зменшенні і є протилежним до основного струму при його зростанні.
1.3. Струм при замиканні та розмиканні кола з індуктивністю
При замиканні та розмиканні кола, в якому є тільки резистори, струм установлюється і зникає практично миттєво. Але в колах із котушками індуктивності при комутаціях виникають індукційні струми, котрі за правилом Ленца уповільнюють зміну основних струмів. Тому при замиканні чи розмиканні кола з індуктивністю струм змінюється поступово.
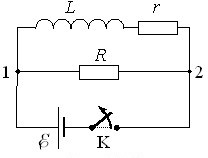
Струм при замиканні кола. Розглянемо процес установлення струму в простому колі, що складається з котушки індуктивності \(L = \textrm{const}\), резистора \(R\), джерела з ЕРС \( {\E}\) та ключа К (рис. 1.3).
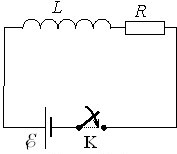
Будемо вважати, що опір дроту котушки включено в \(R\), а опір джерела дорівнює нулю. Також приймемо, що струм є квазістаціонарним (див. розділ III, п. 3.1).
Після замикання в момент \(t = 0\) ключа К у котушці виникне ЕРС самоіндукції \( {\E}_{\text{с}} \), так що струм у колі дорівнюватиме
\begin{equation} {I}=\frac{{\E}+{\E}_{\text{с}}}{R}. \end{equation}
Підставивши сюди вираз (1.6), отримаємо диференціальне рівняння
\begin{equation} \begin{aligned} &{IR}={\E}-L\frac{\mathrm{d}I}{\mathrm{d}t} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \frac{\mathrm{d}I}{\mathrm{d}t}=\frac{{\E}-IR}{L}, \end{aligned} \tag{1.7}\end{equation}
з якого можна знайти закон зміни струму \(I=I(t)\).
Рівняння (1.7) легко інтегрується методом відокремлення змінних. Але задля зручності спочатку введемо позначення :
\begin{equation} {V}={\E}-IR . \tag{1.7а} \end{equation}
Тоді
\begin{equation} \frac{\mathrm{d}I}{\mathrm{d}t} = - \frac{1}{R}\frac{\mathrm{d}V}{\mathrm{d}t} \end{equation}
і рівняння (1.7) набуває вигляду
\begin{equation} \begin{aligned} &\frac{\mathrm{d}V}{\mathrm{d}t}=-\frac{V}{\tau} \quad \Rightarrow \quad \frac{\mathrm{d}V}{V}=-\frac{\mathrm{d}t}{\tau},\\ &\tau= \frac{L}{R}. \end{aligned} \end{equation}
Проінтегрувавши це рівняння від \(t = 0\) до довільного моменту \(t\) і від \(V_{0}\) до \(V\), отримуємо:
\begin{equation} \begin{aligned} &\int\limits_{V_{0}}^{V}\frac{\mathrm{d}V}{V}=-\int\limits_{0}^{\tau}\frac{\mathrm{d}t}{\tau} \quad \Rightarrow {}\\ &\quad{}\Rightarrow\quad \ln\frac{V}{V_{0}}=-\frac{t}{\tau} \quad \Rightarrow \quad {V}=V_{0}e^{-\frac{t}{\tau}}. \end{aligned} \end{equation}
У момент замикання ключа \(t = 0\) струм у колі відсутній: \(I=0\). Отже, відповідно до (1.7а) маємо \( {V}_{0}={\E} \).
Відтак, зробивши зворотню заміну \( {V}={\E}-{IR}\), дістанемо:
\begin{equation} \begin{aligned} &{I}(t)=I_{m}\bigl(1-\mathrm{e}^{-t/\tau}\bigr),\\ &{I}_{m}=\frac{{\E}}{R} . \end{aligned} \tag{1.8}\end{equation}
Отриманий результат має прозорий зміст. А саме: струм у колі складається із двох частин
\begin{equation} {I}=I_{m}+{I^\prime}, \end{equation}
де \( {I}_{m}={\E}/{R} \) — струм, який створюється джерелом, а \( {I}'=-{{I}_{m}}{{e}^{-{t}/{\tau }}}\) — зустрічний струм самоіндукції, що виникає в котушці.
З часом зустрічний струм самоіндукції поступово зменшується, а повний струм \(I\) зростає і наближається до усталеного значення \(I_m\). Наскільки швидко це буде відбуватися, залежить від величини
\begin{equation} \tau=\frac{L}{R}, \tag{1.9} \end{equation}
яка називається часом установлення струму (сталою часу) \(RL\)-ланцюжка.
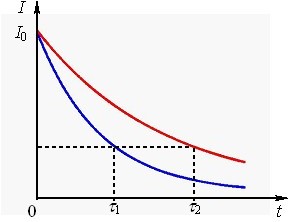
Зокрема, через час \(\tau \) після замикання ключа струм у колі досягає величини \({I}=I_{m}(1-e^{-1})=0{,}63I_{m}\). При цьому чим більша величина \(\tau \), тим повільніше наростає струм (рис. 1.4).
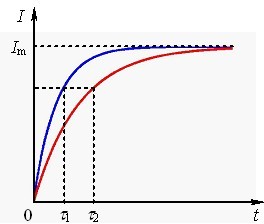
Струм при розмиканні кола. Розглянемо тепер поведінку струму в котушці, яка має індуктивність \(L\) і опір \(r\), після розмикання ключа К у колі рис. 1.5. Як і раніше, опір джерела дорівнює нулю.
Після розмикання ключа струм через котушку та резистор визначається тільки ЕРС самоіндукції і дорівнює
\begin{equation} {I}=\frac{{\E}_{\text{с}}}{R+r}=\frac{{\E}_{\text{с}}}{R_{0}}, \end{equation}
де \(R_{0} = R + r\) — повний опір кола.
Цей струм називається екстраструмом розмикання і відповідно до (1.6) задовольняє диференціальне рівняння
\begin{equation} \begin{aligned} &{I}=-\frac{L}{R_{0}}\frac{\mathrm{d}I}{\mathrm{d}t}\quad \Rightarrow \quad \frac{\mathrm{d}I}{\mathrm{d}t}=-\frac{I}{\tau},\\ &\tau= \frac{L}{R_{0}}, \end{aligned} \end{equation}
що, як і раніше, розв’язується методом відокремлення змінних:
\begin{equation} \begin{aligned} &\frac{\mathrm{d}I}{I}=-\frac{\mathrm{d}t}{\tau} \quad \Rightarrow \quad \int\limits_{I_{0}}^{I}\frac{\mathrm{d}I}{I}=-\int\limits_{0}^{t}\frac{\mathrm{d}t}{\tau} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \ln\frac{I}{I_{0}}=-\frac{t}{\tau}. \end{aligned} \end{equation}
Отже,
\begin{equation} {I}=I_{0}e^{-t/\tau}, \tag{1.10} \end{equation}
де величина \({I}_{0}=I{(0)}\) — струм, який створювався в котушці джерелом \( {\E}\) до розмикання ключа і дорівнював
\begin{equation} {I}_{0}=\frac{{\E}}{r}. \end{equation}
Таким чином, після відключення джерела в котушці виникає струм, що експоненціально спадає з часом як показано на рис. 1.6.
Цей струм тече і через резистор \(R\), тож між точками 1 і 2 створюється напруга
\begin{equation} {U}=IR=I_{0}R\mathrm{e}^{-t/\tau}=\frac{R}{r}{\E}\mathrm{e}^{-t/\tau}. \end{equation}
Позаяк опір котушки зазвичай малий \(r\ll R\), у момент розмикання ключа К створюється стрибок напруги \(U \gg {\E}\). Це може викликати електричний пробій ізоляції, тому в потужних колах з індуктивностями передбачають спеціальні системи захисту від екстраструмів розмикання.
1.4. Енергія магнітного поля
При встановленні струму в контурі з індуктивністю джерело виконує роботу по подоланню ЕРС самоіндукції. Тому його енергія витрачається не тільки на джоульове тепло, а й частково переходить в іншу форму, що називається магнітною енергією струму \(W_m\). Про це свідчить те, що після відключення джерела у колі з індуктивністю продовжує текти струм (1.10) і виділятися тепло. Очевидно, що це відбувається за рахунок магнітної енергії струму, адже ніяких інших джерел енергії в колі немає. З іншого боку, за умови квазістаціонарності струму немає й інших каналів перетворення магнітної енергії.
(Примітка. У випадку нестаціонарних, тобто швидкозмінних, струмів частина цієї енергії йде на електромагнітне випромінювання).
Тому \(W_m=Q\), де \(Q\) — кількість тепла, що виділяється при повному згасанні струму в контурі після відключення зовнішнього джерела. Це дозволяє розрахувати магнітну енергію \(W_m\) через силу струму \(I\) в контурі.
Якщо в колі на рис. 1.5 на момент розмиканні ключа К t = 0 струм у котушці індуктивності дорівнює I, то, згідно з (1.10), надалі він буде зменшуватися за законом \({i}=Ie^{-t/\tau}\). При цьому магнітна енергія котушки буде перетворюватися в тепло на повному опорі кола R0=R+r, згідно із законом Джоуля (розділ III, формула (4.2)). Формально цей процес триватиме необмежений час, тож кількість тепла, що виділиться за час до повного згасання струму, визначається, як:
\begin{equation} {Q}=R_{0}{{I}^{2}}\int\limits_{0}^{\infty }{{{e}^{-{2t}/{\tau }}}\,\mathrm{d}t}=\frac{\tau R_{0}{{I}^{2}}}{2}. \end{equation}
(Довідка. Інтеграли з нескінченними границями називаються невласними інтегралами і обчислюється через граничний перехід:
Але коли границя перехід є очевидною, із символом \({\infty}\) поводяться, як із звичайним числом.
Звідси, враховуючи, що \(W_m=Q\) і \(\tau = L / R_{0}\), отримуємо наступну формулу магнітної енергії струму:
\begin{equation} {W}_{m}=\frac{LI^2}{2}. \tag{1.11} \end{equation}
Вираз (1.11) показує, що крім величини струму магнітна енергія залежить від параметрів контуру. Наприклад, для соленоїда, зважаючи на формулу (1.5),
\begin{equation} {W}_{m}=\frac{\mu_{0}\mu{n^2}I^2}{2}{V}. \tag{1.11а} \end{equation}
Але для соленоїда nI = H — напруженість поля, тож
\begin{equation} {W}_{m}=\frac{\mu_{0}\mu{H^2}}{2}V. \tag{1.11б} \end{equation}
Отже, магнітну енергію соленоїда можна виразити не через конфігурацію контуру та величину струму ньому, а через характеристики магнітного поля в соленоїді та об’єм простору який воно займає. В об’ємі соленоїда зосереджене все його поле, тому отриманий результат дає підстави думати, що магнітна енергія зосереджена не в самій котушці із струмом, а в її магнітному полі. Інакше говорячи, магнітне поле має енергію. Такий висновок повністю підтверджується і теорією, і дослідом.
Магнітне поле ідеального соленоїда є однорідним, і його енергія розподілена у просторі рівномірно з об’ємною густиною
\begin{equation} {w}_{m}=\frac{W}{V}\ (\text{Дж}/\text{м}^3), \end{equation}
що, згідно з виразом (1.11б), визначається формулою
\begin{equation} {w}_{m}=\frac{\mu_{0}\mu{H^2}}{2}. \tag{1.12} \end{equation}
Урахувавши співвідношення B = μ0μH (див. розділ IV), можна записати й такі формули:
\begin{equation} {w}_{m}=\frac{B^2}{2\mu_{0}\mu} \tag{1.12а} \end{equation}
та
\begin{equation} {w}_{m}=\frac{BH}{2}. \tag{1.12б} \end{equation}
Таким чином, енергія заданого об’єму однорідного магнітного поля виражається, як
\begin{equation} {W}_{m}={wV}. \end{equation}
Формули (1.12), (1.12а) і (1.12б) зберігають чинність і для неоднорідного поля, але в такому разі об’ємна густина енергії не скрізь однакова і в кожній точці визначається як
\begin{equation} {w}_{m}=\frac{\mathrm{d}W}{\mathrm{d}V}. \end{equation}
Відповідно, енергія в заданому об’ємі \(V\) неоднорідного поля знаходиться інтегруванням енергій
\begin{equation} \mathrm{d}W_{m}=w\,\mathrm{d}{V}, \end{equation}
зосереджених у всіх елементарних ділянках цього об’єму:
\begin{equation} {W_{m}}=\int\limits_{V}w\,\mathrm{d}{V}. \tag{1.13} \end{equation}
1.5. Природа ЕМІ. Вихрове електричне поле
На початку розділу відзначалося, що є дві різні причини зміни магнітного потоку і виникнення ЕРС індукції та індукційного струму — рух провідників та зміна з часом магнітного поля, в якому знаходиться провідний контур, — але в обох випадках виконується один і той самий закон (1.1). Така універсальність є унікальною рисою явища ЕМІ, бо сторонні сили, що забезпечують рух електронів уздовж контуру, в кожному з указаних випадків мають різне походження.
Індукція в рухомих провідниках. Розглянемо виникнення індукційного струму в провідному контурі утвореному нерухомим металевим каркасом із рухомою дротяною перетинкою, який вміщений у перпендикулярне до його площини однорідне магнітне поле (рис.1.7а).
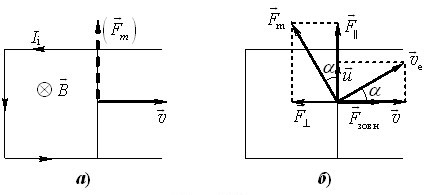
Якщо перетинку привести в рух, як показано, то внаслідок збільшення потоку крізь поверхню контуру, по ньому, відповідно до (1.2), потече індукційний струм \(I_0\), спрямований проти годинникової стрілки. Природа сторонньої сили, яка його створює, на перший погляд є очевидною. Адже з початком руху перетинки вздовж неї на носії струму починає діяти магнітна сила Лоренца \( \vec{F}_{m}\) (розділ IV, ф-ла (1.3)). Тож вона і є причиною переміщення (дрейфу) носіїв по перетинці та виникнення струму. Але в такому поясненні є протиріччя. При протіканні струму сторонні сили мають виконувати над носіями роботу по подоланню електричного опору, тоді як магнітна сила є поперечною і не може виконувати роботу. Пояснення цього "парадоксу" полягає в тому, що насправді швидкість носіїв відносно магнітного поля дорівнює не швидкості перетинки \(\vec{v}\), а величині \(\vec{v}_{e}=\vec{v}+\vec{u}\), де \(\vec{u}\) — дрейфова швидкість, тобто швидкість руху носіїв відносно перетинки. Тому магнітна сила, що діє на носії,
\begin{equation} \vec{F}_{m}=e\bigl[\vec{v}_{e},\vec{B}\bigr] , \tag{1.14} \end{equation}
напрямлена не вздовж перетинки, а під кутом, як показано на рис.1.7б (задля зручності заряд носіїв будемо вважати позитивним). Тому вона має дві складові:
\begin{equation} {{\vec{F}}_{m}}={{\vec{F}}_{\parallel }}+{{\vec{F}}_{\bot }}. \end{equation}
При цьому лише паралельна до перетинки складова
\begin{equation} {{\vec{F}}_{\parallel }}={{\vec{F}}_{\bot }}-{{\vec{F}}_{m}}. \end{equation}
безпосередньо рухає носії по перетинці. А інша складова \(\vec{F}_{\bot}\) гальмує перетинку (це є наочним проявом правила Ленца), і для підтримки руху до неї має бути прикладена якась зовнішня сила
\begin{equation} \vec{F}_{\text{зовн}} = - \vec{F}_{\bot}. \end{equation}
Таким чином, за сторонню силу, що створює струм і визначає ЕРС у контурі, править рівнодійна
\begin{equation} \vec{F}_{\text{стор}} = \vec{F}_{m} + \vec{F}_{\text{зовн}} = \vec{F_{\parallel}}. \end{equation}
При цьому, позаяк магнітна сила роботи не виконує, робота сторонньої сили збігається з роботою зовнішньої сили:
\begin{equation} {{A}_{\text{стор}}}={{A}_{\text{зовн}}}={{A}_{\parallel }} \end{equation}
і виконується за рахунок якогось зовнішнього джерела енергії.
Робота сторонніх сил над носіями струму визначає ЕРС, отже, констатуємо, що
ЕРС індукції в рухомих провідниках зумовлена сумісною дією на носії струму магнітного поля та зовнішніх сил, які підтримують рух. При цьому сили магнітного поля забезпечують дрейф носіїв, а зовнішні сили надають необхідну для цього енергію.
Описаний електронний механізм ЕМІ повністю узгоджується із законом Фарадея, в чому можна переконатися прямим розрахунком ЕРС індукції на основі означення ЕРС (див. розділ III, п. 2.1):
\begin{equation} {\E}=\frac{A_{\text{стор}}}{q}, \end{equation}
де \(A_{\text{стор}}\) — робота сторонньої сили при переміщенні заряду \(q\) по всій довжині перетинки \(l\). Вона дорівнює
\begin{equation} A_{\text{стор}}={F}_{\parallel}l=F_{m}\cos\alpha\cdot{l}. \end{equation}
З урахуванням виразу (1.14)
\begin{equation} A_{\text{стор}}=qBv_e\cos\alpha\cdot{l}=qBvl, \end{equation}
де \({v}\) — швидкість руху перетинки. Відтак для ЕРС індукції в рухомій перетинці отримуємо:
\begin{equation} {\E}_{i}={Blv}. \tag{1.15} \end{equation}
Якщо тепер узяти до уваги, що \( \mathrm{d}v=\mathrm{d}x/\mathrm{d}t \) і \( {l}\,\mathrm{d}x=\mathrm{d}{S}\) — зміна площі контуру за час \(\mathrm{d}t\), то для ЕРС індукції виходить
\begin{equation} {\E}_{i}=\frac{B\,\mathrm{d}S}{\mathrm{d}t}=\frac{\mathrm{d}\Phi}{\mathrm{d}t}, \end{equation}
у відповідності із законом Фарадея.
Наостанку вкажемо, що отримані результати зберігають чинність і при довільній орієнтації та напрямку руху прямого провідника в магнітному полі. При цьому в будь-який момент часу величина ЕРС індукції визначається, як
\begin{equation} {\E}_{i}=B_{\bot}lv_{\bot}, \tag{1.15а} \end{equation}
де \({v_\bot}\) — перпендикулярна до провідника складова його швидкості, а \({B_{\bot}}\) - складова вектора \(\vec{B}\), перпендикулярна до площини руху провідника в цей момент.
Вихрове електричне поле. Коли контур, який знаходиться в стаціонарному магнітному полі \(\vec{B}=\mathrm{const} \), не рухається, то потік крізь нього не змінюється з часом, і електромагнітна індукція не спостерігається. Але щойно магнітне поле починає змінюватись, у контурі з’являється ЕРС та індукційний струм у повній згоді з основним законом ЕМІ (1.1). Пояснити цей факт на основі розглянутого електронного механізму неможливо, бо через хаотичність теплового руху на носії в нерухомому контурі ніяка магнітна сила не діє: \( {{\vec{F}}_{m}} = 0\). Отже, стороння сила, що створює індукційний струм, має чисто електричне походження. А це означає, що в нерухомому контурі вміщеному у змінне магнітне поле з’являється електричне поле \(\vec{E}_{B}\), яке й створює сторонню силу
\begin{equation} \vec{F}=q\vec{E}_{B}, \tag{1.16} \end{equation}
відповідальну за індукційний струм. Такого висновку дійшов Максвелл, який сформулював наступне твердження:
всяке нестаціонарне магнітне поле генерує у просторі відповідне вихрове електричне поле.
На відміну від кулонівського, вихрове поле не створюється зарядами і має замкнені силові лінії. Тому воно не є потенціальним і здатне переміщувати носії струму по замкненому контуру, тобто створювати струм. Робота такого поля віднесена до одиниці перенесеного по контуру заряду — то і є ЕРС індукції. Це дозволяє на основі закону ЕМІ (1.1) і означення ЕРС встановити зв’язок між вихровим електричним полем \(\vec{E}_{B}\) та нестаціонарним магнітним полем \(\vec{B}=\vec{B}{(t)}\), яке його продукує. Згідно з означенням ЕРС,
\begin{equation} {\E}_{i}=\frac{1}{q}\oint\limits_{L}q\vec{E}_{B}\,\mathrm{d}\vec{l} \quad \Rightarrow \quad {\E}_{i}=\oint\limits_{L}\vec{E}_{B}\,\mathrm{d}\vec{l} . \end{equation}
А за основним законом ЕМІ (1.1) та означенням потоку (розділ І, п. 5.2.1) ЕРС індукції можна подати як
\begin{equation} {\E}_{i}=-\frac{\mathrm{d}}{\mathrm{d}t}=\int\limits_{S}\vec{B}\,\mathrm{d}\vec{S}=-\int\limits_{S}\frac{\partial{\vec{B}}}{\partial{t}}\,\mathrm{d}\vec{S}. \end{equation}
(Під інтегралом поставлено знак частинної похідної, позаяк при нерухомому контурі зміна потоку крізь поверхню S зумовлюється тільки явною залежністю індукції поля від часу.)
Таким чином,
\begin{equation} \oint\limits_{L}\vec{E}_{B}\,\mathrm{d}\vec{l}=-\int\limits_{S}\frac{\partial\vec{B}}{\partial{t}}\,\mathrm{d}\vec{S}. \tag{1.17} \end{equation}
Це встановлене Максвеллом рівняння означає, що
циркуляція напруженості вихрового електричного поля по довільному контуру дорівнює взятому з протилежним знаком потокові швидкості зміни індукції магнітного поля через довільну поверхню обмежену цим контуром.
При цьому напрям обходу контуру пов’язаний із векторами \(\mathrm{d}\vec{S}\) правилом правого гвинта, що випливає з правила Ленца. Максвелл також довів, що вектори \(\vec{E}_{B}\) і \(\vec{B}{(t)}\) є завжди взаємно перпендикулярні, тож якщо поле \(\vec{B}{(t)}\) однорідне, то лінії вектора \(\vec{E}_{B}\) лежать у площинах, перпендикулярних до \(\vec{B}{(t)}\) і напрямлені, як на рис. 1.8.
Фарадей трактував електромагнітну індукцію як виникнення струму у замкненому провіднику, вміщеному в магнітне поле. Але за Максвеллом сутність ЕМІ полягає не у виникненні струму в провідниках, а в створенні змінним магнітним полем електричного поля у просторі. А дротяний контур є лишень індикатором цього електричного поля, тому індукційні ефекти мають спостерігатись і в діелектриках та вакуумі. Такий висновок повністю підтверджується дослідом. Ілюстрацією може слугувати бетатрон — один із типів прискорювачів елементарних частинок, у якому електронні пучки у вакуумній камері, вміщеній у змінне магнітне поле, під дією індукованого вихрового електричного поля розганяються майже до швидкості світла.
Таким чином, за Максвеллом співвідношення (1.17) слід трактувати не як вираз ЕРС індукції в дротяному витку, а як рівняння циркуляції вихрового електричного поля по вибраній у просторі замкненій лінії. Але в природі існує ще й кулонівське електричне поле \(\vec{E}_{K}\), створюване зарядами. Тому в загальному випадку електричне поле є суперпозицією полів обох видів, і його напруженість
\begin{equation} \vec{E}=\vec{E}_{K}+\vec{E}_{B}. \end{equation}
При цьому кулонівське поле \(\vec{E}_{K}\) є потенціальним і не дає вкладу в циркуляцію (див. розділ І, п. 5.1). Тож будь-яке електричне поле \(\vec{E}\) задовольняє рівняння
\begin{equation} \oint\limits_{L}\vec{E}\,\mathrm{d}\vec{l}=-\int\limits_{S}\frac{\partial\vec{B}}{\partial{t}}\,\mathrm{d}\vec{S}, \tag{1.17а} \end{equation}
яке є загальним виразом теореми про циркуляцію електричного поля.
Відносність механізмів ЕМІ. Істотна відміна розглянутих умов виникнення індукційного струму в дротяному контурі може навести на думку, що індукційні ефекти пов’язані з двома окремими фізичними явищами. Але насправді це не так, бо однозначно розділити їх неможливо. Це наочно ілюструє наступний позірний дослід. Нехай один спостерігач знаходиться на візку 1 біля нерухомого штабового магніту, другий — на візку 2 із закріпленим дротяним витком, а третій — ще на одному візку 3, як схематично показано на рис. 1.9.
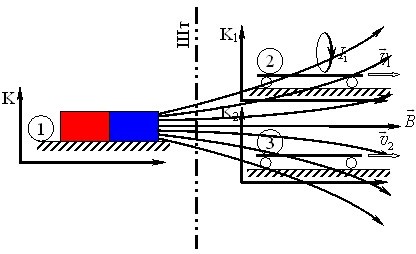
При цьому візки відділені від магніту шторкою Шт із тонованого скла, так що перший спостерігач бачить другого та третього, а вони його — ні. Іншими словами, спостерігачі знаходяться в трьох різних системах відліку \(\text{К}\), \(\text{К}_1\) і \(\text{К}_2\).
Уявімо, що кожен із спостерігачів може реєструвати струм у витку і вимірювати індукцію магнітного поля в місці свого розташування. Тоді, якщо візки 2 і 3 почнуть рухатись із різними швидкостями, всі троє спостерігачів зафіксують появу у витку індукційного струму. Проте вони розійдуться в поясненні причини його виникнення. Перший спостерігач пояснить це дією постійного магнітного поля на носії струму внаслідок руху витка. Другий буде спостерігати струм у нерухомому витку, і пов’яже його з вихровим електричним полем, оскільки виявить, що магнітне поле змінюється з часом. (Ця зміна зумовлена зменшенням величини В у напрямку руху візка з витком.) Третій спостерігач пояснить струм обома причинами, бо для нього й магнітне поле змінюється, й виток рухається. При цьому аргументи кожного спостерігача є неспростовними. Отже, відповідь на запитання, чому виникла ЕМІ і яка її частка зумовлена магнітним, а яка електричним полем, в кожному випадку залежить від умов спостереження, тобто від системи відліку. Це промовисто ілюструє тезу, висловлену ще у Вступі:
носієм електромагнітної взаємодії є єдине електромагнітне поле, поділ якого на електричне та магнітне поля є відносним, залежним від системи відліку.
Іншими словами, електричне та магнітне поля є не різними полями, а різними проявами одного поля, котрі в різній мірі виявляють себе в різних системах відліку. Відповідно, існують встановлені Лоренцом формули перетворень електричного та магнітного полів від однієї до іншої системи відліку, на яких не будемо тут зупинятись. Укажемо лише, що в окремих випадках можна знайти таку систему відліку, в якій існує тільки одне з полів (у розглянутому прикладі це система \(\text{К}_1\), де є лише магнітне поле), а в інших випадках, як, наприклад, для електромагнітних хвиль, таку систему знайти неможливо.
Контрольні запитання
1. У чому полягає відміна між термінами "магнітна індукція" та "електромагнітна індукція"?
2. Що є умовою виникнення в контурі ЕРС індукції та чим визначається її величина?
3. За якої умови в контурі, що рухається в магнітному полі, не буде індукуватись ЕРС? Наведіть приклади.
4. У чому полягає правило Ленца?
5. Поясніть, як визначається напрям індукційного струму в контурі через знак ЕРС індукції за формулою (1.1)?
6. Доведіть, що при будь-якій зміні магнітного потоку крізь дротяний виток унаслідок його руху, магнітне поле буде гальмувати цей рух.
7. Дротяна рамка може обертатися в магнітному полі навколо осі, що лежить у площині рамки і перпендикулярна до напрямку поля. Поясніть, чому рамку легше обертати, коли вона розімкнена.
8. Поясніть, як зміниться індуктивність котушки, щільно намотаної на циліндричне осердя, при її розтяганні в довжину.
9. Кругле дротяне кільце, приєднане через резистор до джерела струму, починають розтягати по діаметру в лінію. Як це вплине на величину струму в резисторі? Чому?
10. Паралельний ланцюжок складається з електричної лампочки та такої самої лампочки послідовно приєднаної до котушки з великою індуктивністю \(L\):
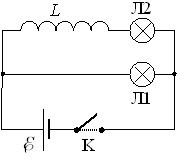
Опишіть та поясніть поведінку лампочок при замиканні та розмиканні ключа К.
11. Поясніть походження сторонніх сил, які є відповідальні за індукційний струм у рухомому та в нерухомому контурі.