physics.zfftt.kpi.ua

Провідниками називаються речовини, що мають у своєму складі багато вільних заряджених частинок, які здатні рухатися по всьому об’єму зразка. Через це вони за впливом на електричне поле дуже відрізняються від діелектриків. Далі розглядаються властивості та поведінка провідників у статичних електричних полях. А саме:

2.1. Електростатичні властивості провідників

Електростатична індукція. Класичними провідниками є метали — речовини, в атомах яких валентні електрони є слабко зв’язані з ядром. Тому при об’єднанні атомів у твердий метал валентні електрони взагалі вивільняються від “своїх” ядер і поводяться подібно до частинок газу в посудині, утворюючи “електронний газ”. Але при внесенні металу в якесь електричне поле \(\vec{E}_{0}\) вільні електрони, окрім хаотичного теплового руху, починають зміщуватися проти напрямку поля під дією сили \(\vec{F}=-e\vec{E}_{0}\). Як наслідок, на поверхні зразка з одного боку з’являється не компенсований негативний заряд –qi, а з протилежного — такий самий позитивний заряд q_i, рис. 2.1.

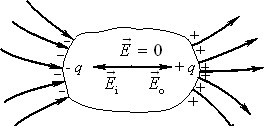
Виникнення макроскопічних зарядів на поверхні незарядженого провідника під дією електричного поля називається електростатичною індукцією, а самі заряди — індукованими зарядами.

Індуковані заряди створюють у провіднику власне поле \(\vec{E}_{i}\), яке напрямлене протилежно до зовнішнього поля \(\vec{E}_{0}\), що нагадує ситуацію в діелектриках. Але, коли в діелектрику на поверхню здатні виходити лише електрони молекул поверхневого шару, то в металі це можуть робити всі вільні електрони, кількість яких є сумірною із кількістю атомів у зразку. Тому можлива величина індукованих зарядів у провіднику по суті є нічим не обмеженою, і їхнє накопичення триває, доки напруженість внутрішнього поля не досягне величини \({{\vec{E}}_{i}}=-{{\vec{E}}_{0}}\), а напруженість результуючого поля — значення \(\vec{E}=\vec{E}_0+\vec{E}_{i}=0\). Відтак переміщення електронів припиняється і в провіднику встановлюється такий рівноважний розподіл зарядів, при якому електричне поле існує тільки на поверхні провідника та поза ним. При цьому поле в кожній точці поверхні спрямоване по нормалі (рис. 2.1), бо інакше вільні заряди продовжували би рухатися по поверхні.

Через кулонівське відштовхування так само поводяться й сторонні (надлишкові) заряди в провіднику: вони виходять на поверхню і розміщуються так, що всередині провідника поля відсутнє, а на поверхні воно напрямлене по нормалі.

Із сказаного випливає загальний висновок про те, що

всередині провідника існування статичного електричного поля є неможливим.

Наостанку зазначимо, що описаний тут розгорнуто в часі процес зникнення поля в провіднику насправді відбувається практично миттєво.

Еквіпотенціальність провідника. Вектор напруженості електричного поля пов’язаний з потенціалом співвідношенням ((3.5), розділ І). Тому відсутність статичного електричного поля в провіднику означає, що

\begin{equation} \mathop{\mathrm{grad}} \varphi = 0 \quad \Rightarrow \quad \varphi = \mathrm{const}, \end{equation}

тобто, всі точки в об’ємі провідника мають однаковий потенціал \(\varphi\). Такий самий потенціал мають і всі точки поверхні. Це теж випливає із співвідношення ((3.5), розділ І), за яким функція потенціалу не може мати розривів, інакше на поверхні було би \(E\to\infty\).

Таким чином,

при рівновазі зарядів усі точки об’єму та поверхні провідника мають однаковий потенціал.

Тому можна говорити про потенціал усього провідника, тоді як в діелектрику — лише про потенціал заданої точки.

Зауваження. Еквіпотенціальність є важливою властивістю провідників, про яку не можна забувати, розв’язуючи задачі. Приміром, при з’єднанні між собою заряджених металевих куль перерозподіл зарядів на них буде тривати до вирівнювання їхніх потенціалів, а не величини зарядів.

Поле біля поверхні провідника. Вістря. Характеристики електричного поля на поверхні провідника визначаються розподілом індукованих і сторонніх зарядів, який задається поверхневою густиною заряду \(\sigma\). Для визначення напруженості \(\vec{E}\) поля провідника оточимо якусь точку на поверхні невеликою замкненою циліндричною оболонкою, як показано на рис. 2.2.

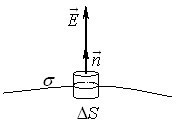
Позаяк поля всередині провідника немає, потік напруженості створюється тільки крізь зовнішню основу циліндрика і наближено дорівнює

\begin{equation} \Delta \Phi\approx E\,\Delta S. \end{equation}

Тому, згідно з теоремою Гаусса (розділ І, п. 5.2.2), можна записати:

\begin{equation} {E}\,\Delta{S}\approx\frac{1}{\varepsilon_0}\sigma\,\Delta{S}, \end{equation}

де \(\sigma\,\Delta{S}=\Delta q\) — заряд ділянки провідника, що охоплена циліндриком. Стягнувши його у вибрану точку на поверхні провідника, отримаємо точний вираз:

\begin{equation} {E}=\frac{\sigma}{\varepsilon_0}, \quad \text{або} \quad \vec{E}=\frac{\sigma}{\varepsilon_0}\vec{n}, \tag{2.1} \end{equation}

де \(\vec{n}\) — орт зовнішньої нормалі до поверхні провідника.

Якщо провідник оточений ізотропним діелектриком з проникністю \(\varepsilon\), то напруженість на поверхні виражається формулою

\begin{equation} \vec{E}=\frac{\sigma}{\varepsilon_0\varepsilon}\vec{n}. \tag{2.1a} \end{equation}

Оскільки напруженість в кожній точці поверхні визначається густиною заряду, з’ясуємо, від чого залежить величина \(\sigma\) в різних точках поверхні. Для цього розглянемо провідник, який складається з двох металевих кульок із радіусами \(R_1\) і \(R_2\), що з’єднані довгою тонкою дротиною (рис. 2.3).

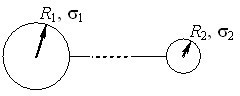
За таких умов кулонівська взаємодія між кульками та заряд, який осідає на дротині, є незначними і можна вважати, що кульки заряджені рівномірно з деякими густинами \(\sigma_1\) і \(\sigma_2\).

Кульки є частинами єдиного провідника і мають однакові потенціали \(\varphi_1=\varphi_2\). Тож згідно з формулою ((2.7), розділ І),

\begin{equation} \frac{q_1}{4\pi\varepsilon_0{R_1}}=\frac{q_2}{4\pi\varepsilon_0{R_2}}. \end{equation}

Підставивши сюди вирази заряду \(q=\sigma S\) і площі поверхні кулі \(S=4\pi R^2\), отримаємо:

\begin{equation} \sigma_1{R_1}=\sigma_2{R_2} \quad \Rightarrow \quad \frac{\sigma_1}{\sigma_2}=\frac{R_2}{R_1}. \tag{2.2} \end{equation}

Таким чином, поверхнева густина зарядів на кульках є обернено пропорційною радіусам, які визначають кривизну \(K=1/R\) їхніх поверхонь.

Для провідника довільної форми співвідношення (2.2), звісно, точно не виконується. Але воно відображає загальну тенденцію:

сторонні заряди у провіднику розподіляються відповідно до форми його поверхні так, що поверхнева густина заряду в кожній точці є тим більшою, чим більша кривизна поверхні в цій точці.

З цієї причини біля вістер і гострих виступів або ребер на поверхні зарядженого провідника електричне поле може виявитися настільки сильним, що викличе електричний пробій у прилеглому шарі діелектрика. Тому в електричному устаткуванні поверхні елементів, що знаходяться під високою напругою, як скажімо ізолятори повітряних ліній передач, роблять гладенькими і закругленими.

Але накопичення зарядів на нерівностях поверхні провідника має і корисні застосування. Одним із прикладів є громовідвід — простий і ефективний пристрій для захисту споруд чи устаткування від ураження блискавкою. Громовідвід являє собою загострений металевий штир, який встановлюється на даху будівлі чи поруч із обладнанням і з’єднується металевою шиною із закопаним у землю листом металу. Громовідвід “працює” так. Перед і під час грози в хмарах і повітрі накопичується багато заряджених частинок — іонів, які й спричинюють блискавки, тобто гігантські іскрові розряди між хмарами та наземними об’єктами. Частина вказаних зарядів осідає на загостреному кінці громовідводу і створює навколо нього сильне неоднорідне поле. Під його дією інші атмосферні заряди притягаються до вістря і далі стікають у землю. Внаслідок цього повітря навколо громовідводу стає збідненим на заряди, і ймовірність потрапляння блискавки в споруду значно зменшується. Тож усупереч поширеній думці, громовідвід не приймає блискавку на себе, хоча таке інколи й трапляється, а “відводить” її від споруди.

На властивостях вістря ґрунтується і робота іонного проектора — надпотужного мікроскопа, який дозволяє спостерігати навіть розташування окремих атомів у металі. Проектор, спрощена схема якого наведена на рис. 2.4, складається із скляного балона та дуже гострої голки з досліджуваного металу, яка є одним з електродів.

Внутрішня поверхня балона вкрита тонким шаром провідної люмінесцентної речовини, що є другим електродом. Балон відкачують і натомість впускають невелику кількість атомарного газу (зазвичай гелію).

Прилад працює так. При подаванні на електроди високої напруги навколо вістря створюється дуже сильне неоднорідне електричне поле, в якому атоми газу поляризуються (див. п. 1.1) і починають рухатися до вістря (див. розділ І, п. 4.2). Радіус кривизни кінчика добре заточеної голки може складати всього 0,1 мкм, а напруженість поля досягати \(\sim 5\cdot 10^7\) В/м. У такому надсильному полі атоми газу біля вістря іонізуються — розділяються на електрони та іони. Електрони падають на голку, а іони відбиваються і рухаються по силових лініях до балона, де вдаряючи в покриття, викликають його свічення, як у телевізійній трубці. Поверхня вістря складається з окремих атомів і є зернистою, тому у місцях виходу атомів напруженість і щільність ліній поля вища, ніж у проміжках між атомами. Відповідно, до таких точок підлітає і відбивається відносно більша кількість іонів, і на поверхні колби утворюється система світлих цяток, положення яких відображає розташування атомів на поверхні вістря.

Із властивостями вістер пов’язані й інші ефекти, зокрема, електризація тертям.

Електростатичне екранування. Якщо провідник є порожнистим, то статичного електричного поля не може бути не лише в самому провіднику, а й у порожнині. Це легко довести. Якщо суцільний провідник зарядити або внести у зовнішнє поле, то заряди розташуються на поверхні, але в об’ємі речовина лишиться електрично нейтральною в кожній точці. Тож, якщо з об’єму видалити частину речовини, утворивши порожнину, то це не призведе до зміни розподілу зарядів на поверхні та появи в порожнині поля. Звідси, до речі, випливає, що у порожнистому провіднику за відсутності зарядів у порожнині сторонні заряди розміщуються тільки на зовнішній поверхні.

Таким чином, ніякі заряди, розміщені на поверхні провідної оболонки чи поза нею, не можуть створити електричного поля всередині. Тому провідна оболонка забезпечує повний захист (екранування) всього, що знаходиться всередині, від впливу будь-яких зовнішніх електростатичних полів. Це широко використовується на практиці. Зокрема, в електроніці задля захисту чутливих елементів схеми їх вміщують у закриті металеві корпуси, а проводи — в металеву обплітку.

Провідна оболонка “працює” і в зворотному напрямку. Наприклад, якщо в порожнині розмістити точковий заряд \(q\) (рис. 2.5а), то його електричне поле індукує на поверхнях провідника заряди \({q}_i^{+}={q}\) і \({q}_i^{-}=-{q}\), які компенсують поле в самому провіднику.

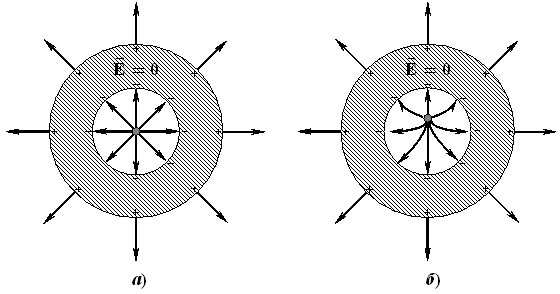
Тому поле назовні провідника буде визначатися тільки величиною та розподілом заряду \({q}_i^{+}\) на зовнішній поверхні, причому зміна поля всередині внаслідок зміщення заряду \(q\) і перерозподіл заряду \({q}_i^{-}\) на внутрішній поверхні порожнини ніяк не вплине на зовнішнє поле (рис. 2.5б). Якщо зовнішню поверхню оболонки заземлити, то ніякого поля назовні взагалі не буде. Таким чином,

замкнена провідна оболонка поділяє весь простір на дві електрично незалежні області.

Фундаментальна причина цього полягає в тому, що у випадку провідної оболонки на шляху із середини назовні обов’язково трапиться область (сама оболонка), в якій немає електричного поля — “передавача” взаємодії між зарядами, розташованими всередині та назовні оболонки.

2.2. Електрична ємність. Конденсатори

Ємність відокремленого провідника. Напруженість електричного поля на поверхні зарядженого провідника в кожній точці визначається густиною заряду (формула (2.1а)) і має різну величину та напрям. Натомість потенціал провідника є скрізь однаковий, тож у кожній точці визначається не густиною заряду в цій точці, а зарядом усього провідника. При цьому дослід свідчить, що потенціал провідника є прямо пропорційним до його заряду:

\begin{equation} \varphi=\frac{1}{C}{q} \quad \text{або} \quad {q=C\varphi}. \end{equation}

Величина

\begin{equation} C=\frac{q}{\varphi } \tag{2.3} \end{equation}

називається електричною ємністю провідника, електроємністю, або просто ємністю.

Одиницею ємності є фарад (Ф). Згідно з (2.3) можна сказати, що

фарад дорівнює ємності провідника, котрому для збільшення потенціалу на \(1\ \text{В}\) треба надати заряд \(1\ \text{Кл}\). Отже, \(1\ \text{Ф} = 1\ \text{Кл/В}\).

Ємність не залежить ані від заряду, ані від потенціалу і для відокремленого провідника визначається тільки його геометричною конфігурацією та властивостями діелектричного середовища, в якому він знаходиться.

Примітка. Відокремленим називається провідник, який є єдиним у всьому просторі. Звичайно, це ідеалізація. Реально провідник можна вважати відокремленим, якщо вплив на нього з боку інших тіл є неістотним.

Задля ілюстрації визначимо ємність провідної кулі радіуса \(R\), що знаходиться в безмежному однорідному ізотропному діелектрику з проникністю \(\varepsilon\). За таких умов заряд розподіляється по поверхні кулі рівномірно, і її електричне поле збігається з полем точкового заряду (1.22). Тож потенціал

\begin{equation} \varphi=\frac{q}{4\pi\varepsilon_0\varepsilon{R}}. \end{equation}

Тоді за означенням (2.3) ємність кулі

\begin{equation} {C}=4\pi\varepsilon_0\varepsilon{R}, \tag{2.4} \end{equation}

як і сказано, визначається тільки геометрією та властивостями середовища, в якому вона знаходиться.

Конденсатори, ємність конденсатора. Електрична ємність як фізична властивість провідників має важливі застосування в електротехніці та електроніці. Але окремі провідники в цьому сенсі мають принципові вади. По-перше, ємність окремо взятого провідника є дуже малою. Наприклад, згідно з формулою (2.4), ємність провідної кулі з розмірами Землі (\(R\approx 6400\) км) у вакуумі складає всього біля \(7\cdot 10^{-4}\) Ф. А по-друге, в реальних умовах ємність окремого провідника не має визначеної величини, бо істотно залежить від оточення. Справді, якщо заряджена металева куля є відокремленою (рис. 2.6а), то її заряд \(q\) розподілений рівномірно, і вона має відповідний потенціал \(\varphi_0\) та ємність \(C_0=q/\varphi_0\). Але коли наблизити до кулі якесь тіло, наприклад, незаряджений кусок металу, то під дією поля кулі на його поверхні з’являться індуковані заряди \({q}_i^{-}\) і \({q}_i^{+}\), як показано на рис. 2.6б. Це призведе до зміщення зарядів кулі ближче до металу, бо індуковані заряди \({q}_i^{-}\) будуть притягати заряди кулі сильніше, ніж заряди \({q}_i^{+}\) — відштовхувати їх. Такий перерозподіл заряду кулі \(q\) змінить її потенціал \(\varphi\), тож і ємність \(C=q/\varphi\). При цьому, як показує глибший аналіз, присутність інших тіл завжди зменшує потенціал і збільшує ємність даного тіла. Крім того, ємність буде змінюватися при будь-якій зміні взаємного розташування кулі та сусіднього тіла.

Указана нестабільність може негативно впливати на роботу апаратури і вимагає спеціального захисту (екранування) чутливих вузлів електронних пристроїв. Але оточення практично не впливає на системи провідників, які називаються конденсаторами. Найпростіший і найуживаніший плоский конденсатор складається з двох паралельних металевих пластин — обкладок, простір між якими заповнений діелектриком, зокрема, повітрям (рис. 2.7).

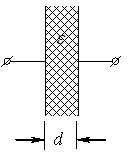
Обкладки розміщують близько одна від одної, тому електричне поле в конденсаторі, за винятком країв пластин, є однорідним, як у випадку нескінченних площин. Спотворення поля на краях пластин (так званий “крайовий ефект”) є незначними, тому в теорії ними нехтують і розглядають конденсатор як ідеальний.

Нечутливість конденсаторів до впливу зовнішніх тіл і полів пояснюється ефектом електростатичного екранування. Це неважко зрозуміти. При підключенні конденсатора до полюсів джерела напруги частина електронів з однієї обкладки переміщується на іншу, й на них з’являться різнойменні заряди однакової величини \(q\) і \(-q\) та відповідна різниця потенціалів \(U=\varphi_+-\varphi_-\).

(Принагідно зазначимо, що величина \(q > 0\) називається зарядом, а \(U\) — напругою конденсатора.)

Заряди в конденсаторі через кулонівське притягання розміщуються на внутрішніх поверхнях пластин. Тож створюване між ними електричне поле є відокремлене від зовнішнього простору самими пластинами, бо всередині них електричного поля не може бути (див. п. 2.1, електростатичне екранування). Тому поле конденсатора не може вийти за його межі, а зовнішнє поле не може потрапити всередину. З цієї причини зовнішні тіла та поля не можуть впливати на конденсатор, а він — на них.

Іншою цінною властивістю конденсаторів є те, що вони при невеликих розмірах можуть мати велику ємність і акумулювати значну кількість електричної енергії. Тому конденсатори мають практичне застосування як накопичувачі електричної енергії.

Типи конденсаторів. Електрична ємність конденсатора визначається відношенням його заряду до напруги:

\begin{equation} {C}=\frac{q}{U}. \tag{2.5} \end{equation}

Тому, аби визначити ємність конденсатора, треба за допомогою відомих методів розрахувати напругу \(U\) на конденсаторі при заданій величині заряду \(q\) і скористатися формулою (2.5). Проілюструємо це на прикладі ідеального плоского конденсатора з площею пластин \(S\), відстанню між ними \(d\) і проникністю діелектрика \(\varepsilon\). Напруженість поля в такому конденсаторі визначається формулою (1.23):

\begin{equation} {E}=\frac{\sigma}{\varepsilon_0\varepsilon}=\frac{q}{\varepsilon_0\varepsilon{S}}. \end{equation}

Це поле є однорідним, тому відповідно до п. 3.1, розділ І, напруга на конденсаторі

\begin{equation} {U}=Ed=\frac{qd}{\varepsilon_0\varepsilon{S}}, \end{equation}

і, згідно з означенням (3.5), ємність плоского конденсатора визначається формулою:

\begin{equation} {C}=\frac{\varepsilon_0\varepsilon{S}}{d}. \tag{2.6} \end{equation}

Отже, чим більша проникність діелектрика та площа обкладок і менша відстань між ними, тим більша ємність конденсатора. У цьому зв’язку слід зазначити, що сучасні технології дозволяють виготовляти конденсатори ємністю \(\sim 1\) Ф розмірами з монету.

На практиці використовують переважно плоскі конденсатори. Але в теорії розглядають ще два типи простих конденсаторів — сферичні та циліндричні. Обкладками сферичного конденсатора є дві концентричні металеві оболонки з якимись радіусами \(R_1\) і \(R_2\) (рис. 2.8а), а циліндричного — коаксіальні циліндри з радіусами \(R_1\) і \(R_2\) і довжиною \(l\) (рис. 2.8б).

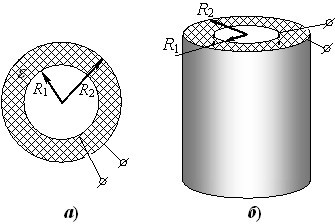
Формули ємності таких конденсаторів розраховуються так само, як для плоского, і мають вигляд:

\begin{equation} C_{\text{сфер}} = \frac{4\pi\varepsilon_0\varepsilon{R_1}{R_2}}{R_2-R_1}, \tag{2.7} \end{equation} \begin{equation} C_{\text{цил}}=\frac{2\pi\varepsilon_0\varepsilon{l}}{\ln(R_2/R_1)}. \tag{2.8} \end{equation}

З’єднання конденсаторів. В електричних колах окрім поодиноких конденсаторів використовують з’єднання (батареї) декількох певним чином сполучених між собою конденсаторів. Виведемо формули ємності найпростіших паралельного та послідовного з’єднань, виходячи з того, що ємність з’єднання, як і одного конденсатора, визначається формулою (2.5) через сумарний заряд батареї та подану на неї напругу.

Паралельне з’єднання. При паралельному з’єднанні всі конденсатори безпосередньо сполучаються між собою, як показано на рис. 2.9а.

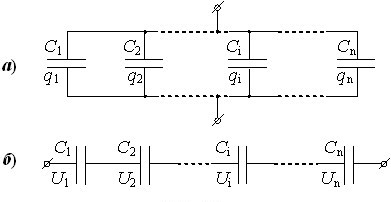
Усі з’єднані обкладки утворюють єдиний провідник і за будь-яких умов мають однаковий потенціал. Тому, якщо подати на батарею напругу \(U\), то напруги \(U_i\) всіх конденсаторів будуть такими самими: \(U_i=U\). Також є очевидним, що заряд батареї дорівнює сумі зарядів усіх з’єднаних конденсаторів: \({q}=\sum\limits{q_i}\). Отже, ємність з’єднання

\begin{equation} \begin{aligned} &C_{\text{пар}}=\frac{q}{U}=\frac{\sum\limits{q_i}}{U}=\sum\limits_i{\frac{q_i}{U_i}}\quad\Rightarrow{}\\ &\quad{}\Rightarrow \quad C_{\text{пар}} = \sum\limits{C_i}. \end{aligned} \tag{2.9} \end{equation}

Таким чином,

при паралельному сполученні конденсаторів ємність з’єднання дорівнює сумі ємностей всіх сполучених конденсаторів.

Зокрема, при паралельному з’єднанні \(n\) конденсаторів однакової ємності \(C\) загальна ємність

\begin{equation} C_{\text{пар}} = nC. \tag{2.9а} \end{equation}

Послідовне з’єднання. В цьому випадку конденсатори утворюють ланцюг, у кожній ланці котрого безпосередньо з’єднуються тільки два конденсатори, як показано на рис.2.9б. При такому сполученні питання про ємність з’єднання не є таким очевидним, як при паралельному, тому проаналізуємо сам процес заряджання послідовного ланцюга конденсаторів. У момент приєднання до джерела заряди \(q\) і \(-q\) подаються тільки на зовнішні пластини першого і останнього конденсаторів \(C_1\) і \(C_n\). Але під дією поля, що виникає, тієї ж миті на всіх з’єднаних між собою парах пластин з’являються індуковані заряди однакової величини \(q_i\) і \(-q_i\), і всі конденсатори виявляються зарядженими. При цьому напруга на ланцюгу дорівнює сумі напруг на окремих конденсаторах: \(U=\sum\limits U_i\), а заряди всіх конденсаторів \(q_i\) однакові і дорівнюють заряду всього ланцюга: \(q_i=q\). Це легко зрозуміти на прикладі ідеальних плоских конденсаторів. У момент підключення до джерела між крайніми пластинами ланцюга виникає однорідне електричне поле \(\vec{E}\). Але всередині з’єднаних пластин поля бути не може, тому індуковані заряди на з’єднаних пластинах мають створювати внутрішнє поле \(\vec{E}_i=-\vec{E}\). А для цього величина індукованих зарядів \(q_i\) повинна дорівнювати величин поданих на ланцюг сторонніх зарядів \(q\).

Таким чином, ємність послідовного з’єднання конденсаторів

\begin{equation} C_{\text{пос}} = \frac{q}{U}=\frac{q}{\sum\limits{U_i}}, \end{equation}

де

\begin{equation} {U_i}=\frac{q_i}{C_i}=\frac{q}{C_i}. \end{equation}

Після такої підстановки виходить наступна формула для розрахунку ємності послідовного з’єднання конденсаторів:

\begin{equation} \frac{1}{C_{\text{пос}}}=\sum\limits\frac{1}{C_i}. \tag{2.10} \end{equation}

Отже,

при послідовному з’єднанні конденсаторів додаються не ємності, а їхні обернені величини.

Із загального виразу (2.10) випливають прості формули прямого розрахунку ємності послідовного з’єднання двох конденсаторів з ємностями \(C_1\) і \(C_2\):

\begin{equation} C_{\text{пос}} = \frac{C_1 C_2}{C_1+C_2} \tag{2.10а} \end{equation}

та \(n\) конденсаторів однакової ємності \(C\):

\begin{equation} C_{\text{пос}} = \frac{C}{n}. \tag{2.10б} \end{equation}

Формули (2.9) і (2.10) дозволяють розраховувати й більш складні комбіновані з’єднання, які можна розчленувати на окремі паралельні та послідовні ділянки.

2.3. Енергія електричного поля

Енергія та її трансформації є універсальними чинниками, що визначають стан будь-якої фізичної системи і процеси в ній. Згадаймо хоча би про механічну енергію та її роль в механічних процесах. Електростатична система, тобто сукупність заряджених частинок або тіл, має відповідний запас електричної енергії. Її походження неважко збагнути. Сили кулонівської взаємодії завжди намагаються звести докупи і нейтралізувати різнойменні заряди та розкидати на нескінченність однойменні. Тому при створенні заданої конфігурації зарядів треба виконувати роботу по подоланню кулонівських сил, тим самим надаючи системі відповідного запасу електростатичної енергії. Позаяк кулонівські сили є консервативними, ця енергія є різновидом потенціальної енергії і, як усяка енергія, може переходити в інші форми. Наприклад, в кінетичну, якщо зарядам системи дозволити рухатися під дією сил кулонівської взаємодії між ними.

Енергія взаємодії системи точкових зарядів. Розглянемо гіпотетичний процес утворення системи з трьох точкових зарядів шляхом перенесення їх з нескінченності, де потенціал поля \(\varphi=0\), в задані точки 1, 2, 3 (рис. 2.10):

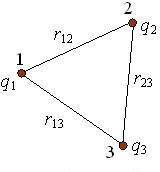
Переміщення першого заряду \(q_1\) в точку 1 відбувається вільно, але наступний заряд \(q_2\) вже рухається в полі заряду \(q_1\) і для його переміщення в точку 2 треба виконати деяку роботу \(A'\) проти сил поля. Ця робота дорівнює взятій з протилежним знаком роботі \(A\) самого поля і визначає потенціальну енергію \(W_{12}\) заряду \(q_2\) в полі заряду \(q_1\). Тож, відповідно до формул ((2.10а) і (2.7), розділ І),

\begin{equation} {W}_{12}=k\frac{q_1 q_2}{r_{12}}. \tag{2.11} \end{equation}

Але, якщо спочатку розташувати заряд \(q_2\) в точці 2, а потім перенести в точку 1 заряд \(q_1\), то нічого не зміниться крім того, що вираз (2.11) буде трактуватись як потенціальна енергію заряду \(q_1\) в полі заряду \(q_2\). Тому величина \(W_{12}\) є “спільним надбанням” обох зарядів і визначає енергію їхньої електричної взаємодії.

При включенні в систему заряду \(q_3\) додасться ще й енергія його взаємодії з першим та другим зарядами, котра виражається аналогічно. Отже, енергія системи з трьох зарядів

\begin{equation} \begin{aligned} &{W}=W_{21}+W_{31}+W_{32}={}\\ &\quad{}=k\frac{q_2 q_1}{r_{12}}+k\frac{q_3 q_1}{r_{13}}+k\frac{q_3 q_2}{r_{23}}. \end{aligned} \end{equation}

Позаяк у кожній парі заряди є рівноправними партнерами взаємодії, перепишемо цей вираз симетрично, як

\begin{equation} \begin{aligned} &{W}=\frac{1}{2}\left(q_1{k}\frac{q_2}{r_{12}}+q_2{k}\frac{q_1}{r_{12}}+q_2{k}\frac{q_3}{r_{23}}+{}\right.\\ &\qquad\left.{}+q_3{k}\frac{q_2}{r_{23}}+q_3{k\frac{q_1}{r_{13}}}+q_1{k}\frac{q_3}{r{13}}\right), \end{aligned} \end{equation}

або, після перегрупування,

\begin{equation} \begin{aligned} &{W}=\frac{1}{2}\left( q_1\left({k}\frac{q_2}{r_{12}}+{k}\frac{q_3}{r_{13}}\right)+{}\right.\\ &\qquad{}\left.{} +q_2\left({k}\frac{q_1}{r_{12}}+{k}\frac{q_3}{r_{23}}\right)+{}\right.\\ &\qquad{}\left.{}+q_3\left({k}\frac{q_1}{r_{13}}+{k}\frac{q_2}{r_{23}}\right) \right). \end{aligned} \end{equation}

Згідно з формулою ((2.7а), розділ І), вираз у кожній малій дужці визначає потенціал поля, що створюється в місці розташування відповідного заряду двома іншими.

Зрозуміло, що при додаванні наступних зарядів нічого принципово не зміниться. Тому електростатична енергія взаємодії довільної системи точкових зарядів виражається загальною формулою

\begin{equation} {W}=\frac{1}{2}\sum\limits{q_i \varphi_i}, \tag{2.12} \end{equation}

де \(\varphi_i\) — потенціали полів, що створюються в місцях розташування зарядів \(q_i\) всіма іншими зарядами системи.

Енергія зарядженого діелектрика та провідника. В протяжних тілах заряд розподіляється в просторі неперервно. Тому для підрахунку електростатичної енергії в зарядженому діелектрику увесь заряд треба подумки розчленувати на елементарні точкові порції \(\mathrm{d}q\) і замінити у виразі (2.12) дискретне додавання на інтегрування по всій зарядженій області:

\begin{equation} {W}=\frac{1}{2}\int\limits{\varphi\,\mathrm{d}q}. \tag{2.13} \end{equation}

Якщо заряд розподілений по об’єму з густиною \(\rho (\vec{r}) \), то \(\mathrm{d}q=\rho\,\mathrm{d}V\), і

\begin{equation} {W}=\frac{1}{2}\int\limits_V{\varphi\rho}\,\mathrm{d}{V}. \tag{2.14} \end{equation}

При розподілі заряду по поверхні з густиною \(\sigma(\vec{r}) \) або по тонкому стержню з лінійною густиною \(\lambda(\vec{r}) \) електростатична енергія виражається, відповідно, як

\begin{equation} {W}=\frac{1}{2}\int\limits_S{\varphi\sigma}\,\mathrm{d}{S} \tag{2.14а} \end{equation}

і

\begin{equation} {W}=\frac{1}{2}\int\limits_{L}\varphi\lambda\,\mathrm{d}{l}. \tag{2.14б} \end{equation}

Провідники в електростатичному стані є еквіпотенціальними. Тому у виразі (2.13) \(\varphi=\text{const}\), і електростатична енергія провідника визначається формулою

\begin{equation} {W}=\frac{1}{2}q\varphi. \tag{2.15} \end{equation}

Стосовно отриманих результатів необхідно зробити важливе зауваження. Хоча вирази (2.12) і (2.13) —(2.15) за загальним змістом видаються ідентичними, між ними є принципова відміна. Це стає зрозумілим, якщо згадати, що точкові заряди є абстракцією. Реально “точкові” заряди є частинками скінченних розмірів, тож заряди в них теж є рознесені в просторі і взаємодіють між собою. З цією взаємодією пов’язана відповідна власна електростатична енергія зарядів, не відображена у формулі (2.12). Напроти, формули (2.13) —(2.15) враховують взаємодію всіх зарядів тіла і визначають власну електростатичну енергію. А ось в електростатичну енергію системи тіл окрім власної енергії \(W_{\text{вл}}=\sum\limits{W_i}\), яка дорівнює сумі енергій всіх тіл, входить іще й енергія взаємодії \(W_{\text{вз}}\) кожного з кожним:

\begin{equation} W=W_{\text{вл}}+W_{\text{вз}}. \end{equation}

Таким чином, електростатична енергія довільної системи не дорівнює сумі енергій окремих її частин (тіл), тобто не є адитивною величиною. Тому в загальному випадку при підрахунках не можна забувати про енергію електростатичної взаємодії \(W_{\text{вз}}\), яка визначається конфігурацією системи — взаємним розташуванням заряджених тіл. Але для точкових заряджених тіл через їхні дуже малі розміри зміна взаємного розташування зарядів в них практично не впливає на власну електростатичну енергію, тож \(W_{\text{вл}}=\text{const}\). Тому власна енергія системи точкових зарядів ніяк не впливає на процеси в ній і може бути відкинута. Отже, хоча формула (2.12) принципово є неповною, фактично вона дає всю необхідну інформацію про електростатичну енергію системи точкових зарядів.

Енергія зарядженого конденсатора. Ця енергія дорівнює роботі по заряджанню конденсатора. Для її підрахунку будемо вважати, що конденсатор заряджається шляхом перенесення нескінченно малих порцій заряду з однієї обкладки на іншу (як це й відбувається в дійсності). Тоді, якщо при напрузі на конденсаторі \(u\) перенести з однієї обкладки на іншу порцію заряду \(\mathrm{d}q\), виконавши роботу \(\delta A'\), то енергія конденсатора збільшиться на величину виконаної роботи:

\begin{equation} \mathrm{d}W=\delta A'=u\,\mathrm{d}q. \end{equation}

Виразивши за формулою (2.5) перенесений заряд через ємність конденсатора та приріст напруги як \(\mathrm{d}q=C\,\mathrm{d}u\), і проінтегрувавши вираз \(\mathrm{d}W\) у границях від \(0\) до кінцевої напруги \(U\), одержимо наступну формулу енергії зарядженого конденсатора:

\begin{equation} {W}=\frac{CU^2}{2}, \tag{2.16} \end{equation}

або рівнозначні формули

\begin{equation} {W}=\frac{q^2}{2C} \tag{2.16а} \end{equation}

і

\begin{equation} {W}=\frac{1}{2}q{U}. \tag{2.16б} \end{equation}

Енергія електричного поля. Всі отримані вище формули виражають електростатичну енергію через характеристики тіл — заряди, потенціали та ємності. Але її можна подати й інакше. Якщо для плоского конденсатора у формулі (2.16) ємність виразити за формулою (2.6), а напругу — за формулою ((3.6а), розділ І), то вийде

\begin{equation} {W}=\frac{\varepsilon_0\varepsilon{E^2}}{2}{V}, \tag{2.17} \end{equation}

де \(Sd=V\) — об’єм області простору між пластинами.

В об’ємі \(V\) зосереджене все поле конденсатора, тож формула (2.17) виражає енергію конденсатора вже не через характеристики пластин, а тільки через характеристики електричного поля між ними. Це наводить на думку, що саме в полі, а не на пластинах, зосереджена електростатична енергія конденсатора. Якщо так, то величина

\begin{equation} {w_e}=\frac{\varepsilon_{0}\varepsilon{E^2}}{2} \tag{2.18} \end{equation}

визначає об’ємну густину енергії електричного поля в ізотропному середовищі, тобто енергію, зосереджену в одиниці об’єму поля.

Слід зауважити, що в електростатиці таке припущення неможливо ані довести, ані спростувати. Але в електродинаміці, де досліджуються явища в нестаціонарних (змінних) полях, теорія й експеримент однозначно доводять, що

електричне поле має енергію, яка в ізотропному середовищі розподілена з об’ємною густиною (2.18).

Об’ємну густину енергії електричного поля можна виразити ще двома рівнозначними формулами, врахувавши зв’язок між векторами \(\vec{E}\) і \(\vec{D}\), а саме:

\begin{equation} {w_{e}}=\frac{D^2}{2\varepsilon_0\varepsilon} \tag{2.18а} \end{equation}

і

\begin{equation} {w_{e}}=\frac{ED}{2}. \tag{2.18б} \end{equation}

У неоднорідному полі об’ємна густина характеризує концентрацію енергії в кожній точці і визначається як

\begin{equation} {w}=\frac{\mathrm{d}W}{\mathrm{d}V}. \tag{2.19} \end{equation}

У цьому випадку енергія поля в заданій області \(V\) є інтегралом (сумою) енергій \(\mathrm{d}W=w\mathrm{V}\) в усіх елементарних областях \(\mathrm{d}V\):

\begin{equation} {W}=\int\limits_{V}w\,\mathrm{d}{V}. \end{equation}

Отже, згідно з формулами (2.18) маємо наступні вирази для обчислення енергії електричного поля в заданому об’ємі:

\begin{equation} {W}=\int\limits_{V}\frac{\varepsilon_0\varepsilon{E^2}}{2}\mathrm{d}{V}; \tag{2.20} \end{equation} \begin{equation} {W}=\int\limits_{V}\frac{D^2}{2\varepsilon_0\varepsilon}\mathrm{d}{V}; \tag{2.20а} \end{equation} \begin{equation} {W}=\int\limits_{V}\frac{ED}{2}\mathrm{d}{V}. \tag{2.20б} \end{equation}

На завершення зазначимо, що всі результати, отримані тут для статичних полів, зберігають чинність і для залежних від часу (нестаціонарних) полів.