ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ
І. ЕЛЕКТРИЧНЕ ПОЛЕ У ВАКУУМІ
5. Циркуляція і потік електричного поля
Окрім напруженості \(\vec{E}\), що визначає електричне поле локально (в кожній точці), існують ще й інтегральні величини, котрі характеризують його не в точці, а на заданій лінії або поверхні. Ці величини називаються “циркуляцією” та “потоком” поля і розглядаються в наступних питаннях:
5.1. Циркуляція потенціального електричного поля
5.2. Електростатична теорема Гаусса
5.1. Циркуляція потенціального електричного поля
Співвідношення (3.5) дозволяє розраховувати напруженість не прямо, а через потенціал. Це може спростити задачу, бо визначати скалярні інтеграли (2.9) зазвичай легше, ніж векторні (1.7). Але такий шлях є прийнятним тільки для потенціальних полів. Тому треба мати формальний (математичний) критерій, який дозволяє розрізняти потенціальні та непотенціальні поля.
Для встановлення такого критерію розглянемо роботу \(A_{12}\) кулонівського поля при переміщенні заряду з точки 1 у точку 2 по двох різних траєкторіях I і II, рис. 5.1.
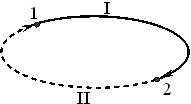
Позаяк таке поле є потенціальним, то за означенням ці роботи однакові:
\begin{equation} {A_{12}^{\mathrm{(I)}}}={A_{12}^{\mathrm{(II)}}}. \end{equation}
Тому, якщо заряд перемістити з точки 1 в точку 2 по шляху (I) і потім повертати назад по шляху (II), то на зворотньому шляху робота \( A_{21}^{( \text{II} )} \) буде відрізнятися від величини \( A_{12}^{( \text{I} )} \) тільки знаком. Отже, на всьому замкненому шляху робота поля
\begin{equation} {A_0}=A_{12}^{\mathrm{(I)}}+A_{21}^{\mathrm{(II)}}={0}. \tag{5.1} \end{equation}
Із механіки відомо, що робота сили \( \vec{F} \) на заданій замкненій траєкторії \(L\) виражається криволінійним інтегралом по цій траєкторії від скалярного добутку сили на переміщення:
\begin{equation} {A_0}=\oint\limits_L\vec{F}\,\mathrm{d}\vec{l}. \end{equation}
В електричному полі \(\vec{F}=q\vec{E}\), отже, враховуючи вираз (5.1), для потенціального (кулонівського) електричного поля маємо:
\begin{equation} \oint\limits_L\vec{E}\,\mathrm{d}\vec{l}=\oint\limits_L{E_l}\,\mathrm{d}{l}={0}, \tag{5.2} \end{equation}
де \({E_l}\) — проекція напруженості на напрям обходу траєкторії інтегрування.
Інтеграл
\begin{equation} {C}=\oint\limits_L\vec{E}\,\mathrm{d}\vec{l}=\oint\limits_L{E_l}\,\mathrm{d}{l} \tag{5.2а} \end{equation}
має спеціальну назву — циркуляція. Тобто,
криволінійний інтеграл від скалярного добутку вектора напруженості поля на вектор елементарного переміщення вздовж заданого замкненого контуру називається циркуляцією поля по цьому контуру.
Можна сказати, що циркуляція дорівнює роботі поля при переміщенні по замкненому контуру одиничного заряду.
Поняття циркуляції і рівність (5.2) дозволяють сформулювати наступний інтегральний критерій потенціальності поля:
умовою потенціальності поля є нульова величина його циркуляції по будь-якому замкненому контуру, що повністю розташований у полі.
Саме таким є кулонівське поле — електричне поле, що створюється зарядженими частинками.
Зауважимо також, що, позаяк циркуляція по суті є питомою роботою поля на замкненому контурі, вона може мати той чи інший знак залежно від обраного напрямку обходу контуру при інтегруванні.
5.2. Електростатична теорема Гаусса
Зміст, властивості та значення другої з інтегральних характеристик електричного поля — потоку розглядаються далі в наступних питаннях:
5.2.1. Потік електричного поля
5.2.1. Потік електричного поля
Поняття та означення потоку походить із механіки суцільних середовищ.
Потік рідини. У повсякденному вжитку слово “потік” означає характерний рух рідини чи газу, скажімо, гірський чи повітряний потік. Але в науковій і технічній лексиці цим терміном позначають також кількісну міру різних процесів переносу: перенесення рідини, газу, чи сипучої речовини при транспортуванні трубопроводами, тощо.
Нехай в якійсь області простору переноситься речовина, приміром, тече вода в річці. Кількісна міра перенесення води через вибрану на її шляху задану поверхню називається потоком крізь цю поверхню і визначається як об’єм води, що проходить крізь неї за одиницю часу (\(\text{м}^3\!/\text{c}\)):
\begin{equation} \Phi=\frac{\mathrm{d}V}{\mathrm{d}t}. \tag{5.3} \end{equation}
Зрозуміло, що потік рідини залежить від швидкості течії та характеристик поверхні. Аби з’ясувати, як саме, виділимо на вибраній поверхні \(S\) (рис. 5.2а) довільну елементарну площинку \(\mathrm{d}S\) і покажемо орт (одиничний вектор) нормалі до неї \(\vec{n}\) та вектор швидкості течії \(\vec{v}\) в цьому місці.
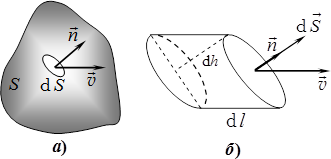
Відтак побудуємо на площинці \(\mathrm{d}S\) як на основі косий циліндрик із твірною \(\mathrm{d}{l}\) та об’ємом \(\mathrm{d}V=\mathrm{d}S\cdot\mathrm{d}h=\mathrm{d}S\cdot\mathrm{d}l\cos\alpha \), як показано на рис. 5.2б. Очевидно, що вся рідина в об’ємі циліндрика проходить крізь площинку \(\mathrm{d}S\) за час \(\mathrm{d}t={\mathrm{d}l}/v \). Тому, згідно з (5.3), елементарний потік \(\mathrm{d}\Phi\) крізь площинку \(\mathrm{d}S\) дорівнює
\begin{equation} \mathrm{d}\Phi=v\,\mathrm{d}S\cos\alpha . \tag{5.4} \end{equation}
Потік \(\Phi\) крізь поверхню \(S\) складається з елементарних потоків \(\mathrm{d}\Phi\) через усі її ділянки: \(\Phi=\int\limits_S\mathrm{d}{\Phi}\), отже
\begin{equation} \Phi=\int\limits_S{v}\,\mathrm{d}S\cos\alpha , \tag{5.4а} \end{equation}
де індекс \(S\) показує, що інтегрування проводиться по всій поверхні \(S\).
Як бачимо, потік крізь задану поверхню визначається як її величиною, так і орієнтацією її ділянок відносно напрямку перенесення рідини. Тому в теорії елементарну площинку трактують як вектор \(\mathrm{d}\vec{S}=\vec{n}\,\mathrm{d}{S}\). Тим самим вектор \(\mathrm{d}\vec{S}\) відображає як величину, так і орієнтацію площинки в просторі. Це дозволяє лаконічно записати вирази (5.4) і (5.4а) у векторній формі:
\begin{equation} \mathrm{d}\Phi=\vec{v}\,\mathrm{d}\vec{S} \end{equation}
і
\begin{equation} \Phi=\int\limits_S\vec{v}\,\mathrm{d}\vec{S}. \tag{5.5} \end{equation}
Швидкість руху частинок \(\vec{v}\) є скрізь визначеною і такою, що закономірно змінюється від точки до точки, тобто є заданою функцією координат: \(\vec{v}=\vec{v}(\vec{r}) \). У математиці векторну функцію координат, визначену в заданій області простору, називають полем вектора, або векторним полем. Отже, мовою математики об’єм рідини, що проходить крізь задану поверхню за одиницю часу, дорівнює потокові поля вектора швидкості течії крізь цю поверхню, або коротко — потокові вектора \(\vec{v}\).
Потік електричного поля. Поняття потоку і означення (5.4) і (5.4а) або (5.5) зберігають чинність та корисність і для векторних полів будь-якої іншої природи. Зокрема,
інтеграл по заданій поверхні \(S\) від скалярного добутку вектора напруженості електричного поля \(\vec{E}\) на вектор елемента поверхні \(\mathrm{d}\vec{S}\) називається потоком напруженості (або потоком поля) крізь цю поверхню:
\begin{equation} \Phi=\int\limits_{S}\vec{E}\,\mathrm{d}\vec{S}. \tag{5.6} \end{equation}
Підінтегральний вираз \(\mathrm{d}\Phi =\vec{E}\,\mathrm{d}\vec{S}\), що визначає потік напруженості крізь довільну елементарну ділянку \(\mathrm{d}S\) поверхні \(S\), можна записати й інакше, розкривши скалярний добуток:
\begin{equation} \begin{aligned} &\mathrm{d}\Phi =\vec{E}\,\mathrm{d}\vec{S}=E\,\mathrm{d}S\cos \alpha ={}\\ &\quad{}={{E}_{n}}\,\mathrm{d}S=E\,\mathrm{d}{{S}_{\bot }}, \end{aligned} \tag{5.7} \end{equation}
де \(E\) і \(\mathrm{d}S\) — модулі векторів \(\vec{E}\) і \(\mathrm{d}\vec{S}\), \(E_n\) — проекція \(\vec{E}\) на нормаль до поверхні, і \(\mathrm{d}{{S}_{\bot }}\) — проекція площинки \(\mathrm{d}\vec{S}\) на площину перпендикулярну до напрямку поля (рис. 5.3).
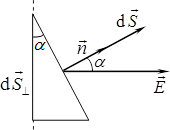
Відповідно, потік поля крізь усю поверхню теж можна подати в різний спосіб:
\begin{equation} \begin{aligned} &\Phi =\int\limits_{S}{\vec{E}\,\mathrm{d}\vec{S}}=\int\limits_{S}E\,\mathrm{d}S\cos\alpha ={}\\ &\quad{}=\int\limits_{S}{{E}_{n}}\,\mathrm{d}S=\int\limits_{S}{E\,\mathrm{d}{{S}_{\bot }}}. \end{aligned} \tag{5.7а} \end{equation}
Говорячи про потік поля, слід зауважити таке. Потік є алгебраїчною величиною і, залежно від кута \(\alpha\) між векторами \(\vec{E}\) і \(\mathrm{d}\vec{S}\), може бути додатнім чи від’ємним. З іншого боку, напрям векторів \(\mathrm{d}\vec{S}\), відтак і знак \(\Phi\), є невизначеними, позаяк орти \(\vec{n}\) можна провести як по один, так і по інший бік поверхні, причому для незамкнених поверхонь — все одно як. Проте у випадку замкнених поверхонь знак потоку набуває суттєвого змісту, тому за домовленістю в усіх точках замкненої поверхні вектори \(\mathrm{d}\vec{S}\) напрямляють назовні (рис. 5.4).
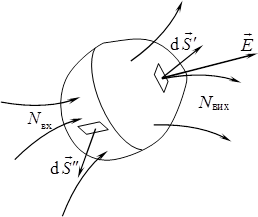
Геометрична інтерпретація потоку. Раніше (п. 1.4) говорилося, що електричне поле можна зображувати за допомогою ліній вектора \(\vec{E}\) (силових ліній), і що такі лінії відображають не лише конфігурацію, а й величину поля в різних областях простору. При цьому за умовою (1.9а) \(E\,\mathrm{d}{{S}_{\bot }} = \mathrm{d}n\). Отже, відповідно до означень (5.7), (5.7а), виконуються числові рівності:
\begin{equation} \left|\mathrm{d}\Phi\right|=\mathrm{d}N\quad \Rightarrow \quad \left|\Phi\right|=N, \tag{5.8} \end{equation}
тобто, можна вважати, що
чисельно потік поля крізь задану поверхню дорівнює кількості ліній поля, що її перетинають.
У випадку замкненої поверхні (оболонки) лінії поля в одних точках заходять усередину, а в інших виходять назовні (рис. 5.4). При цьому в першому випадку \(\alpha>90^\circ\) і створюється від’ємний потік, а в другому \(\alpha<90^\circ\) і потік є додатнім. Тому згідно з (3.6) потік крізь замкнену поверхню \(\Phi_0=\Phi_1+\Phi_2\) можна подати, як
\begin{equation} \Phi_0=N_{\text{вих}}-N_{\text{вх}}, \tag{5.8а} \end{equation}
де \(N_{\text{вих}}\) — кількість ліній поля, що виходять із поверхні назовні, а \(N_{\text{вх}}\) — тих, які входять усередину.
Таке геометричне трактування потоку є зручним у багатьох випадках.
5.2.2. Теорема Гаусса
Потік є важливою характеристикою поля, котра разом із циркуляцією відображає специфічні риси ("обличчя") кожного силового поля. Теорема Гаусса трактує про властивості потоку електричного поля крізь замкнену поверхню.
Потік поля точкового заряду. Визначимо потік \(\Phi\) напруженості крізь довільну замкнену поверхню \(S\) для поля точкового заряду \(q\) у вакуумі (рис. 5.5а).
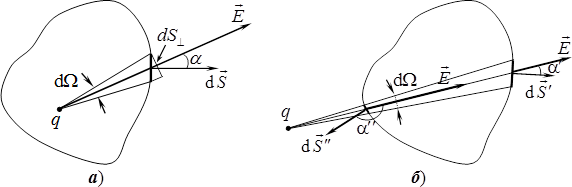
Згідно з виразами (5.7а),
\begin{equation} \Phi =\oint\limits_{S}{E\,\mathrm{d}S\cos \alpha }=\oint\limits_{S}{E\,\mathrm{d}{{S}_{\bot }}}, \end{equation}
де \(\mathrm{d}S\) — площа якоїсь елементарної ділянки замкненої поверхні \(S\).
Проекцію цієї ділянки на площину, перпендикулярну до напрямку поля, можна розглядати як елементарну площадку на поверхні сфери радіуса \(r\) і виразити величину \(\mathrm{d}{{S}_{\bot}}=\mathrm{d}S\cos \alpha \) через відповідний тілесний кут \(\mathrm{d}\Omega\):
\begin{equation} \mathrm{d}{{S}_{\bot }}={{r}^{2}}\,\mathrm{d}\Omega . \tag{5.9} \end{equation}
Довідка. Плоский кут \(\varphi\) визначає частину простору між двома променями, які починаються в одній точці — вершині кута. Його мірою є довжина дуги \(s\), що вирізається сторонами кута на колі заданого радіуса \(r\) із центром у вершині кута. Одиниця плоского кута називається “радіан” (\(\text{рад}\)) і дорівнює кутові, для якого \((s/r) = 1\). За цим означенням усій площині відповідає плоский кут \(\varphi_0=(2\pi r/r)=2\pi\ \text{рад}\). Окрім радіанної, використовують й інші міри, зокрема градусну, де з усією площиною (або довжиною кола) зіставляють кут \(360^\circ\). Тілесний або просторовий кут \(\Omega\) — це частина простору, обмежена певною незамкненою конічною поверхнею. Його мірою є площа сегмента, що вирізається конічною поверхнею на сфері заданого радіуса \(r\) із центром у вершині кута. Одиницею тілесного кута є стерадіан (\(1\ \text{ср}\)) — тілесний кут, для якого \((S/r^2)=1\). Відповідно, всьому тривимірному простору відповідає тілесний кут \({{\Omega }_{0}}=( {4\pi {{r}^{2}}}/{{{r}^{2}}} )=4\pi\ \text{ср} \).
З іншого боку, величина \(E\) визначається формулою (1.4а), тому
\begin{equation} \begin{aligned} &\oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\oint\limits_{S}{\frac{q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}{{r}^{2}}\,\mathrm{d}\Omega }={}\\ &\quad{}=\frac{q}{4\pi {{\varepsilon }_{0}}}\oint\limits_{S}{\mathrm{d}\Omega }. \end{aligned} \end{equation}
Останній інтеграл виражає тілесний кут усього простору і дорівнює \(4\pi \ \text{ср}\), отже,
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{q}{{{\varepsilon }_{0}}}. \tag{5.10} \end{equation}
Тепер розглянемо другий можливий випадок, коли заряд \(q\) знаходиться поза поверхнею \(S\) (рис. 5.5б). В такому разі конічні промені, спрямовані від усіх точок контуру якоїсь площадки \(\mathrm{d}S'\) до заряду й утворюють тілесний кут \(\mathrm{d}\Omega\), виріжуть на протилежному боці відповідну площадку \(\mathrm{d}S''\) з тим самим тілесним кутом. Тому, врахувавши формули (5.9) і (1.4а) та те, що \(\cos\alpha<0\), для потоків крізь указану пару ділянок отримаємо:
\begin{equation} \mathrm{d}\Phi''=-\mathrm{d}\Phi' \quad \Rightarrow \quad \mathrm{d}\Phi'+\mathrm{d}\Phi''=0. \end{equation}
Очевидно, що в такий спосіб можна розчленувати всю замкнену поверхню. Тож сумарний потік крізь замкнену поверхню, що не охоплює заряд,
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=0. \tag{5.10а} \end{equation}
Такого висновку можна дійти і на основі геометричної інтерпретації потоку (5.8а), позаяк у даному випадку кількості ліній поля, що входять усередину поверхні та виходять назовні є однакові.
Відтак, об’єднуючи вирази (5.10) і (5.10а), маємо:
\begin{equation} \oint\limits_{S}\vec{E}\mathrm{d}\vec{S} = \left\{ \begin{aligned} &\frac{q}{\varepsilon_{0}}&&(q\ всередині\ S); \\ &0&&(q\ назовні\ S) .\\ \end{aligned} \right. \tag{5.11} \end{equation}
Теорема Гаусса. Отриманий результат легко узагальнити і на поле, створене довільною системою зарядів (рис. 5.6а).
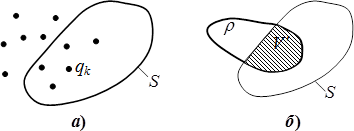
За принципом суперпозиції напруженість поля системи в будь-якій точці
\begin{equation} \vec{E}=\sum\limits_{i}{{{{\vec{E}}}_{i}}}. \end{equation}
Тому потік результуючого поля крізь довільну замкнену поверхню дорівнює сумі потоків полів кожного із зарядів системи:
\begin{equation} \begin{aligned} &\oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\oint\limits_{S}\left( \sum\limits_{i}{{{{\vec{E}}}_{i}}} \right)\mathrm{d}\vec{S}={}\\ &\quad{}=\sum\limits_{i}{\oint\limits_{S}{{{{\vec{E}}}_{i}}\,\mathrm{d}\vec{S}}}. \end{aligned} \end{equation}
Але згідно з (5.11) потік створюють лише заряди, що знаходяться всередині вибраної поверхні. Тому, позначивши такі заряди індексом \(k\), можемо записати:
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{1}{{{\varepsilon }_{0}}}\sum\limits_{k}{{q}_{k}}, \end{equation}
або
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{q}{{{\varepsilon }_{0}}}, \tag{5.12} \end{equation}
де \({q}=\sum\limits_{k}{q}_{k}\).
Це рівняння й виражає інтегральну теорему Гаусса для електричного поля у вакуумі:
потік напруженості електричного поля у вакуумі крізь довільну замкнену поверхню дорівнює сумарному зарядові, що знаходиться всередині цієї поверхні, діленому на \(\varphi_0\).
Рівняння (5.12) є чинним і для заряджених тіл, тобто для полів створених неперервним розподілом заряду в заданому об’ємі (рис. 5.5б). Тільки й того, що величина \(q\) визначається не додаванням зарядів , а інтегруванням заданої густини заряду \(\rho\) по об’єму \(V'\), який займають заряди всередині поверхні \(S\). Але область інтегрування формально поширюють на весь об’єм \(V\) обмежений замкненою поверхнею і записують
\begin{equation} {q}=\int\limits_{V}{\rho \,\mathrm{d}V}. \tag{5.13} \end{equation}
Таким чином,
\begin{equation} \oint\limits_{S}\vec{E}\,\mathrm{d}\vec{S}=\frac{1}{{{\varepsilon }_{0}}}\int\limits_{V}{\rho \,\mathrm{d}V}. \tag{5.14} \end{equation}
Це рівняння є найбільш загальним виразом теореми Гаусса, оскільки інтеграл у правій частині включає як окремі випадки і поверхневий, і лінійний, і дискретний розподіли заряду (див. п. 1.3).
Фізичний зміст теореми Гаусса. Переходячи до аналізу отриманих результатів, одразу звернемо увагу на те, що при незмінній величині заряду всередині замкненої поверхні потік поля крізь неї, тобто значення інтеграла (5.7), не залежить від форми та розмірів поверхні, тим самим і від величини та напрямку напруженості \(\vec{E}\) в різних точках поверхні. Це означає, що на практиці
при визначенні потоку крізь задану складну поверхню можна замінити її зручнішою для обчислень простою поверхнею, що охоплює ті самі заряди.
Друга особливість полягає в тому, що потік поля крізь замкнену поверхню визначається не всіма зарядами, що створюють це поле, а тільки тими з них, які опинилися всередині поверхні. Тому, якщо всередині поверхні зарядів немає, або їхня сума дорівнює нулю, то потік \(\Phi = 0\). Це може спровокувати на хибний висновок, що й напруженість поля \(\vec{E}=0\). Але відсутність потоку ще не означає відсутності поля. Просто в такій ситуації крізь різні ділянки замкненої поверхні створюються потоки різного знаку і такої величини, що сумарний потік виявляється нульовим. Очевидним прикладом є однорідне поле \(\vec{E}=\mathrm{const}\), потік якого крізь будь-яку замкнену поверхню дорівнює нулю.
Походження вказаних особливостей теореми Гаусса можна зрозуміти, повернувшись до її виведення. При цьому легко бачити, що вже у викладці, що передує виразу (5.10), щезає змінна \(r\), яка визначається положенням точок на вибраній поверхні, тож залежить від її розмірів і форми. Це стається через закон Кулона, згідно з яким поле точкового заряду \( E\sim ( {1}/{{{r}^{2}}} )\). При будь-якій іншій залежності \(E(r)\) потік був би залежним від \(r\). За праву частину рівняння (5.12) чи (5.14) “відповідальним” є принцип суперпозиції, який відображає незалежність електричних полів. Завдяки цьому заряди, розташовані назовні замкненої поверхні, не впливають на поле внутрішніх зарядів, отже, й на потік крізь цю поверхню.
Таким чином, теорема Гаусса органічно об’єднує обидва основні закони теорії електричного поля — закон Кулона і принцип суперпозиції. Тому в класичній теоретичній електродинаміці теорема Гаусса розглядається як один із вихідних постулатів (основних законів), а закон Кулона — як один із його наслідків.
Теорема Ірншоу. Позаяк між зарядами спостерігається і притягання, і відштовхування, то можна так підібрати величину та розташування зарядів у системі, що вона буде перебувати в стані механічної рівноваги. Прикладом може слугувати система з двох однакових зарядів \(q\) і розташованого посередині між ними заряду \(q'=-q/4\). Прямим обчисленням можна переконатися, що за таких умов рівнодійна сила, котра діє на кожен заряд з боку двох інших, дорівнює нулю, отже всі заряди перебувають в рівновазі. Але ця рівновага є нестійкою, і зміна положення будь-якого із зарядів призведе до її руйнації. Це відображає теорема Ірншоу, згідно з якою жодна система частинок, між якими діють тільки кулонівські сили, принципово не може перебувати в стані стійкої рівноваги.
Справедливість цього твердження прямо випливає з теореми Гаусса. Доведемо це від зворотнього, припустивши, що якийсь заряд \(-q\) (знак не істотний) системи знаходиться в положенні стійкої рівноваги. Тоді при всякому його зміщенні має з’являтися напрямлена до положення рівноваги сила \(\vec{F}=-q\vec{E}\) (рис. 5.7), що створюється полем \(\vec{E}\) решти зарядів.
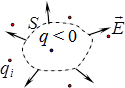
Тому, якщо охопити заряд маленькою замкненою поверхнею так, аби всі інші заряди опинилися поза нею, то вектори \(\vec{E}\) на цій поверхні скрізь мають бути напрямлені назовні і створювати крізь неї потік \(\Phi >0\). Але так не може бути, бо це суперечить теоремі Гаусса: всередині \(S\) немає жодного із зарядів, які створюють указане поле \(\vec{E}\), отже \(\Phi = 0\). Таким чином, стійка рівновага зарядів під дією тільки кулонівських сил є неможливою.
5.3. Обчислення полів за допомогою теореми Гаусса
Напруженість електричного поля, створеного будь-якою заданою системою зарядів, принципово завжди можна прямо розрахувати на основі закону Кулона і принципу суперпозиції, хоча такий розрахунок може виявитися досить трудомістким. Але для високосиметричних полів задачу можна розв’язати набагато легше за допомогою теореми Гаусса. Далі розглянуто декілька прикладів такого розрахунку для полів, що створюються однорідно (із сталою густиною) розподіленим зарядом.
Приклад 4. Циліндрична поверхня
Поле однорідно зарядженої кулі. Поставимо таку задачу: розрахувати напруженість \(\vec{E}(\vec{r})\) поля, що створюється у вакуумі зарядом розподіленим із густиною \(\rho(\vec{r})=\mathrm{const}\) по об’єму кулі радіуса \(R\) (рис. 5.8).
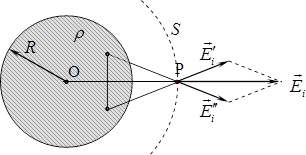
Приступаючи до обчислень, найперше встановимо симетрію поля — проаналізуємо, який воно має напрям і від чого залежить його величина в довільній точці \(P\). Це можна зробити за допомогою закону Кулона та принципу суперпозиції наступним чином. Якщо провести через точку \(P\) радіальну вісь, то при \(\rho=\textrm{const}\) всю кулю можна поділити на пари однакових малих ділянок із зарядами \(q_{i}\), розташованих симетрично до цієї осі. Поля цих зарядів \(\vec{E}{}_i'\) і \(\vec{E}{}_i''\) симетрично орієнтовані і однакові за модулем. Тож зрозуміло, що сумарне поле кожної пари зарядів \(\vec{E}_i=\vec{E}{}_i'+\vec{E}{}_i''\) і поле всієї кулі \(\vec{E}=\sum\limits\vec{E}_{i}\) скрізь мають радіальний напрям і однаковий модуль у рівновіддалених від центра кулі точках.
Таким чином, шукане поле є сферично симетричним (центральним): його лінії напруженості \(\vec{E}\) є радіальними променями, які починаються (або закінчуються) в центрі зарядженої кулі. Тому на концентричній сферичній поверхні довільного радіуса \(r\) проекція напруженості \({E}_n = \textrm{const}\). Через це інтеграл потоку (5.7) крізь таку поверхню легко обчислюється:
\begin{equation} \Phi=\oint\limits_S{E_n\,\mathrm{d}S}=E_n\oint\limits_S{\mathrm{d}S}, \end{equation}
або
\begin{equation} \Phi=E_n S, \tag{5.15} \end{equation}
де \({S}=\oint\limits_S\,\mathrm{d}{S}\) — площа всієї поверхні, крізь яку обчислюється потік.
З іншого боку за теоремою Гаусса потік крізь усяку замкнену поверхню визначається рівнянням (5.14). Тому підставивши в нього вираз (5.13), отримаємо:
\begin{equation} {{E}_{n}}=\frac{q}{{{\varepsilon}_{0}}S}, \tag{5.16} \end{equation}
де \(q\) — величина заряду всередині сфери.
Зауважимо, що позаяк вектор \(\vec{E}\) напрямлений по нормалі до поверхні \(S\), вона є однією з еквіпотенціальних поверхонь поля (див. п. 3.3). Тому зрозуміло, що формула (5.16) годиться не лише для центрального, а й для всякого іншого симетричного поля, що має еквіпотенціальні поверхні простої форми, на яких \(E_n=\textrm{const}\). Що ж до поля кулі, то у формулах (5.15) і (5.16) \(S = 4\pi r^2\), отже
\begin{equation} {E_n}=\frac{q}{4\pi\varepsilon_0{r^2}}. \tag{5.17} \end{equation}
Таким чином, для визначення напруженості поля \(E_n(r)\) треба лишень обчислити заряд зосереджений всередині сфери радіуса \(r\). В загальному випадку він визначається інтегралом (5.11), але при \(\rho=\textrm{const}\)
\begin{equation} q = \rho V', \end{equation}
де \(V'\) — частина об’єму всередині сферичної поверхні, що заповнена зарядом.
Об’єм \(V'\) залежить від того, охоплює сферична поверхня всю заряджену кулю, чи тільки її частину. Тому для визначення напруженості всередині кулі та поза нею розрахунок величини \(q\) треба проводити нарізно.
Поле всередині кулі (\(0\leqslant r \leqslant R\)). У цьому випадку весь обмежений сферичною поверхнею об’єм є заповнений зарядом, і
\begin{equation} {q}=\rho\frac{4}{3}\pi{r^3}. \end{equation}
Отже, згідно з формулою (5.14), всередині зарядженої кулі напруженість електричного поля
\begin{equation} {E_n}=\frac{\rho{r}}{3\varepsilon_0}, \tag{5.18} \end{equation}
або у векторному вигляді
\begin{equation} \vec{E}=\frac{\rho\vec{r}}{3\varepsilon_0}. \tag{5.18а} \end{equation}
Поле назовні кулі (\(r > R\)). За такої умови всередині сферичної поверхні незалежно від її радіуса \(r\) знаходиться весь заряд кулі
\begin{equation} {q}=\rho\frac{4}{3}\pi{R^3}. \end{equation}
Відповідно, напруженість електричного поля у зовнішній області простору
\begin{equation} {E_n}=\frac{\rho{R^3}}{3\varepsilon_0{r^2}}. \tag{5.19} \end{equation}
Аби записати цей вираз у векторній формі, помножимо праву частину на одиничний вектор \((\vec{r}/{r}) \). Тоді
\begin{equation} \vec{E}=\frac{\rho{R^3}}{3\varepsilon_0{r^3}}\vec{r}. \tag{5.19а} \end{equation}
Отримані формули (5.18) і (5.19) показують, що заряджена куля поділяє простір на дві області, в кожній з яких електричне поле залежить від відстані \(r\) до центра кулі за своїм законом. Графік залежності \(E(r)\) показано на рис. 5.9а.
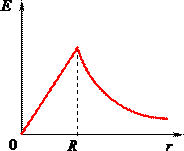
Зауважимо також, що коли у формулі (5.18а) виразити величину \(\rho\) через заряд всієї кулі, як \(\rho=q/(4/3)\pi{R^3}\), то вийде:
\begin{equation} \vec{E}(\vec{r})=\frac{q}{4\pi\varepsilon_0{r^3}}\vec{r}. \tag{5.19б} \end{equation}
Отже, поле назовні рівномірно зарядженої кулі збігається з полем точкового заряду такої самої величини, що розміщений у центрі кулі, рис. 5.9а.
Так виходить і при неоднорідному, але сферично симетричному розподілі заряду \(\rho(r)\).
Поле однорідно зарядженої сфери. Розрахуємо далі поле, що створюється сферичною оболонкою радіуса \(R\), зарядженою з поверхневою густиною заряду \(\sigma=\textrm{const}\). Це поле теж є сферично симетричним, тому його обчислення не відрізняється від попереднього. Відміна лише в тому, що всередині сферичної “гаусової” поверхні при \(r < R\) у формулі (5.16) \(q=0\), а при \(r\geqslant R\) \(q=\sigma\cdot 4\pi r^2\). Тому всередині зарядженої сфери (\(r < R\)) електричного поля немає:
\begin{equation} \vec{E}={0}. \end{equation}
Відповідно, назовні зарядженої сфери (\(r\geqslant R\)) напруженість електричного поля дорівнює
\begin{equation} {E(r)}=\frac{\sigma{R^2}}{\varepsilon_0{r^2}}, \quad \vec{E}(\vec{r})=\frac{\sigma{R^2}}{\varepsilon_0{r^3}}\vec{e}, \tag{5.20} \end{equation}
і, як говорилося, збігається з напруженістю поля точкового заряду \(q=\sigma\cdot 4\pi r^2\). Графік залежності \(E(r)\) показаний на рис. 5.9б.
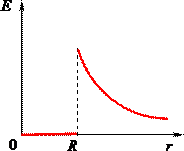
Поле однорідно зарядженого циліндра. Тепер знайдемо електричне поле, що створюється зарядом розподіленим із об’ємною густиною \(\rho=\textrm{const}\) по нескінченному циліндру радіуса \(R\) (рис. 5.10).
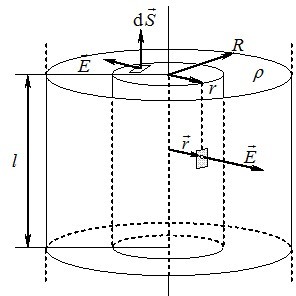
Міркуючи, як раніше, встановлюємо, що шукане має осьову симетрію : в будь-якій точці вектор \(\vec{E}\) напрямлений радіально, і його модуль залежить тільки від відстані до осі циліндра. Отже, якщо охопити частину заряду коаксіальною циліндричною поверхнею довільного радіуса \(r\) і висоти \(l\), то на його основах \(E_n = 0\). Тому потік створюється тільки через бічну поверхню \(S_{\text{біч}}=2\pi rl\), на якій скрізь \(E_n=\textrm{const}\). Відтак
\begin{equation} \Phi=\oint\limits_{S}E_{n}\,\mathrm{d}S=E_{n}\oint\limits_{S_{\text{біч}}}\,\mathrm{d}S=E_{n}\cdot{2}\pi{rl}. \end{equation}
Тож за формулою (5.14) для проекції напруженості на радіальний напрям маємо:
\begin{equation} {E_r}=\frac{q}{2\pi{l}\varepsilon_0{r}}. \tag{5.21} \end{equation}
Далі, як і в попередніх прикладах, обчислення величини \(q\) виконуємо нарізно для областей всередині та назовні зарядженого циліндра.
Поле всередині циліндра (\(r < R\)). У цьому випадку вся замкнена циліндрична поверхня радіуса \(r\) і висоти \({l}\) заповнена зарядом. Тому
\begin{equation} {q}=\rho\pi{r^2}{l}, \end{equation}
і, згідно з формулою (5.19),
\begin{equation} {E_r}=\frac{\rho{r}}{2\varepsilon_0}, \tag{5.22} \end{equation}
а у векторному вигляді
\begin{equation} \vec{E}=\frac{\rho\vec{r}}{2\varepsilon_0}. \tag{5.22а} \end{equation}
Поле назовні циліндра (\(r > R\)). За такої умови всередині замкненої поверхні незалежно від її радіуса \(r\) зосереджений весь заряд охопленої частини циліндра:
\begin{equation} {q}=\rho\pi{R^2}{l}. \end{equation}
Відповідно, формула (5.19):
\begin{equation} {E_r}=\frac{\rho{R^2}}{2\varepsilon_0{r}}. \tag{5.23} \end{equation}
Помноживши праву частину цієї формули на одиничний вектор \({(\vec{r}/r)}\), отримаємо вираз для вектора напруженості:
\begin{equation} \vec{E}=\frac{\rho{R^2}}{2\varepsilon{r^2}}\vec{r}. \tag{5.23а} \end{equation}
Порівнюючи вирази (5.22а) і (5.18а) та (5.23а) і (5.19а), бачимо, що залежності \(\vec{E}(\vec{r}) \) для поля циліндра та кулі є схожими. Відповідно, і графік залежності \(E(r)\) для поля циліндра якісно є таким, як на рис. 5.9а.
Поле однорідно зарядженої циліндричної поверхні. Якщо заряд розподілений із густиною \(\sigma=\textrm{const}\) по нескінченній циліндричній поверхні радіуса \(R\), то, як і у випадку сфери, для точок всередині у формулі (5.21) \(q=0\). Тому всередині зарядженої циліндричної поверхні (\(r < 0\)) поля немає:
\begin{equation} \vec{E}={0}; \end{equation}
Назовні (\(r \geqslant R\)) \( {q}=\sigma\cdot 2\pi{Rl} \), тож
\begin{equation} {E_r}=\frac{\sigma{R}}{\varepsilon_0{r}} \tag{5.24} \end{equation}
і
\begin{equation} \vec{E}=\frac{\sigma{R}} {\varepsilon_0{r^2}}\vec{r}. \tag{5.24а} \end{equation}
Графік залежності \(E(r)\) має вигляд рис. 5.9б.
Поле однорідно зарядженої нитки. Нитку будемо розглядати як нескінченний циліндр гранично малого радіуса, заряджений з лінійною густиною \(\lambda=\textrm{const}\). Тому напруженість поля визначається формулою (5.21), в якій \({q}=\lambda{l}\). Отже,
\begin{equation} {E_r}=\frac{\lambda}{2\pi\varepsilon_0{r}}. \tag{5.25} \end{equation}
У векторній формі
\begin{equation} \vec{E}=\frac{\lambda}{2\pi\varepsilon_0{r^2}}\vec{r}. \tag{5.25а} \end{equation}
Графік \(E(r)\) наведено на рис. 5.11.
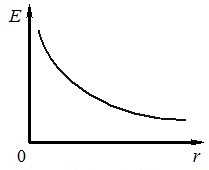
Поле однорідно зарядженої площини. Нарешті визначимо напруженість електричного поля, що створюється нескінченною плоскою поверхнею, зарядженою з поверхневою густиною заряду \(\sigma=\textrm{const}\).
Для встановлення симетрії поля теж можна скористатися законом Кулона та принцип суперпозиції. Але симетрію як цього так і розглянутих полів можна з’ясувати й на основі загальних логічних міркувань, які спираються на однорідність та ізотропність простору. А саме. Уявімо, що вектор \(\vec{E}\) має певний напрям, що складає з площиною кут \(\alpha\ne 90^\circ\). Але тоді виникає запитання, на яке немає відповіді: а чому в такому разі вектор \(\vec{E}\) не може бути спрямований в будь-якому іншому з безлічі напрямків під тим самим кутом \(\alpha\) до площини, адже всі вони є фізично еквівалентними (рівноправними). У той же час подібне запитання не виникає щодо перпендикулярного (\(\alpha=90^\circ\)) до площини напрямку, бо він є один. Отже, у випадку нескінченної однорідно зарядженої площини вектор \(\vec{E}\) скрізь напрямлений перпендикулярно до неї в той чи інший бік залежно від знаку заряду. З таких самих міркувань очевидно, що фізично еквівалентними є і всі точки будь-якої площини паралельної до тієї, що створює поле. Тому на такій площині не тільки напрям, а й модуль напруженості \(E\) скрізь однаковий, тож \(\vec{E}=\textrm{const}\). Іншими словами, дане поле є плоско симетричним і однорідним.
Зауваження. Наведені міркування є придатними для аналізу симетрії будь-якої задачі і мають таку саму доказову силу, як і аналітичні викладки. Але до подібного аналізу слід підходити з уважністю. Наприклад, поле однорідно зарядженої плоскої поверхні у формі диска теж симетричне, але його симетрія не є плоскою. Зокрема, перпендикулярно до площини диска воно напрямлене тільки на осі. Модуль напруженості теж однаковий не скрізь, а тільки на колі з центром на осі й площиною паралельною до площини диска.
Завдяки високій симетрії поле площини теж легко розраховується за допомогою теореми Гаусса. Для цього оточимо частину площини якоюсь замкненою поверхнею, до прикладу, прямим циліндром із паралельними до площини і рівновіддаленими від неї основами, рис. 5.12а.
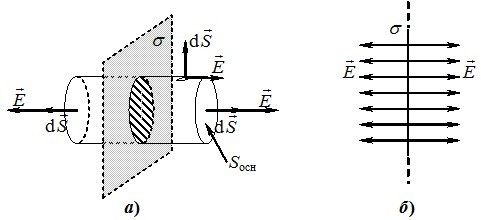
У такому випадку вектори \(\vec{E}\) на основах циліндра мають однакову величину \(E_n=\textrm{const}\), а на бічній поверхні поле є скрізь паралельним до неї і не створює потоку. За таких умов інтеграл потоку (5.5) крізь увесь замкнений циліндр виражається як
\begin{equation} \Phi=2E_{n}\int\limits_{S_{\text{осн}}}\,\mathrm{d}S=2E_{n}S_{\text{осн}}. \end{equation}
При цьому заряд всередині циліндра \(q = \sigma S_{\text{осн}}\). Отже, з рівняння (5.10) маємо:
\begin{equation} {E_n}=\frac{\sigma}{2\varepsilon_0}. \tag{5.26} \end{equation}
У векторному вигляді
\begin{equation} \vec{E}=\frac{\sigma}{2\varepsilon_0}\vec{n}, \tag{5.26а} \end{equation}
де \(\vec{n}\) — орт зовнішньої нормалі до площини.
Таким чином, заряджена з густиною \(\sigma=\textrm{const}\) нескінченна площина створює по обидва боки однорідне електричне поле, що напрямлене від площини при \(\sigma > 0\) і до неї при \(\sigma < 0\). Лінії такого поля являють систему паралельних променів, які розміщені на однаковій відстані один від одного (рис. 5.12б).
Контрольні запитання
1. Що називається циркуляцією силового поля \(\vec{F}\) по заданому контуру \(L\). Який фізичний зміст має ця величина та від чого залежить її знак для заданого контуру?
2. Яку ознаку поля відображає його циркуляція по довільному контуру? Чому вона дорівнює для електричного поля зарядів?
3. Поміркуйте, в яких одиницях вимірюється та що собою являє потік електричного заряду через поверхню поперечного перерізу провідника, по якому тече електричний струм.
4. Потік електричного поля крізь задану замкнену поверхню дорівнює нулю. Чи означає це, що всередині неї немає поля? Немає зарядів?
5. Чому потік поля точкового заряду \(q\) крізь якусь замкнену поверхню дорівнює нулю, коли заряд перебуває поза нею, і не дорівнює нулю, коли він знаходиться всередині?
6. Електричне поле створюється двома паралельними площинами, що різноіменно заряджені з однаковою густиною заряду \(\sigma\) (\(\text{Кл/м}^2\)). Визначте потік електричного поля крізь якусь замкнену поверхню, що розташована: а) поза площинами; б) між площинами. Що спричинює кожну відповідь?
7. Електричне поле створюється двома паралельними площинами, що заряджені з однаковою густиною заряду \(\sigma\) (\(\text{Кл/м}^2\)). Визначте потік електричного поля крізь внутрішню та зовнішню частину поверхні невеликої сфери радіуса \(R\) із центром на одній з пластин, якщо площини заряджені: а) різнойменно і б) однойменно.
8. Із теореми Гаусса випливає, що всередині будь-якої зарядженої провідної оболонки (замкненої поверхні) електричне поле відсутнє. Як це довести?