ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ
IV. МАГНІТНЕ ПОЛЕ
3. Магнітне поле в речовині
Речовина змінює характеристики не лише електричного, а й магнітного поля. Загальною (але не єдиною) причиною цього є інтенсивний рух електронів у атомах, який створює в речовині власні мікроскопічні магнітні поля подібно до мікроскопічних електричних полів у діелектриках. При цьому одні речовини (діелектрики) лише послаблююсь статичне електричне поле, а інші (провідники) повністю його знищують. Але вплив різних речовин на магнітне поле так радикально не відрізняється, і тому всі вони є магнетиками.
Опис магнітного поля в речовині та загальні властивості різних типів магнетиків розглядаються далі в наступних питаннях:
3.2. Вектор \( \vec{H}\). Теорема про циркуляцію магнітного поля в речовині
3.3. Магнітні сприйнятливість і проникність
3.4. Умови на межі двох магнетиків
3.1. Намагнічування речовини
Намагніченість. Замкнений рух електронів в атомах навколо ядер створює мікроскопічні молекулярні струми. Тим самим атоми уподібнюються до мікроскопічних витків із струмом — магнітних диполів, які створюють в околі атомів мікроскопічні магнітні поля. За звичайних умов ці поля в більшості речовин орієнтовані хаотично і є компенсованими. Але при вміщенні магнетика у зовнішнє магнітне поле магнітні моменти і мікрополя атомів частково орієнтуються по зовнішньому полю і перестають бути компенсованими. Як наслідок, у речовині створюється внутрішнє макроскопічне магнітне поле. Цей процес називається намагнічуванням речовини. Він є аналогічним до поляризації діелектриків, при якій відбувається упорядкування електричних моментів молекул і в речовині виникає внутрішнє електричне поле. Подібно до діелектриків уводиться і кількісна характеристика ступеня намагніченості речовини в кожній точці — намагніченість або вектор намагнічування \(\vec{J}\):
\begin{equation} \vec{J}=\frac{1}{\Delta{V}}\sum\limits\vec{p}_{i}=\frac{\vec{p}_{\Sigma}}{\Delta{V}}, \tag{3.1} \end{equation}
де \(\Delta V\) — фізично нескінченно малий об’єм (див. розділ II, п. 1) в околі даної точки речовини, а \(\vec{p}_{\Sigma}=\sum\limits\vec{p}_{i}\) — сумарний магнітний момент атомів у цьому об’ємі. Помноживши і поділивши вираз (3.1) на кількість \(N\) атомів у об’ємі \(\Delta V\), намагніченість можна подати через концентрацію частинок речовини \(n = ( N / \Delta V)\) і середній магнітний момент однієї частинки \(\langle {\vec{p}} \rangle =\frac{1}{N}\sum\limits{{{{\vec{p}}}_{i}}}\):
\begin{equation} \vec{J}=n\langle\vec{p}\rangle. \tag{3.1а} \end{equation}
Струми намагнічування. Переважна орієнтація магнітних моментів атомів уздовж напрямку поля при намагнічуванні речовини означає, що електрони в атомах починають рухають узгоджено. Як наслідок, у намагніченій речовині виникають макроскопічні струми намагнічування. Це можна зрозуміти з рис. 3.1, де стрілками схематично показано циркуляцію заряду в атомах поверхневому шару намагніченого вздовж осі циліндричного зразка.
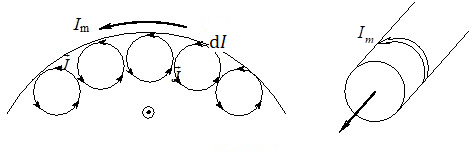
В об’ємі молекулярні струми сусідніх молекул спрямовані взаємно протилежно і є компенсованими, тоді як на поверхні всі молекулярні струми напрямлені однаково. Тому, хоч електрони й не переміщуються від атома до атома, на поверхні відбувається напрямлений рух електричного заряду. Таке своєрідне обтікання зарядом поверхні зразка називається поверхневим струмом намагнічування. Розподіл поверхневих струмів намагнічування визначається лінійною густиною струму намагнічування
\begin{equation} {i}_{m}=\frac{\mathrm{d}I_{m}}{\mathrm{d}l}\ (\text{А/м}), \tag{3.2} \end{equation}
тобто, струмом намагнічування, що припадає на одиницю довжини поверхні зразка в напрямку намагніченості (рис. 3.1).
У неоднорідному магнетику повної компенсації молекулярних струмів усередині зразка немає, тому при намагнічуванні виникають не лише поверхневі, а й об’ємні струми намагнічування, котрі, як і звичайні струми, характеризуються поверхневою густиною струму
\begin{equation} {j}_{m}=\frac{\mathrm{d}I_{m}}{\mathrm{d}S}\ (\text{А/м}^2), \tag{3.3} \end{equation}
яка визначає об’ємний струм намагнічування через одиничну площинку, перпендикулярну до напрямку перенесення заряду.
Ще раз наголосимо, що вказане перенесення заряду не пов’язане з рухом електронів (носіїв) по зразку магнетика. Тому для струмів намагнічування немає поняття електричного опору, вони не супроводжуються виділенням джоульового тепла або електрохімічними процесами і можуть існувати в будь-якому середовищі, а не лише в провідниках. Але струми намагнічування і струми провідності є однаковими щодо спроможності створювати магнітне поле. А саме,
магнітне поле струмів намагнічування нічим не відрізняється від магнітного поля струмів провідності такої самої величини та конфігурації.
Зв’язок між намагніченістю та струмами намагнічування. Уявлення про струми намагнічування дозволяє побудувати послідовну теорію макроскопічного магнітного поля в речовині. Це, зокрема, є зумовлене існуванням безпосереднього зв’язку між струмами намагнічування та намагніченістю. Аби його встановити, виділимо тонкий шар в однорідно намагніченому косому циліндрі з віссю, що складає кут \(\alpha \) з вектором \(\vec{J}\), і перпендикулярними до нього основами площею \(S\) (рис. 3.2).
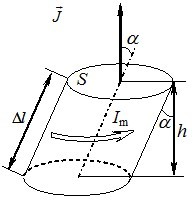
Такий шар можна розглядати як контур із струмом
\begin{equation} {I}_{m}=i_{m}\,\Delta{l}, \end{equation}
де \({i}_{m}\) — лінійна густина поверхневого струму намагнічування, \(\Delta{l}\) — товщина шару уздовж осі циліндра. Тоді магнітний момент шару має величину \({p}=I_{m}{S}\), а намагніченість, згідно з означенням (3.1),
\begin{equation} J=\frac{{{I}_{m}}S}{\Delta V}=\frac{{{i}_{m}}\Delta lS}{\Delta V}. \tag{3.3а} \end{equation}
Звідси, врахувавши, що \(\Delta{V}=S\Delta{l}\cos\alpha \), маємо:
\begin{equation} {J}\cos\alpha={i_{m}}\qquad \text{або}\qquad {J_{l}}=i_{m}, \tag{3.4} \end{equation}
де \({J}_{l}\) — осьова складова намагніченості.
Цей результат дозволяє отримати важливий для теорії магнітного поля в речовині вираз циркуляції намагніченості \(\oint\limits_{L}\vec{J}\,\mathrm{d}\vec{l}=\oint\limits_{L}J_{l}\,\mathrm{d}{l}\) по довільному замкненому контуру \(L\) (рис. 3.3).
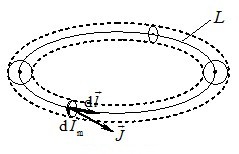
Якщо оточити контур \(L\) дуже тонкою циліндричною трубкою, то згідно з (3.4) на кожній ділянці \(\mathrm{d}{l}\) контуру
\begin{equation} {J}_{l}\,\mathrm{d}l=i_{m}\,\mathrm{d}l=\mathrm{d}{I_{m}}, \end{equation}
де \(\mathrm{d}I_{m}\) — струм намагнічування, що тече по відповідній ділянці поверхні трубки. Таким чином,
\begin{equation} \oint\limits_{L}\vec{J}\,\mathrm{d}\vec{l}=I_{m}, \tag{3.5} \end{equation}
тобто:
циркуляція вектора намагнічування по довільному замкненому контуру дорівнює струмові намагнічування, що охоплюється цим контуром (інакше — перетинає поверхню обмежену цим контуром).
Цей результат, який можна трактувати як теорему про циркуляцію вектора намагнічування, зберігає чинність і при неоднорідній намагніченості речовини.
3.2. Вектор \(\vec{H}\). Теорема про циркуляцію магнітного поля в речовині
При намагнічуванні у речовині створюється внутрішнє макроскопічне магнітне поле \(\vec{{B}}{}^{\,\prime}\), яке разом із зовнішнім полем \(\vec{B}_{0}\) визначає результуюче поле в магнетику
\begin{equation} \vec{B}=\vec{B}_{0}+\vec{B}{}^{\,\prime}. \end{equation}
Зовнішнє поле створюється макроскопічним рухом (дрейфом) електронів у провідниках, а внутрішнє — мікроскопічними рухами електронів навколо ядер в атомах магнетика. Але, як говорилося, ніякої різниці у загальних властивостях між цими полями немає. Тому так само, як поле \(\vec{B}_{0}\) визначається величиною та конфігурацією струмів провідності, поле \(\vec{{B}}{}^{\,\prime}\) визначається величиною та конфігурацією струмів намагнічування. Отже, на основі теореми про циркуляцію магнітного поля струмів у вакуумі (2.4), для поля в речовині можна записати
\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}(I+I_{m}), \tag{3.6} \end{equation}
де \({I}\) та \({I}_{m}\) — сумарна величина струмів провідності та струмів намагнічування, що охоплюються контуром інтегрування.
Записаний вираз формально є подібним до рівняння (2.4). Проте трактувати його як теорему про циркуляцію магнітного поля в речовині по суті не можна, бо він визначає циркуляцію поля \(\vec{B}\) через величину \({I}_{m}\), яка сама залежить від \(\vec{B}\). Тому для опису магнітного поля в речовині, як і в теорії електричного поля в діелектриках, уводиться відповідний допоміжний вектор. Зважаючи на співвідношення (3.5), перетворимо вираз (3.6) наступним чином:
\begin{equation} \begin{aligned} &\oint\limits_{L}\frac{\vec{B}}{\mu_{0}}\,\mathrm{d}\vec{l}=I+\oint\limits_{L}\vec{J}\,\mathrm{d}\vec{l} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \oint\limits_{L}\left(\frac{\vec{B}}{\mu_{0}}-\vec{J}\right)\mathrm{d}\vec{l}={I} \end{aligned} \tag{3.7}\end{equation}
і введемо величину
\begin{equation} \vec{H}=\frac{\vec{B}}{\mu_{0}}-\vec{J}, \tag{3.8} \end{equation}
яку у фізиці зазвичай називають “вектором \(\vec{H}\)”, рідше — “напруженістю” магнітного поля, терміном, який є поширеним в електротехніці. Відтак рівняння (3.7) набуває вигляду
\begin{equation} \oint\limits_{L}\vec{H}\,\mathrm{d}\vec{l}={I} \tag{3.9} \end{equation}
і виражає теорему про циркуляцію магнітного поля струмів у речовині:
циркуляція вектора \(\vec{H}\) по довільному замкненому контуру дорівнює сумарному струмові провідності І, котрий проходить крізь довільну поверхню обмежену цим контуром.
Величина \(I\) залежить від розподілу струмів провідності у просторі і в загальному випадку визначається інтегральною формулою ((1.4а), розділ І). Тому розгорнуто рівняння (3.9) записується, як
\begin{equation} \oint\limits\vec{H}\,\mathrm{d}\vec{l}=\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S}. \tag{3.9а} \end{equation}
Слід сказати, що рівняння (3.9) і (3.9а) як окремий випадок вбирають і доведену раніше теорему про циркуляцію магнітного поля у вакуумі. У цьому легко переконатися, взявши до уваги, що у вакуумі \(\vec{J}={0}\), тож
\begin{equation} \vec{H}=\frac{\vec{B}}{\mu_{0}}. \end{equation}
Отже, рівняння (3.9а) відображує загальні властивості магнітного поля більш повно, ніж рівнянням (2.4а) для циркуляції вектора \(\vec{B}\). У той же час \(\vec{H}\) є допоміжним, а не основним (“польовим”) вектором, бо, згідно з (3.8), у кожній точці він визначається не лише станом поля, а й станом речовини. Але це не зменшує значимість вектора \(\vec{H}\), бо він дозволяє одним рівнянням (3.9а) виразити важливі властивості магнітного поля як у вакуумі, так і в будь-якому середовищі.
3.3. Магнітні сприйнятливість і проникність
Циркуляція вектора \(\vec{H}\) не залежить від струмів намагнічування, тож і від речовини магнетика. Але цього, звичайно, не можна сказати про сам вектор \(\vec{H}\), бо згідно з означенням (3.8) він через вектор \(\vec{J}\) є пов’язаний із струмами намагнічування. Проте в деяких випадках не тільки циркуляція, а й сам вектор \(\vec{H}\) виявляється прямо не залежним від струмів намагнічування, що дозволяє його визначити тільки через струми провідності. З іншого боку, у фізиці матеріалів установлені функціональні зв’язки \(\vec{J}{(\vec{H})}\) між намагніченістю \(\vec{J}\) та вектором \(\vec{H}\) у різних типах магнетиків. За такої умови означення (3.8) перетворюється на функціональне рівняння, з якого можна знайти індукцію \(\vec{B}\) магнітного поля, створеного в магнетику заданим розподілом струмів провідності:
\begin{equation} \begin{aligned} &\vec{H}=\frac{\vec{B}}{\mu_{0}}-\vec{J}(\vec{H}) \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \vec{B}={{\mu}_{0}}\bigl( \vec{H}+\vec{J}({\vec{H}}) \bigr). \end{aligned} \tag{3.10}\end{equation}
Такий розрахунок включає два етапи:
— визначення допоміжного вектора \(\vec{H}(\vec{r}) \) через розподіл сторонніх струмів провідності \(\vec{j}\left( {\vec{r}} \right)\),
— визначення вектора індукції поля \(\vec{B}(\vec{r}) \) за допомогою рівняння (3.10).
У загальному випадку розрахунок є складним через складну залежність \(\vec{J}( {\vec{H}} )\). Але майже всі технологічні магнітні матеріали є ізотропними, тобто їхні властивості не залежать від напрямку поля. А в таких речовинах зв’язок між векторами \( \vec{J} \) і \( \vec{H} \) є простим і має вигляд:
\begin{equation} \vec{J}=\chi\vec{H}, \tag{3.11} \end{equation}
де безрозмірне число \({\chi}\) (читається “хі”) називається магнітною сприйнятливістю і показує наскільки добре дана речовина намагнічується у заданому магнітному полі. Тож підставивши співвідношення (3.11) у рівняння (3.10), отримаємо:
\begin{equation} \vec{B}=\mu_{0}(1+\chi )\vec{H}. \tag{3.12} \end{equation}
Величину \({1+\chi}\) в цьому виразі позначають одним символом \({\mu}\) і називають магнітною проникністю речовини. Отже, за означенням
\begin{equation} \mu = 1+\chi. \tag{3.13} \end{equation}
Слід сказати, що для переважної більшості речовин \(\chi\approx{0}\) і \(\mu\approx{1}\), тобто вони майже не намагнічуються і не впливають на магнітне поле. Але деякі, як до прикладу залізо, є дуже сильними магнетиками, і для них величина \({\chi}\) сягає \(10^5\) і навіть більше.
Із виразів (3.12) і (3.13) випливає важлива формула, що напряму пов’язує вектори \(\vec{B}\) і \({\vec{H}}\) в ізотропному магнетику:
\begin{equation} \vec{B}=\mu_{0}\mu\vec{H}. \tag{3.14} \end{equation}
3.4. Умови на межі двох магнетиків
При переході через межу поділу намагнічених речовин характеристики магнітного поля закономірно змінюються. При цьому співвідношення між векторами \(\vec{B}_{1}\) і \(\vec{B}_{2}\) та \(\vec{H}_{1}\) і \(\vec{H}_{2}\) визначаються умовами на межі, котрі випливають із теорем про потік та про циркуляцію магнітного поля.
Спочатку встановимо зв’язок між нормальними складовими векторів у двох ізотропних магнетиках із проникностями \(\mu _1\) і \(\mu_2\) за відсутності на межі поділу струмів провідності. Для цього розглянемо потік вектора \(\vec{B}\) крізь маленький замкнений циліндр із висотою \(h\) і паралельними до межі поділу основами \(\Delta S\) (рис. 3.4а).
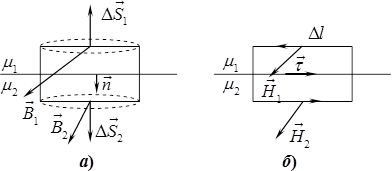
Він складається з потоків через основи циліндра \(\Delta \Phi_1\), \(\Delta \Phi_2\) та бічну поверхню \(\Delta \Phi'\) і за теоремою Гаусса (2.1) дорівнює нулю:
\begin{equation} \Delta \Phi_1+\Delta \Phi_2+\Delta \Phi'=0. \end{equation}
Циліндр малий, тому, спроектувавши вектори на спільну нормаль \(\vec{n}\) до межі поділу, потоки через основи можна наближено виразити, як \(\Delta \Phi_1\approx -B_{1n}\Delta S\) і \(\Delta \Phi_2\approx B_{2n}\Delta S\). Тоді
\begin{equation} -B_{1n}\Delta S + B_{2n}\Delta S + \Delta \Phi'\approx 0. \end{equation}
Неточність цього виразу зумовлена можливою відміною значень \(B_n\) у різних точках площинок \(\Delta S\). Тому для отримання точної рівності треба перейти до границі, “стягнувши” циліндр у якусь точку на межі поділу. Для цього спочатку будемо подумки зменшувати висоту циліндра, поступово наближаючи основи до межі поділу. Тоді у границі \({h}\to{0}\) зникне потік крізь бічну поверхню:
\begin{equation} \begin{aligned} &-B_{1n}\Delta S + B_{2n}\Delta S\approx 0 \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad B_{1n}\Delta S\approx B_{2n}\Delta S. \end{aligned} \end{equation}
При подальшому стяганні основ точність отриманої рівності буде підвищуватись, і в границі \(\Delta S\to 0\) отримаємо:
\begin{equation} B_{1n} = B_{2n}. \tag{3.15а} \end{equation}
Відтак за допомогою співвідношення (3.14) встановлюємо зв’язок між нормальними складовими для векторів \(\vec{H}\):
\begin{equation} \begin{aligned} &\mu_{1}H_{1n}=\mu_{2}H_{2n} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \frac{H_{1n}}{H_{2n}}=\frac{\mu_{2}}{\mu_{1}}. \end{aligned} \tag{3.15б}\end{equation}
Аналогічно за допомогою теореми про циркуляцію вектора \(\vec{H}\) (3.9) і формули (3.14) встановимо межові умови для тангенціальних складових векторів. Для цього розглянемо циркуляцію \(C\) вектора \(\vec{H}\) уздовж малого прямокутника, що охоплює деяку точку на межі поділу магнетиків і орієнтований так, як показано на рис. 3.4б. Ураховуючи малість контуру, інтеграл у рівнянні (2.4) наближено виразимо через вклади окремих сторін:
\begin{equation} {-H_{1\tau}}\Delta{l}+H_{2\tau}\Delta{l}+\Delta{C_{\text{п}}}\approx{0}, \end{equation}
де \(\Delta C_{\text{п}}\) — спільний вклад від поперечних сторін, а проекції векторів поля на напрям переміщення вздовж поздовжніх сторін записані через спільний орт \(\tau \) дотичної до межі поділу.
Далі, стягаючи прямокутник у вибрану точку на межі поділу магнетиків, отримаємо
\begin{equation} {H_{1\tau}}=H_{2\tau} \tag{3.16а} \end{equation}
і, за допомогою формули (3.14),
\begin{equation} \frac{B_{1\tau}}{\mu_{1}}=\frac{B_{2\tau}}{\mu_{2}}. \tag{3.16б} \end{equation}
Зведемо всі отримані результати, які складають умови на межі двох магнетиків за відсутності струмів провідності:
\begin{equation} \begin{gathered} {B_{1n}}=B_{2n},\qquad &\frac{B_{1\tau}}{B_{2\tau}}=\frac{\mu_1}{\mu_2};\\ \frac{H_{1n}}{H_{2n}}=\frac{\mu_2}{\mu_1},\qquad &H_{1\tau}=H_{2\tau}. \end{gathered} \tag{3.17} \end{equation}
Умови (3.17) визначають зв’язок як між модулями, так і між напрямками векторів \(\vec{B}\) і \(\vec{H}\) на межі ізотропних магнетиків. Зокрема, з них випливає, що напрямки цих векторів задовольняють наступний “закон заломлення” (рис. 3.5):
\begin{equation} \frac{\mathrm{tg}\alpha_1}{\mathrm{tg}\alpha_2}=\frac{\mu_1}{\mu_2}. \end{equation}
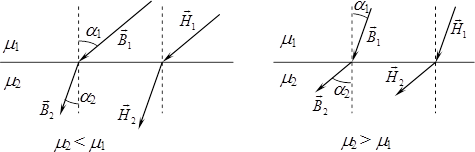
Наостанку зауважимо наступне. Умови на межі (3.17) і зв’язок між векторами магнітного поля (3.14) в ізотропних магнетиках є такий самий, як і в діелектриках ((2.18), (2.14), розділ II). Тож формули для характеристик магнітного поля в ізотропних середовищах, можна отримати з відповідних формул для поля у вакуумі заміною \(\mu_0\) на \(\mu_0\mu\). Зокрема, для поля ідеального соленоїда з ізотропним осердям це дає
\begin{equation} {B}=\mu_{0}\mu{nI} \tag{3.18} \end{equation}
та
\begin{equation} {H=nI}. \tag{3.19} \end{equation}
3.5. Магнетики (пара-, діа- і феромагнетики)
Усі речовини є магнетиками, тобто вони так, чи інакше змінюють характеристики магнітного поля. При цьому за ступенем та характером впливу на магнітне поле виділяють декілька типів магнетиків, серед яких найпоширенішими є парамагнетики, діамагнетики та феромагнетики.
Пара- і діамагнетики. До цих двох типів магнетиків належить переважна більшість речовин. Попри різний механізм намагнічування пара- та діамагнетики єднає те, що вони дуже слабко впливають на магнітне поле, їхня сприйнятливість \(\chi\approx 0\), а проникність \(\mu \approx 1\). При цьому парамагнетики трохи підсилюють, а діамагнетики трохи послаблюють магнітне поле.
Парамагнетиками є речовини, в яких власні магнітні моменти атомів зазвичай орієнтовані хаотично. При внесенні в зовнішнє магнітне поле напрямки магнітних моментів атомів парамагнетика впорядковуються, що зумовлює намагнічування у напрямку поля. Але цьому процесу перешкоджає тепловий рух атомів, отож ступінь упорядкованості моментів і магнітна сприйнятливість парамагнетиків є дуже слабкими і зменшуються при підвищенні температури.
До діамагнетиків належать речовини, в атомах яких магнітні моменти електронів є компенсованими. Тому атоми діамагнетика не мають власного магнітного моменту і, здавалося б, взагалі не повинні намагнічуватись. Але зовнішнє поле діє не на атом як ціле, а на кожен окремий електрон. При цьому рух електронів навколо ядра змінюється так, що у кожного електрона й атома в цілому з’являється індукований магнітний момент, напрямлений протилежно до зовнішнього поля. Тому в діамагнетиках вектори \(\vec{J}=\chi\vec{H}\) і \(\vec{H}\) є антипаралельними, тож \(\chi<{0}\) і \(\mu < 1\).
Ще однією особливістю діамагнетиків є незалежність магнітної сприйнятливості від температури. Це пояснюється тим, що тепловий рух атомів не спроможний впливати на рух електронів навколо ядра. Слід також зауважити, що зовнішнє магнітне поле створює індуковані моменти електронів у будь-яких атомах. Тому діамагнітна намагніченість є притаманною всім магнетикам. Але це практично не впливає на властивості інших видів магнетиків, оскільки діамагнітна намагніченість є значно слабшою, ніж парамагнітна.
Феромагнетики. До цього класу магнетиків належать атоми і деякі сполуки елементів групи заліза (Fe, Co, Ni) та деякі рідкоземельні елементи, а також сплави на їхній основі. Феромагнетики є сильними магнетиками (\({\mu\gg{1}}\)), що зумовлює їхнє практичне застосування в якості технологічних магнітних матеріалів.
Відміна феромагнетиків від слабких магнетиків зумовлена їхньою внутрішньою будовою. З причин, які пояснюються в квантовій фізиці, у феромагнетиках атоми об’єднуються в домени — окремі малі, але макроскопічні (розміром \((1\div 10)\) мкм і навіть більше) області, в яких магнітні моменти атомів є співнапрямленими. Тож домени є спонтанно (самі по собі) намагнічені до теоретичної границі. Наявність доменної структури саме й спричинює особливі магнітні властивості феромагнетиків.
Основна крива намагнічування. У розмагніченому феромагнетику магнітні моменти доменів орієнтовані хаотично, і в ньому, як і в слабких магнетиках, немає власного макроскопічного магнітного поля. Але, на відміну від них, намагнічування феромагнетика при вміщенні у зовнішнє поле зумовлюється упорядкуванням магнітних моментів не окремих атомів, а цілих доменів, і має складний характер. Його можна дослідити, вмістивши залізний сердечник всередину соленоїда із струмом. Оскільки поле соленоїда напрямлене уздовж осі, модулі напруженості в магнетику \(H\) та повітрі \(H_{0}\) збігаються з їхніми проекціями на поверхню сердечника, тож за умовами (3.17) \(H = H_{0}\). Відтак, узявши до уваги формули (2.10) і (3.14), отримуємо
\begin{equation} {H}={nI}. \end{equation}
Отже, величина \(H\) у сердечнику однозначно визначається силою струму в котушці. Тому, поступово збільшуючи величину струму, можна експериментально визначити залежність намагніченості \(J\) та індукції \(B\) від напруженості \(H\). Вигляд графіка \(J ( H)\), який називається основною кривою намагнічування феромагнетика, наведений на рис. 3.6а.
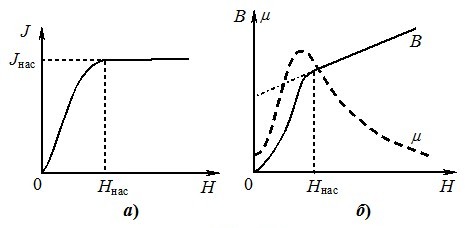
Ця крива наочно відображає особливості намагнічування феромагнетиків — нелінійність і ефект насичення: вже при порівняно невеликій величині \(H_{\text{нас}}\) в сердечнику намагніченість досягає максимального значення \(J_{\text{нас}}\) і далі не змінюється. Такий характер намагнічування пояснюється складними процесами впорядкування магнітних моментів доменів, яке завершується практично повною їхньою орієнтацією в напрямку поля. Тому намагніченість \(J_{\text{нас}}\) є дуже великою і близькою до теоретичного максимуму. Величина індукції \(B ( H)\), яка визначається виразом (3.10), при намагнічуванні теж спочатку зростає подібно до \(J ( H)\), рис. 3.6б, але на відміну індукція після насичення намагніченості продовжує потроху (значно повільніше, ніж зображено) зростати за лінійним законом:
\begin{equation} B(H)=B_m+\mu_0H,\qquad B_m=\mu_0J_{\text{нас}}. \end{equation}
Феромагнетики зазвичай мають полікристалічну структуру, тобто складаються з маленьких неупорядкованих кристалічних зерен — кристалітів. Тому макроскопічно феромагнітна речовина є ізотропним магнетиком, і формула (3.14) зберігає чинність. Але через нелінійність намагнічування проникність феромагнетика \(\mu\ne\textrm{const}\) і є не табличною характеристикою, а залежною від поля величиною
\begin{equation} \mu{(H)}=\frac{B(H)}{\mu_{0}H}. \end{equation}
Із кривої намагнічування випливає, що \(\mu(h)\) спочатку зростає, потім досягає максимуму поблизу насичення, і далі асимптотично спадає до одиниці, як показано на рис. 3.6б штриховою кривою.
Гістерезис. Ще однією особливістю феромагнетиків є часткова необоротність процесу намагнічування, яку ілюструє рис. 3.7.
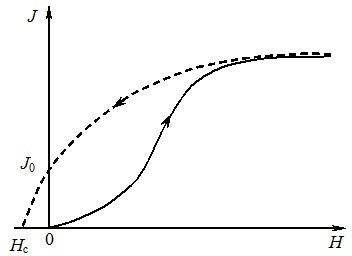
Якщо феромагнітний сердечник намагнітити по основній кривій до насичення (точка А), а потім почати зменшувати струм у котушці, то зміна \(J\) не буде поспівати за зміною \(H\), і феромагнетик буде розмагнічуватися не по шляху намагнічування А — \(0\), а по деякій кривій А — \(J_{0}\). Таке відставання намагніченості називається магнітним гістерезисом (“гістерезис” грецькою саме й означає відставання або спізнення). Через гістерезис при зменшенні напруженості \(H\) до \(0\) феромагнетик повністю не розмагнічується, в ньому зберігається деяка залишкова намагніченість \(J_0\). Тому для повного розмагнічування феромагнетика по котушці треба пропустити струм зворотнього напрямку, котрий створить необхідну для розмагнічування напруженість \(H_{\text{с}}\), яка називається коерцитивною силою.
Залежно від величини коерцитивної сили магнітні матеріали поділяють на магнітном’які та магнітнотверді. Перші мають малу величину \(H_{\text{с}}\), легко перемагнічуються змінним зовнішнім полем і за його відсутності є ненамагніченими. Із таких матеріалів виготовляють сердечники трансформаторів, електромагнітів та інших пристроїв. Напроти, магнітнотверді матеріали мають велику коерцитивну силу і тому зберігають намагніченість навіть у сильних розмагнічуючих полях. Вони, зокрема, використовуються для виготовлення постійних магнітів.
Унаслідок гістерезису при перемагнічуванні феромагнетика змінним струмом залежність \(B ( H)\) зображується на графіку замкненою кривою, що називається петлею гістерезису і виглядає, як на рис. 3.8а для магнітом’яких і на рис. 3.8б для магнітнотвердих матеріалів.
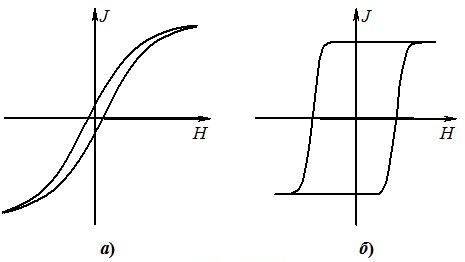
При цьому намагнічений магнітнотвердий феромагнетик фактично може перебувати тільки в якомусь із двох станів насичення, перехід між якими відбувається “стрибком”, тобто при дуже малій зміні напруженості в околі \(H_{\text{с}}\). Це зумовлює використання таких матеріалів у різноманітних логічних електронних схемах та накопичувачах інформації.
Доменна структура і спроможність до феромагнітного намагнічування є не у всіх кристалічних речовин і не при всіх температурах. У більшості феромагнетиків вона зменшується при нагріванні і зовсім зникає при характерній для кожного феромагнетика температурі, що називається точкою Кюрі. Це пояснюється тим, що в точці Кюрі змінюється взаємне розташування атомів (тип кристалічної ґратки) феромагнетика. Відтак існування доменів стає неможливим і феромагнетик перетворюється на звичайний парамагнетик. Але при охолодженні нижче точки Кюрі феромагнітні властивості речовини повністю відновлюються.
Контрольні запитання
1. Якою є загальна причина впливу речовини на магнітне поле?
2. Чим вплив речовини на магнітне поле відрізняється від впливу на електричне поле?
3. Що таке намагнічування та намагніченість речовини?
4. Що таке струми намагнічування? Чим вони відрізняються від “звичайних” струмів (струмів провідності)?
5. Чи придатні рівняння (2.1) і (2.4) для магнітного поля в речовині? Чому?
6. Запишіть і сформулюйте теорему про циркуляцію магнітного поля в речовині. Чи придатна вона для поля у вакуумі? Чому?
7. Чи є напруженість основним вектором магнітного поля? Чому?
8. Чи завжди виконується співвідношення (3.14)?
9. Що є спільного у впливі на магнітне поле між а) пара- та діамагнетиками і б) пара- та феромагнетиками?
10. У чому полягає та чим пояснюється відміна у впливі на магнітне поле між а) пара- та діамагнетиками і б) пара- та феромагнетиками?