physics.zfftt.kpi.ua

У розділі І було показано, що для електричного поля зарядів, окрім напруженості та потенціалу, які характеризують поле в кожній точці (локально), існують й інтегральні величини — потік і циркуляція, — котрі відображують “поведінку” поля на заданій поверхні чи лінії і містять важливу інформацію про його фундаментальні властивості. Нижче подібний аналіз проводиться для магнітного поля струмів у вакуумі. Розглядаються наступні питання:

2.1. Теорема Гаусса для магнітного поля

Магнітне поле, як і електричне, задля наочності зображують за допомогою ліній вектора \( \vec{B}\) або ліній магнітної індукції. Ці лінії відображають напрям і величину магнітного поля, але не є "силовими" лініями, бо безпосередньо не вказують напрямок магнітних сил.

Дослід свідчить, що лінії магнітного поля є завжди замкненими, тож кожна лінія, що входить всередину якоїсь замкненої поверхні, обов’язково десь виходить назовні. Згідно з геометричною інтерпретацією потоку (розділ І, п. 5), це означає, що потоки на вході та на виході замкненої поверхні завжди мають однакову величину і протилежний знак. Тому

потік вектора індукції магнітного поля крізь довільну замкнену поверхню дорівнює нулю:

\begin{equation} \oint\limits_{S}\vec{B}\,\mathrm{d}\vec{S}={0}. \tag{2.1} \end{equation}

У цьому полягає теорема Гаусса для магнітного поля. Вона відображає фундаментальний дослідний факт — відсутність у природі "магнітних зарядів", тобто особливих частинок, які би самі по собі мали здатність створювати магнітне поле подібну до здатності електронів або протони створювати електричне поле. Тому рівняння (2.1) є одним з основних рівнянь класичної електромагнітної теорії.

Наостанок зауважимо, що рівняння (2.1) “завдячує” замкненості ліній магнітного поля, тож є чинним для поля із замкненими лініями, незалежно від його природи. Зокрема, це стосується електричних полів, котрі створюється не зарядами, а нестаціонарними магнітними полями. Картина ліній подібних полів нагадує завихрення, що інколи виникають у потоці води в річці та в повітрі. Тому поля із замкненими лініями називаються вихровими полями. Тож

магнітне поле є вихровим силовим полем.

2.2. Теорема про циркуляцію магнітного поля струмів у вакуумі

Розглянемо тепер другу інтегральну характеристику магнітного поля — циркуляцію вектора \( \vec{B}\), що за означенням (розділ І, ф-ла (5.2а)) визначається як

\begin{equation} {C}=\oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}. \end{equation}

Циркуляція поля прямого струму. Визначимо спочатку циркуляцію поля одного нескінченного прямого провідника із струмом \(I\) по довільному плоскому контуру \(L\), розташованому, як показано на рис. 2.1а.

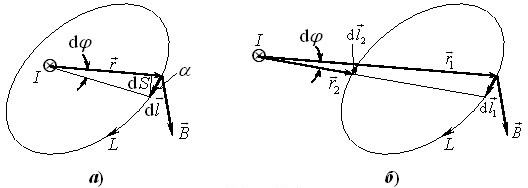
В цьому випадку задача не становить ніяких труднощів. Домовимось обходити контур за годинниковою стрілкою, тоді

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\oint\limits_{L}B\,\mathrm{d}l\cos\alpha, \tag{2.2} \end{equation}

а з рис. 2.1а зрозуміло, що

\begin{equation} \mathrm{d}l\cos\alpha=\mathrm{d}s=r\,\mathrm{d}{\varphi}. \end{equation}

Отже,

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\oint\limits_{L}Br\,\mathrm{d}{\varphi}. \end{equation}

Урахувавши, що індукція поля прямого струму визначається формулою (1.13), отримуємо:

\begin{equation} \begin{aligned} &\oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\frac{\mu_{0}I}{2\pi}\oint\limits_{L}\,\mathrm{d}\varphi \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}{I}. \end{aligned} \tag{2.3}\end{equation}

Для визначення циркуляції у випадку, коли струм не охоплюється контуром, розсічемо його радіальними променями на пари ділянок, як показано на рис. 2.1б. Тоді вклад в інтеграл (2.2) від кожної пари складе

\begin{equation} \begin{aligned} &{B_1}\,\mathrm{d}l_1\cos\alpha_1+B_2\,\mathrm{d}l_2\cos\alpha_2={}\\ &\quad{}=(B_{1}r_{1}-B_{2}r_{2})\mathrm{d}{\varphi}= {0}. \end{aligned} \end{equation}

Отже,

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}={0}. \tag{2.3а} \end{equation}

Теорема про циркуляцію. Отримані результати легко узагальнити на магнітне поле системи паралельних прямих струмів \(I_i\) (рис.2.2).

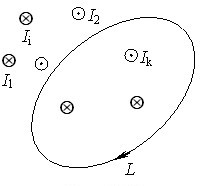
У такому випадку за принципом суперпозиції \( \vec{B}=\sum\limits_{i}\vec{B}_{i}\) і

\begin{equation} \oint\limits_{L}{\vec{B}\,\mathrm{d}\vec{l}} = \oint\limits_{L}{\sum\limits{{{{\vec{B}}}_{i}}\,\mathrm{d}\vec{l}}} = \sum\limits{\oint\limits_{L}{{{{\vec{B}}}_{i}}\,\mathrm{d}\vec{l}}}. \end{equation}

Кожен з інтегралів під знаком суми має значення або (2.3), або (2.3а) залежно від розташування струму \(I_i\) відносно контуру \(L\). Обидва ці випадки можна об’єднати, приписавши всім струмам, які охоплені контуром \(L\), окремий індекс \(k\). Тоді

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}\sum\limits_{k}I_{k}=\mu_{0}{I}, \tag{2.4} \end{equation}

де \(I\) — алгебраїчна сума струмів, які охоплені контуром інтегрування. При цьому знак “\(+\)” мають струми, напрямки яких пов’язані з обраним при інтегруванні напрямом обходу контуру правилом правого гвинта.

Можна довести, що отриманий результат є загальним. Він зберігає чинність і для провідників довільної форми та для об’ємних струмів, розподілених із заданою густиною \( \vec{j}\). Тож у загальному випадку сумарний струм \(I\) в рівнянні (2.4) визначається формулою:

\begin{equation} {I}=\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S}, \end{equation}

де \(S\) — довільна поверхня, що спирається на контур інтегрування \(L\). Відтак рівняння (2.4) набуває вигляду

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=\mu_{0}\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S} \tag{2.4а} \end{equation}

і є загальним виразом теореми про циркуляцію магнітного поля струмів у вакуумі:

циркуляція вектора індукції магнітного поля струмів у вакуумі по довільному замкненому контуру дорівнює сумарній силі струму, що охоплений цим контуром, помноженій на \(\mu_{0}\).

Таким чином, циркуляція магнітного поля по замкненому контуру на загал не дорівнює нулю. Відповідно до критерію потенціальності (розділ І, п. 5.1) це означає, що магнітне поле є непотенціальним полем, тобто, для нього не існує скалярної характеристики подібної до потенціалу \(\varphi \) кулонівського електричного поля.

2.3. Розрахунок магнітного поля струмів за допомогою теореми про циркуляцію

Практична значимість теореми про циркуляцію магнітного поля зумовлена тим, що вона спрощує розрахунки магнітних полів високої симетрії, подібно до теореми Гаусса у випадку електричних полів (розділ І, п. 5.2). Розглянемо декілька конкретних прикладів:

1. Поле прямого струму

2. Поле циліндра із струмом

3. Поле циліндричного шару із струмом

4. Поле ідеального соленоїда

5. Поле тороїда

Поле прямого струму. Перш за все продемонструємо переваги використання теореми про циркуляцію на прикладі поля нескінченного прямого провідника із струмом, для якого вже було отримано формулу індукції за допомогою закону Біо і Савара (п. 1.3).

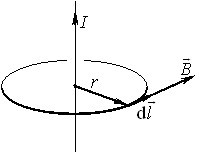
Позаяк індукція такого поля однакова по модулю і напрямлена по дотичній до кола з центром на провіднику, яке є лінією вектора \( \vec{B}\) (рис. 2.3), то

\begin{equation} \begin{aligned} &\oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=B\cdot{2\pi}r=\mu_{0}I \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {B}=\frac{\mu_{0}I}{2\pi{r}}, \end{aligned} \tag{2.5}\end{equation}

що збігається з формулою (1.14).

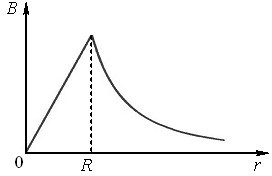
Поле циліндра із струмом. Розрахуємо тепер індукцію магнітного поля струму, що тече вздовж нескінченного суцільного циліндра радіуса \(R\) із немагнітної речовини. Будемо вважати, що в усіх точках перерізу циліндра (рис. 2.4) вектор густини струму \( \vec{j}=\mathrm{const}\) і напрямлений “до нас”.

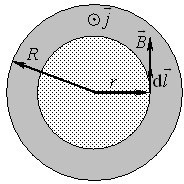
Очевидно, що таке поле, як і в попередньому прикладі, має осьову симетрію, і його індукція теж визначається виразом (2.5). Але тепер величина \(I\) залежить від розмірів контуру інтегрування \(L\) і має визначатися окремо для області всередині циліндра та поза ним.

Поле всередині циліндра (\( {r\le{R}}\)). У цьому випадку контур \(L\) (коло радіуса \(r\) на рис.2.4) охоплює частину всього струму, рівну

\begin{equation} {I}=j\cdot\pi{r^2}. \end{equation}

Отже, модуль індукції магнітного поля всередині циліндра дорівнює

\begin{equation} {B}=\frac{\mu_{0}jr}{2}, \tag{2.6} \end{equation}

вектор \( \vec{B}\) визначається, як

\begin{equation} \vec{B}=\frac{\mu_{0}[\vec{j},\vec{r}]}{2}. \tag{2.6а} \end{equation}

Поле поза циліндром (\( {r>R}\)). За такої умови при будь-якому радіусі контуру \(L\) проходить увесь струм

\begin{equation} {I}=j\cdot\pi{R^2}. \end{equation}

Тож індукція магнітного поля поза циліндром визначається формулою

\begin{equation} {B}=\frac{\mu_{0}jR^2}{2r}, \tag{2.7} \end{equation}

або

\begin{equation} \vec{B}=\frac{\mu_{0}R^2[\vec{j},\vec{r}]}{2r^2}. \tag{2.7а} \end{equation}

На рис. 2.5 показаний графік залежності \(B ( r)\) поля циліндра.

Поле циліндричного шару із струмом. Розглянемо ще й поле, що створюється поздовжнім струмом у циліндричному шарі (циліндрі з коаксіальною порожниною) із радіусами \(R_{1}\) і \(R_{2}\) (рис. 2.6), при рівномірному розподілі струму по перерізу із заданою густиною \( \vec{j}\).

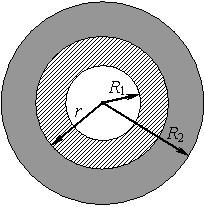
Це поле теж має осьову симетрію, і його розрахунок є аналогічним до попереднього, за винятком того, що він доповнюється розглядом поля в порожнині.

Поле в порожнині (\(r < R_1\)). При осьовій симетрії поля його індукція скрізь визначається загальним виразом (2.5). Але для будь-якого \(r < R_1\) величина \(I=0\), отже,

в порожнині поле відсутнє:

\begin{equation} \vec{B}={0}. \end{equation}

Поле всередині шару (\( {R_{1}}\le{r}\le{R_{2}}\)). У цьому випадку коло радіуса \(r\) охоплює частину всього струму, рівну

\begin{equation} {I}=l\cdot\pi{(r^2-R_{1}^{2})}. \end{equation}

Відповідно, індукція поля всередині циліндричного шару із струмом визначається формулою

\begin{equation} {B}=\frac{\mu_{0}j\left(r^2-R_{1}^{2}\right)}{2r}, \tag{2.8} \end{equation}

або

\begin{equation} \vec{B}=\frac{\mu_{0}[\vec{j},\vec{r}]}{2}\left(1-\frac{R_{1}^{2}}{r^2}\right). \tag{2.8а} \end{equation}

Поле назовні шару (\( {r > R_{2}}\)). Крізь будь-яке коло такого радіуса проходить увесь струм шару. Тому величина \(I\) не залежить від \(r\) і дорівнює

\begin{equation} {I}=j\cdot{\pi}\left(R_{2}^{2}-R_{1}^{2}\right) . \end{equation}

Отже, індукція поля назовні циліндричного шару із струмом визначається формулою

\begin{equation} {B}=\frac{\mu_{0}j\left(R_{2}^{2}-R_{1}^{2}\right)}{2r}, \tag{2.9} \end{equation}

або

\begin{equation} \vec{B}=\frac{\mu_{0}[\vec{j},\vec{r}]\left(R_{2}^{2}-R_{1}^{2}\right)}{2r^2}. \tag{2.9а} \end{equation}

Графік залежності \(B(r)\) наведено на рис. 2.7.

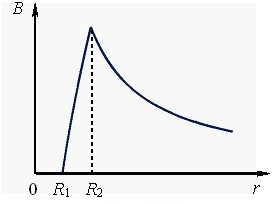
Варто звернути увагу на те, що поле суцільного циліндра і циліндричного шару назовні збігається із полем тонкого провідника розташованого на осі системи, по якому проходить увесь струм. Це ж вірно і для неоднорідного, але симетричного відносно осі розподілу густини струму \( \vec{j}(r)\).

Поле ідеального соленоїда. Ідеальним соленоїдом називається нескінченна циліндрична котушка, щільно намотана гранично тонким дротом в один шар (рис. 2.8а).

Примітка. Реальний соленоїд — це котушка, довжина котрої є сумірною із діаметром.

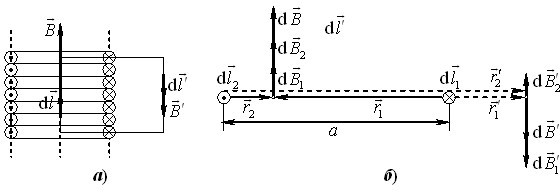
За допомогою закону Біо і Савара можна розрахувати магнітне поле тільки на осі соленоїда. А ось за допомогою теореми про циркуляцію поле ідеального соленоїда можна визначити в усьому просторі. Для цього проаналізуємо симетрію даного поля. Найперше констатуємо, що всі рівновіддалені від осі соленоїда точки є фізично еквівалентними, тож поле в них повинно мати однакову величину. Так само з міркувань симетрії випливає, що поле нескінченного соленоїда має осьовий напрямок, оскільки він є безальтернативним, тобто таким, для якого не існує інших рівноправних напрямів. Всередині соленоїда напрям \( \vec{B}\), як і для окремого витка, пов’язаний із струмом правилом правого гвинта, а назовні має бути протилежним. Це випливає із замкненості ліній \( \vec{B}\) і видно з рис. 2.8б, на якому показані вектори елементарних полів, створюваних парою діаметральних ділянок \( \mathrm{d}\vec{l}_{1}\) і \(\mathrm{d}\vec{l}_{2}\) одного витка всередині (\( {\mathrm{d}\vec{B}}\)) і назовні (\( {\mathrm{d}\vec{B}{}^{\,\prime }}\)). Крім того, поле \( \vec{B}{}^{\,\prime}\) має послаблюватися при віддаленні від соленоїда. Такий висновок випливає із закону Біо і Савара. Справді, відповідно до виразу (1.9а) модуль поля \( \mathrm{d}{B^{\,\prime}}\) двох показаних на рис. 2.8б ділянок дорівнює

\begin{equation} \begin{aligned} &\mathrm{d}B^{\,\prime}=\mathrm{d}B_{1}^{\,\prime}-\,\mathrm{d}B_{2}^{\,\prime} = \frac{\mu_{0}I\,\mathrm{d}l}{4\pi}\left(\frac{1}{r_{1}^{2}}-\frac{1}{r_{2}^{2}}\right)={}\\ &\quad{}=\frac{\mu_{0}I\,\mathrm{d}l}{4\pi}\cdot\frac{(r_{2}-r_{1})(r_{2}+r_{1})}{r_{1}^{2}r_{2}^{2}} . \end{aligned} \end{equation}

У цьому виразі \(r_{2} - r_{1} = d\) — діаметр витка, а \(r_{2} + r_{1} = 2 r\), де \(r\) — відстань від осі соленоїда до даної точки. Крім того, за винятком точок поблизу поверхні соленоїда, \(r_{1}r_{2}\approx r^2\). Отже,

\begin{equation} \mathrm{d}B^{\,\prime}\approx\frac{\mu_{0}Id\,\mathrm{d}l}{2\pi}\cdot\frac{1}{r^{3}}. \end{equation}

Зрозуміло, що так само мають спадати з відстанню поля й інших подібних парних ділянок, а отже й поле \( {B}^{\,\prime}\) всього соленоїда.

Для визначення поля за теоремою про циркуляцію виберемо прямокутний контур, який має бічну сторону \(l\) і розташований у площині діаметрального перерізу соленоїда, як показано на рис. 2.8а. При такій орієнтації контуру вектори індукції спрямовані паралельно до бічних і перпендикулярно до поперечних сторін контуру та на кожній бічній стороні мають незмінний модуль. В такому разі

\begin{equation} \oint\limits_{L}B_{l}\,\mathrm{d}l=Bl+B^{\,\prime}{l}, \end{equation}

і, згідно з теоремою про циркуляцію (2.4),

\begin{equation} \begin{aligned} &\left(B+B^{\,\prime}\right){l}=\mu_{0}NI \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {B}+B^{\,\prime} =\mu_{0}n{I}, \end{aligned} \tag{2.10}\end{equation}

де \(N\) — кількість витків соленоїда, що охоплені контуром, а \( {n}={N/l}\) — щільність намотки (кількість витків на одиницю довжини соленоїда).

Отриманий вираз означає, що при заданій величині \( {I}\) незалежно від розмірів прямокутника

\begin{equation} {B+B^{\,\prime} = \mathrm{const}}. \end{equation}

Але ця умова може виконуватися тільки при \( {B^{\,\prime}}={0}\), бо ця величина не може бути сталою, вона має зменшуватися при віддаленні від соленоїда.

Таким чином,

магнітне поле ідеального соленоїда існує тільки всередині, є однорідним і визначається формулою

\begin{equation} {B}=\mu_{0}{nI}. \tag{2.11} \end{equation}

Поле тороїда. Тороїдом називається дротяна котушка щільно намотана в один шар по всій поверхні тора (рис. 2.9), який будемо вважати немагнітним.

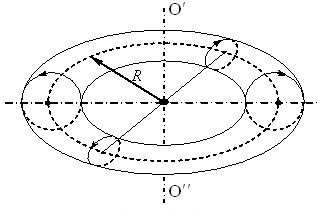
Примітка. Тор являє собою «математичний бублик», тобто тіло, утворене обертанням кола навколо осі, що розташована в площині кола поза його межами.

Розрахуємо поле тороїда з радіусами \(R_1\) і \(R_2\), кількістю витків \(N\), по якому тече струм \(I\).

Поле всередині тороїда. З міркувань симетрії очевидно, що всі точки кола з радіусом \(r\), яке проходить всередині тороїда (\(R_{1}\) < \(r\) < \(R_{2}\)) і має центр на осі системи \(\mathrm{O}'\mathrm{O}''\), є фізично еквівалентними. Тому в кожній з них вектор \( \vec{B}\) напрямлений перпендикулярно до площини витка і має однаковий модуль. Отже, циркуляція \( \vec{B}\) по такому колу

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=B\cdot{2\pi{r}}, \end{equation}

і за теоремою про циркуляцією (10.3)

\begin{equation} {B}=\frac{\mu_{0}NI}{2\pi{r}}, \tag{2.12} \end{equation}

де \(NI\) — повний струм, який охоплюється контуром інтегрування.

Цікаво, що поле всередині тороїда збігається із полем нескінченного прямого провідника із струмом \(I_{0} = NI\) розташованого на осі \(\mathrm{O}'\mathrm{O}''\) тороїда.

Формулу (10.11) можна також записати у вигляді

\begin{equation} {B}=\mu_{0}nI\frac{R_{0}}{r}, \tag{2.12а} \end{equation}

де

\begin{equation} {n}=\frac{N}{2\pi{R_0}} \end{equation}

 — щільність витків, тобто кількість витків на одиницю довжини середньої лінії тороїда (кола з радіусом \(R_{0} =( R_{1} + R_{2})/2\)).

Поле поза тороїдом. Якщо коловий контур радіуса \(r\) розташований поза тороїдом, то при \(r < R_1\) струм узагалі не перетинає поверхню контуру, а при \(r > R_{2}\) струм від кожного витка перетинає її двічі і в протилежних напрямках. Тож в обох випадках

\begin{equation} \oint\limits_{L}\vec{B}\,\mathrm{d}\vec{l}=0\quad \Rightarrow \quad \vec{B}={0}. \end{equation}

Таким чином, як і в соленоїді,

за межами тороїда магнітне поле відсутнє.

Принагідно відмітимо, що з виразу (2.12а) можна отримати формулу індукції магнітного поля ідеального соленоїда, бо його можна формально трактувати як тороїд радіуса \( {R}_{0}\to\infty \). У такому разі \((R_{0} / r) = 1\), і вираз (2.12а) переходить у (2.11).

Наостанку нагадаємо, що в наведених прикладах соленоїд і тороїд розглядалися ідеалізовано, як сукупність щільно складених гранично тонких кілець із струмом. Але насправді кожна з котушок утворює гвинтову лінію. Через це при протіканні струму по витках існує й деяке перенесення заряду, тобто додатковий струм, уздовж осі соленоїда та вздовж середньої лінії тороїда. Тому поза соленоїдом є магнітне поле таке, як поза циліндром із струмом, а поза тороїдом є поле таке, як у кільця радіуса \(R_{0}\). Але, через те, що котушки зазвичай намотують тонким дротом, крок гвинтової лінії й указані поздовжні струми є дуже малими, тож створювані ними поля є неістотними.