physics.zfftt.kpi.ua

Між зарядженими частинками крім електричної спостерігається ще й магнітна взаємодія, яка зумовлена їхнім рухом і здійснюється за допомогою магнітного поля. У цьому можна переконатися на простому досліді. Якщо по двох паралельних дротинах пропустити струми, то вони або притягнуться одна до одної, або відштовхнуться залежно від напрямків струму. Позаяк струм не порушує електричної нейтральності провідників, указана взаємодія зумовлена саме рухом зарядів і здійснюється за польовою схемою: кожен із провідників створює своє магнітне поле, котре діє на інший. При цьому взаємодія припиняється при вимкненні струму в будь-якому з провідників. Це означає, що

магнітне поле створюється рухомими зарядами і діє лише на рухомі заряди.

(Принагідно зауважимо, що магнітні поля породжується також змінними електричними полями (див. розділ V).)

Нижче розглянуті наступні питання:

1.1. Вектор \( \vec{B} \)

Властивості магнітного поля і його кількісні характеристики можна встановити, вивчаючи на досліді магнітні сили, що діють на провідники або контури зі струмом. Але магнітне поле безпосередньо діє не на провідник як такий, а на носії струму, тому логічніше виходити із властивостей сил, які діють у магнітному полі на окремі рухомі заряди. Одразу зауважимо, що, позаяк магнітні сили визначаються не лише величиною заряду, а й величиною та напрямком швидкості його руху, вони мають більш складні властивості, ніж електричні.

Стосовно магнітних сил, які діють на рухомі заряди, дослід показує наступне.

1. У кожній точці магнітного поля серед безлічі напрямів є один такий, при русі зарядженої частинки вздовж котрого магнітне поле на неї не діє. Цей напрям прийнятий за напрям магнітного поля. Інакше говорячи,

при русі зарядженої частинки вздовж напряму магнітного поля магнітна сила на неї не діє.

2. Напрям магнітної сили завжди є перпендикулярним одночасно і до напрямку поля, і до напрямку руху зарядженої частинки, а її модуль \(F_{m}\) є прямо пропорційний величині заряду \(|q|\), його швидкості \({v}\) і синусу кута \(\alpha \) між напрямком швидкості та напрямком поля:

\begin{equation} {F_m}\sim |q|\cdot{v}\cdot\sin\alpha . \end{equation}

Інакше це можна записати як

\begin{equation} {F_m}=B\cdot |q|\cdot{v}\cdot\sin\alpha, \tag{1.1} \end{equation}

де величина

\begin{equation} {B}=\frac{F_m}{|q|\cdot{v}\cdot\sin\alpha} \tag{1.2} \end{equation}

не залежить від заряду та характеристик руху частинки і є силовою характеристикою самого поля. Вона називається індукцією магнітного поля або магнітною індукцією. Аби магнітна індукція вказувала також напрям магнітного поля, її розглядають як вектор \(\vec{B}\), так що формула (1.1) набуває вигляду:

\begin{equation} \vec{F}_{m}=q[\vec{v}\vec{B}], \tag{1.3} \end{equation}

де квадратні дужки означають векторний добуток. Отже, напрям сили, що діє на рухомий точковий заряд у магнітному полі, визначається правилом правого гвинта («свердлика») з урахуванням знаку заряду (рис. 1.1а):

якщо правий гвинт обертати від вектора швидкості заряду до вектора магнітної індукції найкоротшим шляхом, то він буде угвинчуватись у напрямку магнітної сили, що діє на додатній заряд.

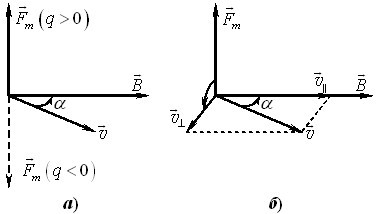
При зміні знаку заряду напрям магнітної сили змінюється на протилежний.

Варто зауважити, що магнітну силу (1.3) зазвичай називають “силою Лоренца”, що не зовсім точно, бо, строго говорячи, силою Лоренца називається повна сила, що діє на заряд в електромагнітному полі; вона складається з електричної та магнітної компонент:

\begin{equation} \vec{F}=\vec{F}_{e}+\vec{F}_{m}=q\bigl(\vec{E}+[\vec{v}\vec{B}]\bigr). \end{equation}

Формула (1.3) є однією з основних у теорії магнітного поля. Зокрема, вона дозволяє дати пряме означення вектора \(\vec{B}\). Якщо швидкість заряду розкласти на паралельну та перпендикулярну до напрямку поля складові так, що \(\vec{v}=\vec{v}_{\parallel}+\vec{v}_{\bot}\) (рис. 1.1б), то, враховуючи, що \({v}_{\bot}=v\sin\alpha \), з виразів (1.1)—(1.3) виходить:

\begin{equation} \vec{B}=\frac{[ \vec{F}{{{\vec{v}}}_{\bot }} ]}{qv_{\bot }^{2}}. \tag{1.4} \end{equation}

Таким чином,

індукція магнітного поля чисельно дорівнює силі, з якою воно діє на одиничний заряд, що рухається перпендикулярно до напрямку поля з одиничною швидкістю.

Одиниця індукції називається тесла (Тл). Її означення буде дано пізніше, а зараз укажемо, що в полі з індукцією \(B=1\) Тл на заряд \(q=1\) Кл при \({v}_{\bot} =1\) м/с діє сила \(F_{m}=1\) H.

1.2. Магнітне поле точкового заряду

Формула (1.3) дозволяє обчислити силу, що діє на заряджену частинку в кожній точці магнітного поля. Відтак за допомогою законів механіки можна знайти закон руху частинки в полі. Тому однією з основних задач теорії є встановлення способів розрахунку магнітних полів. Ці способи, як і у випадку електричного поля, ґрунтуються на виразі індукції магнітного поля окремого точкового заряду та принципі суперпозиції.

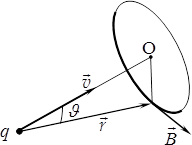
Із експериментальних даних установлено, що для поля заряду \(q\), що рухається з нерелятивістською швидкістю \( \vec{v}\) (рис. 1.2), індукція \(\vec{B}\) в будь-якій точці визначається формулою

\begin{equation} \vec{B}=k\frac{q[\vec{v}\vec{r}]}{r^3},\qquad B=k\frac{qv_{\bot}}{r^2}, \tag{1.5} \end{equation}

в якій \(\vec{r}\) — радіус-вектор даної точки поля відносно заряду і \({v}_{\bot}=v\sin\vartheta \) — перпендикулярна до \(\vec{r}\) складова швидкості заряду.

Коефіцієнт пропорційності \(k\) залежить від вибраної системи одиниць і в СІ дорівнює

\begin{equation} k = 10^{-7} Гн/м, \end{equation}

де Гн (генрі) — одиниця індуктивності (див. розділ V). Числове значення \(k\) є зручним для обчислень, але в літературі при записі формул використовують так звану магнітну сталу \(\mu _{0}=4\pi k\), і формули (1.5) записують у вигляді:

\begin{equation} \vec{B}=\frac{\mu_{0}}{4\pi}\frac{q\left[\vec{v}\vec{r}\right]}{r^3},\qquad B=\frac{\mu_0}{4\pi}\frac{qv_{\bot}}{r^2}. \tag{1.5а} \end{equation}

Згідно з цією формулою, вектор \(\vec{B}\) напрямлений перпендикулярно до площини векторів \(\vec{v}\) і \(\vec{r}\), тобто по дотичній до кола, що проходить в цій площині через задану точку і має центр О на лінії вектора \(\vec{v}\), як показано на рис. 1.2. Зауважимо, що, позаяк величина \(\vec{r}\) змінюється з часом, поле точкового заряду є нестаціонарним (залежним від часу): \(\vec{B}=\vec{B}(t) \).

Вирази (1.3) і (1.5а) дозволяють визначити силу \(\vec{F}_{m1}\), яка діє на заряд \(q_{1}\), що рухається із швидкістю \(\vec{v}_{1}\) у магнітному полі іншого заряду \(q_{2}\), який має швидкість \(\vec{v}_{2}\):

\begin{equation} \vec{F}_{m1}=q_{1}[\vec{v}_{1}\vec{B}_{2}],\quad \text{де} \quad \vec{B}_{2}=\frac{\mu_{0}}{4\pi}\frac{q_{2}[\vec{v}_{2}\vec{r}]}{r^{3}}. \end{equation}

Аналогічно можна виразити і силу \(\vec{F}_{m2}\), що діє на заряд \(q_{2}\) з боку поля заряду \(q_{1}\). Слід зазначити, що позаяк індукції полів і магнітні сили залежать не лише від взаємного розташування, а й від величин та напрямків швидкостей зарядів, магнітна взаємодія між ними є набагато складнішою, ніж електрична. Зокрема, магнітні сили на загал не задовольняють третій закон Ньютона. Виняток становить лише випадок, коли два заряди мають однакову за величиною й напрямом швидкість \({v}_{1}=v_{2}={v}\) і розташовані один проти одного (рис. 1.3).

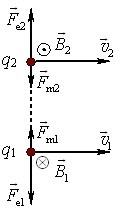
У цьому випадку \(\vec{F}_{m1}=-\vec{F}_{m2}\), причому

\begin{equation} {F}_{m1}=F_{m2}=\frac{\mu_0}{4\pi}\frac{q_1 q_2 v^2}{r^2}. \tag{1.6} \end{equation}

Між зарядами крім магнітних діють ще й електричні сили \(\vec{F}_{e2}=-\vec{F}_{e1}\), величина яких визначається законом Кулона:

\begin{equation} {F}_{e1}=F_{e2}=\frac{1}{4\pi\epsilon_{0}}\frac{q_{1}q_{2}}{r^2}. \tag{1.7} \end{equation}

У випадку, що розглядається, відношення сил магнітної та електричної взаємодії складає

\begin{equation} \frac{F_{m}}{F_{e}}=\mu_{0}\epsilon_{0}{v^2}. \end{equation}

Величина \(\mu _{0}=4\pi \cdot 10^{-7}\) Гн/м, а \(\varepsilon _{0}=9\cdot 10^{-9}/(4\pi )\) Ф/м (див. розділ I, п. 1.2), тож

\begin{equation} \mu_{0}\varepsilon_{0}=\frac{1}{9\cdot 10^{16}}\ \left(\frac{с}{м}\right)^2=\frac{1}{c^2}. \end{equation}

де \(c=3\cdot 10^{8}\) м/с — швидкість світла у вакуумі. Таким чином

\begin{equation} \frac{F_{m}}{F_{e}}=\frac{v^2}{c^2}. \tag{1.8} \end{equation}

1.3. Магнітне поле струмів

Із співвідношення (1.8) видно, що при нерелятивістських швидкостях руху магнітна взаємодія між зарядами є несумірно слабшою за електричну. Тому магнітні сили (1.3) є істотними і знаходять практичне застосування тільки за відсутності помітних електричних полів і тільки в потужних магнітних полях, які створюються не поодинокими зарядами, а інтенсивними потоками заряджених частинок, тобто макроскопічними електричними струмами. На практиці магнітні поля створюють, пропускаючи електричний струм по провідниках відповідної конфігурації, як от обмотки ротора електродвигуна або трансформатора чи електромагніта. Властивості магнітного поля струмів і його дія на заряди та інші струми розглядаються в наступних пунктах:

1.3.1. Закон Біо і Савара

1.3.2. Розрахунок магнітного поля за законом Біо і Савара

1.3.1. Закон Біо і Савара

Індукцію магнітного поля провідника із струмом можна розрахувати на основі виразу (1.5) для поля точкового заряду та принципу суперпозиції, позаяк кожну елементарну ділянку \(\mathrm{d}\vec{l}\) провідника із струмом (рис. 1.4) можна розглядати як рухомий точковий заряд.

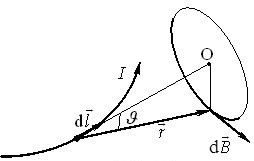
Його величина \(\d q\) дорівнює сумарному заряду зосереджених на цій ділянці носіїв струму, а швидкість руху збігається із їхньою дрейфовою швидкістю \(\vec{u}\). Отже, в заданій точці простору \(\vec{r}\) гранично мала ділянка струму створює елементарне магнітне поле

\begin{equation} \mathrm{d}\vec{B}=k\frac{\mathrm{d}q[\vec{u}\vec{r}]}{r^3}. \end{equation}

Зауважимо, що це поле, на відміну від поля (1.5), є стаціонарним \(\mathrm{d}\vec{B}=\mathrm{const}\), бо кожен носій, який виходить із ділянки \(\mathrm{d}\vec{l}\) тієї ж миті заміщується носієм, який входить в неї.

Величина \(\d q\) у ділянці \(\mathrm{d}\vec{l}\) дорівнює

\begin{equation} \mathrm{d}q=en\,\mathrm{d}V=enS\,\mathrm{d}{l}, \end{equation}

де \(e\), \(n\) — заряд і концентрація носіїв, \(S\) — площа перерізу провідника. Отже,

\begin{equation} \mathrm{d}\vec{B}=k\frac{Sen\,\mathrm{d}l\,[\vec{u},\vec{r}]}{r^3}=k\frac{S[en\,\mathrm{d}l\,\vec{u},\vec{r}]}{r^3}. \end{equation}

Вектори \(\mathrm{d}\vec{l}\) і \(\vec{u}\) мають однаковий напрям, тож \( \d l\, \vec{u}=u\,\mathrm{d}\vec{l}\), і можна записати:

\begin{equation} \mathrm{d}\vec{B}=k\frac{enuS[\mathrm{d}\vec{l},\vec{r}]}{r^3}. \end{equation}

Згідно з формулами (розділ III, (1.3), (1.4б)), \({enuS} ={I}\), отже

\begin{equation} \mathrm{d}\vec{B}=k\frac{I[\mathrm{d}\vec{l},\vec{r}]}{r^3}. \end{equation}

Урахувавши, що \(k = \mu _{0} /4 \pi \), отримуємо остаточні вирази:

\begin{equation} \mathrm{d}\vec{B}=\frac{\mu_{0}I[\mathrm{d}\vec{l},\vec{r}]}{4\pi{r^3}}, \tag{1.9} \end{equation} \begin{equation} \mathrm{d}B=\frac{\mu_{0}I\,\mathrm{d}{l}\sin\vartheta}{4\pi{r^2}}. \tag{1.9а} \end{equation}

Вирази (1.9), (1.9а) спочатку були встановлені на основі дослідних фактів і виражають закон Біо і Савара. Згідно з ними вектор \(\mathrm{d}\vec{B}\) напрямлений перпендикулярно до площини векторів \(\mathrm{d}\vec{l}\) і \(\vec{r}\) так само, як поле \(\vec{B}\) позитивного точкового заряду, що рухається в напрямку струму. Тобто,

напрям магнітного поля струму збігається із напрямом обертання правого гвинта (свердлика), що укручується в напрямку струму.

Зауважимо також, що для точок на напрямку струму на даній ділянці вектори \(\mathrm{d}\vec{l}\) і \(\vec{r}\) є колінеарними, і \(\mathrm{d}\vec{B}={0}\).

1.3.2. Розрахунок магнітного поля за законом Біо і Савара

Закон Біо і Савара разом із принципом суперпозиції дозволяє розрахувати індукцію магнітного поля будь-якого заданого провідника із струмом. Для цього треба знайти вираз (1.9) для довільної нескінченно малої ділянки провідника \(\mathrm{d}\vec{l}\) і проінтегрувати його по всій довжині провідника:

\begin{equation} \vec{B}=\int\limits_{L}\,\mathrm{d}\vec{B}. \tag{1.10} \end{equation}

Визначити індукцію у такий спосіб принципово можна завжди. Але розв’язати задачу аналітично і отримати формулу, що визначає поле в будь-якій точці, можна тільки в окремих випадках за сприятливої конфігурації струму. Розглянемо деякі з них:

1. Поле відрізка та нескінченного прямого струму

2. Поле на осі кільцевого струму. Магнітний момент

Поле відрізка прямого струму. Якщо струм \(I\) протікає по відрізку прямого провідника (рис. 1.5), то в будь-якій точці P, згідно із законом Біо і Савара (1.9), елементарні поля \(\mathrm{d}\vec{B}\) напрямлені перпендикулярно до площини, в якій лежить ця точка та відрізок струму (на рис. 1.5 “до нас”). Тож вектор \(\vec{B}\) результуючого поля напрямлений так само, і його модуль (1.10) визначається інтегралом уздовж відрізка

\begin{equation} {B}=\frac{\mu_{0}I}{4\pi}\int\limits_{1}^{2}\frac{\mathrm{d}{l}\sin\vartheta}{r^2} \tag{1.11} \end{equation}

від початкової точки 1 до кінцевої точки 2.

Для обчислень позначимо як \(R\) відстань від точки P до лінії струму і \(r\) — відстань від точки O до довільної точки на відрізку провідника. Тоді величина

\begin{equation} {l}=R\operatorname{ctg}\vartheta \end{equation}

є функцією \({l}(\vartheta) \) кута \({\vartheta}\) (див. рис. 1.5).

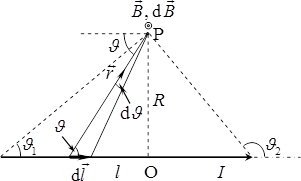
Тому величина \(\mathrm{d}{l}\) під інтегралом (1.11) є модулем приросту цієї функції і за правилами диференціального числення визначається через похідну:

\begin{equation} \mathrm{d}l=|l^{\prime}(\vartheta)\mathrm{d}{\vartheta}| \quad \Rightarrow \quad \mathrm{d}l=R\left(\frac{1}{\sin^2\vartheta}\right)\mathrm{d}{\vartheta}. \end{equation}

Урахуємо також, що \({r}=(R/\!\sin\vartheta) \), тоді

\begin{equation} {B}=\frac{\mu_{0}I}{4\pi{R}}\int\limits_{\vartheta_{1}}^{\vartheta_{2}}\sin\vartheta\,\mathrm{d}\vartheta, \end{equation}

і

\begin{equation} {B}=\frac{\mu_{0}I}{4\pi{R}}(\cos\vartheta_{1}-\cos\vartheta_{2}), \tag{1.12} \end{equation}

де кути \({\vartheta_{1}}\) і \(\vartheta_{2}\) визначають довжину відрізка та положення його кінців відносно заданої точки і відраховуються від напряму струму; \(R\) — відстань від точки до лінії струму.

Поле нескінченного прямого струму. При збільшенні довжини відрізка \({l}\) кут \(\vartheta_{1}\) буде зменшуватись, а \(\vartheta_{2}\) — зростати так, що при \({l}\to\infty\) \(\vartheta_{1}\to{0}\) і \(\vartheta_{2}\to\pi \). Отже, відповідно до виразу (1.12), індукція магнітного поля нескінченного прямого провідника із струмом визначається формулою

\begin{equation} {B}=\frac{\mu_{0}I}{2\pi{R}}. \tag{1.13} \end{equation}

Напрям вектора \(\vec{B}\), як завжди, пов’язаний із напрямом струму правилом правого гвинта.

Поле на осі кільцевого струму. Визначимо тепер індукцію \(\vec{B}\) поля на осі колового контуру (кільця) радіуса \(R\) із струмом \(I\) в залежності від відстані \(r\) до центра (рис. 1.6).

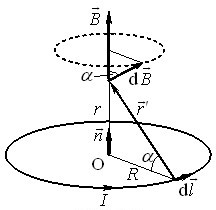
Приступаючи до обчислень за виразом (1.10) одразу врахуємо, що на осі кільця елементарні поля \(\mathrm{d}\vec{B}\) від усіх ділянок орієнтовані під однаковим кутом \(\alpha \) до осі. Тому перпендикулярні відносно осі складові всіх векторів \(\mathrm{d}\vec{B}\) є компенсованими, і результуючий вектор \(\vec{B}\) поля всього кільця напрямлений вздовж осі. Отже, для визначення величини \(B\) слід інтегрувати тільки осьові складові елементарних полів \(\mathrm{d}{{B}_{\parallel }}=\mathrm{d}B\cos \alpha \):

\begin{equation} {B}=\oint\limits\mathrm{d}B\cos\alpha. \tag{1.14} \end{equation}

(Кружальце на символі інтеграла означає, що інтегрування проводиться по замкненому контуру.)

Виражаючи \(\d B\) за формулою (1.9а) і враховуючи, що в ній для точок на осі \(\vartheta=90^{\circ}\) і \({r}=\mathrm{const}\), отримаємо:

\begin{equation} \begin{aligned} &{B}=\frac{\mu_{0}I\cos\alpha}{4\pi{r^{\prime 2}}}\oint\limits\,\mathrm{d}l=\frac{\mu_{0}I\cos\alpha}{4\pi{r^{\prime 2}}}2\pi{R} \quad \Rightarrow \\ &\quad\Rightarrow \quad {B}=\frac{\mu_{0}IR\cos\alpha}{2r^{\prime 2}}. \end{aligned} \end{equation}

Із рис. 1.5 видно, що \(\cos\alpha=R/r^{\prime} \) і \({r^{\prime}}=(r^2+R^2)^{1/2}\), отже,

\begin{equation} {B}=\frac{\mu_{0}IR^2}{2(r^2+R^2)^{3/2}}. \tag{1.15} \end{equation}

У векторному вигляді

\begin{equation} \vec{B}=\frac{\mu_{0}IR^2\vec{n}}{2(r^2+R^2)^{3/2}}, \tag{1.15а} \end{equation}

де \(\vec{n}\) — орт (одиничний вектор) додатньої нормалі до площини кільця, тобто нормалі, що пов’язана з напрямом струму правилом правого гвинта.

При \(r=0\) отримуємо формулу індукції магнітного поля в центрі кільцевого струму:

\begin{equation} \vec{B}=\frac{\mu_{0}I\vec{n}}{2R}. \tag{1.16} \end{equation}

Напрям магнітного поля на осі кільцевого струму теж визначається правилом правого гвинта, котре в даному випадку звучить так:

якщо правий гвинт обертати в напрямку струму в кільці, то він буде вкручуватись у напрямку магнітного поля, створюваного цим струмом на осі кільця.

Магнітний момент контуру зі струмом. Помноживши у формулі (1.15а) чисельник і знаменник на \(2\pi\), отримаємо:

\begin{equation} \vec{B}=\frac{\mu_{0}}{4\pi}\frac{2lS\vec{n}}{(r^2+R^2)^{3/2}}, \end{equation}

де \(S = \pi R^{2}\) — площа кільця.

Цей вираз показує, що індукція магнітного поля в заданій точці на осі кільця визначається не просто струмом \({I}\), а величиною

\begin{equation} \vec{p}=IS\vec{n}\qquad \text{або} \qquad\vec{p}=I\vec{S}, \tag{1.17} \end{equation}

де \(\vec{n}\) — орт (одиничний вектор) додатньої нормалі до поверхні контуру, а \(\vec{S}\) — «вектор поверхні» контуру. Це поняття можна узагальнити і на неплоскі контури.

Вектор (1.17) називається магнітним моментом контуру і є загальною характеристикою його магнітних властивостей. Вектор \(\vec{p}\) визначає магнітне поле кільця також і в інших точках та магнітні поля контурів іншої конфігурації. Дія зовнішнього поля на контур із струмом теж визначається його магнітним моментом. Одиницею магнітного моменту є \(1\ А\cdot м^{2}\).

З урахуванням сказаного формула індукції магнітного поля на осі кільцевого струму набуває вигляду:

\begin{equation} \vec{B}=\frac{\mu_0}{4\pi}\frac{2\vec{p}}{(r^2+R^2)^{3/2}}. \tag{1.18} \end{equation}

Окремий інтерес являють властивості поля на великих відстанях від кільця або при дуже малих його розмірах, коли \(r \gg R\). У такому разі, нехтуючи величиною \(R^{2}\), для поля на осі отримаємо формулу

\begin{equation} \vec{B}=\frac{\mu_0}{4\pi}\frac{2\vec{p}}{r^3}=k_{m}\frac{2\vec{p}}{r^3}, \tag{1.19} \end{equation}

яка є ідентичною до формули ((4.6), розділ I) для напруженості поля на осі електричного диполя. Так само й інші магнітні властивості малого контуру із струмом і відповідні електричні властивості електричного диполя виражаються ідентичними формулами. Тому малий контур із струмом називають магнітним диполем. Принагідно зауважимо, що через дуже малі розміри магнітного диполя форма контура, що його уособлює, не має значення.

1.4. Дія магнітного поля на провідники із струмом

Проходження струму не порушує електричної нейтральності провідників, тому на них не діє зовнішнє електричне поле. Але через дрейф (упорядкований рух) носіїв на провідники зі струмом діє магнітне поле. Далі розглядаються питання:

1.4.1. Сила Ампера

1.4.2. Контур із струмом у магнітному полі

1.4.1. Сила Ампера

Закон Ампера. Сила, що діє в магнітному полі на провідник із струмом, називається силою Ампера. Її походження не важко зрозуміти. За наявності струму електрони-носії дрейфують уздовж провідника, і на них діє відповідна усереднена магнітна сила (1.3), що визначається величиною дрейфової швидкості носіїв. Під дією цієї сили електрони на шляху вільного пробігу отримують поперечний імпульс, який відтак передають іонам кристалічної ґратки провідника при зіткненнях. Як наслідок, виникає сила, що діє на провідник як ціле, тобто — сила Ампера. Таким чином, магнітне поле діє на провідник із струмом опосередковано, через носії струму. Тож сила Ампера діє як на рухомі, так і на нерухомі провідники, і її величина дорівнює результуючій магнітній силі, що діє на всі носії струму в провіднику.

Визначимо згідно з описаним механізмом амперову силу \(\mathrm{d}\vec{F}\), яка діє на елементарну ділянку \(\mathrm{d}\vec{l}\) провідника із струмом \(I\), що вміщений у задане магнітне поле з індукцією \(\vec{B}\) (рис. 1.7).

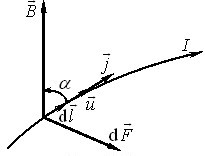
На зосереджені в ділянці носії із сумарним зарядом \(\d q\), що рухаються із дрейфовою швидкістю \(\vec{u}\), діє магнітна сила

\begin{equation} \mathrm{d}\vec{F}=\mathrm{d}q[\vec{u},\vec{B}]. \end{equation}

Якщо позначити заряд носія, їхню концентрацію та площу перерізу провідника відповідно як \(e\), \(n\) і \(S\), то

\begin{equation} \mathrm{d}q=en\,\mathrm{d}V=enS\,\mathrm{d}{l}. \end{equation}

Тут враховано, що для однаково напрямлених векторів \(\mathrm{d}\vec{l}\) і \(\vec{u}\) \(\mathrm{d}l\,\vec{u}\equiv{u}\,\mathrm{d}\vec{l}\). Множник перед векторним добутком, відповідно до формул (1.3) і (1.4б), розділ II, дорівнює силі струму в провіднику, отже,

\begin{equation} \begin{aligned} &\d\vec{F}=I[ \d\vec{l},\vec{B} ],\\ &\mathrm{d}F=IB\,\mathrm{d}l\sin\alpha. \end{aligned} \tag{1.20} \end{equation}

Формули (1.20) виражають закон Ампера, котрий визначає дію магнітного поля на елементарну ділянку струму.

Напрям сили Ампера визначається правилом правого гвинта (рис.1.7):

якщо правий гвинт обертати від напрямку струму в даній ділянці провідника до напрямку магнітного поля, то він буде укручуватись у напрямку сили Ампера, що діє на дану ділянку.

Зауважимо, що це правило є еквівалентним відомому із школи правилу лівої руки.

Сила Ампера, що діє на весь провідник, складається із сил, які діють на окремі його ділянки, і в загальному випадку визначається інтегруванням виразу (1.20) по всій довжині провідника:

\begin{equation} \begin{aligned} &\vec{F}=\int\limits\,\mathrm{d}\vec{F},\\ &\vec{F}=I\int\limits{[ \d\vec{l},\vec{B} ]}. \end{aligned} \tag{1.21} \end{equation}

В окремих випадках формула (1.21) спрощується. До прикладу, якщо довільний провідник знаходиться в однорідному полі \(\vec{B}=\mathrm{const}\), то вектор індукції можна винести з-під інтеграла, не змінюючи порядку множників у векторному добутку. Тоді вийде:

\begin{equation} \begin{aligned} &\vec{F}=I\left[\int\limits\,\mathrm{d}\vec{l},\vec{B}\right] \quad \Rightarrow \quad \vec{F}=I[\vec{l},\vec{B}],\\ &{F}=IlB\sin\alpha, \end{aligned} \tag{1.22} \end{equation}

де \( \int\limits\,\mathrm{d}\vec{l}=\vec{l} \) — вектор проведений від початкової до кінцевої точки провідника (рис. 1.8), \(l\) — відстань між цими точками, а для прямолінійного провідника — його довжина.

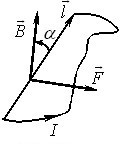
Найпростішою є ситуація, коли маємо прямолінійний провідник розташований перпендикулярно до напрямку однорідного поля. Тоді

\begin{equation} {F}={IBl}. \tag{1.23} \end{equation}

Відмітимо також, що при \(\alpha =0\) або \(\pi \) величина \(F=0\). Отже,

магнітне поле не діє на прямий провідник із струмом, якщо він орієнтований паралельно до напрямку поля.

1.4.2. Контур із струмом у магнітному полі

Вирази (1.20) і (1.21) визначають дію магнітного поля на якусь частину замкненого контуру із струмом. Проте зазвичай у полі перебуває весь контур, і при зміні його орієнтації та переміщенні в полі амперові сили виконують роботу. Тому контур із струмом має відповідну енергію у зовнішньому магнітному полі. Далі розглядаються наступні питання:

1) Момент сил, що діє на контур у магнітному полі.

2) Сила, що діє на магнітний диполь у неоднорідному полі.

3) Енергія магнітного диполя у зовнішньому полі.

4) Робота сили Ампера.

Момент сил, що діє на контур. Аби знайти силу, що діє на контур із струмом \(I\) в зовнішньому магнітному полі \(\vec{B}\), інтегрування у виразі (1.21) треба провести по всьому цьому контуру:

\begin{equation} \vec{F}=I\oint\limits{[ d\vec{l},\vec{B} ]}. \end{equation}

При цьому, якщо поле однорідне (\(\vec{B}=\mathrm{const}\)), то

\begin{equation} \vec{F}=I\left[\oint\limits\,\mathrm{d}\vec{l},\vec{B}\right]={0}, \tag{1.24} \end{equation}

бо інтеграл у цьому виразі є сумою безлічі векторів \(\mathrm{d}\vec{l}\), які утворюють замкнену лінію.

Таким чином, в однорідному магнітному полі сила Ампера, що діє на будь-який замкнений контур як ціле, дорівнює нулю. Але це не означає, що поле ніяк не діє на контур, бо амперові сили, прикладені до окремих ділянок контуру, не є компенсованими. Аби в цьому переконатися, проаналізуємо дію однорідного поля \(\vec{B}\) на жорстку прямокутну рамку із струмом \(I\) і сторонами \(a\) і \(b\) (рис. 1.9а).

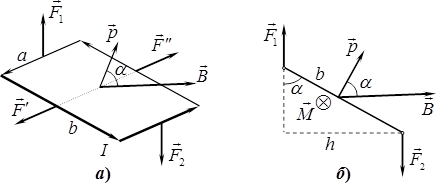
Поле є паралельним, а площина рамки перпендикулярною до площини рисунка (передня сторона рамки і сторона, де струм іде "від нас", наведені жирніше).

При \(\vec{B}=\mathrm{const}\) сили (1.22), прикладені до паралельних сторін рамки, мають однакові модулі і протилежні напрямки: \(\vec{F}{}'=-\vec{F}{}'' \) і \(\vec{F}_{1}=-\vec{F}_{2}\). При цьому перші дві сили діють по одній лінії в площині рамки і є компенсованими. Але дві інші не компенсовані, бо вони намагаються повернути рамку навколо осі \({F}'-{F}'' \) і утворюють так звану "пару сил". Обертальна дія пари сил відносно осі \( {F}'-{F}'' \) визначається вектором моменту пари \(\vec{M}\), який за правилом правого гвинта напрямлений "від нас" (рис. 1.9б) і має модуль \(M\) рівний добутку модуля однієї із сил \(F_{1} = F_{2} = F\) на плече пари (відстань \(h\) між лініями дії сил):

\begin{equation} M = Fh. \end{equation}

Із рис. 1.9б видно, що \( {h}=b\sin\alpha \), а за формулою (1.23) \( {F=IaB}\), отже,

\begin{equation} {M}=IabB\sin\alpha. \end{equation}

Величина \({Iab}=IS={p}\) є модулем магнітного моменту рамки, тож

\begin{equation} {M}=pB\sin\alpha\quad \Rightarrow \quad \vec{M}=[\vec{p},\vec{B}] . \tag{1.25} \end{equation}

Отриманий вираз показує, що магнітне поле намагається повернути рамку так, аби зорієнтувати її магнітний момент у напрямку поля (\(\alpha =0\)), а площину рамки — перпендикулярно до поля. В такому положенні рамки не лише сили \({F}' \) і \({F}'' \), а й \(\vec{F}_{1}\) та \(\vec{F}_{2}\) діють уздовж однієї прямої, тож момент \(\vec{M}={0}\), і контур перебуває у стані рівноваги. Ця рівновага є стійкою, позаяк при повороті рамки навколо осі, напрям якої не збігається з напрямом поля, виникає момент, що намагається повернути рамку у вихідне положення. При протилежній орієнтації (\(\alpha =180\)°) рамка теж буде перебувати в рівновазі, але нестійкій: при щонайменшій зміні орієнтації вона перевернеться у положення \(\alpha =0\).

Можна довести, що в однорідному полі формула (1.25) є правильною для контуру якої завгодно форми та розмірів. Але для довільного контуру в неоднорідному полі вона втрачає чинність. Виняток становить магнітний диполь (малий контур із струмом). У цьому випадку поле в усіх точках контуру можна вважати однаковим, тому для магнітного диполя формула (1.25) лишається придатною. Отже,

на контур із струмом у зовнішньому магнітному полі діє момент сил, який при малих розмірах контуру визначається виразом (1.25).

Сила, що діє на магнітний диполь у неоднорідному полі. В неоднорідному полі вектор \(\vec{B}\ne\mathrm{const}\), тому у виразі (1.22) його не можна винести з-під інтеграла і отримати результат (1.24). А це означає, що

в неоднорідному магнітному поліна на контур із струмом, окрім моменту, діє певна результуюча сила Ампера

\begin{equation} \vec{F}=I\int\limits{[ \d\vec{l},\vec{B} ]}\ne 0. \end{equation}

Це наочно ілюструє рис. 1.10, на якому зображено в профіль круглий контур із струмом (кільце), розміщений в осесиметричному неоднорідному магнітному полі.

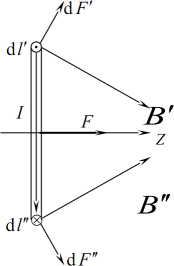
В показаному положенні на всі елементарні ділянки кільця діють однакові за модулем симетричні сили \(\mathrm{d}\vec{F}\), які створюють сумарну силу \(\vec{F}\), спрямовану вздовж осі Z. При іншій орієнтації контуру з’являється ще й момент сил, який намагається перевести контур у показане положення. Тому у неоднорідному полі вільний магнітний диполь під дією амперових сил буде й обертатися, і рухатися поступально. Так само поводиться електричний диполь у зовнішньому електричному полі (див. розділ І, п. 4). При цьому вирази крутних моментів і результуючих сил в обох випадках теж виявляються ідентичними. Зокрема, сила, що діє на магнітний диполь в осесиметричному неоднорідному полі визначається формулою:

\begin{equation} {F}_{z}=p_{z}\frac{\partial{B}}{\partial{z}}, \tag{1.26} \end{equation}

де \({{p}_{z}}=p\cos \alpha \) — проекція магнітного моменту диполя на напрям поля, а \( (\partial{B}/\partial{z}) \) — градієнт індукції, що є мірою неоднорідності поля.

Енергія магнітного диполя в зовнішньому полі. Вище було показано, що в однорідному зовнішньому полі вільний контур із струмом (магнітний диполь) розташовується у площині перпендикулярній до напрямку поля. Це є положення стійкої рівноваги, тож для зміни орієнтації контуру на нього має подіяти момент якихось сторонніх сил, аби подолати момент амперових сил, які утримують контур у положенні стійкої рівноваги. Згідно із законами механіки, робота цих сторонніх сил при повороті контуру йде на зміну його енергії:

\begin{equation} W_2-W_1=A_{стор}. \tag{1.24} \end{equation}

На загал енергія контуру складається із механічної енергії та енергії його взаємодії із зовнішнім полем. Але при повільному повороті навколо нерухомої осі механічна енергія контуру не змінюється, і робота, що виконується моментом прикладених сил, йде тільки на зміну магнітної енергії контуру у зовнішньому полі. З механіки відомо, що робота моменту сили при повороті тіла визначається загальним виразом

\begin{equation} {A}=\int\limits{M}\,\mathrm{d}{\alpha}, \end{equation}

де \(\mathrm{d}{\alpha}\) — елементарний кут повороту. Очевидно, що при повільному повороті контуру моменти сторонніх і амперових сил мають однаковий модуль (1.25). Тому при зміні кута \(\alpha \) від \(\alpha _{1}\) до \(\alpha _{2}\) зміна магнітної енергії контуру в зовнішньому полі складає:

\begin{equation} \begin{aligned} &{W_2}-W_{1}=pB\int\limits_{\alpha_1}^{\alpha_2}\sin\alpha\,\mathrm{d}\alpha \quad \Rightarrow {}\\ &\quad{}\Rightarrow\quad {W}_{2}-W_{1}=pB\cos\alpha_{1}-pB\cos\alpha_{2}. \end{aligned} \end{equation}

Цей результат передбачає, що поле однорідне (\(B = \const\)). Але для малого контуру (магнітного диполя) він зберігає чинність і в неоднорідному полі. Тому на основі отриманого виразу можна зробити висновок, що

магнітний диполь у зовнішньому магнітному полі має енергію, що визначається формулою:

\begin{equation} {W}=-\vec{p}\vec{B}, \tag{1.27} \end{equation}

або

\begin{equation} {W}=-p_{z}{B}, \tag{1.27а} \end{equation}

де \(p_{z}\) — проекція магнітного моменту диполя на напрям зовнішнього поля.

Робота сили Ампера. Сила Ампера здатна рухати провідник із струмом і виконувати над ним механічну роботу. На цьому принципі, зокрема, працюють електричні двигуни. Але провідник із постійним струмом завжди є частиною якогось провідного контуру. Тому не будемо зосереджуватися на окремому провіднику, а одразу розглянемо роботу сил Ампера при переміщенні в магнітному полі замкненого контуру із струмом. У загальному випадку різні точки контуру здійснюють різні переміщення і на них діють різні за величиною та напрямом амперові сили. Тому спочатку розглянемо роботу \({\delta}'A=I\vec{F}\,\mathrm{d}\vec{r}\), що виконується при елементарному переміщенні \(\mathrm{d}\vec{r}\) однієї елементарної ділянки контуру \(\mathrm{d}\vec{l}\) (рис. 1.11).

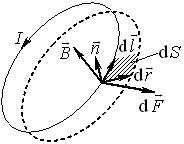
Згідно з виразом (1.20),

\begin{equation} {\delta }'A=I[\mathrm{d}\vec{l},\vec{B}]\cdot \mathrm{d}\vec{r}. \tag{1.28} \end{equation}

Отже, ця робота визначається векторно-скалярним (інакше — мішаним) добутком трьох векторів: \(\mathrm{d}\vec{l}\), \(\vec{B}\) і \(\mathrm{d}\vec{r}\). Властивості мішаного добутку трьох векторів \([\vec{a},\vec{b}]\cdot\vec{c}\) вивчаються у векторній алгебрі. При цьому доводиться, що при так званих циклічних перестановках множників добуток не змінюються, а саме, \([\vec{a},\vec{b}]\cdot\vec{c}\equiv[\vec{c},\vec{a}]\cdot\vec{b}\). Тому вираз (1.28) можна переписати як

\begin{equation} {\delta}'A =I[\mathrm{d}\vec{r},\mathrm{d}\vec{l}]\cdot\vec{B}. \end{equation}

У цьому виразі вектор \([\mathrm{d}\vec{r},\mathrm{d}\vec{l}]\) напрямлений по нормалі \(\vec{n}\) до площинки \(\d S\), а його модуль \(\mathrm{d}r\,\mathrm{d}l\sin\alpha=\mathrm{d}{S}\) дорівнює величині цієї площинки, тож

\begin{equation} [\mathrm{d}\vec{r},\mathrm{d}\vec{l}]=\vec{n}\,\mathrm{d}{S} \end{equation}

і

\begin{equation} \begin{aligned} &{\delta }'A = I\vec{B}\cdot\vec{n}\,\mathrm{d}S=IB_{n}\,\mathrm{d}S \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \delta А = I\d'\Phi, \end{aligned} \end{equation}

де \(\d'\Phi\) — магнітний потік крізь площадку \(\d S\).

Очевидно, що \(\d'\Phi\) є частиною приросту потоку \(\d\Phi\) крізь усю поверхню контуру при його елементарному переміщенні в полі, а \({\delta }'A\) — відповідною частиною повної елементарної роботи \(\delta A\), що виконується при цьому, отже,

\begin{equation} \delta A=I\d \Phi. \tag{1.29} \end{equation}

Повна робота при скінченному переміщенні контуру із струмом у магнітному полі дорівнює

\begin{equation} A=I\cdot\Delta\Phi=I(\Phi_2-\Phi_1). \tag{1.29а} \end{equation}

Таким чином,

при переміщенні контуру із струмом у магнітному полі сили Ампера виконують роботу рівну добутку сили струму в контурі на зміну магнітного потоку крізь поверхню, обмежену цим контуром.

Зауважимо, що коли знак роботи є істотним, при обчисленні потоків слід використовувати додатні нормалі до поверхні контуру, які є пов’язані з напрямом струму правилом правого гвинта.

У зв’язку з отриманим результатом виникає наступне питання. Позаяк амперові сили виконують роботу, вони можуть надавати провідникам із струмом кінетичної, а при наявності, крім магнітного, й інших полів — ще й потенціальної енергії. Але амперові сили є результатом дії на заряди магнітних лоренцових сил (1.3), які є поперечними і ні за яких умов роботи не виконують. То ж звідки береться енергія, за рахунок якої виконують роботу амперові сили? Відповідь полягає в тому, що коли контур із струмом починає рухатися в неоднорідному магнітному полі, то для збереження величини струму на початковому рівні в контурі мають з’явитися додаткові сторонні сили, за рахунок яких і виконується робота (1.29а). Детальніше це питання розглядається в розділі V.