physics.zfftt.kpi.ua

Розглянуті локальні закони електричного струму дозволяють встановити зв’язки між характеристиками струму та електричного поля не лише в кожній точці провідника, а й на кожній ділянці електричного кола, або ланцюга, тобто з’єднаних між собою провідників, приладів і пристроїв, які утворюють систему провідних контурів для струму. Далі розглядаються найпростіші нерозгалужені кола, котрі включають тільки один контур.

Розглянуті такі питання:

2.1. Сторонні сили. ЕРС

Сторонні сили. Раніше говорилося, що для протікання стаціонарного електричного струму потрібний замкнений провідний контур. Але одного цього замало, бо крім носіїв струму в провіднику є й протилежно заряджені частинки, що своїм електричним полем перешкоджають вільному рухові носіїв по контуру. Тому для підтримування струму в провіднику на носії мають діяти якісь інші сили, що діють проти сил указаного електричного поля і здатні переміщувати носії вздовж провідника. Зрозуміло, що такі сили не можуть створюватися зарядами самого провідника і мають зовнішнє походження. Тому вони називаються сторонніми силами.

Через наявність у провіднику із струмом сторонніх сил у виразах закону Ома для густини струму (1.10) і (1.10а) має стояти сумарна напруженість поля кулонівських та сторонніх сил:

\begin{equation} \vec{j}=\sigma \bigl( {{{\vec{E}}}_{\text{к}}}+{{{\vec{E}}}_{\text{cт}}} \bigr). \tag{2.1} \end{equation}

Теоретично сторонні сили можна створити у різний спосіб. Зазвичай для цього в контур включають спеціальні пристрої — джерела струму. Дія джерел струму ґрунтується теж на різних принципах, але в приладах малої потужності найчастіше використовують хімічні джерела — “батарейки” і акумулятори.

Розглянемо, як діє найпростіше коло, що складається із внутрішньої ділянки (джерела) і зовнішньої ділянки у вигляді провідника, котрий через ключ К приєднаний до полюсів (вивідних контактів) джерела (рис. 2.1).

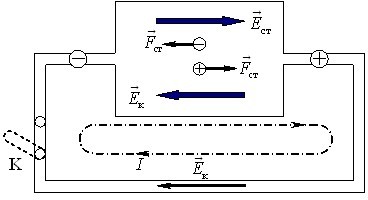
Всередині джерела під дією сторонніх сил певна кількість електронів (носіїв струму) переходить з одного полюса на інший, створюючи між ними відповідну різницю потенціалів і кулонівське електричне поле \(\vec{E}_{\text{к}}\) всередині джерела та на зовнішній ділянці. При розімкненому ключі це поле не спричинює струму, бо всередині джерела воно компенсується полем сторонніх сил, а назовні між полюсами для носіїв немає неперервного провідного шляху. Але після замикання ключа надлишкові електрони з негативного полюса під дією кулонівського поля починають рухатися по зовнішній ділянці і з’єднуватися з надлишковими зарядами на позитивному полюсі. Якби в джерелі на електрони не діяли сторонні сили, це призвело би до практично миттєвої нейтралізації полюсів і припинення руху носіїв по колу. Та насправді електрони, що приходять по зовнішній ділянці кола на позитивний полюс, підхоплюються сторонніми силами і, всупереч дії кулонівського поля всередині джерела, знову переміщуються на негативний полюс. Тож, доки діють сторонні сили, в колі зберігається електричне поле і напрямлений рух (дрейф) носіїв, тобто — електричний струм. Можна сказати, що джерело струму "переганяє" носії струму від одного полюса до іншого, долаючи кулонівське поле всередині джерела, подібно до насоса, котрий переганяє воду від вхідного до вихідного отвору, долаючи опір рухові води в трубопроводі.

Спад напруги та ЕРС. Через розсіювання носіїв у провіднику, вони втрачають енергію впорядкованого руху. Тому для підтримання струму ці втрати мають компенсуватися за рахунок роботи сил, які забезпечують струм. На довільній ділянці кола (рис. 2.2) це можуть бути і кулонівські \(\vec{F}_{\text{к}}\), і сторонні \(\vec{F}_{\text{ст}}\) сили.

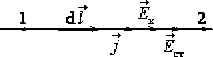
Отже, при елементарному переміщенні \(\mathrm{d}\vec{l}\) уздовж провідника над носіями із загальним зарядом \(q\) виконується робота

\begin{equation} \begin{aligned} &\delta A=\delta A_{\text{к}}+\delta A_{\text{ст}} = \vec F_{\text{к}} \,\mathrm{d}\vec l +\vec F_{\text{ст}}\,\mathrm{d} \vec l ={}\\ &\quad{}= q\vec E_{\text{к}} \,\mathrm{d}\vec l +q\vec E_{\text{ст}}\,\mathrm{d} \vec l. \end{aligned} \end{equation}

Для всієї ділянки між точками 1 і 2 маємо:

\begin{equation} \begin{aligned} &A=A_{\text{к}}+A_{\text{ст}} ={}\\ &\quad{}= q\int\limits_{1\to2}\vec E_{\text{к}} \,\mathrm{d}\vec l +q\int\limits_{1\to2}\vec E_{\text{ст}}\,\mathrm{d} \vec l. \end{aligned} \tag{2.2}\end{equation}

де інтегрування ведеться вздовж провідника.

Робота \(A\) є прямо пропорційною до перенесеного носіями заряду \(q\), тож відношення \(A/q\) не залежить від \(q\) і є характеристикою сумарного силового поля в провіднику. Воно позначається символом \(U\) і називається спадом напруги на заданій ділянці кола:

\begin{equation} {U}=\frac{A}{q}. \tag{2.3} \end{equation}

На елементарній ділянці спад напруги

\begin{equation} \mathrm{d}U=\frac{\delta{A}}{q}. \tag{2.3а} \end{equation}

Таким чином,

спадом напруги на заданій ділянці кола називається відношення роботи всіх сил, які діють на носії струму, до перенесеного по цій ділянці заряду.

Відповідно до даного означення і виразу (2.2),

\begin{equation} U= \int\limits_{1\to2}\vec E_{\text{к}} \,\mathrm{d}\vec l +\int\limits_{1\to2}\vec E_{\text{ст}}\,\mathrm{d} \vec l. \end{equation}

Кулонівське поле є потенціальним (див. розділ І, п. 2), тож перший доданок дорівнює різниці потенціалів на кінцях ділянки:

\begin{equation} \int\limits_{1\to{2}}\vec{E}\,\mathrm{d}\vec{l}=\varphi_1-{\varphi_2}. \tag{2.4} \end{equation}

Другий доданок характеризує поле сторонніх сил. Він позначається символом \(\mathscr{E}\) і називається електрорушійною силою (ЕРС) на даній ділянці кола:

\begin{equation} \mathscr{E}=\frac{{A}_{\text{ст}}}{q} =\int\limits_{1\to2}\vec E_{\text{ст}}\,\mathrm{d} \vec l. \tag{2.5} \end{equation}

Отже,

електрорушійною силою на даній ділянці кола називається відношення роботи сторонніх сил, які діють на носії струму, до перенесеного по цій ділянці заряду.

Ураховуючи означення (2.3) і (2.5), можна записати наступний загальний вираз для спаду напруги на ділянці кола:

\begin{equation} {U}=\varphi_{1}-\varphi_{2}+\mathscr{E}. \tag{2.6} \end{equation}

При цьому на однорідній ділянці, тобто такій, де відсутні сторонні сили, \(\mathscr{E}\) = 0, і спад напруги дорівнює різниці потенціалів на кінцях:

\begin{equation} {U}=\varphi_{1}-\varphi_{2}. \tag{2.6а} \end{equation}

Це означає, що на зовнішній ділянці кола робота по переміщенню зарядів дорівнює

\begin{equation} A=q(\varphi_{1}-\varphi_{2}) \end{equation}

і виконується тільки кулонівським електричним полем. Всередині джерела струму, де \(\mathscr{E}\ne0\), вказана робота виконується обома силовими полями і дорівнює

\begin{equation} {A}=qU=q(\varphi_{1}-\varphi_{2}+\mathscr{E}) . \end{equation}

А ось при обході замкненого контуру \(\varphi_{1}=\varphi_{2}\), і спад напруги у всьому контурі, тобто сума спадів напруги на всіх ділянках,

\begin{equation} {U}=\mathscr{E}. \tag{2.6б} \end{equation}

Отже, відповідно до (2.3), повна робота, що виконується над носіями струму в замкненому контурі дорівнює роботі тільки сторонніх сил:

\begin{equation} {A}=q\mathscr{E}. \tag{2.7} \end{equation}

Це пояснюється тим, що через потенціальність кулонівського поля сума його робіт на зовнішній \( {{A}'_{\text{к}}}=q( {{\varphi }_{1}}-{{\varphi }_{2}} ) \) та на внутрішній \( {{A}''_{\text{к}}}=q( {{\varphi }_{2}}-{{\varphi }_{1}} ) \) ділянках замкненого контуру дорівнює нулю. Тож одні лише кулонівські сили принципово не можуть забезпечити електричний струм. Відповідно,

електричний струм в колі існує виключно завдяки енергії, що надається носіям джерелом струму.

Тому роль сторонніх можуть виконувати тільки ті сили, робота і циркуляція поля котрих на даному провідному контурі є відмінною від нуля:

\begin{equation} \oint\limits\vec E_{\text{ст}}\,\mathrm{d} \vec l\ne0. \end{equation}

При цьому фізична природа та конкретне походження сторонніх сил не має принципового значення.

Що ж до кулонівського поля, то воно, хоч і не дає енергії для протікання струму, виконує в контурі важливу “диспетчерську” функцію — переносить енергію від джерела до інших ділянок.

Наостанок зробимо ще дві ремарки. По-перше, з означень (2.5) і (2.6) випливає, що ЕРС та спад напруги, як і різниця потенціалів, вимірюються у вольтах (\(\text{В}\)). І, по-друге, всі згадані величини є алгебраїчними; їхні знаки визначаються напрямками кулонівського поля та поля сторонніх сил відносно напрямку переміщення від початкової до кінцевої точки заданої ділянки кола. Детальніше про це говориться в п. 2.5.

2.2. Узагальнений закон Ома

Вище говорилося, що для практики важливо знати зв’язок між струмом і полем не лише в точці, а й на окремих ділянках і в усьому колі в цілому. Цей зв’язок визначається відомим законом Ома, який був установлений дослідним шляхом. Але, виходячи із співвідношень (2.2) і (2.3), указаний закон можна отримати й теоретично.

Розглянемо струм у тонкому провіднику, в якому струм рівномірно розподіляється по площі перерізу, так що густина струму

\begin{equation} {j}=\frac{I}{S}, \tag{2.8} \end{equation}

і вектори густини струму \(\vec{j}\) та полів \(\vec{E}_{\text{к}}\), \(\vec{E}_{\text{ст}}\) і \(\vec{E}=\vec{E}_{\text{к}}\) + \(\vec{E}_{\text{ст}}\) спрямовані вздовж провідника.

(Зауважимо, що в теорії термін “тонкий” означає не величину перерізу, а рівномірність розподілу по ньому струму, і на практиці цей критерій задовольняють всі електричні кола.)

На малій ділянці \(\mathrm{d}{l}\) провідника елементарна робота \(\delta A\), яку виконують над носіями всі сили, дорівнює

\begin{equation} \delta{A}=qE\,\mathrm{d}{l}, \end{equation}

або, відповідно до закону Ома (1.9а) і виразу (2.8),

\begin{equation} \delta{A}=q\rho{l}\frac{\mathrm{d}l}{S}. \end{equation}

З іншого боку, згідно з означенням (2.3а),

\begin{equation} \delta{A}=q\,\mathrm{d}{U}, \end{equation}

де \(\mathrm{d}{U}\) — спад напруги на ділянці \(\mathrm{d}{l}\). Отже,

\begin{equation} \mathrm{d}U=\rho{l}\frac{\mathrm{d}l}{S}. \end{equation}

Проінтегрувавши цей вираз по всій довжині провідника з урахуванням того, що для стаціонарного струму \({I}=\mathrm{const}\) по всій довжині, отримаємо:

\begin{equation} {U}=\int\limits_{l}I\rho\frac{\mathrm{d}l}{S}=I\int\limits_{l}\rho\frac{\mathrm{d}l}{S}. \tag{2.9} \end{equation}

У цьому виразі величина

\begin{equation} {R}=\int\limits_{l}\rho\frac{\mathrm{d}l}{S} \tag{2.10} \end{equation}

залежить тільки від розмірів і конфігурації (форми) провідника та властивостей його речовини і називається електричним опором.

Таким чином, струм і спад напруги на довільній ділянці кола пов’язані співвідношеннями

\begin{equation} {U=IR} \tag{2.11} \end{equation}

або

\begin{equation} {I}=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\mathscr{E}}{R}, \tag{2.11а} \end{equation}

які виражають узагальнений закон Ома:

сила струму в довільній ділянці електричного кола дорівнює відношенню спаду напруги на цій ділянці до її опору.

Закон Ома в такій редакції називається узагальненим, оскільки вираз (2.11а) є чинним як для неоднорідної ділянки кола, де на носії діють і кулонівські, і сторонні сили, так і для однорідної ділянки, де діють лише кулонівські сили. В останньому випадку в (2.11а) \(\mathscr{E}=0\), і

\begin{equation} {I}=\frac{\varphi_{1}-\varphi_{2}}{R}. \tag{2.12} \end{equation}

У підручниках з елементарної фізики цей вираз називають законом Ома для ділянки кола:

сила струму в (однорідній) ділянці кола дорівнює відношенню різниці потенціалів на кінцях ділянки до її опору.

Відповідно, при обході всього замкненого контуру \(\varphi_{1}=\varphi_{2}\) і

\begin{equation} {I}=\frac{\mathscr{E}}{R_{0}}, \end{equation}

або

\begin{equation} {I}=\frac{\mathscr{E}}{R+r}, \tag{2.13} \end{equation}

де \(R_{0} = R + r\) — опір всього кола, \(R\) — опір зовнішньої ділянки кола, або навантаження, і \(r\) — внутрішній опір джерела струму (рис. 2.3).

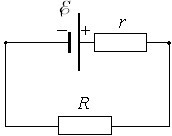
Цю формулу називають законом Ома для повного кола:

сила струму в замкненому колі дорівнює відношенню ЕРС, яка діє в ньому, до повного опору кола.

Формулу (2.13) можна переписати у вигляді

\begin{equation} {IR}+Ir=\mathscr{E}. \tag{2.13а} \end{equation}

Величини \(IR\) та \(Ir\) визначають спади напруги на однорідній зовнішній і неоднорідній внутрішній ділянці кола, відповідно. При цьому згідно з (2.12) \(IR = \varphi _{1}-\varphi _{2}\), тож

\begin{equation} \varphi_{1}-\varphi_{2}=\mathscr{E}-Ir . \tag{2.14} \end{equation}

Отже, різниця потенціалів на полюсах джерела не збігається з ЕРС. Так само не збігаються і спади напруги на цих двох ділянках, попри те, що вони мають спільні крайні точки — полюси джерела.

Зауважимо також, що, тоді як співвідношення (2.11а) виконується для будь-якої ділянки будь-якого кола, формула (2.13) є чинною тільки для найпростішого кола (рис. 2.3), що містить тільки один провідний контур.

2.3. Електричний опір

Опір однорідного провідника. Електричний опір спричинюється розсіюванням носіїв у провіднику із струмом і в загальному випадку визначається інтегральною формулою (2.10). Але на практиці зазвичай використовують однорідні провідники (\(\rho = \mathrm{const}\)) сталого поперечного перерізу (\(S = \mathrm{const}\)) по всій довжині \(l\). В такому разі

\begin{equation} {R}=\frac{\rho}{S}\int\limits_{l}\,\mathrm{d}{l}\quad \Rightarrow \quad {R}=\rho\frac{l}{S}. \tag{2.15} \end{equation}

У деяких випадках замість опору зручніше використовувати обернену величину \(\Lambda=(1/R) \), яка називається провідністю і визначається формулою

\begin{equation} \Lambda=\sigma\frac{S}{l}, \tag{2.15а} \end{equation}

де \(\sigma = (1/ \rho )\) — питома електропровідність речовини провідника.

Електричний опір вимірюється в омах (Ом), а провідність — у сіменсах (См), \(1\ \text{См} = 1\ \text{Ом}^{-1}\).

Опір провідника залежить не лише від його довжини та перерізу, а й від температури. Як показує дослід, при нагріванні опір металів зростає і в доволі широкому діапазоні температур виражається формулою:

\begin{equation} {R}=R_{0}(1+\alpha{t}) , \tag{2.16} \end{equation}

де \(t\) — температура за шкалою Цельсія, \(R_{0}\) — опір провідника при температурі \(0\)°C, і \(\alpha \) (\(1\)/K) — таблична константа, що називається температурним коефіцієнтом опору і показує відносну зміну опору провідника при зміні температури на \(1\) К.

Зростання опору металевих провідників при нагріванні пояснюється зростанням швидкості теплового руху \({v}\) і, згідно з (1.7), зменшенням часу вільного пробігу носіїв \(\langle{\tau}\rangle \). Через це збільшується питомий опір речовини \(\rho \) (1.10а), тож і опір провідника \(R\). В інших провідних середовищах — напівпровідниках і провідниках другого роду (електролітах) — опір теж залежить від температури, але на відміну від металів, при нагріванні зменшується. Це пояснюється тим, що в указаних речовинах при підвищенні температури суттєво зростає концентрація носіїв струму, так що зменшення їхнього часу вільного пробігу перестає бути визначальним.

З’єднання резисторів. Електричний опір є робочим параметром резисторів — найпростіших приладів, які присутні практично в усіх електричних схемах. Резистор по суті є просто зразком провідної речовини із заданим опором \(R\). Для резисторів використовують матеріали з малою електропровідністю, що дозволяє отримувати великі значення опору при малих розмірах резисторів.

В електричних і електронних схемах використовують як поодинокі резистори, так і різні з’єднання (комбінації) резисторів. Але при розрахунках часто буває зручно все з’єднання замінити одним еквівалентним резистором із опором, при якому струми в усіх інших ділянках кола лишаються незмінними. Тож опір еквівалентного резистора має бути таким, що напруга і струм у ньому збігаються з напругою та струмом на всьому з’єднанні.

Встановимо формули для розрахунку еквівалентного опору найпростіших з’єднань резисторів — послідовного та паралельного.

Послідовне з’єднання. В такому з’єднанні всі резистори сполучені в ланцюг так, як показано на рис. 2.4а.

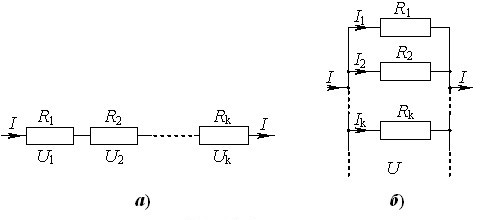
При цьому струм у всіх резисторах однаковий, а напруга на ланцюзі дорівнює сумі напруг на всіх з’єднаних резисторах:

\begin{equation} {I}_{k}={I},\qquad {U}=\sum\limits_{k}U_{k}. \end{equation}

Відповідно, опір з’єднання

\begin{equation} R_{\text{пос}} = \frac{U}{I}=\frac{1}{I}\sum\limits_{k}U_{k}=\sum\limits_{k}\frac{U_k}{I_k}, \end{equation}

тобто

\begin{equation} R_{\text{пос}} = \sum\limits_{k}R_{k}. \tag{2.17} \end{equation}

Отже,

еквівалентний опір послідовного з’єднання дорівнює сумі опорів усіх резисторів, які з’єднані.

Зокрема, коли послідовно з’єднані \(n\) однакових резисторів із опором \(R_{1}\) кожен, то опір з’єднання

\begin{equation} R_{\text{пос}} = nR_{1}. \tag{2.17а} \end{equation}

Паралельне з’єднання. Схема такого з’єднання показана на рис. 2.4б. Очевидно, що в цьому випадку напруга на всіх резисторах однакова і дорівнює напрузі на всьому з’єднанні, а величина струму, що проходить через з’єднання, згідно із законом збереження заряду, дорівнює сумі струмів у кожному із з’єднаних резисторів:

\begin{equation} {U_{k}}={U},\qquad {I}=\sum\limits_{k}{I_k}. \end{equation}

Тому для опору з’єднання маємо:

\begin{equation} \begin{aligned} &R_{\text{пар}}=\frac{U}{I}=\frac{U}{\sum\limits_k I_k} \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad \frac{1}{R_{\text{пар}}}=\frac{\sum\limits_k I_k} {U}=\sum\limits_k\frac{I_k}{U_k}. \end{aligned} \end{equation}

Звідси випливають такі розрахункові формули:

\begin{equation} \frac{1}{R_{\text{пар}}}=\sum\limits_k\frac{1}{R_k} \tag{2.18} \end{equation}

або

\begin{equation} \Lambda_{\text{пар}} = \sum\limits_{k}\Lambda_{k}. \tag{2.18а} \end{equation}

Отже,

еквівалентна провідність паралельного з’єднання резисторів дорівнює сумі провідностей всіх з’єднаних резисторів.

Якщо паралельно з’єднані \(n\) однакових резисторів опором \(R_{1}\) кожен, то згідно з формулою (2.18)

\begin{equation} R_{\text{пар}} = \frac{R_1}{n}. \tag{2.19а} \end{equation}

Для двох паралельно з’єднаних двох резисторів \(R_{1}\) і \(R_{2}\) також можна записати просту пряму формулу розрахунку еквівалентного опору:

\begin{equation} R_{\text{пар}} = \frac{R_{1}R_{2}}{R_1+R_2}. \tag{2.19б} \end{equation}

Отримані формули дозволяють розраховувати й опори більш складних комбінованих з’єднань резисторів, які можна“розбити” на окремі послідовні та паралельні ланцюжки, що в свою чергу, з’єднані між собою послідовно та паралельно.

2.4. З’єднання джерел струму

Хімічне джерело струму має невелику ЕРС і запас енергії (енергоємність). Тому на практиці крім поодиноких елементів живлення використовують батареї, що складаються з декількох з’єднаних між собою елементів. Параметри батареї — ЕРС \(\mathscr{E}\) і внутрішній опір \(r\) — так само, як і опір з’єднань резисторів, можна розрахувати на основі закону збереження заряду та закону Ома.

Послідовне з’єднання джерел (рис. 2.5).

В цьому випадку величина струму в усіх з’єднаних джерелах (\( {{E}_{k}}\), \({{r}_{k}} \)) однакова:

\begin{equation} {I_{k}}={I}, \end{equation}

а різниці потенціалів на полюсах кожного джерела, згідно з (2.14), дорівнюють

\begin{equation} \varphi_{1k}-\varphi_{2k}=\mathscr{E}_{k}-Ir_{k}. \end{equation}

Додавши всі ці вирази, одержимо різницю потенціалів на полюсах батареї:

\begin{equation} \varphi_{1}-\varphi_{2}=\sum\limits\mathscr{E}_{k}-I\sum\limits{r}_{k}. \end{equation}

З іншого боку, для еквівалентного джерела

\begin{equation} \varphi_{1}-\varphi_{2}=\mathscr{E}-{Ir}. \end{equation}

Отже, доходимо висновку, що ЕРС \(\mathscr{E}\) і внутрішній опір \(r\) батареї послідовно з’єднаних елементів визначаються формулами

\begin{equation} \mathscr{E}=\sum\limits\mathscr{E}_{k}, \qquad {r}=\sum\limits{r}_{k}. \tag{2.20} \end{equation}

Зокрема, при узгодженому з’єднанні \(n\) однакових елементів, коли знаки всіх \(\mathscr{E}_i\) однакові,

\begin{equation} \mathscr{E}=n\mathscr{E}_{1}, \qquad {r}=nr_{1}. \tag{2.20а} \end{equation}

У такий спосіб отримують джерела живлення з необхідною величиною ЕРС.

Із приводу з’єднання джерел слід зауважити наступне. На практиці при використанні з’єднань (батарей) джерела завжди сполучають узгоджено. Але в навчальних завданнях свідомо використовуються і неузгодженні з’єднання. Тому при розв’язуванні задач треба пам’ятати, що електрорушійна сила є алгебраїчною величиною, і враховувати не тільки її модуль, а й знак.

Паралельне з’єднання джерел (рис. 2.6).

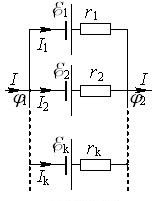
При паралельному з’єднанні різниці потенціалів на полюсах кожного джерела і всієї батареї однакові, а величина струму через батарею відповідно до закону збереження заряду дорівнює сумі струмів у всіх джерелах:

\begin{equation} \varphi _{1k} - \varphi _{2k} = \varphi _{1} - \varphi _{2},\qquad {I}=\sum\limits{I}_{k} . \end{equation}

Згідно із законом Ома (2.11а), для струмів через окремі джерела можна записати:

\begin{equation} {I}_{k}=\frac{1}{r_{k}}(\varphi_{1}-\varphi_{2})+\frac{\mathscr{E}_{k}}{r_{k}}. \end{equation}

Додавши всі струми \({I_{k}}\), отримаємо струм через батарею:

\begin{equation} {I}=(\varphi_{1}-\varphi_{2})\sum\limits\frac{1}{r_{k}}+\sum\limits\frac{\mathscr{E}_{k}}{r_{k}}. \end{equation}

Аналогічно виражається цей струм і через ЕРС \( \mathscr{E}\) та внутрішній опір \(r\) еквівалентного джерела:

\begin{equation} {I}=\frac{1}{r}(\varphi_{1}-\varphi_{2})+\frac{\mathscr{E}}{r}. \end{equation}

Порівнюючи обидва вирази, бачимо, що

при паралельному з’єднанні джерел внутрішній опір \(r\) і ЕРС \( \mathscr{E}\) батареї визначаються формулами:

\begin{equation} \frac{1}{r}=\sum\limits\frac{1}{r_{k}},\qquad \mathscr{E}=r\sum\limits\frac{\mathscr{E}_{k}}{r_{k}}. \tag{2.21} \end{equation}

При узгодженому з’єднанні \(n\) однакових елементів (\( \mathscr{E}_{1}\), \(r_{1}\)) маємо:

\begin{equation} \mathscr{E}=\mathscr{E}_{1},\qquad {r}=\frac{r_{1}}{n}. \tag{2.21а} \end{equation}

Тож при паралельному з’єднанні однакових елементів у джерелі живлення його ЕРС не збільшується, але збільшується запас енергії та потужність, яку джерело може віддавати в навантаження.

Таким чином, комбінуючи послідовні та паралельні з’єднання низьковольтних малопотужних елементів, можна отримувати джерела живлення з потрібною величиною ЕРС і великою енергоємністю. Яскравим свідченням цього є акумуляторні батареї для електромобілів, які забезпечують пробіг у сотні кілометрів без дозарядки.

2.5. Розгалужене коло

Найпростіше електричне коло, приміром, електрична лампа ввімкнена в мережу, складається з одного провідного контуру, що включає одне джерело струму. Але широко використовуються і більш складні розгалужені кола. Характерною ознакою таких кіл є наявність декількох вузлів, гілок і контурів. Вузлом називається точка, в якій сходиться більше, ніж два провідники. Гілкою (або віткою) називають ділянку кола, що з’єднує два вузли. Відповідно, під контуром розуміють сукупність гілок, яка дозволяє носіям рухатися замкненим шляхом, не відгалужуючись.

Для кожної гілки, звичайно, виконується узагальнений закон Ома (2.11а), але потенціали вузлів визначаються не лише “власним” джерелом, а й джерелами, ввімкненими в усі інші гілки кола. Тому струми в різних частинах одного контуру не однакові, і визначити їх безпосередньо за законом Ома неможливо. Для розгалужених кіл використовують спеціальні методи розрахунку, розроблені в теорії електричних кіл. Із них найпрозорішим є метод розрахунку за допомогою двох правил Кірхґофа, що безпосередньо випливають із основних законів електричного струму.

Перше правило Кірхґофа. Це правило стосується струмів у вузлах розгалуженого кола і є прямим наслідком закону збереження електричного заряду. У випадку постійного струму потенціали вузлів не змінюються з часом, отже, в них не відбувається накопичення зарядів. Це означає, що заряд, який підходить до вузла за одиницю часу, точно дорівнює зарядові, що виходить із нього. Іншими словами, сума струмів, які входить у вузол, дорівнює сумі струмів, які виходять із нього. Цю умову прийнято записувати у вигляді

\begin{equation} \sum\limits_{k}I_{k}={0}, \tag{2.22} \end{equation}

розглядаючи величини \(I_k\) як алгебраїчні і приписуючи струмам, які виходять з вузла один знак, наприклад додатній, а тим, що входять — протилежний.

Таким чином, перше правило Кірхґофа твердить, що

алгебраїчна сума струмів, які сходяться в довільному вузлі розгалуженого кола, дорівнює нулю.

Друге правило Кірхґофа. Згідно із узагальненим законом Ома (2.11а), струм у довільній ділянці (гілці) кола із заданим опором визначається різницею потенціалів на її кінцях та електрорушійною силою, що діє на цій ділянці:

\begin{equation} {I}_{k}R_{k}=\varphi_{1k}-\varphi_{2k}+\mathscr{E}_{k}. \end{equation}

Якщо вибрати в розгалуженому колі якийсь замкнений контур і обходити його в заданому напрямку, то кінцева точка \(k\)-ї гілки буде початковою точкою наступної \((k + 1)\)-ої гілки. Тому при додаванні указаних рівнянь для всіх гілок контуру потенціали скоротяться і вийде:

\begin{equation} \sum\limits_{k}I_{k}R_{k}=\sum\limits_{k}\mathscr{E}_{k}. \tag{2.23} \end{equation}

Це рівняння виражає друге правило Кірхґофа, що по суті є узагальненням закону Ома на розгалужене коло. Воно гласить:

алгебраїчна сума добутків сил струму на опори всіх гілок довільного контуру розгалуженого кола дорівнює алгебраїчній сумі ЕРС, які діють у цьому контурі.

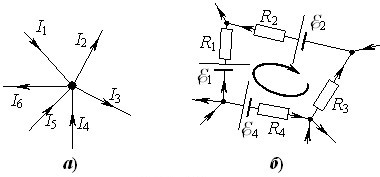
Знаки величин \(I_{k}\) і \( \mathscr{E}_{k}\) є умовними, але мають бути узгодженими. Тому вони визначаються за наступними правилами. Якщо даний струм \(I_k\) за напрямом збігається з напрямом обходу контуру, обраним при складанні рівнянь (2.23), то \(I_k > 0\). Знак ЕРС збігається зі знаком роботи сторонніх сил у джерелі при переміщенні позитивних носіїв у напрямку обходу контуру. Це означає, що \( \mathscr{E}_{k}>{0}\), якщо при обході контуру ми потрапляємо на від’ємний полюс (коротку жирну риску на зображенні джерела на схемі кола). Ці правила ілюструються наступними рівняннями для вузла (рис. 2.7а) та контуру (рис. 2.7б) якогось розгалуженого кола:

\begin{equation} {I}_{1}-I_{2}-I_{3}+I_{4}+I_{5}-I_{6}={0}; \end{equation}

\begin{equation} \begin{aligned} &{I}_{1}R_{1}-I_{2}R_{2}-I_{3}R_{3}-I_{4}R_{4}={}\\ &\quad{}= \mathscr{E}_{1}-\mathscr{E}_{2}+\mathscr{E}_{4}. \end{aligned} \end{equation}

Зауважимо, що величини \(R_k\) в рівнянні (2.23) включають і внутрішні опори джерел \(r_k\). Тому для нерозгалуженого кола, котре можна розглядати як контур із двох гілок з опорами \(R\) і \(r\) та однаковою величиною струму, рівняння (2.23) вироджується в рівняння закону Ома:

\begin{equation} {IR}+Ir=\mathscr{E} \quad \Rightarrow \quad {I}=\frac{\mathscr{E}}{R+r}. \end{equation}

У такому контексті закон Ома можна трактувати як окремий випадок другого правила Кірхґофа.

Порядок розрахунку розгалуженого кола. Склавши та розв’язавши систему рівнянь (2.22) і (2.23), можна розрахувати розгалужене коло, тобто визначити величини та напрями всіх струмів у колі через усі наявні в ньому опори \(R_k\) та ЕРС \( \mathscr{E}_{k}\). Розрахунок варто проводити в такому порядку.

1. Довільно вибрати й позначити на схемі напрямки струмів \(I_k\) у всіх гілках кола;

2. Скласти максимально можливу кількість незалежних рівнянь (2.22) для вузлів, дотримуючись обраного правила знаків.

Примітки. 1) Максимальна кількість рівнянь для вузлів є не обов’язковою, але доцільною, зважаючи на їхню простоту; 2) Аби рівняння були незалежними, кожен наступний вибраний вузол має включати хоча б одну нову гілку. За такої умови максимальна кількість рівнянь (2.22) дорівнює \(N - 1\), де \(N\) — повна кількість вузлів кола.

3. Скласти решту необхідних рівнянь за другим правилом Кірхґофа (2.23) для замкнених контурів. При цьому конфігурацію та напрями обходу контурів можна вибирати довільно, але так, аби кожен наступний включав хоча б одну нову гілку.

4. Розв’язати отриману систему рівнянь. При цьому корені \(I_k\) системи покажуть не тільки величини, а й напрями всіх струмів. А саме, коли \(I_k > 0\), то прийнятий в п. 1 при складанні рівнянь напрям даного струму є правильним. Якщо ж \(I_k < 0\), то дійсний напрям даного струму є протилежним до вибраного при складанні рівнянь.