physics.zfftt.kpi.ua

Електричним струмом називається напрямлений рух заряджених частинок — носіїв струму. Носіями струму можуть бути всякі заряджені частинки. В металах і сплавах це електрони провідності — вивільнені при об’єднанні атомів у тверду речовину валентні електрони, які можуть переміщуватися по всьому об’єму зразка. У рідких провідниках (електролітах) носіями струму є іони, а в газах — і те, й інше. Потоки заряджених частинок у вакуумі теж створюють електричний струм.

Кількісні характеристики та загальні закони струму розглядаються далі в наступних питаннях:

1.1. Сила та густина струму

Сутність явища електричного струму полягає в перенесенні в просторі електричного заряду, а його кількісною характеристикою є сила струму, або величина струму, котра визначається кількістю заряду, що переноситься через задану поверхню за одиницю часу. У випадку стаціонарного (постійного) струму сила струму

\begin{equation} {I=\frac{q}{t}}. \tag{1.1} \end{equation}

Для нестаціонарного (залежного від часу) струму величина (1.1) визначає середню силу струму за час \(t\), а його точна (миттєва) величина в кожен момент часу визначається відношенням елементарної порції перенесеного заряду \(\mathrm{d}q\) до відповідного елементарного проміжку часу \(\mathrm{d}t\):

\begin{equation} {I}=\frac{\mathrm{d}q}{\mathrm{d}t}. \tag{1.1а} \end{equation}

Одиниця сили струму називається ампер (\(\text{А}\)). Вона визначається через магнітну взаємодію струмів і прийнята як одна з основних одиниць міжнародної системи (SІ). Відтак одиниці всіх інших електричних і магнітних величин у кінцевому підсумку визначаються через ампер. Зокрема, одиниця заряду \(1\ \text{Kл}\) = \(1\ \text{А}\cdot \text{с}\) — то є заряд, який проходить через поперечний переріз провідника за одиницю часу при силі струму \(1\ \text{А}\).

Сила струму є скалярною величиною, проте струм як процес має напрям, який визначається напрямом перенесення носіями електричного заряду. При цьому, позаяк існує два знаки заряду, за домовленістю

напрям струму прийнято напрям перенесення позитивного заряду.

Отже в металах, де носіями є електрони, напрям струму є протилежним до напрямку впорядкованого руху носіїв.

У тонких провідниках струм є спрямований уздовж провідника й рівномірно розподілений по перерізу. Але в провідному середовищі маємо справу з об’ємними струмами, котрі в різних точках можуть мати різну величину та напрям. Тому крім інтегральної характеристики — сили струму \(I\) використовують іще й локальну величину — вектор густини струму \(\vec{j}\), який задає інтенсивність і напрям перенесення заряду в кожній точці. Розглянемо, чим визначається вектор \(\vec{j}\) у провідному середовищі з носіями одного сорту. Для цього підрахуємо струм \(\mathrm{d}I=\mathrm{d}q/\mathrm{d}{t}\), який протікає через елементарну ділянку \(\mathrm{d}\vec{S}\) якоїсь поверхні \(S\) (рис. 1.1а).

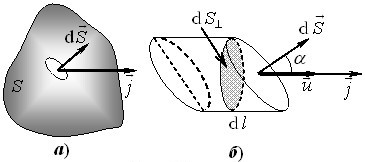
За час \(\mathrm{d}t\) крізь указану ділянку пройдуть усі носії, що знаходилися всередині косого циліндрика (рис. 1.1б) з основою \(\mathrm{d}S\) і твірною \(\mathrm{d}l=u\,\mathrm{d}{t}\), паралельною до швидкості \(\vec{u}\) їхнього упорядкованого руху. Заряд цих носіїв

\begin{equation} \mathrm{d}q=enV\,\mathrm{d}V=enu\,\mathrm{d}t\,\mathrm{d}S\cos\alpha , \end{equation}

де \(e\) — заряд одного носія, \(n\) — їхня концентрація. Отже величина струму через площинку \(\mathrm{d}S\) дорівнює

\begin{equation} \mathrm{d}I=enu\,\mathrm{d}S\cos\alpha=enu\,\mathrm{d}{S}_{\bot}, \tag{1.2} \end{equation}

де \(\mathrm{d}S_{\bot}=\mathrm{d}S\cos\alpha \) — площа проекції ділянки \(\mathrm{d}S\) на площину перпендикулярну до напрямку руху носіїв. Величина

\begin{equation} {j}=\frac{\mathrm{d}I}{\mathrm{d}S_{\bot}}=enu , \end{equation}

яка в кожній точці визначає струм, що припадає на одиницю площі поверхні, перпендикулярної до його напрямку, називається густиною струму і вимірюється в \(\text{А/м}^2\). Аби величина \(j\) відображала ще й напрям струму, її розглядають як вектор:

\begin{equation} \vec{j}=en\vec{u}. \tag{1.3} \end{equation}

У металах і сплавах носіями струму є електрони, але в інших середовищах у створенні струму можуть брати участь різні частинки-носії, кожна із своєю величиною заряду \(q_i\) концентрацію \(n_i\) та швидкістю упорядкованого руху \(\vec{u}_{i}\). Тоді

\begin{equation} \vec{j}=\sum\limits{{{q}_{i}}{{n}_{i}}{{{\vec{u}}}_{i}}}. \tag{1.3а} \end{equation}

Через вектор густини струму можна згорнуто виразити силу струму крізь елементарну площинку \(\mathrm{d}S\) (формула (1.2)) та через довільну поверхню \(S\):

\begin{equation} \mathrm{d}I=\vec{j}\,\mathrm{d}\vec{S}, \tag{1.4} \end{equation} \begin{equation} {I}=\int\limits_{S}\vec{j}\,\mathrm{d}\vec{S}. \tag{1.4а} \end{equation}

Отже, силу струму можна трактувати як потік вектора густини струму через задану поверхню і при необхідності зображувати розподіл струму у просторі лініями вектора \(\vec{j}\) (лініями струму).

Якщо струм по площі поперечного перерізу провідника розподіляється рівномірно, то

\begin{equation} {I}={jS}. \tag{1.4б} \end{equation}

1.2. Рівняння неперервності

Розглянуті характеристики струму дозволяють подати загальній математичний вираз одного із фундаментальних фізичних законів — закону збереження електричного заряду. Якщо виділити в просторі довільну замкнену поверхню, то згідно з означенням (1.1а) і виразом (1.4а) можна записати:

\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}=\frac{\mathrm{d}q_{S}}{\mathrm{d}{t}}, \tag{1.5} \end{equation}

де \(\mathrm{d}q_{s}/\mathrm{d}{t}\) — заряд, який проходить за одиницю часу крізь поверхню \(S\) назовні. Але позаяк заряд не виникає з нічого і не зникає безслідно, ця похідна в точності дорівнює швидкості зменшення величини заряду в об’ємі, що обмежений даною поверхнею. Отже:

\begin{equation} \begin{aligned} &\frac{\mathrm{d}q_{S}}{\mathrm{d}t} =- \frac{\mathrm{d}q_{V}}{\mathrm{d}t}=-\frac{\mathrm{d}}{\mathrm{d}t}\int\limits_{V}\rho\,\mathrm{d}{V}={}\\ &\quad{}= - \int\limits_{V}\frac{\partial \rho }{\partial t}\mathrm{d}{V}, \end{aligned} \end{equation}

де \(\rho\) — об’ємна густина заряду.

Примітка. Під знаком інтеграла стоїть частинна похідна, тому що об’єм V є обмежений фіксованою (нерухомою) поверхнею, і похідна визначається тільки явною залежністю заряду в об’ємі від часу, а не, скажімо, рухом стінок поверхні.

Підставивши цей вираз у (1.5), отримуємо:

\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}=-\int\limits_{V}\frac{\partial \rho }{\partial t}\mathrm{d}{V}. \tag{1.6} \end{equation}

Рівняння (1.6) називається рівнянням неперервності і є загальним виразом закону збереження електричного заряду. Воно, зокрема, вбирає й закон збереження заряду в електрично ізольованій системі, про який говорилося в електростатиці. Справді, крізь будь-яку замкнену поверхню, що відділяє таку систему від оточення, не проходять заряджені частинки, і в усіх її точках \(\vec{j}={0}\). Отже, згідно з (1.6),

\begin{equation} \begin{aligned} &\int\limits_{V}\frac{\partial\rho}{\partial{t}}={0} \quad \Rightarrow \quad \frac{\partial\rho}{\partial{t}}=0 \quad \Rightarrow{}\\ &\quad{}\Rightarrow \quad {q(t)}=\mathrm{const}, \end{aligned} \end{equation}

тобто повний заряд системи не змінюється з часом (зберігається).

Із рівняння неперервності випливають також деякі загальні висновки щодо умов існування електричного струму. Зокрема, це висновок про те, що постійний струм може існувати лишень у замкнених провідних контурах. Дійсно, при постійному струмі розподіл потенціалів і зарядів у провідному середовищі не змінюється з часом, отже, в рівнянні (1.6) похідна \(\partial\rho / \partial{t}=0\) в усіх точках. Тому для будь-якої замкненої поверхні

\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}={0}. \end{equation}

а це означає, що кількість ліній струму (ліній вектора \(\vec{j}\)), які заходять усередину поверхні та виходять назовні є завжди однаковою. Інакше говорячи, лінії стаціонарного струму є неперервними (замкненими) — вони ніде не починаються і ніде не закінчуються. Це одна з причин, чому рівняння (1.6) називають рівнянням неперервності. З нього випливає той загальновідомий факт, що

постійний струм може протікати тільки по замкненому провідному контуру.

Але з рівняння неперервності випливає й зовсім не самоочевидний висновок про те, що

залежний від часу струм може існувати і в незамкнених контурах,

як от у колах із конденсаторами. При цьому в точках розриву контуру (на пластинах конденсатора) відбувається накопичення зарядів того чи іншого знаку, і в них \( (\partial\rho{/}\partial{t})\ne{0}\). Тому відповідно до рівняння (1.6), потік \(\vec{j}\) крізь малу замкнену поверхню, що охоплює таку точку,

\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S} > {0}\quad \text{при} \ \frac{\partial\rho}{\partial{t}}<{0} \end{equation}

і

\begin{equation} \oint\limits_{S}\vec{j}\,\mathrm{d}\vec{S}<{0}\quad \text{при} \ \frac{\partial\rho}{\partial{t}}>{0}. \end{equation}

Згідно з геометричним змістом потоку ці вирази означають, що лінії змінного струму мають початки і кінці: вони починаються в одних точках і закінчуються в інших. (Чому, попри це, рівняння (1.6) називається рівнянням неперервності, див. розділ V, п. 2.) Отже, рівняння неперервності не заперечує можливості існування електричного струму в незамкненому контурі. Але через обмежену кількість носіїв у провіднику, вони не можуть в точках розриву накопичуватися весь час. Тому в незамкненому провіднику довготривалий нестаціонарний струм може існувати лише за умови, що його напрям періодично змінюється на протилежний. Саме такі струми означає термін “змінний струм”.

1.3. Закон Ома в локальній формі

Дрейф носіїв струму. Розглянемо механізм електричного струму в металевому провіднику на основі уявлень класичної фізики, за якими електрони провідності в металі утворюють “електронний газ” і здійснюють інтенсивний тепловий рух. Його усереднену швидкість \({v}\) можна оцінити з відомих формул молекулярної фізики:

\begin{equation} \frac{m\left\langle {{v}^{2}} \right\rangle }{2}=\frac{3}{2}kT \quad \Rightarrow \quad {v}=\sqrt{\frac{3kT}{m}}. \end{equation}

Підставивши значення маси електрона \(m = 9{,}1\cdot10^{-31}\ \text{кг}\), сталої Больцмана \(k = 1{,}38\cdot 10^{-23}\ \text{Дж/К}\) і прийнявши \(T=293\ \text{К}\) (\(20^\circ \,\text{C}\)), отримаємо:

\begin{equation} {v}=\sqrt{\frac{3\cdot{1{,}38\cdot{10^{-23}}}\cdot 293}{9{,}1\cdot{10^{-31}}}}\approx 10^{5}\ \text{м/с}. \end{equation}

Отже, електрони здійснюють дуже інтенсивний тепловий рух. Але він є безладним і не спричинює перенесення заряду, тобто електричного струму. Струм створюється впорядкованим рухом носіїв, і саме його швидкість \(u\), відповідно до формули (1.3), визначає густину струму. Задля кращого уявлення про цей рух оцінимо величину \(u\) в мідному провіднику при густині струму \(j = 10\ \text{А/мм}^2 = 10^7\ \text{А/м}^2\), прийнявши концентрацію носіїв рівною концентрації атомів \(n = 8{,}5\cdot10^{28}\ 1/\text{м}^3\):

\begin{equation} \begin{aligned} &{u}=\frac{j}{en}=\frac{10^7}{1{,}6\cdot{10^{-19}}\cdot{8{,}5}\cdot{10^{28}}}\approx{}\\ &\quad{}\approx 10^{-3}\ \text{м/с} = 1\ \text{мм/с}. \end{aligned} \end{equation}

Це складає всього \(10^{-8}\) від теплової швидкості, й упорядкований рух окремого електрона на тлі хаотичного теплового руху взагалі не можна розрізнити. Тож величина \(u\) визначає не рух окремого електрона, а рух сукупності носіїв струму в цілому. Такий колективний рух називається дрейфом, а швидкість \(u\) — дрейфовою швидкістю носіїв. Дрейф носіїв нагадує знесення (дрейф) рою комах “товкунців” слабким вітерцем.

Закон Ома. Мала величина дрейфової швидкості пояснюється тим, що в металі електрони провідності на своєму шляху натикаються на іони кристалічної ґратки, що перешкоджає їхньому впорядкованому рухові вздовж провідника. Між іонами та електронами діють сили притягання. Через це при зустрічі з масивними іонами електрони повністю втрачають швидкість упорядкованого руху, подібно до того, як пластилінова кулька втрачає швидкість при зіткненні зі стіною. Це й перешкоджає  дрейфові носіїв. Тому для створення та підтримання струму в провіднику має існувати електричне поле. Це не суперечить твердженню про неможливість в провідниках електричного поля, про що говорилося раніше (розділ II, п. 2), бо в провіднику із струмом заряди-носії не перебувають у рівновазі, й указане поле не є електростатичним.

Зауваження. Вільні електрони, звісно, стикаються й між собою. Але ці зіткнення є пружними і, згідно із законом збереження імпульсу, не впливають на сумарний імпульс, тож і на дрейфову швидкість електронів-носіїв струму. Тому зіткнення між електронами не перешкоджає струмові.

Таким чином, через непружні зіткнення з іонами носії вільно рухаються тільки від зіткнення до зіткнення, проходячи в середньому деяку відстань \(\langle\lambda\rangle \), яка називається середньою довжиною вільного пробігу. При цьому середній проміжок часу між двома послідовними зіткненнями електрона з іонами \(\langle\tau{\rangle}\), який називається середнім часом вільного пробігу, складає

\begin{equation} \langle\tau\rangle = \frac{\lambda}{v}, \tag{1.7} \end{equation}

де \({v}\) — швидкість теплового руху електрона.

Атоми в твердих тілах розміщені дуже щільно, майже впритул, Тому величина \(\langle\lambda{\rangle}\) має бути близькою до відстані між атомами в провіднику. Ця відстань для більшості металів складає \((3\div 5)\cdot 10^{-10}\ \text{м}\), а теплова швидкість \({v}\approx{10^5}\ \text{м/с}\). За таких умов час вільного пробігу виявляється настільки малим, що електрони під дією поля не встигають помітно розігнатися, чим пояснюється мала величина дрейфової швидкості носіїв.

Розглянутий класичний механізм руху електронів провідності в металі дозволяє теоретично встановити один з основних законів електричного струму — закон Ома в локальній (інакше диференціальній) формі, який визначає зв’язок між струмом та електричним полем у кожній точці металевого провідника. За час між двома послідовними зіткненнями з іонами кожен електрон під дією поля збільшує швидкість руху уздовж провідника від \(0\) до певної максимальної величини \(\vec{u}_{m}\), яка в середньому дорівнює

\begin{equation} \langle\vec{u}_{m}\rangle=\vec{a}\cdot\langle\tau\rangle=\frac{\vec{F}}{m}\langle\tau\rangle=\frac{e\vec{E}}{m}\langle\tau{\rangle}, \tag{1.8} \end{equation}

де \(\vec{a}\) — прискорення електрона, \(e\) і \(m\) — його заряд і маса, \(\vec{E}\) — напруженість електричного поля в провіднику і \(\langle\tau{\rangle}\) — середній час вільного пробігу електрона.

Дрейфова швидкість носіїв дорівнює половині величини \(u_m\):

\begin{equation} \vec{u}=\frac{1}{2}\langle\vec{u}_{m}\rangle=\frac{e\vec{E}}{2m}\langle\tau{\rangle}. \end{equation}

У такому разі для густини струму відповідно до формули (1.2) маємо:

\begin{equation} \vec{j}=\frac{e^2 n\langle\tau\rangle}{2m}\vec{E}, \end{equation}

або, враховуючи вираз (1.7),

\begin{equation} \vec{j}=\frac{e^2 n\langle\lambda\rangle}{2mv}\vec{E}. \end{equation}

Згорнуто ці формули записують у вигляді

\begin{equation} \vec{j}=\sigma\vec{E} \tag{1.9} \end{equation}

або

\begin{equation} \vec{j}=\frac{\vec{E}}{\rho}. \tag{1.9а} \end{equation}

Величина

показує, наскільки добре дана речовина проводить струм і називається питомою електропровідністю. Відповідно, обернена величина

\begin{equation} \rho=\frac{1}{\sigma}=\frac{2m}{e^2 n\langle\lambda\rangle} \tag{1.10а} \end{equation}

називається питомим опором речовини.

Формули (1.10), (1.10а) виражають один з основних законів електричного струму — закон Ома в локальній формі:

густина електричного струму в кожній точці провідника є прямо пропорційною напруженості поля в цій точці.

Одразу зазначимо, що закон Ома не є загальним. Він виконується тільки в лінійних провідниках — таких, в яких електропровідність не залежить від напруженості поля, тож і від напруги на їхніх кінцях. Окрім металів і сплавів, лінійними є однорідні напівпровідники та електроліти (рідкі провідники) — середовища, в яких концентрація носіїв струму \(n\), відтак і електропровідність \(\sigma\), не залежать від напруженості поля \(E\). А ось гази та контакти різних напівпровідників або напівпровідників із металами є нелінійними провідниками. Тому в газорозрядних і вакуумних лампах, а також у напівпровідникових електронних приладах закон Ома не виконується.

1.4. Питома потужність струму

Стикаючись із іонами металу, електрони провідності передають їм імпульс та енергію, набуті в дрейфовому русі. Ця енергія називається енергією електричного струму і далі перетворюється на ті чи інші види. Наприклад, у газорозрядній лампі частина цієї енергії трансформується в енергію збудження атомів газу і по тому — в енергію світлового випромінювання, а в електричному двигуні майже вся енергія струму перетворюється на кінетичну енергію обертання ротора. При цьому в усіх випадках та чи інша частка енергії струму переходить у внутрішню (теплову) енергію провідників. Зокрема, в нерухомих рідких і твердих провідниках із постійним струмом на тепло перетворюється вся енергія струму.

Кількісною характеристикою перетворень енергії струму на тепло в кожній точці провідника є питома потужність струму (\(\text{Вт/м}^3\)), яка дорівнює енергії, що передається провіднику носіями в одиниці об’єму за одиницю часу

\begin{equation} {w}=\frac{\mathrm{d}W}{\mathrm{d}t\,\mathrm{d}V}. \tag{1.11} \end{equation}

Величину \({w}\) можна визначити, прямо підрахувавши енергію \(\mathrm{d}W\), що виділяється в об’ємі провідника \(\mathrm{d}V\) за час \(\mathrm{d}t\), як

\begin{equation} \mathrm{d}W=\langle{K_1}\rangle\mathrm{d}N\,\mathrm{d}{Z_1}, \end{equation}

де \(\langle{K_1}{\rangle}\) — середня величина кінетичної енергії дрейфового руху одного електрона на момент зіткнення з іоном металу, \(\mathrm{d}N\) — кількість електронів провідності в об’ємі \(\mathrm{d}V\), і \(\mathrm{d}Z_{1}\) — кількість зіткнень з іонами, які відбуває один електрон за час \(\mathrm{d}t\).

Але зручніше у виразі (6.12) величину \(\mathrm{d}W /\mathrm{d}V \) розглядати як роботу, а \(\mathrm{d}W/(\mathrm{d}t\cdot\!\mathrm{d}V) \) — як потужність сил, що діють на всі носії в одиниці об’єму провідника. Тоді, враховуючи відому з механіки формулу \(p=Fu\) для потужності сили \(F\), що діє на частинку при швидкості руху \(u\), можна записати:

\begin{equation} {w}=np={nuF}, \end{equation}

де \(n\) — кількість носіїв в одиниці об’єму. Відтак, урахувавши вираз (1.3), отримаємо:

\begin{equation} {w}=j\frac{F}{e}. \tag{1.12} \end{equation}

Формула (1.12) не пов’язана з природою сил, які діють на носії струму, тож є найбільш загальним виразом питомої потужності струму. Але зазвичай \(F=eE\), де \(E\) — напруженість електричного поля в провіднику із струмом. Тоді

\begin{equation} {w}={jE}, \tag{1.13} \end{equation}

а з урахуванням закону Ома (1.9)

\begin{equation} {w}=\rho{j^2}, \tag{1.13а} \end{equation}

або

\begin{equation} {w}=\sigma{E^2}=\frac{E^2}{\rho}. \tag{1.13б} \end{equation}

У випадку постійного струму всі ці формули є рівносильними і виражають закон Джоуля в локальній (“диференціальній”) формі:

кількість теплоти, що виділяється за одиницю часу (теплова потужність) в одиниці об’єму однорідного провідника із струмом, в кожній точці є прямо пропорційною квадратові густини струму або квадратові напруженості електричного поля в цій точці.

1.5. Обмеженість класичної теорії електропровідності

Отримані в класичній теорії висновки про лінійну залежність густини струму від напруженості електричного поля (закон Ома) та квадратичну залежність потужності струму від напруженості електричного поля (закон Джоуля) в однорідних лінійних провідниках підтверджуються на досліді. Але низка її кількісних передбачень не справджується, тож класична теорія електропровідності металів є неповною. А саме.

Відомо, що концентрація вільних електронів у міді \(n = 8{,}5\cdot10^{28} \text{м}^{-3}\), і питомий опір \(\rho = 1{,}7\cdot 10^{-8}\ \text{Ом}\cdot \text{м}\) при \(t=20^\circ \,\text{C}\). Якщо підставити ці величини, отриману раніше величину теплової швидкості електронів \({v}\approx 10^{5}\ \text{м/с}\), та заряд і масу електрона у формулу (1.10а), то для середньої довжини вільного пробігу електрона виходить \(\langle\lambda\rangle\approx 5{\cdot}{10^{-9}}\ \text{м}\). Позаяк відстань між атомами в міді \(d = 3{,}6\cdot 10^{-10}\ \text{м}\), то виходить, що електрон без зіткнень проходить у середньому півтора десятка іонів, які трапляються на його шляху. В класичній концепції електронного газу цього не можна збагнути, адже атоми в твердому тілі розміщені дуже щільно, практично впритул. Істотні розбіжності між класичною теорією та дослідом існують і щодо температурної залежності опору металевих провідників \(\rho(T)\). Згідно з формулами (1.10а) і (1.7) питомий опір має бути прямо пропорційним величині \(\sqrt{T}\), але насправді в широкому температурному інтервалі залежність \(\rho(T)\) є лінійною. Крім того класична теорія взагалі не здатна пояснити існування явища надпровідності — повного зникнення електричного опору в деяких металах і сплавах при наднизьких температурах.

Обмеженість класичної теорії електропровідності пояснюється тим, що електрони в металі не можна розглядати як матеріальні точки, підпорядковані законам класичної фізики. Як з’ясувалося, електрони мають складні квантові властивості, і їхній рух у твердому тілі радше нагадує не рух кульок, а поширення хвиль. При цьому виявляється, що перешкоду упорядкованому рухові електронів у провіднику, тобто опір, створюють не самі іони, а дефекти кристалічної структури — різні порушення строгої періодичності в розташуванні іонів у вузлах кристалічної ґратки. Такими можуть бути відсутність іонів у деяких вузлах ґратки, їх заміщення чужорідними атомами, розташування власних чи чужорідних атомів у міжвузіллях, з рештою, і тепловий рух атомів. В оптиці подібні дефекти середовища є причиною розсіяння світла (розсіяння фотонів). Відповідно, взаємодію носіїв із дефектами структури провідника називають розсіюванням носіїв струму.

Кількість дефектів у провіднику є набагато меншою за кількість власних атомів, а відстань між ними, відповідно, більшою. Це пояснює аномально велику як для класичної теорії, довжину вільного пробігу носіїв струму. Квантова теорія правильно пояснює й інші властивості провідників, зокрема передбачає лінійну залежність опору від температури і пояснює явище надпровідності. В цьому зв’язку те, що класична теорія при принципово хибних засадах дає правильні основні закони струму (1.9) і (1.13) може викликати подив. Але насправді нічого дивного в цьому немає, позаяк залежності (1.9) і (1.13) є наслідком лише того, що при заданій напруженості поля в провіднику встановлюється постійна швидкість дрейфу носіїв. А це пов’язано тільки із самим фактом розсіювання носіїв, а не з його механізмом.