physics.zfftt.kpi.ua

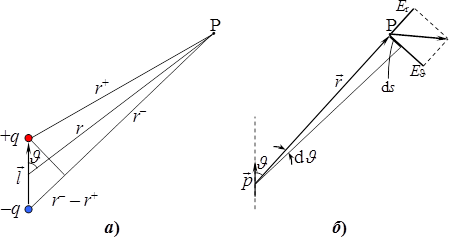
Електричним диполем (двополюсником) називаються два різнойменні заряди (полюси) \(+q\) і \(-q\) однакової величини, що розміщені на малій відстані \(l\) один від одного, рис. 4.1а.

Диполь у цілому є електронейтральним, але через рознесеність полюсів у просторі він створює власне електричне поле та зазнає дії зовнішніх полів. При цьому власне поле диполя та його поведінка у зовнішньому полі визначаються не безпосередньо зарядом полюса, а електричним (дипольним) моментом \(\vec{p}\) — величиною, що визначається як

\begin{equation} \vec{p}=q\vec{l}, \tag{4.1} \end{equation}

де \(q > 0\) — заряд диполя, а вектор \(\vec{l}\), проведений від негативного до позитивного полюса, називається плечем диполя.

Варто завважити, що розглянута система з двох заряджених кульок майже не має прямого практичного застосування. Але диполь є цінною моделлю, що використовується в різних розділах електродинаміки. Зокрема, уявлення про електричний диполь є базовим у теорії електричного поля в діелектриках. Далі розглядаються такі питання:

4.1. Електричне поле диполя

Розглянемо електричне поле, що створюється диполем із моментом \(\vec{p}\) на відстанях \( r\gg l\) від його центра (у так званій дипольній зоні). Очевидно, що це поле має осьову симетрію: його характеристики однакові у всіх точках кола з центром на осі диполя й перпендикулярного до неї. Тому напруженість і потенціал поля диполя у будь-якій точці P залежать тільки від відстані \(r\) та кута \(\vartheta\) (рис. 4.1а):

\begin{equation} \vec{E}=\vec{E}(r,\vartheta) ,\qquad \varphi=\varphi(r,\vartheta) . \end{equation}

Потенціал поля диполя. Розрахунок поля диполя почнемо з потенціалу, який за принципом суперпозиції дорівнює

\begin{equation} \varphi=\varphi_{-}+\varphi_{+}, \end{equation}

де потенціали \(\varphi_-\) і \(\varphi_+\) полів кожного з полюсів визначаються формулою (2.7). Отже,

\begin{equation} \begin{aligned} &\varphi=\frac{-q}{4\pi\varepsilon_0{r_{-}}}+\frac{q}{4\pi\varepsilon_0{r_{+}}} ={}\\ &\quad{}= \frac{q}{4\pi\varepsilon_0}\left(\frac{1}{r_{+}}-\frac{1}{r_{-}}\right) = \frac{q}{4\pi\varepsilon_0}\cdot\frac{r_{-}-r_{+}}{r_{+}r_{-}}. \end{aligned} \end{equation}

Оскільки за умовою \({r}\gg{l}\), різниця довжин відрізків \(r_-\) і \(r_+\) та кут між ними є малими (рис. 4.1), можна прийняти \({r_{-}}-r_{+}=l\cos\vartheta \) і \({r_{+}r_{-}}=r^2 \). Тоді

\begin{equation} \varphi(r,\vartheta)=\frac{p\cos\vartheta}{4\pi\varepsilon_0{r^2}}. \tag{4.2} \end{equation}

Отже, як і говорилося, потенціал поля диполя визначається не окремо величиною зарядів і відстанню між ними, а дипольним моментом.

Напруженість поля диполя. Вектор напруженості теж можна знайти за принципом суперпозиції як \(\vec{E}=\vec{E}_{+}+\vec{E}_{-}\). Але корисніше зробити це за допомогою функції потенціалу (4.2) через проекції \({E_r}\) на радіус-вектор \(\vec{r}\) точки P і \({E}_{\vartheta}\) — на дотичну до кола радіуса \(r\) із центром у центрі диполя (рис. 4.1б). Ці проекції, відповідно до формули (3.3), визначаються як

\begin{equation} {E_r}=-\frac{\partial\varphi}{\partial{r}}, \qquad {E_{\vartheta}=-\frac{\partial\varphi}{\partial{s}}}=-\frac{\partial\varphi}{r\,\partial\vartheta}. \end{equation}

Тут враховано, що елементарне переміщення \(\d s\) у напрямку дотичної збігається з дугою кола: \(\mathrm{d}s=r\,\mathrm{d}{\vartheta}\). Відтак, після указаних диференціювань функції (4.2), отримуємо:

\begin{equation} \left\{ \begin{aligned} E_{r}&=\frac{1}{4\pi\varepsilon_{0}}\frac{2p\cos\vartheta}{r^{3}}, \\ E_{\vartheta}&=\frac{1}{4\pi\varepsilon_{0}}\frac{p\sin\vartheta}{r^{3}}. \\ \end{aligned} \right. \tag{4.3} \end{equation}

Звідси для модуля напруженості \({E}=\sqrt{E_r^2+E_{\vartheta}^2}\) маємо:

\begin{equation} {E}=\frac{p}{4\pi\varepsilon_0{r^3}}\sqrt{1+3\cos^2{\vartheta}}. \tag{4.4} \end{equation}

Напрям вектора \(\vec{E}\) задамо кутом \(\alpha\) між ним і радіусом-вектором \(\vec{r}\) точки P (рис. 4.1б). Тоді, згідно з (4.3),

\begin{equation} \operatorname{tg}\alpha=\frac{1}{2}\operatorname{tg}\vartheta . \tag{4.5} \end{equation}

Формули (2.23) і (2.24) повністю визначають вектор \(\vec{E}\) у будь-якій точці дипольної зони (\({r}\gg{l}\)), хоч і не є дуже наочними. Але для точок на осі диполя та на перпендикулярі до осі, що проходить через центр диполя, вектор напруженості можна визначити однією формулою. В першому випадку кут \(\vartheta\) складає або \(0\), або \(\pi\), тож відповідно до (4.5), такі самі значення має і кут \(\alpha\). Це означає, що на осі напрям поля скрізь збігається з напрямком електричного моменту диполя \(\vec{p}\). Врахувавши це та підставивши в (4.4) значення \(\cos^2\vartheta=1 \), отримуємо:

\begin{equation} {{\vec{E}}_{\parallel }}=\frac{1}{4\pi\varepsilon_0}\cdot\frac{2\vec{p}}{r^3}. \tag{4.6} \end{equation}

Прийнявши \(\vartheta=\pi/2 \), так само одержимо вираз вектора напруженості в другому випадку:

\begin{equation} {{\vec{E}}_{\perp }}=-\frac{1}{4\pi {{\varepsilon }_{0}}}\cdot \frac{{\vec{p}}}{{{r}^{3}}}. \tag{4.7} \end{equation}

З приводу цього виразу корисно зауважити, що в усіх таких точках \(\cos\vartheta={0}\), тож відповідно до (4.2), \(\varphi={0}\). Це наочно ілюструє специфіку зв’язку між напруженістю та потенціалом електричного поля (формула (3.5)). А саме, відсутність потенціалу в заданій точці ще не означає відсутності самого поля. Про відсутність поля свідчить не величина потенціалу, а його незмінність при зміщенні з даної в будь-яку сусідню точку.

Підводячи підсумок, зазначимо, що в цілому електрично нейтральна система зарядів, якою є диполь, навіть на великих порівняно з її розмірами відстанях створює електричне поле. Але його потенціал і напруженість змінюються з відстанню швидше, ніж у випадку поля точкового заряду. Це є характерним і для полів мультиполів — нейтральних систем зарядів складнішої конфігурації. Причому, чим складніша конфігурація, тим сильніша залежність поля від відстані. Тому електричні поля таких систем, як атоми та молекули, існують практично тільки на відстанях порядку розмірів цих частинок.

4.2. Диполь у зовнішньому електричному полі

Момент сил, що діють на диполь. Якщо диполь із зарядом \(q\) і плечем \(\vec{l}\) вміщено в однорідне електричне полі \(\vec{E}= \textrm{const}\), то на полюси діють протилежно напрямлені сили \(\vec{F}_{+}\) і \(\vec{F}_{-}\) (рис. 4.2а), які намагаються повернути диполь за годинниковою стрілкою.

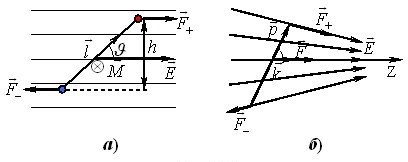
Обертальна дія сил визначається вектором моменту сил \(\vec{M}\). У нашому випадку його легко розрахувати, позаяк сили є однакові за величиною та протилежні за напрямом, тож утворюють так звану “пару сил”. А з механіки відомо, що модуль моменту \(\vec{M}\) пари дорівнює

\begin{equation} {M=Fh}, \end{equation}

де відстань між лініями дії сил, яка називається “плечем” пари.

Напрям вектора моменту сил визначається за правилом правого гвинта. Тут це напрям “від нас”.

(На рис. 4.2а це позначено як \(\otimes \). Аналогічно, напрям “до нас” позначають як \(\odot \).)

З рисунка видно, що \( {h}=l\sin\vartheta \), отже

\begin{equation} {M}=qEl\sin\vartheta=pE\sin{\vartheta}, \tag{4.8} \end{equation}

де \({p=ql}\) — модуль електричного моменту диполя.

З урахуванням напрямків момент сил визначається векторним добуток векторів \(\vec{p}\) і \(\vec{E}\):

\begin{equation} \vec{M}=\bigl[\vec{p}\vec{E}\bigr] . \tag{4.9} \end{equation}

У неоднорідному полі \(\vec{E}\ne\mathrm{const}\) сили \(\vec{F}_{+}\), \(\vec{F}_{-}\) не утворюють пари (див. рис. 4.2б), і формула (4.9) строго є не дійсною. Але для елементарного (із дуже малим плечем) диполя вона зберігає чинність, бо в межах диполя поле лишається практично однорідним. Тому можна сказати, що

будь-яке електричне поле намагається зорієнтувати елементарний диполь так, аби напрям дипольного моменту збігався із напрямом поля.

Сила, що діє на диполь у неоднорідному полі. В однорідному полі результуюча сила, що діє на диполь, \(\vec{F}=\vec{F}_{+}+\vec{F}_{-}={0}\). Тому поле лише повертає диполь навколо нерухомого центра мас. Але в неоднорідному полі (рис. 4.2б) \(\vec{F}_{+}\ne -\vec{F}_{-}\), і на диполь діє ще й деяка результуюча сила \(\vec{F}_{+}+\vec{F}_{-}\ne{0}\). Тому вільний диполь буде не лише повертатися навколо центра мас, а й рухатись як ціле.

Указана сила визначається величиною та орієнтацією електричного моменту диполя \(\vec{p}\) і конфігурацією та ступенем неоднорідності зовнішнього поля. Її загальний вираз легко знайти:

\begin{equation} \vec{F}=\vec{F}_{+}+\vec{F}_{-}=q\bigl(\vec{E}_{+}-\vec{E}_{-}\bigr)=q\,\Delta\vec{E}. \tag{4.10} \end{equation}

де \(\Delta\vec{E}\) — зміна напруженості поля при переміщенні на відстань \(l\) у напрямку плеча диполя. При малій величині \(l\) зміна поля є незначною, тож можна записати:

\begin{equation} \Delta \vec{E}=\frac{\partial \vec{E}}{\partial l}l, \end{equation}

де \(\partial\vec{E}/\partial{l}\) — похідна вектора \(\vec{E}\) у напрямку \({\vec{l}}\), яка визначає швидкість зміни напруженості поля в напрямку плеча диполя. Відтак вираз (4.10) набуває вигляду:

\begin{equation} \vec{F}=p\frac{\partial\vec{E}}{\partial{l}}, \tag{4.11} \end{equation}

де \({p=ql}\) — електричний момент диполя.

Слід зауважити, що попри позірну простоту формули (4.11), властивості сили \(\vec{F}\) у деталях є досить складними. Але ситуація спрощується у випадку елементарного диполя в осесиметричному неоднорідному полі, напруженість якого змінюється тільки у напрямку самого поля, як схематично показано на рис. 4.2б. В такому випадку якщо спрямувати координатну вісь \(\mathrm{Z}\) (орт \(\vec{k}\)) у напрямку поля, то \(\vec{E}=E\vec{k}\), а елементарне переміщення вздовж осі диполя, що фігурує у виразі (4.11), \(\partial{l}=(\partial{z}/\cos\vartheta) \). Отже,

\begin{equation} \vec{F}=p_z\frac{\partial{E}}{\partial{z}}\vec{k}, \tag{4.12} \end{equation}

де \({{p}_{z}}=p\cos \vartheta \) — проекція моменту диполя на напрям поля, а вектор \((\partial{E}/\partial{z})\vec{k}\) — градієнт напруженості поля, в якому знаходиться диполь.

За вказаних умов вектор сили \(\vec{F}\) є колінеарним до осі \(\mathrm{Z}\), тож вираз сили зручно записати через проекцію \({F_z}=\pm{F}\)

\begin{equation} {F_z}=p_z\frac{\partial{E}}{\partial{z}}. \tag{4.13} \end{equation}

Оскільки вісь \(\mathrm{Z}\) на рис. 4.2 спрямована в бік підсилення поля, то у виразах (4.12) і (4.13) \(\partial{E}/\partial{z}\gt{0}\). Це означає, що при орієнтації по полю \(\vartheta\lt{90^{\circ}}\) диполь втягується в область сильнішого поля, а при протилежній орієнтації \((\vartheta\gt{90^{\circ}}) \) — виштовхується в бік слабшого поля. Якщо ж у неоднорідне поле внести диполь у довільній орієнтації та вивільнити, то він почне одночасно повертатися і рухатись у той чи інший бік, але врешті зорієнтується по полю і рухатиметься в бік зростання напруженості.

Енергія диполя в зовнішньому полі. Електричне поле діє не на диполь як ціле, а на кожен заряд окремо. Тому, попри електричну нейтральність, диполь у зовнішньому полі має відповідну потенціальну енергію, яку можна визначити через роботу поля при зміні орієнтації диполя.

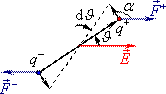
Нехай диполь із зарядом \(q\) і плечем \(\vec{l}\) є зорієнтований під кутом \(\vartheta \) до напрямку електричного поля \(\vec{E}\), рис. 4.3. Тоді при повороті диполя проти годинникової стрілки на елементарний кут \({\mathrm{d}}\vartheta \) заряди диполя переміщуються на відстань \(\mathrm{d}s\), а сили поля \(F=qE\) виконують сумарну роботу \(\delta A=2F\cos \vartheta \,\mathrm{d}s \). Із рис. 4.3 видно, що \(\mathrm{d}s=(l/2)\,\mathrm{d}\vartheta \), і \(\alpha=90^{\circ}-\vartheta \). Отже, \(\cos \alpha =-\sin \vartheta \), і

\begin{equation} \delta{A}=-qEl\sin\vartheta\cdot\mathrm{d}\vartheta=-pE\sin\vartheta\cdot\mathrm{d}\vartheta, \end{equation}

де \({p}={ql}\) — модуль електричного моменту диполя.

Звідси, згідно із співвідношенням (2.10), можна знайти приріст потенціальної енергії диполя при заданій зміні кута \(\vartheta \) від \(\vartheta_1 \) до \(\vartheta_{2}\):

\begin{equation} \begin{aligned} &{W_2-W_1}=-A=pE\int\limits_{\vartheta_{1}}^{\vartheta_{2}}\sin\vartheta\cdot\mathrm{d}\vartheta={}\\ &\quad{}= pE\bigl(\cos\vartheta_{1}-\cos\vartheta_{2}\bigr) . \end{aligned} \end{equation}

Переписавши цей вираз як

\begin{equation} {W_2-W_1}=\bigl(-pE\cos\vartheta_{2}\bigr)-\bigl(-pE\cos\vartheta_{1}\bigr) , \end{equation}

бачимо, що потенціальна енергія диполя у зовнішньому полі визначається формулою

\begin{equation} {W}=-pE\cos\vartheta , \tag{4.14} \end{equation}

або

\begin{equation} {W}=-\vec{p}\vec{E}. \tag{4.14а} \end{equation}

При цьому \(W = 0\), коли \(\cos{\vartheta}={0}\), тобто за нульовий рівень енергії приймається енергія диполя в положенні коли його вісь перпендикулярна до напрямку поля. Відповідно, при \(\vartheta=0{}^{\circ}\) енергія диполя є мінімальною і складає \({W}_{\textrm{min}}=-pE \), а при \(\vartheta=180{}^{\circ}\) вона максимальна і дорівнює \({W}_{\textrm{max}}={pE}\). У відповідності до законів механіки в обох цих положеннях диполь перебуває в рівновазі, але в першому вона є стійкою, тоді як в другому — нестійкою.