physics.zfftt.kpi.ua

Із механіки відомо, що при переміщенні частинки в потенціальному полі роботу поля можна визначити як через силу, так і через потенціальну енергію. Тому роботу при переміщенні заряду в кулонівському електричному полі можна знайти як через напруженість поля, так і через потенціал. Отже, між напруженістю і потенціалом є органічний зв’язок, що дозволяє визначати одну з цих величин за відомою іншою. Далі розглянуто:

3.1. Визначення потенціалу поля через напруженість

Задачу про зв’язок між напруженістю та потенціалом можна розглядати двояко: як установлення способу визначення потенціалу поля \(\varphi(\vec{r}) \) через задану напруженість \(\vec{E}{(\vec{r})}\), та як установлення способу визначення напруженості поля \(\vec{E}{(\vec{r})}\) через заданий потенціал \(\varphi{(\vec{r})}\).

Перша задача по суті вже була розглянута в п. 2.2. Справді, підставляючи у формулу (2.3) вираз роботи поля (2.1), отримуємо загальний вираз різниці потенціалів між заданими точками 1 і 2 через напруженість поля:

\begin{equation} \varphi_1-\varphi_2=\int\limits_{1\to{2}}{\vec{E}\,\mathrm{d}\vec{l}}. \tag{3.1} \end{equation}

Так само, попередньо обравши нульову точку \(P_0\), за формулою (2.6) можна знайти й потенціал в будь-якій точці \(P\):

\begin{equation} \varphi =\int\limits_{P\to {{P}_{0}}}{\vec{E}\,\mathrm{d}\vec{l}}, \tag{3.2} \end{equation}

Як було показано раніше (п. 2.1), ці інтеграли не залежать від траєкторії, що дозволяє при розрахунках обирати найзручніший шлях інтегрування. Часто це силова лінія поля.

3.2. Визначення напруженості поля через потенціал

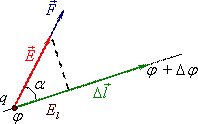
Проекція напруженості \(\vec{E}\) на заданий напрям. Розглянемо роботу поля \(\Delta{A}\) при невеликому переміщенні \(\Delta{\vec{l}}\) заряду \(q\) у заданому напрямку між точками з потенціалами \(\varphi\) та \(\varphi+\Delta\varphi\) (рис. 3.1).

Згідно з (2.3), ця робота складає

\begin{equation} \Delta{A}=-q\,\Delta{\varphi}. \end{equation}

На невеликому переміщенні зміни напруженості поля \({\vec{E}}\) та сили \(\vec{F}=q\vec{E}\), що діє на заряд є незначними. Тому, вказану роботу можна наближено визначити через напруженість в початковій точці:

\begin{equation} \Delta{A}\approx{q}\vec{E}\cdot\Delta\vec{l}. \end{equation}

Прирівнюючи обидва вирази роботи і враховуючи, що \(\vec{E}\,\Delta\vec{l}=E\,\Delta{l}\cos\alpha=E_{l}\,\Delta{l}\) (див. рис. 3.1), отримаємо для проекції вектора \(\vec{E}\) на напрям переміщення заряду \(q\):

\begin{equation} {E_l}\approx-\frac{\Delta\varphi}{\Delta{l}}. \end{equation}

При зменшенні відстані \(\Delta{l}\) похибка буде зменшуватись, і в границі \(\Delta{l}\to{0}\) цей вираз стане точним. Отже,

\begin{equation} E_{l}=-\lim\limits_{\Delta{l}\to{0}}\frac{\Delta{\varphi}}{\Delta{l}}. \end{equation}

Границя у правій частині — то є швидкість зміни величини \(\varphi\) при переміщенні в заданому напрямку \(\vec{l}\). Вона позначається як \(\partial \varphi /\partial l\) і називається похідною функції \( \varphi \) за напрямом \(\vec{l}\):

\begin{equation}\frac{\partial\varphi}{\partial{l}}=\lim\limits_{\Delta{l}\to{0}}\frac{\Delta{\varphi}}{\Delta{l}}.\end{equation}

Таким чином,

\begin{equation} {E_l}=-\frac{\partial{\varphi}}{\partial{l}}, \tag{3.3} \end{equation}

тобто

проекція вектора напруженості електричного поля на заданий напрям дорівнює взятій із зворотнім знаком похідній потенціалу в цьому напрямі.

Зв’язок між \(\vec{E}\) та φ. Попри схожість в означенні та позначенні, похідна за напрямом не є звичною похідною, і в (3.3) символ \(\partial l\) означає не приріст якогось аргументу \(l\), а величину нескінченно малого переміщення у напрямі \(l\). Виняток становить рух уздовж координатних осей, коли елементарні переміщення \(\mathrm{d}x\), \(\mathrm{d}y\), \(\mathrm{d}{z}\) є приростами аргументів \(x\), \(y\), \(z\) функції \(\varphi(x,y,z)\). У такому випадку похідні у напрямках координатних осей вироджуються в частинні похідні по відповідних координатах, і згідно з (3.3)

\begin{equation} \begin{aligned} &{E_x}=-\frac{\partial{\varphi}}{\partial{x}}, \quad {E_y}=-\frac{\partial{\varphi}}{\partial{y}} \quad \text{і} \\ &\quad {E_z}=-\frac{\partial\varphi}{\partial{z}}. \end{aligned} \end{equation}

Це дозволяє виразити через потенціал і вектор напруженості \(\vec{E}=E_x\vec{i}+E_y\vec{j}+e_z\vec{k}\):

\begin{equation} \vec{E}=-\left(\frac{\partial\varphi}{\partial{x}}\vec{i}+\frac{\partial\varphi}{\partial{y}}\vec{j}+\frac{\partial\varphi}{\partial{z}}\vec{k}\right) . \end{equation}

Величина в дужках називається градієнтом потенціалу і позначається як \(\operatorname{grad} \varphi\):

\begin{equation} \operatorname{grad}\varphi=\frac{\partial\varphi}{\partial{x}}\vec{i}+\frac{\partial\varphi}{\partial{y}}\vec{j}+\frac{\partial\varphi}{\partial{z}}\vec{k}. \tag{3.4} \end{equation}

Отже,

\begin{equation} \vec{E}=-\operatorname{grad}\varphi . \tag{3.5} \end{equation}

Вектор напруженості електричного поля в кожній точці дорівнює взятому з протилежним знаком градієнту потенціалу в цій точці.

Ще раз наголосимо, що йдеться тільки про потенціальне (кулонівське) поле.

3.3. Градієнт

Вирази (3.4) і (3.5) показують, як слід обчислювати напруженість поля через потенціал, заданий в декартових координатах, і не дають наочного уявлення про зв’язок напруженості з потенціалом та зміст поняття “градієнт”. Аби висвітлити його, згадаймо, що в кожній точці вектор напруженості \(\vec{E}\) напрямлений уздовж нормалі \(\vec{n}\) до еквіпотенціальної поверхні, і, згідно з (3.3), проекція \(E_n\) і модуль \(E\) напруженості поля визначаються похідною вздовж нормалі:

\begin{equation} {E_n}=\frac{\partial\varphi}{\partial{n}} \qquad \text{і} \qquad {E}=\left|\frac{\partial\varphi}{\partial{n}}\right| . \tag{3.6} \end{equation}

У випадку однорідного поля (\(\vec{E}=\mathrm{const}\)), потенціал у будь-якому напрямку змінюється лінійно, тому

\begin{equation} {E}=\frac{U}{d}, \tag{3.6а} \end{equation}

де \(U=\varphi_1-\varphi_2\) — різниця потенціалів (напруга) між двома точками, розміщеними одна від одної на відстані \(d\) у напрямку поля. На основі цієї формули встановлена одиниця напруженості поля “вольт-на-метр” (В/м):

\(1\ \text{В/м}\) — це напруженість однорідного електричного поля, в якому між точками, розташованими на відстані \(1\ \text{м}\) у напрямку поля, напруга становить \(1\ \text{В}\).

Відповідно до співвідношень (3.6) вектор \(\vec{E}\) виражається, як

\begin{equation} \vec{E}=-\frac{\partial\varphi}{\partial{n}}\vec{n}, \end{equation}

де \(\vec{n}\) — орт (одиничний вектор) нормалі до еквіпотенціальної поверхні, напрямлений в бік зростання потенціалу.

Зіставляючи цей вираз із виразом (3.5), бачимо, що

\begin{equation} \operatorname{grad}\varphi=\frac{\partial\varphi}{\partial{n}}\vec{n}. \tag{3.7} \end{equation}

Цей результат можна розглядати як інваріантне (не залежне від системи координат) означення поняття градієнта потенціалу. Аби зрозуміти його зміст, згадаймо, що модуль вектора більший за модуль його проекції на будь-який інший напрям: \(|\vec{E}|\gt |E| \). Це означає, що \(\left|\frac{\partial\varphi}{\partial{n}}\right|\gt\left|\frac{\partial\varphi}{\partial{l}}\right|\), тобто напрям градієнта є напрямом найшвидшої зміни \(\varphi\). Відтак можна дати наступне формулювання:

градієнтом потенціалу у заданій точці називається вектор, який спрямований в бік найшвидшого зростання потенціалу і має модуль, рівний швидкості його зміни в цьому напрямі.

Примітка. У математиці градієнт трактують як указану міру швидкості зміни будь-якої функції координат.

Відповідно, позаяк у виразі (3.5) фігурує знак “\(-\)”, вектор напруженості електричного поля у кожній точці напрямлений в бік найшвидшого зменшення потенціалу.