ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ
І. ЕЛЕКТРИЧНЕ ПОЛЕ У ВАКУУМІ
2. Потенціал
У вступі говорилося, що в природі існує єдине електромагнітне поле, яке “складається” з електричного та магнітного полів. Але ці поля не є двома окремими полями і за відповідних умов можуть породжувати (індукувати) одне одного. Через це в природі є два види електричних полів: “кулонівські”, що безпосередньо створюються зарядженими частинками, і так звані “вихрові”, які породжуються магнітними полями. Силова дія обох полів, зокрема, їхня робота при переміщенні зарядів визначається вектором напруженості. Але кулонівське поле до того ж є потенціальним, тобто його робота не залежить від траєкторії руху зарядженої частинки та пройденого нею шляху. Тому кулонівське поле, крім напруженості, характеризується ще й скалярною величиною — потенціалом.
Далі розглядаються такі питання:
2.1. Потенціальність електричного поля зарядів
2.2. Різниця потенціалів і потенціал
2.1. Потенціальність електричного поля зарядів
У потенціальності електричного поля зарядів можна переконатися прямими розрахунками. Розглянемо спочатку роботу поля точкового заряду \(q\) при переміщенні іншого точкового заряду \(q'\) вздовж довільної траєкторії між заданими точками 1 і 2 (рис. 2.1).
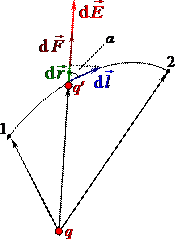
На гранично малому переміщенні \(\mathrm{d}\vec{l}\) поле виконує елементарну роботу \(\delta{A}=\vec{F}\,\mathrm{d}\vec{l}=q'\vec{E}\,\mathrm{d}\vec{l}\). Робота на всьому шляху складається з усіх елементарних робіт \(\delta{A}\) і визначається криволінійним інтегралом по траєкторії:
\begin{equation} {A}=\int\limits_{1\to{2}}E\,|\mathrm{d}\vec{l}|\cos\alpha . \tag{2.1} \end{equation}
З рис. 2.1 видно, що величина \(|\mathrm{d}\vec{l}|\cos\alpha=\mathrm{d}{r}\) є приростом відстані \(r\) при переміщенні \(\mathrm{d}\vec{l}\). Тому, врахувавши формулу (1.4а), отримаємо:
\begin{equation} \begin{aligned} &{A}=\frac{q{'}q}{4\pi\varepsilon_0}\int\limits_{r_1}^{r_2}{\frac{\mathrm{d}r}{r^2}} \quad \Rightarrow\quad {A}={}\\ &\quad= q{'}\left(\frac{q}{4\pi\varepsilon_0{r_1}}-\frac{q}{4\pi\varepsilon_0{r_2}}\right) . \end{aligned} \tag{2.2} \end{equation}
Очевидно, знайдена робота залежить тільки від відстаней \(r_1\) і \(r_2\) від заряду \(q'\) до \(q\), а не від форми траєкторії та пройденого ним шляху. Це вірно і для поля створеного довільною системою зарядів \(q_i\). Дійсно, напруженість поля системи \(\vec{E}=\sum\limits_{i}{\vec{E}_i}\), тому
\begin{equation} \begin{aligned} &{A}=\int\limits_{1\to{2}}q{'}\left(\sum\limits_{i}\vec{E}_i\right)\mathrm{d}\vec{l}={}\\ &\quad{}=\sum\limits_{i}\Biggl(\,\int\limits_{1\to{2}}q{'}\vec{E}_i\,\mathrm{d}\vec{l}\Biggr)= \sum\limits_{i}{A_i}, \end{aligned} \end{equation}
де роботи \(A_i\) складових полів \(\vec{E}_{i}\) визначаються виразом (2.2). Тож
\begin{equation} {A}=q{'}\left(\sum\limits_{i}\frac{q_i}{4\pi\varepsilon_0{r_{i1}}}-\sum\limits_{i}\frac{q_i}{4\pi\varepsilon_0{r_{i2}}}\right) , \tag{2.2а} \end{equation}
де \(r_{i1}\) і \(r_{i2}\) — відстані від початкової та кінцевої точок переміщення заряду \(q_i\) до \(i\)-го заряду системи.
Таким чином, при переміщенні заряду в будь-якому кулонівському полі робота поля не залежить від траєкторії. Отже,
електричне поле, створене зарядженими частинками (кулонівське поле), є потенціальним полем.
Слід зауважити, що це не так для електричних полів, які породжується не зарядами, а змінним магнітним полем.
2.2. Різниця потенціалів і потенціал
Означення. У виразах (2.2) і (2.2a) величина в дужках не залежить від заряду \(q'\) і визначається тільки величиною поля у початковій та кінцевій точках переміщення. Тому вираз роботи поля при переміщенні заряду \(q\) між заданими двома точками по будь-якому шляху можна подати, як
\begin{equation} {A}=q(\varphi_1-\varphi_2)=-q\,\Delta{\varphi} , \tag{2.3} \end{equation}
а при нескінченно малому переміщенні — як
\begin{equation} \delta{A}=-q\,\mathrm{d}{\varphi}. \tag{2.3а} \end{equation}
Величина
\begin{equation} {U}=\varphi_1-\varphi_2 \tag{2.4} \end{equation}
є однією з характеристик електричного поля і називається різницею потенціалів або напругою. Отже:
різницею потенціалів (напругою) між заданими двома точками називається величина, що чисельно дорівнює роботі поля при перенесенні між цими точками одиничного позитивного заряду.
Відтак формулу (2.3) можна записати і як
\begin{equation} {A=qU}. \tag{2.5} \end{equation}
Напруга вимірюється у вольтах (В), причому різниця потенціалів (напруга) двома між точками дорівнює \(1\ \text{В} = 1\ \text{Дж/Кл}\), якщо при перенесенні між ними заряду \(1\) Кл поле виконує роботу \(1\) Дж.
Таким чином, потенціальне поле визначається на лише силовою характеристикою — вектором напруженості \(\vec{E}\), а й скалярною алгебраїчною величиною — потенціалом \(\varphi\), який є енергетичною характеристикою поля. Але вираз (2.4) визначає тільки різницю потенціалів у двох точках. Що ж до потенціалу \(\varphi\), то він сам по собі не є однозначно визначеним — якщо в усіх точках поля до величини \(\varphi\) додати будь-яке задане число, то це ніяк не вплине ні на результати обчислень роботи за формулою (2.3), ні на значення напруженості поля. Тому, аби потенціал у всіх точках був визначений однозначно, треба спочатку вибрати так звану нульову точку (або нульовий рівень) потенціалу — якусь точку \(P_0\) (або множину точок), де потенціал за домовленістю приймається рівним нулю: \(\varphi(P_0)=0\). У такому разі формула (2.3) для роботи поля \(A_0\) при переміщенні заряду з довільної точки \(P\) у нульову точку \(P_0\) запишеться, як
\begin{equation} {A_0}=q\varphi , \end{equation}
і
\begin{equation} {\varphi}=\frac{A_0}{q}. \tag{2.6} \end{equation}
Цей вираз по суті є означенням потенціалу:
потенціал електричного поля є визначеним тільки по відношенню до вибраної нульової точки і чисельно дорівнює роботі поля при перенесенні одиничного позитивного заряду з даної точки в нульову точку.
Слід зазначити, що вибір нульової точки, в принципі, є довільним і лімітується лише міркуваннями зручності. Наприклад, у випадку окремої зарядженої частинки чи системи зарядів обмежених розмірів поле послаблюється з відстанню, тому у фізиці нульову точку потенціалу вибирають “на нескінченності”, тобто в довільній точці віддаленій від системи на необмежено велику відстань. Виняток становлять тільки ідеалізовані поля необмежених розподілів заряду, таких, як нескінченна зарядженою площина, або нескінченний заряджений циліндр, тощо.
На практиці корпуси вузлові (“нульові”) точки схем електричних приладів сполучають із корпусом, а сам корпус із міркувань техніки безпеки “заземлюють”, тобто з’єднують із земною поверхнею. Тому в електротехніці за нуль приймається потенціал Землі.
При виборі нульової точки на нескінченності з виразів (2.2), (2.2а) і (2.3) випливають такі формули потенціалу поля окремого точкового заряду \(q\) та системи зарядів \(q_i\):
\begin{align} \varphi&=\frac{q\mathstrut}{4\pi\varepsilon_0{r}}, \tag{2.7}\\ \varphi&=\sum\limits_{i}\frac{q_i\mathstrut}{4\pi\varepsilon_0{r_i}}. \tag{2.7а} \end{align}
Остання формула показує, що потенціал, як і напруженість поля, задовольняє принцип суперпозиції:
\begin{equation} \varphi=\sum\limits_{i}\varphi_{i}. \tag{2.8} \end{equation}
Це дозволяє розраховувати і потенціали полів неперервно розподілених зарядів за тою самою схемою, що й для напруженості (п. 1.3). А саме, весь заряд поділяють на окремі точкові ділянки \(\mathrm{d}q\), потім за формулою (2.7) записують потенціал поля окремої ділянки \(\mathrm{d}\varphi = k\,\mathrm{d}q/r\), і у виразі (2.8) дискретне додавання замінюють інтегруванням:
\begin{equation} \varphi=k\int\limits{\frac{\mathrm{d}q}{r}} . \tag{2.9} \end{equation}
Відтак, записавши \(\mathrm{d}q\) через густину заряду та розміри ділянки, отримуємо наступні інтегральні формули для обчислення потенціалу при кожному можливому типі розподілу:
\begin{align} \varphi&=k\int\limits_V{\frac{\rho{(\vec{r})}}{r}}\mathrm{d} V = \frac{1}{4\pi\varepsilon_0}\int\limits_{V}\frac{\rho{(\vec{r})}}{r}\mathrm{d}{V} . \tag{2.9а}\\ \varphi&=k\int\limits_{S}{\frac{\sigma{(\vec{r})}}{r}}\mathrm{d}S =\frac{1}{4\pi {{\varepsilon }_{0}}}\int\limits_{S}{\frac{\sigma ( {\vec{r}} )}{r}\mathrm{d}S}, \tag{2.9б}\\ \varphi&=k\int\limits_{L}{\frac{\lambda ( {\vec{r}} )}{r}\mathrm{d}\vec{l}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\int\limits_{L}{\frac{\lambda ( {\vec{r}} )}{r}\mathrm{d}\vec{l}}, \tag{2.9в}\\ \end{align}
де \(\rho{(\vec{r})}\), \(\sigma{(\vec{r})}\) та \(\lambda{(\vec{r})}\) — функція об’ємної, поверхневої та лінійної густини заряду.
Наостанок згадаємо про таке. З механіки відомо, що при переміщенні тіла в потенціальному полі будь-якої природи робота сил поля дорівнює спаду потенціальної енергії тіла:
\begin{equation} {A}=-\Delta{W}=W_1-W_2 . \tag{2.10} \end{equation}
Тож, зваживши на формулу (2.3), маємо такий загальний вираз потенціальної енергії зарядженої частинки в електричному полі:
\begin{equation} W =q\varphi. \tag{2.10а} \end{equation}
2.3. Еквіпотенціальні поверхні
Наочне уявлення про розподіл потенціал поля в просторі можна скласти за допомогою еквіпотенціальних поверхонь, тобто таких,
для кожної з яких потенціал поля в усіх точках однаковий: \(\varphi= \textrm{const}\).
Форма еквіпотенціальних поверхонь визначається видом залежності потенціалу від координат і для кожного значення потенціалу \(\varphi_0\) встановлюється з рівняння \(\varphi(\vec{r})=\varphi_{0}\). Зокрема, для поля точкового заряду, згідно з виразом (2.7), виходить:
\begin{equation} \frac{q}{4\pi\varepsilon_0{r}}=\varphi_{0} \quad\Rightarrow \quad{r}=\frac{q}{4\pi\varepsilon_0\varphi_{0}}=\mathrm{const}. \end{equation}
Отже, еквіпотенціальними поверхнями такого поля є сфери з центром у заряді, як показано штриховими лініями на рис. 1.7а,б (п. 1.4). (Зрозуміло, що на папері зображуються не самі еквіпотенціальні поверхні, а лінії їхнього перетину із площиною рисунка.)
Аби за допомогою еквіпотенціальних поверхонь наочно показати не тільки розподіл, а й зміну потенціалу при переміщенні в полі від точки до точки, їх (поверхні) проводять з однаковим кроком \(\Delta\varphi=\mathrm{const}\). У такому разі чим швидше змінюється потенціал, тим ближче одна до одної розташовуються еквіпотенціальні поверхні. Це стосується як поля точкового заряду, так і інших полів, наприклад, поля двох різнойменних зарядів:
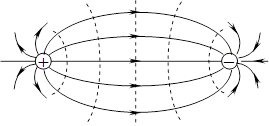
Форма еквіпотенціальних поверхонь, як і форма ліній поля, в загальному випадку є складною і може взагалі не виражатись якимось рівнянням. Але за будь-яких умов у всіх точках
силові лінії та еквіпотенціальні поверхні є взаємно ортогональними,
тобто в точці перетину дотична до силової лінії (напрям \({\vec{E}}\)) і площина, дотична до еквіпотенціальної поверхні, є взаємно перпендикулярними. Це випливає з того, що при будь-якому переміщенні \(\mathrm{d}\vec{l}\) заряду \(q\) по еквіпотенціальній поверхні, згідно з (2.3а), робота поля \(\delta A=q\vec{E}\,\mathrm{d}\vec{l}=-q\,\mathrm{d}\varphi =0\), отже кут між векторами \(\vec{E}\) і \(\mathrm{d}\vec{l}\) дорівнює \(90^\circ\).
Контрольні запитання
1. Що свідчить про потенціальність електричного поля зарядів?
2. Що називається різницею потенціалів у двох точках електричного поля? Потенціалом у заданій точці?
3. Потенціал у деякій точці електричного поля дорівнює \(1\ \text{кВ}\). Що це означає?
4. Запишіть формулу потенціалу поля точкового заряду відносно землі, якщо земна поверхня має потенціал \(\varphi_0\) відносно нескінченності.
5. Електричне поле нескінченної рівномірно зарядженої площини є однорідним (скрізь однаковим). Чи можна записати для нього формулу потенціалу? Чому?
6. Електричне поле створюється двома закріпленими однаковими різнойменними зарядами. Яку форму має і що собою являє еквіпотенціальна поверхня, котра проходить через середину відрізка, що з’єднує заряди?
7. Як, маючи картину еквіпотенціальних поверхонь електричного поля, можна показати вигляд його силових ліній?