ФІЗИКА ДЛЯ БАКАЛАВРІВ. ЕЛЕКТРИКА І МАГНЕТИЗМ
І. ЕЛЕКТРИЧНЕ ПОЛЕ У ВАКУУМІ
1. Напруженість електричного поля
Електромагнітне поле ніяк не впливає на органи чуття людини, тому його властивості можна встановити лише опосередковано через властивості сил, які воно створює. При цьому електричні сили і поле досліджують за допомогою “пробних зарядів” — заряджених частинок з малими розмірами та величиною електричного заряду. Через малі розміри такі частинки відображають властивості електричного поля локально (в точці), а завдяки малій величині заряду не спотворюють його. Цей параграф присвячено основній величині, що характеризує електричне поле — напруженості. Розглянуто такі питання:
1.1. Вектор \(\vec{E}\)
Експериментальні дослідження сил, які діють на пробні заряди в електричному полі, свідчать про таке:
1. У даній точці поля вектор сили \( \vec{F} \), що діє на пробний заряд \(q\), завжди напрямлений вздовж однієї й тієї ж прямій в той чи інший бік, залежно від знаку заряду. Це означає, що електричне поле в кожній точці має визначений напрям.
2. Величина сили, з якою поле діє на пробний заряд, є прямо пропорційною до величини цього заряду:
\begin{equation} {F}\sim|q| . \end{equation}
Це означає, що відношення
\begin{equation} {E}=\frac{F}{|q|} \end{equation}
не залежить від заряду і є мірою “потужності” самого поля. Воно називається напруженістю електричного поля і, аби відображало ще й напрям поля, розглядається як вектор:
\begin{equation} \vec{E}=\frac{\vec{F}}{q} . \tag{1.1} \end{equation}
Сказане ілюструє рис. 1.1.
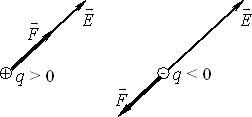
Рис. 1.1
Таким чином, вектор напруженості \( \vec{E} \) є силовою характеристикою (силовим вектором) електричного поля. За модулем і напрямом він збігається із силою, що діє на одиничний позитивний заряд вміщений в дану точку поля.
За одиницю напруженості природньо було би прийняти \(1\ \text{Н/Кл}\), тобто напруженість такого електричного поля, в якому на одиничний заряд діє одинична сила. Але в міжнародній системі одиниць (СІ) одиниця напруженості уводиться інакше і називається “один вольт-на-метр” (\(1\ \text{В/м}\)). Про це буде сказано далі (п. 2.4), а тут лише зауважимо, що \(1\ \text{В/м}\) = \(1\ \text{Н/Кл}\), тобто при Е = \(1\ \text{В/м}\) на заряд \(1\ \text{Кл}\) діє сила \(1\ \text{Н}\).
З означення (1.1) випливає загальна формула сили, що діє в електричному полі на точковий заряд:
\begin{equation} \vec{F}=q\vec{E} . \tag{1.2} \end{equation}
Із цієї формули, зокрема, випливає, що сила, яка діє в полі на позитивний заряд, за напрямком є збіжною, а на негативний — антипаралельною з напрямом поля, як показано на рис. 1.1.
Формула (1.2) є однією з основних у теорії електричного поля, оскільки дозволяє обчислювати силу і відтак визначати рух заряджених частинок в електричних полях. Але для цього треба вміти знаходити напруженість поля незалежно від означення (1.1), тобто без вимірювання сил. Тому встановлення способів визначення напруженості є однією з основних задач теорії електричного поля.
1.2. Напруженість поля точкового заряду
Можливість теоретичного розрахунку напруженості різних електричних полів ґрунтується на двох основних законах, які встановлені на досліді — законі Кулона та принципі суперпозиції.
Закон Кулона. Цей закон був установлений ще до виникнення концепції поля і визначає електричну взаємодію точкових зарядів. Він твердить, що
сили взаємодії між двома точковими зарядами є прямо пропорційні величинам цих зарядів і обернено пропорційні квадратові відстані між ними.
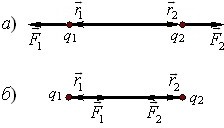
Ці сили задовольняють третій закон Ньютона: вони рівні по модулю і діють у протилежних напрямах уздовж прямої, що проходить через заряди, рис. 1.2.
У векторній формі ці сили виражаються, як
\begin{equation} \vec{F}_1=k\frac{q_1 q_2}{r^2}\vec{e}_{12} ,\quad \vec{F}_2=k\frac{q_1 q_2}{r^2}\vec{e}_{21} , \tag{1.3} \end{equation}
або
\begin{equation} \vec{F}_1=k\frac{q_1 q_2}{r^3}\vec{r}_{1} , \quad \vec{F}_2=k\frac{q_1 q_2}{r^3} \vec{r}_{2} , \tag{1.3а} \end{equation}
де \( \vec{e}_{12}=(\vec{r}_1/{r_1})\) і \( \vec{e}_{21}=(\vec{r}_2 / r_2) \) — одиничні вектори, а \( \vec{r}_{1} \) та \( \vec{r}_{2} \) — радіуси-вектори точки розташування заряду, на який діє сила з боку поля, що створюється в цій точці іншим зарядом; \({r}=|\vec{r}_1|=|\vec{r}_{2}| \) — відстань між зарядами; k — коефіцієнт пропорційності.
Позаяк \(\vec{r}_1 = -\vec{r}_{2} \), напрямки цих сил протилежні, а модулі однакові і дорівнюють
\begin{equation} {F}=k\frac{|q_1|\cdot |q_2|}{r^2} . \tag{1.3б} \end{equation}
Отже, сили кулонівської взаємодії між зарядами задовольняють третій закон Ньютона. Векторні вирази (1.3а) відображають також і характер взаємодії зарядів. Справді, якщо заряди однойменні, то \(q_{1}\cdot q_{2} > 0\), і вектори \(\vec{F}_{1}\) і \(\vec{F}_{2}\) мають напрямки радіусів-векторів \(\vec{r}_{1}\) і \(\vec{r}_{2}\), що відображає відштовхування однойменних зарядів (рис. 1.2а). Для різнойменних зарядів \(q_{1}\cdot q_{2} < 0\), що відповідає притяганню між ними (рис. 1.2б).
Розмірний коефіцієнт \(k\) визначається силою взаємодії між двома одиничними зарядами у вакуумі при одиничній відстані між ними. Його числове значення залежить від системи одиниць і в СІ складає \(k = 9\cdot 10^9\ \text{м/Ф}\) (\(\text{Ф}\) — одиниця електричної ємності “фарад”). Зауважимо, що розмірність \([\text{м/Ф}]\) є рівносильною розмірності \([\text{Н}\cdot \text{м/Кл}^2]\), яка випливає з формули (1.3а). Число \(k\) є зручним для обчислень, але в літературі формули прийнято записувати через електричну сталу \(\varepsilon_{0} \), що визначається як
\begin{equation} \varepsilon_{0}=\frac{1}{4\pi{k}}=8{,}85\cdot{10^{-12}}\ \frac{\text{Ф}}{\text{м}}. \end{equation}
Тому розгорнуто вирази (1.3а), (1.3б) записуються, як
\begin{equation} \begin{aligned} \vec{F}_{1}&=\frac{q_1 q_2\mathstrut}{4\pi\varepsilon_{0}r^3\mathstrut}\vec{r}_{1}, \\ \vec{F}_{2}&=\frac{q_2 q_1\mathstrut}{4\pi\varepsilon_{0}r^{3}\mathstrut}\vec{r}_{2}, \\ {F}&=\frac{|q_1|\cdot{|q_2|}\mathstrut}{4\pi\varepsilon_{0}r^2\mathstrut}. \end{aligned} \tag{1.3в} \end{equation}
Напруженість поля точкового заряду. Сили (1.3в) зумовлені дією на кожен із двох зарядів з боку електричного поля, створеного іншим. Тому відповідно до означення (1.1), поділивши вектор сили, що діє на будь-який із зарядів на його величину, отримаємо загальний вираз вектора напруженості поля точкового заряду:
\begin{equation} \vec{E}=\frac{q}{4\pi\varepsilon_{0}r^{3}}\vec{r}, \tag{1.4} \end{equation}
де \(q\) — алгебраїчна величина заряду, що створює поле, \(\vec{r}\) — радіус-вектор точки, в якій визначається його напруженість (рис. 1.3).
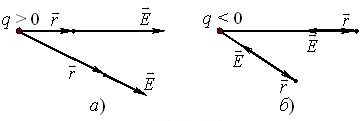
Як видно з формули (1.4) і рис. 1.3, поле точкового заряду є центральним — воно скрізь напрямлене радіально від заряду, якщо \(q > 0\), і до заряду при \(q < 0\), та має модуль
\begin{equation} {E}=\frac{|q|}{4\pi\varepsilon_{0}r^2}, \quad \text{або} \quad {E}=\frac{k|q|}{r^2}. \tag{1.4а} \end{equation}
Зауважимо також, що формули (1.4) і (1.4а) по суті виражають закон Кулона в польовій формі.
1.3. Принцип суперпозиції
Поле системи зарядів. Принцип суперпозиції. Уявімо, що вимірюють напруженість поля системи з двох зарядів у досліді, який складається з наступному трьох частин.
1. Спочатку у вільному просторі в якусь точку 1 вміщують заряд \(q_{1}\) і за допомогою пробного заряду \(q\) та формули (1.1) визначають напруженість поля \(\vec{E}_{1}\) у вибраній точці P (рис. 1.4а).
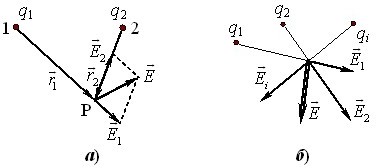
2. Заряд \(q_{1}\) прибирають, а в точку 2 вносять заряд \(q_{2}\) і аналогічно визначають у точці P напруженість \(\vec{E}_{2}\).
3. Не прибираючи заряду \(q_{2}\), в точку 1 повертають заряд \(q_{1}\) і визначають напруженість поля \(\vec{E}\) в точці P, коли присутні обидва заряди.
Цей дослід, проведений реально, дає
\begin{equation} \vec{E}=\vec{E}_{1}+\vec{E}_{2}. \end{equation}
А це означає, що характеристики поля одного заряду не змінюються в присутності іншого. Такий самий результат виходить і при довільній кількості зарядів. Отже, можна зробити висновок, що
електричні поля діють на заряди, але не діють одне на одного.
Указану незалежність полів відображає принцип суперпозиції, який гласить:
вектор напруженості електричного поля, створеного заданою системою зарядів, в будь-якій точці дорівнює сумі векторів напруженості полів, які створюються в цій точці кожним із зарядів системи окремо (тобто за відсутності інших).
Математично принцип суперпозиції виражається загальною формулою
\begin{equation} \begin{aligned} &\vec{E}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}+\cdots +{{\vec{E}}_{i}}+\cdots ={}\\ &\quad{}=\sum{{{\vec{E}}}_{i}}\quad \Rightarrow \quad \vec{E}=\sum{{{{\vec{E}}}_{i}}}. \end{aligned} \tag{1.5} \end{equation}
Згідно з формулою (1.4), для поля системи точкових зарядів \(q_i\) (рис. 1.4б) можна записати:
\begin{equation} \vec{E}=\frac{1}{4\pi {{\varepsilon }_{0}}}\sum{\frac{{{q}_{i}}}{r_{i}^{3}}}{{\vec{r}}_{i}}. \tag{1.6} \end{equation}
Щодо наведеного формулювання принципу суперпозиції слід зауважити таке. Весь ряд доданків у сумі (1.5) можна згрупувати в декілька окремих блоків (наприклад, у два) і спочатку аналогічно обчислити напруженості \(\vec{E}_{\textrm{I}}\) і \(\vec{E}_{\textrm{II}}\) поля кожного блока. Тоді напруженість поля всієї системи виразиться, як
\begin{equation} \vec{E}=\vec{E}_{\textrm{I}}+\vec{E}_{\textrm{II}}. \end{equation}
Це означає, що
напруженість електричного поля довільної системи зарядів дорівнює сумі напруженостей полів будь-яких (не обов’язково точкових) частин цієї системи.
Тому при обчисленні поля за принципом суперпозиції систему можна поділяти на окремі області так, як це найбільш зручно.
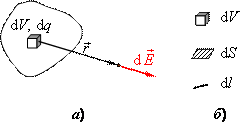
Поле неперервного розподілу заряду. За принципом суперпозиції можна розрахувати і поля, створені неточковими тілами, в яких заряд розподілений неперервно. Для цього тіло слід подумки розділити на елементарні області, кожна з яких містить гранично малий заряд \(\mathrm{d}q\) і створює в заданій точці гранично слабке поле \( \mathrm{d}\vec{E}\) (рис. 1.5а).
Тоді поле, створюване всім тілом,
\begin{equation} \vec{E}=\int\limits{\mathrm{d}\vec{E}}. \end{equation}
Якщо елементарні області точкові, то поля \(\mathrm{d}\vec{E}\) визначаються кулонівською формулою (1.4):
\begin{equation} \mathrm{d}\vec{E}=\frac{k\,\mathrm{d}q}{r^3}\vec{r}. \end{equation}
У такому разі
\begin{equation} \vec{E}=\int\limits\frac{k\,\mathrm{d}q}{r^3}\vec{r}=\frac{1}{4\pi\varepsilon_0}\int\limits\frac{\mathrm{d}q}{r^3}\vec{r}. \tag{1.7} \end{equation}
Ця інтегральна формула, яка є узагальненим виразом принципу суперпозиції, дає алгоритм розрахунку електричного поля створеного будь-яким заданим розподілом електричного заряду.
На практиці окремо розрізняють об’ємний, поверхневий і лінійний розподіли заряду і розділяють область його локалізації на елементарні об’ємчики \(\mathrm{d}V\), площинки \(\mathrm{d}S\), або відрізки \(\mathrm{d}l\) (рис. 1.5б).
Об’ємний розподіл. При розподілі заряду по об’єму тіла величина \(\mathrm{d}q\) у виразі (1.7) у кожній ділянці об’єму \(\mathrm{d}V\) визначається, як \(\mathrm{d}q={\rho}(\vec{r})\mathrm{d}{V}\), через об’ємну густину заряду
\begin{equation} \rho{(\vec{r})}=\frac{\mathrm{d}q}{\mathrm{d}V}\Biggl(\frac{\text{Кл}}{\text{м}^{3}}\Biggr). \end{equation}
У такому разі
\begin{equation} \begin{aligned} &\vec{E}=k\int\limits_{V}\frac{\rho(\vec{r})\vec{r}}{r^3}\mathrm{d}{V}={}\\ &\quad{}=\frac{1}{4\pi\varepsilon_{0}}\int\limits_{V}\frac{\rho(\vec{r}) \vec{r}}{r^3}\mathrm{d}{V}, \end{aligned} \tag{1.8} \end{equation}
де інтегрування проводиться по всьому об’єму зарядженого тіла.
Поверхневий розподіл. Аналогічно, якщо поле створюється зарядженою поверхнею, то заряд її довільної елементарної ділянки \(\mathrm{d}S\) \(\mathrm{d}q=\sigma(\vec{r})\mathrm{d}{S}\), де
\begin{equation} \sigma =\frac{ \d q}{\d s} \ \Biggl(\frac{\text{Кл}}{\text{м}^2}\Biggr) \end{equation}
— поверхнева густина заряду в заданій точці. Тоді
\begin{equation} \begin{aligned} &\vec{E}=k\int\limits_{S}\frac{\sigma\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{S}={}\\ &\quad{}=\frac{q}{4\pi\varepsilon_{0}}\int\limits_{S}\frac{\sigma\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{S}, \end{aligned} \tag{1.8а} \end{equation}
де інтегрування ведеться по всій зарядженій поверхні.
Лінійний розподіл. Нарешті, коли заряд розподілений по заданій лінії («нитці»), то \(\mathrm{d}q=\lambda(\vec{r})\mathrm{d}{l}\), де
\begin{equation} \lambda{(\vec{r})}=\frac{\mathrm{d}q}{\mathrm{d}l}\ \left(\frac{\text{Кл}}{\text{м}}\right) \end{equation}
— лінійна густина заряду. В цьому випадку напруженість визначається через криволінійний інтеграл
\begin{equation} \begin{aligned} &\vec{E}=k\int\limits_{l}\frac{\lambda\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{l}={}\\ &\quad{}=\frac{1}{4\pi\varepsilon_{0}}\int\limits_{l}\frac{\lambda\left(\vec{r}\right)\vec{r}}{r^3}\mathrm{d}{l}. \end{aligned} \tag{1.8б} \end{equation}
Інтегральні вирази (1.8)—(1.8б) випливають із загальної формули (1.7), в основі якої лежить закон Кулона. Тому електричні поля, створювані не лише точковими, а й неперервно розподіленими зарядами, називаються кулонівськими полями.
Принагідно зазначимо, що з усіх наведених формул найбільш загальною є формула (1.8) для об’ємного розподілу заряду, бо поверхневий і лінійний розподіли є просто виродженими випадками об’ємного. Дійсно, заряджена поверхня є не поверхнею в математичному сенсі, а тонкою пластиною із якоюсь товщиною \(h = \mathrm{const}\), тож \(\mathrm{d}q=\rho h\,\mathrm{d}S\). Тому розподіл заряду замість об’ємної густини \(\rho\) зручніше задавати поверхневою густиною \(\sigma=\rho h\) (\(\text{Кл/м}^2\)), яка визначає заряд одиниці поверхні пластинки. Так само нитка являє собою прямий чи викривлений тонкий стержень сталого перерізу \(S\), об’єм елементарної ділянки котрого \(\mathrm{d}V = S\,\mathrm{d}l\). Тоді \(\mathrm{d}q=\rho S\,\mathrm{d}l\), або \(\mathrm{d}q = \lambda\,\mathrm{d}l\), де \(\lambda=\rho S\) — лінійна густина заряду (Кл/м). Нарешті, формула (1.8) вбирає і дискретний розподіл, тобто систему заряджених “кульок” малого об’єму \(\Delta V_i\). У такому разі при інтегруванні у виразі (1.8) в місцях локалізації заряду матимемо \(\rho_i\,\Delta V_i=q_i\), а скрізь у решті об’єму \(\rho\,\mathrm{d}V = 0\). Відтак інтеграл (1.8) вироджується в дискретну суму (1.6).
Що до практичних розрахунків, то способи обчислення наведених інтегралів розглядаються у вищій математиці. Проте в простих випадках достатньо розуміти фізичний зміст виразів (1.8), (1.8а) і (1.8б). У складних випадках, коли задача взагалі не має аналітичних (формульних) розв’язків, використовують комп’ютерні розрахунки. Але принципово використання закону Кулона та принципу суперпозиції є універсальним алгоритмом, який дозволяє розрахувати будь-яке кулонівське електричне поле.
1.4. Лінії напруженості
Поля безпосередньо не впливають на наші органи чуття. Тому, задля отримання наочного уявлення про поле, його в той чи інший спосіб зображують на папері чи екрані монітора. Одним із способів візуалізації поля є лінії напруженості (лінії поля, силові лінії, лінії вектора \(\vec{E}\)), тобто
лінії, в кожній точці яких дотична збігається з вектором напруженості в цій точці (рис. 1.6).
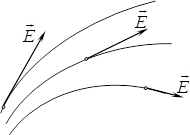
Лінії поля відображають конфігурацію поля, тобто його напрям в різних точках, як це ілюструє рис. 1.7 для полів поодиноких зарядів і пари неподалік один від одного розташованих різнойменних зарядів.
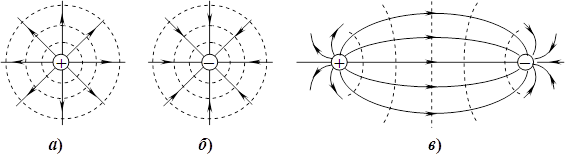
Конфігурація полів інших систем зарядів є складнішою, але їхні силові лінії мають певні спільні властивості. А саме.
Лінії напруженості кулонівського електричного поля є незамкненими; вони виходять із позитивних і сходяться на негативних зарядах.
Також, позаяк в одній точці поле не може мати два різні напрями,
лінії поля не можуть перетинатися.
Окрім того, силові лінії відображають і величину напруженості поля в різних місцях. Як видно з наведених на рис. 1.7 прикладів, поблизу зарядів, де поле є більш сильним, силові лінії розташовані щільніше, ніж на віддаленні. Отже, між лініями поля та величиною напруженості є певний зв’язок. Його легко встановити для поля точкового заряду, яке в усіх рівновіддалених на відстань \(r\) точках має однакову напруженість
\begin{equation} {E}=\frac{q}{4\pi\varepsilon_0{r^2}} \end{equation}
і радіальні силові лінії (рис. 1.7а, б). Тож, якщо для зображення цього поля використати N ліній, то крізь поверхню концентричної сфери з радіусом \(r\) вони будуть проходити з однаковою щільністю
\begin{equation} {n}=\frac{N}{S}=\frac{N}{4\pi{r^2}}. \end{equation}
Якщо в цьому виразі на основі формули (1.4а) зробити заміну
\begin{equation} {4\pi{r^2}}=\frac{q}{\varepsilon_0{E}}, \end{equation}
то отримаємо:
\begin{equation} {E=\frac{q}{\varepsilon_0{N}}n} \quad \Rightarrow \quad {E\sim{n}}. \end{equation}
Тобто на будь-якій відстані від точкового заряду напруженість його поля є прямо пропорційною щільності силових ліній на цій відстані. Такий зв’язок зберігається й для більш складних полів. При цьому щільність ліній \(n\) в кожній точці визначається як
\begin{equation} {n}=\frac{\mathrm{d}N}{\mathrm{d}S_{\bot}}, \end{equation}
де \(\mathrm{d}N\) — кількість ліній поля, що перетинають площадку \(\mathrm{d}S_{\bot}\), перпендикулярну до напрямку поля.
Через будь-яку точку поля можна провести відповідну силову лінію, тож при зображенні поля кількість силових ліній можна вибирати на свій розсуд. Тому домовились уважати, що
в кожній точці щільність ліній поля дорівнює числовому значенню його напруженості:
\begin{equation} E = n. \tag{1.9} \end{equation}
Відтак можна вважати, що кількість силових ліній \(\mathrm{d}N\), які перетинають перпендикулярну до поля елементарну площадку \({\mathrm{d}S_{\bot}}\), дорівнює
\begin{equation} \mathrm{d}N=E\,\mathrm{d}{S}_{\bot}. \tag{1.10} \end{equation}
Така домовленість у деяких ситуаціях виявляється вельми зручною.
Контрольні запитання
1. Що таке фундаментальні взаємодії? Перелічіть їх.
2. Що є схожого і що відмінного між електромагнітною та гравітаційною взаємодією?
3. Що таке електричний заряд і які його основні властивості?
4. Опишіть польовий механізм взаємодій. Чим визначаються загальні властивості електромагнітного поля та його складових — електричного і магнітного полів?
5. Перелічіть загальні властивості електричних сил.
6. Що називається напруженістю електричного поля?
7. Сформулюйте та запишіть у векторній формі закон Кулона. Чи виконується він для довільних заряджених тіл?
8. Якою формулою визначається та як напрямлений вектор напруженості електричного поля точкового заряду?
9. Як записується та який фізичний зміст має принцип суперпозиції електричних полів?
10. Запишіть і поясніть загальний зміст виразів напруженості електричного поля, що створюється зарядженими не точковими тілами при різних типах розподілу заряду.
11. Чи може модуль напруженості поля системи з двох точкових зарядів дорівнювати: 1) сумі модулів і 2) модулю різниці модулів напруженості поля кожного із зарядів? Якщо так, то коли? Окремо розглянути випадки, коли заряди: а) однойменні і б) різнойменні
12. Запишіть вираз напруженості електричного поля посередині між двома однаковими точковими зарядами \(q\) розміщеними не відстані \({l}\) один від одного, коли заряди: а) різнойменні і б) однойменні.
13. Чому дорівнює напруженість електричного поля в центрі правильного трикутника, якщо в його вершинах розміщені однойменні заряди однакової величини.
14. Електричне поле створюється системою з чотирьох однакових зарядів \(q\) розміщених у вершинах квадрата зі стороною \(a\). Чому дорівнює напруженість цього поля на відстані \(r \gg a\) від центра квадрата?
15. Чи можна говорити, що силові лінії збігаються з траєкторіями руху заряджених частинок в електричному полі? Чому?
16. Як за картиною силових ліній електричного поля встановити, де воно сильніше?
17. Чи можуть перетинатися або дотикатися силові лінії електричного поля? Чому?