physics.zfftt.kpi.ua

Вплив діелектриків на характеристики електричного поля розглядається в наступних питаннях:

1.1. Поляризація діелектриків

Полярні та неполярні молекули. Діелектриками називаються речовини, в молекулах яких усі електрони сильно зв’язані з ядрами так, що навіть у сильних електричних полях вони ледь зміщуються відносно ядер. Через це в діелектрику є неможливим електричний струм, тобто переміщення зарядів по всьому об’єму. З цієї причини суцільна діелектрична оболонка ізолює область, яку оточує, від проникнення в неї зарядів. Тому діелектрики інакше називаються “ізоляторами”.

В атомах і молекулах електрони рухаються так швидко, що ядра є немов оточені суцільною хмаринкою від’ємного заряду, або вкриті “електронною оболонкою”. При цьому, залежно від конфігурації електронних оболонок, молекули і діелектричні речовини поділяють на неполярні та полярні. У молекулах неполярних діелектриків, прикладами яких є гелій \(\textrm{He}\) та молекулярний водень \(\textrm{H}_2\), “центри ваги” зарядів електронів і ядер збігаються, як можна зрозуміти із схематичного на рис. 1.1а.

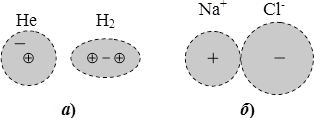
Тому неполярні молекули самі по собі не мають електричного моменту і не створюють власного електричного поля. В молекулах полярних діелектриків, таких як \(\textrm{NaCl}\), заряди електронів і ядер рознесені у просторі (рис. 1.1б) й утворюють елементарні диполі з відповідним власним електричним моментом. Тому в околі полярної молекули існує власне мікрополе \(\vec{E}_{\text{мікро}}\).

Нижче ви можете бачити анімацію, як демонструє поведінку різних молекул в електричному полі.

Поляризація і поляризованість. Унаслідок теплового руху молекул їхні мікрополя в полярному діелектрику орієнтовані хаотично, так що середня величина \(\langle\vec{E}_{\text{мікро}}\rangle=0\). Тому не тільки в неполярних, а й у полярних діелектриках зазвичай ніякого макроскопічного поля немає. Але при внесенні діелектрика в зовнішнє електричне поле \(\vec{E}_{0}\) ситуація змінюється внаслідок поляризації.

Сутність цього явища з’ясуємо на прикладі діелектрика з неполярними молекулами, які будемо розглядати як нейтральні кульки. На перший погляд такі молекули через високий ступінь просторової компенсації зарядів узагалі не мають реагувати на зовнішнє електричне поле. Але поле діє не на молекулу як ціле, а на електрони і на ядра окремо. Через це відбувається деформація електронних оболонок — електрони зміщуються відносно ядер і в кожної молекули з’являється так званий індукований (або наведений) електричний момент \(\vec{p}_{i}\),  орієнтований у напрямку електричного поля  (рис. 1.2а).

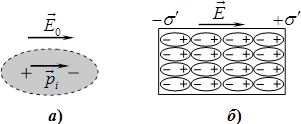
Рознесення негативних і позитивних зарядів частинок діелектрика у взаємно протилежних напрямках під дією електричного поля називається поляризацією.

Примітка. У деяких діелектриках, які називаються п’єзоелектриками, поляризація спостерігається і при механічних деформаціях.

У полярних діелектриках головну роль при поляризації відіграє не деформація електронних оболонок молекул, а переорієнтація їхніх власних електричних моментів під дією поля. Відповідно, поляризацію неполярних діелектриків називають деформаційною, а полярних — орієнтаційною. Слід відмітити, що власні моменти полярних молекул є значно більшими, ніж індуковані. Але через їхню хаотичну орієнтацію та інтенсивний тепловий рух молекул при орієнтаційній поляризації відбувається лише часткове впорядкування власних моментів, так що в обох цих типах діелектриків здатність до поляризації є приблизно однаковою.

При будь-якому виді поляризації молекули під дією електричного поля утворюють систему елементарних диполів із частково впорядкованими (ефетивними) моментами \(\vec{p}_{i}\), фспрямованими по полю, як на рис. 1.2. Тому кожна область діелектрика набуває електричного моменту \(\sum\limits\vec{p}_{i}\ne{0}\). Як наслідок порушується компенсація мікроскопічних полів молекул і в діелектрику виникає внутрішнє (власне) макроскопічне поле \(\vec{E}{'}\). Це поле разом із зовнішнім полем \(\vec{E}_{0}\) формує результуюче макроскопічне поле в діелектрику:

\begin{equation} \vec{E}=\vec{E}_0+\vec{E}{'}. \tag{1.1} \end{equation}

Зрозуміло, що чим сильніша поляризація, тим більша величина \( \sum\limits{\vec{p}_i} \). Тому її використовують для кількісної характеристики ступеня поляризації діелектрика в кожній точці. Відповідна фізична величина називається поляризованістю або вектором поляризації \( \vec{P} \). За означенням

\begin{equation} \vec{P}=\frac{1}{\Delta{V}}\sum\limits\vec{p}_{i}, \tag{1.2} \end{equation}

де \(\Delta V\) — фізично нескінченно малий об’єм діелектрика в околі даної точки, \( \vec{p}_{i} \) — електричні моменти окремих молекул у цьому об’ємі.

Примітка. Як говорилося на початку, фізично нескінченно малим об’ємом називається область у речовині, яка може вважатися точковою, але вміщує макроскопічну кількість молекул. Такі вимоги не є суперечливими через гранично малі розміри молекул. Наприклад, у кубику твердої речовини з ребром \(10^{-6}\) м міститься \(10^{10}\div10^{11}\) молекул.

Отже, можна сказати, що

поляризованість \(\vec{P}\) дорівнює електричному моменту одиниці об’єму поляризованого діелектрика.

Одиницею поляризованості є \(1~\text{Кл/м}^2\), що збігається (і не випадково) з одиницею поверхневої густини заряду.

В однорідному неполярному діелектрику індуковані дипольні моменти всіх молекул однакові, і вираз (1.2) можна записати у вигляді:

\begin{equation} \vec{P}=n\vec{p}, \tag{1.2а} \end{equation}

де \(n\) (\(1/\text{м}^3\)) — концентрація молекул (кількість в одиниці об’єму), \(\vec{p}\) — дипольний момент однієї молекули. Якщо ж вираз (1.2) помножити і поділити на кількість молекул в об’ємі \(\Delta V\), то таким робом можна виразити і поляризованість неоднорідного діелектрика:

\begin{equation} \vec{P}=\frac{N}{\Delta{V}}\cdot\frac{\sum\limits{\vec{p}_{i}}}{N}\quad \Rightarrow \quad \vec{P}=n\langle{\vec{p}_{i}}\rangle, \tag{1.2б} \end{equation}

де \(\langle{\vec{p}_{i}}\rangle \) — дипольний момент, який у середньому припадає на одну молекулу в об’ємі \(\Delta V\).

Поляризаційні та сторонні заряди. В усіх діелектриках поляризація супроводжується появою макроскопічних поляризаційних зарядів.

Механізм виникнення поляризаційних зарядів в однорідному неполярному діелектрику, вміщеному в однорідне електричне поле, ілюструє рис. 1.2б. Унаслідок деформації електронних оболонок молекул електрична нейтральність діелектрика в цілому не порушується, але на його поверхнях з’являються макроскопічні заряди протилежного знаку, що розподіляються з деякою густиною \(\sigma '\) і \(-\sigma '\) і тому називаються поверхневими поляризаційними зарядами. В той же час всередині різнойменні заряди сусідніх молекул розміщені щільно, і в об’ємі діелектрик лишається електрично нейтральним у кожній точці. У полярних діелектриках поверхневі поляризаційні заряди виникають унаслідок повороту дипольних моментів молекул у напрямку поля.

У неоднорідних діелектриках, а також при вміщенні діелектриків у неоднорідне електричне поле, крім поверхневих, виникають і об’ємні поляризаційні заряди, розподілені з деякою об’ємною густиною \(\rho'\). Це легко зрозуміти на прикладі поляризації умовного неоднорідного діелектрика, в якому концентрація молекул зростає в напрямку зовнішнього поля. В такому разі на поверхню зразка, що орієнтована по полю, вийде більше «плюсів» ніж вийде «мінусів» на протилежну поверхню (рис. 1.3)

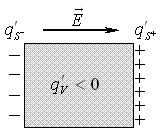
Тож на поверхнях з’явиться сумарний поляризаційний заряд \((q'_{s^+}+q'_{s^-}) > 0\). Тому, враховуючи загальну нейтральність зразка, в об’єм теж стане зарядженим:

\begin{equation} q'_{s^+}+q'_{s^-}+q'_{V}=0 \quad \Rightarrow \quad q'_V=-(q'_{s^+}+q'_{s^-}) < 0 . \end{equation}

Цей об’ємний поляризаційний заряд, розподіляється з відповідною об’ємною густиною \(\rho' < 0\). Зрозуміло, що при зміні напрямку поля на протилежний зміниться і знак \(\rho'\).

При поляризації електрони в молекулах діелектрика зміщуються тільки на дуже малу відстань, лишаючись зв’язаними із своїми ядрами. Тому поляризаційні заряди не можна відокремити один від одного і перемістити в інше місце. Приміром, якщо зразок поляризованого діелектрика розрізати навпіл, то обидві частини лишаться електрично нейтральними і поляризованими так само, як вихідний зразок. Тому поляризаційні заряди інакше називають зв’язаними зарядами.

Принагідно зазначимо, що в теорії електричного поля в діелектриках оперують також поняттям вільних зарядів. Так називають заряди, що, в принципі, можуть довільно розташовуватися і переміщуватися. Вони не належать атомам середовища, тому ще називаються сторонніми зарядами. Такі заряди створюють зовнішнє поле \(\vec{E}_{0}\), яке є першопричиною поляризації. Прикладом сторонніх зарядів можуть бути заряди заряджених кульок, вміщених у діелектричну рідину, або протилежні за знаком заряди на пластинах зарядженого конденсатора, між якими знаходиться діелектрик.

Зв’язок між поляризованістю та поляризаційними зарядами. Із сказаного вище зрозуміло, що величина і розподіл поляризаційних зарядів у діелектрику залежать від ступеня та характеру поляризації.

Установимо спочатку зв’язок між поляризованістю \(\vec P\) і густиною поверхневих поляризаційних зарядів \(\sigma '\). Для цього в шарі однорідно поляризованого діелектрика (\(\vec P = \text{const} \)) товщиною \(h\) виділимо ділянку у вигляді косого циліндра із твірною \(l\) та основами \(\Delta S\), як показано на рис. 1.4.

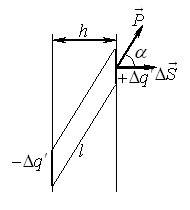
На основах циліндра зосереджені різнойменні поляризаційні заряди однакової величини \(q = \sigma '\Delta S\), отже, він є диполем із плечем \(l = h/\cos \alpha\) і величиною електричного моменту

\begin{equation} p={\sigma }'\Delta Sl= {{\sigma }'\Delta S}\frac{h}{\cos \alpha }. \end{equation}

Поділивши цю величину на об’єм циліндра \(\Delta V = \Delta S h = \Delta S l\cos \alpha \) згідно з означенням (1.2), отримаємо для поляризованості:

\begin{equation} P = \frac{{\sigma '}}{{\cos \alpha }}\quad \Rightarrow \quad P\cos \alpha = \sigma ', \end{equation}

або

\begin{equation} {P_n} = \sigma ', \tag{1.3} \end{equation}

де \({P_n} = P\cos \alpha \) — нормальна до площадки \(\Delta S\) складова поляризованості.

Такий самий результат дістанемо і при неоднорідній поляризації, взявши такі малі значення \(h\) і \(\Delta S\), аби в межах \(\Delta V\) неоднорідність була не істотною. Тому формула (1.3) є загальною й означає, що

на поверхні діелектрика нормальна складова поляризованості в будь-якій точці дорівнює поверхневій густині зв’язаних зарядів у цій точці.

Зокрема, в прямому циліндрі з діелектрика, що однорідно поляризований уздовж осі, поверхнева густина зв’язаних зарядів на основах \(\sigma ' = P\), а повна величина заряду \({q'_s} = PS\) (\(S\) — площа основи). На бічній поверхні \({P_n} = 0\), отже, \(\sigma ' = 0\) і \({q'_S} = 0\).

У загальному випадку зв’язаний заряд на якійсь поверхні \(S\) (рис. 1.5а) визначається інтегруванням зарядів \({\text{d}}q' = \sigma '{\,\text{d}}S\) на всіх її елементарних ділянках:

\begin{equation} {q'_S} = \int\limits_S {{P_n}\,\text{d} S = } \int\limits_S {P\,\text{d} S\cos\alpha = } \int\limits_S {\vec P\,\text{d} \vec S} . \end{equation}

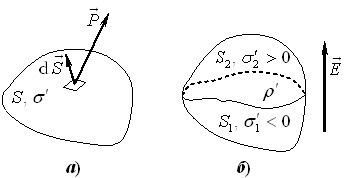
Іншими словами,

поляризаційний заряд на поверхні діелектрика дорівнює потокові вектора \(\vec P\) крізь цю поверхню.

За допомогою виразу (1.3) можна знайти зв’язок і між поляризованістю та об’ємними поляризаційними зарядами. Для цього розглянемо потік вектора \(\vec P\) крізь довільну замкнену поверхню \(S\) (рис. 1.5б). Подумки поділимо її на дві частини \({S_1}\) і \({S_2}\). Тоді потік крізь усю поверхню

\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = \int\limits_{{S_1}} {\vec P\,\text{d} \vec S} + \int\limits_{{S_2}} {\vec P\,\text{d} \vec S} , \end{equation}

і, враховуючи (1.3),

\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = \int\limits_{{S_1}} {{{\sigma '}_1}\,\text{d} S} + \int\limits_{{S_2}} {{{\sigma '}_2}\,\text{d} S} = {q'_{S1}} + {q'_{S2}} = {q'_S}, \tag{1.4} \end{equation}

де \({q'_S} = {q'_{S1}} + {q'_{S2}}\) — поляризаційний заряд на всій замкненій поверхні \(S\).

При однорідній поляризації \({q'_{S1}}\) і \({q'_{S2}}\) відрізняються тільки знаком, так що \({q'_S} = 0\). Але в неоднорідно поляризованому діелектрику \(| {{q'_{S1}}} | \ne {q'_{S2}}\), тож при його загальній електричній нейтральності зразка заряд на всій поверхні \({q'_S} \ne 0\). Це означає, що при неоднорідній поляризації в об’ємі теж виникає поляризаційний заряд \({q'_V} = - {q'_S}\). Відтак вираз (1.4) можна подати у вигляді:

\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = - {q'_V}. \tag{1.5} \end{equation}

або

\begin{equation} \oint\limits_S {\vec P\,\text{d} \vec S} = - \int\limits_V {\rho '\,\text{d} V} , \tag{1.5а} \end{equation}

де \(\rho '\) — об’ємна густина поляризаційного заряду.

Рівняння (1.5), (1.5а) встановлюють загальний зв’язок між поляризованістю та поляризаційними зарядами в діелектрику і по суті виражають теорему Гаусса для вектора \(\vec P\):

потік вектора поляризованості крізь довільну замкнену поверхню в діелектрику дорівнює величині поляризаційного заряду всередині цієї поверхні взятому з протилежним знаком.

1.2. Теорема Гаусса для діелектриків. Вектор \(\vec D\)

Як говорилося на початку, поле в діелектрику складається з поля сторонніх зарядів \({\vec E_0}\) і внутрішнього макроскопічного поля \(\vec E'\):

\begin{equation} \vec E = {\vec E_0} + \vec E'. \end{equation}

При цьому внутрішнє макроскопічне поле \(\vec E'\) є усередненим мікроскопічним полем всіх молекул поляризованого діелектрика. Але речовина діелектрика скрізь, окрім місць розташування поляризаційного заряду, лишається електрично нейтральною і як така участі у створенні поля \(\vec E'\) не бере. Тому при розгляді поля в діелектрику можна вважати, що поляризаційні заряди, як і сторонні, розташовані у вакуумі. Відтак на основі теореми Гаусса ((5.14), розділ І) для результуючого поля \(\vec E\) можна записати:

\begin{equation} \oint\limits_S {\vec E\,\text{d} \vec S = } \frac{1}{{{\varepsilon _0}}}\int\limits_V {( {\rho + \rho '} )\,\text{d} V} , \tag{1.6} \end{equation}

де \(\rho\) i \(\rho '\) — об’ємна густина сторонніх і поляризаційних зарядів, відповідно.

Рівняння (1.6) є подібним до ((5.14), розділ І) але трактувати його як вираз теореми Гаусса для поля в діелектриках не можна, бо воно містить невідомий параметр \(\rho '\), який не визначає поле \(\vec E\), а сам залежить від нього. Тому з огляду на теорію рівняння (1.6) не виражає фундаментальних (загальних) властивостей поля в діелектриках, і не може трактуватись як самодостатній фізичний закон. Воно лише відображає той тривіальний факт, що у створенні електричного поля в діелектрику окрім сторонніх зарядів беруть участь і заряди самого діелектрика. Практичної цінності рівняння (1.6) теж не має, бо шукати з нього невідоме поле \(\vec E\) можна було би тільки знаючи розподіл поляризаційних зарядів \(\rho '\), який визначається тим таки невідомим полем \(\vec E\).

Але вихід з цього хибного логічного кола існує, позаяк поляризаційні заряди є пов’язані з поляризованістю. Розкривши у виразі (1.6) дужки та зробивши заміну (1.5а) матимаемо:

\begin{equation} \oint\limits_{S}{\vec{E}\,\text{d}\vec{S}} = \int\limits_{V}{\rho \,\text{d}V} - \oint\limits_{S}{\vec{P}\,\text{d}\vec{S}}\quad \Rightarrow \quad \oint\limits_{S}{( {{\varepsilon }_{0}}\vec{E}+\vec{P} )\,\text{d}\vec{S}} = \int\limits_{V}{\rho \,\text{d}V}. \tag{1.7} \end{equation}

Величина в дужках, як і напруженість \(\vec E\), є визначеною в усіх точках простору і утворює відповідне векторне поле. Тому вона позначається одним символом \(\vec D\) і називається “вектором \(\vec D\)” або “вектором електричного зміщення”. Таким чином, за означенням

вектором електричного зміщення називається вектор

\begin{equation} \vec D = {\varepsilon _0}\vec E + \vec P. \tag{1.8} \end{equation}

Відтак рівняння (1.7) набуває вигляду:

\begin{equation} \oint\limits_S {\vec D\,\text{d} \vec S = } \int\limits_V {\rho \,\text{d} V} \tag{1.9} \end{equation}

або

\begin{equation} \oint\limits_S {\vec D\,\text{d} \vec S = } q \tag{1.9а} \end{equation}

і виражає теорему Гаусса для електричного поля в діелектриках:

потік вектора \(\vec D\) крізь довільну замкнену поверхню дорівнює сумарній величині вільного заряду всередині цієї поверхні.

Рівняння (1.9), на відміну від (1.7), не містить невідомих параметрів і є чинним як для всіх діелектриків, так і для вакууму. Справді, у вакуумі через відсутності речовини \(\rho ' = 0\), тож \(\vec D = {\varepsilon _0}\vec E\), і рівняння (1.9) трансформується в рівняння (5.14) теореми Гаусса для поля у вакуумі:

\begin{equation} \oint\limits_S {{\varepsilon _0}\vec E\,\text{d} \vec S = } \int\limits_V {\rho \,\text{d} V} \quad \Rightarrow \quad \oint\limits_S {\vec E\,\text{d} \vec S = } \frac{1}{{{\varepsilon _0}}}\int\limits_V {\rho \,\text{d} V} . \end{equation}

Теорема Гаусса виконується і в нестаціонарних полях при не надто швидкій їхній зміні з часом. Тому рівняння (1.9) є одним з основних інтегральних рівнянь класичної теорії електромагнітного поля, створеної Максвеллом. Разом із тим слід усвідомити, що вектор \(\vec D\) є синтетичним утворенням і не має прямого фізичного змісту, як, скажімо, вектор \(\vec E\). Справді, згідно з означенням (1.8), вектор \(\vec D\) є комбінацією двох різних за змістом векторів: вектора \({\varepsilon _0}\vec E\), що визначається станом поля, та вектора \(\vec P\), який відображає стан речовини. Тому

вектор \(\vec D\) не є польовим вектором,

тобто кількісною характеристикою електричного поля.

1.3. Діелектричні сприйнятливість і проникність

Уведення вектора \(\vec D\) є доцільним і в практичному сенсі, бо часто полегшує обчислення електричного поля в діелектриках. Це зумовлено тим, що в деяких випадках поле вектора \(\vec D\) можна розрахувати, знаючи розподіл тільки сторонніх зарядів. З іншого боку, за поляризацію відповідає повне поле в діелектрику, тож поляризованість \(\vec P\) є функцією напруженості \(\vec E: \vec P = \vec P( {\vec E} )\). Тому при відомому зміщенні, вираз (1.8) із означення перетворюється на функціональне рівняння

\begin{equation} \vec{D}( {\vec{r}} )={{\varepsilon }_{0}}\vec{E}( {\vec{r}} )+\vec{P}( \vec{E}( {\vec{r}} ) ) \tag{1.10} \end{equation}

з якого можна визначити напруженість поля, створеного в діелектрику заданим розподілом сторонніх зарядів \(\rho ( {\vec r} )\).

Такий розрахунок включає два етапи:

— визначення допоміжного вектора \(\vec D( {\vec r} )\) через заданий розподіл сторонніх зарядів \(\rho ( {\vec r} )\);

— визначення основного вектора поля \(\vec E( {\vec r} )\) за допомогою рівняння (1.10).

У загальному випадку це може бути не простою задачею через складну залежність поляризованості від напруженості поля \(\vec P = \vec P( {\vec E} )\). Але ізоляційні матеріали, що використовуються в електротехніці та електроніці, є ізотропними діелектриками, і залежність \(\vec P( {\vec E} )\) в них має простий вигляд:

\begin{equation} \vec P=\varepsilon_0\varkappa\vec E, \tag{1.11} \end{equation}

де безрозмірне число \(\varkappa\) називається діелектричною сприйнятливістю діелектрика. Ця величина показує, наскільки сильно, чи слабко поляризується діелектрик в полі заданої напруженості, тобто дійсно характеризує його сприйнятливість до впливу електричного поля.

Підставивши співвідношення (1.11) у рівняння (1.10), отримаємо:

\begin{equation} \vec D=\varepsilon_0(1+\varkappa)\vec E. \tag{1.12} \end{equation}

У цьому виразі число в дужках має той самий, що й \(\varkappa \), загальний зміст. Тому його позначають одним символом \(\varepsilon \) і називають діелектричною проникністю речовини. Отже, за означенням

\begin{equation} \varepsilon=1+\varkappa. \tag{1.13} \end{equation}

Діелектрична проникність є табличною характеристикою речовини і для звичайних діелектриків складає декілька одиниць за винятком води, для якої \(\varepsilon = 81\). Але існують також тверді діелектрики, що звуться сегнетоелектриками, і мають аномально високу (до \( \sim 104\)) проникність. Це зумовлено особливостями їхньої внутрішньої будови.

Із виразів (1.12) і (1.13) випливає важлива формула, що напряму пов’язує вектори \(\vec D\) і \(\vec E\) в ізотропному діелектрику:

\begin{equation} \vec D = {\varepsilon _0}\varepsilon \vec E. \tag{1.14} \end{equation}

1.4. Умови на межі двох діелектриків

Співвідношення (1.14) пов’язує напруженість \(\vec E\) поля в діелектрику з допоміжною величиною \(\vec D\). Але реально напруженість поля в заданому діелектрику визначається полем сторонніх зарядів \({\vec E_0}\), в яке він уміщений і яке є першопричиною його поляризації. Аби встановити зв’язок між векторами \(\vec E\) і \({\vec E_0}\), для початку розглянемо поле у плоскопаралельній пластині однорідного ізотропного діелектрика з проникністю \(\varepsilon \), яка вміщена в однорідне зовнішнє поле \({\vec E_0} = \text{const}\), що перпендикулярне до її поверхонь, рис. 1.6а.

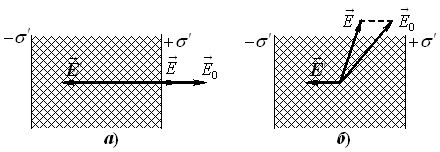
За таких умов внутрішнє поле \(\vec E'\) можна розглядати як поле двох заряджених з густиною заряду \(\sigma'\) і \(-\sigma'\) паралельних площин (поверхонь діелектрика). Воно напрямлене протилежно до зовнішнього поля \({\vec E_0}\) і, згідно з принципом суперпозиції і формулою ((5.23), розділ І), має величину

\begin{equation} E' = \frac{{\sigma '}}{{{\varepsilon _0}}}. \end{equation}

Тому модуль напруженості результуючого поля в діелектрику, відповідно до (1.1), дорівнює

\begin{equation} E = {E_0} - \frac{{\sigma '}}{{{\varepsilon _0}}}. \end{equation}

Звідси, врахувавши співвідношення (1.3) і (1.11), знаходимо зв’язок між полями:

\begin{equation} E=E_0-\varkappa E \quad \Rightarrow \quad (1+\varkappa) E = E_0 \quad \Rightarrow \quad \varepsilon E=E_0\Rightarrow\vec E=\frac{\vec E_0}{\varepsilon} . \tag{1.15} \end{equation}

Отже, пластина послаблює поле в \(\varepsilon \) разів без зміни його напрямку. Тому може здатися, що проникність зразка діелектрика \(\varepsilon \) — то є просто коефіцієнт послаблення ним електричного поля. Але насправді діелектрична проникність не має такого прозорого змісту, а простота виразу (1.15) зумовлена не властивостями речовини діелектрика, а формою та орієнтацією його поверхонь. Це стає зрозумілим, якщо розглянути ту саму пластину вміщену в електричне поле, що спрямоване навкіс, як на рис. 1.6б. Очевидно, що тепер вектори \({\vec E_0}, \vec E'\) і \(\vec E\) вже не є колінеарними, тож і \(\vec E \ne ( \vec E_0/\varepsilon )\). Тому формула (1.15) без застережень виконується лише в абстрактному ізотропному діелектрику, що не має поверхонь, тобто займає увесь безмежний простір. Що ж до обмеженого діелектрика, що має певні розміри та поверхню, співвідношення (1.15) виконується тільки у відповідних випадках, які визначаються так званими умовами на межі — співвідношеннями між векторами \({\vec D_1}\) і \({\vec D_2}\) та \({\vec E_1}\) і \({\vec E_2}\) на поверхні поділу двох діелектриків.

Визначимо указані співвідношення для двох ізотропних діелектриків з проникностями \({\varepsilon _1}\) і \({\varepsilon _2}\) у випадку, коли на межі поділу немає сторонніх зарядів. Для цього спочатку розглянемо потік вектора \(\vec D\) крізь поверхню невеликого замкненого циліндра з паралельними до межі поділу основами \(\Delta S\) і висотою \(h\), рис. 1.7а.

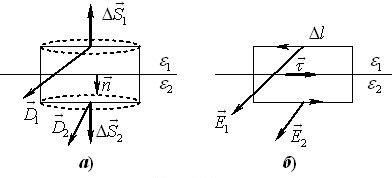
Цей потік складається з потоків через основи циліндра \(\Delta {\Phi _1}, \Delta {\Phi _2}\) і бічну поверхню \(\Delta \Phi '\) і, згідно з теоремою Гаусса (1.9), за відсутності сторонніх зарядів дорівнює нулю:

\begin{equation} \Delta {\Phi _1} + \Delta {\Phi _2} + \Delta \Phi ' = 0. \end{equation}

Позаяк циліндр малий, потоки через основи можна наближено записати як \(\Delta {\Phi _1} \approx - {D_{1n}}\Delta S\) і \(\Delta {\Phi _2} \approx {D_{2n}}\Delta S\), спроектувавши вектори на спільну нормаль \(\vec n\) до межі поділу. Тоді виходить:

\begin{equation} - {D_{1n}}\Delta S + {D_{2n}}\Delta S + \Delta \Phi ' \approx 0. \end{equation}

Неточність цієї рівності зумовлена тим, що в кожному з діелектриків у різних точках площинки \(\Delta S\) величина \({D_n}\) не однакова. Тому для отримання точного виразу треба перейти до границі, “стягнувши” циліндр у якусь точку на межі поділу. Задля більшої прозорості зробимо це в два етапи. Спочатку будемо подумки зменшувати висоту циліндра, поступово наближаючи основи до межі поділу. Тоді у границі \(h \to 0\) зникне потік крізь бічну поверхню:

\begin{equation} - {D_{1n}}\Delta S + {D_{2n}}\Delta S \approx 0\quad \Rightarrow \quad {D_{1n}}\Delta S \approx {D_{2n}}\Delta S. \end{equation}

А тепер будемо зменшувати основи, зменшуючи й похибку в отриманій рівності, аж поки в границі \(\Delta S \to 0\) вона не стане математично точною:

\begin{equation} {D_{1n}} = {D_{2n}}. \tag{1.16а} \end{equation}

Відтак за допомогою співвідношення (1.14) встановлюємо зв’язок між нормальними складовими для векторів напруженості поля:

\begin{equation} {\varepsilon _1}{E_{1n}} = {\varepsilon _2}{E_{2n}}\quad \Rightarrow \quad \frac{{{E_{1n}}}}{{{E_{2n}}}} = \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}}. \tag{1.16б} \end{equation}

Далі за допомогою теореми про циркуляцію ((5.2), розділ І) і формули (1.14) встановимо межові умови для тангенціальних складових векторів. Для цього розглянемо циркуляцію \(C\) вектора \(\vec E\) по малому прямокутнику, що охоплює деяку точку на межі поділу діелектриків і орієнтований так, як показано на рис. 1.7б. Ураховуючи малість контуру, інтеграл у рівнянні ((5.2), розділ І) наближено виразимо через вклади окремих сторін:

\begin{equation} -{{E}_{1\tau }}+{{E}_{2\tau }}+\Delta C\approx 0. \end{equation}

де \(\Delta C\) — спільний вклад від поперечних сторін, а проекції векторів поля на напрям переміщення вздовж поздовжніх сторін записані через спільний орт \(\vec \tau \) дотичної до межі поділу.

Далі, стягаючи спочатку поперечні, а потім поздовжні сторони прямокутника в вибрану точку на межі поділу діелектриків, отримаємо в границі точні співвідношення для напруженості

\begin{equation} {E_{1\tau }} = {E_{2\tau }} \tag{1.17а} \end{equation}

і, за допомогою формули (1.14), — для електричного зміщення.

\begin{equation} \frac{{{D_{1\tau }}}}{{{\varepsilon _1}}} = \frac{{{D_{2\tau }}}}{{{\varepsilon _2}}}. \tag{1.17б} \end{equation}

Зведемо всі отримані результати, які й складають умови на межі двох діелектриків:

\begin{equation} \begin{aligned} {{D}_{1n}}={{D}_{2n}},& \qquad \frac{{{E}_{1n}}}{{{E}_{2n}}}=\frac{{{\varepsilon }_{2}}}{{{\varepsilon }_{1}}};\\\frac{{{D}_{1\tau }}}{{{D}_{2\tau }}}=\frac{{{\varepsilon }_{1}}}{{{\varepsilon }_{2}}},& \qquad {{E}_{1\tau }}={{E}_{2\tau }}. \end{aligned} \tag{1.18} \end{equation}

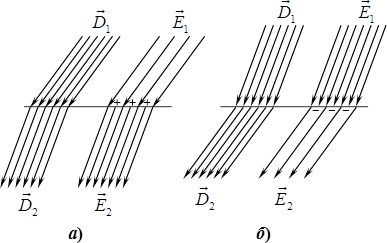
З умов (1.18) випливає, що при переході через межу поділу діелектриків змінюються не тільки модулі, а й напрямки векторів \(\vec D\) і \(\vec E\). При цьому напрямки векторів змінюються однаково, а модулі — ні. Це наочно ілюструє рис. 1.8: коли \({\varepsilon _2} < {\varepsilon _1}\) (рис. 1.8а)), то \({D_2} < {D_1}\), а \({E_2} > {E_1}\), тоді як при \({\varepsilon _2} > {\varepsilon _1}\) (рис. 1.8б)) навпаки \({D_2} > {D_1}\), а \({E_2} < {E_1}\).

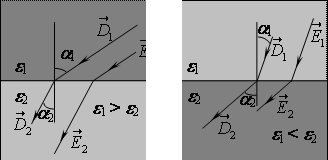
Для межі поділу вакууму (\( {{\varepsilon _1} = 1} \)) і діелектрика (\( {{\varepsilon _2} = \varepsilon } \)) умови (1.18) мають вигляд:

\begin{equation} \begin{aligned} {{D}_{n}}={{D}_{0n}},& \qquad \frac{{{D}_{\tau }}}{{{D}_{0\tau }}}=\varepsilon ;\\ \frac{{{E}_{n}}}{{{E}_{0n}}}=\frac{1}{\varepsilon },& \qquad {{E}_{\tau }}={{E}_{0\tau }}. \end{aligned} \tag{1.18а} \end{equation}

Звідси випливає, що \(E = \sqrt {( E_{0n}/\varepsilon )^2 + E^2_{0\tau }} \). Отже, на загал \(E \ne ( E_0/E_0\varepsilon )\), як і говорилося на початку. Виняток становить тільки випадок, коли поле напрямлене по нормалі до поверхні діелектрика. Тоді \({E_\tau } = {E_{0\tau }} = 0\), і поверхня діелектрика співпадає з однією з еквіпотенціальних поверхонь поля (див. розділ І, п. 2). У такому разі нормальні проекції векторів напруженості збігаються з модулями, і поле в діелектрику

\begin{equation} E = \frac{{{E_0}}}{\varepsilon } \tag{1.19} \end{equation}

так, немов він є безмежним. Відповідно, для двох діелектриків, межа поділу яких є еквіпотенціальною,

\begin{equation} \frac{{{E_1}}}{{{E_2}}} = \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}}. \tag{1.20} \end{equation}

У загальному випадку при переході з одного діелектрика в інший змінюється і напрямок поля. Через це на межі поділу спостерігається ефект заломлення ліній векторів \(\vec D\) і \(\vec E\), рис. 1.9

При цьому з умов (1.18) випливає наступний “закон заломлення”:

\begin{equation} \frac{{\operatorname{tg} {\alpha _1}}}{{\operatorname{tg} {\alpha _2}}} = \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}}. \tag{1.21} \end{equation}

Прийнявши \({\varepsilon _1} = 1\) і \({\varepsilon _2} = \varepsilon \) та відповідно позначивши кути як \({\alpha _0}\) і \(\alpha \), отримаємо зв’язок між напрямками векторів на межі вакууму і діелектрика з проникністю \(\varepsilon \):

\begin{equation} \frac{{\operatorname{tg} {\alpha _0}}}{{\operatorname{tg} \alpha }} = \frac{1}{\varepsilon }. \tag{1.21а} \end{equation}

Зрозуміло, що лінії векторів \(\vec D\) і \(\vec E\) заломлюються однаково, але в їхній поведінці є й істотна відмінність. Якщо розглянути потоки цих векторів крізь замкнену поверхнею у формі диска з основами \(\Delta S\), що прилягають до поверхні поділу діелектриків, як на рис. 1.7, то згідно з (1.18) отримаємо: \({D_{1n}}\Delta S = {D_{2n}}\Delta S\). З урахуванням геометричного змісту потоку це означає, що при переході через межу поділу кількість ліній вектора \(\vec D\) не змінюється, тобто вони є неперервними. Натомість для напруженості \({E_{1n}}\Delta S \ne {E_{2n}}\Delta S\), і лінії вектора \(\vec E\) терплять розрив, як показано на рис. 1.9.

Це не важко пояснити. Через різну проникність діелектриків їхня поляризованість не однакова, і поляризаційні заряди протилежного знаку, що виникають на прилеглих поверхнях мають різну величину. Через це на поверхні дотику існують некомпенсовані зв’язані заряди того, чи іншого знаку. Якщо \({\varepsilon _2} > {\varepsilon _1}\), то ці заряди від’ємні, і на них певна кількість ліній \(\vec E\) закінчується, як на рис. 1.9а. При \({\varepsilon _1} > {\varepsilon _2}\) указані заряди мають знак «\(+\)», і на межі поділу виникають додаткові лінії напруженості, рис. 1.9б.

Наостанку вкажемо наступний корисний для практики висновок, що випливає з проведеного розгляду. Позаяк у безмежному діелектричному середовищі та в діелектрику, обмеженому еквіпотенціальними поверхнями, електричне поле порівняно з вакуумом просто ослаблюється в \(\varepsilon \) разів без зміни напрямку, то будь-яку необхідну формулу можна отримати з відповідної формули для вакууму заміною \({\varepsilon _0}\) на \({\varepsilon _0}\varepsilon \). До прикладу, при наявності діелектрика замість формул (1.4) чи (5.26) з розділу І маємо:

\begin{equation} E = \frac{q}{{4\pi \varepsilon {\varepsilon _0}{r^2}}}, \tag{1.22} \end{equation}

та

\begin{equation} E = \frac{\sigma }{{{\varepsilon _0}\varepsilon }}. \tag{1.23} \end{equation}