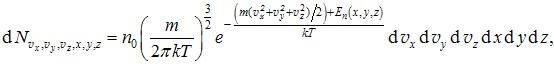ФІЗИКА ДЛЯ БАКАЛАВРІВ. МОЛЕКУЛЯРНА ФІЗИКА ТА ТЕРМОДИНАМІКА
ІІІ. РОЗПОДІЛ МАКСВЕЛЛА-БОЛЬЦМАНА
У Вступі відмічалося, що в молекулярон-кінетичній теорії (МКТ) параметри макроскопічного стану (термодинамічні параметри) системи визначаються через середні значення її мікроскопічних параметрів, тобто, характеристик окремих молекул. Це наочно ілюструють рівняння (1.2), (2.2) або (2.2 а). Тому теоретичне визначення середніх значень мікропараметрів є принциповим завданням МКТ. Так само важливим є визначення кількості частинок у макросистемі, для яких значення того чи іншого мікропараметра лежить у заданих межах. Можливість розв’язання вказаних задач ґрунтується на тому, що в рівноважній термодинамічній системі існують певні статистичні розподіли частинок за різними мікропараметрами. Ці розподіли визначають стан системи й не змінюються з часом.
Далі розглядаються наступні питання:
1. Функція розподілу. Обчислення середніх значень
2. Розподіл Максвелла. Характеристичні швидкості молекул
1. Функція розподілу. Обчислення середніх значень
Поняття про функцію розподілу та про місце, яке вона посідає в МКТ, можна отримати на такому прикладі. Нехай у посудині є N молекул газу, який перебуває в стані термодинамічної рівноваги. Внаслідок випадкових зіткнень усі молекули газу в будь-який момент часу мають різні швидкості[1], а швидкість окремої молекули дуже часто й непередбачувано змінюється з часом. Але кількість молекул із заданими значеннями швидкості лишається незмінною. Зрозуміло, що кількість молекул \(\mathrm{d}N_v \), які мають швидкість у вузькому інтервалі значень від заданого \({v}\) до \({v}+\mathrm{d}v \)[2], є прямо пропорційна загальній кількості молекул і ширині інтервалу: \(\mathrm{d}N_v\approx{N}\mathrm{d}v \). Але вона залежить також і від величини \({v}\). До прикладу, молекул із дуже малими та великими швидкостями, є набагато менше, ніж із середніми. З огляду на це можна записати:
|
\(\mathrm{d}N_v=f(v)N\mathrm{d}v \), |
(3.1) |
де залежна від швидкості величина
|
\({f(v)}=\frac{\mathrm{d}N_v}{N\mathrm{d}v}\) |
(3.2) |
називається функцією розподілу молекул за модулем швидкості. Вона визначає
відносну кількість (частку) молекул, швидкості яких потрапляють в одиничний інтервал біля заданого значення \({v}\).
До цього питання можна підійти й з іншого боку. А саме, якби ми могли “вихоплювати” молекули із посудини по одній і вимірювати їхню швидкість, то з N таких випробувань у деякій кількості випадів \(\mathrm{d}N_v \) отримали б числа в інтервалі від деякого значення \({v}\) до \( v+\mathrm{d}v \). При цьому величина
|
\(\frac{\mathrm{d}N_v}{N}=\mathrm{d}P(v)\) |
(3.3) |
визначає ймовірність (шанси) того, що одна навмання вихоплена молекула буде мати швидкість у вказаному елементарному інтервалі. Отже, вираз (3.2) можна записати як
|
\({f(v)}=\frac{\mathrm{d}P}{\mathrm{d}v}\). |
(3.4) |
Це дозволяє трактувати функцію розподілу як густину імовірності, тобто імовірність того, що швидкість окремої молекули потрапить в одиничний інтервал біля заданого значення \({v}\). У такому разі ймовірність потрапляння швидкості окремої молекули в інтервал ширини \(\mathrm{d}v \)
|
\(\mathrm{d}P=f(v)\mathrm{d}v \). |
(3.4а) |
Відповідно, ймовірність того, що окрема молекула буде мати швидкість у скінченному інтервалі \(\left[v_1;\,v_2\right] \) визначається як
|
\({P}(v_1;\,v_2)=\int\limits_{v_1}^{v_2}f(v)\mathrm{d}v \). |
(3.5) |
Зокрема, якщо інтегрування провести по всіх можливих значеннях швидкості від 0 до нескінченності[3], то вийде одиниця, оскільки молекула достеменно має якесь значення швидкості:
|
\(\int\limits_{0}^{\infty }f(v)\mathrm{d}v=1 \). |
(3.6) |
З цього приводу говорять, що функція розподілу є нормованою на одиницю, а інтеграл (3.6) називають інтегралом нормування.
Функція розподілу \({f(v)}\) безпосередньо дозволяє визначити кількість молекул \(\Delta{N}\), які мають швидкість у заданому інтервалі значень \(\left[v_1;\,v_2\right] \). Для цього треба проінтегрувати вираз (3.1) у відповідних границях:
|
\(\Delta{N}=N\int\limits_{v_1}^{v_2}f(v)\mathrm{d}v\). |
(3.7) |
Для невеликих інтервалів швидкостей \(\Delta{v}<<v \) можна обійтися без інтегрування й використовувати наближений вираз
|
\(\Delta N\approx Nf\left( v \right)\Delta v\). |
(3.7а) |
За допомогою функції розподілу \({f(v)}\) можна визначати також середні значення будь-яких величин, залежних від \({v}\). Справді, нехай у макроскопічній системі з N частинок треба знайти середнє значення \(\left\langle{\Phi}(v)\right\rangle \) певної величини \(\Phi (v) \), яка є функцією швидкості. За означенням середнього
|
\(\langle\Phi{(v)}\rangle=\frac{\Phi_{\Sigma}}{N}\), |
(3.8) |
де \(\Phi_{\Sigma}\) - сума значень цієї величини для всіх N частинок. Через макроскопічну кількість частинок N безпосередньо обчислити \(\Phi_{\Sigma}\) неможливо, але це можна зробити за допомогою функції розподілу. Будь-якому елементарному інтервалу \(\mathrm{d}v \) відповідає кількість частинок \(\mathrm{d}N_v \), яка визначається виразом (3.1). Отже, сумарне значення величини \(\Phi(v) \) на цьому інтервалі дорівнює
\(\mathrm{d}\Phi_{\Sigma}=\Phi(v)\mathrm{d}N_v=N\Phi(v)f(v)\mathrm{d}v \).
Відповідно, для всіх частинок (і всіх значень \({v}\)) маємо
\(\Phi_{\Sigma}=N\int\limits_v\Phi(v)f(v)\mathrm{d}v \).
Отже, шукане середнє значення
|
\(\left\langle\Phi(v)\right\rangle=\int\limits_v \Phi (v) f(v) \mathrm{d}v \). |
(3.9) |
Цей вираз визначає загальний спосіб знаходження середнього значення будь-якої величини, яка є функцією певного мікропараметра системи, через функцію розподілу частинок за цим параметром.
2. Розподіл Максвелла. Характеристичні швидкості молекул
Функція розподілу молекул за проєкцією швидкості на вісь координат, наприклад \({v_x}\), має вигляд:
|
\({f(v_x)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{1}{2}}e^{-\frac{mv_x^2}{2kT}}\), |
(3.10) |
де m - маса молекули, Т - абсолютна температура газу, k - стала Больцмана. Ця функція, згідно з (3.1), визначає кількість молекул, які мають х-проєкцію швидкості в заданому інтервалі \(\mathrm{d}v_x \) і будь-яку величину проєкції швидкості на кожну з двох інших осей координат. Оскільки всі напрямки руху молекул є рівноймовірними, функції розподілу по проєкціях \({v_y}\) і \({v_z}\) є такими самими:
|
\({f(v_y)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{1}{2}}e^{-\frac{mv_y^2}{2kT}}\), |
(3.10а) |
|
|
\({f(v_z)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{1}{2}}e^{-\frac{mv_z^2}{2kT}}\). |
(3.10б) |
Далі розглянемо функцію розподілу молекул по трьох компонентах швидкості \({f(v_x,v_y,v_z)}\), яка визначає молекули із заданим набором проєкцій, а отже, із заданою величиною та напрямком швидкості[4]. Згідно з (3.1), кількість молекул, х-проєкція швидкості котрих лежить в інтервалі від \({v_x}\) до \({v_x}+\mathrm{d}{v_x}\), - це є \(\mathrm{d}N_{v_x}=Nf(v_x)\mathrm{d}{v_x}\). З цих молекул у-проєкцію швидкості в інтервалі від \({v_y}\) до \({v_y}+\mathrm{d}{v_y}\) мають \(\mathrm{d}N_{v_x,v_y}=\mathrm{d}N_{v_x}f(v_y)=Nf(v_x)f(v_y)\mathrm{d}v_x\mathrm{d}v_y \) молекул. Аналогічно визначаються й ті з \(\mathrm{d}N_{v_x,v_y}\) молекул, які мають ще й z-проєкцію швидкості в заданому інтервалі від \({v_z}\) до \({v_z}+\mathrm{d}{v_z}\). Отже, кількість молекул, у яких усі три проєкції швидкості лежать у заданих інтервалах значень, складає
|
\(\mathrm{d}N_{v_x,v_y,v_z}=\mathrm{d}N_{v_x,v_y}f(v_x)f(V_y)f(v_z)\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_x\). |
(3.11) |
Звідси, згідно з (3.2), визначаємо шукану функцію розподілу \({f}(v_x,v_y,v_z) \):
|
\({f(v_x,v_y,v_z)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}e^{-\frac{m(v_x^2+v_y^2+v_z^2)}{2kT}}\). |
(3.12) |
У показнику експоненти стоїть величина \({v_x^2+v_y^2+v_z^2=v^2}\) - квадрат модуля швидкості. Це означає, що, хоча дана функція розподілу враховує як величину, так і напрям швидкості молекули, сама вона від напряму швидкості не залежить. У цьому немає нічого дивного, оскільки через хаотичність теплового руху молекул усі напрями швидкості є рівноймовірними.
Нарешті, розглянемо функцію розподілу молекул газу за модулем швидкості \({f(v)}\), яка визначає кількість молекул із швидкостями з величиною в інтервалі від \({v}\) до \({v+\mathrm{d}v}\) і будь-яким напрямком. Відповідний розрахунок дає такий вираз \({f(v)}\) :
|
\({f(v)}=4\pi\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}v^2e^{-\frac{mv^2}{2kT}}\). |
(3.13) |
|
|
|
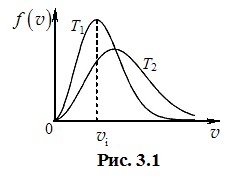
Вигляд графіка цієї функції для двох температур (T2 > T1) показано на рис. 3.1.
Зауважимо, що всі наведені функції розподілу нормовані і, згідно з (3.6), площі під кривими на рис. 3.1 дорівнюють одиниці. Тому при підвищенні температури і зростанні середньої швидкості теплового руху молекул максимум функції розподілу переміщується в область більших швидкостей, а сама крива \({f(v)}\) стає ширшою та нижчою, тобто відбувається певне вирівнювання швидкостей молекул.
Характеристичні швидкості молекул. У різних задачах для характеристики теплового руху молекул використовують три різні так звані характеристичні швидкості: найбільш імовірну, середню арифметичну та середню квадратичну.
Найбільш імовірна швидкість молекул \({v_i}\) відповідає максимуму функції розподілу \({f(v)}\) (рис. 3.1). Її можна визначити, взявши похідну від функції (3.13) і прирівнявши її до нуля. Результат такий:
|
\({v_i}=\sqrt{\frac{2kT}{m}}\). |
(3.14) |
Домноживши чисельник і знаменник під коренем на сталу Авогадро NA, отримаємо інший варіант формули:
|
\({v_i}=\sqrt{\frac{2RT}{M}}\), |
(3.14а) |
де R - універсальна газова стала, М - молярна маса газу.
Середня арифметична швидкість молекул \({\langle{v}\rangle}\), згідно із загальним правилом (3.9), визначається як
\(\langle{v}\rangle=4\pi\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}\int\limits_{0}^{\infty }{v}^{3}e^{-\frac{mv^2}{2cT}}\mathrm{d}{v}\).
Інтеграл у цьому виразі є табличним[5] і дає
|
\(\langle{v}\rangle=\sqrt{\frac{8kT}{\pi{m}}}\) |
(3.15) |
або
|
\( \langle{v}\rangle=\sqrt{\frac{8RT}{\pi{M}}}\). |
(3.15а) |
Середньою квадратичною швидкістю називається величина \({v}\)кв = \(\sqrt{\langle{v^2}\rangle}\). Величина під коренем знаходиться аналогічно до \(\langle{v}\rangle \):
\(\langle{v^2}\rangle=4\pi\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}\int\limits_{0}^{\infty }v^4 e^{-\frac{mv^2}{2kT}}\mathrm{d}{v}=\frac{3kT}{m}\).
Отже, середня квадратична швидкість визначається формулами:
|
\({v}\)кв = \(\sqrt{\frac{3kT}{m}}\). |
(3.16) |
або
|
\({v}\)кв = \(\sqrt{\frac{3RT}{M}}\). |
(3.16а) |
Зауважимо, що всі характеристичні швидкості прямо пропорційні до \(\sqrt{T/m}\) і мало відрізняються за величиною, а саме, \({v_1}:\langle{v}\rangle : v\)кв = 1 : 1,13 : 1,22. Самі ж величини характеристичних швидкостей для газів при кімнатній температурі (~ 300 К) мають 102 ÷ 103 м/с. До прикладу, для кисню О2 \(\langle{v}\rangle\approx \) 450 м/с, а для водню H2 — 900 м/с.
Зведений розподіл молекул за швидкостями. У деяких випадках розгляд задач, пов’язаних із розподілом молекул по швидкостях, спрощується, якщо користуватися безрозмірною зведеною швидкістю молекул \({u=v/v_i}\). Тоді кількість молекул dN із швидкостями в заданому інтервалі значень, яка визначається формулою (3.1), через функцію розподілу \({f(u)}\) виражається, як \({Nf(u)\mathrm{d}u}\). Отже, \({f(v)\mathrm{d}v}={f(u)\mathrm{d}u}\) , звідки
|
\({f(u)}=f(v)\cdot\frac{\mathrm{d}v}{\mathrm{d}u}=f(v) v_i \). |
(3.17) |
Зробивши у виразі \({f(v)}\) (3.13) заміну \({v=uv_i}\) і врахувавши (3.14), із співвідношення (3.17) отримаємо зведену функцію розподілу \({f(u)}\):
|
\({f(u)}=\frac{4}{\sqrt{\pi}}\cdot{u^2}e^{-u^2}\). |
(3.18) |
Розподіл молекул за кінетичними енергіями. Кількість молекул із кінетичними енергіями в заданому інтервалі значень dE дорівнює кількості молекул із швидкостями у відповідному інтервалі \(\mathrm{d}v\), отже \({f(E)\mathrm{d}E}=f(v)\mathrm{d}{v}\), де \({E=mv^2/2}\). Тому, врахувавши (3.13), і зробивши заміни \({v}=\sqrt{2E/m}\) та \(\mathrm{d}E=mv\mathrm{d}v \) , знайдемо функцію розподілу молекул за кінетичними енергіями поступального руху:
|
\({f(E)}=\frac{2\pi}{(\pi kT)^{3/2}}\cdot\sqrt{E}e^{-\frac{E}{kT}}\). |
(3.19) |
За допомогою цієї функції розподілу та виразу (3.9) можна визначити середню енергію поступального руху молекули:
|
\(\langle{E}\rangle=\frac{2\pi}{(\pi kT)^{3/2}}\int\limits_0^{\infty}E\sqrt{E}e^{-\frac{E}{kT}}\mathrm{d}{E}\). |
(3.20) |
Цей інтеграл зводиться до табличного і дає результат:
|
\(\langle{E}\rangle=\frac{3}{2}{kT}\), |
(3.21) |
що співпадає з (1.2). Цей результат можна також отримати, виходячи з того, що
\(\langle{E}\rangle=\frac{m\left\langle{v^2}\right\rangle}{2}=\) 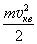 ,
,
і врахувавши вираз (3.16).
За допомогою розподілу Максвелла також можна строго вивести вирази (2.2) і (2.2а) для тиску ідеального газу, і, з урахуванням (3.21), теоретично вивести рівняння стану ідеального газу (2.3) і (2.6), а також і всі наслідки, що випливають з них.
Дослідна перевірка розподілу Максвелла. Всі теоретичні прогнози, про які щойно говорилося, справджуються на дослідіі, що доводить правильність розподілу Максвелла. Але існують і прямі способи його дослідної перевірки. Розглянемо той, що був здійснений Ламмертом.
|
|
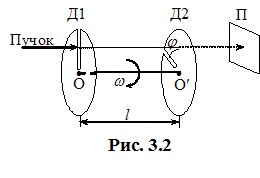
Схема досліду Ламмерта така.У камеру з малим отвором уміщують досліджувану речовину (метал) і підіймають температуру вище точки плавлення. Як наслідок, у камері створюється достатня кількість пари даного металу, котру можна вважати ідеальним газом. З атомів, що вилітають через отвір, за допомогою діафрагм[6] формують вузький і практично нерозбіжний пучок, який спрямовують на вимірювальну установку, схематично показану на рис. 3.2. Вона складається з двох дисків Д1 і Д2, жорстко закріплених на спільній, паралельній до пучка осі ОО′, та скляної пластинки П, на якій осаджуються атоми, що пройшли крізь установку. В дисках зроблені вузькі радіальні прорізи, що зміщені на невеликий кут φ ~ 1° один відносно одного. Відстань \({l}\) між дисками заздалегідь вимірюють. Поки диски нерухомі, всі атоми, що проходять крізь щілину в диску Д1, повністю затримуються диском Д2. Але, коли диски почати обертати з необхідною кутовою швидкістю \({\omega}\) у показаному на рис. 3.2 напрямку, певна частина атомів пройде крізь прорізи в обох дисках і осяде на пластинці П. Зрозуміло, що пройдуть тільки ті атоми, для яких час прольоту \({\tau}\) від першого диска до другого співпаде з часом повороту дисків на кут \({\varphi}\). Це дозволяє знайти швидкість \({v}\) таких атомів. Оскільки \({l=v\tau}\) і \(\varphi=\omega\tau \), то
\({v}=\frac{l}{\varphi}\cdot\omega \).
Таким чином, кожному значенню \(\omega \) відповідає цілком визначена швидкість атомів, які проходять крізь обидва диски. Ці молекули осідають на пластинці П і створюють на ній тонкий напівпрозорий шар, товщина і прозорість якого прямо пов’язані з кількістю атомів, що осіли. Тому, обертаючи диски з різними кутовими швидкостями протягом однакового проміжку часу і, вимірюючи ступінь почорніння пластинок П, отримують залежність відносної кількості атомів у пучку від швидкості їх руху, тобто - функцію розподілу. Результати таких вимірювань, як й інші подібні досліди, повністю узгоджуються з Максвеллівським законом розподілу молекул за швидкостями.
Барометрична формула. Уявімо дуже високий вертикальний циліндр із газом, на молекули якого діє однорідна сила тяжіння, і температура в якому скрізь однакова.
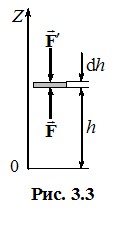
Виділимо на висоті h від основи циліндра шар газу гранично малої товщини dh (рис. 3.3). Цей шар, як і весь газ, перебуває в механічній рівновазі. Отже, сила тиску газу на нижню основу цього шару \(\vec{F}\) зрівноважує силу \(\vec{F}' \), яка створюється силою тиску газу на верхню основу шару та його вагою:
|
\({F=F^{\prime}}\) \( \Rightarrow \) \( {P}S=(P+\mathrm{d}P)S+\mathrm{d}m\cdot{g}\) \( \Rightarrow \) \( {S}\mathrm{d}P=-g\mathrm{d}m \), |
(3.22) |
|
|
|
де S - площа основи циліндра, dт - маса газу в шарі dh, Р і Р + dР - тиск газу на рівні нижньої та верхньої основи шару, відповідно. (Величина dР < 0, оскільки з висотою тиск зменшується). Маса газу в шарі визначається його густиною ρ і об’ємом dV = Sdh: \(\mathrm{d}m=\rho{S}\mathrm{d}h \). Відтак вираз (3.22) набуває вигляду
|
\({\mathrm{d}P}=-\rho{g}{\mathrm{d}h}\). |
(3.23) |
Згідно з рівнянням Клапейрона (2.6), густина газу
\(\rho=\frac{\mathrm{d}m}{\mathrm{d}V}=\frac{PM}{RT}\),
де М - молярна маса газу, Т - його температура, R - універсальна газова стала. Підставляючи цей вираз у (3.23), після інтегрування отримуємо:
|
\( \frac{\mathrm{d}P}{P}=-\frac{Mg}{RT}\mathrm{d}{h}\) \( \Rightarrow \) \( \ln{\frac{P}{P_{0}}}=-\frac{Mg}{RT}\cdot{h}\). |
(3.24) |
Звідси
|
\( {P}=P_0 e^{-\frac{Mg}{RT}h}\), |
(3.25) |
де \( {P_0}\) - тиск біля основи циліндра (при h = 0).
Отримана залежність тиску газу від висоти стовпа (3.25) називається барометричною формулою. Із застереженнями її можна застосовувати й до земної атмосфери, розглядаючи \( {P_0}\) як тиск на рівні моря. Ці застереження такі. Повітря є сумішшю різних газів, тому молярну масу М слід розглядати як усереднену величину, що враховує відсотковий вміст у повітрі різних газів, а тиск Р – як суму парціальних тисків компонент \( {P_i}\). Але для компонент повітря з різними молярними масами \( {M_i}\) тиски \( {P_i}\) і концентрації молекул \({n_i}=P_i/{kT}\), згідно з (3.25), мають по-різному змінюватися з висотою - важчі швидше, ніж легші. Тому вміст компонентів і молярна маса повітря М мали би залежати від висоти h. Насправді цього не спостерігається, позаяк земна атмосфера не є ізотермічною. Температура повітря зменшується з висотою й неоднорідно розподіляється по поверхні Землі. Через це в атмосфері постійно циркулюють потужні повітряні потоки, які й вирівнюють співвідношення концентрацій компонентів повітря на різних висотах. Проте зміна температури повітря з висотою є суттєвою – на висоті 10 - 20 км вона на десятки градусів нижча, ніж на рівні моря. Тому барометрична формулу (3.25) для земної атмосфери є принципово неточною. Але, оскільки на рівні моря температура складає ~ 300 К, відносна зміна температури з висотою є порівняно невеликою, як і спричинена нею неточність формули (3.25). Тому за допомогою барометра, що проградуйований не в одиницях тиску, а в одиницях відстані, можна досить точно визначати висоту. Такі прилади називаються альтиметрами й використовуються на практиці, зокрема, в авіації.
Розподіли Больцмана та Максвелла-Больцмана. У випадку однорідного газу M = mNA (m - маса молекули), а, згідно з (2.3), P = nkT (п - концентрація молекул). Окрім того R = kNA. Зробивши такі підстановки в (3.25), отримаємо залежність концентрації молекул від висоти:
|
\({n=}n_0 e^{-\frac{mgh}{kT}}\) \( \Rightarrow \) \( {n}=n_0 e^{-\frac{E_n}{kT}}\), |
(3.26) |
де \({E_n=mgh}\) - потенціальна енергія молекули в полі сил тяжіння, \({n_0}\) - концентрація молекул на нульовому рівні енергії h = 0. Корисно відмітити, що така залежність концентрації молекул від висоти зумовлена протиборством між двома протилежними тенденціями – тепловим рухом, який намагається “розкидати” молекули рівномірно по всьому об’єму циліндра, та силою тяжіння, що намагається “опустити” всі молекули на дно циліндра.
Л. Больцман довів, що формула (3.26) є чинною не лише для поля сил тяжіння, а й для будь-якого іншого потенціального поля. Тому (3.26) є функцією розподілу частинок за потенціальними енергіями. Вона називається розподілом Больцмана. Оскільки потенціальна енергія частинки в заданому полі визначається тільки її координатами: Eп = Еп(x, y, z) , розподіл Больцмана по суті є розподілом частинок по координатах у силовому полі. Відповідно до цього, кількість частинок dN = ndV в об’ємі dV = dxdydz в околі точки з координатами (x, y, z) визначається, як
|
\(\mathrm{d}N_{x,y,z}=n_0 e^{-\frac{E_n(x,y,z)}{kT}}\mathrm{d}x\mathrm{d}y\mathrm{d}z \). |
(3.27) |
Слід зауважити, що через дуже малу масу молекул (~10-26 кг) помітне зменшення концентрації молекул повітря в полі сил тяжіння спостерігається лише на великих висотах[7]. За таких умов атмосферу не можна вважати ізотермічною, тому безпосередньо експериментально перевірити формули (3.25) і (3.26) неможливо. Але це можна зробити, досліджуючи розподіл за висотою броунівських частинок - дуже малих (~10-7 м) твердих частинок, які зважені в рідині. Броунівські частинки внаслідок ударів з боку молекул рідини здійснюють неупорядкований рух, який відображає тепловий рух молекул рідини. Тому броунівські частинки можна розглядати як гігантські молекули і вважати, що для них є чинними розподіли Максвелла та Больцмана. Такі досліди, що їх виконав Перрен, підтвердили правильність теоретичної формули (3.27) і дозволили експериментально визначити сталу Авогадро.
Розподіл Больцмана (3.27) та розподіл Максвелла (3.12) можна об’єднати в більш загальний розподіл Максвелла-Больцмана, який дозволяє визначати кількості молекул, які знаходяться в заданій елементарній області простору (точці) і мають задану величину та напрям швидкості теплового руху. Вираз (3.27) визначає у кожному місці кількість частинок \(\mathrm{d}N_{x,y,z}\) із будь-якими швидкостями. З цієї кількості, відповідно до (3.11), задану величину й напрям швидкості мають \(\mathrm{d}N_{v_x,v_y,v_z,x,y,z}=\mathrm{d}N_{x,y,z}f(v_x,v_y,v_z)\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z \) частинок. Підставивши сюди вирази (3.27) і (3.12), отримаємо
|
|
(3.28) |
або
|
\(\mathrm{d}N_{v_x,v_y,v_z,x,y,z}=n_0\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}e^{-\frac{E_k+E_n}{kT}}\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z\mathrm{d}x\mathrm{d}y\mathrm{d}z \), |
(3.28а) |
де \({E_k}\) - кінетична енергія частинки.
Вираз (3.28), чи (3.28а) називається розподілом Максвелла-Больцмана. Він визначає кількість частинок маси т із концентрацією n0, швидкості яких за величиною й напрямом нескінченно мало відрізняються від заданого значення і які знаходяться в заданій елементарній області простору (точці).
2. Покажіть на одному кресленні вигляд функції розподілу за швидкостями \({f(v)}\) для водню Н2 та гелію Не при однаковій температурі. Як співвідносяться положення максимумів \( v_1 : v_2 \) та “висоти” піків на графіках \({f(v)}\)?
3. Виходячи з розподілу молекул за модулем швидкості (3.13), отримати функцію розподілу молекул за енергіями (3.19).
4. Виходячи з розподілу молекул за енергіями (3.19), отримати функцію розподілу молекул за модулем швидкості (3.13).
5. Як за допомогою функції розподілу молекул за швидкостями (3.13) можна знайти середню кінетичну енергію поступального теплового руху молекул \(\langle{E}\rangle \)? Як це можна зробити за допомогою функції розподілу молекул за енергіями (3.19)?
6. Знайдіть за допомогою функції розподілу молекул за енергіями (3.19) найбільш імовірну енергію поступального теплового руху молекули.
7. Чи можна при визначепнні атмосферного тиску на деякій висоті h розглядати величину P0 у формулі (3.25) як тиск не на рівні моря, а на довільній висоті H0?
8. При кімнатній температурі молекули газу не осідають на дно, а практично рівномірно розподіляються по всьому об’єму посудини, бо можуть долати сили тяжіння за рахунок кінетичної енергії теплового руху. А як буде при дуже низькій температурі? Перевірте для гелію (M = 4·10-3 кг/моль) при температурі Т = 5 К і нормальному атмосферному тиску.
9. Чому на легких планетах немає атмосфери?
10. Чому в атмосфері Землі кількість водню складає дуже малу частку від кількості кисню, попри те, що загальні кількості Гідрогену та Оксигену на планеті є сумірними?
11. Як би змінювався із часом відсотковий склад атмосфери Землі, якби вона не поповнювалася за рахунок природних і техногенних процесів?
[1] Замість швидкості можна говорити й про будь-який інший мікропараметр системи, наприклад, про імпульс або енергію окремої молекули.
[2] Більш точна, на перший погляд, постановка задачі про кількість молекул, які мають задане значення швидкості насправді є некоректною. Кількість молекул у системі хоча й велика, проте скінченна, тому цілком може статися, що якогось заданого точного значення швидкості не має жодна з них.
[3] Те, що замість граничної швидкості с використовують ∞, є лише зручним формальним прийомом, який спрощує обчислення. Це зумовлено тим, що підінтегральна функція f(v) досить швидко спадає при великих швидкостях, і її вклад в інтеграл стає несуттєвим задовго до досягнення значень v ~ c.
[4] Точніше - молекули, для яких модулі та напрямки вектора швидкості гранично мало відрізняються від заданих значень.
[5] Див., напр, Г.Б.Двайт “Таблицы интегралов”, М., “Наука”, 1977.
[6] Пластинки з малим отвором, які розміщується напроти отвору печі.
[7] До прикладу, на висоті 100 м тиск і концентрація молекул повітря всього на 1 % менші, ніж на рівні моря.