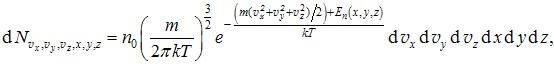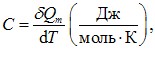ФІЗИКА ДЛЯ БАКАЛАВРІВ. МОЛЕКУЛЯРНА ФІЗИКА ТА ТЕРМОДИНАМІКА
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА ДЛЯ БАКАЛАВРІВ. МОЛЕКУЛЯРНА ФІЗИКА ТА ТЕРМОДИНАМІКА |
| Напечатано:: | |
| Дата: | Суббота, 27 июля 2024, 06:44 |
ВСТУП
У молекулярній фізиці вивчають властивості речовини та явища, що зумовлені її внутрішньою будовою. Загальновідомо, що речовина складається з мікроскопічних частинок - молекул і атомів,- які невпинно рухаються та взаємодіють між собою. Кількість молекул, навіть у мізерній крупинці речовини, є дуже великою (наприклад, навіть порошинка розміром 1 мкм, яку можна побачити тільки в потужний мікроскоп, містить ~1012 молекул), тобто, вона є макроскопічною системою. Через це та через специфічні квантові властивості атомів і молекул, досліджувати властивості речовини, розглядаючи рух окремих частинок на основі законів механіки, принципово неможливо. Але в макроскопічних системах виявляються якісно нові закономірності, котрі досліджують статистичним та термодинамічним методами. Перший використовується в молекулярно-кінетичній теорії (МКТ), де характеристики й поведінка макроскопічної системи встановлюються через усереднені характеристики руху окремих молекул і їхньої взаємодії між собою. Математичною основою МКТ є теорія ймовірностей та математична статистика. Термодинамічний метод, або просто - термодинаміка, ґрунтується на декількох основних законах, або началах термодинаміки, які встановлені з досліду. Закони термодинаміки є універсальними в тому сенсі, що вони є чинні для будь-якої макроскопічної системи незалежно від її внутрішньої будови та індивідуальних властивостей частинок. Через це термодинамічний метод є незамінним, коли внутрішня будова системи та взаємодія між частинками є дуже складною чи недостатньо вивченою. З іншого боку, загальні принципи та положення МКТ дозволяють зрозуміти походження законів термодинаміки та механізми термодинамічних процесів. Отже, статистичний та термодинамічний методи органічно є взаємопов’язані та доповнюють один одного.
Властивості тіл і процеси в них ми спостерігаємо і вивчаємо через величини, які характеризують систему як ціле, і які можна вимірювати приладами. Такі величини називаються макроскопічними або термодинамічними. Для будь-якої системи існує відповідний набір параметрів стану – термодинамічних величин, які визначають макроскопічний (термодинамічний) стан системи, тобто стан системи як цілого. Наприклад, основними параметрами стану газу є об’єм, тиск і температура. Наголосимо ще раз, що макроскопічні (термодинамічні) величини для окремої молекули позбавлені змісту, вони мають сенс тільки для всієї системи чи якоїсь її макроскопічної частини. Сукупність макроскопічних параметрів системи визначає її макроскопічний (термодинамічний) стан. При цьому, якщо всі параметри мають однакові значення по всій системі, її стан називається рівноважним, якщо ні, то – нерівноважним.
Очевидно, що макроскопічний стан системи визначається рухом та взаємодією молекул – мікроскопічних частинок з яких складається система. Відповідно, величини, що характеризують окремі частинки системи називаються мікроскопічними параметрами, а сукупність мікроскопічних параметрів усіх молекул визначає мікроскопічний стан системи. Основним завданням МКТ якраз і є встановлення зв’язку між мікроскопічними та макроскопічними (термодинамічними) станами в різних рівноважних молекулярних системах.
Основні поняття, величини та закони молекулярної фізики і термодинаміки вивчаються в наступних розділах:
III. Розподіл Максвелла-Больцмана
IV. Перше начало термодинаміки
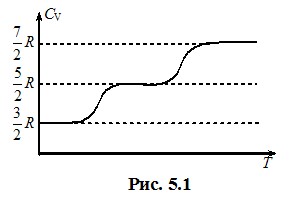
V. Теплоємність. Політропні процеси
І. ОСНОВНІ ПОЛОЖЕННЯ МКТ
У наш час дискретна молекулярна будова речовини не потребує доказів. Достатньо лише вказати, що сучасна техніка дозволяє отримувати зображення не тільки окремих молекул, а й атомів. Нагадаємо деякі основні відомості про характеристики молекул та їхній рух і взаємодію.
2. Рух молекул. Теплова рівновага та температура
1 а.о.м.= 1,660·10-27 кг.
Маса молекули (атома), виражена в а.о.м., називається відносною молекулярною (атомною) масою Мr. Атомні маси хімічних елементів указані в періодичній таблиці Менделєєва. Для наведених вище речовин вони складають, відповідно, 1,008; 12,011 та 31,988[2]. Атомні та молекулярні маси для більшості речовин близькі до цілих чисел і в практичних розрахунках заокруглюються.
Кількість речовини. Молярна маса. Деякі характеристики речовини та процеси визначаються не масою, а кількістю частинок. Це, зокрема, стосується тиску газу або хімічних реакцій. Тому в молекулярній фізиці та хімії поряд з масою широко використовують поняття кількості речовини. Мірою кількості речовини є кількість структурних частинок (атомів, молекул, іонів, тощо), яка в ній міститься. Але через величезну кількість таких частинок для вимірювання кількості речовини використовують, знов таки, відносну одиницю - моль. За означенням 1 моль - це кількість речовини, в якій міститься стільки ж частинок, як у 0,012 кг ізотопу Карбону 12С. Така кількість частинок називається сталою Авогадро й дорівнює
NA = 6,02·1023 1/моль = 6,02·1026 1/кмоль.
Кількість речовини ν виражається через кількість частинок N очевидним співвідношенням:
|
\(\nu=\frac{N}{N_{\mathrm{A}}}\) |
(1.1) |
або, через масу m,
|
\(\nu=\frac{m}{M}\), |
(1.1а) |
де М – маса одного моля речовини, яка називається молярною масою і вимірюється в кг/моль. Зрозуміло, що
|
M = m0NA, |
(1.1б) |
де m0 – маса одного атома (молекули).
Між молярною масою речовини М та відносною масою її молекул Мr існує простий числовий зв’язок:
M(кг/моль) = 10-3·Mr або M(кг/кмоль) = Mr.
Розміри молекул. Уявлення про розміри атомів і молекул можна отримати з таких простих міркувань. Вода (Н2О) масою 1 г, що складає 1/18 моля (М = 18 г/моль), займає об’єм V = 1 см3 і містить N ≈ 3·1022 молекул. Отже, на одну молекулу припадає об’єм V0 = V/N ≈ 3·10-26 м3. Оскільки в рідинах молекули розміщуються впритул одна до одної, поперечний розмір молекули можна оцінити як \( {d}\approx{(V_{0})^{1/3}}\approx{10^{-10}}\) м. Існують і точніші методи визначення розмірів молекул, які дають величини, близькі до наведеної оцінки, причому розміри молекул різних неорганічних речовин виявляються приблизно однаковими[3].
2. Рух молекул. Теплова рівновага та температура
Рух молекул. Молекули речовини завжди перебувають у стані хаотичного руху. Про рух молекул, зокрема, свідчить явище дифузії – взаємопроникнення молекул однієї речовини в іншу. Хаотичність руху молекул наочно відображає броунівський рух - безперервний невпорядкований рух дуже дрібних частинок твердої речовини, що зважені в рідині. Рух молекул як такий не зумовлений якимось причинами або процесами в речовині, він є природнім станом частинок матерії. Водночас хаотичність руху молекул має своє пояснення. Молекула, стикаючись із іншою, змінює величину та напрям своєї швидкості, причому такі зіткнення відбуваються дуже часто. До прикладу, в газі за звичайних умов відбувається ~109 зіткнень за 1 с. Тому величини швидкості та напрямки руху окремих молекул є неконтрольованими, а їхній рух - невпорядкованим (хаотичним).
Рівноважні та нерівноважні стани й процеси. Із хаотичним рухом молекул пов’язані такі фундаментальні поняття, як теплова (термодинамічна) рівновага та температура. Попри невизначеність характеристик руху (мікроскопічних параметрів) окремої молекули, їхні середні значення для всієї системи або окремих її частин, а отже й макроскопічні параметри, у кожен момент часу мають визначену величину[4]. У загальному випадку макроскопічні параметри можуть змінюватися з часом, тоді макроскопічний стан системи називається нерівноважним. Але, як свідчить дослід, якщо система є замкненою, то її макроскопічні параметри в решті-решт обов’язково набувають значень, які надалі лишаються незмінними. Такий стан системи називається рівноважним, а її перехід в рівноважний стан називається релаксацією. Те, що будь-яка ізольована система спонтанно (сама по собі) переходить у рівноважний стан, є фундаментальним законом природи.
Зміна параметрів стану системи із плином часу називається термодинамічним процесом. Як і стани, процеси можуть бути нерівноважними або рівноважними. При нерівноважному процесі всі або деякі термодинамічні параметри не мають визначеної величини для всієї системи. Наприклад, при швидкому стисканні газу в циліндрі внаслідок руху поршня тиск і температура газу будуть різними в різних місцях - найвищими біля поршня й найнижчими біля основи циліндра. Отже, такий процес є нерівноважним або нестатичним. Але, якщо поршень переміщувати дуже повільно, то внаслідок взаємодії між молекулами газу їх концентрація та середня швидкість хаотичного руху будуть устигати вирівнюватися так, що в кожен момент часу термодинамічні параметри (тиск і температура) будуть мати практично однакові значення по всьому об’єму газу. Такий процес називається рівноважним або квазістатичним. Рівноважний процес можна розглядати як неперервну послідовність рівноважних станів системи. Строго рівноважним може бути лише нескінченно повільний процес. Наприклад, для того, щоби зміна об’єму газу в циліндрі під поршнем була рівноважною (квазістатичною), треба щоб у кожен момент часу тиск газу був лише на нескінченно малу величину більшим за зовнішній тиск при розширенні і так само меншим при стисканні газу[5]. Тому напрям процесу можна змінити, змінивши в потрібний бік зовнішній тиск знов-таки на нескінченно малу величину. Як наслідок, провівши такий процес в одному, а потім у зворотному напрямі, ми повернемо газ у вихідний стан так, що в навколишньому середовищі не відбудеться ніяких змін. Процес, який має таку властивість, називається оборотним. Отже, квазістатичні процеси є оборотними. Зрозуміло, що такі процеси є ідеалізацією - усі реальні процеси є необоротні. Проте, не рідко, вирівнювання параметрів у системі відбувається швидко. Наприклад, у газах релаксація йде приблизно із швидкістю звуку. Тому реальні процеси часто можна з достатньою точністю розглядати як оборотні (квазистатичні).
Температура. Індикатором стану термодинамічної рівноваги системи є температура[6]. Якщо система не є рівноважна, то різні її частини (тіла) мають не однакову температуру, але в процесі релаксації більш гарячі тіла охолоджуються, а холодні нагріваються. Відтак, у стані термодинамічної рівноваги температура всіх тіл будь-якої системи або різних частин одного тіла стає однаковою. Слід наголосити, що температура є єдиним термодинамічним параметром, який має вказану властивість. Наприклад, у системі, що складається з декількох гумових кульок із газом і перебуває в стані термодинамічної рівноваги, тиск газу та концентрація молекул у різних кульках може бути різною, але температура - обов’язково є однаковою й рівною температурі навколишнього повітря. Для практичного вимірювання температури використовують якусь залежну від температури властивість певної речовини (“термометричного тіла”) і відповідну температурну шкалу. Так, у побуті найчастіше користуються рідинними термометрами, дія яких ґрунтується на тому, що об’єм термометричної рідини (спирт або ртуть) лінійно залежить від температури в необхідному для практичних потреб інтервалі значень. При цьому найпоширенішою є шкала Цельсія, в якій початок відліку (0 °С) відповідає температурі тверднення води при нормальному атмосферному тиску, а температура кипіння води приймається рівною 100 °С. Є й інші температурні шкали такого типу (шкала Реомюра, шкала Фаренгейта), які відрізняються вибором нульової точки (початку відліку) та розміром одиниці температури.
Згадані температурні шкали не відображають фізичної природи температури, але виражають її зручними для практики умовними числами. Але в науці найчастіще використовують так звану абсолютну термодинамічну шкалу температур або шкалу Кельвіна. Одиниця температури в цій шкалі називається кельвін (К), а температура, виміряна в кельвінах, називається абсолютною температурою. Абсолютна температура Т є пов’язана із температурою t в шкалі Цельсія співвідношенням Т = 273,15 + t. На практиці перший доданок округлюють до цілого і приймають
Т = 273 + t.
Звідси випливає, що розмір одиниці в обох шкалах однаковий і температурі Т = 0 К, яка називається абсолютним нулем, у шкалі Цельсія відповідає температура -273 оС.
Шкала Кельвіна має глибокий фізичний зміст, який розкриває молекулярно-кінетична теорія. Розглянемо молекулярний механізм установлення термодинамічної рівноваги в теплоізольованому циліндрі, що розділений тонкою теплопровідною перегородкою та заповнений газом. Нехай початковий стан газу є нерівноважним, і молекули по обидва боки від перегородки мають різні середні швидкості хаотичного руху. Молекули обох газів стикаються з молекулами перегородки, через що кінетична енергія більш швидких молекул зменшується, а повільних - збільшується. Позаяк в одній частині циліндра кількість швидких молекул більша, ніж в іншій, то через перегородку встановиться потік енергії від газу з у середньому більш швидкими молекулами до газу з повільнішими молекулами. Очевидно, що цей процес триватиме доти, доки не зрівняються середні кінетичні енергії поступального руху молекул газу в одній та в інший частині циліндра. Після цього макроскопічний стан газу в обох частинах буде лишатися незмінним, тобто система перейде в рівноважний стан. Але, як відомо з досліду, так само поводиться й температура. При встановленні рівноваги температура газу в одній частині циліндра знижується, а в іншій - підвищується, доки в усій системі не встановиться однакова температура. Отже, можна зробити висновок про те, що температура пов’язана з хаотичним рухом молекул так, що тіло з більш високою температурою має більшу середню кінетичну енергію молекул[7]. У молекулярно-кінетичній теорії доводиться, що цей зв’язок є універсальним і виражається формулою
|
\(\left\langle{E}\right\rangle=\frac{3}{2}kT \), |
(1.2) |
де \(\left\langle{E}\right\rangle \) - середня кінетична енергія поступального теплового руху однієї молекули, k = 1,38·10-23 Дж/К - універсальна стала, що називається сталою Больцмана, Т - абсолютна температура. Це співвідношення розкриває зміст абсолютного нуля температури:
Т = 0 К - то є температура, при якій припиняється тепловий рух частинок речовини[8].
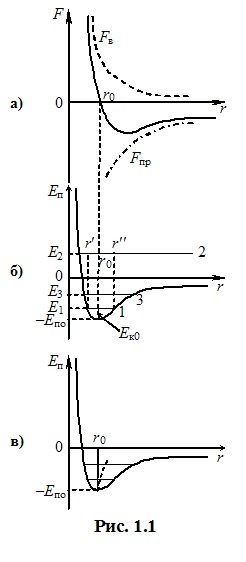 Окрім потенціальної енергії взаємодії Еп кожна молекула має також кінетичну енергію теплового руху Ек та відповідну повну енергію Е = Еп + Ек, яка не змінюється при русі молекули без зіткнення з іншою (горизонтальні лінії Е1, Е2, Е3 на рис 1.1б). Глибина потенціальної ями Еп0 визначається тільки природою молекул і для різних речовин суттєво відрізняється. Кінетична енергія теплового руху молекул Ек0 не залежить від речовини і визначається тільки її температурою. Тому спостерігаються три характерні ситуації.
Окрім потенціальної енергії взаємодії Еп кожна молекула має також кінетичну енергію теплового руху Ек та відповідну повну енергію Е = Еп + Ек, яка не змінюється при русі молекули без зіткнення з іншою (горизонтальні лінії Е1, Е2, Е3 на рис 1.1б). Глибина потенціальної ями Еп0 визначається тільки природою молекул і для різних речовин суттєво відрізняється. Кінетична енергія теплового руху молекул Ек0 не залежить від речовини і визначається тільки її температурою. Тому спостерігаються три характерні ситуації.
1) Сили взаємодії між молекулами великі, тоді Ек0 << Еп0 і повна енергія на рис. 1.1б зображується горизонтальною лінією 1. У такому випадку середня відстань між молекулами має певну величину r0, і вони лише здійснюють малі коливання навколо положень рівноваги. Така поведінка молекул спостерігається в твердих тілах, для яких є характерними здатність зберігати свою форму, твердість і велика механічна міцність.
2) Якщо сили взаємодії між молекулами малі, так що Ек0 > Еп0, то за рахунок своєї кінетичної енергії одна молекула може віддалитися від іншої на необмежену відстань. Така ситуація спостерігається в газах і зумовлює їхні характерні властивості – здатність займати весь наданий об’єм і порівняно легко стискатись.
3) Найскладнішим є молекулярний рух у рідинах. У рідинах глибина потенціальної ями лише трохи більша за середню кінетичну енергію теплового руху молекул і лінія повної енергії займає положення 3 на рис. 1.1б. За таких умов молекули рідини, в основному, здійснюють коливання навколо положень рівноваги як і в твердому тілі. Цим пояснюється те, що рідини зберігають свій об’єм і є майже нестисливими. Але, на відміну від твердого тіла, в рідині завжди присутня помітна кількість “гарячих” молекул, які мають більшу, ніж середня, кінетичну енергію і здатні подолати силу притягання до сусідніх молекул. Такі молекули час від часу переміщуються на декілька міжатомних відстаней (“кочують”) і займають нові рівноважні положення. Завдяки цьому рідина має текучість, і набуває форму посудини, в якій знаходиться.
Наявністю “гарячих” молекул пояснюється й пароутворення, тобто перехід рідини в газоподібний стан - пару[11]. Так само при нагріванні твердого тіла, коли кінетична енергія молекул стає достатньою для подолання жорсткого зв’язку між молекулами, спостерігається плавлення - перехід речовини з твердого стану в рідкий.
Демонстрація теплового руху та взаємодії молекул.
Теплове розширення. Особливості взаємодії між молекулами пояснюють і добре відомий ефект теплового розширення. Він спостерігається через неоднакову залежність сил притягання та відштовхування від відстані між молекулами, крива потенціальної енергії (потенціальна яма) на рис. 1.1б є асиметричною – її права стінка йде більш полого, ніж ліва. Тому при зростанні температури та кінетичної енергії збільшується не тільки амплітуда коливань молекул навколо положень рівноваги, а й середня відстань між ними r = (r′ + r″)/2 (штрихова крива на рис. 1.1в). Саме це є причиною збільшення лінійних розмірів і об’єму рідин та твердих тіл. При порівняно невисоких температурах середня відстань між молекулами змінюється пропорційно до температури, тому лінійні розміри \({l}\) і об’єм \({V}\) тіл лінійно залежать від температури:
\({l=l_0\left(1+\alpha{t{}^\circ}\right)}\),
\({V=V_0\left(1+\beta{t{}^\circ}\right)}\),
де \({l_0},\,\,{V_0}\) – розміри та об’єм при температурі t = 0 °C, α, β – коефіцієнти лінійного та об’ємного розширення, відповідно, причому β = 3α.
Контрольні запитання
1. Які методи дослідження використовуються в молекулярній фізиці? В чому полягає їхня сутність?
2. Що означають терміни “мікроскопічні параметри” та “макроскопічні параметри”?
3. Які одиниці використовують для визначення мас атомів і молекул? Як вони пов’язані муж собою?
4. У чому полягає відмінність між кількістю та масою речовини та як вони пов’язані між собою?
5. Який зв’язок існує між молярною масою речовини та масою однієї молекули, якщо остання виражена в кг і в а.о.м.?
6. Як можна оцінити розміри молекул у рідині через її молярну масу та густину? Чи придатний такий спосіб для твердих тіл? газів?
7. Який фізичний зміст мають поняття “температура” та “абсолютний нуль” температури?
8. У посудині з газом, яка рухається, середня кінетична енергія молекул більша, ніж у нерухомій. Чи означає це, що й температура газу в рухомій посудині вища? Чому?
9. Що таке “термодинамічна рівновага”? Чи є зв’язок між нею та механічною рівновагою?
10. Який характер мають сили взаємодії між атомами та молекулами? Наведіть наочні свідчення існування сил притягання та сил відштовхування між молекулами.
11. Відомо, що дві зіставлені поверхнями гладенькі плоскі пластинки не пристають одна до одної, тоді як дві відполіровані до дзеркального блиску пластинки “склеюються” так, що їх важко відірвати одна від одної. Чому?
12. Чому існують різні агрегатні стани речовини – твердий, рідкий та газоподібний?
13. Чому одна й та сама речовина може перебувати в різних агрегатних станах?
14. Як змінюються розміри тіл при зміні температури? З якою особливістю сил взаємодії між молекулами це пов’язано?
[1] Ізотопи - то є різновиди атомів даного хімічного елемента, що відрізняються кількістю нейтронів у ядрі.
[2] Найменування “а.о.м.”не пишуть.
[3] Це означає, що молекули не можна розглядати просто як зіставлені докупи декілька кульок-атомів. Чому так, пояснює квантова механіка.
[4] Детальніше про це буде сказано при розгляді розподілу Максвелла-Больцмана
[5] Зрозуміло, що це можливо тільки за відсутності будь-якого тертя між поршнем і циліндром.
[6] Суб’єктивно температура пов’язується із відчуттям нагрітості - чим гарячіше тіло, тим вища його температура.
[7] Тому хаотичний рух частинок речовини називають тепловим рухом.
[8] Температура 0 К є граничною величиною: температура реальної фізичної системи може лише наближатися до абсолютного нуля, ніколи не досягаючи його точно. Крім того абсолютний нуль температури означає припинення не будь-якого , а лише теплового руху частинок. Зокрема, при 0 К зберігається рух електронів в атомах і коливання атомів у молекулах (так звані нульові коливання).
[9] Їх називають силами Ван-дер-Ваальса.
[10] Так відбувається тому, що ця робота дорівнює спаду потенціальної енергії (див. МЕХАНІКА, розділ ІV).
[11] Теоретично пароутворення відбувається і в твердих тілах, але в твердому тілі кількість молекул, кінетична енергія котрих достатня для подолання зв’язку з іншими та виходу за межі тіла, є гранично малою.
ІІ. ВЛАСТИВОСТІ ГАЗІВ
У газах сили притягання між молекулами малі, тому молекули не утримуються одна біля одної, а рухаються по всьому наданому об’єму. При не дуже низьких температурах середня кінетична енергія теплового руху молекул у газі істотно перевищує енергію зчеплення між ними. За таких умов можна вважати, що молекули в газах рухаються як вільні частинки, взаємодіючи лише при безпосередніх зіткненнях між собою та зі стінками посудини.
З іншого боку, при не дуже високих тисках концентрація молекул у газах є порівняно невелика, через що власний об’єм молекул виявляється набагато меншим, ніж об’єм посудини, в якій знаходиться газ. Наприклад, при кімнатній температурі й нормальному атмосферному тискові об’єм молекул складає ≈ 0,1% об’єму посудини, і на практиці власні розміри молекул можна не враховувати. Тому, розглядаючи гази, широко використовують спрощену модель “ідеальний газ” - систему, що складається з частинок несуттєвих розмірів, які взаємодіють лише при випадкових пружних зіткненнях між собою та зі стінками посудини. Інакше говорячи молекули ідеального газу не мають власного об’єму та потенціальної енергії взаємодії між собою[1]. Така модель добре відображає властивості справжніх газів за звичайних умов. При екстремальних умовах (наднизькі температури та надвисокі тиски) наявність власного об’єму та взаємодії між молекулами даються взнаки і властивості реальних газів стають більш складними. Але властивості ідеального газу можна теоретично встановити на основі лише простих молекулярно-кінетичних уявлень.
Нижче розглянуті наступні питання
2.1. Тиск ідеального газу
2.2. Рівняння Клапейрона. Ізопроцеси в газах
2.3. Реальний газ
|
|
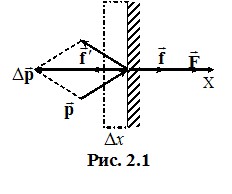
Газ створює тиск на стінки посудини завдяки ударам молекул, причому в ідеальному газі ці удари є абсолютно пружними. Розглянемо дію молекул газу на малу ділянку стінки посудини, рис. 2.1.
Під час зіткнення на молекулу з боку стінки діє мікроскопічна сила, середня величина якої дорівнює відношенню зміни імпульсу молекули до тривалості зіткнення (другий закон Ньютона): \(\vec{f}'=\Delta{\vec{p}}/\tau \). За третім законом Ньютона з боку молекули на стінку діє сила \(\vec{f}=-\vec{f}' \). Можна сказати, що ця сила дорівнює імпульсу, переданому молекулою стінці за одиницю часу. Величина Δp є дуже малою, тому дія молекул газу на стінку посудини має характер мікроскопічних миттєвих “уколів”, урахувати які безпосередньо неможливо. Але у тому й немає потреби - через макроскопічну кількість молекул зіткнення відбуваються так часто та щільно, що створюють рівномірно розподілену по поверхні стінки сталу силу тиску F. Ця сила дорівнює сумарному імпульсу, що передається стінці всіма молекулами, котрі стикаються з нею протягом 1 с. Величину F можна визначити за допомогою таких міркувань. Пружне зіткнення молекули зі стінкою відбувається без утрати кінетичної енергії та величини швидкості. Тому молекула відлітає від стінки з таким самим за модулем імпульсу й під таким самим кутом, як і налітає. При цьому модуль переданого стінці імпульсу складає (див. рис. 2.1):
\(\left|\Delta{\vec{p}}\right|=2p\cos\alpha=2mv\cos\alpha \) \( \Rightarrow \) \( \left|\Delta{\vec{p}}\right|={2mv_x}\),
де m - маса молекули, α – кут між вектором імпульсу молекули та нормаллю до стінки, vx - проекція на вісь Х швидкості, з якою молекула налітає на стінку. Для визначення сили тиску припустимо спочатку, що всі молекули, котрі налітають на стінку, мають однакову величину vx. Тоді сила тиску
\({F}=\nu\cdot{2mv_x}\).
де \(\nu \) - кількість зіткнень молекул зі стінкою за 1 с. Щоб знайти ν, виділимо біля стінки шар молекул настільки малої товщини Δx, що в його межах молекули не стикаються між собою. Тоді всі молекули в шарі, що рухаються до стінки, зіткнуться з нею протягом часу Δt = Δx/vx. Кількість таких молекул ΔN′ дорівнює половині загальної кількості молекул у шарі. Тоді, якщо концентрація молекул газу (кількість в одиниці об’єму) дорівнює n і площа ділянки стінки S, то ΔN′ = nSΔx/2, і кількість зіткнень за одиницю часу
\(\nu=\frac{\Delta{N'}}{\Delta{t}}=\frac{1}{2}nx_xS \) і \({F=nmv_v^2 S}\).
Насправді молекули мають різні швидкості, тому реальна сила тиску визначається середнім значенням квадрата проекції швидкості \(\left\langle{v_x^2}\right\rangle \):
|
\({F}=nm\left\langle{v_x^2}\right\rangle{S}\). |
(2.1) |
Усі напрямки руху молекул є рівноймовірними й незалежними, тому можна записати
\(\left\langle{v_x^2}\right\rangle=\left\langle{v_y^2}\right\rangle=\left\langle{v_z^2}\right\rangle \) і \(\left\langle{v^2}\right\rangle=\left\langle{v_x^2}\right\rangle+\left\langle{v_y^2}\right\rangle+\left\langle{v_z^2}\right\rangle=3\left\langle{v_x^2}\right\rangle \) \(\Rightarrow \) \(\left\langle{v_x^2}\right\rangle=\frac{1}{3}\left\langle{v^2}\right\rangle \). .
Підставивши цей вираз у (2.1) і поділивши на площу S, отримуємо для тиску ідеального газу:
|
\({P}=\frac{1}{3}nm\left\langle{v^2}\right\rangle \) |
(2.2) |
або
|
\({P}=\frac{2}{3}n\left\langle{E}\right\rangle\). |
(2.2а) |
Ці рівняння є принципово важливими, оскільки вони встановлюють теоретичний зв’язок між макроскопічним параметром газу - тиском і мікроскопічними параметрами - масою та швидкістю теплового руху молекул, або їх кінетичною енергією. Тому рівняння (2.2) або (2.2а) часто називають основним рівнянням молекулярно-кінетичної теорії газу. З них випливають важливі наслідки.
Перш за все зауважимо, що в (2.2а) фігурує середня енергія поступального руху молекул, яка визначається тільки температурою газу, згідно з (1.2). Тому для тиску можна записати:
|
\({P=nkT}\). |
(2.3) |
Отже, тиск ідеального газу не залежить від його природи й визначається тільки концентрацією молекул та температурою газу. Зокрема, це означає, що при однакових температурі та тиску всі гази мають однакову концентрацію молекул (закон Авогадро). За нормальних умов (температура 0 оС (273 К) і тиск 760 мм. рт. ст (1,01·105 Па)) вона складає п0 = 2,69·1025 1/м3 і називається числом Лошмідта. При цьому 1 моль будь-якого газу за нормальних умов займає однаковий об’єм V0 = 22,4·10-3 м3. Із незалежності тиску газу від природи молекул випливає, що вираз (2.3) є чинним не лише для однорідних газів, а й для суміші газів, які не вступають між собою в хімічні реакції. У цьому випадку
\( {n}=n_{1}+n_{2}+...+n_{i}+...=\sum_{i}n_{i}\),
де ni - концентрації компонентів суміші. Відповідно, тиск суміші
|
\( {P}=\left(\sum_{i}n_{i}\right){kT}=\sum_{i}(n_{i}kT) \) \( \Rightarrow \) \( {P}=\sum_{i}P_{i}\), |
(2.4) |
де \({P_i}=n_ikT \) - парціальні тиски компонентів, тобто тиски, які створювала би в посудині дана компонента суміші за відсутності всіх інших.
|
\({R=N_Ak}\) = 8,31 Дж/(моль·К) |
(2.5) |
називається універсальною газовою сталою. Врахувавши це, отримуємо рівняння стану ідеального газу, яке називається рівнянням Клапейрона (Клапейрона-Мендєлєєва):
|
\({PV=\nu{RT}=\frac{m}{M}RT}\), |
(2.6) |
де \({\nu}\) - кількість молів, т - маса і М - молярна маса газу. Для одного моля газу.
\({PV=RT}\).
Ізопроцеси в газах. Рівняння Клапейрона (2.6) дозволяє аналізувати не лише рівноважні стани, а й рівноважні процеси в газах, тобто з’ясовувати характер зміни термодинамічних параметрів газу за тих чи інших умов. Для теорії найбільший інтерес викликають так звані ізопроцеси, тобто, процеси, що відбуваються з незмінною кількістю газу і при незмінному значенні одного з параметрів стану. Розрізняють ізотермічний (\(\nu=\mathrm{const}\), T = const), ізобарний (\(\nu=\mathrm{const}\), Р = const) та ізохорний (\(\nu=\mathrm{const}\), V = const) процеси.
В ізотермічному процесі права частина (2.6) не змінюється, отже
|
PV = const, де const = νRT. |
(2.7) |
Це рівняння виражає закон Бойля-Маріотта:
при постійній температурі добуток тиску заданої кількості газу на об’єм є сталим .
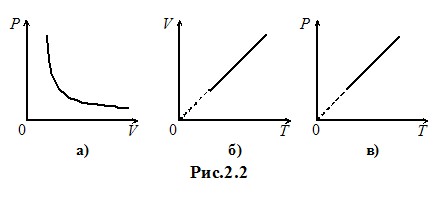
Графік, що показує зв’язок між параметрами стану в ізотермічному процесі, називається ізотермою і на діаграмі (Р, V) для ідеального газу має форму гіперболи (рис. 2.2а).
|
|
Ізобарний (ізобаричний) процес відбувається при сталому тиску газу, тому на основі (2.6) можна записати:
|
\({V=aT}\), де \({a}=\frac{mR}{MP}=\mathrm{const}\). |
(2.8) |
Це є вираз закоу Гей-Люссака:
при сталому тиску об’єм заданої кількості газу змінюється прямо пропорційно абсолютній температурі.
Графік цього процесу (рис. 2.2б називається ізобарою. на діаграмі (V, Т).
В ізохорному (ізохоричному) процесі подібним чином змінюється тиск:
|
\({P=bT}\), де \({b=}\frac{mR}{MV}=\mathrm{const}\). |
(2.9) |
Це є аналітичний вираз закону Шарля:
тиск заданої кількості газу при сталому об’ємі є прямо пропорційним температурі. Вигляд ізохори на діаграмі (P, T) показано на рис. 2.2в.
Рівняння (2.8) і (2.9) інколи записують через температуру в шкалі Цельсія, роблячи в (2.8) і (2.9) заміну Т = 273 + t. Тоді
|
\({V=V_0(1+\alpha{t})}\) і \({P=P_o(1+\beta{t})}\), |
(2.10) |
де V0 = 273 та Р0 = 273 – об’єм і тиск при 0 °С (273 К); α - термічний коефіцієнт об’єму (коефіцієнт об’ємного розширення) і β - термічний коефіцієнт тиску. Очевидно, що
\(\alpha=\beta=\frac{1}{273}\,\,K^{-1}\).
Рівняння Ван дер-Ваальса. Найпроостішим і зручним для якісного аналізу властивостей реальних газів є рівняння стану, що запропонував Ван-дер-Ваальс на основі досить простих міркувань. Об’єм V, який фігурує в рівняннях (2.6), (2.6а) є об’ємом посудини, в якій міститься газ. В дійсності через наявність власних розмірів для молекул доступний не весь об’єм посудини. Тому в рівнянні стану замість V має фігурувати величина V - b, де b - поправка на власний об’єм молекул, яка приблизно дорівнює добутку об’єму однієї молекули на їх кількість[3]. Відповідно, тиск 1 моля реального газу мав би виражатися, як
|
\({P}=\frac{RT}{V_0-b}\), |
(2.11) |
|
|
|
де V0 - молярний об’єм газу (об’єм 1 моля).
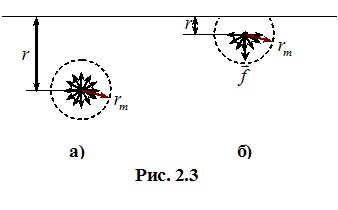
Але на тиск газу впливають і сили притягання між молекулами. Для аналізу цього впливу вводять поняття радіуса молекулярної дії rm, тобто максимальної відстані між молекулами, на якій сили притягання ще мають помітну величину (ця відстань є досить умовною і складає ~10-9 м, тобто декілька поперечників молекули). Якщо молекула знаходиться на відстані r > rm від стінки посудини, то вона оточена сусідніми молекулами з усіх боків у середньому рівномірно і їхня дія є компенсованою (рис.2.3а). Але біля стінки, коли r < rm, кількість сусідніх молекул, які тягнуть дану молекулу донизу, переважає кількість тих, які тягнуть її вгору. Тому на кожну молекулу біля стінки з боку інших діє певна результуюча сила \(\vec{f}\) , спрямована всередину газу (рис. 2.3б). Такі молекулярні сили сповільнюють рух молекул на підльоті до стінки і, згідно з (2.2), зменшують тиск газу на стінку на деяку величину Pi. З урахуванням цього, рівняння (7.13) слід записувати у вигляді
|
\({P}=\frac{RT}{V_0-b}-P_i \). |
(2.11а) |
Величина \({P_i}\) визначається сумарною силою, що діє на молекули в прилеглому до стінки посудини шарі газу. Ця сила є пропорційна як кількості молекул у пристіночному шарі, на які діють молекулярні сили, так і кількості молекул у сусідньому шарі, що створюють її. Обидва шари мають приблизно однакову товщину порядку rm і, відповідно, однакову кількість молекул, прямо пропорційну концентрації газу n. Тому Pi ~ n2 . У свою чергу концентрація молекул є обернено пропорційна об’єму газу (для 1 моля n = NA/V0), отже можна записати \({P_i}=a/V_0^2 \), де а - деяка стала. У підсумку, рівняння (2.11а) набуває вигляду
\({P}=\frac{RT}{V_0-b}-\frac{a}{V_0^2}\),
або
|
\(\left(P+\frac{a}{V_0^2}\right)\left(V_0-b\right)={RT}\). |
(2.12) |
Для \(\nu \) молів газу \({V=\nu{V_0}}\), відповідно, рівняння (2.12) набуває вигляду:
|
\(\left(P+\frac{a\nu^2}{V^2}\right)\left(V-\nu{b}\right)=\nu{RT}\). |
(2.12а) |
Рівняння стану реального газу (2.12) або (2.12 а) називається рівнянням Ван-дер-Ваальса.
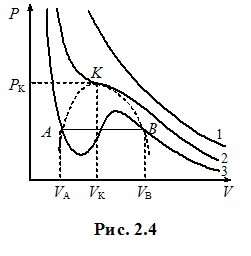
Ізотерми Ван-дер-Ваальса. Критичний стан. Подивимось, які специфічні властивості реальних газів передрікає рівняння Ван-дер-Ваальса та як теоретичні прогнози узгоджуються з дослідними фактами. Для цього проаналізуємо ізотерми Ван-дер-Ваальса, тобто залежності тиску газу від об’єму при сталих температурах, які випливають із рівнянь (2.12), (2.12 а). На рис. 2.4 показаний характерний вигляд теоретичних ізотерм Ван-дер-Ваальса для різних температур газу. При високих температурах, як і слід очікувати, вони нагадують ізотерми ідеального газу - при розширенні тиск монотонно зменшується (крива 1). Але при низьких температурах на кривих з’являється характерна хвиляста ділянка (крива 3).
|
|
Ці два різні типи залежностей розділяються так званою критичною ізотермою (крива 2), яка відповідає певній критичній температурі Тк і має точку перегину К, яка називається критичною точкою. Цій точці, крім критичної температури Тк, відповідає критичнйм тиск Рк і критичний об’єм Vк. Критичні параметри можна знайти, виходячи з того, що в точці К (точці перегину) перша та друга похідні тиску по об’єму дорівнюють нулю. Відповідні розрахунки на основі (2.12) для одного моля газу дають:
|
\( {V}_{0k}=3b \), \( {P}_{0k}=\frac{a}{27b^{2}}\), \( {T}_k=\frac{8a}{27Rb}\) |
(2.13) |
Як видно, критичні параметри визначаються виключно поправками Ван-дер-Ваальса а і b, тобто індивідуальними властивостями молекул. Але величина Кк = RTk/P0kV0k, яка називається критичним коефіцієнтом, є універсальною: згідно з (2.13) її значення, не≈залежно ні від чого, складає Кк = 8/3 ≈ 2,67. Дослід свідчить, що це не зовсім так: критичний коефіцієнт є дещо більшим і залежним від газу[4]. Отже, рівняння Ван-дер-Ваальса не є точним. Про це свідчить і наявність підйомів на хвилястих ділянках ізотерм при T < Tk (крива 3, рис. 2.4), які відповідають зростанню тиску при розширенні газу. Це є неможливо, бо означає збільшення тиску при зменшенні концентрації молекул при незмінній температурі. І дійсно, в експерименті указаний аномальний підйом на ізотермах реального газу не спостерігається. Але натомість виникає “поличка” (відрізок АВ на кривій 3, рис. 2.4): при зменшенні об’єму від VВ до VА тиск газу залишається сталим, а потім стрімко зростає. Спостереження показують, що це пов’язано з конденсацією газу в рідину. У процесі стискання при об’ємі VВ в посудині крім газу з’являється рідина, якої дедалі стає більше, а газу - менше. При об’ємі VА конденсація закінчується, і в посудині міститься лише рідина. Цим пояснюється й дуже стрімке зростання тиску при подальшому стисненні – адже рідина є практично нестисливою.
Таким чином, рівняння Ван-дер-Ваальса показує можливість переходу газу в рідину при ізотермічному стисканні. При цьому об’єм речовини під поршнем без зміни тиску зменшується від значення VА, яка відповідає початковому об’єму газу, до VВ – об’єму рідини, що утворилася з усього газу. Інтервал значень об’єму VВ - VА, при якому в посудині співіснують газоподібна та рідка фази речовини, що показаний штриховою кривою на рис. 2.4, із збільшенням температури зменшується і при Т = Тк зникає зовсім. При цьому, як показує дослід, при V > Vk у посудині спостерігається лише газ, а при V < Vk - лише рідина. Отже, при переході через критичну точку К увесь газ одномоментно перетворюється на рідину, проминаючи двофазну стадію. Самій точці К(Рk, Vk , Тk) відповідає специфічний критичний стан речовини, при якому зникає будь-яка відміна між газом і рідиною. Зокрема, зникає меніск – межа поділу між рідиною та газом і спостерігається опалесценція - різке помутніння речовини по всьому об’єму безпосередньо перед переходом у рідкий стан. При температурах Т > Тк ізотерми Ван-дер-Ваальса не мають розглянутих особливостей, і можна припустити, що за таких умов газ весь час лишається газом, тобто його ніяким способом неможливо перевести в рідкий стан. Це дійсно так: практика отримання скраплених газів свідчить, що будь-який газ можна стисканням перетворити на рідину тільки при температурі, нижче критичної.
Підводячи підсумок, відмітимо, що рівняння Ван-дер-Ваальса якісно правильно відображає властивості реальних газів у широкому діапазоні параметрів стану. І це гідне подиву, оскільки в цьому рівнянні враховані не детальні властивості сил взаємодії між молекулами, а, за великим рахунком, лише сам факт існування таких сил.
1. Що таке“ідеальний газ”? За яких умов природні гази можна розглядати як ідеальні?
2. Чому при високих тисках і низьких температурах властивості природних газів відрізняються від ідеальних?
3. Чим тиск газу на стінки посудини відрізняється від тиску рідини?
4. Якими мікроскопічними параметрами визначається тиск газу на стінки посудини?
5. Якими макроскопічними параметрами визначається тиск газу на стінки посудини?
6. Як визначається тиск суміші газів?
7. Що називається рівнянням стану та який вигляд воно має для ідеальних газів?
8. Чому рівняння Клапейрона можна використовувати для аналізу рівноважних процесів у газі і не можна – для нерівноважних?
9. Що таке ізопроцеси? Перелічіть ізопроцеси в газах.
10. Як виглядають ізотерми на діаграмі (Р, Т)? (V,T)?
11. Як виглядають ізобари на діаграмі (Р, V)? (P,T)?
12. Як виглядають ізохори на діаграмі (Р, V)? (V,T)?
13. Як впливає на тиск реального газу (порівняно з ідеальним) наявність розмірів у молекул? Як це пояснити, виходячи з механізму створення тиску?
14. Як впливає на тиск реального газу (порівняно з ідеальним) наявність сил притягання між молекулами? Як це пояснити, виходячи з механізму створення тиску?
15. Поясніть, які процеси в реальному газі відображають різні характерні ділянки ізотерм Ван-дер-Ваальса.
16. За яких умов газ при стисканні скраплюється (переходить у рідкий стан), а за яких – ні.
17. Що таке критичний стан речовини? Чи можна його спостерігати в експерименті?
[1] Але в деяких випадках доводиться враховувати рух і взаємодію атомів у молекулах.
[2] Атмосферний тиск вимірюють у позасистемних одиницях – міліметрах ртутного стовпчика (1 мм рт. ст. = 133,3 Па).
[3] Насправді вона дещо більша, оскільки навіть при щільній упаковці між молекулами лишаються певні не заповнені проміжки.
ІІІ. РОЗПОДІЛ МАКСВЕЛЛА-БОЛЬЦМАНА
У Вступі відмічалося, що в молекулярон-кінетичній теорії (МКТ) параметри макроскопічного стану (термодинамічні параметри) системи визначаються через середні значення її мікроскопічних параметрів, тобто, характеристик окремих молекул. Це наочно ілюструють рівняння (1.2), (2.2) або (2.2 а). Тому теоретичне визначення середніх значень мікропараметрів є принциповим завданням МКТ. Так само важливим є визначення кількості частинок у макросистемі, для яких значення того чи іншого мікропараметра лежить у заданих межах. Можливість розв’язання вказаних задач ґрунтується на тому, що в рівноважній термодинамічній системі існують певні статистичні розподіли частинок за різними мікропараметрами. Ці розподіли визначають стан системи й не змінюються з часом.
Далі розглядаються наступні питання:
1. Функція розподілу. Обчислення середніх значень
2. Розподіл Максвелла. Характеристичні швидкості молекул
1. Функція розподілу. Обчислення середніх значень
Поняття про функцію розподілу та про місце, яке вона посідає в МКТ, можна отримати на такому прикладі. Нехай у посудині є N молекул газу, який перебуває в стані термодинамічної рівноваги. Внаслідок випадкових зіткнень усі молекули газу в будь-який момент часу мають різні швидкості[1], а швидкість окремої молекули дуже часто й непередбачувано змінюється з часом. Але кількість молекул із заданими значеннями швидкості лишається незмінною. Зрозуміло, що кількість молекул \(\mathrm{d}N_v \), які мають швидкість у вузькому інтервалі значень від заданого \({v}\) до \({v}+\mathrm{d}v \)[2], є прямо пропорційна загальній кількості молекул і ширині інтервалу: \(\mathrm{d}N_v\approx{N}\mathrm{d}v \). Але вона залежить також і від величини \({v}\). До прикладу, молекул із дуже малими та великими швидкостями, є набагато менше, ніж із середніми. З огляду на це можна записати:
|
\(\mathrm{d}N_v=f(v)N\mathrm{d}v \), |
(3.1) |
де залежна від швидкості величина
|
\({f(v)}=\frac{\mathrm{d}N_v}{N\mathrm{d}v}\) |
(3.2) |
називається функцією розподілу молекул за модулем швидкості. Вона визначає
відносну кількість (частку) молекул, швидкості яких потрапляють в одиничний інтервал біля заданого значення \({v}\).
До цього питання можна підійти й з іншого боку. А саме, якби ми могли “вихоплювати” молекули із посудини по одній і вимірювати їхню швидкість, то з N таких випробувань у деякій кількості випадів \(\mathrm{d}N_v \) отримали б числа в інтервалі від деякого значення \({v}\) до \( v+\mathrm{d}v \). При цьому величина
|
\(\frac{\mathrm{d}N_v}{N}=\mathrm{d}P(v)\) |
(3.3) |
визначає ймовірність (шанси) того, що одна навмання вихоплена молекула буде мати швидкість у вказаному елементарному інтервалі. Отже, вираз (3.2) можна записати як
|
\({f(v)}=\frac{\mathrm{d}P}{\mathrm{d}v}\). |
(3.4) |
Це дозволяє трактувати функцію розподілу як густину імовірності, тобто імовірність того, що швидкість окремої молекули потрапить в одиничний інтервал біля заданого значення \({v}\). У такому разі ймовірність потрапляння швидкості окремої молекули в інтервал ширини \(\mathrm{d}v \)
|
\(\mathrm{d}P=f(v)\mathrm{d}v \). |
(3.4а) |
Відповідно, ймовірність того, що окрема молекула буде мати швидкість у скінченному інтервалі \(\left[v_1;\,v_2\right] \) визначається як
|
\({P}(v_1;\,v_2)=\int\limits_{v_1}^{v_2}f(v)\mathrm{d}v \). |
(3.5) |
Зокрема, якщо інтегрування провести по всіх можливих значеннях швидкості від 0 до нескінченності[3], то вийде одиниця, оскільки молекула достеменно має якесь значення швидкості:
|
\(\int\limits_{0}^{\infty }f(v)\mathrm{d}v=1 \). |
(3.6) |
З цього приводу говорять, що функція розподілу є нормованою на одиницю, а інтеграл (3.6) називають інтегралом нормування.
Функція розподілу \({f(v)}\) безпосередньо дозволяє визначити кількість молекул \(\Delta{N}\), які мають швидкість у заданому інтервалі значень \(\left[v_1;\,v_2\right] \). Для цього треба проінтегрувати вираз (3.1) у відповідних границях:
|
\(\Delta{N}=N\int\limits_{v_1}^{v_2}f(v)\mathrm{d}v\). |
(3.7) |
Для невеликих інтервалів швидкостей \(\Delta{v}<<v \) можна обійтися без інтегрування й використовувати наближений вираз
|
\(\Delta N\approx Nf\left( v \right)\Delta v\). |
(3.7а) |
За допомогою функції розподілу \({f(v)}\) можна визначати також середні значення будь-яких величин, залежних від \({v}\). Справді, нехай у макроскопічній системі з N частинок треба знайти середнє значення \(\left\langle{\Phi}(v)\right\rangle \) певної величини \(\Phi (v) \), яка є функцією швидкості. За означенням середнього
|
\(\langle\Phi{(v)}\rangle=\frac{\Phi_{\Sigma}}{N}\), |
(3.8) |
де \(\Phi_{\Sigma}\) - сума значень цієї величини для всіх N частинок. Через макроскопічну кількість частинок N безпосередньо обчислити \(\Phi_{\Sigma}\) неможливо, але це можна зробити за допомогою функції розподілу. Будь-якому елементарному інтервалу \(\mathrm{d}v \) відповідає кількість частинок \(\mathrm{d}N_v \), яка визначається виразом (3.1). Отже, сумарне значення величини \(\Phi(v) \) на цьому інтервалі дорівнює
\(\mathrm{d}\Phi_{\Sigma}=\Phi(v)\mathrm{d}N_v=N\Phi(v)f(v)\mathrm{d}v \).
Відповідно, для всіх частинок (і всіх значень \({v}\)) маємо
\(\Phi_{\Sigma}=N\int\limits_v\Phi(v)f(v)\mathrm{d}v \).
Отже, шукане середнє значення
|
\(\left\langle\Phi(v)\right\rangle=\int\limits_v \Phi (v) f(v) \mathrm{d}v \). |
(3.9) |
Цей вираз визначає загальний спосіб знаходження середнього значення будь-якої величини, яка є функцією певного мікропараметра системи, через функцію розподілу частинок за цим параметром.
2. Розподіл Максвелла. Характеристичні швидкості молекул
Функція розподілу молекул за проєкцією швидкості на вісь координат, наприклад \({v_x}\), має вигляд:
|
\({f(v_x)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{1}{2}}e^{-\frac{mv_x^2}{2kT}}\), |
(3.10) |
де m - маса молекули, Т - абсолютна температура газу, k - стала Больцмана. Ця функція, згідно з (3.1), визначає кількість молекул, які мають х-проєкцію швидкості в заданому інтервалі \(\mathrm{d}v_x \) і будь-яку величину проєкції швидкості на кожну з двох інших осей координат. Оскільки всі напрямки руху молекул є рівноймовірними, функції розподілу по проєкціях \({v_y}\) і \({v_z}\) є такими самими:
|
\({f(v_y)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{1}{2}}e^{-\frac{mv_y^2}{2kT}}\), |
(3.10а) |
|
|
\({f(v_z)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{1}{2}}e^{-\frac{mv_z^2}{2kT}}\). |
(3.10б) |
Далі розглянемо функцію розподілу молекул по трьох компонентах швидкості \({f(v_x,v_y,v_z)}\), яка визначає молекули із заданим набором проєкцій, а отже, із заданою величиною та напрямком швидкості[4]. Згідно з (3.1), кількість молекул, х-проєкція швидкості котрих лежить в інтервалі від \({v_x}\) до \({v_x}+\mathrm{d}{v_x}\), - це є \(\mathrm{d}N_{v_x}=Nf(v_x)\mathrm{d}{v_x}\). З цих молекул у-проєкцію швидкості в інтервалі від \({v_y}\) до \({v_y}+\mathrm{d}{v_y}\) мають \(\mathrm{d}N_{v_x,v_y}=\mathrm{d}N_{v_x}f(v_y)=Nf(v_x)f(v_y)\mathrm{d}v_x\mathrm{d}v_y \) молекул. Аналогічно визначаються й ті з \(\mathrm{d}N_{v_x,v_y}\) молекул, які мають ще й z-проєкцію швидкості в заданому інтервалі від \({v_z}\) до \({v_z}+\mathrm{d}{v_z}\). Отже, кількість молекул, у яких усі три проєкції швидкості лежать у заданих інтервалах значень, складає
|
\(\mathrm{d}N_{v_x,v_y,v_z}=\mathrm{d}N_{v_x,v_y}f(v_x)f(V_y)f(v_z)\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_x\). |
(3.11) |
Звідси, згідно з (3.2), визначаємо шукану функцію розподілу \({f}(v_x,v_y,v_z) \):
|
\({f(v_x,v_y,v_z)}=\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}e^{-\frac{m(v_x^2+v_y^2+v_z^2)}{2kT}}\). |
(3.12) |
У показнику експоненти стоїть величина \({v_x^2+v_y^2+v_z^2=v^2}\) - квадрат модуля швидкості. Це означає, що, хоча дана функція розподілу враховує як величину, так і напрям швидкості молекули, сама вона від напряму швидкості не залежить. У цьому немає нічого дивного, оскільки через хаотичність теплового руху молекул усі напрями швидкості є рівноймовірними.
Нарешті, розглянемо функцію розподілу молекул газу за модулем швидкості \({f(v)}\), яка визначає кількість молекул із швидкостями з величиною в інтервалі від \({v}\) до \({v+\mathrm{d}v}\) і будь-яким напрямком. Відповідний розрахунок дає такий вираз \({f(v)}\) :
|
\({f(v)}=4\pi\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}v^2e^{-\frac{mv^2}{2kT}}\). |
(3.13) |
|
|
|
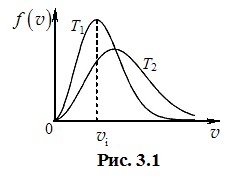
Вигляд графіка цієї функції для двох температур (T2 > T1) показано на рис. 3.1.
Зауважимо, що всі наведені функції розподілу нормовані і, згідно з (3.6), площі під кривими на рис. 3.1 дорівнюють одиниці. Тому при підвищенні температури і зростанні середньої швидкості теплового руху молекул максимум функції розподілу переміщується в область більших швидкостей, а сама крива \({f(v)}\) стає ширшою та нижчою, тобто відбувається певне вирівнювання швидкостей молекул.
Характеристичні швидкості молекул. У різних задачах для характеристики теплового руху молекул використовують три різні так звані характеристичні швидкості: найбільш імовірну, середню арифметичну та середню квадратичну.
Найбільш імовірна швидкість молекул \({v_i}\) відповідає максимуму функції розподілу \({f(v)}\) (рис. 3.1). Її можна визначити, взявши похідну від функції (3.13) і прирівнявши її до нуля. Результат такий:
|
\({v_i}=\sqrt{\frac{2kT}{m}}\). |
(3.14) |
Домноживши чисельник і знаменник під коренем на сталу Авогадро NA, отримаємо інший варіант формули:
|
\({v_i}=\sqrt{\frac{2RT}{M}}\), |
(3.14а) |
де R - універсальна газова стала, М - молярна маса газу.
Середня арифметична швидкість молекул \({\langle{v}\rangle}\), згідно із загальним правилом (3.9), визначається як
\(\langle{v}\rangle=4\pi\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}\int\limits_{0}^{\infty }{v}^{3}e^{-\frac{mv^2}{2cT}}\mathrm{d}{v}\).
Інтеграл у цьому виразі є табличним[5] і дає
|
\(\langle{v}\rangle=\sqrt{\frac{8kT}{\pi{m}}}\) |
(3.15) |
або
|
\( \langle{v}\rangle=\sqrt{\frac{8RT}{\pi{M}}}\). |
(3.15а) |
Середньою квадратичною швидкістю називається величина \({v}\)кв = \(\sqrt{\langle{v^2}\rangle}\). Величина під коренем знаходиться аналогічно до \(\langle{v}\rangle \):
\(\langle{v^2}\rangle=4\pi\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}\int\limits_{0}^{\infty }v^4 e^{-\frac{mv^2}{2kT}}\mathrm{d}{v}=\frac{3kT}{m}\).
Отже, середня квадратична швидкість визначається формулами:
|
\({v}\)кв = \(\sqrt{\frac{3kT}{m}}\). |
(3.16) |
або
|
\({v}\)кв = \(\sqrt{\frac{3RT}{M}}\). |
(3.16а) |
Зауважимо, що всі характеристичні швидкості прямо пропорційні до \(\sqrt{T/m}\) і мало відрізняються за величиною, а саме, \({v_1}:\langle{v}\rangle : v\)кв = 1 : 1,13 : 1,22. Самі ж величини характеристичних швидкостей для газів при кімнатній температурі (~ 300 К) мають 102 ÷ 103 м/с. До прикладу, для кисню О2 \(\langle{v}\rangle\approx \) 450 м/с, а для водню H2 — 900 м/с.
Зведений розподіл молекул за швидкостями. У деяких випадках розгляд задач, пов’язаних із розподілом молекул по швидкостях, спрощується, якщо користуватися безрозмірною зведеною швидкістю молекул \({u=v/v_i}\). Тоді кількість молекул dN із швидкостями в заданому інтервалі значень, яка визначається формулою (3.1), через функцію розподілу \({f(u)}\) виражається, як \({Nf(u)\mathrm{d}u}\). Отже, \({f(v)\mathrm{d}v}={f(u)\mathrm{d}u}\) , звідки
|
\({f(u)}=f(v)\cdot\frac{\mathrm{d}v}{\mathrm{d}u}=f(v) v_i \). |
(3.17) |
Зробивши у виразі \({f(v)}\) (3.13) заміну \({v=uv_i}\) і врахувавши (3.14), із співвідношення (3.17) отримаємо зведену функцію розподілу \({f(u)}\):
|
\({f(u)}=\frac{4}{\sqrt{\pi}}\cdot{u^2}e^{-u^2}\). |
(3.18) |
Розподіл молекул за кінетичними енергіями. Кількість молекул із кінетичними енергіями в заданому інтервалі значень dE дорівнює кількості молекул із швидкостями у відповідному інтервалі \(\mathrm{d}v\), отже \({f(E)\mathrm{d}E}=f(v)\mathrm{d}{v}\), де \({E=mv^2/2}\). Тому, врахувавши (3.13), і зробивши заміни \({v}=\sqrt{2E/m}\) та \(\mathrm{d}E=mv\mathrm{d}v \) , знайдемо функцію розподілу молекул за кінетичними енергіями поступального руху:
|
\({f(E)}=\frac{2\pi}{(\pi kT)^{3/2}}\cdot\sqrt{E}e^{-\frac{E}{kT}}\). |
(3.19) |
За допомогою цієї функції розподілу та виразу (3.9) можна визначити середню енергію поступального руху молекули:
|
\(\langle{E}\rangle=\frac{2\pi}{(\pi kT)^{3/2}}\int\limits_0^{\infty}E\sqrt{E}e^{-\frac{E}{kT}}\mathrm{d}{E}\). |
(3.20) |
Цей інтеграл зводиться до табличного і дає результат:
|
\(\langle{E}\rangle=\frac{3}{2}{kT}\), |
(3.21) |
що співпадає з (1.2). Цей результат можна також отримати, виходячи з того, що
\(\langle{E}\rangle=\frac{m\left\langle{v^2}\right\rangle}{2}=\) 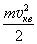 ,
,
і врахувавши вираз (3.16).
За допомогою розподілу Максвелла також можна строго вивести вирази (2.2) і (2.2а) для тиску ідеального газу, і, з урахуванням (3.21), теоретично вивести рівняння стану ідеального газу (2.3) і (2.6), а також і всі наслідки, що випливають з них.
Дослідна перевірка розподілу Максвелла. Всі теоретичні прогнози, про які щойно говорилося, справджуються на дослідіі, що доводить правильність розподілу Максвелла. Але існують і прямі способи його дослідної перевірки. Розглянемо той, що був здійснений Ламмертом.
|
|
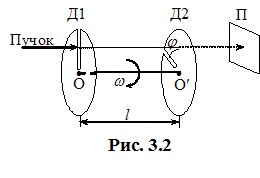
Схема досліду Ламмерта така.У камеру з малим отвором уміщують досліджувану речовину (метал) і підіймають температуру вище точки плавлення. Як наслідок, у камері створюється достатня кількість пари даного металу, котру можна вважати ідеальним газом. З атомів, що вилітають через отвір, за допомогою діафрагм[6] формують вузький і практично нерозбіжний пучок, який спрямовують на вимірювальну установку, схематично показану на рис. 3.2. Вона складається з двох дисків Д1 і Д2, жорстко закріплених на спільній, паралельній до пучка осі ОО′, та скляної пластинки П, на якій осаджуються атоми, що пройшли крізь установку. В дисках зроблені вузькі радіальні прорізи, що зміщені на невеликий кут φ ~ 1° один відносно одного. Відстань \({l}\) між дисками заздалегідь вимірюють. Поки диски нерухомі, всі атоми, що проходять крізь щілину в диску Д1, повністю затримуються диском Д2. Але, коли диски почати обертати з необхідною кутовою швидкістю \({\omega}\) у показаному на рис. 3.2 напрямку, певна частина атомів пройде крізь прорізи в обох дисках і осяде на пластинці П. Зрозуміло, що пройдуть тільки ті атоми, для яких час прольоту \({\tau}\) від першого диска до другого співпаде з часом повороту дисків на кут \({\varphi}\). Це дозволяє знайти швидкість \({v}\) таких атомів. Оскільки \({l=v\tau}\) і \(\varphi=\omega\tau \), то
\({v}=\frac{l}{\varphi}\cdot\omega \).
Таким чином, кожному значенню \(\omega \) відповідає цілком визначена швидкість атомів, які проходять крізь обидва диски. Ці молекули осідають на пластинці П і створюють на ній тонкий напівпрозорий шар, товщина і прозорість якого прямо пов’язані з кількістю атомів, що осіли. Тому, обертаючи диски з різними кутовими швидкостями протягом однакового проміжку часу і, вимірюючи ступінь почорніння пластинок П, отримують залежність відносної кількості атомів у пучку від швидкості їх руху, тобто - функцію розподілу. Результати таких вимірювань, як й інші подібні досліди, повністю узгоджуються з Максвеллівським законом розподілу молекул за швидкостями.
Барометрична формула. Уявімо дуже високий вертикальний циліндр із газом, на молекули якого діє однорідна сила тяжіння, і температура в якому скрізь однакова.
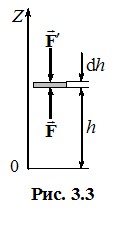
Виділимо на висоті h від основи циліндра шар газу гранично малої товщини dh (рис. 3.3). Цей шар, як і весь газ, перебуває в механічній рівновазі. Отже, сила тиску газу на нижню основу цього шару \(\vec{F}\) зрівноважує силу \(\vec{F}' \), яка створюється силою тиску газу на верхню основу шару та його вагою:
|
\({F=F^{\prime}}\) \( \Rightarrow \) \( {P}S=(P+\mathrm{d}P)S+\mathrm{d}m\cdot{g}\) \( \Rightarrow \) \( {S}\mathrm{d}P=-g\mathrm{d}m \), |
(3.22) |
|
|
|
де S - площа основи циліндра, dт - маса газу в шарі dh, Р і Р + dР - тиск газу на рівні нижньої та верхньої основи шару, відповідно. (Величина dР < 0, оскільки з висотою тиск зменшується). Маса газу в шарі визначається його густиною ρ і об’ємом dV = Sdh: \(\mathrm{d}m=\rho{S}\mathrm{d}h \). Відтак вираз (3.22) набуває вигляду
|
\({\mathrm{d}P}=-\rho{g}{\mathrm{d}h}\). |
(3.23) |
Згідно з рівнянням Клапейрона (2.6), густина газу
\(\rho=\frac{\mathrm{d}m}{\mathrm{d}V}=\frac{PM}{RT}\),
де М - молярна маса газу, Т - його температура, R - універсальна газова стала. Підставляючи цей вираз у (3.23), після інтегрування отримуємо:
|
\( \frac{\mathrm{d}P}{P}=-\frac{Mg}{RT}\mathrm{d}{h}\) \( \Rightarrow \) \( \ln{\frac{P}{P_{0}}}=-\frac{Mg}{RT}\cdot{h}\). |
(3.24) |
Звідси
|
\( {P}=P_0 e^{-\frac{Mg}{RT}h}\), |
(3.25) |
де \( {P_0}\) - тиск біля основи циліндра (при h = 0).
Отримана залежність тиску газу від висоти стовпа (3.25) називається барометричною формулою. Із застереженнями її можна застосовувати й до земної атмосфери, розглядаючи \( {P_0}\) як тиск на рівні моря. Ці застереження такі. Повітря є сумішшю різних газів, тому молярну масу М слід розглядати як усереднену величину, що враховує відсотковий вміст у повітрі різних газів, а тиск Р – як суму парціальних тисків компонент \( {P_i}\). Але для компонент повітря з різними молярними масами \( {M_i}\) тиски \( {P_i}\) і концентрації молекул \({n_i}=P_i/{kT}\), згідно з (3.25), мають по-різному змінюватися з висотою - важчі швидше, ніж легші. Тому вміст компонентів і молярна маса повітря М мали би залежати від висоти h. Насправді цього не спостерігається, позаяк земна атмосфера не є ізотермічною. Температура повітря зменшується з висотою й неоднорідно розподіляється по поверхні Землі. Через це в атмосфері постійно циркулюють потужні повітряні потоки, які й вирівнюють співвідношення концентрацій компонентів повітря на різних висотах. Проте зміна температури повітря з висотою є суттєвою – на висоті 10 - 20 км вона на десятки градусів нижча, ніж на рівні моря. Тому барометрична формулу (3.25) для земної атмосфери є принципово неточною. Але, оскільки на рівні моря температура складає ~ 300 К, відносна зміна температури з висотою є порівняно невеликою, як і спричинена нею неточність формули (3.25). Тому за допомогою барометра, що проградуйований не в одиницях тиску, а в одиницях відстані, можна досить точно визначати висоту. Такі прилади називаються альтиметрами й використовуються на практиці, зокрема, в авіації.
Розподіли Больцмана та Максвелла-Больцмана. У випадку однорідного газу M = mNA (m - маса молекули), а, згідно з (2.3), P = nkT (п - концентрація молекул). Окрім того R = kNA. Зробивши такі підстановки в (3.25), отримаємо залежність концентрації молекул від висоти:
|
\({n=}n_0 e^{-\frac{mgh}{kT}}\) \( \Rightarrow \) \( {n}=n_0 e^{-\frac{E_n}{kT}}\), |
(3.26) |
де \({E_n=mgh}\) - потенціальна енергія молекули в полі сил тяжіння, \({n_0}\) - концентрація молекул на нульовому рівні енергії h = 0. Корисно відмітити, що така залежність концентрації молекул від висоти зумовлена протиборством між двома протилежними тенденціями – тепловим рухом, який намагається “розкидати” молекули рівномірно по всьому об’єму циліндра, та силою тяжіння, що намагається “опустити” всі молекули на дно циліндра.
Л. Больцман довів, що формула (3.26) є чинною не лише для поля сил тяжіння, а й для будь-якого іншого потенціального поля. Тому (3.26) є функцією розподілу частинок за потенціальними енергіями. Вона називається розподілом Больцмана. Оскільки потенціальна енергія частинки в заданому полі визначається тільки її координатами: Eп = Еп(x, y, z) , розподіл Больцмана по суті є розподілом частинок по координатах у силовому полі. Відповідно до цього, кількість частинок dN = ndV в об’ємі dV = dxdydz в околі точки з координатами (x, y, z) визначається, як
|
\(\mathrm{d}N_{x,y,z}=n_0 e^{-\frac{E_n(x,y,z)}{kT}}\mathrm{d}x\mathrm{d}y\mathrm{d}z \). |
(3.27) |
Слід зауважити, що через дуже малу масу молекул (~10-26 кг) помітне зменшення концентрації молекул повітря в полі сил тяжіння спостерігається лише на великих висотах[7]. За таких умов атмосферу не можна вважати ізотермічною, тому безпосередньо експериментально перевірити формули (3.25) і (3.26) неможливо. Але це можна зробити, досліджуючи розподіл за висотою броунівських частинок - дуже малих (~10-7 м) твердих частинок, які зважені в рідині. Броунівські частинки внаслідок ударів з боку молекул рідини здійснюють неупорядкований рух, який відображає тепловий рух молекул рідини. Тому броунівські частинки можна розглядати як гігантські молекули і вважати, що для них є чинними розподіли Максвелла та Больцмана. Такі досліди, що їх виконав Перрен, підтвердили правильність теоретичної формули (3.27) і дозволили експериментально визначити сталу Авогадро.
Розподіл Больцмана (3.27) та розподіл Максвелла (3.12) можна об’єднати в більш загальний розподіл Максвелла-Больцмана, який дозволяє визначати кількості молекул, які знаходяться в заданій елементарній області простору (точці) і мають задану величину та напрям швидкості теплового руху. Вираз (3.27) визначає у кожному місці кількість частинок \(\mathrm{d}N_{x,y,z}\) із будь-якими швидкостями. З цієї кількості, відповідно до (3.11), задану величину й напрям швидкості мають \(\mathrm{d}N_{v_x,v_y,v_z,x,y,z}=\mathrm{d}N_{x,y,z}f(v_x,v_y,v_z)\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z \) частинок. Підставивши сюди вирази (3.27) і (3.12), отримаємо
|
|
(3.28) |
або
|
\(\mathrm{d}N_{v_x,v_y,v_z,x,y,z}=n_0\left(\frac{m}{2\pi{kT}}\right)^{\frac{3}{2}}e^{-\frac{E_k+E_n}{kT}}\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z\mathrm{d}x\mathrm{d}y\mathrm{d}z \), |
(3.28а) |
де \({E_k}\) - кінетична енергія частинки.
Вираз (3.28), чи (3.28а) називається розподілом Максвелла-Больцмана. Він визначає кількість частинок маси т із концентрацією n0, швидкості яких за величиною й напрямом нескінченно мало відрізняються від заданого значення і які знаходяться в заданій елементарній області простору (точці).
2. Покажіть на одному кресленні вигляд функції розподілу за швидкостями \({f(v)}\) для водню Н2 та гелію Не при однаковій температурі. Як співвідносяться положення максимумів \( v_1 : v_2 \) та “висоти” піків на графіках \({f(v)}\)?
3. Виходячи з розподілу молекул за модулем швидкості (3.13), отримати функцію розподілу молекул за енергіями (3.19).
4. Виходячи з розподілу молекул за енергіями (3.19), отримати функцію розподілу молекул за модулем швидкості (3.13).
5. Як за допомогою функції розподілу молекул за швидкостями (3.13) можна знайти середню кінетичну енергію поступального теплового руху молекул \(\langle{E}\rangle \)? Як це можна зробити за допомогою функції розподілу молекул за енергіями (3.19)?
6. Знайдіть за допомогою функції розподілу молекул за енергіями (3.19) найбільш імовірну енергію поступального теплового руху молекули.
7. Чи можна при визначепнні атмосферного тиску на деякій висоті h розглядати величину P0 у формулі (3.25) як тиск не на рівні моря, а на довільній висоті H0?
8. При кімнатній температурі молекули газу не осідають на дно, а практично рівномірно розподіляються по всьому об’єму посудини, бо можуть долати сили тяжіння за рахунок кінетичної енергії теплового руху. А як буде при дуже низькій температурі? Перевірте для гелію (M = 4·10-3 кг/моль) при температурі Т = 5 К і нормальному атмосферному тиску.
9. Чому на легких планетах немає атмосфери?
10. Чому в атмосфері Землі кількість водню складає дуже малу частку від кількості кисню, попри те, що загальні кількості Гідрогену та Оксигену на планеті є сумірними?
11. Як би змінювався із часом відсотковий склад атмосфери Землі, якби вона не поповнювалася за рахунок природних і техногенних процесів?
[1] Замість швидкості можна говорити й про будь-який інший мікропараметр системи, наприклад, про імпульс або енергію окремої молекули.
[2] Більш точна, на перший погляд, постановка задачі про кількість молекул, які мають задане значення швидкості насправді є некоректною. Кількість молекул у системі хоча й велика, проте скінченна, тому цілком може статися, що якогось заданого точного значення швидкості не має жодна з них.
[3] Те, що замість граничної швидкості с використовують ∞, є лише зручним формальним прийомом, який спрощує обчислення. Це зумовлено тим, що підінтегральна функція f(v) досить швидко спадає при великих швидкостях, і її вклад в інтеграл стає несуттєвим задовго до досягнення значень v ~ c.
[4] Точніше - молекули, для яких модулі та напрямки вектора швидкості гранично мало відрізняються від заданих значень.
[5] Див., напр, Г.Б.Двайт “Таблицы интегралов”, М., “Наука”, 1977.
[6] Пластинки з малим отвором, які розміщується напроти отвору печі.
[7] До прикладу, на висоті 100 м тиск і концентрація молекул повітря всього на 1 % менші, ніж на рівні моря.
IV. ПЕРШЕ НАЧАЛО ТЕРМОДИНАМІКИ
Викладені вище відомості про властивості газів добре ілюструють сутність і можливості молекулярно-кінетичного (статистичного) методу (МКТ). Але, як вже говорилося, в молекулярній фізиці широко використовується й термодинамічний метод дослідження, що ґрунтується на декількох основних законах – началах термодинаміки. Ці закони, встановлені дослідним шляхом, відображають такі зв’язки між макроскопічними характеристиками системи, які не пов’язані з її мікроскопічною будовою. Тому закони термодинаміки та всі наслідки, що з них випливають, є універсальними, тобто, чинними для будь-яких систем. Слід також зауважити, що закони термодинаміки мають не лише теоретичне, а й велике практичне значення, оскільки лежать в основі отримання та використання людством різних видів енергії[1].
У термодинаміці, крім параметрів стану, використовують й інші термодинамічні величини. Найперше це стосується внутрішньої енергії, теплоти та роботи.
Нижче розглянуті наступні питання:
2. Макроскопічна робота та теплота
У широкому розумінні до внутрішньої енергії довільної фізичної системи входять усі види енергії, крім кінетичної енергії руху системи як цілого та її потенціальної енергії у зовнішніх полях. Стосовно речовини внутрішня енергія включає кінетичну енергію руху молекул відносно центра мас системи (інакше – теплового руху), потенціальну енергію взаємодії між молекулами, а також енергію руху та взаємодії атомів усередині молекули.
Внутрішня енергія одноатомного ідеального газу. В найпростішій термодинамічній системі - одноатомному ідеальному газі – внутрішня енергія U складається тільки з кінетичної енергії теплового руху атомів і дорівнює добутку кількості частинок N на середню кінетичну енергію однієї частинки \(\langle{E}\rangle\) . Згідно з (1.1), (1.1а), (1.2), (2.5),
|
\({U}=\frac{3}{2}\nu{RT}=\frac{3}{2}\cdot\frac{m}{M}{RT}\). |
(4.1) |
Для одного моля
|
\({U}=\frac{3}{2}{RT}\). |
(4.1а) |
Урахувавши рівняння Клапейрона (2.6), маємо ще один вираз U:
|
\({U}=\frac{3}{2}{PV}\). |
(4.2) |
Записані вирази відображають дуже важливу властивість внутрішньої енергії не лише ідеального газу, а й будь-якої іншої термодинамічної системи. Ця властивість полягає в тому, що
внутрішня енергія однозначно визначається параметрами стану системи.
Відповідно, зміна внутрішньої енергії системи в будь-якому процесі визначається тільки зміною параметрів стану. До прикладу, при переведенні одноатомного газу зі стану 1 (\({P_1,\,V_1,\,T_1,\,}\)) у стан 2 (\({P_2,\,V_2,\,T_2}\)) зміна внутрішньої енергії складає
|
\(\Delta{U}=U_1-U_1=\frac{3}{2}\cdot\frac{m}{M}R(T_2-T_1)=\frac{3}{2}\cdot\frac{m}{M}R\Delta{T}\) |
(4.3) |
або
|
\(\Delta{U}=\frac{3}{2}(P_2 V_2-P_1 V_1) \). |
(4.3а) |
Отже, зміна внутрішньої енергії не залежить від процесу, тобто, способу переведення системи з одного стану в інший. Тому говорять, що
внутрішня енергія є функцією стану системи.
Ступені свободи. Молекули одноатомного ідеального газу не мають якоїсь конфігурації й можуть рухатися тільки поступально. У випадку складніших молекул при визначенні внутрішньої енергії необхідно враховувати й інші види їхніх рухів як цілого, а також рухи та взаємодію атомів усередині молекули. Для цього використовують поняття кількості ступенів свободи.
Кількістю ступенів свободи і системи (молекули) називається кількість незалежних координат, яка є необхідною для однозначного визначення положення молекули в просторі.
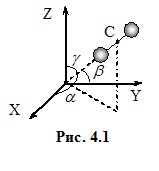
Зміна координат означає рух, отже, можна сказати, що кількість ступенів свободи молекули визначає кількість різних рухів, які вона може здійснювати. До прикладу, поступальний рух тіла визначається зміною з часом трьох координат центра мас. Відповідно, кожна молекула, в тому числі й одноатомна, має iп = 3 поступальні ступені свободи. Для визначення положення жорсткої лінійної молекули[2] (рис. 4.1), окрім положення центра мас, необхідно вказати напрям її осі. Для цього треба задати ще дві координати, наприклад, кути α і β, що їх утворює вісь молекули з двома осями декартової системи (третій кут γ однозначно визначається через два інших умовою: cos2α + cos2β + cos2γ = 1). Зміна цих кутів визначає обертання молекули навколо двох осей, перпендикулярних до осі молекули[3]. Тому жорстка лінійна молекула має iоб = 2 обертальні ступені свободи й повну кількість ступенів свободи i = iп + iоб = 5.
|
|
У випадку жорсткої молекули, що складається з трьох і більше атомів, які не лежать на одній осі, є ще один можливий рух - обертання навколо осі, що проходить через будь-які два атоми. Тому багатоатомна жорстка молекула має iоб = 3 обертальні ступені свободи й повну кількість ступенів свободи і = 6. Якщо в системі з N частинок між ними немає жорсткого зв’язку, то положення кожної частинки треба задавати окремо, через що повна кількість ступенів свободи системи і = 3N. Ця кількість, окрім поступальних і обертальних ступенів свободи, що визначають рух системи як цілого, включає також ступені свободи, які пов’язані з рухом частинок системи відносно центра мас. Як відзначалося на початку цього розділу (п. 1.3), атоми в молекулах зв’язані пружними силами й здійснюють коливальний рух, тому вказані додаткові ступені свободи молекул називаються коливальними. Кількість коливальних ступенів свободи дорівнює різниці між повною кількістю ступенів свободи молекули та сумарною кількістю поступальних і обертальних ступенів свободи: iкол = i - (iп + iоб) . Коливальні ступені свободи молекули визначаються кількістю та конфігурацією атомів, із яких вона складається. При цьому для лінійної молекули з N атомів iкол = 3N - 5, а для всіх інших конфігурацій iкол = 3N - 6. Наприклад, для двохатомної пружної молекули кількість коливальних ступенів свободи iкол = 3·2 - 5 = 1, для трьохатомної лінійної iкол = 3·3 - 5 = 4, а для трьохатомної “трикутної” - iкол = 3·3 - 6 = 3.
Розподіл енергії за ступенями свободи. Згідно з (1.2), середня кінетична енергія поступального руху одноатомної молекули (матеріальної точки) дорівнює
\(\langle{E_n}\rangle=\frac{i_n}{2}{kT}\),
де \({i_n = 3}\) - кількість поступальних ступенів свободи. Отже, на кожен поступальний ступінь свободи припадає середня кінетична енергія, що дорівнює kT/2. Л. Больцман довів, що це вірно й для кінетичної енергії обертального та коливального руху частинок. У цьому полягає класичний закон рівнорозподілу енергії по ступенях свободи:
у стані термодинамічної рівноваги на кожен ступінь свободи системи припадає однакова середня кінетична енергія
\(\langle{E_1}\rangle=\frac{1}{2}{kT}\).
Це зводить проблему визначення внутрішньої енергії довільної системи до підрахунку кількості її ступенів свободи. Правда, розглядаючи внесок в енергію рухів атомів усередині молекули, треба враховувати не лише кінетичну, а й потенціальну енергію їхньої взаємодії. Але це не складно, оскільки коливання атомів у молекулах близькі до гармонічних, а за таких умов середні значення кінетичної та потенціальної енергії коливань виявляються однаковими. Тож середня енергія, що припадає на один коливальний ступінь свободи, дорівнює двом половинкам kT. Через це, при підрахунках, кількість коливальних ступенів свободи подвоюють і обчислюють середню енергію молекули за загальною формулою
|
\(\langle{E}\rangle=\frac{i}{2}{kT}\), |
(4.4) |
де величина і визначається виразом:
|
\({i = i_n+i}\)об + \({2i}\)кол. |
(4.5) |
Відповідно до сказаного, для визначення внутрішньої енергії довільного ідеального газу в (4.1), (4.1а) і (4.2) трійку треба замінити на \({i}\):
|
\({U}=\frac{i}{2}\nu{RT}=\frac{i}{2}\cdot\frac{m}{M}{RT}\), |
(4.6) |
|
|
\({U_m}=\frac{i}{2}{RT}\), |
(4.6а) |
|
|
\({U}=\frac{i}{2}{PV}\). |
(4.7) |
Для інших термодинамічних систем, зокрема для реальних газів, ці формули не підходять, оскільки вони не враховують потенціальну енергію взаємодії між молекулами.
2. Макроскопічна робота та теплота
Фізичні процеси завжди супроводжуються обміном енергією між тілами та її перетвореннями з одних видів на інші. Зокрема, в термодинамічних процесах, за винятком ізотермічних, змінюється внутрішня енергія системи. Внутрішню енергію можна змінювати різними конкретними способами, але є тільки дві різні причини такої зміни. Це – виконання макроскопічної роботи та теплообмін.Макроскопічна робота. Добре відомо, що при швидкому стисканні газу в циліндрі під поршнем його температура, отже й внутрішня енергія, значно зростає[4]. Це пояснюється тим, що при русі поршня молекули газу після зіткнення з ним отримують додатковий імпульс і відлітають із більшими швидкостями, ніж підлітають. З іншого боку, для стискання газу до поршня має бути прикладена зовнішня сила, яка при переміщенні поршня виконує відповідну макроскопічну роботу[5].
|
|
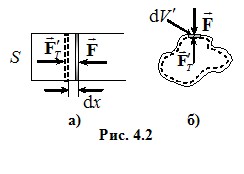
Розглянемо стискання газу в циліндрі з поршнем площею S під дією зовнішньої сили \(\vec{F}\) (рис 4.2 а), вважаючи, що стискання відбувається квазістатично (рівноважно). При переміщенні поршня на нескінченно малу відстань dx сила F виконує елементарну роботу δA′ = Fdx. Оскільки процес є рівноважним, зовнішня сила за модулем дорівнює силі тиску газу на поршень Fт = PS (Р - тиск). Отож, F = PS, і робота δA′ = PSdx, або
|
δA = – PdV, |
(4.8) |
dV - зміна об’єму газу, знак “-” стоїть тому, що δA′ > 0, коли dV < 0, і навпаки. Відповідно, газ виконує таку саму по модулю, але протилежну за знаком роботу
|
δA = – δA′ = PdV. |
(4.8а) |
Отримані вирази є чинними й у загальному випадку. Це легко довести. Нехай газ міститься в еластичній оболонці довільної форми (рис 4.2 б). При нескінченно малому переміщенні dl якоїсь однієї елементарної ділянки оболонки площею dS газ виконує роботу PdV′, де dV′ = dS·dl - часткова зміна об’єму газу, зумовлена переміщенням цієї ділянки. Оскільки тиск газу в усіх точках однаковий, робота, зумовлена елементарним переміщенням усіх ділянок δA = PdV, де dV – сума всіх dV′, тобто елементарний приріст об’єму всього газу. Отже, в термодинаміці робота пов’язана не з переміщенням системи як цілого, а із зміною її об’єму, тобто – із переміщенням стінок, які відокремлюють систему від оточення.
У процесі стискання або розширення газу тиск, на загал, не лишається сталим. Тому при скінченній зміні об’єму газу робота зовнішніх сил A′ та робота газу A визначаються інтегруванням виразів (4.8) і (4.8 а):
|
A′ = \( -\int{P\mathrm{d}V}\). |
(4.9) |
|
|
\({A}=\int{P\mathrm{d}V}\). |
(4.9а) |
Обчислення роботи газу в різних процесах.
В ізохорному (V = const) процесі dV = 0, і робота не виконується: δA = 0.
В ізобарному процесі Р = const і при зміні об’єму від V1 до V2 газ, згідно з (4.9), виконує роботу
|
\({A}=\int\limits_{V_1}^{V_2}P\mathrm{d}V=P\int\limits_{V_1}^{V_2}\mathrm{d}V \) \(\Rightarrow \) \({A}=P(V_2-V_1)=P\Delta{V}\). |
(4.10) |
Робота зовнішніх сил над газом визначається, як
|
A′ = P(V1 - V2) = –PΔV. |
(4.10а) |
За допомогою рівняння Клапейрона (2.6) роботу газу в ізобарному процесі можна виразити й через зміну температури:
|
\({A}=\nu{R}(T_2-T_1)=\nu{R\Delta{T}}\). |
(4.10б) |
В ізотермічному процесі Т = const. Урахувавши це та, підставивши в (4.9) вираз тиску з рівняння Клапейрона (2.6), отримаємо для роботи газу при ізотермічній зміні об’єму від V1 до V2:
|
\({A}=\nu{RT}\int\limits_{V_1}^{V_2}\frac{\mathrm{d}V}{V}=\nu{RT}\ln\frac{V_2}{V_1}=\frac{m}{M}{RT}\ln\frac{V_2}{V_1}\). |
(4.11) |
Оскільки в ізотермічному процесі PV = const, можна також записати:
\({A}=\nu{RT}\ln\frac{P_1}{P_2}=\frac{m}{M}{RT}\ln\frac{P_1}{P_2}\).
Робота зовнішніх тіл над газом при незмінній температурі, відповідно до (4.9), виражається як
|
A′ = \(\nu{RT}\ln\frac{V_1}{V_2}\). |
(4.11а) |
|
|
|
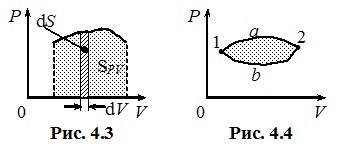
Термодинамічна робота має простий геометричний зміст. На рис. 4.3 показано графік якогось процесу на діаграмі Р-V (“у координатах” (P, V)). Видно, що при нескінченно малій зміні об’єму робота газу δA = PdV чисельно дорівнює площі dS смужки ширини dV під графіком процесу. Так само, робота при скінченній зміні об’єму від V1 до V2 чисельно дорівнює всій площі S під відповідною ділянкою графіка процесу на діаграмі (P, V):
A = SPV.
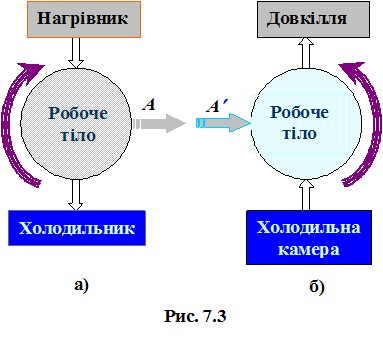
Такий геометричний підхід, звичайно, не знімає необхідності обчислення інтегралів (4.9) при визначенні роботи (крім випадку лінійної залежності P(V)), але він є дуже зручним для якісного аналізу термодинамічних процесів. Наприклад, він дозволяє легко зрозуміти важливу обставину: на відміну від внутрішньої енергії, макроскопічна робота не є функцією стану системи, оскільки залежить від способу переведення системи з початкового стану в кінцевий. Це добре видно з рис. 4.4: роботи, виконані при переході системи із стану 1 в стан 2 у процесах 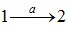 та
та 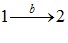 не однакові й відрізняються на величину, що чисельно дорівнює площі заштрихованої області на графіку. Тому говорять, що
не однакові й відрізняються на величину, що чисельно дорівнює площі заштрихованої області на графіку. Тому говорять, що
макроскопічна робота є функцією процесу.
Теплота. Внутрішня енергія може змінюватись і без виконання роботи, наприклад, при безпосередньому контакті тіл із різною температурою.
Процес переходу внутрішньої енергії від одних тіл до інших без виконання макроскопічної роботи називається теплообміном.
У процесі теплообміну частина внутрішньої енергії гарячого тіла переходить до холодного за рахунок зіткнень між більш швидкими молекулами гарячого тіла з повільнішими молекулами холодного. Отже, можна сказати, що при теплообміні внутрішня енергія змінюється за рахунок мікроскопічної роботи, що виконується на рівні окремих молекул. Слід, одначе, зауважити, що внутрішня енергія без виконання макроскопічної роботи може змінюватися й за рахунок випромінювання, та при зміні агрегатного стану речовини (плавлення - тверднення, пароутворення - конденсація), або в хімічних реакціях (як от при горінні).
Величина внутрішньої енергії, яку отримує або втрачає система без виконання макроскопічної роботи називається кількістю теплоти Q.
Дослід свідчить, що для зміни внутрішньої енергії системи на задану величину в різних процесах потрібна не однакова кількість теплоти. Тому, як і робота,
кількість теплоти є функцією процесу.
Формулювання першого начала термодинаміки. Як видно з попереднього, коли не виконується макроскопічна робота (A′ = 0), то зміна внутрішньої енергії системи дорівнює отриманій нею кількості теплоти: ΔU = Q. При виконанні макроскопічної роботи внутрішня енергія також змінюється. Дослідним шляхом установлено, що за відсутності теплообміну зміна внутрішньої енергії системи точно дорівнює виконаній над нею макроскопічній роботі: ΔU = A′ при Q = 0. Отже, у загальному випадку
|
ΔU = Q + A′. |
(4.12) |
Це рівняння виражає перше начало термодинаміки:
зміна внутрішньої енергії довільної термодинамічної системи дорівнює сумі отриманої системою теплоти та виконаної над нею макроскопічної роботи.
Перше начало термодинаміки є законом збереження енергії, узагальненим на теплові процеси.
Для елементарного процесу (тобто, гранично малої зміни стану системи) перше начало записується так:
|
dU = δQ + δA′, |
(4.12а) |
де dU - приріст внутрішньої енергії системи, δQ і δA′ - елементарна кількість теплоти, отримана системою, та елементарна робота, виконана над нею зовнішніми тілами. Слід зауважити, що всі величини в рівняннях (4.12) і (4.12а) є алгебраїчними. Наприклад, якщо система при теплообміні передає енергію іншим тілам, то δQ < 0. Так само, якщо об’єм системи збільшується, то δA < 0.
Рівняння (4.12) і (4.12а) можна записати інакше, якщо в (4.12) і (4.12а) зовнішню роботу замінити на роботу самої системи, згідно з (4.8а). Тоді
|
δQ = dU + δA, |
(4.13) |
|
|
Q = ΔU + A. |
(4.13а) |
Відповідно до цього, можна дати інше формулювання першого начала термодинаміки:
кількість теплоти, передана системі, йде на зміну її внутрішньої енергії та на виконання системою роботи над зовнішніми тілами.
У такій редакції перше начало термодинаміки прямо вказує на можливість виконання системою макроскопічної, тобто механічної, роботи за рахунок теплової енергії. Інакше говорячи, перше начало вказує на принципову можливість перетворення енергії невпорядкованого теплового руху молекул на механічну енергію, тобто енергію руху макроскопічних тіл. На цьому ґрунтується робота так званих теплових двигунів, які складають переважну більшість двигунів, що використовуються людиною.
Історично у становленні термодинаміки як науки вирішальну роль відіграли саме дослідження, спрямовані на підвищення ефективності теплових двигунів. У цьому зв’язку принциповим є висновок, який прямо випливає з (4.13) і показує неможливість так званого вічного двигуна першого роду - пристрою, котрий міг би необмежено довго виконувати роботу, не отримуючи енергію ззовні. Справді, для будь-якої системи, що не отримує енергії від інших тіл або навколишнього середовища, перше начало термодинаміки (4.13а) набуває вигляду
ΔU + A = 0 \(\Rightarrow \) A = –ΔU = U0– Uк,
де U0 і Uк – початкова та кінцева внутрішня енергія системи, відповідно. Звідси очевидно, що максимальна робота, яку міг би виконати будь-який двигун, навіть теоретично, не може перевищити його початкову внутрішню енергію: Amax = U0. Отже, жоден двигун не може бути “вічним”, він за будь-яких умов не зможе працювати довше, ніж доки вистачить запасу внутрішньої енергії[6]. Цей висновок є настільки принциповим, що його розглядають як третє формулювання першого начала термодинаміки:
вічний двигун першого роду є неможливим.
Термодинаміка ізопроцесів. За допомогою першого начала термодинаміки можна з’ясувати істотні деталі стосовно умов здійснення та перебігу різних процесів у термодинамічних системах, зокрема, в газах. Для цього запишемо рівняння (4.13) розлогіше, врахувавши вираз для роботи системи (4.8а), і застосуємо його до різних ізопроцесів.
|
δQ = dU + PdV. |
(4.14) |
1. Ізотермічний процес (Т = const). У цьому процесі, згідно з (4.6) і (4.7), внутрішня енергія не змінюється. Тому в рівнянні (4.12 а) dU = 0, і
|
δQT = PdV = δA і QT = A. |
(4.15) |
Отже, в ізотермічному процесі вся надана системі теплота йде на виконання системою макроскопічної роботи, тобто, перетворюється на механічну енергію. При цьому виникає резонне запитання: яким чином система, отримуючи певну кількість внутрішньої енергії у формі теплоти δQ, зберігає свою температуру незмінною? При довільній зміні об’єму, дійсно, так не може бути. Але, якщо газ помістити в циліндр з ідеально теплопровідними стінками, і проводити процес квазістатично (гранично повільно), то температура скрізь буде лишатись однаковою й рівною температурі навколишнього середовища, тобто такий ідеалізований процес буде строго ізотермічним. Стискання або розширення газу за реальних умов завжди відбувається зі скінченною швидкістю, а стінки циліндра мають скінченну теплопровідність. Тому практично можна здійснювати лише наближено ізотермічні процеси.
2. Ізохорний процес (V = const). У цьому процесі робота не виконується (dV = 0), і перше начало термодинаміки (4.12а) набуває вигляду
|
δQV = dU, |
(4.16) |
або, для скінченних величин,
|
QV = ΔU = U2–U1. |
(4.16а) |
Таким чином, позаяк у газі ізохорний процес здійснюється в циліндрі із закріпленим поршнем, товнутрішня енергія змінюється лише за рахунок теплообміну при контакті системи із більш гарячими чи більш холодними тілами, або за рахунок випромінювання.
3. Ізобарний процес (Р = const). Такий процес у газі завичай здійснюється шляхом повільного нагрівання або охолодження газу в циліндрі, закритому рухомим поршнем. За таких умов газ або розширюється, або стискається так, що його тиск весь час лишається сталим і рівним сумі зовнішнього тиску на поршень і тиску, що створюється його вагою. Тому в ізобарному процесі не лише змінюється внутрішня енергія системи, а й виконується робота. Процес іде відповідно до рівняння (4.10), і, згідно з (4.12 а),
|
QP = ΔU + PdV, або QP = U2 – U1 + P(V2 - V1). |
(4.17) |
1. Чи зміниться внутрішня енергія газу в закритій посудині, якщо вона почне швидко рухатися?
2. Говорять, що внутрішня енергія є функцією стану системи, а робота та теплота – функціями процесу. Що означають ці вислови?
3. Скільки обертальних і скільки коливальних ступенів свободи має лінійна молекула вуглекислого газу О-С-О та молекула води, в якій атоми утворюють трикутник?
4. Який відсоток від повної енергії складає енергія поступального теплового руху в жорсткій та в пружній двохатомній молекулі?
5. Які існують способи зміни внутрішньої енергії системи? Що таке “кількість теплоти”?
6. В якому процесі вся отримана системою теплота йде на зміну внутрішньої енергії?
7. В якому процесі вся отримана системою теплота перетворюється на механічну роботу?
8. Коли для підвищення температури заданої кількості газу на задану величину ΔT доведеться витратити більше тепла, – нагріваючи газ при сталому тиску, чи при сталому об’ємі?
9. Чи може система виконувати механічну роботу за рахунок своєї внутрішньої енергії?
10. Чи можна перетворити всю внутрішню енергію системи на механічну роботу?
[1] У цьому контексті слід сказати, що основи термодинаміки заклав французький інженер С. Карно в дослідженнях, спрямованих на вдосконалення теплових двигунів.
[2] Тобто, такої, в якій атоми нерухомі відносно центра мас і розташовані на одній прямій.
[3] Говорити про обертання двохатомної молекули навколо третьої (власної) осі беззмістовно, оскільки атоми розглядаються як матеріальні точки.
[4] За рахунок цього, зокрема, відбувається самозагоряння паливної суміші в дизельних двигунах.
[5] Термін “макроскопічна робота” у термодинаміці вживають, аби відрізнити роботу, що виконується при переміщенні макроскопічних тіл (тут - поршня) від “мікроскопічної роботи”, що виконується силами взаємодії між окремими молекулами. Але коли це не викликає непорозумінь, слово “макроскопічна” опускають.
[6] Як показує друге начало термодинаміки (Лекція 7, п. 7.3), в дійсності навіть такої максимальної роботи не можна отримати.
V. ТЕПЛОЄМНІСТЬ. ПОЛІТРОПНІ ПРОЦЕСИ
Нижче мова піде про таке:
1. Теплоємності ідеального газу
1. Теплоємності ідеального газу
де δQ – отримана кількість теплоти і dT – зміни температури тіла.
Величина C0 характеризує задане тіло. Але для теорії важливо знати теплові властивості не конкретного тіла, а речовини, з якої воно складається. Для цього уводяться молярна та питома теплоємності речовини.
Молярною теплоємністю С називається теплоємність одного моля даної речовини:
|
|
(5.1) |
де \(\delta{Q_m}=\delta{Q}/\nu \) – кількість теплоти, що припадає на 1 моль, ν – кількість молів речовини, що міститься в тілі. Отже,
\({C}=\frac{C_0}{\nu}\) або \({C}=\frac{MC_0}{m}\),
де М - молярна маса речовини, т - маса тіла. Одиницею молярної теплоємності є 1 Дж/(моль·К).
Питома теплоємність с - це теплоємність одиниці маси речовини:
|
\({c}=\frac{C_0}{m}=\frac{\delta{Q}}{m\mathrm{d}T}\). |
(5.1а) |
Вона вимірюється у Дж/(кг·К) і пов’язана з молярною теплоємністю очевидним співвідношенням:
|
\({c}=\frac{C}{M}\). |
(5.2) |
У попередній лекції було з’ясовано, що в різних процесах заданій зміні внутрішньої енергії та температури тіла відповідає не однакова кількість теплоти. Тому, як і кількість теплоти,
теплоємність є функцією процесу.
Це означає, що теплоємність залежить не лише від властивостей речовини, а й від способу передачі тілу теплової енергії термодинамічній системі (“тілу”). Це випливає з першого начала термодинаміки й добре легко прослідковується в ізобарному та ізохорному процесах. Згідно з виразами (4.14) і (4.16), при наданні системі однакової кількості теплоти зміна внутрішньої енергії, тож і температури, в ізохорному процесі буде більшою, ніж в ізобарному, оскільки при незмінному об’ємі на нагрівання йде все надане тепло, а при сталому тиску – лише його частина. Інша ж частина витрачається на роботу при розширенні (зміні об’єму) тіла. Тому для збільшення температури тіла на 1 К в ізобарному процесі треба витратити більше тепла, ніж в ізохорному. Отже, для будь-якої системи теплоємності при сталому тиску CP та при сталому об’ємі CV, є не однакові, причому CP > CV. Проте, на практиці ця різниця істотна лише для газів, оскільки зміна об’єму й робота розширення при нагріванні рідин і твердих тіл є несуттєвою. Тому для рідин і твердих тіл CP і CV не розрізняють, і в довідкових таблицях їхні теплоємності наводять без указівки на процес.
Теплоємності ідеального газу CV і CP. Внутрішня енергія ідеального газу залежить тільки від температури (формули (4.6), (4.6а)). Тому його молярні теплоємності CV і CP, які посідають важливе місце в теорії, легко визначаються з першого начала термодинаміки. Згідно з означенням (5.1) та виразами (4.16) і (4.14), маємо:
|
\({C_V}=\frac{\delta{Q_V}}{\mathrm{d}T}=\frac{\mathrm{d}U}{\mathrm{d}T}\) |
(5.3) |
і
|
\({C_P}=\frac{\delta{Q_P}}{\mathrm{d}T}=\frac{\mathrm{d}U}{\mathrm{d}T}+\frac{P\mathrm{d}V}{\mathrm{d}T}\). |
(5.3а) |
Зміна внутрішньої енергії, що відповідає заданій зміні температури тіла, не залежить від процесу, то ж вираз CP можна переписати так:
|
\({C_P}=C_V+P\frac{\mathrm{d}V}{\mathrm{d}T}\), |
(5.4) |
де другий доданок визначає роботу, яку виконує 1 моль ідеального газу при ізобарному нагріванні на 1 К. Цю роботу легко визначити з рівняння Клапейрона (2.6 а) з урахуванням умови P = const:
\(\frac{\mathrm{d}V}{\mathrm{d}T}=\frac{R}{P}\) \(\Rightarrow \) \({P}\frac{\mathrm{d}V}{\mathrm{d}T}={R}\).
Отже, робота одного моля ідеального газу при його ізобарному нагріванні на 1 К чисельно дорівнює універсальній газовій сталій[2]. Таким чином, між молярними теплоємностями ідеального газу є універсальне співвідношення, яке називається рівнянням Майєра:
|
\({C_P}=C_V+R \) або \({C_P-C_V=R}\). |
(5.5) |
Що ж до самих теплоємностей, то вони залежать лише від кількості ступенів свободи молекул газу. Справді, із (5.3) і (4.6а) і (5.5) маємо:
|
\({C_V}=\frac{i}{2}{R}\) і \({C_P}=\frac{i+2}{2}{R}\), |
(5.6) |
де і – кількість ступенів свободи молекул, яка визначається виразом (4.5).
Корисно відмітити, що, згідно з отриманим виразом \({C_V}\) і формулами (4.6) і (4.6 а), внутрішня енергія ідеального газу виражається, як
|
\({U=\nu{C_V T}}\) і \({U_m}={C_V T}\). |
(5.7) |
У теорії часто використовується величина
|
\(\gamma=\frac{C_P}{C_V}\), |
(5.8) |
яка називається показником адіабати. З (5.6) випливає, що для ідеального газу
|
\(\gamma=\frac{i+2}{i}\). |
(5.8а) |
Зважаючи на останній вираз, у відповідних формулах замість кількості ступенів свободи і можна оперувати показником адіабати g. Наприклад, формули теплоємностей (5.6) та внутрішньої енергії ідеального газу (4.6) і (4.7) можна подати у вигляді:
|
\({C_V}=\frac{R}{\gamma - 1}\), \({C_P}=\frac{\gamma{R}}{\gamma -1}\); |
(5.9) |
|
|
\({U}=\frac{\nu RT}{\gamma - 1}=\frac{m}{M}\cdot\frac{RT}{\gamma-2}\); |
(5.10) |
|
|
\({U}=\frac{PV}{\gamma-1}\). |
(5.11) |
Неповнота класичної теорії теплоємностей. З формул (5.6) випливає. що теплоємності ідеальних газів визначаються тільки кількістю ступенів свободи, тобто, просторовою структурою молекул. Зокрема, для молекул виходить \({C_V}={3R/2}\) у випадку одноатомних молекул (і = 3), \({C_V}={5R/2}\) для двохатомних жорстких молекул (і = 5) і \({C_V=3R}\) для багатоатомних жорстких молекул (і = 6). Досліди свідчать, що такий прогноз, більшою чи меншою мірою, справджується тільки при не дуже низьких і не дуже високих температурах. Це ілюструє рис. 5.1, де схематично показано температурну залежність теплоємності \({C_V}\) водню Н2.
|
|
При проміжних температурах маємо очікуване для жорстких двохатомних молекул значення \({C_V}={5R/2}\). Але при охолодженні газу теплоємність починає зменшуватись і при дуже низьких температурах набуває значення \({3R/2}\), яке притаманне одноатомному газу. Аналогічно, при значному нагріванні теплоємність зростає, наближаючись до величини \({7R/2}\), яка є характерною для двохатомних пружних молекул через наявність і коливального ступеня свободи. Пояснити ці розбіжності класична фізика не здатна, оскільки вони пов’язані зі специфічними квантовими властивостями молекул та інших мікроскопічних частинок. Як показано у квантовій механіці, енергія обертального та коливального руху мікрочастинок може змінюватися тільки дискретними порціями-квантами, причому енергія квантів обертальної енергії εоб набагато менша, ніж коливальної εкол. З іншого боку, при теплообміні молекули передають одна одній енергію порядку kT. Тому при дуже низьких температурах, коли kT < εоб << εкол, обертальний рух молекул та коливальний рух атомів у них не впливають на процес теплообміну й, відповідно, на теплоємність газу. При цьому молекули поводяться, як одноатомні (і = 3, CV = 3R/2), тому говорять, що при низьких температурах обертальні та коливальні ступені свободи є “замороженими”. При підвищенні температури обертальні ступені свободи поступово починають “розморожуватись”, тобто, все більша кількість молекул H2 починає давати вклад у внутрішню енергію за рахунок не тільки поступального, а й обертального руху. Внаслідок цього теплоємність поступово підвищується до величини \({C_V=5R/2}\), що відповідає жорстким двохатомним молекулам (і = 5). Так само при дуже високих температурах “розморожується” й коливальний ступінь свободи, відтак, згідно з (4.5), i = 5 + 2iкол = 7. Через це теплоємність зростає до значення \({C_V=7R/2}\).
Окрім розглянутих раніше ізопрцесів у газах, важливу роль у термодинаміці відіграють адіабатний процес і політропні процеси, в яких змінюються всі три параметри стану: Р, V, Т.
Адіабатний процес. Так називається процес, який відбувається без теплообміну системи з навколишнім середовищем. Для такого процесу, згідно з (4.14), dU + PdV = 0. Тож, скориставшись виразом (5.11), отримаємо:
\(\frac{\mathrm{d}(PV)}{\gamma-1}+p\mathrm{d}V={0}\) \(\Rightarrow \) \(\mathrm{d}(PV)+(\gamma-1)P\mathrm{d}V={0}\) \(\Rightarrow \)
\({V}\mathrm{d}P+P\mathrm{d}V+(\gamma-1)P\mathrm{d}V={0}\) \(\Rightarrow \) \({V}\mathrm{d}P+\gamma{P}\mathrm{d}V={0}\).
Поділимо останній вираз на PV і врахуємо відоме з диференціального числення співвідношення dx/x = d(lnx). Тоді
\(\frac{\mathrm{d}P}{P}+\gamma\frac{\mathrm{d}V}{V}={0}\) \(\Rightarrow \) \(\mathrm{d}\left(\ln{P}\right)+\gamma\mathrm{d}(\ln{V})={0}\) \(\Rightarrow \) \(\mathrm{d}{(\ln{P})}+\mathrm{d}(\ln{V}^{\gamma})={0}\) \(\Rightarrow \)
\(\Rightarrow \) \(\mathrm{d}(\ln{P}+\ln{V}^{\gamma})=0 \) \(\Rightarrow \) \(\mathrm{d}(\ln{PV}^{\gamma})={0}\).
З цього виразу випливає рівняння адіабатного процесу, яке називається рівнянням Пуассона:
|
\({PV^{\gamma}}=\mathrm{const}\) |
(5.12) |
За допомогою (2.6) це рівняння можна подати і в інших змінних:
|
\({TV^{\gamma-1}}=\mathrm{const}\); |
(5.12а) |
|
|
\({TP^{\frac{1-\gamma}{\gamma}}}=\mathrm{const}\). |
(5.12б) |
Зауважимо, що показником степеня в рівнянні Пуассона є введена в попередньому пункті величина \(\gamma=C_P/C_V \), чим і пояснюється її назва “показник адіабати”.
|
|
Адіабатний процес нагадує ізотермічний тим, що тиск і об’єм знаходяться в оберненому зв’язку. Але в адіабатному процесі зміна тиску відбувається швидше, як це показано на рис. 5.2. Крім того, в адіабатному процесі δQ = 0, і, згідно з (4.13), робота газу виконується не за рахунок теплообміну, як в ізотермічному процесі, а за рахунок зміни внутрішньої енергії системи:
\({0=}\mathrm{d}U+\delta{A}\) \(\Rightarrow \) \(\delta{A}=-\mathrm{d}U \) \(\Rightarrow \) \(\mathrm{d}U=-P\mathrm{d}{V}\).
Звідси випливає, що при адіабатному розширенні газ охолоджується, а при стисканні – нагрівається. Завдяки останньому, як уже відмічалося, відбувається самозапалювання паливної суміші в двигунах дизельного типу. Пониження температури газу при адіабатному розширенні використовується, зокрема, в кріогенній техніці та камері Вільсона – приладі, що дозволяє спостерігати траєкторії руху швидких елементарних частинок. При цьому слід зауважити, що в реальності процес у газі на може бути стого адіабатично через наявність теплообміну з довкіллям. Але при великій швидкості протікання, як у наведених прикладах, він є достатньо близьким до адіабатичного.
Але виявляється, що не будь-яке швидке розширення газу супроводжується його охолодженням. У цьому зв’язку повчальними є результати дослідів по розширенню газу в пустоту, які були здійснені Гей-Люссаком і Джоулем. У цих дослідах використовувалися два балони, що були з’єднані трубкою із закритим краном. Один балон був заповнений повітрям, а інший – відкачаний. Дослід полягав у вимірюванні температури газу до та після відкривання крана. На перший погляд результат досліду легко передбачити: після відкривання крана повітря розширюється дуже швидко, отже практично без теплообміну з оточенням (адіабатно), і тому має охолодитися. Але, навіть при високому початковому тиску, що в 20 разів перевищував атмосферний, ніякої зміни внутрішньої енергії та температури повітря при розширенні не спостерігалось. Цей “парадокс” не важко зрозуміти, взявши до уваги, що при вказаних вище значеннях тиску повітря ще поводиться, як ідеальний газ. Розширюючись у пустоту, повітря не виконує макроскопічної роботи (4.8 а), оскільки не рухає ніяких зовнішніх тіл типу поршня. Не виконується й мікроскопічна робота силами взаємодії між молекулами, оскільки їх в ідеальному газі немає. За таких умов внутрішня енергія, отже й температура повітря, при розширенні не змінюються, що й показали досліди Джоуля. Таким чином, при адіабатному розширенні ідеального газу в пустоту тиск і об’єм значно змінюються при незмінній температурі, що суперечить рівнянням адіабати (5.12 а) і (5.12 б). Але в цьому немає ніякого протиріччя, оскільки всі рівняння термодинаміки стосуються тільки рівноважних процесів, у той час як розширення газу в пустоту відбувається дуже швидко і не є рівноважним.
Політропні процеси. Теплоємність є функцією процесу і, загалом, може змінюватися в ході процесу. Але існують процеси, в яких теплоємність системи лишається сталою: С = const. Такі процеси називаються політропними (говорять також “політропічними”). Установимо рівняння політропного процесу. Для цього запишемо перше начало термодинаміки (4.14) для одного моля газу, виразивши \(\delta{Q}\) і \(\mathrm{d}U\) з (5.1) та (5.3):
\({C\mathrm{d}T}=C_V\mathrm{d}T+P\mathrm{d}{V}\) \(\Rightarrow \) \((C-C_V)\mathrm{d}T-P\mathrm{d}V={0}\).
З рівняння Клапейрона (2.6 а) випливає, що dT = d(PV)/R. Зробивши цю підстановку в попередній вираз і, ввівши позначення \(\alpha=(C-C_V)/R \), отримаємо: \(\alpha\mathrm{d}(PV)-P\mathrm{d}V={0}\). Далі, вчиняючи так, як раніше при виведенні рівняння Пуассона, дістанемо:
\({PV^{1-\frac{1}{\alpha}}}=\mathrm{const}\).
Якщо, підставити в показнику вираз \(\alpha \) і врахувати, що \({R=C_P-C_V}\), то отримаємо рівняння політропи:
|
\({PV^n}=\mathrm{const}\), |
(5.13) |
де число
|
\({n}=\frac{C-C_P}{C-C_V}\) |
(5.14) |
називається показником політропи.
Рівняння (5.13) аналогічне до (5.12), тому за аналогією з (5.12 а) і (5.12 б) можна записати:
|
\({TV^{n-1}}=\mathrm{const}\) і \({T}P^{\frac{1-n}{n}}=\mathrm{const}\). |
(5.14а) |
До політропних належать усі розглянуті раніше процеси. Справді, ізобарний процес Р = const задовольняє рівнянню (5.13) при п = 0, для ізотермічного процесу PV = const і п = 1, для адіабатного– \({n=\gamma}\) . Нарешті, якщо (5.13) переписати у вигляді \({P}^{1/n}V=const \) , стане зрозуміло, що ізохорний процес V = const теж формально можна розглядати як політропний з \( n\to \infty \) . Формула (5.14) дозволяє виразити теплоємність системи в будь-якому політропному процесі через показник політропи:
|
\({C}=\frac{nC_V-C_P}{n-1}\). |
(5.15) |
З цієї формули випливає, що в ізотермічному процесі (п =1) теплоємність \({C}\to \infty \) , що природно, оскільки для цього процесу у виразі (5.1) dT = 0. Для адіабатного процесу n = γ і з (5.15) виходить С = 0. Це теж зрозуміло, адже в цьому процесі δQ = 0. Але для всіх політропних процесів, проміжних між ізотермічним та адіабатним, із формули (5.15) випливає, що С < 0. Щоб переконатися в цьому досить у (5.15) зробити заміну CP = γCV і врахувати, що для таких процесів n < γ. Цей висновок може здатися несподіваним, але в ньому немає нічого парадоксального. Він означає тільки те, що в подібних процесах газ весь час виконує більшу роботу, ніж отримувана ним кількість теплоти. З цієї причини внутрішня енергія зменшується і газ охолоджується, тож dT < 0 i C < 0.
Робота газу в політропних процесах. Найзагальнішим способом обчислення роботи в термодинаміці є визначення інтегралів (4.9). Але для політропного процесу із заданим показником політропи це можна зробити легше за допомогою першого начала термодинаміки (4.13а), згідно з яким A = Q – ΔU. Виразивши Q i ΔU через теплоємності за формулами (5.1) і (5.3), отримаємо для одного моля A = (C - CV)ΔT і для \({\nu}\) молів
|
\({A}=\nu (C-C_V)\Delta{T}\). |
(5.16) |
Різницю теплоємностей легко виразити через показник політропи з (5.14):
\({n}=\frac{C-C_P}{C-C_V}=\frac{(C-C_V)+C_V-C_P}{C-C_V}=1-\frac{R}{C-C_V}\) \(\Rightarrow \) \({C-C_V}=-\frac{R}{n-1}\).
Підставивши цей вираз у (5.16), отримаємо
|
\({A}=\frac{\nu{R}(T_1-T_2)}{n-1}\), |
(5.17) |
або, з урахуванням (2.6),
|
\({A}=\frac{P_1V_1-P_2V_2}{n-1}\). |
(5.17а) |
Слід зауважити, що ці вирази не можна використовувати для ізотермічного процесу (п = 1), оскільки і чисельники, і знаменники дорівнюють нулю.
Усі конкретні питання, пов’язані з першим началом термодинаміки, розглядалися вище на прикладі ідеальних газів. Термодинаміка процесів у реальних газах є значно складнішою. Це зумовлено тим, що у внутрішню енергію реального газу, крім кінетичної, входить ще й потенціальна енергія взаємодії між молекулами Uвз. Остання залежить від відстані між молекулами, тобто, від об’єму газу. Тому при адіабатній (без обміну енергією із зовнішніми тілами) зміні об’єму реального газу має змінюватись не тільки потенціальна, а й кінетична енергія молекул, отже – температура газу. Причому, на відміну від ідеального газу, в реальних газах температура має змінюватись і при розширенні в пустоту, коли зміна об’єму газу не супроводжується виконанням роботи.
Ефект зміни температури при адіабатному розширенні газу в пустоту виявили Джоуль і Томсон, які здійснили дослід за схемою рис. 5.3. Теплоізольована труба розділяється на дві половини “дроселем” Др (пористим корком), по обидва боки від якого розміщені рухомі нетеплопровідні поршні П1 і П2. У початковому стані поршень П2 прилягає до дроселя, а об’єм між поршнем П1 і дроселем заповнений газом. Зовнішні тиски на поршні однакові і дорівнюють тиску газу між поршнем П1 і дроселем. Дослід полягає в повільному продавлюванні газу крізь дросель за рахунок невеликої додаткової сили, прикладеної до поршня П1. При цьому обидва поршні переміщуються з положень 1, 2 в положення 1′, 2′. Такий процес називається “дроселюванням”, або процесом Джоуля-Томсона.
|
|
При повільному переміщенні поршнів дроселювання можна вважати рівноважним (квазістатичним) процесом, так що тиск і температура газу в кожній половині труби (P1, T1) і (P2, T2) лишаються сталими, причому P1 > P2. Застосуємо до цього процесу перше начало термодинаміки (4.12), урахувавши відсутність теплообміну:
ΔU = A′,
де робота A′ складається з робіт \( {A}_{1}^{\prime}\) і \( {A}_{2}^{\prime}\), що їх виконують над газом сили зовнішнього тиску на поршні:
\( {A}^{\prime}=A_{1}^{\prime}+A_{2}^{\prime}\).
Позначивши початковий об’єм зліва V1 і кінцевий об’єм праворуч V2, на основі (4.10а) маємо: \( {A}_{1}^{\prime}=P_{1}V_{1}\) і \( {A}_{2}^{\prime}=-P_{2}V_{2}\). Відтак зміна внутрішньої енергії виражається, як
|
ΔU = A′ = P1V1 – P2V2 \( \Rightarrow \) ΔU =–Δ(PV). |
(5.18) |
Без урахування енергії взаємодії між молекулами Uвз, тобто, за умови ідеальності, внутрішня енергія одного моля газу, згідно з (5.7), U = CVT. Отже, для моля реального газу
U = CVT + Uвз.
Підставивши цей вираз в (5.18), отримаємо:
|
|
(5.19) |
Таким чином, при описаному розширенні в пустоту реального газу температура має змінюватись. Це явище, яке дійсно спостерігається, називається ефектом Джоуля-Томсона, а співвідношення (5.19) є його загальним аналітичним виразом. Для отримання конкретного виразу ΔT треба мати конкретну модель газу, тобто, явні вирази енергії взаємодії між молекулами та рівняння стану газу. Але деякі особливості ефекту Джоуля-Томсона можна з’ясувати й на основі загальних міркувань. По-перше, в процесі Джоуля-Томсона поршні виконують зовнішню роботу \( {A}_{1}^{\prime}\) і \( {A}_{2}^{\prime}\). Тому може здатися, що саме ця робота є причиною зміни температури, і ніякого “ефекту”, власне, немає. Аби відкинути такий сумнів, застосуємо вираз (5.19) до ідеального газу, для якого ΔUвз = 0 і, згідно з (2.6а), \(\Delta (PV)=R\Delta{T}\). Тоді вийде:
\(\Delta{T}=-\frac{R\Delta{T}}{C_V}\) \(\Rightarrow \) \((C_V+R)\Delta{T}={0}\) \(\Rightarrow \) \(\Delta{T}={0}\).
Отже, зміна температури в ефекті Джоуля-Томсона зумовлена саме “неідеальністю” газу. По-друге, для різних газів і при різних тисках і температурах кожен доданок і весь чисельник (5.19) можуть мати різні знаки. Тому температура газу при дроселюванні може як зменшуватися, так і збільшуватися, а в окремих випадках і лишатися незмінною. Практика підтверджує такий прогноз: для кожного газу існує своя температура інверсії, при переході через яку ефект змінює знак.
Наостанок, укажемо, що можливість зменшення температури при дроселюванні використовують у промисловості для скраплення газів і отримання дуже низьких (“кріогенних”) температур.
2. Чи можна твердити, що теплоємність визначається тільки властивостями речовини тіла?
3. Чому в довідниках фізичних характеристик матеріалів є таблиці теплоємностіей для рідин і твердих тіл, але немає – для газів?
4. Чи може теплоємність системи бути від’ємною?
5. Що таке ізохорна теплоємність CV та ізобарна теплоємність системи CP? Чому ізобарна теплоємність більша за ізохорну? На скільки?
6. Що таке показник адіабати? Отримайте формули (5.9) – (5.11).
7. Який процес називається адіабатним? Наведіть різні варіанти запису рівняння адіабати.
8. Як змінюється температура газу в адіабатному процесі? Чи може зменшуватися температура при стисканні газу?
9. Відомо, що при швидкому (адіабатному) розширенні ідеального газу в пустоту його температура не змінюється. Чому?
10. Які процеси називаються політропними? Як пов’язані між собою тиск та об’єм газу в політропному процесі?
11. Отримайте рівняння політропи (5.13) і (5.14а).
12. У чому полягає ефект Джоуля-Томсона? Чому він не спостерігається в ідеальних газах?
[1] Виняток становить тільки ізотермічний процес, у якому внутрішня енергія та температура лишаються незмінними.
[2] Це можна розглядати як термодинамічне означення універсальної газової сталої.
VI. ЯВИЩА ПЕРЕНОСУ
Розглянуті в попередніх лекціях відомості стосуються рівноважних станів і процесів, але за відповідних умов їх можна використовувати й для нерівноважних систем. В різних частинах нерівноважної замкненої системи певні параметри стану (температура, тиск, тощо) та інші характеристики системи ( приміром, концентрація молекул даного сорту в суміші) мають не однакові значення. У процесі встановлення термодинамічної рівноваги відбувається вирівнювання подібних неоднорідностей, яке супроводжується виникненням потоків відповідних фізичних характеристик системи. Скажімо, якщо в одній частині системи температура вища, ніж в іншій, то від більш нагрітої частини до менш нагрітої буде переноситися теплова енергія, при вирівнюванні концентрації частинок від області з більшою їхньою концентрацією до області з меншою буде переноситися маса, тощо. Тому подібні явища називаються явищами переносу.
Явища переносу спостерігаються і в незамкнених системах. При цьому, якщо неоднорідність розподілу характеристик системи штучно підтримувати на незмінному рівні, перенесення відповідних величин буде стаціонарним, тобто, їхні значення не залежитимуть від часу, так само, як у рівноважній системі. Тому для стаціонарних явищ переносу є чинними закони молекулярно-кінетичної теорії та термодинаміки.
Нижче розглянуті наступні питання:
1. Емпіричні закони явищ переносу
2. Середня довжина вільного пробігу молекул
3. Молекулярно-кінетична теорія явищ переносу в газах
1. Емпіричні закони явищ переносу
|
\(\Phi=\frac{\Delta{A}}{\Delta{t}}\), |
(6.1) |
де ΔA – кількість величини А, що переноситься крізь цю поверхню за час Δt.
У загальному випадку потік Ф може бути неоднорідним, коли в різних точках інтенсивність перенесення є не однаковою. Тому для опису перенесення величини А в кожній точці простору вводять густину потоку
|
\({j}=\frac{\Delta\Phi}{\Delta{{S}_{\bot }}}\), |
(6.1а) |
де ΔΦ – потік крізь елементарну площинку \(\Delta{{S}_{\bot }}\), перпендикулярну до напрямку переносу.
Перенесення величини А вздовж певного напряму завжди є зумовлене неоднорідним розподілом у цьому напрямі якоїсь іншої величини В. Наприклад, перенесення теплоти Q від батареї опалення до якоїсь віддаленої точки в кімнаті зумовлене наявністю перепаду температури Т між батареєю та цією точкою. Мірою неоднорідності величини В у заданому напрямку ОХ є її градієнт, тобто швидкість зміни dB/dх у цьому напрямі.
Розглянуті поняття й величини дозволяють аналітично виразити емпіричні (встановлені на досліді) закони стаціонарних явищ переносу, що розглядаються далі.
Теплопровідність. Уявімо дві паралельні плоскі пластини, розміщені в однорідному теплопровідному середовищі, котрі підтримуються при сталих температурах T1 і T2 (T1 > T2). За таких умов між пластинами у показаному на рис. 6.1 напрямі ОХ встановлюється стаціонарне перенесення тепла[1].
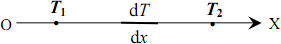
|
\({{j}_{Q}}=-\varkappa \frac{\text{d}T}{\text{d}x}\), |
(6.2) |
де коефіцієнт пропорційності \(\kappa \) коефіцієнтом теплопровідності
Відповідно, кількість теплоти, що переноситься через ділянку перерізу потоку площею ΔS за проміжок часу Δt дорівнює :
|
\(\Delta Q=-\varkappa \frac{\text{d}T}{\text{d}x}\Delta S\Delta t\). |
(6.3) |
(Примітка. Знак “–” у виразах (6.2) і (6.3) є зумовлений тим, що перенесення будь-якої величини (тут Q) завжди відбувається у напрямку менших значень тієї величини (тут T), градієнт якої є причиною переносу. Тож у напрямку перенесення тепла Q > 0, тоді як
Дифузія. Так називається взаємопроникнення різних речовин у сумішах, якщо концентрації частинок у них нерівномірно розподілені по об’єму. До прикладу, проявом дифузії є поширення запаху парфумів у повітрі, або розширення області забарвлення при вміщенні у воду чи на фільтрувальний папір краплі рідкого барвника. Дифузія спостерігається й у хімічно однорідній речовині (газі), якщо концентрація частинок різна в різних місцях. У такому випадку говорять про самодифузію.
Імовірність теплового руху окремої частинки за всіма напрямками однакова, тому будь-якої миті кількість частинок, які рухаються в бік меншої концентрації, більша, ніж кількість частинок, які рухаються в зустрічному напрямку. Через це виникає потік частинок у напрямку зони меншої концентрації. Якщо в газі підтримується сталий градієнт концентрації частинок у напрямку певної осі ОХ, то, як свідчить дослід, сумарна кількість частинок, які проходять за час Δt крізь площинку ΔS, перпендикулярну до напрямку потоку, дорівнює
|
\({N}=-D\frac{\mathrm{d}n}{\mathrm{d}x}\Delta{S}\Delta{t}\), |
(6.4) |
де dn/dx – градієнт концентрації, і D – величина, що залежить від індивідуальних властивостей частинок речовини і називається коефіцієнтом дифузії. Відповідно, густина потоку частинок \({j_n}=N/(\Delta{S}\Delta{t}) \) визначається рівнянням
|
\({j_n}=-D\frac{\mathrm{d}n}{\mathrm{d}x}\), |
(6.5) |
яке називається рівнянням дифузії, або рівнянням Фіка.
Якщо обидві частини рівняння (6.5) помножити на масу однієї молекули m0 і врахувати, що nm0 = ρ – густина речовини, то в правій частині отримаємо градієнт густини dρ/dx, а в лівій – густину потоку маси \({j_m}=m/(\Delta{S}\cdot\Delta{t})\), де \({m=m_0 N}\) – маса речовини, що переноситься. Відтак рівняння (6.5) трансформується в рівняння густини масового потоку:
|
\({j_m}=-D\frac{\mathrm{d}\rho}{\mathrm{d}x}\). |
(6.5а) |
Внутрішнє тертя (в’язкість). До класичних явищ переносу відноситься також внутрішнє тертя, яке спостерігається в рухомій рідині або газі, коли сусідні шари речовини мають різні швидкості течії u1 і u2, як показано на рис. 6.2.
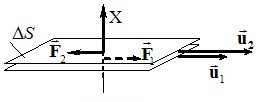
В цьому випадку частинки речовини за рахунок теплового хаотичного руху переходять з одного шару в інший, переносячи із собою відповідний імпульс упорядкованого руху. Унаслідок такого обміну повільний шар буде поповнюватися молекулами, що рухаються у напрямку течії з більшою швидкістю u2, а швидкий – молекулами, що мають меншу швидкість u1. Тому повільний шар буде прискорюватись, а швидкий – сповільнюватись. Це означає, що між шарами є певні сили взаємодії \(\vec{F}_1 \) і \(\vec{F}_2\), які називаються силами внутрішнього тертя. На досліді встановлено, що величина сили внутрішнього тертя залежить від індивідуальних властивостей речовини, площі взаємодіючих шарів ΔS та градієнту їхньої швикості й визначається, як
|
\({F}=\eta\left|\frac{\mathrm{d}u}{\mathrm{d}x}\right|\Delta{S}\). |
(6.6) |
Поділивши цей вираз на ΔS, отримаємо рівняння Ньютона, яке визначає силу внутрішнього тертя між шарами одиничної площі:
|
\({f}=\eta\left|\frac{\mathrm{d}u}{\mathrm{d}x}\right| \). |
(6.6а) |
Похідна під знаком модуля є градієнтом швидкості, який показує, як стрімко змінюється швидкість руху шарів рідини чи газу при переході від одного до іншого шару. Величина η називається коефіцієнтом внутрішнього тертя або динамічною в’язкістю речовини. Крім динамічної, розглядають і так звану кінематичну в’язкість
|
\(\nu=\frac{\eta}{\rho}\), |
(6.7) |
де ρ - густина речовини.
Сила внутрішнього тертя \(\vec{f}\) виникає внаслідок перенесення імпульсу від швидких шарів рідини чи газу до повільних. За другим законом Ньютона \({f}=\left|\mathrm{d}\vec{p}/\mathrm{d}t\right| \), причому в даному випадку права частина – то є імпульс, який переноситься за одиницю часу через одиничну площинку, тобто, густина потоку імпульсу \({j_p}\). Тому, з урахуванням напрямку переносу, рівняння (6.6) можна, подібно до (6.2) – (6.5а), подати як рівняння переносу імпульсу:
|
\({j_p}=-\eta\frac{\mathrm{d}u}{\mathrm{d}x}\). |
(6.8) |
2. Середня довжина вільного пробігу молекул
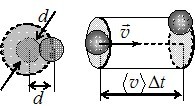
За таких умов середня кількість зіткнень < z′ > на довжині Δl (тобто, за час Δt) дорівнює кількості молекул у вказаному циліндрі: <z′ > = nπd2Δl, де п – концентрація молекул, \(\sigma=\pi{d^2}\) – так званий ефективний переріз молекули[2]. В дійсності рухається не одна, а всі молекули, тому ймовірність зіткнення даної молекули з якоюсь іншою визначається їхньою середньою відносною швидкістю, яка є в \(\sqrt{2}\) разів більша за середню арифметичну швидкість \(\langle{v}\rangle\).[3] Тому коректнішою оцінкою кількості зіткнень є величина
|
\({z}=\sqrt{2}n\pi{d^2}\Delta{l}=\sqrt{2}n\sigma\Delta{l}\). |
(6.9) |
Якщо на відстані \(\Delta{l}\) відбувається z зіткнень даної молекули з іншим, то середня довжина вільного пробігу \(\lambda=\Delta{l}/z \) і, згідно з (6.9),
|
\(\lambda=\frac{1}{\sqrt{2}\pi\sigma{n}}=\frac{1}{\sqrt{2}\pi{d^2{n}}}\). |
(6.10) |
Концентрація молекул пов’язана з тиском газу співвідношенням P = nkT. Тому середня довжина вільного пробігу молекул обернено пропорційна тиску газу, тож
|
\(\lambda_1 P_1=\lambda_2 P_2 \). |
(6.11) |
Середню довжину вільного пробігу молекул у газах можна визначати експериментально на основі явищ переносу. Тому з виразу (6.10) можна знайти ефективний переріз і ефективний діаметр молекули. Щодо точності таких вимірів слід зауважити наступне. По-перше, при підрахунку кількості зіткнень z (6.9) вважалося, що рухома молекула стикається з іншими молекулами в об’ємі прямого циліндра довжини Δl, тобто, що вона при зіткненнях не змінює напрямку руху. Насправді це не так. Тому указаний циліндр є ламаним і має дещо більший об’єм за рахунок “колін”. По-друге, молекули розглядались як кулі, хоча в дійсності довільна молекула складається з декількох атомів і не має симетрії кулі. Тому вираз (6.10) слід розглядати як оціночний. Але, попри це, уявлення про ефективний переріз та ефективний діаметр молекули виявляється досить плідним і загально вживаним.
Наостанок зауважимо, що із середньою довжиною вільного пробігу молекул пов’язане поняття вакуумного стану газу або технічного вакууму. При відкачуванні закритої посудини з газом середня довжина вільного пробігу в міру зниження тиску зростає й при певному тиску P0 стає рівною чи більшою за лінійні розміри посудини. Такий стан газу називається ультрарозрідженим або вакуумним. У вакуумному стані молекули газу практично не стикаються між собою, а тільки зі стінками посудини. Тому властивості ультрарозрідженого газу істотно відрізняються від його властивостей за звичайних умов. Наприклад, при високому вакуумі в газі практично відсутнє внутрішнє тертя та теплопровідність. Останнє використовують у посудинах Дьюара – посудинах із подвійними стінками, простір між якими відкачано до високого вакууму. Такі посудини забезпечують добру теплову ізоляцію від зовнішнього середовища. Прикладом використання посудин Дьюара в побуті є добре відомий кожному термос. В науці та техніці високоякісні посудини Дюара використовують, зокрема, для зберігання скраплених неорганічних газів (азот, кисень, водень, гелій), які мають дуже низькі (кріогенні) температури.
3. Молекулярно-кінетична теорія явищ переносу в газах
Розглянуті явища переносу спостерігаються в будь-яких речовинах мають спільні механізми і, як наслідок, виражаються схожими співвідношеннями (6.2) – (6.8). Але побудувати їхню кількісну теорію на основі молекулярно-кінетичних уявлень можна лише для газів, у яких практично відсутні сили зчеплення між молекулами.Дифузія. Нехай у газі підтримується незалежний від часу нерівномірний розподіл концентрації молекул у напрямку осі ОХ, як показано на рис. 6.4.
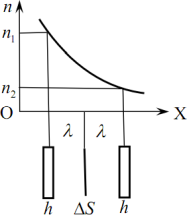
За таких умов у напрямі осі ОХ створюється стаціонарний потік молекул. Визначимо густину цього потоку в довільній точці х. Для цього виділимо в газі два тонкі шари 1 і 2 на відстані вільного пробігу молекул λ від точки х, для кожного з яких площа складає ΔS і товщина h << λ. В такому разі можна вважати, що крізь площинку ΔS проходять усі молекули кожного шару, котрі вилітають в її напрямку паралельно до осі ОХ. Також, ураховуючи рівноймовірність усіх напрямків теплового руху молекул, будемо вважати, що в кожному з двох можливих напрямів кожної з трьох координатних осей рухається (1/6) частина всіх молекул газу. Для виділених шарів це складає, відповідно, \({N_1}=(1/6)n_1\Delta{S}h\) і \({N_2}=(1/6)n_2\Delta{S}h\). Проліт усіх цих молекул крізь площинку ΔS триває протягом часу Δt = h/<v>, який потрібен, аби найвіддаленіші з них подолали відстань h між стінками шару при середній швидкості руху \(\langle{v}\rangle\). Відтак для густини потоку молекул отримуємо:
|
\({j}=\frac{1}{6}n\langle{v}\rangle \) |
(6.12) |
Відтак, згідно з означеннями (6.1а) і (6.1а) , густина зустрічних потоків молекул крізь площинку ΔS виражається, відповідно, як \({j_1}=(1/6)n_1\langle{v}\rangle \) і \({j_2}=(1/6)n_2\langle{v}\rangle \), а результуюча густина потоку дифузії
\({j_n}=\frac{1}{6}(n_1-n_2)\langle{v}\rangle \) = \(-\frac{1}{6}\Delta n\left\langle v \right\rangle \),
де Δn = n2 – n1 — приріст концентрації молекул уздовж осі ОХ на відстані Δx = 2λ.
Позаяк величина λ є дуже малою, то за канонами математичного аналізу можна записати \(\Delta{n}=(\mathrm{d}n/\mathrm{d}x)Δx=2\lambda (\mathrm{d}n/\mathrm{d}x) \)[4].
Відтак для густини потоку частинок при самодифузії остаточно отримаємо:
|
\({j_n}=-\frac{1}{3}\lambda\langle{v}\rangle\frac{\mathrm{d}n}{\mathrm{d}x}\), |
(6.13) |
де (dn/dx) — градієнт концентрації молекул, а множник
|
\({D}=\frac{1}{3}\lambda\langle{v}\rangle \) |
(6.13а) |
— коефіцієнт дифузії.
Таким чином, рівняння (6.13) повністю узгоджується з емпіричним рівнянням (6.5) та теоретично визначає коефіцієнта дифузії D ідеального газу.
Теплопровідність. Як говорилося в п.1, в середовищі між двома паралельними площинами, що підтримуються при сталих температурах T1 і T2, встановлюється певний не залежний від часу розподіл температур уздовж перпендикулярної до площин осі ОХ (рис. 6.5) та стаціонарний тепловий потік, зумовлений теплопровідністю, тобто не пов’язаний з рухом речовини (конвекцією).
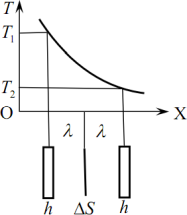
Теоретично закономірності цього процесу в ідеальному газі легко встановити за тією самою формальною схемою, що й у випадку дифузії, врахувавши, що при теплопровідності перенесення тепла спричинюється градієнтом температури, а не концентрації молекул. Тож знову виділимо в газі обабіч площинки ΔS на відстанях вільного пробігу молекул λ два шари 1 і 2 з такою самою площею і товщиною h << λ. Тоді можна вважати, що крізь площинку ΔS проходять усі молекули з кожного шару, котрі рухаються в її напрямі паралельно до осі ОХ. При цьому молекули з шару 1 є більш “гарячими”, ніж із шару 2, тож переносять із собою більшу кінетичну енергію E тепловового руху. Тому зустрічний рух обох пучків молекул супроводжується перенесенням тепловї енергії від гарячих до холодних зон, яку легко розрахувати.
Очевидно, що густина потоку енергії крізь площинку ΔS, що створюється кожним пучком молекул, дорівнює j = jмE, де jм – густина потоку молекул, і E – середня енергія теплового руху однієї молекули в пучку. Тож густина теплового потоку jq = j1 – j2, що створюється крізь площинку ΔS при зустрічному русі обох пучків, дорівнює
jq = jм(E1 – E2)
Енергія полекули визначається її кількістю ступенів свободи і та температурою газу за формулою (4.4): Е = (і/2)kT. Отже,
E1 – E2 = \(\frac{ik}{2}\left( {{T}_{1}}-{{T}_{2}} \right)=-\frac{ik}{2}\Delta T\)
Відтак, урахувавши, що при малій відстані між шарами Δx = 2λ зміна температури \(\Delta{T}=(\mathrm{d}T/\mathrm{d}x)Δx=2\lambda (\mathrm{d}T/\mathrm{d}x) \)[4], а густина потоку молекул виражається формулою (6.12), отримуємо наступний вираз густини теплового потоку при теплопровідності:
\({j_q}=-\frac{1}{3}\lambda\langle{v}\rangle\frac{ikn}{2}\cdot\frac{\mathrm{d}T}{\mathrm{d}x}\).
Множник ikn/2 можна подати зручніше, домноживши чисельник і знаменник на сталу Авогадро NA та масу молекули m0. Тоді, враховуючи, що m0n = ρ – густина, m0NА = М– молярна маса газу, а також формули (2.5), (5.2) і (5.6), отримаємо:
|
\({j_q}=-\frac{1}{3}\lambda\langle{v}\rangle\rho{c_V}\cdot\frac{\mathrm{d}T}{\mathrm{d}x}\). |
(6.14) |
Це і є теоретичне рівняння теплопровідності, причому коефіцієнт теплопровідності визначається виразом
|
\(\kappa=\frac{1}{3}\lambda\langle{v}\rangle\rho{c_V}\), |
(6.15) |
де ρ - густина газу, \({c_V}\) - питома теплоємність при сталому об’ємі.
Внутрішнє тертя (в’язкість). Як відмічалося раніше, внутрішнє тертя між шарами газу є зумовлене переносом імпульсу впорядкованого руху від шару до шару в напрямку зменшення швидкості (від’ємний напрям осі Х на рис. 6.2, що безпосередньо відображено в рівнянні (6.8). Молекулярний механізм в’язкості є повністю аналогічним до щойно розглянутого механізму теплопровідності. Тому для отримання теоретичного рівняння внутрішнього тертя в газі, не повторюючи всіх попередніх міркувань, достатньо заміни у виразах густини потоків енергію Е на імпульс упорядкованого руху молекули p = m0u. Тоді густина потоку імпульсу крізь площинку ΔS дорівнює:
\({j_p}=\frac{1}{6}n\langle{v}\rangle{m_0}(u_1-u_2)=-\frac{1}{6}n\langle{v}\rangle{m_0}\Delta{u}\) \(\Rightarrow \) \({j_p}=-\frac{1}{3}\lambda\langle{v}\rangle{nm_0}\frac{\mathrm{d}u}{\mathrm{d}x}\).
Урахувавши, що m0n = ρ – густина газу, отримаємо теоретичне рівняння густини потоку імпульсу:
|
\({j_p}=-\frac{1}{3}\lambda\langle{v}\rangle\rho\frac{\mathrm{d}u}{\mathrm{d}x}\), |
(6.16) |
а відтак і рівняння Ньютона (6.6 а), з таким виразом коефіцієнта внутрішнього тертя:
|
\(\eta=\frac{1}{3}\lambda\langle{v}\rangle\rho \). |
(6.17) |
Із виразів (6.13). (6.15) і (6.17) випливає, що, визначаючи коефіцієнти переносу дослідним шляхом, можна знайти середню довжину пробігу молекул, і, згідно з (6.10), ефективний переріз та діаметр молекули – параметри, які відіграють важливу роль у багатьох задачах молекулярної фізики. Тому цікаво проаналізувати, наскільки розглянута елементарна теорія узгоджується з експериментом.
Порівняння теоретичних та емпіричних рівнянь переносу показує, що теорія правильно відображає лінійний характер залежності густини потоку величини, які переноситься, від градієнту відповідного термодинамічного параметра газу. Розглянута теорія також адекватно показує, від яких величин залежать коефіцієнти переносу D, η і κ. Зокрема те, що всі коефіцієнти переносу повинні зростати при підвищенні температури, оскільки \(\langle{v}\rangle\sim\sqrt{T}\). Інший теоретичний прогноз полягає в тому, що коефіцієнти теплопровідності (6.15) та внутрішнього тертя (6.17) газів не залежать від тиску, оскільки густина ρ = nm0 є прямо пропорційною, а довжина вільного пробігу молекул λ– обернено пропорційною до концентрації молекул, а отже, й тиску газу. Дослід це підтверджує, що може здатися дивним, – адже зменшуючи концентрацію молекул, ми зменшуємо кількість “переносників” енергії у випадку теплопровідності та імпульсу у випадку внутрішнього тертя. Це справді так, але при тому, такою ж мірою збільшується довжини вільного пробігу молекул, тож і різниця значень величини, що переноситься кожною парою зустрічних молекул, а отже й густина потоку. Водночас, дійсна величина числових множників у коефіцієнтах переносу D, η і κ дещо відрізняється від 1/3 і є не однаковою для різних явищ переносу. Це пояснюється тим, що при виведенні розглянутих рівнянь відповідні процеси в газі розглядалися доволі спрощено.
2. За яких умов до явищ переносу можна застосовувати положення молекулярної фізики рівноважних процесів?
3. Що таке потік даної фізичної величина та густина потоку? Який зв’язок існує між ними?
4. Чи супроводжується тепловий потік переміщенням шарів газу від більш нагрітої області до менш нагрітої?
5. При прокачуванні рідини по трубі швидкість її руху є найбільшою на осі труби й найменша біля стінки. Який напрям має градієнт швидкості зумовлений цим потік імпульсу?
6. Що таке вакуумний стан газу? Якими мають бути розміри посудини, щоб газ у ній перебував у вакуумному стані?
7. Який “принцип дії” термоса? Оцініть, при якому максимальному тиску термос із відстанню між стінками 5 мм ще буде виконувати свою функцію – забезпечувати теплову ізоляцію вмісту від довкілля.
-------------------------
[1] Самі пластини не показані й розташовані перпендикулярно до площини рисунка.
[2] Як видно, ефективний переріз молекули дорівнює площі круга, в який має потрапити центр іншої молекули, щоби вони зіткнулися, тобто, достатньо сильно змінили свої швидкості внаслідок взаємодії. Діаметр та ефективний переріз молекули є певною мірою умовними величинами, зокрема, вони залежать від температури.
[4] Це випливає з того, що при малій зміні аргумента похідну можна наближено розглядати як відношення приросту функції до приросту аргумента: (dn/dx) ≈ (Δn/Δx)
VII. ДРУГЕ НАЧАЛО ТЕРМОДИНАМІКИ
Колові процеси (цикли). Робота циклу. Коловим процесом або циклом називається такий процес, у якому система, пройшовши через низку не співпадаючих станів, повертається у вихідний стан. Графік квазістатичного[2] (рівноважного) колового процесу зображується замкненою кривою, як показано на діаграмі P-V (рис. 7.1).
Коловий процес характеризується і розширенням, і стисканням газу й має певний напрям, тобто, послідовність змін параметрів стану. Якщо цикл іде “за годинниковою стрілкою”, як показано стрілками на рис.7.2а, то цикл називається прямим. При зворотному напрямі зміни параметрів стану (рис.7.2б) цикл називається оберненим.
Квазістатичні цикли є оборотними, тобто, при проведенні такого циклу спочатку в одному, а потім у зворотному напрямі, в зовнішніх тілах не лишається будь-яких змін.
|
|
У коловому процесі газ виконує роботу, яка на ділянках розширення 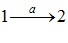 є додатньою, а на ділянках стискання
є додатньою, а на ділянках стискання 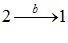 – від’ємною. Тому графічно робота циклу визначається різницею площ під указаними ділянками й чисельно дорівнює взятій з відповідним знаком площі, обмеженій графіком циклу на діаграмі (P, V) (штриховка на рис. 7.2)[3]. У прямому циклі (рис. 7.2а) розширення (ділянка
– від’ємною. Тому графічно робота циклу визначається різницею площ під указаними ділянками й чисельно дорівнює взятій з відповідним знаком площі, обмеженій графіком циклу на діаграмі (P, V) (штриховка на рис. 7.2)[3]. У прямому циклі (рис. 7.2а) розширення (ділянка  ) відбувається при більшому тиску, ніж стискання (ділянка
) відбувається при більшому тиску, ніж стискання (ділянка 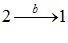 ), тому повна робота циклу має знак “+”. Відповідно, в оберненому циклі знак роботи “–”.
), тому повна робота циклу має знак “+”. Відповідно, в оберненому циклі знак роботи “–”.
Розглянемо детальніше термодинаміку прямого циклу, записавши перше начало термодинаміки (4.13а) для ділянок розширення й стискання газу та для циклу в цілому:
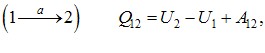
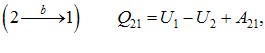
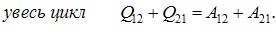
На ділянці розширення об’єм і температура газу зростають, отже A12 > 0 і U2 > U1. Тому Q12 > 0, тобто, газ дійсно отримує тепло від зовнішніх тіл. Але на ділянці стискання A12 < 0, U1 < U2 і Q21 < 0, отже, газ віддає тепло іншим тілам, а роботу реально виконує не сам газ, а зовнішні тіла. Відповідно до цього позначимо отриману газом кількість тепла як Q1 = Q12, віддану кількість тепла як Q′2 = – Q21, і сумарну роботу циклу як A = A12 + A21 = A12 - A′21, де A′21 - додатня робота зовнішніх тіл по стисканню газу. Тоді робота газу в циклі виразиться, як
|
A = Q1 – Q′2. |
(7.1) |
Отже, робота в прямому коловому процесі виконується виключно за рахунок теплової енергії, реально отриманої газом від зовнішніх тіл.
Принцип дії та склад теплового двигуна. В прямому циклі після виконання певної механічної роботи A > 0 газ повертається у вихідний стан. Тому процес можна повторювати знов і знов. На цьому ґрунтується робота теплових двигунів - циклічно діючих пристроїв для отримання механічної енергії за рахунок тепла. Через це прямий коловий процес називають іще циклом теплового двигуна.
З наведеного аналізу дії прямого циклу випливає, що, незалежно від конструкції, тепловий двигун повинен мати три обов’язкових структурних елементи: 1) робоче тіло - речовину (газ), у якій здійснюється робочий цикл двигуна, тобто, прямий коловий процес, в якому відбувається перетворення тепла на механічну енергію; 2) нагрівник - термодинамічну систему з високою температурою та великим запасом теплової енергії, яка може передаватися робочому тілу і 3) холодильник - систему з низькою температурою й дуже великою теплоємністю, котра може приймати від робочого тіла не використане тепло практично без зміни свого стану. Отже, в кожному циклі двигуна робоче тіло: 1) отримує від нагрівника тепло Q1, 2) виконує за рахунок цього корисну роботу А і 3) віддає холодильнику певну кількість тепла \({Q_{2}^{'}}\) , повертаючись у вихідний стан. Описана термодинамічна схема теплового двигуна показана на рис 7.3а. Слід зауважити, що вона відображає лише загальний принцип дії теплового двигуна. Що ж до конструктивного втілення, то всі три елементи у вигляді окремих пристроїв існували тільки в класичних парових машинах – перших і довгий час єдиних теплових двигунах, які використовувалися в техніці. В сучасних теплових двигунах, до прикладу, автомобільних, джерелом теплової енергії є паливна суміш у циліндрах, яка після запалення одночасно стає і нагрівником, і робочим тілом – штовхає поршні й виконує корисну роботу. А в якості холодильника використовується навколишнє повітря, куди викидається відпрацьоване робоче тіло (вихлопні гази) разом із не використаною тепловою енергією.
|
|
Холодильна машина. В робочому тілі (газі) можна здійснити й обернений цикл, умовно показаний на рис. 7.2б. Це можна, приміром, зробити так. Спочатку стиснений газ привести у добрий тепловий контакт із тілом з меншою температурою (холодним тілом), дати йому можливість розширитися при температурі цього тіла (ділянка  ), а потім привести газ у контакт із більш нагрітим (гарячим) тілом і примусовим стисканням повернути його у вихідний стан (ділянка
), а потім привести газ у контакт із більш нагрітим (гарячим) тілом і примусовим стисканням повернути його у вихідний стан (ділянка 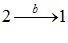 ). У такому разі газ отримує певну кількість тепла \({Q_1}\) від холодного тіла й передає певну кількість тепла \({Q_{2}^{'}}\) гарячому тілу. Як наслідок, холодне тіло ще більше охолоджується, а гаряче нагрівається. Саме це відбувається в кімнатному холодильнику, в якому тепло від холодильної камери, що має низьку температуру, завдяки роботі компресора передається повітрю в кімнаті, яке має вищу температуру. Тому обернений цикл називають циклом холодильної машини. Слід одразу наголосити на тому, що, на відміну від теплового двигуна, цикл холодильної машини можна здійснити тільки примусово за рахунок виконання більшої зовнішньої роботи по стисканню газу на ділянці (
). У такому разі газ отримує певну кількість тепла \({Q_1}\) від холодного тіла й передає певну кількість тепла \({Q_{2}^{'}}\) гарячому тілу. Як наслідок, холодне тіло ще більше охолоджується, а гаряче нагрівається. Саме це відбувається в кімнатному холодильнику, в якому тепло від холодильної камери, що має низьку температуру, завдяки роботі компресора передається повітрю в кімнаті, яке має вищу температуру. Тому обернений цикл називають циклом холодильної машини. Слід одразу наголосити на тому, що, на відміну від теплового двигуна, цикл холодильної машини можна здійснити тільки примусово за рахунок виконання більшої зовнішньої роботи по стисканню газу на ділянці ( ), ніж виконує сам газ на ділянці розширення (
), ніж виконує сам газ на ділянці розширення ( ). Тому холодильна машина може працювати тільки в комбінації з якимось двигуном (зазвичай – електричним), який дає механічну енергію, необхідну для стискання робочого тіла. Принципова схема холодильної машини показана на рис.7.3б.
). Тому холодильна машина може працювати тільки в комбінації з якимось двигуном (зазвичай – електричним), який дає механічну енергію, необхідну для стискання робочого тіла. Принципова схема холодильної машини показана на рис.7.3б.
Ефективність перетворення теплової енергії на механічну в робочому циклі теплового двигуна визначається його коефіцієнтом корисної дії (ККД) η, тобто, відношенням роботи циклу А (формула (7.1)) до кількості тепла Q1, отриманого робочим тілом від нагрівника[4]:
|
\(\eta=\frac{A}{Q_1}=\frac{Q_1-Q_{2}^{'}}{Q_1}\). |
(7.2) |
Отже, ККД теплового двигуна показує, яка частка отриманої теплової енергії перетворюється на механічну, і є тим більшим, чим менша кількість тепла \({Q_{2}^{'}}\) передається холодильнику. Тому виникає природне питання, чи не можна обійтися без холодильника й побудувати тепловий двигун, у якому \({Q_{2}^{'}=0}\) і η = 1, адже це це не суперечить першому началу термодинаміки. Використовуючи в такому двигуні як нагрівник, скажімо, світовий океан із його практично безмежним запасом внутрішньої енергії, можна було би необмежено довго отримувати механічну енергію за рахунок внутрішньої енергії Землі. Оскільки такий гіпотетичний пристрій не суперечить закону збереження енергії, він називається вічним двигуном другого роду. Але, як доводить вся історія розвитку фізики та техніки,
вічний двигун другого роду є неможливим.
У цьому полягає один із фундаментальних законів природи – друге начало термодинаміки. Більш розлого воно виражається формулюванням Кельвіна-Планка, зміст якого полягає в тому, що
принципово неможливо збудувати циклічно працюючий механізм, єдиним результатом дії якого було би виконання роботи за рахунок внутрішньої енергії нагрівника.
Отже, друге начало термодинаміки стверджує неможливість повного перетворення отриманого робочим тілом тепла на механічну енергію в тепловому двигуні (або коловому процесі). Але воно не забороняє цього взагалі. До прикладу, при ізотермічному розширенні газу все отримане тепло перетворюється на роботу (див. Розділ IV, (4.15)), але такий процес не є циклічним і не може бути повторений без того, щоб якась кількість теплоти перейшла від газу до інших тіл.
Існують й інші формулювання другого начала, зокрема, формулювання Клаузіуса:
теплота не може спонтанно (саме по собі) переходити від менш нагрітого тіла до більш нагрітого.
Це твердження теж зовсім не означає, що перехід тепла від холодного тіла до гарячого взагалі неможливий. До прикладу, такий перехід відбувається під час роботи кімнатного холодильника або кондиціонера. Ідеться про те, що ніяким способом неможливо відібрати тепло від тіла з меншою температурою й повністю передати його тілу з більшою температурою так, аби в навколишньому середовищі не відбулося жодних змін. А якщо перехід тепла від холодного тіла до гарячого все ж таки відбувається, то він обов’язково супроводжується якимось іншими процесами. Приміром, перехід тепла в холодильнику від морозильної камери до повітря в кімнаті супроводжується роботою компресора.
Розглянуті формулювання другого начала термодинаміки Кельвіна-Планка та Клаузіуса словесно є істотно різними, і видається дивним, як вони можуть виражати один і той самий закон. Але можна довести, що обидва формулювання є еквівалентними. Припустимо, що якийсь тепловий двигун отримав від нагрівника кількість тепла Q1 і віддав холодильнику кількість тепла \({Q_{2}{'}}\), виконавши додатню роботу \({A}=Q_1-Q_{2}^{'}\). А тепер уявімо, що, всупереч формулюванню Клаузіуса, тепло \({Q_{2}^{'}}\) можна повернути від холодильника до нагрівника так, аби в довкіллі не відбулося ніяких змін. Тоді єдиним наслідком такого комбінованого процесу було б виконання роботи А за рахунок теплоти \({Q}=Q_1-Q_{2}^{'}\) і повернення двигуна у вихідний стан. Але це неможливо, згідно з формулюванням Кельвіна-Планка. Отже, із неможливості повного перетворення теплоти в роботу в коловому процесі з необхідністю випливає неможливість спонтанного переходу тепла від холодного тіла (холодильника) до гарячого (нагрівника). Тобто, із формулювання Клаузіуса випливає формулювання Кельвіна-Планка. Подібним чином можна довести й те, що з формулювання Кельвіна-Планка випливає формулювання Клаузіуса.
Друге начало термодинаміки дозволяє краще зрозуміти, чому при встановленні термодинамічної рівноваги в ізольованій системі всі тіла набувають однакової температури: процеси в замкненій системі є спонтанними й тому супроводжуються переходом тепла виключно від більш нагрітих тіл до менш нагрітих, аж доки ступінь нагрітості всіх тіл, тобто їхні температури, не зрівняються. Отже, можна сказати, що друге начало термодинаміки визначає напрям спонтанних термодинамічних процесів у природі.
Цикл Карно. Позаяк навіть теоретична можливість існування теплового двигуна з ККД η = 1 забороняється другим началом термодинаміки, постає принципове питання, яким може бути максимальний коефіцієнт корисної дії теплових двигунів. Відповідь отримав французький інженер і фізик Саді Карно, котрий винайшов коловий процес (“цикл Карно”), що має найбільший теоретично можливий ККД.
Цикл Карно є оборотним (квазістатичним) коловим процесом, котрий складається з двох ізотерм (ділянки \({1\to{2}}\) і \({3\to{4}}\) на рис.7.4) та двох адіабат (ділянки \({2\to{3}}\) і \({4\to{1}}\)) Висока ефективність такого циклу пояснюється тим, що робоче тіло виконує роботу в ізотермічному та адіабатному процесах (ділянки \({1\to{2}\to{3}}\)), тобто без будь-яких непродуктивних втрат теплової енергії.
|
|
Визначимо ККД циклу Карно, в котрому робочим тілом є ідеальний газ. Згідно з (7.2), можна записати:
|
\(\eta=\frac{A}{Q_1}=1-\frac{Q_2^{'}}{Q_1}\), |
(7.2а) |
де Q1 - кількість тепла, отримана газом від нагрівника, \({Q_2^{'}}\) - тепло, віддане холодильнику. Оскільки цикл Карно є оборотним, всі процеси в ньому є рівноважними. Тому газ отримує тепло, маючи температуру нагрівника T1, а віддає не використане тепло, маючи температуру холодильника T2. В ізотермічному процесі, згідно з (4.15), Q = A, тому в (7.2а) \({Q_1}/Q_2^{'}=A_{12}/A_{34}^{'}\), де A12 - робота газу на ділянці ізотермічного розширення \({1\to{2}}\), і \({A_{34}^{'}}\) - робота зовнішніх тіл на ділянці ізотермічного стискання газу \({3\to{4}}\). Урахувавши це та вирази (4.11) і (4.11а), для ККД отримаємо:
|
\(\eta_c=1-\frac{T_2\ln(V_3/V_4)}{T_1\ln(V_2/V_1)}\). |
(7.3) |
Далі візьмемо до уваги, що пари точок (2, 3) і (4, 1) належать кожна своїй адіабаті. Тому, згідно з (4.29а), можна записати:
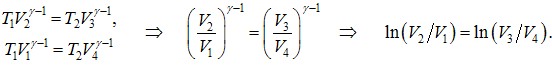
Отже, із (7.3) маємо остаточно:
|
\(\eta_c=1-\frac{T_2}{T_1}\), або \(\eta_c=\frac{T_1-T_2}{T_1}\). |
(7.4) |
Теорема Карно. Вираз (7.4) ми отримали для циклу Карно в ідеальному газі. Але можна довести, що він є універсальним і визначає ККД будь-якого теплового двигуна, що працює на циклі Карно, незалежно ані від речовини робочого тіла, ані від конструкції. Карно також довів, що будь-який інший мислимий цикл має ККД менший, ніж (7.4). Це можна проілюструвати на прикладі циклу, що, як і цикл Карно, складається з двох ізотерм і двох адіабат, але є необоротним (нестатичним). У такому циклі теплообмін відбувається зі скінченною швидкістю, тому температура робочого тіла на ізотермічних ділянках не встигає вирівнюватись і при розширенні є нижчою за температуру нагрівника, а при стисканні – вищою за температуру холодильника. Тому ізотерми проходять, як показано штриховими лініями на рис. 7.4. Через це площа, обмежена графіком необоротного циклу, тож і робота, є меншою, ніж робота (площа) оборотного циклу Карно. Відповідно, меншим є й ККД. Отже, констатуємо, що ККД будь-якого теплового двигуна задовольняє фундаментальній нерівності:
|
\(\eta\le\frac{T_1-T_2}{T_1}\) або \(\eta\le 1-\frac{T_2}{T_1}\), |
(7.5) |
де T1 – максимальна температура, при якій тепло переходить від нагрівника до робочого тіла, а T2 – мінімальна температура, при якій робоче тіло передає тепло холодильнику.
Підводячи підсумок, можна сказати, що
ніякий тепловий двигун не може мати ККД вищий, ніж двигун, який працює на оборотному циклі Карно.
Наведені твердження й підсумковий вираз (7.5) складають зміст теореми Карно, яка посідає провідне місце в термодинаміці.
З практичної точки зору вираз (7.5) показує, що для збільшення ККД теплових двигунів треба підвищувати температуру нагрівника й знижувати температуру холодильника. Але реальні можливості підвищення температури нагрівника обмежені відносно невисокою жаростійкістю матеріалів і тепловим розширенням деталей, що призводить до виходу двигуна з ладу при перегріві. Що ж до температури холодильника, то її мінімальне обґрунтоване значення обмежене температурою довкілля. Причина полягає в тому, що для охолодження холодильника до більш низької, ніж навколишня, температури треба виконувати роботу, що, як випливає з другого начала термодинаміки, є більшою, ніж приріст корисної роботи двигуна за рахунок підвищення ККД. З указаних причин ККД навіть найкращих теплових двигунів є істотно меншим за одиницю.
Теорема Карно має не лише практичне, а й велике теоретичне значення. З попереднього зрозуміло, що теплота, передана холодильнику, вже не може бути ефективно перетворена на механічну енергію. Відбувається своєрідне знецінення теплової енергії, коли все більша її частина стає непридатною для отримання механічної енергії. Причому, це стосується не лише теплових двигунів, а взагалі будь-яких процесів перетворення теплової енергії на механічну.
2. Чому дорівнює робота системи в прямому циклі? Як вона відображаєтся на графіку циклу?
3. Чи можливі процеси, в яких усе отримане системою тепло йде на виконання нею роботи?
4. Чи можливо перетворити на роботу все отримане системою тепло в коловому процесі?
5. Що таке “тепловий двигун”? Наведіть термодинамічну схему теплового двигуна. Чи можна віднести електромотор до теплових двигунів?
6. Що таке “вічний двигун другого роду”? У чому полягає друге начало термодинаміки?
7. Дайте формулювання другого начала термодинаміки Кельвіна-Планка та Клаузіуса і доведіть їхню еквівалентність.
8. Який коловий процес називається циклом Карно? Чому дорівнює ККД циклу Карно?
9. Про що трактує теорема Карно?
[1] Більш за те, це відбувається навіть усупереч нашому бажанню, так що в замкненій системі з часом уся механічна енергія може перетворитися на теплову.
[2] Нагадаємо, що квазістатичним називається достатньо повільний процес, коли можна вважати, що система проходить через низку рівноважних станів.
[4] Це так званий термодинамічний ККД. Реальний ККД, тобто, відношення механічної енергії на валу двигуна до теплової енергії, що виділяється при згорянні палива, ясна річ, менший через недосконалість конструкції та втрати на тертя у вузлах двигуна.
VIII. ЕНТРОПІЯ
Теорема Карно не тільки визначає обмеження, накладені природою на можливість перетворення теплової енергії на механічну. З неї випливає існування фізичної величини, що дозволє аналітично виразити друге начало термодинаміки й висвітлює його фундаментальний зміст. Ця величина, котра називається ентропією, розглядається в наступних питаннях:
2. Обчислення ентропії. Теорема Нернста
3. Нерівність Клаузіуса. Закон зростання ентропії
4. Ентропія й імовірність. Формула Больцмана
\({1+\frac{Q_2}{Q_1}}=1-\frac{T_2}{T_1}\) \(\Rightarrow \) \(\frac{Q_2}{Q_1}=-\frac{T_2}{T_1}\) \(\Rightarrow \) \(\frac{Q_1}{T_1}=\frac{Q_2}{T_2}\),
або
|
\(\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0 \). |
(8.1) |
|
|
Клаузіус назвав відношення кількості теплоти, отриманої системою, до її температури зведеною кількістю теплоти. Тож сума зведених кількостей теплоти, отриманих системою в циклі Карно, дорівнює нулю. Відтак розглянемо оборотний коловий процес, який складається з чотирьох ізотерм і чотирьох адіабат (рис. 8.1а), ділянки а-b і с-d яких лежать на одній адіабаті (точки b і с не з’єднані). Якщо подумки продовжити адіабату ас від точки с до точки b, а адіабату db – від точки b до точки с, то вказаний комбінований процес розпадається на два окремі цикли Карно, котрі здійснюються між температурами Т1 і Т4 та Т2 і Т3. При цьому, позаяк вставлені віртуальні процеси між точками b і с є адіабатичними (Q = 0), то вони ніяк не впливають на зведені теплоти. Відтак для всього “ступінчастого” циклу маємо:
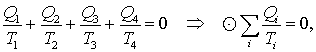 |
(8.2) |
де кружечок біля знаку суми означає, що додавання виконується по всьому коловому процесу (по замкненому “шляху”). Довільний коловий процес (рис. 8.1б) також можна розчленувати віртуальними адіабатами на безліч елементарних циклів Карно (на рис.8.1б штрихами показано один із таких елементарних циклів). При цьому на кожній елементарній ділянці циклу система отримує нескінченно малу зведену кількість теплоти \(\delta{Q}/{T}\), тому дискретна сума (8.2) вироджується в інтеграл по всьому коловому процесу:
|
\(\oint\frac{\delta{Q}}{T}=0 \). |
(8.3) |
Вирази (8.1), (8.2) і (8.3) називаються рівностями Клаузіуса. Вони означають, що
в будь-якому оборотному коловому процесі сумарна зведена кількість теплоти дорівнює нулю.
Зауважимо, що найбільш загальним є вираз (8.3), а (8.1) і (8.2) є його окремими випадками.
Ентропія. Отриманий результат можна подати інакше. Поділимо весь цикл (рис. 8.1 б) на дві ділянки: ![]() та
та  і, відповідно, інтеграл (8.3), на дві частини. Тоді
і, відповідно, інтеграл (8.3), на дві частини. Тоді
|
\(\oint\frac{\delta{Q}}{T}=\int_{1a2}\frac{\delta{Q}}{T}+\int_{2b1}\frac{\delta{Q}}{T}=0 \quad\Rightarrow \quad \int_{1a2}\frac{\delta{Q}}{T}=-\int_{2b1}\frac{\delta{Q}}{T}\). |
(8.3а) |
Оскільки цикл оборотний, то при проведенні процесу 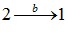 у зворотному напрямку по шляху
у зворотному напрямку по шляху 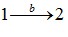 в кожній точці зміниться тільки напрям теплообміну й знак величини \(\delta{Q}/{T}\) , тому
в кожній точці зміниться тільки напрям теплообміну й знак величини \(\delta{Q}/{T}\) , тому
\({-}\int_{2b1}\frac{\delta{Q}}{T}=\int_{1b2}\frac{\delta{Q}}{T}\)
Отже, (8.3а) можна переписати, як
|
\(\int_{1a2}\frac{\delta{Q}}{T}=\int_{1b2}\frac{\delta{Q}}{T}\). |
(8.4) |
Це дуже важливий результат, який означає, що при оборотному переході системи із якогось стану 1 у якийсь стан 2 сумарна зведена кількість теплоти, отримана системою, не залежить від способу переходу (тобто, виду процесу) й визначається тільки параметрами початкового та кінцевого стану системи. Схожа ситуація спостерігається в механіці[1] стосовно роботи консервативних сил, причому незалежність вказаної роботи від траєкторії руху частинки дозволяє ввести поняття потенціальної енергії. Подібним чином у термодинаміці вводиться поняття ентропії S.
Ентропією системи називається величина, зміна котрої при переході системи з одного стану в інший будь-яким квазістатичним (оборотним) способом дорівнює сумарній зведеній кількості теплоти, що її отримує система при цьому переході:
|
\(\Delta{S}=S_2 - S_1=\left(\int_{1\to{2}}\frac{\delta{Q}}{T}\right) \)об. |
(8.5) |
Відповідно, при елементарній зміні стану приріст ентропії
|
\(\mathrm{d}S=\frac{\delta{Q}}{T}\). |
(8.5а) |
Одразу звернімо увагу на такі загальні властивості ентропії. По-перше, хоча кількість теплоти є функцією процесу, величина \(\mathrm{d}S=\delta{Q}/{T}\) і, відповідно, ΔS не залежить від способу зміни стану, отже,
ентропія є функцією стану системи.
По-друге, кількість теплоти, отримана системою в будь-якому квазістатичному процесі, є прямо пропорційною масі (кількості речовини) системи. Тому
ентропія є адитивною величиною,
тобто, ентропія системи дорівнює сумі ентропій її окремих частин. Це дозволяє поширити поняття ентропії на нерівноважні стани системи, якщо її можна поділити на окремі частини (підсистеми), що перебувають у відмінних, але квазірівноважних станах. Нарешті, з (8.3) і (8.5) випливає що в оборотному коловому процесі
|
\(\Delta{S}={0}\), |
(8.6) |
тобто,
в оборотних колових процесах ентропія не змінюється.
Ентропія ідеального газу. Нехай ідеальний газ у кількості ν молів оборотно переходить із стану 1 (P1, V1, T1) у стан 2 (P2, V2, T2). Визначимо зміну ентропії газу. Згідно з першим началом термодинаміки (4.14), при елементарній зміні стану системи \(\delta{Q}=\mathrm{d}U+P\mathrm{d}{V}\). Урахувавши (5.7) і (2.6), будемо мати: \(\delta{Q}=\nu{C_V}\mathrm{d}T+\nu{RT}\mathrm{d}V/{V}\). Звідси для елементарної зведеної кількості теплоти дістанемо:
|
\(\frac{\delta{Q}}{T}=\nu{C_V}\cdot\frac{\mathrm{d}T}{T}+\nu{R}\cdot\frac{\mathrm{d}V}{V}\) |
(8.7) |
Інтегруючи цей вираз відповідно до (8.5), отримаємо
\(\Delta{S}=\nu{C_V}\int_{T_1}^{T_2} \frac{\mathrm{d}T}{T}+\nu{R}\int_{V_1}^{V_2} \frac{\mathrm{d}V}{V}\quad\Rightarrow\)
|
\(\Rightarrow\quad\Delta{S}=S_2-S_1=\nu\left(C_V\ln\frac{T_2}{T_1}+R\ln\frac{V_2}{V_1}\right) \). |
(8.8) |
Величину ΔS можна подати й через інші параметри стану, зробивши у (8.8) відповідні заміни на основі рівняння Клапейрона (2.6). Зокрема, можна отримати такий симетричний вираз:
|
\(\Delta{S}=\nu\left(C_V\ln\frac{P_2}{P_1}+C_P\ln\frac{V_2}{V_1}\right)\). |
(8.8а) |
З (8.8) і (8.8а) випливають прості формули для обчислення зміни ентропії ідеального газу в ізопроцесах. До прикладу, в ізотермічному процесі \(\Delta{S}=\nu{R}\ln (V_2/V_1)\), або \(\Delta{S}=\nu{R}\ln{(P_1/P_2)}\), в ізобарному процесі \(\Delta{S}=\nu{C_P}\ln{(V_2/V_1)}\), або \(\Delta{S}=\nu{C_P}\ln{(T_1/T_1)}\) в ізохорному процесі \(\Delta{S}=\nu{C_V}\ln{(P_2/P_1)}\), або \(\Delta{S}=\nu{C_V}\ln{(T_2/T_1)}\). Принагідно відмітимо, що в адіабатному процесі \(\delta{Q}={0}\), тому й ΔS = 0. Отже, адіабатний процес – то є ізоентропний (ізоентропійний) процес. Відповідно, на діаграмі (T, S) графік циклу Карно зображується прямокутником (рис. 8.2).
 |
Це, зокрема, дозволяє дуже легко отримати вираз (7.4) для ККД циклу Карно. Справді, оскільки в цьому циклі теплообмін відбувається тільки на ізотермах при сталих температурах T1 і T2, то, відповідно до (8.5), Q1 = T1(S2 - S1) і Q2 = T2(S2 - S1). Підставивши ці вирази в (7.2) з урахуванням знаків, одразу отримуємо формулу (7.4).
Зміна ентропії при необоротній зміні стану газу. Нехай в одній із двох теплоізольованих посудин, які з’єднані тонкою трубкою з перекритим краном, знаходиться ν молів ідеального газу, а в другій – вакуум. Об’єми посудин V1 і V2. Кран відкривають і газ, розширюючись в пустоту, заповнює обидві посудини й переходить у новий рівноважний стан. Такий процес є необоротним: для повернення газу у вихідний стан його треба стиснути, а для цього треба виконати роботу та забезпечити теплообмін, що суттєво змінить стан зовнішніх тіл. Тому годі навіть і думати про обчислення зміни ентропії за допомогою виразу (8.5) безпосередньо для цього процесу, адже для необоротного процесу саме поняття зведеної кількості теплоти втрачає зміст через невизначеність температури системи. Але розширення ідеального газу в пустоту відбувається без зміни температури[2], тому замість реального процесу можна розглянути квазістатичне ізотермічне розширення газу від об’єму V1 до об’єму V1 + V2. Тоді, з урахуванням (4.15) і (2.8), із (8.5) отримаємо:
|
\(\Delta{S}=\int_{V_1}^{V_1+V_2}\frac{P\mathrm{d}V}{T}=\nu{R}\int_{V_1}^{V_1+V_2}\frac{\mathrm{d}V}{V}\quad\Rightarrow\quad\Delta{S}=\nu{R}\ln\frac{V_1+V_2}{V_1}\) |
(8.9) |
Отже, в розглянутому процесі ентропія газу зростає.
Теорема Нернста. Означення (8.5) визначає не саму ентропію, а тільки її зміну при заданій зміні стану системи. Тому для визначення самої ентропії необхідно в будь-якому обраному стані покласти ентропію рівною нулю, подібно до того, як це робиться в механіці стосовно потенціальної енергії[2]. Але у випадку ентропії вибір нульового рівня, по суті, є однозначним, завдяки так званій тепловій теоремі Нернста. Нернст на основі емпіричних даних установив, що при наближенні температури до 0 К ентропія будь-якої системи прямує до певної границі, що не залежить від жодних параметрів стану системи. Тому цю границю покладають рівною нулю, і приймають таке формулювання:
при наближенні температури до абсолютного нуля ентропія будь-якої системи прямує до нуля:
|
\({S}\to{0}\), якщо \({T}\to {0}\). |
(8.10) |
Слід зауважити, що теорема Нернста логічно не випливає з інших законів термодинаміки. Тому її ще називають третім началом термодинаміки.
Теорема Нернста дозволяє дати означення не лише для зміни, а й для самої ентропії системи:
|
\({S}=\int_0^T\frac{\delta{Q}}{T}\). |
(8.11) |
|
\( \frac{Q_1}{T_1}+\frac{Q_2}{T_2}\le{0}\), |
(8.12) |
|
|
|
(8.13) |
|
|
\(\oint\frac{\delta{Q}}{T}\le{0}\), |
(8.14) |
в яких знак “<” відноситься до необоротних, а знак “=”– до оборотних колових процесів.
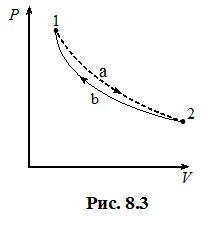 |
Нерівність (8.14) дозволяє з’ясувати загальну поведінку ентропії в необоротних процесах. Нехай система перейшла зі стану 1 у стан 2 в якомусь необоротному процесі, показаному умовно[3] штриховою лінією  на рис. 8.3. Повернемо подумки систему у вихідний стан, здійснивши певний оборотний процес, який показано лінією
на рис. 8.3. Повернемо подумки систему у вихідний стан, здійснивши певний оборотний процес, який показано лінією 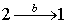 . Відтак отримуємо необоротний цикл, для якого, згідно з (8.14) можна записати:
. Відтак отримуємо необоротний цикл, для якого, згідно з (8.14) можна записати:
\(\int_{1a2}\frac{\delta{Q}}{T}+\int_{2b1}\frac{\delta{Q}}{T}\lt{0}\).
У першому інтегралі під Т слід розуміти температуру навколишнього середовища, при якій відбувається теплообмін, у другому інтегралі ця температура є й температурою системи. Процес 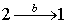 є оборотним, тому, згідно з (8.5), другий інтеграл дорівнює зміні ентропії S1 – S2 при переході системи із стану 2 у стан 1. Отже,
є оборотним, тому, згідно з (8.5), другий інтеграл дорівнює зміні ентропії S1 – S2 при переході системи із стану 2 у стан 1. Отже,
|
\(\int_{1a2}\frac{\delta{Q}}{T}+(S_1-S_2)\lt{0}\quad\rightarrow\quad{S_2-S_1}\gt\int_{1a2}\frac{\delta{Q}}{T}\). |
(8.15) |
Зведена кількість теплоти (інтеграл у правій частині кінцевої нерівності), яку отримує система, може мати будь-який знак, залежно від напрямку та інтенсивності теплообміну на окремих стадіях процесу. Тому в довільному необоротному процесі ентропія системи може як зростати, так і зменшуватись. Але, якщо система є теплоізольованою, тобто, не обмінюється теплом із навколишніми тілами, то інтеграл у (8.15) дорівнює нулю, відтак ΔS = S2 – S1 > 0. Отже, при необоротних процесах у теплоізольваній системі ентропія обов’язково зростає. Об’єднуючи цей результат із (8.6), отримуємо універсальне співвідношення
|
\(\Delta{S}\ge{0}\), |
(8.16) |
яке означає, що
ентропія теплоізольованої системи не може зменшуватися – вона або зростає, або лишається незмінною.
Цей результат називають законом зростання ентропії. Він безпосередньо випливає з теореми Карно, котра, у свою чергу, є прямим наслідком другого начала термодинаміки і, по суті, виражає його. Тому закон зростання ентропії (8.16) розглядають як ще одне формулювання другого начала термодинаміки. З нього, зокрема, випливає висновок про те, що в замкнених системах можливі лише такі процеси, при яких ентропія не зменшується. А практично,позаяк строго оборотних процесів у природі не існує, в усіх процесах у замкнених системах ентропія зростає[4]. Тим самим, друге начало термодинаміки визначає напрям процесів, які можуть відбуватися в природі.
4.Ентропія й імовірність. Формула Больцмана
умовою термодинамічної рівноваги системи є максимум її ентропії.
В цьому сенсі можна говорити про те, що ентропія показує ступінь наближеності системи до стану рівноваги: чим ближча ентропія до свого максимуму, тим ближчим є стан системи до рівноважного. Така думка підтримується й тим, що перехід замкненої системи до рівноваги є необоротним, а саме необоротність термодинамічних процесів є формальною причиною зростання ентропії у замкнених системах. Тому постає питання про причину цієї необоротності, адже термодинамічні процеси визначаються рухом і взаємодією між частинками макроскопічної системи, а в законах руху (законах механіки) ніякої необоротності немає. Наприклад, якби Земля рухалася навколо Сонця в протилежному до існуючого напрямку, ні на Землі, ні у Всесвіті взагалі, нічого б не змінилось.
Виявляється, що причина необоротності теплових процесів полягає в макроскопічності термодинамічних систем, тобто, в тому, що вони містять гігантську кількість частинок. У цьому можна переконатися, позірно[5] розглянцвши явно необоротний процес розширення газу в пустоту на основі статистичного (молекулярно-кінетичного) методу. Отже, нехай маємо посудину, розділену перегородкою на дві однакові частини 1 і 2, причому частина 1 містить N молекул газу, а 2 – порожня. Якщо перегородку прибрати, виникне потік молекул із частини 1 у частину 2. При цьому, внаслідок хаотичності теплового руху, одразу виникне й зустрічний потік молекул з частини 2 в 1. Очевидно, що в міру зменшення кількості молекул в частині 1 і збільшення їхньої кількості в частині 2, перший потік буде з часом послаблюватись, а другий – підсилюватись. Отож через певний час, коли кількості молекул в обох посудинах стануть однаковими, ці потоки зрівняються, перетікання газу з частини 1 у частину 2 припиниться, й у системі встановиться рівноважний стан. Проте ця рівновага є динамічною – перехід молекул з однієї половини посудини в іншу не припиняється, просто кількості молекул, які перетинають у зустрічних напрямках умовну поверхню, що відділяє одну половину посудини від іншої, стають у середньому однаковими. Але в окремі моменти, знову таки через хаотичність теплового руху, вказана рівність порушується й виникає короткочасне перетікання газу з однієї частини посудини в іншу, причому байдуже, в якому напрямку. Отже, спонтанний перехід газу з другої частини в першу, тобто, обернений до розширення процес, є принципово можливим. Але йдеться тільки про дуже незначні частки молекул і про гранично малі проміжки часу. Ніхто й ніколи не спостерігав переходу з другої частини посудини в першу значної частки молекул, тим паче – всього газу. Проаналізуємо, чому? Нехай спочатку N = 1, тобто в частині 1 у початковий момент є лишень одна молекула. Після прибирання перегородки молекула буде рухатися по всій посудині, з однаковою ймовірністю перебуваючи або в другій, або в першій частині посудини. Але щоразу, коли молекула опиняється в першій половині посудини, наш “газ” спонтанно повертається в вихідний стан, причому ймовірність такого переходу дорівнює Р = 1/2, тобто, є дуже великою. Нехай тепер кількість молекул N = 2. Якщо ми будемо спостерігати за цими молекулами певний час, за який зробимо n спостережень, то виявимо, що перша молекула знаходиться в першій частині посудини в n/2 випадків. У свою чергу друга молекула в половині з цих n/2 випадків буде теж знаходиться в першій частині посудини. Тому обидві молекули будуть разом знаходитись у першій половині посудини в (1/2)(n/2) = n/4 випадків. Отже, ймовірність спонтанного повернення у вихідний стан для “газу” з двох молекул уже менша й становить Р = (1/2)·(1/2) = 1/22. Міркуючи так само, для N = 3 отримаємо Р = (1/2)·(1/2)·(1/2) = 1/23, і в загальному випадку Р = 1/2N, де N - кількість молекул у посудині. Як бачимо, спонтанний перехід газу у вихідний стан після встановлення рівноваги є принципово можливим, але ймовірність такого процесу стрімко зменшується при збільшенні кількості молекул у посудині. Так, при N = 10 імовірність Р = 1/210 = 1/1024 ≈ 0,001. Це мала, проте помітна величина: якщо “фотографувати” розподіл молекул у посудині протягом великого часу, то в середньому на кожні 1000 кадрів буде траплятись один, на якому всі молекули знаходяться в першій частині посудини. Це повністю підтверджується комп’ютерним моделюванням. Але вже при N = 100 ймовірність спонтанного повернення у вихідний стан стає Р ≈ 10-30, тобто, виявити таку подію немає жодного шансу. Реальна кількість молекул в 1 см3 газу складає ~1020 і \({P}\approx10^{-310^{19}}\). Наскільки мале це число, неможливо уявити. Тому спонтанний перехід усіх молекул газу знов у першу частину посудини абстракно є можливий, але в дісності ніколи не відбувається, і розширення газу в пустоту є необоротним. Таким чином, молекулярно-кінетична теорія не тільки пояснює причину необоротності термодинамічних процесів, а й уточнює саме поняття необоротності. А саме, необоротні процеси – це не такі процеси, що принципово не можуть самі по собі відбуватись у зворотньому напрямі, а такі, для яких сронтанний зворотній процес є гранично мало ймовірними. Відповідно, й кінцевий стан системи не є математично однозначно заданим, і
рівноважний стан є найбільш імовірним макроскопічним станом системи.
У світлі сказаного важливо з’ясувати, чим визначається ймовірність того чи іншого макроскопічного стану системи. Відповідь не важко знайти, якщо пригадати, що макроскопічний стан системи реалізується через її мікроскопічні стани, тобто, через сукупність станів окремих частинок системи (див. Вступ). Але зв'язок між мікро- та макростанами системи не є взаємно однозначним. Тоді як кожному мікроскопічному станові відповідає визначений макроскопічний стан системи, заданому макроскопічному станові відповідає безліч різних мікроскопічних станів. Наприклад, в розглянутому позірному процесі розширення газу всіх випадках (мікростанах), коли в даній частині посудини знаходиться задана кількість молекул, термодинамічні параметри (концентрація частинок, тиск, внутрішня енергія, тощо) є однаковими, тобто газ перебуває в одному й тому самому макроскопічному стані. Зважаючи на хаотичність руху молекул і величезну частоту зіткнень між ними, в МКТ прийнятий постулат про рівноймовірність усіх мікростанів, які відповідають заданому макроскопічному станові системи, тобто, – що всі мікростани трапляються однаково часто. Відтак стає зрозумілим, що заданий макроскопічний стан буде спостерігатися тим частіше, отже, тим імовірніше, чим більша кількість мікроскопічних станів йому відповідає. Тому в МКТ за міру ймовірності макроскопічного стану системи приймають його термодинамічну ймовірність або статистичну вагу Ω – кількість способів (мікростанів), якою реалізується даний макроскопічний стан системи. Наведена нижче таблиця ілюструє сказане для “газу” з чотирьох молекул 1, 2, 3, 4. У ній показані всі можливі розподіли молекул по частинах посудини (мікростани), відповідні макростани та їхні термодинамічна Ω й математична Р ймовірності. Як видно, рівноважний стан, у якому молекули розподілені по посудині рівномірно, є найбільш імовірним (Ω = 6), а стани, в яких усі молекули самодовільно скупчуються тільки в частині 1, або тільки в частині 2, є найменш імовірними (Ω = 1).
| Способи реалізації макростанів | Ω | P | |
| A | B | ||
|
0 |
1, 2, 3, 4 | 1 | 1/16 |
|
1 2 3 4 |
2, 3, 4 1, 3, 4 1, 2, 4 1, 2, 3 |
4 | 4/16 |
|
1, 2 1, 3 1, 4 2, 3 2, 4 3, 4 |
3, 4 2, 4 2, 3 1, 4 1, 3 1, 2 |
6 | 6/16 |
|
1, 2, 3 1, 2, 4 1, 3, 4 2, 3, 4 |
4 3 2 1 |
4 | 4/16 |
| 1, 2, 3, 4 | 0 | 1 | 1/16 |
| Усього мікростанів 24 = 16 | |||
Поняття термодинамічної ймовірності дозволяє кількісно виразити зв’язок між ентропією та ступенем наближеності системи до термодинамічної рівноваги, про який говорилося вище. Це зробив Л. Больцман, який довів, що ентропія S системи в стані із термодинамічною ймовірністю Ω визначається, як
|
\( {S}=k\ln\Omega\). |
(8.17) |
де k = 1,38·10-23 Дж/К – вже відома нам з МКТ “стала Больцмана”.
Вираз (8.17), який називається формулою Больцмана, є статистичним означенням поняття ентропії. Формула Больцмана відіграє велику роль у статистичній фізиці та термодинаміці. Зокрема, вона розкриває глибинний зміст закону зростання ентропії. А саме, цей закон указує на те, що всі процеси в природі йдуть у напрямку зростання молекулярного безпорядку в системі. Це в свій час спонукало дискусію про так звану “теплову смерть Всесвіту”, тобто, про неминучий перехід нашого Всесвіту до стану термодинамічної рівноваги й припинення в ньому будь-яких процесів. Це, в принципі, не виключено, але сьогодні для однозначної відповіді на це питання наявні знання про походження та еволюцію Всесвіту є недостатніми.
2. Яка фізична величина називається ентропією? В яких одиницях вона вимірюється? Які має основні властивості?
3. Чому не можна безпосередньо визначити зміну ентропії в заданому необоротному процесі?
4. Чи можна взагалі визначити зміну ентропії в необоротному процесі? Чому? Як?
5. У чому полягає закон зростання ентропії? Чи може ентропія термодинамічної системи зменшуватись? За яких умов?
6. Дайте означення рівноважного стану системи на основі поняття ентропії.
7. Який статистичний зміст має ентропія?
8. Що таке “термодинамічна імовірність” макроскопічного стану системи. Який зв’язок існує між нею та ентропією?
[1] Див. «Фізика для бакалаврів. Механіка», розділ IV, п.2.2.
[2] Див. розділ V, п. 3.
[3] Нагадаємо, що в необоротному процесі параметри стану не мають визначених значень для всієї системи, тому процес неможливо зобразити якоюсь лінією на графіку.
[4] Конкретним прикладом цього є результат наведеного в п. 2 розрахунку зміни ентропії при розширенні газу в пустоту.
[5] Це означає “удавано” і є одним із способів доведення. До прикладу, у фізиці нерідко розглядають “позірні експерименти” – удавані досліди, які не суперечить фізичним законам, але технічно є неможливими.