physics.zfftt.kpi.ua

Простір і час у нашій свідомості пов’язуються із нарізним розташуванням предметів та поcлідовним ходом подій. Тому властивості простору та часу найбільш наочно виявляються у властивостях руху тіл і відображаються у формулах перетворень координат і часу та наслідках, які з них випливають.

У цій темі розглянуті наступні питання:

1.1. Принцип відносності Галілея

1.2. Постулати СТВ. Відносність простору та часу

1.3. Перетворення Лоренца

1.4. Перетворення швидкостей в СТВ.  Гранична швидкість

 Контрольні запитання

1.1. Принцип відносності Галілея

Перетворення Галілея. Уявлення класичної фізики про абсолютний простір і абсолютний час відображаются у перетвореннях Галілея — співвідношеннях між координатами тіла (матеріальної точки) в двох інерціальних системах відліку, що рівномірно і прямолінійно рухаються одна віносно одної вздовж осей Х (див. Розділ І, п. 1.4). Таке твердження може здатися дивним, позаяк галілеєві перетворення свідчать про відносність положення тіла в просторі, позаяк \(\vec{r}\ne\vec{r}' \). Але це показує лише, що в просторі не існує якоїсь виділеної точки відліку, відносно якої можна було би визначати положення та рух всіх тіл. Що ж до відстаней між тілами та їхнього взаємного розташування, які власне, й відображають властивості простору, то, згідно з перетвореннями Галілея, вони не залежать від системи відліку, тобто, є абсолютними.

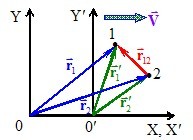
Справді, з рис. 6.1 видно, що положення точки 1 відносно точки 2 визначається радіусом-вектором \( \vec{r}_{12}=\vec{r}_1-\vec{r}_2 \), який, згідно з формулами (1.30) або (1.30а), розділ І, не змінюється при переході від однієї системи відліку до іншої, тобто, є інваріантом перетворень Галілея:

Отож і відстань між двома точками \({l}=\left|\vec{r}_{12}\right| \) є інваріантною, тобто абсолютною величиною:

Отже, лінійні розміри та форма тіла не залежать від системи відліку, що й є наочним відображенням концепції абсолютного простору, тобто, єдиного й ні від чого не залежного “вмістилища речей”.

Так само класична фізика виходить і з уявлення про єдиний і ні від чого не залежний абсолютний час, через що проміжок часу між якимись подіями приймається однаковим для будь-якої системи відліку: Δt = Δt′. Це здається настільки самоочевидним, що навіть не обговорюється. Прямим наслідком концепції абсолютного часу є класичні формули перетворення швидкостей (розділ І, формули (1.33) , (1.33а)), з яких випливає інваріантність (незалежність від системи відліку) відносної швидкості  двох тіл:

Справді, позаяк dt = dt′ і \( \mathrm{d}\vec{r}_{12}=\mathrm{d}\vec{r}_{12}^{\prime}\), то відносні швидкості

В інерціальних системах відліку (ІСВ) інваріантом перетворень Галілея є також прискорення:

\( \vec{a}=\vec{a}^{\prime}\).

Це випливає з того, що інерціальні системи відліку не мають прискорень одна відносно одної .

Принцип відносності класичної механіки. Таким чином, розташування тіла та швидкість і прискорення його руху відносно якогось іншого тіла в усіх інерціальних системах відліку є однаковими. Але на загал саме ці фактори визначають силу взаємодії між тілами (див. розділ ІІ, п. 1.1). Отже, сила взаємодії між тілами теж є інваріантом перетворень Галілея, тобто, є однаковою в усіх інерціальних системах відліку: \( \vec{F}^{\prime}=\vec{F}\). Те саме можна сказати й про масу, оскільки вона є внутрішньою властивістю тіла й ніяк не пов’язана з його рухом. Тож m′ = m. Таким чином, інваріантом перетворень Галілея виявляється й основне рівняння класичної механіки – рівняння другого закону Ньютона (розділ ІІ, рівняння (2.3) і (2.5)). Це означає, що

в усіх інерціальних системах відліку (ІСВ) рух матеріальної точки визначається одним і тим самим основним рівнянням динаміки.

Звідси випливає принцип відносності класичної механіки або принцип відносності Галілея:

за однакових умов у всіх ІСВ всі механічні явища проходять однаково.

Тому

ніякими механічними дослідами всередині даної ІСВ неможливо встановити рухається вона, чи перебуває у спокої.

Таким чином, згідно з принцип відносності Галілея

всі інерціальні системи відліку є повністю еквівалентними щодо механічних явищ.

1.2. Постулати СТВ. Відносність простору і часу

Перетворення Галілея та принцип відносності класичної механіки, що випливає з них і законів Ньютона, довгий час розглядались як непорушний фундамент усієї класичної фізики. Однак у другій половині XIX сторіччя після створення Максвеллом класичної електродинаміки й відкриття електромагнітних хвиль, до яких належить і світло, з’ясувалося, що електромагнітні процеси не задовольняють перетворення Галілея. Зокрема, численними дослідами було неспростовно доведено, що швидкість світла у вакуумі, всупереч перетворенням Галілея (розділ І, формули (1.33) , (1.33а)), не залежить від швидкості руху ані джерела, ані приймача. Це та інші факти, в решті решт,  призвели до радикального перегляду А. Ейнштейном вихідних положень (постулатів) механіки і створення нової науки – спеціальної теорії відносності (СТВ), які розглядаються далі.

1.2.1. Постулати СТВ

1.2.2. Відносність часу

1.2.3. Відносність простору

1.2.1. Постулати СТВ

Незалежність швидкості світла у вакуумі від руху джерела та приймача (“спостерігача”) означає, що вона є однакова в усіх системах відліку. Звідси випливає висновок, що не лише механічними, а й електромагнітними дослідами неможливо розрізнити рух і спокій будь-якої інерціальної системи відліку. На підставі цього А. Ейнштейн поширив принцип відносності на всі фізичні явища і прийняв його за один із постулатів (вихідних положень) нової механіки – принцип відносності Ейнштейна:

в інерціальних системах відліку всі фізичні процеси за однакових умов протікають однаково; всі закони природи та рівняння, що їх описують, є інваріантні, тобто не змінюються при переході від однієї інерціальної системи відліку до іншої.

Інакше кажучи,

всі інерціальні системи відліку є повністю рівноправними (еквівалентними): ніякими дослідами неможливо виділити жодну з них як головну.

Другий постулат СТВ стосується світла. Незалежність швидкості поширення світла від руху джерела та приймача не випливає  як наслідок ні з яких інших положень, тому Ейнштейн прийняв її як другий постулат СТВ – принцип сталості швидкості світла:

швидкість світла у вакуумі не залежить від руху джерела світла і однакова по всіх напрямах.

Це означає, що

швидкість світла у вакуумі однакова в усіх системах відліку.

Отже швидкість світла посідає особливе місце в природі. На відміну від інших швидкостей, скажімо, швидкості звуку, що змінюються при переході від однієї системи відліку до іншої, швидкість світла у вакуумі є інваріантною величиною.

Прийняті Ейнштейном постулати СТВ стоять на міцному фундаменті експерименту – сьогодні невідомо жодного дослідного факту, який би їм суперечив. Разом із тим, аналіз постулатів Ейнштейна призводить до дуже несподіваних для класичної фізики висновків, про які йдеться далі.

1.2.2. Відносність часу

Як уже відмічалося, класична фізика трактує час як абсолютний, тобто єдиний і однаковий для всього Всесвіту. Тому здається самоочевидним, що дві одночасні для даного спостерігача події є таким і для будь-якого іншого спостерігача (абсолютність одночасності). А звідси випливає й висновок про абсолютність проміжку часу між двома подіями. Але таке уявлення є несумісним із постулатами СТВ, у чому можна переконатися на наступному позірному експерименті^[1].

Уявімо довгий стержень, посередині якого розташована лампочка Л, а на кінцях – фотоелементи Ф1 і Ф2 (рис. 6.2).

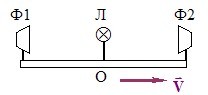
Стержень рухається відносно спостерігача, що знаходиться в точці О. Нехай лампочка в момент проходження повз т. О на мить спалахує (посилає світловий сигнал). Тоді в системі відліку стержня світловий сигнал доходить до фотоелементів за один і той самий час, оскільки він поширюється в обох напрямках з однаковою швидкістю й проходить однакову відстань. Отже, в системі відліку стержня спрацьовування фотоелементів є двома одночасними подіями. Але нерухомий спостерігач в точці О зафіксує зовсім інше. Для нього швидкість світла також однакова в обох напрямках, оскільки вона не залежить від руху джерела. Але відстані, які пройде світло до фотоелементів, будуть різними, позаяк фотоелемент Ф1 рухається назустріч світловому імпульсу, а Ф2 “тікає” від нього. Тож для нерухомого спостерігача фотоелемент Ф1 спрацює раніше, ніж Ф2. Таким чином, із постулатів СТВ впливає неспростовний висновок про відносність одночасності віддалених (таких, що відбуваються в різних точках) подій:

дві відалені події, що є одночасні в даній системі відліку, відбуваються в різні моменти часу в системах відліку, котрі рухаються відносно даної.

Відносність одночасності означає відносність самого плину часу в різних системах відліку. У цьому можна переконатись із ще одного позірного експерименту, запропонованого Ейнштейном. Нехай маємо вертикальний стержень АВ на кінцях котрого закріплено два горизонтальні дзеркала (рис. 6.3), між якими „бігає” короткий світловий імпульс.

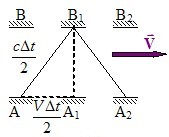
Уявімо, що стержень рухається горизонтально зі швидкістю V, і визначимо час пробігу імпульсу від одного дзеркала до іншого й назад  а) в системі відліку стержня K′ і б) в нерухомій системі відліку К, відносно якої стержень рухається. Очевидно, що в K′-системі цей час дорівнює

де l₀ = AB – відстань між дзеркалами в K′-системі відліку, в якій стержень є нерухомим, c – швидкість світла. Але в К-системі відліку, відносно якої стержень рухається, світловий імпульс відбивається від верхнього дзеркала в точці B₁ і повертається до дзеркала нижнього в точці A₂. Отже, за половину часу пробігу він проходить відстань l = AB₁, яка пов’язана з відстанями AA₁ та A₁B₁ очевидним співвідношенням (AB₁)² = (AA₁)² + (A₁B₁)² . Так само очевидно, що AA₁ = VΔt/2, де V – швидкість стержня, Δt – час пробігу світлового імпульсу від нижнього дзеркала до верхнього й назад у К-системі відліку. Що ж до відстані A₁B₁ у К-системі відліку, то вона, згідно з принципом відносності, як і в K′, дорівнює l₀ ^[2].

Отже, можна записати:

Швидкість світла в К-системі відліку, як і в K′, дорівнює с, отже \( {l}=c\Delta{t}/{2}\). Підставивши цей вираз в (1.5), дістанемо:

Порівнюючи цей вираз із (1.4), знаходимо для двох ІСВ:

Таким чином, одну подію (відбивання імпульсу від дзеркала А) від іншої події (повернення імпульсу на дзеркало А) в різних системах відліку відділяють різні проміжки часу, а це означає, що

час як такий є відносним: його плин у різних системах відліку є не однаковий.

Важливо чітко усвідомити фізичний зміст виразу (1.7). У K′-системі дзеркала є нерухомі, отже, час Δt₀ виміряно нерухомим відносно подій годинником, а час Δt — годинником К-системи відліку, відносно якої “події рухаються” зі швидкістю V. При цьому, як видно з (1.7), Δt > Δt₀, отже спостерігач К-системи відліку дійде висновку, що годинник K′-системи йде повільніше, ніж його власний. У цьому сенсі говорять про уповільнення часу в рухомих системах відліку, і задля однозначності та зручності висловлювань використовують таку термінологію. Систему відліку, в якій точки, де відбуваються дані події є нерухомі, називають власною системою відліку, а час, який показує нерухомий в цій системі відліку годинник (“власний” годинник) називають власним часом. Будь-яка інша система відліку, відносно якої точки, де відбуваються події, рухаються, називається лабораторною системою відліку, а проміжки часу між такими “рухомими” подіями, виміряні годинником лабораторної системи відліку, називають лабораторним часом. Виходячи з цього, можна сказати, що

власний час є найповільнішим.

Слід також нагадати, що тут слово “годинник” означає не якийсь фізичний прилад, а прийнятий принцип вимірювання проміжків часу. Тому розглянутий ефект уповільнення часу є чисто кінематичним і відображає об’єктивну властивість часу як такого, а саме, його відносність. Це добре видно з такої ситуації. Якщо два спостерігачі в двох різних ІСВ виконають описаний дослід з дзеркалами, то кожен з них абсолютно обґрунтовано буде вважати, що годинник колеги з іншої системи відліку йде повільніше, ніж його власний. Тож запитання, який з годинників насправді йде повільніше, є позбавлене змісту.

1.2.3. Відносність простору.

Розглянемо ще один позірний дослід. У системі відліку K′ паралельно до осі O′X′ розміщено нерухомий стержень АВ довжини l′ = l₀, який разом із K′-системою рухається із швидкістю V відносно нерухомої К-системи відліку, рис. 6.4.

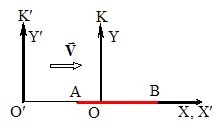
Поставимо завдання визначити довжину стержня АВ в К-системі відліку. Спостерігач К-системи може зробити це, вимірявши час прольоту стержня Δt_ст повз якусь фіксовану точку (наприклад, О) в К-системі відліку. Тоді

Видається “очевидним”, що величина l має збігатися з l_0, але насправді це не так. Уявімо, що описану процедуру вимірювання контролює спостерігач K′-системи, для котрого стержень є нерухомим, а годинник К-системи рухається повз нього із швидкістю V. Отже, він скаже, що спостерігач К-системи вимірює час переміщення свого годинника Δt_год на відстань l₀ між кінцями стержня. Тож

А тепер звернімо увагу на те, що у виразах (1.8) і (1.8а) фігурують проміжки часу між тими самими двома подіями: суміщення годинника із одним (подія 1) та іншим (подія 2) кінцем стержня. При цьому в К-системі (вираз (1.8)) події відбуваються в одній точці і фіксуються нерухомим відносно неї годинником. Отже Δt_ст є власним проміжком часу між цими подіями:

Δt_ст= Δt₀.

Натомість величина Δt_год вимірюється рухомим годинником, отже вона є лабораторним проміжком часу між подіями:

Δt_год = Δt.

Так само довжина l₀ нерухомого в K′-системі відліку стержня є його власною довжиною. Відповідно, довжина l стержня в К-системі, в якій він рухається, є лабораторною довжиною. Відтак із зіставлення виразів (1.8) і (1.8а) виходить:

\(\frac{l}{l_0}=\frac{\Delta{t}_0}{\Delta{t}}\),

і з урахуванням співвідношення (1.7)

Формула (1.9) показує, що довжина рухомого стержня (лабораторна довжина), у напрямку руху в \(\sqrt{1-(V/c)^2}\) раз менша, ніж його власна довжина. Отже

власні поздовжні розміри предмета є найбільшими.

Скорочення довжин у напрямку руху, як і вповільнення часу, є кінематичним ефектом. Менше значення поздовжньої довжини рухомого стержня, порівняно з нерухомим, пояснюється не виникненням у ньому якихось механічних напруг і деформацій, а відносністю самого простору – в різних системах відліку просторові масштаби (розміри одиниці довжини) є не однакові.

Слід іще раз наголосити, що в співвідношенні (1.9) величини l і l₀ – то є поздовжні розміри тіла (стержня), тобто, розміри в напрямку руху. Що ж до поперечних розмірів, то вони не змінюються, позаяк в обох системах відліку відсутній рух тіла вздовж поперечних осей Y, Y′ та Z, Z′.

Розглянуті радикальні висновки, що випливають із постулатів Ейнштейна, ставлять два очевидні запитання: 1) чому класична механіка, що, в очевидь, спирається на принципово хибні уявлення про простір і час, дозволяє визначати рух тіл із винятково високою точністю, і 2) чи мають експериментальне підтвердження ефекти уповільнення часу (1.7) та скорочення масштабів (1.9)? Відповідь на перше запитання дає масштаб величини c = 3·10⁸ м/с. Для макроскопічних тіл, які класична механіка тільки й розглядає, величина с є недосяжною. Навіть найшвидші макроскопічні тіла – космічні тіла і ракети – рухаються із швидкостями не більшими, ніж ~ 10⁴ м/ с. При таких швидкостях (V/c)² ~ 10^–8 , і формули (1.7) і (1.9) з величезною точністю дають Δt = Δt₀ і l = l₀. Тому відносність простору та часу й численні пов’язані з цим релятивістські ефекти стають відчутними лише при гранично високих швидкостях, які, крім світла, притаманні тільки елементарним частинкам високих енергій. Що ж до уповільнення часу, то цей ефект (формула (1.7)) підтверджено на тільки опосередковано, а й безпосередніми вимірами.

1.3. Перетворення Лоренца

Відносність простору та часу означає, що перетворення Галілея (1.30), (1.31), (1.32), які ґрунтуються на концепції абсолютного простору й абсолютного часу, є принципово помилковими й потребують ревізії. Далі розглядаються:

1.3.1. Формули перетворень Лоренца

1.3.2. Відстані і проміжки часу

1.3.3. Інтервал

1.3.1. Формули перетворень Лоренца

Правильні перетворення координат і часу, що задовольняють і постулати Ейнштейна, можна знайти в різний споіб, до прикладу, в такий.

Розглянемо дві “стандартні” інерціальні системи відліку K і K′, осі X та X′ яких співпадають, а осі Y, Y′ і Z, Z′ мають однакові напрямки (рис. 6.5).

За початок відліку часу в обох системах приймаємо момент, коли початки координат O і O′ й відповідні координатні осі обох систем співпадають. Нехай в К-системі в якійсь точці А з координатами (x, y, z) в момент часу t відбулася певна подія, приміром, спалахнула лампочка. Постає питання, які координати (x′, y′, z′) має ця точка і в який момент часу t′ відбувається ця подія для спостерігача K′-системи відліку, що рухається відносно К із швидкістю \(\vec{V}\).

де функціональний множник γ, яний підлягяє визначенню, має прагнути до одиниці при монотонному зменшенні швидкості V.

В обох співвідношеннях фігурує одна й та сама величина γ, тим самим вони задовольняють принцип відносності (І постулат СТВ), адже обидві системи відліку є повністю рівноправними й відрізняються тільки напрямком відносного руху (знаком проєкції \(\vec{V}\)). Через відносність часу, перетворення (t, t′) теж не можуть бути тривіальними, оскільки при t = t′ з перетворень (1.10) і (1.10а) виходить γ = 1, і вони переходять у перетворення Галілея. Загальний вигляд перетворень часу можна встановити, якщо підставити в (1.10а) замість координати х її вираз (1.10) і розв’язати отримане рівняння відносно t:

З урахуванням принципу відносності, зворотне перетворення має вигляд:

У цьому можна переконатися, визначивши t′ безпосередньо з (1.11).

Шукані перетворення мають задовольняти ще й умову сталості швидкості світла с (ІІ постулат СТВ). Аби накласти цю умову розглянемо ще один позірний експеримент. Нехай в момент часу t = t’ = 0, коли точки O і O′ співпадали, спалахнула лампочка, закріплена в початку координат якоїсь із даних двох систем відліку. Оскільки швидкість світла в обох системах дорівнює с, поширення світлового сигналу вздовж осей X, X′ описується рівнянням x = ct, і x′ = ct′. Підставивши ці вирази в (1.10) і (1.10а), отримаємо: ct = γ(c + V)t′ i ct′ = γ(c - V)t. Нарешті, перемноживши ліві та праві частини цих виразів, знайдемо, що

Підставляючи знайдену величину γ у (1.10), (1.10а) і (1.11), (1.11а) та враховуючи збіг поперечних координат, дістанемо перетворення координат і часу, що задовольняють постулати СТВ і називаються перетвореннями Лоренца:

або

1.3.2. Відстані і проміжки часу

Із перетворень Лоренца випливає низка важливих наслідків. Зокрема, розглянуті рпніше ефекти скорочення довжин і уповільнення часу є прямо випливають із формул (1.13) і (1.13а). Переконаємовь у цьому.

Лоренцове скорочення довжин. Розглянемо на основі перетворень Лоренца дослід по визначенню довжини стержні в двох системах відліку, описаний в п.1.2.3. Нехай, як і там, стержень закріплено системі відліку K′, яка рухається із швидкістю V відносно нерухомої К-системи відліку:

Тоді власна довжина стержня l₀ = l′, і дорівнює різниці координат кінців стержня:

Лабораторна довжина стержня в К-системі l = x₂ - x₁ теж дорівнює різниці координат його кінців, але тільки за умови, що вони виміряні одночасно. Відтак, замінивши в (1.14) штриховані величини нештрихованими і врахувавши, що t₂ = t₁, отримаємо співвідношення (1.9):

Цей ефект є прямим наслідком перетворень Лоренца, тому  називається лоренцовим скороченням довжин (або масштабів).

Уповільнення часу. Аналогічно можна отримати й ефект уповільнення часу. Нехай у міжзоряній ракеті, котра віддаляється від Землі із швидкістю V (К′-система відліку), вібуваються дві події, приміром, спалахує й гасне лампочка, що розділені власним проміжком часу

Тоді, зважаючи на те, що на землі обидві події спостерігаються в одній точці \({{{x}}_{1}}={{{x}}_{2}}\), і провівши заміну в (1.15) штрихованих величин на нештриховані за формулою (1.13), для лабораторного проміжку часу між указаними подіями отримаємо вираз (1.7):

1.3.3. Інтервал

Із перетворень Лоренца (1.13) і (1.13а) випливє також  висновок про те, що проміжок часу між двома подіями в одній системі відліку залежить не тільки від проміжку часу між ними в іншій системі відліку, а й від відстані між точками, в яких відбулися ці події. У цьому легко пересвідчитись.

Нехай в К-системі відліку в двох точках на осі ОХ, які розташовані на відстані  Δx = х₂ – х₁   у моменти, відповідно,  t₁ і t₂ вібулися дві події, розділені заданим інтервалом часу  Δt = t₂  – t₁. Аби визначити, чому дорівнює проміжок часу Δt′ = t₂′  – t₁′, що відділяє ці події в системі відліку К′,  треба за допомогою перетворень (1.13а) виразити моменти часу t₂′ і t₁′ через задані величини t₂  і t₁ . Відтак після елементарних перетворень вийде:

\(\Delta {t}'=\frac{\Delta t-\left( {V}/{{{c}^{2}}}\; \right)\Delta x}{\sqrt{1-{{\left( {V}/{c}\; \right)}^{2}}}}\).

Із цього виразу видно, що в загальному випадку співвідношення проміжків часу між двома подіями залежить не лише від ефекту уповільнення часу, а й від відстані муж точками, в яких відбуваються ці події.  Це є свідченням того, що

простір і час є органічно взаємопов’язані.

Тому слід говорити не про окремі простір і час, а про єдиний “простір-час”. Яскравим проявом цього є те, що попри відносність відстаней та проміжків часу, існує така їхня комбінація, котра є інваріантом перетворень Лоренца, тобто, абсолютною кінематичною величиною, що не залежить від інерціальної системи віліку, в якій розглядається. Ця величина називається просторово-часовим інтервалом s (коротко — інтервалом) між двома подіями і визначається виразом:

де (t₁, x₁, y₁, z₁) і (t₂, x₂, y₂, z₂) – просторово-часові координати подій.

Інваріантність інтервалу, (тобто те, що \({s}_{12}^2={s'}_{12}^2 \)), можна довести прямими обчисленнями після заміни у виразі (1.19) нештрихованих величин на штриховані на основі перетворень Лоренца (1.13). Інваріантні величини позначають як “inv”, тож можна записати:

Зауважимо, що інваріантні величини мають велике теоретичне та практичне значення в різних розділах фізики. При цьому в кінематиці СТВ, окрім інтервалу, інваріантами перетворень Лоренца є власний проміжок часу і власна довжина l₀, а також гранична швидкість,  про яку говориться нижче.

В залежності від того, яка складова інтервалу переважає, інтервали поділяють на простороподібні (l₁₂ > cΔt₁₂), часоподібні (cΔt₁₂ > l₁₂) та світлоподібні (l₁₂ = cΔt₁₂).

При цьому, коли інтервал між двома подіями є простороподібним, то при будь-яких можливих відстанях Δl і проміжках часу Δt між подіями в даній К-системі відліку  існує інша система відліку К′, в якій ці події відбуваються одночасно (Δt′₁₂ = 0) на відстані одна від одної

\(\Delta {{{l}'}_{12}}=\sqrt{{{l}_{12}}^{2}-{{c}^{2}}\Delta {{t}^{2}}}\)

Аналогічно при  часоподібному інтервалі між подіями  в К-системі відліку існує К′-система відліку, в якій ці події відбуваються в одному місці (\({l'}_{12}=0 \)) з ітервалом часу

\(\Delta {{{t}'}_{12}}=\sqrt{{{c}^{2}}\Delta {{t}^{2}}-{{l}_{12}}^{2}}\)

Зауважимо також, що у випадку простроподібного інтервалу між подіями (\({l}_{12}>c\Delta{t}_{12}\)), вони є незалежними і не можуть впливати одна на одну, позаяк такий вплив не може передаватись у просторі швидше, ніж із граничною швидкістю c, і за час Δt подолати  відстань Δl. На відміну від цього, при часоподібному або світлоподібному інтервалі, коли \({c}\Delta{t}_{12}\ge{l}_{12}\), причинно-наслідковий зв’язок між подіями є можливим.

1.4. Перетворення швидкостей в СТВ. Гранична швидкість

Перетворення швидкостей. Установимо тепер формули перетворення швидкостей в СТВ, тобто, формули, котрі пов’язують між собою швидкості руху частинки в двох різних інерціальних системах відліку – нерухомій К-системі та в К′-системі, що рухається відносно К із швидкістю V уздовж осі ОХ. Нехай частинка в К-системі відліку рухається із швидкістю \(\vec{v}\),  яка визначається компонентами

Аналогічно швидкість частинки в K′-системі \(\vec{v}' \) визначається компонентами

Аби знайти зв’язок між швидкостями частинки в штрихованій і нештрихованій системі відліку, виразимо проміжок часу та переміщення вздовж осей  в К′-системі відліку через відповідні величини в К-системі. Для цього продиференціюємо співвідношення (1.13):

\(\mathrm{d}{x}'=\frac{\mathrm{d}x-V\mathrm{d}t}{\sqrt{1-{{\left( {V}/{c}\; \right)}^{2}}}}\), \(\mathrm{d}y'=\mathrm{d}y \), \(\mathrm{d}z'=\mathrm{d}z \), \(\mathrm{d}{t}'=\frac{\mathrm{d}t-\frac{V}{{{c}^{2}}}\mathrm{d}x}{\sqrt{1-{{\left( {V}/{c}\; \right)}^{2}}}}\).

Після підстановки цих виразів у (1.15а) і заміни (V/c) = β матимаємо:

\({v'}_x=\frac{\mathrm{d}x-V\mathrm{d}t}{\mathrm{d}t-\frac{V}{c^2}\mathrm{d}x}=\frac{\frac{\mathrm{d}x}{\mathrm{d}t}-V}{1-\frac{V}{c^2}\cdot\frac{\mathrm{d}x}{\mathrm{d}t}}\),

\({{{v}'}_{y}}=\frac{\mathrm{d}y\sqrt{1-{{\beta }^{2}}}}{\mathrm{d}t-\frac{V}{{{c}^{2}}}\mathrm{d}x}\)=\(\frac{\frac{\mathrm{d}y}{\mathrm{d}t}\cdot \sqrt{1-{{\beta }^{2}}}}{1-\frac{V}{{{c}^{2}}}\cdot \frac{\mathrm{d}x}{\mathrm{d}t}}\)

\({v'}_z=\frac{\mathrm{d}z\sqrt{1-\beta^2}}{\mathrm{d}t-\frac{V}{c^2}\mathrm{d}x}\) = \( \frac{\frac{\mathrm{d}z}{\mathrm{d}t}\cdot \sqrt{1-{{\beta }^{2}}}}{1-\frac{V}{{{c}^{2}}}\cdot \frac{\mathrm{d}x}{\mathrm{d}t}}\).

Урахувавши (1.15), отримаємо остаточно:

Ці формули виражають релятивістський закон перетворення швидкостей. При малих швидкостях (V << c і v << c) вони трансформуються в класичний закон додавання швидкостей (розділ І, (1.33), (1.33а)), виражений в координатній формі. В цьому зв’язку звернімо увагу на те, що y- i z- проєкції швидкості частинки в одній системі відліку залежать не тільки від однойменних проєкцій в іншій, а й від х-проєкції швидкості. Тому для релятивістської частинки неможливо виразити зв’язок між швидкостями безпосередньо у векторній формі.

Гранична швидкість. Визначення за формулами (1.16), (1.16а) величини (модуля) та напрямку швидкості частинки в одній системі відліку через ці характеристики, задані в іншій системі відліку, потребує громіздких викладок. Тому при аналізі загальних наслідків з релятивістського закону перетворення швидкостей для більшої прозорості розглядають випадок руху частинки паралельно до осей X, X′ систем відліку. В такому разі поперечні компоненти швидкості дорівнюють нулю, і величина та напрям швидкості частинки в обох системах відліку визначаються тільки однією проєкцією^[8] \({v_x}\) або \({{v'}_x}\).

Розглянемо приклади застосування формул (1.16) і (1.16а) за вказаних умов.

Приклад 1. Нехай спостерігач у рухомій K′-системі відліку вимірює швидкість c′ світлового променя, що йде вздовж осі O′X′ від джерела, закріпленого в початку відліку О нерухомої К-системи відліку. В К-системі швидкість променя дорівнює с, тому, згідно з (1.16),

\( {c}^{\prime}=\frac{c-V}{1-\frac{Vc}{{{c}^{2}}}}=c \)

Отже, в обох системах відліку світловий промінь поширюється з однаковою швидкістю. Взагалі, в цьому немає нічого несподіваного, адже постулат сталості швидкості світла “було закладено” в самі перетворення Лоренца, з яких випливає цей результат.

Приклад 2. Із космічної ракети, що віддаляється від Землі зі швидкістю 0,8с, випустили в напрямку руху зонд із швидкістю 0,6с відносно ракети. Визначимо швидкість зонда v відносно Землі. Для цього пов’яжемо із Землею нерухому К-систему відліку, а з ракетою –  рухому K′-систему. Тоді V = 0,8c i v′ = 0,6c. Підставляємо ці значення у відповідну формулу (1.16а) і отримуємо:

\({v}=\frac{0,6c+0,8c}{1+0,48}\approx0,95c \).

Отже, виходить v < c, тоді як згідно з класичним законом (1.33а) і “здоровим глуздом” мало би вийти 1,4 с.

Приклад 3. Нехай дві елементарні частинки 1 і 2 рухаються назустріч одна одній паралельно осі ОХ К-системи відліку з однаковою швидкістю \({v_1=v_2=nc}\). Визначимо відносну швидкість частинок v, наприклад, швидкість руху другої відносно першої. Для цього перейдемо в K′-систему відліку, котра рухається відносно К із швидкістю першої частинки \({V=v_1}\). Тоді в K′-системі перша частинка є нерухомою, тож швидкість другої частинки в цій системі відліку \({v'}_2={v}\) і є шуканою швидкістю другої частинки відносно першої. Відтак, підставивши в (1.16) проєкції заданих швидкостей, знайдемо:

Знак “–” відображає те, що частинка 2 рухається назустріч частинці 1.

Формальний аналіз виразу (1.17) показує, що відносна швидкість частинок \({v\le{c}}\) при будь-яких значеннях n. Справді, при малих швидкостях (n << 1) модуль відносної швидкості v ≈ 2nc і зростає при збільшенні n. Але при n >> 1 величина v ≈ 2c/n і зменшується при зростанні n. Отже, при деякому значенні n = n_m відносна швидкість має максимум v = v_max . Значення n_m і величину v_max не важко знайти методами вищої математики. А саме, треба взяти похідну від виразу в знаменнику (1.17) і прирівняти її до нуля:

\(\left(\frac{1}{n}+n\right)'=-\frac{1}{n^2}+1 \) \( \Rightarrow \) \( \frac{1}{n_m}=1\,\,\,\,\,\,\,\,n_m=1 \).

Підставивши це значення в (1.17) і отримуємо для модуля v_max = c .

Таким чином, максимальна можлива швидкість руху однієї частинки (одного тіла) відносно іншої частинки (іншого тіла) дорівнює величині с. Але ж саме поняття руху визначене (тобто, має зміст) тільки по відношенню до якогось іншого тіла (тіла відліку). Тому за будь-яких умов швидкість руху тіла

Інакше говорячи, в природі існує гранична швидкість. Це означає, що

швидкість будь-якого матеріального^[3] об’єкта ні за яких умов не може бути більшою, ніж c = 3·10⁸ м/с .

Це, зокрема, пояснює інваріантність швидкості світла у вакуумі: оскільки вона має граничну величину, то не може залежати від системи відліку.

Контрольні запитання

1. 1. Що спонукало створення спеціальної теорії відносності?
   2. Сформулюйте постулати Ейнштейна.
   3. У чому полягає відміна між принципом відносності Ейнштейна та принципом відносності Галілея?
   4. Які висновки про властивості простору й часу випливають із постулатів Ейнштейна?
   5. На підставі яких міркувань можна твердити, що поперечні координати точки в різних системах відліку однакові?
   6. Що таке власна та лабораторна довжина стержня? Як вони пов’язані між собою?
   7. Що таке власний та лабораторний проміжок часу? Як вони пов’язані між собою?
   8. На основі чого можна зробити висновок про те, що простір і час не є незалежними одне від одного ?
   9. Чому говорять, що скорочення поздовжньої довжини тіла та скорочення проміжку часу між подіями є взаємними ефектами?
   10. Що таке релятивістський інтервал між подіями? Які бувають типи інтервалів?
   11. При якому типі інтервалу між подіями не може бути причинно-наслідкового зв’язку?
   12. Згідно з перетвореннями Лоренца, поперечні координати рухомої точки в різних ІСВ однакові (y = y′; z = z′) . Чому ж тоді не однакові поперечні проєкції швидкості (v_y, v′_y та v_z, v′_z ?

       1. [1] Так називають удаваний дослід, який не суперечить законам фізики, але є технічно нездійсненним. У теорії позірний експеримент використовується як один із способів доведення.

       2.  [2] Сравді, коли б це було не так, то, зробивши мітку від верхнього кінця стержня, що пролітає, на нерухомій осі АВ К-системи і побачивши, що вона не співпадає з точкою В, ми б узнали, яка з двох систем відліку рухається, а яка перебуває в спокої. Але це неможливо, відповідно до принципу відносності.

       3. [3] На цьому слід спеціально наголосити: йдеться про рух матеріальних частинок або поширення випромінювання, тобто, про процеси, що супроводжуються перенесенням енергії і, тим самим, можуть бути використані для передачі сигналів (інформаці