physics.zfftt.kpi.ua

Радіус-вектор, траєкторія, шлях, переміщення. Положення точки у просторі можна задати вектором, проведеним із початку відліку в цю точку (рис.1.1), який називається її радіусом-вектором \( \vec{r} \).

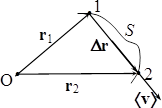
Рухома частинка, отже й кінець її радіуса-вектора, описує в просторі неперервну лінію, котра називається траєкторією руху. Можна сказати, що траєкторія є геометричним місцем точок кінця радіуса-вектора частинки, що рухається. Довжина відрізка траєкторії між двома даними точками називається шляхом, пройденим частинкою за відповідний проміжок часу. Шлях визначає відстань, яку пройшла частинка вздовж траєкторії, але шлях не містить жодної інформації про її кінцеве положення. Тому для визначення зміни положення точки в просторі використовують

переміщення \( \Delta\vec{r} \) – вектор, який проводять із початкового в кінцеве положення точки на траєкторії (рис. 1.1).

Очевидно, що

Модуль вектора переміщення \( |\Delta\vec{r}| \) дорівнює відстані між початковим та кінцевим положенням точки на траєкторії і в загальному випадку не дорівнює пройденому шляху S (рис. 1.1.): \( \left|\Delta\vec{r}\right| \le S \).

Але переміщення \( \mathrm{d}\vec{r} \) за нескінченно малий проміжок часу співпадає з відповідною нескінченно малою ділянкою траєкторії (рис. 1.2).

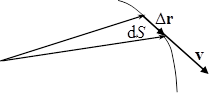
Тому модуль вектора елементарного переміщення \( \left|\mathrm{d}\vec{r}\right| \) і пройдений точкою шлях dS збігаються:

Вектор \( \mathrm{d}\vec{r} \) є напрямлений по дотичній до траєкторії, тож указує напрям руху тіла в даній точці траєкторії.

Швидкість. Стан руху точки визначається не просто зміною її положення в просторі, а тим, як ця зміна відбувається у часі. Наближено це відображає відношення переміщення \( \Delta{\vec{r}} \) до проміжку часу Δt, за який воно здійснене. Така величина називається середнім вектором швидкості (або вектором середньої швидкості переміщення) \( \langle\vec{v}\rangle \):

Напрям вектора \( \langle\vec{v}\rangle \) співпадає з напрямом вектора переміщення (рис.1.1), і його модуль

Слід зазначити, що вектор середньої швидкості є визначеним тільки для заданого проміжку часу Δt, тож для різних проміжків він може відрізнятись як за модулем, так і за напрямком. Але при поступовому зменшенні величини Δt відношення \( \Delta{\vec{r}}/ \Delta{t} \) прямує до визначеної границі \( \vec{v} \), яка є точною характеристикою руху в кожну мить і називається миттєвою швидкістю (або просто швидкістю):

Оскільки переміщення \( \Delta\vec{r} \) є приростом радіуса-вектора, то миттєва швидкість є похідною від радіуса-вектора по часу^[1]. При цьому вектор \( \vec{v} \) є співнапрямлений з вектором \( \mathrm{d}\vec{r} \) , отже,

вектор миттєвої швидкості в кожній точці напрямлений по дотичній до траєкторії .

Вектор \( \vec{v} \) показує не тільки як швидко, а й у якому напрямі переміщується тіло в кожен момент часу. Тому говорять, що вектор швидкості є мірою стану руху тіла. Зокрема, поведінка вектора швидкості дає загальну інформацію про характер руху. До прикладу, якщо \( \vec{v}=\mathrm{const} \), то ані величина, ані напрям швидкості не змінюються, тож тіло рухається рівномірно і прямолінійно. Якщо ж незмінною лишається тільки модуль вектора швидкості, то тіло здійснює рівномірний криволінійний рух, тощо.

У практичних задачах часто буває істотним не напрям руху, а лише швидкість подолання тілом шляху. Тому, крім величин \( \left\langle\vec{v}\right\rangle \) і \( \vec{v} \), використовують середню \( \langle{v}\rangle \) та миттєву v скалярні або шляхові швидкості, які означають через пройдений шлях аналогічно до співвідношень (1.2) і (1.3):

і

Зауважимо, що із співвідношення (1.1а) випливає, що миттєва шляхова швидкість v збігається із модулем вектора миттєвої швидкості, але для середніх швидкостей це, на загал, не так.

Прискорення. Ще однією характеристикою руху є прискорення. Вектор миттєвого прискорення (або просто прискорення) \( \vec{a} \) визначає швидкість зміни вектора швидкості у часі й уводиться аналогічно до миттєвої швидкості:

тобто прискореня – це похідна від вектора швидкості, або ж друга похідна від радіуса-вектора по часу^[2]. Вектор прискорення збігається за напрямом з вектором \( \Delta{\vec{v}}\) і в загальному випадку складає певний кут із напрямом швидкості (рис. 1.3).

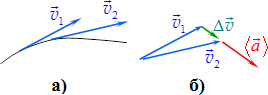
Якщо рух є рівнозмінним (\( \vec{a}=\mathrm{const} \)), то прискорення визначається виразом

де Δt = t₂ - t₁ – проміжок часу, за який швидкість змінюється на величину \( \Delta{\vec{v}} \).

При нерівномірній зміні швидкості цей вираз визначає середнє прискорення \( \langle\vec{a}\rangle \) за час Δt.

Загальні рівняння кінематики точки. Коли задано закон руху точки, тобто залежність радіуса-вектора від часу \( \vec{r}=\vec{r}(t) \), то за допомогою співвідношень (1.2) – (1.7) легко знайти всі інші характеристики руху. Але на практиці найчастіше відомим є  прискорення^[3] \( \vec{a}=\vec{a}(t) \), і завдання полягає у визначенні через нього решти кінематичних величин. Це роблять за допомогою загальних рівнянь швидкості, переміщення (радіуса-вектора) та шляху, котрі встановлюються за допомогою методів інтегрального числення.

З формули (1.6) випливає, що за проміжок часу dt приріст вектора швидкості \( \mathrm{d}\vec{v}=\vec{a}\mathrm{d}t \). Зміна швидкості за скінчений проміжок часу дорівнює сумі (точніше – інтегралу) всіх елементарних змін \( \mathrm{d}\vec{v} \):

Якщо розглядати проміжок часу від початкового t = 0 до довільного моменту t, то з (1.8) отримаємо загальне рівняння швидкості:

де \( \vec{v}_0=\vec{v}(0) \) – початкова швидкість рухомої точки, тобто швидкість у момент часу t = 0.

Аналогічними міркуваннями на основі співвідношення (1.3) встановлюються загальні рівняння для переміщення та радіуса-вектора:

де \( \vec{r}_0=\vec{r}(0) \) – початковий радіус-вектор, який визначає положення рухомої точки в момент t = 0.

Зауважимо, що аби знайти швидкість і положення тіла в заданий момент часу, крім прискорення \( \vec{a}=\vec{a}(t) \), треба знати початкові умови — початкове положення тіла \( \vec{r}_0 \) та його початкову швидкість \( \vec{v}_0 \). Але ці величини не потребують попереднього визначення, позаяк “задаються” вибором системи відліку, в якій розглядається рух.

Рівняння для пройденого точкою шляху встановлюється аналогічно через шляхову швидкість (модуль вектора швидкості) із співвідношення (1.5):

Підставляючи в отримані загальні рівняння заданий закон зміни прискорення \( \vec{a}=\vec{a}(t) \), можна отримати рівняння кінематики для будь-якого конкретного виду руху. Нехай, до прикладу, маємо рух тіла з відомим сталим прискоренням \( \vec{a}=\mathrm{const}\) . Тоді, згідно із рівнянням (1.9),

Це відомий з елементарної фізики закон зміни швидкості при русі зі сталим вектором прискорення. Підставивши отриманий вираз \( \vec{v} \) у рівняння (1.11), так само отримаємо відоме рівняння для радіуса-вектора при вказаному русі:

Аналогічно можна отримати рівняння кінематики й для складніших рухів, у яких прискорення змінюється з часом.

1.2. Координатний спосіб опису руху

Векторні співвідношення компактно і повно відображують фізичний зміст величин і зв’язки між ними, але при розрахунках вектори треба задавати числами. Тому, крім векторного, використовують координатний спосіб опису руху. В такому разі з тілом відліку жорстко зв’язують певну систему координат, найчастіше декартову, і положення точки в просторі визначають координатами – числами x, y, z. Ці числа дорівнюють відстаням (з тим, чи іншим знаком) від початку координат О до проєкції точки на відповідну координатну вісь, рис. 1.4а.

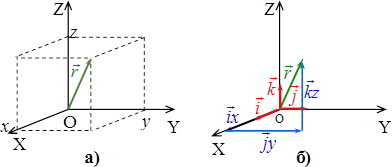
Відтак закон руху точки визначається системою рівнянь залежностей координат від часу:

Очевидно, що декартові координати точки є проєкціями кінця радіуса-вектора на осі координат OX, OY, OZ: x = r_x = rcosα, y = r_y = rcosβ, z = r_z = rcosγ, де α, β, γ – "напрямні кути", тобто кути між напрямками радіуса-вектора \( \vec{r} \) та осей OX, OY, OZ (на рис. 1.4а показано тільки один з них). Тому можна записати:

де \( \vec{i},\,\,\vec{j},\,\,\vec{k} \) – одиничні базисні вектори (орти), які визначають напрямки осей декартової системи координат (рис. 1.4б) і утворюють її базис.

Отже, знаючи координати точки, можна обчислити модуль її радіуса-вектора та, через напрямні косинуси, його напрям:

Продиференціювавши вираз (1.16) по часу і врахувавши означення (1.3), отримаємо вираз швидкості точки в координатній формі:

Отже, похідні координат по часу – то є проєкції вектора швидкості на відповідні осі:

Тому за заданим законом руху в координатній формі (1.15) можна визначити проєкції вектора швидкості (1.19), а також його модуль і напрям:

Аналогічно визначаються й параметри вектора прискорення при координатному способі опису руху:

З усього сказаного в цьому пункті випливає наступний загальний порядок (алгоритм) розв’язування векторних рівнянь. 1. Векторне рівняння “проєктується” на координатні осі, тобто замість нього записується відповідна система алгебраїчних рівнянь для проєкцій. 2. З отриманих алгебраїчних рівнянь визначаються проєкції шуканих векторів і, нарешті, якщо необхідно, через знайдені проєкції визначаються модулі та напрямки шуканих векторів. У нескладних ситуаціях деякі етапи описаного алгоритму ми виконуємо автоматично, не виписуючи їх на папері. Як приклад, отримаємо з векторних рівнянь (1.9) і (1.11) рівняння для проєкцій вектора швидкості та для координат точки через відомі проєкції вектора прискорення:

Аналогічно з рівнянь (1.13) і (1.14) для руху із сталим прискоренням отримаємо:

Із цих рівнянь можна також отримати корисні для розв’язування задач співвідношення:

Для задання напряму руху та вектора швидкості з точкою зв’язують одиничний вектор (орт) \( \vec{\tau} \) дотичної до траєкторії, спрямований в бік збільшення координати рис. 1.5.

В такому разі можна записати:

\( \vec{v}={{v}_{\tau }}\vec{\tau } \)

де \( v_{\tau}=\mathrm{d}l/ \mathrm{d}t \) – проєкція вектора швидкості на напрям \(\vec{\tau} \). Швидкість \( v_{\tau} \) є величиною алгебраїчною, її знак залежить від напрямку руху точки, а модуль дорівнює модулю вектора швидкості:

\( |v_{\tau}|=|\vec{v}|=v. \)

Вектор прискорення точки, котрий при такому способі опису називається повним прискоренням, відповідно до означення (1.6), виражається як

\(\vec{a}=\frac{\mathrm{d}(v_{\tau}\vec{\tau})}{\mathrm{d}t}=\frac{\mathrm{d}v_{\tau}}{\mathrm{d}t}\vec{\tau}+v_{\tau}\frac{\mathrm{d}\vec{\tau}}{\mathrm{d}t} \)

і має дві складові. Перша з них

напрямлена по дотичній до траєкторії (рис. 1.6в) і називається тангенціальним прискоренням і визначає зміну модуля вектора швидкості.

Тому для будь-якого рівномірного руху тангенціальне прискорення \( \vec{a}_{\tau} =0 \).

З’ясуємо зміст другої складової вектора повного прискорення, котра називається нормальним прискоренням:

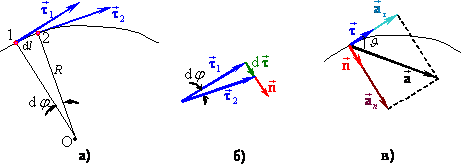
Візьмемо до уваги те, що елементарна ділянка \( \mathrm{d}l \) будь-якої кривої співпадає з дугою певного кола (кола кривизни) з відповідним центром (центром кривизни О) та радіусом R - радіусом кривизни (рис. 1.6а). Урахувавши це, визначимо похідну \( \mathrm{d}\vec{\tau}/\mathrm{d}t \). Приріст орта \(\vec{\tau} \) за гранично малий проміжок часу dt є зумовлений його поворотом на нескінченно малий кут dφ при переміщенні точки по траєкторії на нескінченно малу відстань \( \mathrm{d}l \) (рис. 1.6а,б). Очевидно, що кути повороту орта \( \vec{\tau} \) і радіуса кривизни траєкторії R однакові, отже

\(\left|\frac{\mathrm{d}\tau}{\tau}\right|=\frac{\mathrm{d}l}{R}\,\,\,\,\Rightarrow\,\,\,\,|\mathrm{d}\tau|=\frac{\mathrm{d}l}{R}. \)

Оскільки кут dφ є нескінченно малим, то вектор \( \mathrm{d}\vec{\tau} \) напрямлений перпендикулярно до вектора \( \vec{\tau} \) (рис. 1.6б). Тому, якщо ввести орт (одиничний вектор) нормалі до траєкторії \( \vec{n} \), то вектор \( \mathrm{d}\vec{\tau} \) можна подати у вигляді

\( \mathrm{d}\vec{\tau}=|\mathrm{d}\vec{\tau}|\vec{n}=\frac{\mathrm{d}l}{R}\cdot\vec{n}. \)

Поділивши цей вираз на dt, дістанемо:

\( \frac{\mathrm{d}\vec{\tau}}{\mathrm{d}t}=\frac{1}{R}\cdot\frac{\mathrm{d}l}{\mathrm{d}t}\vec{n}=\frac{v}{R}\vec{n}. \)

Отже, згідно з виразом (1.27),

Цей вектор у кожній точці напрямлений по нормалі до центра кривизни траєкторії і тому називається нормальним (або доцентровим) прискоренням. Він показує, як швидко повертається орт \( \vec{\tau} \), тобто, як швидко змінюється напрям руху точки. Тому при прямолінійному русі \( \vec{a}_n=0 \).

Повне прискорення \(\vec{a} \) (рис. 1.6в) дорівнює сумі тангенціального та нормального:

Його модуль

Напрям вектора повного прискорення визначається кутом \(\vartheta \) (рис. 1.6в), причому

Розглянемо дві системи відліку із збіжними осями X, X′ й однаково напрямленими іншими осями координат – нерухому K і рухому K′, що рухається зі швидкістю \( \vec{V}=\mathrm{const} \) відносно K-системи у додатному напрямку осей X, X′. (рис. 1.7).

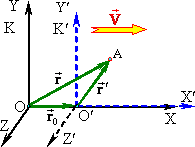
Уважатимемо також, що в початковий момент часу системи K і K′ збігалися. Тоді в довільний момент t положення точки O′ відносно О визначається радіусом-вектором \( \vec{r}_0=\vec{V}t \). Положення довільної точки А в K- і K′-системах визначаються радіусами-векторами \( \vec{r} \) та \( \vec{r}' \), які пов’язані співвідношеннями

або

Ці співвідношення виражають перетворення Галілея у векторній формі. Вони дозволяють визначати положення точки в одній системі відліку, якщо відоме її положення в іншій. При цьому вважається самоочевидним, що час є абсолютним, тобто тривалість будь-яких процесів, приміром руху тіл, не залежить від системи відліку, тож

Перетворення Галілея в координатній формі , згідно з (1.16), мають вигляд:

Взявши першу та другу похідні по часу від виразів (1.30) і (1.30а), знайдемо формули перетворення швидкостей і прискорень: