ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
VI. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ
2. Релятивістська механіка
Радикальний перегляд основ кінематики в СТВ вимагає аналізу та ревізії й основних положень класичної динаміки. Це, зокрема стосується поняття імпульсу, зв’язку між силою та прискоренням, поняття енергії, тощо.
Нижче мова піде про таке:
2.2. Основне рівняння релятивістської динаміки
Релятивістський імпульс. Важливе місце в механіці та інших розділах фізики посідає імпульс – величина, що в класичній механіці визначається добутком маси тіла на його швидкість. Значною мірою це зумовлено тим, що для імпульсу виконується закон збереження, за яким імпульс замкненої системи за будь-яких умов лишається незмінним. Цей закон трактує про поведінку замкненої сукупності тіл всередині заданої інерціальної системи відліку й ніяк не пов’язаний із переходом від однієї системи відліку до іншої та формулами перетворення координат. Тож закон збереження імпульсу виконується і в релятивістській механіці. Але, як показує аналіз, імпульс більш складно, ніж уважалося, залежить від швидкості й визначається формулою:
|
\( \vec{p}=\frac{m\vec{v}}{\sqrt{1-(V/c)^{2}}}\). |
(2.1) |
Таким чином, імпульс нелінійно залежить від швидкості частинки, але, як і в кінематиці, це стає помітним лише при релятивістських (сумірних із с) швидкостях. Тому, за необхідності, величину (2.1) називають релятивістським імпульсом. При малих швидкостях цей вираз переходить у класичну формулу \( \vec{p}=m\vec{v}\).
Релятивістська маса. Інколи вираз імпульсу релятивістської частинки записують у “звичному” вигляді, як
|
\( \vec{p}=m_{r}\vec{v}\), |
(2.1а) |
і число
|
\( {m}_{r}=\frac{m}{\sqrt{1-(V/c)^{2}}}\) |
(2.2) |
називають релятивістською масою частинки. В такому контексті власну масу частинки m називають масою спокою[1].
Це часто спрощує проміжні викладки, але слід одразу зазначити, що поняття релятивістської маси, яке збереглося історично, є формальним і не має визначеного фізичного змісту. Зокрема, величину mr не можна розглядати як міру інертності рухомого тіла.
2.2. Основне рівняння релятивістської динаміки
Із виразу релятивістського імпульсу (2.1) зрозуміло, що \( \mathrm{d}\vec{p}/\mathrm{d}t\ne{m}\vec{a}\), отже, для релятивістської частинки другий закон Ньютона у формі \( {m}\vec{a}=\vec{F}\) не виконується. Але, як доведено, основне рівняння динаміки в більш загальній формі (розділ ІІ, (1.3)) зберігає чинність і в СТВ:
|
\( \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}\). |
(2.3) |
Це рівняння називається основним рівнянням релятивістської динаміки і, природньо, оперує релятивістським імпульсом (2.1). Розгорнуто воно записується так:
|
\( \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{m_{0}\vec{v}}{\sqrt{1-(v/c)^{2}}}\right)=\vec{F}\). |
(2.3а) |
Рівняння (2.3) можна подати й через релятивістську масу:
|
\( \frac{\mathrm{d}(m_{r}\vec{v})}{\mathrm{d}t}=\vec{F} \). |
(2.3б) |
Рівняння (2.3) і (2.3б), начебто, такі самі, як і в класичній механіці, але це є лише видимість. Насправді для релятивістської частинки немає прямого зв’язку між величиною сили та прискоренням. В цьому легко переконатись, якщо виконати диференціювання в (2.3б), взявши до уваги, що mr теж залежить від часу:
|
\( {m}_{r}\vec{a}+\vec{v}\frac{\mathrm{d}m_{r}}{\mathrm{d}t}=\vec{F}\), |
(2.4) |
де \( \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\) – прискорення частинки. При цьому, позаяк другий доданок у лівій частині рівняння (2.4) за напрямом не збігається з \( \vec{F}\) (див. рис. 6.6), то напрям прискорення частинки \(\vec{a}\) відрізняється від напрямку сили, що діє на неї.
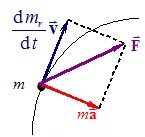
Але є два винятки з такої неординарної поведінки релятивістської частинки.
1. Діюча сила поперечна: \(\vec{F}\bot \vec{v}\). Така сила не виконує роботи, тож рух є рівномірним і mr = const. У такому разі
|
\({{m}_{r}}\vec{a}=\vec{F}\) \( \Rightarrow \) \( \frac{m\vec{a}}{\sqrt{1-{{\left( {v}/{c}\; \right)}^{2}}}}=\vec{F}\)
|
(2.4а) |
2. Діюча сила поздовжня: \(\vec{F}\parallel \vec{v}\). У такому випадку рух частинки є прямолінійним і після диференціювання рівняння (2.3а) набуває вигляду:
|
\(\frac{m\vec{a}}{{{\left( 1-{{\left( {v}/{c}\; \right)}^{2}} \right)}^{{3}/{2}\;}}}=\vec{F}\)
|
(2.4б) |
У кожному цих двох випадків прискорення частинки має напрям діючої на неї сили, а рівняння (2.4а) і (2.4б) нагадують рівняння другого закону Ньютона \(m\vec{a}=\vec{F}\). Тому в них множники при прискоренні іноді називають поперечною \({{m}_{\bot }}\) та поздовжньою \({{m}_{\parallel }}\) масами і записують \(m{{a}_{\bot }}={{F}_{\bot }}\) і \(m{{a}_{\parallel }}={{F}_{\parallel }}\). В цьоиу сенсі можна говорити, що сила дорівнює добутку маси на прискорення. Проте це не означає, що виконується другий закон Ньютона, бо все одно прискорення не є прямо пропорційним діючій на частинку силі. Зокрема, з рівняння (2.4б) видно, що при дії сталої сили прискорення, через зростання поздовжньої “маси” частинки, невпинно зменшуватиметься, простуючи до нуля при наближенні швидкості до значення v = с. Отже, основне рівняння релятивістської динаміки теж доводить граничний характер швидкості с, який раніше було отримано в кінематиці СТВ.
Наостанок відмітимо, що при малих швидкостях руху релятивістські рівняння (2.3а), (2.4а) і (2.4б), як завжди, автоматично переходять у рівняння другого закону Ньютона.
Усі розглянуті досі результати СТВ стосуються понять і величин, які відомі й у класичній механіці. Але Ейнштейн при створенні СТВ відкрив і знаменитий закон зв’язку між енергією та масою, котрому немає аналогів у ньютонівській механіці. На такий зв’язок наводить аналіз співвідношення між кінетичною енергією та роботою сил у релятивістській механіці.
Кінетична енергія релятивістської частинки. Одне з основних положень механіки – теорема про кінетичну енергію, що встановлює зв’язок між нею та роботою сил (розділ IV, п. 2), зберігає чинність і в релятивістській механіці. Але в СТВ кінетична енергія визначається іншою, ніж у класичній механіці, формулою. Для її встановлення розглянемо роботу, яку виконує якась сила \( \vec{F}\) над релятивістською частинкою на переміщенні \( \mathrm{d}\vec{r} \) (рис 6.7).
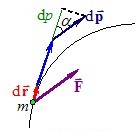
Згідно з означенням роботи
|
\(\delta A=\vec{F}{d}\vec{r}=\vec{F}\vec{v}{d}t\) |
||
Відповідно до (2.3б), \(\vec{F}{d}t={d}({{m}_{r}}\vec{v})={{m}_{r}}{d}\vec{v}+\vec{v}{d}{{m}_{r}}\), де mr – релятивістська маса. Тому
|
\(\delta A=\vec{v}\left( \vec{v}{d}{{m}_{r}}+{{m}_{r}}{d}\vec{v} \right)={{v}^{2}}{d}{{m}_{r}}+{{m}_{r}}v{d}v\), |
(2.5) |
де враховано, що \({{\vec{v}}^{2}}={{v}^{2}}\) і \(\delta A=\vec{v}\left( \vec{v}{d}{{m}_{r}}+{{m}_{r}}{d}\vec{v} \right)={{v}^{2}}{d}{{m}_{r}}+{{m}_{r}}v{d}v\), (див. рис. 6.7).
Для визначення dmr спочатку перетворимо вираз (2.2):
|
\( {m}_{r}^{2}=\frac{m^{2}}{1-(v/c)^{2}}\) \( \Rightarrow \) \( {m}_{r}^{2}-m_{r}^{2}v^{2}/c^{2}\) \( \Rightarrow \) \( {m}_{r}^{2}c^{2}-m_{r}^{2}v^{2}=m^{2}c^{2}\). |
Відтак продиференцюємо отриманий результат:
|
\( {2}m_{r}c^{2}\mathrm{d}m_{r}-2m_{r}v^{2}\mathrm{d}m_{r}-2m_{r}^{2}v\mathrm{d}{v}={0}\). |
Звідси після ділення на 2m одразу дістанемо вираз усієї правої частини (2.5):
|
v2dmr + mrvdv = c2dmr. |
(2.6) |
Отже, з урахуванням (6.8), можна записати:
|
dK = δA = c2dmr. |
(2.7) |
Звідси випливає, що приріст кінетичної енергії частинки визначається приростом її релятивістської маси. Якщо частинка перебуває у спокої, то К = 0 і mr = m. Тому, інтегруючи (2.7) у границях від 0 до К і від m до mr, знаходимо:
|
\( \int\limits_{0}^{K}\mathrm{d}K=\int\limits_{m}^{m_{r}}c^{2}\mathrm{d}{m}_{r}\), \( \Rightarrow \) \( {K}=c^{2}(m_{r}-m) \). |
(2.7а) |
Нарешті, врахувавши (2.2), одержимо формулу кінетичної енергії релятивістської частинки:
|
\( {K}=mc^{2}\left(\frac{1}{\sqrt{1-(v/c)^{2}}}-1\right) \). |
(2.8) |
При малих швидкостях (v << c) формула (2.8) теж переходить у формулу кінетичної енергії ньютонівської механіки. Щоб у цьому переконатися, розкладемо перший доданок (2.8) у степеневий ряд за формулою бінома Ньютона:
\( \frac{1}{\sqrt{1-(v/c)^{2}}}=\left(1+(v/c)^{2}\right)^{-1/2}=1+\frac{1}{2}\cdot\frac{v^{2}}{c^{2}}+\frac{3}{8}\cdot\frac{v^{4}}{c^{4}}+{...}\).
При \( {v}<< {c}\) можна обмежитися першими двома доданками, і тоді вираз (2.8) трансформується в класичну формулу
\( {K}=\frac{mv^{2}}{2}\).
(Застереження. При розв’язуванні задач інколи припускаються грубої помилки, думаючи що ця формула годиться й для релятивістської частинки, якщо під m розуміти релятивістську масу).
Із формули (2.8) випливає, що в релятивістській області при збільшенні швидкості частинки її кінетична енергія стрімко сростає так, що при v → с К → ∞. Це ще одне свідчення того, що жодну частинку неможливо розігнати до швидості с.
Взаємозв’язок енергії і маси. Якщо розкрити дужки в (2.7а), то кінетична енергія релятивістської частинки постає як різниця двох величин:
|
K = mrc2 – mc2. |
(2.9) |
Перша з них
|
E = mrc2 |
(2.10) |
стосується частинки, що рухається, і називається повною (релятивістською) енергією. Друга
|
E0 = mc2 |
(2.11) |
відноситься до тієї ж частинки в стані спокою і, відповідно, називається енергією спокою. При цьому можна подумати, що E0, подібно до релятивістської маси, є формальною величиною. Але з її уведенням кінетична енергія релятивістської частинки відповідно до (2.9) виражається дуже прозоро та природньо. А саме, кінетична енергія, як енергія руху, є різницею енергій частинки в стані руху E та в стані спокою E0:
|
K = E – E0 |
(2.12) |
Відтак Ейнштейн дійшов висновку, що енергія спокою є реальною фізичною величиною, котра визначає узагальнену внутрішню енергію частинки (тіла). Якщо частинка є складною, приміром, як ядро атома, то енергія спокою включає енергію взаємодії складових частинок ядра – нуклонів. Але не тільки це! Згідно з Ейнштейном, будь-яка частинка, навіть така, котра “ні з чого не складається”, теж має відповідну реальну енергію спокою, що здатна перетворюватися на інші види. При цьому зміна енергії спокою частинки супроводжується відповідною зміною її маси спокою:
|
\( \Delta{m}=\frac{\Delta{E}_{0}}{c^{2}}\). |
(2.13) |
Наприклад, при окисленні вуглецю (горінні) виділяється енергія, через що енергія молекули вуглекислого газу є менша, ніж сумарна енергія частинок, які беруть участь у реакції. Тому й маса спокою молекули вуглекислоти повинна бути менша, ніж сума мас спокою атома вуглецю та молекули кисню. Але в хімічних реакціях і взаємодіях макроскопічних тіл зміна маси спокою є настільки мізерною, що її неможливо виявити. Інша річ ядерні реакції, в яких взаємодіють ядра атомів або елементарні частинки надвисоких енергій. В таких процесах енергії, що виділяються та поглинаються, дозволяють не лише виявити, а й визначити на досліді різницю мас ядра та його складових частинок (так званий “дефект мас”). Зокрема, встановлено, що маса ядра будь-якого хімічного елемента менша за сумарну масу складових нуклонів у згоді з формулою (2.13). При цьому ефект є настільки значним, що дозволяє отримувати промислову енергію на атомних електростанціях. Тож формула (2.11) виражає фундаментальний закон природи – органічний зв’язок енергії з масою. Його глибинний зміст полягає в тому, що енергія є невід’ємною характеристикою матерії – будь-яка частинка чи тіло має відповідний (і дуже великий) запас енергії завдяки самому факту свого існування.
Зауважимо також, що завдяки співвідношенню (2.11), в ядерній фізиці та фізиці елементарних частинок масу прийнято вимірювати в одиницях енергії (МеВ).
Зв’язок між енергією та імпульсом. Імпульс (2.1) і повна енергія (2.10) релятивістської частинки залежать від швидкості, отже й від системи відліку. Однак існує певна комбінація цих величин, яка є релятивістським інваріантом, тобто має однакове значення в усіх інерціальних системах відліку. З формули (2.2) маємо
|
\( {m}_{r}^{2}=\frac{m^{2}}{1-(v^{2}/c^{2})}\) \( \Rightarrow \) \( {m}_{r}^{2}c^{2}=m_{r}^{2}v^{2}=m^{2}c^{2}\). |
Помноживши цей вираз на c2 і врахувавши (2.10) і (2.1а), одержимо:
|
\( {E^{2}}-p^{2}c^{2}=m^{2}c^{4}\). |
(2.14) |
Оскільки в правій частині цього виразу стоять величини, що не залежать від системи відліку, ліва частина є релятивістським інваріантом, тобто, не змінюється при переході від однієї ІСВ до іншої:
|
\( {E^{2}}-p^{2}c^{2}=\mathrm{inv} \). |
(2.15) |
Із співвідношення (2.14) безпосередньо випливає корисна формула для обчислення повної енергії релятивістської частинки із заданим імпульсом:
|
\( {E}=c\sqrt{p^{2}+m^{2}c^{2}}\), |
(2.16) |
а з (2.14) і (2.12) можна знайти зв’язок між імпульсом і кінетичною енергією релятивістської частинки:
|
\( pc=\sqrt{{{E}^{2}}-{{m}^{2}}{{c}^{4}}}=\sqrt{{{\left( K+m{{c}^{2}} \right)}^{2}}-{{m}^{2}}{{c}^{4}}}=\sqrt{K\left( K+2m{{c}^{2}} \right)} \), |
звідки
|
\( p=\frac{1}{c}\sqrt{K\left( K+2m{{c}^{2}} \right)}\). |
(2.17) |
Зауважимо, що, відповідно до цього виразу, в ядерній фізиці та фізиці елементарних частинок імпульс прийнято вимірювати в одиницях енергії (МеВ), поділених на швидкість світла c, тобто – в МеВ/с.
Укажемо також, що з формул (2.1а) і (2.10) безпосередньо випливає співвідношення, яке визначає імпульс релятивістської частинки через її енергію та швидкість:
|
\( \vec{p}=\frac{E\vec{v}}{c^{2}}\). |
(2.18) |
Безмасові частинки. Сучасною наукою встановлено, що в природі існують так звані безмасові частинки – частинки, які не мають власної маси (“маси спокою”). Такими є фотони – елементарні частинки, що переносять електромагнітне випромінювання, зокрема, світло. З деякою імовірністю безмасовими є й нейтрино та деякі інші короткоживучі частинки, що народжуються в певних ядерних реакціях.
Для безмасової частинки т = 0, і з (2.16) випливає, що
|
\( {E}={pc}\) або ж \( {p}=\frac{E}{c}\). |
(2.19) |
Ця формула узгоджується з (2.18) тільки за умови, що v = c. Отже, єдиним можливим станом безмасової частинки є рух із граничною швидкістю. Тому, стикаючись з іншими частинками, безмасові частинки або відбиваються без зміни величини швидкості, або поглинаються, тобто, припиняють своє існування. При цьому вони передають свій імпульс тілу, з яким стикаються, згідно з (2.3), створюють відповідну силу тиску. Тиск світла вперше виміряв учений Лебедєв. Отримані ним у дослідах значення тиску світла узгоджуються з теоретичними величинами, розрахованими на основі механізму зіткнень фотонів з частинками опромінюваного тіла. Це є одним із експериментальних підтверджень розглянутої концепції безмасових частинок і їхніх властивостей.
- Як відомо, величина релятивістського імпульсу p = mrv не є прямо пропорційною до величини швидкості частинки. Чи означає це, що її маса залежить від швидкості?
- Частинка має імпульс p = mc (m— маса спокою). Чому дорівнює її швидкість?
- Основне рівняння динаміки і в класичній, і в релятивістській механіці має однаковий загальний вигляд \(\left( {d\vec{p}}/{dt}\; \right)=\vec{F}\). Чи означає це, що й рухи класичної та релятивістської частинки за однакових початкових умов будуть однакові? Чому?
- Кінетична енергія частинки із власною масою m складає К = (mс2/2). Чому дорівнює швидкість частинки?
- При якій швидкості кінетична енергія будь-якої частинки дорівнює її енергії спокою?
- Покажіть, що релятивістський вираз кінетичної енергії К = (mr – m)с2 при v << с переходить у відповідну формулу класичної механіки.
- Покажіть, що вираз релятивістського імпульсу через кінетичну енергію \({p}=\frac{1}{c}\sqrt{T(2E_0+T)}\) при v << с переходить у відповідний вираз класичної механіки.
- Що таке безмасова частинка? Чому дорівнює її імпульс?
- Чим відрізняються зіткнення безмасових частинок від зіткнень “звичайних частинок”?
[1] У навчальній літературі інколи для релятивістської маси використовують символ m, а для власної маси (маси спокою) — m0.