physics.zfftt.kpi.ua

Основу динаміки складають три закони Ньютона, котрі є узагальненням результатів спостережень і спеціально поставлених експериментів і не виводяться з якихось більш простих принципів. Закони Ньютона мають і велике практичне значення, на них ґрунтуються розрахунки різноманітних машин і механізмів, будівельних конструкцій, космічних апаратів, тощо. Щоправда, закони Ньютона навіть у рамках класичної механіки, не є універсальними і виконуються тільки в так званих інерціальних системах відліку. Треба також мати на увазі, що закони Ньютона формулюються для матеріальних точок – тіл, розміри яких є неістотними при розгляді їхнього руху та взаємодії з іншими тілами.

Далі розглянуто:

1.1. Основні величини динаміки

1.2.  Перший закон Ньютона

1.3.  Другий закон Ньютона

1.4. Третій закон Ньютона

       Контрольні запитання

1.1. Основні величини динаміки

Дослідні факти свідчать, що закономірності руху тіла визначається його взаємодією з іншими тілами, інертністю, а також властивостями системи відліку. Відповідно, в динаміці є свої основні величини – сила, маса, імпульс, – які розглядаються нижче.

Сила. Кількісною мірою дії на тіло з боку інших тіл є величина, що називається силою і виявляє себе у зміні швидкості тіла^[1] На досліді встановлені наступні загальні властивості сили.

1). Дія одного тіла на інше завжди є спрямованою, тому сила має певний напрям є векторною величиною \(\vec{F} \).

2). Сила \(\vec{F} \), що діє на дане тіло з боку декількох інших тіл, дорівнює

де \(\vec{F}_i \) – сила, котру створювало б і-те тіло за відсутності інших (рис. 2.1).

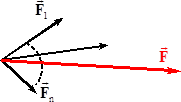
Вираз (1.1) означає, що сила, що діє на дане тіло з боку якогось одного тіла не залежить від присутності інших тіл. У цьому сенсі говорять, що сили \(\vec{F}_i \) підпорядковані принципу суперпозиції. Сили \(\vec{F}\) і \(\vec{F}_i\) називають, відповідно, рівнодійною та складовими силами. Ці поняття є зручними, бо з одного боку дозволяють лаконічно записувати різні співвідношення механіки, а з іншого — “розкладати” задану силу на будь-яку кількість інших так, аби виконувалося співвідношення (1.1). Але слід зауважити, що для не точкових тіл поняття рівнодійної має зміст тільки тоді, коли лінії дії всіх сил \(\vec{F}_i \) перетинаються в одній точц

3). У механіці всі сили поділяють на два види: контактні сили, що виникають при дотику тіл (сили тертя та опору, пружні сили, тощо), та сили, що діють між тілами на відстані (до прикладу, сила всесвітнього тяжіння, або сили електромагнітної взаємодії між зарядженими тілами). В останньому випадку взаємодія від тіла до тіла передається відповідним силовим полем — гравітаційним чи електромагнітим.^[2]

4). Сили різної фізичної природи мають різні властивості, але, незалежно від того, сила взаємодії між двома тілами на загал визначається їхнім взаємним розташуванням і швидкістю їхнього руху одне відносно одного: \(\vec{F}=\vec{F}\left( \vec{r},\vec{v} \right)\).

Маса. Будь-яке тіло “чинить опір” при спробах зміни його швидкості, через що швидкість тіла неможливо змінити миттєво навіть на дуже малу величину. Така властивість тіл називається інертністю, а мірою інертності тіла є його маса. Чим більша інертність, тим більша маса тіла, тож під дією однакової сили швидкість тіла з більшою масою змінюється повільніше, ніж у тіла з меншою масою.

1.2. Перший закон Ньютона

Рух тіла в довільній системі відліку може виявитися доволі складним, причому значною мірою через вплив на його характеристики конкретних властивостей системи відліку^[3]. Але існують так звані інерціальні системи відліку, в яких рух тіл виглядає й описується найбільш природньо і просто. При цьому дослід свідчить, що

в інерціальній системі відліку рух тіла при заданих початкових умовах визначається тільки його взаємодією з іншими тілами.

Цю важливу обставину відображує перший закон Ньютона, згідно з яким

в інерціальній системі відліку тіло за відсутності взаємодії з іншими тілами зберігає стан спокою або рівномірного прямолінійного руху.

Таке тіло називається вільним, і його рух теж називається вільним рухом, або рухом за інерцією. Тому перший закон Ньютона також називають законом інерції.

Як видно, в інерціальній системі відліку рух вільного тіла є найпростішим. При цьому виявляється, що в таких системах відліку й інші закони фізики виражаються найбільш просто й прозоро. Тому для фізики інерціальні системи відліку є переважними. Але в зв’язку з цим постає принципове питання. Інерціальність системи відліку можна встановити тільки за характером руху в ній вільного тіла, проте абсолютно вільних тіл у природі не існує. Тому реально ми можемо мати справу тільки з тілами, дія на котрі з боку інших тіл є або компенсованою, або неістотною. Тож апріорі інерціальність тієї, чи іншої системи відліку встановити неможливо. Це є питання досліду, і саме дослід свідчить, що такі системи відліку існують^[4]. Численні спостереження показують, що з гранично великою точністю інерціальними можна вважати системи відліку, пов’язані із віддаленими “нерухомими” зірками та Сонцем, а також такі, що рухаються відносно зірок поступально, рівномірно та прямолінійно, тобто без будь-яких прискорень. Що ж до систем відліку, пов’язаних із Землею, які найчастіше використовують на практиці, то їх можна вважати інерціальними лише наближено через наявність у них деяких прискорень, зумовлених добовим обертанням Землі та її орбітальним рухом навколо Сонця.

1.3. Другий закон Ньютона

Аналізуючи результати дослідів і спостережень за рухом тіл, Ньютон дійшов висновку, що

швидкість зміни імпульсу тіла^[5] дорівнює силі, що діє на нього:

\(\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}, \)

(1.3)

де \(\mathrm{d}\vec{p} \) – зміна імпульсу за нескінченно малий проміжок часу dt і \(\vec{F} \) – рівнодійна сила, прикладена до тіла^[6].

Це твердження становить другий закон Ньютона. Його також записують у вигляді:

\(\mathrm{d}\vec{p}=\vec{F}\mathrm{d}t. \)

(1.4)

Величина \(\vec{F}\mathrm{d}t \) називається імпульсом сили за час dt. Отже другий закон Ньютона можна сформулювати й так:

приріст імпульсу тіла за певний проміжок часу дорівнює імпульсу сили , що діє на тіло протягом цього часу.

Це вірно й для довільного проміжку часу від t₁ до t₂, але в такому разі імпульс сили знаходиться шляхом інтегрування правої частини (1.4) на проміжку [t₁, t₂] :

\(\Delta\vec{p}=\vec{p}_2-\vec{p}_1=\int\limits_{t_1}^{t_2}\vec{F}\mathrm{d}t.\)

(1.4а)

Якщо маса тіла не змінюється (m = const), то \(\mathrm{d}\vec{p}=\mathrm{d}(m\vec{v})=m\mathrm{d}\vec{v} \) і тоді \(\mathrm{d}\vec{p}/\mathrm{d}t=m\vec{a}\), де \(\vec{a}=\mathrm{d}\vec{v}/\mathrm{d}t \) – прискорення. Отже, для тіла незмінної маси другий закон Ньютона можна записати у вигляді:

\( m\vec{a}=\vec{F}, \)

(1.5)

тобто,

добуток маси тіла на його прискорення дорівнює рівнодійній силі, що прикладена до тіла.

На основі цього рівняння встановлена одиниця сили – ньютон (Н): 1 Н – то є сила, котра тілу маси 1 кг надає прискорення 1 м/с².

У кінематиці (частина І, розділ 1) говорилося, що прискорення є другою похідною від радіуса-вектора точки по часу: \(\vec{a}=\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2} \). Тому другий закон Ньютона (1.5) можна подати у вигляді диференціального рівняння

\(\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}=\frac{\vec{F}}{m},\)

(1.6)

яке принципово вирішує основну задачу динаміки – визначення закону руху точки, тобто залежність її радіуса-вектора від часу \(\vec{r}=\vec{r}(t) \), під дією заданих сил. Для цього треба розв’язати^[7] рівняння (1.4) при відомій залежності \(\vec{F}=\vec{F}\left( t \right)\) і заданих початкових умовах (початкових швидкості \(\vec{v}_0=\vec{v}(0) \) і радіусі-векторі \(\vec{r}_0=\vec{r}(0) \)). З цієї причини рівняння (1.4) називають загальним рівнянням руху матеріальної точки, а ІІ закон Ньютона – основним законом механіки.

Рівняння (1.6) дозволяє розв’язувати й обернені задачі. А саме, визначати силу, що діє на точку, та її швидкість і прискорення, якщо відомий закон руху. Такі задачі є досить простими і зводяться до диференціювання по часу заданої функції \(\vec{r}(t) \).

1.4. Третій закон Ньютона

Важливим дослідним фактом є те, що дія одного тіла на інше завжди має взаємний характер, тобто сили є проявом взаємодії між тілами. Третій закон Ньютона виражає важливу особливість сил взаємодії між тілами:

сили, з якими два тіла діють одне на одне, завжди рівні по модулю і напрямлені у протилежні боки вздовж прямої, що з’єднує тіла (рис.2.2).

Отже

\(\vec{F}_1=-\vec{F}_2. \)

(1.7)

Наведене формулювання треба доповнити двома корисними зауваженнями.

1. Сили взаємодії завжди мають одну й ту саму фізичну природу та походження.

2. Позаяк дія на тіло з боку декількох інших тіл є незалежною (п.1.1), третій закон Ньютона виконується й у довільній системі (сукупності тіл) окремо для кожної пари тіл.

Проте третій закон Ньютона не виконується беззастережно. Зокрема, він не є чинним для сил магнітної взаємодії та на гранично великих відстанях між тілами, що взаємодіють. Але це не створює жодних проблем при розгляді традиційних задач механіки.

Наостанок зазначимо також, що закони Ньютона є системою не розрізнених, а органічно взаємопов’язаних тверджень, тож у будь-якій задачі динаміки “працюють” усі три закони. До прикладу, загальновідомий вираз ваги тіла на горизонтальній опорі P = mg не є прямим наслідком третього закону Ньютона, як це часом говорять учні. Його доведення, хоч і є елементарним, вимагає використання всіх трьох законів Ньютона.

Контрольні запитання

1. Чим відрізняється розгляд руху тіл в кінематиці та в динаміці?

2. Говорять, що маса є мірою інертності тіла. А що таке інертність?

3. Який фізичний зміст має поняття “сила” та які її загальні властивості?

4. Чи можна сказати, що силою називається величина, рівна добутку маси тіла на його прискорення?

5. Сформулюйте І закон Ньютона. Наведіть якийсь приклад, коли він не виконується і поясніть, чому.

6. З другого заону Ньютона (рівняння (1.5)) випливає, що при \(\vec{F} =0 \) \(\vec{a}=0 \) і \(\vec{v}=\mathrm{const}\), тобто, тіло рухається рівномірно й прямолінійно, як вимагає перший закон. Чи означає це, що перший закон Ньютона є наслідком другого? Чому?

7. Чи може мати прискорення тіло, що рухається рівномірно? Якщо так, то коли? Якщо ні, то чому?

8. Два тіла кинуто з однаковою початковою швидкістю одне вертикально, а інше під кутом до горизонту. Чи однакові їхні прискорення та чи однаково змінюються з часом за величиною їхні швидкості?

_______________________________________________________________

  [1] Ще одною ознакою сили є деформації тіл, але як такі вони не впливають на закони руху.

[2] Зазначений поділ є умовним, оскільки на молекулярному рівні поняття дотику втрачає прямий зміст, бо взаємодія між молекулами здійснюється не “безпосередньо”, а через створюване ними електромагнітне поле.

[3] Наприклад, видимий рух планет на небосхилі, тобто відносно Землі, відбувається по дуже складних траєкторіях, в той час як відносно Сонця вони рухаються по простих еліптичних траєкторіях.