ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
Приклади розв'язування задач
Ядерні реакції
|
У задачах на ядерні реакції звичайно потрібно визначити ("розшифрувати") якусь невідому частинку, що бере участь у реакції і розрахувати енергетичний вихід реакції. Іноді завдання включає визначення швидкостей частинок - учасників реакції. 1. Для визначення "невідомого" учасника реакції слід скласти баланси масових і зарядових чисел, тобто прирівняти суми зазначених чисел у лівій і правій частинах реакції. Після цього знаходять A і Z шуканої частинки. 2. Методика розрахунку енергетичного виходу визначається наведеною в тексті задачі довідковою інформацією. Якщо вказані точні значення мас частинок, то використовується формула (21.17a). Якщо задані енергії зв'язку ядер або питомі енергії зв'язку нуклонів, то розрахунок виконується за формулою (21.18). У цих обчисленнях неприпустиме округлення вихідних цифрових даних і проміжних результатів 3. Для визначення величини і напрямку руху зазначених у завданні частинок використовується рівняння енергетичного балансу реакції (21.16) і рівняння балансу імпульсів (див. розділ 3 ("Закон збереження імпульсу"), формули (3.3) і (3.4)). |
Задача 21.3. У приведених нижче рівняннях ядерних реакцій:
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\);
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\);
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\).
Визначити не вказані частинки X.
Задача 21.4. За допомогою табличних значень мас ядер нуклідів та протона й нейтрона
|
mLi = 7,01601 |
|
mBe = 7,01693 |
|
mO = 15,99491 |
|
mH = 2,01410 |
|
mHe = 4,00260 |
|
mN = 14,00307 |
|
mp = 1,00728 |
|
mn = 1,00867 |
(маси подані в а.о.м.). Визначити енергію Q наступних реакцій:
1) \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}p\to{}_{0}^{1}n+{}_{4}^{7}\mathrm{Be}\);
2) \({}_{8}^{16}\mathrm{O}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}+{}_{7}^{14}\mathrm{N}\)
Задача 21.5. Вважаючи, що в одному акті поділу ядра \({}^{235}\mathrm{U}\) вивільняється енергія E = 200 МеВ, визначити: А) енергію W, що виділяється при поділі mU = 1 кг урану \({}^{235}\mathrm{U}\); Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг яка еквівалентна в тепловому відношенні одному кілограму \({}^{235}\mathrm{U}\).
Задача 21.6. З ядер дейтерію (\({}^{2}\mathrm{H}\)) утворився гелій \({}^{4}\mathrm{He}\) масою mHe = 1 г. Визначити: А) енергію Q, що при цьому виділилася; Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг, яку потрібно спалити для одержання такої ж кількості теплової енергії.
Задача 21.7. При бомбардуванні ядер Нітрогену \(\alpha-\)частинками (ядра гелію \({}_{2}^{4}\mathrm{He}\)) утворюються ядра Оксигену та протони:
\({}_{7}^{14}\mathrm{N}+{}_{2}^{4}\mathrm{He}\to{}_{1}^{2}p+{}_{8}^{17}\mathrm{O}\)
Визначити енергетичний вихід Q реакції, якщо кінетична енергія \(\alpha-\)частинки, що налітає, \(T_{\alpha}=4,0\) МеВ, а утворений протон вилітає під кутом \(\theta=60^{\circ}\) до напрямку руху \(\alpha-\)частинки і має кінетичну енергію Tp = 2,09 МеВ.
Задача 21.3
У приведених нижче рівняннях ядерних реакцій:
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\);
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\);
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\).
Визначити
не вказані частинки X.
Розв’язання
У будь-якій ядерній реакції зберігаються зарядове Z і масове A числа:
\(\sum\limits_{i}Z_{ni}=\sum\limits_{i}Z_{ki}\), \(\sum\limits_{i}Z_{ni}=\sum\limits_{i}A_{ki}\),
де індекс "n" відповідає початковому значенню, "k" – кінцевому. Виконавши відповідні підрахунки для заданих реакцій, знаходимо:
|
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\) |
\({}_{11}^{24}\mathrm{X}={}_{11}^{24}\mathrm{Na}\) |
|
|
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\) |
\({}_{0}^{1}\mathrm{X}={}_{0}^{1}n\) |
|
|
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\) |
\({}_{26}^{56}\mathrm{X}={}_{26}^{56}\mathrm{Fe}\) |
Задача 21.4
За допомогою табличних значень мас ядер нуклідів та протона й нейтрона
|
mLi = 7,01601 |
|
mBe = 7,01693 |
|
mO = 15,99491 |
|
mH = 2,01410 |
|
mHe = 4,00260 |
|
mN = 14,00307 |
|
mp = 1,00728 |
|
mn = 1,00867 |
(маси подані в а.о.м.)
Визначити
енергію Q наступних реакцій:
1) \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}p\to{}_{0}^{1}n+{}_{4}^{7}\mathrm{Be}\);
2) \({}_{8}^{16}\mathrm{O}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}+{}_{7}^{14}\mathrm{N}\)
Розв’язання
Згідно з наведеними числовим даними, енергетичний вихід ядерної реакції слід визначати за формулою (21.7a), враховуючи при цьому енергетичний еквівалент \(c^{2}\cdot{1}\) а.о.м. = 931,5 МеВ
\(Q=\Delta{m}\cdot{931,5}\) МеВб
де \(\Delta{m}=m_{1}-m_{2}\) – різниця сумарних мас вихідних та кінцевих ділянок учасників реакції.
Для реакції 1)
Q = ((7,01601 + 1,00728) – (1,00867 + 7,01693))·931,5 = -1,64 МеВ.
Знак "–" свідчить про те, що дана реакція йде з поглинанням енергії (ендотермічна реакція), тобто вихідним продуктам необхідно надавати енергію, щоб дана реакція стала можлива. Звичайно кінетичну енергію надають більш легким частинкам (тут це протон), розганяючи їх в прискорювачах.
Для випадку 2)
Q = ((15,99491 + 2,01410) – (4,0026 + 14,00307)·931,5 = 3,11 МеВ.
В цій реакції енергія виділяється, і її називають екзотермічною реакцією.
Задача 21.5
Вважаючи, що в одному акті поділу ядра \({}^{235}\mathrm{U}\) вивільняється енергія E = 200 МеВ,
визначити:
А) енергію W, що виділяється при поділі mU = 1 кг урану \({}^{235}\mathrm{U}\);
Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг яка еквівалентна в тепловому відношенні одному кілограму \({}^{235}\mathrm{U}\).
|
Дано: \({}^{235}\mathrm{U}\)
E = 200 МеВ
mU = 1 кг
q = 30 МДж/кг
|
|
W - ?
m - ?
|
Розв’язання
Енергія, що виділяється при поділі одного кілограма урану дорівнює
|
W = N·E, |
(1) |
де N – кількість атомів, що розпалися.
Число N знайдемо на підставі виразів (7.3) і (7.6):
|
\(\nu=\frac{m_{U}}{M}=\frac{N}{N_{0}}\) \(\Rightarrow\) \(N=\frac{m_{U}}{M}N_{0}\), |
(2) |
де \(M=235\cdot{10}^{-3}\) кг/моль – атомна маса урану, \(N_{0}=6,02\cdot{10}^{23}\) 1/моль – стала Авагадро. Підставивши значення N (формула (2)) у вираз (1), одержимо:
\(W=\frac{m_{U}}{M}N_{0}\cdot{E}=\frac{1}{235\cdot{10}^{-3}}\cdot{6,02}\cdot{10}^{23}\cdot{200}=5,12\cdot{10}^{26}\) МеВ = \(8,2\cdot{10}^{13}\) Дж.
При згорянні вугілля маси m виділяється кількість тепла (формула (8.18))
Q = qm \(\Rightarrow\) \(m=\frac{Q}{q}\).
За умовою енергії, що виділяються, однакові Q = W, тому еквівалентна маса вугілля
\(m=\frac{W}{q}=\frac{8,2\cdot{10}^{13}}{30\cdot{10}^{6}}=2,37\cdot{10}^{6}\) кг = 2733 т.
Задача 21.6
З ядер дейтерію (\({}^{2}\mathrm{H}\)) утворився гелій \({}^{4}\mathrm{He}\) масою mHe = 1 г.
Визначити:
А) енергію Q, що при цьому виділилася;
Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг, яку потрібно спалити для одержання такої ж кількості теплової енергії.
|
Дано: 2H
4H
mHe = 1 г
q = 30 МДж/кг
|
|
Q - ?
m - ?
|
Розв’язання
Реакція утворення більш важких нуклідів з легких називається реакцією синтезу. Схема цієї реакції має вигляд:
\({}_{1}^{2}\mathrm{H}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}\).
Енергія реакції дорівнює
E = (2mH - mHe)·931,5 МеВ,
де mH = 2,01410 а.о.м. – маса ядра дейтерію, mHe = 4,0026 а.о.м. – маса ядра гелію.
Виконаємо обчислення
E = (2·2,01410 – 4,00260)·931,5 = 23,846 МеВ.
В одному грамі гелію міститься кількість атомів (дивись формули (7.3), (7.6))
\(N=\frac{m_{\mathrm{He}}}{M}N_{0}=\frac{10^{-3}}{3\cdot{10}^{-3}}\cdot{10}^{23}=1,505\cdot{10}^{23}\),
тому загальна енергія, що виділилася, складає
\(Q=E\cdot{N}=3,59\cdot{10}^{24}\) МеВ =\(5,74\cdot{10}^{11}\) Дж.
Для одержання такої ж енергії з вугілля, необхідно спалити масу вугілля
\(m=\frac{Q}{q}=\frac{5,74\cdot{10}^{11}}{3\cdot{10}^{7}}=19140\) кг = 19,14 т.
Зауваження. Якщо порівняти результати цієї і попередньої задач, то стане очевидно, що термоядерна реакція (реакція синтезу) у багато разів ефективніша, ніж реакція поділу урану.
Задача 21.7
При бомбардуванні ядер Нітрогену \(\alpha-\)частинками (ядра гелію \({}_{2}^{4}\mathrm{He}\)) утворюються ядра Оксигену та протони:
\({}_{7}^{14}\mathrm{N}+{}_{2}^{4}\mathrm{He}\to{}_{1}^{2}p+{}_{8}^{17}\mathrm{O}\)
Визначити
енергетичний вихід Q реакції, якщо кінетична енергія \(\alpha-\)частинки, що налітає, \(T_{\alpha}=4,0\) МеВ, а утворений протон вилітає під кутом \(\theta=60^{\circ}\) до напрямку руху \(\alpha-\)частинки і має кінетичну енергію Tp = 2,09 МеВ.
|
Дано: Tα = 4,0 МеВ
θ = 60°
Tp = 2,09 МеВ
|
|
Q - ?
|
Розв’язання
Енергетичний вихід ядерної реакції можна визначити як різницю сумарної кінетичної енергії частинок, що утворилися в реакції, і сумарної кінетичної енергії вихідних ядер (формула (21.16а)):
|
Q = (Tp + TO) – (TN + \(T_{\alpha}\)) = Tp + TO - \(T_{\alpha}\). |
(1) |
Тут враховано, що ядро Нітрогену до реакції перебувало у спокої.
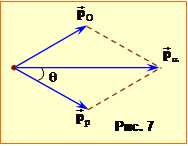
Таким чином, для отримання відповіді необхідно визначити кінетичну енергію ядра \({}^{17}\mathrm{O}\). Для цього скористаємося законом збереження імпульсу:
|
\(\vec{p}_{\alpha}=\vec{p}_{p}+\vec{p}_{O}\), |
(2) |
де \(\vec{p}_{\alpha}\), \(\vec{p}_{p}\), \(\vec{p}_{O}\) – вектори імпульсу відповідно \(\alpha-\)частинки, протона і Оксигену. Векторному рівнянню (2) відповідає діаграма імпульсів на рис.7. З неї очевидно, що модуль вектора \(\vec{p}_{O}\) легко визначити за теоремою косинусів:
\(p_{O}^{2}=p_{\alpha}^{2}-2p_{p}p_{\alpha}\cos\theta\).
Модуль імпульсу і кінетична енергія T зв'язані співвідношенням \(p^{2}=2mT\) (див. формулу (4.3б)), тому
\(2m_{O}T_{O}=2m_{p}T_{p}-4\sqrt{m_{\alpha}m_{p}T_{\alpha}T_{p}}\cos\theta\).
Звідси
\(T_{0}=\eta_{p}T_{p}+\eta_{\alpha}T_{\alpha}-2\sqrt{\eta_{\alpha}\eta_{p} T_{\alpha} T_{p}}\cos\theta\),
де введені позначення \(\eta_{p}=\frac{m_{p}}{m_{O}}=5,9287\cdot{10}^{-2}\), \(\eta_{\alpha}=\frac{m_{\alpha}}{m_{O}}\) = 0,23546.
Підставивши вираз TO в формулу (1), знаходимо
\(Q=(1+\eta)T_{p}-(1-\eta_{\alpha})T_{\alpha}-2\sqrt{\eta_{\alpha}\eta_{p}T_{\alpha}T_{p}}\cos\theta=-1,2\) МеВ.