ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
| Сайт: | physics.zfftt.kpi.ua |
| Курс: | physics.zfftt.kpi.ua |
| Книга: | ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс |
| Напечатано:: | |
| Дата: | Среда, 11 февраля 2026, 07:05 |
Оглавление
- "СУЧАСНА ФІЗИКА". Вчимося розв'язувати задачі.Компенсаційний курс
- Розділ I. Спеціальна теорія відносності
- 2. Приклади розв'язування задач
- Задачі для самостійної роботи
- Розділ II. Квантова оптика
- Приклади розв'язування задач
- Задачі для самостійної роботи
- Розділ ІІІ. Будова атома
- Приклади розв'язування задач
- Задачі для самостійної роботи
- Розділ 4. Атомне ядро
- Приклади розв'язування задач
- Задачі для самостійної роботи
"СУЧАСНА ФІЗИКА". Вчимося розв'язувати задачі.Компенсаційний курс
|
Механіка Ньютона та електродинаміка Максвелла відіграють істотну роль і в інших розділах класичної фізики, приміром, у молекулярній фізиці та оптиці. Але, як з'ясувалося на кінець ХIХ сторіччя, область їхньої застосовності є обмеженою. Так, класична механіка не придатна для опису надшвидких рухів, а класична електродинаміка не здатна адекватно пояснити закономірності світлового випромінювання нагрітих тіл та його взаємодії з речовиною. В процесі з'ясування причин цього сформувалися відповідні частини ''сучасної'' фізики – спеціальна теорія відносності (СТВ), або релятивістська механіка та квантова механіка, – окремі положення котрих розгляднуто в наступних розділах: І. Спеціальна теорії відносності Кожен розділ містить: Короткі теоретичні відомості Приклади розв'язування задач Задачі для самостійної роботи |
Розділ I. Спеціальна теорія відносності
|
Спеціальна теорія відносності (СТВ), інакше – релятивістська механіка, була створена Ейнштейном на початку ХХ сторіччя і стосується руху тіл із субсвітловими (\(\approx{3}\cdot{10}^{8}\) м/с) швидкостями. Такі рухи не узгоджуються із засадами механіки Ньютона, зокрема, із ''самоочевидним'' існуванням абсолютного (єдиного для всього Всесвіту) простору й незалежного від нього абсолютного часу. Також зауважимо, що, вказані швидкості для звичних тіл є практично недосяжні, тому на практиці закони СТВ є актуальні для частинок порядку розмірів атома і менше. Далі розглянуто: |
1.1. Постулати СТВ
|
В основі спеціальної теорії відносності лежать два постулати. (Постулати – вихідні твердження, що приймаються в даній теорії без формально-логічного доказу. У фізиці постулати встановлюються на основі експериментальних фактів. Приміром, у класичної механіці постулатами є встановлені дослідним шляхом закони Ньютона). 1. Принцип відносності Ейнштейна: за однакових умов фізичні процеси в усіх інерціальних системах відліку проходять однаково. Це означає, що
2. Постулат сталості швидкості світла:
Принцип відносності, встановлений для механіки ще Галілеєм, виявився чинним і для електродинаміки Максвелла. Це дало Ейнштейну підставу постулювати, що принцип відносності поширюється на всі фізичні явища, тобто, є абсолютним законом природи. Можна також сказати, що принцип відносності утверджує повну рівноправність усіх інерціальних систем відліку. Що до другого постулату, то на перший погляд він суперечить здоровому глузду. Дійсно, уявімо, що в нерухомій відносно Землі системі відліку закріплено лампочку, тож для нерухомого спостерігача світло від неї поширюється по всіх напрямах із швидкістю с. Тоді за другим постулатом і для спостерігача в космічній ракеті, що пролітає повз, світло від указаної лампочки поширюється зі швидкістю с. І хоча таке твердження може видатися абсурдним, вимірювання повністю підтверджують його істинність. Той факт, що світло від одного джерела у всіх системах відліку поширюється у вакуумі з однаковою швидкістю, свідчить, що c є граничною швидкістю, тобто,
|
1.2. Відносність довжин і проміжків часу
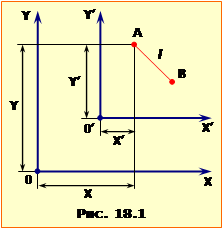
Зрозуміло, що положення тіла в просторі є відносне й визначається системою відліку. Але сам простір у класичній фізиці розглядається як абсолютний – єдиний для усього Всесвіту й однаковий за властивостями незалежно від системи відліку. З такої концепції випливає самоочевидний висновок: хоча в ріних системах відліку XOY і X′O′Y′ (рис.18.1) координати заданої точки відрізняються (\(X\ne{X}^{\prime}\), \(Y\ne{Y}^{\prime}\)), відстань l між двома точками, приміром, кінцями жорсткого срижня АВ, є однаковою в усіх системах відліку. Тим стверджується, що взаємне розташування точок тіла, тож його розміри й форма не залежать від системи відліку, тобто є абсолютними.
|
Абсолютним вважається й час. А саме, хоча моменти часу, в які відбулася якась подія, в різних місцях (часових поясах) виражаються різними числами, видається самоочевидним, що проміжок часу між двома подіями є абсолютним, тобто однаковим для всього Всесвіту. Такі уявлення лежать в основі класичної механіки й відповідають нашому життєвому досвіду. Але є несумісні з постулатами СТВ, з яких випливає, що відстані між точками і проміжку часу між подіями є відносні, залежніі від системи відліку. Одним із проявів цього є ефект скорочення довжин, який полягає в тому, що поздовжня довжина l тіла – стрижня, що рухається в поздовжньому напрямі із швидкістю v (рис.18.1), дорівнює
де \(l_{0}\) – власна довжина стрижня, тобто, відстань \(\Delta{Δx′}\) між кінцями у власній системі відліку X′O′Y′, де він перебуває в спокої. Відповідно, систему XOY, в якій стрижень рухається, називають лабораторною системою відліку, а l – лабораторною довжиною. Указане скорочення стосується лише поздовжніх відстаней. Тож, при довільній орієнтації срижня відносно напрямку руху різниця поперечних координат його кінців в обох системах відліку однакова: \(\Delta{Δy}\) = \(\Delta{Δy′}\). Проміжки часу між двома подіями в деякій точці А, що виміряні в двох різних системах відліку, теж відрізняються й пов'язані співвідношенням:
де \(\Delta{t}_{0}\) – власний проміжок часу, тобто такий, що виміряний нерухомим відносно т. А годинником. Відповідно, \(\Delta{t}\) – лабораторний проміжок часу, тобто такий, що виміряний спостерігачем (годинником) лабораторній системі відліку, яка рухається відносно т. А зі швидкістю v. Згідно з формулою (18.2) \(\Delta{t}\ge\Delta{t}_{0}\), тобто проміжок часу (тривалість процесу) у власній системі відліку подій є менший, ніж у лабораторній, в якій ''події рухаються''. Це означає, що час у різних системах відліку протікає не однаково. Приміром, для спостерігача на Землі він спливає швидше, ніж для космонавтів у міжзоряній ракеті. В цьому полягає ефект уповільнення часу в рухомих системах відліку. Усе сказане означає відносність простору й часу, тобто, що
Окрім того, при \(v\ge{c}\) вирази (18.1) і (18.2) втрачають фізичний зміст, що є формальним ознакою існування в природі граничної швидкості c. Все сказане вище може справити враження, що класична механіка Ньютона та релятивістська механіка Ейнштейна є несумісні. Але це не так, і при \(v/c\to{0}\) з формул (18.1) і (18.2) випливає звичне l = l0 і \(\Delta{t}=\Delta{t}_{0}\). Тож класична кінематика є граничним випадком релятивістської. Варто також зауважити, що на практиці відміна між двома механіками стає помітною лише при неможливихдосяжних для макроскопічних тіл швидкостях. До прикладу, за співвідношеннями (18.1) і (18.2) навіть при швидкості v = 30000 км/с довжина рухомого тіла зменшується тільки на 0,5%. Тому в СТВ термін ''тіло'', реально означає ядра атомів та елементарні частинки, для яких субсвітлові швидкості є досяжні. |
1.3. Релятивістський закон додавання швидкостей
|
де \(v_{x}\), \(v_{x}^{\prime}\) – проєкція швидкості у відповідній системі відліку. В отриманих результатах варто зупинитися на двох моментах: 1. У виразах (18.3), (18.3а) при швидкостях(\(v_{x}\ll{c}\), \(V\ll{c}\)) виходить \(v_{x}V/c^{2}\ll{1}\), \(v_{x}^{\prime}V/c^{2}\ll{1}\), і релятивістські формули (18.3), (18.3а) переходять у класичні (1.9) і (1.10): \(v_{x}=v_{x}^{\prime}+V\), \(v_{x}^{\prime}=v_{x}-V\). 2. За будь-якої швидкості тіла ${{v}_{x}}^{\prime }$ та системи відліку V виходить \(v_{x}\le{c}\) (див. задачу 18.4). Зокрема, якщо ${{v}_{x}}^{\prime }=c$, то й \(v_{x}={c}\). Отже, релятивістський закон додавання швидкостей узгоджується з постулатом сталості швидкості світла у вакуумі, тобто існуванням у Природі граничної швидкості c. |
1.4. Релятивістська маса та імпульс
|
У динаміці кількісною характеристикою руху тіла є імпульс – добут0к його маси на швидкість:
де швидкість визначає інтенсивність руху, а маса – інертність тіла, тобто, природню здатність опиратися зміні швидкості при дії на нього сили. При цьому в класичній механіці вважається, що маса визначається тільки кількістю та індивідуальними властивостями речовини тіла, так що імпульс є прямопропорційний швидкості, а швидкість зміни імпульсу – прискоренню тіла, тож діючій на нього силі. Але виявляється, що при релятивістських (навколосвітлових) швидкостях прискорення тіла під дією сталої сили всупереч другому закону Ньютона поступово зменшується. Це означає, що маса (інертність) залежить не тільки від кількості речовини в тілі, а й від швидкості його руху і, як встановлено в релятивістській механіці (СТВ), визначається формулою:
де m0 називається масою спокою, а m – релятивістською масою тіла. За такої умови загальний вираз імпульсу \(\vec{p}=m \vec{v}\) зберігає чинність і в релятивістській механіці, але m є функцією швидкості й визначається формулою (1.5). Тож релятивістський імпульс розгорнуто визначається як
З цього виразу випливає, що при (\(v\to{c}\)) інертність тіла необмежено зростає: (\(m\to\infty\)). Цим пояснюється постульована в СТВ неможливість руху тіл зі швидкістю, що не тільки перевищує, а й точно дорівнює швидкості світла у вакуумі. Виняток становлять так звані безмасові (m0 = 0) частинки, величина швидкості яких збігається із с. Такими, зокрема, є самі носії світла – фотони. З іншого брку, при малих швидкостях руху (\(v/c\to{0}\)) формули (1.4) і (1.5) дають: \(m=m_{0}\), (const) \(\vec{p}=m_{0}\vec{v}\), тож СТВ не відкидає уявлення класичної механіки про пропорційність імпульсу та маси, а включає його як граничний випадок. |
1.5. Взаємозв'язок енергії і маси
До величини Е, що називається релятивістською енергією, входять кінетична та всі види внутрішньї енергії тіла, але вона не включає енергію, зумовлену дією зовнішніх полів (гравітаційного й електромагнітного). Нерухоме тіло (v = 0) теж має певну енергію спокою
Згідно з виразом (1.7) зміна енергії тягне за собою відповідну зміну маси:
Це, хоч і незвично, не викликає подиву, позаяк може бутибути віднесене на зміну швидкості, тож і маси, при зміні енергії. Але з виразу (1.8) у границі v → 0 виходить
тобто, що маса й енергія спокою можуть змінюватись. Такий висновок видається парадоксальним, але підтверджується на практиці. Про це свідчить ''дефект мас'' в ядерних процесах. До прикладу, добре відомо, що внаслідок виділення дуже великої енергії при об'єднанні нуклонів ядрі атома, його маса спокою є завжди меншою за суму мас нуклонів, із яких воно складається. Сказане свічить, що
так що будь-яка зміна енергії тіла супроводжується еквівалентною зміною його маси і навпаки. Через залежність маси від швидкості для релятивістської механіки, поряд з імпульсом, є непридатною й класична формула кінетичної енергії, але її легко ''виправити'', спираючись на сказане вище. А саме, кінетична енергія T є енергією руху, тож дорівнюєрізниці повної енергії релятивістської частинки (1.7) та її енергії спокою (1.7a):
або, відповідно до виразу (1.4),
Зауважимо, що ця формула, як і інші формули СТВ, при нерелятивістських швидкостях $\left( v/c \right)\ll 1$ переходить у класичну: \(T=\frac{m_{0}v^{2}}{2}\) = $\frac{{{p}^{2}}}{2{{m}_{0}}}$. (У цьому можна переконатися, використавши у виразі (1.9а) відому з математики формулу наближених обчислень \((1+x)^{n}=1+nx\) при $x\ll 1$, де \(x=-v^{2}/c^{2}\), \(n=-1/2\)).
|
2. Приклади розв'язування задач
У даному й наступному пунктах по замовчуванню прийнято таке.
1. Означення ''релятивістський'' без необхідності не використовується.
2. Система відліку, в якій тіло (стрижень, або частинка) перебуває в спокої називається ''власною'', а та, в якій воно рухається – ''лабораторною''.
3. Параметри та характеристики руху тіла, що подано як ''власні'', або без означення, відносяться до власної системи відліку.
4. Рухи тіл розглядаються в системах координат із співнапрямреними осями ординат та збіжними осями абсцис і здійснюються паралельно до останніх.
Задача 1.1. Рухомий стрижень довжиною $l$ = 100 см, який спрямовано під кутом \(\theta=45^{\circ}\) до напрямку руху, має швидкість $v=c/2$. Визначити довжину ${{l}_{0}}$ та орієнтацію (кут ${{\theta }_{0}}$) стрижня у власній системі відліку.
1.2. Визначити довжину вільного пробігу ${{l}}$ нестабільної частинки із часом життя
\(\Delta{t}\) = 20 нс, якщо її власний час життя $\Delta {{t}_{0}}$ є вдвічі менший.Задача1.3. Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c. Визначити: А) відносну швидкість частинок vв та Б) швидкість їхнього зближення u.
1.4. Визначити, на скільки η (%) відрізняється від с швидкість протона з імпульсом $\tilde{p}$ = 10,0 ГеВ/с, якщо його енергія спокою E0 = 938,3 МеВ.
1.5. Визначити імпульс p протона (енеогія спокою E0 = 238,3 Мев) при кінетичній енергії T = 500 МеВ.
1.6. Без урахування втрат в атмосфері на одиницю площі перпендикулярної до сонячних променів поверхні Землі за одинцю часу падає енергія I = 1,4 кДж/(м2·с). Взявши до уваги середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг, визначити: А) щосекундну втрату Сонцем маси μ (кг/с) та Б) час T, за який воно мало би ''полегшати'' на η = 1 % при незмінній величині I.
Задача 1.1
Рухомий стрижень довжиною $l=100$ = 100 см, який спрямовано під кутом \(\theta=45^{\circ}\) до напрямку руху, має швидкість $v=c/2$.
Визначити
довжину ${{l}_{0}}$ та орієнтацію (кут ${{\theta }_{0}}$) стрижня у власній системі відліку.
|
Дано: $v=c/2$
${{l}}$ =100 см
\(\theta=45^{\circ}\)
|
|
l0 - ?,
${{\theta }_{0}}$ - ? |
Розв’язання
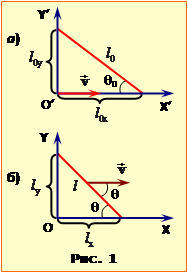 Довжина стрижня l0 у пов'язаній з ним власній системі відліку X′O′Y′ (рис.1а) визначається його проєкцями, як
Довжина стрижня l0 у пов'язаній з ним власній системі відліку X′O′Y′ (рис.1а) визначається його проєкцями, як
|
${{l}_{0}}=\sqrt{l_{{{0x}'}}^{2}+l_{{{0y}'}}^{2}}$, |
(1) |
При цьому, внаслідок скорочення довжин у напрямку руху (п. 1.2), проєкції ${l_{{0x}'}}$, ${l_{{0y}'}}$ є пов'язані такими в лабораторній системі відліку співвідношеннями (1.1):
| ${{l}_{0{x}'}}=\frac{{{l}_{x}}}{\sqrt{1-{{\beta }^{2}}}},\quad \quad {{l}_{0{y}'}}={{l}_{y}}$, |
(2) |
де \(l_{x}=l\cos\theta\), \(l_{y}=l\sin\theta\).
Отже,
| ${{l}_{0}}=l\sqrt{\frac{{{\cos }^{2}}\theta }{1-{{\beta }^{2}}}+{{\sin }^{2}}\theta }$ |
|
У цьому виразі має сенс зробити підстановку ${{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta $ й після спрощень, записати відповідь у більш компактному й зручному для обчислень вигляді:
| \(l_{0}=l\sqrt{\frac{1-\beta^{2}\sin^{2}\theta}{1-\beta^{2}}}\). |
|
З урахуванням заданого значення β = 0,5, числова відповідь складає
\(l_{0}\) = 108 см.
Другу шукану величину ${{\theta }_{0}}$ знайдемо, взявши до уваги відсутність скорочення довжин у поперечному до руху стрижня напрямі. Тож
${{l}_{0y}}={{l}_{y}}=l\sin \theta$ $\Rightarrow $ $\sin {{\theta }_{0}}=\frac{l}{{{l}_{0}}}\sin \theta $,
звідки
$\sin {{\theta }_{0}}$ = 0,655 $\Rightarrow $ ${{\theta }_{0}}$ = 40,9°.
Задача 1.2
Визначити
довжину вільного пробігу ${{l}}$ нестабільної частинки із часом життя $\Delta {{t}}$ = 20 нс, якщо її власний час життя $\Delta {{t}_{0}}$ є вдвічі менший.
|
Дано: $\Delta {{t}}$ = 20 нс
$\Delta {{t}_{0}}$ = $\Delta {{t}}$/2
|
|
${{l}}$ - ?
|
Розв’язання
Довжина вільного пробігу нестабільної частинки – це відстань, яку вона встигає пройти в лабораторній системі відліку за час життяі з часом життя, рухаючись із певною швидкістю $v$:
${{l}}$ = $v$$\Delta {{t}}$ = $\beta c\cdot \Delta t$,
де \(\beta=v/c\).
Тож, аби отримати відповідь, треба визначити параметр $\beta$. Це легко зробити за допомогою співвідношення (1.2), з якого випливає, що
$1-{{\beta }^{2}}={{\left( \frac{\Delta {{t}_{0}}}{\Delta t} \right)}^{2}}\quad \Rightarrow \quad \beta =\sqrt{1-{{\left( \frac{\Delta {{t}_{0}}}{\Delta t} \right)}^{2}}}\quad $.
Відтак, підставивши це значення у вираз (1), дістанемо наступну відповідь:
$l=c\sqrt{\Delta {{t}^{2}}-\Delta t_{0}^{2}}$ = 5,2 м.
Задача 1.3
Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c.
Визначити:
А) відносну швидкість частинок vв та
Б) швидкість їхнього зближення u.
|
Дано: v1 = 0,50c
v2 = 0,75c
|
|
vв - ?
u - ?
|
Розв’язання
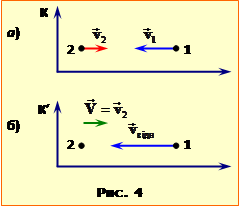
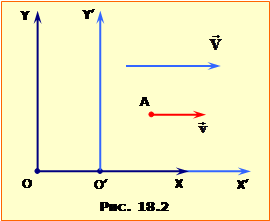
Аби уникнути непорозумінь, уточнимо смисл величин, які належить визначити, а саме. Відносна швидкість є швидкістю руху одного тіла відносно іншого, нехай першого відносно другого. Тоді, якщо з тілом 2 пов'язати систему відліку K′ (рис. 4б), то вона матиме швидість $\vec{V}={{\vec{v}}_{2}}$, тіло 2 в ній перебуватиме в спокої, а тіло 1 рухатиметься із шуканою швидкістю ${{\vec{v}}_{в}}$:
${{{\vec{v}}'}_{1}}={{\vec{v}}_{в}}$.
Натомість швидкість зближення $u$ – то є швидкість зміни відстані між тілами для стороннього спостерігача в нерухомій системі відліку K, рис. 4а. З урахуванням сказаного визначення величин ${{v}_{в}}$ і $u$ не становить труднощів.
A) Значення відносної швидкості vв дорівнює взятій із зворотнім знаком проєкції швидкості першої частинки в K′- системі відліку (рис. 4б) й визначається формулою (1.3а) при \(v_{x}^{{′}}=-{{v}_{в}}\) і $V={{v}_{2}}$:
${{v}_{в}}=\frac{{{v}_{1}}+{{v}_{2}}}{1+\left( {{v}_{1}}\cdot {{v}_{2}} \right)/{{с}^{2}}}=0,91c$
Зауважимо, що при v1 = v2 = c (частинки – фотони), їхня відносна швидкість складала б
${{v}_{в}}=\frac{c+c}{1+\left( c\cdot c \right)/{{с}^{2}}}=c$
у згоді з твердженням про існування в Природі граничної швидкості руху.
Б) У лабораторній системі відліку К частинки за час t проходять відстані l1 = v1t і l2 = v2t, наближаючись одна до одної на відстань l = v1t + v2t = (v1 + v2)t зі швидкістю
\(u=\frac{l}{t}=v_{1}+v_{2}=1,25c\).
Те, що вийшло u > с може видатися парадоксальним, але нічого дивного в цьому результаті немає: адже величина u визначає швидкість зміни відстані між частинками для стороннього спостерігача й не є швидкістю руху однієї частинки відносно іншої.
Задача 1.4
Визначити,
відрізняється від с швидкість протона з імпульсом $\tilde{p}$ = 10,0 ГеВ/с, якщо його енергія спокою E0 = 938,3 МеВ.
|
Дано: $\tilde{p}$ = 10,0ГеВ
E0 = 938,3МеВ
|
|
η (%) - ?
|
Розв’язання
Перед розв'зуванням візьмемо до уваги таку довідку. Елементарні частинки мають гранично малу масу, тому для них, навіть при навколосвітлових швидкостях руху, основні одиниці енергії (Дж) й імпульсу (кг·м/с) є несумірно великі. Тож зазвичай вживають позасистемні одиниці енергії: електрон-вольт (1 еВ = \(1,6\cdot{10}^{-19}\) Дж), мега електрон-вольт (1 МеВ = \(10^{6}\) еВ, читається ''мев'', ) та гіга електрон-вольт ''гев'' (А1 ГеВ = \(10^{9}\) еВ). А для імпульсу використовують умовну одиницю 1 ГеВ/с, де с означає не секунду, а швидкість світла. Розмірністю такої одиниці, як і належить, є (кг·м/с), але числове значення $\tilde{p}$ заданого так імпульсу насправді дорівнює його добутку на швидкість світла: $\tilde{p}$ = (рс).
Шукана відносна відміна швидкості частинки v від швидкості світла с складає
|
\(η=\frac{c-v}{c}=1-\beta\), де $\beta =\left( v/c \right)$. |
(1) |
Отже, для отримання відповіді треба визначити параметр \(\beta\). Для цього використаємо вираз релятивістського імпульсу (1.5), зробивши в ньому заміну $v=c\beta $:
$p=\frac{{{m}_{0}}c\beta }{\sqrt{1-{{\beta }^{2}}}}$.
Далі домножимо обидві частини отрманої рівності на c та за формулою (1. 6б) зробимо підстановку ${{m}_{0}}=\left( {{E}_{0}}/{{c}^{2}} \right)$ і дістанемо:
$pc=\frac{{{E}_{0}}\beta }{\sqrt{1-{{\beta }^{2}}}}$,
або
$\frac{\beta }{\sqrt{1-{{\beta }^{2}}}}=\gamma $, де $\gamma =\frac{pc}{{{E}_{0}}}$.
Звідси отримаємо
$\beta =\frac{1}{\sqrt{1+{{\gamma }^{2}}}}$
і за виразом (1) знайдемо загальну відповідь
$\eta =1-\frac{1}{\sqrt{1+{{\gamma }^{2}}}}$
та після обрахунків (без округлення) числове значення:
$\eta$ $\approx $ 0,44%.
Задача 1.5
Визначити
імпульс p протона (енергія спокою E0 = 238,3 Мев) при кінетичній енергії T = 500 МеВ.
|
Дано: E0 = 238,3 Мев T = 500 МеВ
|
|
p - ?
|
Розв’язання
Імпульс і кінетична енергія є взаємозумовленими характеристиками руху тіла, але для релятивістських (надшвидких) частинок прямого зв'язку між ними немає. Проте його можна встановити через вирази енергії (1.6) і (1.6а), з яких випливає, що
|
$m{{c}^{2}}\left( 1-\frac{{{v}^{2}}}{{{c}_{2}}} \right)={{m}_{0}}{{c}^{2}}$. |
(1) |
Тож, якщо піднести отриманий вираз до квадрата, вийде:
\(m^{2}c^{4}=\frac{m_{0}^{2}c^{4}}{1-\beta^{2}}\) \(\Rightarrow\) \(m^{2}c^{4}-m^{2}v^{2}c^{2}=m_{0}^{2}c^{4}\).
В отриманій рівності \(m_{0}c^{2}=E_{0}\) – енергія спокою і mv = p – релятивістський імпульс, отже, маємо:
|
\(E^{2}-p^{2}c^{2}=E_{0}^{2}\) \(\Rightarrow\) \(p=\frac{1}{c}\sqrt{E^{2}-E_{0}^{2}}\). |
(2) |
Відтак зробимо очевидну підстановку E2 = (E0 + T)2, і, розкривши дужки, отримаємо загальну відповідь:
\(p=\frac{1}{c}\sqrt{T(T+2E_{0})}\).
Числове значення в одиницях СІ складає
p = 5,8·10–19 кг·м/с,
а в (ГеВ/с) (див. попередню задачу)
p = 1,09 ГеВ/с.
Задача 1.6
Без урахування втрат в атмосфері на одиницю площі перпендикулярної до сонячних променів поверхні Землі за одиницю часу падає енергія I = 1,4 кДж/(м2·с). Взявши до уваги середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг,
визначити:
А) щосекундну втрату Сонцем маси μ (кг/с) та
Б) час T, за який воно мало би ''полегшати'' на η = 1 % при незмінній величині I.
|
Дано: I = 1,4 кДж/(м2·с) = 1,4·103 Дж/(м2·с)
R = 149,5·106 км = 1,495·1011 м
M = 2·1030 кг
η = 1 %
|
|
μ - ?, Т - ?
|
Розв’язання
А) Згідно із співвідношенням (1.6б), маса Сонця зменшується з часом зі швидкістю
|
$\mu =\frac{W}{{{c}^{2}}}$, |
(1) |
де W – інтенсивність, тобто, енергія, що випромінюється Сонцем за 1 c.
Зрозуміло, що випромінювання Сонця є однакове по всіх напрямках, отож для спостерігача на Землі його енергія з однаковою щільністю I розподіляється по поверхні сфери радіуса земної орбіти R. Отже,
$W=I\cdot 4\pi {{R}^{2}}$,
і щосекундна втрата маси Сонця складає
$\mu =\frac{4\pi {{R}^{2}}I}{{{c}^{2}}}$.
Відповідно, задана зміна маси Сонця на величину $\Delta M=\eta M$ відбулася б за час
$T=\frac{\eta M{{c}^{2}}}{4\pi {{R}^{2}}I}$.
Обчислення дають
\(\mu\approx4,3\cdot{10}^{9}\) кг/с
і
\(T=4,65\cdot{10}^{18}\) c,
що складає приблизно 150 мільярдів років.
Задачі для самостійної роботи
Рівень 1
|
1.7 |
Стрижень пролітає повз мітку на стіні лабораторії за 20 нс. Визначити власну довжину стрижня l0, якщо мітка проминає його кінці з інтервалом часу 25 нс. [4,5 м] |
|
1.8 |
Визначити, як і у скільки разів довжина стрижня, що рухається у повздовжньому напрямі зі швидкістю 260 Мм/с, відрізняється від його власної довжини. [2] |
|
1.9 |
При якій швидкості руху стрижня в повздовжньому напрямку його довжина буде на 0,5 % меншою за власну? [0,1c] |
|
1.10 |
При якій швидкості руху власний час життя нестабільної частинки буде відрізнятися в 10 разів від часу, що зафіксовано спостерігачем? [0,99c] |
|
1.11 |
Визначити швидкість альфа-частинки, релятивістська маса якої на 10% відрізняється від маси спокою . [0,42c] |
|
1.12 |
У скільки разів релятивістська маса відрізняється від власної частинки при швидкості, що складає 99% швидкості світла? [70] |
|
1.13 |
Обчислити у джоулях та електронвольтах енергію, що відповідає масі 1 а.о.м. та 1 кг. [\(1,48\cdot{10}^{-11}\) Дж; \(931,5\) МеВ; \(8,99\cdot{10}^{16}\) Дж; \(5,61\cdot{10}^{29}\) МеВ] |
|
1.14 |
Яка робота виконується в прискорювачі над електроном при зміні його швидкості від 0,6с до 0,8с? [391 MеВ] |
Рівень 2
|
1.15 |
Стрижень довжиною 1,00 м, орієнтований під кутом 45° до напрямку руху, пролітає повз спостерігача зі швидкістю 0,8c. Яку довжину та орієнтацію стрижня зафіксує спостерігач? [0,93 м; 49,7°] |
|
1.16 |
Визначити швидкість нестабільної частинки, якщо за час життя 2 мкс вона пролітає відстань 6 км. [0,995c] |
|
1.17 |
Визначити повну та кінетичну енергію протона, маса котрого в півтора рази відрізняється від маси спокою 1,67·10–27 кг. [1,41 ГеВ; 470 МеВ] |
|
1.18 |
Визначити швидкість електрона з кінетичною енергією 1,53 МеВ. [0,97с] |
|
1.19 |
Визначити імпульс та кінетичну енергію електрона, що має швидкість 0,9c.[\(5,64\cdot{10}^{-22}\) кг·м/с; \(1,06\cdot{10}^{-13}\) Дж] |
|
1.20 |
Якої відносної похибки буде припущено при обчисленні кінетичної енергії релятивістської частинки за класичною формулою? Виконати обчислення для випадків \(v_1=0,08c\) і \(v_2=0,8c\). [0,5 %; 52 %] |
|
1.21 |
Чому дорівнює кінетична енергія частинки із власною масою \(m_{0}\) й імпульсом \(p=m_{0}c\)? [\(0,414m_{0}c^2\)] |
|
1.22 |
Яку швидкість має релятивістська частинка при кінетичній енергії \(T=500\) МеВ та імпульсі \(p=865/c\) де c – швидкість світла? [0,87c] |
|
1.23 |
Визначити релятивістську масу електрона, що пройшов прискорювальну різницю потенціалів \(U=1\) МВ. [\(2,96m_{0}\), \(m_{0}\) – маса спокою] |
|
1.24 |
Яку прискорювальну різницю потенціалів має пройти протон, аби його маса зрівнялася з масою \(\alpha\)–частинки з кінетичною енергією \(T=1000\) МеВ? [\(3,78\) ГВ] |
|
1.25 |
Частинки рухаються назустріч одна одній з однаковими швидкостями 0,9c. Чому дорівнює відносна швидкість частинок? $\approx 0,99c$ |
|
1.26 |
Електрон зі швидкістю \(0,8c\) перпендикулярно влітає в однорідне магнітне поле \(B=10\) мТл. Визначити радіус кривини траєкторії його подальшого руху. [\(\approx{23}\) см] |
|
1.27 |
Електрон з початковою швидкістю 0,1c входить у смугу прискорювального електричного поля вздовж його напрямку. Визначити швидкість та імпульс електрона на виході зі смуги, якщо поле виконало роботу 515 кеВ. [0,87c; \(4,77\cdot{10}^{-22}\) кг·м/с] |
Розділ II. Квантова оптика
|
Хвильові уявлення про природу світла є неповними. Вони не дозволяють пояснити явища, котрі безпосередньо пов'язані з процесами випускання і поглинання тілами електромагнітного випромінювання. Причина полягає в тому, що в дійсності воно є не неперервною хвилею, а випускається й поглинається у вигляді мікроскопічних порцій, які називають квантами або фотонами. Особливістю фотонів є те, що в залежності від умов вони виявляють властивості і частинок ("корпускул"), і хвиль. Така двоїстість властивостей є характерною й для елементарних частинок речовини, приміром, електронів і є фундаментальною рисою матерії, що називається ''корпускулярно-хвилбовим дуалізмом''. Явища, в яких виявляються хвильові властивості частинок речовини розглядає квантова механіка, корпускулярні властивості світла – квантова оптика, основним положенням якої присвячено даний розділ цього посібника. Далі розглянуто: |
2.1. Фотони
|
Світло випускається джерелом у вигляді потоку особливих мікроскопічних частинок, які називають фотонами (від грецького "фотос" – світло). Фотону притаманні як корпускулярні (енергія, маса, імпульс), так і хвильові (частота і довжина хвилі) характеристики, що є пов'язані між собою. |
|
Енергія фотона E визначається формулою Планка
де \(\nu\) – лінійна частота випромінювання. Величина
є фундаментальною фізичною константою, що називається сталою Планка. У теорії зазвичай використовують циклічну частоту \(\omega=2\pi\nu\) і записують формулу (2.1) у вигляді
де величина
теж називається сталою Планка (читається "аш перекреслене" або "аш з рискою"). Енергію фотона можна виразити і через довжину хвилі випромінювання у вакуумі \(\lambda\):
де c – швидкість світла у вакуумі. |
Маса фотона відповідно до формул (1.6), (2.1), (2.1a) і (2.1б) формально може бути введена як
або
Оскільки швидкість фотона дорівнює c, то, у відповідності до формули (1.5), маса спокою фотона \(\color{darkblue}{m_{0}=0}\). Це означає, що фотон не може існувати в стані спокою. Єдиний можливий стан фотона – це рух зі швидкістю c. Тому при зіткненні з іншими частинками можливе тільки або поглинання фотона, або відбивання без втрати швидкості. |
Імпульс фотона, відповідно до формул (1.4а), (2.2) та (2.2а), визначається формулою
або
Отже, енергія й імпульс фотона є пов'язані співвідношенням
|
2.2. Фотоефект
|
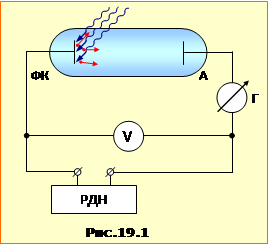
Одним із явищ, які доводять квантову природу світла, є фотоефект – звільнення електронів від зв'язку з атомами речовни під дією світла. Розрізняють зовнішній та внутрішній фотоефект. У першому випадку звільнені електрони виходять за межі тіла, а в другому лишаються всередині. Закономірності фотоефекту можна встановити, досліджуючи вольт-амперні характеристики ВАХ (залежність струму від напруги I(U)) вакуумного фотодіода за різних умов опромінювання світлом. Примітка. Вакуумний фотодіод – це електронна лампа, що має два електроди: анод А і світлочутливий холодний (неророзжарюваний) фотокатод ФК який опромінюється світлом. Для вимірювання ВАХ на фотодіод від регульованого джерела напруги (РДН) за схемою рис.19.1 подають напругу U, полярність і величину котрої можна змінювати й вимірювати вольтметром V. Фотострум I, який з'явлється при опроміненні катода, реєструється гальванометром (чутливим амперметром) Г.
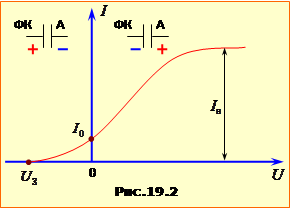
Загальний вигяд ВАХ фотоелемента показано на рис.19.2, на якому область \(U>0\) відповідає прямій (прискорювальній для електронів), а \(U<0\) – зворотній(гальмівній) напрузі для фотоелектронів.
Показаний графік залежності I(U) висвітлює головні властивості фотоефекту. А саме: 1. При підвищенні напруги на фотоелементі зростання струму з певного моменту починає вповільнюватись і припиняється взагалі при деякому струмі I = Iн, що називається ″струмом насичення″. Описана форма ВАХ має наступне пояснення. Електрони вилітають з катода по всіх напрямах, тож при U = 0 лише частина з них потрапляє на анод, створючи невеликий струм І0. Коли ж на фотоелементі починає зростати пряма напруга \(U>0\), то все більша й більша частина фотоелектронів спрямовується електричним полем на анод, і струм істотно зростає. Але електрони вириваються з катода не електричним полем, а світлом, тому з певного моменту починають потрапляти на анод, і настає ″насичення струму″. При цьому його величина
де n – кількість електронів, що вириваються світлом з фотокатода за одиницю часу, і \(e=1,6\cdot{10}^{-19}\) Кл – елементарний заряд. 2. При \(U\le{0}\) у фотоелементі теж тече струм \(I\le{I0}\), для припинення котрого на фотоелемент треба подати гальмівну напругу найменшої необхідної величини Uз, яка називається ″запірною напругою″. Наявність струму при напрузі \(U\le{0}\) пояснюється тим, що фотоелектрони вилітають з катода з деякою початковою швидкістю та кінетичною енергією і, якщо вона є достатньою для виконання роботи (Ч. 3, (1.13а)) по подоланню гальмівного поля, потрапляють на анод. Отож, запірна напруга задовольняє умову
де v – найменша швидкість вильоту електронів із фотокатода, при якій вони здатні дістатися анода. |
|
Із результатів дослідження ВАХ фотоелементів із катодами з різних металів і при різних умовах опромінення випливають наступні загальні закономірності зовнішнього фотоефекту: 1. Кількість електронів, що вилітають із металу за одиницю часу під дією світла, є прямо пропорційна його інтенсивності й не залежить частоти. 2. Максимальна кінетична енергія фотоелектронів лінійно залежить від частоти опромінювального світла й не залежить від його інтенсивності. 3. Для кожного металу існує своя червона межа фотоефекту – мінімальна частота \(\nu_{0}\) (або максимальна довжина хвилі \(\lambda_{0}\)) опромінювального світла, при якій є можливий фотоефект. Окрім цього було встановлено безінерційність фотоефекту, тобто те, що фотострум з'являється практично одночасно з початком опромінювання (із затримкою \(\tau\sim{10}^{-9}\) с). |
|
Прикметно, що жодну з наведених закономірностей неможливо пояснити на основі класичних уявлень. Приміром, якщо світло трактувати як неперервну хвилю, то кінетична енергія фотоелектронів, отож і запірна напруга фотоелемента (п. 2), має залежати від інтенсивності світла, тоді як у дійсності вона визначається тільки його частотою. Так само кількість фотоелектронів і струм насичення (п. 1) мали би бути прямо пропорціні частоті світла, а насправді вона залежить тільки від його інтенсивност. У той же час описані закономірності вичерпно пояснюються квантовою теорією фотоефекту, створеною Ейнштейном, згідно з якою в кожному елементарному акті фотоефекту
При цьому для виходу назовні електрон має подолати зв'язок із кисталічною ґраткою металу, витративши для цього енергію, що називається роботою виходу A і є його табличною характеристикою. Тож, кінетична енергія фотоелектрона при вильоті складає W = ε – A, де ε – енергія поглинутого фотона. Якщо в цьому співвідношенні вирази кінетичної енергії та енергії фотона запишемо розгорнуто, то отримаємо наступні вирази рівняння Ейнштейна для зовнішнього фотоефекту:
|
яке пояснює всі розглянуті закономірності зовнішнього фотоефекту. А саме:
|
1. Через квантову природу світла при його поглинанні електрон потрібну для виконання роботи виходу енергію не поступово накопичує, а отримує одразу. Цим пояснюється безінерційність фотоефекту. 2. З рівнянь (2.7) і (2.7б) прямо випливає висновок про лінійну залежність кінетичної енергії фотоелектрона від частоти опромінюючого світла. 3. З рівнянь (2.7) і (2.7a) очевидно, що вихід електрона з металу є можливий тільки за умови \(h\nu\ge{A}\) або \(hc/\lambda\ge{A}\), тобто при частоті світла $\nu =\frac{A}{h}$, або $\lambda \le \frac{hc}{A}$ Це пояснює існування червоної межі фотоефекту – мінімальної частота (максимальної довжини хвилі) світла, що спроможне виривати електрони з металу.
І останнє. Відповідно до квантових уявлень, інтенсивність світла I (енергія, що переноситься за одиницю часу через одиницю площі) є прямо пропорційна відповідній кількості фотонів:
де ε – енергія одного фотона, \(\Delta{S}_{\perp}\) – площа опромінюваної поверхні, що є перпендикулярна до напрямку променів, \(\Delta{N}\) – кількість фотонів, які падають на поверхню \(\Delta{S}_{\perp}\) за час \(\Delta{t}\), n – те саме за 1с. Очевидно, що кількість електронів ne, які вириваються світлом за одиницю часу, є так само прямо пропорційна величині n. Цим пояснюється перша з розглянутих на початку закономірностей зовнішнього фотоефекту – пряма пропорційна залежність між кількістю вирваних електронів та інтенсивністю опромінювального світла. |
2.3. Тиск світла
|
При зіткненні з поверхнею тіла фотони, подібно до молекул повітря, чинять на неї тиск, який визначається нормальною складовою сумарного імпульсу, що передається одиниці площі освітлюваної поверхні за одиницю часу. Відповідно, тиск паралельного пучка світла залежить від його інтенсивності I, кута падіння α на поверхню, коефіцієнта відбивання R (відношення інтенсивностей відбитого та падаючого пучків) і визначається формулою:
де c – швидкість світла. При нормальному падінні (\(\alpha=0\))
а для абсолютно чорної (R = 0)
Отже, на дзеркальну поверхню світло чинить удвічі більший тиск, аніж на чорну. |
Приклади розв'язування задач
|
Наступні приклади ілюструють застосування основних положень квантової оптики при розв'язуванні типових задач. Задача 2.1. Лазер випускає світлові імпульси з довжиною хвилі \(\lambda=694\) нм, тривалістю \(\tau=2\) мс і прогальністю k = 2. Визначити середню потужність P випромінювання лазера, якщо один імпульс містить \(N=2\cdot{10}^{19}\) фотонів. Задача 2.2. На дзеркало по нормалі падає сфокусоване в цятку діаметром d = 5 мкм випромінювання від імпульсного лазера. Визначити тиск P, який воно створює при енергії імпульсу W =10 Дж і тривалості \(\tau=10\) мкс. Задача 2.3. Кінетична енергія електронів, які вилітають із металу під дією світла, дорівнює W = 2,0 еВ. Визначити, яку частку η% енергії фотона складає робота виходу електрона з цього металу, якщо червона межа фотоефекту для нього складає \(\lambda_{0}=278\) нм. Задача 2.4. При опроміненні фотоелемента світлом один раз із довжиною хвилі \(\lambda_{1}\) = \(\lambda\), а другий – \(n\lambda\), виявилося, що відношення запірних напруг складає (U1/U2) = n2. Визначити червону межу фотоефекту \(\lambda_{0}\) в цьому фотоелементі. Задача 2.5. За певних умов опромінення струм у фотоелементі припиняється при зворотній напрузі Uз = 2 В. Визначити максимальну швидкість v, з якою електрони потраплятимуть на анод фотоелемента при такій самій прямій напрузі Uп = Uз. Задача 2.6. Визначити, до якого максимального потенціалу \(\varphi_{m}\) зарядиться відокремлена металева кулька з роботою виходу електронів A = 4 еВ при опроміненні світлом із довжиною хвилі \(\lambda=140\) нм. Задача 2.1 Лазер випускає світлові імпульси з довжиною хвилі \(\lambda=694\) нм, тривалістю \(\tau=2\) мс і прогальністю k = 2 Визначити середню потужність P випромінювання лазера, якщо один імпульс містить \(N=2\cdot{10}^{19}\) фотонів.
Розв’язання Перш за все зауважимо, що прогальність k (інколи говорять ''шпаруватість'') – то є число, що визначає ступінь заповнення часу даними імпульсами й дорівнює відношенню періоду їхнього повторення T до тривалості \(\tau\). Отже, $T=k\tau $, і середня потужність випромінювання (відношення енергії одного імпульсу до періоду повторення) складає $P=\frac{N\varepsilon }{k\tau }$, (1) де $\varepsilon $ – енергія фотона, що за формулою (2.1б) дорівнює $\varepsilon =\frac{hc}{\lambda }$. Тож, зробивши таку заміну у виразі (1), знайдемо загальну відповідь \(P=\frac{Nhc}{\tau\lambda}\) і числове значення середньої потужності лазерного пучка: \(P=2,86\cdot{10}^{-3}\) Вт = 2,86 мВт. Задача 2.2 На дзеркало по нормалі падає сфокусоване в цятку діаметром d = 5 мкм випромінювання від імпульсного лазера. Визначити тиск P, який воно створює при енергії імпульсу W = 10 Дж і тривалості \(\tau=10\) мкс.
Розв’язання Тиск світла на дзеркальну поверхню визначається формулою (2.10б):
де I – інтенсивність випромінювання і c – швидкість світла. Відповідно до означення (2.9), $I=\frac{W}{\tau S}=\frac{4W}{\pi {{d}^{2}}\tau }$, де \(S=\pi{d}^{2}/4\) – площа поверхні, на яку падає випромінювання лазера. Підставивши цей вираз I у формулу (1), дістанемо відповідь: $P=\frac{8W}{\pi {{d}^{2}}c\tau }$. Обчислення дають P = 0,34 ГПа. Отримана величина є майже в 3,4 тисяч разів більша за атмосферний тиск. Тож на практиці за допомогою сфокусованого потужного лазерного пучка робять отвори в найтвердіших матеріалах, а також використовують його в хірургії як ''лазерний скальпель''. Задача 2.3 Кінетична енергія електронів, які вилітають із металу під дією світла, дорівнює W = 2,0 еВ. Визначити, яку частку η% енергії фотона складає робота виходу електрона з цього металу, якщо червона межа фотоефекту для нього складає \(\lambda_{0}=278\) нм.
Розв’язання Енергія поглинутого фотона ε розподіляється між роботою виходу A та кінетичною енергією фотоелектрона W у відповідності до закону збереження енергії: ε = A + W. Отже, шукана частка енергії η складає:
Згідно з формулою (2.8а) робота виходу дорівнює \(A=\frac{hc}{\lambda_{0}}\), тож, підставивши це значення у вираз (1), дістанемо загальну: $\eta =\frac{1}{1+\left( \lambda W/hc \right)}$ та числову відповідь задачі: η = 0,69 = 69 %.
Задача 2.4 При опроміненні фотоелемента світлом один раз із довжиною хвилі \(\lambda_{1}\) = \(\lambda\), а другий – \(n\lambda\), виявилося, що відношення запірних напруг складає (U1/U2) = n2. Визначити червону межу фотоефекту \(\lambda_{0}\) в цьому фотоелементі.
Розв’язання Спочатку, попередньо виразивши в рівнянні (2.7а) 1) роботу виходу через червону межу λ0 фотоефекту (2.8) і 2) кінетичну енергію через запірну напругу U (2.6), дістанемо для першого випадку: $\frac{hc}{{{\lambda }_{1}}}=\frac{hc}{{{\lambda }_{0}}}+e{{U}_{1}}$ $\Rightarrow \text{ }$ $\frac{1}{{{\lambda }_{1}}}-\frac{1}{{{\lambda }_{0}}}=\frac{e{{U}_{1}}}{hc}$ $\Rightarrow \text{ }$ $\frac{{{\lambda }_{0}}-\lambda_{1} }{\lambda_{1} {{\lambda }_{0}}}=\frac{eU_{1}}{hc}$ (1) Аналогічно для другого випадку: $\frac{{{\lambda }_{0}}-\lambda_{2} }{\lambda_{2} {{\lambda }_{0}}}=\frac{eU_{2}}{hc}$ (2) Відтак, почленно поділивши рівняння (1) і (2), після елементарних викладок отримаємо наступну відповідь: \(\lambda_{0}=(n+1)\lambda\). Задача 2.5 За певних умов опромінення струм у фотоелементі припиняється при зворотній напрузі Uз = 2 В. Визначити максимальну швидкість v, з якою електрони потраплятимуть на анод фотоелемента при такій самій прямій напрузі U = Uз.
Розв’язання За прямої напруги U на фотоелементі кінетична енергія електрона W на момент потрапляння на анод перевищує значення W0 на виході з катода на величину роботи eU прискорювального поля анода:
Відповідно, кінетична енергія електрона W0 при вильоті з катода дорівнює роботі гальмівного поля при запірній напрузі Uз на аноді: W0 = eUз. Отже, враховуючи, що за умовою у виразі (1) U = Uз, знайдемо кінетичну енергію W = 2eUз, та швидкість фотоелектронів при потраплянні на анод: \(\frac{mv^{2}}{2}=2eU_{з}\) \(\Rightarrow\) \(v=2\sqrt{\frac{eU_{з}}{m}}\). Відтак, узявши з таблиць масу електрона m = 9,1·10-31 кг, отримаємо наступну числову відповідь: \(v\approx1,2\cdot{10}^{6}\) м/с.
Задача 2.6 Визначити, до якого максимального потенціалу \(\varphi_{m}\) зарядиться відокремлена металева кулька з роботою виходу електронів A = 4 еВ при опроміненні світлом із довжиною хвилі \(\lambda=140\) нм.
Розв’язання При заданій довжині хвилі опромінювального світла енергія фотона (2.1б) перевищує роботу виходу електрона з кульки, тож вона через вихід електронів буде заряджатися позитивно і створювати для них гальмівне електричне поле. Напочатку опромінення, коли це поле ще буде слабке, фотоелектрони будуть легко його долати й покидати кульку без вороття. Але, при підсиленні гальмівного поля через збільшення кількості втрачених кулькою електронів, вони з якогось моменту почнуть повертатися назад. Відтак позитивний заряд кульки перестане зростати, й вона набуде сталого потенціалу φm, який підлягає визначенню. Аби знайти величину φm, розглянемо описаний процес конкретніше. При переміщенні до точки з певним потенціалом φ′ кінетична енергія фотоелектрона зменшується на величину роботи проти гальмівного поля ${A}'=e\left( \varphi -{\varphi }' \right)$ (ч. 3, ф-ла (1.13)), отже $W-{W}'=e\left( \varphi -{\varphi }' \right)$, де φ – потенціал кульки, W – початкова кінетична енергія фотоелектрона і W′ – його кінетична енергія в зазначеній точці. Як відомо з електрики, при віддаленні від зарядженої кульки її поле монотонно послаблюється. Тож, аби подолати гальмівне поле при потенціалі кульки φ (дістатися точи, де φ′ = 0), початкова кінетична енергія електрона має складати $W\ge e\varphi $. Але в нашому випадку завдання полягає не у визначенні кінетичної енергії фотоелектрона, що необхідна для подолання поля кульки із заданим потенціалом, а у з'ясуванні, при якому потенціалі кульки на подолання її поля піде вся кінетична енергія фотоелектрона. Тож записану нерівність варто обернути: $\varphi \le \frac{W}{e}$. У такому разі стає очевидно, що нижня границя ${{\varphi }_{m}}=\frac{W}{e}$ визначає граничний потенціал кульки, при якому вона вже не здатна (або, рівнозначно, ще здатна) втрачати електрони при заданій кінетичній енергії вильоту з кульки. Отож, урахувавши, що за рівнянням (2.7а) $W=\frac{hc}{\lambda }-A$, отримаємо загальну ${{\varphi }_{m}}=\frac{1}{e}\left( \frac{hc}{\lambda }-A \right)$ і після обчислень – кількісну відповідь задачі: ${{\varphi }_{m}}$ = 4,87 В. |
|||||||||||||||||||
–
Задачі для самостійної роботи
| 2.7. |
Визначити довжину хвилі світла, квант якого має таку саму енергію, що й електрон, прискорений різницю потенціалів 4,1 В. [303 нм] |
| 2.8. |
Визначити частоту та довжину хвилі у вакуумі випромінювання, маса фотона якого дорівнює масі електрона \(9,1\cdot{10}^{-31}\) кг. [\(\approx{1,24}\cdot{10}^{20}\) Гц, \(2,43\cdot{10}^{-12}\) м] |
| 2.9. |
У деякій речовині при довжині хвилі світла \(414\) нм енергія фотона складає ε = 2,0 еВ . Визначити показник заломлення цієї речовини. [1.5] |
|
2.10. |
Визначити енергії фотона, що відповідають найбільшій (\(\0,75\) мкм) і найменшій (\(0,4\) мкм) довжині хвилі видимого світла. [1,6 еВ, 3,1 еВ] |
|
2.11. |
Оцінити відношення маси фотона видимого світла (λ ~ 600 нм) до маси електрона. [~ 4·10–6] |
|
2.12. |
При якій швидкості імпульс електрона дорівнює імпульсу фотона з довжиною хвилі \(\555\) нм? [\(1,3\cdot{10}^{4}\) м/с] |
|
2.13. |
Визначити довжину хвилі випромінювання з масою фотона, що дорівнює подвоєній масі електрона. [1,2 пм] |
|
2.14. |
Скільки фотонів випускається в одному імпульсі лазерного випромінювання з довжиною хвилі \(\lambda=694\) нм при енергії імпульсу \(E=2\) Дж? [\(7\cdot{10}^{18}\)] |
|
2.15. |
Світловий потік з інтенсивністю 120 кВт/м2, падає нормально на дзеркальну поверхню. Який тиск він спричинює? [0,8 мПа] |
| 2.16. |
Імпульсний лазер випромінює в імпульсі 2·1019 фотонів з довжиною хвилі 694 нм. Визначити потужність випромінювання лазера в імпульсі із тривалістю 3 мс. [1,9 кВт] |
| 2.17. |
Потужність випромінювання точкового джерела з довжиною хвилі 1 мкм дорівнює 1 Вт. Скільки фотонів від нього проходить у вакуумі за 1 с через перпендикулярну площинку 1 см2 на відстані 10 км? [\(4\cdot{10}^{5}\)] |
|
2.18. |
Визначити показник заломлення прозорої речовини, якщо довжина світлової хвилі в ній складає 400 нм при енергії фотона 2,07 еВ. [1,5] |
|
2.19. |
Визначити короткохвильову межу випромінювання peнтгенівської трубки при швидкості електронів на підльоті до антикатода (анода) дорівнює 0,85c (c – швидкість світла). [2,7 пм] |
|
2.20. |
При попаданні на антикатод (анод) рентгенівської трубки пучка швидких електронів внаслідок їхнього різкого гальмування виникає рентгенівське випромінювання. Визначити його мінімальну довжину хвилі при напрузі на трубці 50 кВ. [25 пм] |
|
2.21. |
Рентгенівська трубка, що працює при напрузі \(50\) кВ і струмі \(2\) мА, випромінює за \(1\) с \(5\cdot{10}^{13}\) фотонів довжиною хвилі \(0,1\) нм. Визначити ККД трубки, тобто відсоток споживаної енергії, що йде безпосередньо на випромінювання. [0,1 %] |
|
2.22. |
Лазер випромінює в імпульсі енергію \(10\) Дж за час \(0,13\) мс. Визначити середній тиск лазерного імпульсу, якщо його сфокусувати в цятку діаметром \(d=10\) мкм на перпендикулярній до пучка поверхні. Коефіцієнт відбивання поверхні \(\rho=0,5\). [5 МПа] |
|
2. 23 |
Визначити тиск світла на чорну пластинку, котру розташовано на екваторі перпендикулярно до сонячних променів, якщо на 1 см2 її поверхні щосекунди падає при їхній інтенсивності \(12\) Дж світлової енергії. [0,4 мПа] |
|
2.24. |
Об’ємна густина енергії світлового випромінювання \(10\) Дж/м3. Який тиск воно створює при нормальному падінні на поверхню з коефіцієнтом відбивання \(0,5\)? [15 Па] |
|
2.25. |
Лазерний промінь потужністю \(100\) Вт падає під кутом \(\60^{\circ}\) на гладку пластинку з коефіцієнтом поглинання 0,8. Визначити силу тиску променя на пластинку. [0,2 мкН] |
Розділ ІІІ. Будова атома
|
Цей розділ присвячено деяким початковим відомоостям про атом – найменшу структурну частку хімічного елемента. Далі розглянуто: |
3.1. Планетарна модель атома
|
Уявлення про атом (від грецького "атомос" – неподільний) як про найменшу структурну одиницю речовини виникло ще за п'ять віків до нової ери й проіснувало аж до самого кінця ХIХ сторіччя, коли було відкрито легку негативно заряджену частинку – електрон, – а отже існування в атомі позитивно зарядженого ядра. В ядрі зосереджена практично вся маса атома, тож спочатку думали, що електрони є вкраплені в нього, подібно до родзинок у кексі. Та згодом було незаперечно встановлено, що розміри атома в тисячі разів перевищують розміри ядра, тобто, — що електрони знаходяться поза ядром і, аби не впасти, рухаються навколо нього. Так виникла планетарна модель атома, в якій електрони під дією електричного притягання рухаються ядра атома подібно до того, як планети рухаються навколо Сонця під дією гравітації . |
3.2. Постулати Бора
|
Планетарна модель атома є наочною й узгоджується із законами класичної механіки. Одначе вона суперечить класичній електродинаміці, згідно з якою заряджена частинка, що рухається з прискоренням, обов'язково випромінює енергію. Тож електрони в атомі через наявність доцентрового прискорення, як показують розрахунки, мали би майже миттєво попадати на ядро. Але дослідні факти незаперечно свідчить як про розташування електронів поза ядром, так і про стабільність атомів. Виходячи з цього, видатний данський фізик Н. Бор постулював наступні положення (постулати), котрі лягли в основу квантової фізики. Перший постулат Бора (постулат стаціонарних станів):
Другий постулат Бора (правило частот):
Поглинання енергії атомом теж відбувається дискретними порціями (квантами) $\left| \varepsilon \right|$, що задовольняють умови (3.1). Окрім того, Бор сформулював ще й умову стаціонарності електронних орбіт:
де $\hbar =\left( h/2\pi \right)$ – ''зведена'' стала Планка. Слід наголосити, що попри несумісність постулатів Бора із законами класичної фізики, вони відображують незаперечні дослідні факти. |
|||||||||||||||||||
3.3. Атом Гідроґену
Згідно зпланетарною моделлю, атом водню являє собою протон навколо якого по коловій траєкторії рухається електрон. В такій моделі, спираючися на закони класичної механіки та постулати Бора, можна отримати наступні вирази для дозволених радіусів електронних орбіт
| ${{r}_{n}}=\frac{{{\hbar }^{2}}}{k{{m}_{e}}{{e}^{2}}}\cdot {{n}^{2}}$ | (3.4) |
та енергетичних рівнів атома водню:
де me, e – маса і заряд електрона, \(\hbar=1,054\cdot{10}^{-34}\) Дж·с – зведена стала Планка, $k=\left( 1/4\pi {{\varepsilon }_{0}} \right)=9\cdot {{10}^{9}}$ м/Ф – електрична стала, а параметр n = 1, 2, … визначає порядковий номер рівня й називається головним квантовим числом. Зазвичай формулу (3.5) записують у вигляді:
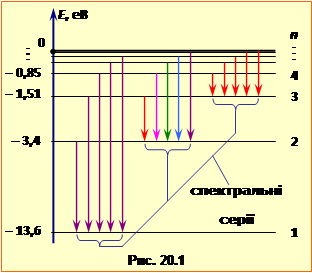
де величина ${{E}_{1}}=\frac{{{k}^{2}}{{m}_{e}}{{e}^{4}}}{2{{\hbar }^{2}}}$ = 13,6 еВ, як видно з формули й рис. 20.1, дорівнює енергії, що необхідна для переведення електрона з основного рівня n = 1 на рівень n → ∞, якому за формулою (3.4) відповідає віддалення електрона від ядра на необмежену відстань r → ∞, тобто іонізація атома. На енергетичні рівні n > 1, атом може переходити тільки внаслідок зовнішнього впливу, приміром, опромінення світлом, і називаються збудженими рівнями. Відповідні стани атома є нестабільні: в них атом перебуває тільки протягом часу \(\tau\sim{10}^{-8}\) c й потому прямо, або каскадно переходить в основний стан із випусканням низки фотонів відповідних частот та довжин хвилі, повний набір яких складає оптичний спектр атома. |
Оптичний спектр водню визначається узагальненою формулою Бальмера, що випливає з умови (3.2) та формули (3.5) і має вигляд:
де величина
називається сталою Рідберґа, а n1 і n2– номери рівнів, між якими відбувається перехід. Всі частоти випромінювання природньо групуються у спектральні серії – сукупності, що відповідають переходам електрона на заданий енергетичний рівень n1 з усіх більш високих рівнів, як схематично показано на рис. 20.1 для перших трьох серій. Частоти у спектрі поглинати визначаються тією самою формулою (3.6) із знаком ''–''. На завершення зауважимо, що борівська теорія стосується й так званих ''водньоподібних атомів'' – іонів із зарядом ядра Zе, які мають тільки один валентний електрон. Прикладом може слугувати іон $H{{e}^{+}}$, або $L{{i}^{++}}$. У такому разі в наведених формулах величину ${{e}^{2}}$ слід замінити на $Z{{e}^{2}}$. |
Приклади розв'язування задач
Нижче наведено декілька прикладів використання постулатів Бора для розв'язування задач про найпростіший з атомів – атом водню. Принагідно відмітимо, що борівська теорія атома є напівкласичною: випромінювання та поглинання енергії в ній визначається квантовими постулатами, а рух електрона навколо ядра розглядається за законми класичної механіки.
Задача 3.1. За одним із постулатів Бора електрон в атомі може рухатися тільки по колових орбітах, на яких добуток його імпульсу та довжини орбіти є кратний до сталої Планка: \(mv\cdot{2}\pi{r}=nh\), n = 1, 2, 3, … , де n – номер орбіти. Виходячи з цього, знайти кутову швидкість електрона \(\omega\) на другій орбіті (n = 2) в атомі водню.
Задача 3.2. За певних умов збудження спектр випромінювання атома водню містить тільки N = 3 лінії. Визначити їхню довжину хвилі \(\lambda_{1}\), \(\lambda_{2}\) і \(\lambda_{3}\).
Задача 3.3. Збуджені атоми водню знаходяться на n-ому енергетичному рівні. Визначити повну кількість ліній N, що спостерігаються у їхньому спектрі випромінювання.
Задача 3.4. Електрон у нерухомому вільному атомі водню знаходиться на першому збудженому енергетичному рівні (n = 2). Визначити, якої швидкості v набуде атом при переході в основний стан.
Задача 3.5. Розглядаючи атоми як звичайні кульки, визначити, за якої найменшої відносної швидкості $v$ при непружному лобовому зіткненні двох атомів водню один із них випустить фотон.
Задача 3.1
За одним із постулатів Бора електрон в атомі може рухатися тільки по колових по колових орбітах, на яких добуток імпульсу електрона та довжини орбіти є кратний до сталої Планка:
|
\(mv\cdot{2}\pi{r}=nh\), n = 1, 2, 3, …, |
(1) |
де n – номер орбіти. Виходячи з цього,
знайти
кутову швидкість електрона \(\omega\) на другій орбіті (n = 2) в атомі водню.
|
Дано: \(mv\cdot{2}\pi{r}=nh\)
n = 2
|
|
ω - ?
|
Розв’язання
В теорії Бора рух електрона в атомі водню розглядається як рух точкового заряду по колу навколо ядра під дією кулонівської сили. Тому згідно з другим законом Ньютона та формулами (ч.3, (1.5)) і (ч.1, (1.28)) можна записати:
|
$\frac{k{{e}^{2}}}{{{r}^{2}}}=m{{\omega }^{2}}r\quad \Rightarrow \quad k{{e}^{2}}=m{{\omega }^{2}}{{r}^{3}}$, |
(2) |
де \(\omega\) – кутова швидкість електрона, m – його маса, e – заряд електрона та ядра, і k – таблична константа, що складає $k=(1/4\pi {{\varepsilon }_{0}})$ $=$ 9·109 (Нм2/Кл2).
Відтак, зробивши у виразі (1) заміни $v=\omega r$ і $h=2\pi \hbar $, де $\hbar =1,05\cdot {{10}^{-34}}$, отримаємо систему рівнянь
\(\left\{ \begin{matrix}n\hbar=m\omega{r}^{2} \\ m\omega^{2}r^{3}=ke^{2} \\ \end{matrix} \right.\)
і, виключивши з неї r, — загальну відповідь задачі:
$\omega =\frac{{{k}^{2}}{{e}^{4}}m}{{{n}^{3}}{{\hbar }^{3}}}$.
Звідси, з урахуванням характеристик електрона \(e=1,6\cdot{10}^{-19}\) Кл і $m= 9,1\cdot {{10}^{-31}}$ кг, виходить:
$\omega =5,2\cdot {{10}^{15}}$$\frac{рад}{с}$.
Задача 3.2
За певних умов збудження спектр випромінювання атома водню містить тільки N = 3 лінії.
Визначити
їхню довжину хвилі \(\lambda_{1}\), \(\lambda_{2}\) і \(\lambda_{3}\).
|
Дано: N = 3 |
|
λ1, λ2, λ3 - ?
|
Розв’язання
Атом випромінює світло при переході електрона із збудженого енергетичного рівня на будь-який нижчий. Враховуючи це, легко бачити, що за умовою для найвищого збудженого рівня головне квантове число n = 3, бо лише в такому випадку є тільки три можливі переходи електрона: з третього й другого рівнів на перший та з третього на другий. Через це й у спектрі випромінювання спостерігається тільки три частоти, що визначаються формулою Бальмера (3.6) і три відповідні довжини хвилі. Отож, підставляючи у вираз (3.6) величину сталої Рідберґа (3.7) та відповідні пари значень n – (3, 1), (2, 1) і (3, 2), – 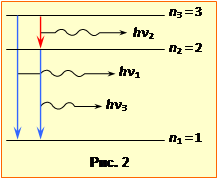 отримаємо частоти
отримаємо частоти
\(\nu_{1}=3,29\cdot{10}^{15}\left(1-\frac{1}{9}\right)=2,93\cdot{10}^{15}\) Гц,
\(\nu_{2}=3,29\cdot{10}^{15}\left(1-\frac{1}{4}\right)=2,47\cdot{10}^{15}\) Гц.
\(\nu_{3}=3,29\cdot{10}^{15}\left(\frac{1}{4}-\frac{1}{9}\right)=4,58\cdot{10}^{14}\) Гц
та шукані довжини хвилі $\lambda =(c/\nu )$ спектральних ліній:
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{2,93\cdot{10}^{15}}=102,7\) нм;
\(\lambda_{2}=\frac{c}{\nu_{2}}=\frac{3\cdot{10}^{8}}{2,47\cdot{10}^{15}}=121\) нм;
\(\lambda_{3}=\frac{c}{\nu_{3}}=\frac{3\cdot{10}^{8}}{4,58\cdot{10}^{14}}=656\) нм.
Задача 3.3
Збуджені атоми водню знаходяться на n-ому енергетичному рівні.
Визначити
повну кількість ліній N, що спостерігаються у їхньому спектрі випромінювання.
|
Дано: n
|
|
N - ?
|
Розв’язання
 Задля наочності на рис. 3 схематично показано енергетичні рівні, на які може переходити електрон атома з n-ого збудженого рівня.
Задля наочності на рис. 3 схематично показано енергетичні рівні, на які може переходити електрон атома з n-ого збудженого рівня.
Відповідь задачі легко отримати, прямо підрахувавши всі можливі переходи електрона на кожен з рівнів від першого до (n –1)-го.
Очевидно, що кількості Nі таких переходів складають:
на перший рівень — N1 = n – 1,
на другий — N2 = n – 2,
на третій — N3 = n – 3,
· · ·
на (n - 1)-й — Nn-1 = 1.
Отримана числова послідовність утворює арифметичну прогресію. Тож за відомою алгебраїчною формулою сумарна кількість можливих переходів, отож і спектральних ліній, дорівнює
$N=\frac{{{N}_{1}}+{{N}_{n-1}}}{2}\left( n-1 \right)=\frac{n\left( n-1 \right)}{2}.$
Задача 3.4
Електрон у нерухомому вільному атомі водню знаходиться на першому збудженому енергетичному рівні (n = 2).
Визначити,
якої швидкості v набуде атом при переході електрона в основний стан.
|
Дано: \(n=2\)
|
|
v - ?
|
Розв’язання
Перехід атома із збудженого в основний стан супроводжується випромінюванням фотона й відбувається спонтанно (без зовнішнього впливу), отже без зміни енргії та імпульсу. Тому при випусканні фотона атом отрмує такий самий, як у фотона, за величиною й протилежний за напрямком імпульс ''віддачі'':
${{\vec{p}}_{а}}=-{{\vec{p}}_{ф}}$
Отже, враховуючи формулу (2.4), швидкість, яку отримує атом, дорівнює
| $v=\frac{\varepsilon }{mc}$, |
(1) |
де m – маса атома водню, а ε – енергія фотона, що випромінюється.
Величина ε дорівнює різниці енергій атома водню (формула (3.5a)) у збудженому (n = 2) та основному (n = 1) стані й складає:
|
\(ε=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)=\frac{3E_{0}}{4}\). |
|
Підставивши цю величину у вираз (1), отримаємо загальну відповідь:
$v=\frac{3{{E}_{0}}}{4{{m}_{a}}c}$.
Відтак урахуємо, що маса атома водню практично збігається із масою протона 1, 67·10–27 кг, і Е0 = 13,6 еВ = 2,2·10–18 Дж, і дістанемо числову відповідь:
v ≈ 3,3 м/с.
Примітка. При розв'язуванні не враховувалося, що при переході зі збудженого в основний стан вільний атом отримує від фотона не лише імпульс віддачі, а й відповідну кінетичну енергію. Але це ніяк не вплинуло на коректність і точність відповіді. Справді, при переході атома з першого збудженого стану в основний енергія випущеного фотона згідно з формулами (3.1) і (3.6) дорівнює 12,5 еВ, тоді як кінетична енергія 10–7 еВ. Тож можна сказати, що ''для фотона атом заввжди є нерухомим''.
Задача 3.5
Розглядаючи атоми як звичайні кульки,
визначити,
за якої найменшої відносної швидкості $v$ при непружному лобовому зіткненні двох атомів водню один із них випустить фотон.
Розв’язання
Згідно з умовою, в задачі не враховується хімічний зв'язок між атомами H і вважається, що при непружному зіткненні вони просто ''склеюються'' без зміни власних властивостей, а не утворюють молекулу H2. В такому разі завдання полягає у визначенні відносної швидкості атомів, за якої при зіткненні один із них перейде у збуджений стан із наступним випроміненням фотона.
Шукана величина $v$ є швидкістю руху одного атома відносно іншого, котрий задля зручності будемо вважати нерухомим. Тоді за законом збереження імпульсу
|
$mv=2m{{v}_{1}}\quad \Rightarrow \quad {{v}_{1}}=\frac{v}{2}$, |
(1) |
де $m$ – маса атома і ${{v}_{1}}$ – швидкість атомів після зіткнення.
При пружних зіткненнях зберігається не лише імпульс, а й кінетична енергія. Але при непружних зіткненнях кульок частина їхньої кінетичної енергії переходить у внутрішню. Для звичайних кульок наслідком цього є нагрівання, а для атомів – перехід у збуджений стан із наступним випромінюванням фотона з енергією
$\varepsilon =\frac{m{{v}^{2}}}{2}-\frac{\left( 2m \right)v_{1}^{2}}{2}$.
Звідси, враховуючи співвідношення (1), виходить:
|
$\varepsilon =\frac{3m{{v}^{2}}}{4}\quad \Rightarrow \quad v=2\sqrt{\frac{\varepsilon }{3m}}$. |
(2) |
Випромінювання фотона є можливе тільки після переведення атома на котрийсь із збуджених енергетичних рівнів, які для атома водню визначаються виразами (3.5) і (3.5а). Отже, шукане найменше значення v відповідає переходу атома при зіткненні з основного (n1 = 1) на перший збуджений рівень (n2 = 2) із наступним випромінюванням фотона з енергією, що за формулами (3.1) і (3.5) складає
$\varepsilon ={{E}_{1}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)=\frac{3}{4}{{E}_{1}}$.
Відтак, підставивши це значення у вираз (2), отримаємо наступну загальну відповідь
$v=\sqrt{\frac{{{E}_{1}}}{m}}$,
і, взявши до уваги значення E1= 13,6 еВ (формула (3.5а)) і масу атома H, яка практично збігається з масою протона m = 1,67·10–27 кг, знайдемо наступну числову відповідь:
v = 3,6·104 м/с.
Зауваження. На перший погляд може здатися, що в рівнянні (1) допущено помилку, позаяк воно не містить імпульсу випущеного при зіткненні атомів фотона. Але це не так, бо зіткнення атомів і випускання фотона становлять дві окремі події.
Задачі для самостійної роботи
|
3.6. |
Визначити довжину хвилі світла, що його випромінює атомом водню при переході з третього на перший збуджені рівні. [486 нм] |
|
3.7. |
Визначити ширину (інтервал довжин хвилі Δλ) першої спектральної серії (\(n_1=1\)) атома водню . [≈30 нм] |
|
3.8. |
Визначити граничні довжини хвилі в спектральній сері Бальмера атома водню (переходи на рівень \(n=2\)). [365 нм; 656 нм] |
| 3.9. |
Визначити швидкість та прискорення електрона на першій борівський орбіті в атомі водню. [\(2,2\) Мм/с; \(9\cdot{10}^{22}\) м/с2] |
| 3.10. |
Визначити період обертання електрона навколо ядра в незбудженому атомі водню та величину еквівалентного струму, що створюється орбітальним рухом електрона. [\(1,5\cdot{10}^{-16}\) c; \(1,1\) мА] |
|
3.11. |
Визначити кількість обертів за секунду, що їх здійснює електрон на другій борівській орбіті в атомі водню. [$8,3\cdot {{10}^{14}}$ c-1] |
|
3.12. |
Як і в скільки разів зміниться частота обертання електрона навколо ядра в атомі водню при переході з першої борівської орбіти на другу? [Зменшиться у 8 разів] |
|
3.13. |
У скільки разів змінюється радіус борівської орбіти електрона в атомі водню при переході з п'ятого рівня на другий? [6,25] |
| 3.14. |
Визначити потенціал другої іонізації атома гелію, тобто — іонізації йона Не+. [54,4 В] |
| 3.15. |
Визначити потенціальну та кінетичну енергію електрона в основному (\(n=1\)) стані атома водню. [–43,5·10–19 Дж; 21,75·10–19 Дж] |
| 3.16. |
З якою швидкістю вилітають електрони з атомів водню під дією рентгенівських променів із довжиною хвилі 50 нм? [2,95 Мм/с] |
|
3.17. |
Найбільша довжина хвилі у видимій частині оптичного спектра атома водню складає \(656\) нм. Визначити довжини хвиль трьох наступних спектральних ліній. [486 нм; 434 нм; 410 нм] |
|
3.18. |
Скільки ліній міститься в спектрі випромінювання атомів водню при їхньому збудженні світлом з довжиною хвилі 102,6 нм? [3] |
|
3.19. |
Випромінювання атомарного водню по нормалі падає на дифракційну ґратку з періодом \(5\)мкм. Визначити, переходами між якими енергетичними рівнями в атомі є зумовлена лінія, що в спектрі другого порядку має кут дифракції \(15,3^{\circ}\)? [\(3\to{2}\)] |
|
3.20. |
Визначити швидкість, якої набуває атом водню при переході із першого збудженого стану в основний. [3,25 м/с] |
|
3.21. |
В удаваній термостійкій камері нагрівають гелій та речовину з великою атомною вагою. При якій температурі її атоми, стикаючись із атомами гелію, почнуть випромінювати світло з довжиною хвилі 0,63 мкм? [15 кК] |
|
3.22. |
Визначити довжину хвилі випромінювання, що спостерігається при захопленні повільним протоном електрона, який має швидкість \(v=1,9\) Мм/с. [122 нм] |
|
3.23. |
Прискорений різницею потенціалів \(U=18\) В електрон налітає на нерухомий атом водню й відбивається у зворотньому напрямі зі швидкістю \(v=1,65\) Мм/с. Визначити довжину хвилі фотона, що при цьому випромінюється. Маси атома та електрона \(1,67\cdot{10}^{-27}\) кг і \(9,1\cdot{10}^{-31}\) кг, відповідно. [122 нм] |
Розділ 4. Атомне ядро
|
Не тільки атом, а і його ядро складається з відповідних елементарних частинок – протонів і нейтронів, або узагальнено – нуклонів. При цьому, якщо кількість електронів і їхня взаємодія між собою та з ядром визначає хімічні властивості даного елемента, то кількість і взаємодія між нуклонами визначає сам елемент і його специфічні ''ядерні'' властивості. Зокрема, це стосується здібності ядер до перетворень і дуже сильного зв'язку між нуклонами, який призводить до виділення надзвичайно великої енергії при розщепленні та синтезі ядер й інтенсивного радіоактивного випромінювання, котре має сильну біологічну дію.
|
4.1. Склад атомного ядра
Ядро, як і атом, не є ''неподільним'' і складається з елементарних частинок ''нуклонів'' — незаряджених нейтронів і позитивних протонів, які мають електричний заряд +е = 1,6·10–19 Кл. Маси нуклонів майже однакові й з великою точністю дорівнюють 1 а.о.м. = 1,66·10–27 кг. Через це в теорії указані характеристики ядра задають цілими числами. А саме, кількість протонів і заряд виражають протонним (зарядовим) числом Z, тож електричний заряд ядра
| \(q_{я}=Ze\). | (4.1) |
Відповідно, масу ядра задають масовим числом (або ''атомною вагою'') A:
| \(m_{я}=A\) а.о.м., |
Відповідно кількість нейтронів у ядрі
| N = A – Z |
(4.2) |
називається нейтронним числом N.
Кількість протонів у ядрі Z, тож і кількість електронів у атомі даного хімічного елемента є фіксованою й визначає його положення в періодичній системі елементів. А от кількість нейтронів у ядрі заданого хімічного елемента може вар'ювати, утворюючи його ізотопи (у перекладі – ''ті, що займають одне місце''). Ізотопи є хімічно однакові, але можуть істотно різнитися за іншими властивостями. Зокрема це стосується стабільності ядра, так що в окремих випадках ізотопи одного хімічного елемента можуть перетворюватися на ізотопи іншого. Тому в ядерній фізиці ядра та атоми заданого ізотопу хімічного елемента Х іменують "нуклідами" й позначають як \({}_{Z}^{A}\mathrm{X}\), або $_{A}{{X}^{Z}}$.
4.2. Енергія зв'язку атомного ядра
|
Нуклони в ядрі атомному ядрі утримуються ядерними силами, котрі є: – зарядонезалежні – однакові для протонів і нейтронів; – на порядки більші за електричні; – близькодійні – виявляються лише на відстанях до \(r\le{10}^{-15}\)м порядку розмірів аомного ядра; – насичувані – один нуклон може взаємодіяти тільки з обмеженою кількістю ''сусідів''. |
|
Наскільки міцно нуклони утримуються в ядрі визначає його енергія зв'язку \(E_{зв}\),– найменша енергія, потрібна, аби поділити ядро на складові нуклони. Зрозуміло, що здійснити таке розщеплення нереально, але величину \(E_{зв}\) можна знайти опосередковано через зв'язок енергії з масою (Розділ І, п. 1.5). Справді, за законом збереження енергії
де \(E_{я}\) і \(E_{нк}\) – енергія ядра та сумарна енергія складових нуклонів. Тож, у відповідності до формули (1.7), сумарна власна маса складових нуклонів \(m_{нк}\) має перевищувати масу ядра \(m_{я}\), як і є насправді. Отож, згідно з виразом (4.3) і формулою (1.7),
де різниця мас
називається дефектом маси атомного ядра. Тож, подавши величину \(m_{нк}\) через маси нуклонів mp і mn та зарядове й масове числа Z і A, як \(m_{нк}=Zm_{p}+(A-Z)m_{n}\), отримаємо розгорнутий вираз енергії зв'язку ядра:
У довідкових таблицях маси нуклонів і атомів подають в атомних одиницях (а.о.м.), а енергію в мегаелектрон-вольтах (МеВ). У такому разі енергетичний еквівалент $m{{c}^{2}}$ маси складає \(931,5\) МеВ/(а.о.м.), і з виразу (4.5) випливає розрахункова формула: |
|
Зчеплення кожного нуклона в ядрі з іншими залежить від їхньої кількості й усереднино визначається питомою енергією зв'язку
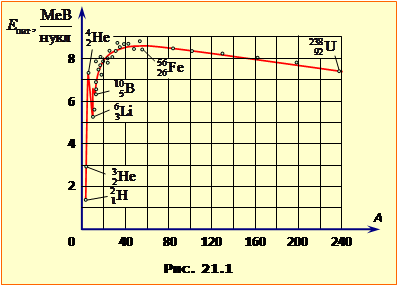
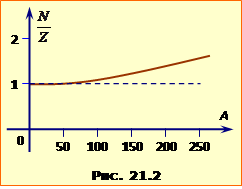
Такий вигляд залежності \(E_{пит}(A)\) пояснюється відміною у власивостях ядерного притягання між нуклонами та електричнго відштовхування між протонами. А саме, через велику потужність ядерних сил при збільшенні кількості нуклонів ''ядерна'' частка питомої енергії зв'язку спочатку стрімко зростає. Але, через насичуваність ядерних сил, це зростання поступово уповільнюється, так що при А = 40÷50 досягає величини насичення порядку 9 МеВ/нукл і далі не змінюється. Але електричне відштовхування між протонами не насичується, і чим далі, то сильніше послаблює міцність ядра. Як наслідок, повна питома енергія зв'язку на другій половині графіка \(E_{пит}(A)\) монотонно спадає до приблизно 7,5 Мев/нукл при А = 240. При цьому зі збільшенням масового числа A співвідношення між кількістю протонів Z, і нейтронів N = A – Z поступово змінюється на користь нейтронів (рис. 4.2), що частково компенсує деструктивний вплив на міцність ядра з боку протонів. У цьому виявляється однин із глибоких законів природи, за яким будь-яка надана сама собі фізична система прагне набути максимальної стійкості.
|
4.3. Радіоактивний розпад ядер
|
Атомні ядра, як і самі атоми, за відповідних умов вступають у ядерні реакції. Але в ядерній реакцї яедра не просто утворюють зв'язану систему, як атоми в хімічній, а зливаються в одне нове ядро. Такі перетворення ядер називаються радіоактивними, бо супроводжуються радіацією (від латинського "radiātiō" – випромінювання) – випусканням різних елементарних частинок, зокрема, –\({\mathbf{\alpha}}\)-частинок, що є ядрами ізотопу Гелію \({}_{2}^{4}\mathrm{He}\) і мають позитивний електричний заряд \(q_{\alpha}=3,2\cdot{10}^{-19}\) Кл і масу \(m_{\alpha}=4,00260\) а.о.м, котра майже збігається з атомною масою гелію. –\({\mathbf{\beta}}\)-частинок, які являють собою електрони. Через це їх позначають ще як \(e^{-}\), або \({}_{-1}^ {0}e\)). –\({\gamma}\)-квантів – фотонів надвисокої енергії (> 105 еВ) і малої довжини хвилі (\(<5\cdot{10}^{-12}\) м). |
|
Ядерні реакції бувають самовільними та вимушеними. Прикладом перших є\(\alpha\)- і \(\beta\)- розпад – самовільне перетворення ядра Х на ядро Y за спрощеною схемою:
із виконанням наступного правила зміщення: 1. При \(\alpha-\)розпаді утворюється нуклід, розташований у таблиці елементів на дві позиції попередух вихідного; 2. При \(\beta-\)розпаді утворюється нуклід, який займає наступне за вихідним елементом місце. Варто також зазначити, що при \(\beta-\)розпаді зарядове число дочірнього ядра відрізняється від вихідного, а масове – ні. Це є виявом ''закону збереження кількості нуклонів'', за яким, загальна кількість нуклонів, що беруть участь у ядерній реакції, лишається незмінною. При розпаді наявна кількість ядер вихдного нукліда N з часом зменшується за експоненціальним законом радіоактивного розпаду:
де N0 – кількість ядер на момент початку відліку t = 0, e – основа натуральних логарифмів. Величина \(\lambda\) (1/с) показує швидкість зменшення кількості ядер, що розпадаються, й називається сталою розпаду. Те саме опосередковано визначає й обернена величина
тож закон розпаду (4.10) можна подати як
Звідси випливає, що на момент \(t=\tau\)
тобто, за проміжок часу $\Delta t=\tau $ наявна кількість ядер, що розпадаються, зменшується в \(e\approx{2,72}\) разів. (див. рис. 21.3). Отже, чим більша величина $\tau $, тим повільніше зменшується наявна кількість ядер даного радіоактивного нукліду й тому називається його часом життя. Зазначимо також, що ''живучість'' нукліду задають також періодом напіврозпаду
– інтервалом часу, за який кількість радіоактивних ядер зменшується вдвічі. В такому разі виразом закону розпаду набуває вигляду:
На завершення заувжимо, що наведені вирази ґрунтуються на тому, що ,розпад окремого ядра є випадковою подією, тож його ймовірність ,не залежить від наявності, чи відсутності інших ядер. |
Склад ядра; енергія зв'язку
|
При розв'язуванні задач на склад ядра кількість протонів визначається з періодичної таблиці елементів (таблиці Д.І. Менделєєва) за порядковим номером елемента. Якщо в умові задачі на обчислення енергії зв'язку ядра не вказані точні значення мас необхідних частинок і нуклідів, їх беруть з довідкових таблиць. Увага! У таких розрахунках неприпустиме округлення вихідних даних. Необхідно використовувати всі значущі цифри, зазначені в довідкових даних. Необхідно також звертати увагу на те, що саме подано в довідковій таблиці: маси ядер чи маси нейтральних атомів. У першому випадку для розрахунку використовується формула (21.7), а в другому – (21.7a) або (21.7б). |
Задача 21.1. Визначити питому енергію зв'язку Eпит нуклонів в ядрах \({}_{3}^{7}\mathrm{Li}\), \({}_{27}^{58}\mathrm{Co}\), \({}_{92}^{235}\mathrm{U}\) за заданими масами протона, нейтрона та нейтральних атомів.
Задача 21.2. Визначити енергію зв'язку ядра, яке має однакову кількість протонів і нейтронів, а його радіус у k = 1,5 разів менший, ніж у ядра \({}^{27}\mathrm{Al}\). Вважати середню густину ядерної речовини однаковою для всіх ядер.
Задача 21.1
Визначити
питому енергію зв'язку Eпит нуклонів в ядрах \({}_{3}^{7}\mathrm{Li}\), \({}_{27}^{58}\mathrm{Co}\), \({}_{92}^{235}\mathrm{U}\) за заданими масами протона, нейтрона та нейтральних атомів:
mp = 1,00728 а.о.м.,
mn = 1,00867 а.о.м.,
mLi = 7,01601 а.о.м.,
mCo = 57,93575 а.о.м.,
mU = 235,04394 а.о.м.
Розв’язання
Питома енергія зв'язку нуклонів визначається співвідношенням (21.8):
\(E_{пит}=\frac{E_{зв}}{A}\),
де \(E_{зв}\) – енергія зв'язку ядра, A – число нуклонів в ядрі, рівне масовому числу ізотопа.
Маси задані в а.о.м. тому для енергії зв'язку \(E_{зв}\) зручно використати формулу (21.7б).
Згідно з заданими величинами обчислюємо:
\({}_{3}^{7}\mathrm{Li}\): \(E_{зв}=\frac{3\cdot{1,00728}+4\cdot{1,00867}-7,01601}{7}\cdot{931,5}=5,36\) МеВ/нукл;
\({}_{27}^{58}\mathrm{Co}\): \( E_{зв}=\frac{27\cdot{1,00728}+31\cdot{1,00867}-57,93575}{58}\cdot{931,5}=8,51\) МеВ/нукл;
\({}_{92}^{235}\mathrm{U}\): \( E_{зв}=\frac{92\cdot{1,00728}+143\cdot{1,00867}-235,04394}{235}\cdot{931,5}=7,39\) МеВ/нукл;
Задача 21.2
Визначити
енергію зв'язку ядра, яке має однакову кількість протонів і нейтронів, а його радіус у k = 1,5 разів менший, ніж у ядра \({}^{27}\mathrm{Al}\). Вважати середню густину ядерної речовини однаковою для всіх ядер.
Маси:
протона mp = 1,00867 а.о.м.,
нейтрона mn = 1,00728 а.о.м.,
ядра \({}^{27}\mathrm{Al}\) mAl = 26,96661 а.о.м.
|
Дано: k = 1,5
mAl = 26,96661 а.о.м.
|
|
\(E_{зв}\) - ?
|
Розв’язання
З урахуванням рівності кількості протонів і нейтронів (Z = N A – Z), формула (21.7 б) для енергії зв'язку ядра набуває вигляду:
|
\(E_{зв}=(N(m_{p}+m_{n})-m)\cdot{931,5}\), |
(1) |
де mp, mn, m – маса протона, нейтрона і ядра, виражена в а.о.м.
Таким чином, розв'язування задачі зводиться до визначення m і N. Обидві величини знайдемо з умови незмінності середньої густини ядерної речовини \(\rho=m/V\) (V – об'єм ядра):
|
\(\frac{m}{V}=\frac{m_{Al}}{V_{Al}}\) \(\Rightarrow\) \(\frac{m}{m_{Al}}=\frac{V}{V_{Al}}\). |
(2) |
Будемо вважати ядра кулями, тоді \(V=\frac{4}{3}\pi{R}^{3}\) і \(V_{Al}=\frac{4}{3}\pi{(kR)^{3}}\). Врахувавши, що за умовою k = 3/2, із співвідношення (2) отримуємо:
|
\(m=\frac{8}{27}m_{Al}\). |
(3) |
Маса ядра приблизно дорівнює добутку маси одного нуклона mн на їх кількість у ядрі A. Тому m = 2Nmн, mAl = 27mн (27 – масове число для \({}^{27}\mathrm{Al}\)). Підставивши ці значення у вираз (2), знаходимо
\(2Nm_{н}=\frac{8}{27}27m_{н}\) \(\Rightarrow\) N = 4.
Знайдені значення N і m (формула (3)) підставляємо у формулу (1) і остаточно одержуємо:
\(E_{зв}=\left(4(m_{p}+m_{n})-\frac{8}{27}m_{Al}\right)\cdot{931,5}\).
Виконаємо обчислення:
\(E_{зв}=\left(4(1,00728+1,00867)-\frac{8}{27}\cdot{26,96661}\right)\cdot{931,5}=68,6\) МеВ.
Ядерні реакції
|
У задачах на ядерні реакції звичайно потрібно визначити ("розшифрувати") якусь невідому частинку, що бере участь у реакції і розрахувати енергетичний вихід реакції. Іноді завдання включає визначення швидкостей частинок - учасників реакції. 1. Для визначення "невідомого" учасника реакції слід скласти баланси масових і зарядових чисел, тобто прирівняти суми зазначених чисел у лівій і правій частинах реакції. Після цього знаходять A і Z шуканої частинки. 2. Методика розрахунку енергетичного виходу визначається наведеною в тексті задачі довідковою інформацією. Якщо вказані точні значення мас частинок, то використовується формула (21.17a). Якщо задані енергії зв'язку ядер або питомі енергії зв'язку нуклонів, то розрахунок виконується за формулою (21.18). У цих обчисленнях неприпустиме округлення вихідних цифрових даних і проміжних результатів 3. Для визначення величини і напрямку руху зазначених у завданні частинок використовується рівняння енергетичного балансу реакції (21.16) і рівняння балансу імпульсів (див. розділ 3 ("Закон збереження імпульсу"), формули (3.3) і (3.4)). |
Задача 21.3. У приведених нижче рівняннях ядерних реакцій:
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\);
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\);
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\).
Визначити не вказані частинки X.
Задача 21.4. За допомогою табличних значень мас ядер нуклідів та протона й нейтрона
|
mLi = 7,01601 |
|
mBe = 7,01693 |
|
mO = 15,99491 |
|
mH = 2,01410 |
|
mHe = 4,00260 |
|
mN = 14,00307 |
|
mp = 1,00728 |
|
mn = 1,00867 |
(маси подані в а.о.м.). Визначити енергію Q наступних реакцій:
1) \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}p\to{}_{0}^{1}n+{}_{4}^{7}\mathrm{Be}\);
2) \({}_{8}^{16}\mathrm{O}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}+{}_{7}^{14}\mathrm{N}\)
Задача 21.5. Вважаючи, що в одному акті поділу ядра \({}^{235}\mathrm{U}\) вивільняється енергія E = 200 МеВ, визначити: А) енергію W, що виділяється при поділі mU = 1 кг урану \({}^{235}\mathrm{U}\); Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг яка еквівалентна в тепловому відношенні одному кілограму \({}^{235}\mathrm{U}\).
Задача 21.6. З ядер дейтерію (\({}^{2}\mathrm{H}\)) утворився гелій \({}^{4}\mathrm{He}\) масою mHe = 1 г. Визначити: А) енергію Q, що при цьому виділилася; Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг, яку потрібно спалити для одержання такої ж кількості теплової енергії.
Задача 21.7. При бомбардуванні ядер Нітрогену \(\alpha-\)частинками (ядра гелію \({}_{2}^{4}\mathrm{He}\)) утворюються ядра Оксигену та протони:
\({}_{7}^{14}\mathrm{N}+{}_{2}^{4}\mathrm{He}\to{}_{1}^{2}p+{}_{8}^{17}\mathrm{O}\)
Визначити енергетичний вихід Q реакції, якщо кінетична енергія \(\alpha-\)частинки, що налітає, \(T_{\alpha}=4,0\) МеВ, а утворений протон вилітає під кутом \(\theta=60^{\circ}\) до напрямку руху \(\alpha-\)частинки і має кінетичну енергію Tp = 2,09 МеВ.
Задача 21.3
У приведених нижче рівняннях ядерних реакцій:
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\);
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\);
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\).
Визначити
не вказані частинки X.
Розв’язання
У будь-якій ядерній реакції зберігаються зарядове Z і масове A числа:
\(\sum\limits_{i}Z_{ni}=\sum\limits_{i}Z_{ki}\), \(\sum\limits_{i}Z_{ni}=\sum\limits_{i}A_{ki}\),
де індекс "n" відповідає початковому значенню, "k" – кінцевому. Виконавши відповідні підрахунки для заданих реакцій, знаходимо:
|
а) \({}_{13}^{27}\mathrm{Al}+{}_{0}^{1}n\to{X}+ {}_{2}^{4}\mathrm{He}\) |
\({}_{11}^{24}\mathrm{X}={}_{11}^{24}\mathrm{Na}\) |
|
|
б) \({}_{6}^{12}\mathrm{C}+{X}\to{}_{6}^{13}\mathrm{C}\) |
\({}_{0}^{1}\mathrm{X}={}_{0}^{1}n\) |
|
|
в) \({}_{25}^{56}\mathrm{Mn}\to\mathrm{X}+{}_{-1}^{0}e\) |
\({}_{26}^{56}\mathrm{X}={}_{26}^{56}\mathrm{Fe}\) |
Задача 21.4
За допомогою табличних значень мас ядер нуклідів та протона й нейтрона
|
mLi = 7,01601 |
|
mBe = 7,01693 |
|
mO = 15,99491 |
|
mH = 2,01410 |
|
mHe = 4,00260 |
|
mN = 14,00307 |
|
mp = 1,00728 |
|
mn = 1,00867 |
(маси подані в а.о.м.)
Визначити
енергію Q наступних реакцій:
1) \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}p\to{}_{0}^{1}n+{}_{4}^{7}\mathrm{Be}\);
2) \({}_{8}^{16}\mathrm{O}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}+{}_{7}^{14}\mathrm{N}\)
Розв’язання
Згідно з наведеними числовим даними, енергетичний вихід ядерної реакції слід визначати за формулою (21.7a), враховуючи при цьому енергетичний еквівалент \(c^{2}\cdot{1}\) а.о.м. = 931,5 МеВ
\(Q=\Delta{m}\cdot{931,5}\) МеВб
де \(\Delta{m}=m_{1}-m_{2}\) – різниця сумарних мас вихідних та кінцевих ділянок учасників реакції.
Для реакції 1)
Q = ((7,01601 + 1,00728) – (1,00867 + 7,01693))·931,5 = -1,64 МеВ.
Знак "–" свідчить про те, що дана реакція йде з поглинанням енергії (ендотермічна реакція), тобто вихідним продуктам необхідно надавати енергію, щоб дана реакція стала можлива. Звичайно кінетичну енергію надають більш легким частинкам (тут це протон), розганяючи їх в прискорювачах.
Для випадку 2)
Q = ((15,99491 + 2,01410) – (4,0026 + 14,00307)·931,5 = 3,11 МеВ.
В цій реакції енергія виділяється, і її називають екзотермічною реакцією.
Задача 21.5
Вважаючи, що в одному акті поділу ядра \({}^{235}\mathrm{U}\) вивільняється енергія E = 200 МеВ,
визначити:
А) енергію W, що виділяється при поділі mU = 1 кг урану \({}^{235}\mathrm{U}\);
Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг яка еквівалентна в тепловому відношенні одному кілограму \({}^{235}\mathrm{U}\).
|
Дано: \({}^{235}\mathrm{U}\)
E = 200 МеВ
mU = 1 кг
q = 30 МДж/кг
|
|
W - ?
m - ?
|
Розв’язання
Енергія, що виділяється при поділі одного кілограма урану дорівнює
|
W = N·E, |
(1) |
де N – кількість атомів, що розпалися.
Число N знайдемо на підставі виразів (7.3) і (7.6):
|
\(\nu=\frac{m_{U}}{M}=\frac{N}{N_{0}}\) \(\Rightarrow\) \(N=\frac{m_{U}}{M}N_{0}\), |
(2) |
де \(M=235\cdot{10}^{-3}\) кг/моль – атомна маса урану, \(N_{0}=6,02\cdot{10}^{23}\) 1/моль – стала Авагадро. Підставивши значення N (формула (2)) у вираз (1), одержимо:
\(W=\frac{m_{U}}{M}N_{0}\cdot{E}=\frac{1}{235\cdot{10}^{-3}}\cdot{6,02}\cdot{10}^{23}\cdot{200}=5,12\cdot{10}^{26}\) МеВ = \(8,2\cdot{10}^{13}\) Дж.
При згорянні вугілля маси m виділяється кількість тепла (формула (8.18))
Q = qm \(\Rightarrow\) \(m=\frac{Q}{q}\).
За умовою енергії, що виділяються, однакові Q = W, тому еквівалентна маса вугілля
\(m=\frac{W}{q}=\frac{8,2\cdot{10}^{13}}{30\cdot{10}^{6}}=2,37\cdot{10}^{6}\) кг = 2733 т.
Задача 21.6
З ядер дейтерію (\({}^{2}\mathrm{H}\)) утворився гелій \({}^{4}\mathrm{He}\) масою mHe = 1 г.
Визначити:
А) енергію Q, що при цьому виділилася;
Б) масу m кам'яного вугілля з теплотворною здатністю q = 30 МДж/кг, яку потрібно спалити для одержання такої ж кількості теплової енергії.
|
Дано: 2H
4H
mHe = 1 г
q = 30 МДж/кг
|
|
Q - ?
m - ?
|
Розв’язання
Реакція утворення більш важких нуклідів з легких називається реакцією синтезу. Схема цієї реакції має вигляд:
\({}_{1}^{2}\mathrm{H}+{}_{1}^{2}\mathrm{H}\to{}_{2}^{4}\mathrm{He}\).
Енергія реакції дорівнює
E = (2mH - mHe)·931,5 МеВ,
де mH = 2,01410 а.о.м. – маса ядра дейтерію, mHe = 4,0026 а.о.м. – маса ядра гелію.
Виконаємо обчислення
E = (2·2,01410 – 4,00260)·931,5 = 23,846 МеВ.
В одному грамі гелію міститься кількість атомів (дивись формули (7.3), (7.6))
\(N=\frac{m_{\mathrm{He}}}{M}N_{0}=\frac{10^{-3}}{3\cdot{10}^{-3}}\cdot{10}^{23}=1,505\cdot{10}^{23}\),
тому загальна енергія, що виділилася, складає
\(Q=E\cdot{N}=3,59\cdot{10}^{24}\) МеВ =\(5,74\cdot{10}^{11}\) Дж.
Для одержання такої ж енергії з вугілля, необхідно спалити масу вугілля
\(m=\frac{Q}{q}=\frac{5,74\cdot{10}^{11}}{3\cdot{10}^{7}}=19140\) кг = 19,14 т.
Зауваження. Якщо порівняти результати цієї і попередньої задач, то стане очевидно, що термоядерна реакція (реакція синтезу) у багато разів ефективніша, ніж реакція поділу урану.
Задача 21.7
При бомбардуванні ядер Нітрогену \(\alpha-\)частинками (ядра гелію \({}_{2}^{4}\mathrm{He}\)) утворюються ядра Оксигену та протони:
\({}_{7}^{14}\mathrm{N}+{}_{2}^{4}\mathrm{He}\to{}_{1}^{2}p+{}_{8}^{17}\mathrm{O}\)
Визначити
енергетичний вихід Q реакції, якщо кінетична енергія \(\alpha-\)частинки, що налітає, \(T_{\alpha}=4,0\) МеВ, а утворений протон вилітає під кутом \(\theta=60^{\circ}\) до напрямку руху \(\alpha-\)частинки і має кінетичну енергію Tp = 2,09 МеВ.
|
Дано: Tα = 4,0 МеВ
θ = 60°
Tp = 2,09 МеВ
|
|
Q - ?
|
Розв’язання
Енергетичний вихід ядерної реакції можна визначити як різницю сумарної кінетичної енергії частинок, що утворилися в реакції, і сумарної кінетичної енергії вихідних ядер (формула (21.16а)):
|
Q = (Tp + TO) – (TN + \(T_{\alpha}\)) = Tp + TO - \(T_{\alpha}\). |
(1) |
Тут враховано, що ядро Нітрогену до реакції перебувало у спокої.
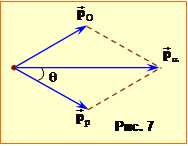
Таким чином, для отримання відповіді необхідно визначити кінетичну енергію ядра \({}^{17}\mathrm{O}\). Для цього скористаємося законом збереження імпульсу:
|
\(\vec{p}_{\alpha}=\vec{p}_{p}+\vec{p}_{O}\), |
(2) |
де \(\vec{p}_{\alpha}\), \(\vec{p}_{p}\), \(\vec{p}_{O}\) – вектори імпульсу відповідно \(\alpha-\)частинки, протона і Оксигену. Векторному рівнянню (2) відповідає діаграма імпульсів на рис.7. З неї очевидно, що модуль вектора \(\vec{p}_{O}\) легко визначити за теоремою косинусів:
\(p_{O}^{2}=p_{\alpha}^{2}-2p_{p}p_{\alpha}\cos\theta\).
Модуль імпульсу і кінетична енергія T зв'язані співвідношенням \(p^{2}=2mT\) (див. формулу (4.3б)), тому
\(2m_{O}T_{O}=2m_{p}T_{p}-4\sqrt{m_{\alpha}m_{p}T_{\alpha}T_{p}}\cos\theta\).
Звідси
\(T_{0}=\eta_{p}T_{p}+\eta_{\alpha}T_{\alpha}-2\sqrt{\eta_{\alpha}\eta_{p} T_{\alpha} T_{p}}\cos\theta\),
де введені позначення \(\eta_{p}=\frac{m_{p}}{m_{O}}=5,9287\cdot{10}^{-2}\), \(\eta_{\alpha}=\frac{m_{\alpha}}{m_{O}}\) = 0,23546.
Підставивши вираз TO в формулу (1), знаходимо
\(Q=(1+\eta)T_{p}-(1-\eta_{\alpha})T_{\alpha}-2\sqrt{\eta_{\alpha}\eta_{p}T_{\alpha}T_{p}}\cos\theta=-1,2\) МеВ.
Закон радіоактивного розпаду
|
При розв'язуванні задач на закон радіоактивного розпаду необхідно бути уважним в операціях зі степенями: множення - ділення і логарифмування - потенціювання. |
Задача 21.8. В урановій руді відношення кількості ядер \({}^{238}\mathrm{U}\) до кількості ядер \({}^{206}\mathrm{Pb}\) складає \(\eta=2,8\). Оцінити вік \(\tau\) уранової руди. Період піврозпаду \({}^{238}\mathrm{U}\) \(T_{1/2}=4,5\cdot{10}^{9}\) років. Вважати, що весь Плюмбум \({}^{206}\mathrm{Pb}\) є кінцевим продуктом розпаду урану.
Задача 21.9. У калориметр вмістили \(\beta-\)радіоактивний препарат \({}^{24}\mathrm{Na}\) масою m = 1 мг. Період піврозпаду препарату T = 15 годин. Оцінити кількість тепла Q, що виділяється в калориметрі за добу. Вважати, що всі частинки мають кінетичну енергію, рівну \(\eta=1/3\) максимально можливої в цій реакції.
Задача 21.8
В урановій руді відношення кількості ядер \({}^{238}\mathrm{U}\) до кількості ядер \({}^{206}\mathrm{Pb}\) складає \(\eta=2,8\).
Оцінити
вік \(\tau\) уранової руди.
Період піврозпаду \({}^{238}\mathrm{U}\) \(T_{1/2}=4,5\cdot{10}^{9}\) років. Вважати, що весь Плюмбум \({}^{206}\mathrm{Pb}\) є кінцевим продуктом розпаду урану.
|
Дано: η = 2,8
T1/2 = 4,5·109 років
|
|
\(\tau\) - ?
|
Розв’язання
Число радіоактивних ядер, що не розпалися на момент часу \(\tau\), визначається законом радіоактивного розпаду (21.11):
NU = \(N_{0}e^{-\lambda\tau}\)
де N0 – число вихідних ядер, \(\lambda\) – стала розпаду.
Із співвідношень (21.12) і (21.14) випливає, що
\(\lambda=\frac{\ln{2}}{T}\).
Тоді можна записати:
|
\(N_{U}=N_{0}e^{-\frac{\tau\ln{2}}{T}}=N_{0}\cdot{2}^{-\frac{\tau}{T}}\). |
(1) |
Число ядер, що розпалися, яке дорівнює числу ядер свинцю Pb, що утворилися:
|
NPb = \(N_{0}-N=N_{0}(1-2^{-\frac{\tau}{T}})\). |
(2) |
Розділивши вирази (1) на (2), одержимо:
|
\(\eta=\frac{N_{\mathrm{U}}}{ N_{\mathrm{Pb}}}=\frac{1}{2^{-\frac{\tau}{T}}-1}\) \(\Rightarrow\) \(2^{\frac{\tau}{T}}=\frac{\eta+1}{\eta}\). |
|
Із цього виразу після логарифмування отримуємо
\(\tau=T\cdot{}\frac{\ln\frac{\eta+1}{\eta}}{\ln{2}}\approx2\cdot{10}^{9}\) років.
Задача 21.9
У калориметр вмістили \(\beta-\)радіоактивний препарат \({}^{24}\mathrm{Na}\) масою m = 1 мг. Період піврозпаду препарату T = 15 годин
Оцінити
кількість тепла Q, що виділяється в калориметрі за добу. Вважати, що всі частинки мають кінетичну енергію, рівну \(\eta=1/3\) максимально можливої в цій реакції.
Енергія зв'язку: ядра \({}^{24}\mathrm{Na}\) E1 = 193,5 МеВ ядра \({}^{24}\mathrm{Mg}\) E2 = 198,3 МеВ.
|
Дано: m = 1 мг = 10-6 кг
T = 15 годин
η = 1/3
E1 = 193,5 МеВ
E2 = 198,3 МеВ
|
|
Q - ?
|
Розв’язання
Згідно з виразом (21.10) реакція \(\beta-\)розпаду \({}^{24}\mathrm{Na}\) має вигляд
\({}_{11}^{24}\mathrm{Na}\to{}_{12}^{24}\mathrm{Mg}+{}_{-1}^{0}e\).
Енергетичний вихід реакції Q1 через енергії зв'язку визначається формулою (21.18):
\(Q_{1}=E_{2}-E_{1}=4,8\) MeВ.
В реакції \(\beta-\)розпаду крім електрона \({}_{-1}^{0}e\) утворюється ще одна елементарна частинка – антинейтрино, яка не показана в схемі реакції (21.10). Антинейтрино відносить енергію, що може мати величину від 0 і аж до \(Q_{1}\). Тому \(Q_{1}\) є максимально можливою енергією електрона, а її середнє значення набагато менше і, згідно з умовою, становить
\(Q^{\prime}=Q/3=1,6\) МеВ = \(2,56\cdot{10}^{-13}\) Дж.
Кінетичну енергію ядра \({}^{24}\mathrm{Mg}\) можна не брати до уваги. Справді, згідно з законом збереження імпульсу, імпульси ядра \({}^{24}\mathrm{Mg}\) та електрона за величиною однакові. Тому відношення їх кінетичних енергій (формула (4.3б)
\(T_{я}/T_{e}=m_{e}/m_{я}=0,00055/24=2\cdot{10}^{-5}\).
Загальна енергія, що виділяється в калориметрі, дорівнює енергії \(Q^{\prime}\), помноженій на кількість ядер \(N^{\prime}\), що розпалися:
|
\(Q=Q^{\prime}N^{\prime}\). |
(1) |
Відповідно до закону розпаду (21.15) число ядер, що розпалися \(N^{\prime}=N-N_{0}\), визначається виразом:
|
\(N^{\prime}=N_{0}\left(1-e^{-\lambda\tau}\right)=N_{0}\left(1-2^{-\frac{\tau}{T}}\right)\). |
(2) |
Кількість ядер \({}^{24}\mathrm{Na}\) у початковий момент \(N_{0}\) знаходимо згідно з основними положеннями молекулярно-кінетичної теорії (формули (7.3) і (7.6)):
|
\(N_{0}\frac{m}{M}N_{A}\), |
(3) |
де \(M=24\cdot{10}^{-3}\) кг/моль – молярна маса ізотопу \({}^{24}\mathrm{Na}\), \(N_{A}=6,02\cdot{10}^{23}\) 1/моль – стала Авогадро.
Підставивши значення (3) у вираз (2), а його – у формулу (1), дістанемо:
\(Q=Q^{\prime}N^{\prime}=Q^{\prime}\frac{m}{M}N_{A}\left(1-2^{-\frac{\tau}{T}}\right)\) =
=\(2,56\cdot{10}^{-13}\cdot\frac{10^{-6}}{24\cdot{10}^{-3}}\cdot{6,02}\cdot{10}^{23}\left(1-2^{-\frac{24}{15}}\right)=4,3\cdot{10}^{6}\) Дж \(\approx{4,3}\) МДж.
Склад ядра. Енергія зв'язку
|
21.1. |
Визначити кількість протонів і нейтронів в ядрах \({}_{13}^{23}\mathrm{Na}\); \({}_{47}^{107}\mathrm{Ag}\); {}_{92}^{238}\mathrm{U}\)? [Na: p -13, n – 10; Ag: p -47, n – 60; U: p -92, n – 146] |
|
21.2. |
Визначити енергію зв'язку, що припадає на один нуклон, в ядрах: \({}_{3}^{7}\mathrm{Li}\); \({}_{3}^{16}\mathrm{O}\); \({}_{26}^{56}\mathrm{Fe}\); \({}_{92}^{235}\mathrm{U}\). [\(5,387\) МеВ; \(7,46\) МеВ; \(8,554\) МеВ; \(7,39\) МеВ] |
|
21.3. |
Атомна маса хлору прийнята рівною 35,5. Хлор має два стабільних ізотопи \({}_{}^{35}\mathrm{Cl}\) і \({}_{}^{37}\mathrm{Cl}\). Визначити їх процентне співвідношення у природній суміші. [\({}_{}^{35}\mathrm{Cl}\) – \(75\) %; \({}_{}^{37}\mathrm{Cl}\) – \(25\) %] |
Ядерні реакції
Рівень 1
| 21.4 |
Визначити невказані частинки, які приймають участь у ядерних реакціях:
[1) \({}_{11}^{24}\mathrm{Na}\); 2) \({}_{+1}^{0}\mathrm{e}\) 3) \({}_{14}^{30}\mathrm{Si}\); 4) \({}_{7}^{14}\mathrm{N}\); 5) \({}_{1}^{1}\mathrm{H}\); 6) \({}_{26}^{56}\mathrm{Fe}\);] |
||
| 21.5 | При бомбардуванні ядра Феруму \({}_{26}^{56}\mathrm{Fe}\) нейтронами утвориться \(\beta\)-радіоактивний ізотоп Мангану з атомною масою 56. Реакція відбувається в два етапи. Записати обидві реакції і визначити, які частинки з'являються в цих перетвореннях. [\({}_{26}^{56}\mathrm{Fe}+{}_{0}^{1}\mathrm{n}\to{}_{25}^{56}\mathrm{Mn}+{}_{1}^{1}\mathrm{H}\) \(\Rightarrow\) \({}_{25}^{56}\mathrm{Mn}+{}_{-1}^{0}\mathrm{e}\)] | ||
| 21.6 | Визначити енергетичний вихід реакції \({}_{3}^{7}\mathrm{Li}+{}_{1}^{1}\mathrm{p}\to{2}{}_{2}^{4}\mathrm{He}\), якщо енергія зв'язку на один нуклон у ядрі \(\mathrm{Li}\) дорівнює 5,6 МеВ, а в ядрі \(\mathrm{He}\) – 7,06 МеВ. [17,3 МеВ] | ||
| 21.7 | Яка мінімальна енергія необхідна для розщеплення ядра Нітрогену \({}_{7}^{14}\mathrm{N}\) на протони і нейтрони? [105 МеВ] | ||
| 21.8 | Яке ядро утвориться з ядра радіоактивного Радію \({}_{88}^{206}\mathrm{N}\) в результаті п'яти \(\alpha\)-розпадів і чотирьох \(\beta\)-розпадів? [\({}_{82}^{206}\mathrm{N}\)] | ||
| 21.9 | Скільки \(\alpha\) і \(\beta\)-розпадів відбувається при перетворенні ізотопу Урану \({}_{92}^{238}\mathrm{U}\) на стабільний ізотоп Плюмбуму \({}_{82}^{206}\mathrm{N}\)? [\(8\alpha\)-розпадів, \(6\beta\)-розпадів] | ||
|
Рівень 2 |
|||
| 21.10 | Яку мінімальну енергію повинен мати \(\gamma\)-квант для "виривання" нейтрона з ядра \({}_{6}^{12}\mathrm{C}\)? [\(18,6\) МеВ] | ||
| 21.11 | При анігіляції електрона і позитрона утворюється два однакових \(\gamma\)-кванта. Визначити їхню довжину хвилі, нехтуючи кінетичною енергією частинок до реакції. [\(2,4\) пм] | ||
| 21.12 | Яку мінімальну енергію повинна мати альфа-частинка, щоб відбулася ядерна реакція: \({}_{3}^{7}\mathrm{Li}+{}_{2}^{4}\mathrm{He}\to{}_{5}^{10}\mathrm{B}{}_{0}^{1}\mathrm{n}\). [\(2,8\) МеВ] | ||
| 21.13 | У результаті взаємодії повільних ядер дейтерію \({}_{1}^{2}\mathrm{H}\) і тритію \({}_{1}^{3}\mathrm{H}\) утвориться нейтрон і невідома частинка. Що це за частинка? Яку частину всієї енергії вона несе? [\(\alpha\)-частинка; \(1/5\)] | ||
| 21.14 | Скільки теплоти виділиться при утворенні \(m=1\) г Гелію \({}_{2}^{4}\mathrm{He}\) з дейтерію \({}_{1}^{2}\mathrm{H}\)? Чому дорівнює маса кам'яного вугілля з питомою теплотою згорання \(q=30\) МДж/кг, яку необхідно спалити, щоб отримати таку ж кількість енергії? [\(57,4\) МДж; \(20\) т] | ||
| 21.15 | Визначити енергію, що виділяється при синтезі \(m=1\) г гелію з дейтерію і тритію. [\(4\cdot{10}^{11}\) Дж] | ||
| 21.16 | Яка енергія виділяється у водневій бомбі при синтезі \(m=1\) г гелію? [\(0,42\) ПДж] | ||
| 21.17 | Внаслідок ділення ядра \({}_{92}^{235}\mathrm{U}\) виділяється енергія \(E=200\) МеВ. Скільки енергії вивільняється в ядерному реакторі з \(m=1\) гядерного пального? Скільки вугілля треба спалити, щоб отримати таку ж кількість енергії? [\(23\) МВт×год; \(2,8\) т] | ||
| 21.18 | Підводний човен «Наутілус» (США) має атомний реактор потужністю \(P=14,7\) МВт, у якому паливом служить збагачений уран \({}_{92}^{235}\mathrm{U}\). Визначити місячний запас палива, якщо вміст урану в ньому становить \(\eta=25\) %. При діленні ядра урану виділяється енергія \(E=200\) МеВ. [\(2,2\) кг] | ||
| 21.19 | В урановому реакторі атомної електростанції за \(t=1,5\) року розщеплюється \(m=1,5\) кг \({}_{92}^{235}\mathrm{U}\). Визначити електричну потужність станції, якщо її ККД \(\eta=10\) %, а при діленні одного ядра урану виділяється енергія \(E=200\) МеВ. [\(96,5\) МВт] | ||
| 21.20 | Записати реакцію альфа-розпаду радію \({}_{88}^{226}\mathrm{Ra}\). Визначити відношення імпульсів і кінетичних енергій утворених ядер, вважаючи, що до розпаду ядро радію перебувало у спокої. [\(1\); \(5,5\)] | ||
| 21.21 | Ядро \({}_{}^{200}\mathrm{Po}\), що знаходиться в стані спокою, випромінює альфа-частинку з енергією \(T=5,77\) МеВ. Записати схему цієї реакції. Визначити: А) швидкість ядра, що утворилося; Б) яку частину енергії, що вивільняється в цьому процесі, уносить утворене ядро. [\(0,34\) Мм/с; \(2\) %] |