ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс: Приклади розв'язування задач

ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс

◄ Предыдущая: 3.3. Атом Гідроґену Следующая: Задачі для самостійної роботи ►

Приклади розв'язування задач

Нижче наведено декілька прикладів використання постулатів Бора для розв'язування задач про найпростіший з атомів – атом водню. Принагідно відмітимо, що борівська теорія атома є напівкласичною: випромінювання та поглинання енергії в ній визначається квантовими постулатами, а рух електрона навколо ядра розглядається за законми класичної механіки.

Задача 3.1 . За одним із постулатів Бора електрон в атомі може рухатися тільки по колових орбітах, на яких добуток його імпульсу та довжини орбіти є кратний до сталої Планка: $mv\cdot{2}\pi{r}=nh$, n = 1, 2, 3, … , де n – номер орбіти. Виходячи з цього, знайти кутову швидкість електрона $\omega$ на другій орбіті (n = 2) в атомі водню.

Задача 3.2 . За певних умов збудження спектр випромінювання атома водню містить тільки N = 3 лінії. Визначити їхню довжину хвилі $\lambda_{1}$, $\lambda_{2}$ і $\lambda_{3}$.

Задача 3.3. Збуджені атоми водню знаходяться на n-ому енергетичному рівні. Визначити повну кількість ліній N, що спостерігаються у їхньому спектрі випромінювання.

Задача 3.4. Електрон у нерухомому вільному атомі водню знаходиться на першому збудженому енергетичному рівні (n = 2). Визначити, якої швидкості v набуде атом при переході в основний стан.

Задача 3.5 . Розглядаючи атоми як звичайні кульки, визначити, за якої найменшої відносної швидкості $v$ при непружному лобовому зіткненні двох атомів водню один із них випустить фотон.

Задача 3.1

За одним із постулатів Бора електрон в атомі може рухатися тільки по колових по колових орбітах, на яких добуток імпульсу електрона та довжини орбіти є кратний до сталої Планка:

$mv\cdot{2}\pi{r}=nh$, n = 1, 2, 3, …,

(1)

де n – номер орбіти. Виходячи з цього,

знайти

кутову швидкість електрона $\omega$ на другій орбіті (n = 2) в атомі водню.

Дано:

$mv\cdot{2}\pi{r}=nh$

n = 2

ω - ?

Розв’язання

В теорії Бора рух електрона в атомі водню розглядається як рух точкового заряду по колу навколо ядра під дією кулонівської сили. Тому згідно з другим законом Ньютона та формулами (ч.3, (1.5)) і (ч.1, (1.28)) можна записати:

$\frac{k{{e}^{2}}}{{{r}^{2}}}=m{{\omega }^{2}}r\quad \Rightarrow \quad k{{e}^{2}}=m{{\omega }^{2}}{{r}^{3}}$,

(2)

де $\omega$ – кутова швидкість електрона, m – його маса, e – заряд електрона та ядра, і k – таблична константа, що складає $k=(1/4\pi {{\varepsilon }_{0}})$ $=$ 9·10⁹ (Нм²/Кл²).

Відтак, зробивши у виразі (1) заміни $v=\omega r$ і $h=2\pi \hbar $, де $\hbar =1,05\cdot {{10}^{-34}}$, отримаємо систему рівнянь

$\left\{ \begin{matrix}n\hbar=m\omega{r}^{2} \\ m\omega^{2}r^{3}=ke^{2} \\ \end{matrix} \right.$

і, виключивши з неї r, — загальну відповідь задачі:

$\omega =\frac{{{k}^{2}}{{e}^{4}}m}{{{n}^{3}}{{\hbar }^{3}}}$.

Звідси, з урахуванням характеристик електрона $e=1,6\cdot{10}^{-19}$ Кл і $m= 9,1\cdot {{10}^{-31}}$ кг, виходить:

$\omega =5,2\cdot {{10}^{15}}$$\frac{рад}{с}$.

Задача 3.2

За певних умов збудження спектр випромінювання атома водню містить тільки N = 3 лінії.

Визначити

їхню довжину хвилі $\lambda_{1}$, $\lambda_{2}$ і $\lambda_{3}$.

Дано:

N = 3

λ₁, λ₂, λ₃ - ?

Розв’язання

Атом випромінює світло при переході електрона із збудженого енергетичного рівня на будь-який нижчий. Враховуючи це, легко бачити, що за умовою для найвищого збудженого рівня головне квантове число n = 3, бо лише в такому випадку є тільки три можливі переходи електрона: з третього й другого рівнів на перший та з третього на другий. Через це й у спектрі випромінювання спостерігається тільки три частоти, що визначаються формулою Бальмера (3.6) і три відповідні довжини хвилі. Отож, підставляючи у вираз (3.6) величину сталої Рідберґа (3.7) та відповідні пари значень n – (3, 1), (2, 1) і (3, 2), – 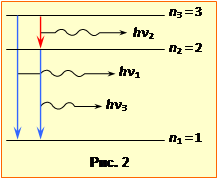отримаємо частоти

$\nu_{1}=3,29\cdot{10}^{15}\left(1-\frac{1}{9}\right)=2,93\cdot{10}^{15}$ Гц,

$\nu_{2}=3,29\cdot{10}^{15}\left(1-\frac{1}{4}\right)=2,47\cdot{10}^{15}$ Гц.

$\nu_{3}=3,29\cdot{10}^{15}\left(\frac{1}{4}-\frac{1}{9}\right)=4,58\cdot{10}^{14}$ Гц

та шукані довжини хвилі $\lambda =(c/\nu )$ спектральних ліній:

$\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{2,93\cdot{10}^{15}}=102,7$ нм;

$\lambda_{2}=\frac{c}{\nu_{2}}=\frac{3\cdot{10}^{8}}{2,47\cdot{10}^{15}}=121$ нм;

$\lambda_{3}=\frac{c}{\nu_{3}}=\frac{3\cdot{10}^{8}}{4,58\cdot{10}^{14}}=656$ нм.

Задача 3.3

Збуджені атоми водню знаходяться на n-ому енергетичному рівні.

Визначити

повну кількість ліній N, що спостерігаються у їхньому спектрі випромінювання.

Дано:

N - ?

Розв’язання

Задля наочності на рис. 3 схематично показано енергетичні рівні, на які може переходити електрон атома з n-ого збудженого рівня.

Відповідь задачі легко отримати, прямо підрахувавши всі можливі переходи електрона на кожен з рівнів від першого до (n –1)-го.

Очевидно, що кількості N_і таких переходів складають:

на перший рівень — N₁ = n – 1,

на другий — N₂ = n – 2,

на третій — N₃ = n – 3,

· · ·

на (n - 1)-й — N_n-1 = 1.

Отримана числова послідовність утворює арифметичну прогресію. Тож за відомою алгебраїчною формулою сумарна кількість можливих переходів, отож і спектральних ліній, дорівнює

$N=\frac{{{N}_{1}}+{{N}_{n-1}}}{2}\left( n-1 \right)=\frac{n\left( n-1 \right)}{2}.$

Задача 3.4

Електрон у нерухомому вільному атомі водню знаходиться на першому збудженому енергетичному рівні (n = 2).

Визначити,

якої швидкості v набуде атом при переході електрона в основний стан.

Дано:

$n=2$

v - ?

Розв’язання

Перехід атома із збудженого в основний стан супроводжується випромінюванням фотона й відбувається спонтанно (без зовнішнього впливу), отже без зміни енргії та імпульсу. Тому при випусканні фотона атом отрмує такий самий, як у фотона, за величиною й протилежний за напрямком імпульс ''віддачі'':

${{\vec{p}}_{а}}=-{{\vec{p}}_{ф}}$

Отже, враховуючи формулу (2.4), швидкість, яку отримує атом, дорівнює

$v=\frac{\varepsilon }{mc}$,

(1)

де m – маса атома водню, а ε – енергія фотона, що випромінюється.

Величина ε дорівнює різниці енергій атома водню (формула (3.5a)) у збудженому (n = 2) та основному (n = 1) стані й складає:

$ε=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)=\frac{3E_{0}}{4}$.

Підставивши цю величину у вираз (1), отримаємо загальну відповідь:

$v=\frac{3{{E}_{0}}}{4{{m}_{a}}c}$.

Відтак урахуємо, що маса атома водню практично збігається із масою протона 1, 67·10^–27 кг, і Е₀ = 13,6 еВ = 2,2·10^–¹⁸ Дж, і дістанемо числову відповідь:

v ≈ 3,3 м/с.

Примітка. При розв'язуванні не враховувалося, що при переході зі збудженого в основний стан вільний атом отримує від фотона не лише імпульс віддачі, а й відповідну кінетичну енергію. Але це ніяк не вплинуло на коректність і точність відповіді. Справді, при переході атома з першого збудженого стану в основний енергія випущеного фотона згідно з формулами (3.1) і (3.6) дорівнює 12,5 еВ, тоді як кінетична енергія 10^–7 еВ. Тож можна сказати, що ''для фотона атом заввжди є нерухомим''.

Задача 3.5

Розглядаючи атоми як звичайні кульки,

визначити,

за якої найменшої відносної швидкості $v$ при непружному лобовому зіткненні двох атомів водню один із них випустить фотон.

Розв’язання

Згідно з умовою, в задачі не враховується хімічний зв'язок між атомами H і вважається, що при непружному зіткненні вони просто ''склеюються'' без зміни власних властивостей, а не утворюють молекулу H₂. В такому разі завдання полягає у визначенні відносної швидкості атомів, за якої при зіткненні один із них перейде у збуджений стан із наступним випроміненням фотона.

Шукана величина $v$ є швидкістю руху одного атома відносно іншого, котрий задля зручності будемо вважати нерухомим. Тоді за законом збереження імпульсу

$mv=2m{{v}_{1}}\quad \Rightarrow \quad {{v}_{1}}=\frac{v}{2}$,

(1)

де $m$ – маса атома і ${{v}_{1}}$ – швидкість атомів після зіткнення.

При пружних зіткненнях зберігається не лише імпульс, а й кінетична енергія. Але при непружних зіткненнях кульок частина їхньої кінетичної енергії переходить у внутрішню. Для звичайних кульок наслідком цього є нагрівання, а для атомів – перехід у збуджений стан із наступним випромінюванням фотона з енергією

$\varepsilon =\frac{m{{v}^{2}}}{2}-\frac{\left( 2m \right)v_{1}^{2}}{2}$.

Звідси, враховуючи співвідношення (1), виходить:

$\varepsilon =\frac{3m{{v}^{2}}}{4}\quad \Rightarrow \quad v=2\sqrt{\frac{\varepsilon }{3m}}$.

(2)

Випромінювання фотона є можливе тільки після переведення атома на котрийсь із збуджених енергетичних рівнів, які для атома водню визначаються виразами (3.5) і (3.5а). Отже, шукане найменше значення v відповідає переходу атома при зіткненні з основного (n₁ = 1) на перший збуджений рівень (n₂ = 2) із наступним випромінюванням фотона з енергією, що за формулами (3.1) і (3.5) складає

$\varepsilon ={{E}_{1}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)=\frac{3}{4}{{E}_{1}}$.

Відтак, підставивши це значення у вираз (2), отримаємо наступну загальну відповідь

$v=\sqrt{\frac{{{E}_{1}}}{m}}$,

і, взявши до уваги значення E₁= 13,6 еВ (формула (3.5а)) і масу атома H, яка практично збігається з масою протона m = 1,67·10^–27 кг, знайдемо наступну числову відповідь:

v = 3,6·10⁴ м/с.

Зауваження. На перший погляд може здатися, що в рівнянні (1) допущено помилку, позаяк воно не містить імпульсу випущеного при зіткненні атомів фотона. Але це не так, бо зіткнення атомів і випускання фотона становлять дві окремі події.

◄ Предыдущая: 3.3. Атом Гідроґену Следующая: Задачі для самостійної роботи ►